Pb₉Cu(PO₄)₆O: a room-temperature superconductor? electronic-structure features assessed via the flat/steep band model

Abstract

The recent claim of room-temperature superconductivity in copper-doped lead apatite Pb_10−xCu_x(PO₄)₆O (0.9 < x <1.1) (LK-99) has stimulated widespread research, yet experimental validations consistently attribute its resistivity drops to impurities and find no evidence of zero resistivity and Meissner effect. To clarify the electronic properties of this system, we conduct systematic first-principles calculations incorporating multi-Cu doping configurations of Pb₉Cu(PO₄)₆O beyond previously studied single substitutions. Our results demonstrate that while certain single-Cu models exhibit metallicity, all proposed structures, including double-Cu-doped supercells and c-axis chain models, display extremely narrow bandwidths (≤0.25 eV) and a lack of steep dispersive bands near the Fermi level. These features, incompatible with the flat/steep band model of superconductivity, along with the absence of characteristic electronic structures found in known superconductors, strongly suggest that LK-99 derivatives are not superconducting.

---

1. Introduction

The quest for room-temperature superconductivity at ambient pressure is one of the most significant challenges in condensed matter physics, promising revolutionary advancements in energy transmission¹ and quantum computing.² While the discovery of superconductivity dates back to 1911 ³, our understanding has been significantly advanced by key discoveries in the field, such as high-temperature cuprate superconductors,⁴ iron-based superconductors,⁵ and more recently nickelate superconductors.⁶ Despite these milestones, the goal of a practical, room-temperature superconductor has remained elusive. Recently, Lee et al.^7,8 ignited an intense debate by claiming superconductivity above 400 K in copper-substituted lead apatite, Pb_10−xCu_x(PO₄)₆O (0.9 < x <1.1) (LK-99) at ambient conditions. However, many researchers remain doubtful about its precise crystal structure and superconductivity.

In the past two years, many experimental groups have reported the successful synthesis of LK-99, but failed to reproduce the room-temperature superconductivity of LK-99. For instance, Puphal et al.⁹ grew single crystals of Pb_10−xCu_x(PO₄)₆O (x ≈ 1) using the traveling solvent floating zone (TSFZ) method. They observed highly insulating behavior and extremely weak diamagnetism, with a volume susceptibility of only −1.452 × 10⁻⁴—far from the theoretical value of −1 for ideal superconductors—and display an uneven distribution of substituted Cu. Similarly, Zhang et al.¹⁰ synthesized the Pb_9.06(7)Cu_0.94(6)(PO_3.92(4))₆O_0.96(3) and, through neutron diffraction and inelastic neutron scattering, revealed minimal Cu substitution on the Pb2 (4f) site, with most Cu occupying the Pb1 (6h) site (Fig. 1). They detected no long-range magnetic order down to 10 K, no superconducting resonances, and no electron behavior correlated with superconductivity. Interestingly, many groups have identified Cu₂S impurities in their LK-99 samples via X-ray diffraction.^9–11 Notably, Zhu et al.¹¹ and Chen et al.¹² reported that Cu₂S undergoes a first-order structural phase transition from hexagonal to monoclinic near 380 K, accompanied by a sharp drop in resistivity. Lei et al.¹³ directly addressed this issue by synthesizing LK-99 containing Cu₂S and then chemically removing it with ammonia solution. Their comparative analysis demonstrated that the apparent superconducting-like resistivity drop originates from the Cu₂S impurity—a conclusion supported by several groups.^11–13 In addition, magnetic susceptibility measurements consistently show that LK-99 exhibits only weak diamagnetism. Although Guo et al.¹⁴ observed partial magnetic levitation and a mix of diamagnetic and soft ferromagnetic behavior in multi-phase LK-99-like samples, the definitive Meissner effect (key evidence for superconductivity) has not been observed, as emphasized by Hou et al.¹⁵ and Thakur et al.¹⁶ In summary, it seems that extensive experimental work on synthesized LK-99 has found no evidence of room-temperature superconductivity. The observed superconducting-like properties are largely attributed to Cu₂S impurities, while magnetic measurements confirm only weak diamagnetism and a consistent absence of the Meissner effect.^17–20 Despite these collective results, Hyun-Tak Kim, one of the original authors, still insists that LK-99 is a superconductor.²¹ Thus, the question of whether LK-99 is superconducting remains controversial within the scientific community.

Fig. 1 (a) Crystal structure of experimental Pb₁₀(PO₄)₆O, illustrating the coordination polyhedron of Pb1O1₆O2₂ and Pb2O₉. (b) Crystal structure of defect-free Pb₁₀(PO₄)₆O model, showing the Pb1O₆ and Pb2O₉ coordination polyhedrons. (c) and (d) Band structure of defect-free Pb₁₀(PO₄)₆O model (c) without and (d) with SOC effect.

Initial DFT studies on Cu substitution in the parent compound Pb₁₀(PO₄)₆O predicted that Cu occupancy at the Pb2 (4f) site would induce flat bands crossing the Fermi level (E_F), despite also indicating a thermodynamic preference for occupation at the Pb1 (6h) site. Griffin²² proposed that such Pb2 (4f) substitution might exhibit features relevant to high-T_C superconductivity. Sun et al.²³ and Lai et al.²⁴ further suggested that substitution at the Pb2 (4f) site metallizes the system, whereas substitution at Pb1 (6h) results in a semiconducting or insulating state. In contrast, Si et al.²⁵ described Pb₉Cu(PO₄)₆O as a strongly correlated Mott or charge-transfer insulator, even in the presence of flat bands crossing the E_F. Celiberti et al.²⁶ supported the insulating state, classifying it as a charge-transfer insulator when electron correlations are considered. Yue et al.²⁷ also suggested Mott insulating or correlated non-Fermi-liquid metallic states, rather than superconducting behavior. Regarding dynamic stability, harmonic phonon calculations^28–30 revealed dynamic instabilities at 0 K in both undoped and Cu-doped compounds. However, Kim et al.³¹ employed anharmonic calculations and reported dynamic stability at room temperature. Liu et al.³² emphasized that symmetry breaking is essential for realizing the insulating state in doped lead apatite, thereby correcting their earlier metallic predictions.²⁴ Supporting this, Li et al.³³ demonstrated that the intrinsic triclinic P1 symmetry of LK-99 leads to semiconducting behavior, while the P3 symmetry is linked to correlated electronic states. Finally, Bai et al.³⁴ incorporated spin–orbit coupling (SOC) and confirmed the semiconducting nature of LK-99 in magnetic phases. Thus, although a number of theoretical studies incorporating electron correlations, SOC, and symmetry breaking strongly suggest that LK-99 is an insulator or correlated semiconductor (challenging the experimentally reported superconductivity by Kim et al.^7,8), several studies still support the possibility of superconducting behavior. Therefore, whether LK-99 is a superconductor remains controversial.

In recent years, a “flat/steep band model” has been proposed from a chemical perspective to explain electron pairing and superconductivity in metals.^35–39 According to this model, the coexistence of a flat band and a steep band near the E_F, along with peaked electron–phonon coupling structures, constitutes a key electronic feature of superconducting materials. This model has not only provided an important theoretical basis for the discovery of new superconductors—such as the superconducting transition in boron-doped diamond⁴⁰—but has also been successfully applied to explain the superconducting mechanisms in a variety of systems, including Hg,⁴¹ Ca,⁴² Te,⁴³ CaC₆,⁴⁴ and MgB₂.^45,46 Given the ongoing controversy surrounding LK-99, it is essential to examine its electronic structure through the lens of the flat/steep band model to evaluate its potential superconductivity.

In this study, we systematically investigated the structural and electronic properties of Pb₉Cu(PO₄)₆O derivatives with various Cu doping configurations using DFT+U and SOC calculations. A series of structural models—including both single and double Cu doping—were constructed and evaluated based on their band characteristics near the E_F. Our results consistently show extremely narrow bandwidths (≤0.25 eV) across all configurations, with the largest value observed in a c-axis-aligned double Cu-doped chain model. These bandwidths are significantly smaller than those of known conventional and unconventional superconductors, and the electronic structures lack the necessary coexistence of flat and steep bands required for superconductivity. We therefore conclude that Pb₉Cu(PO₄)₆O is unlikely to exhibit superconducting behavior under the current structural models.

2. Computational details

The structural optimization and electronic properties of the Pb₁₀(PO₄)₆O and Pb₉Cu(PO₄)₆O were calculated within the framework of DFT^47,48 by using the Vienna Ab initio Simulation Package (VASP)^49,50 with the projector augmented wave (PAW) method.⁵¹ The generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE)-type exchange-correlation potentials⁵² was used throughout this work. The employed PAW-PBE pseudopotentials of Pb, Cu, P and O treat 6s²5d¹⁰6p², 3d¹⁰4s¹, 3s²3p³ and 2s²2p⁴ as valence states, respectively. The cutoff energy for the expansion of wave functions in plane waves was set as 600 eV and the tetrahedron method with Blöchl corrections was utilized in the integrations. The Brillouin zone integrations were carried out using Monkhorst–Pack k-point meshes of dimensions 7 × 7 × 6, 6 × 6 × 4, and 2 × 4 × 5 for the 1 × 1 × 1 unit cell, the 1 × 1 × 2 supercell, and the 2 × 1 × 1 supercell of Pb₉Cu(PO₄)₆O, respectively. Electron correlation effects were treated using the L(S)DA+U approach, with Hubbard U = 5.00 eV and exchange parameter J = 1.00 eV applied to the Cu-3d states, which aligns with values used in some DFT+U investigations of LK-99.^{22,28,30,32–34}

3. Results and discussion

3.1 Undoped Pb₁₀(PO₄)₆O

The experimental Pb₁₀(PO₄)₆O crystalizes in a hexagonal structure (P6₃/m) with two types of inequivalent Pb atoms: six Pb1 (6h) and four Pb2 (4f) sites (Fig. 1a). The structure also contains one type of P atoms and two types of O atoms. The first type of O atoms forms a PO₄ coordination polyhedron by bonding with the P atom. Notably, the second type of O atom, situated at the 4e site, is only 1/4 occupied and does not directly bond with any P atom. To handle the partial occupancy of O₂ at the 4e site, we constructed a defect-free Pb₁₀(PO₄)₆O model using a supercell program⁵³ that systematically samples symmetry-inequivalent configurations. The candidate structures were screened based on electrostatic energy considerations, and the most stable symmetric arrangement was selected for further study. This approach effectively converts the fractional oxygen site into a fixed, integer-occupied position while preserving the structural symmetry and minimizing coulombic interactions. As shown in Fig. 1b, the defect-free Pb₁₀(PO₄)₆O model crystalizes in a trigonal structure (P3) with six different Wyckoff sites of Pb atoms (provided in Table S2). To concisely describe the Pb atoms in the crystal structure, we classify the six Pb atoms occupying the 3d Wyckoff sites as the first type (Pb1), and the four Pb atoms at other Wyckoff sites as the second type (Pb2). Each Pb1 atom is coordinated by six oxygen atoms, forming a Pb1O₆ polyhedron. Among the six Pb1-centered polyhedron in the unit cell, three are coordinated exclusively by O1 atoms, while the remaining three each contain five O1 atoms and one extra-O atom. In contrast, each Pb2 atom is coordinated by nine O1 atoms, forming a Pb2O₉ polyhedron. The lattice constants and space groups for the undoped and the defect-free 1 × 1 × 1 Pb₁₀(PO₄)₆O model is provided in Tables S1 and S2. Subsequent structural optimization of the defect-free model resulted in a negligible increase in lattice constants and a modest expansion of the unit cell volume by 3.94%. The optimization process led to subtle changes in the Pb–O coordination environments. The Pb1O1₆O2₂ coordination polyhedron present in the undoped structure is transformed into a Pb1O₆ coordination polyhedron in the defect-free model, with an average bond length shifting from 2.635 Å to 2.611 Å. Simultaneously, while the Pb2O₉ coordination polyhedron was preserved, its average bond length increased from 2.721 Å to 2.764 Å. These minimal changes in structural parameters validates the accuracy of the defect-free model.

Given the strong SOC effect inherent to the heavy Pb element, we explicitly incorporated SOC into our calculations to achieve a more accurate description of the electronic properties. We performed electronic structure calculations for Pb₁₀(PO₄)₆O using both the PBE and SOC methods to evaluate the impact of SOC on the electronic properties. Our PBE calculations (Fig. 1c) confirm that Pb₁₀(PO₄)₆O is an insulator, revealing an indirect band gap of E^PBE_g = 2.76 eV from L to M, which is in excellent agreement with previous DFT studies.^23,24 The band gap of Pb₁₀(PO₄)₆O is further calculated by HSE06 to be 3.89 eV, consistent with the ∼3.8 eV value reported by Cabezas-Escares et al.²⁸ The inclusion of SOC (Fig. 1d) leads to a band structure that is qualitatively similar to the PBE result; however, it causes a reduction in the band gap to E^SOC_g = 2.54 eV (from H to A). PBE calculations show that the two bands near the E_F split into four bands in SOC calculations, with a slight increase in bandwidth. These bands are composed mainly of O-2p states and a small part of Pb-6s and Pb-6p states. The density of states (DOS) analysis (Fig. S1a and S2) provides further insight into the electronic structure. The top of the valence band consists mainly of O-2p states and a small part of Pb-6s and Pb-6p states, while the bottom of the conduction band consists mainly of Pb-6p and O-2p states. Furthermore, the analysis of the crystal orbital Hamiltonian population (COHP) (Fig. S1b) reveals a pronounced P–O bonding interaction near −5 eV, resulting from hybridization between P-3p and O-2p orbitals, while the strong antibonding P–O interaction is observed in the conduction band (CB) between 8 eV and 10 eV. Notably, the top of the valence band (VB, from −3.5 eV to E_F) is predominantly composed of nonbonding O-2p states, with negligible contributions from either bonding or antibonding P–O or Pb–O interactions. Throughout both the VB and CB, Pb–O interactions remain weak, exhibiting only minor bonding and antibonding character.

3.2 Model construction

Considering the presence of two distinct Pb sites and a partially occupied oxygen site (O, occ. = 0.25) in Pb₁₀(PO₄)₆O, we constructed various Cu substitution models using supercells of different sizes to systematically explore possible doping configurations. A schematic illustration of the model construction workflow is presented in Fig. 2. The substitution at the Pb1 (6h) site within a 1 × 1 × 1 unit cell initially yielded 24 distinct configurations. Symmetry analysis revealed that only two of these are unique, labelled as mod1-00 and mod1-01. Similarly, substitution at the Pb2 (4f) site within a 1 × 1 × 1 unit cell initially generated 16 configurations, which were reduced by symmetry to four unique structures, designated as mod2-00, mod2-01, mod2-02, and mod2-03. From each set of unique configurations, we selected the lowest-energy structure (mod1-00 for Pb1 substitution and mod2-00 for Pb2 substitution, see Table 1 and Fig. 4a and b) as representative models for electronic structures analysis (Fig. 4 and 5).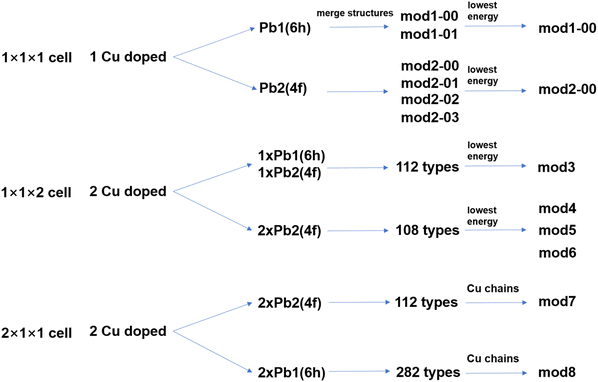

Fig. 2 Schematic illustration of the construction process for the Cu doped Pb₁₀(PO₄)₆O structural models.

Table 1 Structural parameters and total energies of Cu-doped Pb₁₀(PO₄)₆O configurations after full relaxation, including number of atoms, space group, and total energy per atom

Model	Number of atoms	Space group	Total energy (eV per atom)
mod1-00	41	P1	−6.494
mod1-01	41	P1	−6.492
mod2-00	41	P3	−6.485
mod2-01	41	P3	−6.480
mod2-02	41	P3	−6.480
mod2-03	41	P3	−6.485
mod3	82	P1	−6.492
mod4	82	P3	−6.485
mod5	82	P3	−6.486
mod6	82	P3	−6.482
mod7	82	P1	−6.490
mod8	82	P1	−6.496

---

Furthermore, to systematically explore double Cu substitutions at distinct Pb sites, we constructed six additional models (mod3–mod8) using 1 × 1 × 2 and 2 × 1 × 1 supercells. Within the 1 × 1 × 2 supercell, we considered two substitution schemes: (i) one Cu at a Pb1 site and another at a Pb2 site, from which 112 configurations were generated and the lowest-energy structure was selected as mod3 (Fig. 6a); and (ii) both Cu atoms at Pb2 sites, yielding 108 configurations, from which the three most stable ones were chosen as mod4, mod5, and mod6 (Fig. 7a–c).

Moreover, in all previously reported Cu-doped models, the possibility of Cu atoms forming one-dimensional chains has not been considered. To explicitly address this, we constructed 2 × 1 × 1 supercells to explore such ordered arrangements. Substituting two Cu atoms at Pb2 sites resulted in 112 distinct configurations, from which we selected a structure exhibiting a continuous Cu chain aligned along the c-axis, denoted as mod7 (Fig. 8a). Similarly, for substitutions at two Pb1 sites, 282 configurations were generated, and a structure with a Cu chain along the c-axis was identified and labeled as mod8 (Fig. 8b). Then, we systematically analyzed the electronic structure of each model, with particular emphasis on the region near the E_F, to evaluate whether their band structures satisfy the criteria of the flat/steep band model of superconductivity.

We have simulated the XRD patterns for all proposed structural models using VESTA.⁵⁴ The experimental XRD pattern for Pb_7.629Cu_2.371(PO₄)₆O is downloaded from the ICSD (collection code 175670). As shown in Fig. 3, the simulated XRD patterns of the Cu-doped Pb2 (4f) models (mod2-00, mod4, mod5, and mod6) are in close agreement with the experimental XRD data. In contrast, the patterns for mod1-00, mod3, mod7, and mod8 exhibit obvious deviations from the experimental results, particularly with the occurrence of additional weak peaks in the low-angle region (Fig. S5). This discrepancy may be attributed to the fact that mod1-00, mod3, and mod8 all involve Cu doping at the Pb1 (6h) sites, which may introduce local structural changes that are inconsistent with the experimental structure. Additionally, in mod7, the relatively short Cu–Cu distances may lead to significant structural distortion, further contributing to the mismatch.

Fig. 3 Simulated XRD patterns for mod2-00, mod4, mod5, mod6 and the experimentally reported XRD pattern for Pb_7.629Cu_2.371(PO₄)₆O from ICSD.

3.3 Single Cu doped 1 × 1 × 1 Pb₁₀(PO₄)₆O models

The optimized crystal structures of mod1-00 and mod2-00 are shown in Fig. 4a and b, with their lattice parameters and atomic positions summarized in Tables S4 and S5. In these models, Cu substitutes the Pb1 (6h) and Pb2 (4f) sites, respectively. A key structural difference lies in the Cu–O coordination environment: in mod1-00, the Cu atom is four-coordinated, forming a CuO₄ polyhedron with Cu–O bond lengths ranging from 1.93 to 2.07 Å. In contrast, the Cu atom in mod2-00 is six-coordinated, forming a distorted CuO₆ octahedron with longer and more dispersed Cu–O bonds (2.06–2.62 Å), suggesting significantly weaker Cu–O interactions.

Fig. 4 (a) Crystal structure of the mod1-00 configuration, highlighting the Cu-centered O coordination environment (CuO₄ polyhedron). (b) Crystal structure of mod2-00, featuring the corresponding CuO₆ polyhedron. (c) Band structure of mod1-00 and (d) mod2-00 at five different levels: standard PBE (non-spin-polarized), spin-polarized PBE, spin-polarized PBE+U, SOC, and SOC+U.

To comprehensively evaluate the electronic properties of both models, we performed calculations using five different approaches: standard PBE (non-spin-polarized), spin-polarized PBE, PBE+U, with SOC, and with both SOC and U (SOC+U), as summarized in Fig. 4c and d. A clear contrast emerges between the two models. mod1-00 exhibits insulating/semiconducting behavior with band gaps measured at the L point as follows: E^PBE_g = 0.43 eV, E^spin_g = 0.61 eV, E_g^spin+U = 0.89 eV, E^SOC_g = 0.62 eV and E_g^SOC+U = 0.91 eV. The smallest gap (0.43 eV) is given by standard PBE, while the largest (0.91 eV) is obtained with SOC+U—a difference of approximately 0.48 eV. Notably, all computed band gaps for mod1-00 are significantly smaller than that of the defect-free Pb₁₀(PO₄)₆O (E^SOC_g = 2.54 eV), indicating that Cu substitution substantially reduces the band gap and modifies the electronic structure.

To elucidate the origin of the band gap reduction in mod1-00, we analyzed its DOS (Fig. S3(a)). The VB is mainly composed of hybridized states from extra-O, Cu, O, and to a lesser extent, Pb1 atoms. Notably, the CBM is formed by a very flat band just above the E_F, which mainly consists of Cu states. This finding directly implicates Cu substitution in introducing in-gap states that reduce the band gap. At higher energies (∼3 eV), the conduction band resembles that of defect-free Pb₁₀(PO₄)₆O, dominated by O and Pb states, indicating that the influence of Cu doping is primarily confined to energies near the E_F.

In sharp contrast, mod2-00 exhibits two flat bands crossing the E_F, indicative of metallic behavior. This finding is consistent with recent r²SCAN calculations by Sukhenko et al.⁵⁵ on Pb₉Cu(PO₄)₆O, where the Cu doping approach aligns with that employed in our mod2-00 model. Notably, both their r²SCAN results and our PBE+U calculations yield broadly similar band structures. These flat bands are also predominantly contributed by O and Cu states (Fig. S3(b)). Such flat bands at the E_F have been previously proposed in DFT studies of LK-99 as a potential signature of superconductivity.²² However, the extremely narrow bandwidth of these crossing bands (only 0.12 eV) makes them unlikely to support superconductivity.

Furthermore, we find that symmetry breaking dramatically alters the electronic structure of mod2-00. When symmetry constraints are removed (ISYM = 0), a band gap of 0.16 eV opens, indicating a transition to an insulating state. This gap opening arises from lifted orbital degeneracies and electronic state redistribution under reduced symmetry, which eliminates the band crossings present in the symmetric case (ISYM = 2). As shown in Fig. 5a and b, the bands crossing the E_F under symmetric conditions and the lowest conduction band in the symmetry-broken case are primarily derived from hybridized Cu-3d (d_xy, d_yz, d_xz) and O-2p orbitals, with a minor contribution from the partially occupied extra-O-2p states. In contrast, the two valence bands between −0.6 eV and −0.1 eV are dominated by extra-O-2p_x and extra-O-2p_y states, consistent with the DOS results in Fig. S4 and in agreement with previous reports.³² These results demonstrate that symmetry breaking induces a metal–insulator transition in mod2-00. Under reduced symmetry, no bands cross the E_F, suggesting that the system is more likely to be an insulator rather than a superconductor. This sensitivity to symmetry conditions underscores the importance of considering structural relaxations and symmetry-breaking effects in evaluating the electronic ground state of candidate materials.

Fig. 5 Band structure of mod2-00 (a) with symmetry (ISYM = 2) and (b) without symmetry (ISYM = 0).

3.4 Double Cu doped 1 × 1 × 2 Pb₁₀(PO₄)₆O models

Fig. 6 illustrates the crystal structure and electronic properties of mod3, in which two Cu atoms substitute on one Pb1 and one Pb2 site, respectively. The structure features two distinct CuO₄ coordination units, with average bond lengths of 2.02 Å and 2.01 Å. The shortest Cu1–Cu2 distance is 3.66 Å. Band structure calculations reveal four flat bands near the E_F; however, none of them cross it, and the system exhibits an extremely narrow band gap of E_g^spin+U = 0.038 eV. DOS analysis indicates that these flat bands are predominantly composed of O-2p and Cu-3d states, with a minor contribution from extra-O-2p orbitals. Approximately 0.5 eV below the E_F, the states are mainly derived from extra-O-2p and Pb1-6s orbitals, with a small contribution from Pb1-6p states. Between −1.0 eV and −0.7 eV, the electronic states consist of a hybrid of O-2p and extra-O-2p orbitals, along with a modest contribution from Pb2-6s states. Taken together, these electronic features, particularly the finite band gap, indicate that mod3 behaves as an insulator rather than a superconductor.

Fig. 6 (a) Crystal structure of mod3 and the Cu1O₄ and Cu2O₄ polyhedron. (b) Calculated band structure and PDOS of mod3 within LSDA+U.

Fig. 7 displays the crystal structures and electronic properties of mod4, mod5, and mod6, all of which involve double Cu substitutions at Pb2 sites. Each model contains two CuO₆ octahedra with slightly varying average bond lengths: 2.28 Å and 2.27 Å in mod4, 2.28 Å and 2.24 Å in mod5, and 2.25 Å and 2.24 Å in mod6 (Fig. 7a–c). The shortest Cu–Cu distances are 6.71 Å in mod4, 5.70 Å in mod5, and 3.26 Å in mod6. Electronic structure analysis shows that all three models exhibit flat bands crossing the E_F, primarily composed of Cu-3d and O-2p orbitals, with a minor contribution from extra-O-2p states. A notable distinction lies in the number of bands crossing the E_F: mod4 and mod5 each have only one band crossing near the K point, whereas mod6 features four such bands. In addition, mod4 and mod5 each host two non-crossing flat bands above the E_F. PDOS results further confirm a substantially higher DOS at the E_F in mod6 compared to mod4 and mod5. As illustrated in Fig. 7c, this electronic behavior can be attributed to the structural characteristic of mod6, which contains Cu₂O₉ polyhedron with three O-bridged Cu1–O–Cu2 and the shortest Cu–Cu distance (3.26 Å) among the three models.

Fig. 7 (a–c) Crystal structures of mod4, mod5, and mod6, respectively, with their corresponding Cu-centered coordination polyhedron highlighted. (d–f) Calculated electronic band structures and PDOS for mod4, mod5, and mod6, respectively.

The bandwidth of the E_F-crossing flat bands remains consistently narrow (∼0.10 eV) across all three models (Fig. 7d–f and Table 2), showing no enhancement compared to mod2-00. This indicates that double Cu substitution at Pb2 sites within a 1 × 1 × 2 supercell does not lead to broader bandwidths. The corresponding effective electron mass in these bands is exceptionally high, suggesting strongly localized carriers, consistent with electronic confinement and lack of dispersion. Given the absence of steep bands crossing the E_F, these electronic structures are incompatible with the flat/steep band model required for superconductivity. Therefore, it is highly unlikely that mod4, mod5, or mod6 support superconducting behavior.

Table 2 Bandwidths and DOS near the E_F for the proposed structural models in this work, along with representative metals and conventional superconductors for comparison

Model and compounds	Bandwidth (eV)	DOS at EF (spin up)	DOS at EF (spin down)	References
mod2-00	∼0.12 eV	12.35	0	This work
mod4	∼0.14 eV	0	0
mod5	∼0.11 eV	18.55	0
mod6	∼0.08 eV	90.28	30.92
mod7	∼0.20 eV	11.86	8.36
mod8	∼0.25 eV	12.60	15.53
Cu metal	∼5.5 eV	—	—	56
Ni metal	∼5.0 eV	—	—	56
YBa2Cu3O7	∼2.0 eV	∼8.0 (Total)	—	57
Bi2Sr2CaCu2O8	∼3.0 eV	—	—	58
HgBa2Ca2Cu3O8	∼3.6 eV	—	—	59
La3Ni2O7	∼3.5 eV	—	—	60
CeCu2Si2	∼1.4 eV	—	—	61
β-(BEDT-TTF)2IBr2	∼0.5 eV	∼5.0 (Total)	—	62
LaH10	∼8.0 eV	—	—	63
Y2O2.125Bi	∼1.3 eV	—	—	64

---

3.5 Double Cu doped 2 × 1 × 1 Pb₁₀(PO₄)₆O model

Within the 2 × 1 × 1 supercell, we selected two structural models, mod7 and mod8, both capable of forming one-dimensional Cu–Cu zig-zag chains along the c-axis, with the aim of enhancing metallic behavior and inducing distinctive electronic features near the E_F. In mod7, the zig-zag chain exhibits alternating Cu–Cu distances of 3.36 Å and 4.57 Å. The chain is composed of Cu₂O₇ units formed by corner-sharing CuO₄ polyhedron, which are further bridged by PO₄ groups, as illustrated in Fig. 8a. In mod8, the chain similarly consists of corner-sharing CuO₄ units forming Cu₂O₇ motifs; however, these units are not connected via PO₄ tetrahedra. This structural distinction results in a nearest-neighbor Cu–Cu distance of 3.58 Å and a second-nearest-neighbor distance of 5.83 Å (Fig. 8b). Furthermore, the average Cu–O bond lengths in the CuO₄ polyhedrons are 2.011 Å and 2.034 Å in mod7, and 2.016 Å and 2.028 Å in mod8, indicating very similar local coordination environments between the two models.

Fig. 8 (a and b) Crystal structures of mod7 and mod8, respectively, both exhibiting one-dimensional zig-zag Cu–Cu chains along the c-axis. (c and d) Corresponding band structures and PDOS for mod7 and mod8, respectively.

Electronic structure calculations (Fig. 8c and d) reveal two bands crossing the E_F in both mod7 and mod8, primarily derived from hybridized Cu-3d, O-2p, and extra-O-2p orbitals. Notably, mod8 exhibits an additional flat band located approximately 0.5 eV above the E_F, dominated by Cu1-3d and extra-O-2p states. Although the bandwidths of the Fermi-crossing bands in mod7 and mod8 (up to 0.25 eV) show some increase compared to that of mod2-00 (0.12 eV), they remain narrow and indicative of strong electron localization. The absence of significant dispersion near E_F, coupled with the lack of simultaneous flat and steep band features as required by the flat/steep band model of superconductivity, suggests that these systems are unlikely to support superconducting behavior. Thus, despite the structural variation and the formation of extended Cu–O chains, the electronic characteristics of mod7 and mod8 remain inconsistent with those of conventional superconductors.

3.6 Discussion

Our computational results indicate that Cu-doped Pb₁₀(PO₄)₆O structural models consistently exhibit flat bands near the E_F. Across all models studied, these bands display extremely narrow bandwidths (ranging from 0.08 eV to 0.25 eV, Table 2) and exhibit minimal dispersion. The DOS at E_F values are notably high and significantly exceed those of known superconductors, which provides clear quantitative evidence for the extremely flat nature of the bands near E_F. From a band structure perspective, such features correspond to very high effective electron masses, indicating strongly localized carriers with limited mobility. Moreover, the significant energy separation between these flat bands and the conduction band minimum renders interband electronic transitions highly unfavorable. Notably, such pronounced flat, non-dispersive bands are not characteristic of conventional metals or established high-temperature superconductors. As summarized in Table 2, typical bandwidths of known metallic or superconducting systems are substantially broader. For instance, the Fermi-crossing bandwidth in Cu metal reaches ∼5.5 eV,⁵⁶ while those in cuprate and nickelate superconductors range between 2.0–3.6 eV.^57–60 Even among unconventional superconductors with inherently narrower bands, such as the heavy-fermion compound CeCu₂Si₂ (∼1.4 eV)⁶¹ and the organic superconductor β-(BEDT-TTF)₂IBr₂ (∼0.5 eV),⁶² the reported values remain several times larger than those computed here. Similarly, the bandwidths of pressurized LaH₁₀ ⁶³ and Y₂O_2.125Bi⁶⁴ are considerably wider.

Our calculations further reveal that increasing the system size does not substantially enhance bandwidth or dispersion. Models within the 1 × 1 × 2 supercell (mod4-mod6) show no noticeable improvement compared to the 1 × 1 × 1 case (mod2). Although the 2 × 1 × 1 supercell models (mod7 and mod8) exhibit a modest increase in bandwidth, approximately doubling that of mod2, the values remain critically low (≤0.25 eV). The resulting electronic dispersion remains insufficient to support superconducting behavior.

In conclusion, the extreme flatness and narrow bandwidth of the bands near the E_F across all Cu-doped Pb₁₀(PO₄)₆O models are incompatible with the “flat/steep band” model proposed for superconductivity. These electronic features, coupled with the absence of steeply dispersive carriers, suggest that LK-99 is highly unlikely to exhibit superconductivity, whether conventional or unconventional in nature.

4. Conclusion

Based on a DFT+U and SOC study of Cu-doped Pb₁₀(PO₄)₆O systems with various doping configurations and supercell sizes, we found that LK-99 is highly unlikely to exhibit superconducting behavior. Our calculations reveal that all 8 proposed structural models, including those with single and double Cu substitutions, different Pb site preferences, and extended Cu–Cu chain motifs, consistently exhibit extremely narrow bandwidths (≤0.25 eV) crossing the E_F. These non-dispersive electronic states imply strongly localized carriers with high effective mass and severely limited mobility, which are incompatible with the conventional metallic behavior prerequisite for superconductivity. Furthermore, the electronic structures lack the essential combination of flat and steep bands, and instead show a tendency toward insulating or weakly metallic ground states. Notably, even models with intentionally designed one-dimensional Cu–Cu zig-zag chains along the c-axis fail to produce substantial band dispersion or enhanced DOS at the E_F. Comparative analysis with established conventional and unconventional superconductors confirms that the bandwidths in LK-99 are consistently less than 10% of those observed in known cuprate superconducting systems. In light of these results, LK-99 does not satisfy the electronic structure criteria required for either conventional or high-temperature superconductor.

Author contributions

Cheng X and Deng S conceived the project. Liu G and Cheng X carried out the DFT calculations. Liu G, Xiang M and Cheng X contributed to data analysis. Liu G wrote the drafts. Liu G, Cheng X and Deng S revised the manuscript. All authors discussed the results and provided comments during the manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available within the article. Further inquiries can be directed to the corresponding authors.

Supplementary information (SI): density of states; average-pCOHP; simulated XRD patterns; atomic coordinates and Wyckoff positions; coulomb energy and relaxed total energy. See DOI: https://doi.org/10.1039/d5ra07404e.

Acknowledgements

This work was financially supported by the National Natural Science Foundation (NSF) of China (22031009, 62475265); National Key R&D Program of China (2021YFB3601501); the Self-deployed Key Project of State Key Laboratory of Functional Crystals and Devices (GNJT-2025-ZD01); the NSF of Fujian Province (2023J01212). Computational resources have been provided by the supercomputing facilities of National Supercomputer Center in Tianjin.

References

1. D. Uglietti, Supercond. Sci. Technol., 2019, 32, 053001.
2. M. H. Devoret and R. J. Schoelkopf, Science, 2013, 339, 1169–1174.
3. H. Kamerlingh Onnes, Commun. Phys. Lab. Univ. Leiden, 1911, 122, 122–124.
4. J. G. Bednorz and K. A. Muller, Z. Phys. B:Condens. Matter, 1986, 64, 189–193.
5. Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296–3297.
6. H. L. Sun, M. W. Huo, X. W. Hu, J. Y. Li, Z. J. Liu, Y. F. Han, L. Y. Tang, Z. Q. Mao, P. T. Yang, B. S. Wang, J. G. Cheng, D. X. Yao, G. M. Zhang and M. Wang, Nature, 2023, 621, 493–498.
7. S. Lee, J.-H. Kim and Y.-W. Kwon, arXiv, 2023, preprint arXiv:2307.12008,  DOI:10.48550/arXiv.2307.12008.
8. S. Lee, J. Kim, H.-T. Kim, S. Im, S. An and K. H. Auh, arXiv, 2023, preprint arXiv:2307.12037,  DOI:10.48550/arXiv.2307.12037.
9. P. Puphal, M. Y. P. Akbar, M. Hepting, E. Goering, M. Isobe, A. A. Nugroho and B. Keimer, APL Mater., 2023, 11, 101128.
10. Q. Zhang, Y. D. Guan, Y. Q. Cheng, L. J. Min, J. K. Keurn, Z. Q. Mao and M. B. Stone, Phys. Rev. Mater., 2024, 8, 014605.
11. S. L. Zhu, W. Wu, Z. Li and J. L. Luo, Matter, 2023, 6, 4401–4407.
12. H. Y. Chen, X. R. Zhou, Z. Meng, X. N. Wang, Z. Y. Duan, L. Liu, G. J. Zhao, H. Yan, P. X. Qin and Z. Q. Liu, Nano Lett., 2024, 24, 584–591.
13. Z. J. L. Lei, C. W. Lin, I. N. Chen, C. T. Chou, Y. L. Lin, J. H. Chen, H. H. Sung and L. M. Wang, APL Mater., 2024, 12, 021104.
14. K. Z. Guo, Y. Li and S. Jia, Sci. China:Phys., Mech. Astron., 2023, 66, 107411.
15. Q. Hou, W. Wei, X. Zhou, X. Y. Wang, T. Y. Wang, Y. Sun and Z. X. Shi, Matter, 2023, 6, 4408–4418.
16. G. S. Thakur, M. Schulze and M. Ruck, Supercond. Sci. Technol., 2024, 37, 015013.
17. K. Kumar, N. K. Karn, Y. Kumar and V. P. S. Awana, ACS Omega, 2023, 8, 41737–41743.
18. B. P. Cho, J. Park, D. Y. Yun, J. Seo and K. Park, Curr. Appl. Phys., 2024, 62, 22–28.
19. L. Liu, Z. Meng, X. N. Wang, H. Y. Chen, Z. Y. Duan, X. R. Zhou, H. Yan, P. X. Qin and Z. Q. Liu, Adv. Funct. Mater., 2023, 33, 2308938.
20. K. Kumar, N. K. Karn and V. P. S. Awana, Supercond. Sci. Technol., 2023, 36, 10LT02.
21. H.-T. Kim, S. Lee, S. Im, S. M. An and K. H. Auh, 2024 APS March Meeting, Session A16, Abstract A16.00002, 2024.
22. S. M. Griffin, arXiv, 2023, preprint arXiv:2307.16892,  DOI:10.48550/arXiv.2307.16892.
23. Y. Sun, K.-M. Ho and V. Antropov, Phys. Rev. Mater., 2023, 7, 114804.
24. J. W. Lai, J. X. Li, P. T. Liu, Y. Sun and X. Q. Chen, J. Mater. Sci. Technol., 2024, 171, 66–70.
25. L. Si and K. Held, Phys. Rev. B, 2023, 108, L121110.
26. L. Celiberti, L. Varrassi and C. Franchini, Phys. Rev. B, 2023, 108, L201117.
27. C. M. Yue, V. Christiansson and P. Werner, Phys. Rev. B, 2023, 108, L201122.
28. J. Cabezas-Escares, N. F. Barrera, R. H. Lavroff, A. N. Alexandrova, C. Cardenas and F. Munoz, Phys. Rev. B, 2024, 109, 144515.
29. Y. Jiang, S. B. Lee, J. Herzog-Arbeitman, J. B. Yu, X. L. Feng, H. Y. Hu, D. Calugaru, P. S. Brodale, E. L. Gormley, M. G. Vergniory, C. Felser, S. Blanco-Canosa, C. H. Hendon, L. M. Schoop and B. A. Bernevig, Phys. Rev. B, 2023, 108, 235127.
30. J. H. Shen, D. Gaines, S. Shahabfar, Z. Li, D. H. Kang, S. Griesemer, A. Salgado-Casanova, T. C. Liu, C. T. Chou, Y. Xia and C. Wolverton, Chem. Mater., 2023, 36, 275–285.
31. S. W. Kim, K. Wang, S. Y. Chen, L. J. Conway, G. L. Pascut, I. Errea, C. J. Pickard and B. Monserrat, npj Comput. Mater., 2024, 10, 16.
32. J. X. Liu, T. Y. Yu, J. X. Li, J. T. Wang, J. W. Lai, Y. Sun, X. Q. Chen and P. T. Liu, Phys. Rev. B, 2023, 108, L161101.
33. J. Li and Q. An, J. Phys. Chem. C, 2023, 128, 580–587.
34. H. Bai, J. R. Ye, L. Gao, C. H. Zeng and W. M. Liu, Sci. Rep., 2023, 13, 21085.
35. A. Simon, Angew. Chem., Int. Ed., 1997, 36, 1789–1806.
36. S. Q. Deng, A. Simon and J. Köhler, Angew. Chem., Int. Ed., 1998, 37, 640–643.
37. S. Deng, A. Simon and J. Köhler, J. Supercond., 2004, 17, 227–231.
38. S. Deng, A. Simon and J. Köhler, in Superconductivity in Complex Systems, ed. K. A. Muller and A. BussmannHolder, 2005, vol. 114, pp. 103–141.
39. S. Deng, C. Felser and J. Köhler, J. Mod. Phys., 2013, 04, 10–13.
40. S. Deng, J. Köhler and A. Simon, Z. Kristallogr. Cryst. Mater., 2010, 225, 495–497.
41. S. Deng, A. Simon and J. Köhler, J. Am. Chem. Soc., 2002, 124, 10712–10717.
42. S. Deng, A. Simon and J. Köhler, Solid State Sci., 2000, 2, 31–38.
43. S. Deng, J. Köhler and A. Simon, Angew. Chem., Int. Ed., 2006, 45, 599–602.
44. S. Deng, A. Simon and J. Köhler, Angew. Chem., Int. Ed., 2008, 47, 6703–6706.
45. S. Deng, A. Simon and J. Köhler, J. Supercond., 2003, 16, 477–481.
46. S. Deng, A. Simon, J. Köhler and A. Bussmann-Holder, J. Supercond., 2003, 16, 919–922.
47. P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, B864–B871.
48. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
49. G. Kresse and J. Hafner, Phys. Rev. B: condens. Matter Mater. Phys., 1993, 47, 558–561.
50. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
51. P. E. Blochl, Phys. Rev. B: condens. Matter Mater. Phys., 1994, 50, 17953–17979.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
53. K. Okhotnikov, T. Charpentier and S. Cadars, J. Cheminf., 2016, 8, 17.
54. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
55. I. V. Sukhenko and V. L. Karbivskyy, J. Phys.: Condens. Matter, 2025, 37, 083002.
56. A. Yamasaki and T. Fujiwara, J. Phys. Soc. Jpn., 2003, 72, 607–610.
57. L. F. Mattheiss and D. R. Hamann, Solid State Commun., 1987, 63, 395–399.
58. R. Manzke, T. Buslaps, R. Claessen, M. Skibowski and J. Fink, Phys. Scri., 1990, 41, 579–583.
59. C. O. Rodriguez, N. E. Christensen and E. L. P. Blanca, Physica C, 1993, 216, 12–16.
60. C. L. Xia, H. Q. Liu, S. J. Zhou and H. H. Chen, Nat. Commun., 2025, 16, 1054.
61. A. Jabar, S. Idrissi, N. Tahiri and L. Bahmad, Rev. Mexic. Fisica, 2024, 70, 061001–061008.
62. Y. J. Lee, R. M. Nieminen, P. Ordejon and E. Canadell, Phys. Rev. B: condens. Matter Mater. Phys., 2003, 67, 180505.
63. H. Y. Liu, I. I. Naumov, R. Hoffmann, N. W. Ashcroft and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6990–6995.
64. X. Y. Cheng, E. E. Gordon, M. H. Whangbo and S. Q. Deng, Angew. Chem., Int. Ed., 2017, 56, 10123–10126.

---