DOI:
10.1039/D5RA03555D
(Paper)
RSC Adv., 2025,
15, 24002-24018
Half-metallic ferromagnetism and thermoelectric-efficient behavior in chalcogenide spinels MgNi2X4 (X = S, Se): a first-principles approach
Received
20th May 2025
, Accepted 1st July 2025
First published on 10th July 2025
Abstract
We present a comprehensive first-principles investigation of the structural, electronic, magnetic, thermoelectric, and optical properties of MgNi2X4 (X = S, Se) spinels. Both compounds are confirmed to be mechanically and dynamically stable in the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure. Energy–volume calculations establish ferromagnetism as the ground state, and phonon dispersion curves obtained via density functional perturbation theory (DFPT) exhibit no imaginary frequencies, confirming dynamic stability. Electronic structure calculations using both GGA and TB-mBJ functionals reveal half-metallic ferromagnetism having total magnetic moments of approximately 4 μB per formula unit predominantly arising from Ni2+ ions. Thermoelectric properties, including Seebeck coefficient, electrical and thermal conductivities, and the dimensionless figure of merit (zT) has been evaluated in the temperature range of 100–800 K as a function of chemical potential. The maximum zT values of ∼1.00 for MgNi2S4 and ∼0.98 for MgNi2Se4 are attained near room temperature, indicating its efficient thermoelectric performance. High See beck coefficients in the spin-down channel 180 μV K−1 for MgNi2S4 and 450 μV K−1 for MgNi2Se4 reflect their spin-polarized electronic structures. Additionally, low lattice thermal conductivities derived from phonon-based calculations further enhance their thermoelectric potential. Optical analyses reveal strong absorption, high photoconductivity, and significant dielectric response in the visible to ultraviolet range, making these materials suitable for optoelectronic applications. These results establish both MgNi2S4 and MgNi2Se4 as promising multifunctional candidates for the use in next-generation spintronic, thermoelectric, and optoelectronic devices.
m structure. Energy–volume calculations establish ferromagnetism as the ground state, and phonon dispersion curves obtained via density functional perturbation theory (DFPT) exhibit no imaginary frequencies, confirming dynamic stability. Electronic structure calculations using both GGA and TB-mBJ functionals reveal half-metallic ferromagnetism having total magnetic moments of approximately 4 μB per formula unit predominantly arising from Ni2+ ions. Thermoelectric properties, including Seebeck coefficient, electrical and thermal conductivities, and the dimensionless figure of merit (zT) has been evaluated in the temperature range of 100–800 K as a function of chemical potential. The maximum zT values of ∼1.00 for MgNi2S4 and ∼0.98 for MgNi2Se4 are attained near room temperature, indicating its efficient thermoelectric performance. High See beck coefficients in the spin-down channel 180 μV K−1 for MgNi2S4 and 450 μV K−1 for MgNi2Se4 reflect their spin-polarized electronic structures. Additionally, low lattice thermal conductivities derived from phonon-based calculations further enhance their thermoelectric potential. Optical analyses reveal strong absorption, high photoconductivity, and significant dielectric response in the visible to ultraviolet range, making these materials suitable for optoelectronic applications. These results establish both MgNi2S4 and MgNi2Se4 as promising multifunctional candidates for the use in next-generation spintronic, thermoelectric, and optoelectronic devices.
1 Introduction
The growing global demand for sustainable energy and efficient electronic systems has intensified the search for multifunctional materials capable of addressing these technological challenges.1 In parallel, achieving high levels of spin polarization in materials has become crucial for developing next-generation spin-based electronic devices.2,3 Additionally, increasing attention is being directed toward identifying materials that are non-toxic, earth-abundant, and cost-effective, thereby ensuring their compatibility with environmental and economic constraints.4–6 Among various material classes, spinel-type chalcogenides have emerged as promising candidates owing to their structural flexibility, electronic tunability, and mechanical robustness.7–10 In particular, thiospinels with a general formula AB2X4 (A = divalent cation, B = transition metal, X = S, Se) typically crystallize in a cubic spinel structure and exhibit a range of functional properties including structural phase transitions, metal-insulator behavior, magnetism, superconductivity, and thermoelectric performance.11–14 In such materials, magnetism is primarily governed by the hybridization between the d orbitals of transition metals and the p orbitals of chalcogen atoms, which has been extensively explored for spintronic applications.15–20 A particularly desirable property in this context is half-metallic ferromagnetism (HMF),21 where one spin channel exhibits metallic conductivity while the opposite spin channel remains semiconducting or insulating—resulting in 100% spin polarization at the Fermi level.22,23 This makes half-metallic materials ideal for spintronic applications involving spin injection, detection, and spin-polarized current transport in semiconductor devices.21 Beyond magnetism, thermoelectric energy conversion is another frontier where spinel chalcogenides show strong promise. Materials that can convert waste heat into usable electrical energy are characterized by a high dimensionless figure of merit, zT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, and κ is the total thermal conductivity (electronic + lattice contributions).24 Strategies to enhance zT often involve reducing lattice thermal conductivity through methods such as bandgap tuning or phonon scattering engineering.25 Recent studies have highlighted several transition-metal-based thiospinels for their potential in spintronic and thermoelectric applications, including HgY2(S/Se)4 and ZnMn2(S/Se/Te)4,26,27 Mg(Lu/La)2Z4 (Z = S, Se),28,29 and SrX2S4 (X = Mn, Fe, Co).30 Other researchers have reported magnetism in doped SrS systems and explored the role of transition metals like Ti, V, Cr, and Mn for spintronic behavior.31 However, among the various spinel families, Mg-based thiospinels remain underexplored, despite their potential advantages in terms of low toxicity, earth abundance, and lightweight composition. To date, no comprehensive theoretical study has been conducted on MgNi2S4 and MgNi2Se4, which are expected to exhibit a combination of strong spin polarization, electronic tunability, and favorable thermoelectric parameters.
This study presents a systematic first-principles investigation of MgNi2S4 and MgNi2Se4 thiospinels using density functional theory (DFT) with advanced exchange-correlation functionals. The electronic band structures are calculated with the modified Becke–Johnson (mBJ) potential, which provides reliable estimates of bandgaps and spin splitting. Furthermore, the thermoelectric properties are predicted using the Boltzmann transport theory, incorporating energy-dependent carrier transport under the constant relaxation time approximation. The analysis confirms that these Mg-based thiospinels are promising candidates for spintronic and thermoelectric applications, encouraging experimental synthesis and further functional characterization.
2 Method of calculations
The density functional theory (DFT) framework serves as an indispensable approach for investigating material properties across a wide spectrum of applications. In this study, the Wien2k software and the full-potential linear augmented plane wave (FP-LAPW) method were employed32 to comprehensively analyze the electronic and magnetic characteristics of MgNi2(S/Se)4. Structural optimizations and energy computations for ferromagnetic (FM) and non-magnetic (NM) spin configurations were performed using the Perdew–Burke–Ernzerhof (PBE) functional.33 Although PBE is robust for determining lattice parameters and total energies, it exhibits limitations in accurately predicting electronic properties, particularly the band gap. To overcome these shortcomings, the Tran-Blaha modified Becke–Johnson (TB-mBJ) potential was adopted for precise evaluation of the electronic states and energy gaps.34 The TB-mBJ potential stands out as a highly efficient and reliable alternative to computationally intensive methods like PBE + U and hybrid functionals (e.g., HSE06). While the Hubbard parameter is essential for systems with heavy-element interactions, the hybridization of Ni 3d electrons with Mg and S/Se electrons in this study is relatively straightforward. Consequently, the TB-mBJ potential proves to be more suitable, offering superior accuracy with reduced computational cost and simpler implementation. This choice ensures an optimal balance between computational efficiency and accuracy in capturing the electronic structure. For electronic structure calculations, the system was partitioned into muffin-tin and interstitial regions. The muffin-tin region was treated using spherical harmonic solutions, while the interstitial region employed plane wave solutions. A k-mesh of 12 × 12 × 12 was used to sample the first Brillouin zone for harmonic solutions. Additional computational parameters included Kmax × RMT = 8.0, where Kmax represents the maximum wave vector in the reciprocal lattice, and RMT is the muffin-tin radius. The angular momentum expansion was limited to lmax = 10, and energy convergence was achieved with an iterative process at a threshold of 0.1 mRy. Thermoelectric properties were calculated using the BoltzTrap code,35 grounded in Boltzmann transport theory. This method derives key transport parameters such as electrical conductivity (σ) and the Seebeck coefficient from quantum integrals as functions of chemical potential and temperature. These calculations provide critical insights into the transport behavior of MgNi2(S/Se)4, emphasizing their potential utility in thermoelectric applications using certain relations reported elsewhere:36| |
 | (1) |
| |
 | (2) |
| |
 | (3) |
Here, Ξ(ε) is a transport distribution function specified by 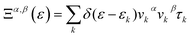 where vkα represent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100
where vkα represent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-k points.
000-k points.
3 Results and discussion
3.1 Structural properties
The structure of these magnesium-based spinels crystallizes in a cubic phase with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227), comprising a unit cell with 8 Mg, 16 Ni, and 32 S/Se atoms, as shown in Fig. 1. Within the crystal structure, magnesium atoms occupy the tetrahedral 8a Wyckoff positions at (0.125, 0.125, 0.125), nickel atoms reside at the octahedral 16 d sites at (0.5, 0.5, 0.5), and chalcogen atoms (S or Se) are situated at the 32e sites with positional coordinates (0.25, 0.25, 0.25). The cubic symmetry is preserved through careful adjustment of the positional parameter. The energy–volume (E–V) relationships for MgNi2X4 (X = S, Se) spinel compounds have been calculated self-consistently via structural optimization procedures Structural optimization was performed using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, and the resulting total energy as a function of volume was fitted to the Murnaghan equation of state to derive equilibrium structural parameters. The equation employed is as:37
m (No. 227), comprising a unit cell with 8 Mg, 16 Ni, and 32 S/Se atoms, as shown in Fig. 1. Within the crystal structure, magnesium atoms occupy the tetrahedral 8a Wyckoff positions at (0.125, 0.125, 0.125), nickel atoms reside at the octahedral 16 d sites at (0.5, 0.5, 0.5), and chalcogen atoms (S or Se) are situated at the 32e sites with positional coordinates (0.25, 0.25, 0.25). The cubic symmetry is preserved through careful adjustment of the positional parameter. The energy–volume (E–V) relationships for MgNi2X4 (X = S, Se) spinel compounds have been calculated self-consistently via structural optimization procedures Structural optimization was performed using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, and the resulting total energy as a function of volume was fitted to the Murnaghan equation of state to derive equilibrium structural parameters. The equation employed is as:37  where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus, and
where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus, and  is its pressure derivative. The computed E–V curves Fig. 2a and b for both ferromagnetic (FM) and non-magnetic (NM) phases demonstrate well-optimized structures. Positive energy differences (ΔE = ENM − EFM) confirm that the FM phase is energetically more favorable than the NM one, suggesting the magnetic ground state stability of both MgNi2S4 and MgNi2Se4. Thermodynamic stability is further validated by the negative formation energies calculated using the relation: ΔHf = Etotal (MgNimS/Sen) − (EMg + mENi + nES/Se). The resulting values are ΔHf = −0.815 eV for MgNi2S4 and −0.575 eV for MgNi2Se4, which are consistent with previously reported theoretical data.36 Following the structural and thermodynamic assessment, key parameters such as the equilibrium lattice constant (a0), bulk modulus (B0), and its pressure derivative
is its pressure derivative. The computed E–V curves Fig. 2a and b for both ferromagnetic (FM) and non-magnetic (NM) phases demonstrate well-optimized structures. Positive energy differences (ΔE = ENM − EFM) confirm that the FM phase is energetically more favorable than the NM one, suggesting the magnetic ground state stability of both MgNi2S4 and MgNi2Se4. Thermodynamic stability is further validated by the negative formation energies calculated using the relation: ΔHf = Etotal (MgNimS/Sen) − (EMg + mENi + nES/Se). The resulting values are ΔHf = −0.815 eV for MgNi2S4 and −0.575 eV for MgNi2Se4, which are consistent with previously reported theoretical data.36 Following the structural and thermodynamic assessment, key parameters such as the equilibrium lattice constant (a0), bulk modulus (B0), and its pressure derivative  were extracted from the E(V) curves using the second-order Birch–Murnaghan equation of state. The computed values are reported in Table 1 and show good agreement with earlier DFT theoretical studies.38 Notably, the substitution of sulfur by selenium results in a reduced bulk modulus, attributable to the larger ionic radius of Se, which leads to an expansion in lattice volume and consequently a softer mechanical response. These results collectively confirm that both MgNi2S4 and MgNi2Se4 are structurally, thermodynamically, and magnetically stable, and are thus promising candidates for functional applications.
were extracted from the E(V) curves using the second-order Birch–Murnaghan equation of state. The computed values are reported in Table 1 and show good agreement with earlier DFT theoretical studies.38 Notably, the substitution of sulfur by selenium results in a reduced bulk modulus, attributable to the larger ionic radius of Se, which leads to an expansion in lattice volume and consequently a softer mechanical response. These results collectively confirm that both MgNi2S4 and MgNi2Se4 are structurally, thermodynamically, and magnetically stable, and are thus promising candidates for functional applications.
 |
| | Fig. 1 Plot of the crystal structure of MgNi2X4 (X = S/Se). | |
 |
| | Fig. 2 Energy–volume optimization curve of MgNi2X4 (X = S, Se) spinel compounds in non-magnetic and ferromagnetic phases. | |
Table 1 Lattice parameter (Å), bulk modulus (GPa), energies differences (eV), enthalpy of formation eV per atom, spin-down gap (↓Eg (eV)), half-metallic gap, ghm (eV) are calculated for spinels MgNi2S4 and MgNi2Se4
| Parameters |
Present |
Work |
Reported work38 |
| MgNi2S4 |
MgNi2Se4 |
MgTi2S4 |
MgMn2S4 |
| a0 |
10.07 |
10.52 |
10.19 |
10.17 |
| B0 |
82.32 |
65.50 |
83.17 |
86.25 |
| ΔE1 |
1.36 |
0.095 |
— |
— |
| ΔHf |
−0.815 |
−0.575 |
−1.22 |
−0.98 |
| ↓Eg |
1.77 |
1.24 |
1.65 |
2.00 |
| ghm |
0.44 |
0.12 |
0.15 |
0.75 |
3.2 Phonon dynamics
The phonon dispersion analysis of MgNi2S4 and MgNi2Se4 provides critical insights into their vibrational and dynamical stability. To evaluate this, phonon dispersion curves (Fig. 3) were computed using density functional perturbation theory (DFPT) as implemented in the Quantum ESPRESSO package. A 2 × 2 × 2 supercell was constructed from the fully optimized conventional unit cell, and a 3 × 3 × 3 q-point mesh was employed to compute the interatomic force constants. The underlying density functional theory (DFT) calculations were performed within the generalized gradient approximation (GGA) for the exchange-correlation functional39,40 Each primitive cell of these spinel compounds contains seven atoms, resulting in 21 vibrational modes in total three acoustic and eighteen optical. The symmetry analysis at the Brillouin zone centre (Γ-point), based on the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (No. 227), yields the following irreducible representation of vibrational modes: Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g, where the modes 3Eu, Tg, 2Tu, and Eg exhibit degeneracy. Among these, A1g, Eg, and T2g modes are Raman-active, while T1u modes are infrared-active. The remaining modes (A2u, Eu, and T2u) are classified as silent modes. Although no experimental Raman spectroscopy was conducted in this study, this classification follows group-theoretical selection rules derived from the crystal symmetry. The calculated phonon dispersion curves exhibit no imaginary frequencies throughout the Brillouin zone, affirming the dynamical stability of both compounds. In the low-frequency region (approximately 2–4 THz), the vibrations are primarily governed by magnesium atoms due to their low atomic mass and their wagging and translational motion with surrounding chalcogen atoms. The intermediate-frequency modes (6–8 THz) involve nickel atoms, contributing more complex lattice vibrations through their coupling with both Mg and S/Se atoms. At higher frequencies (11–13 THz), the modes arise predominantly from the stretching vibrations of Ni–S and Ni–Se bonds, which are relatively stiff and energetically strong compared to other atomic interactions. These high-frequency optical phonons are particularly relevant in polar semiconductors, where they mediate long-range electron–phonon interactions via the Fröhlich mechanism, influencing both carrier scattering and lattice thermal conductivity. This has direct consequences for thermoelectric efficiency. Overall, the phonon structure confirms the dynamical robustness of MgNi2S4 and MgNi2Se4 and provides a microscopic foundation for understanding their thermal transport properties and suitability in thermoelectric applications.
m space group (No. 227), yields the following irreducible representation of vibrational modes: Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g, where the modes 3Eu, Tg, 2Tu, and Eg exhibit degeneracy. Among these, A1g, Eg, and T2g modes are Raman-active, while T1u modes are infrared-active. The remaining modes (A2u, Eu, and T2u) are classified as silent modes. Although no experimental Raman spectroscopy was conducted in this study, this classification follows group-theoretical selection rules derived from the crystal symmetry. The calculated phonon dispersion curves exhibit no imaginary frequencies throughout the Brillouin zone, affirming the dynamical stability of both compounds. In the low-frequency region (approximately 2–4 THz), the vibrations are primarily governed by magnesium atoms due to their low atomic mass and their wagging and translational motion with surrounding chalcogen atoms. The intermediate-frequency modes (6–8 THz) involve nickel atoms, contributing more complex lattice vibrations through their coupling with both Mg and S/Se atoms. At higher frequencies (11–13 THz), the modes arise predominantly from the stretching vibrations of Ni–S and Ni–Se bonds, which are relatively stiff and energetically strong compared to other atomic interactions. These high-frequency optical phonons are particularly relevant in polar semiconductors, where they mediate long-range electron–phonon interactions via the Fröhlich mechanism, influencing both carrier scattering and lattice thermal conductivity. This has direct consequences for thermoelectric efficiency. Overall, the phonon structure confirms the dynamical robustness of MgNi2S4 and MgNi2Se4 and provides a microscopic foundation for understanding their thermal transport properties and suitability in thermoelectric applications.
 |
| | Fig. 3 Phonons dispersion plots of MgNi2X4 (X = S/Se). | |
3.3 Electronic properties and half-metallicity of MgNi2X4 (X = S, Se) chalcogenides
The electronic characteristics of magnesium-based chalcogenides, specifically MgNi2S4 and MgNi2Se4, were systematically explored using two exchange–correlation potential approaches: the generalized gradient approximation (GGA) and the modified Becke–Johnson scheme combined with GGA (mBJ-GGA). These functionals were employed to assess the materials' viability for optoelectronic and spintronic applications. The calculated band structures incorporate the contributions from all atomic orbitals present in the system. While both functionals produce qualitatively similar trends in the electronic structure, the mBJ-GGA functional consistently predicts larger band gaps. This difference underscores the superior capability of the mBJ-GGA method in accurately describing the electronic behavior of transition metal-based systems, where precise band gap prediction is essential for evaluating device performance.41 Fig. 4 clearly demonstrates that both MgNi2S4 and MgNi2Se4 exhibit half-metallic ferromagnetism, characterized by a distinct spin asymmetry. The spin-up (↑) channel displays metallic behavior, with the Fermi level intersecting the valence band, while the spin-down (↓) channel behaves as a semiconductor, exhibiting a clear energy gap where the Fermi level lies within the band gap region. In the majority-spin (up) states, the Fermi level aligns with the valence band maximum, whereas in the minority-spin (down) states, the Fermi level is located in a gap region, affirming the semiconducting nature of this spin channel. The band gap, defined as the energy difference between the valence band maximum and the conduction band minimum, was computed under both GGA and mBJ-GGA schemes. The values are listed in Table 1. As expected, GGA underestimates the band gaps due to the inadequacy of treating the strong electron correlation effects associated with Ni-d orbitals. The mBJ-GGA, in contrast, provides band gap values that are in closer agreement with previously reported theoretical data,38 thereby offering a more consistent and realistic depiction of the electronic structure for these spinel systems. A detailed inspection of the band dispersion reveals notable differences between the two spin channels. In the spin-up direction, the electronic states in both the valence and conduction bands are more dispersive, suggesting a reduced effective mass for charge carriers, which in turn implies higher mobility. Conversely, the spin-down bands are less dispersive, resulting in a larger effective mass, which may hinder charge transport in the minority-spin channel but is beneficial for spin-dependent transport characteristics. The presence of an indirect band gap in the spin-down channel, situated near the Fermi level, is attributed to strong exchange interactions that stabilize the ferromagnetic configuration. These interactions are instrumental in maintaining the spin polarization and magnetic ordering essential for spintronic functionality. To gain deeper insight, the spin-splitting gap was calculated. This parameter measures the energy difference between the Fermi level and the valence band maximum or conduction band minimum for each spin channel and is tabulated in Table 1. To quantify the extent of spin polarization at the Fermi level, the degree of spin polarization (P) was calculated using the expression:  where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A value of P = 100% confirms complete spin polarization, reinforcing the half-metallic character of these compounds. Furthermore, the half-metallic gap ghmg defined as the energy separation between the highest occupied and lowest unoccupied states in the spin-down channel was computed. This gap is critical for ensuring spin-filtering performance and plays a vital role in stabilizing the half-metallic state, making these materials promising candidates for spintronic switches and magneto-optoelectronic applications.
where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A value of P = 100% confirms complete spin polarization, reinforcing the half-metallic character of these compounds. Furthermore, the half-metallic gap ghmg defined as the energy separation between the highest occupied and lowest unoccupied states in the spin-down channel was computed. This gap is critical for ensuring spin-filtering performance and plays a vital role in stabilizing the half-metallic state, making these materials promising candidates for spintronic switches and magneto-optoelectronic applications.
 |
| | Fig. 4 Plot of the electronic band structure for MgNi2X4 (X = S/Se) in spin up and spin down channels under GGA + mBJ potential approximation. | |
3.3.1 Density of states analysis. The total and partial DOS profiles, illustrated in Fig. 5a–d, are consistent with the band structures and offer further insights into the nature of electronic states. In MgNi2S4, significant hybridization occurs between S 2p and Ni 3d orbitals within the energy window of −2 eV to +2 eV in the spin-up channel. In contrast, the spin-down states are primarily distributed between −4.5 eV and −2 eV. A similar pattern is observed in MgNi2Se4, where the spin-down sub-bands extend from −4 eV to −2 eV, while the spin-up sub-bands are located between −4.1 eV and −2.3 eV. These observations emphasize the dominant role of Ni 3d states in governing the electronic, magnetic, and half-metallic properties of these compounds. Moreover, the observed exchange splitting the energy difference between spin-up and spin-down channels further corroborates the stability of the ferromagnetic ground state. The combination of complete spin polarization, visible-range spin-down band gaps, and stable exchange interactions positions MgNi2S4 and MgNi2Se4 as promising candidates for next-generation multifunctional devices that integrate spintronic, optoelectronic, and magneto-transport functionalities.
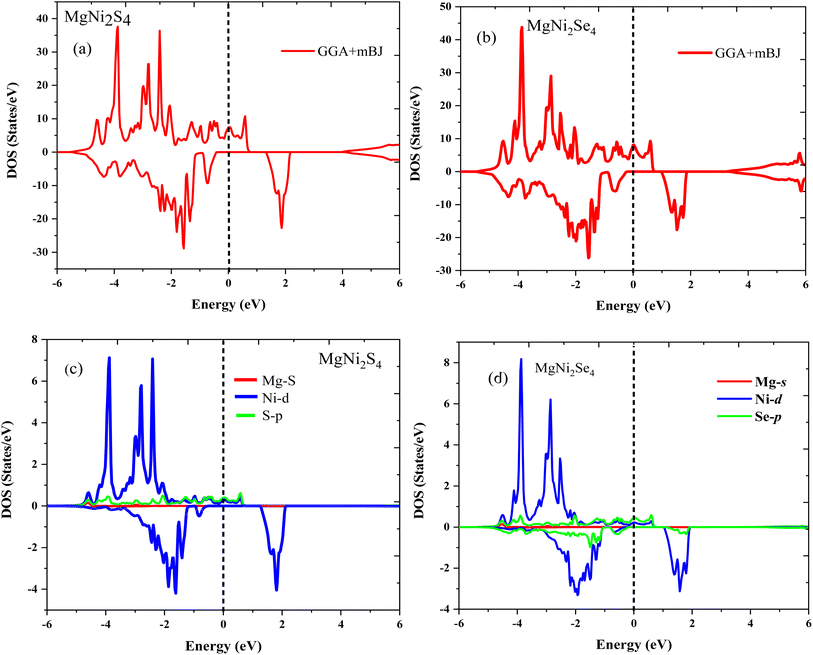 |
| | Fig. 5 (a) and (b) represents total density (TDOS) of states in spin up and spin down channels for MgNi2X4 (X = S/Se) and (c) and (d) represents partial density of states in spin up and spin down channels for MgNi2X4 (X = S/Se) respectively under GGA-mBJ potential approximation. | |
3.4 Optical properties
Light is an eco-friendly, renewable, and abundant energy source with tremendous potential for driving advancements in various technological applications, particularly in the field of optoelectronics. Recent research efforts have increasingly focused on the development of highly efficient materials capable of harnessing and converting light energy into electrical energy. In this context, magnesium-based spinel compounds, such as MgNi2X4 (X = S, Se), have attracted considerable attention due to their promising physical and electronic characteristics. The optical properties of these spinel compounds have been systematically investigated by analyzing their dielectric function both the real ε1(ω) and imaginary ε2(ω) parts along with other related optical parameters such as the absorption coefficient, reflectivity, refractive index, and energy loss function, over a broad photon energy range of 0 to 14 eV. These properties provide crucial insights into how these materials interact with electromagnetic radiation, influencing their suitability for optoelectronic and photonic applications. The real part,  determines the material's response to light propagation and polarization, while the imaginary part, ε2(ω),
determines the material's response to light propagation and polarization, while the imaginary part, ε2(ω),  measures its light absorption capability, where higher values indicate stronger absorption.42 The real part of the dielectric function, ε1(ω) (Fig. 6a and b), represents the material's polarization response to an electric field and affects how light propagates through the material. For MgNi2S4, the static dielectric constant at zero photon energy is approximately 43, indicating strong polarizability and dielectric screening at low frequencies. As the photon energy increases, ε1(ω) rapidly decreases and stabilizes between 5 and 10 beyond 5 eV, implying diminished polarization response in the ultraviolet (UV) range. MgNi2Se4 exhibits an even higher static dielectric constant of about 85, nearly twice that of MgNi2S4, likely due to the larger atomic size and polarizability of selenium atoms. Its ε1(ω) follows a similar trend, sharply declining with photon energy and stabilizing around 10 in the high-energy region. This high static dielectric constant implies strong internal electric field screening and potential for enhanced light-matter interactions at low photon energies.The imaginary part ε2(ω), indicative of energy absorption through interband electronic transitions, shows significant peaks near 0.25 eV for both compounds, revealing intense absorption in the infrared region. This peak corresponds to electronic transitions that contribute strongly to light absorption at low photon energies, a property beneficial for infrared sensing and photovoltaic applications. Beyond this region, ε2(ω) oscillates with smaller peaks extending into the visible and UV spectrum, confirming that these materials absorb across a broad energy range, with MgNi2Se4 generally showing stronger absorption than MgNi2S. The optical conductivity (Fig. 6c) complements the dielectric response by quantifying the ability of the materials to conduct electric current under light excitation. Both compounds exhibit negligible optical conductivity below 2 eV, indicating limited interband transitions at very low energies. A steep increase in optical conductivity begins near 2 eV, with a prominent peak around 9.5 eV reaching approximately 6.8 Ω−1 cm−1 for MgNi2S4 and slightly lower values for MgNi2Se4. This peak in the UV region signals strong electronic transitions and efficient electron-photon interaction, making these materials suitable for UV optoelectronic devices, such as photodetectors and UV filters. The absorption coefficient (Fig. 6d) provides a direct measure of how strongly the materials absorb incident photons. Both MgNi2S4 and MgNi2Se4 show minor absorption peaks below 4 eV, indicating some activity in the visible spectrum but relatively weak. Beyond 5 eV, absorption sharply increases and reaches values near 2 × 106 cm−1 at 14 eV, confirming strong absorption in the UV region. Such high absorption coefficients are critical for applications like UV photodetection, photocatalysis, and solar energy harvesting, where efficient photon capture at high energies is required. The refractive index (Fig. 6e), derived from ε1(ω), describes how light bends when entering the material. Both compounds display very high static refractive indices of around 10.5 at zero photon energy, reflecting strong optical density and polarizability. As photon energy rises, the refractive index steadily decreases and stabilizes between 1.5 and 2 in the UV region, indicating less light bending at higher energies. This large variation with energy indicates strong dispersion effects, relevant for optical lensing and waveguiding applications. Lastly, the extinction coefficient (Fig. 6f) quantifies the attenuation or loss of light intensity inside the material due to absorption and scattering. It begins at approximately 4.2 at low photon energies (∼0.5 eV), showing significant attenuation due to strong absorption in the infrared region. The extinction coefficient fluctuates between 1.0 and 2.5 across the 5–14 eV range, corresponding to multiple interband transitions and complex loss mechanisms in the UV region. These values affirm the results from the absorption and conductivity spectra, highlighting considerable optical losses at higher energies that are characteristic of electronic transitions in these materials. Overall, MgNi2S4 and MgNi2Se4 spinels demonstrate pronounced optical activity across a wide energy spectrum from infrared to ultraviolet. Their large static dielectric constants (43 and 85, respectively), high optical conductivity (∼6.8 Ω−1 cm−1 in the UV), strong absorption coefficients (∼2 × 106 cm−1), and significant extinction coefficients emphasize their potential for advanced optoelectronic applications. Such properties make them promising candidates for UV photodetectors, infrared sensors, solar cells, and optical coatings where efficient light absorption, polarization control, and strong electron-photon interactions are essential. The larger dielectric response and absorption in MgNi2Se4 compared to MgNi2S4 also suggest that chemical substitution in the spinel structure can tune optical properties for targeted applications. Values of some important optical parameters are presented in Table 2.
measures its light absorption capability, where higher values indicate stronger absorption.42 The real part of the dielectric function, ε1(ω) (Fig. 6a and b), represents the material's polarization response to an electric field and affects how light propagates through the material. For MgNi2S4, the static dielectric constant at zero photon energy is approximately 43, indicating strong polarizability and dielectric screening at low frequencies. As the photon energy increases, ε1(ω) rapidly decreases and stabilizes between 5 and 10 beyond 5 eV, implying diminished polarization response in the ultraviolet (UV) range. MgNi2Se4 exhibits an even higher static dielectric constant of about 85, nearly twice that of MgNi2S4, likely due to the larger atomic size and polarizability of selenium atoms. Its ε1(ω) follows a similar trend, sharply declining with photon energy and stabilizing around 10 in the high-energy region. This high static dielectric constant implies strong internal electric field screening and potential for enhanced light-matter interactions at low photon energies.The imaginary part ε2(ω), indicative of energy absorption through interband electronic transitions, shows significant peaks near 0.25 eV for both compounds, revealing intense absorption in the infrared region. This peak corresponds to electronic transitions that contribute strongly to light absorption at low photon energies, a property beneficial for infrared sensing and photovoltaic applications. Beyond this region, ε2(ω) oscillates with smaller peaks extending into the visible and UV spectrum, confirming that these materials absorb across a broad energy range, with MgNi2Se4 generally showing stronger absorption than MgNi2S. The optical conductivity (Fig. 6c) complements the dielectric response by quantifying the ability of the materials to conduct electric current under light excitation. Both compounds exhibit negligible optical conductivity below 2 eV, indicating limited interband transitions at very low energies. A steep increase in optical conductivity begins near 2 eV, with a prominent peak around 9.5 eV reaching approximately 6.8 Ω−1 cm−1 for MgNi2S4 and slightly lower values for MgNi2Se4. This peak in the UV region signals strong electronic transitions and efficient electron-photon interaction, making these materials suitable for UV optoelectronic devices, such as photodetectors and UV filters. The absorption coefficient (Fig. 6d) provides a direct measure of how strongly the materials absorb incident photons. Both MgNi2S4 and MgNi2Se4 show minor absorption peaks below 4 eV, indicating some activity in the visible spectrum but relatively weak. Beyond 5 eV, absorption sharply increases and reaches values near 2 × 106 cm−1 at 14 eV, confirming strong absorption in the UV region. Such high absorption coefficients are critical for applications like UV photodetection, photocatalysis, and solar energy harvesting, where efficient photon capture at high energies is required. The refractive index (Fig. 6e), derived from ε1(ω), describes how light bends when entering the material. Both compounds display very high static refractive indices of around 10.5 at zero photon energy, reflecting strong optical density and polarizability. As photon energy rises, the refractive index steadily decreases and stabilizes between 1.5 and 2 in the UV region, indicating less light bending at higher energies. This large variation with energy indicates strong dispersion effects, relevant for optical lensing and waveguiding applications. Lastly, the extinction coefficient (Fig. 6f) quantifies the attenuation or loss of light intensity inside the material due to absorption and scattering. It begins at approximately 4.2 at low photon energies (∼0.5 eV), showing significant attenuation due to strong absorption in the infrared region. The extinction coefficient fluctuates between 1.0 and 2.5 across the 5–14 eV range, corresponding to multiple interband transitions and complex loss mechanisms in the UV region. These values affirm the results from the absorption and conductivity spectra, highlighting considerable optical losses at higher energies that are characteristic of electronic transitions in these materials. Overall, MgNi2S4 and MgNi2Se4 spinels demonstrate pronounced optical activity across a wide energy spectrum from infrared to ultraviolet. Their large static dielectric constants (43 and 85, respectively), high optical conductivity (∼6.8 Ω−1 cm−1 in the UV), strong absorption coefficients (∼2 × 106 cm−1), and significant extinction coefficients emphasize their potential for advanced optoelectronic applications. Such properties make them promising candidates for UV photodetectors, infrared sensors, solar cells, and optical coatings where efficient light absorption, polarization control, and strong electron-photon interactions are essential. The larger dielectric response and absorption in MgNi2Se4 compared to MgNi2S4 also suggest that chemical substitution in the spinel structure can tune optical properties for targeted applications. Values of some important optical parameters are presented in Table 2.
 |
| | Fig. 6 (a) represents the real part ε1(ω) and imaginary part ε2(ω) of dielectric constant of MgNi2S4 and (b) represents real part ε1(ω) and imaginary part ε2(ω) of dielectric constant of MgNi2Se4 (c) represents optical conductivity, (d) represents absorption coefficient (e) represents reflective index and (f) excitation coefficient under GGA-mBJ potential approximation. | |
Table 2 Represents the important optical parameters calculated in different energy ranges
| Property |
MgNi2S4 |
MgNi2Se4 |
| Static dielectric constant ε1 (0) |
43 |
85 |
| Dielectric constant at UV (>5 eV) |
∼5 to 10 |
∼10 |
| Imaginary dielectric peak near 0.25 eV |
∼40 (peak height) |
∼60 (peak height) |
| Optical conductivity peak (∼9.5 eV) |
6.8 Ω−1 cm−1 |
∼6.0 Ω−1 cm−1 |
| Absorption coefficient at 14 eV |
2.0 × 106 cm−1 |
2.0 × 106 cm−1 |
| Static refractive index (n0) |
∼10.5 |
∼10.5 |
| Refractive index in UV (5–14 eV) |
∼1.5 to 2 |
∼1.5 to 2 |
| Extinction coefficient at ∼0.5 eV |
∼4.2 |
∼4.2 |
| Extinction coefficient (5–14 eV) |
1.0 to 2.5 |
1.0 to 2.5 |
3.5 Thermoelectric properties
The phenomenon known as the thermoelectric effect occurs when a temperature gradient is introduced across a material, causing an electric voltage or current to be generated. The functioning of thermoelectric devices, which are used in applications like temperature control and power generation, is supported by this effect. The dimensionless figure of merit (zT), characterises the efficiency of a thermoelectric material which is determined by the following relation  . Where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (comprising both electronic and lattice contributions), and T is the absolute temperature. Maximizing zT requires high See beck coefficient and electrical conductivity, along with low thermal conductivity. The electron relaxation time (τ), a crucial factor in determining transport coefficients, represents the average time interval between successive scattering events of charge carriers. The constant relaxation time approximation assumes that τ varies slowly with energy on the scale of kBT, the thermal energy. Under this assumption, the thermoelectric coefficients such as the electrical conductivity per unit time (σ/τ), electronic thermal conductivity per unit time (κe/τ), and the power factor per unit time can be conveniently expressed in terms of τ. Due to the unavailability of sufficient computational resources and power to compute the relaxation time (τ) from first principles for our studied system, we followed the same CRTA methodology. In both our study and the cited work, the relaxation time is not explicitly calculated but assumed to be constant typically of the order of 10−15 seconds, the carrier concentration used was 1 × 1020 cm−3, a typical value used for semiconducting thermoelectric materials, as supported by prior DFT-based studies on similar materials. These interdependent parameters were evaluated using Boltzmann transport theory within the rigid band approximation and constant relaxation time (τ) approximation, as implemented in the BoltzTrap code. Thermoelectric properties were calculated using the BoltzTrap code,35 grounded in Boltzmann transport theory while κl was estimated using the Slack model.
. Where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (comprising both electronic and lattice contributions), and T is the absolute temperature. Maximizing zT requires high See beck coefficient and electrical conductivity, along with low thermal conductivity. The electron relaxation time (τ), a crucial factor in determining transport coefficients, represents the average time interval between successive scattering events of charge carriers. The constant relaxation time approximation assumes that τ varies slowly with energy on the scale of kBT, the thermal energy. Under this assumption, the thermoelectric coefficients such as the electrical conductivity per unit time (σ/τ), electronic thermal conductivity per unit time (κe/τ), and the power factor per unit time can be conveniently expressed in terms of τ. Due to the unavailability of sufficient computational resources and power to compute the relaxation time (τ) from first principles for our studied system, we followed the same CRTA methodology. In both our study and the cited work, the relaxation time is not explicitly calculated but assumed to be constant typically of the order of 10−15 seconds, the carrier concentration used was 1 × 1020 cm−3, a typical value used for semiconducting thermoelectric materials, as supported by prior DFT-based studies on similar materials. These interdependent parameters were evaluated using Boltzmann transport theory within the rigid band approximation and constant relaxation time (τ) approximation, as implemented in the BoltzTrap code. Thermoelectric properties were calculated using the BoltzTrap code,35 grounded in Boltzmann transport theory while κl was estimated using the Slack model.
In this study, we examined the temperature dependence and chemical potential dependence of the thermoelectric coefficients, as illustrated in Fig. 7a–c and 8a–c. Given the anticipated ferromagnetic nature of the investigated compounds, we also explored the influence of magnetism on their thermoelectric properties. To this end, we adopted the two-current model, a theoretical framework that separates electronic transport into spin-up (↑) and spin-down (↓) channels—especially relevant for ferromagnetic systems.43 In such materials, magnetization leads to spin-dependent scattering and mobility due to interactions between conduction electrons and localized magnetic moments. As a result, key transport quantities Seebeck coefficient (S), electrical conductivity (σ), and electronic thermal conductivity (κe) become spin-dependent, denoted as S↑, S↓, σ↑, σ↓, κe↑, and κe↓.Using this model, the total transport coefficients are obtained as: total electrical conductivity: σ = σ↑ + σ↓, total electronic thermal conductivity: κe = κe↑ + κe↓, and total Seebeck coefficient:  . These spin-resolved calculations enable a more accurate understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. The variation of thermoelectric coefficients across the 100–800 K temperature range is thoroughly analyzed in the following section.
. These spin-resolved calculations enable a more accurate understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. The variation of thermoelectric coefficients across the 100–800 K temperature range is thoroughly analyzed in the following section.
 |
| | Fig. 7 (a–d) Variation in (a) Seebeck coefficient, (b) electrical conductivity, (c) thermal conductivity against temperature. | |
 |
| | Fig. 8 (a–c) Thermoelectric parameters (a) Seebeck coefficient, (b) electrical conductivity and figure of merit (zT) against chemical potential. | |
3.5.1 Seebeck coefficient. Thermoelectric materials generate an electric voltage in response to a temperature gradient (ΔT), quantified by the Seebeck coefficient (S), where ΔV = SΔT. The magnitude and sign of S depend on carrier concentration, scattering mechanisms, and temperature.44 Fig. 7a illustrates the temperature dependence of the See beck coefficient for MgNi2S4 and MgNi2Se4. In the spin-down channel, S decreases with rising temperature from approximately 200 μV K−1 (MgNi2S4) and 900 μV K−1 (MgNi2Se4) at 100 K to 140 μV K−1 and 250 μV K−1 at 800 K, respectively highlighting the semiconducting nature of this spin channel. In contrast, the spin-up channel shows an increasing S with temperature, ranging from 60–80 μV K−1 at 100 K to about 150–160 μV K−1 at 800 K, consistent with metallic transport. Fig. 8a presents the variation of S with chemical potential (μ) at 300 K and 800 K. Both compounds display symmetrical peaks and troughs, representing p-type (μ < 0) and n-type (μ > 0) doping regimes. MgNi2Se4 exhibits higher peak values, indicating stronger voltage generation under the same temperature gradient. Around the intrinsic Fermi level (μ = 0), both materials show moderate S values, suggesting bipolar conduction. Though the magnitude of S slightly decreases at higher temperatures due to increased thermal excitation of carriers, the overall profile remains stable, indicating good thermoelectric resilience across temperature.44 The sign of S also reveals the type of dominant carriers: positive for p-type (holes), and negative for n-type (electrons). Our results confirm that the spin-down channel of MgNi2S4 demonstrates n-type conduction, while MgNi2Se4 exhibits p-type behaviour both hallmarks of semiconducting transport. This spin-dependent response reflects the half-metallic ferromagnetic character of these spinels, where one spin channel is metallic and the other semiconducting. The Seebeck coefficient in semiconductors can be expressed as S = (8π2kB2/3eh2) × m* × T × (π/3n)2/3 where kB is the Boltzmann constant, e is the elementary charge, h is Planck's constant, T is temperature, m* is the effective mass, and n is the carrier concentration. These spin-polarized thermoelectric characteristics make MgNi2S4 and MgNi2Se4 excellent candidates for spin-caloritronic and advanced energy conversion applications, where control over both spin and heat transport is critical.
3.5.2 Electrical conductivity. The temperature-dependent variation of the electrical conductivity per unit relaxation time (σ/τ) is shown in Fig. 7b, calculated using the constant relaxation time approximation (RTA) within the BoltzTrap code. This method enables evaluation of electrical transport properties without requiring a specific τ value and assumes negligible lattice thermal conductivity.46 The thermoelectric potential of MgNi2S4 and MgNi2Se4 is evident from their favourable band structures and high carrier mobilities. In both materials, σ/τ increases with temperature from 100 to 800 K, reflecting enhanced carrier excitation and mobility. In MgNi2S4, the spin-up channel shows a non-linear increase in σ/τ from (1.8 to 3.8) × 1019 (Ω m s) −1, indicating metallic transport behaviour due to the absence of a band gap. Meanwhile, the spin-down channel increases nonlinearly from (1.7 to 3.9) × 1019 (Ω m s) −1, attributed to semiconducting behaviour governed by an indirect band gap above 1.7 eV. A similar trend is observed in MgNi2Se4, where the spin-up channel exhibits a linear increase in σ/τ from (1.5 to 3.0) × 1019 (Ω m s)−1, while the spin-down channel rises nonlinearly from (0.1 to 0.3) × 1019 (Ω m s)−1, consistent with its semiconducting nature. These trends are explained by the relation σ = neμ, where σ depends on carrier concentration (n) and mobility (μ), both of which are influenced by temperature. Furthermore, Fig. 8b presents σ/τ as a function of chemical potential at 300, 600, and 800 K. In both materials, σ/τ is lowest near μ = 0 eV, reflecting minimal intrinsic carrier activity. As μ shifts toward the conduction or valence band, σ/τ increases sharply, indicating enhanced electrical conductivity through doping. At elevated temperatures, σ/τ increases further across the entire chemical potential range, confirming thermally activated transport.47 This temperature and doping dependence of σ/τ plays a critical role in determining the thermoelectric performance of these spinel compounds by balancing electrical transport efficiency with thermal losses. Such tunable electrical conductivity is essential for designing high-performance thermoelectric devices that rely on precise control of carrier transport under thermal gradients.
3.5.3 Thermal conductivity. Thermal conductivity, which describes a material's ability to transport heat via charge carriers and lattice vibrations, is a critical parameter for evaluating thermoelectric performance. For optimal efficiency, materials must exhibit low thermal conductivity to sustain a strong temperature gradient and generate thermoelectric voltage. In solids, the total thermal conductivity (κtotal) includes electronic (κe) and lattice (κl) components, the latter mediated by phonons. In this study, κe was computed using the BoltzTrap code, while κl was estimated using the Slack model due to typically weak phonon contributions in large-lattice spinels.45 Fig. 7c shows that κe/τ increases with temperature for both MgNi2S4 and MgNi2Se4, from approximately (0.5 to 1.2) × 1014 and (0.5 to 0.9) × 1014 W m−1 K−1 s−1, respectively, due to enhanced carrier mobility. Despite this increase, κe remains relatively low, minimizing parasitic heat losses beneficial for thermoelectric applications. According to the Wiedemann–Franz law (κ/σ = LT), electrical and thermal conductivities are interconnected; however, the moderate rise in κe/τ does not significantly increase κtotal preserving thermoelectric potential. Lattice thermal conductivity (κl) also shown in Fig. 7c, decreases from ∼0.65 W mK−1 at 300 K to ∼0.2 W mK−1 at 800 K due to increased phonon–phonon Umklapp scattering, which shortens the phonon mean free path. While low κl high temperatures is generally favourable, the peak zT is observed at room temperature against chemical potential as shown in Fig. 8c, indicating that favourable electronic properties such as high See beck coefficient and adequate electrical conductivity play a more dominant role in enhancing zT. Overall, κtotal shows a decreasing trend from ∼1.2–1.4 W mK−1 at room temperature to below 0.5 W mK−1 at 800 K, mainly due to the suppression of κlwhich supports high zT by maintaining a strong thermal gradient.
3.5.4 Figure of merit (zT). The figure of merit (zT) is a critical dimensionless parameter that quantifies the thermoelectric efficiency of a material by evaluating its ability to convert thermal energy into electrical power. Fig. 8c illustrates the variation of zT as a function of chemical potential (μ) for the spinel compounds MgNi2S4 and MgNi2Se4 at different temperatures. At room temperature (300 K), both materials exhibits pronounced peaks near the Fermi level (μ = 0 eV), with MgNi2S4 reaching a maximum zT of 1.0 and MgNi2Se4 attaining a peak value of approximately 0.98. These high zT values under moderate doping conditions underscore the effectiveness of carrier concentration tuning in optimizing thermoelectric performance. These values are in good agreement with those reported in the literature.44 The observed increase in zT as μ shifts away from zero indicates that both n-type (μ > 0) and p-type (μ < 0) doping can significantly enhance charge carrier contributions, thereby improving the power factor. At an elevated temperature of 800 K, the zT curves broaden due to increased thermal excitation and carrier scattering, yet the maximum values remain close to those observed at 300 K. This behaviour suggests that the reduction in lattice thermal conductivity at higher temperatures is counterbalanced by less favourable electronic transport properties, making room-temperature conditions more suitable for peak thermoelectric performance in these materials. The nearly symmetric profile of the zT curves across a chemical potential range from −1.5 eV to +1.5 eV further highlights the dual doping compatibility and stability of thermoelectric response. Overall, these findings demonstrate that MgNi2S4 and MgNi2Se4 possess a robust and tunable thermoelectric character, making them strong candidates for use in practical energy conversion applications, especially in devices that operate near ambient temperatures.
3.6 Magnetic properties
The ferromagnetic behavior of MgNi2S4 and MgNi2Se4 was confirmed through spin-dependent volume optimization, establishing that both compounds possess a ferromagnetic (FM) ground state. The strength of this magnetism was evaluated by computing both the total magnetic moment and the local magnetic moments associated with individual ions. The magnetic moment in these materials emerges due to the presence of spin-polarized electrons, which was quantified by calculating the difference in the integral of the spin-polarized density of states (DOS). In addition to the total magnetic moment, the local magnetic moments contributed by individual atoms were also computed to assess their specific roles in the magnetic character of both compounds. The magnetism in these systems is primarily due to the Ni atoms. Under the influence of crystal field splitting, the d-orbitals of Ni split into d-eg (higher energy) and d-t2g (lower energy) levels. This splitting causes previously paired electrons in the Ni d-orbitals to become unpaired and align in a particular direction, giving rise to a net magnetic moment.46,47 For MgNi2S4, the calculated total magnetic moment is 3.9997 μB per formula unit, indicating strong ferromagnetic ordering (Table 3). Magnesium (Mg) contributes about 0 μB, confirming its non-magnetic nature and negligible effect on the compound's magnetism. The nickel (Ni) atoms are the primary contributors, each contributing a significant 1.38152 μB. The overall ferromagnetic property is slightly opposed by a small negative magnetic moment from sulfur (−0.1283 μB), indicating a weak diamagnetic or antiferromagnetic tendency. Furthermore, the interstitial region contributes −0.53028 μB, reinforcing this minor opposition, but without disrupting the dominant ferromagnetic alignment. In a similar manner, MgNi2Se4 displays substantial ferromagnetic behavior, with a total magnetic moment of 4.0000 μB per formula unit (Table 3). Here again, magnesium contributes 0 μB, maintaining its non-magnetic character. The Ni atoms contribute 1.38152 μB per atom, making them the principal source of magnetism. The selenium atoms contribute a slightly larger negative magnetic moment of −0.1479 μB compared to sulfur, indicating a somewhat stronger diamagnetic or antiferromagnetic effect. Additionally, the interstitial region contributes −0.12 μB, slightly counteracting the overall ferromagnetic alignment. In both compounds, the primary ferromagnetic nature is dominated by the nickel atoms. The minor opposing effects introduced by sulfur, selenium, and the interstitial regions do not significantly alter the compounds' overall magnetic properties. Notably, the slightly greater negative contributions from selenium and the interstitial region in MgNi2Se4 suggest more intricate magnetic interactions compared to MgNi2S4. However, both systems retain their strong ferromagnetic character.
Table 3 The total and partial spin magnetic moments for MgNi2X4 Spinels
| Compound |
Total (μB) |
Int (μB) |
Mg (μB) |
Ni (μB) |
S/Se (μB) |
| MgNi2S4 |
3.9997 |
−0.53028 |
0.00 |
1.38152 |
−0.1283 |
| MgNi2Se4 |
4.0001 |
−0.12 |
0.00 |
1.37615 |
−0.1309 |
3.7 Elastic properties
The atomic arrangement within a crystal lattice significantly influences its resistance to external forces, thereby determining its mechanical stability. Assessing mechanical stability is thus essential for guiding industrial and technological applications. For the studied magnesium-based chalcogenides, we determined the second-order elastic constants using the energy–volume method while incorporating tetrahedral and octahedral distortions via the cubic elastic package. The eigenvalues of the elastic constant matrix for MgNi2X4 (X = S, Se), presented in Table 4, are all positive and comply with the Born stability criteria: C11 > 0, C44 > 0, C11 − C12 > 0, C11 + 2C12 > 0, and C11 > B > C12.48 This confirms the mechanical stability of these magnesium-based chalcogenides in the symmetric cubic phase (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The calculated elastic constants enable the derivation of various moduli bulk (B), shear (G), and Young's modulus (Y) using well-established relations. The results, detailed in Table 4, reveal that the Young's modulus, which represents the stiffness of the material, is greater than the bulk modulus, which reflects resistance to uniform compression. The shear modulus, indicative of resistance to shape deformation, is lower, suggesting that these materials can undergo shape changes more readily than volumetric changes. The order Y > B > G highlights the high stiffness and flexibility against shear deformation. To further assess the mechanical response, we computed the Kleinman parameter (ζ), which lies within the range 0 ≤ ζ < 1. A lower ζ value indicates stronger resistance to bond angle distortions and bond bending, implying greater rigidity of the crystal framework. Table 4 also presents metrics used to evaluate material ductility. Cauchy's pressure (C12 − C44) is a reliable indicator of ductility, with a positive value signifying ductile behavior. Similarly, Pugh's ratio (B/G), with a threshold of 1.75, distinguishes ductile (>1.75) from brittle (<1.75) materials.49 Poisson's ratio (ν) also supports this classification; values greater than 0.26 denote ductility. The computed values of these parameters collectively affirm the ductile nature of the MgNi2X4 compounds.
m). The calculated elastic constants enable the derivation of various moduli bulk (B), shear (G), and Young's modulus (Y) using well-established relations. The results, detailed in Table 4, reveal that the Young's modulus, which represents the stiffness of the material, is greater than the bulk modulus, which reflects resistance to uniform compression. The shear modulus, indicative of resistance to shape deformation, is lower, suggesting that these materials can undergo shape changes more readily than volumetric changes. The order Y > B > G highlights the high stiffness and flexibility against shear deformation. To further assess the mechanical response, we computed the Kleinman parameter (ζ), which lies within the range 0 ≤ ζ < 1. A lower ζ value indicates stronger resistance to bond angle distortions and bond bending, implying greater rigidity of the crystal framework. Table 4 also presents metrics used to evaluate material ductility. Cauchy's pressure (C12 − C44) is a reliable indicator of ductility, with a positive value signifying ductile behavior. Similarly, Pugh's ratio (B/G), with a threshold of 1.75, distinguishes ductile (>1.75) from brittle (<1.75) materials.49 Poisson's ratio (ν) also supports this classification; values greater than 0.26 denote ductility. The computed values of these parameters collectively affirm the ductile nature of the MgNi2X4 compounds.| |
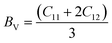 | (4) |
| |
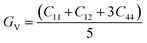 | (5) |
| |
 | (6) |
| |
 | (7) |
| |
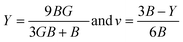 | (8) |
In addition to calculating the bulk modulus (B0) from the elastic constants (Cij), the present study also reports the magnitude of B0 derived from the Birch–Murnaghan equation by incorporating the data of the optimized volume. From the computed values of the elastic moduli, it is evident that substituting selenium (Se) in the composition results in a decrease in the elastic moduli, indicating that MgNi2Se4 is less rigid compared to MgNi2S4. This reduction in stiffness is attributed to the relatively smaller electronegativity difference between Se and the constituent cations, which weakens the bond strength and, consequently, lowers the elastic moduli.
Table 4 Mechanical parameters for MgNi2S4/Se4 spinels
| Parameter |
C11 |
C12 |
C44 |
B |
G |
Y |
B/G |
v |
Cp |
Az |
AU |
ζ |
| MgNi2S4 |
182.4 |
52.02 |
39.2 |
82.32 |
45.0 |
118.8 |
1.82 |
0.31 |
12.82 |
0.60 |
2.54 |
0.82 |
| MgNi2Se4 |
108.2 |
34.03 |
24.6 |
65.50 |
36.3 |
74.6 |
1.80 |
0.29 |
9.43 |
0.65 |
1.78 |
0.68 |
In the field of crystallophysics, anisotropy metrics such as the Zener anisotropy index (AZ) and the universal anisotropy factor (AU) are vital for assessing the directional dependence of elastic properties. To quantify elastic anisotropy, we evaluated AZ and AU  .50,51 Deviation of either value from unity implies anisotropic behavior, whereas values equal to one suggest isotropy. The results in Table 4 clearly indicate notable anisotropy in these compounds, reflecting directional dependence in their elastic response. Additionally, to gain deeper insight into the anisotropic and elastic characteristics of the studied compounds, we employed the Elate code52 to generate three-dimensional (3D) contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (ν). These 3D visualizations provide a clear depiction of the directional dependence of elastic properties for MgNi2S4 and MgNi2Se4, as presented in Fig. 9 and 10, respectively. It is evident from the plots that all parameters, except linear compressibility, exhibit notable deviations from an ideal spherical shape emphasizing the anisotropic nature of these spinels. Moreover, the degree of anisotropy appears consistent across various crystallographic directions, further confirming the directional variation in their mechanical response.
.50,51 Deviation of either value from unity implies anisotropic behavior, whereas values equal to one suggest isotropy. The results in Table 4 clearly indicate notable anisotropy in these compounds, reflecting directional dependence in their elastic response. Additionally, to gain deeper insight into the anisotropic and elastic characteristics of the studied compounds, we employed the Elate code52 to generate three-dimensional (3D) contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (ν). These 3D visualizations provide a clear depiction of the directional dependence of elastic properties for MgNi2S4 and MgNi2Se4, as presented in Fig. 9 and 10, respectively. It is evident from the plots that all parameters, except linear compressibility, exhibit notable deviations from an ideal spherical shape emphasizing the anisotropic nature of these spinels. Moreover, the degree of anisotropy appears consistent across various crystallographic directions, further confirming the directional variation in their mechanical response.
 |
| | Fig. 9 (a–d) Directional dependence of (a) Young's modulus (Y), (b) linear compressibility (β), (c) shear modulus (G), and (d) Poisson's ratio (v) for MgNi2S4 compound. | |
 |
| | Fig. 10 (a–d) Directional dependence of (a) Young's modulus (Y), (b) linear compressibility (β), (c) shear modulus (G), and (d) Poisson's ratio (v) for MgNi2Se4 compound. | |
3.8 Electron density
We analyze the electron density distributions of magnesium-based chalcogenides, specifically MgNi2X4 (X = S, Se), along the (001) crystallographic plane to explore charge sharing and bonding interactions among the constituent atoms (Fig. 11). The electron density maps demonstrate notable overlapping charge regions between nickel and sulfur/selenium (Ni–S/Se) as well as magnesium and sulfur/selenium (Mg–S/Se), indicating the presence of covalent bonding interactions. These maps provide valuable insights into the charge transfer dynamics between the cations (Mg and Ni) and anions (S and Se), which are essential for understanding the bonding nature and stability of these materials. To further investigate the bonding characteristics, we calculated the electronegativity differences between the cations and anions. The differences are determined to be 0.67/0.64 for Ni–S/Se and 1.25/1.22 for Mg–S/Se. These values, being below the critical threshold of 2.0, confirm the predominance of covalent bonding with a polar nature.52 This indicates that the bonds in MgNi2S4 and MgNi2Se4 exhibit a mixed ionic-covalent character. The findings highlight that while the materials display ionic traits due to the metal and non-metal constituents, the covalent nature significantly influences their stability and electronic properties.
 |
| | Fig. 11 Graphical plot of electron density distribution along 100 plane for MgNi2S4/Se4. | |
4 Conclusion
A comprehensive first-principles investigation of the mechanical, optoelectronic, magnetic, and thermoelectric properties of chalcogenide spinels MgNi2X4 (X = S, Se) has been performed using density functional theory. Mechanical stability and ductility are confirmed by Poisson's ratios above 0.26 and Pugh's ratios exceeding 1.75. Negative formation energies (−0.815 eV for MgNi2S4 and −0.575 eV for MgNi2Se4), along with the absence of imaginary phonon modes, attest to their thermodynamic and dynamic stability. Electronic structure calculations reveal half-metallic ferromagnetism, with metallic spin-up channels and semiconducting spin-down channels exhibiting indirect band gaps of 1.77 eV and 1.24 eV for MgNi2S4 and MgNi2Se4, respectively. Optically, both compounds show broad-spectrum activity from visible to ultraviolet, marked by high static dielectric constants (43 and 85), strong optical conductivity (∼6.8 Ω−1 cm−1 in the UV), large absorption coefficients (∼2 × 106 cm−1), and significant extinction coefficients. These attributes support potential applications in UV photodetectors, IR sensors, solar cells, and optical coatings. The superior dielectric response and absorption in MgNi2Se4 suggest tunability through chemical substitution. Magnetically, both spinels exhibit robust ferromagnetism with total magnetic moments around 4.0 μB, primarily originating from Ni atoms. Thermoelectrically, Seebeck coefficients range between 180–450 μV K−1 across 100–800 K. MgNi2S4 exhibits n-type and MgNi2Se4 p-type behavior in the spin-down channel. Maximum figures of merit (zT) of 1.00 and 0.98, respectively, are observed near room temperature against chemical potential, indicating strong potential for efficient thermoelectric energy conversion. Collectively, MgNi2X4 spinels emerge as multifunctional materials promising for integrated applications in spintronics, optoelectronics, and thermoelectrics.
Data availability
The data sets generated and thereafter analyzed would be available from the corresponding author upon reasonable request.
Author contributions
All the authors have significantly contributed to the research. Ashiq Ramzan: conceptualization, methodology (partially), writing – original draft, revision; Mudasir Younis Sofi: methodology (partially), data curation and analysis, editing write-up, writing – review & modification; Mohammad Ishfaq-ul-Islam: formal analysis, Mohd. Shahid Khan: formal analysis; M. Ajmal Khan: supervision, software, validation, writing – review & modification.
Conflicts of interest
The authors declare no competing interests.
References
- T. Naito, Functional Materials: Advances and Applications in Energy Storage and Conversion, 1st edn, Jenny Stanford Publishing, 2018 Search PubMed.
- Z. Szotek, W. M. Temmerman, A. Svane, L. Petit, P. Strange, G. M. Stocks, D. Kodderitzsch, W. Hergert and H. Winter, Electronic structure of half-metallic ferromagnets and spinel ferromagnetic insulators, J. Phys.:Condens. Matter, 2004, 16, S5587–S5600 CrossRef CAS.
- A. Hirohata, K. Yamada, Y. Nakatani, I. L. Prejbeanu, B. Dieny, P. Pirro and B. Hillebrands, Review on spintronics: Principles and device applications, J. Magn. Magn. Mater., 2020, 509, 166711 CrossRef CAS.
- W. Zeng, L. Shu, Q. Li, S. Chen, F. Wang and X. M. Tao, Fiber-based wearable electronics: A review of materials, fabrication, devices, and applications, Adv. Mater., 2014, 26, 5310–5336 CrossRef CAS PubMed.
- F. Ozel, et al., A general review on the thiospinels and their energy applications, Mater. Today Energy, 2021, 21, 100822 CrossRef CAS.
- R. M. Fleming, F. J. DiSalvo, R. J. Cava and J. V. Waszczak, Observation of charge-density waves in the cubic spinel structure CuV2S4, Phys. Rev. B, 1981, 24, 2850–2853 CrossRef CAS.
- F. K. Lotgering and R. P. Van Stapele, Magnetic properties and electrical conduction of copper-containing sulfo- and selenospinels, J. Appl. Phys., 1968, 39, 417–423 CrossRef CAS.
- N. H. Van Maaren, G. M. Schaeffer and F. K. Lotgering, Superconductivity in sulpho- and selenospinels, Phys. Lett. A, 1967, 25, 238–239 CrossRef.
- F. Majid, M. T. Naisr, E. Algrafy, M. Sajjad, N. A. Noor, A. Mahmood and S. M. Ramay, Optical and magnetic properties of thiospinels for multifunctional applications, J. Mater. Res. Technol., 2020, 9, 6135–6142 CrossRef CAS.
- N. Imanishi, K. Inoue, Y. Takeda and O. Yamamoto, Thiospinels as cathode for lithium secondary battery, J. Power Sources, 1993, 44, 619–625 CrossRef CAS.
- S. A. Abbas, I. Mahmood, M. Sajjad, N. A. Noor, Q. Mahmood, M. A. Naeem, A. Mahmood and S. M. Ramay, Spinel-type Na2MoO4 and Na2WO4 as promising optoelectronic materials: First-principle DFT calculations, Chem. Phys., 2020, 538, 1109022 CrossRef.
- G. J. Snyder, T. Caillat and J. P. Fleurial, Thermoelectric properties of chalcogenides with the spinel structure, Mater. Res. Innovations, 2001, 5, 67–73 CrossRef CAS.
- K. Hashikuni, K. Suekuni, H. Usui, M. Ohta, K. Kuroki and T. Takabatake, High power factor in thiospinels Cu2TrTi3S8 (Tr = Mn, Fe, Co, Ni) arising from TiS6 octahedron network, Appl. Phys. Lett., 2016, 109, 182110 CrossRef.
- M. Yousaf, S. A. Dalhatu, G. Murtaza, R. Khenata, M. Sajjad, A. Musa, H. A. R. Aliabad and M. A. Saeed, Optoelectronic properties of XIn2S4 (X = Cd, Mg) thiospinels through highly accurate all-electron FP-LAPW method coupled with modified approximations, J. Alloys Compd., 2015, 625, 182–187 CrossRef CAS.
- O. Volnianska and P. Bogusławski, Magnetic and structural properties of IIA–V nitrides, Phys. Rev. B, 2007, 75, 224418 CrossRef.
- S. C. Middleburgh, D. M. King, G. R. Lumpkin, M. Cortie and L. Edwards, Segregation and migration of species in the CrCoFeNi high entropy alloy, J. Alloys Compd., 2014, 599, 179–182 CrossRef CAS.
- S. Roqan, S. Venkatesh, Z. Zhang, S. Hussain, I. Bantounas and J. B. Franklin, Obtaining strong ferromagnetism in diluted Gd-doped ZnO thin films through controlled Gd-defect complexes, J. Appl. Phys., 2015, 117, 073904 CrossRef.
- I. S. Roqan, K. P. O'Donnell, R. W. Martin, P. R. Edwards, S. F. Song and A. Vantomme, Identification of the prime optical center in GaN: Eu3+, Phys. Rev. B, 2010, 81, 085209 CrossRef.
- Q. Mahmood, M. Hassan, G. Murtaza, M. Sajjad, A. Laref and B. Haq, Theoretical investigation of electronic, magnetic, and thermoelectric behavior of LiZ2O4 (Z = Mn, Fe, Co, Ni) by modified Becke–Johnson approach, J. Supercond. Novel Magn., 2019, 32, 1231–1239 CrossRef CAS.
- T. H. Flemban, V. Singaravelu, A. A. S. Devi and I. S. Roqan, Homogeneous vertical ZnO nanorod arrays with high conductivity on an in situ Gd nanolayer, RSC Adv., 2015, 5, 94670–94678 RSC.
- R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50, 2024 CrossRef CAS.
- J. M. D. Coey and M. Venkatesan, Half-metallic ferromagnetism: Example of CrO2 (invited), J. Appl. Phys., 2002, 91, 8345 CrossRef CAS.
- M. Horne, P. Strange, W. M. Temmerman, Z. Szotek, A. Svane and H. Winter, The electronic structure of europium chalcogenides and pnictides, J. Phys.:Condens. Matter, 2004, 16, 5061 CrossRef CAS.
- Y. Lang, L. Pan, C. Chen and Y. Wang, Thermoelectric properties of thiospinel type CuCo2S4, J. Electron. Mater., 2019, 48, 4179–4187 CrossRef CAS.
- W. Tahir, G. M. Mustafa, N. A. Noor, S. M. Alay-e-Abbas, Q. Mahmood and A. Laref, Analysis of optoelectronic and transport properties of magnesium based MgSc2X4 (X = S, Se) spinels for solar cell and energy storage device applications, Ceram. Int., 2020, 46, 26637–26645 CrossRef CAS.
- G. M. Mustafa, S. Saba, N. A. Noor, A. Laref, M. Abd El-Rahman, Z. Farooq, R. B. Behram and Z. Ullah, First-principles calculations to investigate HgY2S/Se4 spinel chalcogenides for optoelectronic and thermoelectric applications, J. Mater. Res. Technol., 2023, 22, 97–106 CrossRef CAS.
- N. A. Noor, M. Rashid, G. M. Mustafa, A. Mahmood, W. Al Masry and S. M. Ramay, Zinc based chalcogenides ZnMn2X4 (X = S, Se, Te) as promising spintronic and sustainable energy materi als: Ab-initio DFT investigations, J. Alloys Compd., 2021, 856, 157198 CrossRef CAS.
- G. M. Mustafa, N. A. Noor, M. W. Iqbal, M. Sajjad, M. A. Naeem, Q. Mahmood, H. M. Shaikh, A. Mahmood and W. Al-Masry, Study of optoelectronic and transport properties of MgLu2Z4 (Z = S, Se) spinels for optoelectronic and energy harvesting applications, Mater. Sci. Semicond. Process., 2021, 121, 105452 CrossRef CAS.
- G. M. Mustafa, T. Zelai, S. Bouzgarrou, M. H. Alhossainy, Q. Mahmood, A. Mera, H. H. Hegazy, S. Alharthi and M. A. Amin, First principle study of magnesium-based chalcogenides MgLa2(S/Se)4 for solar cells and renewable energy applications, Appl. Phys. A, 2022, 128, 38 CrossRef CAS.
- S. A. Rouf, H. Albalawi, T. Zelai and O. Hakami, Half-metallic fer romagnetism and thermoelectric effect in spinel chalcogenides SrX2S4 (X = Mn, Fe, Co) for spintronics and energy harvesting, J. Phys. Chem. Solids, 2023, 182, 111601 CrossRef CAS.
- Q. Mahmood, G. Nazir, J. Alzahrani and N. A. Kattan, Room tem perature ferromagnetism and thermoelectric behavior of cal cium-based spinel chalcogenides CaZ2S4 (Z = Ti, V, Cr, Fe) for spintronic applications, J. Phys. Chem. Solids, 2022, 167, 110742 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowsk, F. Tran and L. Marks, WIEN2k: an Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, TechnischeUniversitat, Vienna, 2019, p. 287 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- D. Koller, F. Tran and P. Blaha, Improving the modified Becke-Johnson exchange potential, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85(15), 155109 CrossRef.
- G. K. H. Madsen and D. J. Singh, BoltzTraP: a code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- M. Y. Sofi, M. S. Khan and M. A. Khan, Eco-friendly lead-free halide double perovskites A2CuMCl6 (A= K, Rb; M= Sb, Bi): stability, thermoelectric, and optoelectronic advancements through theoretical insights, J. Mater. Chem. C, 2024, 12(39), 16045–16058 RSC.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247 CrossRef CAS PubMed.
- M. Khalid, M. W. Iqbal, M. Asghar, N. A. Noor, G. M. Mustafa and S. M. Ramay, Exchange mechanism, ferromagnetic and transport characteristics of Mg-based spinel chalcogenides for spintronic applications, Eur. Phys. J. Plus, 2022, 137(1), 1 Search PubMed.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- P. Giannozzi, et al., Quantum Espresso: A modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- M. Y. Sofi, M. S. Khan, J. Ali and M. A. Khan, Unlocking the role of 3d electrons on ferromagnetism and spin-dependent transport properties in K2GeNiX6 (X= Br, I) for spintronics and thermoelectric applications, J. Phys. Chem. Solids, 2024, 192, 112022 CrossRef CAS.
- A. Ramzan, M. Y. Sofi, M. S. Khan, J. Ali and M. A. Khan, First-principles investigation of Mg-based MgAl2X4 (X= S, Se) spinels for optoelectronic and energy harvesting applications, Eur. Phys. J. B, 2025, 98(5), 1 CrossRef.
- M. Y. Sofi, M. S. Khan and M. A. Khan, Harnessing the half-metallicity and thermoelectric insights in Cs2AgMBr6 (M= V, Mn, Ni) double halide perovskites: A DFT study, Mater. Sci. Semicond. Process., 2025, 186, 109023 CrossRef CAS.
- S. A. Khandy, K. Kaur, S. Marutheeswaran and I. Islam, Understanding the ultralow thermal conductivity and strong anharmonicity of a lanthanum-based germanium halide monolayer for possible thermoelectric applications, ACS Appl. Energy Mater., 2024, 11(20), 9279–9288 CrossRef.
- G. A. Slack, Non-metallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34(2), 321–335 CrossRef CAS.
- G. Matsumoto, K. Ohbayashi, K. Kohn and S. Iida, Magnetic properties of ZnMn2S4, ZnMn2Se4 and ZnMn2Te4, J. Phys. Soc. Jpn., 1966, 21(11), 2429 CrossRef.
- H. Yilin, W. Yang, L. Tingzhou, Y. Tie and W. Xiaotian, Electronic, magnetic, half-metallic, and mechanical properties of a new equiatomic quaternary Heusler compound YRhTiGe: a first-principles study, Materials, 2018, 11, 797 CrossRef PubMed.
- M. Born, On the stability of crystal lattices, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160 CrossRef CAS.
- M. Y. Sofi, A. Ramzan, M. S. Khan, A. Kumar, M. R. Rather, S. A. Sofi, S. A. Khandy and M. A. Khan, Pioneering computational insights into the structural, magnetic, and thermoelectric properties of A3XN (A= Co, Fe; X= Cu, Zn) anti-perovskites for advanced material applications, Mater. Sci. Semicond. Process., 2025, 1(185), 108925 CrossRef.
- W. Hume-rothery, Elasticity and anelasticity of metals, Nature, 1949, 164(4159), 84–85 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101(5), 055504 CrossRef PubMed.
- R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: An open-source online application for analysis and visualization of elastic tensors, J. Phys.:Condens. Matter, 2016, 28(27), 275201 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure. Energy–volume calculations establish ferromagnetism as the ground state, and phonon dispersion curves obtained via density functional perturbation theory (DFPT) exhibit no imaginary frequencies, confirming dynamic stability. Electronic structure calculations using both GGA and TB-mBJ functionals reveal half-metallic ferromagnetism having total magnetic moments of approximately 4 μB per formula unit predominantly arising from Ni2+ ions. Thermoelectric properties, including Seebeck coefficient, electrical and thermal conductivities, and the dimensionless figure of merit (zT) has been evaluated in the temperature range of 100–800 K as a function of chemical potential. The maximum zT values of ∼1.00 for MgNi2S4 and ∼0.98 for MgNi2Se4 are attained near room temperature, indicating its efficient thermoelectric performance. High See beck coefficients in the spin-down channel 180 μV K−1 for MgNi2S4 and 450 μV K−1 for MgNi2Se4 reflect their spin-polarized electronic structures. Additionally, low lattice thermal conductivities derived from phonon-based calculations further enhance their thermoelectric potential. Optical analyses reveal strong absorption, high photoconductivity, and significant dielectric response in the visible to ultraviolet range, making these materials suitable for optoelectronic applications. These results establish both MgNi2S4 and MgNi2Se4 as promising multifunctional candidates for the use in next-generation spintronic, thermoelectric, and optoelectronic devices.
m structure. Energy–volume calculations establish ferromagnetism as the ground state, and phonon dispersion curves obtained via density functional perturbation theory (DFPT) exhibit no imaginary frequencies, confirming dynamic stability. Electronic structure calculations using both GGA and TB-mBJ functionals reveal half-metallic ferromagnetism having total magnetic moments of approximately 4 μB per formula unit predominantly arising from Ni2+ ions. Thermoelectric properties, including Seebeck coefficient, electrical and thermal conductivities, and the dimensionless figure of merit (zT) has been evaluated in the temperature range of 100–800 K as a function of chemical potential. The maximum zT values of ∼1.00 for MgNi2S4 and ∼0.98 for MgNi2Se4 are attained near room temperature, indicating its efficient thermoelectric performance. High See beck coefficients in the spin-down channel 180 μV K−1 for MgNi2S4 and 450 μV K−1 for MgNi2Se4 reflect their spin-polarized electronic structures. Additionally, low lattice thermal conductivities derived from phonon-based calculations further enhance their thermoelectric potential. Optical analyses reveal strong absorption, high photoconductivity, and significant dielectric response in the visible to ultraviolet range, making these materials suitable for optoelectronic applications. These results establish both MgNi2S4 and MgNi2Se4 as promising multifunctional candidates for the use in next-generation spintronic, thermoelectric, and optoelectronic devices.


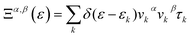 where vkα represent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100
where vkα represent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-k points.
000-k points.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227), comprising a unit cell with 8 Mg, 16 Ni, and 32 S/Se atoms, as shown in Fig. 1. Within the crystal structure, magnesium atoms occupy the tetrahedral 8a Wyckoff positions at (0.125, 0.125, 0.125), nickel atoms reside at the octahedral 16 d sites at (0.5, 0.5, 0.5), and chalcogen atoms (S or Se) are situated at the 32e sites with positional coordinates (0.25, 0.25, 0.25). The cubic symmetry is preserved through careful adjustment of the positional parameter. The energy–volume (E–V) relationships for MgNi2X4 (X = S, Se) spinel compounds have been calculated self-consistently via structural optimization procedures Structural optimization was performed using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, and the resulting total energy as a function of volume was fitted to the Murnaghan equation of state to derive equilibrium structural parameters. The equation employed is as:37
m (No. 227), comprising a unit cell with 8 Mg, 16 Ni, and 32 S/Se atoms, as shown in Fig. 1. Within the crystal structure, magnesium atoms occupy the tetrahedral 8a Wyckoff positions at (0.125, 0.125, 0.125), nickel atoms reside at the octahedral 16 d sites at (0.5, 0.5, 0.5), and chalcogen atoms (S or Se) are situated at the 32e sites with positional coordinates (0.25, 0.25, 0.25). The cubic symmetry is preserved through careful adjustment of the positional parameter. The energy–volume (E–V) relationships for MgNi2X4 (X = S, Se) spinel compounds have been calculated self-consistently via structural optimization procedures Structural optimization was performed using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional, and the resulting total energy as a function of volume was fitted to the Murnaghan equation of state to derive equilibrium structural parameters. The equation employed is as:37  where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus, and
where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus, and  is its pressure derivative. The computed E–V curves Fig. 2a and b for both ferromagnetic (FM) and non-magnetic (NM) phases demonstrate well-optimized structures. Positive energy differences (ΔE = ENM − EFM) confirm that the FM phase is energetically more favorable than the NM one, suggesting the magnetic ground state stability of both MgNi2S4 and MgNi2Se4. Thermodynamic stability is further validated by the negative formation energies calculated using the relation: ΔHf = Etotal (MgNimS/Sen) − (EMg + mENi + nES/Se). The resulting values are ΔHf = −0.815 eV for MgNi2S4 and −0.575 eV for MgNi2Se4, which are consistent with previously reported theoretical data.36 Following the structural and thermodynamic assessment, key parameters such as the equilibrium lattice constant (a0), bulk modulus (B0), and its pressure derivative
is its pressure derivative. The computed E–V curves Fig. 2a and b for both ferromagnetic (FM) and non-magnetic (NM) phases demonstrate well-optimized structures. Positive energy differences (ΔE = ENM − EFM) confirm that the FM phase is energetically more favorable than the NM one, suggesting the magnetic ground state stability of both MgNi2S4 and MgNi2Se4. Thermodynamic stability is further validated by the negative formation energies calculated using the relation: ΔHf = Etotal (MgNimS/Sen) − (EMg + mENi + nES/Se). The resulting values are ΔHf = −0.815 eV for MgNi2S4 and −0.575 eV for MgNi2Se4, which are consistent with previously reported theoretical data.36 Following the structural and thermodynamic assessment, key parameters such as the equilibrium lattice constant (a0), bulk modulus (B0), and its pressure derivative  were extracted from the E(V) curves using the second-order Birch–Murnaghan equation of state. The computed values are reported in Table 1 and show good agreement with earlier DFT theoretical studies.38 Notably, the substitution of sulfur by selenium results in a reduced bulk modulus, attributable to the larger ionic radius of Se, which leads to an expansion in lattice volume and consequently a softer mechanical response. These results collectively confirm that both MgNi2S4 and MgNi2Se4 are structurally, thermodynamically, and magnetically stable, and are thus promising candidates for functional applications.
were extracted from the E(V) curves using the second-order Birch–Murnaghan equation of state. The computed values are reported in Table 1 and show good agreement with earlier DFT theoretical studies.38 Notably, the substitution of sulfur by selenium results in a reduced bulk modulus, attributable to the larger ionic radius of Se, which leads to an expansion in lattice volume and consequently a softer mechanical response. These results collectively confirm that both MgNi2S4 and MgNi2Se4 are structurally, thermodynamically, and magnetically stable, and are thus promising candidates for functional applications.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (No. 227), yields the following irreducible representation of vibrational modes: Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g, where the modes 3Eu, Tg, 2Tu, and Eg exhibit degeneracy. Among these, A1g, Eg, and T2g modes are Raman-active, while T1u modes are infrared-active. The remaining modes (A2u, Eu, and T2u) are classified as silent modes. Although no experimental Raman spectroscopy was conducted in this study, this classification follows group-theoretical selection rules derived from the crystal symmetry. The calculated phonon dispersion curves exhibit no imaginary frequencies throughout the Brillouin zone, affirming the dynamical stability of both compounds. In the low-frequency region (approximately 2–4 THz), the vibrations are primarily governed by magnesium atoms due to their low atomic mass and their wagging and translational motion with surrounding chalcogen atoms. The intermediate-frequency modes (6–8 THz) involve nickel atoms, contributing more complex lattice vibrations through their coupling with both Mg and S/Se atoms. At higher frequencies (11–13 THz), the modes arise predominantly from the stretching vibrations of Ni–S and Ni–Se bonds, which are relatively stiff and energetically strong compared to other atomic interactions. These high-frequency optical phonons are particularly relevant in polar semiconductors, where they mediate long-range electron–phonon interactions via the Fröhlich mechanism, influencing both carrier scattering and lattice thermal conductivity. This has direct consequences for thermoelectric efficiency. Overall, the phonon structure confirms the dynamical robustness of MgNi2S4 and MgNi2Se4 and provides a microscopic foundation for understanding their thermal transport properties and suitability in thermoelectric applications.
m space group (No. 227), yields the following irreducible representation of vibrational modes: Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g, where the modes 3Eu, Tg, 2Tu, and Eg exhibit degeneracy. Among these, A1g, Eg, and T2g modes are Raman-active, while T1u modes are infrared-active. The remaining modes (A2u, Eu, and T2u) are classified as silent modes. Although no experimental Raman spectroscopy was conducted in this study, this classification follows group-theoretical selection rules derived from the crystal symmetry. The calculated phonon dispersion curves exhibit no imaginary frequencies throughout the Brillouin zone, affirming the dynamical stability of both compounds. In the low-frequency region (approximately 2–4 THz), the vibrations are primarily governed by magnesium atoms due to their low atomic mass and their wagging and translational motion with surrounding chalcogen atoms. The intermediate-frequency modes (6–8 THz) involve nickel atoms, contributing more complex lattice vibrations through their coupling with both Mg and S/Se atoms. At higher frequencies (11–13 THz), the modes arise predominantly from the stretching vibrations of Ni–S and Ni–Se bonds, which are relatively stiff and energetically strong compared to other atomic interactions. These high-frequency optical phonons are particularly relevant in polar semiconductors, where they mediate long-range electron–phonon interactions via the Fröhlich mechanism, influencing both carrier scattering and lattice thermal conductivity. This has direct consequences for thermoelectric efficiency. Overall, the phonon structure confirms the dynamical robustness of MgNi2S4 and MgNi2Se4 and provides a microscopic foundation for understanding their thermal transport properties and suitability in thermoelectric applications.
 where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A value of P = 100% confirms complete spin polarization, reinforcing the half-metallic character of these compounds. Furthermore, the half-metallic gap ghmg defined as the energy separation between the highest occupied and lowest unoccupied states in the spin-down channel was computed. This gap is critical for ensuring spin-filtering performance and plays a vital role in stabilizing the half-metallic state, making these materials promising candidates for spintronic switches and magneto-optoelectronic applications.
where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A value of P = 100% confirms complete spin polarization, reinforcing the half-metallic character of these compounds. Furthermore, the half-metallic gap ghmg defined as the energy separation between the highest occupied and lowest unoccupied states in the spin-down channel was computed. This gap is critical for ensuring spin-filtering performance and plays a vital role in stabilizing the half-metallic state, making these materials promising candidates for spintronic switches and magneto-optoelectronic applications.

 determines the material's response to light propagation and polarization, while the imaginary part, ε2(ω),
determines the material's response to light propagation and polarization, while the imaginary part, ε2(ω),  measures its light absorption capability, where higher values indicate stronger absorption.42 The real part of the dielectric function, ε1(ω) (Fig. 6a and b), represents the material's polarization response to an electric field and affects how light propagates through the material. For MgNi2S4, the static dielectric constant at zero photon energy is approximately 43, indicating strong polarizability and dielectric screening at low frequencies. As the photon energy increases, ε1(ω) rapidly decreases and stabilizes between 5 and 10 beyond 5 eV, implying diminished polarization response in the ultraviolet (UV) range. MgNi2Se4 exhibits an even higher static dielectric constant of about 85, nearly twice that of MgNi2S4, likely due to the larger atomic size and polarizability of selenium atoms. Its ε1(ω) follows a similar trend, sharply declining with photon energy and stabilizing around 10 in the high-energy region. This high static dielectric constant implies strong internal electric field screening and potential for enhanced light-matter interactions at low photon energies.The imaginary part ε2(ω), indicative of energy absorption through interband electronic transitions, shows significant peaks near 0.25 eV for both compounds, revealing intense absorption in the infrared region. This peak corresponds to electronic transitions that contribute strongly to light absorption at low photon energies, a property beneficial for infrared sensing and photovoltaic applications. Beyond this region, ε2(ω) oscillates with smaller peaks extending into the visible and UV spectrum, confirming that these materials absorb across a broad energy range, with MgNi2Se4 generally showing stronger absorption than MgNi2S. The optical conductivity (Fig. 6c) complements the dielectric response by quantifying the ability of the materials to conduct electric current under light excitation. Both compounds exhibit negligible optical conductivity below 2 eV, indicating limited interband transitions at very low energies. A steep increase in optical conductivity begins near 2 eV, with a prominent peak around 9.5 eV reaching approximately 6.8 Ω−1 cm−1 for MgNi2S4 and slightly lower values for MgNi2Se4. This peak in the UV region signals strong electronic transitions and efficient electron-photon interaction, making these materials suitable for UV optoelectronic devices, such as photodetectors and UV filters. The absorption coefficient (Fig. 6d) provides a direct measure of how strongly the materials absorb incident photons. Both MgNi2S4 and MgNi2Se4 show minor absorption peaks below 4 eV, indicating some activity in the visible spectrum but relatively weak. Beyond 5 eV, absorption sharply increases and reaches values near 2 × 106 cm−1 at 14 eV, confirming strong absorption in the UV region. Such high absorption coefficients are critical for applications like UV photodetection, photocatalysis, and solar energy harvesting, where efficient photon capture at high energies is required. The refractive index (Fig. 6e), derived from ε1(ω), describes how light bends when entering the material. Both compounds display very high static refractive indices of around 10.5 at zero photon energy, reflecting strong optical density and polarizability. As photon energy rises, the refractive index steadily decreases and stabilizes between 1.5 and 2 in the UV region, indicating less light bending at higher energies. This large variation with energy indicates strong dispersion effects, relevant for optical lensing and waveguiding applications. Lastly, the extinction coefficient (Fig. 6f) quantifies the attenuation or loss of light intensity inside the material due to absorption and scattering. It begins at approximately 4.2 at low photon energies (∼0.5 eV), showing significant attenuation due to strong absorption in the infrared region. The extinction coefficient fluctuates between 1.0 and 2.5 across the 5–14 eV range, corresponding to multiple interband transitions and complex loss mechanisms in the UV region. These values affirm the results from the absorption and conductivity spectra, highlighting considerable optical losses at higher energies that are characteristic of electronic transitions in these materials. Overall, MgNi2S4 and MgNi2Se4 spinels demonstrate pronounced optical activity across a wide energy spectrum from infrared to ultraviolet. Their large static dielectric constants (43 and 85, respectively), high optical conductivity (∼6.8 Ω−1 cm−1 in the UV), strong absorption coefficients (∼2 × 106 cm−1), and significant extinction coefficients emphasize their potential for advanced optoelectronic applications. Such properties make them promising candidates for UV photodetectors, infrared sensors, solar cells, and optical coatings where efficient light absorption, polarization control, and strong electron-photon interactions are essential. The larger dielectric response and absorption in MgNi2Se4 compared to MgNi2S4 also suggest that chemical substitution in the spinel structure can tune optical properties for targeted applications. Values of some important optical parameters are presented in Table 2.
measures its light absorption capability, where higher values indicate stronger absorption.42 The real part of the dielectric function, ε1(ω) (Fig. 6a and b), represents the material's polarization response to an electric field and affects how light propagates through the material. For MgNi2S4, the static dielectric constant at zero photon energy is approximately 43, indicating strong polarizability and dielectric screening at low frequencies. As the photon energy increases, ε1(ω) rapidly decreases and stabilizes between 5 and 10 beyond 5 eV, implying diminished polarization response in the ultraviolet (UV) range. MgNi2Se4 exhibits an even higher static dielectric constant of about 85, nearly twice that of MgNi2S4, likely due to the larger atomic size and polarizability of selenium atoms. Its ε1(ω) follows a similar trend, sharply declining with photon energy and stabilizing around 10 in the high-energy region. This high static dielectric constant implies strong internal electric field screening and potential for enhanced light-matter interactions at low photon energies.The imaginary part ε2(ω), indicative of energy absorption through interband electronic transitions, shows significant peaks near 0.25 eV for both compounds, revealing intense absorption in the infrared region. This peak corresponds to electronic transitions that contribute strongly to light absorption at low photon energies, a property beneficial for infrared sensing and photovoltaic applications. Beyond this region, ε2(ω) oscillates with smaller peaks extending into the visible and UV spectrum, confirming that these materials absorb across a broad energy range, with MgNi2Se4 generally showing stronger absorption than MgNi2S. The optical conductivity (Fig. 6c) complements the dielectric response by quantifying the ability of the materials to conduct electric current under light excitation. Both compounds exhibit negligible optical conductivity below 2 eV, indicating limited interband transitions at very low energies. A steep increase in optical conductivity begins near 2 eV, with a prominent peak around 9.5 eV reaching approximately 6.8 Ω−1 cm−1 for MgNi2S4 and slightly lower values for MgNi2Se4. This peak in the UV region signals strong electronic transitions and efficient electron-photon interaction, making these materials suitable for UV optoelectronic devices, such as photodetectors and UV filters. The absorption coefficient (Fig. 6d) provides a direct measure of how strongly the materials absorb incident photons. Both MgNi2S4 and MgNi2Se4 show minor absorption peaks below 4 eV, indicating some activity in the visible spectrum but relatively weak. Beyond 5 eV, absorption sharply increases and reaches values near 2 × 106 cm−1 at 14 eV, confirming strong absorption in the UV region. Such high absorption coefficients are critical for applications like UV photodetection, photocatalysis, and solar energy harvesting, where efficient photon capture at high energies is required. The refractive index (Fig. 6e), derived from ε1(ω), describes how light bends when entering the material. Both compounds display very high static refractive indices of around 10.5 at zero photon energy, reflecting strong optical density and polarizability. As photon energy rises, the refractive index steadily decreases and stabilizes between 1.5 and 2 in the UV region, indicating less light bending at higher energies. This large variation with energy indicates strong dispersion effects, relevant for optical lensing and waveguiding applications. Lastly, the extinction coefficient (Fig. 6f) quantifies the attenuation or loss of light intensity inside the material due to absorption and scattering. It begins at approximately 4.2 at low photon energies (∼0.5 eV), showing significant attenuation due to strong absorption in the infrared region. The extinction coefficient fluctuates between 1.0 and 2.5 across the 5–14 eV range, corresponding to multiple interband transitions and complex loss mechanisms in the UV region. These values affirm the results from the absorption and conductivity spectra, highlighting considerable optical losses at higher energies that are characteristic of electronic transitions in these materials. Overall, MgNi2S4 and MgNi2Se4 spinels demonstrate pronounced optical activity across a wide energy spectrum from infrared to ultraviolet. Their large static dielectric constants (43 and 85, respectively), high optical conductivity (∼6.8 Ω−1 cm−1 in the UV), strong absorption coefficients (∼2 × 106 cm−1), and significant extinction coefficients emphasize their potential for advanced optoelectronic applications. Such properties make them promising candidates for UV photodetectors, infrared sensors, solar cells, and optical coatings where efficient light absorption, polarization control, and strong electron-photon interactions are essential. The larger dielectric response and absorption in MgNi2Se4 compared to MgNi2S4 also suggest that chemical substitution in the spinel structure can tune optical properties for targeted applications. Values of some important optical parameters are presented in Table 2.
 . Where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (comprising both electronic and lattice contributions), and T is the absolute temperature. Maximizing zT requires high See beck coefficient and electrical conductivity, along with low thermal conductivity. The electron relaxation time (τ), a crucial factor in determining transport coefficients, represents the average time interval between successive scattering events of charge carriers. The constant relaxation time approximation assumes that τ varies slowly with energy on the scale of kBT, the thermal energy. Under this assumption, the thermoelectric coefficients such as the electrical conductivity per unit time (σ/τ), electronic thermal conductivity per unit time (κe/τ), and the power factor per unit time can be conveniently expressed in terms of τ. Due to the unavailability of sufficient computational resources and power to compute the relaxation time (τ) from first principles for our studied system, we followed the same CRTA methodology. In both our study and the cited work, the relaxation time is not explicitly calculated but assumed to be constant typically of the order of 10−15 seconds, the carrier concentration used was 1 × 1020 cm−3, a typical value used for semiconducting thermoelectric materials, as supported by prior DFT-based studies on similar materials. These interdependent parameters were evaluated using Boltzmann transport theory within the rigid band approximation and constant relaxation time (τ) approximation, as implemented in the BoltzTrap code. Thermoelectric properties were calculated using the BoltzTrap code,35 grounded in Boltzmann transport theory while κl was estimated using the Slack model.
. Where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (comprising both electronic and lattice contributions), and T is the absolute temperature. Maximizing zT requires high See beck coefficient and electrical conductivity, along with low thermal conductivity. The electron relaxation time (τ), a crucial factor in determining transport coefficients, represents the average time interval between successive scattering events of charge carriers. The constant relaxation time approximation assumes that τ varies slowly with energy on the scale of kBT, the thermal energy. Under this assumption, the thermoelectric coefficients such as the electrical conductivity per unit time (σ/τ), electronic thermal conductivity per unit time (κe/τ), and the power factor per unit time can be conveniently expressed in terms of τ. Due to the unavailability of sufficient computational resources and power to compute the relaxation time (τ) from first principles for our studied system, we followed the same CRTA methodology. In both our study and the cited work, the relaxation time is not explicitly calculated but assumed to be constant typically of the order of 10−15 seconds, the carrier concentration used was 1 × 1020 cm−3, a typical value used for semiconducting thermoelectric materials, as supported by prior DFT-based studies on similar materials. These interdependent parameters were evaluated using Boltzmann transport theory within the rigid band approximation and constant relaxation time (τ) approximation, as implemented in the BoltzTrap code. Thermoelectric properties were calculated using the BoltzTrap code,35 grounded in Boltzmann transport theory while κl was estimated using the Slack model.
 . These spin-resolved calculations enable a more accurate understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. The variation of thermoelectric coefficients across the 100–800 K temperature range is thoroughly analyzed in the following section.
. These spin-resolved calculations enable a more accurate understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. The variation of thermoelectric coefficients across the 100–800 K temperature range is thoroughly analyzed in the following section.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The calculated elastic constants enable the derivation of various moduli bulk (B), shear (G), and Young's modulus (Y) using well-established relations. The results, detailed in Table 4, reveal that the Young's modulus, which represents the stiffness of the material, is greater than the bulk modulus, which reflects resistance to uniform compression. The shear modulus, indicative of resistance to shape deformation, is lower, suggesting that these materials can undergo shape changes more readily than volumetric changes. The order Y > B > G highlights the high stiffness and flexibility against shear deformation. To further assess the mechanical response, we computed the Kleinman parameter (ζ), which lies within the range 0 ≤ ζ < 1. A lower ζ value indicates stronger resistance to bond angle distortions and bond bending, implying greater rigidity of the crystal framework. Table 4 also presents metrics used to evaluate material ductility. Cauchy's pressure (C12 − C44) is a reliable indicator of ductility, with a positive value signifying ductile behavior. Similarly, Pugh's ratio (B/G), with a threshold of 1.75, distinguishes ductile (>1.75) from brittle (<1.75) materials.49 Poisson's ratio (ν) also supports this classification; values greater than 0.26 denote ductility. The computed values of these parameters collectively affirm the ductile nature of the MgNi2X4 compounds.
m). The calculated elastic constants enable the derivation of various moduli bulk (B), shear (G), and Young's modulus (Y) using well-established relations. The results, detailed in Table 4, reveal that the Young's modulus, which represents the stiffness of the material, is greater than the bulk modulus, which reflects resistance to uniform compression. The shear modulus, indicative of resistance to shape deformation, is lower, suggesting that these materials can undergo shape changes more readily than volumetric changes. The order Y > B > G highlights the high stiffness and flexibility against shear deformation. To further assess the mechanical response, we computed the Kleinman parameter (ζ), which lies within the range 0 ≤ ζ < 1. A lower ζ value indicates stronger resistance to bond angle distortions and bond bending, implying greater rigidity of the crystal framework. Table 4 also presents metrics used to evaluate material ductility. Cauchy's pressure (C12 − C44) is a reliable indicator of ductility, with a positive value signifying ductile behavior. Similarly, Pugh's ratio (B/G), with a threshold of 1.75, distinguishes ductile (>1.75) from brittle (<1.75) materials.49 Poisson's ratio (ν) also supports this classification; values greater than 0.26 denote ductility. The computed values of these parameters collectively affirm the ductile nature of the MgNi2X4 compounds.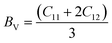
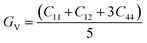


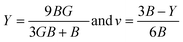
 .50,51 Deviation of either value from unity implies anisotropic behavior, whereas values equal to one suggest isotropy. The results in Table 4 clearly indicate notable anisotropy in these compounds, reflecting directional dependence in their elastic response. Additionally, to gain deeper insight into the anisotropic and elastic characteristics of the studied compounds, we employed the Elate code52 to generate three-dimensional (3D) contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (ν). These 3D visualizations provide a clear depiction of the directional dependence of elastic properties for MgNi2S4 and MgNi2Se4, as presented in Fig. 9 and 10, respectively. It is evident from the plots that all parameters, except linear compressibility, exhibit notable deviations from an ideal spherical shape emphasizing the anisotropic nature of these spinels. Moreover, the degree of anisotropy appears consistent across various crystallographic directions, further confirming the directional variation in their mechanical response.
.50,51 Deviation of either value from unity implies anisotropic behavior, whereas values equal to one suggest isotropy. The results in Table 4 clearly indicate notable anisotropy in these compounds, reflecting directional dependence in their elastic response. Additionally, to gain deeper insight into the anisotropic and elastic characteristics of the studied compounds, we employed the Elate code52 to generate three-dimensional (3D) contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (ν). These 3D visualizations provide a clear depiction of the directional dependence of elastic properties for MgNi2S4 and MgNi2Se4, as presented in Fig. 9 and 10, respectively. It is evident from the plots that all parameters, except linear compressibility, exhibit notable deviations from an ideal spherical shape emphasizing the anisotropic nature of these spinels. Moreover, the degree of anisotropy appears consistent across various crystallographic directions, further confirming the directional variation in their mechanical response.






