Open Access Article
Open Access ArticleTheoretical insight and molecular recognition of fluconazole molecularly imprinted polymers: a combined computational and experimental analysis†
Untung Gunawan *a,
Slamet Ibrahim
*a,
Slamet Ibrahim b,
Atthar Luqman Ivansyah
b,
Atthar Luqman Ivansyah cd and
Sophi Damayanti
cd and
Sophi Damayanti ef
ef
aDepartment of Pharmacy, School of Medicine and Health Sciences, Atma Jaya Catholic University of Indonesia, 14440, Indonesia. E-mail: untung.gunawan@atmajaya.ac.id
bFaculty of Pharmacy, Universitas Jenderal Achmad Yani, Cimahi, 40531, Indonesia
cInstrumentation and Computational Physics Research Group, Department of Physics, Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung, 40132, Indonesia
dMaster Program in Computational Science, Faculty of Mathematics and Natural Science, Institut Teknologi Bandung, 40132, Indonesia
eDepartment of Pharmacochemistry, School of Pharmacy, Institut Teknologi Bandung, 40132, Indonesia
fUniversity Center of Excellence on Artificial Intelligence for Vision, Natural Language Processing & Big Data Analytics (U-CoE Al-VLB), Institut Teknologi Bandung, 40132, Indonesia
First published on 5th June 2025
Abstract
Insufficient surveillance and diagnosis result in a minimum of 150 million cases of serious fungal infections reported annually. The WHO has compiled a list of priority pathogens to encourage research and investment in fungal infections and antifungal resistance in late 2022. Among these, Candida albicans is classified as a critical pathogen. Fluconazole is widely recognized as an effective medication for the treatment and prevention of both mucosal and invasive candidiasis. Molecularly imprinted polymer (MIP) could enhance separation selectivity in fluconazole bioanalysis. The objective of this research is to develop an MIP for fluconazole by analyzing interactions identified in prior research and incorporating established improvements for MIP synthesis that cannot be observed through laboratory experimentation. Based on binding affinity, intermolecular hydrogen bonds, complexation energy, and thermodynamic characteristics, 2-acrylamido-1-ethanesulfonic acid was chosen as the optimal monomer. The HOMO–LUMO investigation revealed the localization of the orbitals from the guest to the host. The FMO study indicated that chloroform was the most suitable solvent for complex formation. The QTAIM, NBO, and NCI-RDG analyses identified the hydrogen bond formed between the H51 atom of the monomer and the N33 atom of fluconazole, determined to be the most significant hydrogen bond in the host–guest interaction. The interaction energy from multi-monomer interaction showed that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ratio is the best ratio in forming a pre-polymerization complex between the template and monomer. Based on the findings of this study, it is anticipated that the computational analysis may be utilized for rational design for the enhancement of prior studies and future laboratory investigations.
6 ratio is the best ratio in forming a pre-polymerization complex between the template and monomer. Based on the findings of this study, it is anticipated that the computational analysis may be utilized for rational design for the enhancement of prior studies and future laboratory investigations.
1 Introduction
Insufficient surveillance and diagnostic invasive fungal infections cause at least 150 million severe fungal infections and a total of 1.5 million deaths annually. Existing reports show the annual incidence rates for aspergillosis, candidiasis, and invasive mucormycosis are estimated to exceed 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 750
000, 750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 10
000, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cases, respectively.1–3 The epidemiology of invasive fungal infections causes a mortality rate of 30–70% in invasive aspergillosis, 40% in invasive candidiasis, and 35–100% in invasive mucormycosis.4 The use of antifungal drugs only demonstrates partial success in improving the prognosis of infected patients, and this is compounded by the rapid evolution of drug resistance among fungal species.5 Due to an increase in critically ill and immunocompromised patients, as well as an increase in fungal infections, there have been changes in the evolution, prognosis, diagnosis, and treatment of fungal diseases lately.6 In late 2022, the World Health Organisation (WHO) published a list of fungal priority pathogens (FPPL) to promote worldwide research in fungal illnesses and antifungal resistance. Three priority groups classify the nineteen species linked to invasive fungal diseases: critical, high, and medium. Four pathogens, Candida auris, Cryptococcus neoformans, Aspergillus fumigatus, and Candida albicans, are considered to be critical fungi.7 C. albicans, a pathogenic fungus, has the ability to invade healthy humans and induce invasive candidiasis or infections of the mucosae. Invasive candidiasis is a severe and sometimes fatal illness characterized by a high death rate. However, the treatment for candidiasis is feasible, and the occurrence of antifungal resistance is generally unusual.8 The Infectious Diseases Society of America (IDSA) recommends using echinocandins, triazole antifungals, flucytosine, and amphotericin B as treatment options for invasive candidiasis.9 The initial treatment of choice for C. albicans is echinocandin, whereas fluconazole is an alternative option for initial treatment. Additionally, fluconazole is employed as a step-down therapy. Although included in the essential medicines list (EML) in 2021, echinocandins remain inaccessible in many countries. Consequently, fluconazole continues to be the preferred choice in these countries.10,11
000 cases, respectively.1–3 The epidemiology of invasive fungal infections causes a mortality rate of 30–70% in invasive aspergillosis, 40% in invasive candidiasis, and 35–100% in invasive mucormycosis.4 The use of antifungal drugs only demonstrates partial success in improving the prognosis of infected patients, and this is compounded by the rapid evolution of drug resistance among fungal species.5 Due to an increase in critically ill and immunocompromised patients, as well as an increase in fungal infections, there have been changes in the evolution, prognosis, diagnosis, and treatment of fungal diseases lately.6 In late 2022, the World Health Organisation (WHO) published a list of fungal priority pathogens (FPPL) to promote worldwide research in fungal illnesses and antifungal resistance. Three priority groups classify the nineteen species linked to invasive fungal diseases: critical, high, and medium. Four pathogens, Candida auris, Cryptococcus neoformans, Aspergillus fumigatus, and Candida albicans, are considered to be critical fungi.7 C. albicans, a pathogenic fungus, has the ability to invade healthy humans and induce invasive candidiasis or infections of the mucosae. Invasive candidiasis is a severe and sometimes fatal illness characterized by a high death rate. However, the treatment for candidiasis is feasible, and the occurrence of antifungal resistance is generally unusual.8 The Infectious Diseases Society of America (IDSA) recommends using echinocandins, triazole antifungals, flucytosine, and amphotericin B as treatment options for invasive candidiasis.9 The initial treatment of choice for C. albicans is echinocandin, whereas fluconazole is an alternative option for initial treatment. Additionally, fluconazole is employed as a step-down therapy. Although included in the essential medicines list (EML) in 2021, echinocandins remain inaccessible in many countries. Consequently, fluconazole continues to be the preferred choice in these countries.10,11
Several techniques have been established for the analysis of fluconazole bioanalysis. Each biological matrix possesses advantages and disadvantages, and the data's clinical interpretation relies highly on the matrix.12,13 Optimizing the sample preparation in biological matrices will improve the recoveries and minimize any interferences, such as endogenous compounds, during the analysis.14 The current techniques employed for the separation of triazole antifungals in biological samples encompass liquid–liquid extraction (LLE), protein precipitation, and solid-phase extraction (SPE).15 The utilization of molecularly imprinted polymer (MIP) has emerged as a separation technique aimed at enhancing the selectivity of analyte separation. MIP refers to artificially synthesized receptors designed to bind to a specific substance selectively. Therefore, they can be considered analogous to the natural antibody–antigen systems.16 Compared to other separation methods, MIP offers several advantages, such as the ability to specifically recognize analyte molecules and a wide range of applications in different fields. As a result, MIPs are useful for various purposes, including sorbents for solid phase extraction and stationary phases in column chromatography.17,18 The widespread use of MIP as a novel approach for preparation methods shows its effectiveness in analyzing compounds in complex matrices while simultaneously requiring relatively small sample quantities.19,20
Nowadays, the utilization of computational methods in this design provides the production of high-affinity polymers through a systematic approach, resulting in significant time and resource savings.21 The use of computational design for MIP is anticipated to become a standard practice in the pre-synthesis stage, enabling the creation of polymers that exhibit enhanced affinity and selectivity towards specific target molecules.22 The computational methodology commonly utilized for the synthesis of MIP involves the application of molecular modeling techniques, such as quantum mechanics (QM), molecular mechanics (MM), or molecular dynamics (MD). The computational expense associated with MM optimization is significantly lower than QM, resulting in a much higher computational speed, which is much faster than QM.23 Nevertheless, this approach lacks to compensate for electron interactions and is incapable of accurately simulating that in chemical reactions, thereby diminishing the accuracy of the calculation.24
Previous studies have demonstrated the application of multi-template MIP for the investigation of triazole antifungals, including voriconazole, itraconazole, and fluconazole. The multi-template MIP facilitates the simultaneous extraction of analytes, which minimizes the effort needed to prepare different MIPs for each analyte individually. However, MIPs utilizing multiple template molecules exhibit several drawbacks that require consideration, such as competition in the MIP's ability to recognize template molecules, which causes lower selectivity and adsorption capacity compared to single templates due to the reduction in binding sites. This is evidenced by the low selectivity of MIP towards fluconazole between multi-template compared to a single-template MIP.25,26 This study aims to develop a MIP for fluconazole by analyzing interactions identified in prior research and incorporating established improvements for MIP synthesis that cannot be observable through laboratory experimentation. This is expected to enhance comprehension of designing a rational MIP design for fluconazole bioanalysis.
2 Methodology
2.1. Materials
2.2. Analysis interaction of fluconazole with the monomer
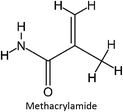
The intermolecular interactions between fluconazole and the monomers were analyzed by performing an association constant (Ka) experiment, which involved fluconazole and four functional monomers: acrylic acid (AA), itaconic acid (IA), acrylamide (ACR), and 2-hydroxyethyl methacrylate (HEMA). A continuous increment of functional monomers was added to the fluconazole solution in acetonitrile, initially at a concentration of 0.025 mM, until a 20-fold excess was reached. Absorbance measurements were taken for each increase in the functional monomer concentration at the maximum wavelength of fluconazole (260 nm). A graph was generated to illustrate the correlation between the change in absorbance (Δabsorbance) and the concentration of the functional monomer. This graph was subsequently used to determine the association constant (Ka) via the Benesi–Hildebrand equation. The Ka value obtained experimentally was compared to the Ka value derived from the mathematical calculations presented in prior research. To ensure reproducibility and reliability, the study was replicated three times. After the laboratory study, fluconazole–monomer complexes were analyzed using Discovery Studio Visualizer software to investigate the intermolecular interactions formed in the prepolymerization complex solution.27
 | (1) |
2.3. Computational investigations to enhance the performance of MIP fluconazole
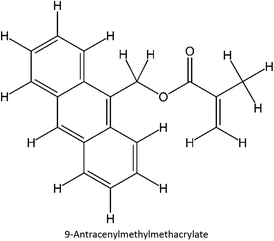
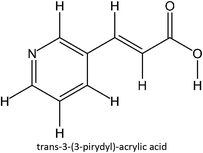
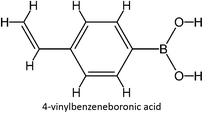
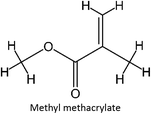
The design for MIP fluconazole enhancement was carried out computationally by improving the theoretical level calculation, enlarging the number of monomers used in the interaction, and increasing the method used associated with interactions, which is expected to offer further understanding of establishing a rational MIP design for fluconazole bioanalysis. MarvinSketch was utilized for illustrating the structures of 39 functional monomers as shown in Table 1. Additionally, we applied a data-driven approach to group the monomers based on their acid–base properties. Specifically, monomers 1–8 were classified as acidic, monomers 9–24 as neutral, and monomers 25–39 as basic. This clustering strategy enabled a more systematic investigation of the interactions between fluconazole and the monomers, facilitating the identification of key characteristics that influence rational MIP design. The method employed molecular recognition as the host–guest interaction. Fluconazole serves as the host, whereas monomers act as guest molecules. Enhancements were implemented in the calculation methodology to achieve conditions that closely approximate experimental results by transitioning from HF 3-21G to DFT B3LYP/6-311G++(d,p) level theory equipped with the DFT-D3 dispersion correction method. The 3D structure of fluconazole and monomers was built using Avogadro28 followed by the optimization geometry of all initial structures using Gaussian.29 Structural parameters are assessed to verify the appropriateness of the computational approaches.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio between the host and guest was maintained throughout the simulations. Post-docking analysis was conducted to examine the complexes generated from the simulations. This analysis focused on evaluating the structures formed between fluconazole and the monomers, assessing the binding affinity, and analyzing the intermolecular interactions between fluconazole and the monomers.
1 mole ratio between the host and guest was maintained throughout the simulations. Post-docking analysis was conducted to examine the complexes generated from the simulations. This analysis focused on evaluating the structures formed between fluconazole and the monomers, assessing the binding affinity, and analyzing the intermolecular interactions between fluconazole and the monomers.3 Results and discussion
3.1. Analysis interaction of complex
The choice of functional monomers is a critical factor influencing the selectivity and performance of molecularly imprinted polymers (MIPs). The functional groups of the monomers interact with the template molecule during the pre-polymerization stage, forming complexes that dictate the MIP's characteristics. These interactions significantly impact the final properties of the MIP, including its binding capacity and selectivity for the target molecule. The stronger the interaction between the template and the monomer, the more pronounced the MIP's bonding capacity and selectivity.34 In this study, the strength of the interaction between fluconazole, as the template molecule, and the selected monomers was assessed using the UV spectrophotometry method to determine the association constant (Ka). The association constant is determined by evaluating the slope and intercept values through the Benesi–Hildebrand equation by plotting a graph of 1/[monomer] [M−1] vs. 1/Δabsorbance.35 The Ka value exhibits a broad spectrum; it is below 25 M−1 for weak intermolecular interactions and exceeds 100 M−1 for strong intermolecular interactions.36,37 The results reveal that Ka values obtained with the complex formed between fluconazole and four monomers above 100 M−1, demonstrate a strong interaction between the template and the monomer.The interaction of the complex generated during UV titration was examined using computational analysis. The complex that formed through molecular docking between fluconazole and each monomer was observed. The findings in Fig. 1 demonstrate that the intermolecular interactions within the complex formed by the template and monomer comprise hydrogen bonds, hydrophobic interactions, and halogen bonds. Intermolecular hydrogen bond interaction that formed between the template–monomer complex plays an essential role in enhancing the affinity of MIP, particularly for low molecular weight organic molecules in aprotic solvents38 which is related to the UV titration study.
 | ||
| Fig. 1 Intermolecular interaction between FLU and monomer, green: hydrogen bond, cyan: halogen bond, pink: hydrophobic bond. | ||
The computational method can be employed to assess hydrogen bond interactions between the template and monomer.39 The Ka value acquired from the experiment was compared with the Ka value determined from the computational analysis utilized in prior research which included computational analysis utilizing the HF-321 G method, focusing on the assessment of geometry optimization and complex frequencies. A universally applicable thermodynamic relationship was established for the complexation constant in a dilute solution. The relationship is founded on a thermodynamic concept of the complexation equilibrium.40 The free Gibbs energy of the complex, obtained from the frequency calculation of the optimal structure, can be utilized to determine the K value, which serves as a benchmark for the Ka value in laboratory experiments. The results in Fig. 2 indicate a difference between the Ka value derived from the UV titration experiment and the K value obtained from the computational calculation. While computational methods provide valuable theoretical insights into host–guest interactions, it is important to acknowledge that experimental data can be influenced by various factors such as sample preparation, solvent conditions, and instrumental limitations. These factors can introduce uncertainties that may not be captured by the computational models. Therefore, both sources of error, computational and experimental must be considered.
 | ||
| Fig. 2 UV spectrum of FLU-monomer complex (top), association constant from experiment and computational study (bot). | ||
Among the four monomers investigated, acrylic acid was the only monomer that demonstrated a close correlation between the Ka and K values, indicating a strong interaction between fluconazole and this monomer. Acrylic acid was identified as the optimal monomer due to its higher yield compared to the other monomers, a finding consistent with previous study.26 However, the discrepancy between the Ka and K values can be attributed to several factors inherent in the computational and experimental methodologies used. Firstly, the computational calculations were performed exclusively under vacuum conditions, which do not accurately reflect the actual experimental conditions. The UV titration experiments were conducted in acetonitrile, a solvent that can significantly influence the intermolecular interactions between the fluconazole (FLU) template and the monomers. The solvent environment plays a critical role in modulating the binding affinity by affecting the solvation of the molecules and their interaction dynamics. Computational models that do not incorporate solvent effects may overlook these essential interactions, leading to discrepancies between the theoretical and experimental results. Furthermore, the computational approach used in this study relied on the HF 3-21G method, which, while widely utilized for investigating the binding energies of monomer–template complexes, has limitations. Specifically, the HF 3-21G method does not adequately account for dispersion interactions, which are crucial for accurately modeling non-covalent interactions such as hydrogen bonding, van der Waals forces, and hydrophobic interactions.41 Dispersion interactions are particularly significant in weak binding systems like host–guest complexes, where these forces play a critical role in stabilizing the complex. The lack of proper treatment of dispersion forces can therefore result in an incomplete or inaccurate representation of the binding energy.
To address these limitations and improve the accuracy of our MIP design, it is essential to employ a more advanced level of theory that incorporates explicit solvation effects and better treatment of dispersion interactions. Methods such as Density Functional Theory (DFT) with dispersion corrections (e.g., DFT-D3) would provide a more accurate description of the intermolecular interactions in solvated environments. Additionally, molecular dynamics simulations could be used to capture the flexibility of the system and the solvent's influence on the host–guest interactions, thus providing a more reliable and comprehensive prediction of the binding behavior. By refining our computational approach to include these advanced methods, we aim to improve the design of the MIP, ensuring that the computational predictions are better aligned with experimental results and enhancing the overall performance of the MIP in bioanalytical applications.
3.2. Computational investigations to enhance performance of MIP fluconazole
With the limitations of the previous level of theory used, computational calculations can be developed with better methods and further analysis to be able to determine the type of intermolecular interactions that occur. The first improvement was carried out by improving the theoretical level calculation. The B3LYP/6-311G method was used because extensively employed to determine the optimal functional monomer for constructing highly selective MIP by computing reaction energy.42–44 Numerous research studies on host–guest interactions have examined this level theory because of its effectiveness in investigating second-period atoms. In addition, the computational cost is acceptable while maintaining high accuracy.45,46 The diffuse (++) and polarization (d,p) basis functions were added in order to enhance the computation method. Diffusion and polarization functions are essential in identifying non-covalent interactions that include hydrogen bonds, which play an essential part in the systematic design of MIPs.47 Additionally, the DFT D3 correction was established to enhance the accuracy of our calculations by including intermolecular interactions in the calculation.48,49 The structural parameter calculation was conducted by comparing the experimental crystal structure50 and the optimized fluconazole structure from this method. No significant differences were observed when comparing the experimental results with the computational simulation of geometric parameters (Table 2). Thus, the theoretical levels can be utilized to examine the interactions between the host and guest that involve fluconazole as template molecules and functional monomers.| Geometric parameter | Experimental | Computational | Difference (%) |
|---|---|---|---|
| Distance F11–C5 | 1.356 | 1.351 | 0.33 |
| Distance F10–C1 | 1.348 | 1.350 | 0.15 |
| Distance O13–C12 | 1.408 | 1.421 | 0.92 |
| Distance N27–N32 | 1.361 | 1.362 | 0.05 |
| Distance N27–C18 | 1.459 | 1.451 | 0.56 |
| Distance (N27–C28) | 1.340 | 1.352 | 0.90 |
| Distance N32–C29 | 1.321 | 1.323 | 0.15 |
| Distance N33–C28 | 1.327 | 1.321 | 0.45 |
| Distance N33–C29 | 1.350 | 1.362 | 0.89 |
| Distance N21–N34 | 1.358 | 1.358 | 0.02 |
| Distance C12–C4 | 1.528 | 1.534 | 0.39 |
| Distance C4–C5 | 1.389 | 1.400 | 0.79 |
| Angle N32–N27–C18 | 120.7 | 120.9 | 0.14 |
| Angle C18–N27–C28 | 129.6 | 129.4 | 0.12 |
| Angle N27–N32–C29 | 102.3 | 102.4 | 0.05 |
| Angle C28–N33–C29 | 103.0 | 102.9 | 0.15 |
| Angle C12–C4–C5 | 122.2 | 120.5 | 1.43 |
| Angle F11–C5–C4 | 119.5 | 120.1 | 0.53 |
| Angle N27–C28–N33 | 110.0 | 110.3 | 0.23 |
| Angle N32–C29–N33 | 115.0 | 114.9 | 0.02 |
The molecular docking simulations generated a total of 39 complex molecules. The binding energies of each complex were negative, as shown in Fig. 3. A negative binding affinity signifies that the complex is bonded spontaneously without requiring energy consumption. Lower binding energy values resulted in a more stable and stronger interaction between fluconazole and functional monomers.53 The nature of intermolecular interactions within the complex was investigated. In the MIP synthesis, two main kinds of interactions are employed: covalent and non-covalent. The non-covalent method, which encompasses hydrogen bonds, dipole–dipole interactions, electrostatic interactions, and van der Waals bonds, is preferred due to its practical synthesis procedure, easy template removal, versatility in binding targets by monomers, and the potential to use a wide range of monomers.54 A summary of the intermolecular interactions of all complexes is provided in Table S1 ESI.† The monomer that is capable of establishing hydrogen bonds with fluconazole was favored. Due to low-accuracy docking simulations, it is necessary to compare the obtained binding energy with the alternative method to determine the most stable conformation.55 The coordinate input for further geometry optimization calculations was established from the conformation with the lowest binding energy obtained by molecular docking simulation.
| ΔEcomplex = Ecomplex − (Efluconazole + Emonomer) | (2) |
Among several implicit solvation models, SMD model has gained popularity for computing condensed phase properties and has been employed in prior host–guest studies.56–58
Fig. 4 shows that all complexes had significantly negative energy values in their ΔEcomplex profiles, implying an energy-driven process. The system's stability increases with a decrease in the value of ΔEcomplex.59 The ΔEcomplex value was found to be minimal under vacuum conditions, and the ΔEcomplex value changed under solvated conditions, indicating that the solvent influences the intermolecular interactions within the complex. Intermolecular interactions are exclusively observed between the host and guest molecules in a vacuum condition. Nevertheless, under solvated conditions, the possibility for interaction expands to include host, guest, and solvent molecules. The complex molecule demonstrates a remarkable interaction with the solvent, therefore resulting in a modification of the intermolecular hydrogen bonds.60,61 The basic properties of the solvent are crucial to guarantee the stability of the complexation process. The solvating capacity of the solvent has a considerable impact on the selectivity of complexation and the stability of the complexes. This can lead to significant changes in the binding characteristics of the template molecule.62
In addition to having a strong interaction with the template, the monomer must spontaneously bind to the template. Thermodynamic parameters are the most suitable for determining whether a process occurs spontaneously. The thermodynamic parameters were represented in terms of Gibbs free energy (ΔG), enthalpy (ΔH), and entropy (ΔS). The optimal compound from previous research was calculated for its thermodynamics in vacuum and dissolved conditions, both at a temperature of 298.15 K and a pressure of 1 atm. The utilization of the following calculation determined the parameters:
| ΔGcomplex = Gcomplex − (Gfluconazole + Gmonomer) | (3) |
| ΔHcomplex = Hcomplex − (Hfluconazole + Hmonomer) | (4) |
| ΔScomplex = Scomplex − (Sfluconazole + Smonomer) | (5) |
The complexation process will proceed spontaneously if the Gibbs free energy is negative. The result demonstrated that only a limited number of monomers had a negative ΔGcomplex, suggesting that not all monomers possess the ability to bind spontaneously with the fluconazole as a template molecule. Compatibility between the template and functional monomer is essential for their interaction. The acid functional monomer exhibits a stronger interaction with the base template molecule, and conversely, the base template compound also shows a stronger interaction with the acid functional monomer.63
Table S2 ESI† provides a comprehensive overview of all complex thermodynamic parameters (ΔH, ΔS, and ΔG). The results indicate that an exothermic process characterizes the formation of all complexes in both vacuum and solvents and is primarily influenced by changes in enthalpy. The molecular interaction between the monomers and the template is likely responsible for the negative value of this enthalpy.64 A negative change in entropy (ΔS < 0) suggests that the formation of all complexes was not favored under both vacuum and solvated conditions. If a reaction is exothermic and the entropy is positive (indicating increased disorder), the change in free energy will always be negative, resulting in a spontaneous reaction.59 The selection of the 39 monomers used in our study was based on those commonly employed in MIP synthesis. Fluconazole, being a weakly basic triazole antifungal compound, is theoretically expected to interact most strongly with basic monomers compared to neutral or acidic monomers. As a result, we prioritized the study of acidic monomers (1–8), followed by neutral monomers (9–24), and finally, basic monomers (25–39). Based on binding energy docking, hydrogen bond formation in intermolecular interaction, complexation energy, and thermodynamic parameters, 2-acrylamido-1-ethanesulfonic acid (monomer 7) was the optimal monomer and was selected for further study.
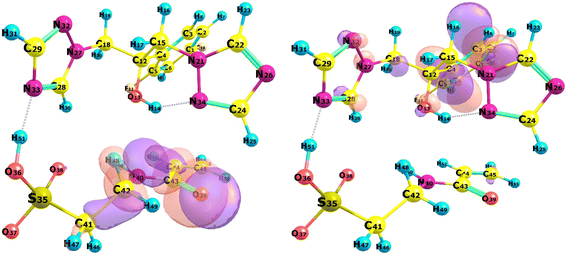
The orbital distribution that defines the HOMO–LUMO transition is illustrated in Fig. 5. LUMO is mainly located in the host molecule; meanwhile, the HOMO is primarily located in the guest molecule suggesting fluconazole is more electrophilic than monomer 7. Complex 7's HOMO and LUMO orbitals were found to be localized from the guest to the host, as indicated by the observed result, which induced the charge transfer from monomer 7 to fluconazole.59 Further explanation of complex 7 charge transfer was identified through natural population analysis (NPA). Both fluconazole and monomer 7 natural charge before interactions were zero (Table 3). When monomer 7 docked with fluconazole as the host, the overall natural charge changed. Fluconazole's total natural charge turns positive, whereas monomer 7 acquires a negative charge. The highest charge transfer was exhibited in a vacuum, with chloroform showing the second highest in solvated conditions. The complex 7 charge transfer was confirmed using structure parameterization, which involved comparing the structure of the complex in both vacuum and solvated conditions. An investigation was carried out between the intermolecular interaction of the host and guest molecule, specifically the bonding between atoms N33 in fluconazole and H51 in monomer 7. The bond length between N33–H51 in vacuum and solvated environment is detailed in Table 3. The most minimal shift existed in chloroform, which exhibited a correlation with the charge transfer investigation.
| Conditions | Total NPA | N33–H51 bond | ||
|---|---|---|---|---|
| Fluconazole | Monomer 7 | Bond length (Å) | Difference (%) | |
| Vacuum | 0.0837 | −0.0837 | 1.630 | — |
| Acetone | 0.1197 | −0.1197 | 1.516 | 6.96 |
| Acetonitrile | 0.1257 | −0.1257 | 1.499 | 8.00 |
| Chloroform | 0.1108 | −0.1108 | 1.542 | 5.38 |
| Dichloromethane | 0.1231 | −0.1231 | 1.500 | 7.97 |
| DMSO | 0.1206 | −0.1206 | 1.514 | 7.13 |
The FMO parameters were analyzed to further examine the complex 7 structure's stability. The parameters that were assessed included: energy gap (Eg), ionization potential (IP), electron affinity (EA), hardness (η), softness (S), electrophilicity index (ω), stabilization energy (SE), chemical potential (µ), and electronegativity (X). The HOMO–LUMO energy derivation was used to derive all the parameters.70
| Eg = ELUMO − EHOMO | (6) |
| IP = −EHOMO | (7) |
| EA = −ELUMO | (8) |
| η = (ELUMO − EHOMO)/2 | (9) |
| S = 1/2η | (10) |
| ω = µ2/2η | (11) |
| SE = −µ2/2η | (12) |
| µ = 1/2(EHOMO + ELUMO) | (13) |
| X = (IP + EA)/2 | (14) |
The energy gap between the HOMO and the LUMO can be utilized to figure out the molecule's kinetic stability. A smaller gap corresponds to lower chemical stability, higher molecular reactivity, and weakened orbital interactions between host and guest molecules since it takes smaller energy to move an electron from HOMO to LUMO conditions.71 The quantum chemical properties of complex 7 are presented in Table 4, while all the FMO parameters for all 39 complexes are provided in Table S3 ESI.† Chloroform was determined to be the best solvent compared to the others for the formation of complexes between fluconazole as the host and monomer 7 as the guest molecule, based on the computation of the FMO parameters. Chloroform is a widely utilized solvent in MIP synthesis. During polymerization, it works as a dispersion medium and pore-forming agent. Chloroform is a polar aprotic solvent that is regularly used in non-covalent imprinting techniques due to its outstanding ability to provide substantial imprinting performance. During polymerization, it acts as a dispersion medium and a pore-forming agent.72,73 Chloroform as the optimum solvent corresponds with the prior charge transfer studies and structural parameterization. The interaction mechanisms in complex 7 will be examined in more detail.
| Conditions | Eg | IP | EA | η | S | ω | SE | µ | X |
|---|---|---|---|---|---|---|---|---|---|
| Vacuum | 5.728 | 7.332 | 1.604 | 2.864 | 0.175 | 3.485 | −3.485 | −4.468 | 4.468 |
| Acetone | 5.814 | 7.074 | 1.260 | 2.907 | 0.172 | 2.987 | −2.987 | −4.167 | 4.167 |
| Acetonitrile | 5.794 | 7.064 | 1.265 | 2.897 | 0.173 | 2.996 | −2.996 | −4.167 | 4.167 |
| Chloroform | 5.876 | 7.141 | 1.269 | 2.938 | 0.170 | 3.006 | −3.006 | −4.203 | 4.203 |
| Dichloromethane | 5.814 | 7.070 | 1.256 | 2.907 | 0.172 | 2.981 | −2.981 | −4.163 | 4.163 |
| DMSO | 5.807 | 7.051 | 1.245 | 2.903 | 0.172 | 2.963 | −2.963 | −4.148 | 4.148 |
| ∇2ρ = λ1 + λ2 + λ3 | (15) |
| HBCP = GBCP + VBCP | (16) |
In accordance with the AIM theory, the properties of bonds, specifically hydrogen bonds is validated by: (a) hydrogen bonds are confirmed by the existence of BCP between the acceptor and the donor groups, (b) at the BCP point, the value of ρ(r) must be minimal, falling within the interval of 0.0020 to 0.0400 a.u., (c) the value of the ∇2ρ(r) must be a positive number within the range of 0.0240 to 0.1390 a.u.75 Furthermore, the interaction characteristics were determined based on the ∇2ρ, the HBCP parameter, and were classified into three distinct categories according to Rozas et al.76,77 (i) weak hydrogen bonds and primarily electrostatic interactions are indicated by both the positive values of ∇2ρ and HBCP, (ii) the presence of strong hydrogen bonds with a covalent character is indicated by both negative ∇2ρ and HBCP values, (iii) moderate hydrogen bonds with partial covalent characteristics are recognized when ∇2ρ is positive while HBCP is negative. The interaction strength may also be classified using the parameter |V/G|. Weak interaction is defined as |V/G| value below 1, whereas moderate interaction is identified as an |V/G| ranging from 1 to 2. The strong interaction is present when the |V/G| value is more than 2.78
Table S4 ESI† reveals the topological properties of complex 7 in both vacuum and solvated states. Ten intermolecular BCPs exist between fluconazole and monomer 7. The hydrogen bonds in system 9, formed between the H51 atom from monomer 7 and the N33 atom from fluconazole, were determined to be moderate hydrogen bonds, characterized by a positive ∇2ρ (0.0983) and a negative HBCP (−0.0176). Nine others intermolecular BCPs exhibited weak hydrogen bonds, as indicated by a negative value for ∇2ρ and HBCP. Furthermore, the bond between H51 and N33 in system 9 exhibited a moderate interaction with a |V/G| value of 1.4171, whereas the other BCPs displayed a weak interaction with a |V/G| value below 1. The presence of a reliable hydrogen bond between the hydrogen atom in monomer 7 and the nitrogen atom in fluconazole is responsible for a moderate interaction in system 9. Further QTAIM analysis will be conducted on the effect of solvated conditions utilizing system 9. The vacuum and all solvated conditions exhibited positive ∇2ρ and negative HBCP values. Moderate covalent hydrogen bonds were consistently detected throughout all conditions, with the difference in the ratio of |V/G| between solvated and vacuum conditions. The enhancement of the |V/G| ratio in the solvated state indicated a stronger interaction. Chloroform outperformed other solvents with the highest |V/G| ratio (1.6461). Chloroform as a solvent in the complex formation will enhance the hydrogen bonds in complex 7. The BCP of complex 7 in vacuum and chloroform is illustrated in Fig. 6, while the full BCP of complex 7 is provided in Fig. S1 ESI.†
The QTAIM study shows that systems 2 (O39–H25) and 4 (C43–N34) only exhibit BCP in vacuum conditions. In contrast, the BCP of systems 5 (C44–N34) and 6 (H48–N33) is exclusively observable in solvated states. Under vacuum situations, intermolecular interactions exclusively exist between fluconazole as host and monomer 7 as guest molecules. However, an interaction between the molecules and the solvent is potentially possible under solvated conditions. Interactions of complex molecules with the solvent can strengthen or weaken intermolecular hydrogen bonds.
 | (17) |
A larger E(2) value indicated stronger and more persistent donor–acceptor orbital connections that increased the interactions between host and guest molecules.81 The population trends and distribution of interaction types are presented in Table S5 ESI.† This table summarizes and simplifies the data gathered, specifically focusing on the complex 7 intermolecular interactions under both vacuum and solvated conditions. Complex 7 exhibited ten intermolecular interactions according to its BCP. Compared to vacuum circumstances, the overall E(2) value significantly rises in solvated conditions. The solvents influence intermolecular interactions between the host and guest molecule. Vacuum conditions restrict interactions with host–guest molecules, leading to a decreased stabilization energy compared to the solvated conditions. In contrast to other solvents, chloroform exhibited the greatest total E(2) value, which aligns with prior studies. System 9 (H51–N33) provides the largest contribution to the total E(2) value in complex 7, confirming that a moderate hydrogen bond was formed between fluconazole and monomer 7 in the QTAIM analysis. Based on the E(2) value in system 9, the hydrogen bond between the lone pair (LP) as donors in the N33 atom and the LP* orbital as acceptors in the H51 atom was the most energetic and potential interaction in the formation of intermolecular hydrogen bonds in complex 7.
 | (18) |
By examining the RDG isosurface of complex 7, we can observe that there is a noticeable decrease in the population of strong interaction in chloroform compared to vacuum conditions, especially for bonding between H51–N3. The RDG isosurface in chloroform is missing the blue area (shown by the orange circle in vacuum), which validates the effect of solvated conditions in host–guest interaction in complex 7. Scatter plots of complex 7 later supported this conclusion in the vacuum and chloroform conditions, which were the best solvents in the prior investigation. In contrast to chloroform, the vacuum condition demonstrated a decreased sign(λ2)ρ value, which signifies the existence of a strong interaction (intermolecular hydrogen bond) within the complex denoted by the yellow circle.83 The lack of this specific region in chloroform and other solvated conditions of complex 7 suggests that the solvent will affect the intramolecular hydrogen bonds between fluconazole as the host and monomer 7 as the guest in the complex. This finding is consistent with the results of QTAIM and NBO investigations.
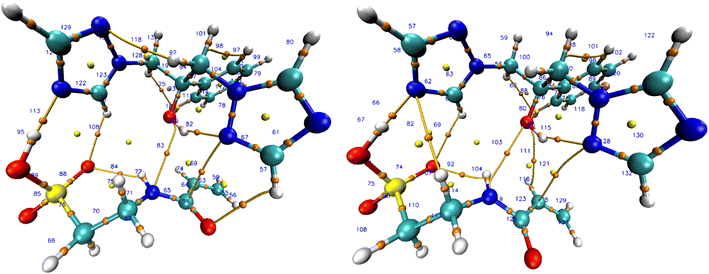
Fluconazole was docked with one to eight molecules of the monomer, based on the maximum number of hydrogen bonds fluconazole can potentially form, consisting of one hydrogen bond donor and up to seven hydrogen bond acceptors. As shown in Fig. 8, the optimization energy of the complex decreased with the increasing number of 2-acrylamido-1-ethanesulfonic acid molecules docked to fluconazole. Larger systems tend to exhibit more degrees of freedom, enabling a broader exploration of the potential energy landscape and typically resulting in lower energy values. The interaction energy analysis revealed that the lowest Einter value occurred at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ratio, which was determined to be the optimal ratio for forming the pre-polymerization complex between fluconazole and 2-acrylamido-1-ethanesulfonic acid. This ratio can be considered for future template–monomer stoichiometry in MIP synthesis.
6 ratio, which was determined to be the optimal ratio for forming the pre-polymerization complex between fluconazole and 2-acrylamido-1-ethanesulfonic acid. This ratio can be considered for future template–monomer stoichiometry in MIP synthesis.
4 Conclusions
This work enhances the computational method of MIP design for fluconazole bioanalysis based on prior studies. The analysis of fluconazole's interaction with the monomer revealed that fluconazole exhibits a robust interaction with AA, IA, ACR, and HEMA, characterized by a high Ka value. The Ka value obtained from the UV titration experiment was compared with the K value generated through computational calculations. Acrylic acid demonstrated a strong correlation between Ka and K values, establishing it as the optimum monomer, providing higher synthesis yield than the other monomers from the prior study, suggesting that computational analysis can assist in the design of MIP. The design of MIP fluconazole was enhanced through computational methods by refining theoretical calculations, increasing the number of interacting monomers, and improving the methodologies associated with these interactions, which is anticipated to provide deeper insights into the rational design of MIP for fluconazole bioanalysis.The geometric parameters generated from the structural parameterization indicate that the DFT calculation using B3LYP/6-311G++(d,p) level theory and DFT-D3 dispersion was suitable for the investigation. The method evaluated the host–guest interactions of fluconazole and 39 monomers. The negative binding affinity observed in all complexes resulting from molecular docking indicates the favorable complex formation between the template and the monomer molecule. All complexes had a significantly negative value for ΔEcomplex, with minimal value observed under vacuum conditions. The thermodynamic study revealed that only a few monomers can spontaneously bind with fluconazole, as a negative ΔGcomplex shown. The thermodynamic study revealed that only a few monomers can spontaneously bind with fluconazole, as a negative ΔGcomplex shows 2-acrylamido-1-ethanesulfonic acid (monomer 7) was chosen as a optimal monomer. The stability of complex formation in various solvents was observed through the FMO study, which indicated that chloroform was the optimal solvent for the formation of complexes between fluconazole and monomer 7, surpassing the other solvents.
The QTAIM study revealed the presence of ten intermolecular BCPs between fluconazole and monomer 7. The hydrogen bonds in system 9, generated from the H51 atom from monomer 7 and the N33 atom from fluconazole, were found to be the strongest bond as revealed in the NBO study by the largest E(2) value. Hydrogen bonds, van der Waals forces, and hydrophobic interactions between guest and host molecules dominated the 2D scatter plots and RDG isosurface with chloroform as the optimal solvent. The interaction energy from multi-monomer interaction showed that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ratio is the best ratio in forming a pre-polymerization complex between fluconazole and 2-acrylamido-1-ethanesulfonic acid. Based on the results obtained from this investigation and the confirmation and validation of the outstanding stability exhibited by complex 7, the computational study provides an enhancement of prior studies and gives insight for further laboratory investigations.
6 ratio is the best ratio in forming a pre-polymerization complex between fluconazole and 2-acrylamido-1-ethanesulfonic acid. Based on the results obtained from this investigation and the confirmation and validation of the outstanding stability exhibited by complex 7, the computational study provides an enhancement of prior studies and gives insight for further laboratory investigations.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Untung Gunawan: Data curation, investigation, methodology, visualization, writing – original draft. Slamet Ibrahim: Supervision, writing – review & editing. Atthar Luqman Ivansyah: Resources, software, supervision, writing – review & editing. Sophi Damayanti: Conceptualization, supervision, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.Acknowledgements
This work was supported by Center for Higher Education Fund, Ministry of Education, Culture, Research, and Technology of the Republic of Indonesia and Indonesia Endowment Fund for Education (LPDP) from the Ministry of Finance of the Republic of Indonesia.References
- F. Bongomin, S. Gago, R. O. Oladele and D. W. Denning, J. Fungi, 2017, 3, 57 CrossRef PubMed.
- K. Kainz, M. A. Bauer, F. Madeo and D. Carmona-Gutierrez, Microb. Cell, 2020, 7, 143–145 CrossRef PubMed.
- L. Chen, E. H. J. Krekels, P. E. Verweij, J. B. Buil, C. A. J. Knibbe and R. J. M. Brüggemann, Drugs, 2020, 80, 671–695 CrossRef CAS PubMed.
- C. Firacative, Mem. Inst. Oswaldo Cruz, 2020, 115, 1–9 Search PubMed.
- J. T. Loh and K. P. Lam, Adv. Drug Delivery Rev., 2023, 196, 114775 CrossRef CAS PubMed.
- C. P. Eades and D. P. H. Armstrong-James, Med. Mycol., 2019, 57, S307–S317 CrossRef CAS PubMed.
- WHO Fungal Priority Pathogens List to Guide Research, Development and Public Health Action, WHO, 2022, vol. 43 Search PubMed.
- S. P. B. Tamo, Infect. Dis. Clin. Microbiol., 2020, 2, 91–102 Search PubMed.
- P. G. Pappas, C. A. Kauffman, D. R. Andes, C. J. Clancy, K. A. Marr, L. Ostrosky-Zeichner, A. C. Reboli, M. G. Schuster, J. A. Vazquez, T. J. Walsh, T. E. Zaoutis and J. D. Sobel, Clin. Infect. Dis., 2016, 62, e1–e50 CrossRef PubMed.
- S. Pathadka, V. K. C. Yan, C. F. Neoh, D. Al-Badriyeh, D. C. M. Kong, M. A. Slavin, B. J. Cowling, I. F. N. Hung, I. C. K. Wong and E. W. Chan, Drugs, 2022, 82, 1193–1205 CrossRef CAS PubMed.
- N. Barantsevich and E. Barantsevich, Antibiotics, 2022, 11, 718 CrossRef CAS PubMed.
- M. A. Acquavia, L. Foti, R. Pascale, A. Nicolò, V. Brancaleone, T. R. I. Cataldi, G. Martelli, L. Scrano and G. Bianco, Talanta, 2021, 224, 121862 CrossRef CAS PubMed.
- G. Wong, A. Brinkman, R. J. Benefield, M. Carlier, J. J. De Waele, N. El Helali, O. Frey, S. Harbarth, A. Huttner, B. McWhinney, B. Misset, F. Pea, J. Preisenberger, M. S. Roberts, T. A. Robertson, A. Roehr, F. B. Sime, F. S. Taccone, J. P. J. Ungerer, J. Lipman and J. A. Roberts, J. Antimicrob. Chemother., 2014, 69, 1416–1423 CrossRef CAS PubMed.
- L. Xia, J. Yang, R. Su, W. Zhou, Y. Zhang, Y. Zhong, S. Huang, Y. Chen and G. Li, Anal. Chem., 2020, 92, 34–48 CrossRef CAS PubMed.
- U. Gunawan, S. Ibrahim, A. L. Ivansyah and S. Damayanti, Pharmacia, 2023, 70, 1265–1281 CrossRef CAS.
- J. J. Belbruno, Chem. Rev., 2019, 119, 94–119 CrossRef CAS PubMed.
- W. J. Cheong, S. H. Yang and F. Ali, J. Sep. Sci., 2013, 36, 609–628 CrossRef CAS PubMed.
- M. Arabi, A. Ostovan, A. R. Bagheri, X. Guo, L. Wang, J. Li, X. Wang, B. Li and L. Chen, TrAC, Trends Anal. Chem., 2020, 128, 115923 CrossRef CAS.
- M. Szultka, R. Krzeminski, M. Jackowski and B. Buszewski, J. Chromatogr. B:Anal. Technol. Biomed. Life Sci., 2013, 940, 66–76 CrossRef CAS PubMed.
- Z. R. Zad, S. S. H. Davarani, A. Taheri and Y. Bide, J. Mol. Liq., 2018, 253, 233–240 CrossRef CAS.
- Z. Dai, J. Liu, S. Tang, Y. Wang, Y. Wang and R. Jin, J. Mol. Model., 2015, 21, 290 CrossRef PubMed.
- S. Suryana, Mutakin, Y. Rosandi and A. N. Hasanah, Molecules, 2021, 26, 1891 CrossRef CAS PubMed.
- Z. Liu, Z. Xu, H. Liu, D. Wang, Y. Yang, Y. Duan, L. Ma and T. Lin, Polymers, 2021, 13, 1–18 Search PubMed.
- K. B. Lipkowitz and M. A. Peterson, Chem. Rev., 1993, 93, 2463–2486 CrossRef CAS.
- S. Manzoor, R. Buffon and A. V Rossi, Talanta, 2015, 134, 1–7 CrossRef CAS PubMed.
- U. Gunawan, S. Ibrahim, A. L. Ivansyah and S. Damayanti, React. Funct. Polym., 2024, 200, 105915 CrossRef CAS.
- D. SYSTÈMES, Dassault Syst MES, 2016, preprint Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14(27–28), 33–38 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- The GIMP Development Team, GNU Image Manipulation Program (GIMP), Version 3.0.4. Community, Free Software (license GPLv3), 2025, https://www.gimp.org Search PubMed.
- S. Li, S. Cao, M. J. Whitcombe and S. A. Piletsky, Prog. Polym. Sci., 2014, 39, 145–163 CrossRef CAS.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- R. Wang and Z. Yu, Acta Phys.-Chim. Sin., 2007, 23, 1353–1359 CrossRef CAS.
- D. Huo, L. Yang, C. Hou, H. Fa, X. Luo, Y. Lu, X. Zheng, J. Yang and L. Yang, Spectrochim. Acta, Part A, 2009, 74, 336–343 CrossRef PubMed.
- E. Verheyen, J. P. Schillemans, M. van Wijk, M.-A. Demeniex, W. E. Hennink and C. F. van Nostrum, Biomaterials, 2011, 32, 3008–3020 CrossRef CAS PubMed.
- A. N. Hasanah, N. Safitri, A. Zulfa, N. Neli and D. Rahayu, Molecules, 2021, 26, 5612 CrossRef CAS PubMed.
- R. D. Groot, J. Chem. Phys., 1992, 97, 3537–3549 CrossRef CAS.
- E. R. Johnson, I. D. Mackie and G. A. DiLabio, J. Phys. Org. Chem., 2009, 22, 1127–1135 CrossRef CAS.
- J. Liu, Z. Zhang, L. Yang, Y. Fan and Y. Liu, J. Mol. Graphics Modell., 2019, 88, 228–236 CrossRef CAS PubMed.
- T. A. Sales and T. C. Ramalho, Theor. Chem. Acc., 2020, 139, 31 Search PubMed.
- U. Gunawan, S. Ibrahim, A. L. Ivansyah and S. Damayanti, Pharmacia, 2023, 70, 1265–1281 Search PubMed.
- A. H. Mazurek and Ł. Szeleszczuk, Molecules, 2022, 27, 3874 Search PubMed.
- N. Bensouilah, H. Fisli, H. Bensouilah, S. Zaater, M. Abdaoui and B. Boutemeur-Kheddis, J. Mol. Struct., 2017, 1146, 179–190 CrossRef CAS.
- E. Papajak and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 597–601 CrossRef CAS PubMed.
- D. Imane, N. Leila, M. Fatiha, G. Abdelkrim, C. Mouna, L. Ismahan, B. Abdelazize and H. Brahim, J. Mol. Liq., 2020, 309, 113233 CrossRef CAS.
- J. Hostaš and J. Řezáč, J. Chem. Theory Comput., 2017, 13, 3575–3585 CrossRef PubMed.
- C. M. Orben and B. Dittrich, Acta Crystallogr., Sect. C:Struct. Chem., 2014, 70, 580–583 CrossRef CAS PubMed.
- J. S. Murray and P. Politzer, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2011, 1, 153–163 CrossRef CAS.
- C. H. Suresh and S. Anila, Acc. Chem. Res., 2023, 56, 1884–1895 CrossRef CAS PubMed.
- T. Pantsar and A. Poso, Molecules, 2018, 23, 1 CrossRef PubMed.
- T. Sajini and B. Mathew, Talanta Open, 2021, 4, 100072 CrossRef.
- G. Fitzgerald, J. DeJoannis and M. Meunier, in Woodhead Publishing Series in Electronic and Optical Materials, ed. V. K. Tewary and Y. B. T.-M. Zhang Characterization, and Production of Nanomaterials, Woodhead Publishing, 2015, pp. 3–53 Search PubMed.
- Y. Eken, N. M. S. Almeida, C. Wang and A. K. Wilson, J. Comput.-Aided Mol. Des., 2021, 35, 63–77 CrossRef CAS PubMed.
- S. A. Fahmy, F. Ponte, I. M. Fawzy, E. Sicilia and H. M. E.-S. Azzazy, RSC Adv., 2021, 11, 24673–24680 RSC.
- S. Mirzaei, M. V Ivanov and Q. K. Timerghazin, J. Phys. Chem. A, 2019, 123, 9498–9504 CrossRef CAS PubMed.
- Z. Jia, H. Pang, H. Li and X. Wang, Theor. Chem. Acc., 2019, 138, 1–11 Search PubMed.
- U. Gunawan, S. Ibrahim, A. Luqman Ivansyah and S. Damayanti, J. Mol. Liq., 2023, 383, 122130 CrossRef CAS.
- M. F. Akmal, D. Wahyuningrum and A. L. Ivansyah, J. Mol. Liq., 2022, 366, 120195 CrossRef CAS.
- M. Payehghadr and S. E. Hashemi, J. Inclusion Phenom. Macrocyclic Chem., 2017, 89, 253–271 CrossRef CAS.
- I. S. Ibarra, J. M. Miranda, I. Pérez-Silva, C. Jardinez and G. Islas, Anal. Methods, 2020, 12, 2958–2977 RSC.
- B. C. Deka and P. K. Bhattacharyya, Comput. Theor. Chem., 2017, 1110, 40–49 CrossRef CAS.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- R. G. Parr and P. K. Chattaraj, J. Am. Chem. Soc., 1991, 113, 1854–1855 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Parr, Horizons of Quantum Chemistry, ed. K. Fukui and B. Pullman, Springer Netherlands, Dordrecht, 1980 Search PubMed.
- Y. Li and J. N. S. Evans, J. Am. Chem. Soc., 1995, 117, 7756–7759 CrossRef CAS.
- J. Yu, N. Q. Su and W. Yang, JACS Au, 2022, 2, 1383–1394 CrossRef CAS PubMed.
- C. D. D. Sundari, A. L. Ivansyah, O. Floweri, I. M. Arcana and F. Iskandar, New J. Chem., 2022, 46, 3966–3977 RSC.
- L. Chen, X. Wang, W. Lu, X. Wu and J. Li, Chem. Soc. Rev., 2016, 45, 2137–2211 RSC.
- W. Dong, M. Yan, Z. Liu, G. Wu and Y. Li, Sep. Purif. Technol., 2007, 53, 183–188 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161 CrossRef CAS.
- I. Alkorta, I. Rozas and J. Elguero, Int. J. Quantum Chem., 2001, 86, 122–129 CrossRef.
- A. Kazachenko, F. Akman, M. Medimagh, N. Issaoui, N. Vasilieva, Y. N. Malyar, I. G. Sudakova, A. Karacharov, A. Miroshnikova and O. M. Al-Dossary, ACS Omega, 2021, 6, 22603–22615 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- S. Ghosh, P. Chopra and S. Wategaonkar, Phys. Chem. Chem. Phys., 2020, 22, 17482–17493 RSC.
- M. P. M. Costa, L. M. Prates, L. Baptista, M. T. M. Cruz and I. L. M. Ferreira, Carbohydr. Polym., 2018, 198, 51–60 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- M. Panneerselvam, M. D. Kumar, M. Jaccob and R. V. Solomon, ChemistrySelect, 2018, 3, 1321–1334 CrossRef.
- T. Sajini and B. Mathew, Talanta Open, 2021, 4, 100072 CrossRef.
- S. D. Jackman, T. Mozgacheva, S. Chen, B. O'Huiginn, L. Bailey, I. Birol and S. J. M. Jones, Bioinformatics, 2019, 35, 4448–4450 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra03211c |
| This journal is © The Royal Society of Chemistry 2025 |