Open Access Article
Open Access ArticleHalf-metallicity of novel halide double perovskites K2CuVCl6 and Rb2CuVCl6: application in next-generation spintronic devices
Mohammed El Amine Monira,
Hadj Baltacha,
K. Bouferrachebc,
M. Fatmi b,
M. A. Gheboulibd,
Faisal Katib Alanazi*e,
B. Gheboulif,
Maroua Imène Benamranig and
Rabah Boudissabf
b,
M. A. Gheboulibd,
Faisal Katib Alanazi*e,
B. Gheboulif,
Maroua Imène Benamranig and
Rabah Boudissabf
aFaculty of the Exact Sciences, Mustapha Stambouli University of Mascara, B. P. 305, 29000 Mascara, Algeria
bResearch Unit on Emerging Materials (RUEM), University Ferhat Abbas of Setif 1, Setif, 19000, Algeria
cDepartment of Physics, Faculty of Sciences, University of M'sila University Pole, Road Bourdj Bou Arreiridj, 28000, M'sila, Algeria
dDepartment of Chemistry, Faculty of Sciences, University of M'sila University Pole, Road Bourdj Bou Arreiridj, 28000, M'sila, Algeria
eDepartment of Physics, College of Sciences, Northern Border University, P. O. Box 1321, 91431 Arar, Saudi Arabia. E-mail: faisal.katib.al@gmail.com
fLaboratory for the Study of Surfaces and Interfaces of Solid Materials (LESIMS), University Ferhat Abbas of Setif 1, Setif, 19000, Algeria
gLaboratoire de Croissance et Caractérisation de Nouveaux Semiconducteurs (LCCNS), Faculté de Technologie, Université Ferhat Abbas Setif 1, 19000 Setif, Algeria
First published on 27th May 2025
Abstract
This work reports the determination of structural, electronic, half-metallic and magnetic properties of new double perovskites K2CuVCl6 and Rb2CuVCl6 using the full-potential linearized augmented plane wave plus local orbitals method incorporated in the WIEN2k code. The calculations performed for this prediction were framed using the density functional theory, and the exchange and correlation potential were described using the generalized gradient approximation of TB-mBJ (Tran–Blaha modified Becke–Johnson). The structural properties confirmed the stable ferromagnetic ground state of the two studied compounds. The equilibrium structural parameters, such as lattice constant (a0), bulk modulus (B0), their first pressure derivative (B′) and minimum of the total energy (E0), were determined for both the compounds. The electronic properties showed that the studied perovskite compounds were completely half-metallic materials. The half-metallic gap (EHM) values for the compounds were 1.119 eV (for K2CuVCl6) and 1.088 eV (for Rb2CuVCl6). The exchange-splitting energy (Δ(d)) was found to be large for both the compounds (Δ(d) = 3.482 eV for K2CuVCl6 and Δ(d) = 3.380 eV for Rb2CuVCl6). The calculated total magnetic moments of the two studied materials indicated major contributions from V atoms and minor contributions from Cu atoms. Owing to p–d hybridization, feeble magnetic moments were exhibited by the non-magnetic K, Rb, Cu and Cl sites, while the atomic magnetic moment of V atoms decreased from its free space charge of 3.00 μB.
1. Introduction
Half-metallic materials play vital roles in the development of new devices based on spintronic and optoelectronic technologies. In the last decade, half-metallic materials have attracted increasing attention of researchers owing to their excellent electronic, magnetic and optical properties. Generally, half-metallic compounds exhibit two different electronic behaviors depending on the two spin directions: a semiconducting character in one spin direction and a metallic nature in the other spin direction.1 Research in this domain was initiated by the prediction of the electronic structure of half-Heuslers NiMnS and PtMnS by Groot et al.2 The most prominent works after this prediction were on perovskite materials, such as La0.70Sr0.30MnO3 and Sr2FeMoO6;3,4 Heusler alloys, such as Co2MnSi and Co2FeSi;5,6 and TM-doped chalcogenide and pnictide semiconductors.7In the present time, the half-metallicity has appeared in several types of materials, such as: TM (transition metal) doped semiconductors, exploring half-metallicity in NiO via TM and NTM doping: Insights from LDA and LDA-SIC approaches,8 investigating half-metallic behavior of MnO doped with TM and NTM: LDA, LDA-SIC and LDA + U analysis;9 half-Heusler alloys, study on the phase stability, mechanical and half-metallic properties of half-Heusler alloys FeMnZ (Z = Si, Ge and Sn),10 half-metallicity and thermoelectric performance: A multifaceted investigation of Zr-based half-Heusler alloys;11 full-Heusler alloys, a spin-polarized analysis of the half-metallicity, mechanical, structural and optoelectronic attributes of full-Heusler XVCo2 (X = B and P) alloys,12 revealing half-metallicity: predicting large band-gaps in halogen-based full-Heusler alloys;13 quaternary Heusler alloys, systematic study of structural, elastic, electronic, magnetism and half-metallic properties for the quaternary alloys: Heusler type VZrReZ (Z = Si, Ge and Sn),14 ab initio study of quaternary Heusler alloys LiAEFeSb (AE = Be, Mg, Ca, Sr or Ba) and prediction of half-metallicity in LiSrFeSb and LiBaFeSb;15 perovskites materials, a DFT theoretical prediction of new half-metallic ferromagnetism, mechanical stability, optoelectronic and thermoelectric properties of ZnCrO3 perovskites for spintronic applications,16 half-metallic ferromagnetic and optical properties of YScO3 (Y = Ni, Pd, and Pt) perovskite: a first principles study;17 and double perovskite materials, harnessing the half-metallicity and thermoelectric insights in Cs2AgMBr6 (M = V, Mn, Ni) double halide perovskites: a DFT study,18 tunability of half metallicity and thermoelectric indicators in Na2TaX6 (X = Cl, Br) vacancy ordered double perovskites.19 Moreover, recent studies have highlighted the growing interest in simple and double perovskites owing to their tunable properties and potential in optoelectronics, catalysis, and energy applications.20–33
In this study, we computed the structural, electronic and magnetic features of the new double perovskites K2CuVCl6 and Rb2CuVCl6 in order to prove their complete half-metallic property, and the calculations were carried out using the full-potential linearized augmented plane waves with local orbitals (FP-LAPW + lo) method embedded in the WIEN2k package. This study was conducted in order to determine the large half-metallic energy gap (EHM) and high Curie temperature (TC) corresponding to the new double perovskites K2CuVCl6 and Rb2CuVCl6 using the TB-mBJ–GGA approximation. This study is crucial for the development of spintronics, enabling low-energy storage and computing devices. It also highlights the prospects of these materials in optoelectronics, particularly for advanced LEDs and solar cells. Finally, these findings can be utilized in thermoelectricity to enhance the energy efficiency of industrial systems.
The rest of this article is given as follows: simulation method and calculation details are mentioned in Section 2. Obtained results are discussed in Section 3. The conclusions of this prediction are listed in Section 4.
2. Computational details
In this work, the DFT (density functional theory)34 calculations were carried out by employing the full-potential linearized augmented plane waves plus local orbitals (FP-LAPW + lo) method35,36 implemented in the WIEN2k code.37 The potential of exchange and correlation is described using both Perdew–Burke–Ernzerhof generalized gradient approximation (PBE–GGA)38 and Tran–Blaha modified Becke–Johnson potential of the generalized gradient approximation (TB-mBJ–GGA).39,40 The computational parameters employed in this prediction approach are as follows: the matrix size RMT × Kmax parameter, which represents the extension of the plane waves and the convergence of the energy eigenvalues, is taken as 8, where Kmax denotes the large modulus of the reciprocal lattice vector, and RMT denotes the small radius of muffin-tin spheres. The cut-off energy (Ecut-off), which evaluates the number of plane waves used in the basic function, was chosen as −6 eV. The Fourier expansion factor (GMax) that describes charge density translation and wave function expansion was set to 12. The irreducible Brillouin zone integrations were founded on the 11 × 11 × 11 mesh, in which 56 k-points were produced. The maximum norm of the angular momentum was equal to lmax = 10. The computed radii of the K, Rb, Cu, V, and Cl atoms reported in this study were 2.50, 2.50, 2.35, 2.30 and 2.02 a.u., respectively. The K (4s1), Rb (5s1), Cu (3d104s1), V (3d34s2) and Cl (3s23p5) states were treated as valence electrons. The anti-ferromagnetic calculations were carried out using the super-cell size of 1 × 1 × 2. Furthermore, the self-consistent process was set to stop iterations when the convergence energy becomes greater than 10−4 Ry.3. Results and discussion
3.1. Structural properties
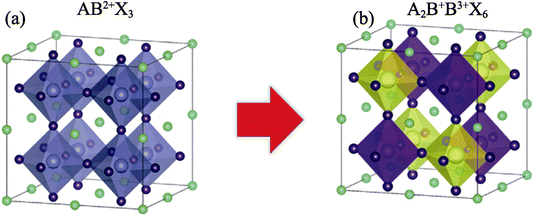
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 225).41 The atomic positions are given as follows: the X atoms occupy the 8c (1/4, 1/4, 1/4) positions, the Cu and V atoms occupy the 4a (0, 0, 0) and 4b (1/2, 0, 0) positions, respectively, and Cl atoms are located at the 24e (0.2504, 0, 0) positions.41 The crystal structure of the double perovskite compound is depicted in Fig. 1.
m (no. 225).41 The atomic positions are given as follows: the X atoms occupy the 8c (1/4, 1/4, 1/4) positions, the Cu and V atoms occupy the 4a (0, 0, 0) and 4b (1/2, 0, 0) positions, respectively, and Cl atoms are located at the 24e (0.2504, 0, 0) positions.41 The crystal structure of the double perovskite compound is depicted in Fig. 1.
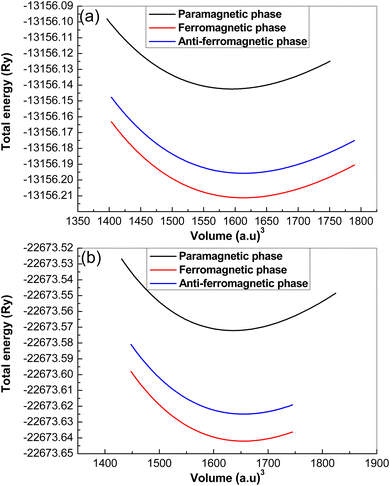 | ||
| Fig. 2 Plot of total energy fitting versus cell-volume of (a) K6CuVCl6 and (b) Rb6CuVCl6 double perovskite compounds. | ||
| Material | Configuration | Lattice constant a0 (Å) | Bulk modulus B0 (GPa) | B′ | Minimum of the total energy E0 (Ry) |
|---|---|---|---|---|---|
| K2CuVCl6 | PM phase | 9.8142 | 40.7357 | 4.8572 | −13156.1424 |
| FM phase | 9.8513 | 39.0165 | 5.1508 | −13156.2112 | |
| AFM phase | 9.8417 | 39.0712 | 4.9912 | −13156.1957 | |
| Rb2CuVCl6 | PM phase | 9.8978 | 39.6915 | 4.9354 | −22673.5721 |
| FM phase | 9.9357 | 38.3989 | 4.9421 | −22673.6420 | |
| AFM phase | 9.9214 | 38.4157 | 4.9321 | −22673.6249 | |
| K2ScCuCl6 (ref. 44) | PM phase | 9.98 | 35.76 | 5.00 | −12786.28 |
| Rb2ScCuCl6 (ref. 44) | PM phas | 10.08 | 49.09 | 8.47 | −22303.72 |
3.1.3.1. Cohesive energy. In a solid, the atoms are bound together by cohesive energy (ECoh). The ECoh energy value is estimated as the difference between the total energy of the material and the sum of different atomic energies of the constituents at infinite separation.45 The ECoh energy of the X2CuVCl6 (X = K and Rb) materials was calculated using the following formula:
| ECoh(X2CuVCl6) = (2EX + ECu + EV + 6ECl) − E0 | (1) |
| Material | E0 | EX | ECu | EV | ECl | ECoh |
|---|---|---|---|---|---|---|
| K2CuVCl6 | −13156.211232 | −1204.191254 | −3309.685742 | −1898.056927 | −922.888706 | 2.753819 |
| Rb2CuVCl6 | −22673.642044 | −5962.915605 | −3309.685748 | −1898.056928 | −922.888707 | 2.735916 |
3.1.3.2. Formation energy. Formation energy (Ef) is the energy required for maintaining material stability in its favorable crystalline structure under the theoretical temperature of 0 K; the negative value of Ef denotes the stable structure of the material and confirms the strong bonding between the atoms in their favorable crystal structure.46
The Ef energy of the studied X2CuVCl6 (X = K and Rb) compounds was calculated according to the following relationship:
| Ef(X2CuVCl6) = E0 − (2EX + ECu + EV + 6ECl) | (2) |
3.2. Elastic properties
The elasticity tensor of a cubic system is defined by three independent elastic constants, namely C11, C12 and C44. The elastic constants (C11, C12 and C44) of the X2CuVCl6 (X = K and Rb) materials were computed using the IRelast program47 implemented in the WIEN2k package,23 and the values obtained by the GGA approximation are shown in Table 4. The Born's criteria48,49 for assessing the mechanical stability of materials that crystallize in the cubic system are as follows:48,49
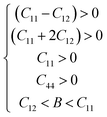 | (3) |
Therefore, the GGA results confirm that the studied X2CuVCl6 (X = K and Rb) compounds are mechanically stable.
The shear modulus (G) is defined as a parameter for evaluating the resistance of a material to plastic strain; it is calculated as the average of the Voigt50 and Reuss51 approaches, and it is reformulated according to the Hill's approach:52
 | (4) |
 | (5) |
Bulk modulus (B0) is the factor that determines the resistance to fracture.53 Moreover, Pugh's ratio (B0/G) is another parameter that identifies the brittleness and ductility of materials.54,55 The material becomes brittle when the B0/G parameter is less than 1.75; when the value is higher (B0/G > 1.75), the material will have a ductile nature. According to the Pugh ratios reported in Table 4, the present materials are ductile materials. Therefore, the two studied materials are held in their form by metallic bonding.
3.3. Electronic properties
In this work, the electronic band structures and density of states of the double perovskite materials K2CuVCl6 and Rb2CuVCl6 were predicted using both GGA and TB-mBJ–GGA functionals, aiming to explore their electronic properties and assess their potential for practical applications. | ||
| Fig. 4 Spin-polarized electronic structure of the equilibrium double perovskite K2CuVCl6 calculated using (a) PBE–GGA and (b) TB-mBJ–GGA functionals. | ||
 | ||
| Fig. 5 Spin-polarized electronic structure of the equilibrium double perovskite Rb2CuVCl6 calculated using (a) PBE–GGA and (b) TB-mBJ–GGA functionals. | ||
 | ||
| Fig. 6 Spin-polarized partial density of states (PDOS) of the equilibrium double perovskite K2CuVCl6 calculated using (a) PBE–GGA and (b) TB-mBJ–GGA approximations. | ||
 | ||
| Fig. 7 Spin-polarized partial density of states (PDOS) of the equilibrium double perovskite Rb2CuVCl6 calculated using (a) PBE–GGA and (b) TB-mBJ–GGA approximations. | ||
For the K2CuVCl6 material (Fig. 6), the PDOS curves determined by the TB-mBJ–GGA scheme reveal the following: the 4s-Cu electrons in the spin-up and spin-down states appear in the energy spectra from −6 to −5 eV and from 4.5 to 8 eV, respectively; energy bands of the 4p-Cu spin-up and spin-down electrons are spotted in the energy range from −4.50 to −4 eV; the spin-up 3d-V electrons are located in the energy zones between −4.50 and −2 eV, around the Fermi level (EF), and between 2.75 and 3.80 eV, while the spin-down 3d-V electrons are spotted in the energy regions between −4.50 and −2 eV and between 2.80 and 3.75 eV; moreover, the energy bands of the 3s-Cl spin-down electrons are located in the energy spectrum between −3.40 and −3 eV. Therefore, the PDOS of the K2CuVCl6 compound is mainly contributed by the 3d electrons of V atoms, where they are at the origin of the half-metallic aspect of the material. In addition, strong hybridization is also observed between the 3d-V states and the 4p-Cu states in the energy spectrum between −4.50 and −4 eV.
For the Rb2CuVCl6 material, Fig. 7 depicts that the bands in the energy ranges from −5.90 to −5 eV and 4.50 to 7 eV belong to the spin-up and spin-down 4s-Cu states, respectively; the energy bands between −4.50 and −3.75 eV and between 7 and 11 eV arise from the 4p-Cu spin-up and spin-down components; the spin-up and spin-down energy bands observed at around −10 eV and from 7 to 11 eV belong to the 3p states of the Cl atoms; on the other hand, the 3d-V states occupy the spin-up energy bands located in the energy regions from −4.25 to −2 eV, around the Fermi level (EF), and from 2.30 to 3.50 eV; whereas, the spin-down 3d-V states lead to bands in the energy regions from −4.25 to −2 eV and 2.40 to 3.55 eV. We can conclude that the 3d-V states are responsible for the half-metallicity of the equilibrium Rb2CuVCl6 double perovskite as they produce an energy gap in the spin-down direction and metallic behavior in the spin-up direction around the Fermi level. Furthermore, the hybridization of the 3d-V states and the 4p-Cu states is observed in the energy range of −4.50 to −3.75 eV.
In the X2CuVCl6 (X = K and Rb) halide double perovskites, the 3d-V states influence the electronic structure by introducing an exchange and splitting process (Δ(d)), where Δ(d) energy is defined as the energy difference between the highest d-orbital peaks of the corresponding spin-down and spin-up states.58 It is expressed as follows:
| Δ(d) = Ed(↓) − Ed(↑) | (6) |
The computed Δ(d) energy values of the studied K2CuVCl6 and Rb2CuVCl6 compounds are reported in Table 5. The TB-mBJ–GGA results are considered relatively improved owing to the high Δ(d) energy observed for the studied compounds (Table 5).
3.4. Magnetic properties
| Material | Magnetic moment (μB) | Curie temperature (K) | |||||
|---|---|---|---|---|---|---|---|
| MTot | M (interstitial) | M (X) | M (Cu) | M (V) | M (Cl) | TC | |
| K2CuVCl6 | 2.1082 (2.0000) | 0.2402 (0.2454) | 0.0006 (0.0002) | −0.0133 (−0.4792) | 1.9546 (2.3109) | −0.0124 (−0.0129) | 814.0870 |
| Rb2CuVCl6 | 1.9748 (2.0004) | 0.2353 (0.2321) | 0.0007 (0.0002) | −0.1337 (−0.4792) | 1.9543 (2.3223) | −0.0137 (−0.0125) | 898.1217 |
 | (7) |
 | (8) |
The calculated TC temperatures of the equilibrium X2CuVCl6 (X = K and Rb) halide double perovskites using the TB-mBJ–GGA scheme are listed in Table 6. Notably, the TC values of both compounds are high.
4. Conclusions
In summary, the FP-LAPW + lo method was applied in this work to evaluate the structural, elastic, electronic and magnetic properties of X2CuVCl6 (X = K and Rb) halide double perovskite compounds at equilibrium. The main conclusions of this prediction model are summarized below:(i) Analyses of the structural properties of both compounds show that the ferromagnetic state is the stable ground phase.
(ii) The optimized structural parameters (a0, B0, B′ and E0) of the compounds are reported in this study.
(iii) The calculated elastic constants of both materials confirm their mechanical stability and ductility.
(iv) The calculated electronic properties of the compounds using both GGA and TB-mBJ–GGA parameterizations prove that they are entirely half-metals with a large half-metallic gap.
(v) The half-metallic gaps corresponding to the two halide double perovskites are calculated using GGA and TB-mBJ–GGA functionals.
(vi) The 3d-V exchange-splitting energy (Δ(d)) calculated using this approach was found to be large for both studied compounds.
(vii) The estimated magnetic properties of the two compounds reveal that:
(1) The atomic magnetic moment of the V atom contributes mainly to the total magnetic moment.
(2) The opposite signs of the atomic magnetic moments of V and Cu atoms reveal that the valence electrons of V and Cu atoms interact in an antiparallel manner during the exchange and splitting process.
(3) The hybridization between 3d-V and 4p-Cu electrons reduces the magnetic moment of the V atom from its free space charge and produces weak magnetic moments at the non-magnetic X, Cu and Cl sites.
Data availability
Data supporting the results presented in this paper are not publicly available at this time but may be obtained from the corresponding author (E-mail: fatmimessaud@yahoo.fr) upon reasonable request.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number NBU-FFR-2025-310-11.References
- W. E. Pickett and J. S. Moodera, Phys. Today, 2001, 54, 39–44 CrossRef CAS.
- R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027 CrossRef CAS.
- R. J. Soulen Jr, J. M. Byers, M. S. Osofsky, B. Nadgorny, T. Ambrose and A. Barry, Science, 1998, 282, 85–88 CrossRef PubMed.
- K. L. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680 CrossRef CAS.
- I. Galanakis, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 012413 CrossRef.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H.-J. Lin, Appl. Phys. Lett., 2006, 88, 032503 CrossRef.
- M. Nakao, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 214429 CrossRef.
- A. Nfissi, R. El Fdil, A. Samih, D. Kabouchi, Z. Fadil, C. J. Raorane, A. A. Ifseisi, M. E. Assal and E. Salmani, J. Magn. Magn. Mater., 2024, 610, 172563 CrossRef CAS.
- A. Nfissi, D. Kabouchi, R. El Fdil, A. Samih, Z. Fadil, C. J. Raorane, K. H. Mahmoud, A. S. A. Alsubaie and E. Salmani, Solid State Commun., 2024, 389, 115596 CrossRef CAS.
- G. Li, Z. Li and Z. Liu, J. Magn. Magn. Mater., 2025, 614, 172742 CrossRef CAS.
- B. Gurunani and D. C. Gupta, Mater. Sci. Eng., B, 2025, 311, 117783 CrossRef CAS.
- F. Firdous, Q. Ain, S. A. M. Issa, H. M. H. Zakaly and J. Munir, RSC Adv., 2024, 14, 34679–34689 RSC.
- I. Muhammad, S. Ahmed, N. Ullah, M. Mushtaq, M. Liaqat, X. Tian and J.-M. Zhang, Results Phys., 2024, 57, 107419 CrossRef.
- F. Faid, H. Mebarki, K. Mokadem, F. M. Abdalilah, A. Benmakhlouf, M. Khatiri and T. Helaimia, J. Magn. Magn. Mater., 2024, 605, 172345 CrossRef CAS.
- J. K. Sharma, A. Dhamija, A. Pal and J. Kumar, Comput. Mater. Sci., 2024, 232, 112679 CrossRef CAS.
- M. Jamil, M. Manzoor, A. Kumar, A. Agrawal, R. Almeer, Y. A. Kumar and R. Sharma, Solid State Commun., 2024, 394, 115702 CrossRef CAS.
- H. Kerrai, A. Zaim and M. Kerouad, Vacuum, 2024, 226, 113341 CrossRef CAS.
- M. Y. Sofi, M. S. Khan and M. A. Khan, Mater. Sci. Semicond. Process., 2025, 186, 109023 CrossRef CAS.
- M. A. Yasir, G. M. Mustafa, M. A. Ameer, N. A. Noor, S. Mumtaz and I. M. Moussa, Mater. Sci. Eng., B, 2025, 311, 117830 CrossRef CAS.
- M. Husain, H. Albalawi, M. Al Huwayz, N. Al Saqri, R. Khan and N. Rahman, Phys. Scr., 2023, 98, 105935 CrossRef CAS.
- N. Rahman, A. Rauf, M. Husain, N. Sfina, V. Tirth, M. Sohail, R. Khan, A. Azzouz-Rached, G. Murtaza, A. A. Khan and S. A. Khattak, RSC Adv., 2023, 13, 15457–15466 RSC.
- M. Husain, N. Rahman, H. Albalawi, S. Ezzine, M. Amami, T. Zaman, A. U. Rehman, M. Sohail, R. Khan, A. A. Khan, Tahir and A. Khan, RSC Adv., 2022, 12, 32338–32344 RSC.
- S. A. Shah, M. Husain, N. Rahman, M. Sohail, R. Khan, A. Alataway, A. Z. Dewidar, H. O. Elansary, L. Abu El Maati, K. Yessoufou, A. Ullah and A. Khan, Materials, 2022, 15, 5684 CrossRef CAS PubMed.
- S. A. Shah, M. Husain, N. Rahman, M. Sohail, R. Khan, A. A. Khan, A. Ullah, S. A. M. Abdelmohsen, A. M. M. Abdelbacki, A. M. El-Sabrout, H. O. Elansary and A. Khan, RSC Adv., 2022, 12, 8172–8177 RSC.
- N. Rahman, M. Husain, V. Tirth, A. Algahtani, H. Alqahtani, T. Al-Mughanam, A. H. Alghtani, R. Khan, M. Sohail, A. A. Khan, A. Azzouz-Rached and A. Khan, RSC Adv., 2023, 13, 18934–18945 RSC.
- A. A. Pasha, H. Khan, M. Sohail, N. Rahman, R. Khan, O. H. Alsalmi, D. Abduvalieva, K. M. Abualnaja, A. El Jery and M. Adrdery, Mater. Adv., 2023, 4, 6645–6654 RSC.
- W. Ullah, M. Husain, N. Rahman, N. Sfina, M. Elhadi, R. Khan, M. Sohail, A. Azzouz-Rached, M. Uzair, A. A. Khan and A. Khan, Silicon, 2024, 16, 3021–3032 CrossRef CAS.
- U. Hameed, H. Ullah, S. Z. Abbas, K. Safeen, K. M. Alotaibi, A. Safeen, S. Yasin, G. Murtaza, F. Khalil, S. Ali, G. Asghar and R. Khan, J. Phys. Chem. Solids, 2025, 199, 112519 CrossRef CAS.
- M. S. Khan, M. Sohail, N. Rahman, R. Khan, H. E. Ali, J. Jamil, B. S. Abdullaeva, K. M. Abualnaja, G. Alosaimi, Y. Khairy and H. Algarni, Chem. Pap., 2025, 79, 107 CrossRef CAS.
- N. S. Alsaiari, I. Ahmed, S. Hanf, M. M. Rekha, M. Kundlas, M. Ouladsmane, K. Muhammad and J. Rehman, J. Inorg. Organomet. Polym., 2025 DOI:10.1007/s10904-025-03746-z.
- N. Rahman, K. M. Abualnaja, S. Belhachi, N. Sfina, M. Husain, B. M. Al-Khamiseh, A. Azzouz-Rached, H. A. Althobaiti, S. Ullah, R. Khan and M. Asghar, J. Inorg. Organomet. Polym., 2025, 35, 1439–1452 CrossRef CAS.
- N. Sfina, N. Rahman, S. Belhachi, M. Husain, B. M. Al-Khamiseh, K. M. Abualnaja, G. Alosaimi, A. Azzouz-Rached, S. Ullah, A. U. Rashid and R. Khan, J. Inorg. Organomet. Polym., 2024, 34, 6102–6113 CrossRef CAS.
- M. Husain, N. Rahman, A. Azzouz-Rached, N. Sfina, K. M. Abualnaja, G. Alosaimi, M. Asad, R.-D. Hamza, V. Tirth, N. U. Khan, Q. Humayun, R. Khan, R. Ahmad, A. Samreen, A. A. Khan and J. Lu, Inorg. Chem. Commun., 2024, 164, 112424 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- K. M. Wong, S. M. Alay-e-Abbas, A. Shaukat, Y. Fang and Y. Lei, J. Appl. Phys., 2013, 113, 014304 CrossRef.
- K. M. Wong, S. M. Alay-e-Abbas, Y. Fang, A. Shaukat and Y. Lei, J. Appl. Phys., 2013, 114, 034901 CrossRef.
- P. Blaha, K. Schwarz, P. Sorantin and S. K. Trickey, Comput. Phys. Commun., 1990, 59, 339 CrossRef.
- J. P. Perdew, S. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 195134 CrossRef.
- G. M. Mustafa, R. Waqar, S. Saba, N. A. Noor, Z. Farooq, M. Imran, R. B. Behram and Y. M. Alanazi, Phys. Scr., 2023, 98, 065703 CrossRef CAS.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS PubMed.
- S. L. Shang, Y. Wang, D. Kim and Z.-K. Liu, Comput. Mater. Sci., 2010, 47, 1040–1048 CrossRef CAS.
- A. Ayyaz, G. Murtaza, A. Usman, N. Sfina, A. S. Alshomrany, S. Younus, S. Saleem and Urwa-tul-Aysha, J. Inorg. Organomet. Polym., 2024, 34, 3560–3575 CrossRef CAS.
- J. J. Kim, H. W. Seong and H. J. Ryu, J. Nucl. Mater., 2022, 566, 153780 CrossRef CAS.
- A. Yakoubi, O. Baraka and B. Bouhafs, Results Phys., 2012, 2, 58–65 CrossRef.
- J. B. Kramers-Kronig, Am. J. Phys., 2011, 79, 1053–1059 CrossRef.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1956 Search PubMed.
- J. Wang and S. Yip, Phys. Rev. Lett., 1993, 71, 4182 CrossRef CAS PubMed.
- W. Voigt, Lehrbuch der Kristallphysik, Taubner, Leipzig, 1928 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 55 CrossRef.
- R. Hill, Proc. Phys. Soc., London, 1953, 65, 909 Search PubMed.
- G. Vaitheeswaran, V. Kanchana, R. S. Kumar, A. L. Cornelius, M. F. Nicol, A. Svane, A. Delin and B. Johansson, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 014107 CrossRef.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CAS.
- G. Simmon and H. Wang, Single Crystal Elastic Constants and Calculated Aggregate Properties: a Handbook, M.I.T Press, Cambridge, 1971 Search PubMed.
- K. L. Yao, G. Y. Gao, Z. L. Liu and L. Zhu, Solid State Commun., 2005, 133, 301–304 CrossRef CAS.
- G. Y. Gao, K. L. Yao, E. Sasioglu, L. M. Sandratskii, Z. L. Liu and J. L. Jiang, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 75, 174442 CrossRef.
- A. Zunger, Solid State Phys.: Condens. Matter, 1986, 39, 275 CAS.
- J. Kubler, G. H. Fecher and C. Felser, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 024414 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |