Thermal behavior in FeCuCrCoNi high entropy alloy nanoparticles: an atomistic approach

Abstract

High Entropy Alloy nanoparticles (HEA NPs) have been synthetized because they are promising materials to improve nanoscale performance. However, little theoretical study has been carried out regarding the thermal stability of HEA NPs. Here, atomistic simulations have been conducted to study the thermal response of FeCuCrCoNi HEA NPs as a function of size. Atomistic modeling shows that melting point can be explained in terms of a two-phase model without the contribution of surface melting as is predicted through liquid shell models. On the other hand, it is observed that premelting starts with a preferential mobility of Fe and Cu atoms. Simulations show that due to the enhanced diffusion there is no evidence of precipitation or clustering during the thermal load, which is independent of the HEA NP size.

---

Introduction

The synthesis of high entropy alloy nanoparticles (HEA NPs) has been conducted in the last year due to their outstanding behavior in catalysis, sensing, energy storage, corrosion, and many other applications.^1–4 The origin of their unique behavior is attributed to the chemical complexity introduced by the different atom types coexisting in the ordered crystalline structure.^5–9 In particular, the design and functionalization of the NPs have been addressed as a route to improve the surface activation process in order to boost their application in different fields.^10,11 The current demands in many fields have motivated understanding of the NPs’ physical and chemical responses under different scenarios.¹²

The novelty of HEA NPs arises from the different atomic sizes leading to modification of the electronic structure in terms of the atomic environment. Metallic HEA NPs of a few atoms showed that even the same component atoms display different local density of states that change in terms of the atomic neighborhood.^5,13 Similar results have been conducted in body cubic centered TiZrHfNb HEA.¹⁴ The unique electronic structure has motivated several applications, such as an enhanced performance in hydrogen production on sub-20 Å NiCoFePtRh NPs, or superior electrocatalysis in alkaline oxygen reactions.¹⁵ Even more, nano–micro particles have been referred to as excellent materials for supercapacitors, or electrocatalyzer structures.^15,16 The latter is motivated by the complex surfaces and chemical composition of HEA NPs, rendering different absorption energies which enable favorable adsorption to enhance the surface activity.

The previously mentioned applications have fueled the synthesis methods in the micro and nanoscale.¹⁷ To date, HEA nano and microparticles have been synthesized by means of different strategies such as carbothermal shock synthesis, fast moving bed pyrolysis, mechanical alloying, combinatorial sputtering, ultrasonic assisted wet chemistry, kinetically controlled laser synthesis, microwave assisted combustion synthesis, among many other methods.^18–20 From all the mentioned synthesis strategies, at least five of them are based on thermal treatments that heat the precursors at high temperature to drive the element diffusion and mixing. The temperature cooling rate is also a fundamental factor that helps the consolidation of the solid solution before atomic diffusion could promote the segregation of the constituents.

The thermal response of NPs is currently addressed as a technique to understand how they will respond under more complex scenarios,^21–23 and synthesis conditions.^24–26 Besides, melting and premelting are crucial to delimit the NP applicability for diverse applications.^27–29 Molecular dynamics simulations are typically introduced to unveil the atomistic mechanism that governs the phase transition on NPs of diverse morphology and composition.^30–33 Samsonov et al.³⁴ showed that the continuous melting in Ag and Au NPs is driven by means of a surface pre-melting mechanism. Al NPs with less than 1000 atoms have shown an interesting bi-stable behavior near to the melting point, which is attributed to the coexistence of a solid-to-liquid state at temperatures lower than the melting point.³⁵ Pd NPs have shown very interesting behavior related to the NP shape, where cuboctahedron nanostructures display a melting from the NP corners. This is attributed to the surface stress as a consequence of the high facet indexes.³⁶

Chemical complexity has been used as a tool to improve the performance of NPs. In this aspect, the coexistence of more than one element renders bimetallic NPs with different phases or complex morphology such as Core@Shell or Janus-like NPs. Au–Ag NPs have shown that alloying structures have a negative formation energy in comparison with Janus or Core@Shell nanostructures, demonstrating that for this kind of system the alloying is the more stable configuration.³⁷ FeCu NPs have displayed a morphology dependence in terms of the atomic concentrations.³⁸ By means of atomistic modeling, it was shown that the final configuration strongly depends on the surface energy of the respective Fe and Cu NPs. Although, in the current literature, many studies have been carried out on metallic NPs, studies on HEA NPs are still missing.^39,40

It is worth mentioning that current experimental studies have achieved the synthesis of HEA nanostructures of diverse compositions.² Even more recent studies have achieved the synthesis of HEA NPs with a hollow central cavity,^41,42 which has been reported in the literature as a convenient morphology to boost the material performance in catalysis, sensing, energy storage, and many other applications.⁴² Size effects on melting point on HEA NPs were conducted through atomistic simulations on a system composed of PdPtRhCo atoms.³⁹ Complementary studies have shown that there is no segregation on multiprincipal alloys.⁴³ Other studies on AgAuPdPtNi HEAs have shown a size-dependent melting point typical of metallic NPs.³⁹ Besides, some elements show a faster diffusion that could be relevant in the early stages of premelting of NPs.^39,40 All in all, chemical complexity is a relevant factor that seems to influence thermal behavior in HEA NPs, however, theoretical understanding is still limited.

For this reason, this contribution is focused on the study of the melting of HEA NPs composed by FeNiCrCoCu atoms. Even more, possible size effects and atomistic understanding to unveil the fundamental physics processes that unleash the melting and premelting of HEA NPs will be discussed.

Methods

We carried out simulations to study the thermal behavior of FeNiCrCoCu HEA NPs, performed by classical Molecular Dynamics with the help of the LAMMPS package.⁴⁴ The atoms interactions were modeled using the embedded atom method⁴⁵ with the parameterization proposed by Pasianot and Farkas.^46,47 DFT calculations on the FeNiCrCuCo alloy⁴⁸ were performed, where the lattice parameter found for a face-centered cubic (FCC) HEA with x = 0.2 was 3.395 Å, by solving the Kohn–Sham equations with the PBE exchange functional. This value differs only 3.7% from the value used in this work (3.52 Å). Experimentally, the same paper reports a lattice parameter of 3.6 Å for the FCC HEA, which is 3% higher than the value used here. Although this potential does not precisely replicate any particular alloy, it is specifically designed to capture overall trends in alloy properties, such as heats of mixing, elastic constants, and thermodynamic behavior, by matching known experimental ranges, as can be seen in works of Farkas et al.⁴⁹ and Deluigi et al.⁴⁷ In particular, the potential consistently reproduces the stability of the FCC structure across Fe–Ni–Cr–Co–Cu mixtures and aligns with observed formation enthalpies and stacking fault energies,⁴⁶ enabling reliable insights into general trends and guiding further investigation of alloy behavior.

The construction of the HEA NPs was performed by cutting a sphere of a given radius R from a FCC bulk, with a lattice parameter of 3.52 Å, which has been reported by Pasianot et al.⁴⁶ as the lattice parameter of FeNiCrCoCu bulk, as is observed in Fig. 1a–c. Considering the reported lattice parameter, we built a bulk HEA, assigning the Fe, Cu, Cr, Co, and Ni atoms to random positions of the FCC lattice. The result was an equiatomic HEA with a concentration of 20% for each element. For the construction of the HEA NPs, we followed the steps proposed by Valencia et al.⁵⁰ The HEA NPs studied in the present work have radius sizes of 7.5, 10, 15, 20, 25, 30, 35, and 40 Å, as shown in Fig. 1c.

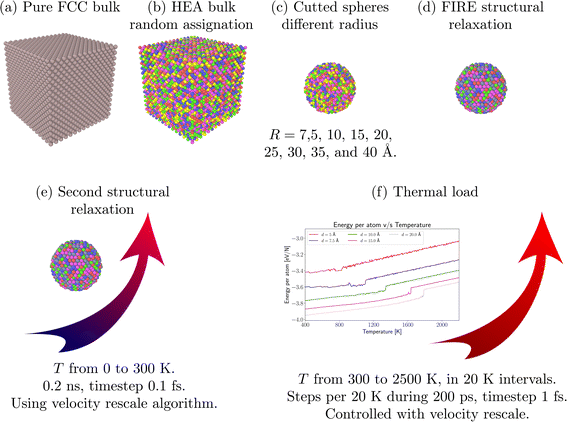Fig. 1 NP simulation setup. (a–d) correspond to NP construction. (e and f) depict the relaxation and thermal load.

Due to the mentioned considerations on the construction of the HEA NPs, the geometrical configuration could have possible residual forces on the atoms. Therefore, the structures were firstly relaxed using the Fast Inertial Relaxation Engine algorithm (FIRE).⁵¹ After this first energy minimization, a second relaxation was introduced by raising the system temperature from 0 to 300 K. To this end, the temperature was controlled using a velocity rescale algorithm while the atomic motion was integrated, assuming a microcanonical NVE ensemble. The relaxation was performed over 0.2 ns using a timestep of 1.0 fs to ensure energy conservation.

The thermal load was performed by increasing the system temperature from 300 to 2500 K in 20 K temperature intervals. Each temperature increase was held at 200 ps, where the first 100 ps were used to allow the system equilibration, and the remaining time was used to calculate average thermodynamic quantities such as potential energy, temperature, and mean square displacement (MSD), among others. In some cases, rotational or translational movement in the NP could lead to overestimation of MSD calculations. For this reason, motion equations are integrated with the constraints to add zero angular and linear momentum during the thermal load to not introduce spurious effects in the calculations of thermodynamic quantities. The system temperature during annealing was controlled using the velocity rescale algorithm adopting a timestep of 1.0 fs (Fig. 1f).

For the post-processing of the results, we used the OVITO software.⁵² Possible segregation of clustering of elements was analyzed with the pair correlation function, and the atomic displacement and mobility were studied with the MSD which is calculate as

where N is the number of atoms, is the position of the i-atom at the given time t, 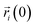corresponds to the initial position of the i-atom. In eqn (1), 〈…〉 brackets correspond to the time average in an interval of 100 ps. To avoid any possible spurious effect due to any possible translational displacement of the NP, the distances 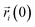and were computed concerning the position of the HEA NP’s center of mass.

The Von Mises shear strain at the i-atom, η^VM_i, is calculated from the second shear strain invariant:

where η_αβ corresponds to the local strain of the i-atom with its neighbors, and the subscripts α and β correspond to the strain components in the x, y, and z axes. To define the Von Mises shear strain it is necessary to adopt a cutoff radius to define the numbers of neighbors that contribute in the calculation of η^VM_i, here a cutoff of 3.0 Å was adopted.^53,54

Results

A good description of the thermal resistance of any NP is to calculate the melting temperature, which allows us to follow the evolution of the potential energy as a function of the temperature. In Fig. 2, we show this curve for our system for the mentioned radius. We can observe that even small NPs are stable for temperatures of 800 K to undergo a phase transformation from liquid to solid. This transformation is dependent on the nanocluster size. It is worth noticing that the smaller radii considered in this publication (R = 5 and 7.5 Å cases) appear to have a slight fall in the potential energy curve later giving rise to the melting of the HEA NPs. This effect could be associated with the surface reconstruction because of the small size of the nanocluster. Besides, NPs with d > 10 Å behave like a bulk material, avoiding structural transition until the melting point.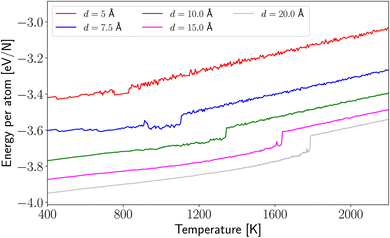

Fig. 2 Potential energy curves as a function of temperature. For illustrative purposes, only R = 5, 7.5, 10, 15, 20 Å are depicted in the figure.

A summary of melting temperature as a function of the HEA NP radius is illustrated in Fig. 3. As expected, the melting point grows as a function of the NP size, with a slight saturation at the size of R = 40 Å. However, many theoretical models assume that NPs’ melting points increase as a function of radius using an exponent of −1.⁵⁵ In Fig. 3, it is shown that theoretical models for spherical NPs show excellent agreement with simulation data, where the usual models assume that temperature scales with HEA NP size as:

where T₀ is the bulk melting point, X is a constant that depends on the material and R is the NP radius. The exponent c adopts a −1 value close to our c = −0.978 value from our model. Even our fit assumes a bulk melting point T₀ = 2184 K, in line with values reported by Deluigi⁴⁷ for the bulk FeCuCrCoNi HEA. The latter supports the assumption of a two-phase model with melting temperature depending on competition from solid and liquid phases.

Fig. 3 (a) T_melt as a function of the NP size, dashed line shows an analytical fit model. (b) T_melt as a function of the reciprocal radius, the dashed line shows an analytical fit model. For both adjustments made, we highlight the equation used and the parameters obtained.

The size effect dependence in melting models is usually attributed to unbound atoms on the surface that promote the melting of NPs. In some cases, a premelting from the surface influences the melting point, so it is necessary to include the presence of a liquid–shell model to describe the phase transition in terms of NP size accurately.^56,57 A simpler formulation can be obtained from the Gibbs–Thomson equation, which assumes a direct phase transformation from solid to liquid utilizing the reciprocal radius 1/R. Fig. 3b, displays an excellent relation predicting a C = 1, which not only shows that the models are valid in the nanoscale but also that melting behavior does not present contributions from the surface.

To understand the diffusion mechanism, we inspected the mean square displacement in terms of different elements. As shown in Fig. 4, each MSD curve follows the same trend, independent of the NP size. However, differences appear when we inspect the mean square displacement of each element, where Cu and Fe atoms show more mobility at lower temperatures than other components. This effect is almost negligible at R = 5 Å, but becomes more pronounced with size with the increase in atoms and the decrease in the surface-to-volume ratio.

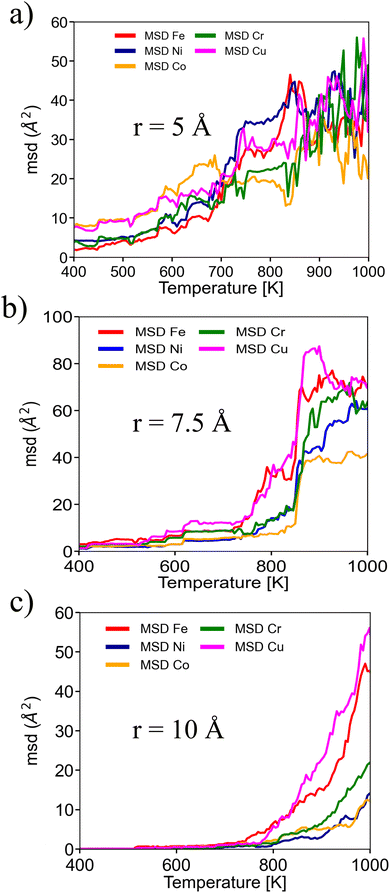Fig. 4 MSD for different NP radii. To illustrate early states of atomic mobility, MSD was plotted until a temperature of 1000 K.

In Fig. 5, we show the calculated pair correlation function (PDF) for different HEA NP sizes. From here, we can study the atomic distribution during the temperature ramp in detail. Each of the simulated nanostructures shows a well-defined peak that matches the first neighbor distance of the FCC lattice of the HEA NP; the same applies to second and subsequent neighbors. We want to highlight that it is independent of the NP size, with 7.5 Å and 20 Å cases only showing small fluctuations of the peaks, mainly attributed to the small number of atoms considered for the calculations. At higher temperatures, peak intensities decrease, but there is no creation of new peaks during the thermal load. This effect is observed even in the 7.5 Å case, where the smaller size should increase probabilities for clustering as a consequence of the shorter exploration path of the atoms. In short, the behavior observed for each NP is consistent with the absence of clustering of the elements, ruling out the possible precipitation of some elements due to the increase in diffusion through the thermal load. It is worth noticing that clustering or precipitation has been observed in other HEA NPs, particularly those with a high mismatch between atomic sizes.

Fig. 5 Pair correlation function for selected HEA NPs with different radii (in panel (a) 7.5 Å, and in panel (b) 20 Å). Each curve shows a different temperature (300, 1200, 1500 and 2000 K). It is illustrated with the pair correlation function per atomic species which separates the contribution of each element from the total contribution.

In Fig. 6, we show an atomistic representation during the thermal loading of the NP. For R = 5 Å, there is an apparent change in the shape of the NP with temperature. Besides, inspecting each element confirms no evidence of clustering or precipitation because the atoms do not form stable structures or crystalline domains for atomic species. Ultrasmall nanoclusters are known to tend to form icosahedral shape configurations,^58–60 the inspection of elements does not confirm the formation of any subcluster inside the HEA NP, as can be expected of few atom monoatomic clusters.

Fig. 6 Illustration of atom distribution as a function of temperature for the case R = 5 Å. Figure shows the whole NP, and the atom positions per element.

At R = 20 Å (Fig. 7), HEA NPs retain a spherical shape, but atoms show apparent mobility with a thermal load as could be seen from a visual inspection of the whole structure. On the other hand, the distribution per atomic species is relatively homogeneous over the whole NP (Fig. 7), which confirms the observation from the pair correlation function. Even more, we employed two algorithms to identify local crystalline structures. In both cases, the common neighbor analysis⁶¹ and the polyhedral template matching algorithm⁶² (both implemented in OVITO code) used over the mono-elemental NP do not show evidence of any crystalline structures.

Fig. 7 Illustration of atom distribution as a function of temperature for the case R = 20 Å. Figure shows the whole NP, and the atom positions per element.

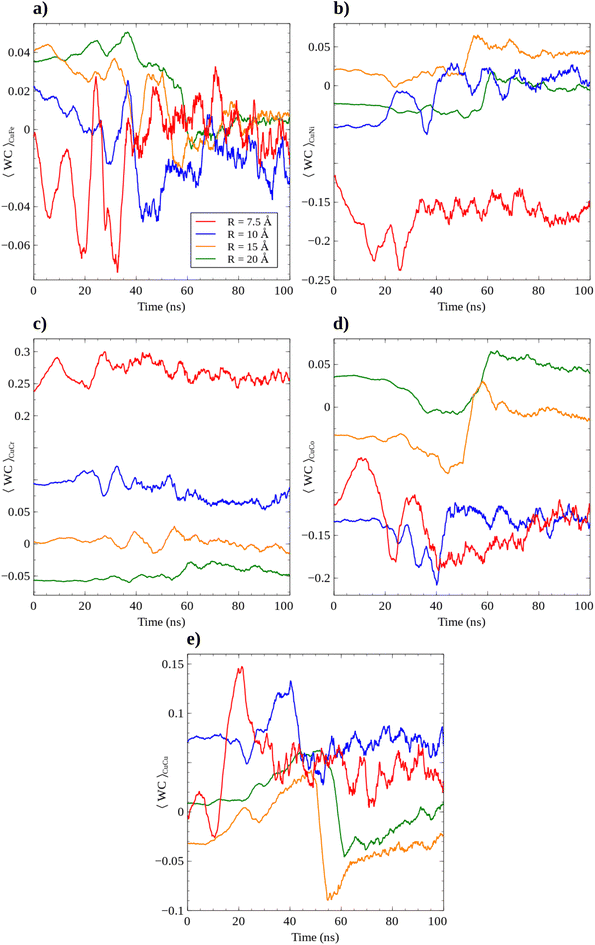
Possible segregation mechanisms are quantitatively evaluated by means of the Warren–Cowley parameter (WC). The WC parameter is studied in terms of Cu atoms, as shown in Fig. 8. As shown for Fe, and Ni, the close to zero values suggest a random distribution. The major difference is associated with R = 7.5 and 10 Å, showing a slight clustering for CuNi and CuCo, and a repulsive effect for CuCr. Almost zero values (random distribution) are found for CuCu and CuFe. The larger the cluster size, the smaller the possible short-range ordering effect observed. All in all the close to zero values are consistent with the lack of a Short-Range Order (SRO) effect in FeNiCrCoCu.

Fig. 8 WC parameters for Cu at different NP sizes and temperatures. (a–e) correspond to the correlations with Fe, Ni, Cr, Co, and Cu, respectively. The colors red, blue, yellow, and green correspond to NP radii of 7.5, 10.0, 15.0, and 20.0 Å, respectively.

To understand the high mobility of Fe atoms, Fig. 9 illustrates the potential energy contribution by atomic species as a function of the temperature. The curves show that for each NP radius (5, 10, and 20 Å) the Fe atoms have a higher potential energy than the other elements. In every curve, the difference in potential energy is at least 0.5 eV compared to the other elements. The higher potential energy levels can explain the enhanced mobility of Fe atoms since it can be interpreted as a higher local pressure as a consequence of their atomic environment. It is worth noticing that Fe atoms show an abrupt increase in potential energy at temperatures around 1000 K, which matches with the increase in MSD and premelting of the NP.

Fig. 9 Average potential energy per element as a function of temperature, for r = 5, 15, and 20 Å (a–c).

The Von Mises shear strain for different temperatures is illustrated in Fig. 10. The figure shows that shear strain is rather homogeneous at a temperature of 600 K. For 900 K, a yellow shell is observed with atoms with Von Mises strains higher than 0.5. This high value of strain is the consequence of atomic displacement due to the surface diffusion rather than an effective strain leading to tensile stress in the NP shell. Even more, the atoms with high strain are found in 2–3 atomic layers, which is a small value to adopt a core@shell effect in the premelting of the NP. At higher temperatures, Von Mises propagates to the core but shows a shell of 10–20 Å thickness; however, the NPs tend to lose their crystalline structure.

Fig. 10 Von Mises strain at different temperatures for a NP with R = 20 Å. Color coding display the Von Mises shear strain intensity.

Conclusion

Many theoretical works have addressed the size-dependence effect on melting temperature. In some particular mono elemental NPs or core@shell NPs, the melting process is the consequence of collective enhanced diffusion promoted by the surface. In HEA, the chemical complexity introduces internal strain as a consequence of the different atomic sizes; this way, the surface stress of unbound atoms is not the unique contribution as can be expected in conventional alloys. PtPdRhCo multi-element alloys have shown that Von Mises strain increases continuously with temperature, contributing to the formation of a liquid shell. In that case, NPs are larger than the ones simulated by us with melting temperature close to the respective bulk material. Alarifi et al.²⁸ studied the premelting in Ag NPs, showing that a 40 Å NP behaves differently to larger size NPs. In the Ag case, the melting layers were set at 18 Å, which is larger than the few atomic layers found by us, also suggesting that the size of the NP has a major role in the melting stages of the nanostructure.^29,63 The surface contribution to potential energy reported in monocrystalline NPs shows a difference with bulk atoms close to 0.5 eV. In HEA NPs, a potential energy difference of 0.5 eV is observed not only on the surface but also on the Fe atoms product of the chemical complexity. The latter suggests that for the NP sizes simulated here, the melting not only originates in the NP shell but also in the NP core as a consequence of the coexistence of different atom types in the crystalline lattice.

To conclude, our results show that melting temperature strongly depends on the HEA NP size, which agrees with classical melting models. Besides, we found a linear dependence of temperature with R⁻¹, which confirms that melting does not have a liquid contribution from the surface melting. Instead, enhanced mobility of Fe and Cu atoms at lower temperatures is observed, suggesting that the diffusion of some particular elements in the HEA NP can dominate melting. While direct experiments on the thermal behavior of FeCrCoNiCu have not been addressed, there exists indirect evidence that grain boundaries have shown migration of Cu towards the surface without complementary analysis. On the other hand, Zhang et al.⁶⁴ after cold-rolling and melting observed phase separation of FCC FeCrCoNiCu in a Cu-rich phase and a second FCC structure composed of FeCrCoNi. Both phases coexist forming dendritic like structures. Other works on AuCoCuNiPt NPs, show the precipitation of Au and Cu towards the NP surface.⁶⁵ AlSiCrMnFeNiCu HEA NPs,⁶⁶ and AlCuFe⁶⁷ show the precipitation of Al forming an oxide layer, they explain the results based on single element melting points and lower enthalpy of mixing, similar to that observed here for Cu. Recent experiments performed on FeCoNiCuPd NPs,⁶⁸ showed a melting point in line with that reported here, in addition in situ TEM demonstrated that melting is initiated by Cu atoms due to their lower melting temperature, in excellent agreement with the prediction of our simulations in a different HEA. Finally, a CoCrFeNiGa NP shows at least three stages of melting related to some phase transitions from FCC to BCC, and segregation or precipitation of some elements,⁶⁹ the interesting point is that the experiments also report a loss of Ga during the heating as the first melting event due to its low melting point. Cu atoms have the lowest melting point among all the elements in the HEA, which, in agreement with experimental evidence, is expected to lead to early diffusion as the temperature increases. On the other hand, Fe has a similar melting point to Cr and Ni, but this comparison is made considering the BCC phase. A possible explanation is that Fe atoms adopt an FCC structure in the NPs, causing melting to occur before any structural transition from BCC to FCC takes place. Finally, we note that the results provided by simulations have also been observed in HEA NPs with different compositions. Considering that the number of studies on HEA NPs has increased in recent years,^70,71 it is necessary to carry out modeling of different multi-elemental NPs, taking into account their sizes and geometries in order to support and guide future experiments.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Fondo Nacional de Investigaciones Científicas y Tecnológicas (FONDECYT, Chile) under grants #1240655 (MR, AP, JR, FV), #1240663 (MR), and FONDECYT de Iniciación #11190484 (FV). The authors thank the Financiamiento Basal para Centros Científicos y Tecnológicos de Excelencia AFB180001 and AFB220001. FR acknowledges the Human Capital Subdirectorate/National Doctorate/2025-21251417. WS thanks Fomento de Vinculación Internacional (FOVI, Chile) under Grant #FOVI230054, and scholarship Doctorado Nacional from Agencia Nacional de Investigación y Desarrollo (ANID, Chile) under Grant #21250704. FC and SB acknowledge the support of POSTDOCT_DICYT project 042431BR_Postdoc Vicerrectoría de investigación, Innovación y Creación. This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).

References

1. Y. Yao, Z. Huang, P. Xie, S. D. Lacey, R. J. Jacob, H. Xie, F. Chen, A. Nie, T. Pu and M. Rehwoldt, et al., Carbothermal shock synthesis of high-entropy-alloy nanoparticles, Science, 2018, 359, 1489–1494.
2. P.-C. Chen, X. Liu, J. L. Hedrick, Z. Xie, S. Wang, Q.-Y. Lin, M. C. Hersam, V. P. Dravid and C. A. Mirkin, Polyelemental nanoparticle libraries, Science, 2016, 352, 1565–1569.
3. Y. Sun and S. Dai, High-entropy materials for catalysis: A new frontier, Sci. Adv., 2021, 7, eabg1600.
4. Y. Ma, Y. Ma, Q. Wang, S. Schweidler, M. Botros, T. Fu, H. Hahn, T. Brezesinski and B. Breitung, High-entropy energy materials: challenges and new opportunities, Energy Environ. Sci., 2021, 14, 2883–2905.
5. D. Wu, K. Kusada, Y. Nanba, M. Koyama, T. Yamamoto, T. Toriyama, S. Matsumura, O. Seo, I. Gueye and J. Kim, et al., Noble-metal high-entropy-alloy nanoparticles: atomic-level insight into the electronic structure, J. Am. Chem. Soc., 2022, 144, 3365–3369.
6. N. K. Katiyar, K. Biswas, J.-W. Yeh, S. Sharma and C. S. Tiwary, A perspective on the catalysis using the high entropy alloys, Nano Energy, 2021, 88, 106261.
7. T. Zuo, M. C. Gao, L. Ouyang, X. Yang, Y. Cheng, R. Feng, S. Chen, P. K. Liaw, J. A. Hawk and Y. Zhang, Tailoring magnetic behavior of CoFeMnNiX (X = Al, Cr, Ga, and Sn) high entropy alloys by metal doping, Acta Mater., 2017, 130, 10–18.
8. A. Ferrari and F. Körmann, Surface segregation in Cr-Mn-Fe-Co-Ni high entropy alloys, Appl. Surf. Sci., 2020, 533, 147471.
9. C. M. Clausen, M. L. Nielsen, J. K. Pedersen and J. Rossmeisl, Ab initio to activity: machine learning-assisted optimization of high-entropy alloy catalytic activity, High Entropy Alloys Mater., 2023, 1, 120–133.
10. G. Feng, F. Ning, J. Song, H. Shang, K. Zhang, Z. Ding, P. Gao, W. Chu and D. Xia, Sub-2 nm ultrasmall high-entropy alloy nanoparticles for extremely superior electrocatalytic hydrogen evolution, J. Am. Chem. Soc., 2021, 143, 17117–17127.
11. D. Wu, K. Kusada, T. Yamamoto, T. Toriyama, S. Matsumura, S. Kawaguchi, Y. Kubota and H. Kitagawa, Platinum-group-metal high-entropy-alloy nanoparticles, J. Am. Chem. Soc., 2020, 142, 13833–13838.
12. T. Löffler, A. Ludwig, J. Rossmeisl and W. Schuhmann, What makes high-entropy alloys exceptional electrocatalysts?, Angew. Chem., Int. Ed., 2021, 60, 26894–26903.
13. X. Wang, Q. Liu and X. Wang, High-Entropy Materials: from Bulk to Sub-nano, Adv. Funct. Mater., 2025, 2504275.
14. S. Uporov, R. Ryltsev, V. Sidorov, S. K. Estemirova, E. Sterkhov, I. Balyakin and N. Chtchelkatchev, Pressure effects on electronic structure and electrical conductivity of TiZrHfNb high-entropy alloy, Intermetallics, 2022, 140, 107394.
15. Y. Wang and Y. Wang, High-entropy Alloys in Catalyses and Supercapacitors: A Review, Nano Energy, 2022, 104, 107958.
16. S. Perumal, D. B. Han, T. Marimuthu, T. Lim, H. W. Kim and J. Seo, Active Learning-Driven Discovery of Sub-2 nm High-Entropy Nanocatalysts for Alkaline Water Splitting, Adv. Funct. Mater., 2025, 2424887.
17. L. Yang, R. He, J. Chai, X. Qi, Q. Xue, X. Bi, J. Yu, Z. Sun, L. Xia and K. Wang, et al., Synthesis Strategies for High Entropy Nanoparticles, Adv. Mater., 2025, 37, 2412337.
18. Y. Chen, T. Duval, U. Hung, J. Yeh and H. Shih, Microstructure and electrochemical properties of high entropy alloys—a comparison with type-304 stainless steel, Corros. Sci., 2005, 47, 2257–2279.
19. D. Tejero-Martin, M. Rezvani Rad, A. McDonald and T. Hussain, Beyond traditional coatings: a review on thermal-sprayed functional and smart coatings, J. Therm. Spray Technol., 2019, 28, 598–644.
20. Y. Zhang, B. Zhang, K. Li, G.-L. Zhao and S. Guo, Electromagnetic interference shielding effectiveness of high entropy AlCoCrFeNi alloy powder laden composites, J. Alloys Compd., 2018, 734, 220–228.
21. S. Link and M. A. El-Sayed, Size and temperature dependence of the plasmon absorption of colloidal gold nanoparticles, J. Phys. Chem. B, 1999, 103, 4212–4217.
22. Y. Hatakeyama, T. Morita, S. Takahashi, K. Onishi and K. Nishikawa, Synthesis of gold nanoparticles in liquid polyethylene glycol by sputter deposition and temperature effects on their size and shape, J. Phys. Chem. C, 2011, 115, 3279–3285.
23. L. H. Fischer, G. S. Harms and O. S. Wolfbeis, Upconverting nanoparticles for nanoscale thermometry, Angew. Chem., Int. Ed., 2011, 50, 4546–4551.
24. D. Vorkapic and T. Matsoukas, Effect of temperature and alcohols in the preparation of titania nanoparticles from alkoxides, J. Am. Ceram. Soc., 1998, 81, 2815–2820.
25. K. S. Rao, K. El-Hami, T. Kodaki, K. Matsushige and K. Makino, A novel method for synthesis of silica nanoparticles, J. Colloid Interface Sci., 2005, 289, 125–131.
26. R. Grisel, K.-J. Weststrate, A. Gluhoi and B. E. Nieuwenhuys, Catalysis by gold nanoparticles, Gold Bull., 2002, 35, 39–45.
27. G. Parravicini, A. Stella, P. Tognini, P. Merli, A. Migliori, P. Cheyssac and R. Kofman, Insight into the premelting and melting processes of metal nanoparticles through capacitance measurements, Appl. Phys. Lett., 2003, 82, 1461–1463.
28. H. Alarifi, M. Atis, C. Ozdogan, A. Hu, M. Yavuz and Y. Zhou, Determination of complete melting and surface premelting points of silver nanoparticles by molecular dynamics simulation, J. Phys. Chem. C, 2013, 117, 12289–12298.
29. N. Wang, S. Rokhlin and D. Farson, Nonhomogeneous surface premelting of Au nanoparticles, Nanotechnology, 2008, 19, 415701.
30. H. Tafrishi, S. Sadeghzadeh and R. Ahmadi, Molecular dynamics simulations of phase change materials for thermal energy storage: a review, RSC Adv., 2022, 12, 14776–14807.
31. N. Wang, S. Rokhlin and D. Farson, Ultrafast laser melting of Au nanoparticles: atomistic simulations, J. Nanopart. Res., 2011, 13, 4491–4509.
32. P. Tian, Molecular dynamics simulations of nanoparticles, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2008, 104, 142–164.
33. H. Akbarzadeh, E. Mehrjouei, M. Abbaspour and A. N. Shamkhali, Melting behavior of bimetallic and trimetallic nanoparticles: a review of MD simulation studies, Top. Curr. Chem., 2021, 379, 22.
34. V. Samsonov, I. Talyzin, S. Vasilyev, V. Puytov and A. Romanov, On surfacepre-melting of metallic nanoparticles: molecular dynamics study, J. Nanopart. Res., 2023, 25, 105.
35. S. Alavi and D. L. Thompson, Molecular dynamics simulations of the melting of aluminum nanoparticles, J. Phys. Chem. A, 2006, 110, 1518–1523.
36. X. Zhang, W. Li, D. Wu, Y. Deng, J. Shao, L. Chen and D. Fang, Size and shape dependent melting temperature of metallic nanomaterials, J. Phys.: Condens. Matter, 2019, 31, 075701.
37. W. Qi and S. Lee, Phase stability, melting, and alloy formation of Au-Ag bimetallic nanoparticles, J. Phys. Chem. C, 2010, 114, 9580–9587.
38. J. Rojas-Nunez, R. I. Gonzalez, E. M. Bringa, S. Allende, P. Sepúlveda, N. Arancibia-Miranda and S. E. Baltazar, Toward controlled morphology of FeCu nanoparticles: Cu concentration and size effects, J. Phys. Chem. C, 2018, 122, 8528–8534.
39. S.-P. Ju, I.-J. Lee and H.-Y. Chen, Melting mechanism of Pt–Pd–Rh–Co high entropy alloy nanoparticle: an insight from molecular dynamics simulation, J. Alloys Compd., 2021, 858, 157681.
40. O. Kushnerov, AlCoCuFeNi high-entropy alloy nanoparticle melting and solidification: a classical molecular dynamics simulation study, J. Phys. Electron., 2019, 27, 41–46.
41. X. Wang, Q. Dong, H. Qiao, Z. Huang, M. T. Saray, G. Zhong, Z. Lin, M. Cui, A. Brozena and M. Hong, et al., Continuous synthesis of hollow high-entropy nanoparticles for energy and catalysis applications, Adv. Mater., 2020, 32, 2002853.
42. X. Zuo, R. Yan, L. Zhao, Y. Long, L. Shi, Q. Cheng, D. Liu and C. Hu, A hollow PdCuMoNiCo high-entropy alloy as an efficient bi-functional electrocatalyst for oxygen reduction and formic acid oxidation, J. Mater. Chem. A, 2022, 10, 14857–14865.
43. Z. Zeng, J. Zhao, X. Zhou, J. Li and B. Liang, Thermal stability of Al-Cu-Fe-Cr-Ni high entropy alloy bulk and nanoparticle structure: A molecular dynamics perspective, Chem. Phys., 2019, 517, 126–130.
44. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171.
45. M. S. Daw, S. M. Foiles and M. I. Baskes, The embedded-atom method: a review of theory and applications, Mater. Sci. Rep., 1993, 9, 251–310.
46. R. Pasianot and D. Farkas, Atomistic modeling of dislocations in a random quinary high-entropy alloy, Comput. Mater. Sci., 2020, 173, 109366.
47. O. R. Deluigi, R. C. Pasianot, F. Valencia, A. Caro, D. Farkas and E. M. Bringa, Simulations of primary damage in a High Entropy Alloy: Probing enhanced radiation resistance, Acta Mater., 2021, 213, 116951.
48. S. Q. Wang and H. Q. Ye, First-principles studies on the component dependences of High-Entropy Alloys, Adv. Mater. Res., 2011, 338, 380–383.
49. D. Farkas and A. Caro, Model interatomic potentials and lattice strain in a high-entropy alloy, J. Mater. Res., 2018, 33, 3218–3225.
50. F. J. Valencia, M. Ramírez, A. Varas and J. Rogan, Understanding the Stability of Hollow Nanoparticles with Polycrystalline Shells, J. Phys. Chem. C, 2020, 124, 10143–10149.
51. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural relaxation made simple, Phys. Rev. Lett., 2006, 97, 170201.
52. A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
53. M. L. Falk and J. S. Langer, Deformation and failure of amorphous, solidlike materials, Annu. Rev. Condens. Matter Phys., 2011, 2, 353–373.
54. F. Shimizu, S. Ogata and J. Li, Theory of shear banding in metallic glasses and molecular dynamics calculations, Mater. Trans., 2007, 48, 2923–2927.
55. G. Guenther and O. Guillon, Models of size-dependent nanoparticle melting tested on gold, J. Mater. Sci., 2014, 49, 7915–7932.
56. H. Reiss and I. B. Wilson, The effect of surface on melting point, J. Colloid Sci., 1948, 3, 551–561.
57. K.-J. Hanszen, Theoretische Untersuchungen über den Schmelzpunkt kleiner Kügelchen: Ein Beitrag zur Thermodynamik der Grenzflächen, Z. Phys., 1960, 157, 523–553.
58. J. Rogan, G. García, J. A. Valdivia, W. Orellana, A. Romero, R. Ramírez and M. Kiwi, Small Pd clusters: A comparison of phenomenological and ab initio approaches, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115421.
59. J. Rogan, A. Varas, J. A. Valdivia and M. Kiwi, A strategy to find minimal energy nanocluster structures, J. Comput. Chem., 2013, 34, 2548–2556.
60. F. Muñoz, J. Rogan, G. García, M. Ramírez, J. Valdivia, R. Ramírez and M. Kiwi, Collisions between a single gold atom and 13 atom gold clusters: an ab initio approach, Eur. Phys. J. D, 2011, 61, 87–93.
61. H. Tsuzuki, P. S. Branicio and J. P. Rino, Structural characterization of deformed crystals by analysis of common atomic neighborhood, Comput. Phys. Commun., 2007, 177, 518–523.
62. P. M. Larsen, S. Schmidt and J. Schiøtz, Robust structural identification via polyhedral template matching, Modell. Simul. Mater. Sci. Eng., 2016, 24, 055007.
63. F. G. Shi, Size dependent thermal vibrations and melting in nanocrystals, J. Mater. Res., 1994, 9, 1307–1313.
64. L. Zhang, J. Fan, D. Liu, M. Zhang, P. Yu, Q. Jing, M. Ma, P. Liaw, G. Li and R. Liu, The microstructural evolution and hardness of the equiatomic CoCrCuFeNi high-entropy alloy in the semi-solid state, J. Alloys Compd., 2018, 745, 75–83.
65. S. Krouna, A. Acheche, G. Wang, N. O. Pena, R. Gatti, C. Ricolleau, H. Amara, J. Nelayah and D. Alloyeau, Atomic-Scale Insights Into the Thermal Stability of High-Entropy Nanoalloys, Adv. Mater., 2025, 37, 2414510.
66. R. Rawat, B. K. Singh, A. Tiwari, N. Arun, A. P. Pathak, Y. Shadangi, N. Mukhopadhyay, S. R. Nelamarri, S. V. Rao and A. Tripathi, Formation of Cu-Ni enriched phases during laser processing of non-equiatomic AlSiCrMnFeNiCu high entropy alloy nanoparticles, J. Alloys Compd., 2022, 927, 166905.
67. R. Rawat, A. Tiwari, N. Arun, S. N. Rao, A. Pathak, Y. Shadangi, N. Mukhopadhyay, S. V. Rao and A. Tripathi, Nanosecond pulsed laser ablation of Al–Cu–Fe quasicrystalline material: effects of solvent and fluence, J. Alloys Compd., 2021, 859, 157871.
68. N. Hashimoto, K. Mori, H. Yoshida, N. Kamiuchi, R. Kitaura, R. Hirasawa and H. Yamashita, Thermal Stability of High-Entropy Alloy Nanoparticles Evaluated by In Situ TEM Observations, Nano Lett., 2024, 24, 7063–7068.
69. N. Shkodich, T. Smoliarova, H. Ali, B. Eggert, Z. Rao, M. Spasova, I. Tarasov, H. Wende, K. Ollefs, B. Gault and M. Farle, Effect of high energy ball milling, heat treatment and spark plasma sintering on structure, composition, thermal stability and magnetism in CoCrFeNiGa_x (x = 0.5; 1) high entropy alloys, Acta Mater., 2025, 284, 120569.
70. D. Alloyeau, N. Ortiz Pena, G. Wang, C. Ricolleau and J. Nelayah, In situ and operando transmission electron microscopy for the synthesis, fundamental understanding and catalytic applications of nanoalloys, Adv. Phys.: X, 2025, 10, 2481277.
71. W. Wan, K. Liang, P. Zhu, P. He and S. Zhang, Recent advances in the synthesis and fabrication methods of high-entropy alloy nanoparticles, J. Mater. Sci. Technol., 2024, 178, 226–246.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra08595g

---