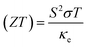DOI:
10.1039/D5RA02609A
(Paper)
RSC Adv., 2025,
15, 20397-20406
Above-room-temperature strain-stable half-metallic phase owing to a high thermoelectric response in CaCu3Cr2Re2O12†
Received
14th April 2025
, Accepted 26th May 2025
First published on 17th June 2025
Abstract
We present the electronic, magnetic, and thermoelectric properties of the CaCu3Cr2Re2O12 quadruple double perovskite oxide (QDPO) using ab initio calculations. Strong antiferromagnetic interactions between Cu2+↑Cr3+↑Re5+↓ result in a ferrimagnetic (FiM) ground state. A half-metallic (HM) state is evident with a finite energy gap (Eg) of 1.62 eV in the spin-majority channel (N↑), which is large enough to ensure a long mean free path for spin and prevent spin-flipping with a colossal spin-filtering ability. Due to a significant Eg in N↑, the system displays a high figure of merit (0.76) at 300 K. The calculated spin moments of +0.48/+2.55/−0.92 μB and spin-magnetization densities on the Cu/Cr/Re further verify the FiM state. The magnetic phase transition yields a Curie temperature (TC) of 340 K, which is below the experimental value (360 K). Because thermal energy near TC disrupts the magnetic ordering, magnetization is consequently reduced, which is also reflected in the susceptibility curve. Additionally, the FiM state of the structure was confirmed under modulated applied magnetic fields. Finally, the HM FiM state is also verified under a moderate biaxial ([110]) strain of ±5%. Hence, this work provides deep insights into this QDPO, highlighting its stable HM FiM behavior, above-room-temperature TC and high thermoelectric response, which promises potential applications in spintronics.
1 Introduction
In the realm of magnetic materials fabricated at the ultra-small scale, special focus is placed on those composed of transition metals (TMs) such as Fe, Co, and Ni, along with their alloys.1 One of the most promising types of magnetic materials is half-metallic (HM) compounds, such as ferromagnetic (FM) and ferrimagnetic (FiM) materials. These compounds exhibit metallic conductivity in one spin channel while behaving as semiconductors or insulators in the opposite spin channel.2 This means that the electron carriers are entirely (100%) spin-polarized (SP) at the Fermi level (EF), producing HM magnetic motifs that are highly essential for spintronics applications, essentially enabling the manipulation and storage of information based on electron spins, such as in tunneling devices, spin transistors, and magnetic logic gates.3–9 It has been observed that tunneling conduction in a spin-based trilayer essentially depends on the SP of the electrodes,10,11 consequently resulting in a giant tunneling magnetoresistance (TMR), which can be utilized in high-density data storage and extremely efficient magnetic sensors.12 However, an enormous TMR ratio in trilayer devices is susceptible to temperature (temp.), and it sharply decreases with rising temp. due to a substantial reduction in SP magnitude near the magnetic transition temp. (MTT). Hence, materials that maintain maximum (100%) SP charge carriers at room temp. with an MTT > 300 K are highly beneficial for developing future high-temp. spintronic devices. The first predicted HM FM material was the NiMnSb half-Heusler alloy13 followed by CrO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14,15 and Fe3O4
14,15 and Fe3O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16,17, which were also proposed as HM and investigated comprehensively. In this regard, perovskite oxides (POs) have become very important candidates, especially after the discovery of sizable magnetoresistance in La1−xSrxMnO3
16,17, which were also proposed as HM and investigated comprehensively. In this regard, perovskite oxides (POs) have become very important candidates, especially after the discovery of sizable magnetoresistance in La1−xSrxMnO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 and Tl2Mn2O7
18 and Tl2Mn2O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19, further emphasizing the importance of HM structures. Similarly, double perovskite oxides (DPOs) with an ordered A2BB′O6 form, where the B and B′ ions are usually 3d and 4/5d TMs,20,21 are highly beneficial for spintronic applications.22 Excitingly, an HM FiM state is anticipated in the Sr2FeMoO6 DPO, which has a metal-to-insulator transition (MIT) at 410 K and also demonstrates a large TMR ratio at room temperature. In this context, the Fe3+ 3d5 and Mo5+ 5d1 ions with
19, further emphasizing the importance of HM structures. Similarly, double perovskite oxides (DPOs) with an ordered A2BB′O6 form, where the B and B′ ions are usually 3d and 4/5d TMs,20,21 are highly beneficial for spintronic applications.22 Excitingly, an HM FiM state is anticipated in the Sr2FeMoO6 DPO, which has a metal-to-insulator transition (MIT) at 410 K and also demonstrates a large TMR ratio at room temperature. In this context, the Fe3+ 3d5 and Mo5+ 5d1 ions with  are coupled antiferromagnetically, resulting in a FiM spin-ordering (SO).3 Similarly, an HM FiM behavior is observed in Sr2CrReO6 owing to it having the highest Curie temp. (TC) of 635 K among the DPO family.23,24 However, it is theoretically established that SP in HM DPOs such as Sr2FeMoO6 substantially depends on temp. and cation disorder, as well as being proportional to the spin-magnetization of the cores.25 In the past decade, numerous efforts have been dedicated to develop robust 2D FM/FiM materials with high TC. One effective approach involves modulating the magnetism in existing 2D layered materials through post-treatment techniques, such as doping, ion or charge implantation,26,27 strain engineering,28,29 and defect engineering.30,31 The research discovered that the stress-induced transformation of two-dimensional materials from an indirect to a direct energy gap (Eg) significantly enhances photoluminous (PL) efficiency, making them more suitable for optoelectronic devices.32–41 Thus, novel nano-electronic and optoelectronic devices with stress-adjustable properties hold significant potential for spintronic applications. Moreover, to optimize material properties, the doping/ion implantation strategy has been explored, in which additional magnetic cations are introduced at the A-site in the DPO with a ratio of 1 to 3. This results in a new A- and B-site ordered quadruple DPO (QDPO) keeping an
are coupled antiferromagnetically, resulting in a FiM spin-ordering (SO).3 Similarly, an HM FiM behavior is observed in Sr2CrReO6 owing to it having the highest Curie temp. (TC) of 635 K among the DPO family.23,24 However, it is theoretically established that SP in HM DPOs such as Sr2FeMoO6 substantially depends on temp. and cation disorder, as well as being proportional to the spin-magnetization of the cores.25 In the past decade, numerous efforts have been dedicated to develop robust 2D FM/FiM materials with high TC. One effective approach involves modulating the magnetism in existing 2D layered materials through post-treatment techniques, such as doping, ion or charge implantation,26,27 strain engineering,28,29 and defect engineering.30,31 The research discovered that the stress-induced transformation of two-dimensional materials from an indirect to a direct energy gap (Eg) significantly enhances photoluminous (PL) efficiency, making them more suitable for optoelectronic devices.32–41 Thus, novel nano-electronic and optoelectronic devices with stress-adjustable properties hold significant potential for spintronic applications. Moreover, to optimize material properties, the doping/ion implantation strategy has been explored, in which additional magnetic cations are introduced at the A-site in the DPO with a ratio of 1 to 3. This results in a new A- and B-site ordered quadruple DPO (QDPO) keeping an  form, which possesses a very high MTT and magnetization (M). For instance, the antiferromagnetic (AFM) interaction between the magnetic cations induces a FiM state in the CaCu3Fe2Re2O12 QDPO, which features a very high MIT of 560 K and 100% SP. In this state, the spin-majority and spin-minority channels (N↑ and N↓) exhibit nonconductive and conductive traits, respectively, along with a large total magnetic moment (mt) of 8.7 μB.42 In this continuum, a newly ordered NaCu3Fe2Os2O12 QDPO was synthesized, which exhibits an HM FiM nature with a wide energy gap (Eg) in N↑ and spin ordering of Cu2+↑Fe3+↑Os5.5+↓, showing a TC above 380 K.43 Combined experimental and theoretical studies demonstrate that the FiM LaCu32+Co22+Re25.5+O12 QDPO is nearly 100% ordered with Cu2+↑Fe3+↑Os5.5+↓ SO and a TC of 150 K.44 Wang et al. theoretically predicted a series of HM FiM ACu3Fe2Re2O12 (A = Ca, Sr, Ba, Pb, Sc, Y, La) QDPOs, where the AFM coupling between CuFe and Re is dominant.45 It was established that compounds with A2+ = Ca/Sr/Ba/Pb and A3+ = Sc/Y/La ions exhibit TC values greater than 405 K and 502 K, respectively. Similarly, LaCu3Fe2Re2O12 is a HM material with a very large TC of 710 K, where a strong AFM coupling of Cu2+↑Fe3+↑Os4.5+↓ results in a FiM lowest energy state.46 It was also observed that the saturated total mt of 7.0 μB at 710 K increases to 8.0 μB at 2 K. Very recently, Zhang et al. experimentally verified the HM FiM nature in the CaCu3Cr2Re2O12 (CCCRO) system, maintaining a spin ordering of Cu2+↑ Cr3+↑ Re5+↓ above room temp. (360 K).47 However, in this stable charge configuration, the calculated mt of 5.0 μB is significantly greater than the experimentally measured value of 1.6 μB per f.u. Therefore, the intriguing features of this new class of materials, as outlined above, motivate us to explore the different characteristics of the recently synthesized CCCRO QDPO through density functional theory (DFT) calculations. These calculations demonstrate a FiM spin ordering, accompanied by a mt of 5.0 μB per formula unit (f.u.), and a half-metallic nature, featuring a 1.62 eV gap in the N↑ channel. This results in a high TC of 340 K. The material shows metallic behavior in the N↓ channel, with a p-type thermoelectric (TE) response. Moreover, the HM phase of the system remains stable under biaxial strain, and the material exhibits promising TE and catalytic properties, making it a strong candidate for future device applications. Finally, this paper aims to develop a theory of the magnetization process for CCCRO QDPO-based ultra-thin spin valves, which have proven to be effective as high-temperature storage devices.
form, which possesses a very high MTT and magnetization (M). For instance, the antiferromagnetic (AFM) interaction between the magnetic cations induces a FiM state in the CaCu3Fe2Re2O12 QDPO, which features a very high MIT of 560 K and 100% SP. In this state, the spin-majority and spin-minority channels (N↑ and N↓) exhibit nonconductive and conductive traits, respectively, along with a large total magnetic moment (mt) of 8.7 μB.42 In this continuum, a newly ordered NaCu3Fe2Os2O12 QDPO was synthesized, which exhibits an HM FiM nature with a wide energy gap (Eg) in N↑ and spin ordering of Cu2+↑Fe3+↑Os5.5+↓, showing a TC above 380 K.43 Combined experimental and theoretical studies demonstrate that the FiM LaCu32+Co22+Re25.5+O12 QDPO is nearly 100% ordered with Cu2+↑Fe3+↑Os5.5+↓ SO and a TC of 150 K.44 Wang et al. theoretically predicted a series of HM FiM ACu3Fe2Re2O12 (A = Ca, Sr, Ba, Pb, Sc, Y, La) QDPOs, where the AFM coupling between CuFe and Re is dominant.45 It was established that compounds with A2+ = Ca/Sr/Ba/Pb and A3+ = Sc/Y/La ions exhibit TC values greater than 405 K and 502 K, respectively. Similarly, LaCu3Fe2Re2O12 is a HM material with a very large TC of 710 K, where a strong AFM coupling of Cu2+↑Fe3+↑Os4.5+↓ results in a FiM lowest energy state.46 It was also observed that the saturated total mt of 7.0 μB at 710 K increases to 8.0 μB at 2 K. Very recently, Zhang et al. experimentally verified the HM FiM nature in the CaCu3Cr2Re2O12 (CCCRO) system, maintaining a spin ordering of Cu2+↑ Cr3+↑ Re5+↓ above room temp. (360 K).47 However, in this stable charge configuration, the calculated mt of 5.0 μB is significantly greater than the experimentally measured value of 1.6 μB per f.u. Therefore, the intriguing features of this new class of materials, as outlined above, motivate us to explore the different characteristics of the recently synthesized CCCRO QDPO through density functional theory (DFT) calculations. These calculations demonstrate a FiM spin ordering, accompanied by a mt of 5.0 μB per formula unit (f.u.), and a half-metallic nature, featuring a 1.62 eV gap in the N↑ channel. This results in a high TC of 340 K. The material shows metallic behavior in the N↓ channel, with a p-type thermoelectric (TE) response. Moreover, the HM phase of the system remains stable under biaxial strain, and the material exhibits promising TE and catalytic properties, making it a strong candidate for future device applications. Finally, this paper aims to develop a theory of the magnetization process for CCCRO QDPO-based ultra-thin spin valves, which have proven to be effective as high-temperature storage devices.
2 Computational details
To study the physical aspects of the considered material, DFT calculations were performed within the framework of the full-potential linearized augmented plane-wave (FP-LAPW) method as implemented in the WIEN2k code.48 The generalized gradient approximation (GGA)49 was used for the exchange–correlation function along with the Hubbard parameter (U) of 4.0, 3.5, and 2.4 eV for the Cu 3d, Cr 3d, and Re 5d orbitals, respectively, to account for correlation effects.50 Additionally, spin–orbit coupling (SOC) effects were included in the scalar relativistic form due to the presence of a heavy Re element. Inside the atomic sphere, lmax = 12 was set as an upper limit, and the plane-wave cutoff was chosen as Rmt × Kmax = 7 and Gmax = 24. The Kmax was chosen to ensure no charge leakage occurred and the total energy converged. A 10 × 10 × 10 k-mesh was used, generating 76 points within the full Brillouin zone, sufficient for energy convergence. Moreover, the energy convergence as a function of the k-grid has been checked carefully, as shown in Fig. 1S of the ESI.† This clearly displays that the chosen k-point grid is large enough for the energy convergence. The atomic positions were fully relaxed until the atomic forces reached ∼5 mRy per a.u. Self-consistency was ensured by total energy (Et) and charge convergence criteria of 10−5 Ry and 10−4 C, respectively. Furthermore, TC calculations were carried out using the Vampire code.51 To perform the calculations, first, the experimental atomic sites are fully relaxed until the charge and forces converged to a minimum criterion mentioned above. After that, the Self-Consistent Field method is used to converge the Et up to five decimal places, which is a very high metric to accurately described the electronic structure of the compound.
3 Results and discussion
The crystal diagrams of the A–B site ordered CCCRO QDPO are shown in Fig. 1, with different magnetic orderings (unconstrained system), exhibiting the space group Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (No. 201).47 The experimentally observed lattice constants of a = b = c = 7.4152 Å
(No. 201).47 The experimentally observed lattice constants of a = b = c = 7.4152 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 were used for the present study and our DFT calculated value of 7.4097 Å is in excellent agreement with the experiment. The Wyckoff positions for Ca, Cu, Cr, Re, and O ions are 2a(0.25, 0.25, 0.25), 6d(0.25, 0.75, 0.75), 4b(0, 0, 0), 4c(0.5, 0.5, 0.5), and 24h(0.5583, 0.7559, 0.0662), respectively. First, we investigated the magnetically stable state of the system by considering four possible spin orderings (SOs): FM (Cu2+↑, Cr3+↑, Re5+↑), FiM-1 (Cu2+↑, Cr3+↑, Re5+↓), FiM-II (Cu2+↓, Cr3+↑, Re5+↓), and FiM-III (Cu2+↓, Cr3+↑, Re5+↑), as displayed in Fig. 1(a–d), respectively. In the case of the FM SO, the spins of all magnetic ions are aligned in the same direction (see Fig. 1(a)). However, in FiM-1 SO, the Cu and Cr spins are parallel to each other, but anti-parallel to that of Re (see Fig. 1(b)). For FiM-II SO, the Cu and Re spins are aligned with each other but anti-aligned to that of Cr (see Fig. 1(c)). Finally, in FiM-III SO, the spins of Cr and Re are aligned in the same direction as each other, whereas they are anti-aligned with the Cu spin (see Fig. 1(d)). Henceforth, the Cu2+↑Cr3+↑Re5+↓ (FiM-1) configuration is the lowest energy state with energy differences of −105/−78/−55 meV to the FM/FiM-II/FiM-III SO. This state has a mt of 5.0 μB per f.u., which is in excellent agreement with recent experimental observations.47 Notably, the lengths of the arrows in the figures represent the magnitude of each atom’s spin magnetic moment (ms). Next, we studied the structural stability of the CCCRO material in its stable FiM-I phase by calculating the formation and cohesive energies (Efor. and Ecoh.) as:
47 were used for the present study and our DFT calculated value of 7.4097 Å is in excellent agreement with the experiment. The Wyckoff positions for Ca, Cu, Cr, Re, and O ions are 2a(0.25, 0.25, 0.25), 6d(0.25, 0.75, 0.75), 4b(0, 0, 0), 4c(0.5, 0.5, 0.5), and 24h(0.5583, 0.7559, 0.0662), respectively. First, we investigated the magnetically stable state of the system by considering four possible spin orderings (SOs): FM (Cu2+↑, Cr3+↑, Re5+↑), FiM-1 (Cu2+↑, Cr3+↑, Re5+↓), FiM-II (Cu2+↓, Cr3+↑, Re5+↓), and FiM-III (Cu2+↓, Cr3+↑, Re5+↑), as displayed in Fig. 1(a–d), respectively. In the case of the FM SO, the spins of all magnetic ions are aligned in the same direction (see Fig. 1(a)). However, in FiM-1 SO, the Cu and Cr spins are parallel to each other, but anti-parallel to that of Re (see Fig. 1(b)). For FiM-II SO, the Cu and Re spins are aligned with each other but anti-aligned to that of Cr (see Fig. 1(c)). Finally, in FiM-III SO, the spins of Cr and Re are aligned in the same direction as each other, whereas they are anti-aligned with the Cu spin (see Fig. 1(d)). Henceforth, the Cu2+↑Cr3+↑Re5+↓ (FiM-1) configuration is the lowest energy state with energy differences of −105/−78/−55 meV to the FM/FiM-II/FiM-III SO. This state has a mt of 5.0 μB per f.u., which is in excellent agreement with recent experimental observations.47 Notably, the lengths of the arrows in the figures represent the magnitude of each atom’s spin magnetic moment (ms). Next, we studied the structural stability of the CCCRO material in its stable FiM-I phase by calculating the formation and cohesive energies (Efor. and Ecoh.) as:| |
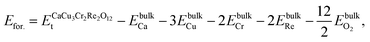 | (1) |
| |
 | (2) |
where  is the DFT-computed Et of the CCCRO structure, while EbulkCa, EbulkCu, EbulkCr, EbulkRe, and
is the DFT-computed Et of the CCCRO structure, while EbulkCa, EbulkCu, EbulkCr, EbulkRe, and  are the DFT-determined Et for the Ca, Cu, Cr and Re ions and O molecules in their bulk stable phases, respectively. Similarly, Eiso.Ca, Eiso.Cu, Eiso.Cr, Eiso.Re, and
are the DFT-determined Et for the Ca, Cu, Cr and Re ions and O molecules in their bulk stable phases, respectively. Similarly, Eiso.Ca, Eiso.Cu, Eiso.Cr, Eiso.Re, and  are the DFT-measured Et for the isolated Ca, Cu, Cr and Re ions, and oxygen molecule, accordingly. The calculated Efor./Ecoh. per atom is −2.31 eV/−4.89 eV. The negative signs for both energies confirm that the structure is thermodynamically stable and supports an exothermic reaction. Moreover, the mechanical stability of the structure is utilized by calculating the elastic tensors (Cij). The computed three independent elastic parameters, namely C11, C12, and C44, satisfied the basic demands and Born criteria as (C11 − C12) > 0, (C11 + 2C12) > 0, C11 > 0, C44 > 0, and C12 < B < C11 (ref. 52) for the mechanical stability. Hence, the determined C11, and C12, and C12 are 289, 211, and 140, correspondingly, which satisfies the above-mentioned mechanical stability standard.
are the DFT-measured Et for the isolated Ca, Cu, Cr and Re ions, and oxygen molecule, accordingly. The calculated Efor./Ecoh. per atom is −2.31 eV/−4.89 eV. The negative signs for both energies confirm that the structure is thermodynamically stable and supports an exothermic reaction. Moreover, the mechanical stability of the structure is utilized by calculating the elastic tensors (Cij). The computed three independent elastic parameters, namely C11, C12, and C44, satisfied the basic demands and Born criteria as (C11 − C12) > 0, (C11 + 2C12) > 0, C11 > 0, C44 > 0, and C12 < B < C11 (ref. 52) for the mechanical stability. Hence, the determined C11, and C12, and C12 are 289, 211, and 140, correspondingly, which satisfies the above-mentioned mechanical stability standard.
 |
| | Fig. 1 Crystal structures of the CaCu3Cr2Re2O12 quadruple structure in a (a) ferromagnetic (FM), (b) ferrimagnetic (FiM)-I, (c) FiM-II, and (d) FiM-III spin ordering. | |
To describe the electronic structure of the CCCRO, we calculated and presented the SP total/partial density of states (TDOS/PDOS) within the GGA+U and TDOS for GGA+U+SOC methods in Fig. 2(a, a′ and b), respectively. Fig. 2(a) suggests that the system is HM within the GGA+U method with fully SP conduction electrons, which is consistent with the experimental findings.47 A large Eg of 1.62 eV remains in the N↑ channel, and a few TDOS states appear at the Fermi level (EF) in N↓, leading to a metallic behavior of N↓. Consequently, the entire system illustrates an HM phase. The broad Eg in N↑ is sufficiently large to prevent spin-flipping, which helps to avoid thermal excitation of the electrons and ensures that the HM nature of the system is stable at or above room temp. to some extent. From Fig. 2(a′), we observe that only Re 5d and O 2p states (where hybridization occurs between Re 5d and O 2p states near the EF) cross the EF in N↓, transitioning from the valence band (VB) to the conduction band (CB), which is responsible for the metallicity. In contrast, no ion states cross or lie at the EF in the N↑, confirming the 100% SP at the EF. Additionally, the GGA+U+SOC calculated TDOS (see Fig. 2(b)) exhibits the metallic behavior of the system. Furthermore, the calculated SP band structures within the GGA+U and GGA+U+SOC methods (shown in Fig. 3(a/a′ and b), respectively), validate the HM and metallic nature of the structure as demonstrated by the TDOS in Fig. 2(a and b). To further confirm the HM state of the structure, we calculated the spin-polarized TDOS of the system using the hybrid functional PBE0, as shown in Fig. 2S of the ESI,† which is implemented in Wien2K and gives almost the same high accuracy in results as found in the case of HSE06, which is implemented in the VASP code. One can see that the calculated TDOS exhibits a HM state where N↑ contains a large Eg, while N↓ is showing a metallic behavior within PBE0 (see Fig. 2S of the ESI†), as predicted in the case of the GGA+U method (see Fig. 2(b)).
 |
| | Fig. 2 Calculated spin-polarized density of states (DOS) in the CaCu3Cr2Re2O12 quadruple structure: (a/a′) total/partial DOS for the GGA+U and (b) total DOS for the GGA+U+SOC method,. | |
 |
| | Fig. 3 Calculated spin-polarized band structures in the CaCu3Cr2Re2O12 quadruple structure, for the (a/a′) spin-majority/spin-minority channel within the GGA+U (1st-row) and (b) GGA+U+SOC (2nd-row) methods. | |
Next, we discuss the system’s magnetism, where the energetically stable FiM-I configuration Cu2+↑Cr3+↑Re5+↓ produces an mt of 5.0 μB per f.u., which is higher than that of other spin configurations. This value is reasonable, as also mentioned in ref. 47. However, it remains considerably higher than the experimentally measured value of 1.6 μB per f.u.47 The calculated ms for the Cu, Cr, and Re ions within the muffin-tin sphere are 0.48/2.54/−0.92 μB using the GGA+U method, which changes slightly to 0.47/2.53/−0.89 μB upon including spin–orbit coupling (SOC). The “−” sign in the Re ms indicates that its spin is oppositely aligned with the Cu and Cr spins, confirming the FiM state. The Cu, Cr, and Re ions are in the +2 (3d9), +3 (3d3), and +5 (5d2) states, respectively, holding electronic configurations of t32g↑t32g↓e2g↑e1g↓, t32g↑t02g↓e0g↑e0g↓, and t22g↑t02g↓e0g↑e0g↓ with spin quantum numbers  , respectively. Hence, the computed ms on each ion also verifies their respective valence states. The induced orbital magnetic moment (morb.) on the Cu/Cr/Re ion is 0.06/−0.05/0.23 μB. Compared to that on the Cu and Cr, the sizable magnitude of morb. on the Re ion highlights the strong SOC influence. Furthermore, as Cu lies in a more than half-occupied d state, its ms and morb. are aligned with each other (i.e., both have a “+” sign), as discussed in ref. 53. Conversely, Cr and Re ions lie in less than half-filled d states, so their ms and morb. are anti-aligned. For Cr, the signs are “+/−” for ms/morb., while for Re, they are “−/+”, as described in ref. 54. Thus, the above discussions support the AFM interactions between the Cu/Cr and Re ions.
, respectively. Hence, the computed ms on each ion also verifies their respective valence states. The induced orbital magnetic moment (morb.) on the Cu/Cr/Re ion is 0.06/−0.05/0.23 μB. Compared to that on the Cu and Cr, the sizable magnitude of morb. on the Re ion highlights the strong SOC influence. Furthermore, as Cu lies in a more than half-occupied d state, its ms and morb. are aligned with each other (i.e., both have a “+” sign), as discussed in ref. 53. Conversely, Cr and Re ions lie in less than half-filled d states, so their ms and morb. are anti-aligned. For Cr, the signs are “+/−” for ms/morb., while for Re, they are “−/+”, as described in ref. 54. Thus, the above discussions support the AFM interactions between the Cu/Cr and Re ions.
To further directly confirm the ms magnitude on the magnetic ions and the FiM SO in the system, we visualized the three-dimensional spin-magnetization density iso-surfaces with an iso-value of ±0.005 e Å−3 in Fig. 4. Firstly, the high densities around the Cr ion, compared to those around the Cu and Re ones, establish that Cr is the primary contributor to the system magnetism and confirm the calculated ms values on each ion. Secondly, the Cu and Cr density colors are the same (red), in contrast to that of Re (light green). This indicates that the Cu and Cr spins are aligned in the same direction (parallel to each other), but they are anti-aligned to the Re-spin, which further supports the FiM-I (Cu2+↑Cr3+↑Re5+↓) SO. Additionally, the combined eg and t2g orbital features are evident in the Cu and Cr/Re ion densities as they occupy +2 (e2g↑e1g↓) and +3 (t32g↑)/+5 (t22g↑) states, respectively. Therefore, the AFM coupling between Cu/Cr and Re ions can be understood using the super-exchange interaction concept, where the possible electron transfer between them is illustrated in Fig. 5. Since Cr and Re maintain +3 and +5 valence states, as t2g states are less than half-filled in both cases (see Fig. 5), virtual hopping between these t2g orbitals leads to AFM coupling, resulting in a FiM state.
 |
| | Fig. 4 Calculated three-dimensional spin-magnetization density iso-surfaces with an iso-value of ±0.005 e Å−3 in the CaCu3Cr2Re2O12 quadruple structure. For simplicity, Ca and oxygen ions are omitted. | |
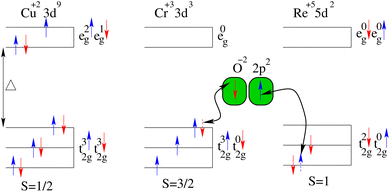 |
| | Fig. 5 Schematic representation of the antiferromagnetic superexchange coupling between Cu2+ (3d9)/Cr3+ (3d3) and Re2+ (5d2) orbitals via O−2 (2p2) in the CaCu3Cr2Re2O12 quadruple structure. | |
The total ms of an atom is the result of the combined contributions from the ms values of its electrons, including the morb. component. In FiM materials, the magnetism primarily originates from the ms of the unpaired metal ions within the crystalline lattice. Consequently, these materials display magnetic moments with spontaneous long-range ordering, driven by a quantum mechanical phenomenon called the exchange or interchange interaction. The exchange interaction, which governs SO, can be categorized into short-range (direct), long-range, or indirect exchange interactions. This interaction is characterized by the presence of two distinct sublattices, A and B, and at least three different exchange interactions: JAA, JAB, and JBB.55 The ions in sublattice A are oriented in one direction, whereas those in sublattice B are oriented in the opposite direction. For example, the exchange interaction results from the parallel alignment of atomic ms in FiM materials. Hence, to figure out the origin of the high TC in the CCCRO system, the magnetic exchange couplings were computed using the Heisenberg spin method:56,57
| |
 | (3) |
Here,
Jij represents the interaction between the magnetic ions
i and
j due to exchange forces. If
Jij is positive (
Jij > 0), an FM interaction occurs, allowing the spins to align in a parallel configuration (↑↑). In contrast, if
Jij is negative (
Jij < 0), an AFM interaction arises, resulting in an antiparallel spin alignment (↑↓). FM materials exhibit the former behavior, while AFM and FiM are associated with the latter.
Si/
Sj is the spin vector of the Cu/Cr/Re ion at the
i/
j site and represents the spin variables. For simplicity, only the three nearest neighbors
Jij, namely
JCu–Cr,
JCu–Re, and
JCr–Re, are taken into account. To do this,
Jij in four varying SOs, namely FM (Cu
2+↑Cr
3+↑Re
5+↑), FiM-I (Cu
2+↑Cr
3+↑Re
5+↓), FiM-II (Cu
2+↓Cr
3+↑Re
5+↓), and FiM-III (Cu
2+↓Cr
3+↑Re
5+↑), as shown in
Fig. 1, is calculated as:
46| | |
Et(FM) = E0 + 12JCu–CrSCuSCr + 12JCu–ReSCuSRe + 12JCr–ReSCrSRe
| (4) |
| | |
Et(FiM-I) = E0 + 12JCu–CrSCuSCr − 12JCu–ReSCuSRe − 12JCr–ReSCrSRe
| (5) |
| | |
Et(FiM-II) = E0 − 12JCu–CrSCuSCr + 12JCu–ReSCuSRe − 12JCr–ReSCrSRe
| (6) |
| | |
Et(FiM-III) = E0 − 12JCu–CrSCuSCr − 12JCu–ReSCuSRe+ 12JCr–ReSCrSRe
| (7) |
Our results show that the three considered couplings are AFM. In the case of Cu2+↑–Cr3+↑, Jij = 0.957 meV for the atom interactions closest to Cu–Cr and becomes −0.374 meV for the second-to-nearest ones, hinting at the AFM coupling between Cu2+↑ and Cr3+↑. However, the AFM Cu2+↑–Re5+↓ and Cr3+↑–Re5+↓ interactions are much stronger than those of Cu2+↑–Cr3+↓, resulting in a long-ranged Cu2+↑–Cr3+↑–Re5+↓ SO (FiM-I) as the lowest energy state of CCCRO. The calculated values of the AFM exchange coupling constants JCr–Re = −30.21 meV and JCu–Re = −28.57 meV for the interactions SCr↑–SRe↓ and SCu↑–SRe↓ are substantially higher than the 5.85 meV for JCu–CrSCu↑SCr↑. Therefore, the much stronger AFM interactions between the Cu/Cr and Re ions result in a high TC = 340 K for the system.
Magnetic materials typically form magnetic domains, regions where the magnetic moments are highly aligned, and the boundaries between the magnetic domains (domain walls) shift in the presence of an external magnetic field (H), leading to changes in the material’s M. The domain structure organizes itself to minimize the overall magnetostatic energy of the material. The domains’ size, shape, and orientation are determined by the interactions between the exchange, magnetostatic, and anisotropic energies of the system. Consequently, exposure of a material to an external H induces an M within the material. The magnitude of the M is directly proportional to the applied H, as given by the relation:
In this equation,
χ represents the material’s magnetic susceptibility, a dimensionless quantity in SI units. The behavior of solid materials under an external
H is affected by factors including their atomic structure, electromagnetic excitation, pressure, and temperature. Hence, to visualize the magnetic phase transition at
TC in the CCCRO QDPO,
M versus TC calculations have been performed (presented in
Fig. 6) using the Vampire code.
51,58 The computed
TC is 340 K, ∼7% lower than the experimentally observed value of 360 K.
47 This discrepancy can primarily be attributed to inherent differences in computational modeling and experimental conditions. As the temp. approaches
TC, thermal energy disrupts the ordered alignment of
ms, corresponding to a sharp decrease in
M. This results in a corresponding decrease in the
ms of the constituent ions due to the reduced number of unpaired d-electrons. This phase transition is critical as it signifies the loss of spontaneous
M and the onset of enhanced thermal fluctuations, which can be seen in the
χ curve shape as depicted in
Fig. 6. This implies some level of anisotropy within the material and the influence of opposing magnetic interactions.
59 Importantly, the sharp peak in
χ observed at
TC indicates the material’s heightened sensitivity to
H due to increased SO.
 |
| | Fig. 6 Calculated susceptibility and magnetization curves versus Curie temperature of the CaCu3Cr2Re2O12 quadruple structure. | |
Recently, a material which is applicable for spintronics application, contain the M process of the spin valve of HM ferrites, has been attracting deep attention. M as a function of the applied H is represented by the M–H curve, which reveals the saturation M that is reached beyond a certain threshold of H. As H decreases to zero after saturation, M does not revert to zero, a behavior referred to as hysteresis. This property is critical for various applications, such as magnetic sensing devices. Therefore, the magnetic properties of CCCRO are evaluated by measuring M in terms of the applied H and temp. of 2 T/5 T and 2/100/200/300 K, respectively, as shown in Fig. 7(a) and (b). At low temp. (2 K), as shown in Fig. 7(a), the material exhibits strong SO and quickly drives the system to saturation, displaying sharp transitions in the hysteresis loop. As the temp. increases to 100 K, thermal fluctuations begin to reduce the M, however, the material still reaches a saturation, as found under 2 T (see Fig. 7(a)), though more gradually. At 5 T (see Fig. 7(b)), the material achieves saturation more effectively, but the saturated M is lower at 2 K. At higher temp. (200 K and 300 K), the material’s M continues to decrease due to an increase in thermal agitation, and the transition to saturation becomes more gradual. However, the high field (5 T) still drives the material towards saturation, but the overall M is lower.
 |
| | Fig. 7 Variation of the saturated magnetization (M) with applied magnetic field (H) for (a) 2 T and (b) 5 T at a fixed temperature of 2/100/200/300 K in the CaCu3Cr2Re2O12 quadruple structure. | |
By analyzing the band structure, the material’s metallic, semiconducting, or insulating nature can be inferred from its transport properties. A decrease in the Hall coefficient (RH) with increasing temp. suggests metallic behavior, while a Seebeck coefficient (S) greater than zero signifies p-type semiconducting characteristics. Thus, the transport properties of the CCCRO QDPO were computed using the BoltzTraP2 software60 under the constant relaxation time approximation (τ = 1 × 10−19 s). The electrical conductivity per unit relaxation time 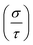 exhibits a distinct temp. dependence due to the SP electronic structure. There is a significant increase in σ for non-metallic N↑, from 3.18 × 1019 S m−1 at 300 K to 4.0 × 1019 S m−1 at 800 K, as thermal excitation promotes electrons across the gap. In contrast, N↓ shows a weaker temp. dependence, from 2.58 × 1019 S m−1 at 300 K to 2.80 × 1019 S m−1 at 800 K, as conductivity is primarily limited by electron-phonon scattering (see Fig. 8(a)). Initially, N↑ has a higher S (1.92 × 10−5 V K−1) at 300 K due to limited thermally excited carriers, while N↓ exhibits a lower S (−2.94 × 10−6 V K−1) at 300 K. As temp. increases (up to 800 K), the S for N↑ decreases (−3.73 × 10−6 V K−1) as thermal excitation saturates available states, while the S for N↓ increases (8.66 × 10−6 V K−1) due to enhanced carrier diffusion (Fig. 8(b)). After a certain temp., S stabilizes for both channels, indicating saturation in the TE potential.
exhibits a distinct temp. dependence due to the SP electronic structure. There is a significant increase in σ for non-metallic N↑, from 3.18 × 1019 S m−1 at 300 K to 4.0 × 1019 S m−1 at 800 K, as thermal excitation promotes electrons across the gap. In contrast, N↓ shows a weaker temp. dependence, from 2.58 × 1019 S m−1 at 300 K to 2.80 × 1019 S m−1 at 800 K, as conductivity is primarily limited by electron-phonon scattering (see Fig. 8(a)). Initially, N↑ has a higher S (1.92 × 10−5 V K−1) at 300 K due to limited thermally excited carriers, while N↓ exhibits a lower S (−2.94 × 10−6 V K−1) at 300 K. As temp. increases (up to 800 K), the S for N↑ decreases (−3.73 × 10−6 V K−1) as thermal excitation saturates available states, while the S for N↓ increases (8.66 × 10−6 V K−1) due to enhanced carrier diffusion (Fig. 8(b)). After a certain temp., S stabilizes for both channels, indicating saturation in the TE potential.
 |
| | Fig. 8 Calculated (a) electrical conductivity per unit relaxation time  , (b) Seebeck coefficient (S), (c) thermal conductivity per unit relaxation time , (b) Seebeck coefficient (S), (c) thermal conductivity per unit relaxation time  , (d) molar magnetic susceptibility (χ), (e) Hall-coefficient (RH), and (f) figure of merit (ZT) of the CaCu3Cr2Re2O12 quadruple structure. , (d) molar magnetic susceptibility (χ), (e) Hall-coefficient (RH), and (f) figure of merit (ZT) of the CaCu3Cr2Re2O12 quadruple structure. | |
The thermal conductivity per unit relaxation time  increases linearly with temp. primarily due to phonon–electron scattering, peaking around 800 K for both channels. For N↑, the conductivity is slightly higher, with the value increasing from 2.88 × 1014 W m−1 K at 300 K to 1.02 × 1015 W m−1 K at 800 K (Fig. 8(c)). This difference arises from the increased availability of high-energy states in N↑ due to thermal excitation across the Eg. N↓, being metallic, shows a less pronounced increase, from 2.01 × 1014 W m−1 K at 300 K to 6.27 × 1014 W m−1 K at 800 K, due to the relatively constant DOS at the EF. χ is higher for N↓ than N↑ at lower temp. as N↓ is metallic and has a higher DOS at the EF. At 300 K, χ for N↓ is 1.59 × 10−11 and decreases to 1.57 × 10−11 at 800 K due to thermal excitation disrupting spin alignment. For N↑, χ increases from 1.35 × 10−11 at 300 K to 1.47 × 10−11 at 800 K as thermal excitation promotes electrons across the Eg, allowing for stronger spin alignment. However, χ for N↑ saturates around the TC due to phase transition effects (Fig. 8(d)). The Hall coefficient (RH) for N↑ remains positive across this temp. range, indicating hole conduction, while for N↓, it decreases with increasing temp., signifying metallic behavior (shown in Fig. 8(e)). In N↓, RH decreases with temp. as thermally activated carriers dominate, signaling the metallic behavior. For N↑, RH increases as thermal excitation generates additional carriers, enhancing the RH. Further, the molar specific heat capacity (CV) increases with temp. following the Debye Law, reflecting stronger atomic binding and activation of additional vibrational modes. Despite differing electronic properties, CV remains nearly identical for both spin channels because it is governed primarily by phonon vibrations in the lattice, which are independent of the SP electronic structure. Finally, the thermal performance of the systems as quantified by the figure of merit,
increases linearly with temp. primarily due to phonon–electron scattering, peaking around 800 K for both channels. For N↑, the conductivity is slightly higher, with the value increasing from 2.88 × 1014 W m−1 K at 300 K to 1.02 × 1015 W m−1 K at 800 K (Fig. 8(c)). This difference arises from the increased availability of high-energy states in N↑ due to thermal excitation across the Eg. N↓, being metallic, shows a less pronounced increase, from 2.01 × 1014 W m−1 K at 300 K to 6.27 × 1014 W m−1 K at 800 K, due to the relatively constant DOS at the EF. χ is higher for N↓ than N↑ at lower temp. as N↓ is metallic and has a higher DOS at the EF. At 300 K, χ for N↓ is 1.59 × 10−11 and decreases to 1.57 × 10−11 at 800 K due to thermal excitation disrupting spin alignment. For N↑, χ increases from 1.35 × 10−11 at 300 K to 1.47 × 10−11 at 800 K as thermal excitation promotes electrons across the Eg, allowing for stronger spin alignment. However, χ for N↑ saturates around the TC due to phase transition effects (Fig. 8(d)). The Hall coefficient (RH) for N↑ remains positive across this temp. range, indicating hole conduction, while for N↓, it decreases with increasing temp., signifying metallic behavior (shown in Fig. 8(e)). In N↓, RH decreases with temp. as thermally activated carriers dominate, signaling the metallic behavior. For N↑, RH increases as thermal excitation generates additional carriers, enhancing the RH. Further, the molar specific heat capacity (CV) increases with temp. following the Debye Law, reflecting stronger atomic binding and activation of additional vibrational modes. Despite differing electronic properties, CV remains nearly identical for both spin channels because it is governed primarily by phonon vibrations in the lattice, which are independent of the SP electronic structure. Finally, the thermal performance of the systems as quantified by the figure of merit,
, is significantly higher for the
N↑ channel at room temp. This is due to its enhanced
S and lower
κe, which collectively results in improved TE performance. At ambient temp., the
ZT values for
N↑ and
N↓ are 0.76 and 0.001, respectively, highlighting the superior TE efficiency of the
N↑ channel. This behavior is depicted in
Fig. 8(f), which illustrates the temp. dependence and contrast in
ZT values for the two spin channels.
4 Strained system
DOS and Eg are crucial descriptors of the electronic properties of materials. The DOS represents the number of electronic states at each energy level, while the Eg refers to the energy difference between the CB and VB. Thus, the orbital hybridization between the O 2p orbitals and the Cr 3d and Cu 3d orbitals plays a central role in determining these properties. Changes in atomic distance, induced by strain, affect the overlap between these orbitals, thereby influencing the Eg and DOS peak height. Interatomic distances are reduced in materials under compressive (comp.) strain, leading to more substantial orbital overlap and hybridization. This typically results in a narrowing of the Eg and a reduction in the sharpness of the DOS peak. Conversely, under tensile (tens.) strain, interatomic distances are increased, which weakens orbital overlap and can lead to a widening of the Eg and a sharper DOS peak. Therefore, we perform DFT calculations to simulate the effects of comp. and tens. strain on the CCCRO QDPO. A comp. strain is applied by reducing the lattice constant, bringing the atoms closer together, and tens. strain is applied by increasing the lattice constant, causing the atoms to move farther apart. To assess the stability of the HM phase in the CCCRO QDPO, we examine the effects of biaxial ([110]) strain on the electronic and magnetic properties within a reasonable range of ±5%. First, the structural robustness of the aforementioned systems is evaluated by plotting the Efor./Ecoh. in blue/red with respect to the strain, as shown in Fig. 9(a). Both quantities remain negative throughout the entire applied strain range. However, structures under comp. strain exhibit lower stability compared to those under tensile strain, as the values of Efor./Ecoh. shift toward higher (more positive) energies with increasing strain from 0% to −5%. Next, to quantitatively analyze the variations in the electronic structure of the system resulting from strain, we display only the calculated Eg of N↑ in Fig. 9(b), since N↓ remains metallic across the entire strain range considered. It is observed that Eg decreases solely from 1.62 to 1.24 eV with the varying compressive strain from 0% to −5%. The change in Eg is mainly due to the charge re-distribution (Cu 3d, Cr 3d and O 2p) state hybridization. It is observed that the Re–Cr bond lengths are least affected for the entire strain ranges, but the Cr–Cu bond lengths increase significantly (from 3.21 Å to 3.70 Å). This also changes the interaction forces among the ions linked with the stretched bond lengths. As a result, the energies around the EF change (the ground state energies of the CB/VB show a decreasing/increasing trend, respectively). This causes the decrease in Eg. However, small changes were found for the cases of tensile strain compared to the ones without stress (0%).
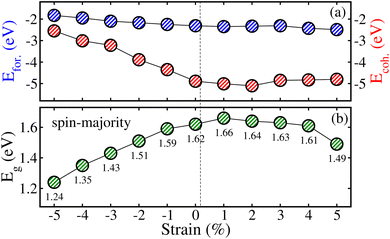 |
| | Fig. 9 Calculated (a) formation/cohesive energy (Efor./Ecoh.) in blue/red color and (b) energy gap (Eg) in the spin-majority channel with respect to ±5% biaxial ([110]) strain in the CaCu3Cr2Re2O12 quadruple structure. | |
Under comp. strain, the interatomic distances between O, Cr, and Cu atoms decrease, bringing their atomic orbitals into closer proximity. This leads to stronger orbital hybridization between the O 2p and the Cr 3d and Cu 3d orbitals. The closer proximity of the orbitals causes the electronic states to become more delocalized, reducing the band gap Eg as the conduction and valence bands move closer together. This narrowing of the Eg indicates a transition toward a more metallic or semiconducting state. Also, the DOS peak height decreases because the increased overlap between the atomic orbitals leads to a broader distribution of electronic states near the EF. As a result, the DOS peak becomes less sharp due to the more delocalized electronic states. As shown in Fig. 3S of the ESI,† this effect is observed for the Cr and Cu 3d states. Fig. 4S of the ESI† shows similar behavior for the O 2p states under comp. strain. In contrast, under tens. strain, the interatomic distances between the atoms increase, which causes the O 2p orbitals and Cr/Cu 3d orbitals to become more localized. This increases the distance of the O 2p orbitals from the Fermi level EF, while the Cr and Cu 3d orbitals are pushed even further away due to decreased orbital overlap. The reason for this decrease is the increasing localization of these orbitals, which leads to a reduction in the number of available electronic states near the EF, thus decreasing the DOS peak height. For the O 2p orbitals, the peak height increases under tens. strain. This is because as the strain increases, the O 2p orbitals become more localized near the EF, which increases the DOS in this region. Despite the increase in peak height for the O 2p orbitals, the total DOS does not show a significant increase under tens. strain. This is because, although the O 2p orbitals become more localized and their peak height increases, the overall distribution of electronic states remains narrow, and the states of the Cr and Cu 3d orbitals are less delocalized. Therefore, the overall DOS profile does not exhibit a significant broadening, and the peak height for the TDOS remains nearly unchanged.
For qualitative evaluation, we plotted the TDOS for various comp. and tens. strains of the motif, as shown in Fig. 10. This established the fact that N↑ maintained a definite Eg value, while in N↓, states lie at the EF for −1/−3/−5% (comp.) and +1/+3/+5% (tens.) strained systems, as shown in (Fig. 10(a–c) and 10(a′)–(c′)), respectively. Hence, this ensures the robustness of the HM nature of the system under the considered ±5% biaxial strain and maybe above it. Finally, we plotted the calculated ms values on the Cu/Cr/Re ion as a function of strain in Fig. 11. In the case of the Cr/Re ion, a small reduction/increment in ms magnitude is observed when comp./tens. strain is adjusted from −1% to −5%/+1% to +5%. However, it almost remains the same for the whole strain range on the Cu ion. So, an increase/decrease in ms value for the comp./tens. strain can be readily explained by taking the hybridization factor into account. As the comp. strain amplitude increases, the ions move closer together, resulting in stronger hybridization. This leads to greater charge transfer among the ions, reducing the ms magnitude of the individual magnetic ions. In contrast, the ions move further apart for tensile strained systems, which weakens the hybridization between them. This causes less charge transfer among ions and enhances the ms value, as illustrated in this article.61 Additionally, both Cu and Cr ions have “+” signs on their ms, whereas it’s a “−” for that of the Re ion over the whole strain range. This further endorses the AFM coupling between Cu/Cr and Re, which turns out to have a FiM SO.
 |
| | Fig. 10 GGA+U calculated total density of states (TDOS) for (a/a′) −/+1%, (b/b′) −/+3%, and (c/c′) −/+5% compressive/tensile biaxial ([110]) strains in the stable ferrimagnetic-I spin ordering of the CaCu3Cr2Re2O12 quadruple structure. | |
 |
| | Fig. 11 Calculated partial spin magnetic moments (ms) on the Cu, Cr, and Re ions for ±5% biaxial ([110]) strain in the stable ferrimagnetic-I ordering of the CaCu3Cr2Re2O12 quadruple structure. | |
5 Conclusion
These ab initio calculations lay a foundational understanding for developing a quadruple-double perovskite oxide, CaCu3Cr2Re2O12, with potential applications in spintronics. We demonstrated that magnetic properties can be engineered through doping (charge/ion implantation) to create ferromagnetic (FM) and various ferrimagnetic (FiM) spin orderings (SOs) to figure out the magnetic ground state of the system, which is Cu2+↑Cr3+↑Re5+↓, while keeping a reasonable total magnetic moment of 5.0 μB per f.u. along with partial spin moments of 0.48/2.54/−0.92 μB on the Cu/Cr/Re ions. This leads the system into a FiM phase, which is further confirmed by plotting the three-dimensional spin-magnetization density isosurfaces. Interestingly, the system exhibits a half-metallic (HM) nature with a sufficiently large energy gap (Eg) of 1.62 eV in the spin majority channel (N↑), which is an essential parameter to avoid spin-flipping above room temperature (temp.), with a Curie temperature (TC) of 340 K. Moreover, the transport properties of the system reveal its metallic nature in the spin minority channel (N↓) and an insulating trait in the spin majority channel (N↑), as evidenced by the increasing/decreasing Hall coefficient (RH) for N↑/N↓ and increasing electrical conductivity with temperature. The positive Seebeck coefficient confirms p-type behavior, while thermal conductivity trends reflect the influence of phonon–electron interactions. These findings underscore the material’s potential for thermoelectric (TE) applications, driven by its favorable charge carrier dynamics and heat transport traits. Moreover, the computed TC is further explained regarding magnetization (M) and magnetic susceptibility parameters. We have explicitly discussed the behavior of the spin-polarized (SP) electron population within the material by applying an external magnetic field (H) of varying strength (2 T and 5 T), enabling the tuning of magnetic properties. Further, it is predicted that the system demonstrates a robustness of its HM state against a reasonable range of ±5% biaxial ([110]) strains. Hence, the combination of a robust HM FiM state, large Eg in N↑, high TC (above room temp.), and reasonable TE response of the CaCu3Cr2Re2O12 structure opens pathways for further research in spintronics, offering insight into how materials can be tailored for applications such as memory devices, quantum computing, and spin-based transistors at high temperature.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Author contributions
Shehla Yasmeen: writing – original draft, investigations, formal analysis, data curation. S. Nazir: writing – review and editing, validation, supervision, project administration, conceptualization.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
The computational work was supported by University of Sargodha, Sargodha, Pakistan.
References
- M. D. Nguyen, H. V. Tran, S. Xu and T. R. Lee, Appl. Sci., 2021, 11, 11301 CrossRef CAS PubMed.
- R. J. Celotta and D. T. Pierce, Science, 1986, 234, 333–340 CrossRef CAS PubMed.
- K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680 CrossRef CAS.
- X. Xiong, J. Kang, Q. Hu, C. Gu, T. Gao, X. Li and Y. Wu, Adv. Funct. Mater., 2020, 30, 1909645 CrossRef CAS.
- I. Zutic, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef CAS.
- A. Fert, Rev. Mod. Phys., 2008, 80, 1517–1530 CrossRef CAS.
- M. I. Katsnelson, V. Y. Irkhin, L. Chioncel, A. I. Lichtenstein and R. A. de Groot, Rev. Mod. Phys., 2008, 80, 315–378 CrossRef CAS.
- W. A. Borders, A. Z. Pervaiz, S. Fukami, K. Y. Camsari, H. Ohno and S. Datta, Nature, 2019, 573, 390–393 CrossRef CAS PubMed.
- K. Premasiri and X. P. Gao, J. Phys.: Condens. Matter, 2019, 31, 193001 CrossRef CAS PubMed.
- J. Z. Sun, W. J. Gallagher, P. R. Duncombe, L. Krusin-Elbaum, R. A. Altman, A. Gupta, Y. Lu, G. Q. Gong and G. Xiao, Appl. Phys. Lett., 1996, 69, 3266–3268 CrossRef CAS.
- T. Obata, T. Manako, Y. Shimakawa and Y. Kubo, Appl. Phys. Lett., 1999, 74, 290–292 CrossRef CAS.
- W. tin Chen, M. Mizumaki, H. Seki, M. S. Senn, T. Saito, D. Kan, J. P. Attfield and Y. Shimakawa, Nat. Commun., 2014, 5, 3909 CrossRef PubMed.
- R. A. de Groot, F. M. Mueller, P. G. V. Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027 CrossRef CAS.
- K. Schwarz, J. Phys. F: Metal. Phys., 1986, 16, 211 CrossRef.
- R. Wiesendanger, H.-J. Guntherodt, G. Guntherodt, R. J. Gambino and R. Ruf, Phys. Rev. Lett., 1990, 65, 247–250 CrossRef CAS PubMed.
- A. Yanase and K. Siratori, J. Phys. Soc. Jpn., 1984, 53, 312–317 CrossRef CAS.
- I. Shvets, R. Wiesendanger, D. Burgler, G. Tarrach, H.-J. Guntherodt and J. Coey, J. Appl. Phys., 1992, 71, 5489–5499 CrossRef CAS.
- S. Jin, T. H. Tiefel, M. McCormack, R. A. Fastnacht, R. Ramesh and L. H. Chen, Science, 1994, 264, 413–415 CrossRef CAS PubMed.
- A. P. Ramirez, J. Phys.:Condens. Matter, 1997, 9, 8171 CrossRef CAS.
- M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197–233 CrossRef CAS.
- G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785–5796 RSC.
- T. Saha-Dasgupta, J. Supercond. Novel Magn., 2013, 26, 1991–1995 CrossRef CAS.
- H. Kato, T. Okuda, Y. Okimoto, Y. Tomioka, K. Oikawa, T. Kamiyama and Y. Tokura, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 184412 CrossRef.
- P. Majewski, S. Geprägs, O. Sanganas, M. Opel, R. Gross, F. Wilhelm, A. Rogalev and L. Alff, Appl. Phys. Lett., 2005, 87, 202503 CrossRef.
- O. Erten, O. N. Meetei, A. Mukherjee, M. Randeria, N. Trivedi and P. Woodward, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 165105 CrossRef.
- J. Hong, C.-J. Kang and J. Kim, Phys. Rev. B, 2022, 106, 195428 CrossRef CAS.
- S. Jiang, L. Li, Z. Wang, K. F. Mak and J. Shan, Nat. Nanotechnol., 2018, 13, 549–553 CrossRef CAS PubMed.
- X.-J. Dong, J.-Y. You, B. Gu and G. Su, Phys. Rev. Appl., 2019, 12, 014020 CrossRef CAS.
- X. Hu, Y. Zhao, X. Shen, A. V. Krasheninnikov, Z. Chen and L. Sun, ACS Appl. Mater. Interfaces, 2020, 12, 26367–26373 CrossRef CAS PubMed.
- A. Avsar, A. Ciarrocchi, M. Pizzochero, D. Unuchek, O. V. Yazyev and A. Kis, Nat. Nanotechnol., 2019, 14, 674–678 CrossRef CAS PubMed.
- Y. Zhao, L. Lin, Q. Zhou, Y. Li, S. Yuan, Q. Chen, S. Dong and J. Wang, Nano Lett., 2018, 18, 2943–2949 CrossRef CAS PubMed.
- X. Cong, Y. Liao, Q. Peng, Y. Yang, C. Cheng, W. Zhang, P. Fang, C. Chen, L. Miao and J. Jiang, RSC Adv., 2015, 5, 59344–59348 RSC.
- P. Nayebi and M. Shamshirsaz, Eur. Phys. J. B, 2020, 93, 170 CrossRef.
- L. Song, H. Cao, X. Chai, X. Chen, Z. Ye, Y. Zhou, X. Huang, H. Zhu and X. Zheng, Phys. E, 2020, 120, 114057 CrossRef CAS.
- W. Miao, L. Wang, J. Wang and M. Sun, ACS Appl. Nano Mater., 2023, 6, 20074–20081 CrossRef CAS.
- Q. Zheng, G. Luo, Q. Liu, R. Quhe, J. Zheng, K. Tang, Z. Gao, S. Nagase and J. Lu, Nanoscale, 2012, 4, 3990–3996 RSC.
- M. Serlin, C. Tschirhart, H. Polshyn, Y. Zhang, J. Zhu, K. Watanabe, T. Taniguchi, L. Balents and A. Young, Science, 2020, 367, 900–903 CrossRef CAS PubMed.
- C. Chen, J. Li and X.-L. Sheng, Phys. Lett. A, 2017, 381, 3337–3341 CrossRef CAS.
- X. Gao, H. Liu, D. Wang and J. Zhang, Chem. Soc. Rev., 2019, 48, 908–936 RSC.
- Z.-Z. Lin, Q. Wei and X. Zhu, Carbon, 2014, 66, 504–510 CrossRef CAS.
- J. Xi, Y. Nakamura, T. Zhao, D. Wang and Z. Shuai, Acta Phys–Chim. Sin., 2018, 34, 961–976 CAS.
- W. T. Chen, M. Mizumaki, H. Seki, M. S. Senn, T. Saito, D. Kan, J. P. Attfield and Y. Shimakawa, Nat. Commun., 2014, 5, 3909 CrossRef CAS PubMed.
- X. Wang, M. Liu, X. Shen, Z. Liu, Z. Hu, K. Chen, P. Ohresser, L. Nataf, F. Baudelet and H.-J. Lin, et al., Inorg. Chem., 2019, 58, 320–326 CrossRef CAS PubMed.
- Z. Liu, Q. Sun, X. Ye, X. Wang, L. Zhou, X. Shen, K. Chen, L. Nataf, F. Baudelet and S. Agrestini, et al., Appl. Phys. Lett., 2020, 117, 152402 CrossRef CAS.
- D. Wang, M. Shaikh, S. Ghosh and B. Sanyal, Phys. Rev. Mater., 2021, 5, 054405 CrossRef CAS.
- Z. Liu, S. Zhang, X. Wang, X. Ye, S. Qin, X. Shen, D. Lu, J. Dai, Y. Cao, K. Chen, F. Radu, W.-B. Wu, C.-T. Chen, S. Francoual, J. R. L. Mardegan, O. Leupold, L. H. Tjeng, Z. Hu, Y.-f. Yang and Y. Long, Adv. Mater., 2022, 34, 2200626 CrossRef CAS PubMed.
- J. Zhang, Z. Liu, X. Ye, X. Wang, D. Lu, H. Zhao, M. Pi, C.-T. Chen, J.-L. Chen, C.-Y. Kuo, Z. Hu, X. Yu, X. Zhang, Z. Pan and Y. Long, Inorg. Chem., 2024, 63, 3499–3505 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- J. P. Perdew, B. Kieron and E. Matthias, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. C. Calderon, J. J. Plata, C. Toher, C. Oses, O. Levy, M. Fornari, A. Natan, J. M. Mehl, G. Hart, B. M. Nardelli and S. Curtarolo, Comput. Mater. Sci., 2015, 108, 233–238 CrossRef.
- R. F. L. Evans, W. J. Fan, P. Chureemart, T. A. Ostler, M. O. A. Ellis and R. W. Chantrell, J. Phys.: Condens. Matter, 2014, 26, 103202 CrossRef CAS PubMed.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- K. Samanta and S.-D. Tanusri, J. Phys. Soc. Jpn., 2018, 87, 041007 CrossRef.
- H. L. Feng, M. Arai, Y. Matsushita, Y. Tsujimoto, Y. Guo, C. I. Sathish, X. Wang, Y.-H. Yuan, M. Tanaka and K. Yamaura, J. Am. Chem. Soc., 2014, 136, 3326–3329 CrossRef CAS PubMed.
- Z. Jirák, S. Krupička, Z. Šimša, M. Dlouhá and S. Vratislav, J. Magn. Magn. Mater., 1985, 53, 153–166 CrossRef.
- M. Pajda, J. Kudrnovsky, I. Turek, V. Drchal and P. Bruno, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 64, 174402 CrossRef.
- E. Sasioglu, E. lu, L. M. Sandratskii and P. Bruno, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 70, 024427 CrossRef.
- R. F. L. Evans, U. Atxitia and R. W. Chantrell, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 91, 144425 CrossRef.
- A. A. Belik, R. Liu, M. Tanaka and K. Yamaura, Molecules, 2024, 29, 5488 CrossRef CAS PubMed.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- K. Yang, R. Wu, L. Shen, Y. P. Feng, Y. Dai and B. Huang, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 125211 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b
*b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14,15 and Fe3O4
14,15 and Fe3O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16,17, which were also proposed as HM and investigated comprehensively. In this regard, perovskite oxides (POs) have become very important candidates, especially after the discovery of sizable magnetoresistance in La1−xSrxMnO3
16,17, which were also proposed as HM and investigated comprehensively. In this regard, perovskite oxides (POs) have become very important candidates, especially after the discovery of sizable magnetoresistance in La1−xSrxMnO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 and Tl2Mn2O7
18 and Tl2Mn2O7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19, further emphasizing the importance of HM structures. Similarly, double perovskite oxides (DPOs) with an ordered A2BB′O6 form, where the B and B′ ions are usually 3d and 4/5d TMs,20,21 are highly beneficial for spintronic applications.22 Excitingly, an HM FiM state is anticipated in the Sr2FeMoO6 DPO, which has a metal-to-insulator transition (MIT) at 410 K and also demonstrates a large TMR ratio at room temperature. In this context, the Fe3+ 3d5 and Mo5+ 5d1 ions with
19, further emphasizing the importance of HM structures. Similarly, double perovskite oxides (DPOs) with an ordered A2BB′O6 form, where the B and B′ ions are usually 3d and 4/5d TMs,20,21 are highly beneficial for spintronic applications.22 Excitingly, an HM FiM state is anticipated in the Sr2FeMoO6 DPO, which has a metal-to-insulator transition (MIT) at 410 K and also demonstrates a large TMR ratio at room temperature. In this context, the Fe3+ 3d5 and Mo5+ 5d1 ions with  are coupled antiferromagnetically, resulting in a FiM spin-ordering (SO).3 Similarly, an HM FiM behavior is observed in Sr2CrReO6 owing to it having the highest Curie temp. (TC) of 635 K among the DPO family.23,24 However, it is theoretically established that SP in HM DPOs such as Sr2FeMoO6 substantially depends on temp. and cation disorder, as well as being proportional to the spin-magnetization of the cores.25 In the past decade, numerous efforts have been dedicated to develop robust 2D FM/FiM materials with high TC. One effective approach involves modulating the magnetism in existing 2D layered materials through post-treatment techniques, such as doping, ion or charge implantation,26,27 strain engineering,28,29 and defect engineering.30,31 The research discovered that the stress-induced transformation of two-dimensional materials from an indirect to a direct energy gap (Eg) significantly enhances photoluminous (PL) efficiency, making them more suitable for optoelectronic devices.32–41 Thus, novel nano-electronic and optoelectronic devices with stress-adjustable properties hold significant potential for spintronic applications. Moreover, to optimize material properties, the doping/ion implantation strategy has been explored, in which additional magnetic cations are introduced at the A-site in the DPO with a ratio of 1 to 3. This results in a new A- and B-site ordered quadruple DPO (QDPO) keeping an
are coupled antiferromagnetically, resulting in a FiM spin-ordering (SO).3 Similarly, an HM FiM behavior is observed in Sr2CrReO6 owing to it having the highest Curie temp. (TC) of 635 K among the DPO family.23,24 However, it is theoretically established that SP in HM DPOs such as Sr2FeMoO6 substantially depends on temp. and cation disorder, as well as being proportional to the spin-magnetization of the cores.25 In the past decade, numerous efforts have been dedicated to develop robust 2D FM/FiM materials with high TC. One effective approach involves modulating the magnetism in existing 2D layered materials through post-treatment techniques, such as doping, ion or charge implantation,26,27 strain engineering,28,29 and defect engineering.30,31 The research discovered that the stress-induced transformation of two-dimensional materials from an indirect to a direct energy gap (Eg) significantly enhances photoluminous (PL) efficiency, making them more suitable for optoelectronic devices.32–41 Thus, novel nano-electronic and optoelectronic devices with stress-adjustable properties hold significant potential for spintronic applications. Moreover, to optimize material properties, the doping/ion implantation strategy has been explored, in which additional magnetic cations are introduced at the A-site in the DPO with a ratio of 1 to 3. This results in a new A- and B-site ordered quadruple DPO (QDPO) keeping an  form, which possesses a very high MTT and magnetization (M). For instance, the antiferromagnetic (AFM) interaction between the magnetic cations induces a FiM state in the CaCu3Fe2Re2O12 QDPO, which features a very high MIT of 560 K and 100% SP. In this state, the spin-majority and spin-minority channels (N↑ and N↓) exhibit nonconductive and conductive traits, respectively, along with a large total magnetic moment (mt) of 8.7 μB.42 In this continuum, a newly ordered NaCu3Fe2Os2O12 QDPO was synthesized, which exhibits an HM FiM nature with a wide energy gap (Eg) in N↑ and spin ordering of Cu2+↑Fe3+↑Os5.5+↓, showing a TC above 380 K.43 Combined experimental and theoretical studies demonstrate that the FiM LaCu32+Co22+Re25.5+O12 QDPO is nearly 100% ordered with Cu2+↑Fe3+↑Os5.5+↓ SO and a TC of 150 K.44 Wang et al. theoretically predicted a series of HM FiM ACu3Fe2Re2O12 (A = Ca, Sr, Ba, Pb, Sc, Y, La) QDPOs, where the AFM coupling between CuFe and Re is dominant.45 It was established that compounds with A2+ = Ca/Sr/Ba/Pb and A3+ = Sc/Y/La ions exhibit TC values greater than 405 K and 502 K, respectively. Similarly, LaCu3Fe2Re2O12 is a HM material with a very large TC of 710 K, where a strong AFM coupling of Cu2+↑Fe3+↑Os4.5+↓ results in a FiM lowest energy state.46 It was also observed that the saturated total mt of 7.0 μB at 710 K increases to 8.0 μB at 2 K. Very recently, Zhang et al. experimentally verified the HM FiM nature in the CaCu3Cr2Re2O12 (CCCRO) system, maintaining a spin ordering of Cu2+↑ Cr3+↑ Re5+↓ above room temp. (360 K).47 However, in this stable charge configuration, the calculated mt of 5.0 μB is significantly greater than the experimentally measured value of 1.6 μB per f.u. Therefore, the intriguing features of this new class of materials, as outlined above, motivate us to explore the different characteristics of the recently synthesized CCCRO QDPO through density functional theory (DFT) calculations. These calculations demonstrate a FiM spin ordering, accompanied by a mt of 5.0 μB per formula unit (f.u.), and a half-metallic nature, featuring a 1.62 eV gap in the N↑ channel. This results in a high TC of 340 K. The material shows metallic behavior in the N↓ channel, with a p-type thermoelectric (TE) response. Moreover, the HM phase of the system remains stable under biaxial strain, and the material exhibits promising TE and catalytic properties, making it a strong candidate for future device applications. Finally, this paper aims to develop a theory of the magnetization process for CCCRO QDPO-based ultra-thin spin valves, which have proven to be effective as high-temperature storage devices.
form, which possesses a very high MTT and magnetization (M). For instance, the antiferromagnetic (AFM) interaction between the magnetic cations induces a FiM state in the CaCu3Fe2Re2O12 QDPO, which features a very high MIT of 560 K and 100% SP. In this state, the spin-majority and spin-minority channels (N↑ and N↓) exhibit nonconductive and conductive traits, respectively, along with a large total magnetic moment (mt) of 8.7 μB.42 In this continuum, a newly ordered NaCu3Fe2Os2O12 QDPO was synthesized, which exhibits an HM FiM nature with a wide energy gap (Eg) in N↑ and spin ordering of Cu2+↑Fe3+↑Os5.5+↓, showing a TC above 380 K.43 Combined experimental and theoretical studies demonstrate that the FiM LaCu32+Co22+Re25.5+O12 QDPO is nearly 100% ordered with Cu2+↑Fe3+↑Os5.5+↓ SO and a TC of 150 K.44 Wang et al. theoretically predicted a series of HM FiM ACu3Fe2Re2O12 (A = Ca, Sr, Ba, Pb, Sc, Y, La) QDPOs, where the AFM coupling between CuFe and Re is dominant.45 It was established that compounds with A2+ = Ca/Sr/Ba/Pb and A3+ = Sc/Y/La ions exhibit TC values greater than 405 K and 502 K, respectively. Similarly, LaCu3Fe2Re2O12 is a HM material with a very large TC of 710 K, where a strong AFM coupling of Cu2+↑Fe3+↑Os4.5+↓ results in a FiM lowest energy state.46 It was also observed that the saturated total mt of 7.0 μB at 710 K increases to 8.0 μB at 2 K. Very recently, Zhang et al. experimentally verified the HM FiM nature in the CaCu3Cr2Re2O12 (CCCRO) system, maintaining a spin ordering of Cu2+↑ Cr3+↑ Re5+↓ above room temp. (360 K).47 However, in this stable charge configuration, the calculated mt of 5.0 μB is significantly greater than the experimentally measured value of 1.6 μB per f.u. Therefore, the intriguing features of this new class of materials, as outlined above, motivate us to explore the different characteristics of the recently synthesized CCCRO QDPO through density functional theory (DFT) calculations. These calculations demonstrate a FiM spin ordering, accompanied by a mt of 5.0 μB per formula unit (f.u.), and a half-metallic nature, featuring a 1.62 eV gap in the N↑ channel. This results in a high TC of 340 K. The material shows metallic behavior in the N↓ channel, with a p-type thermoelectric (TE) response. Moreover, the HM phase of the system remains stable under biaxial strain, and the material exhibits promising TE and catalytic properties, making it a strong candidate for future device applications. Finally, this paper aims to develop a theory of the magnetization process for CCCRO QDPO-based ultra-thin spin valves, which have proven to be effective as high-temperature storage devices.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (No. 201).47 The experimentally observed lattice constants of a = b = c = 7.4152 Å
(No. 201).47 The experimentally observed lattice constants of a = b = c = 7.4152 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47 were used for the present study and our DFT calculated value of 7.4097 Å is in excellent agreement with the experiment. The Wyckoff positions for Ca, Cu, Cr, Re, and O ions are 2a(0.25, 0.25, 0.25), 6d(0.25, 0.75, 0.75), 4b(0, 0, 0), 4c(0.5, 0.5, 0.5), and 24h(0.5583, 0.7559, 0.0662), respectively. First, we investigated the magnetically stable state of the system by considering four possible spin orderings (SOs): FM (Cu2+↑, Cr3+↑, Re5+↑), FiM-1 (Cu2+↑, Cr3+↑, Re5+↓), FiM-II (Cu2+↓, Cr3+↑, Re5+↓), and FiM-III (Cu2+↓, Cr3+↑, Re5+↑), as displayed in Fig. 1(a–d), respectively. In the case of the FM SO, the spins of all magnetic ions are aligned in the same direction (see Fig. 1(a)). However, in FiM-1 SO, the Cu and Cr spins are parallel to each other, but anti-parallel to that of Re (see Fig. 1(b)). For FiM-II SO, the Cu and Re spins are aligned with each other but anti-aligned to that of Cr (see Fig. 1(c)). Finally, in FiM-III SO, the spins of Cr and Re are aligned in the same direction as each other, whereas they are anti-aligned with the Cu spin (see Fig. 1(d)). Henceforth, the Cu2+↑Cr3+↑Re5+↓ (FiM-1) configuration is the lowest energy state with energy differences of −105/−78/−55 meV to the FM/FiM-II/FiM-III SO. This state has a mt of 5.0 μB per f.u., which is in excellent agreement with recent experimental observations.47 Notably, the lengths of the arrows in the figures represent the magnitude of each atom’s spin magnetic moment (ms). Next, we studied the structural stability of the CCCRO material in its stable FiM-I phase by calculating the formation and cohesive energies (Efor. and Ecoh.) as:
47 were used for the present study and our DFT calculated value of 7.4097 Å is in excellent agreement with the experiment. The Wyckoff positions for Ca, Cu, Cr, Re, and O ions are 2a(0.25, 0.25, 0.25), 6d(0.25, 0.75, 0.75), 4b(0, 0, 0), 4c(0.5, 0.5, 0.5), and 24h(0.5583, 0.7559, 0.0662), respectively. First, we investigated the magnetically stable state of the system by considering four possible spin orderings (SOs): FM (Cu2+↑, Cr3+↑, Re5+↑), FiM-1 (Cu2+↑, Cr3+↑, Re5+↓), FiM-II (Cu2+↓, Cr3+↑, Re5+↓), and FiM-III (Cu2+↓, Cr3+↑, Re5+↑), as displayed in Fig. 1(a–d), respectively. In the case of the FM SO, the spins of all magnetic ions are aligned in the same direction (see Fig. 1(a)). However, in FiM-1 SO, the Cu and Cr spins are parallel to each other, but anti-parallel to that of Re (see Fig. 1(b)). For FiM-II SO, the Cu and Re spins are aligned with each other but anti-aligned to that of Cr (see Fig. 1(c)). Finally, in FiM-III SO, the spins of Cr and Re are aligned in the same direction as each other, whereas they are anti-aligned with the Cu spin (see Fig. 1(d)). Henceforth, the Cu2+↑Cr3+↑Re5+↓ (FiM-1) configuration is the lowest energy state with energy differences of −105/−78/−55 meV to the FM/FiM-II/FiM-III SO. This state has a mt of 5.0 μB per f.u., which is in excellent agreement with recent experimental observations.47 Notably, the lengths of the arrows in the figures represent the magnitude of each atom’s spin magnetic moment (ms). Next, we studied the structural stability of the CCCRO material in its stable FiM-I phase by calculating the formation and cohesive energies (Efor. and Ecoh.) as: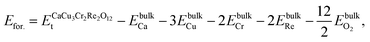

 is the DFT-computed Et of the CCCRO structure, while EbulkCa, EbulkCu, EbulkCr, EbulkRe, and
is the DFT-computed Et of the CCCRO structure, while EbulkCa, EbulkCu, EbulkCr, EbulkRe, and  are the DFT-determined Et for the Ca, Cu, Cr and Re ions and O molecules in their bulk stable phases, respectively. Similarly, Eiso.Ca, Eiso.Cu, Eiso.Cr, Eiso.Re, and
are the DFT-determined Et for the Ca, Cu, Cr and Re ions and O molecules in their bulk stable phases, respectively. Similarly, Eiso.Ca, Eiso.Cu, Eiso.Cr, Eiso.Re, and  are the DFT-measured Et for the isolated Ca, Cu, Cr and Re ions, and oxygen molecule, accordingly. The calculated Efor./Ecoh. per atom is −2.31 eV/−4.89 eV. The negative signs for both energies confirm that the structure is thermodynamically stable and supports an exothermic reaction. Moreover, the mechanical stability of the structure is utilized by calculating the elastic tensors (Cij). The computed three independent elastic parameters, namely C11, C12, and C44, satisfied the basic demands and Born criteria as (C11 − C12) > 0, (C11 + 2C12) > 0, C11 > 0, C44 > 0, and C12 < B < C11 (ref. 52) for the mechanical stability. Hence, the determined C11, and C12, and C12 are 289, 211, and 140, correspondingly, which satisfies the above-mentioned mechanical stability standard.
are the DFT-measured Et for the isolated Ca, Cu, Cr and Re ions, and oxygen molecule, accordingly. The calculated Efor./Ecoh. per atom is −2.31 eV/−4.89 eV. The negative signs for both energies confirm that the structure is thermodynamically stable and supports an exothermic reaction. Moreover, the mechanical stability of the structure is utilized by calculating the elastic tensors (Cij). The computed three independent elastic parameters, namely C11, C12, and C44, satisfied the basic demands and Born criteria as (C11 − C12) > 0, (C11 + 2C12) > 0, C11 > 0, C44 > 0, and C12 < B < C11 (ref. 52) for the mechanical stability. Hence, the determined C11, and C12, and C12 are 289, 211, and 140, correspondingly, which satisfies the above-mentioned mechanical stability standard.


 , respectively. Hence, the computed ms on each ion also verifies their respective valence states. The induced orbital magnetic moment (morb.) on the Cu/Cr/Re ion is 0.06/−0.05/0.23 μB. Compared to that on the Cu and Cr, the sizable magnitude of morb. on the Re ion highlights the strong SOC influence. Furthermore, as Cu lies in a more than half-occupied d state, its ms and morb. are aligned with each other (i.e., both have a “+” sign), as discussed in ref. 53. Conversely, Cr and Re ions lie in less than half-filled d states, so their ms and morb. are anti-aligned. For Cr, the signs are “+/−” for ms/morb., while for Re, they are “−/+”, as described in ref. 54. Thus, the above discussions support the AFM interactions between the Cu/Cr and Re ions.
, respectively. Hence, the computed ms on each ion also verifies their respective valence states. The induced orbital magnetic moment (morb.) on the Cu/Cr/Re ion is 0.06/−0.05/0.23 μB. Compared to that on the Cu and Cr, the sizable magnitude of morb. on the Re ion highlights the strong SOC influence. Furthermore, as Cu lies in a more than half-occupied d state, its ms and morb. are aligned with each other (i.e., both have a “+” sign), as discussed in ref. 53. Conversely, Cr and Re ions lie in less than half-filled d states, so their ms and morb. are anti-aligned. For Cr, the signs are “+/−” for ms/morb., while for Re, they are “−/+”, as described in ref. 54. Thus, the above discussions support the AFM interactions between the Cu/Cr and Re ions.



 exhibits a distinct temp. dependence due to the SP electronic structure. There is a significant increase in σ for non-metallic N↑, from 3.18 × 1019 S m−1 at 300 K to 4.0 × 1019 S m−1 at 800 K, as thermal excitation promotes electrons across the gap. In contrast, N↓ shows a weaker temp. dependence, from 2.58 × 1019 S m−1 at 300 K to 2.80 × 1019 S m−1 at 800 K, as conductivity is primarily limited by electron-phonon scattering (see Fig. 8(a)). Initially, N↑ has a higher S (1.92 × 10−5 V K−1) at 300 K due to limited thermally excited carriers, while N↓ exhibits a lower S (−2.94 × 10−6 V K−1) at 300 K. As temp. increases (up to 800 K), the S for N↑ decreases (−3.73 × 10−6 V K−1) as thermal excitation saturates available states, while the S for N↓ increases (8.66 × 10−6 V K−1) due to enhanced carrier diffusion (Fig. 8(b)). After a certain temp., S stabilizes for both channels, indicating saturation in the TE potential.
exhibits a distinct temp. dependence due to the SP electronic structure. There is a significant increase in σ for non-metallic N↑, from 3.18 × 1019 S m−1 at 300 K to 4.0 × 1019 S m−1 at 800 K, as thermal excitation promotes electrons across the gap. In contrast, N↓ shows a weaker temp. dependence, from 2.58 × 1019 S m−1 at 300 K to 2.80 × 1019 S m−1 at 800 K, as conductivity is primarily limited by electron-phonon scattering (see Fig. 8(a)). Initially, N↑ has a higher S (1.92 × 10−5 V K−1) at 300 K due to limited thermally excited carriers, while N↓ exhibits a lower S (−2.94 × 10−6 V K−1) at 300 K. As temp. increases (up to 800 K), the S for N↑ decreases (−3.73 × 10−6 V K−1) as thermal excitation saturates available states, while the S for N↓ increases (8.66 × 10−6 V K−1) due to enhanced carrier diffusion (Fig. 8(b)). After a certain temp., S stabilizes for both channels, indicating saturation in the TE potential. increases linearly with temp. primarily due to phonon–electron scattering, peaking around 800 K for both channels. For N↑, the conductivity is slightly higher, with the value increasing from 2.88 × 1014 W m−1 K at 300 K to 1.02 × 1015 W m−1 K at 800 K (Fig. 8(c)). This difference arises from the increased availability of high-energy states in N↑ due to thermal excitation across the Eg. N↓, being metallic, shows a less pronounced increase, from 2.01 × 1014 W m−1 K at 300 K to 6.27 × 1014 W m−1 K at 800 K, due to the relatively constant DOS at the EF. χ is higher for N↓ than N↑ at lower temp. as N↓ is metallic and has a higher DOS at the EF. At 300 K, χ for N↓ is 1.59 × 10−11 and decreases to 1.57 × 10−11 at 800 K due to thermal excitation disrupting spin alignment. For N↑, χ increases from 1.35 × 10−11 at 300 K to 1.47 × 10−11 at 800 K as thermal excitation promotes electrons across the Eg, allowing for stronger spin alignment. However, χ for N↑ saturates around the TC due to phase transition effects (Fig. 8(d)). The Hall coefficient (RH) for N↑ remains positive across this temp. range, indicating hole conduction, while for N↓, it decreases with increasing temp., signifying metallic behavior (shown in Fig. 8(e)). In N↓, RH decreases with temp. as thermally activated carriers dominate, signaling the metallic behavior. For N↑, RH increases as thermal excitation generates additional carriers, enhancing the RH. Further, the molar specific heat capacity (CV) increases with temp. following the Debye Law, reflecting stronger atomic binding and activation of additional vibrational modes. Despite differing electronic properties, CV remains nearly identical for both spin channels because it is governed primarily by phonon vibrations in the lattice, which are independent of the SP electronic structure. Finally, the thermal performance of the systems as quantified by the figure of merit,
increases linearly with temp. primarily due to phonon–electron scattering, peaking around 800 K for both channels. For N↑, the conductivity is slightly higher, with the value increasing from 2.88 × 1014 W m−1 K at 300 K to 1.02 × 1015 W m−1 K at 800 K (Fig. 8(c)). This difference arises from the increased availability of high-energy states in N↑ due to thermal excitation across the Eg. N↓, being metallic, shows a less pronounced increase, from 2.01 × 1014 W m−1 K at 300 K to 6.27 × 1014 W m−1 K at 800 K, due to the relatively constant DOS at the EF. χ is higher for N↓ than N↑ at lower temp. as N↓ is metallic and has a higher DOS at the EF. At 300 K, χ for N↓ is 1.59 × 10−11 and decreases to 1.57 × 10−11 at 800 K due to thermal excitation disrupting spin alignment. For N↑, χ increases from 1.35 × 10−11 at 300 K to 1.47 × 10−11 at 800 K as thermal excitation promotes electrons across the Eg, allowing for stronger spin alignment. However, χ for N↑ saturates around the TC due to phase transition effects (Fig. 8(d)). The Hall coefficient (RH) for N↑ remains positive across this temp. range, indicating hole conduction, while for N↓, it decreases with increasing temp., signifying metallic behavior (shown in Fig. 8(e)). In N↓, RH decreases with temp. as thermally activated carriers dominate, signaling the metallic behavior. For N↑, RH increases as thermal excitation generates additional carriers, enhancing the RH. Further, the molar specific heat capacity (CV) increases with temp. following the Debye Law, reflecting stronger atomic binding and activation of additional vibrational modes. Despite differing electronic properties, CV remains nearly identical for both spin channels because it is governed primarily by phonon vibrations in the lattice, which are independent of the SP electronic structure. Finally, the thermal performance of the systems as quantified by the figure of merit,