Tuning the RKKY interaction in bilayer graphene: the pivotal role of electron–phonon coupling and external fields

Abstract

In this work, the effects of electron–phonon coupling are uniquely integrated in a state-of-the-art study of RKKY interaction in simple bilayer graphene. We investigate the Holstein model Hamiltonian using Green's function approaches, taking into account three crucial parameters: an interlayer bias voltage, a perpendicular magnetic field, and a chemical potential to regulate electron density. We provide a detailed perspective of the behavior of the RKKY exchange interaction under different conditions by first calculating the static spin susceptibility and then computing the interaction with great precision. Our new method reveals how important the electron–phonon interaction strength is in forming this magnetic coupling, and the results, which are backed up by a thorough graphical analysis, show how it varies subtly depending on the parameters that are included. These discoveries open the door for creative approaches to the creation of adjustable quantum systems for next-generation technologies and greatly advance our understanding of indirect exchange in two-dimensional materials.

---

1 Introduction

By stacking two graphene layers on top of one another, bilayer graphene is produced.^1,2 Modifying the bandgap in reaction to an external electric field is one of the structure's distinctive characteristics. Hence bilayer graphene is ideal for use in optoelectronics and nanoelectronics.^3,4 Due to the interplay between interlayer coupling and external disturbances, this tunability offers a versatile platform for studying quantum processes in low-dimensional systems.⁵ Overall, the existence of gap states and the small size of bilayer graphene limit its performance in transistor applications, despite the fact that its tunable band gap offers unique potential.⁶ These problems must be fixed if its use in electrical devices is to be maximized. The work explores the transport properties of bilayer graphene with a focus on conductivity and localization effects. It investigates the consequences of an energy gap caused by interlayer asymmetry by applying the effective mass model and the Born approximation.⁷ Furthermore, bilayer graphene has exceptional mechanical strength and flexibility. Factors such as fracture development and twist angles may alter its mechanical characteristics.^8,9 Recent advancements in experimental techniques have further demonstrated its potential as a mechanically robust material for flexible electronics.¹⁰ The mechanical properties of bilayer graphene enable effective performance in various scenarios, but its lower chemical reactivity compared to monolayer graphene makes functionalization harder, potentially complicating the chemical changes needed for specific applications.¹¹ Bilayer graphene is also used in a variety of applications, including as transistors, sensors, and spintronic devices.^12–16 Its ability to produce high on/off current ratios in transistors⁴ adds to its potential in digital electronics.¹⁷ Bilayer graphene is acknowledged as a crucial component for developing contemporary technology when all is said and done.^18–20 The manufacture of high-quality, large-area bilayer graphene remains a challenge. The sizes generated by existing methods are often limited, and achieving uniformity in layer stacking is a significant obstacle.²¹

In solid-state physics, the electron–phonon interaction²² is vital, affecting electrical resistance, superconductivity,^23–26 and hot electron dynamics. Furthermore, the magnetic properties of layered materials must be adjusted by this interaction in order to influence phenomena like indirect exchange couplings.²⁷ The understanding of electron–phonon interactions is crucial for improving heat transfer in microelectronics and thermoelectric materials.^28,29 This knowledge aids in the design of materials with efficient heat management, which is essential for the longevity and functionality of devices. According to a research on theory and applications, electron–phonon effects including mobility and superconductivity are predicted by ab initio calculations.³⁰ Electron–phonon interactions play a major role in cavity quantum electrodynamics (QED) in silicon quantum dots.³¹ They have an impact on the coherence and emission characteristics of quantum states, which are crucial for creating reliable quantum computing systems.^32–34 Using a modified technique, researchers showed that photoexcited charge carriers in silicon reduce thermal conductivity by scattering phonons, revealing electron–phonon interaction's role in heat transport and hinting at light-based thermal control.³⁵ Across our earlier research, we have systematically analyzed how spin–orbit coupling,^36,37 electron–electron interactions,³⁸ and notably electron–phonon coupling^39–42 shape the electronic, magnetic, and thermodynamic properties of diverse low-dimensional materials.

In 1954, Ruderman and Kittel originally proposed⁴³ the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction, an indirect quantum mechanical exchange mechanism that Kasuya⁴⁴ and Yosida⁴⁵ later improved. It explains how conduction electrons in a host material mediate the magnetic coupling between localized spins (such as magnetic impurities). Depending on the density of electronic states at the Fermi level, the RKKY interaction in ordinary metallic systems exhibits either ferromagnetic or antiferromagnetic behavior as it oscillates with the distance between spins.⁴⁶ This interaction's classical form is provided by H_RKKY = J(r) S₁ × S₂ where J(r) is the oscillatory exchange coupling function dependent on the distance r between two localized spins S₁ and S₂.^47–50 In bilayer graphene, the RKKY interaction differs from 3D materials due to its 2D nature and symmetry. The slower decay (e.g. 1/r²) in bilayer graphene, which may be adjusted by electric fields or doping, is caused by its parabolic band structure and effective mass, in contrast to single-layer graphene, where J(r) decays as 1/r³ and is antiferromagnetic owing to linear density of states. The reliance of the RKKY interaction in twisted bilayer graphene on the twist angle is another intriguing feature. According to theoretical research, the density of states sharply rises at particular angles, such the magic angle (∼1.1°), resulting in the creation of flat bands.^51–53 These flat bands can enhance the RKKY interaction, resulting in unexpected magnetic behaviors that are amplified in the presence of Holstein phonons. By introducing scattering and changing electron mass, Holstein phonons further affect this. Bilayer graphene is a perfect testbed for examining quantum magnetism because of the added complexity introduced by the interaction between these phonons and electronic degrees of freedom.⁵⁴ A complex subject of both basic and applied importance is the RKKY interaction in bilayer graphene, especially when Holstein phonons are present.^55–59 This interaction, which is influenced by the electrical and vibrational characteristics of the material, provides a means of advancing knowledge and technological advancement. Moreover, external fields such as magnetic fields can further tune this interaction, offering a pathway to control magnetic order at the nanoscale.⁶⁰ Previous work by our group has investigated the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction in a variety of material systems, including graphene and its derivatives,^61–63 with a focus on clarifying how lattice dynamics, in particular electron–phonon interaction,^64–66 influence this basic magnetic exchange process.

A technique for calculating the spatial dependency and Lindhard function of the RKKY interaction for any dimension n is presented in an article, exposing sign shifts in metallic layers that promote antiferromagnetic stacking.⁶⁷ In another work researchers studied the RKKY interaction between magnetic impurities in graphene using perturbation theory in imaginary time, evaluating its symmetry on a bipartite lattice at half filling via real-space spin susceptibility.⁶⁸ The RKKY interaction in CNTs and graphene nanoribbons, influenced by spin–orbit and magnetic fields, varies by sublattice in metallic CNTs and is ferromagnetic in semiconducting ones. Anisotropic terms arise from spin–orbit, tunable by Fermi level, with spin noise calculated from frequency analysis.⁶⁹ According to lattice Green's function, the RKKY interaction in graphene decays as 1/R³, oscillates with (K − K′) × R and phases, and exhibits ferromagnetic (antiferromagnetic) coupling for the same (opposite) sublattices, which is consistent with long-range analytics.⁷⁰ Recent studies have demonstrated that electron–phonon interactions in bilayer graphene alter its strength and spatial variation, and that Fermi level tweaking can change its behavior from ferromagnetic to antiferromagnetic.^{57,58,71–74}

2 Hamiltonian and Green's function

The structure of a simple (AA-stacked) bilayer graphene arrangement is depicted in Fig. 1. It consists of two graphene honeycomb lattices that are exactly positioned on top of one another, separated by around 0.3 nanometers. Only the visible layer is discernible when seen perpendicular to one of these layers, making the underlying layer indistinguishable. We have labeled the lower layer atoms with the number 1 and the upper layer atoms with the number 2. This method helps us easily identify the differences between the atoms in each layer. The unit cell in this structure is similar to graphene, with the difference that the primitive unit cell in bilayer graphene has four bases, and its generating vectors are as follows:where the unit vectors in the x and y directions are î and ĵ, respectively; and a defines the carbon–carbon bonding length between nearest neighbor atomic sites. The vectors a₁ and a₂ define the lattice in the x–y plane, with the armchair direction aligned along the x-axis and the zigzag direction along the y-axis, as illustrated in Fig. 1 and 2.

Fig. 1 The structure of AA-stacked bilayer graphene, consisting of two graphene honeycomb lattices positioned directly on top of each other, separated by approximately 0.3 nm. The lower layer atoms are labeled as 1, and the upper layer atoms as 2. The primitive lattice vectors a₁ and a₂ are shown, with the armchair direction along the x-axis and the zigzag direction along the y-axis, within a Cartesian coordinate system (x, y, z), where the z-axis is perpendicular to the graphene planes.

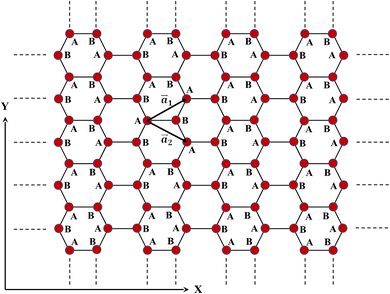Fig. 2 Top view of AA-stacked bilayer graphene, showing the primitive lattice vectors a₁ and a₂ within a Cartesian coordinate system.

We analyze electrons in the π-orbital of carbon atoms utilizing the tight-binding Hamiltonian, together with the influence of electron–phonon coupling resulting from localized phonons. For this purpose, the Holstein model Hamiltonian can be used to characterize the electronic characteristics of the interaction between dispersionless local vibrational modes and tight-binding electrons in graphene-like materials. The interlayer hopping integral γ in the Hamiltonian facilitates electron tunneling between the two graphene layers, splitting the electronic bands and enhancing the tunability of the RKKY interaction compared to monolayer graphene, where such interlayer coupling is absent. The Hamiltonian of the spin-dependent Holstein model for bilayer graphene in the presence of bias voltage and magnetic field perpendicular to the plane is provided by

where in this equation the nearest neighbor hopping integral for itinerant electrons on a honeycomb lattice is represented by t,⁷⁵ and within the honeycomb lattice, the wave vector k is located in the first Brillouin zone. At sublattice A(B), an electron with wave vector k and spin quantum number σ = ↑, ↓ is created by Additionally, μ presents the electron gas's chemical potential. In addition, the annihilation phonon operator at wave vector k on each sublattice is indicated by the symbol c_k. The frequency of the out-of-plane vibrations of each atom's optical phonon on the lattice is denoted by ω₀. Also g determines the electron–phonon couplings for sublattices A and B. The magneton Bohr constant is denoted by μ_B and magnetic field along perpendicular to the plane of the structure is introduced by B. To provide physical context, typical values are t ≈ 2.8 eV, γ ≈ 0.2 eV, g/t ≈ 0.01–0.1 (corresponding to 0.028–0.28 eV), V/t ≈ 0.1–1 (0.28–2.8 eV), and k_BT/t ≈ 0.01–0.1 (300–3000 K), which are realistic for experimental graphene-based devices. The interlayer hopping of electrons between graphene sheets is described by the second term in eqn (2). Between an A(B) site in one layer and the closest A(B) site in the other layer, the hopping parameter γ has a value of about 0.2.^76,77 Using unitary transformations, we transfer the non-interacting part of this Hamiltonian (H₀) expressed in the reciprocal space (wave vector k) to the band space, as a result of which the matrix form of this Hamiltonian is transformed into a diagonal matrix form, Hamiltonian and eigenvalues of the AA-stacked bilayer graphene system in the presence of magnetic field and bias voltage without considering Encryption failed: Data to encrypt is empty. Interactions with phonons are obtained as follows:where E^σ_η(k) represent the energy eigenvalues for each spin direction of electron, while the correspond to the creation and annihilation operators for electrons in the conduction and valence bands. σ in the right hand of each relation in eqn (3) gets amounts +1(−1) for spin up (down) electron.

In solid state physics, Green's functions are an essential mathematical tool that help analyze complicated problems including correlated electron systems, lattice dynamics, and electrical resistance in metals.⁷⁸ Green's functions provide a distinct method for modeling and resolving solid state physics issues when compared to other mathematical tools, especially in systems with intricate boundary conditions or strong confinement. It is a useful tool in the physicist's toolbox because of its capacity to deal with a variety of physical events. Additionally, Green's functions are used to calculate determinants and inverses of matrices relevant to solid state physics and quantum chemistry in the Huckel (tight binding) paradigm.^79,80

The matrix elements of the non-interacting single-particle Green's function can be calculated using its definition in terms of electronic creation and annihilation operators, which obey a specific anti-commutation relation

where {α, β} = {a₁, b₁, a₂, b₂} and ω_n denotes the fermionic Matsubara frequency. τ is the imaginary time and T implies the equilibrium temperature of the bilayer graphene. The calculation of eqn (4) necessitates a transformation between the electronic creation and annihilation operators, transitioning from the atomic orbital basis to the band basis, which are expressed as follows:

Appendix (6) lists the u_ij coefficients in this equation. In the case of bilayer graphene, since the number of atoms in the unit cell is four, and considering that the symmetry of the Green's function matrix arises from the symmetry of the Hamiltonian, a total of sixteen single-particle Green's functions can be written for this system. Finally, the following expression for Green's functions in Fourier presentation is produced after some algebraic computations:

As previously mentioned, the analytical form of the u_jα, u_jβ coefficients in eqn (6) is provided in Appendix 6.

To apply the impacts of phonon presence, we intend to assess the electron–phonon interaction, another statement included in the Holstein model Hamiltonian (H_int) in eqn (2), and use it to rectify the Green's functions and the band structure. Using Matsubara's formalism and perturbative expansion for the interacting spin-dependent Green's function matrix, Dyson's equation yields the perturbed Green's function matrix with

(G^σ(k,iω_n))⁻¹ = (G^(0)σ(k,iω_n))⁻¹ − Σ^σ(k,iω_n). (7)

We use the Migdal theorem⁸¹ to compute the elements of the self-energy matrix in eqn (7). This theory states that we can use the lowest order perturbation theory to discover the self-energy diagram since the phonon energy scale is substantially smaller than the electronic one. Using the Fourier transform of the phononic propagator and its definition as

where the bosonic Matsubara's frequency is implied by ν_m = 2πmk_BT with an integer value m. Since momentum has no effect on the Holstein phonon propagator D⁽⁰⁾(p, iν_m), the noninteracting phononic propagator (unperturbed phononic Green's function) is determined by

The off-diagonal components of the self-energy matrix have zero value because of the dispersionless nature of the Holstein phonon frequency. In the context of second-order perturbation theory for electron–phonon interaction, Feynman's diagrammatic methods⁸² can be used to derive the constituents of the spin-dependent self-energy matrix as outlined below

Phononic self-energy is insignificant for materials that resemble graphene because screening effects that correspond to static transverse spin susceptibility⁸³ have been derived from the electronic density of states at the Fermi surface. Thus, the Holstein phonon propagator in eqn (10) is regarded as unscreened (D⁽⁰⁾(iν_m)). We define the relationship between the noninteracting Matsubara electronic Green's function and the imaginary portion of the noninteracting ones in order to compute the self-energy elements using Lehman's theorem:⁸²

By converting eqn (11) into eqn (10) and applying Matsubara's frequency summation algorithm over bosonic Matsubara energies ν_m, the spin-dependent self-energy matrix elements are produced as follows:

where introduce the Bose–Einstein and Fermi–Dirac distribution functions, respectively. Moreover, refers to the unit cell number in the lattice structure of simple stacked bilayer graphene. Finally, the interacting Green's functions of the AA bilayer graphene structure are produced by inserting these components into the matrix of eqn (7).

3 Dynamical spin susceptibility and RKKY interaction

In order to obtain the spatial dependence of RKKY interaction for transverse spin components, static spin susceptibilities need to be calculated. Linear response theory gives us the noninteracting spin response functions based on the correlation function of both transverse and longitudinal components of spin operators. The dynamical spin susceptibility is defined as the Fourier transformation of the correlation function between spin components of localized electrons at different times. Based on the correlation function between transverse components of spin operators of electron gas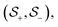 linear response theory provides us with the interacting spin response function in the presence of quantum effects of electronic interactions. The Fourier transform of Matsubara representation of transverse spin susceptibility, which is a spin–spin correlation function, has the following relationship:where q describes the wave vector belonging to the first Brillouin zone of the honeycomb monolayer. Also ν_n = 2nπk_BT is the bosonic Matsubara's frequency. 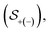The Fourier transformations of transverse components of spin density operators, are given by

Substitute in eqn (13) and following Wick's theorem implementation⁸⁵ and Fourier transformation, the one bubble level (obl) dynamical transverse spin susceptibility can be expressed as follows in terms of the Fourier representation of interacting Green's function matrix elements⁸²

Summation over fermionic Matsubara energies iω_m is accomplished by utilizing the Lehman representation,⁸² which connects Matsubara Green's function to the imaginary component of retarded Green's function as

After substituting eqn (17) into (16) and performing Matsubara frequency summation, the one bubble level dynamical transverse spin susceptibility function of bilayer graphene is finally obtained as the following expression

One technique for taking into consideration how electron–phonon interactions affect transverse spin susceptibility is the Random Phase Approximation (RPA). The interactions in a dense electron gas^86–88 are represented by leading-order chain Feynman diagrams, which are the source of this summation. By concentrating on particle-hole excitations, RPA streamlines the consideration of these interactions and successfully captures the fundamental physics of the system while ignoring higher-order correlations.⁸⁹ RPA has been used to examine spin, charge, and orbital fluctuations, among other phenomena, in the context of superconductivity and electron–phonon interaction.⁹⁰ Feynman diagrams,⁹¹ which offer a visual depiction of the interactions under consideration, are frequently used to assess the method's efficacy. The random phase approximation states that one bubble transverse spin susceptibility is used to express the transverse magnetic response function of interacting electrons on AA-stacked bilayer graphene.

where denotes the Fourier transformation of the effective phonon-mediated electron–electron interaction.

The Fourier transformation of the longitudinal component of the spin, i.e., is given in terms of fermionic operators as

Also, χ_zz is introduced as longitudinal spin susceptibility and its relation can be expressed in terms of the correlation function between the z component of spin operators as

After some algebraic calculations similar to the transverse spin susceptibility case, we arrive at the final results for the Matsubara representation of one bubble level longitudinal dynamical spin susceptibility, as

Using random phase approximation, the longitudinal magnetic response function of interacting electrons on AA-stacked bilayer graphene can be expressed in terms of one bubble longitudinal spin susceptibility as

Our system incorporates two localized magnetic moments whose interaction is mediated through an electron liquid in the presence of electron–phonon interaction and magnetic field. We assume that the magnetic field is applied perpendicular to the simple stacked bilayer graphene first, and then we add the magnetic moments. The contact interaction between the spin of itinerant electrons and two magnetic impurities with magnetic moments S₁ and S₂, located respectively at R₁ and R₂, is given by

where ζ is the coupling constant between conduction electrons and impurity, s(r) is the spin density operator of electrons. The RKKY interaction which arises from the quantum effects is obtained by using a second order perturbation^43,92which is the honored XXZ model. R denotes the spatial distance between two local moments S₁ and S₂. On the other hand, the coupling exchange constants are related to longitudinal and transverse static spin susceptibilities of the electron gas^43,92 aswhere J_zz(R) and J_xx(R) are named longitudinal and in-plane exchange coupling constants, respectively. The longitudinal (in-plane) coupling exchange states the strength of exchange interaction between longitudinal (transverse) spin components of localized moments. Longitudinal (transverse) components of spin of localized moments imply spin components perpendicular (parallel) to the plane of honeycomb layer in bilayer graphene. The effects of both magnetic field and electron–phonon coupling strength as well as bias voltage on the RKKY interactions have been addressed in this study. In AA-stacked bilayer graphene, the RKKY interaction exhibits sublattice dependence similar to monolayer graphene due to the direct alignment of layers. As shown in prior studies,^72,93 same-sublattice couplings (A–A, B–B) are typically stronger and ferromagnetic, while different-sublattice couplings (A–B) are weaker and antiferromagnetic, due to interference effects in the Green's function.

4 Results and analysis

In this section, we outline the numerical outcomes concerning the behaviors of both longitudinal and in-plane exchange coupling constants between two external local moments. Such external magnetic moments can be coupled via mediating electron gas in simple stacked bilayer graphene. Here electron gas in bilayer graphene acts as host medium for two external magnetic moments. The electron dynamics in bilayer graphene is described within the Holstein model framework. We intend to investigate the effects of electron–phonon coupling strength, bias voltage, and longitudinal magnetic field in electrons of host medium on the exchange coupling constants J_xx and J_zz. For achieving these purposes, we should numerically calculate self-energy matrix elements by using eqn (12). The required electronic band structure relations for numerical calculating eqn (12) have been given by eqn (3). Moreover, the Einstein phonon mode is evaluated at the amount ω₀ ≈ 0.1 eV.⁸⁴ Using matrix elements of noninteracting Green's function in eqn (6) and self-energy matrix elements in eqn (12), the matrix elements of interacting Green's function of simple stacked bilayer graphene can be obtained based on Dyson's equation in eqn (7). By using interacting Green's function, transverse spin susceptibility of simple stacked bilayer graphene can be derived via eqn (18) and (19). Moreover, longitudinal spin susceptibility is derived by using eqn (22) and (23). By inserting the numerical results of spin susceptibilities into eqn (26), longitudinal and in-plane exchange coupling constants strengths between two external magnetic moments localized into bilayer graphene are numerically determined. In order to obtain the numerical results of all mentioned equations, summation over wave vectors, k, have been performed into the first Brillouin zone of the honeycomb plane. The dependences of in-plane (J_xx(R)) and longitudinal (J_zz(R)) RKKY interactions on distance between two localized impurities are studied. We have considered both magnetic external moments are located into bilayer graphene along the zigzag direction so that the distance vector between two moments is R = R R̂, according to Fig. 1. The unit vector R̂ is aligned along the zigzag direction in the x–y plane, consistent with the coordinate system shown in Fig. 1. We initiate the exploration of the exchange coupling constant strengths between two localized moments by mediating simple bilayer graphene. The exchange coupling constants are investigated by delving into analysis of behaviors under the influences of magnetic fields, electron–phonon coupling, and bias voltage effects. The dominance of the antiferromagnetic regime (J_xx, J_zz > 0) over the ferromagnetic regime (J_xx, J_zz < 0) at small R/a arises from the oscillatory nature of the RKKY interaction, driven by the Fermi wavevector and the phase of the Green's function, which favors antiferromagnetic alignment at short distances.⁷⁰

The curves of RKKY exchange couplings in terms of normalized distance between two localized external moments, i.e., R/a, for undoped simple stacked bilayer graphene with μ = 0.0 for different normalized electron–phonon couplings g/t have been plotted in panels of Fig. 3. The bias voltage and magnetic field have been fixed at V/t = 0.3 and gμ_BB/t = 0.3, respectively. In the left panel, the in-plane exchange constant has been plotted in terms of distance between two localized external moments. For each value of g/t, the exchange coupling J_xx(R) exhibits an oscillatory behavior as a function of R so that the increase of electron–phonon coupling constant has considerable effect on the amplitude of oscillation of J_xx(R). Also, the period of this oscillation is independent of g. It is clearly observed that the range of antiferromagnetic exchange values (J_xx(R) > 0) is more than that of ferromagnetic (J_xx(R) < 0) ones. Longitudinal exchange coupling J_zz between two impurities localized in bilayer graphene in terms of normalized distance R/a for different values of g/t has been shown in the right panel of Fig. 3. The amplitude of longitudinal RKKY interaction oscillation decreases with distance parameter R/a, based on the right panel of Fig. 3. Also, at fixed value of R/a, the value of exchange constant J_zz reduces with electron–phonon coupling strength. It is obvious that the range of antiferromagnetic exchange values (J_zz(R) > 0) is more than that of ferromagnetic (J_zz(R) < 0) ones.

Fig. 3 Left (Right) Panel: in-plane (longitudinal) RKKY interaction (J_xx(R) (J_zz(R))) between two localized moments in undoped simple stacked bilayer graphene as a function of the distance R for different electron–phonon coupling strengths g/t for fixed temperature k_BT/t = 0.01. The magnetic field and bias voltage have been fixed at amounts gμ_BB/t = 0.3 and V/t = 0.3, respectively. The distance vector R = RR̂ is along the zigzag direction in the x–y plane, as shown in Fig. 1.

The influences of bias voltage on behaviors of RKKY exchange coupling constants have been depicted in panels of Fig. 4. We have considered the fixed values for electron–phonon coupling strength and magnetic field as g/t = 0.01 and gμ_BB/t = 0.3, respectively. The left panel of Fig. 4 shows the behavior of in-plane exchange coupling J_xx between two localized impurities in undoped bilayer graphene as a function of normalized distance R/a for different values of bias voltage. This panel indicates the amplitude of oscillation increases with bias voltage. The amplitude of oscillation of exchange constant J_xx indicates a remarkable reduction in the distance region R/a < 1 for all amounts of V/t. The coupling exchange constant at higher distances above normalized value 6 approximately tends to zero so that the curves of J_xx fall on each other in this range of distance. In the right panel of Fig. 4, we present the behavior of longitudinal exchange coupling J_zz between two localized external moments in undoped bilayer graphene as a function of normalized distance R/a for different values of bias voltage. This figure indicates the amplitude of oscillation increases with bias voltage. The amplitude of oscillation of exchange constant indicates a remarkable reduction in the distance region R/a < 1 for all amounts of bias voltages. The coupling exchange constant at higher distances above 6 approximately tends to zero so that the curves of J_zz fall on each other in this range of distance.

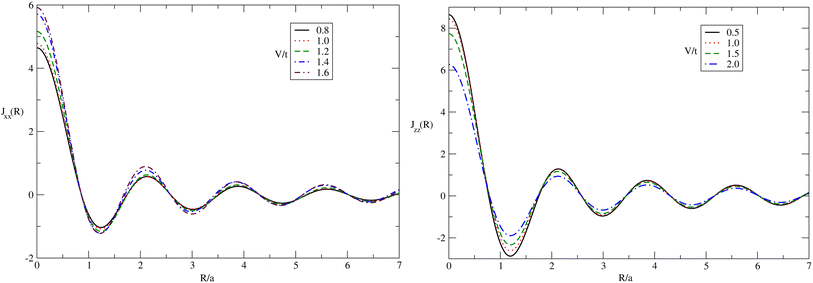Fig. 4 Left (Right) panel: in-plane (longitudinal) RKKY interaction (J_xx(R) (J_zz(R))) between two localized moments in undoped simple stacked bilayer graphene as a function of the distance R for different bias voltages V/t for fixed temperature k_BT/t = 0.01. The magnetic field and electron–phonon coupling strength have been fixed at amounts gμ_BB/t = 0.3 and g/t = 0.01, respectively. The distance vector R = RR̂ is along the zigzag direction in the x–y plane, as shown in Fig. 1.

In the left panel of Fig. 5, results for in-plane coupling exchange constant J_xx are presented versus normalized distance between localized moments R/a in undoped bilayer graphene for different applied magnetic field gμ_BB/t and fixed g/t = 0.01 and V/t = 0.3. Temperature is assumed to be k_BT/t = 0.01. For each value of magnetic field value, the exchange coupling J_xx(R) exhibits an oscillatory behavior as a function of R so that the increase of magnetic field leads to enhance the amplitude of oscillation of J_xx(R) at distances R/a < 0.5. Although the values of in-plane exchange constant are approximately independent of magnetic field strength at R/a > 0.5. Moreover, the period of this oscillation is independent of gμ_BB/t according to the left panel of Fig. 5. It is also clearly observed that the range of antiferromagnetic exchange values (J_xx(R) > 0) is more than that of ferromagnetic (J_xx(R) < 0) ones. The trend of increasing J_xx with magnetic field strength is expected to persist for higher magnetic fields (gμ_BB/t up to 2.5), consistent with prior studies.⁶¹ The right panel of Fig. 5 shows the behavior of longitudinal exchange constant J_zz between two localized external moments in bilayer graphene as a function of normalized distance R/a for different values of magnetic field strengths at V/t = 0.3 and g/t = 0.01. The temperature has been fixed at k_BT/t = 0.05. Our findings reveal that the amplitude of oscillation in distance dependence of J_zz enhances with magnetic field strength at fixed distance between external local moments. The coupling exchange constant curves for all magnetic fields at higher distances above 6 move to zero according to the right panel of Fig. 5. In contrast to the in-plane coupling exchange constant in the left panel, the sensitivity of J_zz to the magnetic strength at higher distances is preserved as shown in the right panel of Fig. 5.

Fig. 5 Left (Right) panel: in-plane (longitudinal) RKKY interaction (J_xx(R) (J_zz(R))) between two localized moments in undoped simple stacked bilayer graphene as a function of the distance R for different magnetic field strengths gμ_BB/t at fixed temperature k_BT/t = 0.01 (left) and k_BT/t = 0.05 (right). The bias voltage and electron–phonon coupling constant values have been assumed to be at V/t = 0.3 and g/t = 0.01, respectively. The distance vector R = RR̂ is along the zigzag direction in the x–y plane, as shown in Fig. 1. The increasing trend of J_xx with magnetic field is expected to persist for higher gμ_BB/t up to 2.5.⁶¹

Fig. 6 displays the dependence of in-plane exchange constant J_xx on electron–phonon coupling constant for different magnetic fields. The distance between two magnetic external moments has been fixed at R/a = 1.0. Normalized temperature and bias voltage are assumed to be k_BT/t = 0.01 and V/t = 0.3, respectively. Observing the data, it is evident that the in-plane exchange constant declines with increasing g/t strength for each value of magnetic field. Rising temperature enhances the scattering rate of electrons of the host medium from vibrated atoms, which leads to reducing the exchange coupling constant between two external local moments in the bilayer graphene as the host medium. In addition, at fixed electron–phonon coupling constant below normalized value 0.05, J_xx rises with an increase of magnetic field. However, the variation of magnetic field has no considerable effect on the in-plane exchange constant at g/t > 0.05 based on Fig. 6.

Fig. 6 In-plane RKKY interaction (J_xx(R)) between two localized moments in undoped simple stacked bilayer graphene as a function of normalized electron–phonon coupling strength at fixed distance R/a = 1.0 for different magnetic field strengths gμ_BB/t. The temperature and bias voltage have been fixed at k_BT/t = 0.01 and V/t = 0.3, respectively. The distance vector R = RR̂ is along the zigzag direction in the x–y plane, as shown in Fig. 1.

We demonstrated the relationship between in-plane exchange coupling constant J_xx and electron–phonon coupling strength under various bias voltages, as depicted in Fig. 7. We set R/a = 1.0, k_BT/t = 0.01, and gμ_BB/t = 0.3 for calculations. The figure illustrates that as g/t increases, the intensity of the in-plane exchange constant between two localized moments decreases for all values of bias voltages. As bias voltage escalates within the electron–phonon coupling strength range g/t < 0.05, exchange coupling constant J_xx experiences an increase in intensity. For g/t > 0.05, the in-plane exchange coupling constant is independent of bias voltage.

Fig. 7 In-plane RKKY interaction (J_xx(R)) between two localized moments in undoped simple stacked bilayer graphene as a function of normalized electron–phonon coupling strength at fixed distance R/a = 1.0 for different bias voltages V/t. The temperature and magnetic field strength have been fixed at k_BT/t = 0.01 and gμ_BB/t = 0.3, respectively. The distance vector R = RR̂ is along the zigzag direction in the x–y plane, as shown in Fig. 1.

We have plotted the in-plane exchange constant J_xx between localized moments in bilayer graphene versus normalized bias voltage V/t for several values of electron–phonon coupling constant g/t, namely g/t = 0.012, 0.014, 0.016, 0.018, 0.02 for the temperature k_BT/t = 0.01 at fixed distance R/a = 1.0 in Fig. 8. There is a peak in each curve of J_xx for each value of electron–phonon coupling strength at bias voltage V/t ≈ 1.5. The height of this peak reduces with an increase of electron–phonon coupling strength as shown in Fig. 8. In addition, at a fixed value of V/t, the in-plane exchange constant decreases with electron–phonon coupling strength. For bias voltages below normalized value 0.5, it is obvious that J_xx is less bias voltage dependent for each value of g/t.

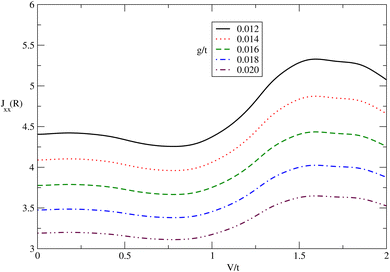Fig. 8 In-plane RKKY interaction (J_xx(R)) between two localized moments in undoped simple stacked bilayer graphene as a function of normalized bias voltage at fixed distance R/a = 1.0 for different normalized electron–phonon coupling strengths g/t. The temperature and magnetic field have been fixed at k_BT/t = 0.01 and gμ_BB/t = 0.3, respectively. The distance vector R = RR̂ is along the zigzag direction in the x–y plane, as shown in Fig. 1.

It is worthwhile to discuss that the amplitude of longitudinal RKKY interaction is higher than the transverse exchange constant at fixed magnetic field and electron–phonon coupling constant. Such a difference between J_xx and J_zz leads to an anisotropic Heisenberg model Hamiltonian for describing exchange coupling between two localized moments according to eqn (25). Also, this difference between longitudinal RKKY interaction and transverse exchange constant arises from the applied external magnetic field perpendicular to the plane. In fact, applying a magnetic field along the z direction (longitudinal magnetic field) causes magnetic ordering of the electronic system along the z-direction perpendicular to the honeycomb plane. Thus, the external magnetic field along the z-direction leads to an increase of the coupling exchange constant for longitudinal components of spin angular momenta of localized magnetic moments because the system tends to orient magnetic moments along the external magnetic field, i.e., the z-direction or longitudinal direction. This implies the coupling exchange constant for longitudinal components of magnetic moments is higher than that for transverse components of magnetic moments.

5 Discussion

The RKKY interaction in AA-stacked bilayer graphene exhibits a decay behavior similar to that of monolayer graphene, following a 1/r³ dependence due to its linear band dispersion near the Fermi level, in contrast to the 1/r² decay in AB-stacked bilayer graphene, which arises from its parabolic band structure.⁵⁶ This distinction is modulated by electron–phonon coupling and external fields, which adjust the amplitude and oscillatory behavior of the interaction, as demonstrated in our results. The interlayer hopping integral γ in AA-stacked bilayer graphene enhances the electronic band splitting, making the RKKY interaction more tunable compared to monolayer graphene, where such interlayer coupling is absent.

An interlayer offset in AA-stacked bilayer graphene would reduce the interlayer hopping integral γ, weakening the RKKY interaction due to decreased interlayer overlap, as observed in studies transitioning to AB-stacking.⁷ Additionally, the phonon modes in AA-stacked bilayer graphene, particularly out-of-plane modes, induce stronger modulation of the RKKY interaction compared to AB-stacked graphene due to direct interlayer coupling. This is consistent with prior studies on phonon-mediated interactions,²⁷ although a quantitative comparison requires further investigation beyond the scope of this study.

The interplay of temperature and magnetic field strength further influences the RKKY interaction. Higher temperatures increase electron–phonon scattering, reducing the exchange coupling, as seen in Fig. 6 and 7, while stronger magnetic fields enhance the oscillatory amplitude, particularly for J_zz, due to Zeeman splitting.⁶¹ These trends underscore the potential of bilayer graphene for tunable quantum magnetic systems.

6 Conclusion

This study demonstrates the critical role of electron–phonon coupling, bias voltage, and magnetic fields in tuning the RKKY interaction in AA-stacked bilayer graphene. Key findings include the oscillatory behavior of the exchange coupling constants J_xx and J_zz, with a 1/r³ decay, modulated by external parameters, and a stronger longitudinal interaction due to magnetic field-induced ordering. The results highlight bilayer graphene's potential for designing adjustable quantum systems for spintronics and nanotechnology. Future research should explore experimental validation of these tunability mechanisms and the impact of structural disorder or interlayer offsets, which remain open questions for advancing practical applications.

Appendix

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author contributions

All authors contributed to the conceptualization and methodology of the study. F. Azizi performed the quantum many-particle calculations to derive the Green's functions and spin susceptibilities, and analyzed the numerical results. H. Rezania developed the theoretical framework, provided insights into charge susceptibility properties, and validated the computational approach. Both authors contributed to writing, reviewing, and editing the manuscript, ensuring its scientific accuracy and clarity.

Conflicts of interest

The authors have no competing interests to declare that are relevant to the content of this article. The interests within the last three years of beginning this present work are along electronic properties of nanostructure systems. Specifically, our interests include the optical and transport properties of nanostructures due to the effects of quantum interactions and scattering between particles in the structure. Such interests are along the content of this article.

References

1. E. McCann and M. Koshino, Rep. Prog. Phys., 2013, 76, 056503.
2. A. V. Rozhkov, A. O. Sboychakov, A. L. Rakhmanov and F. Nori, Phys. Rep., 2016, 648, 1–104.
3. D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Adv. Phys., 2010, 59, 261–482.
4. F. Xia, D. B. Farmer, Y.-M. Lin and P. Avouris, Nano Lett., 2010, 10, 715–718.
5. E. V. Castro, K. S. Novoselov and S. V. Morozov, et al., Phys. Rev. Lett., 2009, 102, 216804.
6. Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen and F. Wang, Nature, 2009, 459, 820–823.
7. M. Koshino, New J. Phys., 2009, 11, 095010.
8. A. Liu and Q. Peng, Micromachines, 2018, 9, 440.
9. T. Yu, J. Li, Z. Yang, H. Li, Q. Peng and H.-K. Tang, Crystals, 2023, 13, 584.
10. S.-J. Kim, S. Lee and K.-B. Lee, Carbon, 2019, 150, 465–471.
11. Q. H. Wang, C.-J. Shih, G. L. C. Paulus and M. S. Strano, J. Am. Chem. Soc., 2013, 135, 18866–18875.
12. W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794–807.
13. E. C. Ahn, npj 2D Mater. Appl., 2020, 4, 17.
14. S. C. Ray, N. Soin, T. Makgato, C. H. Chuang, W. F. Pong, S. S. Roy, S. K. Ghosh, A. M. Strydom and J. A. McLaughlin, Sci. Rep., 2014, 4, 3862.
15. P. Michetti and P. Recher, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 125438.
16. T. S. Ghiasi, A. A. Kaverzin, A. H. Dismukes, D. K. de Wal, X. Roy and B. J. van Wees, Nat. Nanotechnol., 2021, 16, 788–794.
17. G. Fiori, D. Neumaier, B. N. Szafranek and G. Iannaccone, IEEE Trans. Electron Devices, 2014, 61, 729–733.
18. B. N. Szafranek, D. Schall, M. Otto, D. Neumaier and H. Kurz, Nano Lett., 2011, 11, 2640–2643.
19. P. Wu, M. Liu, Y. Ma, Y. Xiao, D. Wang, H. Zhang, L. Zhang and J. Li, Adv. Mater. Interfaces, 2017, 4, 1700477.
20. M. Cheli, G. Fiori and G. Iannaccone, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 80, 235422.
21. Y. Guan, D. J. Lewis, H. Yang and S. Han, Adv. Mater. Interfaces, 2020, 7, 2000899.
22. L. J. Sham and J. M. Ziman, Solid State Phys., 1963, 15, 221–298.
23. F. Marsiglio, Phys. Rep., 2008, 468, 1–83.
24. A. Lanzara, P. V. Bogdanov, X. J. Zhou, S. A. Kellar, D. L. Feng, E. D. Lu, T. Yoshida, H. Eisaki, A. Fujimori, K. Kishio, J.-I. Shimoyama, T. Noda, S. Uchida, Z. Hussain and Z.-X. Shen, Nature, 2001, 412, 510–514.
25. S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133.
26. J. Bardeen and M. J. Stephen, Phys. Rev. B:Condens. Matter Mater. Phys., 1973, 7, 2897–2909.
27. H. L. Calvo, L. Classen, S. Wickenburg, M. M. Ugeda, A. J. Bradley, M. F. Crommie and F. J. García de Abajo, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 125411.
28. J. Quan, C. Yu, X. Zhang, X. Zhang, Y. Guo, J. Zhang and L. Xi, Nano Energy, 2021, 83, 105843.
29. X. Qian, X. Zhou and G. Chen, MRS Bull., 2021, 46, 208–217.
30. F. Giustino, Rev. Mod. Phys., 2017, 89, 015003.
31. T. Ota, T. Hayashi, K.-H. Ahn, S. Katsumoto and Y. Iye, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 80, 081306.
32. R. J. Hughes, A. D. Günther, J. A. Hodges, C. A. Merchant, D. E. Savage, M. G. Lagally, J. R. Eriksson, S. N. Coppersmith and M. A. Eriksson, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 085303.
33. D. E. Reiter, Adv. Quantum Technol., 2019, 2, 1900072.
34. P. Kaer, T. R. Nielsen, P. Lodahl, A.-P. Jauho and J. Mørk, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 245314.
35. Y. Zhou, J. Zhang, J. Wang, Y. Zhao, S. Cao, B. Peng, F. Qi, X. Liu, K. J. Tielrooij and M. Bonn, Nat. Commun., 2020, 11, 6254.
36. F. Azizi and H. Rezania, Phys. E, 2021, 134, 114833.
37. F. Azizi and H. Rezania, J. Magn. Magn. Mater., 2021, 523, 167606.
38. H. Rezania, M. Abdi and F. Azizi, J. Phys.: Condens. Matter, 2018, 30, 145601.
39. H. Rezania, M. Abdi and F. Azizi, Phys. Rev. B, 2019, 100, 155404.
40. F. Azizi and H. Rezania, Physica B, 2021, 614, 413032.
41. F. Azizi and H. Rezania, J. Magn. Magn. Mater., 2025, 589, 171548.
42. H. Rezania and F. Azizi, Phys. Lett. A, 2025, 522, 129766.
43. M. A. Ruderman and C. Kittel, Phys. Rev., 1954, 96, 99–102.
44. T. Kasuya, Prog. Theor. Phys., 1956, 16, 45–57.
45. K. Yosida, Phys. Rev., 1957, 106, 893–898.
46. D. T. Thi and G. T. Hoa, J. Magn. Magn. Mater., 2010, 322, 1757–1761.
47. Z. P. Shi, D. L. Lin, T. H. Lin and T. George, Solid State Commun., 1994, 90, 517–520.
48. Z. Liang, Y. Liu, Z. Zhao, J. Tian and S. Feng, Nano Lett., 2023, 23, 6951–6957.
49. H. Kundu, V. N. Smolyaninova, J. D. Cochran, A. T. Lee, J. J. Heremans and I. Žutić, Phys. Rev. B, 2023, 108, 155419.
50. Y. Duan, T. Qin, W. Zhang, Y. Liu, Z. Zhao and S. Feng, Phys. Rev. B, 2022, 106, 165418.
51. N. R. Chebrolu, B. L. Chittari and J. Jung, Phys. Rev. B, 2019, 99, 235417.
52. A. L. Sharpe, E. J. Fox, A. W. Barnard, J. Finney, K. Watanabe, T. Taniguchi, M. A. Kastner and D. Goldhaber-Gordon, Science, 2019, 365, 605–608.
53. G. Ciepielewski, E. McCann and V. I. Fal’ko, Phys. Rev. B, 2024, 109, 165422.
54. S. A. Jafari, J. Magn. Magn. Mater., 2018, 458, 1–5.
55. E. H. Hwang and S. Das Sarma, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 115449.
56. F. Parhizgar, H. Rostami and A. G. Moghaddam, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 125401.
57. N. Klier, S. Shallcross and O. Pankratov, Phys. Rev. B, 2016, 94, 125432.
58. H. Zhang, C. Du, Y. Liu, Z. Zhao, J. Tian and S. Feng, Phys. Rev. B, 2020, 102, 115402.
59. M. Killi, D. Heidarian and A. Paramekanti, New J. Phys., 2011, 13, 053043.
60. L. Brey, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 205405.
61. H. Rezania and F. Azizi, J. Magn. Magn. Mater., 2016, 419, 463–469.
62. F. Azizi and H. Rezania, Superlattices Microstruct., 2020, 141, 106496.
63. F. Azizi and H. Rezania, J. Phys.: Condens. Matter, 2024, 36, 255801.
64. H. Rezania, M. Abdi and F. Azizi, J. Magn. Magn. Mater., 2019, 489, 165451.
65. H. Rezania and F. Azizi, Physica E, 2020, 121, 114098.
66. F. Azizi and H. Rezania, J. Phys. Chem. Solids, 2021, 150, 109860.
67. D. N. Aristov, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 55, 8064–8068.
68. E. Kogan, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 115119.
69. J. Klinovaja and D. Loss, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 045422.
70. M. Sherafati and S. Satpathy, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 125429.
71. S. Das Sarma and E. H. Hwang, Phys. Rev. B, 2020, 102, 195405.
72. Y. Mohammadi and R. Moradian, J. Magn. Magn. Mater., 2015, 396, 121–127.
73. Y. Wang, X. Zhang, J. Tian, Z. Zhao and S. Feng, Nano Lett., 2025, 25, 123–129.
74. Z. Liu, Y. Wang, J. Tian, Z. Zhao and S. Feng, Phys. Rev. B, 2024, 109, 045418.
75. M. S. Dresselhaus, G. Dresselhaus and P. C. Eklund, Science of Fullerenes and Carbon Nanotubes, Academic Press, 1998.
76. C. Xu, H. Li and K. Banerjee, IEEE Trans. Electron Devices, 2010, 57, 2104–2110.
77. I. Lobato and B. Partoens, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 165429.
78. S. Doniach and E. H. Sondheimer, Green's Functions for Solid State Physicists, Imperial College Press, 1998.
79. E. N. Economou, Green's Functions in Quantum Physics, Springer, 2006.
80. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2017, 29, 373001.
81. A. B. Migdal, Sov. Phys. JETP, 1958, 7, 996–1001.
82. G. D. Mahan, Many-particle Physics, Springer, 2013.
83. G. Grosso and G. P. Parravicini, Solid State Physics, Academic Press, 2013.
84. O. Gunnarsson, M. W. Haverkort and G. Sangiovanni, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 035125.
85. G. C. Wick, Phys. Rev., 1950, 80, 268–272.
86. D. Bohm and D. Pines, Phys. Rev., 1951, 82, 625–634.
87. D. Bohm and D. Pines, Phys. Rev., 1953, 92, 609–625.
88. M. Gell-Mann and K. A. Brueckner, Phys. Rev., 1957, 106, 364–368.
89. M. Altmeyer, S. A. Jäger, M. J. Schön, M. C. Lüdl, S. Karna and R. A. Wilhelm, J. Phys.: Condens. Matter, 2016, 28, 215301.
90. Y. He, D. Li, G. Zhang and Y. Liang, J. Phys. Chem. C, 2018, 122, 19266–19272.
91. R. D. Mattuck, A Guide to Feynman Diagrams in the Many-Body Problem, Courier Corporation, 2012, 23, p. 1202.
92. H. Imamura, P. Bruno and Y. Utsumi, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 121303.
93. A. M. Black-Schaffer, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 205416.

---