Interpretable machine learning models for predicting the antitumor effects of metal and metal oxide nanomaterials

Abstract

Understanding the toxic behavior of metal and metal oxide nanoparticles (M/MOx NPs) is essential for effective tumor diagnosis and treatment, yet generalizing findings remains challenging due to limited data, sampling variability, unreported complexities, low model accuracy, and a lack of interpretability. To address these issues and minimize extensive experimentation, we combined quantum chemistry calculations with published toxicity data to develop a machine learning model achieving over 90% accuracy in cross-validation. Utilizing 39 descriptors extracted from 152 articles, our dataset comprises 2765 instances covering various nanoparticle types, detection methods, and cell types. We enhanced data representation with the Jaccard similarity coefficient and employed Feature Importance and Shapley Additive Explanations (SHAP) to identify key factors influencing cytotoxicity, such as concentration, exposure time, zeta potential, diameter, COSMO area (CA), coating, testing methods, cell types, metal electronegativity, HOMO energy, and molecular weight. Additionally, we analyzed the interactions among these features and their influence on predictions, synthesized novel metal oxide nanoparticles, and assessed their physicochemical properties and anti-tumor toxicity. Cytotoxicity experiments with newly synthesized nanoparticles further validated the model's accuracy and generalizability, revealing hidden relationships and enabling predictions for previously unseen samples. This approach supports preliminary computer-aided screenings, significantly reducing the need for labor-intensive experimentation.

---

1 Introduction

Cancer remains a leading cause of death worldwide, with its incidence continually rising.^1,2 Nanotechnology has garnered increasing research attention for addressing the diagnosis and treatment of conventional diseases.^3–6 In particular, metal and metal oxide nanomaterials play a significant role in the diagnosis and treatment of tumors.^7–10

Nanomaterials' toxic effects are generally influenced by their various physicochemical properties, such as size, shape, surface area, chemical composition, and stability.¹¹ Among the various biological assays used to evaluate nanomaterial toxicity, in vitro cytotoxicity assays are one of the most important toxicological measurement methods.¹² These assays use live cells to observe and detect the toxic effects of nanomaterials and are favored due to their relative simplicity, speed, and cost-effectiveness. Moreover, since cytotoxicity tests do not use animals, they avoid ethical issues. Consequently, extensive research has been published on the cytotoxic effects of nanoparticles.^13–17 However, the complexity and heterogeneity of nanomaterials, differing testing conditions, detection methods, and cell lines complicate comparisons and analyses across studies. Additionally, in vitro and in vivo toxicity assessments of metal and metal oxide nanomaterials can be very time-consuming and costly.

Computational toxicology, an alternative to in vitro and in vivo experiments, has been widely applied in toxicology research. Various in silico methods have been developed and applied, including pharmacological modeling,¹⁸ comparative molecular field analysis,^19,20 molecular docking,^21–23 molecular dynamics simulations,^24,25 network-based algorithms,^26–29 and machine learning methods like quantitative structure activity relationship (QSAR) modeling,^30–40 and deep learning.^41,42

Among these, machine learning has recently become one of the most popular methods for studying the cytotoxicity of nanomaterials. As a branch of artificial intelligence, machine learning aims to develop computational algorithms to infer mathematical models from existing data, providing a promising tool for accelerating the development of needed nanoparticles.⁴³ When applied to the complex relationships between variables and unknown outcomes, machine learning can reveal hidden features in data, offering deeper insights into the characteristics leading to nanotoxicity. For instance, researchers used partial least squares (PLS) regression to establish a nano-QSAR model and found that charge density and surface charge were the main factors in gold nanoparticle exudation.⁴⁴ Another study predicted the bioactivity of gold nanoparticles using several linear and nonlinear machine learning algorithms based on the composition of the protein corona, identifying key proteins as promoters or inhibitors of cellular association.⁴⁵ A recent study used decision tree modeling and feature selection algorithms to find that cytotoxicity test indicators were significant determinants of viability outcomes.⁴⁶

Current research predominantly focuses on the effects of inorganic nanomaterials on the environment and general cells, rather than on tumor cells specifically.^47–62 Furthermore, despite the presence of some related data in datasets, significant issues such as data scarcity, extensive missing critical data, low model accuracy, and insufficient model interpretability persist.

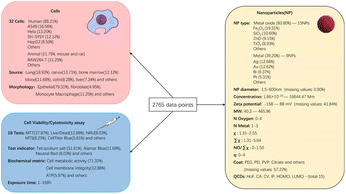
In this study, as shown in Fig. 1, we collected and organized data on the toxicity of metal and metal oxide nanomaterials towards tumor cells and their intrinsic characteristics (chemical composition, metal electronegativity, number of oxygen atoms, number of metal atoms, molecular weight, metal cation charge, coating/functional group, particle size, concentration, zeta potential, and tumor cell type, source, morphology, and exposure time, detection method, interference check, colloidal stability, and positive control setting) totaling 2765 groups of literature data. In addition, in order to better understand the relationship between structure and activity in nano-QSAR research, we calculated and introduced 16 quantum chemical descriptors⁶³ including Heat of formation (HoF), COSMO area (CA), COSMO volume (CV), ionization potential (IP), Highest Occupied Molecular Orbital (HOMO), Lowest Unoccupied Molecular Orbital (LUMO), No. of Filled Levels (NFL), molecular weight, point group, cluster electronegativity (T_χ), molecular hardness, electrophilicity, bandgap energy (E_g), polarizability (Pol), softness (S) by PM7 semi-empirical method. We used the Jaccard similarity coefficient^64–66 to supplement missing data and selected nine classical algorithm models for training. Among them, the LightGBM⁶⁷ model achieved the highest prediction accuracy of 90.78% and an area under the curve (AUC) of 95%. To enhance the interpretability of the model and identify the optimal decision making process, we use feature importance, partial dependence plot (PDP), and individual conditional expectation (ICE).⁶⁸ To further validate the model's accuracy and explore its generalization capability, we supplemented our dataset with 240 new groups of data involving three common metals (ZnO, CdO, Cu₂O) and three rare earth metals (CeO₂, Er₂O₃, Nd₂O₃). The new experimental results confirmed the reliability and accuracy of our model. These results will significantly reduce the time and financial costs for researchers, eliminating excessive labor-intensive experiments and enabling the rapid development of nanomaterials for biomedical purposes.

Fig. 1 Experimental flowchart.

2 Materials and methods

2.1 Data sets

2.1.1 Literature search and harmonization. Initially, a systematic iterative literature search was conducted using multiple databases, including Google/Google Scholar, PubMed, and Web of Science, with various combinations of keywords (e.g., “metal and metal oxide nanoparticles + tumor cytotoxicity,” “metal and metal oxide nanoparticles + cells + response,” “metal and metal oxide nanoparticles + survival rate”). This stage yielded approximately 400 peer-reviewed original research articles reporting in vitro cytotoxicity assessments of nanoparticles (NPs) with diameters <1000 nm. All studies identified through this search were evaluated for inclusion in the publication database for analysis.

Eligibility for inclusion in the meta-analysis was determined based on the following criteria: NPs were described with respect to at least the core material, size, and dosage; the specific cell type and NP exposure duration were specified; and the average cell survival rate/toxicity ± standard deviation/error was clearly reported. To limit heterogeneity and ensure meaningful conclusions, only data points developed using common cell viability/cytotoxicity assays were selected. These included the neutral red uptake assay (NR), mitochondrial toxicity assays using tetrazolium salts (MTT, MTS, XTT, WST-1, WST-8), ATP bioluminescence assays, lactate dehydrogenase (LDH) re-lease assays, resazurin (Alamar Blue) cell viability assays, and live/dead (membrane integrity) assays. Metalloid-based NPs and loaded NPs were excluded from the scope of this study.

2.1.2 Data extraction and harmonization. After organizing the data into a more relevant list, all publications were thoroughly reviewed, and the following physicochemical parameters of nanoparticles (NPs) were manually extracted: core and coating materials, particle size, zeta potential, cell type, NP exposure time, cell viability/cyto-toxicity assays, and the percentage of cell survival post-NP exposure. It should be noted that the particle sizes included in the dataset were measured using different techniques, such as Zetasizer and microscopy. If multiple particle sizes were reported, the hydrodynamic diameter in solution, which better simulated experimental conditions, was selected for our analysis.

Additional data extracted included whether NP interference checks were conducted, colloidal stability checks in the culture medium, and the use of positive controls. To prepare the data for machine learning, the units for NP size (nm), zeta potential (mV), concentration (μM), and exposure time (h) were standardized. Further descriptive attributes were added for the cells, including whether the cells were cell lines or primary cells, whether they were of human or animal origin, cell morphology, cell age, and organ or tissue origin, as well as detection methods (including reagents and biochemical markers). For more detailed information, please refer to ESI, Sheet 1.†

To account for variability and potential systematic errors across different studies, several data cleaning and harmonization steps were conducted. First, only studies reporting essential experimental details (e.g., exposure time, NP concentration, viability values, and assay method) were included. Data points showing clear indications of experimental artifacts, such as nanoparticle agglomeration, instability in culture media, or known assay interference, were excluded. Furthermore, to reduce systematic bias, we selected the most comparable measurement type across studies—specifically, hydrodynamic diameter for size and zeta potential in deionized water rather than in complex media. Assay types were recorded, and studies using incompatible or non-standard cytotoxicity protocols were omitted. Where ranges or inconsistent formats were used, midpoints or standardized metrics were calculated (e.g., converting ranges to averages or normalizing concentration units). Despite these efforts, we acknowledge inherent inter-study variability; however, by using a sufficiently large dataset and feature-based modeling, the machine learning approach can account for such noise and still identify robust, generalizable patterns.

2.1.3 Data supplementation. To address missing values in the dataset, this study employs an imputation method based on the Jaccard similarity coefficient, implemented through the following steps: (i) similarity calculation phase: for each data sample containing missing values, the Jaccard similarity coefficient is computed between its complete features and those of all other samples; (ii) imputation execution phase: the complete sample exhibiting the highest Jaccard similarity coefficient with the deficient sample is selected, and its corresponding feature values are used for imputation. The algorithm used for this imputation process, along with the complete machine learning workflow, is available in the GitHub repository listed in the Data availability section.

In this study, similarity between data points was measured using the S_ϕ coefficient (formula (1)) and the Jaccard similarity coefficient (formula (2)). The similarity metrics were based on a contingency table (Table 1).

Table 1 Contingency table for similarity evaluation

	Value 1	Value 0
Value 1	a	b
Value 0	c	d

---

In Table 1: represents the number of positions where both variables are 1.

b-represents the number of positions where the first variable is 1 and the second variable is 0.

c-represents the number of positions where the first variable is 0 and the second variable is 1.

d-represents the number of positions where both variables are 0.

J = a/(a + b + c) (2)

2.2 Machine learning

2.2.1 Light Gradient Boosting Machine (LightGBM). LightGBM is an efficient gradient boosting framework that utilizes histogram-based learning algorithms to handle large-scale and high-dimensional data effectively. In this study, a grid search was performed to optimize key parameters such as learning rate, tree depth, and the number of leaves. The best parameter combination was selected using cross-validation, and the optimized LightGBM model was used for model building and performance evaluation.

2.2.2 Convolutional neural network (CNN). Convolutional Neural Networks (CNNs) are deep learning models designed for automatic feature extraction and classification from one-dimensional data. The architecture consists of two convolutional layers, utilizing 32 and 64 filters, respectively, with a kernel size of 3. Each convolutional layer is followed by a max pooling layer (pooling size of 2) to reduce the dimensionality of the feature maps. After the convolution and pooling operations, the data is flattened and processed through two fully connected layers. The final output is obtained through a sigmoid activation function, which facilitates binary classification. This model is flexible and can accommodate varying input dimensions.

2.2.3 Multi-Layer Perceptron (MLP). The Multi-Layer Perceptron (MLP) is a classical feedforward neural network that learns the nonlinear relationships between input features. The model comprises three fully connected layers, where the input features first pass through a layer with 128 neurons, followed by a hidden layer containing 64 neurons, and a final output layer producing a single prediction. The output layer applies a sigmoid activation function for binary classification. MLP is particularly well-suited for processing flattened input data and for capturing complex nonlinear relationships among descriptors to make accurate predictions.

2.2.4 Random Forest (RF). Random Forest is an ensemble method based on decision trees that is robust and effective for handling high-dimensional features. In this study, the WEKA implementation of Random Forest was used, constructing trees based on the default number and selecting features randomly. The majority voting (classification) or mean calculation (regression) of individual trees produces the final prediction. This method serves as a baseline model for comparing complex nonlinear data.

2.2.5 Extreme Gradient Boosting (XGBoost). XGBoost is an efficient implementation of gradient boosting with strong regularization and parallel computing capabilities. In this study, XGBoost was used with default parameters, including a fixed learning rate and maximum tree depth, to assess its predictive power on the dataset.

2.2.6 Support Vector Machine (SVM). The Support Vector Machine (SVM) leverages kernel functions to map data into higher-dimensional spaces, optimizing the classification boundary for maximum margin. A radial basis function (RBF) kernel was used in this study, with regularization parameters set to their default values. SVM is employed to model both linear separability and complex boundaries in descriptor data.

2.2.7 Logistic regression. Logistic regression is a linear classification method based on the sigmoid function to output probabilities. In this study, logistic regression was used as a baseline model without tuning the regularization parameters to evaluate the linear separability of descriptors.

2.2.8 k-Nearest Neighbors (kNN). k-Nearest neighbors (kNN) is an instance-based method for prediction, where the target sample is assigned the majority class (classification) or mean value (regression) of its k nearest neighbors in the feature space. The optimal value of k was automatically chosen via cross-validation, with Euclidean distance as the distance measure.

2.2.9 Naive Bayes. Naive Bayes is a classification method based on Bayes' theorem, assuming independence between features. In this study, the model assumes conditional independence among descriptors and outputs posterior probabilities for classification.

2.3 Model validation and evaluation

The accuracy of the models was estimated using five-fold cross-validation and by predicting the test sets. The test sets were obtained through cell experiments on a series of synthesized metal oxide nanoparticles.

To evaluate the performance of the models, the following metrics were calculated: ROC, AUC, precision, recall, F1 score, and balanced accuracy. Additionally, confusion matrices were plotted to assess the classification performance, showing the number of correctly classified instances as well as the misclassified compounds (false positives and false negatives).

The formulas for the calculated parameters are as follows:

Sensitivity (Sn), also known as true positive rate, measures the proportion of actual positives correctly identified by the model.

Sn = TP/(TP + FN)

where TP is the number of true positives and FN is the number of false negatives.

Specificity (Sp), also known as true negative rate, measures the proportion of actual negatives correctly identified.

Sp = TN/(TN + FP)

where TN is the number of true negatives and FP is the number of false positives.

Precision (Pr) measures the proportion of positive predictions that are actually correct.

Pr = TP/TP + FP

Recall (R) is equivalent to sensitivity (Sn), as it also measures the proportion of actual positives that are correctly identified.

Recall = Sn

F1 score is the harmonic mean of precision and recall, providing a balance between the two.

F1 = 2 × (Pr × recall)/(Pr + recall)

Balanced accuracy (AC) is the average of sensitivity and specificity, providing a single metric for classification quality when the class distribution is imbalanced.

AC = 0.5 × (Sn + Sp)

These metrics were calculated using standard Python libraries, allowing for the comprehensive evaluation of model performance in the context of nanoparticle toxicity prediction.

2.4 Synthesis experiments

2.4.1 ZnO. Add 98 mL of anhydrous ethanol to a 250 mL round-bottom flask and heat it to a constant temperature of 80 °C using an oil bath. Add 0.577 g of SDS to the flask and stir until completely dissolved. Then, quickly add 2 mL of 0.5 mol L⁻¹ zinc acetate solution, initiating the reaction with zinc acetate in the amount of 1 × 10⁻³ mol. After 30 minutes, stop heating, cool the sample to room temperature, and centrifuge. Wash the resulting powder with deionized water and anhydrous ethanol at least three times, then air-dry to obtain white powder.

2.4.2 CdO. Dissolve 1 g of cadmium sulfate (3CdSO₄·8H₂O) in 50 mL of a Teflon-lined stainless-steel autoclave, adding 3 mL of 30% hydrogen peroxide and 27 mL of distilled water. Adjust the solution pH to 10 using ammonia, then react at 100 °C for 12 hours in an oven. After cooling, filter and wash with distilled water and anhydrous ethanol, then dry at 80 °C in the air for 2 hours to obtain white powder.

2.4.3 Cu₂O. Prepare a reaction solution of CuSO₄ and maintain it at 70 °C in a water bath with stirring. Add 1.6 g L⁻¹ of polyvinylpyrrolidone (PVP) to the CuSO₄ solution, followed by NaOH solution (2 mol L⁻¹). Gradually add N₂H₄·H₂O solution. The reaction solution turns from blue to green, producing an orange-yellow precipitate. After 4 hours, wash the precipitate with anhydrous ethanol and dry under vacuum at 70 °C for 8 hours to obtain a powder sample.

2.4.4 CeO₂. Stir a microemulsion containing Ce(NO₃)₃ on a magnetic stirrer for about 5 minutes, introducing N₂ gas during the reaction. Add a microemulsion containing ammonia while stirring, forming a pale yellow precipitate at pH = 10. Centrifuge and wash the precipitate with ethanol and water twice, then dry in a vacuum oven at 373 K.

2.4.5 Er₂O₃. Dissolve an appropriate amount of erbium oxide in hydrochloric acid to prepare a solution of erbium chloride (0.05 mol L⁻¹) with pH 1.0–2.0. Add urea to maintain a concentration of 1.0 mol L⁻¹. Incubate at 85 °C for 85 minutes, cool quickly, and add 20% n-pentanol, stirring vigorously for 30 minutes before standing for 10–12 hours. Filter and wash the precipitate with water 2–3 times, then dry at 90 °C for 4 hours. Finally, calcine at 700 °C for 2 hours to obtain high-purity nano erbium oxide.

2.4.6 Nd₂O₃. Prepare solutions of neodymium nitrate and ammonium carbonate, adding a small amount of CTMAB surfactant to the neodymium nitrate solution. Mix with stirring, then add ammonium carbonate solution dropwise (about 1 mL min⁻¹) to the neodymium nitrate solution, maintaining pH 7–8 to obtain the precursor of neodymium oxide. Age the mixture, filter, wash with deionized water and anhydrous ethanol, and dry. Calcine the precursor at 800 °C for 3 hours to obtain neodymium oxide.

2.5 Characterization

Measure zeta potential using a Zetasizer Nano ZS90. Perform XRD using a Rigaku D/MAX 2500V. Obtain SEM images with a TESCAN MIRA LMS.

2.6 Cell experiments

2.6.1 Cell culture. Cultivate HeLa and A549 cells from the cell bank of Guangxi University Medical School Laboratory. Grow cells in high-glucose DMEM medium containing 10% fetal bovine serum and 1% penicillin/streptomycin at 37 °C and 5% CO₂.

2.6.2 In vitro cytotoxicity experiments. Seed HeLa and A549 cells into 96-well plates and treat with increasing concentrations of metal oxide nanoparticles (five concentration gradients per material) for 24 or 48 hours. After co-culture, replace the medium with DMEM containing 10% CCK8 or MTT, incubate for 1–4 hours, remove the medium, and add 100 μL of DMSO per well. Measure absorbance at 450 nm to assess relative cell viability using a microplate reader.

3 Results and discussion

3.1 Data retrieval and mining

A dataset was compiled from 152 studies on the cytotoxicity of nanomaterials published between 2004 and 2023. Keywords such as “nanoparticles/nanomaterials/nanometals + toxicity/cytotoxicity” were used to filter extensive online resources, including Google, Scopus, CNKI, ACS, Wiley, Science, and PubMed. The initial selection criteria required detailed descriptions of the core material, diameter, identified cell types, exposure duration, and mean cell viability/toxicity with standard deviations. From this preliminary selection, data specific to nanometals, their oxides, and tumor cells were extracted, resulting in 2765 instances. These instances encom-passed characteristics such as nanoparticle type, size, shape, coating, surface charge, concentration, cell properties, assay type, exposure duration, and the resulting cell viability values. The distribution of these data features is illustrated in Fig. 2.

Fig. 2 Overview of nano particle data attributes/features in literature (2765 data points).

Notably, the dataset exhibited a degree of class imbalance, with 656 samples categorized as toxic (cell viability < 50%) and 2109 as non-toxic. This imbalance is primarily associated with the focus of our study, which centers on metal and metal oxide nanoparticles relevant to cancer therapy. In this domain, nanomaterials with favorable biocompatibility and low toxicity are generally prioritized due to their translational potential and suitability for biomedical applications.

The cytotoxicity of nanoparticles is a complex process influenced by various parameters, including surface charge, surface coating, chemical composition, hydrodynamic diameter, surface area, nanoparticle concentration, and cell descriptors that determine the nanoparticle environment. To build a reliable and interpretable machine learning model, it is essential to collect extensive data that incorporates all these parameters. To enhance the model's predictive accuracy and deepen the understanding of the cytotoxic mechanisms of nanoparticles, we included 17 features of M/MOx NPs extracted from various references. In addition to 15 quantum chemical features, we have also added 7 molecular features: metal electronegativity (x), the sum of metal electronegativities in a single metal oxide (∑x), the ratio of the number of oxygen atoms to the sum of metal electronegativities in a specific metal oxide (n_O/∑x), the number of metal atoms (N_Metal), the number of oxygen atoms (N_Oxygen), the metal cation charge corresponding to a given oxide (q), and molecular weight (MW). These features can be easily derived from molecular formulas and obtained from the periodic table. All data visualization is shown in Fig. 3a. Feature selection was implemented to reduce the number of correlated features, resulting in a low level of correlation among the parameters (Fig. 3b).

Fig. 3 (a) Data visualization of the dataset; (b) process the correlation matrix on the dataset.

3.2 Quantum chemistry calculations

A cluster structure describing M/MOx NPs was prepared. Firstly, spherical clusters of M/MOx NPs were constructed using experimental crystal structures. In the design of the model cluster, Materials Studio⁶⁹ was used to extend the unit Celsius on each axis to generate a polycrystalline cell, and then atoms within 4.5 Å of the center of the poly-crystalline cell were selected based on the point symmetry of the crystal structure as a constraint. The design of spherical clusters takes into account the influence of M/MOx NP surface curvature on its molecular orbital (MO) structure. The clusters are generated in a similar manner at a distance of 4.5 Å to fairly compare their reactivity. In QM calculations, the semi empirical PM7 (ref. 70) method implemented in MOPAC2016 (ref. 71) was used to optimize the geometric shape of the model cluster model with model symmetry as a constraint.

In order to calculate further descriptors related to reactivity, the coefficients of each atomic orbital in the MO linear combination in the density matrix are further utilized to calculate descriptors related to reactivity of M/MOx NP.⁷² The summary of QM descriptor preparation is shown in Fig. 4.

Fig. 4 Quantum chemistry features and computational processes.

Quantum chemical descriptors reflect the intrinsic electronic, structural, and reactive properties of M/MOx NPs and provide mechanistic insights into how these nanomaterials interact with biological systems. For instance, the HOMO energy level indicates the tendency of nanoparticles to donate electrons; higher HOMO values are associated with stronger electron-donating ability, which can facilitate redox reactions with cellular components and induce oxidative stress. Similarly, E_g relates to the material's electronic excitability; a narrower bandgap often implies higher reactivity and a greater likelihood of generating ROS, a key factor in nanoparticle-induced cytotoxicity. Electronegativity reflects the tendency of metal centers to attract electrons, where materials with low electronegativity are typically more reducing and prone to ROS generation. ω, S, and η influence the stability and reactivity of nanoparticles toward biological nucleophiles, such as proteins or DNA bases. A higher electrophilicity value implies a greater capacity to accept electrons from biomolecules, potentially leading to adduct formation or enzyme inhibition. Pol affects how the electronic cloud of a particle responds to external fields, such as those found in biological environments; greater polarizability may enhance interactions with charged cellular surfaces or macromolecules. CA and CV provide spatial metrics that reflect the particle's surface exposure and its interaction potential with surrounding molecules or membranes. These descriptors, combined, allow the model to capture subtle structural and electronic features that directly relate to nanotoxicity pathways, such as oxidative damage, membrane penetration, or macromolecular binding.

3.3 Data supplementation

Due to unknown or missing values in the available datasets, including the zeta potential—a crucial parameter that characterizes the environment around nanoparticles and is vital for describing toxicity phenomena—a significant portion of all dataset parameters were blank (Fig. 2A). Removing all such samples significantly reduced the dataset size, presenting limitations in current methods. Incomplete observations could adversely affect the performance of machine learning algorithms. To address this issue, we supplemented the data using similarity-based methods.

Through our analysis of similarity results, we found that the Jaccard similarity coefficient more effectively measures the similarity within our dataset. We hypothesize this is because the S_ϕ coefficient⁷³ typically assesses symmetric correlation between two binary variables and is suitable for balanced situations where the number of 1s and 0s is roughly equal. However, our dataset has an uneven distribution of 1s and 0s, which makes the performance of the S_ϕ coefficient less effective compared to the Jaccard similarity coefficient. The Jaccard similarity coefficient, which measures similarity based on the proportion of shared 1s and ignores shared 0s, is more appropriate for our data, where 1s are fewer but significantly impactful for analysis.

Thus, despite the usefulness of the S_ϕ coefficient in certain symmetric and balanced binary variable analyses, the Jaccard similarity coefficient is better suited for our specific dataset and research context due to its focus on matching 1s while ignoring shared 0s. We used the Jaccard similarity coefficient to evaluate the similarity within the dataset, calculating it pairwise for each nanoparticle. The most similar results were used to fill in missing data.

The complete dataset is available in the attached excel sheet (excel sheet1). Before conducting machine learning experiments, some feature values (e.g. NP concentration) were standardized (NP concentration is expressed in μM). The red sections in the dataset represent supplemented missing data.

3.4 Model construction and comparison

To train our models, we selected nine mainstream and representative machine learning algorithms, including Convolutional Neural Networks (CNN),⁷⁴ Multi-Layer Perceptron (MLP),⁷⁵ Random Forest,⁷⁶ Extreme Gradient Boosting (XGBoost),⁷⁷ Light Gradient Boosting Machine (LightGBM),⁷⁸ Support Vector Machine (SVM),⁷⁹ logistic regression,⁸⁰ k-Nearest Neighbors (kNN),⁸¹ and Naive Bayes.⁸²

The dataset of 2765 samples was split into a training set and a test set in a 2 : 1 ratio, with the external validation set composed of subsequent experimental data. Model training and evaluation were implemented using Python 3.9.13 with PyTorch, Scikit-learn, XGBoost, and LightGBM libraries.

Given the class-imbalanced nature of the dataset, model evaluation focused primarily on the F1 score and the area under the receiver operating characteristic curve (AUC-ROC), as both metrics are more informative than accuracy under skewed class distributions. The F1 score was selected as the core metric for its ability to balance precision and recall, with particular emphasis placed on recall to reduce false negatives and improve sensitivity to toxic samples.

To address class imbalance during model training, we employed tailored strategies: for neural network models (CNN and MLP), a weighted cross-entropy loss was applied, assigning higher weights to the minority (toxic) class. For gradient boosting models (XGBoost and LightGBM), we used consistent hyperparameters (200 trees, learning rate = 0.1, max depth = 8), as these models inherently mitigate imbalance via split gain functions. Parameters for other classifiers were optimized individually. SVM and kNN were included as baseline methods to assess robustness under imbalanced conditions.

Model evaluation was initially performed using the fixed test set to simulate a realistic single-pass prediction scenario. The corresponding ROC curves and confusion matrices are shown in Fig. 5a and b. Among all models, LightGBM achieved the highest test performance with an AUC of 0.9534 and a strong F1 score, demonstrating its superior discrimination ability (Table 2).

Fig. 5 (a) ROC curves of various models. (b) Test set confusion matrix. (c) F1 score of cross-validation. (d) AUC score of cross-validation.

Table 2 Prediction scores of each model

Model	Accuracy	AUC	Precision	Recall	F1
CNN (100 epoch)	0.8564	0.9125	0.89	0.9185	0.904
MLP (100 epoch)	0.8564	0.9103	0.8701	0.9461	0.9066
Random forest	0.8853	0.9278	0.894	0.9578	0.9248
XGBoost	0.9025	0.9414	0.9116	0.9607	0.9355
LightGBM	0.9078	0.9534	0.9168	0.9622	0.9389
SVM	0.8081	0.8763	0.8113	0.9636	0.8809
Logistic regression	0.7996	0.8584	0.8289	0.917	0.8708
kNN	0.8339	0.8739	0.8519	0.9374	0.8926
Naive Bayes	0.4244	0.7801	0.9688	0.2256	0.366

---

To further validate model robustness and account for variability due to random data partitioning, we performed stratified five-fold cross-validation. Cross-validation results (Fig. 5c, d and Table 3) were subjected to pairwise t-tests at a 95% confidence level to compare LightGBM with other representative models (CNN, MLP, SVM, kNN, and Naive Bayes). LightGBM significantly outperformed all other models in terms of F1 score (p < 0.05), confirming its superior sensitivity to toxic samples. Although CNN and MLP achieve slightly better average AUCs, with the differences reaching statistical significance, their performance on the other four evaluation metrics is inferior, and their models exhibit greater instability, suggesting limited applicability and reliability in class-imbalanced tasks.

Table 3 5-Fold CV results of each model

Model	Accuracy	AUC	Precision	Recall	F1
CNN (100 epoch)	0.8683	0.9190	0.9085	0.9223	0.9153
MLP (100 epoch)	0.8650	0.9090	0.9064	0.9202	0.9132
Random forest	0.8920	0.8153	0.9086	0.9566	0.9319
XGBoost	0.9082	0.8474	0.9246	0.9594	0.9416
LightGBM	0.9098	0.8459	0.9230	0.9636	0.9428
SVM	0.8305	0.6639	0.8362	0.9706	0.8984
Logistic regression	0.7943	0.6028	0.8116	0.9552	0.8775
kNN	0.8407	0.7304	0.8698	0.9335	0.9004
Naive Bayes	0.7155	0.6234	0.8312	0.7929	0.8108

---

While both LightGBM and XGBoost performed well, LightGBM was ultimately selected for downstream analysis due to its faster training speed, higher computational efficiency, and direct support for categorical features.⁶⁷ Additionally, the final model trained on the supplemented dataset showed a marked improvement in predictive performance, with AUC increasing from 82% to 95%, indicating that similarity-based data augmentation significantly enhanced model accuracy in predicting the cytotoxicity of M/MOx nanoparticles in tumor cells.

3.5 Model interpretability analysis

3.5.1 Importance analysis. Beyond developing a successful model, each artificial intelligence method should both validate existing knowledge and generate new insights. To uncover potential associations between nanoparticles and tumor cell cytotoxicity, we analyzed the importance of each descriptor and the model's SHAP (Shapley Additive Explanations) values. This analysis aimed to reveal how changes in each numerical parameter affect the predicted viability values (Fig. 6).

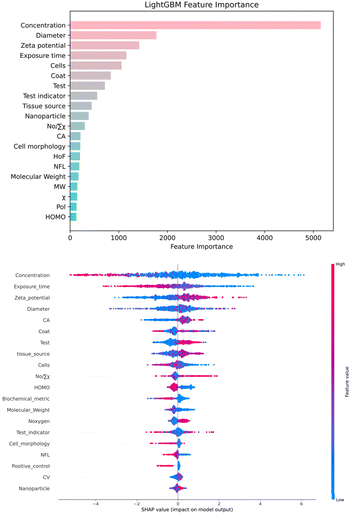Fig. 6 (a) Comparison of the importance of various descriptors in LightGBM. (b)SHAP analysis of dataset features.

The global contribution comparison (Fig. 6a) in the LightGBM model, an ensemble decision tree model, evaluates feature importance by calculating the frequency and information gain of features at splitting nodes. The top ten features in importance are concentration, diameter, zeta potential, exposure time, cells, coat, test, nanoparticle, n_O/∑x and CA. These features significantly impact the prediction of cell survival rates, aligning with researchers' experimental experience. However, feature importance does not show how each feature influences the final outcome. Therefore, SHAP values were introduced for further analysis to uncover more hidden information.

SHAP values clearly display the well-known concentration and time-dependent effects (Fig. 6b), where increasing these parameters generally reduces tumor cell viability. Interestingly, an increase in the absolute value of the zeta potential of M/MOx enhances tumor cell survival rates. This could be because nanoparticles with lower zeta potential are more readily taken up by tumor cells,⁸³ which is less noticeable in limited experimental data. CA is a molecular surface area related parameter based on the Continuous Solvent Model (COSMO), which typically reflects the interaction between molecules and their surrounding environment. For nanomaterials, a higher CA value may indicate a larger contact area with the external environment (such as cell membranes or proteins), thereby increasing the likelihood of interaction with cells.⁸⁴ But in our SHAP analysis, this situation seems to be the opposite, which may be related to the interaction with the cell membrane. A smaller surface area sometimes means high local reactivity, increasing interaction with the cell membrane or internal structure, thereby increasing toxicity.⁸⁵ Additionally, increases in metal electronegativity, the number of oxygen atoms, and metal cation charge also boost cell survival rates, consistent with Hu et al.'s experimental results.⁵⁵ This can be explained by the increased production of reactive oxygen species (ROS) by highly reducing substances and materials containing less electronegative elements, leading to higher toxicity.⁵⁷ Contrary to general expectations, nanoparticles with smaller hydrodynamic diameters did not significantly decrease tumor cell viability in our analysis. While smaller nanoparticles are typically believed to have higher surface areas and be more easily taken up by cells,⁸⁶ recent literature suggests that size effects cannot always be easily separated from concentration effects. Larger nanoparticles may exhibit greater toxicity at moderate to high concentrations.⁸⁷ Moreover, characteristics such as coating, testing, and cells also have a significant impact on cell toxicity, for example, the surface properties of nanomaterials play a key role in determining the outcome of their interactions with cells.⁸⁸ Thus, our model not only confirmed previous research but also provided insights for the design of M/MOx targeting tumor cell cytotoxicity.

3.5.2 Feature effects. Although feature importance can explain which features significantly affect the prediction of black box machine learning models, the relationship between the predicted target and features is still unclear (linear, monotonic, or more complex). Here, three model agnostic methods are applied to understand feature effects from a local or global perspective. PDP aims to display the marginal effect of one or two features on model prediction by averaging the model output of different values of a feature.⁸⁹ PDP can easily visualize the relationship between predicted targets and selected features, but due to average marginal effects, heterogeneity effects may be hidden (i.e. the same feature may have different impacts on individuals). ICE decomposes this mean by highlighting the estimated functional relationships of individual observations.⁹⁰ In the ICE graph, each line reflects the change in the predicted target of an instance when the selected feature changes. PDP is the average value of all lines in the ICE graph. The visualization results of the feature effects are shown in Fig. 7. The impact of corresponding features on the results can be directly observed from the PDP and ICE plots, such as the decrease in cytotoxicity of M/MOx NPs with increasing concentration, exposure time, molecular weight, and HOMO (7a, b, g and h). A high HOMO value usually means that the electrons of the material are more easily transferred or involved in reactions, especially in interactions with biological systems. A higher HOMO value increases the tendency of the material to undergo oxidation resulting in the generation of free radicals or electron transfer with biomolecules (such as proteins and DNA) in the cell, leading to cell damage or cytotoxicity. The cytotoxicity of M/MOx NPs is inversely proportional to zeta potential, CA, n_O/∑x and Pol (7d, e, f and i). Interestingly, we found that M/MOx NPs with particle sizes between 10–110 nm have stronger cytotoxicity (6c). Generally speaking, small-sized nanoparticles usually have higher surface energy and activity, making them easy to penetrate cell membranes or trigger oxidative stress reactions, resulting in higher cytotoxicity. However, in our PDP results, 0–10 nm did not show the expected high cytotoxicity. This may be because small-sized nanoparticles tend to aggregate in solution, forming larger particles that reduce their direct interaction with cells.⁹¹ Additionally, smaller nanoparticles in biological systems may be more easily recognized and cleared by defense mechanisms such as autophagosomes and macrophages, thereby reducing their toxicity.⁹²

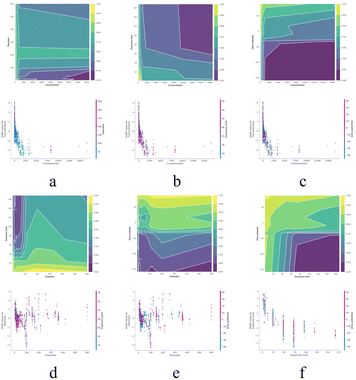
Fig. 7 Feature effects of the nine important features. (a–i) PDP and ICE results with different features. The thick line with a yellow shadow is PDP.

When features interact, the combined effect between two features may be nonadditive. In most practical situations, there are more or less interactions. Therefore, in order to make learning models interpretable, it is necessary to consider the strength and effectiveness of feature interactions. Feature interaction is often considered as the interaction between two features, as the interaction between more features is difficult to visualize and interpret. The partial dependency relationship between two features can be visualized in an interactive contour map. It is worth noting that this interaction may only be a correlation rather than a causal relationship, as the graph shows a global explanation of feature interactions without effect decomposition. SHAP dependency graph is another method of visualizing the interaction between two features, where the vertical dispersion of a single feature value on the x-axis represents the interaction effect with another feature. However, this visualization tool is difficult to display the interaction between two classification features without inherent logical relationships. Fig. 8 shows the combination effect between two of the first four features. Concentration shows a strong influence in all graphs, with higher concentrations indicating stronger cytotoxicity (8a–c). There is a complex relationship between zeta potential and particle size (8e), especially at negative zeta potential, where toxicity increases with larger particle size. The exposure time also increased cytotoxicity to a certain extent (8d and f), especially at smaller particle sizes and negative zeta potentials. The longer the exposure time, the stronger the toxicity. Overall, there is a highly non-linear interaction between cytotoxicity and the concentration, particle size, zeta potential, and exposure time of nanomaterials. Reasonable control of these factors may reduce the cytotoxicity of nanomaterials.

Fig. 8 PDP and SHAP dependency graphs are used to visualize the combination effect between two features. (a–c) Concentration with particle size, exposure time, and zeta potential, respectively; (d and e) particle size with exposure time and zeta potential; (f) exposure time with zeta potential.

3.6 Experimental results comparison

To further demonstrate the model's practical application, we synthesized six different types of metal oxide nanoparticles in the lab (ZnO, CdO, Cu₂O, CeO₂, Er₂O₃, Nd₂O₃) and characterized them using zeta potential measurements, X-ray powder diffraction (XRD), and scanning electron microscopy (SEM) to extract key parameters (Fig. 9). Two tumor cell lines (A549 and HeLa) were cultured, and their toxicity predictions were assessed. Notably, CeO₂, Er₂O₃, Nd₂O₃ nanoparticles, not presenting the training dataset, were included to test the model's generalization capability. Five concentration gradients were designed for each nanoparticle, with two exposure times (24 h and 48 h) and two detection methods (MTT and CCK8), resulting in a dataset of 240 instances (attached as Excelsheet2). The model's prediction results are shown in Table 4. To further assess the reliability and practical applicability of the predictive model in real experimental settings, SHAP analysis was conducted on experimental data to elucidate the contributions of individual features to cell viability outcomes. One representative metal oxide nanoparticle—ZnO, CdO, Cu₂O, CeO₂, Er₂O₃, and Nd₂O₃—was randomly selected from each material category for SHAP-based prediction and interpretation, as illustrated in Fig. 10. In the SHAP plots, arrows represent influential features such as zeta potential, concentration, and exposure time; red arrows indicate positive contributions (i.e., enhanced cell survival), while blue arrows reflect negative impacts (i.e., increased cytotoxicity). The final SHAP output F(x) represents the predicted level of cell viability. For instance, ZnO yielded a low F(x) value of −1.71, suggesting high cytotoxicity, whereas CdO showed a high F(x) value of 7.43, indicative of low toxicity. The SHAP interpretations reveal that cytotoxicity arises from complex interactions among multiple features. In general, higher nanoparticle concentrations tend to reduce cell viability, negatively charged surfaces may intensify cellular interactions, and longer exposure durations increase toxicity. These mechanistic insights can inform future experimental strategies, such as optimizing concentration and exposure time to minimize adverse biological effects.

Fig. 9 SEM and XRD characterization of metal oxide nanoparticles (ZnO, CdO, Cu₂O, CeO₂, Er₂O₃, Nd₂O₃).

Table 4 LightGBM model predicts scores for experimental results

Model	Accuracy	AUC	Precision	Recall	F1
LightGBM	0.9125	0.7887	0.9353	0.9731	0.9538

---

Fig. 10 The SHAP prediction and interpretation diagram of cytotoxicity of different nano metal oxides (ZnO, CdO, Cu₂O, CeO₂, Er₂O₃, Nd₂O₃) in the external validation set.

4 Conclusions

In this study, we compiled 2765 toxicity data points of metal and metal oxide (M/MOx) nanoparticles against tumor cells from published literature and addressed data gaps using the Jaccard similarity coefficient. We developed an interpretable machine learning model, incorporating physicochemical, molecular, and quantum chemical descriptors, to predict the in vitro cytotoxicity of 26 nanoparticle types across 32 tumor cell lines. Feature selection based on correlation analysis enhanced model performance, and the final LGBM model achieved over 90% accuracy in cross-validation. Feature importance and effect analysis revealed key variables consistent with experimental understanding, supporting the model's interpretability. Experimental validation with newly synthesized rare earth metal oxide nanoparticles confirmed the model's predictive ability. This approach provides a robust, scalable, and efficient computational tool for toxicity screening, offering practical guidance for the rational design of tumor-targeting nanomaterials (Fig. 10).

Data availability

The data that support the findings of this study are available in the ESI.† All code used for data preprocessing, similarity-based imputation, and model construction is available at: https://github.com/mcurcumin/mayoufu-rcs-I-ML-Predicts-Antitumor-Effects-of-Metal-Metal-Oxide-NMs.

Author contributions

Methodology, Houlin Su; software, Yu Jiang; validation, Youfu Ma; formal analysis, Jiajia Lei; investigation, Wenguang Xiao, Haijun Tian, Yawei Ma, Li Zhu, Yuxi Liang; resources, Lisheng Wang and Mingqing Yuan; data curation, Youfu Ma; writing – original draft, Youfu Ma; writing – review & editing, Xu Liu; supervision, Lisheng Wang and Xu Liu; project administration, Xu Liu; funding acquisition, Mingqing Yuan and Xu Liu. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Innovation Project of Guangxi Graduate Education (YCSW2024027) and Guangxi Natural Science Foundation (2020GXNSFAA297178). This work was supported by Center for Instrumental Analysis of Guangxi University (https://www.fxcszx.gxu.edu.cn).

References

1. R. L. Siegel, K. D. Miller and A. Jemal, Ca-Cancer J. Clin., 2016, 66, 7–30.
2. F. Bray, J. Ferlay, I. Soerjomataram, R. L. Siegel, L. A. Torre and A. Jemal, Ca-Cancer J. Clin., 2018, 68, 394–424.
3. S. S. Lucky, K. C. Soo and Y. Zhang, Chem. Rev., 2015, 115, 1990–2042.
4. P. Gao, M. Wang, Y. Chen, W. Pan, P. Zhou, X. Wan, N. Li and B. Tang, Chem. Sci., 2020, 11, 6882–6888.
5. W. Ngo, B. Stordy, J. Lazarovits, E. K. Raja, C. L. Etienne and W. C. W. Chan, J. Am. Chem. Soc., 2020, 142, 17938–17943.
6. C. M. Alexander, K. L. Hamner, M. M. Maye and J. C. Dabrowiak, Bioconjugate Chem., 2014, 25, 1261–1271.
7. P. Gao, Y. Chen, W. Pan, N. Li, Z. Liu and B. Tang, Angew. Chem., Int. Ed., 2021, 60, 16763–16776.
8. X. Sun, Y. Zhang, J. Li, K. S. Park, K. Han, X. Zhou, Y. Xu, J. Nam, J. Xu, X. Shi, L. Wei, Y. L. Lei and J. J. Moon, Nat. Nanotechnol., 2021, 16, 1260–1270.
9. X. Zhong, X. Dai, Y. Wang, H. Wang, H. Qian and X. Wang, Wiley Interdiscip. Rev.:Nanomed. Nanobiotechnol., 2022, 14, e1797.
10. M. Cordani and Á. Somoza, Cell. Mol. Life Sci., 2019, 76, 1215–1242.
11. M. A. Gatoo, S. Naseem, M. Y. Arfat, A. Mahmood Dar, K. Qasim and S. Zubair, BioMed Res. Int., 2014, 2014, 498420.
12. A. Adan, Y. Kiraz and Y. Baran, Curr. Pharm. Biotechnol., 2016, 17, 1213–1221.
13. J. G. Rouse, J. Yang, A. R. Barron and N. A. Monteiro-Riviere, Toxicol. In Vitro, 2006, 20, 1313–1320.
14. P. Wick, P. Manser, L. K. Limbach, U. Dettlaff-Weglikowska, F. Krumeich, S. Roth, W. J. Stark and A. Bruinink, Toxicol. Lett., 2007, 168, 121–131.
15. K. S. Choi, B. K. Bang, P. K. Bae, Y. R. Kim and C. H. Kim, J. Nanosci. Nanotechnol., 2013, 13, 1820–1823.
16. T. R. Pisanic 2nd, J. D. Blackwell, V. I. Shubayev, R. R. Fiñones and S. Jin, Biomaterials, 2007, 28, 2572–2581.
17. K. Müller, J. N. Skepper, M. Posfai, R. Trivedi, S. Howarth, C. Corot, E. Lancelot, P. W. Thompson, A. P. Brown and J. H. Gillard, Biomaterials, 2007, 28, 1629–1642.
18. X. Lu, H. Yang, Y. Chen, Q. Li, S. Y. He, X. Jiang, F. Feng, W. Qu and H. Sun, Curr. Pharm. Des., 2018, 24, 3424–3439.
19. L. Shi, W. Tong, H. Fang, Q. Xie, H. Hong, R. Perkins, J. Wu, M. Tu, R. M. Blair, W. S. Branham, C. Waller, J. Walker and D. M. Sheehan, SAR QSAR Environ. Res., 2002, 13, 69–88.
20. H. Hong, H. Fang, Q. Xie, R. Perkins, D. M. Sheehan and W. Tong, SAR QSAR Environ. Res., 2003, 14, 373–388.
21. H. W. Ng, M. Shu, H. Luo, H. Ye, W. Ge, R. Perkins, W. Tong and H. Hong, Chem. Res. Toxicol., 2015, 28, 1784–1795.
22. S. Sakkiah, W. Guo, B. Pan, R. Kusko, W. Tong and H. Hong, J. Environ. Sci. Health, Part C:Environ. Carcinog. Ecotoxicol. Rev., 2018, 36, 192–218.
23. H. W. Ng, W. Zhang, M. Shu, H. Luo, W. Ge, R. Perkins, W. Tong and H. Hong, BMC Bioinf., 2014, 15(suppl. 11), S4.
24. C. Selvaraj, S. Sakkiah, W. Tong and H. Hong, Food Chem. Toxicol., 2018, 112, 495–506.
25. S. Sakkiah, R. Kusko, W. Tong and H. Hong, in Advances in Computational Toxicology: Methodologies and Applications in Regulatory Science, ed. H. Hong, Springer International Publishing, Cham, 2019, pp. 181–212,  DOI:10.1007/978-3-030-16443-0_10.
26. F. Cheng, H. Hong, S. Yang and Y. Wei, Briefings Bioinf., 2016, 18, 682–697.
27. H. Luo, H. Ye, H. W. Ng, L. Shi, W. Tong, W. Mattes, D. Mendrick and H. Hong, BMC Bioinf., 2015, 16, S9.
28. H. Luo, H. Ye, H. W. Ng, S. Sakkiah, D. L. Mendrick and H. Hong, Sci. Rep., 2016, 6, 32115.
29. H. Ye, H. Luo, H. W. Ng, J. Meehan, W. Ge, W. Tong and H. Hong, Environ. Int., 2016, 89–90, 81–92.
30. H. Hong, S. Thakkar, M. Chen and W. Tong, Sci. Rep., 2017, 7, 17311.
31. H. W. Ng, S. W. Doughty, H. Luo, H. Ye, W. Ge, W. Tong and H. Hong, Chem. Res. Toxicol., 2015, 28, 2343–2351.
32. G. Idakwo, J. Luttrell, M. Chen, H. Hong, Z. Zhou, P. Gong and C. Zhang, J. Environ. Sci. Health, Part C:Environ. Carcinog. Ecotoxicol. Rev., 2018, 36, 169–191.
33. H. Luo, H. Ye, H. W. Ng, L. Shi, W. Tong, D. L. Mendrick and H. Hong, Bioinf. Biol. Insights, 2015, 9(suppl. 3), 21–29.
34. J. Shen, L. Xu, H. Fang, A. M. Richard, J. D. Bray, R. S. Judson, G. Zhou, T. J. Colatsky, J. L. Aungst, C. Teng, S. C. Harris, W. Ge, S. Y. Dai, Z. Su, A. C. Jacobs, W. Harrouk, R. Perkins, W. Tong and H. Hong, Toxicol. Sci., 2013, 135, 277–291.
35. H. Hong, W. Tong, Q. Xie, H. Fang and R. Perkins, SAR QSAR Environ. Res., 2005, 16, 339–347.
36. G. Idakwo, J. Luttrell Iv, M. Chen, H. Hong, P. Gong and C. Zhang, in Advances in Computational Toxicology: Methodologies and Applications in Regulatory Science, ed. H. Hong, Springer International Publishing, Cham, 2019, pp. 119–139,  DOI:10.1007/978-3-030-16443-0_7.
37. H. Hong, J. Zhu, M. Chen, P. Gong, C. Zhang and W. Tong, in Drug-Induced Liver Toxicity, ed. M. Chen and Y. Will, Springer New York, New York, NY, 2018, pp. 77–100,  DOI:10.1007/978-1-4939-7677-5_5.
38. S. Sakkiah, C. Selvaraj, P. Gong, C. Zhang, W. Tong and H. Hong, Oncotarget, 2017, 8(54), 92989–93000.
39. Z. Wang, J. Chen and H. Hong, Environ. Sci. Technol., 2021, 55, 6857–6866.
40. G. Idakwo, S. Thangapandian, J. Luttrell, Y. Li, N. Wang, Z. Zhou, H. Hong, B. Yang, C. Zhang and P. Gong, J. Cheminf., 2020, 12, 66.
41. A. Maxwell, R. Li, B. Yang, H. Weng, A. Ou, H. Hong, Z. Zhou, P. Gong and C. Zhang, BMC Bioinf., 2017, 18, 523.
42. W. Tang, J. Chen, Z. Wang, H. Xie and H. Hong, J. Environ. Sci. Health, Part C:Environ. Carcinog. Ecotoxicol. Rev., 2018, 36, 252–271.
43. Y. Wei, J. Wu, Y. Wu, H. Liu, F. Meng, Q. Liu, A. C. Midgley, X. Zhang, T. Qi, H. Kang, R. Chen, D. Kong, J. Zhuang, X. Yan and X. Huang, Adv. Mater., 2022, 34, e2201736.
44. A. Bigdeli, M. R. Hormozi-Nezhad and H. Parastar, RSC Adv., 2015, 5, 57030–57037.
45. E. Papa, J. P. Doucet, A. Sangion and A. Doucet-Panaye, SAR QSAR Environ. Res., 2016, 27, 521–538.
46. H. I. Labouta, N. Asgarian, K. Rinker and D. T. Cramb, ACS Nano, 2019, 13, 1583–1594.
47. N. Shirokii, Y. Din, I. Petrov, Y. Seregin, S. Sirotenko, J. Razlivina, N. Serov and V. Vinogradov, Small, 2023, 19, e2207106.
48. N. Sizochenko, M. Syzochenko, N. Fjodorova, B. Rasulev and J. Leszczynski, Ecotoxicol. Environ. Saf., 2019, 185, 109733.
49. G. Gul, R. Yildirim and N. Ileri-Ercan, Environ. Sci.: Nano, 2021, 8, 937–949.
50. G. L. Edwards, D. S. C. Black, G. B. Deacon and L. P. Wakelin, Can. J. Chem., 2005, 83, 969–979.
51. D. E. Jones, H. Ghandehari and J. C. Facelli, Beilstein J. Nanotechnol., 2015, 6, 1886–1896.
52. L. Horev-Azaria, G. Baldi, D. Beno, D. Bonacchi, U. Golla-Schindler, J. C. Kirkpatrick, S. Kolle, R. Landsiedel, O. Maimon, P. N. Marche, J. Ponti, R. Romano, F. Rossi, D. Sommer, C. Uboldi, R. E. Unger, C. Villiers and R. Korenstein, Part. Fibre Toxicol., 2013, 10, 32.
53. V. Kovalishyn, N. Abramenko, I. Kopernyk, L. Charochkina, L. Metelytsia, I. V. Tetko, W. Peijnenburg and L. Kustov, Food Chem. Toxicol., 2018, 112, 507–517.
54. Y. Luo, C. Wang, Y. Qiao, M. Hossain, L. Ma and M. Su, J. Mater. Sci.:Mater. Med., 2012, 23, 2563–2573.
55. X. Hu, S. Cook, P. Wang and H.-m. Hwang, Sci. Total Environ., 2009, 407, 3070–3072.
56. T. Puzyn, B. Rasulev, A. Gajewicz, X. Hu, T. P. Dasari, A. Michalkova, H.-M. Hwang, A. Toropov, D. Leszczynska and J. Leszczynski, Nat. Nanotechnol., 2011, 6, 175–178.
57. S. Kar, A. Gajewicz, T. Puzyn, K. Roy and J. Leszczynski, Ecotoxicol. Environ. Saf., 2014, 107, 162–169.
58. K. Pathakoti, M.-J. Huang, J. D. Watts, X. He and H.-M. Hwang, J. Photochem. Photobiol., B, 2014, 130, 234–240.
59. F. Luan, V. V. Kleandrova, H. González-Díaz, J. M. Ruso, A. Melo, A. Speck-Planche and M. N. Cordeiro, Nanoscale, 2014, 6, 10623–10630.
60. V. V. Kleandrova, F. Luan, H. González-Díaz, J. M. Ruso, A. Speck-Planche and M. N. Cordeiro, Environ. Sci. Technol., 2014, 48, 14686–14694.
61. J. Cao, Y. Pan, Y. Jiang, R. Qi, B. Yuan, Z. Jia, J. Jiang and Q. Wang, Green Chem., 2020, 22, 3512–3521.
62. C. Leone, E. E. Bertuzzi, A. P. Toropova, A. A. Toropov and E. Benfenati, Chemosphere, 2018, 210, 52–56.
63. H. K. Shin, K. Y. Kim, J. W. Park and K. T. No, SAR QSAR Environ. Res., 2017, 28, 875–888.
64. N. Sizochenko, M. Syzochenko, N. Fjodorova, B. Rasulev and J. Leszczynski, Ecotoxicol. Environ. Saf., 2019, 185, 109733.
65. S. M. Shafer and D. F. Rogers, Int. J. Prod. Res., 1993, 31, 1133–1142.
66. Y. Yin and K. Yasuda, Comput. Ind. Eng., 2005, 48, 471–489.
67. G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, 2017.
68. H. Yu, Z. Zhao and F. Cheng, Chemosphere, 2021, 276, 130164.
69. I. Accelrys Software, 2023.
70. J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32.
71. J. J. P. Stewart, Stewart Computational Chemistry, MOPAC2016, Colorado Springs, CO, 2016.
72. R. Todeschini and V. Consonni, in Methods and Principles in Medicinal Chemistry, ed. R. Manhold, H. Kubinyi and G. Folkers, Wiley-VCH, Weinheim, Germany, 2009, vol. 41, pp. 625–627.
73. M. E. Hohn, J. Int. Assoc. Math. Geol., 1976, 8, 137–150.
74. Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, Proc. IEEE, 1998, 86, 2278–2324.
75. D. E. Rumelhart, G. E. Hinton and R. J. Williams, Nature, 1986, 323, 533–536.
76. L. Breiman, Mach. Learn., 2001, 45, 5–32.
77. T. Chen and C. Guestrin, Proc. ACM SIGKDD Int. Conf. Knowl. Discov. Data Min., 2016, vol. 22, pp. 785–794.
78. G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Adv. Neural Inf. Process Syst., 2017, 30, 3149–3157.
79. M. A. Hearst, S. T. Dumais, E. Osuna, J. Platt and B. Scholkopf, IEEE Intelligent Systems and Their Applications, 1998, vol. 13, pp. 18–28.
80. X. Zou, Y. Hu, Z. Tian and K. Shen, Proc. IEEE Int. Conf. Comput. Sci. Netw. Technol. (ICCSNT), 2019, pp. 135–139.
81. K. Taunk, S. De, S. Verma and A. Swetapadma, Proc. Int. Conf. Intell. Comput. Control Syst. (ICCS), 2019, pp. 1255–1260.
82. H. Zhou, in Learn Data Mining Through Excel: A Step-by-Step Approach for Understanding Machine Learning Methods, ed. H. Zhou, Apress, Berkeley, CA, 2023, pp. 143–159,  DOI:10.1007/978-1-4842-9771-1_9.
83. Kenry, T. Yeo, P. N. Manghnani, E. Middha, Y. Pan, H. Chen, C. T. Lim and B. Liu, ACS Nano, 2020, 14, 4509–4522.
84. A. Nel, T. Xia, L. Mädler and N. Li, Science, 2006, 311, 622–627.
85. A. Verma, O. Uzun, Y. Hu, Y. Hu, H.-S. Han, N. Watson, S. Chen, D. J. Irvine and F. Stellacci, Nat. Mater., 2008, 7, 588–595.
86. T.-H. Kim, M. Kim, H.-S. Park, U. S. Shin, M.-S. Gong and H.-W. Kim, J. Biomed. Mater. Res., Part A, 2012, 100, 1033–1043.
87. L. Li, W. S. Xi, Q. Su, Y. Li, G. H. Yan, Y. Liu, H. Wang and A. Cao, Small, 2019, 15, e1901687.
88. V. Colvin, Environ. Mol. Mutagen., 2007, 48, 533.
89. J. H. Friedman, Ann. Stat., 2001, 29, 1189–1232.
90. A. Goldstein, A. Kapelner, J. Bleich and E. Pitkin, Journal of Computational and Graphical Statistics, 2015, 24, 44–65.
91. S. Bhattacharjee, J. Controlled Release, 2016, 235, 337–351.
92. T. Xia, M. Kovochich, M. Liong, L. Mädler, B. Gilbert, H. Shi, J. I. Yeh, J. I. Zink and A. E. Nel, ACS Nano, 2008, 210, 2121–2134.

---

Footnotes

† Electronic supplementary information (ESI) available: The source code is publicly available at https://github.com/mcurcumin/mayoufu-rcs-I-ML-Predicts-Antitumor-Effects-of-Metal-Metal-Oxide-NMs. See DOI: https://doi.org/10.1039/d5ra02309b

‡ Youfu Ma and Yu Jiang contributed equally to this work.

---