Open Access Article
Open Access ArticleNew strategy for optimizing the microstructure and giant dielectric properties of TiO2 via acceptor/donor ratio tuning†
Wattana Tuichaia,
Jurimart Wongsrichaa,
Nutthakritta Phromviyob,
Bundit Putasaengc,
Supamas Danwittayakul c,
Pornjuk Srepusharawoot
c,
Pornjuk Srepusharawoot ab and
Prasit Thongbai
ab and
Prasit Thongbai *ab
*ab
aGiant Dielectric and Computational Design Research Group (GD-CDR), Department of Physics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand. E-mail: pthongbai@kku.ac.th; Fax: +66 43 202374; Tel: +66 84 4190266
bInstitute of Nanomaterials Research and Innovation for Energy (IN-RIE), Khon Kaen University, Khon Kaen 40002, Thailand
cNational Metal and Materials Technology Center, 114 Thailand Science Park, Paholyothin Road, Klong 1, Klong Luang, Pathumthani 12120, Thailand
First published on 9th June 2025
Abstract
In this study, we investigated how the acceptor/donor doping ratio influences the microstructure and giant dielectric behavior of co-substituted TiO2 ceramics. ScxTa0.025Ti0.975−xO2 ceramics, with Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, and 2.0, were synthesized via solid-state reactions. All samples crystallized into dense rutile TiO2, and Raman spectroscopy revealed that increasing the Sc3+/Ta5+ ratio promotes the formation of oxygen vacancies, leading to larger average grain sizes. The dielectric constant (ε′) decreased significantly with higher Sc3+/Ta5+ ratios, and no giant dielectric response was observed for ratios above 1.0. Notably, samples with Sc3+/Ta5+ ratios of 0.4 and 0.8 achieved ε′ values of 5.9 × 104 and 4.8 × 104, respectively, alongside low loss tangents (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of 0.024 and 0.043 at 1 kHz and 25 °C. These ceramics also exhibited excellent temperature stability, with their ε′ values varying by less than ±15% from −60 to 210 °C—sufficient for X9R capacitor applications. Impedance spectroscopy and nonlinear electrical measurements revealed that the enhanced dielectric performance arises primarily from interfacial polarization effects due to insulating grain boundaries and conductive grains, as further confirmed by X-ray photoelectron spectroscopy. Interestingly, the optimal dielectric properties, commonly reported at an acceptor/donor ratio of 1.0 in other co-doped systems, were not observed in this study. These findings challenge the conventional assumption that a 1
δ) of 0.024 and 0.043 at 1 kHz and 25 °C. These ceramics also exhibited excellent temperature stability, with their ε′ values varying by less than ±15% from −60 to 210 °C—sufficient for X9R capacitor applications. Impedance spectroscopy and nonlinear electrical measurements revealed that the enhanced dielectric performance arises primarily from interfacial polarization effects due to insulating grain boundaries and conductive grains, as further confirmed by X-ray photoelectron spectroscopy. Interestingly, the optimal dielectric properties, commonly reported at an acceptor/donor ratio of 1.0 in other co-doped systems, were not observed in this study. These findings challenge the conventional assumption that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acceptor/donor ratio is universally optimal for co-doped TiO2 ceramics. This work provides a new strategy for enhancing dielectric performance by adjusting the doping ratio in systems dominated by extrinsic mechanisms such as IBLC.
1 acceptor/donor ratio is universally optimal for co-doped TiO2 ceramics. This work provides a new strategy for enhancing dielectric performance by adjusting the doping ratio in systems dominated by extrinsic mechanisms such as IBLC.
1. Introduction
Giant dielectric oxides with dielectric permittivities (ε′) exceeding 103 have garnered significant interest due to their potential applications in ceramic capacitors (CCs) and high-energy-density storage (HEDS) devices.1,2 Many non-ferroelectric complex and simple oxides exhibit remarkably high dielectric properties without undergoing ferroelectric phase transitions.3–8 Several mechanisms have been proposed to explain these giant dielectric phenomena, including the internal barrier layer capacitor (IBLC) model,4–6 surface barrier layer capacitor (SBLC) model,9 polaronic stacking fault defects,10 small polaron hopping,11 and the non-ohmic sample-electrode (SE) contact model.12,13 Despite significant progress, the temperature stability of ε′ remains a key challenge for their practical implementation in CCs and HEDS applications.Titanium dioxide (TiO2) ceramics have attracted widespread attention due to their excellent dielectric properties, structural versatility (anatase, rutile, and brookite phases), and broad applicability in areas such as energy storage, environmental science, and medicine.7,8 Among these polymorphs, rutile TiO2 stands out due to its high ε′ and relatively low loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), making it a promising material for dielectric and capacitor applications.
δ), making it a promising material for dielectric and capacitor applications.
Recent research has highlighted the remarkable dielectric performance of co-substituted rutile TiO2 materials, which exhibit very high ε′ and low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ over a broad temperature range, making them promising candidates for high-performance CCs and HEDS applications. For instance, In3+, Nb5+ co-doped TiO2 (InNb-TO) ceramics have demonstrated ε′ ≈ 64
δ over a broad temperature range, making them promising candidates for high-performance CCs and HEDS applications. For instance, In3+, Nb5+ co-doped TiO2 (InNb-TO) ceramics have demonstrated ε′ ≈ 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and tan
000 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ < 0.025.8 This behavior is primarily attributed to the electron pinned defect-dipole (EPDD) model, where In3+ doping induces oxygen vacancy
δ < 0.025.8 This behavior is primarily attributed to the electron pinned defect-dipole (EPDD) model, where In3+ doping induces oxygen vacancy  -related complex defects that confine the free electrons introduced by Nb5+ doping.
-related complex defects that confine the free electrons introduced by Nb5+ doping.
Understanding the origins of the giant dielectric response and the roles of dopants in TiO2-based ceramics remains a critical research topic. While the EPDD model is widely recognized as a key mechanism in co-doped TiO2, alternative mechanisms such as IBLC and SBLC have also been proposed.9,14–17 Despite the diversity of these models, high ε′, excellent temperature stability, and low dielectric loss are crucial properties for practical applications. Recent broadband dielectric spectroscopy studies have confirmed that multiple dielectric responses can achieve ε′ > 103, further emphasizing the importance of elucidating the underlying mechanisms.18,19
To enhance dielectric performance, researchers have explored a variety of dopant combinations in co-doped TiO2, including (Gd3+, Nb5+),20 (Cu2+, Nb5+),21 (In3+, Ta5+),22 (Ag+, Ta5+),23 (Tm3+, Nb5+),24 (Eu3+, Nb5+),25 (Pr3+, Ta5+),26 (Zr4+, Ta5+),27 (Ga3+, Nb5+),11 (Al3+, Nb5+),28 (Zn2+, W6+),29 (Ag+, Mo6+),30 and (Ca2+, Ta5+).31 In most of these studies, trivalent and pentavalent dopants were introduced at equal concentrations (+3/+5 ratio = 1), based on the assumption that donor dopants primarily enhance the dielectric response, while acceptor dopants regulate tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. However, recent findings suggest that this assumption may be oversimplified, and the interactions between donor and acceptor dopants are more complex than previously thought.
δ. However, recent findings suggest that this assumption may be oversimplified, and the interactions between donor and acceptor dopants are more complex than previously thought.
For example, in aluminum–niobium co-doped TiO2 (InAl-TO) ceramics,28 Nb5+ doping was expected to increase ε′ by generating free electrons. In other words, a reduction in ε′ should be attributed solely to the decrease in Nb5+, while Al3+ doping is expected to primarily regulate tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. However, contrary to these expectations, ε′ was found to decrease with increasing Al3+ concentration. This suggests that ε′ is influenced not only by Nb5+ but also by the presence of Al3+. The unexpected decline in ε′ was attributed to Al3+, which primarily induces
δ. However, contrary to these expectations, ε′ was found to decrease with increasing Al3+ concentration. This suggests that ε′ is influenced not only by Nb5+ but also by the presence of Al3+. The unexpected decline in ε′ was attributed to Al3+, which primarily induces  and typically does not significantly alter ε′ or the concentration of free electrons. However, Al3+ appears to interact with Nb5+, indicating a possible self–charge compensation mechanism between these ions. Unfortunately, this interaction remains largely unexplored. In practice, partial self-charge compensation between trivalent (+3) and pentavalent (+5) ions may occur without the formation of additional point defects, implying that an equal acceptor/donor ratio may not always be optimal. To achieve better dielectric performance, acceptor dopants should primarily reduce dielectric loss while minimizing any perturbation to ε′. This leads to an important hypothesis: the acceptor/donor ratio should be lower than 1.0 rather than strictly equal to 1.0.
and typically does not significantly alter ε′ or the concentration of free electrons. However, Al3+ appears to interact with Nb5+, indicating a possible self–charge compensation mechanism between these ions. Unfortunately, this interaction remains largely unexplored. In practice, partial self-charge compensation between trivalent (+3) and pentavalent (+5) ions may occur without the formation of additional point defects, implying that an equal acceptor/donor ratio may not always be optimal. To achieve better dielectric performance, acceptor dopants should primarily reduce dielectric loss while minimizing any perturbation to ε′. This leads to an important hypothesis: the acceptor/donor ratio should be lower than 1.0 rather than strictly equal to 1.0.
Many previous studies have assumed that an acceptor/donor ratio of 1.0 is necessary for maximizing dielectric properties in co-doped TiO2, particularly in systems where EPDD is the dominant mechanism, such as InNb-TO.8 In such cases, In3+ and Nb5+ work synergistically to create complex defect structures that enhance the dielectric response. However, in co-doped TiO2 systems where giant dielectric properties arise primarily from extrinsic mechanisms such as IBLC and SBLC—rather than EPDD—the situation may be entirely different. This is evident in Sc3+, Ta5+ co-doped TiO2 (ScTa-TO), where Sc3+ (acceptor) promotes the formation of insulating grain boundaries, while Ta5+ (donor) enhances conductivity in the grain interiors.9 Unlike the InNb-TO system, where both dopants cooperate to form a defect complex, Sc3+ and Ta5+ do not work together in the same way. This suggests that the commonly assumed +3/+5 ratio of 1.0 may not always yield optimal dielectric performance in TiO2 ceramics. These findings indicate that the optimal acceptor/donor ratio is closely related to the predominant dielectric mechanism. In systems governed by EPDD, such as InNb-TO or In3+, Ta5+ co-doped TiO2 (InTa-TiO2),8,32 a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio is theoretically expected to be optimal for forming electron–trapping complex defects that enhance the dielectric response. In contrast, for systems dominated by the IBLC mechanism, such as ScTa-TiO, a reduced acceptor concentration may help maintain free electron generation and strengthen interfacial polarization. This work, therefore, introduces a design strategy that can be adapted to other extrinsically driven dielectric systems. The insight gained here offers a new conceptual basis for tailoring co-doped TiO2 ceramics by adjusting the acceptor/donor ratio in accordance with the underlying dielectric mechanism.
1 ratio is theoretically expected to be optimal for forming electron–trapping complex defects that enhance the dielectric response. In contrast, for systems dominated by the IBLC mechanism, such as ScTa-TiO, a reduced acceptor concentration may help maintain free electron generation and strengthen interfacial polarization. This work, therefore, introduces a design strategy that can be adapted to other extrinsically driven dielectric systems. The insight gained here offers a new conceptual basis for tailoring co-doped TiO2 ceramics by adjusting the acceptor/donor ratio in accordance with the underlying dielectric mechanism.
Our previous study investigated ScTa-TiO ceramics with selected Sc3+ concentrations (1, 2.5, and 5%), focusing primarily on humidity sensitivity.33 It was found that the ε′ value for the sample with a Sc3+/Ta5+ ratio of 1.0 remained below 104, even when sintered at 1500 °C. In contrast, the sample with a Sc3+/Ta5+ ratio of 0.4 exhibited a much higher ε′ (∼105), but this was accompanied by a relatively high tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. These observations suggested that the optimal dielectric behavior might not occur at the conventional 1
δ. These observations suggested that the optimal dielectric behavior might not occur at the conventional 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, yet the underlying origin and systematic relationship between microstructure and dielectric properties were not clarified.
1 ratio, yet the underlying origin and systematic relationship between microstructure and dielectric properties were not clarified.
The present work expands upon those findings by systematically investigating the influence of the Sc3+/Ta5+ ratio over a broader and finer compositional range (0.4, 0.8, 1.0, 1.2, 1.6, and 2.0), under identical processing conditions. By decoupling the effects of different mechanisms, this study seeks to establish the correlation between doping ratio, microstructure, and dielectric properties, and to determine whether the optimal performance truly aligns with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acceptor/donor ratio. This research introduces a new strategy for tailoring co-doped TiO2 ceramics, especially in systems dominated by IBLC effects. Through targeted control of grain boundary characteristics and dopant interactions, the work aims to provide guiding principles for developing high-performance dielectric materials with excellent temperature stability and low tan
1 acceptor/donor ratio. This research introduces a new strategy for tailoring co-doped TiO2 ceramics, especially in systems dominated by IBLC effects. Through targeted control of grain boundary characteristics and dopant interactions, the work aims to provide guiding principles for developing high-performance dielectric materials with excellent temperature stability and low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ.
δ.
2. Experimental details
The ScTa-TO ceramics were designed with various acceptor/donor ratios of 0.4, 0.8, 1.0, 1.2, 1.6 and 2.0. Correspondingly, the ScxTa0.025Ti0.975−xO2 ceramics, where Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, and 2.0, were synthesized using a conventional solid-state reaction (SSR) method. The preparation steps for obtaining the mixed powders are detailed in previous work.9 The mixed powders were pressed into pellets with a diameter of 9.5 mm and a thickness of 1.5 mm using uniaxial compression at approximately 210 MPa, without the use of a binder. The ceramic samples were then sintered at 1400 °C for 5 h with a heating rate of 2 °C min−1, followed by natural furnace cooling to room temperature. The sintered ceramics with the specified acceptor/donor ratios were referred to as (Sc/Ta)0.4, (Sc/Ta)0.8, (Sc/Ta)1.0, (Sc/Ta)1.2, (Sc/Ta)1.6, and (Sc/Ta)2.0, respectively. The densities of the sintered samples were measured using the Archimedes method.To characterize the sintered ScTa-TO specimens, a comprehensive suite of analytical techniques was employed, including UV-Vis Raman spectroscopy, scanning electron microscopy (SEM), X-ray diffraction (XRD), field-emission scanning electron microscopy (FE-SEM) with energy-dispersive X-ray analysis (EDS), and X-ray photoelectron spectroscopy (XPS). Detailed descriptions of these techniques can be found in our previous publication.9
For the dielectric and nonlinear electrical measurements, both surfaces of the sintered samples were polished, cleaned, and dried at 100 °C for 2 h. Silver (Ag) paint was then applied to form electrodes, followed by heating at 600 °C for 0.5 h to ensure proper adhesion. The dielectric and electrical properties were measured using a KEYSIGHT E4990A Impedance Analyzer with an oscillation voltage of 0.5 V. Dielectric measurements were conducted over a frequency range of 40 Hz to 1 MHz and a temperature range of −180 to 200 °C. The nonlinear current density–electric field (J–E) characteristics were evaluated at ∼25 °C using a Keithley Model 247 high-voltage measurement unit. The breakdown field (Eb) was determined at J = 1 mA cm−2, while the nonlinear coefficient (α) was calculated over the J range of 1–10 mA cm−2.
3. Results and discussion
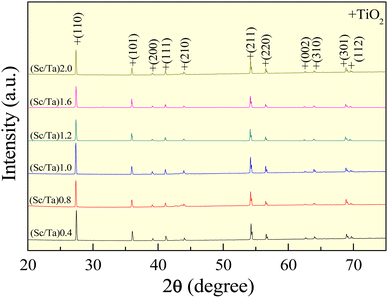
The XRD patterns of ScTa-TO ceramics, with Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, 1.2, 1.6, and 2.0, are presented in Fig. 1. The diffractograms reveal distinct peaks corresponding to the rutile TiO2 phase (JCPDS card no. 21-1276),19,20,24,27 indicating that all compositions retain the rutile structure after doping with Sc3+ and Ta5+. The peaks at 2θ positions ∼27.4, 36.1, 41.2, 54.3, and 69.1° are indexed to the (110), (101), (200), (211), and (301) planes,34 respectively, confirming the maintenance of the tetragonal rutile phase across all doping levels. No secondary phases or impurity peaks were detected, suggesting incorporation of Ta5+ and Sc3+ ions into the rutile lattice without forming new phases. However, while no Sc-related secondary phase is detectable in the XRD pattern of the (Sc/Ta)2.0 ceramic, due to the resolution limitations of the technique, segregation of Sc-related phases was observed in the SEM mapping, which will be discussed further in the microstructure analysis section.The lattice parameters (a and c values) derived from Rietveld refinements of the XRD patterns are summarized in Table 1 and Table S1 (ESI),† with the full refinement details provided in Fig. S1 (ESI).† The quality of the Rietveld refinements is reflected in the reliability factors Rexp, Rp, Rwp, and χ2, with all samples exhibiting χ2 values below 1.5, indicating robust structural models. The lattice expansion observed in the ScTa-TO ceramics compared to undoped TiO2 is attributed to the substitution of smaller Ti4+ ions (ionic radius: 0.605 Å) by larger Sc3+ (0.745 Å) and Ta5+ (0.64 Å) ions.9 Interestingly, while the lattice parameters exhibit some changes with increasing Sc3+ content, the c/a ratio remains relatively stable. This contrasts with what is observed in InNb-TO ceramics, where a significant increase in the c/a ratio with increasing In3+ content suggests preferential In3+ location along the c-axis, leading to the formation of extended planar defects (EPDDs).8 The absence of a significant change in the c/a ratio in the ScTa-TO ceramics, as indicated by XRD analysis, suggests that EPDDs do not preferentially form in these materials, aligning with theoretical predictions from previous work.9
| Sample | TiO2 | (Sc/Ta)0.4 | (Sc/Ta)0.8 | (Sc/Ta)1.0 | (Sc/Ta)2.0 |
|---|---|---|---|---|---|
| Rietveld refinement | |||||
| a = b (Å) | 4.593 | 4.597 | 4.596 | 4.596 | 4.598 |
| c (Å) | 2.961 | 2.964 | 2.964 | 2.965 | 2.966 |
| c/a | 0.644(7) | 0.644(8) | 0.644(9) | 0.645(1) | 0.645(1) |
| V (Å)3 | 62.475 | 62.631 | 62.597 | 62.620 | 62.708 |
| Rexp (%) | 4.209 | 5.834 | 6.603 | 6.072 | 6.071 |
| Rp (%) | 3.266 | 4.203 | 4.608 | 3.968 | 4.234 |
| Rwp (%) | 4.839 | 6.910 | 8.076 | 7.283 | 6.876 |
| χ2 | 1.321 | 1.403 | 1.496 | 1.439 | 1.283 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Raman shift | |||||
| Eg | 447.9 | 446.4 | 446.4 | 445.4 | 445.1 |
| A1g | 611.3 | 611.8 | 611.5 | 610.9 | 609.9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Microstructure | |||||
| ρ (g cm−3) | 4.13 | 4.06 | 4.11 | 4.14 | 3.92 |
| Ḡ (μm) | 41.7 ± 14.3 | 6.1 ± 1.8 | 7.9 ± 2.2 | 17.0 ± 6.3 | 17.7 ± 7.3 |
The microstructure of the ScTa-TO ceramics, where Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, and 2.0, was analyzed using SEM, and the resulting images are presented in Fig. 2. As observed, the grain sizes (Ḡ) of the ceramics exhibit noticeable changes with varying Sc3+ concentrations, as summarized in Table 1. Generally, as the Sc3+ concentration increases, the Ḡ appears to increase as well, particularly when comparing the ceramics with Sc3+/Ta5+ ratios = 0.4 and 2.0. The Ḡ values in the ScTa-TO ceramics are larger than those of 2.5%Ta5+-doped TiO2 alone (∼8.3 μm) at the sintering temperature of 1400 °C for 4 h, as reported in previous work,16 suggesting that the function of Sc3+ in the co-doped system is similar to that of Ga3+ in promoting grain growth. In the 2.5%Ta5+-doped TiO2 ceramic, Ta5+ acts as a grain growth inhibitor, leading to smaller grain sizes by reducing grain boundary mobility due to its segregation at grain boundaries.35 In contrast, both Ga3+ and Sc3+ are known to produce  during the sintering process, which enhances grain boundary mobility and promotes grain growth via the increase in diffusion rate of oxygen ions and
during the sintering process, which enhances grain boundary mobility and promotes grain growth via the increase in diffusion rate of oxygen ions and  .9,16 In the case of ScTa-TO ceramics, it is evident that Sc3+ counteracts the grain size reduction caused by Ta5+, resulting in larger grains, particularly in the higher Sc3+ concentration samples, e.g., (Sc/Ta)2.0 ceramic. The micrographs of the (Sc/Ta)1.0 ceramic (Fig. 2c) show relatively uniform grain distribution, and a slightly increased grain size compared to the (Sc/Ta)0.4 ceramic (Fig. 2a). However, the (Sc/Ta)2.0 ceramic (Fig. 2d) displays the most significant grain growth, with larger grains and more pronounced grain boundary mobility. The (Sc/Ta)2.0 ceramic show the largest pore size and large number of pores, corresponding to its lowest density. This behavior is consistent with the function of Sc3+ as a promoter of grain boundary diffusion, facilitating the migration of grain boundaries and leading to enhanced grain growth. Additionally, future studies could explore how variations in grain size, along with the electrical properties of the grains and grain boundaries, affect the material's dielectric properties, as grain size is a critical factor in determining overall dielectric behavior.
.9,16 In the case of ScTa-TO ceramics, it is evident that Sc3+ counteracts the grain size reduction caused by Ta5+, resulting in larger grains, particularly in the higher Sc3+ concentration samples, e.g., (Sc/Ta)2.0 ceramic. The micrographs of the (Sc/Ta)1.0 ceramic (Fig. 2c) show relatively uniform grain distribution, and a slightly increased grain size compared to the (Sc/Ta)0.4 ceramic (Fig. 2a). However, the (Sc/Ta)2.0 ceramic (Fig. 2d) displays the most significant grain growth, with larger grains and more pronounced grain boundary mobility. The (Sc/Ta)2.0 ceramic show the largest pore size and large number of pores, corresponding to its lowest density. This behavior is consistent with the function of Sc3+ as a promoter of grain boundary diffusion, facilitating the migration of grain boundaries and leading to enhanced grain growth. Additionally, future studies could explore how variations in grain size, along with the electrical properties of the grains and grain boundaries, affect the material's dielectric properties, as grain size is a critical factor in determining overall dielectric behavior.
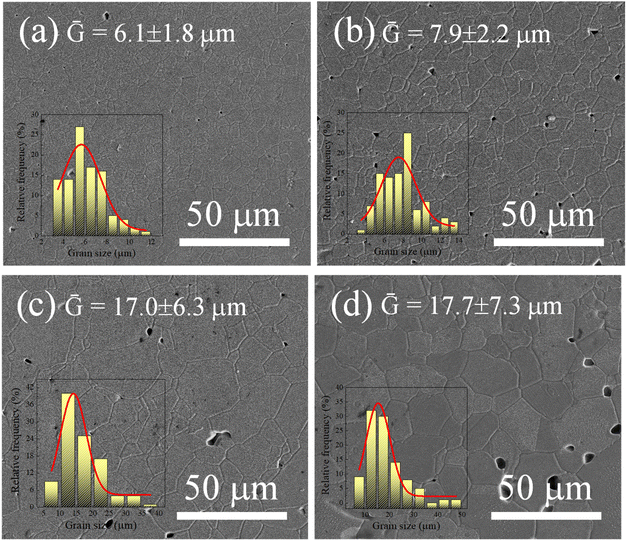 | ||
| Fig. 2 SEM images of ScTa-TO ceramics with Sc3+/Ta5+ ratios of (a) 0.4, (b) 0.8, (c) 1.0, and (d) 2.0. | ||
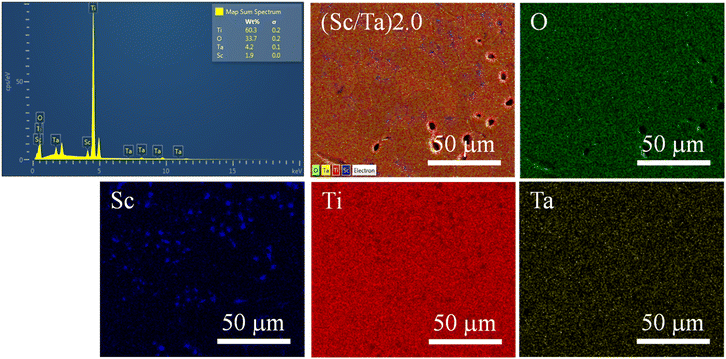
The SEM-mapping images of the ScTa-TO ceramics, as shown in Fig. 3 and 4, illustrate the elemental distribution for (Sc/Ta)1.0 and (Sc/Ta)2.0 ceramics. In the (Sc/Ta)1.0 ceramic (Fig. 3), the mapping images indicate that Ti, O, Ta, and Sc are homogeneously distributed throughout the microstructure. Similar result is also observed in the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics, as shown in Fig. S2 and S3,† respectively. This uniform dispersion suggests that the dopants are well-incorporated into the TiO2 matrix at this doping level. Conversely, the (Sc/Ta)2.0 ceramic (Fig. 4) reveals notable segregation of Sc-rich phase particles, particularly evidenced by the scattered blue regions in the Sc mapping image, indicating the formation of secondary phases at higher doping concentrations. This observation is consistent with the increasing Sc3+ content detected by the EDS spectra, which show a progressive rise in the Sc percentage as the Sc3+ doping concentration increases. These findings suggest that the solubility limit of Sc3+ in the TiO2 matrix is exceeded in the (Sc/Ta)2.0 ceramic, leading to the observed phase segregation.
Fig. 5 presents the Raman spectra of ScTa-TO ceramics Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, and 2.0 compared to pure TiO2. The spectra reveal the characteristic Eg and A1g modes of rutile TiO2, which correspond to oxygen vibrations within the lattice.24,36–38 A noticeable shift in both Raman modes occurs as the Sc3+ concentration increases, indicating the impact of Sc3+ substitution on the TiO2 structure. The Eg mode is detected at 446.4 cm−1 for both the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics, and it downshifts slightly to 445.4 cm−1 and 445.1 cm−1 for the (Sc/Ta)1.0 and (Sc/Ta)2.0 ceramics, respectively. This consistent downshift of the Eg mode is attributed to the formation of  , which tend to slightly increase as the Sc3+ concentration rises. Sc3+ substitution into the TiO2 lattice requires charge compensation, typically achieved by generating
, which tend to slightly increase as the Sc3+ concentration rises. Sc3+ substitution into the TiO2 lattice requires charge compensation, typically achieved by generating  .38 The observed shift in the Eg mode of ScTa-TO ceramics compared to pure TiO2 aligns well with previously reported studies.9 For example, Parker et al. observed a shift in the Eg mode from 447 to 443 cm−1 as the [O]/[Ti] decreased from 2.0 to 1.99.39 The presence of
.38 The observed shift in the Eg mode of ScTa-TO ceramics compared to pure TiO2 aligns well with previously reported studies.9 For example, Parker et al. observed a shift in the Eg mode from 447 to 443 cm−1 as the [O]/[Ti] decreased from 2.0 to 1.99.39 The presence of  due to Sc3+ doping ions can be explained by the following charge compensation reaction9,15
due to Sc3+ doping ions can be explained by the following charge compensation reaction9,15
 | (1) |
The shift in the Eg peak position corroborates the increase in  concentration, as predicted by eqn (1). However, it should be noted that a Sc-rich second phase was observed in the (Sc/Ta)2.0 ceramic (Fig. 4). This suggests that the solubility limit of Sc3+ in the ScTa-TO ceramics is slightly higher than 2.5%. Beyond this point, additional Sc3+ substitution may not be observed, and no further creation of
concentration, as predicted by eqn (1). However, it should be noted that a Sc-rich second phase was observed in the (Sc/Ta)2.0 ceramic (Fig. 4). This suggests that the solubility limit of Sc3+ in the ScTa-TO ceramics is slightly higher than 2.5%. Beyond this point, additional Sc3+ substitution may not be observed, and no further creation of 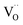 occurs. This may explain the relatively small difference in the Eg peak position between the (Sc/Ta)1.0 and (Sc/Ta)2.0 ceramics.
occurs. This may explain the relatively small difference in the Eg peak position between the (Sc/Ta)1.0 and (Sc/Ta)2.0 ceramics.
The A1g mode also shows a gradual downshift, from 611.8 cm−1 in the (Sc/Ta)0.4 ceramic to 610.9 cm−1 for the (Sc/Ta)1.0 ceramic, and finally to 609.9 cm−1 in the (Sc/Ta)2.0 ceramic. This shift in the A1g mode can be attributed to O–Ti–O bond vibrations, which may be altered by local distortions in the lattice caused by the substitution of Ti4+ with Sc3+ and Ta5+. While the A1g mode is less sensitive to  than the Eg mode, the consistent downshift indicates that the Ta5+ and Sc3+ substitution modifies the bonding environment within the lattice. The observed shifts in both the Eg and A1g modes suggest that increasing Sc3+ concentration results in the introduction of more
than the Eg mode, the consistent downshift indicates that the Ta5+ and Sc3+ substitution modifies the bonding environment within the lattice. The observed shifts in both the Eg and A1g modes suggest that increasing Sc3+ concentration results in the introduction of more  concentrations, confirming the presence of an oxygen-deficient environment. These vacancies are likely responsible for the enlarged grain size observed in the (Sc/Ta)2.0 ceramic, as oxygen ions and
concentrations, confirming the presence of an oxygen-deficient environment. These vacancies are likely responsible for the enlarged grain size observed in the (Sc/Ta)2.0 ceramic, as oxygen ions and  diffusion contributes to grain growth.40
diffusion contributes to grain growth.40
Fig. 6 presents the frequency dependence of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 25 °C for the ScTa-TO ceramics with different Sc3+/Ta5+ ratios. The ε′ and tan
δ at 25 °C for the ScTa-TO ceramics with different Sc3+/Ta5+ ratios. The ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values exhibit distinct trends across the frequency range (40–106 Hz), depending on the Sc3+ concentration or Sc3+/Ta5+ ratios. As shown in Fig. 6a, the ceramics with Sc3+/Ta5+ ratios of 0.4, 0.8, and 1.0 exhibit exceptionally high ε′ values (>104), consistent with previous studies on various co-doped TiO2 systems. In contrast, the (Sc/Ta)1.2, (Sc/Ta)1.6, and (Sc/Ta)2.0 ceramics do not display a giant dielectric response, despite containing the same Ta5+ concentration as the other compositions. Notably, its ε′ value is on the order of 102, comparable to that of pure rutile TiO2,7 which is primarily attributed to ionic polarization. Furthermore, the ε′ value of the (Sc/Ta)1.0 ceramic is not the highest among the compositions. If there were no interaction between Sc3+ and Ta5+, ε′ should remain unchanged across all ceramics, as Ta5+—the primary source of free electrons—is present at the same concentration in each sample. Table 2 summarizes the ε′ and tan
δ values exhibit distinct trends across the frequency range (40–106 Hz), depending on the Sc3+ concentration or Sc3+/Ta5+ ratios. As shown in Fig. 6a, the ceramics with Sc3+/Ta5+ ratios of 0.4, 0.8, and 1.0 exhibit exceptionally high ε′ values (>104), consistent with previous studies on various co-doped TiO2 systems. In contrast, the (Sc/Ta)1.2, (Sc/Ta)1.6, and (Sc/Ta)2.0 ceramics do not display a giant dielectric response, despite containing the same Ta5+ concentration as the other compositions. Notably, its ε′ value is on the order of 102, comparable to that of pure rutile TiO2,7 which is primarily attributed to ionic polarization. Furthermore, the ε′ value of the (Sc/Ta)1.0 ceramic is not the highest among the compositions. If there were no interaction between Sc3+ and Ta5+, ε′ should remain unchanged across all ceramics, as Ta5+—the primary source of free electrons—is present at the same concentration in each sample. Table 2 summarizes the ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values at 25 °C and 1 kHz for all ceramics, where a clear trend is observed: ε′ decreases with increasing Sc3+/Ta5+ ratio, despite the consistent Ta5+ doping level. This behavior is similar to that reported for AlNb-TO ceramics.28 Based on the IBLC model,3 the observed reduction in ε′ may be attributed to an increase in grain boundary thickness or a decrease in free charge carriers within semiconducting grains. Although grain boundary thickness measurements require TEM analysis, it is evident that the decrease in ε′ correlates with the increasing Sc3+/Ta5+ ratio. Theoretically, ε′ should depend solely on the Ta5+ concentration, but these results suggest that Sc3+ also plays a role, likely by influencing the availability of free charge carriers. Although the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics exhibit higher ε′ values than the (Sc/Ta)1.0 ceramic, it is premature to conclude that they possess optimized dielectric properties.
δ values at 25 °C and 1 kHz for all ceramics, where a clear trend is observed: ε′ decreases with increasing Sc3+/Ta5+ ratio, despite the consistent Ta5+ doping level. This behavior is similar to that reported for AlNb-TO ceramics.28 Based on the IBLC model,3 the observed reduction in ε′ may be attributed to an increase in grain boundary thickness or a decrease in free charge carriers within semiconducting grains. Although grain boundary thickness measurements require TEM analysis, it is evident that the decrease in ε′ correlates with the increasing Sc3+/Ta5+ ratio. Theoretically, ε′ should depend solely on the Ta5+ concentration, but these results suggest that Sc3+ also plays a role, likely by influencing the availability of free charge carriers. Although the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics exhibit higher ε′ values than the (Sc/Ta)1.0 ceramic, it is premature to conclude that they possess optimized dielectric properties.
 | ||
Fig. 6 Frequency dependence of (a) ε′ and (b) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 25 °C for ScTa-TO ceramics with Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, 1.2, 1.6, and 2.0. δ at 25 °C for ScTa-TO ceramics with Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, 1.2, 1.6, and 2.0. | ||
| Sample | Dielectric properties | Temperature range of Δε′(T)/ε′25 ≤±15% | Ea (eV) | |
|---|---|---|---|---|
| ε′ (25 °C) | Tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (25 °C) δ (25 °C) |
|||
| (Sc/Ta)0.4 | 5.94 × 104 | 0.024 | −60–200 °C | ∼0.831 |
| (Sc/Ta)0.8 | 4.81 × 104 | 0.043 | −60–200 °C | ∼1.214 |
| (Sc/Ta)1.0 | 2.05 × 104 | 0.070 | −40–190 °C | ∼1.246 |
| (Sc/Ta)1.2 | 1.46 × 102 | 0.060 | — | — |
| (Sc/Ta)1.6 | 1.92 × 102 | 0.058 | — | — |
| (Sc/Ta)2.0 | 1.55 × 102 | 0.040 | — | — |
Fig. 6b shows the variation of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ with frequency at 25 °C for the ScTa-TO ceramics. At low frequencies (<104 Hz), tan
δ with frequency at 25 °C for the ScTa-TO ceramics. At low frequencies (<104 Hz), tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ remains relatively low for all compositions. As summarized in Table 2, the (Sc/Ta)1.0 ceramic exhibits the highest tan
δ remains relatively low for all compositions. As summarized in Table 2, the (Sc/Ta)1.0 ceramic exhibits the highest tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, further indicating that the Sc3+/Ta5+ ratio of 1.0 is not optimal. This trend is consistent with our previous findings for the same composition sintered at 1500 °C with Au-sputtered electrodes, where the dielectric properties were also not optimized despite using a 1
δ, further indicating that the Sc3+/Ta5+ ratio of 1.0 is not optimal. This trend is consistent with our previous findings for the same composition sintered at 1500 °C with Au-sputtered electrodes, where the dielectric properties were also not optimized despite using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio.33 The sharp increase in tan
1 ratio.33 The sharp increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at higher frequencies suggests the presence of a dielectric relaxation mechanism,3,14,24 similar to those observed in other giant dielectric materials such as CaCu3Ti4O12 (CCTO),41 CuO,6 and NiO.3 The relatively low tan
δ at higher frequencies suggests the presence of a dielectric relaxation mechanism,3,14,24 similar to those observed in other giant dielectric materials such as CaCu3Ti4O12 (CCTO),41 CuO,6 and NiO.3 The relatively low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ observed in the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics indicate their potential suitability for high-performance capacitor applications.
δ observed in the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics indicate their potential suitability for high-performance capacitor applications.
Beyond achieving a high ε′ and low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, the temperature dependence of ε′ is a crucial factor in determining the suitability of dielectric materials for ceramic applications.42 To assess thermal stability, ε′ was thoroughly investigated for the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics, all of which exhibit giant ε′ values exceeding 104. As shown in Fig. 7, ε′ remains exceptionally stable over a broad temperature range from −180 to 210 °C at 1 kHz. The inset of Fig. 7 reveals that tan
δ, the temperature dependence of ε′ is a crucial factor in determining the suitability of dielectric materials for ceramic applications.42 To assess thermal stability, ε′ was thoroughly investigated for the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics, all of which exhibit giant ε′ values exceeding 104. As shown in Fig. 7, ε′ remains exceptionally stable over a broad temperature range from −180 to 210 °C at 1 kHz. The inset of Fig. 7 reveals that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ remains below 0.1 between −60 and 200 °C, with the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics exhibiting lower tan
δ remains below 0.1 between −60 and 200 °C, with the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics exhibiting lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values than (Sc/Ta)1.0 within this range.
δ values than (Sc/Ta)1.0 within this range.
 | ||
Fig. 7 Temperature dependence of ε′ at 1 kHz for ScTa-TO ceramics with Sc3+/Ta5+ ratios of 0.4, 0.8, and 1.0; inset shows tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 1 kHz. δ at 1 kHz. | ||
To further quantify the thermal stability of ε′, the temperature coefficient Δε′(T)/ε′25 (where ε′25 represents ε′ at 25 °C) was calculated for all compositions. As illustrated in Fig. 8, the (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics exhibit excellent stability, with fluctuations within ±15% over the entire range of −60 to 200 °C. In contrast, the (Sc/Ta)1.0 ceramic shows more pronounced variations, indicating a less stable dielectric response at higher Sc3+ doping levels. The remarkable thermal stability observed in (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics is particularly notable when compared to other giant dielectric materials, such as CCTO, CuO, NiO-based oxides, La2−xSrxNiO4, and AFe1/2B1/2O3 (B = Nb and Ta) compounds.3,6,41,43,44 These comparisons highlight the superior temperature performance of (Sc/Ta)0.4 and (Sc/Ta)0.8, making them promising candidates for applications requiring highly stable dielectric properties in fluctuating thermal environments. This stability likely arises from a combination of intrinsic factors, such as charge compensation between Sc3+ and Ta5+ ions, and extrinsic effects related to grain boundary characteristics.
 | ||
| Fig. 8 Temperature coefficient of ε′ at 1 kHz for ScTa-TO ceramics with Sc3+/Ta5+ ratios of 0.4, 0.8, and 1.0. | ||
The (Sc/Ta)0.4 and (Sc/Ta)0.8 ceramics likely exhibit the most stable dielectric behavior, characterized by low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and consistent ε′ values across a wide temperature range. This superior dielectric performance is attributed to a well-balanced interaction between interfacial polarization and the electrical properties of both grains and grain boundaries. These findings emphasize the critical role of Sc3+/Ta5+ ratio in tuning the dielectric properties of ScTa-TO ceramics. Interestingly, the optimal dielectric performance was not observed in the (Sc/Ta)1.0 ceramic, where the Sc3+/Ta5+ ratio is 1.0, a condition commonly reported in other co-doped systems such as InTa-TO and InNb-TO.8,32 This suggests that the optimal dielectric properties may not necessarily be achieved at a +3/+5 ion ratio of 1.0, a phenomenon that remains underexplored in existing literature. In contrast, studies on AlxNb0.03Ti0.97−xO2 ceramics indicate that the best dielectric properties were still obtained at x = 0.03 (Al3+/Nb5+ ratio = 1.0).28
δ and consistent ε′ values across a wide temperature range. This superior dielectric performance is attributed to a well-balanced interaction between interfacial polarization and the electrical properties of both grains and grain boundaries. These findings emphasize the critical role of Sc3+/Ta5+ ratio in tuning the dielectric properties of ScTa-TO ceramics. Interestingly, the optimal dielectric performance was not observed in the (Sc/Ta)1.0 ceramic, where the Sc3+/Ta5+ ratio is 1.0, a condition commonly reported in other co-doped systems such as InTa-TO and InNb-TO.8,32 This suggests that the optimal dielectric properties may not necessarily be achieved at a +3/+5 ion ratio of 1.0, a phenomenon that remains underexplored in existing literature. In contrast, studies on AlxNb0.03Ti0.97−xO2 ceramics indicate that the best dielectric properties were still obtained at x = 0.03 (Al3+/Nb5+ ratio = 1.0).28
Typically, the enhancement of dielectric properties in TiO2 ceramics is attributed to the incorporation of Ta5+ into the rutile TiO2 matrix, which generates free electrons through the following reactions:9,16,18,32
 | (2) |
| Ti4+ + e → Ti3+ | (3) |
The introduction of Ta5+ results in a high ε′ due to the generation of free electrons; however, it also leads to an increased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ.14 The observed reduction in tan
δ.14 The observed reduction in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is attributed to the substitution of Sc3+ ions. Based on eqn (2) and (3), the dielectric response of all ScTa-TO ceramics should, in theory, remain similar, as ε′ is primarily governed by the donor (Ta5+) concentration, which is consistent across all samples. However, experimental results indicate that ε′ decreases with increasing Sc3+ concentration. This decline in dielectric response cannot be attributed to grain size variations, as the average grain size increases with higher Sc3+ doping levels. Instead, the observed reduction in ε′ is likely associated with extrinsic factors, particularly the electrical properties of grains and grain boundaries, which will be discussed in subsequent sections.
δ is attributed to the substitution of Sc3+ ions. Based on eqn (2) and (3), the dielectric response of all ScTa-TO ceramics should, in theory, remain similar, as ε′ is primarily governed by the donor (Ta5+) concentration, which is consistent across all samples. However, experimental results indicate that ε′ decreases with increasing Sc3+ concentration. This decline in dielectric response cannot be attributed to grain size variations, as the average grain size increases with higher Sc3+ doping levels. Instead, the observed reduction in ε′ is likely associated with extrinsic factors, particularly the electrical properties of grains and grain boundaries, which will be discussed in subsequent sections.
To further elucidate the origin of the giant dielectric response in the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics and to clarify the influence of the Sc3+/Ta5+ ratio on dielectric properties, impedance spectroscopy was used to investigate the electrical characteristics of grains and grain boundaries. As shown in Fig. 9a, all three compositions exhibit a nonzero intercept on the Z′ axis at 25 °C, confirming the presence of semiconducting grains,5,9,14 which is due to Ta5+ doping (as described in eqn (2) and (3)) and insulating grain boundaries formed by Sc3+ doping. In contrast, the (Sc/Ta)2.0 ceramic shows no intercept on the Z′ axis, indicating the absence of semiconducting grains and, consequently, the lack of an IBLC structure—which is consistent with its low ε′. In conventional BaTiO3-based ceramics, the formation of IBLC structures typically requires complex processing procedures, including high-temperature sintering under carefully controlled reducing atmospheres, followed by partial reoxidation to form thin insulating grain boundary layers.45 In contrast, the ScTa-TO ceramics examined in this study successfully develop a stable IBLC structure through a much simpler route—sintering in ambient air. This approach is similar to that used for CCTO-based materials but offers better control over tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. The formation of the IBLC structure in ScTa-TO ceramics is attributed to the deliberate tuning of acceptor and donor dopant concentrations, eliminating the need for strict atmosphere control during processing.
δ. The formation of the IBLC structure in ScTa-TO ceramics is attributed to the deliberate tuning of acceptor and donor dopant concentrations, eliminating the need for strict atmosphere control during processing.
Fig. S4† and its inset provide additional evidence supporting the IBLC effect. At 25 °C, the insulating grain boundary arc is not fully resolved, and only a partial semicircular arc is visible in all ceramics. However, the presence of these partial arcs strongly suggests that these ceramics are electrically heterogeneous, consisting of semiconducting grains and insulating grain boundaries. Furthermore, the nonzero intercept on the Z′ axis increases with the Sc3+/Ta5+ ratio, indicating a corresponding increase in grain resistance (Rg).5 This trend culminates in the (Sc/Ta)2.0 ceramic, where no semiconducting grains are present, leading to a complete suppression of the IBLC effect. The increase in Rg with higher Sc3+ content can be attributed to self-charge compensation between Sc3+ and Ta5+, following the reaction:
 | (4) |
The absence of the IBLC effect in (Sc/Ta)2.0 suggests that excessive Sc3+ doping promotes self-charge compensation, eliminating the formation of semiconducting grains due to the absence of free electrons (as described in eqn (2) and (3)), thereby significantly reducing the ε′. This supports the hypothesis that an optimal balance between donor (Ta5+) and acceptor (Sc3+) concentrations is essential for maintaining the IBLC structure and maximizing the dielectric response. Even at the highest measured temperature (i.e., 250 °C), none of the (Sc/Ta)0.4, (Sc/Ta)0.8, or (Sc/Ta)1.0 ceramics exhibit a fully developed semicircle, as shown in the inset of Fig. 9b. However, the persistence of partial semicircular arcs at higher temperatures further confirms that their giant dielectric response originates from interfacial polarization at the boundaries between semiconducting grains and insulating grain layers, consistent with the IBLC mechanism.3,5,9,41 The inability to fully resolve the grain boundary response at elevated temperatures suggests that the insulating grain boundaries retain high resistance (Rgb). Furthermore, a strong correlation between the ε′ value and the electrical properties of the semiconducting grains can be established. The observed increase in Rg directly indicates a reduction in free charge concentration within the semiconducting grains. Under an applied electric field, as the free charge concentration decreases, the accumulated charges at the grain boundaries are reduced, weakening interfacial polarization and consequently lowering the ε′ value as the Sc3+/Ta5+ ratio increases. This behavior closely resembles that observed in Li and Ti co-doped NiO, where the dielectric response declines with decreasing free charge concentration in the semiconducting grains due to the reduced Li+ doping levels.3
To further investigate the influence of the Sc3+/Ta5+ ratio on the electrical properties of semiconducting grains, XPS was employed to analyze the valence states of Ti in the ScTa-TO ceramics. As shown in Fig. 10, the Ti 2p spectra of (Sc/Ta)0.4, (Sc/Ta)1.0, and (Sc/Ta)2.0 exhibit characteristic Ti 2p3/2 and Ti 2p1/2 peaks at 458.4 eV and 464.2 eV, respectively, which are indicative of Ti4+.8,16,22 Spectral deconvolution, performed using a combination of Gaussian and Lorentzian functions, revealed the presence of Ti3+ at ∼457.3 eV8, 22 in the (Sc/Ta)0.4 and (Sc/Ta)1.0 ceramics. In contrast, no Ti3+ signal was detected in the (Sc/Ta)2.0 ceramic, confirming that only Ti4+ is present in this composition. Quantitative analysis further showed that the Ti3+/Ti4+ ratios in (Sc/Ta)0.4 and (Sc/Ta)1.0 were 2.34% and 1.78%, respectively, indicating a partially reduced Ti state. This reduction is associated with free-electron generation, which facilitates the formation of semiconducting grains. These findings correlate with the Rg trends observed in Fig. 9a, as the Ti3+/Ti4+ ratio decreases, Rg increases, suggesting a lower concentration of charge carriers. Notably, the (Sc/Ta)2.0 ceramic exhibits neither Ti3+ nor a nonzero intercept in the impedance spectrum, confirming the absence of semiconducting grains. The dominance of Ti4+ in the (Sc/Ta)2.0 ceramic supports the hypothesis that excessive Sc3+ doping promotes self-charge compensation, effectively suppressing free-electron generation and eliminating the IBLC effect. The XPS analysis provides direct evidence that variations in the Sc3+/Ta5+ ratio influence the reduction state of Ti, which in turn governs the formation of semiconducting grains. A higher concentration of Ti3+ promotes free-electron availability, leading to lower Rg, which enhances interfacial polarization and giant dielectric behavior.
 | ||
| Fig. 10 XPS spectra of Ti 2p for ScTa-TO ceramics with Sc3+/Ta5+ ratios of (a) 0.4, (b) 1.0, and (c) 2.0. | ||
To further investigate the influence of the Sc3+/Ta5+ ratio on the electrical properties of insulating grain boundaries, impedance spectroscopy was used to analyze their Rgb values. Although a fully developed semicircular arc, which represents the electrical response of insulating grain boundaries,5 was not observed even at the highest measured temperature (250 °C), the onset of curvature was detected at 210 °C. This indicates the initial formation of a discernible grain boundary response at elevated temperatures. To estimate Rgb, the impedance data were fitted using the following equation4
 | (5) |
 ), Cgb represents the grain boundary capacitance, and ω is the angular frequency of the applied electric field. As shown in Fig. 11a, the Z* plots of the (Sc/Ta)0.8 ceramic in the 210–250 °C range were well fitted using eqn (5). Similar fitting was successfully applied to the (Sc/Ta)0.4 and (Sc/Ta)1.0 ceramics, enabling the determination of Rgb values at different temperatures. The temperature dependence of Rgb was further analyzed using the Arrhenius equation:
), Cgb represents the grain boundary capacitance, and ω is the angular frequency of the applied electric field. As shown in Fig. 11a, the Z* plots of the (Sc/Ta)0.8 ceramic in the 210–250 °C range were well fitted using eqn (5). Similar fitting was successfully applied to the (Sc/Ta)0.4 and (Sc/Ta)1.0 ceramics, enabling the determination of Rgb values at different temperatures. The temperature dependence of Rgb was further analyzed using the Arrhenius equation:
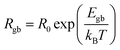 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ observed in these ceramics can be attributed to the high electrostatic potential barrier (Schottky barrier) at the grain boundaries, which plays a crucial role in maintaining excellent dielectric stability.
δ observed in these ceramics can be attributed to the high electrostatic potential barrier (Schottky barrier) at the grain boundaries, which plays a crucial role in maintaining excellent dielectric stability.
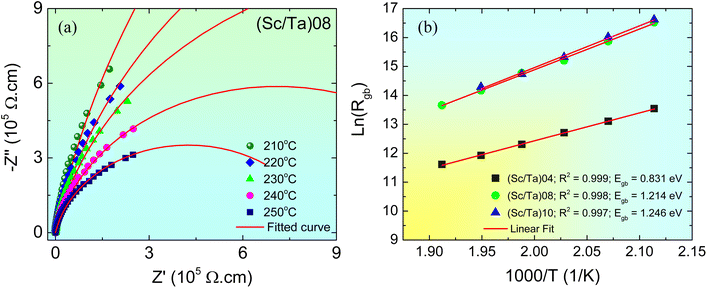 | ||
| Fig. 11 (a) Z* plots of (Sc/Ta)0.8 ceramic at different temperatures from 210 to 250 °C fitted by eqn (5). (b) Arrhenius plots of temperature dependence of Rgb for (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics. | ||
The J–E characteristics of the ScTa-TO ceramics with different Sc3+/Ta5+ ratios are displayed in Fig. 12, further confirming the existence of Schottky barriers at the grain boundaries in the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics. These ceramics exhibited a distinct nonlinear J–E response, while the (Sc/Ta)2.0 ceramic displayed purely ohmic behavior, consistent with the absence of semiconducting grains observed in impedance spectroscopy (Fig. 9). For the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics, the nonlinearity in J–E curves with α values in the range of 1.5 to 2.0 arises from the potential barrier at the grain boundaries, supporting the IBLC model as the dominant mechanism governing the dielectric properties of these materials. It is worth noting that the α values observed in this study are consistent with those of surface-polished samples reported in our previous work on 2.5% (Sc1/2Ta1/2) co-doped TiO2.9 In that study, α dropped significantly from ∼37 (as-fired) to ∼2.6 after polishing, confirming that the SBLC effect was effectively removed. This validates that the dielectric behavior observed here is primarily governed by the IBLC mechanism.
The nonzero intercepts in the impedance spectra and the observed nonlinear J–E behavior collectively demonstrate that these compositions possess electrically heterogeneous structures, consisting of semiconducting grains and insulating grain boundaries. In contrast, the (Sc/Ta)2.0 ceramic lacks a nonlinear J–E response due to absence of semiconducting grains in this sample, which suggests that excessive Sc3+ doping promotes self-charge compensation, reducing the availability of free electrons and preventing the formation of an IBLC structure. Consequently, the (Sc/Ta)2.0 ceramic does not exhibit giant dielectric properties, further confirming that the interfacial polarization effect at the grain boundaries is critical to the observed high ε′ in the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics. The Eb values of the (Sc/Ta)0.4, (Sc/Ta)0.8, and (Sc/Ta)1.0 ceramics were determined to be 66, 117, and 214 V cm−1, respectively. These values correlate well with the Egb and Rgb observed in the Arrhenius plots, Fig. 11b. Although these relatively low breakdown fields may limit their applicability in high-voltage devices, the combination of high ε′, low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, and excellent temperature stability makes these ceramics promising candidates for embedded capacitors and low-power electronic components. Moreover, the chemical stability of the TiO2 matrix and the thermal robustness of the Sc3+ and Ta5+ dopants suggest good long-term reliability. The ability to achieve IBLC structures through air sintering further enhances their compatibility with scalable and cost-effective fabrication processes. However, due to the extrinsic nature of the dielectric response, which relies on grain boundary effects, these materials may not be suitable for applications requiring thin films, multilayer architectures, or dielectric composites, where the formation of IBLC structures is typically constrained.
δ, and excellent temperature stability makes these ceramics promising candidates for embedded capacitors and low-power electronic components. Moreover, the chemical stability of the TiO2 matrix and the thermal robustness of the Sc3+ and Ta5+ dopants suggest good long-term reliability. The ability to achieve IBLC structures through air sintering further enhances their compatibility with scalable and cost-effective fabrication processes. However, due to the extrinsic nature of the dielectric response, which relies on grain boundary effects, these materials may not be suitable for applications requiring thin films, multilayer architectures, or dielectric composites, where the formation of IBLC structures is typically constrained.
Taken together, the combination of surface polishing to suppress SBLC contributions, the observed electrical heterogeneity from impedance analysis, the nonlinear J–E characteristics associated with Schottky-type grain boundary barriers, and the absence of EPDD-related defects strongly confirms that the dielectric response in ScTa-TO ceramics9 is primarily governed by the IBLC mechanism. It should be noted that no secondary phases or abnormal structural distortions were detected in the XRD and Raman spectra, suggesting that extrinsic factors such as impurities or local structural defects have negligible influence on the dielectric response in these ceramics.
By challenging the conventional assumption that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acceptor/donor ratio is necessary for optimal performance in co-doped TiO2 ceramics, this work demonstrates a new strategy for achieving enhanced dielectric properties—characterized by high ε′, low tan
1 acceptor/donor ratio is necessary for optimal performance in co-doped TiO2 ceramics, this work demonstrates a new strategy for achieving enhanced dielectric properties—characterized by high ε′, low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, and excellent temperature stability. Unlike our previous study, which focused primarily on humidity sensing performance and observed only moderate dielectric values,33 the present work systematically tunes the Sc3+/Ta5+ ratio and establishes a clear relationship between doping ratio, microstructure, and dielectric response. These insights provide a more comprehensive understanding of defect control and interfacial polarization mechanisms in IBLC-dominated systems. Beyond its fundamental contributions, this study offers a broadly applicable framework for designing high-permittivity ceramics, with implications for capacitors, energy storage devices, and advanced dielectric materials through precise control of defect chemistry and microstructural engineering. This approach is particularly well suited for co-doped TiO2 systems where the dielectric response is governed primarily by extrinsic mechanisms, such as interfacial polarization via IBLC, and where EPDD-related effects are negligible or absent. In such systems, tuning the acceptor/donor ratio provides a powerful strategy to enhance dielectric properties without relying on complex defect dipole formation.
δ, and excellent temperature stability. Unlike our previous study, which focused primarily on humidity sensing performance and observed only moderate dielectric values,33 the present work systematically tunes the Sc3+/Ta5+ ratio and establishes a clear relationship between doping ratio, microstructure, and dielectric response. These insights provide a more comprehensive understanding of defect control and interfacial polarization mechanisms in IBLC-dominated systems. Beyond its fundamental contributions, this study offers a broadly applicable framework for designing high-permittivity ceramics, with implications for capacitors, energy storage devices, and advanced dielectric materials through precise control of defect chemistry and microstructural engineering. This approach is particularly well suited for co-doped TiO2 systems where the dielectric response is governed primarily by extrinsic mechanisms, such as interfacial polarization via IBLC, and where EPDD-related effects are negligible or absent. In such systems, tuning the acceptor/donor ratio provides a powerful strategy to enhance dielectric properties without relying on complex defect dipole formation.
4. Conclusions
We investigated how the acceptor/donor doping ratio influenced the microstructure and giant dielectric behavior of co-substituted TiO2 ceramics. Specifically, we synthesized ScxTa0.025Ti0.975−xO2 ceramics, with Sc3+/Ta5+ ratios of 0.4, 0.8, 1.0, and 2.0, via SSR method. All samples exhibited a dense rutile TiO2 phase. Raman spectroscopy revealed that increasing the Sc3+/Ta5+ ratio led to the formation of , which in turn resulted in larger average grain sizes. As this ratio increased, the ε′ dropped markedly, and no giant dielectric response was observed for ratios above 1.0. By contrast, ratios of 0.4 and 0.8 yielded high ε′ values of 5.9 × 104 and 4.8 × 104, respectively, along with low tan
, which in turn resulted in larger average grain sizes. As this ratio increased, the ε′ dropped markedly, and no giant dielectric response was observed for ratios above 1.0. By contrast, ratios of 0.4 and 0.8 yielded high ε′ values of 5.9 × 104 and 4.8 × 104, respectively, along with low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values of 0.024 and 0.043 at 1 kHz and 25 °C. These ceramics also retained stable dielectric characteristics over a broad temperature range (−60 to 210 °C), with variations less than ±15%, thereby satisfying the X9R capacitor standard. Impedance spectroscopy and nonlinear electrical measurements confirmed that the enhanced dielectric performance was primarily governed by interfacial polarization between semiconducting grains and insulating grain boundaries, supported by XPS analysis. Notably, the optimal dielectric response commonly associated with an acceptor/donor ratio of 1.0 in other co-doped systems was not observed in this work, emphasizing the importance of tailoring the doping ratio based on the dominant mechanism involved. These findings demonstrate that the ideal acceptor/donor ratio is not universal across all co-doped TiO2 ceramics but is instead dependent on the primary dielectric mechanism. While a 1
δ values of 0.024 and 0.043 at 1 kHz and 25 °C. These ceramics also retained stable dielectric characteristics over a broad temperature range (−60 to 210 °C), with variations less than ±15%, thereby satisfying the X9R capacitor standard. Impedance spectroscopy and nonlinear electrical measurements confirmed that the enhanced dielectric performance was primarily governed by interfacial polarization between semiconducting grains and insulating grain boundaries, supported by XPS analysis. Notably, the optimal dielectric response commonly associated with an acceptor/donor ratio of 1.0 in other co-doped systems was not observed in this work, emphasizing the importance of tailoring the doping ratio based on the dominant mechanism involved. These findings demonstrate that the ideal acceptor/donor ratio is not universal across all co-doped TiO2 ceramics but is instead dependent on the primary dielectric mechanism. While a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio may be essential for systems driven by EPDD, our results show that lower ratios can be more effective in IBLC-dominated systems by reducing self-compensation and maintaining semiconducting grain behavior. This approach offers a useful framework for optimizing extrinsically governed co-doped TiO2 ceramics.
1 ratio may be essential for systems driven by EPDD, our results show that lower ratios can be more effective in IBLC-dominated systems by reducing self-compensation and maintaining semiconducting grain behavior. This approach offers a useful framework for optimizing extrinsically governed co-doped TiO2 ceramics.
Data availability
All data are included in the manuscript. The data supporting this article have been included as part of the ESI.†Author contributions
Wattana Tuichai; conceptualization, methodology, validation, data curation, formal analysis, investigation, visualization. Jurimart Wongsricha; methodology, investigation. Nutthakritta Phromviyo; methodology, investigation. Bundit Putasaeng; methodology, resources. Supamas Danwittayakul; conceptualization, resources, funding acquisition. Pornjuk Srepusharawoot; software, formal analysis. Prasit Thongbai; conceptualization, methodology, validation, formal analysis, investigation, resources, writing – original draft, writing – review & editing, visualization, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Fundamental Fund of Khon Kaen University and the National Science, Research, and Innovation Fund (NSRF). Additional support was provided by the Research of Khon Kaen University. W. Tuichai would like to thank the Thailand Graduate Institute of Science and Technology (TGIST) for his PhD scholarship.References
- L. Yang, H. Wang, F. Zhang, Y. Yang, S. Qu, D. Leng and X. Ma, Nano Energy, 2023, 114, 108609 CrossRef CAS.
- Y. Wang, W. Jie, C. Yang, X. Wei and J. Hao, Adv. Funct. Mater., 2019, 29, 1808118 CrossRef.
- J. Wu, C.-W. Nan, Y. Lin and Y. Deng, Phys. Rev. Lett., 2002, 89, 217601 CrossRef.
- J. Liu, C.-G. Duan, W.-G. Yin, W. Mei, R. Smith and J. Hardy, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 70, 144106 CrossRef.
- T. Adams, D. Sinclair and A. West, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 094124 CrossRef.
- S. Sarkar, P. K. Jana, B. K. Chaudhuri and H. Sakata, Appl. Phys. Lett., 2006, 89, 212905 CrossRef.
- C. C. Homes and T. Vogt, Nat. Mater., 2013, 12, 782–783 CrossRef CAS.
- W. Hu, Y. Liu, R. L. Withers, T. J. Frankcombe, L. Norén, A. Snashall, M. Kitchin, P. Smith, B. Gong, H. Chen, J. Schiemer, F. Brink and J. Wong-Leung, Nat. Mater., 2013, 12, 821–826 CrossRef CAS.
- W. Tuichai, P. Srepusharawoot, S. Danwittayakul and P. Thongbai, Sci. Rep., 2024, 14, 2593 CrossRef CAS.
- W. C. Ribeiro, E. Joanni, R. Savu and P. R. Bueno, Solid State Commun., 2011, 151, 173–176 CrossRef CAS.
- W. Dong, W. Hu, A. Berlie, K. Lau, H. Chen, R. L. Withers and Y. Liu, ACS Appl. Mater. Interfaces, 2015, 7, 25321–25325 CrossRef CAS.
- P. Lunkenheimer, R. Fichtl, S. Ebbinghaus and A. Loidl, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 70, 172102 CrossRef.
- M. Li, A. Feteira and D. C. Sinclair, J. Appl. Phys., 2009, 105, 114109 CrossRef.
- W. Tuichai, S. Danwittayakul, N. Chanlek and P. Thongbai, Mater. Res. Bull., 2019, 116, 137–142 CrossRef CAS.
- W. Tuichai, S. Danwittayakul, N. Chanlek, P. Thongbai and S. Maensiri, J. Alloys Compd., 2017, 703, 139–147 CrossRef CAS.
- W. Tuichai, N. Thongyong, S. Danwittayakul, N. Chanlek, P. Srepusharawoot, P. Thongbai and S. Maensiri, Mater. Des., 2017, 123, 15–23 CrossRef CAS.
- J. Li, F. Li, C. Li, G. Yang, Z. Xu and S. Zhang, Sci. Rep., 2015, 5, 8295 CrossRef CAS PubMed.
- N. Thongyong, K. Sreejivungsa, P. Kawee, N. Chanlek, M. Takesada and P. Thongbai, J. Alloys Compd., 2024, 989, 174341 CrossRef CAS.
- N. Thongyong, N. Chanlek, P. Srepusharawoot, M. Takesada, D. P. Cann and P. Thongbai, J. Eur. Ceram. Soc., 2022, 42, 4944–4952 CrossRef CAS.
- J. Fan, G. He, Z. Cao, Y. Cao, Z. Long and H. Zhanggui, J Materiomics, 2023, 9, 157–165 CrossRef.
- P. Qiao, Y. Zhang, J. Wang, Z. Peng, D. Wu, X. Chao, Z. Yang and P. Liang, Ceram. Int., 2024, 50, 2242–2248 CrossRef CAS.
- Y. Xue, Z. Wang, Y. Li, Z. Yi, X. Li and D. Wu, J. Mater. Sci.: Mater. Electron., 2023, 34, 864 CrossRef.
- J.-J. Ma, Y. Gao, Y. Chen and M.-H. Wang, J. Electron. Mater., 2023, 52, 3698–3705 CrossRef.
- J. Fan, Z. Long, H. Zhou, G. He and Z. Hu, J. Alloys Compd., 2022, 921, 166200 CrossRef.
- H. Zhang, X. Huang, X. Liao and D. Zhu, Mater. Sci. Semicond. Process., 2023, 163, 107568 CrossRef.
- T. Yang and J. Liang, J. Alloys Compd., 2022, 929, 167323 CrossRef.
- Y. Mingmuang, N. Chanlek and P. Thongbai, J Materiomics, 2022, 8, 1269–1277 CrossRef.
- Y. Song, X. Wang, X. Zhang, Y. Sui, Y. Zhang, Z. Liu, Z. Lv, Y. Wang, P. Xu and B. Song, J. Mater. Chem. C, 2016, 4, 6798–6805 RSC.
- L. Zhou, Z. Peng, M. Jiang, G. Yang, H. Liu, D. Wu, P. Liang, L. Wei, X. Chao and Z. Yang, Ceram. Int., 2024, 50, 3252–3259 CrossRef.
- L. Zhou, Z. Peng, J. Zhu, Q. Shi, P. Liang, L. Wei, D. Wu, X. Chao and Z. Yang, Mater. Chem. Phys., 2023, 295, 127072 CrossRef.
- Z. Yang, X. Wang, L. Zhang, H. Li, H. Zhang and D. Xu, Ceram. Int., 2024, 50(11), 18993–19001 CrossRef.
- W. Dong, W. Hu, T. J. Frankcombe, D. Chen, C. Zhou, Z. Fu, L. Candido, G. Hai, H. Chen, Y. Li, R. L. Withers and Y. Liu, J. Mater. Chem. A, 2017, 5, 5436–5441 RSC.
- K. Phuion, W. Tuichai, J. Wongsricha, K. Sreejivungsa, N. Thanamoon, N. Phromviyo, W. Jarernboon and P. Thongbai, J. Alloys Compd., 2025, 1010, 177639 CrossRef CAS.
- W. Hao, P. Xu, L. Sun and E. Cao, Ceram. Int., 2023, 49, 40650–40658 CrossRef CAS.
- A. J. Atanacio, M. A. Alim, T. Bak, M. Ionescu and J. Nowotny, J. Am. Ceram. Soc., 2017, 100, 419–428 CrossRef CAS.
- W. Hu, K. Lau, Y. Liu, R. L. Withers, H. Chen, L. Fu, B. Gong and W. Hutchison, Chem. Mater., 2015, 27, 4934–4942 CrossRef CAS.
- G. Liu, H. Fan, J. Xu, Z. Liu and Y. Zhao, RSC Adv., 2016, 6, 48708–48714 RSC.
- L. Wang, J. Li, X. Liu, M. Zhang, X. Li, S. Liu and X. Sun, Ceram. Int., 2023, 49, 32116–32126 CrossRef CAS.
- J. C. Parker and R. W. Siegel, Appl. Phys. Lett., 1990, 57, 943–945 CrossRef.
- M. N. Rahaman, Ceramic Processing and Sintering, M. Dekker, New York, 2nd edn, 2003 Search PubMed.
- L. M. Jesus, L. B. Barbosa, D. R. Ardila, R. S. Silva and J. C. M'Peko, Ceram. Int., 2023, 49, 25594–25601 CrossRef.
- M. Pan and C. A. Randall, IEEE Electr. Insul. Mag., 2010, 26, 44–50 Search PubMed.
- X. Q. Liu, G. Liu, P. P. Ma, G. J. Li, J. W. Wu and X. M. Chen, J. Electroceram., 2016, 37, 73–78 CrossRef CAS.
- M. Amara, J. Hellara, J. Laifi, F. Bourguiba, J. Dhahri, K. Khirouni and E. K. Hlil, J. Inorg. Organomet. Polym. Mater., 2024, 34, 664–679 CrossRef CAS.
- D. C. Sinclair, T. B. Adams, F. D. Morrison and A. R. West, Appl. Phys. Lett., 2002, 80, 2153 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra02034d |
| This journal is © The Royal Society of Chemistry 2025 |