Modeling the melting temperature of metallic nanocrystals: dependencies on size, dimensionality, and composition

Abstract

The melting temperature is an extremely important property in describing the stability of metallic nanocrystals and can be modulated by the size, dimensionality, and composition. In this study, a new model was developed to comprehend these effects on the melting temperature by considering the surface stress and the size-dependent surface energy. The developed model predicts a decrease in the melting temperature with decreasing size or dimensionality. Moreover, for nanoalloys with identical size and dimensionality, the model suggests that the melting temperature decreases as the component with lower surface energy increases. Importantly, our model's predictions are consistent with experimental and simulation data, validating its accuracy and universality.

---

Introduction

As a fundamental property in practical applications, the melting temperature T_m holds significant importance.^1–4 Some useful material properties are functions of the ratio of working temperature (T_w) to T_m.^5,6 Usually, for bulk materials, these functions become irrelevant due to the constant T_m(∞), where ∞ denotes the bulk. Nevertheless, as the size (D) of metallic nanocrystals (MNCs) decreases into the nanoscale range, their melting temperature T_m(D) also decreases due to the significant increase in surface-to-volume ratio (A/V).^7–9 Simultaneously, T_w/T_m(D) increases with decreasing D and associated functions start to come into play. Consequently, at equivalent T_w values, MNCs can exhibit superior properties compared to bulk materials, which is advantageous for practical applications.^10,11 Furthermore, the decrease in T_m(D) will be a critical factor contributing to failure of many MNCs that operate at elevated temperatures.¹² For efficient applications of MNCs, we should consider the trade-off between stability and properties to determine the optimal size at which both coexist. Additionally, certain properties of MNCs are directly or indirectly related to T_m(D).^13,14 Once we know how T_m(D) behaves, it can serve as a bridge towards determining those size-dependent properties. Therefore, investigating the melting behavior of MNCs is crucial for determining the optimal size as well as identifying other size-dependent properties.

In order to understand the melting behavior of MNCs, extensive research has been conducted in both experimental and simulation fields. For example, electron diffraction patterns were used to analyze the thermostability of Pb nanoparticles (NPs).¹⁵ Additionally, the molecular dynamics method was utilized to study the melting behaviors of Pb nanowires (NWs)¹⁶ and Cu_xNi_1−x nanoalloys (NAs),¹⁷ with x representing the composition. In summary, the aforementioned references suggest that T_m(x, D, d) can be customized by varying D, dimensionality (d) and x. To enhance our understanding of the melting behavior of MNCs and facilitate the design of nanodevices, it is imperative to comprehend the impact of these parameters.

Apart from experiments and simulations, theoretical studies are also effective in illustrating the melting mechanism. Many theoretical works have been conducted, such as Wautelet's Gibbs free energy model (FEM)¹⁸ and Nanda's Liquid-drop model (LDM).¹⁹ These two models share a common feature: T_m(D) is inversely proportional to D, which can be expressed as:

Although β is defined as a material constant, it has no explicit physical meaning and its value depends on the models employed. For instance, in the case of Pb, β can be 1.4 nm (ref. 18) in FEM or 1.8 nm (ref. 19) in LDM. In deriving these models, surface energy γ – an important thermodynamic parameter – was taken into account to determine the value of β. However, it should be noted that γ is size-dependent,^20,21 whereas both LDM and FEM models treated it as a size-independent parameter, resulting in inaccurate values for β. Additionally, the reorganization of surface atoms when a new surface is formed can create surface stress. This surface stress, denoted as f, can result in surface strain and ultimately impact the T_m(x, D, d) function.^21–24 Specifically, both γ(D) and f can affect the T_m(x, D, d) function. Therefore, to achieve a comprehensive understanding of the melting behavior of MNCs, it is essential to incorporate both factors into the model. In this contribution, the objective is to propose an analytical model that incorporates both γ(D) and f to predict the T_m(x, D, d) function of MNCs. The accuracy and universality of our proposed model will be validated through comparison with corresponding experimental and simulation data.

Model

As previously noted in our research, the role of cohesive energy per atom (E_c) plays an equivalent role to that of T_m in determining thermostability,²⁵ Specifically, T_m(∞) is proportional to E_c(∞). The absence of structural change should result in T_m and E_c being continuous functions as size decreases from bulk to nanoscale, with A/V increasing as the sole variable.²⁵ Consequently, this relationship can be extended to the nanoscale level:

Therefore, the determination of T_m(D) relies on knowledge of the E_c(D) function. Compared with bulk crystals, MNCs possess a larger surface area, leading to the breaking of bonds of surface atoms and subsequent reorganization. The total energy of MNCs can be divided into three components: internal energy E_c(D), surface free energy γ(D) arising from new surface formation, and distortion energy U caused by reorganization of surface atoms. According to the law of the conservation of energy, it can be expressed as:

nE_c(∞) = nE_c(D) + Aγ(D) + U (3)

where n represents the total atoms number of MNCs.

For crystals with varying structures, the atoms arrange themselves in distinct patterns, resulting in diverse packing densities η. In the case of MNCs with a given volume V, n can be mathematically expressed as:

where V_a is the atomic volume.

According to our previous model and Qi's work, the approximate relationship between γ and E_c has been assessed as ^26,27 where A_a is the surface area of one atom. By extending this expression to the nanoscale, it can be reformulated as:

In eqn (3), U is another parameter that needs to be discussed. As mentioned above, U originates from the reorganization of surface atoms, resulting in the surface strain and imposing an additional internal pressure P_in at the surface. The distortion energy can be written as U = P_inV.²⁸ In accordance with the Laplace–Young equation, P_in is expressed as P_in = 2Af/3V, where A/V = 2(3 − d)/D and d takes values of 0, 1, 2 for NPs, NWs and nanofilms (NFs), respectively.²⁹ Furthermore, the expression for f has been derived in Jiang's work:^30,31

f = [(3σ_sl0D₀B)/8]^1/2 (6)

where D₀ represents the critical diameter and can be represented by D₀ = 2(3 − d)h.³² B denotes the bulk modulus. σ_sl0 indicates the solid–liquid interface energy and has been deduced as follows:³³

σ_sl0 = 2hH_m(∞)S_vib(∞)/[3V_m(∞)R] (7)

where h is the nearest neighbor atomic distance, H_m(∞) and S_vib(∞) represent the bulk melting enthalpy and vibration entropy, respectively, while V_m(∞) and R represent the molar volume and ideal gas constant. By substituting eqn (6) and (7) into the expression of U, we can derive:

By combining eqn (3)–(5) and (8), T_m(D, d) or E_c(D, d) can be written as:

For NAs, the parameters required for calculation in eqn (9) are composition-dependent due to component interactions and can be approximated using the Fox equation:³⁴

where B denotes parameters used in eqn (9).

Results and discussion

Fig. 1 shows the model's prediction of T_m(D) for Pb NPs based on eqn (9), represented by the black line. The parameters utilized in eqn (9) are detailed in Table 1. The general trend is that T_m(D) decreases as D decreases, with a significant decrease occurring at D < 10 nm, indicating that size has a noticeable effect on T_m(D) at smaller sizes. This tendency can be attributed to an increase in A/V. As the decline of D, a multitude of atoms attach to the surface, leading to an increase in A/V. Subsequently, the surface atoms take precedence in determining the properties of MNCs. Given that surface atoms possess higher energetic states than inner atoms, thermal vibration of MNCs intensifies as D declines. Based on this analysis and the Lindemann criterion, it is reasonable to anticipate a reduction in T_m(D). During derivation of eqn (9), this decrease in T_m(D) is attributed to synergistic effects between f and γ(D), however, existing analytical models scarcely consider the effect of f on T_m(D). To determine whether f affects the T_m(D) or not, we also plotted the prediction of ignoring the effect of f in eqn (9) as a red line in Fig. 1. As shown in Fig. 1, the red line is higher than both the present model prediction and the experimental (■¹⁵) and simulation (□³⁵) data. However, good consistency can be observed between our present model prediction and these symbols. Therefore, it can be concluded that the existence of f has a decreasing effect on T_m(D). From the perspective of energy, the presence of f can enhance the free energy of MNCs and subsequently decrease the T_m(D). Additionally, Lu's research has demonstrated that f effectively reduces T_m(D),²¹ thereby confirming the aforementioned analysis. Consequently, it is imperative to consider the impact of f as disregarding its effect may lead to an overestimation of T_m(D).

Fig. 1 T_m(D) function of Pb NPs. The symbols ■¹⁵ and □³⁵ are the corresponding experimental and simulation data. The illustration expounds on the influences of γ(D) and f on the ΔT_m(D).

Table 1 The relevant parameters are used in the calculation of the present model^a

	h	Hm(∞)	Tm(∞)	Svib(∞)	Vm(∞)	B	Ec(∞)	η^44
a The units for B, h, Hm(∞), Tm(∞), Svib(∞), Vm(∞) and Ec(∞) are GPa, nm, kJmol^−1, K, cm^3 mol^−1, J mol^−1 K^−1 and eV, respectively. The values of B, h, Hm(∞), Tm(∞) and Vm(∞) are taken from the reference,^45 the values of Svib and Ec(∞) are taken from the references.^46,47.b The parameters are calculated by eqn (11).
Pb	0.350	4.77	600.6	6.65	18.26	46.00	2.03	0.74
Au	0.270	12.50	1337.3	7.62	10.21	220.00	3.82	0.74
Sn	0.290	7.00	505.1	9.22	16.29	58.00	3.06	0.53
Al	0.250	10.70	933.5	6.15	10.00	76.00	3.40	0.74
Bi	0.320	10.90	544.7	7.20	21.31	31.00	2.18	0.44
Ag	0.289	11.30	1234.9	7.82	21.31	100.00	2.94	0.74
In	0.368	3.26	429.8	7.58	15.76	43.00	2.52	0.68
Cu	0.270	13.10	1357.8	7.85	7.11	140.00	3.48	—
Ni	0.270	17.20	1728.0	8.11	6.59	180.00	4.47	—
Pd	0.275	16.70	1828.1	7.22	8.56	121.00	3.90	—
Pt	0.270	20.00	2041.4	7.80	9.09	230.00	5.85	—
Cu0.2Ni0.8^b	0.270	16.20	1677.1	8.05	6.69	170.27	4.23	0.74
Cu0.5Ni0.5^b	0.270	14.87	1520.7	7.98	6.84	157.50	3.92	0.74
Cu0.8Ni0.2^b	0.270	13.76	1418.6	7.90	7.00	146.51	3.64	0.74
Pd0.25Ni0.75^b	0.255	17.07	1752.0	7.87	6.99	160.44	4.55	0.74
Pd0.5Pt0.5^b	0.272	17.44	1928.8	7.49	8.82	158.58	4.68	0.74
Pd0.5Cu0.5^b	0.265	14.68	1558.2	7.52	7.77	128.33	3.69	0.74
Pb0.5Bi0.5^b	0.335	6.64	571.1	6.92	19.67	37.00	4.72	0.74

---

In addition, the prediction of FEM is also shown in Fig. 1 with an orange line for comparison. It is evident that the prediction of FEM is lower than both the symbols and the prediction of present model. During the derivation of FEM, γ was considered size-independent.¹⁸ However, it actually decreases with the decrease of D.^14,36 According to FEM's expression, T_m (D) declines as increasing γ.¹⁸ Therefore, neglecting the size effect on γ(D) would lead to an overestimation of the impact of surface energy and a subsequent underestimation of T_m(D). In light of the above analysis, it is imperative to consider the effects of f and γ(D), as failing to do so could lead to either an underestimation or overestimation of the size effect.

Based on the aforementioned analysis, both f and γ(D) are essential factors in determining the T_m(D) function. To comprehend the individual impact of f and γ(D), one can express the difference in melting temperature (ΔT_m(D) = T_m(D) − T_m(∞)) as follows using eqn (9):

with denoting the influences of γ(D) and f, respectively. The influences on ΔT_m(D) are depicted in the inserted graph of Fig. 1, where the green and pink lines represent their respective effects. As illustrated in the graph, both lines are below zero, suggesting that either γ(D) or f contributes to the decrease in T_m(D). Additionally, the green line shows a more significant decline than the pink line, suggesting that f causes a greater depression in T_m(D) depression compared to γ(D), as verified by Jiang's work.³⁷

Fig. 2 depicts the T_m(D, d) function of Pb MNCs in light of eqn (9). The red, black and blue lines represent Pb NFs, NWs and NPs respectively from top to bottom. It is evident that all three lines decrease as D decreases. Furthermore, for a given D value, the T_m(D, d) values can be ranked in descending order as follows: T_m(D, 2) > T_m(D, 1) > T_m(D, 0). For MNCs with identical D but different d values, A/V can be sequenced as: (A/V)_NFs < (A/V)_NWs < (A/V)_NPs. Based on the aforementioned analysis, the depression of T_m(D, d) is caused by the increase in A/V. Henceforth, in terms of size effect, NPs exhibit the most significant impact followed by NWs while NFs exert a relatively weaker influence; this means that as d decreases, T_m(D, d) also declines.

Fig. 2 T_m(D, d) functions of Pb MNCs. The symbols ▲⁴⁸ and ●¹⁶ are the simulation data for Pb NFs, NWs, ■¹⁵ and □³⁵ are the experimental and simulation data for Pb NPs, respectively.

To further demonstrate the universality of eqn (9), Fig. 3 presents a comparison between our model's predictions and experimental/simulation data for various MNCs, including Au, Ag, Al, Sn, Bi NPs and In MNCs. It is evident that the T_m(D, d) curves of above MNCs are in agreement with their corresponding symbols. By combining Fig. 1–3, the validity and universality of the eqn (9) are fully demonstrated due to the remarkable consistency with both experimental and simulation data.

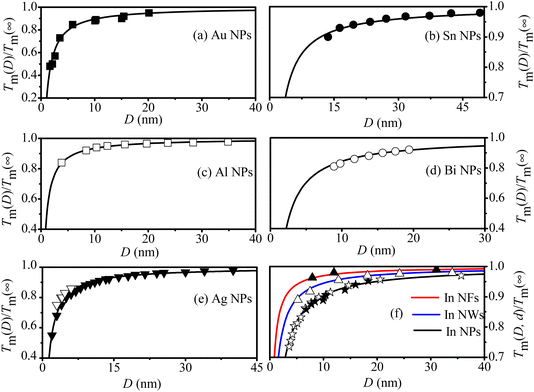Fig. 3 T_m(D, d) functions of (a) Au NPs, (b) Sn NPs, (c) Al NPs, (d) Bi NPs, (e) Ag NPs and (f) in MNCs. The symbols ■,⁴⁹ ●,⁵⁰ □,⁵¹ ○⁵² ☆,⁵³ ★,⁵⁴ △⁵⁵ and ▲⁵⁶ are the experimental results, ▼⁵⁷ and ▽⁵⁸ are the simulation data.

For bimetallic NAs, the variation in component x can alter the interatomic interaction and subsequently impact melting temperature.³⁸ Fig. 4 illustrates the comparison between model predictions (Eq. (9)) and simulation results for T_m (x, D) of Cu_xNi_1−x NPs with x = 0.2, 0.5 and 0.8. It is evident that both of them exhibit a high degree of consistency. For instance, when D equals 4 nm, the simulation results are recorded at temperatures of 1250 K, 1150 K, and 1073 K,¹⁷ while the corresponding predicted values are 1260 K, 1167 K, and 1089 K for x equal to 0.2, 0.5, and 0.8, respectively. The margin of error between the two sets of data is approximately 1%. Furthermore, it also can be observed that, as Cu content increases, T_m (x, D) decreases. For NAs, the distribution of components is non-uniform, exhibiting surface segregation. The segregation phenomenon can be described as follows: the component with the lowest γ value preferentially segregates to the surface.^39,40 Consequently, for the Cu_xNi_1−x NAs, Cu atoms will preferentially segregate to the surface due to their lower surface energy compared to Ni (γ_Cu = 1.566 J m⁻² vs. γ_Ni = 2.080 J m⁻²).⁴¹ With the increase of Cu, more surface segregation of Cu atoms leads to a decrease in the bond energy of Cu–Ni NAs, especially for surface atoms, and then leads to an increase in the thermal vibration of surface atoms. According to the Lindemann criterion,⁴² the decrease in T_m(x, D) can be expected with the increase of the Cu component. The alignment between model predictions and simulation data confirmed the effectiveness of eqn (9).

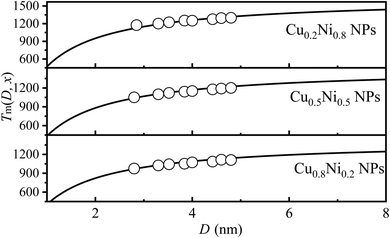Fig. 4 T_m(x, D) functions of Cu_xNi_1−x NPs with x = 0.2, 0.5 and 0.8. The symbol ■¹⁷ is the simulation data.

Furthermore, the T_m(x, D, d) functions for Pd_0.25Ni_0.75, Pd_0.5Cu_0.5, Pb_0.5Bi_0.5 NPs and Pd_0.5Pt_0.5 NWs are depicted in Fig. 5 to demonstrate the validity and universality of eqn (9), which is supported by both experimental and simulation data.

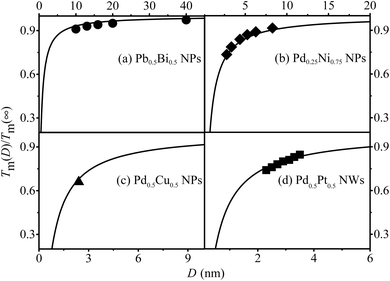Fig. 5 T_m(x, D, d) functions of (a) Pb_0.5Bi_0.5 NPs, (b) Pd_0.25Ni_0.75 NPs, (c) Pd_0.5Cu_0.5 NPs and (d) Pd_0.5Pt_0.5 NWs. The symbol ●⁵⁹ denotes the experimental results. ♦,⁶⁰ ▲⁶¹ and ■⁶² are the corresponding simulation data, respectively.

The model introduced in this study offers valuable insights into modifying T_m(x, D, d) in MNCs by manipulating their size, dimensionality and composition. The parameters required for model prediction possess clear physical significance, which ensures the model's applicability not only to metallic nanocrystals but also to non-metallic nanocrystals. Given the critical importance of T_m(x, D, d) in characterizing fundamental property variations,^13,14 this model facilitates a quantitative exploration of key challenges in MNCs ' research. It is noteworthy that the model's applicability is currently restricted to MNCs under ambient pressure conditions. While as the pressure increases, the intermolecular distance of most substances decreases, leading to more stable solid structures that require higher temperatures to melt. Consequently, the melting temperature generally increases with increasing pressure,^3,43 demonstrating an inverse relationship with the size effect. Therefore, our subsequent research will focus on exploring the competition between size-induced undercooling and pressure-induced overheating.

Conclusions

In summary, a novel model is established by taking into account both f and γ(D), which can be utilized to predict the T_m(x, D, d) of MNCs. The depression of T_m(x, D, d) with decreasing D or d results from the synergistic effects of f and γ(D). While both f and γ(D) contribute to the reduction in T_m(x, D, d), the impact of f is more pronounced than that of γ(D). Neglecting either factor would lead to an underestimation or overestimation of T_m(x, D, d). Furthermore, as the component with the lowest γ increases, surface segregation causes a decrease in NAs' T_m(x, D, d). By comparing it to corresponding experimental and simulation data, the validity and universality of the newly constructed model are confirmed, providing guidance for designing and applying new nanodevices.

Abbreviation

A/V	Surface-to-volume ratio
Aa	Surface area of one atom
B	Bulk modulus
D	Size
d	Dimensionality
D0	Critical diameter
Ec	Cohesive energy per atom
f	Surface stress
FEM	Gibbs free energy model
h	Nearest neighbor atomic distance
Hm	Melting enthalpy
LDM	Liquid-drop model
MNCs	Metallic nanocrystals
NAs	Nanoalloys
NFs	Nanofilms
NPs	Nanoparticles
NWs	Nanowires
Pin	Addition internal pressure
R	Ideal gas constant
σsl0	Solid-liquid interface energy
Svib	Vibration entropy
Tm	Melting temperature
Tw	Working temperature
U	Distortion energy
Vm	Molar volume
x	Composition
γ	Surface energy
η	Packing density
β	Material constant
∞	Bulk

Data availability

All data that support the findings of this study are included within the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (51301073, 11774148).

References

1. F. Wang, D. Zhou and Y. Han, Adv. Funct. Mater., 2016, 48, 8903–8919.
2. G. Guisbiers, Adv. Phys.:X, 2019, 4, 1668299.
3. G. de With, Chem. Rev., 2023, 123, 13713–13795.
4. L. Delgado-Callico, K. Rossi, R. Pinto-Miles, P. Salzbrenner and F. Baletto, Nanoscale, 2021, 13, 1172–1180.
5. M. Li and T. S. Zhu, Phys. Chem. Chem. Phys., 2016, 18, 16958–16963.
6. H. Gleiter, Prog. Mater. Sci., 1989, 33, 223–315.
7. Z. Yan, M. G. Taylor, A. Mascareno and G. Mpourmpakis, Nano Lett., 2018, 18, 2696.
8. C. C. Yang and Y. W. Mai, Mater. Sci. Eng., R, 2014, 79, 1–40.
9. X. Jiang, H. Sheng and B. Xiao, Phys. Chem. Chem. Phys., 2023, 25, 29310–29314.
10. T. Mallát, Z. Bodnár, S. Szabó and J. Petró, Appl. Catal., 1991, 69, 85–95.
11. L. Lu, M. Sui and K. Lu, Science, 2000, 287, 1463–1466.
12. Z. L. Wang, J. M. Petroski, T. C. Green and M. A. El-Sayed, J. Phys. Chem. B, 1998, 102, 6145–6151.
13. C. C. Yang and Y. W. Mai, J. Phys. Chem. C, 2013, 117, 2421–2426.
14. Q. Jiang and H. Lu, Surf. Sci. Rep., 2008, 63, 427–464.
15. C. Coombes, Met. Phys., 1972, 2, 441.
16. O. Gülseren, F. Ercolessi and E. Tosatti, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 7377.
17. G. Li, Q. Wang, D. Li, L. Xiao and J. He, Mater. Chem. Phys., 2009, 114, 746–750.
18. M. Wautelet, Eur. Phys. J.:Appl. Phys., 2004, 29, 51–54.
19. K. Nanda, S. Sahu and S. Behera, Phys. Rev. A, 2002, 66, 013208.
20. E. H. Kim and B. J. Lee, Met. Mater. Int., 2009, 15, 531–537.
21. Q. S. Mei and K. Lu, Prog. Mater. Sci., 2007, 52, 1175–1262.
22. H. Wang and H. Zhu, Nanoscale Res. Lett., 2015, 10, 1–9.
23. H. Sheng, R. Gao, B. Xiao and X. Jiang, Vacuum, 2021, 192, 110428.
24. Y. Ma, W. Li, P. Dong, M. Yang, Y. He, S. Zheng, Z. Zhao, R. Zhang, Z. Zhang and M. Li, Eur. Phys. J. Plus, 2022, 137, 824.
25. H. M. Lu, D. N. Ding, Z. H. Cao, S. C. Tang and X. K. Meng, J. Phys. Chem. C, 2007, 111, 12914–12917.
26. Q. Jiang, H. M. Lu and M. Zhao, J. Phys.: Condens. Matter, 2004, 16, 521–530.
27. W. H. Qi and M. P. Wang, J. Mater. Sci. Lett., 2002, 21, 1743–1745.
28. S. Li, J. Lian and Q. Jiang, Chem. Phys. Lett., 2008, 455, 202–206.
29. R. C. Cammarata and K. Sieradzki, Annu. Rev. Mater. Sci., 1994, 24, 215–234.
30. M. Zhao, X. Zhou and Q. Jiang, J. Mater. Res., 2001, 16, 3304–3308.
31. L. H. Liang, J. C. Li and Q. Jiang, Solid State Commun., 2002, 121, 453–455.
32. Z. Zhang, X. X. Lü and Q. Jiang, Phys. B, 1999, 270, 249–254.
33. Q. Jiang, H. X. Shi and M. Zhao, Acta Mater., 1999, 47, 2109–2112.
34. T. G. Fox, Bull. Am. Phys. Soc., 1956, 1, 123.
35. H. Lim, C. Ong and F. Ercolessi, Zeitschrift für Physik D Atoms, Molecules and Clusters, 1993, 26, 45–47.
36. T. D. Chen, Y. L. Ma, X. D. Fu and M. Li, ACS Appl. Nano Mater., 2020, 3, 1583–1591.
37. X. Jiang, B. Xiao, R. Lan, X. Gu, H. Sheng, H. Yang and X. Zhang, J. Phys. Chem. C, 2018, 122, 26260–26266.
38. S. P. Huang and P. B. Balbuena, J. Phys. Chem. B, 2002, 106, 7225–7236.
39. A. V. Ruban, H. L. Skriver and J. K. Nørskov, Phys. Rev. B, 1999, 59, 15990–16000.
40. M. J. Cui, H. M. Lu, H. P. Jiang and X. K. Meng, ACS Nano, 2016, 10, 10618–10619.
41. W. R. Tyson and W. A. Miller, Surf. Sci., 1977, 62, 267–276.
42. F. A. Lindemann, Phys. Z., 1910, 11, 609–612.
43. Z. Chen, C. Q. Sun, Y. Zhou and G. Ouyang, J. Phys. Chem. C, 2008, 112, 2423–2427.
44. H. Lu and Q. Jiang, Phys. Status Solidi A, 2004, 241, 2472–2476.
45. R. Rossetti, R. Hull, J. M. Gibson and L. E. Brus, J. Chem. Phys., 1985, 82, 552–559.
46. H. M. Lu, Z. Wen and Q. Jiang, Colloids Surf., A, 2006, 278, 160–165.
47. C. Kittel, Introduction to Solid State Physics, 5th edn Wiley, 2005.
48. W. H. Qi and M. P. Wang, Chin. J. of Nonferrous Met., 2006, 16, 1161–1165.
49. K. Dick, T. Dhanasekaran, Z. Zhang and D. Meisel, J. Am. Chem. Soc., 2002, 124, 2312–2317.
50. S. Lai, J. Guo, V. Petrova, G. Ramanath and L. Allen, Phys. Rev. Lett., 1996, 77, 99.
51. S. Lai, J. Carlsson and L. Allen, Appl. Phys. Lett., 1998, 72, 1098–1100.
52. V. Skripov, V. Koverda and V. Skokov, Phys. Status Solidi A, 1981, 66, 109–118.
53. M. Zhang, M. Y. Efremov, F. Schiettekatte, E. Olson, A. Kwan, S. Lai, T. Wisleder, J. Greene and L. Allen, Phys. Rev. B, 2000, 62, 10548.
54. G. Allen, R. Bayles, W. Gile and W. Jesser, Thin Solid Films, 1986, 144, 297–308.
55. K. M. Unruh, T. E. Huber and C. A. Huber, Phys. Rev. B, 1993, 48, 9021–9027.
56. G. Krausch, T. Detzel, H. Bielefeldt, R. Fink, B. Luckscheiter, R. Platzer, U. Wöhrmann and G. Schatz, Appl. Phys. A:Mater. Sci. Process., 1991, 53, 324–329.
57. W. Luo, W. Hu and S. Xiao, J. Phys. Chem. C, 2008, 112, 2359–2369.
58. S. Xiao, W. Hu and J. Yang, J. Phys. Chem. B, 2005, 109, 20339–20342.
59. W. A. Jesser, R. Z. Shneck and W. W. Gile, Phys. Rev. B, 2004, 69, 144121.
60. U. Domekeli, S. Sengul, M. Celtek and C. Canan, Philos. Mag., 2017, 98, 1–17.
61. S. K. R. S. Sankaranarayanan, V. R. Bhethanabotla and B. Joseph, J. Phys. Chem. C, 2007, 111, 2430–2439.
62. S. K. R. S. Sankaranarayanan, V. R. Bhethanabotla and B. Joseph, Phys. Rev. B, 2006, 71, 155441.

---