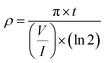Effects of carbon nanotube and curing agent concentrations on the mechanical, thermal and electrical properties of polydimethylsiloxane: optimization and statistical analysis

Abstract

This study examined the combined impact of carbon nanotubes (CNTs) and curing agents on the mechanical properties (tensile strength and modulus of elasticity) and thermal and electrical conductivities of polydimethylsiloxane (PDMS) using statistical analysis. PDMS composites were created by varying the concentrations of CNTs (0% to 5%) and curing agents (0% to 0.5%), and their properties such as tensile strength, modulus of elasticity, and thermal and electrical conductivities were comprehensively analyzed. Mechanical tests revealed that adding 5% CNT and 0.5% curing agent increased the tensile strength by 50% and modulus of elasticity (Young's modulus) by 65%, indicating a substantial reinforcing effect. Thermal conductivity remarkably improved from 0.2 W m⁻¹ K⁻¹ in pure PDMS to 1.1 W m⁻¹ K⁻¹ in the composite containing 5% CNT and 0.5% curing agent. The electrical conductivity improved significantly from an insulating 10⁻¹⁴ S m⁻¹ to 10⁻² S m⁻¹. This indicated a shift to conductive PDMS at higher CNT concentrations. Statistical analysis showed that CNTs had more significant impact on electrical and thermal properties, while the curing agent mainly enhanced the mechanical stability. These results highlight the combined potential of CNTs and curing agents in modifying PDMS properties for advanced engineering applications.

---

1 Introduction

Silicon-based materials, particularly polydimethylsiloxane (PDMS), have gained significant attention for applications in flexible electronics, bio-integrated devices, and thermal management systems owing to their flexibility, chemical resistance, and dielectric properties.^1,2 Recent works have demonstrated PDMS composites integrated into stretchable sensors,³ thermal interface layers for electronics,² and nanostructured surfaces with tunable wettability and conductivity.¹ Polydimethylsiloxane (PDMS) or silicone rubber is renowned for its unique combination of properties that make it a highly adaptable material. It exhibits exceptional thermal stability, maintaining its flexibility and mechanical integrity across a broad temperature range from −60 °C to 250 °C. This material is also highly resistant to environmental factors, such as UV radiation, ozone, and moisture, which contributes to its long-term durability in outdoor applications. PDMS's mechanical properties include excellent modulus of elasticity and tensile strength, enabling its shape recovery after deformation.^4–6 Additionally, it has outstanding electrical insulating properties, making it ideal for use in electronic and electrical applications. Its chemical inertness further enhances its suitability for medical and food-grade applications as it does not react with bodily fluids or food substances. Overall, the combination of thermal stability, mechanical resilience and chemical resistance makes PDMS a versatile material for a wide range of demanding applications.^7–10

Carbon nanotubes (CNTs) are versatile nanomaterials with a wide range of applications owing to their exceptional mechanical, electrical and thermal properties. They are used in electronics to create highly conductive materials in energy storage devices such as batteries and super capacitors to enhance their performance and in composite materials to improve their strength and durability while reducing their weight. CNTs are also employed in medical devices for drug delivery, as sensors and diagnostic tools, and in environmental applications, such as water purification and pollutant detection. Their unique structure enables innovations across various fields, making them invaluable in advancing technology and materials science.^11–13

The incorporation of carbon nanotubes (CNTs) and curing agents significantly enhanced the properties of PDMS. CNTs serve as reinforcing agents within the PDMS matrix, improving tensile strength, modulus of elasticity (Young's modulus), thermal conductivity, and electrical conductivity. As CNT concentration increases, the material becomes stronger, stiffer, and more thermally and electrically conductive, making it suitable for high-performance applications.¹⁴ On the other hand, curing agents facilitate cross-linking within PDMS, which increases the material's toughness, durability, and resistance to deformation under stress. The combination of CNTs and curing agents results in a PDMS composite with superior mechanical, thermal, and electrical properties, expanding its applicability in demanding environments such as electronics, automotive components, and high-temperature seals. Thus, statistical estimation and optimization of additives such as CNT to PDMS and their effect on mechanical, thermal and electrical properties is essential for many application and it is the main objective of this study.^7,14–17 Recent advancements in polysiloxane-based composites have primarily focused on the development of multifunctional materials for high-performance applications, including wearable electronics, thermal interface materials, and self-healing polymers.^1,2,18–20 These studies often involve surface modification of nanofillers, incorporation of conductive or responsive additives, or complex structural designs to enhance specific functionalities. In contrast, the present study takes a statistical optimization approach, focusing on the combined influence of CNT concentration and curing agent content on the mechanical, thermal, and electrical properties of polydimethylsiloxane (PDMS) composites. Unlike conventional one-variable-at-a-time methods, the use of a central composite design (CCD) and design of experiments (DOE) enables a systematic, data-driven evaluation of multiple factors, allowing for predictive modeling and multi-property optimization. This approach offers a scalable and reproducible pathway for simultaneously tuning performance across several domains, using commercially available materials and a simple fabrication process, making it attractive for industrial and engineering applications.

2 Methodology

2.1 Materials

Polydimethylsiloxane (PDMS) base material was supplied by Wacker Chemie with a brand name of HELISOL® 10A. HELISOL® 10A is a linear, non-reactive polydimethylsiloxane with a viscosity of approx. 0.1 cm² s⁻¹. Fullerene carbon nanotube (CNTs) with multi-walled, <8 nm OD, 2–5 nm ID, 0.5–2 micron long, and purity of ≥96.0% was supplied by Thermo Scientific Chemicals. Dicumyl peroxide of 98% purity ({2-[(2-phenylpropan-2-yl)peroxy]propan-2-yl}benzene) was used as a curing agent and purchased from Thermo Scientific Chemicals. Sodium dodecyl sulfate (SDS) was purchased from Thermo Scientific Chemicals and used as a dispersing agent. Anhydrous toluene of 99.8% purity was used as a solvent medium and purchased from Thermo Scientific Chemicals.

2.2 Experimental design and statistical analysis

To investigate the influence of carbon nanotube (CNT) concentration and curing agent (CA) levels on the properties of PDMS, experimental design and statistical analysis were performed using Design Expert software (version 13). A central composite design (CCD) was employed, consisting of 13 experimental runs: 8 factorial points and 5 center points. This design allowed for efficient evaluation of both the individual and interactive effects of CNT and CA. These variables were set at high and low levels as detailed in Table 1. The levels were determined based on initial runs covering the maximum and minimum values for each factor. Each sample formulation was tested in five replicates, and results are reported as the mean ± standard deviation to ensure accuracy and reproducibility. Statistical significance was assessed using analysis of variance (ANOVA), with the significance level set at p < 0.05. Where significant differences were found, least significant difference (LSD) tests were used to separate the means and identify specific group differences.

Table 1 Independent variables and their high and low levels

Factor	Name	Unit	Minimum	Maximum
A	CNT	wt%	0	5
B	CA	wt%	0	0.5

---

2.3 Preparation of PDMS nanocomposite

Incorporating carbon nanotubes (CNTs) into PDMS involves several steps to ensure proper dispersion and integration which can significantly affect the material properties. CNTs were dispersed in a mixture of toluene solvent and 0.5 wt% of sodium dodecyl sulfate using an ultrasonicator for 30 minutes to achieve a uniform dispersion. Then, the CNT–solvent dispersion was added to PDMS base material and mixed thoroughly. The solvent was evaporated by gentle heating to remove any residual solvent. Then, the curing agent was added to the CNT–PDMS mixture and thoroughly mixed to ensure even distribution of the curing agent. In the end, the mixture was poured into molds to get the desired shape. The samples were cured at room temperature followed by a post-cure at an elevated temperature of 150 °C for 2 hours. Fig. 1 illustrates the preparation steps of the samples. Five samples were formulated for each run and the average value was reported and used for the statistical analysis. The composition of the samples detail is shown in Table 2.

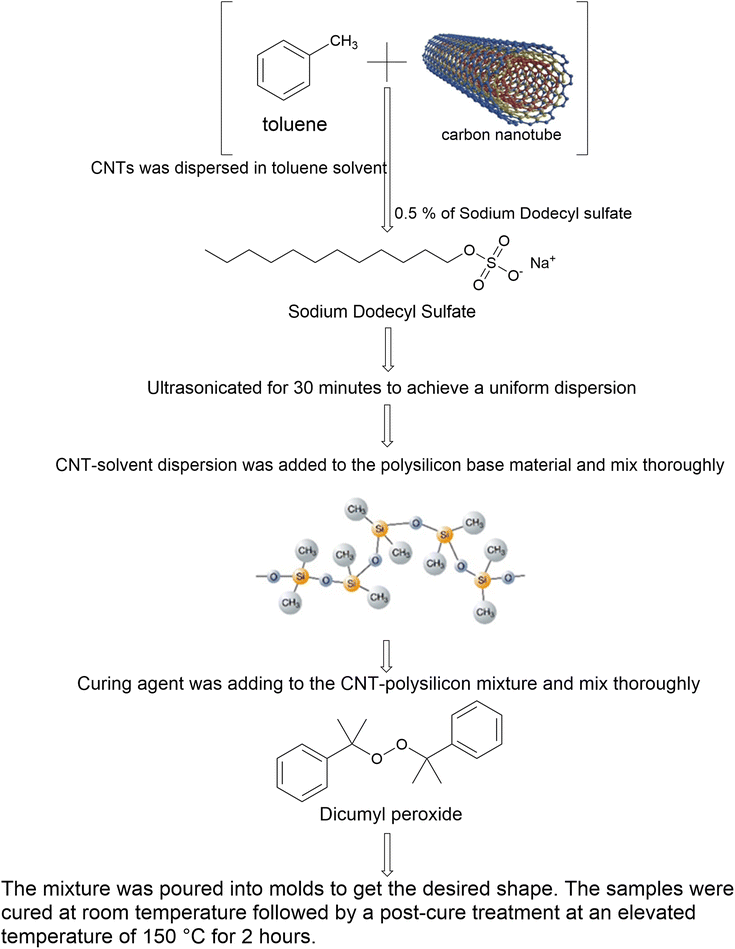Fig. 1 Steps for the preparation of samples.

Table 2 Formulation details for incorporating different percentages of CNT and CA into PDMS

Run	CNT (wt%)	CA (wt%)
1	2.5	0.25
2	2.5	0.25
3	2.5	0.5
4	2.5	0.25
5	0	0
6	2.5	0.25
7	5	0.5
8	0	0.25
9	2.5	0.25
10	5	0
11	5	0.25
12	2.5	0
13	0	0.5

---

2.4 Sample testing

2.4.1 Mechanical testing. A universal testing machine (UTM) was used for mechanical testing of the samples under standard test methods for vulcanized rubber and thermoplastic elastomers (tension) (ASTM D412) and the data for TS and E were recorded.^21,22

2.4.2 Thermal conductivity. A guarded hot plate steady-state method (ASTM C177) was used to investigate the effect of CNT and CA on thermal conductivity of PDMS. This method involves placing the sample between a hot plate and a cold plate. The heat flows through the sample from the hot side to the cold side. A guarded hot plate apparatus containing a heater, temperature sensors and insulating guard helps to minimize heat losses. The sample was placed between the heated plate and the cold plate and the steady-state heat flow was achieved. The heat flux through the sample was measured, and the temperature difference recorded across the sample. Thermal conductivity (K) of the sample was calculated using eqn (1):where q is the heat flux, d is the thickness of the sample, A is the cross-section area of the sample, and ΔT is the temperature difference across the sample.²³

2.4.3 Electrical conductivity. The electrical conductivity of the samples was measured using a four-point probe device (four-point probe method) according to ASTM D257. This device has four aligned probes (electrodes) placed equidistant from each other. The outer two probes pass current through the sample, while the inner two probes measure the voltage drop across the sample. The samples were prepared in a flat thin film with dimensions of 55 mm × 10 mm × 5 mm^24,25 and cleaned from any contamination before testing. A stable current source was connected to the outer probes to ensure a consistent current flow through the sample. The voltage drop was measured using a high-precision voltmeter which was connected to the inner probes. The resistivity of the samples was calculated using eqn 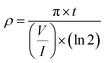(2):where t is the sample thickness, V is the measured voltage, and I is the current.

The electrical conductivity was reported as the inverse of resistivity as shown in eqn (3).^26–28

3 Results and discussion

The results of mechanical, thermal conductivity and electrical conductivity testing for all sample formulations are reported in Table 3. These data are inserted into the DOE to conduct the statistical analysis.

Table 3 Results of mechanical property, thermal conductivity and electrical conductivity for all sample formulations

Run	TS (MPa)	E (MPa)	TC (W m^−1 K^−1)	EC (S m^−1)
1	9.65	1.49	0.74	1.0000 × 10^−5
2	9.64	1.49	0.74	1.0000 × 10^−5
3	8.11	1.36	0.7	1.0000 × 10^−5
4	9.64	1.49	0.74	1.0000 × 10^−5
5	3.23	0.54	0.21	1.0000 × 10^−9
6	9.65	1.49	0.74	1.0000 × 10^−5
7	11.43	1.65	0.82	1.0000 × 10^−5
8	4.32	0.98	0.38	1.0000 × 10^−9
9	9.64	1.49	0.74	1.0000 × 10^−5
10	10.31	1.43	0.65	1.0000 × 10^−4
11	10.98	1.54	0.76	1.0000 × 10^−4
12	4.56	0.24	0.42	1.0000 × 10^−6
13	6.57	1.21	0.41	1.0000 × 10^−9

---

3.1 Statistical analysis of mechanical testing

The ANOVA analysis in Table 4 for tensile strength (TS) indicates that the model F-value is 11.80 and the P-value is less than 0.05, which is a sign of significant model terms (CNT and CA are significant model terms). The final quadratic equation in terms of actual factors (eqn (4)) can be used to make predictions about the response (TS) for given levels of each factor. The levels were specified in the original units for each factor.

TC = 2.28397 + 1.68848 CNT + 20.34483 CA − 0.888000 CNT× CA − 0.045297 CNT² − 25.56966 CA² (4)

Table 4 ANOVA data for linear model response 1: TS

Source	Sum of square	Mean square	F-Value	P-Value
Model	79.21	15.84	11.80	0.0027	Significant
A-CNT	57.66	57.66	42.93	0.0003
B-CA	10.69	10.69	7.96	0.0257
AB	1.23	1.23	0.9174	0.3701
A^2	0.2214	0.2214	0.1648	0.6969
B^2	7.05	7.05	5.25	0.0557

---

A similar finding is recorded for the modulus of elasticity (E) as shown in Table 5. The result of ANOVA analysis in Table 5 indicates that the model F-value is 5.58 and P-value is less than 0.05, which is a sign of significant model terms (CNT and CA are significant model terms). The final quadratic equation in terms of actual factors (eqn (5)) can be used to make predictions about the response (E) for the given levels of each factor. The levels were specified in the original units for each factor.

TC = 0.335086 + 0.108793 CNT + 4.8793 CA − 0.180000 CNT× CA + 0.012441 CNT² − 6.11586 CA² (5)

Table 5 ANOVA data for linear model response 2: E

Source	Sum of square	Mean square	F-Value	P-Value
Model	1.74	0.3475	5.58	0.0217	Significant
A-CNT	0.5953	0.5953	9.56	0.0175
B-CA	0.6733	0.6733	10.81	0.0133
AB	0.0506	0.0506	0.8131	0.3972
A^2	0.0167	0.0167	0.2682	0.6205
B^2	0.4035	0.4035	6.48	0.0383

---

The results of mechanical properties in terms of TS and E are illustrated in Fig. 2 and 3. The results indicate that the incorporation of carbon nanotubes (CNTs) and curing agents significantly influenced the mechanical properties of PDMS. However, the effects differ in magnitude and impact. The results in Fig. 2 indicate that CNTs have significant effects on the tensile strength of PDMS. As CNTs were added to the polymer matrix, they act as reinforcing agents and distribute the stress more evenly, making the material stronger and more resistant to breaking under tension. In addition, the CNTs increased the stiffness of PDMS as reflected in the high Young's modulus. CNTs restrict the movement of the polymer chains, thus making the material more rigid. This is beneficial in applications that require structural integrity.^4,29,30

Fig. 2 Effects of CNT and CA concentrations on TS in a 3D surface.

Fig. 3 Effects of CNT and CA concentration on E in a 3D surface.

The result in Fig. 3 indicates a positive effect of curing agents (CA) on the mechanical properties of PDMS. The positive effect is primarily due to the cross-linking density. Increased cross-linking led to improved tensile strength, toughness and modulus of elasticity. PDMS becomes more resistant to permanent deformation and retains its shape better under stress. Curing agents led to an increase in E, which can lead to an enhanced ability of PDMS to recover its original shape after being deformed. This is critical in application areas such as seals and gaskets where the material must maintain a tight seal.^4,29–32

In addition, the results of mechanical analysis indicated that both CNTs and curing agents enhance the mechanical properties of PDMS. The sample with the highest mechanical properties was recorded at 5 wt% CNT load and 0.5 wt% CA. Generally, CNTs have a more pronounced effect on properties like tensile strength and Young's modulus due to their ability to reinforce the polymer matrix at the molecular level. CNTs primarily affect the matrix of PDMS strength and stiffness while curing agents have a more significant impact on modulus of elasticity and shape retention. The improved properties of PDMS nanocomposites can be attributed not only to the physical reinforcement from the carbon nanotubes (CNTs) but also to chemical interactions at the molecular level. Although CNTs are chemically inert, they can interact with the silicone matrix through van der Waals forces and interfacial adhesion promoted by surfactants like SDS, which aid in their dispersion. The curing agent, dicumyl peroxide, generates free radicals during the curing process, which can initiate cross-linking reactions in PDMS chains. These free radicals may also facilitate limited covalent bonding or enhanced interfacial entanglement between the CNT surfaces and the silicone matrix. This chemical network contributes to better stress transfer, thermal pathways, and electron mobility. Moreover, the presence of CNTs may influence the cross-linking density by altering the mobility and spatial arrangement of the polymer chains during curing, thus creating a more tightly packed structure that enhances mechanical and thermal stability.

3.2 Statistical analysis of thermal conductivity (TC) testing

The result of ANOVA analysis in Table 6 for thermal conductivity (TC) indicated that the model F-value is 38.38 and the P-value is less than 0.0500, which is a sign of significant model terms (CNT, and CA are significant model terms). The final quadratic equation in terms of actual factors (eqn (6)) can be used to make predictions about the response (TC) for given levels of each factor. The levels were specified in the original units for each factor.

TC = 0.178822 + 0.169828 CNT + 1.39161 CA − 0.012000 CNT × CA − 0.016966 CNT² − 1.85655 CA² (6)

Table 6 ANOVA data for linear model response 3: TC

Source	Sum of square	Mean square	F-Value	P-Value
Model	0.4329	0.0866	38.38	<0.0001	Significant
A-CNT	0.2521	0.2521	111.78	<0.0001
B-CA	0.0704	0.0704	31.21	0.0008
AB	0.0002	0.0002	0.0997	0.7614
A^2	0.0311	0.0311	13.77	0.0076
B^2	0.0372	0.0372	16.48	0.0048

---

Fig. 4 shows that the thermal conductivity of PDMS is significantly influenced by the addition of carbon nanotubes (CNTs) and curing agents, although the effects differ in nature and magnitude. CNTs are known for their exceptional thermal conductivity, which can reach up to 6000 W m⁻¹ K⁻¹ in individual nanotubes.³³ When CNTs were incorporated into the PDMS matrix, they created conductive pathways that allow heat to be transferred more efficiently through the material. As the concentration of CNTs increases, the thermal conductivity of PDMS improves substantially. This makes the material better suited in application areas that require effective heat dissipation, such as in electronics or thermal interface materials. The result suggests that the improvement in thermal conductivity is not linear; it increases significantly once a critical concentration (percolation threshold) is reached. At this point, a continuous network of CNTs is formed, which greatly enhances the thermal performance of PDMS composite. Other researchers have made similar submissions.^34–36 The result also shows that higher cross-linking density was obtained due to the addition of CA, which slightly improved the thermal conductivity of the material. The improvement in thermal conductivity is due to the reduction in the amount of free volume within PDMS, thus allowing heat to be transferred more efficiently. Also, the effect of CA can prevent the degradation of PDMS at higher temperatures. The primary role of CNTs is to ensure that the material maintains its mechanical integrity at elevated temperatures, rather than enhancing heat transfer. Therefore, CNTs have a far more significant impact on the thermal conductivity of PDMS compared with curing agents. The addition of CNTs can dramatically increase thermal conductivity, especially when the concentration is high enough to form a conductive network. While curing agents improve the material's ability to withstand heat without degrading, they do not substantially alter the material's ability to conduct heat. On the other hand, CNTs directly enhance PDMS thermal conductivity by providing a conductive network for heat transfer.^{30,32,37–39}

Fig. 4 Effects of CNT and CA concentrations on TC in a 3D surface.

3.3 Statistical analysis of electrical conductivity (EC) testing

The result of ANOVA analysis in Table 7 for electrical conductivity (EC) indicated that the model F-value is 9.87 and the P-value is less than 0.0500, which is a sign of significant model terms (CNT and CA are significant model terms). The final quadratic equation in terms of actual factors (eqn (7)) can be used to make predictions about the response (EC) for given levels of each factor. The levels were specified in the original units for each factor.

EC = −0.000013 − 2.04888 × 10⁻⁶ CNT + 0.000142 CA − 0.000036 CNT × CA + 5.00974 × 10⁻⁶ CNT² − 0.000211 CA² (7)

Table 7 ANOVA data for linear model response 4: EC

Source	Sum of square	Mean square	F-Value	P-Value
Model	1.318 × 10^−8	2.636 × 10^−9	9.87	0.0045	Significant
A-CNT	7.350 × 10^−9	7.350 × 10^−9	27.51	0.0012
B-CA	1.094 × 10^−9	1.094 × 10^−9	4.09	0.0828
AB	2.025 × 10^−9	2.025 × 10^−9	7.58	0.0284
A^2	2.708 × 10^−9	2.708 × 10^−9	10.13	0.0154
B^2	4.805 × 10^−10	4.805 × 10^−10	1.80	0.2218

---

Fig. 5 indicates that the electrical conductivity (EC) of PDMS is significantly affected by the addition of carbon nanotubes (CNTs) and curing agents, with CNTs having a much more pronounced effect. CNTs are inherently conductive materials with electrical conductivity values ranging from 10³ to 10⁵ S m⁻¹, depending on the type and quality of the nanotubes. When dispersed within PDMS matrix, CNTs form conductive pathways that allow electrons to flow through the material. The results showed that the electrical conductivity of the composite rose sharply as the concentration of CNTs increased, especially when the percolation threshold was reached. This is adduced to the establishment of continuous network of CNTs within PDMS networks. Similar to thermal conductivity, the electrical conductivity experienced a dramatic increase once a critical concentration of CNTs was reached. Below this threshold, the material remains largely insulating. This makes CNTs a powerful tool for tuning the electrical properties of PDMS.^40–42 The result also shows that the curing agents themselves do not contribute to electrical conductivity and generally maintain the insulating nature of PDMS.^43,44 However, CA might indirectly influence electrical conductivity by affecting the dispersion and alignment of CNTs within PDMS networks. Thus, if no conductive fillers like CNTs are added, curing agents will typically enhance the electrical insulation properties of PDMS by increasing the density of the polymer network, thereby reducing the likelihood of electrical conduction. Therefore, CNTs directly contribute to the electrical conductivity of PDMS, while curing agents influence PDMS mechanical and thermal properties without significantly altering its electrical characteristics.

Fig. 5 Effect of CNT and CA concentrations on EC in a 3D surface.

The improvements in thermal and electrical conductivity seen in this study go beyond the high conductivity of carbon nanotubes (CNTs) themselves. What truly drives these enhancements is how CNTs interact with the PDMS matrix on a microscopic level. When CNTs are well-dispersed and reach a critical concentration, they form a continuous network that allows heat and electricity to travel efficiently through the composite, a concept known as the percolation threshold.^33,45 The curing agent, dicumyl peroxide, also plays an important role here. During the curing process, it creates free radicals that link PDMS chains together, increasing the crosslink density. This tighter network restricts polymer chain movement, which in turn helps hold the CNTs in place. As a result, the CNTs are more likely to stay evenly dispersed and form stronger, more stable conductive paths. The curing process may also enhance how well CNTs stick to the polymer at the molecular level, reducing resistance at their interfaces.^16,32,43 While this paper focuses on statistical optimization, previous studies using tools like SEM, FTIR, and swelling experiments have shown that similar systems benefit from this kind of interaction. These techniques revealed improved CNT dispersion, stronger interfacial bonding, and denser crosslinking, all of which support the trends observed here.^30,46

4 Conclusion

The CNTs were observed to enhance the mechanical strength and stiffness of PDMS composite, thereby making it suitable in application areas that require high performance materials. The curing agents were observed to primarily contribute to the modulus of elasticity and shape retention, thus improving the reinforcing effects of the CNTs. Also, the CNTs have a much greater effect in enhancing the thermal and electrical conductivity of the PDMS material than the curing agents. This study presents a straightforward yet effective strategy for enhancing and optimizing the multifunctional performance of PDMS composites through the synergistic use of carbon nanotubes and curing agents, guided by statistical modeling. Unlike recent works that emphasize nano-engineered surfaces or functionalized filler interfaces, this research demonstrates that substantial improvements in tensile strength, modulus, thermal conductivity, and electrical conductivity can be achieved through a data-centric optimization framework, using a cost-effective and scalable fabrication method. Therefore, this study, provides a practical foundation for engineering PDMS-based materials with tailored properties for real-world applications.

Data availability

The data supporting the findings of this study are available within the article. All relevant numerical data used in the statistical analysis and optimization models are presented in the main text (tables and figures). No custom code was developed for this study.

Conflicts of interest

There are no conflicts to declare.

References

1. H. Zhan, W. Cheng and F. Liu, et al., Resilient and robust mechanoresponsive polydimethylsiloxane/SiO₂ composites induced by interfacial enhancement, J. Colloid Interface Sci., 2025, 690, 137361.
2. M. He, X. Zhong and X. Lu, et al., Excellent Low-Frequency Microwave Absorption and High Thermal Conductivity in Polydimethylsiloxane Composites Endowed by Hydrangea-Like CoNi@BN Heterostructure Fillers, Adv. Mater., 2024, 36(48), 2410186.
3. M. He, J. Hu and H. Yan, et al., Shape Anisotropic Chain-Like CoNi/Polydimethylsiloxane Composite Films with Excellent Low-Frequency Microwave Absorption and High Thermal Conductivity, Adv. Funct. Mater., 2025, 35(18), 2316691.
4. H. Kahn and A. H. Heuer, Polysilicon: Mechanical Properties, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, R. W. Cahn and M. C. Flemings, Oxford, Elsevier, 2001, pp. 7724–7727.
5. V. P. Jaecklin, C. Linder and J. Brugger, et al., Mechanical and optical properties of surface micromachined torsional mirrors in silicon, polysilicon and aluminum, Sens. Actuators, A, 1994, 43(1), 269–275.
6. R. Xu and K. Komvopoulos, Fatigue crack growth in polysilicon microstructures subjected to multi-axial loading: a Poisson–Voronoi-based finite element analysis, Int. J. Fatigue, 2023, 177, 107898.
7. S. M. Yang, L. A. Chung and H. R. Wang, Review of polysilicon thermoelectric energy generators, Sens. Actuators, A, 2022, 346, 113890.
8. M. Rydberg and U. Smith, Long-term stability and electrical properties of fluorine doped polysilicon IC-resistors, Mater. Sci. Semicond. Process., 2001, 4(4), 373–382.
9. L. Jalabert, P. Temple-Boyer and F. Olivié, et al., Relation between residual stress and electrical properties of polysilicon/oxide/silicon structures, Microelectron. Reliab., 2000, 40(4), 597–600.
10. M. Zaghdoudi, M. M. Abdelkrim and M. Fathallah, et al., Phosphorus doping and deposition pressure effects on optical and electrical properties of polysilicon, Mater. Sci. Eng., C, 2006, 26(2), 177–180.
11. M. M, S. Sagadevan and B. E, et al., Enhancing biocompatibility and functionality: carbon nanotube-polymer nanocomposites for improved biomedical applications, J. Drug Delivery Sci. Technol., 2024, 99, 105958.
12. A. Taurbekov, V. Fierro and Z. Kuspanov, et al., Nanocellulose and carbon nanotube composites: a universal solution for environmental and energy challenges, J. Environ. Chem. Eng., 2024, 12(5), 113262.
13. I. K. R. A. Dipta and C. W. Lee, Recent advances and perspectives in carbon nanotube production from the electrochemical conversion of carbon dioxide, J. CO2 Util., 2024, 82, 102745.
14. S. M. Ubnoske, E. J. Radauscher and E. R. Meshot, et al., Integrating carbon nanotube forests into polysilicon MEMS: growth kinetics, mechanisms, and adhesion, Carbon, 2017, 113, 192–204.
15. Q. Wu, H. Ye and X. Yang, et al., Synthesis of epoxy resin/silicone rubber interpenetrating polymer network for ablation thermal protection coating, Polym. Degrad. Stab., 2023, 215, 110454.
16. G. Xiong, P. Kang and J. Zhang, et al., Improved adhesion, heat resistance, anticorrosion properties of epoxy resins/POSS/methyl phenyl silicone coatings, Prog. Org. Coat., 2019, 135, 454–464.
17. P. Karamanolevski, A. Bužarovska and G. Bogoeva-Gaceva, The Effect of Curing Agents on Basic Properties of Silicone-epoxy Hybrid Resin, Silicon, 2018, 10(6), 2915–2925.
18. H. Zhang, Y. Guo and Y. Zhao, et al., Liquid Crystal-Engineered Polydimethylsiloxane: Enhancing Intrinsic Thermal Conductivity through High Grafting Density of Mesogens, Angew. Chem., Int. Ed., 2025, 64(14), e202500173.
19. Y. Guo, L. Zhang and K. Ruan, et al., Enhancing hydrolysis resistance and thermal conductivity of aluminum nitride/polysiloxane composites via block copolymer-modification, Polymer, 2025, 323, 128189.
20. M. He, L. Zhang and K. Ruan, et al., Functionalized Aluminum Nitride for Improving Hydrolysis Resistances of Highly Thermally Conductive Polysiloxane Composites, Nano-Micro Lett., 2025, 17(1), 134.
21. P. Santhaveesuk, P. Serichetaphongse and S. Kiat-amnuay, Microwave disinfection of facial silicone prostheses, part 2: mechanical properties, J. Prosthet. Dent., 2024, 131(2), 340.
22. N. A. S. Abdullah, F. F. Abdullah and A. H. Sufian, et al., Effect of degradation by temperature onto nitrile rubber elastomer mechanical properties, Mater. Today: Proc., 2022, 48, 1941–1946.
23. A. Elkholy and R. Kempers, An accurate steady-state approach for characterizing the thermal conductivity of additively manufactured polymer composites, Case Stud. Therm. Eng., 2022, 31, 101829.
24. H. Tanabi and M. Erdal, Effect of CNTs dispersion on electrical, mechanical and strain sensing properties of CNT/epoxy nanocomposites, Results Phys., 2019, 12, 486–503.
25. M. Wen, X. Sun and L. Su, et al., The electrical conductivity of carbon nanotube/carbon black/polypropylene composites prepared through multistage stretching extrusion, Polymer, 2012, 53(7), 1602–1610.
26. S. Kane, S. Warnat and C. Ryan, Improvements in methods for measuring the volume conductivity of electrically conductive carbon powders, Adv. Powder Technol., 2021, 32(3), 702–709.
27. T. E. Warner and T. Graf, On the measurement of the electrical conductivity of graphite-polymer composite bipolar plates, J. Power Sources, 2024, 594, 233871.
28. R. Waremra and P. Betaubun, Analysis of Electrical Properties Using the Four Point Probe Method, E3S Web Conf., 2018, 73, 13019.
29. M. Yang, P. Song and D. Kong, et al., Wear and corrosion properties of HVOF sprayed WC-Cr₃C₂ composite coating for application in polysilicon cyclone separator, J. Mater. Res. Technol., 2024, 29, 78–89.
30. Y. Cao, Y. Teng and P. Zhang, et al., UV ageing of epoxy resin-based glass fiber-reinforced polymer composites incorporating with various curing agents, Mater. Today Commun., 2024, 40, 110061.
31. A. Kausar, Chapter 7 – Cutting-Edge Shape Memory Nanocomposite Sponges, in Shape Memory Polymer-Derived Nanocomposites, ed. A. Kausar, Elsevier, 2024, pp. 133–156.
32. F. Jeyranpour, G. Alahyarizadeh and B. Arab, Comparative investigation of thermal and mechanical properties of cross-linked epoxy polymers with different curing agents by molecular dynamics simulation, J. Mol. Graphics Modell., 2015, 62, 157–164.
33. Z. Han and A. Fina, Thermal conductivity of carbon nanotubes and their polymer nanocomposites: a review, Prog. Polym. Sci., 2011, 36(7), 914–944.
34. L. Li, H. Jiang and Y. Liu, et al., Improvement of thermal conductivity and wear property of Gr/EP composites with CNTs/Cu foam as 3-dimensional reinforcing skeleton, J. Mater. Res. Technol., 2024, 29, 1172–1182.
35. Y. Sheng, C. Li and J. Wang, et al., Multiscale modeling of thermal conductivity of hierarchical CNT-polymer nanocomposite system with progressive agglomeration, Carbon, 2023, 201, 785–795.
36. M. K. Hassanzadeh-Aghdam, M. J. Mahmoodi and J. Jamali, Effect of CNT coating on the overall thermal conductivity of unidirectional polymer hybrid nanocomposites, Int. J. Heat Mass Transfer, 2018, 124, 190–200.
37. M. Wójcik-Bania, TG/MS/FTIR study on thermal degradation process of clay mineral–polysiloxane nanocomposites, Polym. Degrad. Stab., 2022, 206, 110200.
38. W. Si, N. Wang and Y. Zong, et al., Investigation of heat transfer mechanism affecting temperature homogeneity at polysilicon rods in a Siemens reduction furnace, J. Cryst. Growth, 2024, 636, 127693.
39. S. Moradian, M. J. Modarres-Zadeh and R. Abdolvand, Thermal conductivity in nanoscale polysilicon structures with applications in sensors, Sens. Actuators, A, 2019, 295, 596–603.
40. S. Sinha Ray, 15 – Electrical and thermal conductivity of environmentally friendly polymer nanocomposites (EFPNCs) using biodegradable polymer matrices and clay/carbon nanotube (CNT) reinforcements, in Environmentally Friendly Polymer Nanocomposites, ed. S. Sinha Ray, Woodhead Publishing, 2013, pp. 450–464.
41. T. Lalire, C. Longuet and A. Taguet, Electrical properties of graphene/multiphase polymer nanocomposites: a review, Carbon, 2024, 225, 119055.
42. R. Gopika, K. Arun and M. T. Ramesan, Optimizing the structural, thermal, gas sensing and electrical properties of in-situ polymerized poly(thiophene-co-indole)/silicon carbide nanocomposites for energy storage applications, J. Alloys Compd., 2024, 988, 174226.
43. J. Shu, Y. Wang and B. Guo, et al., Effect of Curing Agents on Electrical Properties of Low-Temperature Curing Conductive Coatings and Thermodynamic Analysis, Coatings, 2021, 11(6), 656.
44. W. Jilani, N. Mzabi and N. Fourati, et al., Effects of curing agent on conductivity, structural and dielectric properties of an epoxy polymer, Polymer, 2015, 79, 73–81.
45. K. Zhao, W. Wang and Y. Yang, et al., From Taylor cone to solid nanofiber in tri-axial electrospinning: size relationships, Results Phys., 2019, 15, 102770.
46. P. Karamanolevski, A. Bužarovska and G. Bogoeva-Gaceva, The Effect of Curing Agents on Basic Properties of Silicone-epoxy Hybrid Resin, Silicon, 2018, 10(6), 2915–2925.

---