Open Access Article
Open Access ArticleA comprehensive exploration of Na+ ion transport in NaSICONs using molecular dynamics simulations†
Judith Schuett ab,
Steffen Neitzel-Grieshammer
ab,
Steffen Neitzel-Grieshammer *a,
Shuta Takimotoc,
Ryo Kobayashi
*a,
Shuta Takimotoc,
Ryo Kobayashi d and
Masanobu Nakayama
d and
Masanobu Nakayama c
c
aFaculty of Chemical Engineering, FH Münster – University of Applied Sciences, Stegerwaldstraße 39, 48565 Steinfurt, Germany. E-mail: steffen.neitzel-grieshammer@fh-muenster.de
bInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52056 Aachen, Germany
cDepartment of Advanced Ceramics, Nagoya Institute of Technology, Gokiso, Showa, Nagoya 466-8555, Japan
dDepartment of Applied Physics, Nagoya Institute of Technology, Gokiso, Showa, Nagoya 466-8555, Japan
First published on 2nd June 2025
Abstract
Scandium-substituted Na1+x+yScyZr2−ySixP3−xO12 NaSICONs have emerged as promising electrolyte materials for all-solid-state sodium batteries. However, the comprehensive investigation of these multi-element structures is challenging due to their vast compositional space, leading to a limited number of compositions explored thus far. In this study, we address this issue by employing low-cost, yet high-precision force field molecular dynamics simulations based on density functional theory to investigate the Na+ mobility and resulting conductivity in Na1+x+yScyZr2−ySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2). Our findings show that the incorporation of Sc3+- and Si4+-substituents enhances the conductivity, achieving values of 10−2 S cm−1 at room temperature for moderate to high substitution degrees. Moreover, our study demonstrates the efficacy of the applied methodology for large-scale screening, enabling the exploration of extensive configurational spaces of NaSICONs and other materials for potential use as solid-state electrolytes.
1. Introduction
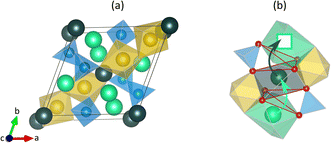
Sodium-based energy storage systems have a longstanding history, but it is only in recent years that they stepped into the spotlight as concerns about limited resource availability of the market-dominating lithium-ion batteries prompted exploration of alternative solutions.1–4 Sodium-ion batteries (NIBs) hold great promise as they provide a broad range of new possibilities, particularly for large-scale energy storage applications owing to the similar chemical properties of sodium and lithium, the abundance of sodium resources, and potential cost reduction.1–15 Meanwhile, all-solid-state batteries (ASS) are being considered as the next generation of batteries due to their prolonged lifetimes, wide temperature ranges, and high energy and power densities.16–26The performance of ASS batteries depends crucially on the applied solid-state electrolyte (SSE), which must provide high conductivity at ambient temperatures. Among Na+-based SSEs, sodium superionic conductors (NaSICONs) have garnered significant attention, given their good thermal and (electro-)chemical stability, high ionic conductivity, and promising performance for ASS-NIBs.17–22,27–40 Several articles provide an overview of the developments of NaSICONs.41–49 The parent NaSICON composition Na1+xZr2SixP3−xO12 (NZSP) exhibits the rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structure above 150 °C, but undergoes a monoclinic (C2/c) phase transformation for 1.6 ≤ x ≤ 2.4 at room temperature.50–58 As shown in Fig. 1a, the structure consists of a rigid three-dimensional framework composed of corner-sharing ZrO6-octahedra and PO4-tetrahedra, between which Na1 (6b) and Na2 (18e) sodium ion sites are located. In the non-substituted structure (x = 0), the energetically more favorable Na1 sites are fully occupied. As the P5+ sites are substituted by Si4+, the Na2 site occupation increases to satisfy the overall charge neutrality.50,51,54,55,57–67 The diffusion of the Na+ charge carriers is based on the correlated knock-off mechanism which involves the potential energy transfer from higher energy Na2 ions to lower energy Na1 ions.68 This diffusion mechanism has already been proposed and studied in detail for various Na+ and Li+ conductors, such as NaSICONs,68–70 garnets,68 and Li2CO3.71 As illustrated in Fig. 1b, a Na2 ion jumps onto an adjacent occupied Na1 site and pushes the Na1 ion onto a neighboring unoccupied Na2 site. The bottlenecks of the migration are formed by opposing ZrO6-octahedra and PO4-tetrahedra adjacent to the pathway.50,51,55,60,61,63,65,72–79
c) structure above 150 °C, but undergoes a monoclinic (C2/c) phase transformation for 1.6 ≤ x ≤ 2.4 at room temperature.50–58 As shown in Fig. 1a, the structure consists of a rigid three-dimensional framework composed of corner-sharing ZrO6-octahedra and PO4-tetrahedra, between which Na1 (6b) and Na2 (18e) sodium ion sites are located. In the non-substituted structure (x = 0), the energetically more favorable Na1 sites are fully occupied. As the P5+ sites are substituted by Si4+, the Na2 site occupation increases to satisfy the overall charge neutrality.50,51,54,55,57–67 The diffusion of the Na+ charge carriers is based on the correlated knock-off mechanism which involves the potential energy transfer from higher energy Na2 ions to lower energy Na1 ions.68 This diffusion mechanism has already been proposed and studied in detail for various Na+ and Li+ conductors, such as NaSICONs,68–70 garnets,68 and Li2CO3.71 As illustrated in Fig. 1b, a Na2 ion jumps onto an adjacent occupied Na1 site and pushes the Na1 ion onto a neighboring unoccupied Na2 site. The bottlenecks of the migration are formed by opposing ZrO6-octahedra and PO4-tetrahedra adjacent to the pathway.50,51,55,60,61,63,65,72–79
The three-dimensional Na+ mobility results in high ionic conductivities, e.g. up to 5.2 × 10−3 S cm−1 for Na3.4Zr2Si2.4P0.6O12 at room temperature.33 However, NZSP is associated with a number of challenges. First, obtaining stoichiometric pure compositions is difficult due to the formation of secondary phases, such as ZrO2. Second, the microstructure depends strongly on the sample preparation method. Both aspects have significant impact on the ionic conductivity.21,45,80
Thus, numerous efforts in the past have been made to further improve NaSICONs in competition with liquid electrolytes. An outstanding feature of NaSICONs with the general formula NaM2(AO4)3 is the ability of accommodating a wide range of M and A cations in the structural framework,49 making multi-element substitution a feasible strategy for enhancing the performance of NaSICONs. For example, the substitution of Zr4+ by Sc3+ in NZSP leads to the suppression of secondary phases, optimization of the microstructure, and thus high Na+ conductivities.81–94 Ma et al. reported a remarkable total conductivity of 4.0 × 10−3 S cm−1 for Na3.4Sc0.4Zr1.6Si2P1O12 at room temperature.81 In addition, Sc3+-substituted structures exhibit a wide electrochemical stability window, suggesting both the application of high voltage cathode materials and the direct utilization of sodium metal anodes to boost the energy density.35,81
However, the multi-element substitution of NaSICONs results in a vast compositional search space that requires fast, low-cost methods for investigating Na+ mobility and resulting conductivity. In this regard, computational techniques, such as molecular dynamics (MD) simulations, have proven as a powerful tool. MD provides comprehensive structural information and the dynamic evolution of conducting systems without relying on prior assumptions about the migration mechanism and pathways. Ionic jump events are directly observed from the modelled real-time dynamics and trajectories of the ions are used to identify the diffusion mechanism and quantify the diffusion properties. However, MD does require the accurate description of interatomic interactions, i.e. the potential energy surface (PES).95,96
In ab initio MD (AIMD) simulations, the interactions between atoms are described by first-principles methods such as density functional theory (DFT), providing high reliability and accuracy as well as great transferability. However, due to its high computational expenses, AIMD is only feasible for small systems in terms of length scale (<1000 atoms) and timescale (∼100 ps) limiting the number of diffusion events.95,96 As a result, diffusion properties estimated from AIMD simulations are often compromised by poor statistics and require high simulation temperatures to ensure a sufficient number of ion jumps.95,97
In contrast, classical force field MD (FFMD) simulations employ interatomic potentials to model the interactions between the ions. The PES is described as a function of the atom positions rather than a variational ground state energy as in AIMD, which significantly reduces computational demands. Consequently, FFMD simulations are amenable for larger systems with up to millions of ions and longer simulation times (>1 ns), resulting in lower statistical variances in the determined diffusion properties. However, the accuracy of FFMD simulations depends on the availability and suitability of the FF parameter sets, which are usually restricted to a limited number of compounds and properties.95,96
To tackle the trade-off between accuracy and efficiency in MD simulations, Kobayashi et al. introduced a high-throughput method for producing reliable FFs using a metaheuristic Cuckoo Search (CS) approach based on structure information from first-principles calculations. In this way, low-cost and accurate FFMD simulations are ensured.98,99
It should be noted that data-driven machine learning potentials (MLP) has emerged as a powerful tool for materials exploration and development, providing an alternative to AIMD and classical FFMD simulations.100–104 In particular, Neural Network Potentials (NNPs) have been demonstrated to reproduce AIMD results with high accuracy.105,106 However, NNPs evaluate energy and forces in a purely empirical manner, which requires large amounts of training data. Additionally, their use in extrapolated spaces, beyond the training set, presents challenges. In contrast, the FF employed in this study, based on a physical model, is expected to maintain a higher degree of consistency even in extrapolated spaces. Moreover, NNPs face limitations in terms of computational time. For instance, in this study, the simulation of 1 ns (106 steps) of a system with approximately 3500 atoms requires about 12 hours on 2 CPU cores. By comparison, performing the same calculation using M3GNet.py,107,108 which is known for its relatively fast performance,109,110 along with the Atomic Simulation Environment (ASE)111 on 16 CPU cores, requires 458 hours. Thus, FFMD simulations are considered advantageous for studies that comprehensively evaluate a large number of compositions at multiple temperatures.
Here, DFT based FFMD simulations of Na1+x+yScyZr2−ySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2), an example of a promising NaSICON compound, are performed to comprehensively investigate the Na+ transport behavior in multi-substituted NaSICONs. Initially, the FF parameters are optimized with the CS algorithm leveraging structural information acquired from short AIMD simulations of a training system. We show that the FF parameters obtained for the training system with a specific composition can be transferred to target systems with arbitrary compositions. The optimized potential parameters are then employed in the subsequent FFMD simulations across the entire compositional range of Na1+x+yScyZr2−ySixP3−xO12. Na+ diffusion coefficients are derived from the collective diffusion events described by their mean squared displacement. In addition, estimated radial distribution functions are analyzed to understand the influence of Sc3+- and Si4+-substitutions on the Na+ transport behavior.
On the one hand, this study aims to deepen the understanding of the influences of multi-element substitution on the transport of Na+ in NaSICONs, all in pursuit of achieving high ionic conductivity for ASS-NIBs applications. On the other hand, this study showcases the efficacy of the applied methodology for large-scale screening, enabling the exploration of extensive configurational spaces of NaSICONs and other materials promising as SSEs.
2. Methods
2.1 Force field model
FFMD simulations of Na+ diffusion in Na1+x+yScyZr2−ySixP3−xO12 require an FF model that describes the ion pair interactions and structural framework of NaSICONs. Thus, the FF model proposed by Kobayashi et al.99 is applied, which consists of two-body potentials112,113 and three-body angular potentials.114The Morse potential is applied to describe the attractive interactions and short-range repulsions of cation–anion pairs,112
 | (1) |
The screened Coulomb potential is added to account for the repulsive interactions among cations or anions. Since the Coulomb potential prevents cation or anion pairs with a small distance, their short-range repulsion can be neglected,112
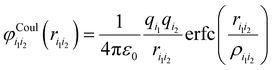 | (2) |
 is a function of the ion distances over the screening length ρi1i2 = f(ri1 + ri2), which is determined by the sum of the effective radii ri1 and ri2 of the ions i1 and i2 and the screening factor f defining the radius of the Coulomb potential.
is a function of the ion distances over the screening length ρi1i2 = f(ri1 + ri2), which is determined by the sum of the effective radii ri1 and ri2 of the ions i1 and i2 and the screening factor f defining the radius of the Coulomb potential.
To avoid discontinuities in the potential energy and force, the following smoothing function with the cutoff radius rc2b is applied to both the Morse and Coulomb pair potential:
 | (3) |
In addition, the Stillinger–Weber (SW) angular potential is applied to describe the framework of the non-migrating cations and oxygen anions,114
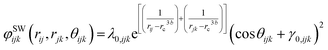 | (4) |
In previous studies, this FF model has been successfully applied to other solid state materials, such as LiZr2(PO4)3,99,115 La(1−x)/3LixNbO3,116 LiAl5O8,117 Li3MCl6,118 and La1−xMxF3−x,99 demonstrating rapid FF production with sufficient accuracy, as described below.
2.2 Force field parameterization
The FF parameters D0,ij, αij and r0,ij of the Morse potential, ρi1i2 of the Coulomb potential, and λijk and γijk of the SW potential must be determined for the Na1+x+yScyZr2−ySixP3−xO12 system. Thus, FF parametrization was conducted using a training system with 120 atoms according to the following steps:(i) AIMD simulations were performed to obtain the equilibrium volume (V0), the radial distribution function (RDF) and the bond angular distribution function (ADF) by averaging the ionic configurations of every 10th step, omitting the first 800 steps to ensure that the system is in equilibrium.
The RDF gij(r) describes the particle density as a function of the distance r from the reference atom i to a surrounding atom j according to eqn (5),
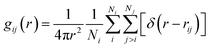 | (5) |
The ADF hijk(θ) describes the particle density as a function of the bond angle θijk between the reference atom i and two other atoms j and k within a given distance (2.8 Å) according to eqn (6),
 | (6) |
Both RDF and ADF are determined by averaging the same element combinations, such as Sc–O, Zr–O, Si–O, P–O, and O–Sc–O, O–Zr–O, O–Si–O, O–P–O for Na1+x+yScyZr2−ySixP3−xO12. The RDF, ADF and V0 are used as reference data in the subsequent FF fitting process.
(ii) The metaheuristic optimization of the FF parameters was performed by the CS algorithm119–121 employing the AIMD reference data obtained in step (i).98,99 The hyperparameters in the CS algorithm are the number of individuals (nests) in each generation (Nn) and the fraction of individuals replaced in the next generation by nests with new random solution (Pn).121
(iii) To evaluate the optimization process, FFMD simulations were performed using the obtained FF parameters. The results of the simulations were analyzed in the same way as for AIMD in step (i). The optimization process was checked for consistency using the loss function L assessing the differences between the RDF, ADF, and V0 values obtained by FFMD and AIMD simulations (eqn (S1)–(S4) in ESI†).122
Step (ii) and (iii) were repeated until the loss function value met the defined convergence criteria.98,99
2.3 Force field molecular dynamics simulations and analysis
With the optimized FF parameters, FFMD simulations were performed for a total of 119 compositions of Na1+x+yZr2−yScySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2) in the temperature range of 298 ≤ T/K ≤ 798 in 100 K steps.From the FFMD simulations, the mean squared displacement MSD of the migrating Na+ (eqn (7)) is obtained, which is used to determine the tracer diffusion coefficient D* (eqn (8)):
 | (7) |
 | (8) |
| D* = HRDσ | (9) |
 | (10) |
Assuming HR = 1, which is expected to have minimal impact on the results, the ionic conductivity is determined using the MSD, and the activation energy EA is derived from the Arrhenius relationship:
 | (11) |
Hereafter, D* will be referred to as D for simplicity.
2.4 Computational details
With the optimized FF parameters, FFMD simulations of supercells with composition Na1+x+yZr2−yScySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2) with up to 4013 atoms were performed in the temperature range of 298 ≤ T/K ≤ 798 in 100 K increments. First, NpT-FFMD simulations were conducted for 10 ps with 1 fs time steps to optimize the cell volume. Subsequently, NVT-FFMD simulations were performed for 1 ns with 1 fs time steps.
The Langevin thermostat, with a relaxation time of 50 fs, was used to control the temperature in both the NpT and NVT ensembles. For pressure regulation in the NpT ensemble, the Berendsen barostat with isotropic coupling and a relaxation of 50 fs was employed. To evaluate the influence of the thermostat on ionic diffusion, additional FFMD simulations were conducted under the NVE ensemble, omitting a heat bath. These simulations show that the diffusion coefficients increase by approximately a factor of 1.4 on average (Fig. S1†). Nevertheless, the overall trend of concentration-dependent diffusion behavior remains largely unchanged.
3. Results
3.1 Validation of optimized force field parameters
The optimization of the FF parameters of the six-component NaSICON structure Na1+x+yScyZr2−ySixP3−xO12 follows a multiple-step process detailed in Section 2 of the ESI.† The FF parameters were optimized using the training system Na3ScZrSiP2O12. For further validation, the obtained FF parameters are applied in FFMD simulations across the entire compositional range of Na1+xZr2SixP3−xO12 (0 ≤ x ≤ 3) at 598 K and the resulting conductivities are compared with literature values. These compositions and temperature are chosen due to the extensive data available in the literature, allowing a comprehensive comparison. Fig. 2 shows the comparison of the resulting conductivities with literature data from experiments and KMC simulations.51,52,55,60,66,135 Although, the data in the literature exhibit significant variation that exceed the uncertainty of the simulation, the conductivities obtained from FFMD simulations in this work and the literature data show similar dependence on the substitution degree x. This indicates that the FF parameters not only adequately describe the NaSICON structure but also capture the interactions between the migrating Na+ and both the structural framework and the neighboring Na+, which are crucial for the Na+ transport in NaSICONs, as highlighted in our previous studies.135,136 It is shown that the parameters originally obtained for the training system with the specific composition Na3ScZrSiP2O12 can be applied to the entire compositional range of Na1+x+yScyZr2−ySixP3−xO12. | ||
| Fig. 2 Comparison of Na+ conductivity of Na1+xZr2SixP3−xO12 (0 ≤ x ≤ 3) at 598 K obtained by FFMD simulations using FF parameters derived from the CS optimization in the Na3ScZrSiP2O12 training system with literature data obtained from experimental studies51,52,55,66 and KMC simulations60,135 at 573 K. | ||
3.2 Microscopic Na+ diffusion
Since the optimized FF parameter adequately describe the NaSICON system, NVT-MD simulations are conducted using this FF parameter set (Table S3†) to investigate the Na+ diffusion behavior in Na1+x+yZr2−yScySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2) over the temperatures range of 298 ≤ T/K ≤ 798. Information about the microscopic Na+ diffusion behavior can be directly obtained from the MD simulations.Fig. 3 depicts the resulting density plot of the accumulated trajectories of the Na+ in Na3Sc1.5Zr0.5Si0.3P2.7O12 over the simulation time, revealing the well-connected three-dimensional Na+ diffusion pathways between the Na1 and Na2 sites that enable the long-range Na+ transport. This conduction pathway is in excellent agreement with the findings of Deng et al.,137 who used a combination of FFMD simulations with parameters of the interatomic potentials developed by Pedone et al.,138 bond valence energy landscape method, maximum-entropy method/Rietveld analysis method.
Fig. 4a depicts the resulting MSDs of the Na+ in Na3Sc1.5Zr0.5Si0.3P2.7O12 at all simulation temperatures. In Fig. 4b, the MSDs of all other ions in the same compound are shown for 698 K. As anticipated, solely the Na+ diffuse in the cell, whereas O2−, Sc3+, Zr4+, Si4+, P5+ vibrate around their initial equilibrium sites.
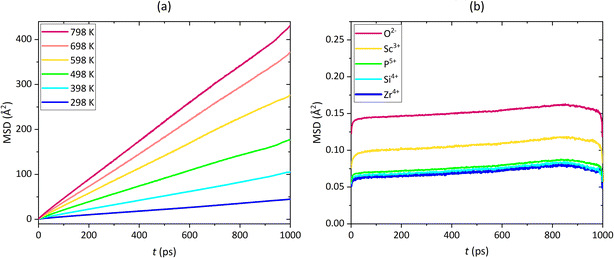 | ||
| Fig. 4 MSD of (a) Na+ in the temperature range of 298 ≤ T/K ≤ 798 and (b) O2−, Sc3+, Zr4+, Si4+, P5+ at 698 K in Na3Sc1.5Zr0.5Si0.5P2.5O12. | ||
3.3 Exploration of the configurational space
The microscopic Na+ diffusion behavior is accurately captured using the optimized FF parameter set. Consequently, the diffusion coefficient, conductivity, and activation energy are predicted across the entire configurational space of Na1+x+yScyZr2−ySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2). As most current studies focus on only a few compositions, this comprehensive prediction offers a broader picture of Na+ diffusion in the Sc3+- and Si4+-substituted NaSICON system.The Na+ tracer diffusion coefficients D are calculated using the MSDs according to eqn (8). Following the approach proposed by Usler et al.,139 the error u(D) in D is estimated, indicating that u(D) is two orders of magnitude smaller than D for temperatures above 498 K. Fig. S9† illustrates the Arrhenius plots for various compositions with different substitution ratios and Na+ concentrations, showing the anticipated linear relationship between D and temperatures above 498 K. Below this temperature, however, deviations from the linearity are observed, probably due to insufficient statistics of Na+ hopping events. The Na+ conductivities σ and activation energies EA are derived from eqn (11). For the determination of EA, only diffusion coefficients obtained at temperatures between 498 ≤ T/K ≤ 798 are considered to ensure a statistically significant number of Na+ jumps. The calculated values of D and σ at 598 K, EA and the cell volumes V of Na1+x+yScyZr2−ySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2) are depicted in Fig. 5. Note that the Na+ diffusion coefficients and conductivities are shown for 598 K rather than room temperature because the conductivity values below 498 K fall within the extrapolated range. Additionally, 598 K is particularly relevant for practical applications, as it corresponds to the operating temperature of NAS batteries.140
It is noted that in this study, the Sc/Zr and Si/P arrangements were randomly configured, and thus the impact of such cation arrangements on the diffusion coefficient of Na+ are investigated. For ten randomly selected compositions, four random initial arrangements were created and the relative deviation of the diffusion coefficient among these was evaluated. The distribution of the obtained diffusion coefficients is shown in Fig. S10.† The variation in diffusion coefficients due to differences in arrangement are very small, with the relative standard error being a maximum of 5.6% and an average of 2.6% across the 10 compositions. Therefore, it is concluded that the supercell size and simulation time (1 ns) applied in this study are sufficiently large.
In our previous studies on Na1+xM2SixP3−xO12, we have revealed the dependence of the Na+ mobility in NaSICONs on both the local ionic environment of the Na+ lattice sites and the Na+ migration energy.135,136 The introduction of Si4+-substituents on P5+ sites corresponds to a charged defect of −1, leading to favorable Na+–Si4+ pair interactions which influence the Na+ mobility. Three compositional ranges in Na1+xM2SixP3−xO12 can be distinguished:
(i) At small substitution concentrations (x < 0.5), there are only a few Na+ charge carriers, that are trapped in low energy states near the introduced Si4+ due to the attractive Na+–Si4+ interactions. The depth and number of traps increases with the number of Si4+, resulting in low conductivities and an increase of the activation energies.
(ii) At intermediate to high substitution concentrations (0.5 ≤ x ≤ 2.0), Na+ percolation pathways form between favorable Si4+-rich positions. The Na+ mobility is thus determined by the migration energy. As a result, the conductivity increases, and the activation energy decreases with substitution content.
(iii) At high substitution concentrations (x > 2.0), the insufficient number of vacant Na+ lattice sites lead to a decrease in ionic conductivity while the activation energy is the lowest due to the low migration energy. However, strong unfavorable Na+–Na+ repulsion may lead to an increase in activation energy.
Accordingly, the behavior of D (Fig. 5a), σ (Fig. 5b), and EA (Fig. 5c) can be described as a function of the substitution degree in Na1+x+yScyZr2−ySixP3−xO12. In this system, the substitution of Sc3+ for Zr4+ and Si4+ for P5+ creates charged defects of −1. At minor substituents concentrations, both D and σ remain low, while EA increases, although less pronounced than previously observed in Na1+xM2SixP3−xO12.135 This behavior can be attributed to the limited number of Na+ charge carriers being trapped in low energy states near the introduced Sc3+ and Si4+ ions. With increasing substitution level, percolation pathways form between Sc3+- and Si4+-rich environments, leading to an increase in both D and σ and a decrease in EA. At high substitution concentrations, D and σ decrease due to the lack of available vacant Na+ sites. But the activation energy is lowest, particularly in the single-substituted structures, as previously observed in Na1+xZr2SixP3−xO12. Though, at high Sc3+- and intermediate Si4+-content, the activation energy is elevated. This can be attributed to strong Na+–Na+ repulsive interactions that prevent the occupation of Na+ sites, as found in Na1+xSn2SixP3−xO12.135 In summary, the simulations reveal that the region of high diffusivity and conductivity follows a diagonal pattern, with increasing values observed at high Sc content (1.3 ≤ y ≤ 1.9) and medium to high Si content (1.3 ≤ x ≤ 2.7).
The comparison of σ (Fig. 5b) and EA (Fig. 5c) with cell volume V (Fig. 5d) shows that there is no clear relation, suggesting that the enlargement of the bottleneck area with increased cell volume has a less pronounced impact on conductivity and activation energy than previously proposed in the literature.49,50,55,65,74–76,78,79
Earlier studies have already experimentally investigated some compositions of Na1+x+yScyZr2−ySixP3−xO12. For example, Lunghammer et al. employed time-domain nuclear magnetic resonance (NMR) and broadband conductivity spectroscopy to investigate the Na+ motion in the Si4+-rich composition Na3.4Sc0.4Zr1.6Si2PO12 on both short- and long-range scales revealing activation energies of 0.13 eV to 0.15 eV and 0.29 eV to 0.31 eV, respectively.82 Rapid Na+ exchange leads to ionic conductivities of 2 × 10−3 S cm−1 at 25 °C.82 For the same composition, Ma et al. reported bulk conductivities of 6.2 × 10−3 S cm−1 at 298 K.81 For the Sc3+-rich composition Na3.4Sc2Si0.4P2.6O12, Kaus et al. observed values of EA = 0.2 eV and σ = 4 × 10−3 S cm−1 at 350 K using NMR relaxometry.83 In a separate study, Guin et al. conducted impedance measurements on the same composition, reporting an activation energy of 0.14 eV, which corresponds to the bulk transport.84 In comparison, MD simulations of this study yield values of EA = 0.11 eV and σ = 2.6 × 10−2 S cm−1 at 298 K for the Si4+-rich composition Na3.4Sc0.4Zr1.6Si2PO12, and EA = 0.08 eV and σ = 1 × 10−1 S cm−1 at 350 K for the Sc3+-rich composition Na3.4Sc2Si0.4P2.6O12. The values obtained for EA in this study are consistent with the values for short-range bulk Na+ transport, capturing the elementary diffusion processes involving local, correlated motions influenced by Coulomb interactions and structural disorder.82 However, the obtained values for σ are one to two orders of magnitude higher than those reported in previously cited studies.81–84 Nevertheless, our findings are in good agreement with the conductivities determined by Subramanian et al. at 573 K, using impedance measurements for various compositions, such as σ = 1.35 × 10−1 S cm−1 versus σ = 1.07 × 10−1 S cm−1 for Na3Sc0.5Zr1.5Si1.5P1.5O12.90 Moreover, similar general behavior of conductivity and activation energy as a function of the substitution concentration have been reported in the literature for Na3+yScyZr2−ySi2PO12 (0 ≤ y ≤ 0.6) and of Na3+xSc2SixP3−xO12 (0.05 ≤ x ≤ 0.8).81,84,94
The effect of Sc3+- and Si4+-substitution on the Na+ diffusion behavior in NaSICONs is further clarified by estimating RDFs of cations adjacent to the Na+ sites. Fig. 6a illustrates der RDFs of Si4+–Na+ and P5+-Na+ in Na1.5Zr2Si0.5P2.5O12. At smaller distances, the peak of the RDF of Si4+–Na+ pairs is larger compared to that of P5+–Na+ pairs, which indicates that more Na+ are adjacent to Si4+ than to P5+, suggesting the Na+ trapping by the Si4+-substituents.
 | ||
| Fig. 6 Comparison of (a) RDFs of Si4+–Na+ (solid line) and P5+–Na+ (dashed line) in Na1.5Zr2Si0.5P2.5O12 and (b) RDFs of Sc3+–Na+ (solid line) and Zr4+–Na+ (dash line) in Na1.3Sc0.3Zr1.7P3O12. | ||
Similarly, Fig. 6b shows the comparison of the RDFs of Sc3+–Na+ and Zr4+–Na+ pairs in Na1.3Sc0.3Zr1.7P3O12. The RDF of Sc3+–Na+ pairs exhibit larger peak than that of Zr4+–Na+ pairs at small distances, indicating that the Na+ are trapped by Sc3+ substituents.
4. Conclusion
The Na+ transport properties in NaSICONs were exhaustively investigated in Na1+x+yScyZr2−ySixP3−xO12 (0 ≤ x ≤ 3; 0 ≤ y ≤ 2) using FFMD simulations. For this purpose, FF parameters were determined based on the structural information of the training system Na3ScZrSiP2O12 obtained from short AIMD simulations. The obtained FF parameters can be applied to target systems with arbitrary compositions, which they describe with performance comparable to DFT calculations. This underscores the effectiveness of the FF model in characterizing the structure and interactions in NaSICONs and in describing the Na+ transport behavior without necessitating explicit consideration of the ion migration and transition state structure. In this way, the exhaustive exploration of the Na+ transport in NaSICONs across a broad spectrum of compositions is feasible using fast, low-cost, and yet accurate FFMD simulations.NVT-MD simulations revealed the three-dimensional diffusion pathways of Na+ ions between the Na1 and Na2 sites. The resulting Na+ diffusion coefficients D, ionic conductivities σ, and activation energies EA show similar dependence on the substitution concentration as previously observed for the single-substituted structures Na1+xM2SixP3−xO12. The Na+ transport behavior is primarily governed by the effects of Na+ trapping and percolation caused by the introduced substituents. At minor substitution concentrations, Na+ are trapped in low energy states near the substituents, resulting in low values of D and σ and high values of EA. At intermediate substitution levels, Na+ percolation pathways are formed, leading to an increase in D and σ and decrease in EA. However, at very high substitution levels, D and σ decrease due to the lack of available Na+ sites. Overall, the simulations indicate that the highest diffusivity and conductivity occur along a diagonal compositional trend, corresponding to elevated Sc contents (1.3 ≤ y ≤ 1.9) and moderate to high Si contents (1.3 ≤ x ≤ 2.7). The activation energies are found to be in good agreement with experimental values describing short-range Na+ ion motions.
In addition, the Na+ trapping effects of the introduced Sc3+- and Si4+-substitution was verified by estimating RDFs, providing further insights into the Na+ migration behavior.
This study demonstrates the efficacy of the applied methodology in exploring large configurational spaces of NaSICONs and predicting promising materials for use in ASS-NIBs. The FFMD simulations, applying FF parameters optimized for the particular system under investigation, offer a computationally efficient way to identify substitution levels that lead to the highest conductivities. This allows further investigations to focus on this optimal range instead of exploring large compositional spaces. The key advantage of the applied method is its simplicity and versatility, making it applicable to a wide range of compounds and structures. In addition, the crucial impact of substitution in NaSICONs is further elucidated, indicating the high potential of these materials, especially Na1+x+yScyZr2−ySixP3−xO12.
Data availability
The data supporting this article have been included as part of the ESI.† The raw data is available from the authors upon request.Author contributions
M. N., J. S. and S. N. conceived the study. J. S. and S. T. performed the simulations. All the authors contributed to the discussion and the paper writing.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
This research was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project number 452855747. J. S. is International Research Fellow of Japan Society for the Promotion of Science.References
- C. Delmas, Sodium and sodium-ion batteries: 50 years of research, Adv. Energy Mater., 2018, 8, 1703137 CrossRef
.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Research development on sodium-ion batteries, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed
.
- D. Larcher and J.-M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed
.
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, The emerging chemistry of sodium ion batteries for electrochemical energy storage, Angew. Chem., Int. Ed., 2015, 54, 3431–3448 CrossRef CAS PubMed
.
- B. L. Ellis and L. F. Nazar, Sodium and sodium-ion energy storage batteries, Curr. Opin. Solid State Mater. Sci., 2012, 16, 168–177 CrossRef CAS
.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Na-ion batteries, recent advances and present challenges to become low cost energy storage systems, Energy Environ. Sci., 2012, 5, 5884–5901 RSC
.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Sodium-ion batteries, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS
.
- H. Pan, Y.-S. Hu and L. Chen, Room-temperature stationary sodium-ion batteries for large-scale electric energy storage, Energy Environ. Sci., 2013, 6, 2338–2360 RSC
.
- S. Y. Hong, Y. Kim, Y. Park, A. Choi, N.-S. Choi and K. T. Lee, Charge carriers in rechargeable batteries: Na ions vs. Li ions, Energy Environ. Sci., 2013, 6, 2067–2081 RSC
.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Sodium-ion batteries: present and future, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC
.
- A. Eftekhari and D.-W. Kim, Sodium-ion batteries: new opportunities beyond energy storage by lithium, J. Power Sources, 2018, 395, 336–348 CrossRef CAS
.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, A cost and resource analysis of sodium-ion batteries, Nat. Rev. Mater., 2018, 3, 1–11 CrossRef
.
- L. Chen, M. Fiore, J. E. Wang, R. Ruffo, D.-K. Kim and G. Longoni, Readiness level of sodium-ion battery technology: a materials review, Adv. Sustainable Syst., 2018, 2, 1700153 CrossRef
.
- T. Liu, Y. Zhang, Z. Jiang, X. Zeng, J. Ji, Z. Li, X. Gao, M. Sun, Z. Lin and M. Ling, Exploring competitive features of stationary sodium ion batteries for electrochemical energy storage, Energy Environ. Sci., 2019, 12, 1512–1533 RSC
.
- Y. E. Durmus, H. Zhang, F. Baakes, G. Desmaizieres, H. Hayun, L. Yang, M. Kolek, V. Küpers, J. Janek and D. Mandler, Side by side battery technologies with lithium-ion based batteries, Adv. Energy Mater., 2020, 10, 2000089 CrossRef CAS
.
- C. Jiang, H. Li and C. Wang, Recent progress in solid-state electrolytes for alkali-ion batteries, Sci. Bull., 2017, 62, 1473–1490 CrossRef CAS PubMed
.
- W. Hou, X. Guo, X. Shen, K. Amine, H. Yu and J. Lu, Solid electrolytes and interfaces in all-solid-state sodium batteries: Progress and perspective, Nano Energy, 2018, 52, 279–291 CrossRef CAS
.
- C. Zhao, L. Liu, X. Qi, Y. Lu, F. Wu, J. Zhao, Y. Yu, Y.-S. Hu and L. Chen, Solid-state sodium batteries, Adv. Energy Mater., 2018, 8, 1703012 CrossRef
.
- C. Zhou, S. Bag and V. Thangadurai, Engineering materials for progressive all-solid-state Na batteries, ACS Energy Lett., 2018, 3, 2181–2198 CrossRef CAS
.
- L. Fan, S. Wei, S. Li, Q. Li and Y. Lu, Recent progress of the solid-state electrolytes for high-energy metal-based batteries, Adv. Energy Mater., 2018, 8, 1702657 CrossRef
.
- Q. Ma and F. Tietz, Solid-state electrolyte materials for sodium batteries: towards practical applications, ChemElectroChem, 2020, 7, 2693–2713 CrossRef CAS
.
- V. Thangadurai and B. Chen, Solid Li-and Na-Ion Electrolytes for Next Generation Rechargeable Batteries, Chem. Mater., 2022, 34, 6637–6658 CrossRef CAS
.
- H. Che, S. Chen, Y. Xie, H. Wang, K. Amine, X.-Z. Liao and Z.-F. Ma, Electrolyte design strategies and research progress for room-temperature sodium-ion batteries, Energy Environ. Sci., 2017, 10, 1075–1101 RSC
.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed
.
- D. H. S. Tan, A. Banerjee, Z. Chen and Y. S. Meng, From nanoscale interface characterization to sustainable energy storage using all-solid-state batteries, Nat. Nanotechnol., 2020, 15, 170–180 CrossRef CAS PubMed
.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Development of solid-state electrolytes for sodium-ion battery–a short review, NMS, 2019, 1, 91–100 Search PubMed
.
- Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J. Yamaki, Fabrication and performances of all solid-state symmetric sodium battery based on NASICON-related compounds, Electrochim. Acta, 2013, 101, 59–65 CrossRef CAS
.
- F. Lalère, J.-B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, An all-solid state NASICON sodium battery operating at 200 °C, J. Power Sources, 2014, 247, 975–980 CrossRef
.
- S. Song, H. M. Duong, A. M. Korsunsky, N. Hu and L. Lu, A Na+ superionic conductor for room-temperature sodium batteries, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed
.
- W. Zhou, Y. Li, S. Xin and J. B. Goodenough, Rechargeable sodium all-solid-state battery, ACS Cent. Sci., 2017, 3, 52–57 CrossRef CAS PubMed
.
- Z. Zhang, Q. Zhang, J. Shi, Y. S. Chu, X. Yu, K. Xu, M. Ge, H. Yan, W. Li and L. Gu, A self-forming composite electrolyte for solid-state sodium battery with ultralong cycle life, Adv. Energy Mater., 2017, 7, 1601196 CrossRef
.
- T. Lan, C.-L. Tsai, F. Tietz, X.-K. Wei, M. Heggen, R. E. Dunin-Borkowski, R. Wang, Y. Xiao, Q. Ma and O. Guillon, Room-temperature all-solid-state sodium batteries with robust ceramic interface between rigid electrolyte and electrode materials, Nano Energy, 2019, 65, 104040 CrossRef CAS
.
- Q. Ma, C.-L. Tsai, X.-K. Wei, M. Heggen, F. Tietz and J. T. S. Irvine, Room temperature demonstration of a sodium superionic conductor with grain conductivity in excess of 0.01 S cm−1 and its primary applications in symmetric battery cells, J. Mater. Chem., 2019, 7, 7766–7776 RSC
.
- P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, Electrochemical performance of all-solid-state sodium-ion model cells with crystalline NaxCoO2 thin-film cathodes, J. Electrochem. Soc., 2019, 166, A5328 CrossRef CAS
.
- P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, Sc-substituted Nasicon solid electrolyte for an all-solid-state NaxCoO2/Nasicon/Na sodium model battery with stable electrochemical performance, J. Power Sources, 2019, 409, 86–93 CrossRef CAS
.
- Y. Lu, J. A. Alonso, Q. Yi, L. Lu, Z. L. Wang and C. Sun, A high-performance monolithic solid-state sodium battery with Ca2+ doped Na3Zr2Si2PO12 electrolyte, Adv. Energy Mater., 2019, 9, 1901205 CrossRef
.
- E. Matios, H. Wang, C. Wang, X. Hu, X. Lu, J. Luo and W. Li, Graphene regulated ceramic electrolyte for solid-state sodium metal battery with superior electrochemical stability, ACS Appl. Mater. Interfaces, 2019, 11, 5064–5072 CrossRef CAS PubMed
.
- Z. Zhang, S. Wenzel, Y. Zhu, J. Sann, L. Shen, J. Yang, X. Yao, Y.-S. Hu, C. Wolverton and H. Li, Na3Zr2Si2PO12: a stable Na+-ion solid electrolyte for solid-state batteries, ACS Appl. Energy Mater., 2020, 3, 7427–7437 CrossRef CAS
.
- J. Yang, G. Liu, M. Avdeev, H. Wan, F. Han, L. Shen, Z. Zou, S. Shi, Y.-S. Hu and C. Wang, Ultrastable all-solid-state sodium rechargeable batteries, ACS Energy Lett., 2020, 5, 2835–2841 CrossRef CAS
.
- X. Wang, W. Mei, J. Chen, D. Wang and Z. Mao, Rare Earth Oxide-Assisted Sintered NASICON Electrolyte Composed of a Phosphate Grain Boundary Phase with Low Electronic Conductivity, ACS Appl. Energy Mater., 2021, 5, 777–783 CrossRef
.
- J. Alamo and R. Roy, Crystal chemistry of the NaZr2(PO4)3, NZP or CTP, structure family, J. Mater. Sci., 1986, 21, 444–450 CrossRef CAS
.
- N. a. Anantharamulu, K. Koteswara Rao, G. Rambabu, B. Vijaya Kumar, V. Radha and M. Vithal, A wide-ranging review on Nasicon type materials, J. Mater. Sci., 2011, 46, 2821–2837 CrossRef CAS
.
- R. Rajagopalan, Z. Zhang, Y. Tang, C. Jia, X. Ji and H. Wang, Understanding crystal structures, ion diffusion mechanisms and sodium storage behaviors of NASICON materials, Energy Storage Mater., 2021, 34, 171–193 CrossRef
.
- Z. Yang, B. Tang, Z. Xie and Z. Zhou, NASICON-type Na3Zr2Si2PO12 solid-state electrolytes for sodium batteries, ChemElectroChem, 2021, 8, 1035–1047 CrossRef CAS
.
- Y. B. Rao, K. K. Bharathi and L. N. Patro, Review on the synthesis and doping strategies in enhancing the Na ion conductivity of Na3Zr2Si2PO12 (NASICON) based solid electrolytes, Solid State Ionics, 2021, 366, 115671 CrossRef
.
- C. Li, R. Li, K. Liu, R. Si, Z. Zhang and Y.-S. Hu, NaSICON: a promising solid electrolyte for solid-state sodium batteries, Interdiscip. Mater., 2022, 1, 396–416 Search PubMed
.
- L. Zhang, Y. Liu, Y. You, A. Vinu and L. Mai, NASICONs-type solid-state electrolytes: the history, physicochemical properties, and challenges, Interdiscip. Mater., 2023, 2, 91–110 Search PubMed
.
- K. Singh, A. Chakraborty, R. Thirupathi and S. Omar, Recent advances in NASICON-type oxide electrolytes for solid-state sodium-ion rechargeable batteries, Ionics, 2022, 28, 5289–5319 CrossRef CAS
.
- M. Guin and F. Tietz, Survey of the transport properties of sodium superionic conductor materials for use in sodium batteries, J. Power Sources, 2015, 273, 1056–1064 CrossRef CAS
.
- H.-P. Hong, Crystal structures and crystal chemistry in the system Na1+xZr2SixP3−xO12, Mater. Res. Bull., 1976, 11, 173–182 CrossRef CAS
.
- J. B. Goodenough, H.-P. Hong and J. A. Kafalas, Fast Na+-ion transport in skeleton structures, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS
.
- J. P. Boilot, J. P. Salanie, G. Desplanches and D. Le Potier, Phase transformation in Na1+xSixZr2P3−xO12 compounds, Mater. Res. Bull., 1979, 14, 1469–1477 CrossRef CAS
.
- U. von Alpen, M. F. Bell and W. Wichelhaus, Phase transition in nasicon (Na3Zr2Si2PO12), Mater. Res. Bull., 1979, 14, 1317–1322 CrossRef CAS
.
- J.-J. Didisheim, E. Prince and B. J. Wuensch, Neutron Rietveld analysis of structural changes in NASICON solid solutions Na1+xZr2SixP3−xO12 at elevated temperatures: x = 1.6 and 2.0 at 320 °C, Solid State Ionics, 1986, 18, 944–958 CrossRef
.
- W. H. Baur, J. R. Dygas, D. H. Whitmore and J. Faber, Neutron powder diffraction study and ionic conductivity of Na2Zr2SiP2O12 and Na3Zr2Si2PO12, Solid State Ionics, 1986, 18, 935–943 CrossRef
.
- T. Feist, P. K. Davies and E. Vogel, The energetics of phase transitions in the system Na1+xSixZr2P3−xO12 1.9 ≤ x ≤ 2.5, Thermochim. Acta, 1986, 106, 57–61 CrossRef CAS
.
- J. P. Boilot, G. Collin and P. Colomban, Crystal structure of the true NASICON: Na3Zr2Si2PO12, Mater. Res. Bull., 1987, 22, 669–676 CrossRef CAS
.
- J.-P. Boilot, G. Collin and P. Colomban, Relation structure-fast ion conduction in the NASICON solid solution, J. Solid State Chem., 1988, 73, 160–171 CrossRef CAS
.
- L.-O. Hagman, P. Kierkegaard, P. Karvonen, A. I. Virtanen and J. Paasivirta, The crystal structure of NaMe2IV(PO4)3; MeIV = Ge, Ti, Zr, Acta Chem. Scand., 1968, 22, 1822–1832 CrossRef CAS
.
- Z. Deng, T. P. Mishra, E. Mahayoni, Q. Ma, A. J. K. Tieu, O. Guillon, J.-N. Chotard, V. Seznec, A. K. Cheetham, C. Masquelier, G. S. Gautam and P. Canepa, Fundamental investigations on the sodium-ion transport properties of mixed polyanion solid-state battery electrolytes, Nat. Commun., 2022, 13, 4470 CrossRef CAS PubMed
.
- P. P. Kumar and S. Yashonath, Structure, Conductivity, and Ionic Motion in Na1+xSixZr2P3−xO12: A Simulation Study, J. Phys. Chem. B, 2002, 106, 7081–7089 CrossRef CAS
.
- S. Roy and P. Padma Kumar, Framework flexibility of sodium zirconium phosphate: role of disorder, and polyhedral distortions from Monte Carlo investigation, J. Mater. Sci., 2012, 47, 4946–4954 CrossRef CAS
.
- S. Roy and P. P. Kumar, Influence of Cationic ordering on ion transport in NASICONs: molecular dynamics study, Solid State Ionics, 2013, 253, 217–222 CrossRef CAS
.
- Z. Deng, G. Sai Gautam, S. K. Kolli, J.-N. Chotard, A. K. Cheetham, C. Masquelier and P. Canepa, Phase Behavior in Rhombohedral NaSiCON Electrolytes and Electrodes, Chem. Mater., 2020, 32, 7908–7920 CrossRef CAS
.
- Z. Zou, N. Ma, A. Wang, Y. Ran, T. Song, Y. Jiao, J. Liu, H. Zhou, W. Shi, B. He, D. Wang, Y. Li, M. Avdeev and S. Shi, Relationships Between Na+ Distribution, Concerted Migration, and Diffusion Properties in Rhombohedral NASICON, Adv. Energy Mater., 2020, 10, 2001486 CrossRef CAS
.
- D. T. Qui, J. J. Capponi, J. C. Joubert and R. D. Shannon, Crystal structure and ionic conductivity in Na4Zr2Si3O12, J. Solid State Chem., 1981, 39, 219–229 CrossRef CAS
.
- C. Delmas, R. Olazcuaga, G. Le Flem, P. Hagenmuller, F. Cherkaoui and R. Brochu, Crystal chemistry of the Na1+xZr2−xLx(PO4)3 (L = Cr, In, Yb) solid solutions, Mater. Res. Bull., 1981, 16, 285–290 CrossRef CAS
.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed
.
- Y. Noda, K. Nakano, H. Takeda, M. Kotobuki, L. Lu and M. Nakayama, Computational and Experimental Investigation of the Electrochemical Stability and Li-Ion Conduction Mechanism of LiZr2(PO4)3, Chem. Mater., 2017, 29, 8983–8991 CrossRef CAS
.
- Y. Noda, K. Nakano, M. Otake, R. Kobayashi, M. Kotobuki, L. Lu and M. Nakayama, Research Update: Ca doping effect on the Li-ion conductivity in NASICON-type solid electrolyte LiZr2(PO4)3: a first-principles molecular dynamics study, APL Mater., 2018, 6, 60702 CrossRef
.
- S. Shi, P. Lu, Z. Liu, Y. Qi, L. G. Hector JR, H. Li and S. J. Harris, Direct Calculation of Li-Ion Transport in the Solid Electrolyte Interphase, J. Am. Chem. Soc., 2012, 134, 15476–15487 CrossRef CAS PubMed
.
- S. Roy and P. Padma Kumar, Influence of Si/P ordering on Na+ transport in NASICONs, Phys. Chem. Chem. Phys., 2013, 15, 4965–4969 RSC
.
- Z. Zhang, Z. Zou, K. Kaup, R. Xiao, S. Shi, M. Avdeev, Y.-S. Hu, D. Wang, B. He, H. Li, X. Huang, L. F. Nazar and L. Chen, Correlated Migration Invokes Higher Na+-Ion Conductivity in NaSICON-Type Solid Electrolytes, Adv. Energy Mater., 2019, 9, 1902373 CrossRef CAS
.
- Z. Zou, N. Ma, A. Wang, Y. Ran, T. Song, B. He, A. Ye, P. Mi, L. Zhang, H. Zhou, Y. Jiao, J. Liu, D. Wang, Y. Li, M. Avdeev and S. Shi, Identifying Migration Channels and Bottlenecks in Monoclinic NASICON-Type Solid Electrolytes with Hierarchical Ion-Transport Algorithms, Adv. Funct. Mater., 2021, 31, 2107747 CrossRef CAS
.
- H. Kohler, H. Schulz and O. Melnikov, Composition and conduction mechanism of the NASICON structure X-ray diffraction study on two crystals at different temperatures, Mater. Res. Bull., 1983, 18, 1143–1152 CrossRef CAS
.
- H. Kohler and H. Schulz, NASICON solid electrolytes part I: the Na+-diffusion path and its relation to the structure, Mater. Res. Bull., 1985, 20, 1461–1471 CrossRef CAS
.
- H. Kohler and H. Schulz, NASICON solid electrolytes part II – X-ray diffraction experiments on sodium-zirconium-phosphate single crystals at 295 K and at 993 K, Mater. Res. Bull., 1986, 21, 23–31 CrossRef CAS
.
- E. R. Losilla, M. A. G. Aranda, S. Bruque, M. A. París, J. Sanz and A. R. West, Understanding Na Mobility in NASICON Materials: a Rietveld, 23Na and 31P MAS NMR, and Impedance Study, Chem. Mater., 1998, 10, 665–673 CrossRef CAS
.
- H. Park, K. Jung, M. Nezafati, C.-S. Kim and B. Kang, Sodium Ion Diffusion in Nasicon (Na3Zr2Si2PO12) Solid Electrolytes: Effects of Excess Sodium, ACS Appl. Mater. Interfaces, 2016, 8, 27814–27824 CrossRef CAS PubMed
.
- S. Naqash, D. Sebold, F. Tietz and O. Guillon, Microstructure–conductivity relationship of Na3Zr2(SiO4)2(PO4) ceramics, J. Am. Ceram. Soc., 2019, 102, 1057–1070 CrossRef CAS
.
- Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Scandium-substituted Na3Zr2(SiO4)2(PO4) prepared by a solution-assisted solid-state reaction method as sodium-ion conductors, Chem. Mater., 2016, 28, 4821–4828 CrossRef CAS
.
- S. Lunghammer, D. Prutsch, S. Breuer, D. Rettenwander, I. Hanzu, Q. Ma, F. Tietz and H. M. Wilkening, Fast Na ion transport triggered by rapid ion exchange on local length scales, Sci. Rep., 2018, 8, 1–8 CAS
.
- M. Kaus, M. Guin, M. Yavuz, M. Knapp, F. Tietz, O. Guillon, H. Ehrenberg and S. Indris, Fast Na+ ion conduction in NASICON-type Na3.4Sc2(SiO4)0.4(PO4)2.6 observed by 23Na NMR relaxometry, J. Phys. Chem. C, 2017, 121, 1449–1454 CrossRef CAS
.
- M. Guin, F. Tietz and O. Guillon, New promising NASICON material as solid electrolyte for sodium-ion batteries: correlation between composition, crystal structure and ionic conductivity of Na3+xSc2SixP3−xO12, Solid State Ionics, 2016, 293, 18–26 CrossRef CAS
.
- M. Guin, E. Dashjav, C. M. Kumar, F. Tietz and O. Guillon, Investigation of crystal structure and ionic transport in a scandium-based NASICON material by neutron powder diffraction, Solid State Sci., 2017, 67, 30–36 CrossRef CAS
.
- S. K. Pal, R. Saha, G. V. Kumar and S. Omar, Designing high ionic conducting NASICON-type Na3Zr2Si2PO12 solid-electrolytes for Na-ion batteries, J. Phys. Chem. C, 2020, 124, 9161–9169 CrossRef CAS
.
- J. M. Winand, A. Rulmont and P. Tarte, Ionic conductivity of the Na1+xMxIIIZr2−x(PO4)3 systems (M = Al, Ga, Cr, Fe, Sc, In, Y, Yb), J. Mater. Sci., 1990, 25, 4008–4013 CrossRef CAS
.
- P. J. Squattrito, P. R. Rudolf, P. G. Hinson, A. Clearfield, K. Volin and J. D. Jorgensen, Sodium and oxygen disorder in a scandium-substituted nasicon: a time of flight neutron powder diffraction study of Na2.5Zr1.8Sc0.2Si1.3P1.7O12, Solid State Ionics, 1988, 31, 31–40 CrossRef CAS
.
- G. Collin, R. Comes, J. P. Boilot and P. Colomban, Disorder of tetrahedra in Nasicon-type structure—I.: Na3Sc2(PO4)3: structures and ion-ion correlations, J. Phys. Chem. Solids, 1986, 47, 843–854 CrossRef CAS
.
- M. A. Subramanian, P. R. Rudolf and A. Clearfield, The preparation, structure, and conductivity of scandium-substituted NASICONs, J. Solid State Chem., 1985, 60, 172–181 CrossRef CAS
.
- S. Susman, C. J. Delbecq, T. O. Brun and E. Prince, Fast ion transport in the NASICON analog Na3Sc2(PO4)3: structure and conductivity, Solid State Ionics, 1983, 9, 839–844 CrossRef
.
- L. Ladenstein, S. Lunghammer, E. Y. Wang, L. J. Miara, H. M. R. Wilkening, G. J. Redhammer and D. Rettenwander, On the dependence of ionic transport on crystal orientation in NASICON-type solid electrolytes, JPhys Energy, 2020, 2, 35003 CrossRef CAS
.
- F. Sun, Y. Xiang, Q. Sun, G. Zhong, M. N. Banis, Y. Liu, R. Li, R. Fu, M. Zheng and T.-K. Sham, Origin of high ionic conductivity of Sc-doped sodium-rich NASICON solid-state electrolytes, Adv. Funct. Mater., 2021, 31, 2102129 CrossRef CAS
.
- T. Zinkevich, A. Fiedler, M. Guin, F. Tietz, O. Guillon, H. Ehrenberg and S. Indris, Na+ ion mobility in Na3+xSc2(SiO4)x(PO4)3−x (0.1 < x < 0.8) observed by 23Na NMR spectroscopy, Solid State Ionics, 2020, 348, 115277 CrossRef CAS
.
- Y. Gao, A. M. Nolan, P. Du, Y. Wu, C. Yang, Q. Chen, Y. Mo and S.-H. Bo, Classical and Emerging Characterization Techniques for Investigation of Ion Transport Mechanisms in Crystalline Fast Ionic Conductors, Chem. Rev., 2020, 120, 5954–6008 CrossRef CAS PubMed
.
- A. van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Rechargeable Alkali-Ion Battery Materials: Theory and Computation, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed
.
- X. He, Y. Zhu, A. Epstein and Y. Mo, Statistical variances of diffusional properties from ab initio molecular dynamics simulations, npj Comput. Mater., 2018, 4, 18 CrossRef
.
- R. Kobayashi, nap: a molecular dynamics package with parameter-optimization programs for classical and machine-learning potentials, J. Open Source Softw., 2021, 6, 2768 CrossRef
.
- R. Kobayashi, Y. Miyaji, K. Nakano and M. Nakayama, High-throughput production of force-fields for solid-state electrolyte materials, APL Mater., 2020, 8, 81111 CrossRef CAS
.
- R. Jalem, K. Kanamori, I. Takeuchi, M. Nakayama, H. Yamasaki and T. Saito, Bayesian-Driven First-Principles Calculations for Accelerating Exploration of Fast Ion Conductors for Rechargeable Battery Application, Sci. Rep., 2018, 8, 5845 CrossRef PubMed
.
- T. Atsumi, K. Sato, Y. Yamaguchi, M. Hamaie, R. Yasuda, N. Tanibata, H. Takeda, M. Nakayama, M. Karasuyama and I. Takeuchi, Chemical Composition Data-Driven Machine-Learning Prediction for Phase Stability and Materials Properties of Inorganic Crystalline Solids, Phys. Status Solidi B, 2022, 259, 2100525 CrossRef CAS
.
- S. Sekine, T. Hosaka, H. Maejima, R. Tatara, M. Nakayama and S. Komaba, Na[Mn0.36Ni0.44Ti0.15Fe0.05]O2 predicted via machine learning for high energy Na-ion batteries, J. Mater. Chem., 2024, 12, 31103–31107 RSC
.
- Q. Zhao, L. Zhang, B. He, A. Ye, M. Avdeev, L. Chen and S. Shi, Identifying descriptors for Li+ conduction in cubic Li-argyrodites via hierarchically encoding crystal structure and inferring causality, Energy Storage Mater., 2021, 40, 386–393 CrossRef
.
- Q. Zhao, M. Avdeev, L. Chen and S. Shi, Machine learning prediction of activation energy in cubic Li-argyrodites with hierarchically encoding crystal structure-based (HECS) descriptors, Sci. Bull., 2021, 66, 1401–1408 CrossRef CAS PubMed
.
- S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi, Y. Asano, T. Onodera, T. Ishii, T. Kudo, H. Ono, R. Sawada, R. Ishitani, M. Ong, T. Yamaguchi, T. Kataoka, A. Hayashi, N. Charoenphakdee and T. Ibuka, Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements, Nat. Commun., 2022, 13, 2991 CrossRef CAS PubMed
.
- R. Iwasaki, N. Tanibata, H. Takeda and M. Nakayama, Universal-neural-network-potential molecular dynamics for lithium metal and garnet-type solid electrolyte interface, Commun. Mater., 2024, 5, 148 CrossRef CAS
.
- J. Qi, T. W. Ko, B. C. Wood, T. A. Pham and S. P. Ong, Robust training of machine learning interatomic potentials with dimensionality reduction and stratified sampling, npj Comput. Mater., 2024, 10, 43 CrossRef
.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed
.
- K. Makino, N. Tanibata, H. Takeda and M. Nakayama, Computational studies on Mg ion conductivity in Mg2xHf1−xNb(PO4)3 using neural network potential, J. Solid State Electrochem., 2024, 28, 4471–4481 CrossRef CAS
.
- D. Kwon and D. Kim, Machine learning interatomic potentials in engineering perspective for developing cathode materials, J. Mater. Chem., 2024, 12, 23837–23847 RSC
.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.:Condens. Matter, 2017, 29, 273002 CrossRef PubMed
.
- H. Chen, L. L. Wong and S. Adams, SoftBV–a software tool for screening the materials genome of inorganic fast ion conductors, Acta Crystallogr., Sect. B, 2019, 75, 18–33 CrossRef CAS PubMed
.
- H. Chen and S. Adams, Bond softness sensitive bond-valence parameters for crystal structure plausibility tests, IUCrJ, 2017, 4, 614–625 CrossRef CAS PubMed
.
- F. H. Stillinger and T. A. Weber, Computer simulation of local order in condensed phases of silicon, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 31, 5262 CrossRef CAS PubMed
.
- K. Nakano, N. Tanibata, H. Takeda, R. Kobayashi, M. Nakayama and N. Watanabe, Molecular dynamics simulation of Li-ion conduction at grain boundaries in NASICON-Type LiZr2(PO4)3 solid electrolytes, J. Phys. Chem. C, 2021, 125, 23604–23612 CrossRef CAS
.
- Z. Yang, R. E. Ward, N. Tanibata, H. Takeda, M. Nakayama and R. Kobayashi, Exploring the diffusion mechanism of Li ions in different modulated arrangements of La(1−x)/3LixNbO3 with fitted force fields obtained via a metaheuristic algorithm, Solid State Ionics, 2021, 366, 115662 CrossRef
.
- S. Miyakawa, S. Matsuda, N. Tanibata, H. Takeda, M. Nakayama, T. Saito and S. Fukuchi, Computational studies on defect chemistry and Li-ion conductivity of spinel-type LiAl5O8 as coating material for Li-metal electrode, Sci. Rep., 2022, 12, 16672 CrossRef PubMed
.
- S. Aizu, S. Takimoto, N. Tanibata, H. Takeda, M. Nakayama and R. Kobayashi, Screening chloride Li-ion conductors using high-throughput force-field molecular dynamics, J. Am. Ceram. Soc., 2023, 106, 3035–3044 CrossRef CAS
.
- X.-S. Yang and S. Deb, in 2009 World congress on nature & biologically inspired computing (NaBIC), IEEE, pp. , pp. 210–214 Search PubMed.
- X.-S. Yang and S. Deb, Engineering optimisation by cuckoo search, Int. J. Math. Model. Numer. Optim., 2010, 1, 330–343 Search PubMed
.
- X.-S. Yang and S. Deb, Cuckoo search: recent advances and applications, Neural Comput. Appl., 2014, 24, 169–174 CrossRef
.
- J. Rodrigues and A. Zellner, Weighted balanced loss function and estimation of the mean time to failure, Commun. Stat. Theor. Methods, 1994, 23, 3609–3616 CrossRef
.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864 CrossRef
.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133 CrossRef
.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements, J. Phys.:Condens. Matter, 1994, 6, 8245 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- M. Parrinello and A. Rahman, Crystal Structure and Pair Potentials: A Molecular-Dynamics Study, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS
.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13, 5188 CrossRef
.
- J. Schuett, A. S. Kuhn and S. Neitzel-Grieshammer, Predicting the Na+ ion transport properties of NaSICON materials using density functional theory and Kinetic Monte Carlo, J. Mater. Chem., 2023, 11, 9160–9177 RSC
.
- J. Schuett, F. Pescher and S. Neitzel-Grieshammer, The origin of high Na+ ion conductivity in Na1+xZr2SixP3−xO12 NASICON materials, Phys. Chem. Chem. Phys., 2022, 24, 22154–22167 RSC
.
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J.-N. Chotard, C. P. Grey and M. S. Islam, Crystal structures, local atomic environments, and ion diffusion mechanisms of scandium-substituted sodium superionic conductor (NASICON) solid electrolytes, Chem. Mater., 2018, 30, 2618–2630 CrossRef CAS
.
- A. Pedone, G. Malavasi, M. C. Menziani, A. N. Cormack and U. Segre, A new self-consistent empirical interatomic potential model for oxides, silicates, and silica-based glasses, J. Phys. Chem. B, 2006, 110, 11780–11795 CrossRef CAS PubMed
.
- A. L. Usler, D. Kemp, A. Bonkowski and R. A. de Souza, A general expression for the statistical error in a diffusion coefficient obtained from a solid-state molecular-dynamics simulation, J. Comput. Chem., 2023, 44, 1347–1359 CrossRef CAS PubMed
.
- A. Bito, in IEEE Power Engineering Society General Meeting, 2005, vol. 2, pp. 1232–1235 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01549a |
| This journal is © The Royal Society of Chemistry 2025 |