DOI:
10.1039/D5RA01165E
(Paper)
RSC Adv., 2025,
15, 9295-9304
Solid-state synthesized Li4GeO4 germanate: an exploration of its structure, vibrational characteristics, electrical conductivity, and dielectric properties
Received
17th February 2025
, Accepted 17th March 2025
First published on 26th March 2025
Abstract
Orthogermanate materials have obtained considerable interest due to their unique physical and chemical properties, enabling diverse applications in the field of optoelectronics. This study explores the synthesis, vibrational properties, and electrical conduction mechanisms of the ceramic compound Li4GeO4. The sample was successfully synthesized using a high-temperature solid-state reaction. The Li4GeO4 compound crystallizes in the orthorhombic system (Bmmb space group). The morphological distribution and grain size of the titled compound were analyzed using SEM studies. The crystal structure was examined using Raman spectroscopy, confirming the presence of the functional group [GeO4]4−. Additionally, a detailed analysis of Nyquist plots demonstrates the sensitivity of the material's electrical characteristics to variations in frequency and temperature. Applying Jonscher's power law to the ac conductivity versus temperature reveals a change in the exponent “S”, which is explained by a change in the conduction mechanism, and consistent with the OLPT model below 573 K and the CBH model above. Utilizing the Maxwell–Wagner effect as proposed by the Koop phenomenological theory, the thermal variation of permittivity has been analyzed. The compound exhibits low dielectric loss values and a high permittivity (ε ∼ 106 F m−1). Additionally, its electrical capacitance reaches a promising value of 123 μF at 673 K, making it a strong candidate for energy storage applications, such as lithium-ion batteries.
1. Introduction
Orthogermanate materials with the chemical formula A2MGeO4 (where A = K, Li, Na, Cs, Rb and M = Zn, Co, Mg, Mn) have gained increasing attention due to their fascinating physical applications, including their use in supercapacitors,1 solid electrolytes for batteries,2,3 and dielectrics.4 Sodium-ion and lithium-ion batteries, in particular, are popular for their high performance, notably their high specific capacity. These materials have also garnered significant interest for applications in optoelectronic devices, including light-emitting diodes (LEDs), solar cells, lasers, detectors, and photodetectors.5,6 Numerous studies have concentrated on the metal orthogermanate Na2MGeO4 (M = Co, Mn, Fe) as a promising cathode material.7 Ionic conductivity is closely linked to structural rearrangement. Nonetheless, the maximum energy storage and ionic conductivity of Li-ion batteries are insufficient to meet society's long-term needs.8 Since 1965,9 the conductivity of Na2BGeO4 (with B = Zn, Co) has been examined across various sodium environments, demonstrating that orthogermanate compounds exhibit excellent conductivity. Recently, numerous studies have highlighted the impact of Co2+ on both structural stability and the electronic and electrical properties of these materials. Additionally, the Ag2ZnGeO4 compound is recognized as an electronic semiconductor with a conductivity of (σ60 °C ≈ 1 × 10−2) (Ω−1 cm−1).10 Studies by S. Ben Yahya and B. Louati on the electric properties of A2ZnGeO4 (where A = Li and K) revealed electrical conductivities of approximately 10−3 Ω−1 m−1 for K2ZnGeO4 and 10−5 Ω−1 m−1 for Li2ZnGeO4. (ref. 11 and 12) This paper details the synthesis and structural characterization of the Li4GeO4 compound. Given that this material has not been extensively studied previously, this investigation provides a comprehensive analysis of its electrical and dielectric properties. To examine the dielectric characteristics, we employ impedance spectroscopy, a practical and effective technique. The dielectric study, which varies with frequency and temperature, offers valuable insights into the conduction mechanisms, loss factor, permittivity, and localized charge carriers. Although there is limited literature on AC conductivity and dielectric relaxation for this material, our study rigorously explores these aspects, focusing on conductivity, electrical modulus, and impedance spectroscopy. The results are analyzed using various theoretical models. Moreover, our paper includes in-depth discussions on the dielectric constant, dielectric loss, AC and DC conductivity, as well as the electrical modulus and impedance analysis of the Li4GeO4 sample.
2. Experimental section
The ceramic compound Li4GeO4 was synthesized through a conventional solid-state reaction method. Starting materials included high-purity raw powders of Li2CO3 and GeO2 (∼99%, Sigma Aldrich). The raw materials were weighed according to their stoichiometric ratios according to the reaction below (eqn (1)) and thoroughly mixed for 1 hour using an agate pestle and mortar. The obtained powder was then calcined in an alumina crucible at 400 °C for 15 hours, followed by calcination at 600 °C for an additional 15 hours to ensure complete dehydration of the product. Following a second grinding and drying process, the powders were compacted into cylindrical pellets measuring 1.2 mm in height and 8 mm in diameter. These pellets were subsequently sintered at 800 C° for 15 hours (Fig. 1).| | |
2Li2CO3 + GeO2 → Li4GeO4 + ↑2CO2
| (1) |
 |
| | Fig. 1 Schematic representation of the Li4GeO4 synthesis via the solid-state method. | |
The obtained pellet was reground to obtain a powder to carry out the characterizations using XRD, SEM and Raman techniques. The Powder X-ray Diffraction (PXRD) experiment for Li4GeO4 was conducted at room temperature using a Bruker D8 ADVANCE diffractometer equipped with Cu Kα radiation (λ Kα = 1.5406 Å) over a wide 2θ angular range. The structure of the title compound was determined using the FullProf software through direct methods, and the atomic positions were refined with a full-matrix least-squares method.13 The microstructure and grain distribution were examined using a Scanning Electron Microscope (Zeiss ULTRA) equipped with 0 energy-dispersive system: INCA-X (Oxford Instruments). The Raman spectra were recorded at room temperature in the 100–1000 cm−1 range on a Renishaw Invia reflex spectrometer using a 10 mW laser power with a wave length of 633 nm. The electrical measurements were accomplished using A Solartron 1260 impedance examined by a microcomputer in the frequency and temperature range from 0.1 Hz to 10 MHz and (413–673) K, respectively. To achieve the precise contact, pellets are masked on the opposite surfaces with a thin layer of gold and were fixed between two copper electrodes in a special holder.
3. Results and discussion
3.1. X-ray diffraction and crystal structure
The X-ray diffraction pattern of the title compound at room temperature is shown in Fig. 2(a). The Rietveld refinement was performed to receive the detailed information about the crystal structure. The absence of impurity peaks and secondary phases indicates that we have successfully created a pure and high-quality sample. Based on JCPDS 01-072-1587 for Li4GeO4 all the diffraction peaks associated with the 2θ values have been accurately indexed in the orthorhombic system, specifically within the Bmmb space group. The quality factor, which reflects the strong correspondence between the experimental (red points) and theoretical (black solid line) profiles, is χ2 = 1.26, while the reliability factors are within acceptable ranges, with Rp = 10.5% and Rwp = 12.6%. From the refinement results, the cell parameters were determined to be a = 7.768(0) Å, b = 6.005(1) Å, c = 7.369 (1) Å, and the volume V = 346.676(1) Å3. These parameters are in good agreement with those found by Von H. Völlen Kle.14 The crystal structure of our compound is shown in Fig. 2(b). It contains two distinct Li+ positions, in each site the Li+ ion is coordinated to four O2− ions forming distorted LiO4 tetrahedra that share corners with four equivalent GeO4 tetrahedra, other corners with six LiO4 tetrahedra, and edges with three LiO4 tetrahedra. The Li–O bond lengths in the first site range from 2.01 to 2.14 Å, while in the second site, the shorter Li–O bonds range from 1.93 Å to 1.98 Å. Additionally, the Ge4+ ion is bonded to four O2− ions to create GeO4 tetrahedra that share corners with the LiO4 tetrahedra, exhibiting two shorter Ge–O bond lengths of 1.78 Å and two longer bond lengths of 1.79 Å.
 |
| | Fig. 2 (a) The Rietveld refinement was performed on the X-ray powder diffraction pattern of Li4GeO4 that was sintered at 800 °C, and (b) the crystal structural of Li4GeO4. | |
The average crystallite size of our compound was determined using the Debye–Scherrer equation:
| |
 | (2) |
Here,
θ represents the diffraction angle, and
β denotes the half-height width (FWHM) of the diffraction peak. The wavelength of the X-rays used is
λ = 1.5406 Å. We employed the most intense XRD peak (111) within the 2
θ range of 10–70° to determine
β, resulting in a crystallite size value of
DSC = 73 nm.
3.2. Scanning electron microscopy and Raman spectroscopy
The SEM and EDX techniques were employed to investigate the composition and morphology of our sample. The SEM analysis highlights essential microstructural features, including grain size, surface morphology, and porosity, which critically influence charge transport pathways. In particular, grain boundaries and surface textures impact charge carrier scattering, contributing to variations in electrical conductivity.15 Additionally, specific microstructural characteristics may be linked to the relaxation phenomena observed in the impedance data. Fig. 3(a) illustrates the formation of uniformly distributed, randomly oriented fine grains (Gs) separated by well-defined grain boundaries (GBs). While the grains appear largely homogeneous, their size distribution is non-uniform and falls within the sub-micron range. This heterogeneity likely arises from the sintering process, where low activation energy facilitates shifts in GBs within the sample.16 Such shifts lower the system's total free energy, thereby influencing the dynamics of grain growth. Consequently, the uneven grain size distribution results from cation diffusion across the boundaries, as recrystallization does not occur concurrently with the sintering process.17 The average grain size was determined using ImageJ software, and the results are presented as a histogram in Fig. 3(b). This histogram shows that the particle sizes primarily fall within the range of 0.2 to 1.1 μm, with an average size of 0.64 μm. As illustrated in Fig. 3(c), the EDX spectrum indicates the presence of various elements, including oxygen and germanium. Notably, lithium is absent from the spectrum in Fig. 3(c), despite having the same atomic number as beryllium, which is the reference element used for this compound.5 The average grain size calculated from the SEM images is larger than that determined by the Debye–Scherrer formula. This discrepancy arises because scanning electron microscopy provides the average size of secondary particles, while X-ray diffraction analysis of the line profile reveals the size of primary particles. Each secondary particle observed by SEM is composed of a significant number of primary particles, and the resolution of X-rays enables accurate calculation of these primary particle sizes.18
 |
| | Fig. 3 (a) SEM image of title compound; (b) grain size distribution histogram and (c) the elemental analysis by EDX. | |
Fig. 4 displays the intensity variation of the Raman spectrum as a function as wavenumber within the range of 100–1200 cm−1. Based on other results in the literature, the Raman bands of orthorhombic Li4GeO4 can be classified into three distinct regions.19,20 Some vibrational modes were not detectable because of the overlap among the Raman-active modes. The assignments for the Li4GeO4 ceramic sintered at 800 °C can be found in Table 1.
 |
| | Fig. 4 The Raman spectrum of Li4GeO4 at room temperature. | |
Table 1 The experimental Raman-active modes of Li4GeO4 ceramic
| Band |
Wavenumber (cm−1) |
Assignments |
| 1 |
100.19 |
T Ge/Ge |
| 2 |
175.19 |
T Li/Li |
| 3 |
199.14 |
T Ge/Ge |
| 4 |
300.35 |
R + T Li/Li |
| 5 |
363.87 |
R + T Li/Li |
| 6 |
503.99 |
δ O–Ge–O |
| 7 |
729.53 |
ν3 GeO4 |
| 8 |
743.53 |
ν3 GeO4 |
| 9 |
762.15 |
ν1 GeO4 |
3.3. Complex impedance spectroscopy study
The modeling process for complex impedance is extremely valuable for identifying the individual contributions of ionic conduction from grain and grain boundary in the material being studied. Fig. 5(a) illustrates the Nyquist plots of the ceramic Li4GeO4 across a temperature range of 413 to 673 K. These spectra show that as the temperature rises, the diameter of the semicircle diminishes, illustrating the thermally activated conduction process.21 These plots indicate that the material behaves like a typical ceramic, characterized by more resistive grain boundaries compared to the grains. Additionally, the semicircle shows some depression (i.e., the centers of the semicircle are below the abscissa axis) rather than being centered on the axis, which suggests a distribution of relaxation times. The electrical processes occurring within the material have been modeled and are represented by an equivalent electrical circuit that comprises a series combination of two subcircuits: the first is a parallel combination of (Rg//C1//CPE1), representing the grain contribution, while the second consists of (Rgb//CPE2), related to the grain boundary contributions. The Constant Phase Element (CPE) is employed in the equivalent circuit to account for non-ideal capacitance behavior that may arise from the presence of multiple relaxation phenomena in the Li4GeO4 system, which exhibit nearly equal or comparable relaxation periods.22 Its expression is as follows:12| |
 | (3) |
where the parameter α (where 0 ≤ α ≤ 1) represents the deviation from Debye-type behavior in the relaxation mechanism. A value of zero indicates purely resistive behavior, while a value of one signifies a pure capacitive behavior. Fig. 5(b) and (c) show the angular frequency-dependent real (Z′) and imaginary (−Z′′) components of the impedance at different temperatures. A reduction in Z′ with rising temperature suggests a negative temperature coefficient of resistance.23 This behavior implies that an enhancement in AC conductivity could be possible, attributed to an increase in charge carrier mobility and a reduction in the density of trapped charges. The frequency dependence of −Z′′ shows a peak  at every measured temperature. As the temperature rises, the asymmetric peak of
at every measured temperature. As the temperature rises, the asymmetric peak of  shifts to higher frequencies and becomes thinner. The broadening of the peak indicates a distribution of relaxation times, while the shift toward higher frequencies signifies a reduction in the relaxation time. The behavior of Z′ and –Z′′ for the title compound in the frequency range is consistent with that observed in other ceramic systems documented in the literature, such as the compounds K2ZnGeO4 (ref. 11) and KSr0.5Fe2O4.24 Fig. 5(d) illustrates how the resistance related to both the grain (Rg) and the grain boundary (Rgb) changes as a function of temperature. It is important to note that the resistance near the grain boundary is higher than that of the grain itself. Generally, the increased disorder and instability in atomic arrangement at grain boundaries contribute to grain growth at elevated temperatures. Consequently, both the resistance of the grain and that of the grain boundary decrease as the temperature rises.25
shifts to higher frequencies and becomes thinner. The broadening of the peak indicates a distribution of relaxation times, while the shift toward higher frequencies signifies a reduction in the relaxation time. The behavior of Z′ and –Z′′ for the title compound in the frequency range is consistent with that observed in other ceramic systems documented in the literature, such as the compounds K2ZnGeO4 (ref. 11) and KSr0.5Fe2O4.24 Fig. 5(d) illustrates how the resistance related to both the grain (Rg) and the grain boundary (Rgb) changes as a function of temperature. It is important to note that the resistance near the grain boundary is higher than that of the grain itself. Generally, the increased disorder and instability in atomic arrangement at grain boundaries contribute to grain growth at elevated temperatures. Consequently, both the resistance of the grain and that of the grain boundary decrease as the temperature rises.25
 |
| | Fig. 5 (a) The −Z′′ vs. Z′ curves at various temperatures for Li4GeO4, the solid lines associating the data points are adjusted curves employing an equivalent circuit model, as depicted in the respective inset. (b) Real (Z′) and (c) imaginary (−Z′′) parts of the complex impedance of Li4GeO4 as functions of angular frequency. (d) Variation of Rg (grain resistance) and Rgb (grain boundary resistance) as a function of temperature. | |
3.4. Electrical conductivity studies
The electrical conductivity of the compound being studied was calculated using the measured values of the impedance's real part Z′ and imaginary Z′′ through the following relation:| |
 | (4) |
Fig. 6(a) displays the angular frequency dependence of the electrical conductivity as a function of angular frequency at various temperatures. These spectra reveal the existence of two regions. The first region, found at low frequencies, presents as a plateau and is associated with DC conductivity behavior. The second region, observed at higher frequencies, is referred to as the AC conductivity “conductivity scattering area”. This behavior can be explained by Jonscher's power law:
| | |
σac(T,ω) = σdc(T) + A(T)ωS(T)
| (5) |
where “
A” is the temperature dependent factor,
ω refers to the angular frequency and
S(
T) is the power exponent that indicates the degree of interaction between mobile ions and their surrounding environment (0 <
S < 2). Previous studies reported various conduction models, primarily categorized into two distinct processes: classical hopping over a barrier and quantum tunneling. However, modifications have been made over the years. The final proposed models include quantum mechanical tunneling (QMT), correlated barrier hopping (CBH), non-overlapping small polaron tunneling (NSPT), and overlapping large polaron tunneling (OLPT).
26,27 These models were suggested to link the conduction mechanism of AC conductivity with the behavior of
S(
T) as a function of temperature. The thermal evolution of
S(
T) as shown in
Fig. 6(b). It's important to highlight that in the
I region,
S decreases with increasing temperature until it reaches a minimum, then begins to rise again before decreasing once more after the phase transition temperature. This behavior aligns with the OLPT model. When the value of
S is greater than 1, it suggests that electron hopping takes place between neighboring sites. In region II,
S decreases with increasing temperature, which is consistent with the CBH model. In this case, since
S is less than 1, it indicates that the charge carriers exhibit translational motion characterized by abrupt jumps.
12 Fig. 6(c) illustrates the variation of ln(
σdc ×
T) as a function of 1000/
T at 10
4 Hz as an example. Its variation shows an increase with rising temperature, following Arrhenius' law:
| |
 | (6) |
 |
| | Fig. 6 (a) The variation of the AC conductivity as a function of frequency at various temperatures for Li4GeO4. Solid lines connecting the data points illustrate the fitting of the AC conductivity data using Jonscher's power law (eqn (5)). (b) The power exponent (S), (c) the variation of ln(σdcT) as a function of the inverse temperature at a frequency of 104 Hz, and (d) the variation of the activation energy as a function of frequency. | |
In this context, σ0 represents the pre-exponential factor, Ea denotes the activation energy, and KB stands for the Boltzmann constant. A change in the slope of the DC conductivity curve is observed at T = 573 K, which closely aligns with the observation that this modification results from a change in the conduction mechanism. The activation energy values for charge transport obtained from the linear fit are Ea1 = (0.73 ± 0.02) eV at low temperatures and Ea2 = (0.58 ± 0.02) eV at higher temperatures. The evolution of activation energy as a function as frequency (Fig. 6(d)) shows that the activation energy decreases as frequency increases. This reduction in activation energy at higher frequencies demonstrates that the system exhibits frequency-activated ionic conductivity. Additionally, the lower activation energy at these elevated frequencies suggests that more neighboring sites become accessible during alternating current (ac) conduction.
3.5. Dielectric properties
Fig. 7(a) illustrates the variation of the dielectric constant (ε′) as function as frequency at various temperatures. The materials studied showed higher ε′ = 106 F m−1 values at low frequencies, suggesting that they would be suitable low-frequency energy storage candidates.28,29 Moreover, ε′ values tend to increase with temperature at a specific frequency. This article discusses how thermal activation of charge carriers impacts polarization. The four main categories of polarization are ionic, orientational, electronic, and interfacial. In this context, orientational and interfacial polarizations are considered relaxation components, while electronic and ionic polarizations are classified as deformational components of polarizability.30 Koop's phenomenological theory suggests that the variation of ε′ with frequency can be attributed to Maxwell–Wagner interfacial polarization. Fig. 7(b) displays the variation of the imaginary part (ε′′) as a function as frequency. The value of ε′′ decreases consistently with the increase of frequency. The imaginary component of the dielectric constant relates with the energy dissipation in the compound. Additionally, the frequency-dependent imaginary component of the dielectric constant is modeled using a universal power law:where A(T) and m(T) represent the temperature-dependent variables. Fig. 7(c) shows the variation of the exponent m(T) as a function of temperature. As the temperature increases, the value of m(T) decreases and approaches −1 (the overall value of m(T) remains close to −1 across all temperatures), this suggests that the conduction in title compound is primarily of the dc type.31 It is worth noting that the exponent m has two distinct parts: in the first part, the OLPT model is found, while in the second part, the CBH model is the most adequate. This result is in good agreement with the findings from AC conductivity studies (Fig. 6(b)). The dielectric loss factor measures the intrinsic loss of electrical energy in a dielectric medium when an alternating electric field is applied. The frequency dependence of loss factor for Li4GeO4 at various temperature is shown in Fig. 7(d). The value of loss factor at low frequency is very high. The loss factor is significantly high at low frequencies. As the frequency increases, the loss factor decreases and approaches nearly zero beyond 105 Hz, indicating that the hopping of charge carriers increases with rising frequency. Table 2 compares the permittivity values of the studied compound with those reported in previous studies, highlighting the potential of Li4GeO4 as a promising candidate for energy storage applications.
 |
| | Fig. 7 (a) Frequency dependence of the dielectric constant (ε′). (b) Variation of the imaginary part (ε′′) as a function of frequency, fitted using the universal power law as shown in eqn (7) (inset of figure). (c) Variation of the exponent m(T) as a function of temperature. (d) Frequency dependence of the loss factor. | |
Table 2 Comparison of permittivity values of the current compound with previous studies
| Compound |
Temperature (K) |
ε′ (F m−1) |
| Li2CaGeO4 |
573 |
120 (ref. 32) |
| Na2CoGeO4 |
573 |
1.2 × 104 (ref. 33) |
| Present study |
573 |
1.6 × 106 |
3.6. Electric modulus
Fig. 8(a) illustrates the frequency dependence of the imaginary part of the electrical modulus (M′′) at different temperatures ranging from 413 to 673 K. As the frequency increases, the value of M′′ steadily rises until it reaches a maximum point 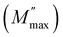 and then rapidly falls, as depicted in the graph. The shift of the peak towards higher frequencies with increasing temperature suggests the occurrence of a relaxation process. The peak's asymmetrical broadening, which signifies non-Debye-type conduction phenomena, reflects the transmission of relaxation processes within the material. Electrical capacitance is a key parameter for assessing the performance of ceramic materials in energy storage applications. Fig. 8(b) presents the variation of capacitance, measured at constant frequencies and temperatures, to provide a comprehensive understanding of the studied compound's energy storage behavior. At low frequencies, the capacitance reaches its highest values, exceeding 132 μF at 673 K, making Li4GeO4 a promising candidate for electronic capacitor systems and energy storage devices, such as Li-ion batteries, before gradually decreasing with increasing frequency. The observed capacitance behavior suggests the presence of interface states, leading to the formation of an inhomogeneous barrier at the interface.34 Additionally, as temperature increases, capacitance in the low-frequency region exhibits a noticeable rise, accompanied by significant dispersion. The nearly linear dependence of capacitance in the frequency range of 0.1–104 Hz is likely associated with a reduction in space charge density. Previous studies35,36 have attributed the temperature-induced capacitance enhancement to a decrease in bond energies, which facilitates stronger orientational vibrations and weakens interatomic forces, ultimately contributing to improved capacitance.
and then rapidly falls, as depicted in the graph. The shift of the peak towards higher frequencies with increasing temperature suggests the occurrence of a relaxation process. The peak's asymmetrical broadening, which signifies non-Debye-type conduction phenomena, reflects the transmission of relaxation processes within the material. Electrical capacitance is a key parameter for assessing the performance of ceramic materials in energy storage applications. Fig. 8(b) presents the variation of capacitance, measured at constant frequencies and temperatures, to provide a comprehensive understanding of the studied compound's energy storage behavior. At low frequencies, the capacitance reaches its highest values, exceeding 132 μF at 673 K, making Li4GeO4 a promising candidate for electronic capacitor systems and energy storage devices, such as Li-ion batteries, before gradually decreasing with increasing frequency. The observed capacitance behavior suggests the presence of interface states, leading to the formation of an inhomogeneous barrier at the interface.34 Additionally, as temperature increases, capacitance in the low-frequency region exhibits a noticeable rise, accompanied by significant dispersion. The nearly linear dependence of capacitance in the frequency range of 0.1–104 Hz is likely associated with a reduction in space charge density. Previous studies35,36 have attributed the temperature-induced capacitance enhancement to a decrease in bond energies, which facilitates stronger orientational vibrations and weakens interatomic forces, ultimately contributing to improved capacitance.
 |
| | Fig. 8 (a) Variation of the imaginary part of the electric module as a function of frequency. (b) Frequency-dependent capacitance spectra. | |
The analysis of −Z′′ (ω) and M′′ (ω) plots allows for the determination of the nature of relaxation in a material, whether it is Debye/delocalized or non-Debye/localized, as well as the displacement of charge carriers. When the peaks of impedance and modulus  align at the same frequency, it signifies long-range motion. In contrast, a discrepancy between the two peaks indicates short-range motion in the conduction process. In Fig. 9(a), a significant mismatch between
align at the same frequency, it signifies long-range motion. In contrast, a discrepancy between the two peaks indicates short-range motion in the conduction process. In Fig. 9(a), a significant mismatch between  and
and 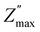 peaks is observed at temperature of 413 K. This discrepancy suggests a short-range motion of polarons within Li4GeO4, deviating from the ideal Debye response. Fig. 9(b) illustrates the combined modulus and impedance spectra (M′′ and −Z′′) at 673 K. The maxima of (−Z′′ and M′′) occur at nearly the same frequency, it indicates that the relaxation process is influenced by the displacement of long-range charge carriers.36 Significantly, as the temperature increases, the gap between the peaks decreases, suggesting that the rise in temperature facilitates the relaxation of polarons into a delocalized state, related to a Debye-type response.
peaks is observed at temperature of 413 K. This discrepancy suggests a short-range motion of polarons within Li4GeO4, deviating from the ideal Debye response. Fig. 9(b) illustrates the combined modulus and impedance spectra (M′′ and −Z′′) at 673 K. The maxima of (−Z′′ and M′′) occur at nearly the same frequency, it indicates that the relaxation process is influenced by the displacement of long-range charge carriers.36 Significantly, as the temperature increases, the gap between the peaks decreases, suggesting that the rise in temperature facilitates the relaxation of polarons into a delocalized state, related to a Debye-type response.
 |
| | Fig. 9 Variation of −Z′′ and M′′ as a function of frequency at 413 K (a) and 673 K (b). | |
4. Conclusions
The powder Li4GeO4 was synthesized using a solid-state method. Several complementary techniques, along with XRPD analysis, were employed to investigate the surface morphology, stoichiometry, and purity of the compound. SEM analysis confirmed the crystalline nature and surface quality of the powder, indicating that the Li4GeO4 compound is of good quality. The vibrational analysis conducted with Raman spectra recorded at room temperature provided insights into the internal and external vibrational modes of the [GeO4]4− ions. The electrical, dielectric, and relaxation properties of the sample were studied using impedance spectroscopy to characterize the material's intrinsic electrical behavior. Following the structural analysis, this behavior was interpreted to establish a connection between the nature of the migrating species and their impact on the macroscopic properties. The Nyquist plots revealed the presence of two electrical relaxation phenomena, indicative of non-Debye-type relaxation, and the observation of two semicircular arcs suggested a dominant contribution from the grains. These plots were fitted with an equivalent circuit comprising a series combination of two subcircuits; the first was a parallel combination of (Rg//C1//CPE1), representing the grain contribution, while the second consisted of (Rgb//CPE2), related to grain boundary contributions. The AC conductivity was successfully described using Jonscher's power law. The variation of the deduced S(T) indicates that the OLPT model effectively interprets the charge transport mechanism in Li4GeO4 for T < 573 K transitioning to a CBH model above 573 K. Additionally, a change in the slope of the DC conductivity curve is observed around the same temperature as the phase transition detected in S(T). The activation energy values of charge transport are Ea1 = (0.73 ± 0.02) eV (T < 573 K) and Ea2 = (0.58 ± 0.02) eV (T > 573 K). These values were found to stand out for the interstitial Li+ ions. In the dielectric study, as a function of angular frequency, the findings of the electrical study were confirmed, showing that space charge and free charge conductivity could be determined through the modified Cole–Cole plot.
Data availability
Data will be shared upon reasonable request to the corresponding author.
Author contributions
Sourour Ben Yahya: writing—review & editing, writing—original draft, visualization, validation, software, investigation, formal analysis, data curation. Iheb Garoui: software, investigation. Mustapha Zaghrioui: review, methodology, Abderrazek Oueslati: review and supervision and Bassem Louati: supervision and review.
Conflicts of interest
The authors declare no competing interests.
References
- J. Yan, S. Li, B. Lan, Y. Wu and P. S. Lee, Multifunctional Supercapacitors: Rational Design of Nanostructured Electrode Materials toward Multifunctional Supercapacitors, Adv. Funct. Mater., 2020, 30(2) DOI:10.1002/adfm.202070008.
- S. Chakraborty, A. Banerjee, T. Watcharatharapong, R. B. Araujo and R. Ahuja, Current computational trends in polyanionic cathode materials for Li and Na batteries, J. Phys.: Condens. Matter, 2018, 30(28), 283003, DOI:10.1088/1361-648x/aac62d.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Na-ion batteries, recent advances and present challenges to become low cost energy storage systems, Energy Environ. Sci., 2012, 5(3), 5884, 10.1039/c2ee02781j.
- M. Panda, V. Srinivas and A. K. Thakur, On the question of percolation threshold in polyvinylidene fluoride/nanocrystalline nickel composites, Appl. Phys. Lett., 2008, 92, 132905, DOI:10.1063/1.2900710.
- S. Ben Yahya, R. Barillé and B. Louati, Synthesis, optical and ionic conductivity studies of a lithium cobalt germanate compound, RSC Adv., 2022, 12(11), 6602–6614, 10.1039/d2ra00721e.
- B. E. Liebert and R. A. Huggins, Ionic conductivity of Li4GeO4, Li2GeO3 and Li2Ge7O15, Mater. Res. Bull., 1976, 11(5), 533–538, DOI:10.1016/0025-5408(76)90235-x.
- K. J. McDonald, et al., Hydrothermal synthesis, structure refinement, and electrochemical characterization of Li2CoGeO4 as an oxygen evolution catalyst, J. Mater. Chem. A, 2014, 2(43), 18428–18434, 10.1039/c4ta03325f.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Li–O2 and Li–S batteries with high energy storage, Nat. Mater., 2011, 11(1), 19–29, DOI:10.1038/nmat3191.
- J. Grins, Structure and Ionic Conductivity of Na2BeGeO4, J. Solid State Chem., 1995, 118(1), 62–65, DOI:10.1006/jssc.1995.1310.
- G. Vaivars, Synthesis, structure and conductivity of Ag2ZnSiO4, Ag2ZnGeO4 and Ag2BeSiO4, Solid State Ionics, 1995, 78(3–4), 259–267, DOI:10.1016/0167-2738(95)00000-v.
- S. B. Yahya and B. Louati, Characterization of the structure and conduction behavior of overlapping polaron tunnel of dipotassium zinc orthogermanate, J. Alloys Compd., 2021, 876, 159972, DOI:10.1016/j.jallcom.2021.159972.
- S. Ben yahya and B. Louati, Vibrational analysis and AC electrical conduction behavior of lithium zinc orthogermanate, Ionics, 2021, 27(7), 3027–3034, DOI:10.1007/s11581-021-04061-6.
- J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192(1–2), 55–69, DOI:10.1016/0921-4526(93)90108-i.
- H. Völlenkle and A. Wittmann, Die Kristallstruktur von Li4GeO4, Z. Kristallogr. Cryst. Mater., 1969, 128(1–6), 66–71, DOI:10.1524/zkri.1969.128.16.66.
- M. Javed, et al., Variable range hopping transport and dielectric relaxation mechanism in GdCrO3 rare-earth orthochromite perovskite, J. Rare Earths, 2024, 42(7), 1304–1316, DOI:10.1016/j.jre.2023.07.006.
- V. Yu. Novikov, Grain growth in nanocrystalline materials, Mater. Lett., 2015, 159, 510–513, DOI:10.1016/j.matlet.2015.07.092.
- J. Hojo, Sintering Behavior of Ultrafine Silicon Carbide Powder, Silicon Carbide Ceram., 1991, 1, 149–168, DOI:10.1007/978-94-011-3842-0_7.
- A. Peña, et al., Magnetism in La0.7Pb0.3(Mn0.9TM0.1)O3 (TM = Fe, Co, Ni) CMR perovskites, J. Magn. Magn. Mater., 2001, 226–230, 831–833, DOI:10.1016/s0304-8853(01)00077-4.
- V. V. Fomichev and E. V. Proskuryakova, Vibrational Spectra and Energy Characteristics of the Superionics Li4SiO4 and Li4GeO4, J. Solid State Chem., 1997, 134(2), 232–237, DOI:10.1006/jssc.1997.7539.
- H. L. Zheng, Z. C. Zhang, J. G. Zhou, S. S. Yang and J. Zhao, Vibrational spectra of CaGa2O4, Ca2GeO4, CaIn2O4 and CaSnO3 prepared by electrospinning, Appl. Phys. A:Mater. Sci. Process., 2012, 108(2), 465–473, DOI:10.1007/s00339-012-6916-4.
- M. Ben Bechir and M. H. Dhaou, Study of charge transfer mechanism and dielectric relaxation of all-inorganic perovskite CsSnCl3, RSC Adv., 2021, 11(35), 21767–21780, 10.1039/d1ra02457d.
- M. Javed, et al., Investigation on electrical transport and dielectric relaxation mechanism in TbCrO3 perovskite orthochromite, J. Alloys Compd., 2023, 955, 170181–170189, DOI:10.1016/j.jallcom.2023.170181.
- H. Zhang, A. Chang and C. Peng, Preparation and characterization of Fe3+-doped Ni0.9Co0.8Mn1.3−xFexO4 (0 ≤ x ≤0.7) negative temperature coefficient ceramic materials, Microelectron. Eng., 2011, 88(9), 2934–2940, DOI:10.1016/j.mee.2011.04.023.
- M. M. Bouzayani, I. Soudani, M. B. Abdessalem, S. Znaidia, A. Oueslati and A. Aydi, Electrical conduction mechanism and dielectric properties of the KSr0.5Fe2O4 spinel ferrite, J. Mater. Sci.: Mater. Electron., 2024, 35(18), 1–17, DOI:10.1007/s10854-024-13077-3.
- X. Lu, et al., Effects of grain size and temperature on mechanical properties of nano-polycrystalline nickel-cobalt alloy, J. Mater. Res. Technol., 2020, 9(6), 13161–13173, DOI:10.1016/j.jmrt.2020.09.060.
- I. G. Austin and N. F. Mott, Polarons in crystalline and non-crystalline materials, Adv. Phys., 1969, 18(71), 41–102, DOI:10.1080/00018736900101267.
- I. Ahmad, M. J. Akhtar and M. M. Hasan, Impedance spectroscopic investigation of electro active regions, conduction mechanism and origin of colossal dielectric constant in Nd1−xSrxFeO3 (0.1 ≤ x ≤ 0.5), Mater. Res. Bull., 2014, 60, 474–484, DOI:10.1016/j.materresbull.2014.08.046.
- W. B. Weir, Automatic measurement of complex dielectric constant and permeability at microwave frequencies, Proc. IEEE, 1974, 62(1), 33–36, DOI:10.1109/proc.1974.9382.
- T. Dabbebi, et al., Structural and dielectric behaviors for Mg0.5Co0.5Fe2O4 spinel ferrite synthesized by sol–gel route, J. Mater. Sci.: Mater. Electron., 2021, 33(1), 490–504, DOI:10.1007/s10854-021-07322-2.
- A. Sahoo, T. Paul, S. Maiti and R. Banerjee, Temperature-dependent dielectric properties of CsPb2Br5: a 2D inorganic halide perovskite, Nanotechnology, 2022, 33(19), 195703–195708, DOI:10.1088/1361-6528/ac4fe5.
- H. Jodi, S. Supardi, E. Kartini and A. Zulfia, Synthesis And Electrochemical characterization of Li3PO4 for solid state electrolytes, Jurnal Sains Materi Indonesia, 2018, 18(1), 1, DOI:10.17146/jsmi.2016.18.1.4181.
- S. Ben yahya and B. Louati, Investigation of the structural, morphological, electrical and dielectric properties of Li2CaGeO4 compound, Ionics, 2024, 27(7), 5325–5340, DOI:10.1007/s11581-024-05670-7.
- S. Ben Yahya, R. Barillé and B. Louati, Synthesis and investigation of the morphological, optical, electrical and dielectric characteristics of a disodium cobalt orthogermanate, RSC Adv., 2023, 13(39), 27262–27273, 10.1039/d3ra04829b.
- A. Kalam, et al., Interpretation of Resistance, Capacitance, Defect Density, and Activation Energy Levels in Single-Crystalline MAPbI3, J. Phys. Chem. C, 2020, 124(6), 3496–3502, DOI:10.1021/acs.jpcc.9b11343.
- M. Mnakri, I. Gharbi, M. Enneffati and A. Oueslati, Synthesis and investigation on the optical and complex impedance analysis in LiCrO2 prepared using solid-state reaction, Mater. Today Commun., 2024, 38, 107714, DOI:10.1016/j.mtcomm.2023.107714.
- I. Garoui, M. Mallek, F. N. Almutairi, W. Rekik and A. Oueslati, Synthesis, structural characterization and complex impedance analysis of a novel organic-inorganic hybrid compound based on mercury (II) chloride, J. Mol. Struct., 2024, 1315, 138881, DOI:10.1016/j.molstruc.2024.138881.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Iheb Garouia,
Mustapha Zaghriouib,
Abderrazek Oueslati
*a,
Iheb Garouia,
Mustapha Zaghriouib,
Abderrazek Oueslati a and
Bassem Louatia
a and
Bassem Louatia




 at every measured temperature. As the temperature rises, the asymmetric peak of
at every measured temperature. As the temperature rises, the asymmetric peak of  shifts to higher frequencies and becomes thinner. The broadening of the peak indicates a distribution of relaxation times, while the shift toward higher frequencies signifies a reduction in the relaxation time. The behavior of Z′ and –Z′′ for the title compound in the frequency range is consistent with that observed in other ceramic systems documented in the literature, such as the compounds K2ZnGeO4 (ref. 11) and KSr0.5Fe2O4.24 Fig. 5(d) illustrates how the resistance related to both the grain (Rg) and the grain boundary (Rgb) changes as a function of temperature. It is important to note that the resistance near the grain boundary is higher than that of the grain itself. Generally, the increased disorder and instability in atomic arrangement at grain boundaries contribute to grain growth at elevated temperatures. Consequently, both the resistance of the grain and that of the grain boundary decrease as the temperature rises.25
shifts to higher frequencies and becomes thinner. The broadening of the peak indicates a distribution of relaxation times, while the shift toward higher frequencies signifies a reduction in the relaxation time. The behavior of Z′ and –Z′′ for the title compound in the frequency range is consistent with that observed in other ceramic systems documented in the literature, such as the compounds K2ZnGeO4 (ref. 11) and KSr0.5Fe2O4.24 Fig. 5(d) illustrates how the resistance related to both the grain (Rg) and the grain boundary (Rgb) changes as a function of temperature. It is important to note that the resistance near the grain boundary is higher than that of the grain itself. Generally, the increased disorder and instability in atomic arrangement at grain boundaries contribute to grain growth at elevated temperatures. Consequently, both the resistance of the grain and that of the grain boundary decrease as the temperature rises.25




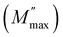 and then rapidly falls, as depicted in the graph. The shift of the peak towards higher frequencies with increasing temperature suggests the occurrence of a relaxation process. The peak's asymmetrical broadening, which signifies non-Debye-type conduction phenomena, reflects the transmission of relaxation processes within the material. Electrical capacitance is a key parameter for assessing the performance of ceramic materials in energy storage applications. Fig. 8(b) presents the variation of capacitance, measured at constant frequencies and temperatures, to provide a comprehensive understanding of the studied compound's energy storage behavior. At low frequencies, the capacitance reaches its highest values, exceeding 132 μF at 673 K, making Li4GeO4 a promising candidate for electronic capacitor systems and energy storage devices, such as Li-ion batteries, before gradually decreasing with increasing frequency. The observed capacitance behavior suggests the presence of interface states, leading to the formation of an inhomogeneous barrier at the interface.34 Additionally, as temperature increases, capacitance in the low-frequency region exhibits a noticeable rise, accompanied by significant dispersion. The nearly linear dependence of capacitance in the frequency range of 0.1–104 Hz is likely associated with a reduction in space charge density. Previous studies35,36 have attributed the temperature-induced capacitance enhancement to a decrease in bond energies, which facilitates stronger orientational vibrations and weakens interatomic forces, ultimately contributing to improved capacitance.
and then rapidly falls, as depicted in the graph. The shift of the peak towards higher frequencies with increasing temperature suggests the occurrence of a relaxation process. The peak's asymmetrical broadening, which signifies non-Debye-type conduction phenomena, reflects the transmission of relaxation processes within the material. Electrical capacitance is a key parameter for assessing the performance of ceramic materials in energy storage applications. Fig. 8(b) presents the variation of capacitance, measured at constant frequencies and temperatures, to provide a comprehensive understanding of the studied compound's energy storage behavior. At low frequencies, the capacitance reaches its highest values, exceeding 132 μF at 673 K, making Li4GeO4 a promising candidate for electronic capacitor systems and energy storage devices, such as Li-ion batteries, before gradually decreasing with increasing frequency. The observed capacitance behavior suggests the presence of interface states, leading to the formation of an inhomogeneous barrier at the interface.34 Additionally, as temperature increases, capacitance in the low-frequency region exhibits a noticeable rise, accompanied by significant dispersion. The nearly linear dependence of capacitance in the frequency range of 0.1–104 Hz is likely associated with a reduction in space charge density. Previous studies35,36 have attributed the temperature-induced capacitance enhancement to a decrease in bond energies, which facilitates stronger orientational vibrations and weakens interatomic forces, ultimately contributing to improved capacitance.

 align at the same frequency, it signifies long-range motion. In contrast, a discrepancy between the two peaks indicates short-range motion in the conduction process. In Fig. 9(a), a significant mismatch between
align at the same frequency, it signifies long-range motion. In contrast, a discrepancy between the two peaks indicates short-range motion in the conduction process. In Fig. 9(a), a significant mismatch between  and
and 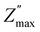 peaks is observed at temperature of 413 K. This discrepancy suggests a short-range motion of polarons within Li4GeO4, deviating from the ideal Debye response. Fig. 9(b) illustrates the combined modulus and impedance spectra (M′′ and −Z′′) at 673 K. The maxima of (−Z′′ and M′′) occur at nearly the same frequency, it indicates that the relaxation process is influenced by the displacement of long-range charge carriers.36 Significantly, as the temperature increases, the gap between the peaks decreases, suggesting that the rise in temperature facilitates the relaxation of polarons into a delocalized state, related to a Debye-type response.
peaks is observed at temperature of 413 K. This discrepancy suggests a short-range motion of polarons within Li4GeO4, deviating from the ideal Debye response. Fig. 9(b) illustrates the combined modulus and impedance spectra (M′′ and −Z′′) at 673 K. The maxima of (−Z′′ and M′′) occur at nearly the same frequency, it indicates that the relaxation process is influenced by the displacement of long-range charge carriers.36 Significantly, as the temperature increases, the gap between the peaks decreases, suggesting that the rise in temperature facilitates the relaxation of polarons into a delocalized state, related to a Debye-type response.



