Predicting pK_a of flexible polybasic tetra-aza macrocycles

Abstract

We present physics-based pK_a predictions for a library of tetra-aza macrocycles. These flexible, polybasic molecules exhibit highly charged states and substantial prototropic tautomerism, presenting a challenge for pK_a prediction. Our computational protocol combines CREST/xTB conformational sampling, density functional theory (DFT) refinement in continuum solvent, and a linear empirical correction (LEC). This approach predicts known tetra-aza macrocycle pK_a to within a root-mean-square deviation 1.2 log units. This approach also provides reasonable predictions for the most stable protomers at different pH. We use this protocol to predict pK_a values for four novel, synthetically achievable, previously un-synthesized tetra-aza macrocycles, providing new leads for future experiments.

---

1. Introduction

Predicting pK_a and pH-dependent speciation (prototropic tautomerization) was¹ and is² a critical component of computational medicinal chemistry.^3,4 The pH-dependent speciation of drug molecules governs their solubility,⁵ docking poses,⁶ and membrane permeability.⁷ Modern density functional theory (DFT) approximations can routinely predict gas-phase pK_a of rigid small molecules possessing a single acid/base site.⁸ Predicting aqueous-phase pK_a requires a model for solvent.^9–12 Predicting aqueous-phase pK_a of large, flexible, polybasic molecules remains a challenge. Polybasic molecules are abundant in pharmaceutical design, possess prototropic tautomerism,^13,14 and can be highly charged in solution.¹⁵ Flexible macrocycles can access multiple conformations within each tautomer (chameleonicity).¹⁶ Molecules that are both flexible and polybasic are particularly challenging for pK_a prediction.

1.1. Tetra-aza macrocycles

Our goal in this work is to validate and use a computational protocol capable of predicting the pK_a and pH-dependent speciation of flexible, polybasic, tetra-aza macrocycles (Fig. 1). Tetra-aza macrocycles combine high water solubility, tunable metal binding,^17,18 and antioxidant activitiy.^19,20 Tetra-aza macrocycles have been employed as catalysts, luminescent bioprobes,²¹ MRI contrast agents,²² and drug candidates for treating oxidative stress.^23,24 Some tetra-aza macrocycles dis-aggregate amyloids.²⁵ Other tetra-aza macrocycles have demonstrated activity as Nrf2 activators.²⁶ The Green group has devised synthetic methods capable of accessing a broad range of substituted tetra-aza macrocycles, and has advanced these molecules' application as potential therapeutics. Initial experimental studies include the measured pK_a of ten substituted macrocycles (molecules 1–10) and the protonation sites of molecules 1 and 2 (Table 1).^23,27 These molecules possess between four and six acid/base sites and are positively charged at physiological pH.^23,27 Proton NMR methods can be used to accurately measure the pK_a and the dominant tautomers at varying pH. These studies demonstrate that substitution significantly changes the pK_a.^23,27,28 Synthesis and testing of the thousands of synthetically accessible tetra-aza macrocycle derivatives represents a major technical hurdle. Reliable predictions of the structures, docking poses, solubility, membrane permeability, and other properties of un-synthesized tetra-aza macrocycles could significantly accelerate development of lead compounds for the applications discussed above. Reliable prediction of pK_a and charge state at physiological pH is a prerequisite for such predictions. The broad range of possible synthetically accessible macrocycles, and the demonstrated impact of chemical substitution on pK_a and protonation site, motivate the use of physics-based pK_a prediction protocols for tetra-aza macrocycles.

Fig. 1 Structures of existing molecules 1–10 and previously un-synthesized molecules 11–14. Atom numbering is indicated in blue.

Table 1 Comparison of computed and measured pK_a values for macrocycles 1–10

Molecule	pKa	Experiment	QM	QM + LEC
a Ref. 31 and 32.b Ref. 27.c Ref. 32.d Ref. 23.
1	1	11.37^a	10.73	9.63
	2	8.22^a	3.83	6.15
	3	1.61^a	−1.22	3.60
2	1	11.56^b	14.10	11.34
	2	9.05^b	9.90	9.22
	3	5.45^b	3.41	5.94
	4	1.68^b	−1.90	3.26
3	1	10.50^a	12.25	10.40
	2	7.27^a	1.73	5.09
	3	1.37^a	−6.88	0.74
4	1	10.54^a	13.35	10.96
	2	8.27^a	8.04	8.28
	3	1.73^a	−4.04	2.18
5	1	11.14^a	10.06	9.30
	2	7.47^a	3.02	5.74
6	1	10.6^a	12.28	10.42
	2	7.00^a	3.90	6.18
	3	0.85^a	−3.71	2.34
7	1	10.32^c	10.52	9.53
	2	8.00 ^c	5.87	7.18
	3	1.75^c	−2.15	3.13
8	1	11.16^b	13.92	11.25
	2	9.46^b	11.13	9.84
	3	6.91^b	3.61	6.04
	4	2.17^b	−6.47	0.95
9	1	8.27^d	8.50	8.50
	2	7.36^d	5.62	7.05
10	1	11.31^d	16.82	12.71
	2	9.35^d	15.58	12.08
	3	5.25^d	3.75	6.11
	4	4.21^d	2.40	5.43
	5	0.98^d	−5.16	1.61
RMSD			3.88	1.21

---

1.2. Physics-based pK_a prediction

Physics-based computational protocols for pK_a prediction explicitly treat conformational change, making them suitable for capturing the interplay of conformation, pK_a, and prototropic tautomerism in tetra-aza macrocycles. The Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) physical property challenges provide a snapshot of the state-of-the-art in physics-based pK_a prediction.²⁹ In the SAMPL6 challenge, participants predicted the Gibbs free energies and pK_a values of 22 N-acetylsulfonamides possessing up to three acid/base sites. The most accurate physics-based quantum mechanical (QM) methods combined conformational sampling, DFT, model solvent, and a linear empirical correction (QM + LEC). The best QM + LEC methods gave root-mean-square errors (RMSE) below 0.7 log units.² In the SAMPL7 challenge, participants predicted pK_a values for 22 N-acylsulfonamides and related bioisosteres. Participants determined experimental values (“macroscopic pK_a”) from the computed free energies of individual protonation tautomers (“microscopic pK_a”). Only one physics-based method gave RMSE below 1 log unit.²⁹ Moreover, there was significant disagreement as to which microscopic transitions produced the measured pK_a, i.e., which prototropic tautomers were most stable at each pH. In the SAMPL8 challenge, participants considered more diverse compounds including several polybasic species. A QM protocol combining conformational sampling, DFT, and the COSMO-RS solvation model yielded RMSE 1.65 log units when using assignment based on the experimental transition curves.³⁰

1.3. Overview

We use state-of-the-art physics-based computational protocols to predict the pK_a of previously un-synthesized polybasic tetra-aza macrocycles. We employ protocols similar to those applied in the SAMPL6 and SAMPL7 challenges. We use these protocols to predict the pK_a and pH-dependent speciation of molecules 11–14, four previously un-synthesized tetra-aza macrocycles. Table 2 reports the final predictions. We validate these protocols against the experimental pK_a and pH-dependent speciation behavior of previously synthesized macrocycles. Table 1 shows the experimental pK_a values and predictions of our preferred protocol. This protocol provides useful accuracy consistent with results from the SAMPL challenges. In an attempt to further refine our predictions, we systematically test the effects of the different approximations employed. We find that solvation of highly charged species is a significant source of remaining errors. Future studies will experimentally test the predictions for molecules 11–14 and will use this protocol to predict pK_a values of other tetra-aza macrocycles.

Table 2 Predicted pK_a values for macrocycles 11–14

Molecule	pKa	Prediction
11	1	7.73
	2	5.83
12	1	10.06
	2	9.11
13	1	8.52
	2	7.14
14	1	6.67
	2	6.39

---

2. Methods

Most calculations in this work use a common computational workflow. For each molecule of interest, the user provides a three-dimensional structure in which all N protonation sites are occupied, along with a list of the N exchangeable protons (ESI Fig. SI1,† blue nitrogen atoms). To illustrate, molecule 1 starts with a structure of the charge +4 species with N = 4 protonated nitrogen atoms. The approach is “black-box” in that any molecule of interest may be treated, as long as the protonated 3D structure and possible protonation sites are known. A Python script using the itertools library automatically generates all possible protonation isomers by removing all possible combinations of exchangeable protons. To illustrate, molecule 1 gives 14 protonation isomers spanning five charge states: one neutral isomer, four protonation isomers with charge +1, six isomers with charge +2, four with charge +3, and one (the original input structure) with charge +4. Spatial symmetry is not used: for example, two of the charge +1 structures for molecule 1 are redundant, with protonation on either of the two symmetry-equivalent secondary amines adjacent to the pyridine.

The computed three-dimensional structure of each protonation isomer is used as input for a metadynamics and molecular dynamics simulation using the Conformer-Rotamer Ensemble Sampling Tool (CREST).³³ CREST calculations use the GFN2-xTB tight binding Hamiltonian,³⁴ the generalized Born with surface area contributions (GBSA) continuum model for water solvent,³⁵ and the iMTD-GC metadynamics-based exploration of conformational space employing a biasing potential expressed with the root-mean-square deviation in Cartesian space as a metric for the collective variables.³⁶ The five lowest-energy conformations generated by CREST are refined using a Gaussian 16 DFT geometry optimization and free energy calculation.³⁷ These calculations use density functional theory in an atomic orbital (AO) basis set to treat the molecule, and a continuum solvent model to treat the water solvent. Solvent is modeled using either the SMD or IEFPCM continuum models for water solvent, employing the default parameters for, e.g., solvent static dielectric constant.^38,39 The calculations also use 6-31G(d) or def2-TZVP atomic orbital basis sets,^40,41 and the B3LYP^42,43 or M06-2X⁴⁴ exchange-correlation functionals. All geometry optimizations and vibrational frequency calculations are performed in continuum solvent.^45,46 Gibbs free energies are taken to be the free-particle-rigid-rotor-harmonic-oscillator free energy of the lowest energy conformation of each protonation state. All calculations treat temperature T = 298.15 K. The workflow is implemented as a set of Python and Perl scripts which write and process CREST and Gaussian input and output files. This implementation is freely available at the Janesko group GitHub site.

QM calculations compute the pK_a as ΔG*/RT(ln 10). For any acid HAⁿ with charge n, we compute ΔG* as the Gibbs free energy of the dissociation reaction

HAⁿ (aq) ⇄ H⁺ (aq) + Aⁿ⁻¹ (aq) (1)

G* = G_comput (Aⁿ⁻¹, aq) + G_expt (H⁺, aq) − G_comput (HAⁿ, aq) (2)

The computed Gibbs free energies of HAⁿ and Aⁿ⁻¹ are taken directly from the Gaussian output files. G_expt (H⁺, aq) denotes the experimental Gibbs free energy of the hydrated proton at 298.15 K and standard state concentration 1 mol L⁻¹. This is computed as described in ref. 47.

G_expt(H⁺, aq) = G⁰_g (H⁺) + ΔG^{1atm → 1 M} + ΔG_aq,solv (H⁺) (3)

The standard Gibbs energy of the gas phase proton, treated as an ideal gas at gas-phase concentration 1 bar, is taken as G⁰_g (H⁺) = −6.28 kcal mol⁻¹. This is calculated as G⁰_g= H⁰_g − TS⁰_g where H⁰_g = (5/2) RT and S⁰_g = 26.05 cal (mol⁻¹·K⁻¹).⁴⁸ The factor ΔG^{1atm → 1 M} = 1.89 kcal mol⁻¹ accounts for change of the state from 1 bar to 1 mol L⁻¹. The aqueous solvation free energy of the proton at concentration 1 mol L⁻¹ ΔG_aq,solv (H⁺) = −265.9 kcal mol⁻¹ is taken from the work of Tissandier et al.,⁴⁹ corrected to treat an ideal gas at a gas-phase concentration of 1 mol L⁻¹ dissolving as an ideal solution at a liquid-phase concentration of 1 mol L⁻¹ as discussed by Kelley et al.⁵⁰ QM + LEC calculations employ a linear empirical correction (LEC)

pK_a (corrected) = a × pK_a (computed) + b (4)

Parameters a and b are obtained as a best-fit to the experimental data in Table 1. In addition to the tests of basis set, continuum solvent, and exchange-correlation functional discussed above, several test calculations treat other aspects of the computational workflow. Test calculations using only computed solvation free energies compute ΔG* as

HAⁿ (aq) + H₂O (aq) ⇄ H₃O⁺ (aq) + Aⁿ⁻¹ (aq) (5)

ΔG* = G_comput (Aⁿ⁻¹, aq) + ΔG_expt (H₃O⁺, aq) − ΔG_comput (HAⁿ, aq) − ΔG_comput (H₂O, aq) (6)

Other test calculations combine eqn (5) and (6) with the pK-Yay correction.⁵¹ Test calculations employing explicit + implicit water solvent use the QCG quantum cluster growth approach to determine the conformations of the added water molecules.⁵² This approach uses combined metadynamics and molecular dynamics with the intermolecular force field xTB-IFF⁵³ to grow molecule-solvent clusters, one solvent molecule at a time. The DFT approximations are tested by comparison to the CBS-QB3 ab initio composite approach as implemented in Gaussian 16.⁵⁴ We compare DFT and CBS-QB3 calculations on the aqueous-phase pK_a of six small molecules structurally similar to the tetra-aza macrocycles: dimethyl amine DMA, trimethyl amine TMA, pyridine, 3-hydroxy pyridine 3HP, 4-hydroxy pyridine 4HP, and phenol. Experimental pK_a of these molecules are taken from the Bordwell tables.^34,55–57

3. Results

3.1 Validation

Table 1 compares measured pK_a values to those computed with our preferred QM and QM+LEC method: CREST structure optimization, M06-2X/def2-TZVP structure refinement with the SMD continuum solvent model, and pK_a computed from the experimental proton solvation free energy. Fig. 2 shows a scatter plot of experimental vs. QM+LEC predicted pK_a. Uncorrected QM results give root-mean-square-deviation (RMSD) 3.88 log units. LEC significantly improves the results, with RMSD 1.21 log units comparable to those seen in previous SAMPL challenges. We regard this as significant in that the present work includes flexible species with up to six exchangeable protons and measured pK_a spanning a range of ten log units.

Fig. 2 Scatter plot of experimental vs. computed pK_a from Table 1. Selected points are labelled as “molecule, pK_a (n)”.

Fig. 3 compares measured lowest-energy protomers to those computed with our preferred QM+LEC method. The predicted most stable protomers show excellent agreement with experiment. The charge +1 state of molecule 1 is correctly predicted to be protonated at nitrogen N2 (see atom labeling in Fig. 1). The charge +2 state is correctly predicted to be protonated at N2 and pyridine nitrogen N4. The charge +3 state is correctly predicted to show tautomerism, protonated at nitrogen N1, N2, N3 and not protonated at pyridine nitrogen N4.

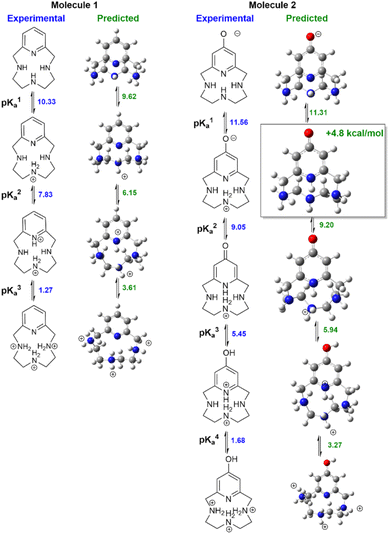Fig. 3 Speciation of molecules 1–2. Left columns show experimentally determined stable protomers, right columns show the predicted stable protomers.

Our protocol also provides reasonable predictions for molecule 2. The charge +1 state is correctly predicted to have the 4-pyridone structure with protonation at N2. The charge +3 state is correctly predicted to be protonated at oxygen, yielding protonated 4-hydroxy-pyridine and protonation at N2. The charge +2 state is correctly predicted to show a significant rearrangement with protonation at N1–N3. The only discrepancy is that the most stable charge-neutral state is predicted to be the 4-pyridone tautomer. This is predicted to be 4.8 kcal mol⁻¹ more stable than the zwitterion assigned in ref. 27. Calculations of NMR chemical shifts upon protonation confirm that the zwitterionic structure best reproduces experimental NMR titration data (ESI Table SI1†). Calculations suggest that the zwitterionic structure has a degree of proton sharing between N2 and N4 (ESI Fig. SI2†). The suggestion of proton sharing is consistent with the basicity of the moieties involved: the measured pK_a of 4-pyridone in water is 11.09 at 20° (ref. 58 ), significantly higher than the measured pK_a of aliphatic secondary amines (dimethylamine 10.922 at 20° ref. 59) and quite close to the measured first pK_a of molecule 2. We regard this agreement as particularly significant given the discrepancies in predicted protonation tautomers seen in previous SAMPL challenges.²⁹

3.2. Other computational protocols

Table 3 reports RMSD in pK_a computed with different choices of approximate density functional, basis set, solvent model, and choice of ΔG. Here “TZP” denotes the def2-TZVP basis set and "DZ" denotes the 6-31+G basis set. For each choice, we report RMSD from QM and QM + LEC calculations and include the LEC parameters a, b (eqn (4)). The choice of density functional has a relatively small effect, with B3LYP and M06-2X giving comparable QM + LEC RMSD. The basis set has a modest effect, with TZP giving an ∼0.1 log unit improvement over DZ. The solvent model significantly affects the uncorrected results, with IEFPCM giving RMSD values 6–8 log units larger than those with SMD. This is true for both B3LYP and M06-2X DFT calculations. This appears to be a systematic error corrected by the LEC. QM+LEC RMSD are comparable between SMD and IEFPCM models. The source of this systematic error appears to involve an insufficient charge screening leading to progressive destabilization of highly charged species. To illustrate this in detail, we consider the difference between the first and fourth pK_a for molecule 2. Experiments give a difference of 9.9 log units. M06-2X/def2-TZVP calculations give a difference of 33 log units for the IEFPCM model, but a difference of only 16 log units for the SMD model. This difference is reflected in the slope a of the LEC, which is around 0.5 for SMD solvent and around 0.3 for IEFPCM solvent. QM calculations using only computed solvation free energies (eqn (3) and (4)) give a much larger RMSD, a result which is improved by the pK-Yay correction. Eqn (3) and (4) and the pK-Yay correction do not change the results obtained after LEC.

Table 3 RMSD in pK_a (log units) computed with different model chemistries (density functional, basis set, continuum solvent), different choices of ΔG, and linear empirical corrections LEC. Column “Eqn (4) LEC a, b” denotes the optimum values of the fitted parameters in the LEC eqn (4)

	ΔG	RMSD		Eqn (4) LEC
Model chemistry		QM	QM + LEC	a, b
M06-2X/TZP/SMD	Eqn (2)	3.88	1.20	0.50, 4.22
M06-2X/DZ/SMD	Eqn (2)	3.75	1.33	0.52, 4.19
M06-2X/TZ/PCM	Eqn (2)	11.54	1.20	0.28, 7.08
B3LYP/TZP/SMD	Eqn (2)	3.84	1.30	0.49, 3.18
B3LYP/TZP/PCM	Eqn (2)	10.36	1.18	0.28, 6.45
M06-2X/TZP/SMD	Eqn (5)	13.7	1.21	0.28, 5.17
M06-2X/TZP/SMD	pKYaY	9.45	1.21	0.50, −3.20

---

To confirm that the density functional and basis set have a limited effect on the accuracy, ESI Table SI2† reports a small benchmark study of rigid molecules structurally similar to tetra-aza macrocycles. For these molecules, the effect of conformational flexibility and prototropic tautomerism are minimized. RMSD obtained with the accurate ab initio composite approach CBS-QB3 in model solvent are comparable to that obtained with DFT. This strongly suggests that errors in the QM+LEC results in Table 1 arise mostly from the model solvent.

3.3 Explicit solvent

Additional insight comes from considering the role of explicit solvent. Hybrid explicit+continuum solvation models can significantly improve pK_a prediction, especially for sets of related molecules where the position of explicit solvent is well-defined (e.g., two explicit water molecules hydrogen-bonded to a monocarboxylic acid).^60,61 However, for flexible polybasic macrocycles, the optimum position and orientation of explicit solvent is difficult to determine a priori.

Fig. 4 presents an initial study for molecule 1, showing pK_a computed (QM) with increasing numbers of explicit solvent molecules. Geometries are obtained using the quantum cluster growth (QCG) algorithm.⁵² ESI Fig. SI3† shows results for the hydroxypyridines used in the ab initio benchmark. Explicit solvent improves the computed pK_a values, consistent with previous studies.⁶² The predicted low-energy solvent configurations appear chemically reasonable. However, the improvement is not monotonic with increasing number of solvent molecules. This is not a special limitation of the QCG conformation search, it is an intrinsic limitation of any hybrid explicit+continuum solvent model.

Fig. 4 Explicit solvent calculations for molecule 1. (left) First (blue), second (red), and third (black) pK_a. Horizontal dashed lines are experimental values, other lines are calculations with 0–5 explicit water molecules. (right) Computed structures for charge +2 state with 0–5 explicit water molecules.

3.4. Predicted pK_a

We conclude by reported the predicted pK_a values for novel tetra-aza macrocycles 11–14. Table 2 reports the QM+LEC results. These are computed with our preferred method: CREST/xTB structure optimization, M06-2X/def2-TZVP structure refinement with the SMD continuum solvent model, pK_a computed from the experimental proton solvation free energy, and LEC a = 0.5 and b = 4.22. The computed values are chemically reasonable. Electron-withdrawing groups R = Cl and R = CF₃ reduce the pK_a values relative to molecule 9 (R = H). Electron-donating groups R = NMe₂ and R = OMe increase the pK_a values relative to molecule 9. Molecule 12 (R = NMe₂) is predicted to have both pK_a well above 7, suggesting that it will be doubly protonated at physiological pH. Molecules 11 and 14 (R = Cl and R = CF₃) are predicted to have both pK_a around or less than 7, suggesting that both molecules may have an appreciable concentration of charge-neutral tautomer at physiological pH.

4. Conclusions

Accurate prediction of the pK_a values, protonation sites, and pH-dependent speciation of polybasic drug candidates remains a significant challenge in computational medicinal chemistry. Here we used black-box methods to predict the pK_a and speciation of four previously un-tested tetra-aza macrocycle small molecules. These flexible molecules possess four to six acid/base sites and pose a significant challenge for pK_a prediction. This work included 32 pK_a values measured for 10 different aza-macrocyclic molecules as a baseline. The computational workflow employed combines exhaustive search over protonation tautomers, continuum models for water, CREST metadynamics and molecular dynamics for conformational sampling, modern density functional theory (DFT), SMD continuum solvent, and a linear empirical correction. Baseline studies give an RMSD within 1.2 log units of experimentally measured values and accurate predictions of the most stable protomer at each charge state. The predicted pK_a values for the previously un-tested macrocycles are chemcially reasonable. Our results highlight a significant step toward predicting the pK_a of large flexible molecules.

Data availability

The data supporting this article have been included as part of the ESI.† Scripts for executing the computational workflow are available at https://github.com/bjanesko/DFTPropertyPredictionWorkflows.

Author contributions

Investigation (T. K. H, K. P., M. M., D. M. F.), formal analysis (T. K. H, D. M. F., B. G. J, K. N. G.), writing (B. G. J., K. N. G.).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support from NIH NIGMS 2R15GM123463, Robert A. Welch Foundation grant P-2195-20240404, and Flatley Foundation through TCU. The authors are grateful for the support provided by the TCU High Performance Computing Center.

Notes and references

1. J. D. Watson and F. H. C. Crick, Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid, Nature, 1953, 171(4356), 737–738.
2. M. Işık, A. S. Rustenburg, A. Rizzi, M. R. Gunner, D. L. Mobley and J. D. Chodera, Overview of the SAMPL6 pKa challenge: evaluating small molecule microscopic and macroscopic pKa predictions, J. Comput. Aided Mol. Des., 2021, 35(2), 131–166.
3. D. Garcia Jimenez, M. Vallaro, M. Rossi Sebastiano, G. Apprato, G. D'Agostini, P. Rossetti, G. Ermondi, G. Caron and A. Chamelogk, Chromatographic Chameleonicity Quantifier to Design Orally Bioavailable Beyond-Rule-of-5 Drugs, J. Med. Chem., 2023, 66(15), 10681–10693.
4. P. D. Leeson, A. P. Bento, A. Gaulton, A. Hersey, E. J. Manners, C. J. Radoux and A. R. Leach, Target-Based Evaluation of “Drug-Like” Properties and Ligand Efficiencies, J. Med. Chem., 2021, 64(11), 7210–7230.
5. B. Faller and P. Ertl, Computational approaches to determine drug solubility, Adv. Drug Deliv. Rev., 2007, 59(7), 533–545.
6. J. L. Domínguez, M. C. Villaverde and F. Sussman, Effect of pH and ligand charge state on BACE-1 fragment docking performance, J. Comput. Aided Mol. Des., 2013, 27(5), 403–417.
7. S. Ono, M. R. Naylor, C. E. Townsend, C. Okumura, O. Okada, H.-W. Lee, R. S. Lokey and A. Cyclosporin, Conformational Complexity and Chameleonicity, J. Chem. Inf. Model., 2021, 61(11), 5601–5613.
8. M. Marín-Luna, I. Alkorta and J. Elguero, A theoretical study of the gas phase (proton affinity) and aqueous (pKa) basicity of a series of 150 pyrazoles, New J. Chem., 2015, 39(4), 2861–2871.
9. E. L. Jones, A. J. Mlotkowski, S. P. Hebert, H. B. Schlegel and C. S. Chow, Calculations of pKa Values for a Series of Naturally Occurring Modified Nucleobases, J. Phys. Chem. A, 2022, 126(9), 1518–1529.
10. B. Thapa and H. B. Schlegel, Calculations of pKa's and Redox Potentials of Nucleobases with Explicit Waters and Polarizable Continuum Solvation, J. Phys. Chem. A, 2015, 119(21), 5134–5144.
11. J. Ho, Predicting pKa in Implicit Solvents: Current Status and Future Directions<a class, Aust. J. Chem., 2014, 67(10), 1441–1460.
12. J. Ho and M. L. Coote, A universal approach for continuum solvent pKa calculations: are we there yet?, Theor. Chem. Acc., 2010, 125(1), 3–21.
13. R. Casasnovas, J. Frau, J. Ortega-Castro, A. Salvà, J. Donoso and F. Muñoz, Absolute and relative pKa calculations of mono and diprotic pyridines by quantum methods, J. Mol. Struct.:THEOCHEM, 2009, 912(1), 5–12.
14. A. H. Göller, Reliable gas-phase tautomer equilibria of drug-like molecule scaffolds and the issue of continuum solvation, J. Comput.-Aided Mol. Des., 2022, 36(11), 805–824.
15. M. Schilling and S. Luber, Determination of pKa Values via ab initio Molecular Dynamics and its Application to Transition Metal-Based Water Oxidation Catalysts, Inorganics, 2019, 7(6), 73.
16. E. Danelius, V. Poongavanam, S. Peintner, L. H. E. Wieske, M. Erdélyi and J. Kihlberg, Solution Conformations Explain the Chameleonic Behaviour of Macrocyclic Drugs, Chem.–Eur. J., 2020, 26(23), 5231–5244.
17. K. M. Lincoln, M. E. Offutt, T. D. Hayden, R. E. Saunders and K. N. Green, Structural, Spectral, and Electrochemical Properties of Nickel(II), Copper(II), and Zinc(II) Complexes Containing 12-Membered Pyridine- and Pyridol-Based Tetra-aza Macrocycles, Inorg. Chem., 2014, 53(3), 1406–1416.
18. M. A. Mekhail, K. Pota, T. M. Schwartz and K. N. Green, Functionalized pyridine in pyclen-based iron (iii) complexes: evaluation of fundamental properties, RSC Adv., 2020, 10(52), 31165–31170.
19. K. M. Lincoln, P. Gonzalez, T. E. Richardson, L. Rutter, D. A. Julovich, J. W. Simpkins and K. N. Green, A potent antioxidant small molecule aimed at targeting metal-based oxidative stress in neurodegenerative disorders, Chem. Commun., 2013, 49, 2712–2714.
20. M. A. Mekhail, K. J. Smith, D. M. Freire, K. Pota, N. Nguyen, M. E. Burnett and K. N. Green, Increased Efficiency of a Functional SOD Mimic Achieved with Pyridine Modification on a Pyclen-Based Copper(II) Complex, Inorg. Chem., 2023, 62(14), 5415–5425.
21. N. Hamon, A. Roux, M. Beyler, J. C. Mulatier, C. Andraud, C. Nguyen, M. Maynadier, N. Bettache, A. Duperray, A. Grichine, S. Brasselet, M. Gary-Bobo, O. Maury and R. Tripier, Pyclen-Based Ln(III) Complexes as Highly Luminescent Bioprobes for In Vitro and In Vivo One- and Two-Photon Bioimaging Applications, J. Am. Chem. Soc., 2020, 142(22), 10184–10197.
22. C. Robic, M. Port, O. Rousseaux, S. Louguet, N. Fretellier, S. Catoen, C. Factor, S. Le Greneur, C. Medina, P. Bourrinet, I. Raynal, J. M. Idée and C. Corot, Physicochemical and Pharmacokinetic Profiles of Gadopiclenol A New Macrocyclic Gadolinium Chelate With High T1 Relaxivity, Invest. Radiol., 2019, 54(8), 475–484.
23. H. M. Johnston, K. Pota, M. M. Barnett, O. Kinsinger, P. Braden, T. M. Schwartz, E. Hoffer, N. Sadagopan, N. Nguyen, Y. Yu, P. Gonzalez, G. Tircsó, H. Wu, G. Akkaraju, M. J. Chumley and K. N. Green, Enhancement of the Antioxidant Activity and Neurotherapeutic Features through Pyridol Addition to Tetraazamacrocyclic Molecules, Inorg. Chem., 2019, 58(24), 16771–16784.
24. D. M. Freire, D. Beeri, K. Pota, H. M. Johnston, P. Palacios, B. S. Pierce, B. D. Sherman and K. N. Green, Hydrogen peroxide disproportionation with manganese macrocyclic complexes of cyclen and pyclen, Inorg. Chem. Front., 2020, 7, 1573–1582.
25. K. M. Lincoln, T. E. Richardson, L. Rutter, P. Gonzalez, J. W. Simpkins and K. N. Green, An N-heterocyclic amine chelate capable of antioxidant capacity and amyloid disaggregation, ACS Chem. Neurosci., 2012, 3(11), 919–927.
26. J. Zhang, Y. Yu, M. A. Mekhail, H. Wu and K. N. Green, A macrocyclic molecule with multiple antioxidative activities protects the lens from oxidative damage, Front. Chem., 2022, 10 DOI:10.3389/fchem.2022.996604.
27. K. N. Green, K. Pota, G. Tircsó, R. A. Gogolák, O. Kinsinger, C. Davda, K. Blain, S. M. Brewer, P. Gonzalez, H. M. Johnston and G. Akkaraju, Dialing in on pharmacological features for a therapeutic antioxidant small molecule, Dalton Trans., 2019, 48, 12430–12439.
28. A. Yepremyan, A. Mehmood, S. M. Brewer, M. M. Barnett, B. G. Janesko, G. Akkaraju, E. E. Simanek and K. N. Green, A new triazine bearing a pyrazolone group capable of copper, nickel, and zinc chelation, RSC Adv., 2018, 8(6), 3024–3035.
29. T. D. Bergazin, N. Tielker, Y. Zhang, J. Mao, M. R. Gunner, K. Francisco, C. Ballatore, S. M. Kast and D. L. Mobley, Evaluation of log P, pKa, and log D predictions from the SAMPL7 blind challenge, J. Comput. Aided Mol. Des., 2021, 35(7), 771–802.
30. M. Diedenhofen, F. Eckert and S. Terzi, COSMO-RS blind prediction of distribution coefficients and aqueous pKa values from the SAMPL8 challenge, J. Comput. Aided Mol. Des., 2023, 37(8), 395–405.
31. M. A. Mekhail, K. Pota, T. M. Schwartz and K. N. Green, Functionalized pyridine in pyclen-based iron (iii) complexes: evaluation of fundamental properties, RSC Adv., 2020, 10(52), 31165–31170.
32. A. Yepremyan, M. A. Mekhail, B. P. Niebuhr, K. Pota, N. Sadagopan, T. M. Schwartz and K. N. Green, Synthesis of 12-Membered Tetra-aza Macrocyclic Pyridinophanes Bearing Electron-Withdrawing Groups, J. Org. Chem., 2020, 85(7), 4988–4998.
33. P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22(14), 7169–7192.
34. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671.
35. A. V. Onufriev and D. A. Case, Generalized Born Implicit Solvent Models for Biomolecules, Annu. Rev. Biophys., 2019, 48(1), 275–296.
36. S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15(5), 2847–2862.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel; G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci; H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Williams; Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. C.01, Wallingford, CT, 2016.
38. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396.
39. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105(8), 2999–3094.
40. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
41. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72(1), 650–654.
42. A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98(2), 1372–1377.
43. J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, A comparison of models for calculating nuclear magnetic resonance shielding tensors, J. Chem. Phys., 1996, 104(14), 5497–5509.
44. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215.
45. J. Ho, A. Klamt and M. L. Coote, Comment on the Correct Use of Continuum Solvent Models, J. Phys. Chem. A, 2010, 114(51), 13442–13444.
46. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation, J. Phys. Chem. B, 2011, 115(49), 14556–14562.
47. B. Thapa and H. B. Schlegel, Calculations of pKa's and Redox Potentials of Nucleobases with Explicit Waters and Polarizable Continuum Solvation, J. Phys. Chem., 2015, 119(21), 5134–5144.
48. G. J. Tawa, I. A. Topol, S. K. Burt, R. A. Caldwell and A. A. Rashin, Calculation of the aqueous solvation free energy of the proton, J. Chem. Phys., 1998, 109(12), 4852–4863.
49. M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, The Proton's Absolute Aqueous Enthalpy and Gibbs Free Energy of Solvation from Cluster-Ion Solvation Data, J. Phys. Chem., 1998, 102(40), 7787–7794.
50. C. P. Kelly, C. J. Cramer and D. G. Truhlar, Aqueous Solvation Free Energies of Ions and Ion−Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton, J. Phys. Chem. B, 2006, 110(32), 16066–16081.
51. R. W. Pereira and R. O. Ramabhadran, pK-Yay: A Black-Box Method Using Density Functional Theory and Implicit Solvation Models to Compute Aqueous pKa Values of Weak and Strong Acids, J. Phys. Chem., 2020, 124(43), 9061–9074.
52. J. Gorges, S. Grimme, A. Hansen and P. Pracht, Towards understanding solvation effects on the conformational entropy of non-rigid molecules, Phys. Chem. Chem. Phys., 2022, 24(20), 12249–12259.
53. S. Grimme, C. Bannwarth, E. Caldeweyher, J. Pisarek and A. Hansen, A general intermolecular force field based on tight-binding quantum chemical calculations, J. Chem. Phys., 2017, 147(16), 161708.
54. J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A complete basis set model chemistry. VI. Use of density functional geometries and frequencies, J. Chem. Phys., 1999, 110(6), 2822–2827.
55. F. G. Bordwell, Equilibrium acidities in dimethyl sulfoxide solution, Acc. Chem. Res., 1988, 21(12), 456–463.
56. F. G. Bordwell, X. Zhang and M. S. Alnajjar, Effects of adjacent acceptors and donors on the stabilities of carbon-centered radicals, J. Am. Chem. Soc., 1992, 114(20), 7623–7629.
57. S. Yadav, S. Rana, M. Manish, S. Singh, A. Lynn and P. Mathur, In silico design of dehydrophenylalanine containing peptide activators of glucokinase using pharmacophore modelling, molecular dynamics and machine learning: implications in type 2 diabetes, J. Comput. Aided Mol. Des., 2024, 39(1), 5.
58. A. Albert and A. Hampton, Analogues of 8-hydroxyquinoline having additional cyclic nitrogen atoms. Part II. Further preparations, and some physico-chemical properties, J. Chem. Soc., 1954, 505–513.
59. D. H. Everett, W. F. K. Wynne-Jones and H. B. Hartley, The dissociation constants of the methylammonium ions and the basic strengths of the methylamines in water, Proc. Roy. Soc. Lond. Math. Phys. Sci., 1941, 177(971), 499–516.
60. S. Pezzola, M. Venanzi, P. Galloni, V. Conte and F. Sabuzi, Easy to Use DFT Approach for Computational pKa Determination of Carboxylic Acids, Chem.–Eur. J., 2024, 30(1), e202303167.
61. S. Pezzola, S. Tarallo, A. Iannini, M. Venanzi, P. Galloni, V. Conte and F. Sabuzi, An Accurate Approach for Computational pK_a Determination of Phenolic Compounds, Molecules, 2022, 27(23), 8590.
62. S. A. Rodriguez, J. V. Tran, S. J. Sabatino and A. S. Paluch, Predicting octanol/water partition coefficients and pKa for the SAMPL7 challenge using the SM12, SM8 and SMD solvation models, J. Comput. Aided Mol. Des., 2022, 36(9), 687–705.

---

Footnote

† Electronic supplementary information (ESI) available: M06-2X/def2TZVP/SMD geometries and free energies of all species. See DOI: https://doi.org/10.1039/d5ra01015b

---