Tension-compression asymmetry of gradient nanograined high-entropy alloys

Abstract

This study investigates the mechanical responses and deformation mechanisms of CoCrFeMnNi high-entropy alloy (HEA) with varying grain size gradients through molecular dynamics simulations, and explores the tension-compression asymmetry of gradient nanograined high-entropy alloy (G-HEA) under different loading conditions. In the early stage of plastic deformation, the normal stress and shear strain of G-HEA both exhibit gradient distribution characteristics under compression and tension. However, as the engineering strain increased, these gradient distribution characteristics gradually diminished and ultimately disappeared. Grain boundary (GB) migration and grain merging are the main GB activities of G-HEA, and fine grains in the soft zone have stronger grain boundary vitality compared to coarse grains in the hard zone. G-HEA exhibits multiple plastic deformation mechanisms, including dislocation slip, deformation twinning, and hexagonal close-packed (HCP) phase transformation. There are both synergy and competition among various deformation mechanisms, which collectively enhance the mechanical properties of materials. This work has found that the differences in GB activities are the main cause of stress and strain asymmetry in G-HEA, while the different nucleation positions of dislocations are the reasons for the asymmetry in dislocation density, yield stress, and average flow stress. In addition, when g = 0.32, the yield stress and flow stress of G-HEA both reach their maximum/minimum values, further demonstrating the role of gradient nanostructures in regulating stress and strain distribution. Therefore, the research results of this article provide a theoretical basis for designing G-HEA suitable for different application scenarios.

---

1. Introduction

High-entropy alloys (HEAs) are a class of multi-principal element alloys¹ that break traditional alloy design principles, which are also a new class of alloys with chemical long-range disorder,² prepared by special manufacturing processes from four or more base metal elements. Unlike traditional alloys, HEAs have excellent solid solution strengthening ability due to their ease of forming solid solutions. By adjusting the atomic ratios of metals, adding interstitial atoms, and improving manufacturing processes, HEA with outstanding mechanical properties,^3–5 high-temperature performance,^6–8 corrosion resistance,⁹ and wear resistance¹⁰ can be designed to accommodate the requirements of specific working environments. HEAs have attracted the attention of numerous researchers due to their excellent comprehensive performance and have quickly become a research hotspot. CoCrFeMnNi HEA is a single-phase high entropy alloy with a face-centered cubic (FCC) structure, first proposed by Cantor and his colleagues.¹¹ This alloy, characterized by high mixing entropy, large lattice distortion, and slow diffusion rates due to similar atomic ratios, is widely studied in the field of metallic materials.

CoCrFeMnNi HEA has low stacking fault energy and can activate both dislocation slip and deformation twinning (DT) mechanisms simultaneously. Additionally, It may undergo hexagonal closed-packed (HCP) phase transformation^12,13 under low temperature, high pressure, high strain rate, and severe plastic deformation environments. The synergistic effect of multiple deformation mechanisms gives it good plastic deformation ability. However, the yield strength and tensile strength of CoCrFeMnNi HEA at room temperature are relatively low. Adding interstitial atoms for solid solution strengthening,¹ forming refined grains through Severe Plastic Deformation (SPD),¹⁴ and forming supersaturated strengthening phases¹⁵ through heat treatment are typical methods for improving alloy strength. CoCrFeMnNi HEA with nanostructures prepared using SPD technology exhibit ultra-high strength, but low extensibility. Adding a short-term annealing process after SPD can optimize the microstructure of the alloy, making it possess both high strength and good plasticity. Common SPD craft include ultrasonic shot peening (USP),^16,17 surface mechanical rolling treatment (SMRT),¹⁸ laser shock peening (LSP),^19,20 and surface mechanical attrition treatment (SMAT).^21,22 Chen et al.²³ used USP to treat equiatomic CrMnFeCoNi HEA, forming a nanocrystalline layer with compressive residual stress on the alloy surface, significantly improving its strength and hardness without sacrificing ductility. Additionally, Wang et al.²⁴ combined USP with SMRT to enhance the mechanical and fatigue properties of 2024 aluminum alloys, they believed that the synergistic effect of compressive residual stress and gradient structural layers from USP enhanced the mechanical properties, whereas SMRT reduced the surface roughness of the surface of alloys and improved the fatigue properties of the material. Tong et al.²⁵ prepared CoCrFeMnNi HEA with excellent wear and corrosion properties through laser additive manufacturing (LAM) and laser shock peening (LSP), they insisted that residual compressive stress enhanced the adhesion of the friction layer on the worn surface to protect the bottom layer from damage and improve its wear performance. Furthermore, the synergistic effects of grain refinement and residual compressive stress facilitated the formation of a dense passivation film on the surface of the material, suppressing the intrusion of corrosive ions and enhancing the corrosion resistance of HEAs. Tsai et al.²⁶ used SMAT craft to treat two single-phase HEAs (FeCoNiCrMn and FeCoNiCrMn-Al). By designing appropriate SMAT paths, the grain sizes of the alloys were reduced from ∼50 μm to ∼0.1–1 μm, the hardness increased from ∼2.5–5 GPa to ∼5–8.5 GPa, and the tensile strength and ductility were two times greater than those of the original alloys.

After undergoing SPD, the surfaces of metallic materials can form nanostructured layers with certain thicknesses, but the grain size of the substrate remains in the micrometer scale. This type of metallic material with gradient nanograined (GNG) has been proven to possess both high strength and ductility^27–30 and has become a research hotspot in materials science in recent years. Compared with experimental studies on the mechanical properties, corrosion resistance, wear resistance, and micro-deformation mechanisms of GNG metals, computational simulations are low-cost, efficient, and environmentally friendly scientific research methods. Among these methods, the crystal plasticity finite element method (CPFEM), discrete dislocation dynamics (DDD) method, and molecular dynamics (MD) method are typical computational means applied to meso-, micro-, and atomic-scale studies, respectively. Jang et al.³¹ developed a constitutive model for FCC CoCrFeMnNi HEA based on dislocation slip and deformation twinning mechanisms and validated the effectiveness of the model through compression tests and microstructural characterizations. Zhai et al.³² combined in situ Electron Backscatter Diffraction (EBSD) and CPFEM to investigate the deformation mechanisms of Al_0.6CoCrFeNi HEA and reported that the dislocation density distribution was uniform in fine-grained samples, whereas high dislocation densities were mainly concentrated near the BCC phase in coarse-grained samples. Lu et al.³³ used three-dimensional multiscale DDD to study the mechanical properties and deformation mechanisms of GNG aluminum and discovered that the synergistic strengthening induced by the gradient structure resulted in yield stress and strain-hardening exceeding those predicted by the properties of simply mixed materials. Moreover, the prominent Bauschinger effects observed in the materials confirmed the role of back-stress strengthening in GNG structures, providing valuable insights into the optimization of alloy mechanical properties. At the atomic scale, Zhou et al.³⁴ performed MD simulations on the plastic deformation characteristics of GNG copper films and observed a synergistic effect caused by GNG layers, which led to strain strengthening. Furthermore, they found that plastic deformation first occurred in the fine-grained regions and propagated to the coarse-grained regions as the strain increased, and considered this plastic attribute was independent of the strain rate and temperature. Lu et al.³⁵ used MD to study the mechanical responses of GNG metals at different temperatures and pointed out that the mechanical properties of the metals decreased with increasing temperature. Xian et al.³⁶ used MD to investigate crack propagation behaviors in GNG coppers with different grain sizes and concluded that increasing the grain size gradient improved the crack resistance of the material, remarkably increased its dislocation density, but led to increasingly severe crack blunting phenomena.

To date, numerous studies on the mechanical properties and deformation mechanisms of gradient nanograined high-entropy alloy (G-HEA) have been reported. An et al.³⁷ prepared a GNG CoCrFeMnNi HEA with hierarchical grain sizes and many nano-twins via rotational accelerated shot peening and composition design and found that the alloy exhibited multiple deformation mechanisms, resulting in ultrahigh strength and comparable ductility relative to those of cast alloys. Qiao et al.³⁸ investigated the deformation behavior of CoCrFeMnNi HEA under impact tensile using the split Hopkinson tensile bar (SHTB) technique and concluded that the collaborative reinforcement of twinning and dislocation was the primary reason for the increased strength and ductility. Tong et al.³⁹ applied LSP to modify the surface stress states and microstructures of CoCrFeMnNi HEA and considered that the residual compressive stress and GNG introduced by LSP enhanced both the strength and ductility of the alloy. Most of the aforementioned studies rely on experimental methods, which are often time-consuming and costly. In contrast, atomic simulations offer advantages such as high efficiency, low cost, and reliable results, making them an ideal approach for investigating HEA. They have been widely applied to study aspects such as size effects, impact toughness, and orientation effects in HEA. Additionally, Du et al.⁴⁰ utilized molecular dynamics (MD) to explore the additional strengthening mechanisms and the Bauschinger effect in G-HEA. They proposed that dislocation pinning ahead of grain boundaries (GBs) is a significant source of extra strengthening of G-HEA, while the reverse motion of dislocations facilitated by sessile dislocations contributes to the Bauschinger effect. However, there are few MD studies reported on the influence of grain size gradient rates on the mechanical properties of G-HEA, particularly regarding the tension-compression asymmetry and the underlying mechanisms under compressive and tensile loading conditions.

Based on the aforementioned factors, this work employs MD to investigate the mechanical responses and deformation mechanisms of CoCrFeMnNi HEA with varying grain size gradients under uniaxial compression and tension. This work aims to elucidate the intrinsic mechanisms responsible for the tension-compression asymmetry in G-HEA, identify the optimal grain size gradient for different loading conditions, and provide a theoretical foundation for designing G-HEA suitable for diverse application scenarios. The remainder of this paper is organized as follows: Section 2 introduces the establishment of geometric models with different grain size gradient rates and the simulation process; Section 3 presents the simulation results for different models under uniaxial compression and uniaxial tension; Section 4 discusses the gradient distribution characteristics of stress and strain, grain boundary (GB) activities during plastic deformation, and plastic deformation mechanisms; and Section 5 features a summary of the main conclusions of this study.

2. Simulation details

MATLAB was used for programming and generating polycrystalline seed point files. The open-source software Atomsk⁴¹ uses these seed point coordinates and the Voronoi algorithm to generate an equiatomic CoCrFeMnNi HEA quasi-three-dimensional atomic model with a random orientation. To investigate the role of gradient nanostructures, the G-HEA models and the homogeneous nanocrystalline HEA (H-HEA) models were constructed simultaneously. These models have the same geometric dimensions, simulation, and analysis methods, except for differences in grain size and distribution. Fig. 1 is a schematic diagram of the sample with grain size changing along the x-direction. The grain size gradient g is defined as the first derivative of the average grain size with respect to the x-direction position, expressed as follows:

Fig. 1 (a) Variation in the average grain size of polycrystalline HEA along the x-axis, showing smaller average grain sizes in the regions on both sides and larger grain sizes in the central region. Four linear gradients and two uniform HEA atomic models were constructed. (b) Microstructural morphology of the model with a gradient of g = 0.23, where d₀ represents the minimum grain size.

Keeping the average grain size of the region on both sides constant at 6 nm and adjusting the average grain size in the middle region, G-HEA samples with g = 0.18, g = 0.23, g = 0.32, and g = 0.49 were constructed. The average grain sizes were 12.3, 13.7, 15.4, and 17.4 nm respectively. The calculation method for these values is as follows:

where S is the area of the xy plane of the sample, and N is the number of grains.

The atomic numbers of these G-HEA models are not significantly different, about 1.95 million, but the grain numbers are 188, 152, 120, and 94, respectively. Additionally, two H-HEA models for comparison have average grain sizes of 6 nm and 40 nm with corresponding grain numbers 520 and 15 respectively. The geometric dimensions of all the models were 186 × 120 × 0.96 nm³ (x × y × z), with a lattice constant of 3.595 Å, where the size along the z direction is larger than the cutoff radius 0.45 nm for meeting the periodicity along the z direction.⁴² The simulation process and analysis methods were consistent across all the models.

The open-source software LAMMPS⁴¹ was used for atomic-level simulations of tension and compression of the G-HEA and H-HEA models. The 2NN MEAM potential function developed by Choi et al.⁴³ was applied to calculate the interatomic forces between Co, Cr, Fe, Mn, and Ni atoms. This potential function has been used in simulations of the tension deformation, cyclic plasticity, radiation damage, nanoindentation behavior, impact-induced spallation, and temperature effects of CoCrFeMnNi HEA, with high simulation accuracy. Periodic boundary conditions were exerted in all directions and the simulation time step was set to 0.001 ps. First, the conjugate gradient method was operated to minimize the model energy and eliminate the internal atomic stress. Next, an NPT ensemble was used for isothermal relaxation at 300 K under constant pressure, with the pressure on all axes being maintained at 0 bar and the relaxation time being set to 50 ps. Finally, the NPT ensemble was employed again to control the atomic pressure in the system, with the x- and z-axes maintaining a pressure of 0 bar and uniaxial tension and compression being applied along the y-axis with a strain amplitude of ±20%. To avoid the influence of strain rate sensitivity on the simulation results, we investigated some similar literature and performed a series of trial calculations. Ultimately, after considering factors such as computational cost and accuracy, the strain rate for this study was determined to be ±1 × 10⁹ s⁻¹. The open-source software OVITO was utilized for result analysis and visualization. The common neighbor analysis (CNA) module was employed for atomic structure analysis, and the dislocation extraction algorithm (DXA) module was applied for dislocation analysis. Additionally, CoCrFeMnNi HEA possesses lattice distortion (LD) and short-range order (SRO) phenomena; however, when studying the mechanical behaviors and deformation mechanisms of polycrystalline HEA, the grain sizes and gradient effects at the microstructural level are the primary influencing factors.⁴⁰ Therefore, this work did not consider the effects of LD and SRO in this study.

3. Results

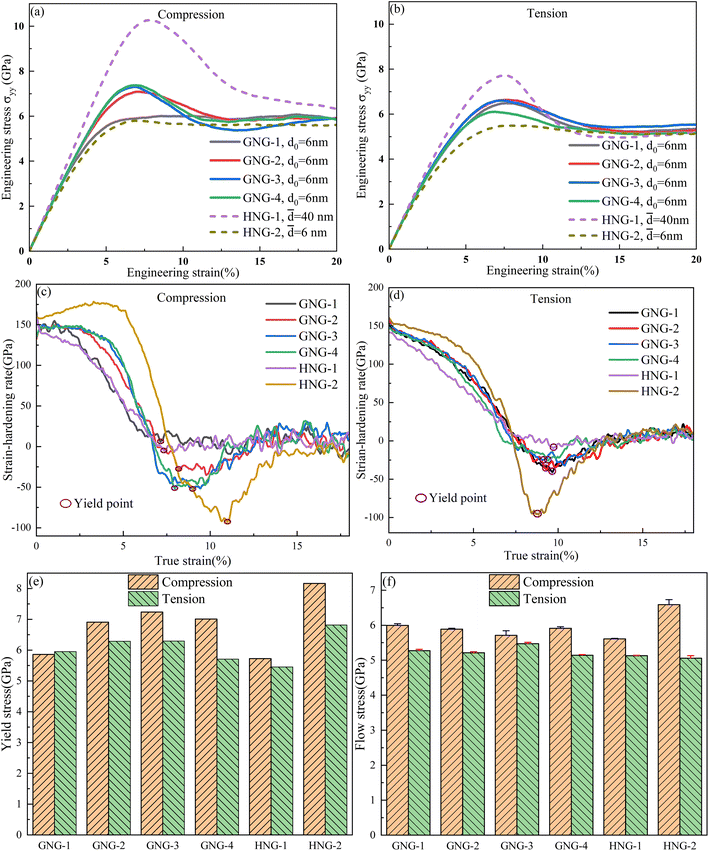
Fig. 2 shows the mechanical behaviors of G-HEA and H-HEA under different loading conditions. As shown in Fig. 2(a), when the compressive strain is less than 3%, the normal stress and shear strain exhibit a roughly linear relationship, indicating that it is in the elastic stage. Afterward, the material enters the plastic deformation stage, where the stress continues to increase with engineering strain increase, exhibiting a typical strain-hardening behavior until the maximum is reached. However, the rate of change of stress in the initial stage of plastic deformation is smaller than that in the elastic stage. After the peaks, the stress first rapidly decreases and then gradually stabilizes when the engineering strain reaches 13%. It is worth noting that the GNG-1 and HNG-2 with smaller average grain sizes do not exhibit an obvious stress drop, whose stress directly enters a stable plastic stage after reaching the maximum. This stress drop is a common engineering phenomenon, especially in single-crystal simulations.⁴⁴ For polycrystals, the stress drop is related to the grain size, and it weakens as the grain size decreases.⁴⁵ The results of this work confirm the conclusion just mentioned. In MD simulations, the stress drop is often associated with dislocation burst phenomena,⁴⁶ which is consistent with the results of micropillar compression experiments.^47,48 As shown in Fig. 1(a) and 2(a), atomic models with big gradient values have larger average grain sizes and higher peak stress than those with small gradient values, and the result of peak stress complies with inverse Hall–Petch effects. Compared to compression, tension has a relatively lower stress status, and its stress–strain curve also satisfies the inverse Hall–Petch relationship. The maximum stress under tension occurs in GNG-2, while the maximum stress under compression occurs in GNG-4. It indicates that there is a tension-compression asymmetry in the stress of HEA.

Fig. 2 Mechanical responses of G-HEA and H-HEA at 300 K. (a) Uniaxial compression stress–strain curve. (b) Uniaxial tension stress–strain curve. (c)–(d) Strain-hardening rate under compression and tension. (e) Yield stress under uniaxial compression and tension. (f) Flow stress under uniaxial compression and tension.

For metals such as HEA, which do not have a clear yield point, the stress at the strain ε = 0.2% usually represents the yield stress. Alternatively, the yield stress of a material can be determined by combining the stress–strain curve with the strain-hardening rate (the first derivative of true stress with respect to true strain) curve. Cereceda et al.⁴⁹ used this method to estimate the yield stress of materials and achieved good results. Since the stress–strain curves of the HEA studied in this work show no significant change in slope at the traditional yield point ε = 0.2%, the second method was applied to calculate the yield stress of the HEA. As shown in Fig. 2(c) and (d), at high strain rates, as the strain increases, the strain-hardening rate first decreases, then briefly stabilizes, and finally slowly increases (except for HNG-2). The yield point is the turning point of metal materials from elastic deformation to plastic deformation, and its strain-hardening rate is usually the lowest. Therefore, this work takes the strain corresponding to the first minimum value of strain hardening rate in the temporary stable zone as the yield point, and the stress corresponding to the yield point as the yield stress. HGN-2, with the highest grain boundary density and the largest initial dislocation density, is more prone to grain boundary merging than the other models. The strain-hardening rate of HGN-2 first increases and then rapidly decreases before increasing again and finally stabilizing. As shown in Fig. 2(e), the yield stress of G-HEA increases first and then decreases with the increase of average grain size, and reaches its maximum at g = 0.32, which is consistent with the research results of Liu et al.⁵⁰ The average stress value of the local plastic strain interval has been widely served as the flow stress of metals in MD simulation research.^51,52 In this work, the strain range for calculating the flow stress is from ±15% to ±20%, the outcome of flow stress as shown in Fig. 2(f). The flow stress of G-HEA under compressive load decreases first and then increases with the increase of average grain size, reaching its minimum when g = 0.32; but under tensile load, the flow stress increases first and then decreases with the increase of average size, reaching its maximum at g = 0.32. The flow stress of G-HEA exhibits tension-compression asymmetry. It is worth noting that under the same strain conditions, the yield stress and flow stress under compression are greater than their corresponding values under tension. This finding is similar to the results obtained for nanocrystalline Ni,⁵³ which may be attributed to the decrease in the atomic spacing under compression that leads to an increase in the atomic interaction forces.

Because the yield stress and flow stress of G-HEA reach their maximum or minimum both at g = 0.32, GNG-3 will be the main model for analysis and discussion in Part 4. Moreover, gradient nanostructures can coordinate stress and strain distributions, and by changing the grain size gradient rate, the constraints of the inverse Hall–Petch effect can be broken.

4. Discussion

4.1 Effects of gradient nanostructures on the stress and strain distributions

To study the effect of the grain size gradient on the normal stress and shear strain of HEA, this work divided GNG-3 along the x-axis into 50 regions and calculated the average normal stress and average shear strain for each region. This method is commonly used to analyze the correlation between normal stress, shear strain, and the geometric position of a model. Fig. 3 shows the average normal stresses and average shear strains of GNG-3 in the stage of plastic deformation under different loading methods. The solid and dashed lines represent the variables of compression and stretching, respectively. The red curve and red icon show the variable values in the early stage of plastic deformation, while the blue curve and blue graph represent the variable values in the later stage of plastic deformation. Here, the average normal stress σ_yy is calculated as the sum of the stress in the y-direction for all the atoms in each region divided by the volume of that region,⁵⁴ and the average shear strain is similarly calculated.

Fig. 3 Distribution of the average normal stress and shear strain in GNG-3. (a) Normal stress σ_yy. (b) Average shear strain.

Fig. 3(a) displays the distribution of normal stress σ_yy of GNG-3 at engineering strains of ±5% and ±20%. The grain size gradient distribution leads to varying gradient distribution characteristics for the normal stresses under different loading conditions. When the strain is ±5%, the material has just entered the plastic deformation stage. The coarse grains (CGs) in the middle of the sample exhibit greater normal stresses under both compression and tension, whereas the fine grains (FGs) on either side experience lower normal stresses under the same conditions. Overall, the stress shows a “C”-shaped gradient distribution along the x-axis, with the gradient effect under compression being more pronounced than that under tension. However, as the engineering strain increases, the feature of stress gradient distribution gradually weakens, and by the time the strain reaches ±20%, the stress in the grains across different regions becomes approximately the same, leading to a uniform stress distribution (as indicated by the red dashed line in Fig. 3(a)). Under compressive loading, when the strain reaches 20%, the average normal stress in the FGs region is lower than that in the CGs region, showing a gradient distribution of normal stress opposite to that observed at 5% strain. Liu et al.⁵⁰ have shown that the yield stress of CoCrFeMnNi HEA follows the classic Hall–Petch relationship concerning grain size, with a critical grain size of 48.6 nm. Therefore, the grain sizes of all models in this study are within the inverse Hall–Petch effect range. The CGs region in the middle of GNG-3 can be considered a hard zone with higher stiffness, whereas the FGs regions on the sides can be considered a soft zone with weaker resistance to deformation. When the material enters the plastic deformation stage, the CGs in the hard zone owing to their higher resistance to deformation, exhibit higher stress, whereas the FGs in the soft zone, owing to their lower stiffness, exhibit lower stress, resulting in a stress gradient distribution effect. As the engineering strain increases, the GBs in the soft zone begin to slip and migrate, the boundaries become blurred, and small grains gradually merge into larger grains. The performance difference between FGs and CGs decreases with increasing engineering strain, and the gradient distribution effect of stress gradually disappears or reverses.

Fig. 3(b) shows the distribution of the average shear strain for GNG-3 at strains of ±5% and ±20%. Similar to the normal stress distribution, the average shear strain distribution is nonuniform in the early stages of plastic deformation. The strain in the hard zone is smaller, whereas the strain in the soft zone is larger, exhibiting an obvious gradient distribution characteristic. As the engineering strain increases, the strain gradient distribution effect gradually weakens, eventually evolving into a uniform distribution.

In summary, in the early stages of uniaxial loading, the CGs in the hard zone exhibit high stiffness, low shear strain, and relatively high normal stress. In contrast, the FGs in the soft zone on either side have relatively low stiffness, high shear strain, and low stress. It can be considered that the gradient nanostructure causes the stress gradient distribution and strain gradient distribution of CoCrFeMnNi HEA, and the tension-compression asymmetry of the stress distribution and strain distribution may be related to the dislocation nucleation position and grain boundary movement. Specific reasons can be found in Section 4.2.

4.2 Plastic deformation mechanisms under uniaxial loading

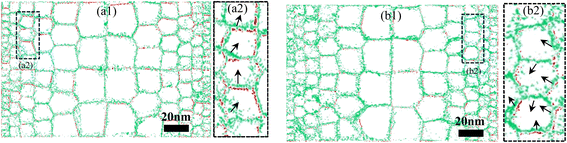
When gradient nanostructured metals transition from elastic deformation to plastic deformation, mechanically driven GB migration and accompanying grain growth dominate the plastic deformation process.⁵⁵ Fig. 4 shows the GB migration map obtained using a method similar to that of Cao,⁵⁶ where the GBs before deformation are shown in red and the GBs at a strain of 10% are shown in green. The affine displacements have been removed to display pure GB migration characteristics.⁵⁷ The right sides of Fig. 4(a1) and (b1) show enlarged views of the corresponding region, with black arrows indicating the direction of grain boundary migration. GB migration occurs in the CoCrFeMnNi HEA under both uniaxial compression and uniaxial tension. However, the amount of GB migration under compression is greater than that under tension, and the FGs in the soft zone possess more significant GB vitality than the CGs in the hard zone. This phenomenon is related to the relatively low stiffnesses of FGs, which are prone to plastic deformation in the inverse Hall–Petch region. Furthermore, when ε < 3%, the deformed GBs after affine removal largely overlap the initial GBs, which indicates that the material undergoes almost no grain boundary migration during the elastic deformation stage. After plastic deformation, dislocations nucleate at GBs and are emitted into the crystal, ultimately being absorbed by the opposite GBs. As the engineering strain increases, dislocations gradually accumulate at GBs, forming back stresses that hinder their continued movement. The reverse force of back stresses drives grain boundary movement, causing the deformed GBs to no longer coincide with the initial GBs. Fig. 4(a2) and (b2) show that the GBs on the left almost all migrate to the upper right, whereas the GBs on the right mostly move to the upper left. The GB migration in the hard zone is much smaller than that in the soft zone, which is just why the grains in the soft zone on each side exhibit greater average shear strain. Therefore, GB migration is the physical mechanism driving the plastic deformation of CoCrFeMnNi HEA, and it is also one of the reasons for the distribution of shear strain gradient.

Fig. 4 The result of GB migration in GNG-3 at ε = 10%. (a) Uniaxial compression. (b) Uniaxial tension. (a1) and (b1) Are the GBs of GNG-3 under different loads. (a2) and (b2) Are the enlarged views of the corresponding regions of the left pictures, with black arrows indicating the direction of GBS motion.

The CNA module of OVITO software labels GB atoms, atoms near dislocations, and unrecognized atoms as “Other” atoms. However, other atoms are mainly composed of GB atoms, especially in the early and middle stages of metal material deformation. Therefore, the fraction of “Other” atoms can reflect the changes in GB movement. As shown in Fig. 5, models with smaller average grain sizes have higher initial grain boundary densities. As the engineering strain increases, the number of “Other” atoms gradually increases. When the engineering strain is less than 3%, GNG CoCrFeMnNi HEA is still in the elastic stage, the GB movement is inactive, and the proportion of Other atoms remains unchanged. When the engineering strain reaches 5–10%, due to factors such as GB migration, dislocation motion, DT, and HCP phase transformation, the number of “Other” atoms increases rapidly. When ε > 10%, grain merging reduces the number of “Other” atoms, whereas dislocation nucleation increases their number. However, the overall trend is an increase in the number of “Other” atoms.

Fig. 5 Curves of the ratio of “Other” atoms under different loads. (a) Compression. (b) Tension.

Notably, the GB movement in the plastic deformation stage of the GNG CoCrFeMnNi HEA exhibits tension-compression asymmetry. This difference in GB motion also indirectly leads to the asymmetry of stress distribution and strain distribution. As shown in Fig. 5(a), the number of “Other” atoms in GNG HEA increases rapidly in the early stage of compression (indicated by the red dashed box), whereas this phenomenon does not occur under tensile loading (Fig. 5(b)). This difference may be related to the presence of residual tensile stress between grain boundary atoms during the relaxation stage. In the early stage of deformation, the compressive stress formed by the external compressive load is first neutralized with the residual tensile stress at the grain boundary. After the residual tensile stress is canceled out, compressive stress begins to form at GBs. The stress mutation in the early stage of deformation caused a brief increase in the number of other atoms, resulting in greater displacement of GB atoms. This also is the main reason why the migration of compressed grain boundaries is greater than that of stretched grain boundaries.

Under compression, except for the models GNG-4 and HNG-1, which have relatively large average grain sizes, the number of “Other” atoms in other models increases approximately linearly with engineering strain. However, under tension, the number of “Other” atoms exhibits a three-stage variation pattern: a stable period, a rapid growth period, and a slow growth period. The phenomenon of a three-stage pattern becomes increasingly pronounced as the average grain size increases. Additionally, the elastoplastic transition point under compression is ε = 3%, but the elastoplastic transition point under tension is ε = 4.5%. Under compression load, due to the continuous reduction of atomic spacing, the repulsive force between atoms drives dislocation nucleation and intragranular movement, while promoting the material to enter the plastic deformation stage. This may be a potential reason why the elastoplastic transition point of compression is smaller than that of tension.

Since nonaffine square displacement (NSD) can capture the GB sliding process,^58,59 we plotted the NSD (the definition and calculation method can be found in ref. 56) curves of the GNG CoCrFeMnNi HEA under different loads to further investigate GB migration. Fig. 6(a) and (b) show the NSD curves for compression and tension, respectively. As the engineering strain increases, the NSD curve first experiences a brief rapid increase, followed by a rough increase linearly (except for GNG-3). This variation trend is similar to that of the “Other” atoms. This result once again proves that HEA did not occur in GB migration during the elastic deformation stage. When the engineering strain reaches approximately 5%, the NSD curve continues to rise and maintains a nearly constant growth rate during subsequent deformation.

Fig. 6 NSD curves and cloud maps of G-HEA. (a) Compressive load. (b) Tensile load. (c) The NSD cloud map of GNG-3 at 5% compressive strain. (d) The NSD cloud map of GNG-3 at 5% tensile strain.

Similar to the variation in “Other” atoms, the NSD curves of the GNG CoCrFeMnNi HEA exhibit tension-compression asymmetry. Under compression load, GNG-3 has the highest initial NSD value and the lowest final NSD value. The NSD of GNG-3 slowly increases at a very small growth rate in the early stage of deformation and begins to linearly increase at a larger rate after the elastic deformation ends. However, GNG-3 has a higher NSD value at the end of tension compared to other models. G-HEA with varying gradient rates exhibited nearly identical NSD magnitudes and evolutionary trends during the elastic stage, with their NSD curves beginning to diverge only during the intermediate-to-late stages of plastic deformation. As illustrated in Fig. 2(f), under compressive load, GNG-3 has the lowest flow stress compared to other models, and the lower flow stress is not sufficient to drive the model to produce too much deformation, resulting in the minimal NSD for it at compressive termination. Conversely, under tensile load, GNG-3 has the highest average flow stress, which results in it possessing a maximum NSD value at the end of the stretch. Therefore, it can be considered that the tension-compressive asymmetry of the NSD of G-HEA is related to the average flow. In addition, as shown in Fig. 6(c) and (d), when the strain is 5%, G-HEA just enters plastic deformation, and GB movement begins to be active, with the NSD at the GB being larger than that inside the grain. As the engineering strain increases, the GBs begin to migrate, and the FGs in the soft zone gradually merge, with high NSD regions also appearing inside the grains.

In addition to GB migration, grain coalescence is a dominant GB activity that adjusts the plastic deformation of the CoCrFeMnNi HEA. During the relaxation stage, the atomic forces are not fully released, and some dislocations nucleate at the GBs. As shown in Fig. 7(a)–(c), as the compressive strain increases, dislocations nucleating at GBs are emitted into the interior of the grains, causing the GBs to gradually disappear, and two adjacent grains merge into a larger grain. As shown in Fig. 7(d)–(f), as the tensile strain increases, more dislocations nucleate within the grains and move towards two sides of the GBs. The “Other” atoms near the dislocations cause the GBs to become blurry, and two grains merge into a larger grain.

Fig. 7 The schematic diagram of grain merging in GNG-3 under different loads. (a)–(c) Compression. (d)–(f) Tension.

A comparison of the morphologies of grain 1 and grain 2 before and after deformation reveals that smaller grains are more prone to merge, whereas the boundaries of larger grains are largely maintained (as shown in Fig. 8). The smaller grains undergo significant morphological changes before and after deformation, whereas the morphologies of the larger grains change relatively little. Furthermore, The dislocation movement of grains with the same average grain size may differ significantly during plastic deformation. For example, grain a and grain c have a higher dislocation density, while dislocation activity in grain b is minimal. This phenomenon is related to the differences in grain orientation.⁴¹

Fig. 8 Particularity of plastic deformation of different grains in GNG-3 (the right part). (a) ε = 0 (b) ε = 15% FCC atoms have been removed.

Notably, the dislocation density of the CoCrFeMnNi HEA also shows tension-compression asymmetry. Fig. 9 shows the evolution curves of the dislocation density for GNG-3 under different loads. Similar to the variation in the fraction of “Other” atoms, models with smaller average grain sizes have higher initial dislocation densities, whereas models with larger average grain sizes tend to exhibit a three-stage dislocation density evolution trait. In the elastic stage, dislocations stored at GBs move from one side of the GB to the other, with a very small increment of dislocation density and a stable total dislocation density. When the engineering strain reaches a critical value (approximately 4.5% for compression and 6% for tension), many dislocations nucleate at the GBs or within the grains (under tensile load), causing a sharp increase in the dislocation density. When the engineering strain reaches approximately 12%, the rate of increase in the dislocation density slows or becomes constant. Compared with those under compressive loading, HEA has a more pronounced three-stage dislocation density evolution feature under tensile load, where the dislocation density remains nearly constant in the early and late stages of deformation and increases rapidly only during the middle stage of plastic deformation.

Fig. 9 Evolution curves of the dislocation densities in GNG-3 under different loads. (a) Compression. (b) Tension.

The reason for the difference in dislocation density evolution mentioned earlier may be due to the different nucleation positions of dislocations. As illustrated in Fig. 10(b) and (c), under compressive load, dislocations mainly nucleate at GBs and then move in one direction to the opposite GB. A dislocation source forms a dislocation, and the dislocation density increases at a relatively small rate. However, under tensile load, dislocations mainly nucleate within the crystal and then move in two directions to the grain boundaries on both sides. One dislocation source forms two dislocations, and the dislocation density increases significantly at a higher rate. In addition, the different nucleation positions of dislocations are still the main reason for the dislocation density in the later stage of plastic deformation under tensile load to maintain stability and one of the reasons for the tension-compression asymmetric of stress and strain.

Fig. 10 Microstructures and dislocations of the GNG-3 under different loads. (a) The left half of the atomic model before loading. (b) and (c) The enlarged view at ε = 10% under compression. (d) and (e) The enlarged view at ε = 10% under tension. The four images on the right are enlarged views of the same grain selected by the rectangular box in (a). Among them, green, red, and purple represent FCC, HCP, and GBs respectively, and the back dashed line is also GBs.

Dislocation slip, DTs, and HCP phase transition are the main plastic deformation mechanisms of CoCrFeMnNi HEA, with dislocation slip being the main mechanism, followed by HCP phase transformation and deformation twinning being the least.³¹ Otto et al.⁶⁰ attributed the twinning of CoCrFeMnNi HEA to its low dislocation energy. Studies^12,61 have shown that the stacking fault energies of CoCrFeMnNi HEA at 293 K are 20–25 mJ m⁻², which suggests that twins may be activated at room temperature. Additionally, CoCrFeMnNi HEA can trigger a transformation of the FCC phase to the HCP phase with high strain rates and SPD at room temperature.^62–64 The microstructures of different G-HEA models are shown in Fig. 10, with FCC atoms being removed for better observation. The microstructures (including intrinsic stacking faults (ISFs), extrinsic stacking faults (ESFs), DTs, and HCP phase⁶⁵), and partial dislocations^21–23 can be clearly observed. G-HEAs under compressive load have high dislocation density and abundant microstructures, and a large number of Shockley dislocations nucleate at GBs and move inward, forming ISFs, ESFs, DTs, and HCP phase, In addition, a small amount of stair-rod also forms at the GBs. However, under tensile load, numerous dislocations nucleate within the crystal and move toward the grain boundaries on both sides, forming different microstructures. Furthermore, near grain boundaries, different dislocations move relative to each other to form Shockley dislocation loops and Hirth dislocation locks under different loads.

Fig. 11 exhibits the evolution of the ISFs, ESFs, DTs, and HCP phases in GNG-3. As shown in Fig. 11(a1) and (a2), during the elastic deformation stage, Shockley dislocations that nucleate in the relaxation stage and are stored at the GBs continuously emit in the same direction into the crystal, forming several ISFs of different lengths. These ISFs are the prerequisite and foundation for the formation of ESFs and HCP phases during the plastic stage. It should be noted that these dislocations that cause ISFs are not newly generated, but stored at GBs during the relaxation stage, which is just the reason why the dislocation density remains stable during elastic deformation. As shown in Fig. 11(b1) and (b2), after the dislocations stored at the grain boundary are released, the new dislocations not only continue to nucleate at the grain boundary but also nucleate inside the crystal. Shockley dislocations nucleating at the grain boundary and inside the crystal are marked as S1 (black dashed rectangular box) and S2 (black solid rectangular box), respectively. S1 moves in one direction, while S2 moves in two opposite directions simultaneously. There are two evolutionary pathways for ESFs, one approach is for two dislocations separated by an atomic layer to move towards each other, causing collinear HCP atoms to transform into FCC atoms and form ESFs. Another one is for dislocations to tightly adhere to the original ISF nucleation and move inward to form ESFs. As shown in Fig. 11(c1) and (c2), dislocations nucleate adjacent to existing ISFs at the GB and move inward with the increasing engineering strain to form the HCP phase. In addition, dislocations crossing two ISFs that are only two atomic layers apart can also form HCP phases. As shown in Fig. 11(d1) and (d2), a large number of dislocations nucleate at grain boundaries or within grains during plastic deformation. Dislocations in different directions interlock with each other to form dislocation locks and dislocation loops, and new dislocations are formed at the intersection points, which cross the previous HCP phase and form DTs.

Fig. 11 Microstructural evolution of GNG-3. (a) ISFs. (b) ESFs. (c) HCP phase. (d) DTs. (a1) and (a2) Show the evolution of ISFs. (b1) and (b2) Show the evolution of ESFs. (c1) and (c2) Show the evolution of HCP phase. (d1) and (d2) Show the evolution of DTs.

According to Laplanche's report, CoCrFeMnNi HEA exhibits DTs at a true strain of ∼7.4% at 77 K, while at 293 K, DTs are only activated when the material is close to fracture, with a true strain of 25%.⁶⁶ Moreover, Jang et al.⁶⁷ confirmed through CPFEM compression tests and microstructural characterizations that CoCrFeMnNi HEA can activate DTs at room temperature, but the contribution of DTs to shear strain is very tiny at approximately 0.5%. Therefore, it can be considered that DT is not the primary plastic deformation mechanism of the CoCrFeMnNi HEA at room temperature.

As shown in Fig. 12, dislocation slip persists throughout the entire deformation process of CoCrFeMnNi HEA. It serves as the prerequisite for the formation of microstructures such as ISFs, ESFs, HCP phases, and DTs, and is also the dominant plastic deformation mechanism. During the middle to late stages of plastic deformation, the proportion of ISFs and HCP phases within the grains increases significantly, leading to a reduction in the independent motion space for dislocations and a gradual increase in their movement resistance. The movement of dislocations that closely adhere to or pass through existing microstructures (as indicated by the dislocation labeled D1 in Fig. 12(b) and (c)) promotes the formation of new microstructures, forming new microstructures. It can be said that dislocation slip promotes the formation of DTs and HCP phases. However, the newly formed DTs and HCP phases, in turn, hinder dislocation slip and even keep the dislocation in place (as indicated by the dislocation labeled D2 in Fig. 12 (a)–(c)). Additionally, as shown in the region labeled G3 in Fig. 12(b) and (c), the pre-existing microstructures also hinder the motion of dislocations nucleated at the bottom grain boundary, leading to the formation of sub-grain boundaries at the interface. The increase in dislocation resistance enhances the flow stress of the material. Therefore, during the plastic deformation stage, dislocation slip, DT, and HCP phase transformation compete and promote each other, jointly enhancing the mechanical properties of HEAs.

Fig. 12 The interaction of different deformation mechanisms of GNG-3. (a) ε = 5%. (b) ε = 10%. (c) ε = 15%. (d) ε = 20%. (a–d) Show the same grain, which is also the grain below the rectangular box in Fig. 10(a).

In the CNA analysis, the atoms forming the ISFs, ESFs, DTs, and HCP phases are all marked as HCP atoms. Therefore, the fraction of HCP atoms can indirectly reflect the activity of dislocation motion. As shown in Fig. 13, models with smaller average grain sizes have higher grain boundary densities and initial dislocation densities than those with larger average grain sizes, resulting in a higher initial HCP fraction. As the engineering strain increases, the HCP fraction increases more rapidly in larger grain size models than in smaller grain size models because larger grain size models have more internal space to generate microstructures such as ISFs, ESFs, and DTs rather than having a higher dislocation density. However, in the later stages of compressive deformation, owing to the reduction of atomic spacing, dislocation motion becomes increasingly difficult, and the HCP atom fraction remains stable or slightly decreases. In contrast, during the later stages of tensile deformation, the HCP atom fraction continues to increase, although the rate of increase slightly decreases.

Fig. 13 Evolution curves of the HCP atom fraction. (a) Compression. (b) Tension. The HCP atoms include ISFs, ESFs, HCP phases, and DTs, which are generated by dislocation slip and GB movement.

4.3 Effect of the grain gradient on uniaxial tension-compression asymmetry

As mentioned earlier, G-HEA transforms from elastic deformation to plastic deformation at an engineering strain of 3–4.5%, and their flow stress first increases and then decreases with increasing strain, eventually stabilizing. To study the effect of the grain size gradient on tension-compression asymmetry, the average flow stresses of HEA during ε = 3–10% were calculated, and the difference in average flow stress under compression and tension was determined. As shown in Fig. 14(a), except for GNG-1, all the other models exhibit higher average flow stresses under compression than those under tension. The average flow stress under compression increases with increasing grain size gradient, whereas the average flow stress under tension first increases and then decreases as the grain size gradient size increases. Additionally, the difference in the average flow stress between compression and tension increases as the grain size gradient becomes greater. This phenomenon is related to the larger deformation discrepancy in models with a higher grain size gradient.

Fig. 14 Average flow stresses and average dislocation densities of GNG HEA. (a) Average flow stress. (b) Average dislocation density.

Although CoCrFeMnNi HEA exhibits DT and HCP phase transformation during deformation, dislocation slip remains the main deformation mechanism. To further investigate the effect of the grain size gradient on tension-compression asymmetry, the average dislocation densities of HEA with different grain size gradients under ε = 3–10% were extracted, and the difference in average dislocation density under compression and tension was calculated. As shown in Fig. 14(b), the average dislocation density decreases with increasing grain size gradient, indicating an obvious size effect. The average dislocation density under tension is greater than that under compression, suggesting that tension is more conducive to dislocation nucleation and slip. Furthermore, the difference in average dislocation density between compression and tension increases as the gradient increases, which is consistent with the trend observed for the average flow stress.

Fig. 15 shows the density curves of partial dislocations under compressive and tensile loading for CoCrFeMnNi HEA. The initial partial dislocations density is closely related to the grain size, with models with smaller average grain sizes owning higher partial dislocations densities than those with larger average grain sizes. However, the differences in partial dislocation density between the models decrease as the strain increases. When ε < 5%, the partial dislocation changes are relatively small, indicating that few new dislocation nuclei are formed during the elastic deformation. Especially under tension load, partial dislocations remain roughly unchanged during the elastic deformation stage. Additionally, both the HNG-2 and GNG-2 models show slight decreases in their partial dislocation densities at the early stage of tensile deformation, which may be related to dislocation absorption by the grain boundaries. Similar to the evolution of the total dislocation density, the partial dislocation density under tensile loading follows a distinct three-stage evolution pattern, whereas the partial dislocation density under compressive loading nearly linearly increases after a horizontal segment. This result once again proves that the dislocation density of G-HEA exhibits tension-compression asymmetry.

Fig. 15 Evolution of the partial dislocation density in HEA under different loads. (a) Compression. (b) Tension.

5. Conclusion

This study employed MD simulations to investigate the mechanical response and deformation behavior of CoCrFeMnNi G-HEA under uniaxial loading. The results demonstrated that the gradient nanostructure induced the characteristic of gradient distribution of stress and strain during the initial plastic deformation stage. However, these gradient distribution characteristics progressively diminished with increasing engineering strain and ultimately vanished.

GB migration and grain merging are the main grain boundary activities of CoCrFeMnNi HEA, and FGs in the soft zone have stronger GB vitality compared to CGs in the hard zone. G-HEA has multiple plastic deformation mechanisms including dislocation slip, DT, and HCP phase transformation. However, dislocation slip is the main deformation mechanism. DT only appears briefly in the middle and later stages of deformation, and its quantity is very small, which is a secondary deformation mechanism of the material. HCP phase transformation is a deformation mechanism that mainly occurs in the later stage of plastic deformation due to the nucleation and movement of dislocations adjacent to the original ISFs. The three deformation mechanisms have both synergy and competition, jointly enhancing the mechanical properties of materials.

This work has found that the yield stress, dislocation density, and average flow stress of CoCrFeMnNi G-HEA all exhibit tension-compression asymmetry. The residual tensile stress during the relaxation stage and the atomic repulsion force during the initial deformation stage are the main reasons for the tension-compression asymmetry of GB vitality, and the differences in GB vitality indirectly lead to the tension-compression asymmetry of stress and strain. In the middle stage of plastic deformation, dislocations nucleate at grain boundaries under compressive load but nucleate within grains under tensile load. The different nucleation positions of dislocations result in differences in the evolution of dislocation density and are also one of the reasons for the tension-compression asymmetry of average flow stress and yield stress.

Data availability

The data that support the findings of this study are available on request from the corresponding author, [Yin], upon reasonable request. The e-mail of the corresponding author is E-mail: fyin@whut.edu.cn.

Author contributions

Xingguo Yang: writing – original draft, visualization, methodology, formal analysis, data curation, conceptualization, investigation. Fei Yin: writing – review & editing, conceptualization, supervision, project administration.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was financially supported by the National Key Research and Development Program of China (No. 2020YFA0714900), the Taihang National Laboratory (THL-K-2024-092), the National Natural Science Foundation of China (No. 51975441), the Independent Innovation Projects of the Hubei Longzhong Laboratory (2022ZZ-26 and 2024 KF-18), the Fundamental Research Funds for the Central Universities (WUT: 2020IVA020), and the Innovative Research Team Development Program of the Ministry of Education of China (IRT_17R83), Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN 202404004), the Key Scientific Research Project of Chongqing Open University (No: NDZD2024-03).

References

1. X. C. Lu, J. F. Zhao, C. Yu, Z. M. Li, Q. H. Kan, G. Z. Kang and X. Zhang, Cyclic plasticity of an interstitial high-entropy alloy: experiments, crystal plasticity modeling, and simulations, J. Mech. Phys. Solids, 2020, 142, 103971,  DOI:10.1016/j.jmps.2020.103971.
2. A. Karati, K. Guruvidyathri, V. S. Hariharan and B. S. Murty, Thermal stability of AlCoFeMnNi high-entropy alloy, Scr. Mater., 2019, 162, 465–467,  DOI:10.1016/j.scriptamat.2018.12.017.
3. P. J. Shi, W. L. Ren, T. X. Zheng, Z. M. Ren, X. L. Hou, J. C. Peng, P. F. Hu, Y. F. Gao, Y. B. Zhong and P. K. Liaw, Enhanced strength-ductility synergy in ultrafinegrained eutectic high-entropy alloys by inheriting microstructural lamellae, Nat. Commun., 2019, 10(1), 489–496,  DOI:10.1038/s41467-019-08460-2.
4. Y. P. Lu, X. Z. Gao, L. Jiang, Z. N. Chen, T. M. Wang, J. C. Jie, H. J. Kang, Y. B. Zhang, S. Guo, H. H. Ruan, Y. H. Zhao, Z. Q. Cao and T. J. Li, Directly cast bulk eutectic and near-eutectic high entropy alloys with balanced strength and ductility in a wide temperature range, Acta Mater., 2017, 124, 143–150,  DOI:10.1016/j.actamat.2016.11.016.
5. W. H. Liu, J. Y. He, H. L. Huang, H. Wang, Z. P. Lu and C. T. Liu, Effects of Nb additions on the microstructure and mechanical property of CoCrFeNi high-entropy alloys, Intermetallics, 2015, 60, 1–8,  DOI:10.1016/j.intermet.2015.01.004.
6. Y. Y. Liu, Z. Chen, Y. Z. Chen, J. C. Shi, Z. Y. Wang, S. Wang and F. Liu, Effect of Al content on high temperature oxidation resistance of AlxCoCrCuFeNi high entropy alloys (x=0, 0.5, 1, 1.5, 2), Vacuum, 2019, 169, 108837,  DOI:10.1016/j.vacuum.2019.108837.
7. D. Kumar, Recent Advances in Tribology of High Entropy Alloys: A Critical Review, Prog. Mater. Sci., 2023, 136, 101106,  DOI:10.1016/j.pmatsci.2023.101106.
8. O. N. Senkov, G. B. Wilks, J. M. Scott and D. B. Miracle, Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys, Intermetallics, 2011, 19, 698–706,  DOI:10.1016/j.intermet.2011.01.004.
9. K. Kuwabara, H. Shiratori, T. Fujieda, K. Yamanaka, Y. Koizumi and A. Chiba, Mechanical and Corrosion Properties of AlCoCrFeNi High-Entropy Alloy Fabricated with Selective Electron Beam Melting, Addit. Manuf., 2018, 23, 264–271,  DOI:10.1016/j.addma.2018.06.006.
10. N. Haghdadi, T. Guo, A. Ghaderi, P. D. Hodgson, M. R. Barnett and D. M. Fabijanic, The scratch behaviour of AlXCoCrFeNi (x=0.3 and 1.0) high entropy alloys, Wear, 2019, 428–429, 293–301,  DOI:10.1016/j.wear.2019.03.026.
11. B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Microstructural development in equiatomic multicomponent alloys, J. Mater. Sci. Eng. A, 2004, 375–377, 213–218,  DOI:10.1016/j.msea.2003.10.257.
12. S. Huang, W. Li, S. Lu, F. Y. Tian, J. Shen, E. Holmstrom and L. Vitos, Temperature dependent stacking fault energy of FeCrCoNiMn high entropy alloy, Scr. Mater., 2015, 108, 44–47,  DOI:10.1016/j.scriptamat.2015.05.041.
13. F. Zhang, H. B. Lou, S. Y. Chen, X. H. Chen, Z. D. Zeng, J. Y. Yan, W. X. Zhao, Y. Wu, Z. P. Lu and Q. S. Zeng, Effects of non-hydrostaticity and grain size on the pressure-induced phase transition of the CoCrFeMnNi high-entropy alloy, J. Appl. Phys., 2018, 124, 115901,  DOI:10.1063/1.5046180.
14. P. Dolzhenko, M. Tikhonova, M. Odnobokova, R. Kaibyshev and A. Belyakov, Ultrafine-Grained Stainless Steels after Severe Plastic Deformation, Metals, 2023, 13(674), 1–35,  DOI:10.3390/met13040674.
15. B. Indranil, T. M. Jeff and H. De, Strengthening mechanisms in high entropy alloys: Fundamental issues, Scr. Mater., 2020, 187, 148–156,  DOI:10.1016/j.scriptamat.2020.06.019.
16. C. Song, S. Hu, Q. Y. Han, X. H. Han, L. C. Xie, W. H. Zhuang, F. Yin and L. Hua, Ultrastrong gradient nanostructured CSS-42L bearing steel and its enhanced wear resistance at elevated temperature, Surf. Coat. Technol., 2023, 470, 129881,  DOI:10.1016/j.surfcoat.2023.129881.
17. F. Yin, S. Hu, R. Xu, X. H. Han, D. S. Qian, W. T. Wei, L. Hua and K. J. Zhao, Strain rate sensitivity of the ultrastrong gradient nanocrystalline 316L stainless steel and its ratedependent modeling at nanoscale, Int. J. Plast., 2020, 129, 102696,  DOI:10.1016/j.ijplas.2020.102696.
18. G. S. Dong, B. Gao and Z. B. Wang, Rotary bending fatigue behavior of a rare earth addition bearing steel: The effects of a gradient nanostructured surface layer formed by surface mechanical rolling treatment, Int. J. Fatigue, 2023, 168, 107425,  DOI:10.1016/j.ijfatigue.2022.107425.
19. M. Wang, X. Z. Chen, F. Z. Dai, K. Peng, A. Singh Ramachandra and S. Konovalov, Simulation of residual stress and micro-plastic deformation induced by laser shock imprinting on TC4 titanium alloy aero-engine blade, J. Mater. Res. Technol., 2023, 26, 9419–9436,  DOI:10.1016/j.jmrt.2023.09.225.
20. K. Y. Luo, S. K. Xu, L. J. Xu, Y. Xing, H. M. Zhang, C. Wang and J. Lu, Wear behaviors of AISI 316L stainless steel with a gradient structured surface layer induced by laser shock peening, Surf. Coat. Technol., 2024, 481, 130608,  DOI:10.1016/j.surfcoat.2024.130608.
21. K. Han, X. Q. Li, X. C. Liu, J. X. Zang, W. W. He and J. Z. Chen, Integrated modeling of the gradient structure evolution during surface mechanical grinding treatment: Formation mechanism and mechanical properties, Mater. Des., 2023, 230, 111979,  DOI:10.1016/j.matdes.2023.111979.
22. W. L. Li, N. R. Tao and K. Lu, Fabrication of a gradient nano-micro-structured surface layer on bulk copper by means of a surface mechanical grinding treatment, Scr. Mater., 2008, 59(5), 546–549,  DOI:10.1016/j.scriptamat.2008.05.003.
23. Y. Chen, J. Du, D. S. Tian and L. L. Hu, KaixiongEffect of Ultrasonic Shot Peening Duration on the Microstructure and Mechanical Properties of CrMnFeCoNi High-Entropy Alloy, J. Alloys Compd., 2023, 934, 168023,  DOI:10.1016/j.jallcom.2022.168023.
24. C. Wang, X. Liu, Q. Y. Song, K. H. Tian, S. H. Fei, H. S. Deng and G. Shen, Effects of ultrasonic shot peening followed by surface mechanical rolling on mechanical properties and fatigue performance of 2024 aluminum alloy, Eng. Fract. Mech., 2024, 311, 110538,  DOI:10.1016/j.engfracmech.2024.110538.
25. Z. P. Tong, X. Y. Pan, W. F. Zhou, Y. Yu, Y. X. Ye, D. S. Qian and X. D. Ren, Achieving excellent wear and corrosion properties in laser additive manufactured CrMnFeCoNi high-entropy alloy by laser shock peening, Surf. Coat. Technol., 2021, 422, 127504,  DOI:10.1016/j.surfcoat.2021.127504.
26. M. T. Tsai, J. C. Huang, W. Y. Tsai, T. H. Chou, C. F. Chen, T. H. Li and J. S. C. Jang, Effects of ultrasonic surface mechanical attrition treatment on microstructures and mechanical properties of high entropy alloys, Intermetallics, 2018, 93, 113–121,  DOI:10.1016/j.intermet.2017.11.018.
27. X. Zhou, X. Y. Li and K. Lu, Strain hardening in gradient nano-grained Cu at 77K, Scr. Mater., 2018, 153, 6–9,  DOI:10.1016/j.scriptamat.2018.04.039.
28. Z. Cheng, H. F. Zhou, Q. H. Lu, H. J. Gao and L. Lu, Extra strengthening and work hardening in gradient nanotwinned metals, Science, 2018, 362(6414), 559–566,  DOI:10.1126/science.aau1925.
29. J. F. Zhao, Q. H. Kan, L. C. Zhou, G. Z. Kang and X. Zhang, Deformation mechanisms based constitutive modelling and strength-ductility mapping of gradient nano-grained materials, Mater. Sci. Eng. A, 2019, 742, 400–408,  DOI:10.1016/j.msea.2018.10.096.
30. X. C. Lu, X. Zhang, M. X. Shi, F. Roters, G. Z. Kang and D. Raabe, Dislocation mechanism based size-dependent crystal plasticity modeling and simulation of gradient nano-grained copper, Int. J. Plast., 2019, 113, 52–73,  DOI:10.1016/j.ijplas.2018.09.007.
31. M. J. Jang, D. H. Ahn, J. Moon, J. W. Bae, D. Yim, J. W. Yeh, Y. Estrin and H. S. Kim, Constitutive modeling of deformation behavior of high-entropy alloys with face-centered cubic crystal structure, Mater. Res. Lett., 2017, 5(5), 350–356,  DOI:10.1080/21663831.2017.1292325.
32. H. L. Zhai, B. M. Yao, W. J. Zhang, H. Y. Lin, X. F. Ma, Y. J. Li, W. D. Zhai, J. Y. Zhong and S. Wang, On the plastic deformation mechanism of Al0.6CoCrFeNi high entropy alloy: In-situ EBSD study and crystal plasticity modeling, Mater. Sci. Eng. A, 2024, 915, 147108,  DOI:10.1016/j.msea.2024.147108.
33. S. J. Lu, J. F. Zhao, M. S. Huang, Z. H. Li, G. Z. Kang and X. Zhang, Multiscale discrete dislocation dynamics study of gradient nano-grained materials, Int. J. Plast., 2022, 156, 103356,  DOI:10.1016/j.ijplas.2022.103356.
34. K. Zhou, T. Zhang, B. Liu and Y. J. Yao, Molecular dynamics simulations of tensile deformation of gradient nano-grained copper film, Comput. Mater. Sci., 2018, 142, 389–394,  DOI:10.1016/j.commatsci.2017.10.043.
35. Y. S. Lu, M. P. Chang, T. H. Fang and S. W. Liang, Effects of microstructure and temperature on mechanical properties of gradient nano-grained nickel-titanium-copper films, Mater. Today Commun., 2022, 31, 103294,  DOI:10.1016/j.mtcomm.2022.103294.
36. F. K. Xian, J. J. Zhou, X. F. Lian, J. C. Shen and Y. P. Chen, Molecular dynamics simulation of crack propagation in very small grain size nanocopper with different grain size gradients, RSC Adv., 2024, 14(1), 616–625,  10.1039/d3ra07374b.
37. Z. B. An, S. C. Mao, Y. N. Liu, H. Zhou and X. D. Han, Hierarchical grain size and nanotwin gradient microstructure for improved mechanical properties of a non-equiatomic CoCrFeMnNi high-entropy alloy, J. Mater. Sci. Technol., 2021, 92, 195–207,  DOI:10.1016/j.jmst.2021.02.059.
38. Y. Qiao, Y. Chen, F. H. Cao, H. Y. Wang and L. H. Dai, Dynamic behavior of CrMnFeCoNi high-entropy alloy in impact tension, Int. J. Impact Eng., 2021, 158, 104008,  DOI:10.1016/j.ijimpeng.2021.104008.
39. Z. P. Tong, H. L. Liu, J. F. Jiao, W. F. Zhou, Y. Yang and X. D. Ren, Improving the strength and ductility of laser directed energy deposited CrMnFeCoNi high-entropy alloy by laser shock peening, Addit. Manuf., 2020, 35, 101417,  DOI:10.1016/j.addma.2020.101417.
40. X. Du, S. Y. Shuang, Z. J. Zhao, Z. H. Fu, Q. H. Kan and X. Zhang, Extra strengthening and Bauschinger effect in gradient high-entropy alloy: A molecular dynamics study, Int. J. Mech. Sci., 2024, 264, 108829,  DOI:10.1016/j.ijmecsci.2023.108829.
41. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1–19,  DOI:10.1006/jcph.1995.1039.
42. Q. H. Fang, L. Li, J. Li and H. Wu, Strengthening mechanism of gradient nanostructured body-centred cubic iron film: From inverse Hall-Petch to classic Hall-Petch, Comput. Mater. Sci., 2018, 152, 236–242,  DOI:10.1016/j.commatsci.2018.06.001.
43. W. M. Choi, Y. H. Jo, S. S. Sohn, S. Lee and B. J. Lee, Understanding the physical metallurgy of the CoCrFeMnNi high-entropy alloy: an atomistic simulation study, npj Comput. Mater., 2018, 4(1), 1–9,  DOI:10.1038/s41524-017-0060-9.
44. L. Zhang, C. Lu and A. K. Tieu, Nonlinear elastic response of single crystal Cu under uniaxial loading by molecular dynamics study, Mater. Lett., 2018, 227, 236–239,  DOI:10.1016/j.matlet.2018.05.094.
45. J. Sun, H. F. Ye, J. Tao, Q. Li, J. Y. Zhang, L. M. Shen, Y. G. Zheng Yonggang and H. W. Zhang, Gradient structure regulated plastic deformation mechanisms in polycrystalline nanotwinned copper, J. Phys. Appl. Phys., 2019, 52, 365304,  DOI:10.1088/1361-6463/ab29ca.
46. J. Li, J. R. Greer and A. T. Jennings, Emergence of strain-rate sensitivity in Cu nanopillars: transition from dislocation multiplication to dislocation nucleation, Acta Mater., 2011, 59(14), 5627–5637,  DOI:10.1016/j.actamat.2011.05.038.
47. J. T. Pürstl, H. O. Jones, T. E. J. Edwards, R. P. Thompson, F. Di Gioacchino, N. G. Jones and W. J. Clegg, On the extraction of yield stresses from micro-compression experiments, Mater. Sci. Eng., A, 2011, 800, 140323,  DOI:10.1016/j.msea.2020.140323.
48. A. Kunz, S. Pathak and J. R. Greer, Size effects in Al nanopillars: single crystalline vs. Bicrystalline, Acta Mater., 2011, 59(11), 4416–4424,  DOI:10.1016/j.actamat.2011.03.065.
49. D. Cereceda, M. Diehl, F. R. D. Raabe, J. M. Perlado and J. Marian, Unraveling the temperature dependence of the yield strength in single-crystal tungsten using atomistically-informed crystal plasticity calculations, Int. J. Plast., 2016, 78, 242–265,  DOI:10.1016/j.ijplas.2015.09.002.
50. R. G. Liu, J. Tang, J. X. Jiang, X. Y. Li and Y. J. Wei, Stacking fault induced hardening and grain size effect in nanocrystalline CoNiCrFeMn high-entropy alloy, Extreme Mech. Lett., 2022, 56, 101875,  DOI:10.1016/j.eml.2022.101875.
51. K. Zhou, S. F. Shao and Y. J. Yao, Molecular dynamics simulations of tension-compression asymmetry in nanocrystalline copper, Phys. Lett. A, 2017, 381, 1163–1168,  DOI:10.1016/j.physleta.2017.01.027.
52. F. Sansoz and X. Ke, Hall-Petch strengthening limit through partially active segregation in nanocrystalline Ag-Cu alloys, Acta Mater., 2022, 225, 117560,  DOI:10.1016/j.actamat.2021.117560.
53. A. C. Lund, T. G. Nieh and C. A. Schuh, Tension/compression strength asymmetry in a simulated nanocrystalline metal, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(1), 012101,  DOI:10.1103/PhysRevB.69.012101.
54. D. Surblys, H. Matsubara, G. Kikugawa and T. Ohara, Application of atomic stress to compute heat flux via molecular dynamics for systems with many-body interactions, Phys. Rev. E, 2019, 99(5), 051301,  DOI:10.1103/PhysRevE.99.051301.
55. T. H. Fang, W. L. Li, N. R. Tao and K. Lu, Revealing Extraordinary Intrinsic Tensile Plasticity in Gradient Nano-Grained Copper, Science, 2011, 331(6024), 1587–1590,  DOI:10.1126/science.1200177.
56. P. Cao, The strongest size ingradien tnanograined metals, Nano Lett., 2020, 20(2), 1440–1446,  DOI:10.1021/acs.nanolett.9b05202.
57. S. Zhou, Z. Y. Hou, N. N. Liu, Y. Niu, C. Li, Z. Wang, J. G. Wang, L. Gao and K. J. Dong, Optimal grain size distribution in gradient nano-grained nickel, Vacuum, 2023, 210, 111854,  DOI:10.1016/j.vacuum.2023.111854.
58. M. L. Falk and J. S. Langer, Dynamics of viscoplastic deformation in amorphous solids, Phys. Rev. E, 1998, 57(6), 7192–7205,  DOI:10.1103/PhysRevE.57.7192.
59. L. K. Xu, Z. F. Huang, M. S. Wu and F. Chen, Grain size gradient effect on grain boundary mediated deformation of nano-grained metals, Eng. Fract. Mech., 2024, 304, 110151,  DOI:10.1016/j.engfracmech.2024.110151.
60. F. Otto, C. Somsen and A. Dlouhy, The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy, Acta Mater., 2013, 61(15), 5743–5755,  DOI:10.1016/j.actamat.2013.06.018.
61. C. C. KOCH, C. NIU and A. J. ZADDACH, Mechanical properties and stacking fault energies of NiFeCrCoMn High-entropy alloy, JOM, 2013, 65(12), 1780–1789,  DOI:10.1007/s11837-013-0771-4.
62. D. Thürmer, S. T. Zhao, O. R. Deluigi, C. V. Stan, L. A. Alhafez, H. M. Urbassek, M. A. Meyers, E. M. Bringa and N. Gunkelmann, Exceptionally high spallation strength for a highentropy alloy demonstrated by experiments and simulations, J. Alloys Compd., 2022, 895, 162567,  DOI:10.1016/j.jallcom.2021.162567.
63. S. T. Zhao, Z. Z. Li, C. Y. Zhu, W. Yang, Z. R. Zhang, D. E. J. Armstrong, P. S. Grant, R. O. Ritchie and M. A. Meyers, Amorphization in extreme deformation of the CrMnFeCoNi high-entropy alloy, Sci. Adv., 2021, 7(5), eabb3108,  DOI:10.1126/sciadv.abb3108.
64. H. Wang, D. K. Chen, X. H. An, Y. Zhang, S. J. Sun, Y. Z. Tian, Z. F. Zhang, A. G. Wang, J. Q. Liu, M. Song, S. P. Ringer, T. Zhu and X. Z. Liao, Deformation-induced crystalline-to-amorphous phase transformation in a CrMnFeCoNi high-entropy alloy, Sci. Adv., 2021, 7(14), eabe3105,  DOI:10.1126/sciadv.abe3105.
65. S. Jiang, H. W. Zhang, Y. G. Zheng and Z. Chen, Atomistic study of the mechanical response of copper nanowires under torsion, J. Phys. Appl. Phys., 2009, 42(130), 135408,  DOI:10.1088/0022-3727/42/13/135408.
66. G. Laplanche, A. Kostka, O. M. Horst, G. Eggeler and E. P. George, Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy, Acta Mater., 2016, 118(16), 152–163,  DOI:10.1016/j.actamat.2016.07.038.
67. M. J. Jang, D. H. Ahn, J. Moon, J. W. Bae, D. Yim, J. W. Yeh, Y. Estrin and H. S. Kim, Constitutive modeling of deformation behavior of high-entropy alloys with face-centered cubic crystal structure, Mater. Res. Lett., 2017, 5(5), 350–356,  DOI:10.1080/21663831.2017.1292325.

---