Open Access Article
Open Access ArticleThe importance of measuring diffusion coefficients in reactor design and simulation†
Francesco Taddeo a,
Ornella Ortonaa,
Donato Ciccarellia,
Riccardo Tessera,
Henrik Grénmanb,
Martino Di Serio
a,
Ornella Ortonaa,
Donato Ciccarellia,
Riccardo Tessera,
Henrik Grénmanb,
Martino Di Serio a,
Vincenzo Russo
a,
Vincenzo Russo *a and
Luigi Paduano*a
*a and
Luigi Paduano*a
aDepartment of Chemical Sciences, University of Naples Federico II, Via Cintia, IT-80126 Naples, Italy. E-mail: v.russo@unina.it; luigi.paduano@unina.it
bLaboratory of Industrial Chemistry and Reaction Engineering, Åbo Akademi, Henrikinkatu 2, FI-20500 Turku/Åbo, Finland
First published on 13th May 2025
Abstract
Glucose is extensively employed to produce sorbitol through catalytic hydrogenation. In the process development, parameters such as fluid dynamic conditions, temperature, and diffusion coefficients must be evaluated. To optimize the production of sorbitol, it is necessary to know the diffusion coefficients of the reacting system. In this study, they were determined at different solute concentrations and temperatures. Diffusion coefficients can also be estimated using models, such as Wilke–Chang and Hayduk and Minhas correlations. The values between 25 °C and 45 °C are similar to the experimental data, while at 65 °C, both models significantly overestimate the experimental results. As for the ternary systems, at 25 °C, both glucose and sorbitol are essentially transported by their concentration gradient. Finally, simulations of reactors operating in laminar flow conditions were made, estimating the diffusion coefficients using the Wilke–Chang correlation and determining them experimentally, showing that the glucose conversion profile along the axis of the reactor was different.
1 Introduction
In most industrialized countries, the importance of sugars is widely recognized not only as a valuable food resource but also as a raw material in the industrial field. The use of saccharides as raw material is increasingly spreading, providing the opportunity to develop new commercially relevant products.1,2 A wide variety of sugars are used for various purposes, including glucose, which is extensively employed in the industrial context to produce sorbitol through catalytic hydrogenation.3 Sorbitol is widely used not only in nutrition but also in cosmetics, medical applications, and industrial settings.4 Its global production ranges between 650![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 900
000 and 900![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons per year through the catalytic hydrogenation of glucose.5 Currently, the most widely used catalysts are nickel, rhodium, or ruthenium-based supported catalysts.4,6–8 Generally, catalytic hydrogenation of glucose can be carried out in both batch and continuous reactors at high pressures. In the past, most of the global sorbitol production was obtained through batch processes, but nowadays, there is an increasing trend towards sorbitol production through continuous hydrogenation.9–11 Among the continuous reactors extensively used in the industrial context to carry out this type of reaction there is the trickle-bed reactor.12,13 It is a type of three-phase reactor where the reactants are in the gas and/or liquid phase, while the catalyst is in the solid phase. Gas–liquid–solid catalytic reactions are often characterized by high reactivity. An essential quality of a three-phase reactor is, therefore, to facilitate contact between the phases as simply and effectively as possible to achieve optimal catalyst utilization. The thermodynamics and kinetics of the involved reactions often require the use of high temperatures. However, this results in the expansion of the gas phase and if operating at atmospheric pressure, the increase in the volume of the gas phase causes it to occupy more space than the liquid phase. As a result, the gas–liquid interfacial area is reduced because of larger bubbles form, leading to gas–liquid mass transfer limitation. To address this problem, high pressures are frequently used which enable increased heat and mass transport, slowing down the deactivation of the catalytic bed.14 Diffusion represents a crucial aspect in catalytic applications and is a significant phenomenon in many areas of chemistry, as mass transfer is often limited by diffusion. The literature provides several examples of processes in which diffusion plays an important role.15,16 Other relevant cases include processes involving polymeric materials, such as polyvinyl alcohol–water, cellulose acetate–tetrahydrofuran, and cellulose triacetate–dichloromethane systems, where authors have demonstrated how diffusion coefficients can be obtained from experimental data using mathematical models or the determination of methane diffusion coefficient, in which the development of an optimization method through numerical simulation has proven to be a highly effective approach.17,18 In a binary system, the mutual diffusion of a solute is described by Fick's law:
000 tons per year through the catalytic hydrogenation of glucose.5 Currently, the most widely used catalysts are nickel, rhodium, or ruthenium-based supported catalysts.4,6–8 Generally, catalytic hydrogenation of glucose can be carried out in both batch and continuous reactors at high pressures. In the past, most of the global sorbitol production was obtained through batch processes, but nowadays, there is an increasing trend towards sorbitol production through continuous hydrogenation.9–11 Among the continuous reactors extensively used in the industrial context to carry out this type of reaction there is the trickle-bed reactor.12,13 It is a type of three-phase reactor where the reactants are in the gas and/or liquid phase, while the catalyst is in the solid phase. Gas–liquid–solid catalytic reactions are often characterized by high reactivity. An essential quality of a three-phase reactor is, therefore, to facilitate contact between the phases as simply and effectively as possible to achieve optimal catalyst utilization. The thermodynamics and kinetics of the involved reactions often require the use of high temperatures. However, this results in the expansion of the gas phase and if operating at atmospheric pressure, the increase in the volume of the gas phase causes it to occupy more space than the liquid phase. As a result, the gas–liquid interfacial area is reduced because of larger bubbles form, leading to gas–liquid mass transfer limitation. To address this problem, high pressures are frequently used which enable increased heat and mass transport, slowing down the deactivation of the catalytic bed.14 Diffusion represents a crucial aspect in catalytic applications and is a significant phenomenon in many areas of chemistry, as mass transfer is often limited by diffusion. The literature provides several examples of processes in which diffusion plays an important role.15,16 Other relevant cases include processes involving polymeric materials, such as polyvinyl alcohol–water, cellulose acetate–tetrahydrofuran, and cellulose triacetate–dichloromethane systems, where authors have demonstrated how diffusion coefficients can be obtained from experimental data using mathematical models or the determination of methane diffusion coefficient, in which the development of an optimization method through numerical simulation has proven to be a highly effective approach.17,18 In a binary system, the mutual diffusion of a solute is described by Fick's law:
 | (1) |
In the presence of three or more components, mutual diffusion is referred to as multicomponent diffusion. Multicomponent diffusion in liquids plays a significant role in many chemical engineering processes such as distillation, extraction, and chemical reactions.19–22 In a ternary system consisting of solute (1), solute (2), and solvent, the equations of Fick are the following:23,24
 | (2) |
Over time, various methods have been developed to determine mutual diffusion coefficients, including interferometric methods by Gouy and Rayleigh, conductometric method, and Taylor dispersion method.25–27 Among these, the Taylor dispersion technique is now used almost exclusively for several reasons, such as easy assembly of the experimental system and ease of measurement execution.28 The Taylor Dispersion Method is based on a 1953 work by the homonymous scientist Taylor29 valid for two-component systems; this study is based on the dispersion of a pulse of a solution in a current of slightly different concentration, flowing through a very thin tube with circular cross-section, characterized by laminar flow. Subsequently, studies conducted by Alizadeh et al.30 showed that the Taylor method can also be used for systems consisting of three or more components. The Taylor dispersion method assumes that the flow velocity in the tube is constant over time and shows a parabolic profile along the z-direction; moreover, it assumes that the pipe is sufficiently long, about 10–20 m. Direct current of fixed composition flows along the capillary tube while the pulse with different concentrations introduced into the flow induces the formation of a concentration gradient that for t = 0 corresponds to a Dirac δ of concentration, while for t > 0 it takes the form of a Gaussian that tends to widen over time.
Based on Taylor's work, the differential equation holds:
 | (3) |
In order to apply the Taylor dispersion method, and obtain reliable and accurate diffusion coefficients, it is necessary the occurrence of the laminar regime inside the tube. This is achieved by working with low flow rates and using extremely small diameter tubes. Considering a binary system, when a solute is injected into a laminar flow stream of solvent, the solute at the center of the tube flows more rapidly than the solute near the tube walls. As a result, the injected solute disperses as it flows along the capillary tube. The difference in concentration between the stream and the pulse at the outlet of the capillary pipe is revealed by the difference in the refractive index. Over the years, numerous scientists have conducted studies and experiments to determine the diffusion coefficients of both binary and ternary mixtures. These studies are crucial as they provide a direct measurement of the mobility of molecules. Despite the significance of understanding these diffusion coefficients, there is still a lack of data in the literature for glucose-water, sorbitol-water, and glucose-sorbitol-water systems at different temperatures. The limited amount of data available in the scientific panorama has been obtained through the study of various systems. For instance, Sano and Yamamoto31 used a capillary cell method to determine the mutual diffusion coefficients of glucose at T = 303 K and T = 323 K in concentrated solutions (C > 1.0 mol L−1). Additionally, diffusion coefficients have been measured by the Taylor dispersion method for aqueous glucose solutions at temperatures ranging from T = 298 K to T = 328 K.32 Van de Ven-Lucassen et al.33 conducted studies using the Taylor method to determine the diffusion coefficients of a binary glucose-water system at T = 298 K and different molar fractions of glucose. Experiments were performed in a membrane structure containing yeast cells to examine the diffusion of certain sugars, including glucose.34 This method revealed that the infinite dilution diffusion coefficient of L-glucose was found to be 8.9 × 10−6 cm2 s−1. It was observed that the diffusion coefficient of saccharides decreases as molecular weight and membrane size increase. Although fructose and glucose have the same molecular weight and chemical formula, their different structures result in small differences in their diffusion properties, as can be seen with their diffusion coefficients. Temperature is a key factor influencing the value of diffusion coefficients.35 In the case of a liquid, the relationship between D and T can be understood through the Stokes–Einstein relation
 | (4) |
The diffusion coefficient in liquids therefore increases by increasing temperature, as evidenced by eqn (4), due to the proportionality of the numerator with T, and the presence of the term η that instead decreases by increasing temperature. In this work, the diffusion coefficients of glucose(1)-water(0) and sorbitol(2)-water(0) binary systems and glucose(1)-sorbitol(2)-water(0) ternary system were determined at different concentrations and different temperatures, in particular in a range from 25 °C to 65 °C. Additionally, simulations of reactors operating in laminar flow conditions for the synthesis of sorbitol were made estimating the diffusion coefficients both using the Wilke–Chang correlation and determining experimentally the diffusion coefficient values.
2 Experimental
2.1. Materials
D(+)-Glucose (≥99.5% purity) and D-sorbitol (≥98% purity) were supplied by Merck. All solutions were prepared using water with a conductivity of 1.6 μS, obtained from an Elix 3 system by Millipore.2.2. Experimental setup
To measure diffusion coefficients, a solution with a slightly different composition was introduced into a Teflon tube (length 20 m and inner diameter 3.945 × 10−4 m) using a peristaltic pump. The tube was coiled to form a 40 centimeters diameter helix and immersed in a thermostat to maintain a constant temperature throughout the measurements. An injector was used to feed 0.5 cm3 of the solution, and samples were analyzed at the tube outlet by a differential refractive index analyzer with a sensitivity of 8 × 10−8 RIU, which continuously sent the measured signal to a data acquisition system. The sketch of the apparatus is reported in Fig. S.1.†2.3. Experimental procedure
To simulate the different compositions, several solutions were prepared, including binary solutions of glucose-water and sorbitol-water, and ternary solutions of glucose-sorbitol-water at various concentrations. Firstly, the diffusion coefficients at infinite dilution for both glucose and sorbitol were measured by injecting three pulses with a decreasing concentration of either glucose or sorbitol. The solutions were prepared by dissolving weighed amounts of solutes (glucose or sorbitol), previously dried at T = 40 °C for 2 hours, in distilled water. Measurements were conducted at T = 25, 30, 35, 45, and 65 °C. The binary systems glucose-water and sorbitol-water were prepared to determine their diffusion coefficients. As in the previous case, the solutes were dried in an oven at T = 40 °C for 2 hours. Then, a stock solution of glucose-water or sorbitol-water was made by weighing the solutes, and starting from this, the feed solution was obtained. Four different solutions were prepared by diluting the feed. The concentrations of these four solutions were slightly different from each other and from the concentration of the feed solution itself. Two of them had concentrations slightly higher than the feed, while the other two, were slightly lower. All four solutions were injected into the flow system at regular intervals as pulses. The measurements were taken at four different temperatures, namely 25, 35, 45, and 65 °C, for each of the systems. These temperature and concentration values were selected based on the experimental conditions used in the glucose hydrogenation process. To measure the diffusion coefficients of the ternary systems glucose-sorbitol-water, the same procedure as previously described was followed. Three different ternary glucose-sorbitol-water systems were prepared with varying concentrations of solutes for both the feed and the eight ternary solutions to be injected. The concentration of one of the two solutes (glucose or sorbitol) was kept constant and equal to that of the feed, while the concentration of the other component was varied. The operative conditions used to determine the infinite diffusion coefficients of glucose and sorbitol, glucose-water and sorbitol-water binary systems, and glucose-sorbitol-water ternary system are reported in the ESI (Tables S.1–S.4).†2.4. Applicability of the Taylor dispersion method
The diffusion coefficients of binary glucose-water and sorbitol-water systems, as well as the ternary glucose-sorbitol-water system, were determined at different concentrations and temperatures using the Taylor dispersion method. This knowledge will enable accurate simulation of the compositions of reactants and products in flow reactors during the hydrogenation reaction of glucose to produce sorbitol. As mentioned before, to use the Taylor dispersion method, specific conditions must be satisfied. These conditions include ensuring the laminar regime, verified for Re < 2000,36 and additionally, it is necessary to confirm the Taylor condition:29
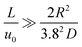 | (5) |
Therefore, to ascertain the applicability of the Taylor method for the measures made at various temperatures, the Reynolds number was first calculated. This value changes with the temperature as it includes viscosity and density, which both vary with temperature.
 | (6) |
The values of μ and ρ are tabulated, the diameter of the tube is known, while the average rate and the volumetric flowrate are respectively calculated as in eqn (7) and (8):
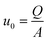 | (7) |
 | (8) |
In Table 1, the parameters for both the tube and the pump are reported.
| Parameter | Value | Unit |
|---|---|---|
| L | 20 | m |
| R | 3.945 × 10−4 | m |
| A | 4.89 × 10−7 | m2 |
| V | 9.77 × 10−6 | m3 |
| Q | 1.95 × 10−9 | m3 s−1 |
| tr | 5000 | s |
| u | 4.00 × 10−3 | m s−1 |
2.5. Diffusion coefficients for the binary and ternary systems
Diffusion coefficients for an infinite dilution system were determined according to the following function:37
 | (9) |
The Wilke and Chang correlation38 is a fairly dated but still widely adopted estimation method for determining diffusion coefficients at infinite dilution (eqn (10)).
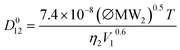 | (10) |
Another correlation still widely used today is that of Hayduk and Minhas39 (eqn (11)).
| D012 = 1.25 × 10−8(V1−0.19 − 0.292)T1.52ηwε* | (11) |
The Wilke and Chang correlation suggests selecting Φ based on the solvent, e.g., 2.6 for water, 1.9 for methanol, 1.5 for ethanol, and 1.0 for unassociated solvents. An average error of approximately 10% was observed from the authors when testing 251 solute–solvent systems. By using the Hayduk and Minhas correlation it is possible to predict diffusion coefficients with an average deviation of slightly below 10%. However, several restrictions must be taken into account when applying this correlation. It should not be applied to diffusion in viscous solvent (η > 20–30 cP); if the solute is water, dimer values for VA and PA should be used; for organic acids in solvents different from water, methanol, or butanol, the acid should be treated as a dimer, with VA and PA values doubled; for nonpolar solutes diffusing in monohydroxy alcohols, VB and PB should be multiplied by 8ηB, where ηB represents the solvent viscosity in cP.40
As for the ternary systems, the experimental refractive index, acquired through the Abbe refractometer of the different solutions at the various temperatures were determined. RI1 and RI2 i.e., the dependence of the refractive index on the composition of one of the two components, keeping the composition of the other constant were therefore determined.
 | (12) |
2.6. Simulation of flow reactor for glucose hydrogenation to sorbitol
To verify the influence of diffusion coefficients on the performance of a flow reactor for hydrogenation reactions of glucose to sorbitol, two models were developed. One model included diffusion coefficients obtained using the Wilke–Chang correlation, while the other used experimentally determined diffusion coefficient values.Both models are based on the following assumptions: (i) the system consists of a single liquid phase and the solution is saturated with hydrogen. The catalyst can either be dissolved in the liquid phase (homogeneous catalysis) or operate without fluid-solid or intraparticle mass transfer limitations (heterogeneous catalysis); (ii) the kinetics is of the first order with respect to glucose; (iii) the system is isothermal, with T = 65 °C; (iv) the models are developed in stationary conditions; (v) a laminar flow condition is imposed; (vi) molecular diffusion along the axis of the tube is neglected, being the Taylor condition verified.
The solution to the mass balance equations was predicted by two models using infinite dilution binary coefficients, estimated by the Wilke–Chang correlations (eqn (13a) and (13b)) and mutual diffusion coefficients determined experimentally via the Taylor dispersion method (eqn (14a) and (14b))
 | (13a) |
 | (13b) |
 | (14a) |
 | (14b) |
The Wilke–Chang correlations was used to determine the values of D1 and D2 at T = 65 °C. The values obtained were D1 = 18.0 × 10−6 cm2 s−1 and D2 = 17.1 × 10−6 cm2 s−1. In the case of the model involving the use of mutual diffusion coefficients determined experimentally through the Taylor dispersion method, empirical functions were used. These functions describe the trend of the experimental data of the Dij collected at T = 65 °C (eqn (15a)–(15d)).
| D11 = 1.44 × 10−5 + 1.85 × 10−5C1 − 1.10 × 10−2C12 + 2.26 × 10−1C13 − 1.17C14 | (15a) |
D12 = 3.75 × 10−5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−8.31 × 10−2/(C1 + 2.85 × 10−11)] exp[−8.31 × 10−2/(C1 + 2.85 × 10−11)]
| (15b) |
| D21 = [1.14 × 10−4/(1.14 × 10−4 + 8.38)]·[exp(8.38C2) − exp(−1.14 × 10−4C2)] | (15c) |
| D22 = 1.56 × 10−5 − 3.23 × 10−4C2 + 8.31 × 10−3C22 − 8.31 × 10−2C23 + 3.30 × 10−1C24 | (15d) |
To solve both models, it is necessary to introduce typical boundary conditions for single-phase flow reactors:
(i) Constant concentration at the tube inlet: ci|z=0 = ci,0.
(ii) Zero concentration derivative at the tube exit:  .
.
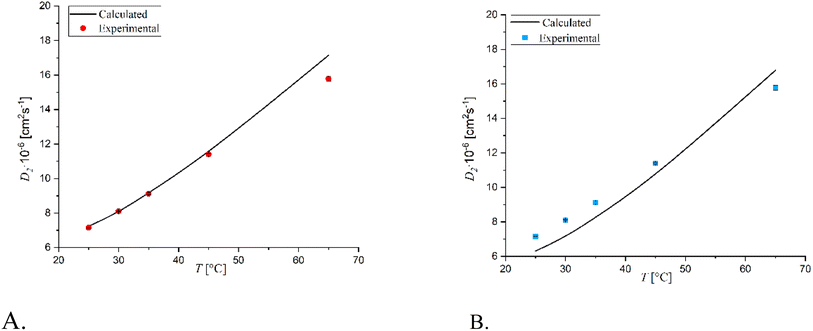
(iii) Symmetrical concentration profile in the center of the tube: 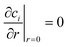 .
.
(iv) Derivative of zero concentration on the walls of the tube:  .
.
To solve the system, values reported in Table 2 were imposed.
| Value | Unit | |
|---|---|---|
| L | 100 | cm |
| R | 2.5 × 10−1 | cm |
| ci,0 | 0.10 | mol L−1 |
| k | 10−3 | s−1 |
The glucose conversion was calculated according to eqn (16), where an average glucose concentration is used.
 | (16) |
3 Results & discussion
3.1. Reynolds number and Taylor condition
Reynolds numbers were calculated at different temperatures and the Taylor condition was verified, as shown in Table 3.The Reynolds number is much lower than 2000 in all cases. To verify the Taylor condition, as expressed in eqn (5), the ratio of the second member is calculated. To satisfy the Taylor condition, this ratio must be much lower than the L/u0 ratio, which is approximately 6000 s. Since the diffusion coefficient varied with temperature, the Taylor condition was verified to be satisfied by calculating the ratio at different temperatures.
3.2. Diffusion coefficients for glucose-water, sorbitol-water, and glucose-sorbitol-water systems
Diffusion coefficients for an infinite dilution system, in the case of both glucose and sorbitol, are reported in Table 4. All measurements were repeated three times to determine the uncertainty.| T [°C] | D1 [cm2 s−1] | D2 [cm2 s−1] |
|---|---|---|
| 25 | (7.294 ± 0.032) × 10−6 | (7.149 ± 0.004) × 10−6 |
| 30 | (7.917 ± 0.106) × 10−6 | (8.115 ± 0.017) × 10−6 |
| 35 | (9.361 ± 0.277) × 10−6 | (9.124 ± 0.065) × 10−6 |
| 45 | (11.482 ± 0.007) × 10−6 | (11.405 ± 0.046) × 10−6 |
| 65 | (14.503 ± 0.770) × 10−6 | (15.783 ± 0.137) × 10−6 |
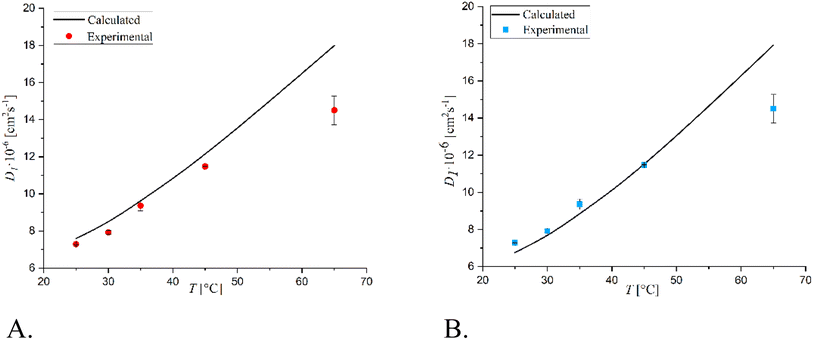
As it is possible to note, the diffusion coefficients increased by increasing the temperature, as expected. A comparison was made between the infinite dilution diffusion coefficients of glucose and sorbitol as calculated with the previously described Wilke–Chang and Hayduk–Minhas33 correlations and those obtained experimentally (see Fig. 1 and 2).
 | ||
| Fig. 1 Comparison between experimental infinite dilution diffusion coefficients and those calculated with (A) Wilke–Chang and (B) Hayduk–Minhas correlations for glucose. | ||
 | ||
| Fig. 2 Comparison between experimental infinite dilution diffusion coefficients and those calculated with (A) Wilke–Chang and (B) Hayduk–Minhas correlations for sorbitol. | ||
These two correlations are normally adopted in the literature as well suited for dilute solutions of organic molecules, where water is the solvent.
It can be stated that the two models well describe the experimental data within the temperature range of 25–45 °C. However, the Hayduk–Minhas model is not reliable for sorbitol, as it always estimates diffusion coefficients lower than the actual values. The most significant finding is that both models overestimate the experimental data at 65 °C. This comparison surely indicates that the classical correlations used to estimate diffusion coefficients must be always verified when using them at high temperatures, where the trends of the main physico chemical parameters (e.g., viscosity, molar volumes, association factors) could deviate from the functionalities adopted in describing diffusion coefficients at lower temperature values. De facto, the deviation can be considered natural as the interaction between the diffusing molecules in the solvent can change very much when temperature is varied.
The diffusion coefficients of the glucose-water binary system at different solute concentrations are reported in Table 5, confirming results comparable to those reported in the literature for a temperature range of 25 to 45 °C.32
| T [°C] | C1 [mol L−1] | D1 [cm2 s−1] |
|---|---|---|
| 25 | 0.0250 | (7.433 ± 0.029) × 10−6 |
| 35 | (9.434 ± 0.042) × 10−6 | |
| 45 | (11.797 ± 0.088) × 10−6 | |
| 65 | (17.348 ± 0.348) × 10−6 | |
| 25 | 0.0500 | (7.443 ± 0.045) × 10−6 |
| 35 | (9.132 ± 0.114) × 10−6 | |
| 45 | (11.091 ± 0.072) × 10−6 | |
| 65 | (15.744 ± 0.241) × 10−6 | |
| 25 | 0.0753 | (7.096 ± 0.226) × 10−6 |
| 35 | (8.953 ± 0.301) × 10−6 | |
| 45 | (11.036 ± 0.254) × 10−6 | |
| 65 | (16.361 ± 0.661) × 10−6 | |
| 25 | 0.1000 | (6.897 ± 0.056) × 10−6 |
| 35 | 0.0953 | (8.999 ± 0.137) × 10−6 |
| 45 | (10.705 ± 0.111) × 10−6 | |
| 65 | (15.613 ± 0.183) × 10−6 |
In Table 6, the data relating to sorbitol solutions are reported.
| T [°C] | C2 [mol L−1] | D2 [cm2 s−1] |
|---|---|---|
| 25 | 0.0256 | (6.979 ± 0.672) × 10−6 |
| 35 | (9.131 ± 0.305) × 10−6 | |
| 45 | (11.476 ± 0.581) × 10−6 | |
| 65 | (15.919 ± 0.531) × 10−6 | |
| 25 | 0.0490 | (6.910 ± 0.065) × 10−6 |
| 35 | (8.459 ± 0.189) × 10−6 | |
| 45 | (11.099 ± 0.197) × 10−6 | |
| 65 | (15.633 ± 0.258) × 10−6 | |
| 25 | 0.0722 | (6.766 ± 0.128) × 10−6 |
| 35 | (8.767 ± 0.164) × 10−6 | |
| 45 | (10.922 ± 0.192) × 10−6 | |
| 65 | (15.607 ± 0.146) × 10−6 | |
| 25 | 0.0956 | (6.665 ± 0.099) × 10−6 |
| 35 | (8.530 ± 0.307) × 10−6 | |
| 45 | (10.528 ± 0.351) × 10−6 | |
| 65 | (15.774 ± 0.498) × 10−6 |
The diffusion coefficients for both glucose-water and sorbitol-water binary systems decrease slightly with concentration, which, due to the low concentration, is mainly due to the decrease in activity coefficients with concentration according to the Hartley equation.32 While the increase in temperature produces an increase in the diffusion coefficients that follows the trend predicted by the Stokes–Einstein equation. Both evidences allow the exclusion of association or interaction phenomena between molecules in the considered concentration range. Table 7 shows a summary of the values obtained of the diffusion coefficients of the glucose-sorbitol-water ternary systems at the different concentrations of solute and the respective temperatures.
| T [°C] | Cstream [mol L−1] | D11 [cm2 s−1] | D12 [cm2 s−1] | D21 [cm2 s−1] | D22 [cm2 s−1] |
|---|---|---|---|---|---|
| 25 | 0.0248 | 6.729 ± 0.287 | 0.044 ± 0.002 | 0.148 ± 0.017 | 6.266 ± 0.827 |
| 0.0742 | |||||
| 25 | 0.0496 | 6.355 ± 0.706 | −0.040 ± 0.003 | 0.223 ± 0.017 | 6.548 ± 0.742 |
| 0.0496 | |||||
| 25 | 0.0742 | 6.521 ± 0.611 | 0.068 ± 0.003 | −0.0020 ± 0.0001 | 6.495 ± 0.379 |
| 0.0248 | |||||
| 45 | 0.0248 | 6.949 ± 0.134 | 0.162 ± 0.242 | 4.728 ± 0.134 | 11.000 ± 1.021 |
| 0.0742 | |||||
| 45 | 0.0496 | 7.000 ± 0.601 | 0.346 ± 0.956 | 0.161 ± 0.017 | 10.453 ± 1.309 |
| 0.0496 | |||||
| 45 | 0.0742 | 10.116 ± 1.321 | 1.336 ± 0.232 | −0.396 ± 0.043 | 8.642 ± 0.123 |
| 0.0254 | |||||
| 65 | 0.0248 | 11.169 ± 1.035 | 0.046 ± 0.002 | 13.913 ± 1.247 | 13.585 ± 1.165 |
| 0.0742 | |||||
| 65 | 0.0496 | 8.804 ± 0.136 | 8.540 ± 0.186 | 5.562 ± 0.135 | 12.019 ± 1.166 |
| 0.0496 | |||||
| 65 | 0.0743 | 12.214 ± 1.221 | 11.506 ± 1.254 | 2.593 ± 0.115 | 11.697 ± 1.239 |
| 0.0248 |
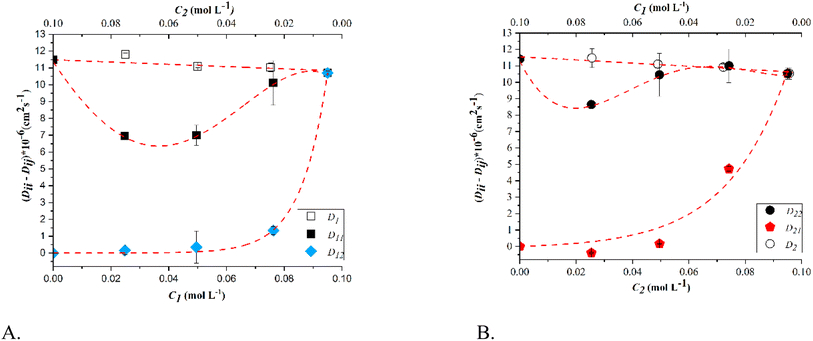
Fig. 3–5 display the diffusion coefficients of the ternary system at varying concentrations of solutes. Additionally, the diffusion coefficients of the binary systems glucose-water and sorbitol-water are shown at the same concentrations of solute as a function of the solutes' concentration (C1 represents glucose, while C2 represents sorbitol).
Observing the graphs, it is evident that the experimental results validate the theoretical condition:29
 | (17a) |
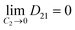 | (17b) |
At T = 25 °C, both glucose and sorbitol are transported through their concentration gradient, as the cross-coefficients D12 and D21 remain low and constant regardless of the composition range. As temperature increases, however, there is a marked difference in the behavior of the main diffusion coefficients, which for both substances go through a minimum that increases with temperature and then tends to the corresponding binary diffusion coefficients as the concentration of the substance increases.
In fact, at 45 °C, the main diffusion coefficients D11 and D22 exhibit a different trend, with a minimum and deviation from the respective binaries. This may suggest that the presence of sorbitol in high concentrations prevents the movement of glucose under the same gradient. The same behaviour is noticed for sorbitol in the presence of glucose. For instance, focusing on the trend of the diffusion coefficients where the sorbitol concentration is higher, one possible explanation for the trend could be the formation of a network of hydrogen bonds with a conformation that is not favorable to the diffusion of glucose. The same is valid also for glucose (Fig. 3b). At T = 45 °C, as the concentration of glucose increases, the hindering effect of sorbitol tends to disappear. These effects are more noticeable at T = 65 °C, where the transport of glucose is generated equally by its gradient and that of sorbitol. As shown in Fig. 5, the crossing coefficients at 65 °C are positive and have similar values of the main diffusion coefficients as the concentration of glucose or sorbitol increases. This implies that, under these conditions, there is a significant additional flux for each component generated by the cross gradient of the other.
However, it remains evident that probably even in this case, the formation of a certain type of hydrogen bond network hinders diffusion and does not allow obtaining the same transport efficiency that is observed in the corresponding binary systems.41
3.3. Simulation of flow reactor for glucose hydrogenation to sorbitol
The trends of the experimental data of the Dij collected at T = 65 °C are reported in Fig. 6 while glucose profiles obtained with the two previously mentioned approaches are depicted in Fig. 7.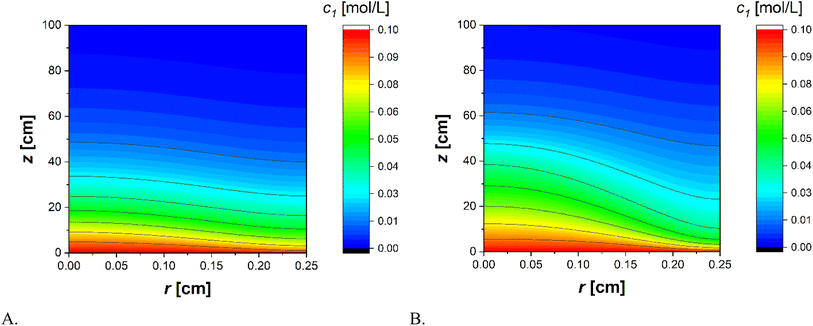 | ||
| Fig. 7 Contour diagrams for the glucose concentration profiles calculated with (A) Wilke–Chang correlation and (B) Taylor method. | ||
In the first case, the simulation leads to less pronounced concentration gradients along the radius of the tube compared to the second case. Furthermore, the glucose concentration at the outlet is lower in the first model compared to the second one. This leads to an overestimation of calculated glucose conversion using the less stringent approach. This phenomenon can be better appreciated in Fig. 8, where the calculated glucose conversions according to the two models are compared.
The most significant difference between the two models occurs between 15% and 90% of the tube length. The first model not only overestimates the conversion but also produces a qualitatively different profile compared to the more rigorous approach. Since the rate obtained using the Taylor method is lower than that of the Wilke–Chang method, a longer reactor is required to achieve the same conversion. Furthermore, the shape of the curve differs in the two cases. Therefore, in deriving the kinetic data, the analysis may lead to an incorrect estimation of parameters and, consequently, an imprecise determination of the rate law.
4 Conclusions
The diffusion coefficients of the binary systems glucose-water, sorbitol-water, and the ternary system glucose-sorbitol-water were determined at different concentrations of the two solutes and different temperatures. Knowing these coefficients is important for accurately simulating chemical reactors in flow. This study emphasizes the importance of measuring diffusion coefficients, providing new data that were previously not available in the literature. The Wilke–Chang and Hayduk–Minhas models accurately predict diffusion coefficients for water-glucose and water-sorbitol systems between 25 and 45 °C, except for the Hayduk model applied to sorbitol, which underestimates the values. At 65 °C, both models significantly overestimate experimental results. In ternary systems at 25 °C, glucose and sorbitol diffuse primarily by their concentration gradient, as the cross coefficients D12 and D21 remain small and constant across compositions. At 45 °C, the main diffusion coefficients (D11, D22) show deviations from binary values, with a minimum suggesting that high sorbitol concentrations hinder glucose diffusion, and viceversa. However, as glucose concentration increases, this hindering effect weakens. At 65 °C, this effect is even more pronounced, and glucose transport is influenced equally by its own gradient and that of sorbitol. To verify the usefulness of the study, two reactor simulations for glucose conversion to sorbitol under laminar flow were conducted, one using the Wilke–Chang model and another incorporating mutual diffusion. Results showed that the Wilke–Chang model overestimates glucose conversion in the central section of the tube. Thus, more rigorous models provide more reliable insights for process optimization. The results of this study can be applied to real catalytic data by using the model and the obtained parameters, enhancing its practical relevance.Abbreviations
Greek letters
| η | Solvent viscosity [cP] |
| ηw | Water viscosity [cP] |
| μ | Dynamic viscosity of the fluid [Pa s] |
| ρ | Density of the fluid [kg m−3] |
| Φ | Solvent association factor [—] |
Data availability
The results of this study are available within the manuscript and the ESI file.†Author contributions
Francesco Taddeo: investigation, writing – original draft; Ornella Ortona: conceptualization, methodology; Donato Ciccarelli: investigation, data curation; Riccardo Tesser: software, data curation; Henrik Grénman: methodology, formal analysis; Martino Di Serio: conceptualization, supervision, project administration; Vincenzo Russo: conceptualization, supervision, writing – review and editing; Luigi Paduano: supervision, project administration, writing – review and editing.Conflicts of interest
There are no conflicts to declare.References
- J. Tomaszewska, D. Bieliński, M. Binczarski, J. Berlowska, P. Dziugan, J. Piotrowski, A. Stanishevsky and I. A. Witońska, RSC Adv., 2018, 8, 3161–3177 RSC.
- A. Barone, B. A. De Liso, H. Grénman, K. Eränen, F. Taddeo, C. Imparato, A. Aronne, V. Russo, M. Di Serio and T. Salmi, Processes, 2023, 12, 27 CrossRef.
- H. Röper, Starch/Staerke, 2002, 54, 89–99 CrossRef.
- B. Kusserow, S. Schimpf and P. Claus, Adv. Synth. Catal., 2003, 345, 289–299 CrossRef CAS.
- S. Schimpf, C. Louis and P. Claus, Appl. Catal., A, 2007, 318, 45–53 CrossRef CAS.
- Y. Fu, L. Ding, M. L. Singleton, H. Idrissi and S. Hermans, Appl. Catal., B, 2021, 288, 119997 CrossRef CAS.
- J. Wisnlak and R. Simon, Ind. Eng. Chem. Prod. Res. Dev., 1979, 18, 50–57 CrossRef.
- P. A. Lazaridis, S. Karakoulia, A. Delimitis, S. M. Coman, V. I. Parvulescu and K. S. Triantafyllidis, Catal. Today, 2015, 257, 281–290 CrossRef CAS.
- T. Kilpiö, A. Aho, D. Murzin and T. Salmi, Ind. Eng. Chem. Res., 2013, 52, 7690–7703 CrossRef.
- A. Aho, S. Roggan, K. Eränen, T. Salmi and D. Murzin, Catal. Sci. Technol., 2015, 5, 953–959 RSC.
- E. Crezee, Appl. Catal., A, 2003, 251, 1–17 CrossRef CAS.
- P. Gallezot, N. Nicolaus, G. Flèche, P. Fuertes and A. Perrard, J. Catal., 1998, 180, 51–55 CrossRef CAS.
- D. Durante, T. Kilpiö, P. Suominen, V. S. Herrera, J. Wärnå, P. Canu and T. Salmi, Comput. Chem. Eng., 2014, 66, 22–35 CrossRef CAS.
- A. K. Saroha and K. D. P. Nigam, Rev. Chem. Eng., 1996, 12, 207–347 CAS.
- F. Taddeo, R. Tesser, M. Di Serio and V. Russo, Chem. Eng. Process., 2024, 197, 109712 CrossRef CAS.
- F. Orabona, S. Capasso, W. Y. Perez-Sena, F. Taddeo, K. Eränen, L. Verdolotti, R. Tesser, M. Di Serio, D. Murzin, V. Russo and T. Salmi, Chem. Eng. J., 2024, 493, 152677 CrossRef CAS.
- A. M. Asoltanei, E. T. Iacob-Tudose, M. S. Secula and I. Mamaliga, Processes, 2024, 12, 1266 CrossRef CAS.
- S. Shen, H. Wang, T. Ren, Z. Wang, T. Cao and Z. Xin, ACS Omega, 2024, 9, 3950–3961 CAS.
- R. B. Bird and D. J. Klingenberg, Adv. Water Resour., 2013, 62, 238–242 CrossRef.
- M. Castaldi, L. Costantino, O. Ortona, L. Paduano and V. Vitagliano, Langmuir, 1998, 14, 5994–5998 CrossRef CAS.
- A. Vergara, L. Paduano and R. Sartorio, Macromolecules, 2002, 35, 1389–1398 CrossRef CAS.
- L. Paduano, R. Sartorio and V. Vitagliano, J. Phys. Chem. B, 1998, 102, 5023–5028 CrossRef CAS.
- A. Vergara, L. Paduano, V. Vitagliano and R. Sartorio, Phys. Chem. Chem. Phys., 1999, 1, 5377–5383 RSC.
- G. Palazzo and L. Paduano, in Colloidal Foundations of Nanoscience, ed. D. Berti and G. Palazzo, Elsevier, 2022 Search PubMed.
- D. G. Miller, J. Phys. Chem., 1988, 92, 4222–4226 CrossRef CAS.
- D. G. Leaist, J. Phys. Chem., 1990, 94, 5180–5183 CrossRef CAS.
- L. Paduano, R. Sartorio, V. Vitagliano, J. G. Albright, D. G. Miller and J. Mitchell, J. Phys. Chem., 1990, 94, 6885–6888 CrossRef CAS.
- V. Russo, O. Ortona, R. Tesser, L. Paduano and M. Di Serio, ACS Omega, 2017, 2, 2945–2952 CrossRef CAS PubMed.
- W. E. Price, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 2431 RSC.
- A. Alizadeh, C. A. Nieto De Castro and W. A. Wakeham, Int. J. Thermophys., 1980, 1, 243–284 CrossRef CAS.
- Y. Sano and S. Yamamoto, J. Chem. Eng. Jpn., 1993, 26, 633–636 CrossRef CAS.
- A. C. F. Ribeiro, O. Ortona, S. M. N. Simões, C. I. A. V. Santos, P. M. R. A. Prazeres, A. J. M. Valente, V. M. M. Lobo and H. D. Burrows, J. Chem. Eng. Data, 2006, 51, 1836–1840 CrossRef CAS.
- I. M. J. J. Van De Ven-Lucassen and P. J. A. M. Kerkhof, J. Chem. Eng. Data, 1999, 44, 93–97 CrossRef CAS.
- T. Lebeau, T. Jouenne and G. A. Junter, Enzyme Microb. Technol., 1998, 22, 434–438 CrossRef CAS.
- T. Waluga and S. Scholl, Chem. Eng. Technol., 2013, 36, 681–686 CrossRef CAS.
- R. H. Perry, D. Green and J. O. Maloney, Perry's Chemical Engineers' Handbook, McGraw-Hill, 7th edn, 1997 Search PubMed.
- D. G. Leaist and H. Ling, J. Phys. Chem., 1995, 99, 12896–12901 CrossRef CAS.
- K. Miyabe and R. Isogai, J. Chromatogr. A, 2011, 1218, 6639–6645 CrossRef CAS PubMed.
- W. Hayduk and B. S. Minhas, Can. J. Chem. Eng., 1982, 60, 295–299 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The properties of gases and liquids, McGraw-Hill Education, New York, 5th edn, 2001 Search PubMed.
- A. Vergara, L. Paduano, G. D'Errico and R. Sartorio, Phys. Chem. Chem. Phys., 1999, 1, 4875–4879 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra00669d |
| This journal is © The Royal Society of Chemistry 2025 |