Synthesis and adsorption performance of a novel pyridinium-functionalized hypercrosslinked resin for the removal of chromium(VI) ions

Abstract

This study presents the synthesis and characterization of a novel anion exchange hypercrosslinked resin (HPR1) designed for the removal of high-concentration hexavalent chromium Cr(VI) from aqueous solutions. The resin was synthesized via a one-step Friedel–Crafts alkylation reaction using a low-crosslinking copolymer of divinylbenzene and vinylbenzyl chloride (DVB-co-VBC), prepared by suspension polymerization with toluene as a porogen. The successful incorporation of pyridinium groups into the resin network was confirmed using elemental analysis, FTIR spectroscopy, and solid-state ¹³C NMR spectroscopy. The adsorption performance of HPR1 was evaluated at various pH (2, 4, and 6.5) and initial Cr(VI) concentrations. The nonlinear Langmuir isotherm model provided the best fit for the experimental data compared with tc Freundlich and Redlich–Peterson isotherms. Notably, the adsorption equilibrium was achieved within 4 min, with a maximum capacity of 207 mg g⁻¹ at pH 2. Kinetic studies indicated that the adsorption process was best described by a pseudo-second-order model, with higher rates observed at pH 4 than at pH 2. Additionally, intraparticle diffusion has been identified as the mechanism that controls the adsorption process. The high adsorption capacity of HPR1 at acidic pH values suggests its potential for treating industrial wastewater containing elevated concentrations of Cr(VI).

---

Introduction

Water pollution caused by toxic heavy metals is a significant global environmental issue. Industrial discharges have led to the accumulation of non-biodegradable heavy metal ions, posing serious risks to ecosystems, human health, and animal life.^1,2 Chromium is widely utilized in various industrial processes, including corrosion inhibition, leather tanning, electroplating, dyeing, chromate preparation, and alloying.^3–6 Hexavalent chromium Cr(VI) is particularly hazardous due to its high solubility across a wide pH range, making it more toxic than trivalent chromium Cr(III).⁷ Therefore, controlling Cr(VI) levels in industrial effluents before discharge into sewage systems or natural water bodies is crucial to prevent environmental degradation. Numerous methods have been reported for the removal of Cr(VI) from aqueous solutions, including chemical precipitation, adsorption, membrane separation, reverse osmosis, electrodialysis, and ion exchange.^8–11

However, these techniques often fail to meet the permissible limit for hexavalent chromium in industrial wastewater (0.1 mg L⁻¹).¹² Consequently, there is a pressing need to explore alternative methods capable of achieving this standard. Adsorption has emerged as one of the most effective techniques for heavy metal removal due to its simplicity and efficiency. Synthetic porous polymers have gained attention in various fields such as water purification and gas separation because of their ease of preparation, well-defined porous structures, high specific surface areas, low cost, and potential for regeneration.^13,14 Macroporous polymers based on poly(styrene-co-divinylbenzene) (poly(PS-co-DVB)) are typically synthesized through suspension polymerization in the presence of inert solvents (porogens). These resins often utilize high levels of crosslinking agents—up to 50 vol%—which can limit the availability of active sites on the adsorbent polymer.^14–16 Hypercrosslinked polymers (HCPs) represent another class of adsorbent materials characterized by their high micropore content and specific surface areas comparable to activated carbon (up to 2000 m² g⁻¹).^17–20 Recent advancements in hypercrosslinked polymer synthesis have utilized Friedel–Crafts reactions to generate novel materials with diverse applications.^21–27

In this study, we report the synthesis and characterization of a novel anion exchange hypercrosslinked resin (HPR1) obtained via Friedel–Crafts alkylation. The low-crosslinking poly(DVB-co-VBC) copolymer matrix was prepared by suspension polymerization followed by quaternization of pyridine groups in a single step. The incorporation of pyridinium groups into the hypercrosslinked resin network was confirmed using FTIR spectroscopy and elemental analysis. The adsorption performance of HPR1 was evaluated for the removal of hexavalent chromium from aqueous solutions at various pH levels (2, 4, and 6.5) and initial Cr(VI) concentrations. The nonlinear Langmuir isotherm provided the best fit for the experimental data compared with the Freundlich and Redlich–Peterson isotherms. Notably, the adsorption equilibrium was reached within 4 min, with a maximum capacity of 207 mg g⁻¹ at pH 2. Kinetic studies indicated that the adsorption process followed the pseudo-second-order model with faster rates observed at pH 4 than at pH 2. Finally, intraparticle diffusion was identified as the mechanism control the adsorption process.

Experimental

Materials

All reagents used in the synthesis of the anion exchange hypercrosslinked resin were purchased from Sigma Aldrich. Poly(vinyl alcohol) PVA (80–87% hydrolyzed, M_w 85 000–124 400) was used as suspension agent without further purification, pyridine (Py), 1,2-dichloroethane (DCE), zinc chloride (ZnCl₂), and azobisisobutyronitrile (AIBN) were used as received without further purification. 4-Vinylbenzyl chloride (VBC) and divinylbenzene DVB (80% isomeric mixture) were washed with a 5% NaOH aqueous solution prior to use.

Synthetic route for anion exchange hypercrosslinked HPR1 resin

The synthetic route to the anion exchange hypercrosslinked resin (HPR1) is shown in Scheme 1. The scheme demonstrates that the post-crosslinking reaction, involving Friedel–Crafts alkylation and quaternization of pyridine groups, occurs in a single step. Initially, the low-crosslinked copolymer was synthetized using vinylbenzyl chloride (VBC) as monomer along with an internal crosslinking agent.^16,28 Posteriorly, the copolymer R1 was utilized in the post-crosslinked reaction to form of pyridinium groups.^29,30

Scheme 1 Synthesis route of the anion exchange hypercrosslinked resin (HPR1).

Synthesis of the low-crosslinked copolymer R1

The low-crosslinked precursor resin R1 was synthetized using suspension polymerization technique. A four-necked, 1 L reaction vessel equipped with a thermostat, a mechanical stirrer, water condenser and nitrogen inlet were used. The organic phase was prepared by mixing divinylbenzene (DVB) (1.9 g, 14.4 mmol) and 4-vinylbenzyl chloride (VBC) (20 g, 130.7 mmol) and 0.1 wt% AIBN (0.33 g, 0.60 mmol) and toluene (33 mL) as the porogen agent. This organic mixture was stirred for 30 min under a nitrogen atmosphere. The aqueous phase consisted of deionized water (700 mL), NaCl 8.37 g and polyvinyl alcohol (PVA) (1.40 g, 1 wt%). The organic phase was then added dropwise to the aqueous phase while maintaining nitrogen flow. The suspension was then stirred and heated at 70 °C for 12 h. The resulting poly(VBC-co-DVB) copolymer was filtered, washed with a methanol–water mixture and placed in a Soxhlet apparatus for extraction with methanol for 24 h to remove residual monomer and PVA. Finally, the precursor resin R1 was dried in a vacuum oven at 50 °C for 24 h.

Synthesis of the HPR1 resin

The synthesis of the anion exchange hypercrosslinked resin was achieved through Friedel–Crafts alkylation. Initially, 18 g of the low-crosslinked precursor copolymer R1 was placed in a 100 mL round-bottomed flask, to which 54 mL of 1,2-dichloroethane was added as the solvent. The mixture was slowly stirred for 12 h to facilitate the swelling of the beads. Subsequently, 17 mL of pyridine (Py) and 0.19 g ZnCl₂ were introduced as catalyst. The molar ratio used was 2 : 1 concerning the chloromethyl content and the Friedel–Crafts catalyst (CH₂Cl : ZnCl₂), as well as and 2 : 1 for the formation of pyridinium groups (Py : CH₂Cl). The solution was then heated to 90 °C for 10 h. Upon completion of the reaction, the HPR1 resin was filtered, washed with a methanol–water mixture, and subjected to Soxhlet extraction for 24 h to eliminate residual pyridine. Finally, the resin was dried in a vacuum oven at 50 °C for 24 h.

Characterization of HPR1 resin

The low-crosslinked precursor R1 and HPR1 anion exchange resin were characterized using several analytical techniques. Fourier Transformed Infrared (FTIR) spectroscopy was conducted with a PerkinElmer 1500 spectrometer in Attenuated Total Reflection mode (ATR). Elemental analysis was performed using a PerkinElmer CHNSO 2400 Analyzer and Scanning electron microscopy (SEM) analysis was carried out using a DSM 940 microscope from Zeiss, operated in high vacuum mode at an acceleration voltage of 10–30 kV with a secondary detector. The thermal properties of the synthesized resins were analyzed using thermogravimetric analysis (TGA) over a temperature range of 30 to 800 °C. The concentration of hexavalent chromium Cr(VI) ions in the solution was quantified using a PerkinElmer Lambda 40 ultraviolet-visible spectrophotometer.

Adsorption experiments

The contact time and the influence of initial concentration of Cr(VI) ions were investigated at pH values of 2, 4 and 6.5 through a batch experiment conducted at room temperature (25 °C) with continuous stirring. A precisely weighed 0.10 g of the HPR1 anion exchange resin was introduced into flasks containing 10 mL of chromium aqueous solution. The initial concentration of the adsorbate C₀ (mg L⁻¹) was set to 500, 1000, 1500, 2000, 2250, 2500, 2750 and 3000 mg L⁻¹. The pH was adjusted using aqueous solution of HCl or NaOH. Each flask was completely sealed and continuously shaken at 200 rpm until equilibrium was reached.

The equilibrium concentration capacity of the adsorbate was calculated using the following eqn (1).

where C₀ (mg L⁻¹) and C_e are the initial Cr(VI) concentration and the concentrations at the equilibrium liquid phase, respectively. q_e (mg g⁻¹) is the amount of Cr(VI) adsorbed per resin unit mass at equilibrium, V (L) is the volume of the solution, and m (g) is the mass of dry resin.

Kinetic study

The kinetic study was conducted in a manner similar to the adsorption equilibrium isotherms at pH values of 2 and 4. The adsorption capacity at contact time q_t (mg g⁻¹) was determined in real-time until equilibrium was reached and calculated using the following eqn (2).where C_t (mg L⁻¹) is the concentration of Cr(VI) at contact time.

To evaluate the ion exchange performance of the hypercrosslinked resin, two kinetic models were employed: the nonlinear pseudo-first-order and pseudo-second-order models. These models were calculated using the following eqn (3) and (4).³¹

q_t = q_e(1 − e^−k₁t) (3)

where q_e and q_t are the adsorption capacities of Cr(VI) (mg g⁻¹) at equilibrium time and at any instant t (min), respectively. Where k₁ is the rate constant of nonlinear pseudo-first order adsorption (1/min) and k₂ is the rate constant of nonlinear pseudo-second order (g mg⁻¹ min⁻¹).

Additionally, the kinetics parameters were determined using the linearized form of pseudo-first order, eqn (5) and pseudo-second order, eqn (6) models.^31,32

ln(q_e − q_t) = ln q_e − k₁t (5)

where q_e is the amount of chromium adsorbed at equilibrium (mg g⁻¹), q_t is the amount de chromium adsorbed at time t (mg g⁻¹), k₁ is the rate constant of the pseudo-first order adsorption (1/min).

The Weber–Morris diffusion model was applied to analyze the intra-particle diffusion mechanisms of the anion exchange hypercrosslinked resin.³² This model is described by the following eqn (7).

q_t = k_ipt^1/2 + C (7)

where q_t is adsorption capacity at time t (mg g⁻¹), C is the intercept related to the thickness of the boundary layer (mg g⁻¹) and k_ip is the rate constant of intra-particle diffusion (mg g⁻¹ min^−1/2).

Adsorption isotherm study

The adsorption performance of the HPR1 resin was evaluated using the Langmuir, Freundlich, and Redlich–Peterson isotherm models. The Langmuir equation describes monolayer coverage on a structurally homogeneous adsorbent, where all the adsorption sites are energetically identical and exhibit equal affinity for the adsorbate.³³ The Langmuir model is represented by the following eqn (8).where q_m is the maximum adsorption capacity (mg g⁻¹), and k_L is a constant related to the adsorption energy (L mg⁻¹).

In contrast, the Freundlich eqn (9) models multi-layer adsorption on a heterogeneous surface, indicating that the amount of adsorbed adsorbate increases indefinitely with concentration.³⁴

q_e = k_FC_e^1/n (9)

where k_F [(mg g⁻¹) (L mg⁻¹)1/n], and n are the characteristic constants.

The Redlich–Peterson isotherm is an empirical model that combines features of both Langmuir and Freundlich isotherms,¹⁴ it provides a linear dependence on concentration in the numerator and a potential function in the denominator, making it applicable over a wide concentration range; it can be expressed by eqn (10).

This model can be applied in both homogeneous or heterogeneous systems due to its adaptability. The mechanism of adsorption described by this model is hybrid and does not conform to ideal monolayer adsorption. Where the β constant is an exponent that lies between 0–1. The constants k_R and a_R have units (L g⁻¹) and (L mg⁻¹), respectively. While C_e is the equilibrium liquid phase concentration of the adsorbate (mg L⁻¹) and q_e is the equilibrium adsorbate loading onto the adsorbent (mg g⁻¹).

Results and discussion

Chemical characterization of HPR1 anion exchange resin

Scanning electron microscopy (SEM) revealed a narrow particle size distribution for the R1 resin, with an average diameter ranging from 80 μm to 120 μm, obtained through suspension polymerization (Fig. 1a). After the formation of pyridinium groups and subsequent crosslinking, SEM micrographs at ×27 000 magnification illustrated the development of porous structure within the HPR1 resin, displaying a rough surface texture (Fig. 1b). At ×9000 magnification, some spherical particles exhibited signs of cleavage, revealing a smooth surface with lamellar morphology (Fig. 1c). These observations indicate structural changes resulting from the synthetic process.

Fig. 1 Scanning Electron Microscopy (SEM) Images of synthetized resins. (a) Spherical particles obtained through suspension polymerization of the R1 resin. (b) The surface of a single particles of the HPR1 resin (c) morphology of cleaved particles after the post-crosslinked of the HPR1 resin.

Prior to the post-crosslinking reaction, the poly(VBC-co-DVB) precursor copolymer contained 18.9% chlorine groups, determined by elemental analysis (Table 1). After Friedel–Crafts alkylation, the percentage of pyridinium groups incorporated was 43% as calculated from the elemental analysis data (Table 1).

Table 1 Elemental analysis data of the precursor copolymer and anion exchange hypercrosslinked resin

Resin	Elemental analysis
	% C	% H		% N		% Cl		% O
	Theoretical	Exp	Theoretical	Exp	Theoretical	Exp	Theoretical	Exp	Theoretical
R1	73.0	73.8	6.0	7.3	—	—	21	18.9	—
HPR1	68.6	68.3	7.0	7.6	4.7	4.7	—	19.4	19.7

---

The FTIR spectrum of the R1 precursor copolymer displays vibrational bands at 1610, 1510, and 1421 cm⁻¹, corresponding to the C=C bonds of the aromatic ring and the out-of-plane C–H bond at 813 cm⁻¹. In addition, two adsorption bands at 1263 cm⁻¹ and 671 cm⁻¹ were attributed to the C–Cl bond (Fig. 2a).³⁵ after the post-crosslinked and the incorporation of pyridine ring. In the FTIR spectrum, the vibrational bands C=C of the aromatic rings were shifted to 1484, 1448, and 1424 cm⁻¹ attributed to the post-crosslinking reaction and the incorporation of the pyridine ring. In addition, a new band appeared at 1630 cm⁻¹, indicating the successful quaternization of pyridine groups (R–N⁺⁻Cl).²⁹ Furthermore, the intensity of the vibrational band at 1213 cm⁻¹, associated with the C–Cl bond, decreased, suggesting that not all chlorine groups reacted during the post-crosslinking process and that not all pyridine groups were incorporated in the in situ reaction. Indicated that only 43% of the chlorine groups participated in this reaction with pyridine and the post-crosslinking reaction. Finally, a vibrational band at 802 cm⁻¹ was observed, indicating crosslinking between the aromatic rings of divinylbenzene and vinylbenzyl chloride (Fig. 2b).³⁶

Fig. 2 FTIR spectra of the materials synthetized. (a) R1 poly(DVB-co-VBC) copolymer synthetized by suspension polymerization. (b) HPR1 resin obtained through the Friedel–Crafts alkylation reaction and subsequent formation of the pyridinium group (R–N⁺–Cl).

Solid-state ¹³C CP/MAS NMR spectroscopy confirmed the results of FTIR spectroscopy and elemental analysis. In the solid-state ¹³C CP/MAS NMR spectrum of the R1 precursor copolymer, the aliphatic region displayed two signals at 45.79 ppm and 39.95 ppm, corresponding to the ClCH₂Ar and CH₂–CHAr–CH₂ carbons in the copolymer network, respectively. In the aromatic region, signals for the aromatic carbons of divinylbenzene (DBV) and vinylbenzyl chloride (VBC) were observed at 145.49, 136.46 and 128.29 ppm (Fig. 3a). Additionally, the signal at 63.70 ppm, corresponding to the HOCH₂Ar, which was also observed in the FTIR spectrum at 3226 cm⁻¹, due to presence of water molecules and the hydrolysis of the VBC monomer during the polymerization.³⁵

Fig. 3 Solid-state (118 MHz) ¹³C CP/MAS NMR spectrum. (a) Precursor copolymer synthetized from divinylbenzene (DBV) and vinylbenzyl chloride (VBC). (b) Anion exchange hypercrosslinked resin obtained in a single step.

In contrast, in the spectrum of the HPR1 resin showed a reduction in the intensity of the signal at 45.01 ppm, in the aliphatic region, due to the post-crosslinking reaction of the chloromethylated VBC copolymer network and the incorporation of pyridine units in the formation de pyridinium groups. The signal at 64.1 ppm was assigned to the quaternization of the pyridinium groups (R–N⁺–Cl).²⁹ These results collectively confirmed the successful synthesis of the anion exchange hypercrosslinked resin in a single step.

Finally, in the aromatic region, the signal at 145.02 ppm increased in intensity due to the addition of pyridine rings.

Thermal properties of the HPR1 resin

Thermogravimetric analysis is a valuable tool for studying the thermal behavior and functionalization of synthetized resins. The R1 resin exhibited thermal stability with a T_5% of 352 °C, indicating a 5% weight loss at this temperature. The R1 precursor showed a rapid decomposition stage at 466 °C, corresponding to a 37% weight loss, attributed to the decomposition or oxidation of the polymer backbone. The copolymer precursor retained its residual weight at 538 °C, losing 79% of its total weight (Fig. 4).

Fig. 4 TGA curves of the R1 resin and HRP1 resin synthetized in a single step.

In contrast, HPR1 exhibited three distinct thermal decomposition stages, which differed from those observed for the R1 resin. At 100 °C, the HPR1 resin exhibited a 7% weight reduction, which can be attributed to the evaporation of water molecules or other volatile solvents. The second stage, occurring between 227 °C and 311 °C, involves the decomposition of pyridinium or chloromethyl groups.^37,38 The maximum decomposition was observed at 264 °C, with a weight loss of 19%. The third stage was attributed to the degradation of the polymer backbone. At 540 °C, HPR1 lost 84% of its total weight (Fig. 4).

Effect of pH on adsorption performance of the hypercrosslinked resin

The pH levels is a crucial factor that influences the efficiency of an adsorbent, as it determines the species present in acidic or basic media, thereby affecting metal adsorption behavior.³⁹ At pH < 2, Cr(VI) mainly exists as H₂CrO₄; in the pH range of 2 to 6.8, Cr(VI) is mainly found as HCrO₄⁻and Cr₂O₇²⁻. At pH > 6.8, Cr(VI) predominantly exists as CrO₄²⁻.⁴⁰

Fig. 5 shows a three-dimensional plot illustrating the adsorption capacity for Cr(VI) ions in the anion exchange hypercrosslinked resin. The z-axis represents the adsorption capacity, the x-axis indicates pH values of 2, 4 and 6.5, and the y-axis shows the initial Cr(VI) concentrations ranging from 500 to 3000 mg L⁻¹. The plot demonstrates that the selectivity for different chromate oxyanions varies with pH and initial concentration. The HPR1 resin exhibited high adsorption capacity for Cr(VI) ions at pH 2. At an initial concentration of 500 mg L⁻¹, the hypercrosslinked resin showed an affinity for the HCrO₄⁻ species, which was predominant in the pH range of 2 to 6.8.⁴¹ This chromate oxyanion is more readily adsorbed by the hypercrosslinked resin because of its smaller ionic size and favorable diffusion kinetics.

Fig. 5 Effect of initial concentration hexavalent chromium Cr(VI) concentration as a function of pH of the anion exchange hypercrosslinked resin (HPR1).

At pH 6.5, the HRP1resin reached a maximum equilibrium capacity of 1000 mg L⁻¹ owing to the presence of dichromate oxyanions Cr₂O₇²⁻. The larger ionic size of Cr₂O₇²⁻ compared to that HCrO₄⁻ is likely responsible for its lower adsorption capacity. However, at pH 4 and 2, the hypercrosslinked resin demonstrated enhanced adsorption capacity, achieving an initial concentration of up to 1500 mg L⁻¹. It is hypothesized that higher concentrations of chromium oxyanions facilitate the formation of more polymerized chromium oxide species. At pH 2, the HPR1 resin attained a maximum equilibrium capacity of 2500 mg L⁻¹, while at pH 4, it reached equilibrium at 2000 mg L⁻¹. The dependence on metal adsorption is related to the type and ionic state of the functional groups present in the hypercrosslinked resin network and the surface characteristics of the adsorbent.

Kinetic study of the HPR1 resin

Kinetic data are essential to understand whether the adsorption rate is limited by diffusion or chemical reactions. The HPR1 resin was evaluated at pH 2 and pH 4 with an initial Cr(VI) concentration of 300 mg L⁻¹. Kinetic data were analyzed using the nonlinear forms of both the pseudo-first-order and pseudo-second-order kinetic models. The parameters are listed in Table 2.

Table 2 Kinetic parameters for nonlinear and linear forms of pseudo-first-order and pseudo-second-order models of anion exchange hypercrosslinked resin

Pseudo First order	No linearized form				Linearized form
	qe (mg g^−1)	k1 (min^−1)	R^2	χ^2	qe (mg g^−1)	K (min^−1)	R^2
pH 2	27.9841	0.79703	0.9999	0.08703	1.047	0.4782	0.7202
pH 4	29.5165	1.84212	0.9984	0.15099	1.026	0.5281	0.6561

---

Pseudo Second Order	No linearized form				Linearized form
	qe (mg g^−1)	k2 (g mg^−1 min^−1)	R^2	χ^2	qe (mg g^−1)	K (g mg^−1 min^−1)	R^2
pH 2	29.26	0.04358	0.8059	0.9914	28.08	0.186	0.9997
pH 4	29.93	0.16407	0.9993	0.05998	29.58	2.858	0.9999

---

As shown in Fig. 6, The HPR1 resin reaches equilibrium within 5 min. Both kinetic models exhibited high correlation coefficients (R² ≈ 0.999) at pH 2 and 4. At pH 2, the rate constants were k₁ = 0.797 (1/min) and k₂ = 0.043 (mg g⁻¹ min⁻¹) for the pseudo-first-order and pseudo-second-order kinetic models, respectively.

Fig. 6 Kinetic curves of the nonlinear pseudo-first-order and pseudo-second-order kinetic models at pH = 2 and pH = 4 of HPR1 resin.

At pH 4, these values increase to k₁ = 1.842 (1/min) and k₂ = 0.169 (mg g⁻¹ min⁻¹). These results indicate that the adsorption rate of Cr(VI) ions was faster at pH 4 than at pH 2.

To elucidate the adsorption mechanism further, the experimental data were fitted to the linear form of the pseudo-second-order model, as shown in Fig. 7. The pseudo-second-order rate equation demonstrated a high correlation coefficient (R² = 0.999) at both pH values, whereas the pseudo-first-order model exhibited a low correlation coefficient (R² = 0.720), as shown in Table 2. This suggested that the adsorption process on the HPR1 resin is primarily dominated by chemical adsorption involving ion exchange.⁴² The rate constants k₂ were found to be 0.18 (1/min) at pH 2 and 2.85 (mg g⁻¹ min⁻¹) at pH 4, confirming that Cr(VI) ion adsorption is significantly faster at pH 4 compared to pH 2.

Fig. 7 Linear form of the pseudo-second-order model for the HPR1 resin at pH 2 and pH 4 at room temperature of HPR1.

To study the diffusion mechanism of the HPR1 resin, the intraparticle diffusion model established by Weber and Morris was applied to investigate the mass transfer of adsorbates until equilibrium was reached. The intraparticle diffusion process involves three steps:

(1) Transportation of the adsorbate from the solution to the external surface of the adsorbent.

(2) Intra-particle diffusion: where adsorbate molecules diffuse from the external surface into the pores or along the pore walls.

(3) Equilibrium adsorption of adsorbate onto the active sites of the adsorbent.

The parameters related to this model are summarized in Table 3. The diffusion mechanism of HPR1 was characterized by two distinct steps, as shown in Fig. 8. The first step corresponds to film diffusion, representing the instantaneous adsorption stage, while the second step involves slower intra-particle diffusion into the pores, indicating that equilibrium adsorption has been achieved. The value of the intra-particle diffusion rate constant k_ip, suggest that the adsorption process is faster at pH 4 than at pH 2. The C_ip values from the intraparticle diffusion model indicate a significant influence of both the boundary layer and the film diffusion effect on the overall process.⁴³

Table 3 Parameters obtained of the diffusion model associated with the adsorption of Cr(VI)

	kip (mg g^−1 min^−0.5)	C (mg g^−1)	R^2
pH 2
First linear segment	11.3	1.294	0.8677
Second linear segment	1.405	28.46	0.7687
pH 4
First linear segment	24.84	22.85	0.999
Second linear segment	2.27	2.92	0.999

---

Fig. 8 Inter-particle diffusion of the anion exchange hypercrosslinked resin at pH = 2 and pH = 4 at room temperature.

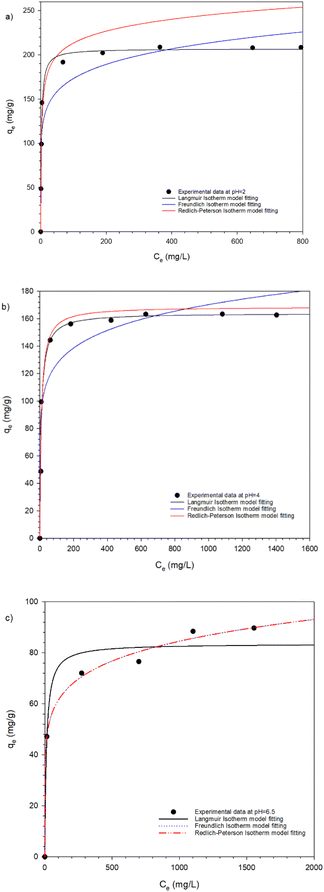
Adsorption isotherms

The equilibrium adsorption isotherm is crucial for understanding the interactions between the adsorbate and the adsorbent. The adsorption equilibrium was evaluated using nonlinear Langmuir, Freundlich and Redlich–Peterson isotherms at initial Cr(VI) concentrations ranging from 500 to 3000 mg L⁻¹ at room temperature. The parameters obtained from the equilibrium isotherms are summarized in Table 4.

Table 4 Parameters of nonlinear Langmuir, Freundlich and Redlich–Peterson isotherm models for the removal of Cr(VI)

pH	Langmuir model					Freundlich model			Redlich–Peterson model
	qm (mg g^−1)	kL (mL mg^−1)	R^2	χ^2	n	kF (mL mg^−1)	R^2	χ^2	aR (L mg^−1)	kR (L g^−1)	β	R^2	χ^2
2	207.0	0.454	0.969	254.76	7.843	96.30	0.952	397.51	0.816	124.486	0.923	0.979	167.70
4	164.1	0.119	0.970	109.08	7.846	70.58	0.882	427.39	0.113	19.069	1	0.965	126.93
6.5	83.6	0.082	0.977	34.93	7.200	32.39	0.997	4.92	226.738	7350.17	7350.17	0.997	6.16

---

As illustrated in Fig. 9a–c, the experimental data fit the Langmuir isotherm models better than the Freundlich and Redlich–Peterson model at both pH 2 and pH 4. This suggests that Cr(VI) ions adsorption occurred uniformly on the active sites of HPR1. The high Langmuir constant k_L values indicate strong sorption at pH 2 (k_L = 0.454 mL mg⁻¹) and weaker sorption at pH 6.5 (k_L = 0.082 mL mg⁻¹), which is attributed to protonation of pyridine group at lower pH. The maximum adsorption capacity (q_m) also varied with 207 mg g⁻¹ at pH 2, 164 mg g⁻¹ at pH 4 and 83.6 mg g⁻¹ at pH 6.5.

Fig. 9 Adsorption equilibrium isotherms of the HPR1 resin analyzed using nonlinear Langmuir, Freundlich and Redlich–Peterson isotherm models. (a) At pH 2, the adsorption parameters were best fit by the nonlinear Langmuir isotherm model. (b) At pH 4, the data were also well described by the nonlinear Langmuir model. (c) At pH 6.5 the experimental data were best fit by the Redlich–Peterson isotherm model.

This variation is linked to the different species of chromate oxyanion present at varying pH levels.⁴⁴ Additionally, the porous structure of HPR1 and the ionic character of its matrix play significant roles in its adsorption capacity. Freundlich isotherm analysis showed that the sorption process between the anion exchange hypercrosslinked resin and Cr(VI) ions was favorable. A value of 1/n > 1implies favorable physisorption, while 1/n > 1 indicates favorable chemisorption. At both pH 2 and pH 4, chemisorption predominated during the adsorption process on HPR1. The Freundlich constant k_F increased with decreasing pH: 96.30 (mL mg⁻¹) at pH 2, 70.58 (mL mg⁻¹) at pH 4 and 32.34 (mL mg⁻¹) at pH 6.5. This suggests that adsorption was more efficient at pH 2 than at pH 6.5.

The Redlich–Peterson isotherm model serves as a bridge between the Langmuir and Freundlich models. When the value of β approaches 1, the system aligns more closely with the Langmuir model, whereas a value approaching 0 indicates an alignment with the Freundlich model. In this study, the adsorption behavior of the HPR1resin was primarily described by the Langmuir model.

Comparation with other adsorbents

The HPR1 resin exhibited a high adsorption capacity for Cr(VI) ions at pH 2, surpassing that of many conventional adsorbents. A comparative analysis of adsorption capacities is provided in Table 5, which summarizes the maximum adsorption capacity q_max as a function of pH. For instance, the chitosan–graphene oxide composite (Cs–GO nanocomposite), a biosorbent, demonstrated a q_max of 104.16 mg g⁻¹. In contrast, the adsorbent studied by Revalthi achieved a q_max of 195.99 mg g⁻¹, a value closely approaching that of the HPR1 resin. Other hypercrosslinked adsorbents, such as thiol-functionalized black carbon, showed a q_max of 201 mg g⁻¹ at pH 3.5. A similar system reported by Xuanbo, hypercrosslinked nanofibrous tubes synthesized via Friedel–Crafts alkylation and quaternization reactions achieved a q_max of 191.07 mg g⁻¹ at pH 2. Notably, the HPR1 resin synthesized in this study outperforms all adsorbents examined, highlighting its superior adsorption efficiency.

Table 5 Performance comparison of recent adsorbents for removal of Cr(VI) ions

Adsorbent	qmax mg g^−1	pH	Reference
CS-GO nanocomposite	104.16	2	45
CS/CMC/BAG	195.99	3	46
M0ntomorillonite/Humic acid/polyvinyl alcohol-polypyrrole	106.9	2	47
HCNT-C4	191.07	2	48
S-BC40	201	3.5	49
HPR1	207	2	This work

---

Conclusions

In this study, an anion exchange hypercrosslinked resin was prepared by the copolymerization of divinylbenzene (DVB) and vinylbenzyl chloride (VBC) using a porogen agent. The incorporation of pyridine units occurred in a single step during the post-crosslinking reaction. Elemental analysis indicated that 43% of the chloromethyl groups reacted in the Friedel–Crafts alkylation reaction, which was further confirmed by FTIR and solid-state ¹³C NMR spectroscopy.

The resin HPR1 demonstrated a high adsorption capacity for Cr(VI) ions, particularly at acidic pH values. The nonlinear Langmuir isotherm model indicated a maximum adsorption capacity of 207 mg g⁻¹ at pH 2. Kinetic studies revealed that the adsorption rate was higher at pH 4 that at pH 2, whereas the overall adsorption process was most efficient at pH 2. Additionally, intraparticle diffusion was identified as the rate-limiting step in the adsorption mechanism. These findings underscore the potential of HPR1 to effectively treat industrial wastewater containing high concentrations of hexavalent chromium.

Data availability

https://doi.org/10.5061/dryad.p5hqbzkzv.

Author contributions

Cardoso Judith: funding acquisition, supervision, methodology. Ramírez-Arreola Daniel E: visualization, writing original draft, writing review and editing. Ortiz-Palacios, Jesús: investigation, writing original draft, writing review and editing, visualization, methodology.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Patricia Castillo for her invaluable assistance with Scanning electron microscopy. This research was financially supported by Secretaría de Educación, Ciencia, Tecnología e Innovación (Project SECTEI/288/2019/8994c19).

References

1. F. Fu and Q. Wang, J. Environ. Manage., 2011, 92, 407–418.
2. S. Rengaraj, C. K. Joo, Y. Kim and J. Yi, J. Hazard. Mater., 2003, 102, 257–275.
3. I. Campos, J. A. Álvarez, P. Villar, A. Pascual and L. Herrero, Environ. Technol., 2013, 34, 1267–1281.
4. H. Cui, M. Fu, S. Yu and M. K. Wang, J. Hazard. Mater., 2011, 186, 1625–1631.
5. S. Rengaraj, K. H. Yeon and S. H. Moon, J. Hazard. Mater., 2001, 87, 273–287.
6. L. Tian, G. Xie, R. X. Li, X. H. Yu and Y. Q. Hou, Desalin. Water Treat., 2011, 36, 334–343.
7. Y. Zeng, H. Woo, G. Lee and J. Park, Microporous Mesoporous Mater., 2010, 130, 83–91.
8. N. Balkaya and N. Bektasb, Desalin. Water Treat., 2009, 3, 43–49.
9. S. De Gisi, G. Lofrano, M. Grassi and M. Notarnicola, Sustain. Mater. Technol., 2016, 9, 10–40.
10. D. Mohan and C. U. Pittman, J. Hazard. Mater., 2006, 137, 762–811.
11. R. M. Schneider, C. F. Cavalin, M. A. S. D. Barros and C. R. G. Tavares, Chem. Eng. J., 2007, 132, 355–362.
12. N. T. Tavengwa, E. Cukrowska and L. Chimuka, Talanta, 2013, 116, 670–677.
13. M. A. Abdullah, L. Chiang and M. Nadeem, Chem. Eng. J., 2009, 146, 370–376.
14. N. Fontanals, R. M. Marcé and F. Borrull, Solid-Phase Extr., 2019, 55–82.
15. V. V. Azanova and J. Hradil, React. Funct. Polym., 1999, 41, 163–175.
16. D. C. Sherrington, Chem. Commun., 1998, 2275–2286.
17. C. Cai, Z. Hou, T. Huang, K. Li, Y. Liu, N. Fu, S. Han and Y. Zhou, Macromol. Chem. Phys., 2017, 218, 1–6.
18. S. Shen, X. Zhang and L. Fan, Mater. Lett., 2008, 62, 2392–2395.
19. L. Tan and B. Tan, Chem. Soc. Rev., 2017, 46, 3322–3356.
20. M. P. Tsyurupa and V. A. Davankov, React. Funct. Polym., 2002, 53, 193–203.
21. R. Castaldo, G. Gentile, M. Avella, C. Carfagna and V. Ambrogi, Polymers, 2017, 9(12), 651.
22. Y. Xie, J. Lin, J. Liang, M. Li, Y. Fu, H. Wang, S. Tu and J. Li, Chem. Eng. J., 2019, 378, 122107.
23. G. Xiao, R. Wen, A. Liu, G. He and D. Wu, J. Hazard. Mater., 2017, 329, 77–83.
24. L. Shao, M. Liu, J. Huang and Y. N. Liu, J. Colloid Interface Sci., 2018, 513, 304–313.
25. W. Kuang, Y. N. Liu and J. Huang, J. Colloid Interface Sci., 2017, 487, 31–37.
26. T. Zhang and J. Huang, J. Colloid Interface Sci., 2017, 505, 383–391.
27. J. Germain, J. M. J. Fréchet and F. Svec, J. Mater. Chem., 2007, 17, 4989–4997.
28. D. Bratkowska, N. Fontanals, F. Borrull, P. A. G. Cormack, D. C. Sherrington and R. M. Marcé, J. Chromatogr. A, 2010, 1217, 3238–3243.
29. K. Wieszczycka, K. Filipowiak, I. Wojciechowska and P. Aksamitowski, Sep. Purif. Technol., 2020, 236, 116313.
30. X. Wang, H. Ou and J. Huang, J. Colloid Interface Sci., 2019, 538, 499–506.
31. Y. S. Ho, J. Hazard. Mater., 2006, 136, 681–689.
32. T. W. Weber and R. K. Chakravorti, AIChE J., 1974, 20, 228–238.
33. M. H. Armbruster and J. B. Austin, J. Am. Chem. Soc., 1938, 60, 467–475.
34. G. Crini, H. N. Peindy, F. Gimbert and C. Robert, Sep. Purif. Technol., 2007, 53, 97–110.
35. N. Fontanals, J. Cortés, M. Galià, R. M. Marcé, P. A. G. Cormack, F. Borrull and D. C. Sherrington, J. Polym. Sci. Part A Polym. Chem., 2005, 43, 1718–1728.
36. A. V. Pastukhov, M. P. Tsyurupa and V. A. Davankov, J. Polym. Sci. Part B Polym. Phys., 1999, 37, 2324–2333.
37. Q. B. Meng, G. S. Yang and Y. S. Lee, Microporous Mesoporous Mater., 2013, 181, 222–227.
38. H. A. Ezzeldin, A. Apblett and G. L. Foutch, Int. J. Polym. Sci., 2010, 2010(1), 684051.
39. S. Mor, K. Ravindra and N. R. Bishnoi, Bioresour. Technol., 2007, 98, 954–957.
40. X. Sun, Q. Li, L. Yang and H. Liu, Particuology, 2016, 26, 79–86.
41. B. Pan, B. Pan, W. Zhang, L. Lv, Q. Zhang and S. Zheng, Chem. Eng. J., 2009, 151, 19–29.
42. R. D. C. Soltani, G. S. Khorramabadi, A. R. Khataee and S. Jorfi, J. Taiwan Inst. Chem. Eng., 2014, 45, 973–980.
43. S. K. Singh, T. G. Townsend, D. Mazyck and T. H. Boyer, Water Res., 2012, 46, 491–499.
44. D. G. Trikkaliotis, A. K. Christoforidis, A. C. Mitropoulos and G. Z. Kyzas, Carbohydr. Polym., 2020, 234, 115890.
45. M. S. Samuel, Int. J. Biol. Macromol., 2019, 121, 285.
46. S. Revathi, M. Amanullah, A. S. Al-Samghan, J. J. Joseph, P. Pazhanisamy, M. Addich and T. Gomathi, Int. J. Biol. Macromol., 2024, 278, 134769.
47. X. Zhang, Y. Li, W. Zou, L. Ding and J. Chen, J. Inorg. Organomet. Polym. Mater., 2024, 34(2), 745–758.
48. X. Liu, Z. Zhu, X. Wang, J. Yang, Y. Zhang, X. Yan and S. Qin, Environ. Res., 2024, 263, 119980.
49. K. Huangmee, L. C. Hsu, Y. M. Tzou, Y. L. Cho, C. H. Liao, H. Y. Teah and Y. T. Liu, J. Environ. Manage., 2024, 360, 12074.

---