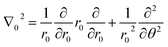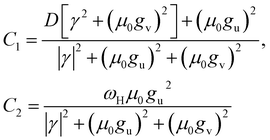DOI:
10.1039/D5RA00635J
(Paper)
RSC Adv., 2025,
15, 6854-6862
Radially evolving spiral wave patterns in the Gierer–Meinhardt reaction–diffusion system†
Received
27th January 2025
, Accepted 25th February 2025
First published on 3rd March 2025
Abstract
Spiral wave formation in spatially extended systems is a fascinating phenomenon that has garnered significant attention in reaction–diffusion systems. In this study, we explore the emergence of spiral wave-like patterns in the Gierer–Meinhardt reaction–diffusion model. By employing a multiple-time scale perturbation technique, we derive amplitude equations that reveal the conditions for spiral wave formation. Notably, our analysis shows that the amplitude of these spiral waves varies with the radial distance, introducing a distinctive feature to this pattern. Our theoretical predictions are further substantiated by numerical simulations, which confirm the emergence of spiral wave structures and validate the distinct radial dependence of their amplitude.
1 Introduction
Self-organized pattern formation, one of the most captivating out-of-equilibrium phenomena, has drawn immense attention over recent decades. Beyond biological systems, such phenomena have been observed in a wide variety of chemical and physical systems.1,2 Alan Turing's pioneering work on reaction–diffusion systems, which proposed diffusion-driven instability in activator–inhibitor kinetics as the fundamental mechanism behind self-organization, has laid the foundation for extensive research in this field.3,4 This framework has revealed a plethora of spatiotemporal structures, such as stripes, spots, traveling waves, labyrinthine patterns, and others, both experimentally5–7 and theoretically.8–10 Among these, spiral wave patterns stand out as a particularly fascinating example of spatiotemporal organization.
A spiral wave is a two-dimensional structure that propagates either outward from or inward toward a central core, forming a characteristic spiral geometry. The Belousov–Zhabotinsky (BZ) reaction, a classical example of a homogeneous reaction–diffusion system, has been widely studied for its ability to generate oscillatory behavior and spatially extended patterns such as spiral and target waves. The first experimental observation of spiral waves was achieved in the Belousov–Zhabotinsky (BZ) reaction,11–14 followed by similar findings in other chemical systems such as the sodium silicate–cobalt chloride reaction,15 the photosensitive chlorine dioxide iodine malonic acid reaction.16 Similarly, heterogeneous autocatalytic reactions, including the oxidation of CO on platinum surfaces, exhibit rich spatiotemporal dynamics governed by reaction–diffusion mechanisms.17 Beyond these, precipitating reaction–diffusion systems have also been shown to produce intricate patterns, including Liesegang rings and reaction-driven waves, which share similarities with spiral and target waves observed in classical reaction–diffusion models.18–21 In electrochemical and metal co-deposition systems, reaction–diffusion dynamics play a crucial role in the formation of complex spatiotemporal structures, including spiral waves and target patterns, influenced by the coupling between reaction kinetics and mass transport.22–24
Spiral waves have also been observed in numerous biological processes, including the aggregation of slime molds,25 the development of frog eggs,26 cardiac arrhythmias,27 fertilized starfish eggs,28 and dense bacterial populations,29 among others. From a theoretical perspective, various reaction–diffusion models have successfully captured spiral wave dynamics. These include chemical models such as the Oregonator model for the BZ reaction,30,31 the CDIMA reaction–diffusion model,8,32,33 and the delayed-feedback induced spiral in Brusselator model.34 Similarly, biological self-organization processes have been described using models such as the FitzHugh–Nagumo,35,36 Hastings–Powell,37 and Decroly–Goldbeter38 models. The Gierer–Meinhardt (GM) model is another widely studied reaction–diffusion framework, originally developed to elucidate spatial pattern formation during morphogenesis.39 This model has been instrumental in simulating a range of patterns, including spots, stripes, combinations of spots and stripes,40–43 as well as traveling wave-like patterns.44 However, the dynamics of spiral waves within the GM model remain underexplored, particularly from a numerical analysis perspective. Bhattacharyay et al.45 analytically demonstrated the potential for spiral and target wave formation in the GM system using multiple-scale analysis. However, numerical validation of these insights is lacking, highlighting the need for further investigation. These diverse systems highlight the universality of RD-driven pattern formation and motivate further investigation into the underlying mechanisms that govern the emergence of novel structures. Understanding the conditions under which these patterns arise, particularly the variation of spiral wave amplitudes or frequency modulation, has broad implications for nonlinear chemical dynamics, biological morphogenesis, and materials science.
In this study, we undertake a comprehensive exploration of spiral wave dynamics in the GM reaction–diffusion system from both analytical and numerical perspectives. Employing the multiple-scale analysis technique,45–48 a weakly nonlinear analysis, we derive amplitude equations to elucidate the conditions for spiral wave formation. To corroborate these analytical findings, we perform numerical simulations and examine the emergence of spiral waves under both zero-flux and periodic boundary conditions. Furthermore, we investigate the dependence of spiral wave formation on domain size and grid resolution, to ensure the robustness of the spiral waves providing deeper insights into the system's behavior. Remarkably, our findings reveal the existence of amplitude variations of the developed spiral waves in GM model, radially-varying spiral wave patterns, a phenomenon not previously reported to the best of our knowledge. The derived amplitude equations predict this unique behavior, offering valuable insights into the radially-evolving spiral wave dynamics in the GM model. This distinctive characteristic sets our study apart from existing research on spiral wave dynamics and highlights the novel contributions of our work. Understanding the variation of spiral wave amplitudes in reaction–diffusion (RD) systems is essential for advancing multiple scientific fields. In nonlinear chemical dynamics, such variations reveal instabilities and mode selection, refining models of self-organization in chemical systems. In biological morphogenesis, they influence processes like cell signaling, cardiac waves, and tissue development, with implications for disease modeling. In materials science, amplitude variations impact pattern formation in electrochemical and metal co-deposition systems, affecting surface morphology, nanoscale fabrication, and corrosion control. Similarly, in precipitating RD systems, they offer pathways for designing ordered material structures with specific functionalities.
2 The model
In this study, we consider the two-variable Gierer–Meinhardt (GM) model,39,40 which was originally proposed to describe the emergence of spatial patterns in tissue structures, starting from nearly homogeneous conditions during embryological development and regeneration. The model builds upon Alan Turing's groundbreaking concept of reaction–diffusion systems, specifically emphasizing the autocatalytic behavior of an activator and the cross-catalytic inhibition mediated by an inhibitor. The governing equations of the original two-variable GM model are given as follows:| |
 | (1a) |
| |
 | (1b) |
Here, U and V represent the concentration of the activator and inhibitor species, respectively, and thus have the dimension of concentration. In accordance with the activator–inhibitor dynamics of a reaction–diffusion system, the activator species promotes the production of both itself and the inhibitor, while the inhibitor suppresses the activator's production. The term 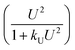 captures the saturable nature of activator production, with kU serving as the saturation constant. The parameters σU and σV are the basic production term of the activator and inhibitor, respectively, while the removal rates of the two species are represented by μU, μV. ρU and ρV are the cross-reaction coefficients and are related to the product of the rate constant and source densities of the activator and inhibitor species, respectively. The diffusion coefficients for the activator and inhibitor are denoted by DU and DV. Although this model was originally proposed to explain the development of spatial patterns in tissue structures during morphogenesis, it can also describe spatiotemporal pattern formation observed in various chemical systems. To reduce the complexity of the equation, we set the saturation constant (kU) and the basic production term of the inhibitor (σV) to zero in the current investigation.40 This scenario closely resembles a chemical reaction occurring in a continuously stirred tank reactor (CSTR),49 where reactants and products are continuously introduced and removed. During these reactions, intermediate species50 generated in the system act as activator and inhibitor components. The following dimensionless quantities have been introduced to render the overall eqn (1) dimensionless:
captures the saturable nature of activator production, with kU serving as the saturation constant. The parameters σU and σV are the basic production term of the activator and inhibitor, respectively, while the removal rates of the two species are represented by μU, μV. ρU and ρV are the cross-reaction coefficients and are related to the product of the rate constant and source densities of the activator and inhibitor species, respectively. The diffusion coefficients for the activator and inhibitor are denoted by DU and DV. Although this model was originally proposed to explain the development of spatial patterns in tissue structures during morphogenesis, it can also describe spatiotemporal pattern formation observed in various chemical systems. To reduce the complexity of the equation, we set the saturation constant (kU) and the basic production term of the inhibitor (σV) to zero in the current investigation.40 This scenario closely resembles a chemical reaction occurring in a continuously stirred tank reactor (CSTR),49 where reactants and products are continuously introduced and removed. During these reactions, intermediate species50 generated in the system act as activator and inhibitor components. The following dimensionless quantities have been introduced to render the overall eqn (1) dimensionless:
Substituting these transformations, eqn (1) becomes:
| |
 | (2a) |
| |
 | (2b) |
Here,

,

, and

are dimensionless parameters. Setting the reaction terms in
eqn (2) to zero provides the system's homogeneous steady state, given by (
uss,
vss) = [(1 +
σ), (1 +
σ)
2].
2.1 Linear stability analysis: Hopf and Turing instability
We performed a systematic linear stability analysis around the homogeneous steady state of the system in the absence of diffusion. This analysis provides the condition for Hopf bifurcation in the parameter space as  . The Hopf bifurcation curve separates the parameter space into regions of temporally stable and unstable states. Subsequently, we carried out the stability analysis of the spatially extended GM model around the homogeneous steady state in the presence of diffusion. This yields the Turing condition as:
. The Hopf bifurcation curve separates the parameter space into regions of temporally stable and unstable states. Subsequently, we carried out the stability analysis of the spatially extended GM model around the homogeneous steady state in the presence of diffusion. This yields the Turing condition as:  . The Turing curve divides the parameter space into two regions, indicating the presence of diffusion-driven instability. Fig. 1 illustrates the corresponding bifurcation diagram for a fixed value of D = 0.25 in the μ vs. σ parameter space. The three distinct regions, marked with different colors, represent the relevant spatiotemporal instabilities identified through linear stability analysis. Based on prior literature,48 the oscillatory region near the Turing curve will be our primary focus for spiral wave formation.
. The Turing curve divides the parameter space into two regions, indicating the presence of diffusion-driven instability. Fig. 1 illustrates the corresponding bifurcation diagram for a fixed value of D = 0.25 in the μ vs. σ parameter space. The three distinct regions, marked with different colors, represent the relevant spatiotemporal instabilities identified through linear stability analysis. Based on prior literature,48 the oscillatory region near the Turing curve will be our primary focus for spiral wave formation.
 |
| | Fig. 1 Bifurcation diagram obtained from linear stability analysis of eqn (2) of the GM model for the parameter values: D = 0.25. The region above and below the Hopf curve (green line) represents temporally stable and unstable regions, respectively. The region above and below the Turing curve (blue line) represents spatially stable and unstable regions, respectively. | |
3 Derivation of amplitude equation for spiral waves: a multiple timescale based analysis
To explore the existence of spiral wave solutions in the spatially extended system, we employ the well-established multiple-scale perturbation technique, as mentioned earlier. The multiple time-scale perturbation method is a well-established technique within the broader framework of weakly nonlinear analysis (WNL). It has been successfully applied to predict the emergence of target and spiral waves, as well as other spatiotemporal instabilities, in various reaction–diffusion systems, including biological morphogenesis,45 the chlorine dioxide–iodine–malonic acid system,46,47 and prey-predator models.48,51 This method allows for the systematic derivation of amplitude equations governing spiral wave formation near the bifurcation. Additionally, other weakly nonlinear analysis techniques have been effectively used to study the emergence of spiral waves, Turing patterns, and other spatiotemporal structures in electrochemical and metal co-deposition systems.23,52 The general reaction–diffusion equations for the Gierer–Meinhardt (GM) model, as described in Section 2, are given by:| |
 | (3a) |
| |
 | (3b) |
Here, μ serves as our control bifurcation parameter, determining how far we can move from the Hopf curve to achieve the spiral wave-like structure. As done earlier when deriving the Hopf and Turing conditions, we introduce a small perturbation [δu(x,y,t), δv(x,y,t)] around the system's homogeneous steady state (uss,vss). The key distinction in this instance lies in how this small perturbation is expressed, which will now follow the framework of multiple scales. Performing a Taylor series expansion of the reaction terms and neglecting higher-order terms, eqn (3) reduces to the following linearized form:| |
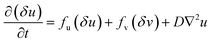 | (4a) |
| |
 | (4b) |
where fu, fv, gu, and gv are the partial derivatives of the reaction terms with respect to u and v, evaluated at the steady state.
We expand the control parameter μ around the Hopf bifurcation point (μ0) as μ = μ0 + εμ1, where 0 < ε < 1. The choice of ε is not unique, so our focus will be on deriving the expression for εμ1 as a whole. This provides valuable information regarding how far from the Hopf curve the spiral solution can be observed. Given the intrinsic spiral nature of the solution, it is advantageous to work in polar coordinates. Thus, we scale the spatial coordinates in two dimensions (polar coordinates) as θ = ε1/2θ1 and r = r0 + εr1. Similarly, the time variable is written as t = t0 + ετ. The perturbations (δu,δv) are expanded in the following form:
Substituting these expressions into eqn (4) we get:
| |
 | (6) |
| |
 | (7) |
where,
Next, we collect the coefficients of O(ε) from both sides of eqn (6) and (7), yielding the following equations:
| |
 | (8) |
Now, since the spirals are observed near the Hopf bifurcation threshold, we assume the trial solution (u1,v1) to take the following form:
| |
 | (9) |
where
A(
r1,
θ1,
τ) is the amplitude function, and (
ū1,
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 1
1) are the eigenvectors corresponding to the eigenvalue
γ. The eigenvalue (
γ) can be obtained by solving
eqn (8) in the absence of the diffusion terms. The corresponding solution for
γ is given as:
| |
 | (10) |
From this equation, we may infer that when (fu + μ0gv) > 0, the growth rate γ will increase. This condition allows us to determine the Hopf curve as:
| |
 | (11) |
This result is consistent with our earlier expression for the Hopf curve. Additionally, we obtain the Hopf frequency as:
| |
 | (12) |
Furthermore, substituting the trial solution eqn (9) into eqn (8), we can explicitly solve for ū1 and ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 1. Consequently, the explicit form of the trial solution becomes:
1. Consequently, the explicit form of the trial solution becomes:
| |
 | (13) |
Next, we seek the higher-order terms, O(ε2). As before, we compare the coefficients of ε2 from both sides of the governing equations. This yields the following set of equations:
| |
 | (14) |
The operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) acts on u1 and v1 in eqn (8), leading to zero eigenvalues. However, in eqn (14), a non-trivial term arises on the right-hand side due to the action of the operator
acts on u1 and v1 in eqn (8), leading to zero eigenvalues. However, in eqn (14), a non-trivial term arises on the right-hand side due to the action of the operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) on u2 and v2. Therefore, the solvability criterion (Fredholm theorem) must be applied. According to this condition, the right-hand side of eqn (14) must be orthogonal to the left eigenvector of
on u2 and v2. Therefore, the solvability criterion (Fredholm theorem) must be applied. According to this condition, the right-hand side of eqn (14) must be orthogonal to the left eigenvector of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) corresponding to the zero eigenvalue. This condition ultimately leads to the following equation:
corresponding to the zero eigenvalue. This condition ultimately leads to the following equation:
| |
 | (15) |
where,

and

are the complex conjugate of
u1 and
v1, respectively. Expanding
eqn (15) leads to the following equation:
| |
 | (16) |
Since the amplitude (A) depends on r1, θ1, and t, we revert to the original scale. Ultimately, we obtain the dynamics of the amplitude as follows:
| |
 | (17) |
Here,
To solve eqn (17), we assume a generic solution for the spiral wave53,54 of the form:
| |
 | (18) |
where
Ā(
r) is the amplitude of the spiral,
η is the growth rate of the spiral,
ω is the angular frequency,
ψ(
r) determines the type of spiral, and
m is the number of arms on the spiral. The sign of
m governs the direction of rotation:
m = +1 for an anticlockwise spiral wave rotating clockwise, and
m = −1 for a clockwise spiral wave rotating counterclockwise.
Substituting eqn (18) into eqn (17) and comparing the real and imaginary components, we obtain:
| |
 | (19) |
| |
 | (20) |
It follows from eqn (19) that if the amplitude (A(r)) varies with respect to r, there is a possibility that the spiral's growth rate (η) will be positive. Our analysis predicts the formation of spiral waves with varying amplitude, a feature that aligns with the general predictions of WNL theory. However, while our approach confirms the existence of amplitude variations, it does not fully resolve the nature of the amplitude evolution in space and time. Nonetheless, our results demonstrate that if a spiral wave forms, it will inherently exhibit a radially varying amplitude. Additionally, a spiral with a nonzero frequency requires that eqn (20) be satisfied. Assuming that the spiral type does not change significantly with respect to r, then we can approximate  . In this case, eqn (20) can be simplified and expressed as:
. In this case, eqn (20) can be simplified and expressed as:
| |
 | (21) |
Finally, we can infer that, in addition to the spiral's amplitude fluctuating with r, if eqn (21) is satisfied, a fully developed spiral wave can be observed. Since ωH represents the Hopf frequency of homogeneous oscillation in this case, we can consider it as a zero-order approximation of the spiral's natural frequency ω. Consequently, ωH can be equated to ω within a numerical factor ζ, such that ω = ζωH. Using this relation, eqn (21) can be written as:
| |
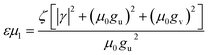 | (22) |
To compare with the numerical findings, we must now determine the value of eqn (22). The only unknown term is ζ. First, we use the formula (μ − μ0) to determine the value of εμ1 numerically. Where μ0 is the Hopf curve  and μ is the numerical value at which the first spiral arises. Once we have the value of εμ1 eqn (22) allows us to determine the value of ζ using this value along with the other parameters. Keeping ζ constant for the rest of the parameter set, we can then compare the value of εμ1 value obtained from eqn (22) with the numerical simulations.
and μ is the numerical value at which the first spiral arises. Once we have the value of εμ1 eqn (22) allows us to determine the value of ζ using this value along with the other parameters. Keeping ζ constant for the rest of the parameter set, we can then compare the value of εμ1 value obtained from eqn (22) with the numerical simulations.
4 Numerical analysis
We conducted detailed numerical simulations of eqn (2a) and (2b) for parameter values within the oscillatory region near the Turing curve, as shown in Fig. 1. The explicit Euler method was used for numerical integration, with spatial and temporal discretization. The simulations were performed on a finite system of size Lx = Ly = 200 with a grid size of δx = δy = 1 and a time step of dt = 0.001. A zero-flux boundary condition was applied throughout the simulations unless otherwise specified. To initiate the dynamics, the system was perturbed at the center of the domain (10 × 10 mesh) by introducing ±1% random noise around the homogeneous steady state, ensuring the breaking of spatial symmetry. Numerical simulations confirm the feasibility of obtaining spiral waves in the system. Fig. 2(a) shows the concentration profile of the activator (u) for the parameter values D = 0.25, σ = 0.2, and μ = 0.37. The corresponding time evolution of the activator concentration at a fixed point (100, 100) is presented in Fig. 2(b), from which the spiral's frequency was determined to be ≈0.0765. A detailed video representation, available in SM (Movie 1), illustrates the observed spiral's temporal dynamics-rotating inwardly in an anticlockwise direction while spatially exhibiting a clockwise geometry.
 |
| | Fig. 2 (a) Numerically simulated concentration profile for the activator concentration (u) obtained by solving eqn (2a) and (2b) shows the emergence of a spiral wave-like structure for the parameter values D = 0.25, μ = 0.37, and σ = 0.2. Domain size of the square box (200 × 200), grid spacing (δx = δy) = 1.0, time step (dt) = 0.001. In the colorbar, the dark blue region represents a low concentration value, while the yellow region demonstrates a high concentration. (b) The corresponding time profile for a fixed point of (100, 100) of (a). Temporal frequency of oscillation is found to be ≈0.0765. | |
A closer examination of the spiral wave pattern reveals that its amplitude is not constant with respect to the radial distance r. Notably, one of the insights derived from the analytical investigation suggests that the spiral's amplitude must vary with r for it to grow. To better visualize this behavior, Fig. 3(a) provides a contour diagram of the activator concentration (u), highlighting regions where amplitude changes are most prominent. To further elucidate, Fig. 3(b) displays heatmaps of the spiral arm's concentration profile for two specific regions, A and B, marked by blue arrows in Fig. 3(a), extending from the spiral perimeter toward the core. The differing color intensities between regions A and B indicate a clear variation in the spiral's amplitude with respect to r, corroborating the analytical predictions. Interestingly, there are only a few documented instances where the amplitude of spiral waves varies with respect to the radial distance r. Elmegreen et al.55 observed variations in spiral arm amplitude in the grand design galaxies M51, M81, and M100. Beyond amplitude fluctuations, Li et al.56 demonstrated the formation of dense-sparse and sparse-dense spiral waves in complex Ginzburg–Landau reaction–diffusion systems, where the breadth of the spiral arm changes with r. As far as reaction–diffusion systems are concerned, our study is the first to demonstrate the emergence of spirals with variable amplitude with respect to r.
 |
| | Fig. 3 (a) Colored contour diagram of spiral wave for the activator concentration (u) for the parameter values D = 0.25, μ = 0.37, and σ = 0.2. Two regions highlighted with a white dotted line demonstrate the region where there is a change of amplitude with respect to radial distance (r). rc is the perpendicular distance from the periphery of the spiral arm towards the inner side. How the r increases for a spiral is indicated by the black arrow line. (b) Represents the heatmap for two regions, A and B, on the spiral arms and how their color is changing with rc. Since the color of the heatmap is not equivalent, it indicates that there is a change of the spiral's amplitude with respect to r. | |
In the following stage, we wish to numerically test the analytical prediction for obtaining a spiral for those εμ1 values that satisfy eqn (22). To achieve this, we first present the theoretical εμ1 values for various σ values (which are associated with the source densities of the inhibitor and activator concentrations). In Fig. 4, we provide the corresponding diagram in the εμ1 vs. σ parameter space with a solid curve. To obtain spiral wave patterns, μ is suitably adjusted numerically as the σ value is varied. By subtracting μ0 from μ (numerical), the numerical values of εμ1 are determined. For various values of σ, these are represented by the triangular points in Fig. 4. This diagram clearly demonstrates that the predictions derived from analytical calculations align well with our numerical simulations. Furthermore, we have computed numerically the frequency (νs) of the spiral obtained for various σ and εμ1 combinations. It is worth noting that we observed a nearly linear decrease in frequency values with respect to both σ and εμ1. The dependence of frequency values on εμ1 further corroborates our analytical claim in eqn (21). Fig. 5 displays the associated diagram. Blue triangular points in the curve indicate the dependence of frequency values on εμ1, whereas green circular points in the curve indicate the dependence of frequency values on σ.
 |
| | Fig. 4 Bifurcation curves of analytical prediction and numerical simulations in the εμ1 vs. σ parameter space. Other parameter is D = 0.25. The green solid line represents the prediction obtained from analytical analysis. Blue triangle points depict the points where numerically spirals have been observed. The diagram shows a well-matching between the analytical predictions and numerical simulations. | |
 |
| | Fig. 5 Numerically estimated frequency (νs) values for different spirals perceived for various combinations of εμ1 and σ values. The blue triangle points depict how the frequency values are changing with respect to the numerically calculated εμ1, whereas the green circular points represent how the frequency is varying with respect to the σ values. | |
Now, we aim to analyze the influence of domain size, grid spacing, and boundary conditions, which are critical characteristics for maintaining spiral waves, as highlighted in a previous study.8
4.1 Effect of system size, spatial grid length and boundary condition
We first investigate the impact of box size while maintaining a fixed grid spacing. Numerical simulations reveal that increasing the box length from 200 to 800 significantly affects the formed spiral, even with the same grid spacing (δx = δy = 1.0). With a larger box length, numerous spiral sources emerge, some rotating counterclockwise and others clockwise. Furthermore, neighboring spirals continuously annihilate each other and form new ones. Notably, for a box size of 300 (Movie 2 in SM), all spiral sources rotate counterclockwise. However, for larger boxes (L = 400, 800), both clockwise and counterclockwise rotating spirals appear (Movie 3 and Movie 4 in SM). The corresponding spatial patterns are shown in Fig. 6, where it is evident that with a box size of 300, four spiral sources emerge [Fig. 6(a)], whereas for a box size of 800, the number of spiral sources increases significantly [Fig. 6(c)].
 |
| | Fig. 6 Effect of box size on the formations of the spiral patterns for a fixed grid spacing (δx = δy = 1.0): numerically simulated concentrated profile for activator u for box size-(a) Lx = Ly = 300, (b) Lx = Ly = 400, and (c) Lx = Ly = 800. Other parameter values are D = 0.25, μ = 0.37, and σ = 0.2. With increasing box size, multiple spiral sources arise in the system. | |
Next, keeping the box length (Lx = Ly = 200) fixed, we vary the grid spacing (δx = δy) for the numerical simulations. We find that spirals can form even with smaller grid spacings, though in this case, multiple spiral sources appear, similar to the behavior observed with larger box sizes. Additionally, spiral annihilation and formation occur simultaneously. This differs from the case of larger grid spacing (δx = 1.0), where the system tends to maintain a single spiral wave. Finally, we applied periodic boundary conditions in our numerical simulations to assess the effect of boundary conditions on spiral waves. The systematic modification of box sizes, grid spacing, and initial random perturbation of the box domain consistently led to the formation of spiral waves. However, in none of the cases did we observe a single spiral wave. Instead, multiple spiral sources, with both clockwise and counterclockwise rotation, always appeared in the system. Remarkably, in all of these instances, the spirals formed consistently exhibited amplitude fluctuations as a function of radial distance (r). These observations strongly support our analytical conclusion that the amplitude of the spiral must change with respect to the radial distance in order for it to grow highlighting a novel and unique aspect of the system's spatiotemporal dynamics.
While our study primarily focuses on theoretical and numerical aspects, we recognize the importance of linking our findings to experimentally realizable systems. Spiral waves have been observed in a variety of reaction–diffusion systems, including the classic Belousov–Zhabotinsky (BZ) reaction, electrochemical deposition processes, and biological systems such as cardiac tissue and cell signaling networks. However, most reported spiral waves in these contexts exhibit nearly constant amplitudes. The amplitude variation we predict could potentially be observed in experimental systems with specific kinetic and diffusion properties and suitable boundary conditions. In particular, electrochemical systems and metal co-deposition processes,23,52 where diffusion anisotropy, kinetic feedback mechanisms and boundary effects play a crucial role, may provide a suitable testbed for verifying our findings.
5 Concluding remarks
In this work, we have explored the dynamics of spiral waves in the Gierer–Meinhardt (GM) reaction–diffusion model. Despite extensive studies of this model over the years,39–44 the numerical observation of spiral wave-like patterns has not been thoroughly investigated. We employed the multiple-scale analysis perturbative technique to analytically establish the possibility of spiral wave formation. Our analytical results indicate that if the amplitude of the spiral varies with the radial distance, the spiral will grow positively. Additionally, we derived a condition that defines the spatial extent within which the spiral pattern can emerge from the Hopf bifurcation zone.
Our comprehensive numerical analysis of the GM reaction–diffusion model corroborates the theoretical predictions. In all numerically simulated spirals, we observed that the amplitude changes with respect to the radial distance (r). Our findings confirm that the observed amplitude variation is not an artifact of numerical discretization or initial conditions. To ensure the robustness of our results, we performed extensive numerical checks by varying the discretization schemes, using different grid sizes, and altering the domain sizes. Additionally, we tested a range of initial conditions and consistently observed the emergence of spiral waves with varying amplitude. These checks validate that the amplitude modulation is an intrinsic feature of the system rather than a numerical anomaly. Intriguingly, the observed spiral consistently exhibited amplitude modulation as a function of r, regardless of the variations in simulation parameters. This phenomenon, to the best of our knowledge, has not been previously documented in any reaction–diffusion system.
This work not only demonstrates the feasibility of generating spiral waves in the GM reaction–diffusion model but also highlights the potential for creating a novel class of spirals with variable amplitude, opening avenues for further exploration in reaction–diffusion systems. The variation of spiral wave amplitudes in reaction–diffusion (RD) systems is a crucial aspect of pattern formation that can have significant implications across multiple scientific domains:
5.1 Nonlinear chemical dynamics
Spiral waves are fundamental structures in RD systems, and their amplitude variations can indicate underlying instabilities, mode selection, or the influence of external perturbations. Understanding these variations helps refine theoretical models of chemical oscillations and pattern formation, which are essential for predicting and controlling self-organization in synthetic and natural chemical systems.
5.2 Biological morphogenesis
Many biological processes, such as cell signaling, tissue development, and neural activity, involve RD-based mechanisms. Amplitude variations in spiral waves could influence how biochemical signals propagate in systems like calcium waves in cells, cardiac electrical waves, and embryonic development. Recognizing these effects could improve models of morphogenesis and disease states (e.g., cardiac arrhythmias linked to spiral wave instabilities).
5.3 Materials science
In electrochemical and metal co-deposition systems, spiral waves and other RD patterns influence the deposition morphology and material properties. Understanding amplitude variations can provide insights into the control of surface structures, leading to advances in material fabrication techniques, corrosion prevention, and nanoscale patterning. Similarly, in precipitating RD systems, controlling these variations could allow for the design of ordered structures with specific functionalities.
By studying the mechanisms governing amplitude variations in spiral waves, we gain deeper insights into pattern robustness, stability, and the interplay between reaction kinetics and diffusion. This knowledge not only advances fundamental science but also has potential applications in designing controllable self-organizing systems across chemistry, biology, and materials engineering.
Data availability
The data supporting this article have been included as part of the ESI.†
Author contributions
Tarpan Maiti and Achal Jadhav contributed equally to this study.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Tarpan Maiti thanks Ministry of Education (MoE) of India for the PMRF. Achal Jadhav thanks IISER Thiruvananthapuram (IISERTVM) for the Institute fellowship. Pushpita Ghosh acknowledges Start-up Research Grant (No. SRG/2022/000043) by Science and Engineering Research Board (SERB), India. All the authors acknowledge IISERTVM for the computational resources.
Notes and references
- I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos, Oxford University Press, New York, 1998 Search PubMed.
- M. Cross and H. Greenside, Pattern Formation and Dynamics in Nonequilibrium Systems, Cambridge University Press, 2009 Search PubMed.
- A. M. Turing, Philos. Trans. R. Soc., B, 1952, 237, 37–72 Search PubMed.
- M. C. Cross and P. C. Hohenberg, Rev. Mod. Phys., 1993, 65, 851–1112 CrossRef CAS.
- V. Castets, E. Dulos, J. Boissonade and P. De Kepper, Phys. Rev. Lett., 1990, 64, 2953 CrossRef CAS PubMed.
- B. Rudovics, E. Barillot, P. Davies, E. Dulos, J. Boissonade and P. De Kepper, J. Phys. Chem. A, 1999, 103, 1790–1800 CrossRef CAS.
- I. Berenstein, L. Yang, M. Dolnik, A. M. Zhabotinsky and I. R. Epstein, Phys. Rev. Lett., 2003, 91, 058302 CrossRef PubMed.
- P. Ghosh, Phys. Rev. E, 2019, 100, 042217 CrossRef CAS PubMed.
- T. Maiti and P. Ghosh, J. Chem. Phys., 2022, 157, 224907 CrossRef CAS PubMed.
- T. Maiti and P. Ghosh, J. Chem. Phys., 2023, 159, 174902 CrossRef CAS PubMed.
- A. Zaikin and A. Zhabotinsky, Nature, 1970, 225, 535–537 CrossRef CAS PubMed.
- A. T. Winfree and W. Jahnke, J. Phys. Chem., 1989, 93, 2823–2832 CrossRef CAS.
- T. Plesser, S. C. Mueller and B. Hess, J. Phys. Chem., 1990, 94, 7501–7507 CrossRef CAS.
- S. Dutta and O. Steinbock, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 83, 056213 CrossRef PubMed.
- F. Haudin, J. H. Cartwright, F. Brau and A. De Wit, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17363–17367 CrossRef CAS PubMed.
- I. Berenstein, A. P. Muñuzuri, L. Yang, M. Dolnik, A. M. Zhabotinsky and I. R. Epstein, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 78, 025101 CrossRef PubMed.
- S. Nettesheim, A. Von Oertzen, H. Rotermund and G. Ertl, J. Chem. Phys., 1993, 98, 9977–9985 CrossRef CAS.
- A. Volford, F. Izsák, M. Ripszám and I. Lagzi, Langmuir, 2007, 23, 961–964 CrossRef CAS PubMed.
- M. R. Tinsley, D. Collison and K. Showalter, J. Phys. Chem. A, 2013, 117, 12719–12725 CrossRef CAS PubMed.
- M. M. Ayass, M. Al-Ghoul and I. Lagzi, J. Phys. Chem. A, 2014, 118, 11678–11682 CrossRef CAS PubMed.
- M. M. Ayass, I. Lagzi and M. Al-Ghoul, Phys. Chem. Chem. Phys., 2015, 17, 19806–19814 Search PubMed.
- B. Bozzini, D. Lacitignola and I. Sgura, Math. Biosci. Eng., 2010, 7, 237–258 Search PubMed.
- B. Bozzini, D. Lacitignola, C. Mele and I. Sgura, Acta Appl. Math., 2012, 122, 53–68 Search PubMed.
- B. Bozzini, D. Lacitignola and I. Sgura, J. Solid State Electrochem., 2013, 17, 467–479 Search PubMed.
- F. Siegert and C. Weijer, J. Cell Sci., 1989, 93, 325–335 CrossRef CAS.
- P. Camacho and J. D. Lechleiter, Science, 1993, 260, 226–229 CrossRef CAS PubMed.
- R. A. Gray and J. Jalife, Int. J. Bifurc. Chaos Appl. Sci., 1996, 6, 415–435 Search PubMed.
- T. H. Tan, J. Liu, P. W. Miller, M. Tekant, J. Dunkel and N. Fakhri, Nat. Phys., 2020, 16, 657–662 Search PubMed.
- S. Liu, Y. Li, Y. Wang and Y. Wu, Nat. Phys., 2024, 20, 1015–1021 Search PubMed.
- O. Steinbock, V. Zykov and S. C. Müller, Nature, 1993, 366, 322–324 Search PubMed.
- Y. Gong and D. J. Christini, Phys. Rev. Lett., 2003, 90, 088302 CrossRef PubMed.
- S. Sen, P. Ghosh, S. S. Riaz and D. S. Ray, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046212 Search PubMed.
- S. Sen, P. Ghosh and D. S. Ray, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81, 056207 Search PubMed.
- H. Hu, X. Li, Z. Fang, X. Fu, L. Ji and Q. Li, Chem. Phys., 2010, 371, 60–65 Search PubMed.
- J. Yang and A. Garfinkel, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2003, 68, 066312 Search PubMed.
- B.-W. Li, Y. He, L.-D. Li, L. Yang and X. Wang, Commun. Nonlinear Sci. Numer. Simul., 2021, 99, 105830 Search PubMed.
- X. Tang, T. Yang, I. R. Epstein, Y. Liu, Y. Zhao and Q. Gao, J. Chem. Phys., 2014, 141, 024110 Search PubMed.
- J. Gao and C. Gu, IEEE Access, 2019, 7, 140391–140401 Search PubMed.
- A. Gierer and H. Meinhardt, Kybernetik, 1972, 12, 30–39 CAS.
- A.-J. Koch and H. Meinhardt, Rev. Mod. Phys., 1994, 66, 1481 Search PubMed.
- Y. Song, R. Yang and G. Sun, Appl. Math. Model., 2017, 46, 476–491 Search PubMed.
- G.-Q. Sun, C.-H. Wang and Z.-Y. Wu, Nonlinear Dyn., 2017, 88, 1385–1396 Search PubMed.
- L. Guo, X. Shi and J. Cao, Nonlinear Dyn., 2021, 105, 899–909 Search PubMed.
- S. Ghosh, S. Paul and D. S. Ray, Phys. Rev. E, 2016, 94, 042223 Search PubMed.
- A. Bhattacharyay, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2001, 64, 016113 Search PubMed.
- S. S. Riaz and D. S. Ray, J. Chem. Phys., 2005, 123, 174506 Search PubMed.
- P. Ghosh and D. S. Ray, J. Chem. Phys., 2011, 135, 104112 Search PubMed.
- M. Banerjee, S. Ghorai and N. Mukherjee, Int. J. Bifurc. Chaos Appl. Sci., 2017, 27, 1750038 CrossRef.
- J. Boissonade and P. De Kepper, J. Phys. Chem., 1980, 84, 501–506 CrossRef CAS.
- I. Lengyel and I. R. Epstein, Science, 1991, 251, 650–652 Search PubMed.
- R. Yadav, N. Mukherjee and M. Sen, Nonlinear Dyn., 2022, 107, 1397–1410 Search PubMed.
- B. Bozzini, G. Gambino, D. Lacitignola, S. Lupo, M. Sammartino and I. Sgura, Comput. Math. Appl., 2015, 70, 1948–1969 Search PubMed.
- S. Koga, Prog. Theor. Phys., 1982, 67, 164–178 Search PubMed.
- M. Ipsen, L. Kramer and P. G. Sørensen, Phys. Rep., 2000, 337, 193–235 CrossRef CAS.
- B. G. Elmegreen, D. M. Elmegreen and P. E. Seiden, Astrophys. J., 1989, 343, 602–607 Search PubMed.
- B.-W. Li, H. Zhang, H.-P. Ying, W.-Q. Chen and G. Hu, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 77, 056207 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Achal Jadhav‡
,
Achal Jadhav‡ and
Pushpita Ghosh
and
Pushpita Ghosh *
*


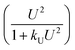 captures the saturable nature of activator production, with kU serving as the saturation constant. The parameters σU and σV are the basic production term of the activator and inhibitor, respectively, while the removal rates of the two species are represented by μU, μV. ρU and ρV are the cross-reaction coefficients and are related to the product of the rate constant and source densities of the activator and inhibitor species, respectively. The diffusion coefficients for the activator and inhibitor are denoted by DU and DV. Although this model was originally proposed to explain the development of spatial patterns in tissue structures during morphogenesis, it can also describe spatiotemporal pattern formation observed in various chemical systems. To reduce the complexity of the equation, we set the saturation constant (kU) and the basic production term of the inhibitor (σV) to zero in the current investigation.40 This scenario closely resembles a chemical reaction occurring in a continuously stirred tank reactor (CSTR),49 where reactants and products are continuously introduced and removed. During these reactions, intermediate species50 generated in the system act as activator and inhibitor components. The following dimensionless quantities have been introduced to render the overall eqn (1) dimensionless:
captures the saturable nature of activator production, with kU serving as the saturation constant. The parameters σU and σV are the basic production term of the activator and inhibitor, respectively, while the removal rates of the two species are represented by μU, μV. ρU and ρV are the cross-reaction coefficients and are related to the product of the rate constant and source densities of the activator and inhibitor species, respectively. The diffusion coefficients for the activator and inhibitor are denoted by DU and DV. Although this model was originally proposed to explain the development of spatial patterns in tissue structures during morphogenesis, it can also describe spatiotemporal pattern formation observed in various chemical systems. To reduce the complexity of the equation, we set the saturation constant (kU) and the basic production term of the inhibitor (σV) to zero in the current investigation.40 This scenario closely resembles a chemical reaction occurring in a continuously stirred tank reactor (CSTR),49 where reactants and products are continuously introduced and removed. During these reactions, intermediate species50 generated in the system act as activator and inhibitor components. The following dimensionless quantities have been introduced to render the overall eqn (1) dimensionless:

 ,
,  , and
, and  are dimensionless parameters. Setting the reaction terms in eqn (2) to zero provides the system's homogeneous steady state, given by (uss,vss) = [(1 + σ), (1 + σ)2].
are dimensionless parameters. Setting the reaction terms in eqn (2) to zero provides the system's homogeneous steady state, given by (uss,vss) = [(1 + σ), (1 + σ)2].
 . The Hopf bifurcation curve separates the parameter space into regions of temporally stable and unstable states. Subsequently, we carried out the stability analysis of the spatially extended GM model around the homogeneous steady state in the presence of diffusion. This yields the Turing condition as:
. The Hopf bifurcation curve separates the parameter space into regions of temporally stable and unstable states. Subsequently, we carried out the stability analysis of the spatially extended GM model around the homogeneous steady state in the presence of diffusion. This yields the Turing condition as:  . The Turing curve divides the parameter space into two regions, indicating the presence of diffusion-driven instability. Fig. 1 illustrates the corresponding bifurcation diagram for a fixed value of D = 0.25 in the μ vs. σ parameter space. The three distinct regions, marked with different colors, represent the relevant spatiotemporal instabilities identified through linear stability analysis. Based on prior literature,48 the oscillatory region near the Turing curve will be our primary focus for spiral wave formation.
. The Turing curve divides the parameter space into two regions, indicating the presence of diffusion-driven instability. Fig. 1 illustrates the corresponding bifurcation diagram for a fixed value of D = 0.25 in the μ vs. σ parameter space. The three distinct regions, marked with different colors, represent the relevant spatiotemporal instabilities identified through linear stability analysis. Based on prior literature,48 the oscillatory region near the Turing curve will be our primary focus for spiral wave formation.



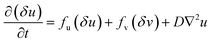





![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 1) are the eigenvectors corresponding to the eigenvalue γ. The eigenvalue (γ) can be obtained by solving eqn (8) in the absence of the diffusion terms. The corresponding solution for γ is given as:
1) are the eigenvectors corresponding to the eigenvalue γ. The eigenvalue (γ) can be obtained by solving eqn (8) in the absence of the diffusion terms. The corresponding solution for γ is given as:


![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 1. Consequently, the explicit form of the trial solution becomes:
1. Consequently, the explicit form of the trial solution becomes:

![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) acts on u1 and v1 in eqn (8), leading to zero eigenvalues. However, in eqn (14), a non-trivial term arises on the right-hand side due to the action of the operator
acts on u1 and v1 in eqn (8), leading to zero eigenvalues. However, in eqn (14), a non-trivial term arises on the right-hand side due to the action of the operator ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) on u2 and v2. Therefore, the solvability criterion (Fredholm theorem) must be applied. According to this condition, the right-hand side of eqn (14) must be orthogonal to the left eigenvector of
on u2 and v2. Therefore, the solvability criterion (Fredholm theorem) must be applied. According to this condition, the right-hand side of eqn (14) must be orthogonal to the left eigenvector of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) corresponding to the zero eigenvalue. This condition ultimately leads to the following equation:
corresponding to the zero eigenvalue. This condition ultimately leads to the following equation:
 and
and  are the complex conjugate of u1 and v1, respectively. Expanding eqn (15) leads to the following equation:
are the complex conjugate of u1 and v1, respectively. Expanding eqn (15) leads to the following equation:




 . In this case, eqn (20) can be simplified and expressed as:
. In this case, eqn (20) can be simplified and expressed as:
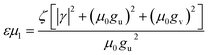
 and μ is the numerical value at which the first spiral arises. Once we have the value of εμ1 eqn (22) allows us to determine the value of ζ using this value along with the other parameters. Keeping ζ constant for the rest of the parameter set, we can then compare the value of εμ1 value obtained from eqn (22) with the numerical simulations.
and μ is the numerical value at which the first spiral arises. Once we have the value of εμ1 eqn (22) allows us to determine the value of ζ using this value along with the other parameters. Keeping ζ constant for the rest of the parameter set, we can then compare the value of εμ1 value obtained from eqn (22) with the numerical simulations.