Open Access Article
Open Access ArticleDevelopment of bixbyite microdice fabricated cathode for aqueous rechargeable zinc ion batteries†
Nusrat Tazeen Tonu ab,
Mohammad Abu Yousuf
ab,
Mohammad Abu Yousuf *a,
Parbhej Ahamed
*a,
Parbhej Ahamed a and
Md. Mahfujul Hasanc
a and
Md. Mahfujul Hasanc
aDepartment of Chemistry, Khulna University of Engineering and Technology, Khulna, 9203, Bangladesh. E-mail: yousuf@chem.kuet.ac.bd; nusrattazeen@ku.ac.bd; parbhej@chem.kuet.ac.bd
bChemistry Discipline, Khulna University, Khulna, 9208, Bangladesh
cFood and Toxicology Research Section, IFST, BCSIR, Dhaka, Bangladesh. E-mail: raihanacce@gmail.com
First published on 9th May 2025
Abstract
In this study, an ultrasonic-aided reverse micelle formation, followed by the calcination route, was developed for the synthesis of bixbyite microdice aimed at the fabrication of a cathode for ARZIBs. The prepared product was Mn2O3 having crystallinity and grain size of 65.12% and 25.61 nm, respectively, with a small percentage of other Mn-based oxides within it. The FESEM image showed dice like microsized Mn2O3, revealing the possible formation of a reverse micelle core of approximately 500 nm. XPS narrow spectra revealed the presence of Mn3+ in a mixture of Mn with +2 and +4 oxidation states. The crystal planes from the TEM images matched with XRD results and strengthened the formation of bixbyite Mn2O3 nanoparticles. The optical band gap of 3.21 eV specified the semiconducting property of the prepared Mn2O3, and therefore, the prepared Mn2O3 was used as a cathode material in a CR-2032 coin cell of ARZIBs. CV showed a reversible reaction within the cell, indicating the (de)intercalation of Zn2+ ions between the anode and cathode. The fresh cell showed high conductivity and low resistance compared with the used cell after BCD testing, confirmed by EIS. The cell delivered high specific discharge capacities of 293.59 ± 4.75 and 252.10 ± 4.66 mA h g−1 at applied current densities of 0.1 and 0.3 A g−1, respectively. Consequently, BCD was performed for 1000 cycles at a current density of 0.3 A g−1. Throughout the cycling, the capacity retention and coulombic efficiency were maintained at 90.35 ± 0.30% and 98.44 ± 0.27%, respectively, suggesting the resilient reversibility of charging and discharging.
1. Introduction
The environment and its energy systems are essential for human survival and prosperity. Since natural resources are finite, fossil fuel usage and energy demand have increased worldwide interest in energy technologies. Moreover, since smartphones, computers, electronic automobiles, etc. are so popular, rechargeable batteries are in demand.1,2 In recent decades, rechargeable batteries such as lead-acid (LABs), Li+-ion (LIBs), Na+-ion, and Zn2+-ion (ZIBs) batteries have been developed.3 Among the oldest and most popular rechargeable batteries are LABs. However, Pb toxicity, limited energy density, and deep discharge with overcharging restrict LABs.4,5 Unlike LABs, LIBs are the most popular rechargeable batteries for electrical and electronic vehicles owing to their extended lifespan, high voltage, and high energy density. Unfortunately, volatile organic electrolytes and the scarcity and flammability of Li make LIBs unfeasible.6,7 LIBs pose a major threat to those who dominate the current energy market; thus, the development of new batteries is imminent.8Aqueous rechargeable batteries appear promising over LIBs for two reasons. First, organic electrolytes are replaced with aqueous ones to avoid fires, reducing short circuit costs. Second, water's stronger ionic conductivity than organic solvents' allows higher battery operation.9 Meanwhile, aqueous rechargeable zinc ion batteries (ARZIBs) are gaining popularity because of their environmental friendliness, safety, availability, affordability (US$2.4 kg−1), high theoretical capacities (820 mA h g−1 and 5855 mA h cm−3), low potential, and suitable Zn2+|Zn reduction potential (−0.76 V vs. SHE).10 Zn-based aqueous batteries were first fabricated in the 1980s. Zn-air and Zn–MnO2 batteries use alkaline media for charge–discharge electrochemistry. Zinc dendrite development and aqueous electrolyte-induced side reaction have delayed water-based ZIB commercialization.11 Electrostatic repulsions between host materials and divalent Zn2+ ions make ARZIB cathode materials difficult to find. Prussian blue analogues, V-based cathodes have been developed. However, Mn-based cathodes provide better electrochemical storage performance compared with Zn2+|Zn potential, and are a suitable voltage platform (1.25 V).12,13
At present, a variety of Mn-based oxides has been verified for the Zn2+ ion storage in ARZIBs, including α-MnO2, β-MnO2, γ-MnO2, δ-MnO2, Ω-MnO2, λ-MnO2, ε-MnO2, Mn2O3, Mn3O4, ZnMn2O4, etc., consisting of the same fundamental structure of MnO6, but are linked differently.14 Among these, MnO2 is the most explored cathode, but it has weak electrical and ionic conductivities. Besides, it is temperature sensitive, and undergoes a phase transformation to other Mn-oxide above 200 °C.15 While charging, H+ ions intercalate to the cathode, competing with Zn2+ and leading to sluggish diffusion of Zn2+ ion within MnO2.16 These simultaneous acts of structural deformation and indolent Zn2+ ion diffusion makes MnO2 problematic for ARZIB. Therefore, Mn2O3 has received a lot of focus lately for its easy preparation process, high energy intensity,17 and high thermal stability up to 850 °C,18 although they are barely reported for ARZIBs.
A variety of efforts has been made to stabilize and enrich Mn2O3 for the storage of Zn2+ ion in aqueous media, e.g., preparation process optimization, surface alteration, etc. A sacrificial template-based thermal decomposition approach was utilized to create Mn2O3, which had a specific discharge capacity of 225.0 and 92.7 mA h g−1 at 0.05 and 2.0 A g−1, respectively, and retained its initial discharge capacity after 1700 cycles.19 Mn2O3 was doped with Ni to triple its specific capacity (252 mA h g−1 at 0.1 A g−1), and it retained its capacity to 85.6% after 2500 cycles.20 Precipitation followed by calcination was used to synthesize Mn2O3 nanopowder, which showed a specific discharge capacity of 211 mA h g−1 at 0.5 A g−1 after 200 cycles, and it retained 70% of its initial capacity after 1100 cycles at 2.0 A g−1.21 Since porosity increases ionic conductivity, porous 3D polymer polypyrrole (PPy)-coated Mn2O3 microspheres were developed by applying hydrothermal treatment followed by calcination and polymerization with a conductive PPy, which provided 287.7 mA h g−1 at 1.0 A g−1 over 300 cycles.22 Porosity in semiconductors creates additional ion transport pathways. Due to larger linked pores in Mn2O3, electron/ion conduction is faster. For smaller surface area and porosity, commercial Mn2O3 has poor Zn2+ ion capacity. Altering its preparation technique might boost this capacity.20
When ultrasound is introduced in a reaction system, it enhances the solubility of reactants with the media, creates heat to enhance mass transport in the system, and produces a vibration which could create cavities or pores within the product, which accelerates the reaction rate.23 Previously, ultrasound was used to increase the porosity of polyurethane foam.24 It was also used for homogeneous distribution of nano-SiO2 within plastomer matrix, and the resultant nano-SiO2 had a smaller size.25 Ultrasound was employed to hasten the distribution of Se particles in the hyperbranched polysaccharide dispersion and the size of Se nanoparticle decreased from 100 to 50 nm on average.26
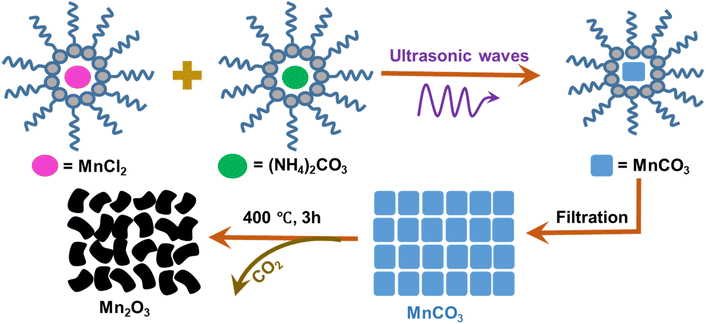
MnCl2 and (NH4)2CO3 were used as raw materials to prepare nano-sized MnCO3, which is a well-known substitution reaction,27 followed by the calcination route to prepare Mn2O3.28 However, there are limitations to control the size and shape. In this study, a high frequency ultrasonic assisted novel reverse micelle route was adopted using MnCl2 and (NH4)2CO3 to prepare bixbyite Mn2O3 microdice where size, shape and porosity have been tuned successfully, which was characterized by physico-chemical and spectroscopic techniques, and applied as cathode material in Zn-ion batteries for electrochemical applications which hasn't been done so far.
2. Materials and methods
2.1 Chemicals and instruments
Manganese(II) chloride tetrahydrate, MnCl2·4H2O and ammonium carbonate, (NH4)2CO3 were purchased from Loba Chemie, India. Cyclohexane (C6H12), cyclohexanol (C6H12OH) and Triton X-100 were purchased from PT. Smart Lab Indonesia. Zinc sulphate heptahydrate, (ZnSO4·7H2O) was obtained from Sigma-Aldrich (USA). Polyvinylidene fluoride (PVDF), carbon black (C-black), N-methyl pyrrolidone, zinc foil, and stainless steel (SS) foil (304 grades) having thickness t-0.01 × w-100 mm were used for CR-2032 coin cell battery fabrication. All of the work was done using deionized (DI) water. For ultrasonic irradiation, ultrasonic bath (Powersonic 603) was used. To identify the functional groups in the prepared sample, Fourier transform infra-red spectroscopy (FTIR) experiments were done using a FTIR spectrometer (IR Tracer-100, Shimadzu Corporation, Japan). The structure and surface morphology and elemental mapping of the prepared material was analyzed by a field emission scanning electron microscope (FESEM, JSM-7610F, Japan). A small amount of sample was taken for gold coating, then analyzed by the FESEM. Powder X-ray diffractometer (XRD: Bruker, D2PHASER) was used to analyze X-ray diffraction (XRD) of the prepared material with a Cu-Kα radiation source at 2θ from 10° to 80°. A Raman spectroscopic study was performed with a DXR smart Raman spectrometer (Thermo Fisher Scientific Co., Ltd., USA) with an excitation wavelength of 780 nm and full range grating. The elemental composition and valency state of Mn were analyzed by X-ray photoelectron spectroscopy (XPS) (XPS; L-Alpha, Thermo Scientific, UK). The prepared materials shape and crystal planes were evaluated using transmission electron microscopy (TEM) (JEM 2100 PLUS, JEOL, Japan). A small amount of prepared material was taken in a sample vial containing ethanol and shaken well. After that, the vial was enclosed by a cork and sonicated until the particles of the materials were resuspended. The vial was kept at rest for 24 h. A drop of the sample was placed onto a copper grid in a vacuum chamber overnight for degassing. Then, the copper grid containing the sample was analyzed by a TEM analyzer. Solid state UV visible spectroscopy was applied to find out the optical band gap and recorded within the range of 300–800 nm using a UV-1800 spectrophotometer (Shimadzu Corporation, Japan). Cyclic voltammetry (CV), electrochemical impedance spectroscopy (EIS) and battery charging–discharging (BCD) experiments were carried out using a Biologic potentiostat (SP-300).2.2 Preparation of Mn2O3 via an ultrasonic assisted reverse micelle route
Cyclohexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Triton X-100
Triton X-100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cyclohexanol
cyclohexanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (5
water (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was added into a beaker and mixed using an ultrasonic bath at room temperature until a clear mixture was formed, indicating the formation of a microemulsion. The microemulsion was divided equally into two beakers (B-1 and B-2). 0.005 mole of MnCl2 and (NH4)2CO3 were added to B-1 and B-2, respectively and they were kept in an ultrasonic bath until the materials were completely dissolved. Then, the mixture from B-2 was added dropwise into B-1. As the process started with a cloudy appearance, this indicated the production of MnCO3. Ultrasonication was continued for 30 min and all the MnCl2 and (NH4)2CO3 were reacted to form MnCO3, which was sedimented as the reaction ended. Then, the product was filtered, air dried and calcined at 400 °C for 3 h. The product was cooled to room temperature and black colored Mn2O3 was formed.29,30 A similar experiment was also carried out using magnetic stirring instead of ultrasonic irradiation. It took longer to produce MnCO3 by magnetic stirring and the amount of product was 61.06% less compared with ultrasonic irradiation. Fig. 1 shows the schematic diagram for the preparation of Mn2O3.
1) was added into a beaker and mixed using an ultrasonic bath at room temperature until a clear mixture was formed, indicating the formation of a microemulsion. The microemulsion was divided equally into two beakers (B-1 and B-2). 0.005 mole of MnCl2 and (NH4)2CO3 were added to B-1 and B-2, respectively and they were kept in an ultrasonic bath until the materials were completely dissolved. Then, the mixture from B-2 was added dropwise into B-1. As the process started with a cloudy appearance, this indicated the production of MnCO3. Ultrasonication was continued for 30 min and all the MnCl2 and (NH4)2CO3 were reacted to form MnCO3, which was sedimented as the reaction ended. Then, the product was filtered, air dried and calcined at 400 °C for 3 h. The product was cooled to room temperature and black colored Mn2O3 was formed.29,30 A similar experiment was also carried out using magnetic stirring instead of ultrasonic irradiation. It took longer to produce MnCO3 by magnetic stirring and the amount of product was 61.06% less compared with ultrasonic irradiation. Fig. 1 shows the schematic diagram for the preparation of Mn2O3.
2.3 Fabrication of CR-2032 coin cell
Here, the active material is prepared Mn2O3, and C-black was used to increase the conductivity of Mn2O3, while PVDF was used as the gluing agent and NMP was the solvent; together PVDF and NMP were used as the binding agent. Mn2O3, C-black and PVDF were mixed in an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, followed by the addition of NMP. They were further mixed using a manual mortar and pestle until a smooth slurry was formed. Then, the slurry was applied on a stainless steel foil to form a thin layer.31 Thereafter, the foil was dried at 70 °C and cut using a die cutting machine which was the final cathode of the battery. The fabrication of the CR-2032 coin cell of ARZIB was done through the arrangement of cathode metal case, fabricated cathode, separator soaked with aqueous 2.0 M ZnSO4 as electrolyte, Zn foil as the anode, with a spacer, spring, and anode metal case.32 About 20 batteries were made for electrochemical testing.
1 ratio, followed by the addition of NMP. They were further mixed using a manual mortar and pestle until a smooth slurry was formed. Then, the slurry was applied on a stainless steel foil to form a thin layer.31 Thereafter, the foil was dried at 70 °C and cut using a die cutting machine which was the final cathode of the battery. The fabrication of the CR-2032 coin cell of ARZIB was done through the arrangement of cathode metal case, fabricated cathode, separator soaked with aqueous 2.0 M ZnSO4 as electrolyte, Zn foil as the anode, with a spacer, spring, and anode metal case.32 About 20 batteries were made for electrochemical testing.
3. Results and discussion
Fig. 2 shows the FTIR spectra of the prepared products between a wavenumber range of 400 to 4000 cm−1. The peak positions were also labelled with dotted straight lines. For MnCO3, a broad peak with high intensity at 3404 cm−1 represents the stretching vibrations of O–H, a sharp peak with low intensity at 2489 cm−1 indicates the bending vibration of O–H in H2O, which is due to moisture in the KBr plate. Sharp peaks with low intensity at 1799 and 1073 cm−1, and high intensity at 1457, 867 and 718 cm−1 represented the vibration of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in MnCO3. For Mn2O3, a broad peak at 566 cm−1 represented the Mn–O vibration in MnO6–octahedral moiety, which indicated the presence of Mn–oxide. These results indicated that the ultrasonic assisted reverse micelle route produced MnCO3 that formed Mn-based oxide after calcination. Furthermore, the line intensity of Mn2O3 decreased as the wave number increased, which implies it's crystalline and/or semiconducting behavior.33,34
O in MnCO3. For Mn2O3, a broad peak at 566 cm−1 represented the Mn–O vibration in MnO6–octahedral moiety, which indicated the presence of Mn–oxide. These results indicated that the ultrasonic assisted reverse micelle route produced MnCO3 that formed Mn-based oxide after calcination. Furthermore, the line intensity of Mn2O3 decreased as the wave number increased, which implies it's crystalline and/or semiconducting behavior.33,34
The prepared Mn2O3 was subjected to powder XRD analysis to determine the crystalline structure and purity. An X-ray diffractogram of the prepared Mn2O3 is shown in Fig. 3. Diffraction peaks were found at 2θ = 18.14°, 18.85°, 21.69°, 23.13°, 26.13°, 28.70°, 30.85°, 31.96°, 32.96°, 33.93°, 35.61°, 36.36°, 37.17°, 38.23°, 39.62°, 40.72°, 42.93°, 45.16°, 47.79°, 49.33°, 51.18°, 53.28°, 53.71°. 55.17°, 57.13°, 57.94°, 60.62°, 62.32°, 64.06°, 65.77°, 66.01°, 67.41°, 69.11°, 73.89°, and 73.91°. This spectrum was analyzed using X'pert Highscore Plus software and a mixture of Mn based oxides were found by matching with the Crystallographic Open Database (COD). The spectrum primarily matched with Mn2O3 (77% with bixbyte, COD_Pdf # 96-210-5792), along with Mn5O8 (34% with Mn10O16, COD_Pdf # 96-151-4101), Mn2O4 (18% with pyrolusite, COD_Pdf # 96-210-5791), Mn3O4 (13% with hausmannite, COD_Pdf # 96-151-4241), Mn4O8 (10% with ramsdellite, COD_Pdf # 96-900-3476), α-MnO2 (8%, COD_Pdf # 96-151-4117) and Mn6C6O18 (10% with rhodochrosite, COD_Pdf # 96-900-7691). The suspected planes of the prepared Mn2O3 w. r. to 2θ compared with the references are listed in Table 1. Therefore, the prepared Mn-oxide is mainly Mn2O3 with a small amount of Mn5O8, which also contains a trace amount of MnO2 and Mn3O4; thus, it was being considered as Mn2O3. This could be credited to the cubic crystal system of the I a![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group (no. 206).
space group (no. 206).
| 2θ (°) | Planes (h k l) compared with Mn2O3 (COD_Pdf # 96-210-5792) | 2θ (°) | Planes (h k l) Compared with Mn5O8 (COD_Pdf # 96-151-4101) |
|---|---|---|---|
| 18.85 | (0 2 0) | 18.14 | (2 0 0) |
| 23.13 | (1 2 1) | 21.69 | (-2 0 2) |
| 26.13 | (0 2 2) | 28.70 | (1 1 1) |
| 33.93 | (2 2 2) | 30.85 | (2 0 1) |
| 35.61 | (1 3 2) | 31.96 | (3 1 0) |
| 38.23 | (0 4 0) | 32.96 | (-3 1 1) |
| 40.72 | (1 4 1) | 36.36 | (2 2 0) |
| 42.93 | (0 4 2) | 37.17 | (-2 0 2) |
| 45.16 | (2 3 3) | 39.62 | (0 0 2) |
| 49.33 | (1 4 3) | 47.79 | (-4 2 1) |
| 53.28 | (1 5 2) | 51.18 | (0 2 2) |
| 55.17 | (0 4 4) | 53.71 | (1 3 1) |
| 57.13 | (3 4 3) | 57.94 | (4 2 1) |
| 60.62 | (1 6 1) | 64.62 | (-7 1 1) |
| 62.32 | (0 6 2) | 66.01 | (6 2 0) |
| 64.06 | (1 5 4) | ||
| 65.77 | (2 6 2) | ||
| 67.41 | (1 6 3) | ||
| 69.11 | (4 4 4) | ||
| 73.91 | (1 2 7) |
The Scherer eqn (1) was used to calculate the average crystal size of prepared Mn2O3:
 | (1) |
The d-spacing calculation was done using Bragg's law (2):
 | (2) |
For the cubic cell, the lattice constant was calculated using eqn (3):
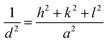 | (3) |
| Unit cell volume, V = a3 | (4) |
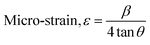 | (5) |
 | (6) |
| Peak positions, 2Theta (°) | Interplanar spacing, d (Å) | Miller indices, (h k l) |
|---|---|---|
| 18.85 | 4.703938 | (0 2 0) |
| 23.13 | 3.842288 | (1 2 1) |
| 26.13 | 3.407558 | (0 2 2) |
| 33.93 | 2.717783 | (2 2 2) |
| 35.61 | 2.519145 | (1 3 2) |
| 38.23 | 2.352310 | (0 4 0) |
| 40.72 | 2.214030 | (1 4 1) |
| 42.93 | 2.105031 | (0 4 2) |
| 45.16 | 2.006130 | (2 3 3) |
| 49.33 | 1.845861 | (1 4 3) |
| 53.28 | 1.717950 | (1 5 2) |
| 55.17 | 1.663485 | (0 4 4) |
| 57.13 | 1.610982 | (3 4 3) |
| 60.62 | 1.526319 | (1 6 1) |
| 62.32 | 1.488705 | (0 6 2) |
| 64.06 | 1.452401 | (1 5 4) |
| 65.77 | 1.418719 | (2 6 2) |
| 67.41 | 1.388135 | (1 6 3) |
| 69.11 | 1.358082 | (4 4 4) |
| 73.91 | 1.281297 | (1 2 7) |
The Raman spectra of the prepared Mn2O3 is given in Fig. 4. The presence of five well resolved peaks are located at 343, 530, 569, 633 and 749 cm−1, which are characteristic spectral features of Mn-based oxide. Raman shifts at 343 and 633 cm−1 can be qualified as asymmetric stretching of bridge oxygen species (Mn–O–Mn) and symmetric stretching of Mn2O3 groups, respectively.39 The peak located at 569 cm−1 represented the terminal Mn–O stretching in the basal plane of MnO6 sheet in the MnO2 skeleton.40 Other peaks were observed due to the mixture of a small amount of Mn3O4 in the prepared Mn2O3,41 which complemented the results of previously discussed XRD. Therefore, the prepared Mn2O3 is a mixture of Mn2O3, MnO2 and Mn3O4.
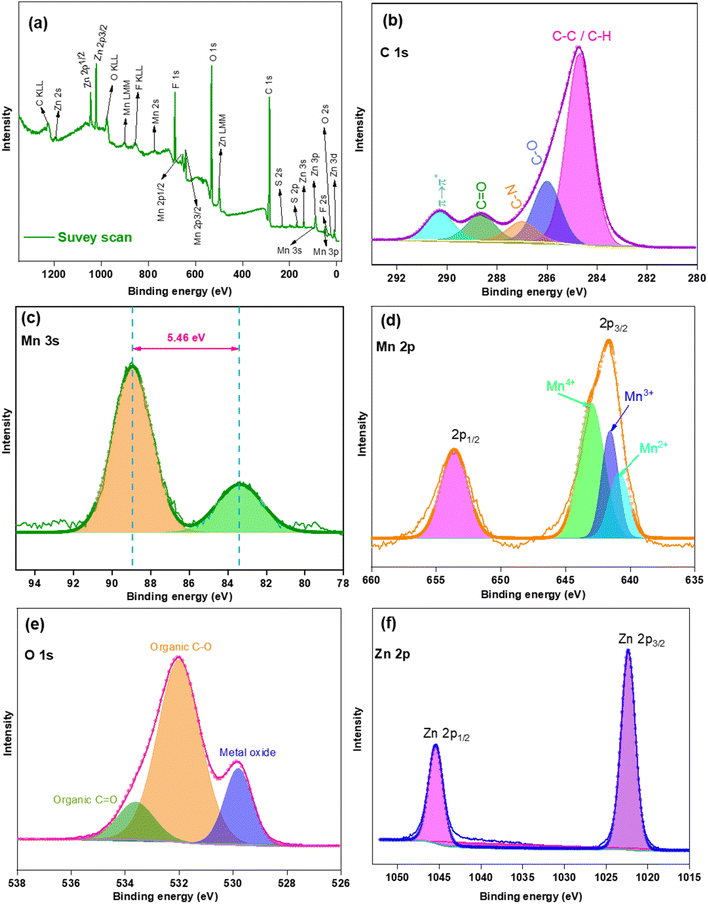
To understand the surface chemical composition of prepared Mn2O3, XPS was carried out. Fig. 5(a) shows the total XPS survey scan of prepared Mn2O3 within a binding energy range of +1350 to −10 eV. The presence of Mn (945.03, 902.86, 849.22, 772.32, 652.63, 641.47, 82.09, and 47.05 eV) and O (1011.39, 995.27, 975.11, and 531.69) was confirmed with a negligible amount of C (1223.17 and 284.26 eV) and Cl (1301.93, 267.51, and 198.68 eV). The amount of Mn and O was 34.11% and 51.26%, respectively (by the no. of atoms present). The ratio of Mn and O is very close to Mn2O3. C might come from calcination of the adhered shell of the reverse micelle during filtration of MnCO3 and the presence of Cl might be derived from tap water contamination during the course of apparatus cleaning.
From Fig. 5(b), two sharp and well defined peaks at 652.81 and 641.63 eV indicated Mn 2p1/2 and Mn 2p3/2 states having a separation of 11.15 eV. A small broad satellite peak at 661.14 eV that is 10.89 eV higher than that of Mn 2p state confirmed the presence of the Mn3+ oxidation state. Therefore, the prepared Mn2O3 could be Mn2O3 with a mixture of Mn(II), Mn(III) and Mn(IV) oxidation states. At the lower energy level [Fig. 5(c)], two sharp and well defined peaks at 21.05 and 4.18 eV were for the O 2 s and O 2p state with the Mn 3d state indicated by a tailing peak at 9.91 eV. These values are well matched with previously reported values.42,43
To understand the oxidation states of Mn, core level binding energy narrow spectra were taken [Fig. 5(d)–(f)]. All the Mn 2p, Mn 3s and O 1s spectra were broad due to multiple splitting. The presence of Mn4+, Mn3+, and Mn2+ was confirmed by Gaussian fitted peaks at 643.78, 641.63 and 640.54 eV, respectively. The values of multiple splitting energies of the Mn 3s spectra were 88.47 and 82.98 eV, with a distance of 5.49 eV. This peak splitting arose by the coupling of non-ionized 3s electron with 3d valence-band electrons. This splitting is directly proportional to the remaining electron in the 3s orbital and other unpaired electrons having parallel spins. The energy difference of this splitting designated the particular state of Mn. In this case, the formation of the Mn2O3 phase was confirmed due to the Mn3+ oxidation state. Narrow peaks appearing at binding energies of 530.83 eV (OII) and 529.26 eV (OI) in O correspond to the Mn–O–Mn bond of manganese oxide. The broad peak of OII at lower intensity corresponds to Mn–OH bonding. The presence of the –OH group in the O 1s narrow spectra was due to the absorption of moisture of prepared Mn2O3. Fig. 5(g) shows the valence band spectra of prepared Mn2O3. The valence band maximum (VBM) positions were determined by Gaussian deconvolution of the leading peak edges. Here, the binding energy of Mn eg of the Mn 3d orbital is 1.32 eV higher than the Fermi level (EF). Some other states were also found: Mn t2g, O 2p, Mn t2g-O 2p, and Mn eg-O 2p were at binding energies of 2.75, 4.16, 5.05, and 6.33 eV. This result indicated the primary formation of Mn2O3, with a small amount of MnO2 and Mn3O4 mixed with it, which also complemented the results of % of Mn and O already acquired from XPS spectral data.43,44
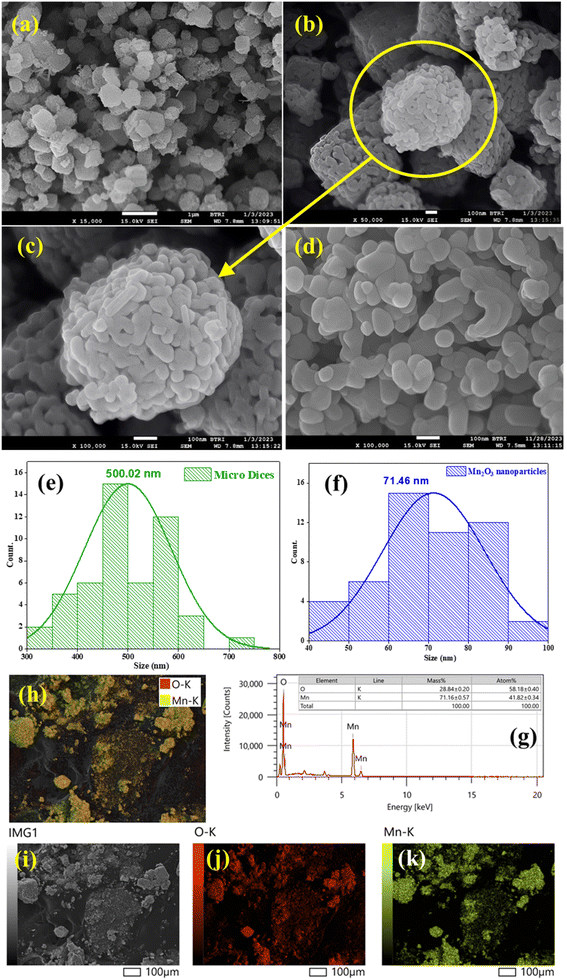
The surface morphology and average particle size were assessed using FESEM. Fig. 6(a–d) shows the surface morphology of Mn2O3 before and after grinding. Before grinding, the particles were distorted porous microdice with a histogram average size of 500.02 nm [Fig. 6(e)]. Tiny Mn2O3 nanoparticles aggregated with each other, resulting in porous Mn2O3 microdice. After breaking the microdice, the histogram showed Mn2O3 particles of an average size of 71.46 nm [Fig. 6(f)]. In this case, all the particles were of different shapes and sizes.45,46 In the reverse micelle core, only water exists. The water media of the reverse micelle core might generate MnCO3. Calcination of MnCO3 at 400 °C produced Mn2O3, releasing CO2. As predicted, CO2 emission did not affect the reactor core's structure, leaving a porous micro dice of 500.02 nm. Ultrasonic waves twisted the reactor core from a spherical shape to a somewhat distorted cube-like dice shape. Some fractured dice were also observed in Fig. 6(b), which arose during transfer of the sample after calcination.
The composition and stoichiometry of prepared Mn2O3 were examined with the help of the energy dispersive X-ray microanalysis (EDX) technique. Fig. 6(g) portrays the EDX spectrum of prepared Mn2O3. The presence of Mn and O were established as major elements with a very small amount of impurities. These elements were uniformly distributed over the whole Mn2O3 sample, as confirmed by the elemental mapping illustration in Fig. 6(h–k). The EDX lines located at 5.9 and 0.53 keV are the K lines of Mn and O, respectively. The quantification result from EDX data revealed the percentage of each element with corresponding energy distribution held in the matrix enabling us to determine the composition of the prepared sample. Here, Mn and O are the main components and the % of atoms for Mn and O are 41.82 and 58.18%, respectively, which is almost 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and suggests that the prepared Mn2O3 could be primarily Mn2O3 with a small amount of other manganese oxides (Mn5O8, MnO2 and/or Mn3O4) within it.47,48 The literature says that Mn2O3 belongs to the orthorhombic system with MnO as the basic unit, where Mn3+ exhibits an octahedral coordination and O2− shows a tetrahedral coordination. Mn2O3 also suffers a phase transition from an orthorhombic structure to a layered structure of MnO2. Therefore, Mn2O3 could be considered as an individual constituent and/or as a combination of MnO and MnO2. Similarly, Mn3O4 possesses two oxidation states, Mn2+ and Mn3+, that could be individual constituents and/or a combination of MnO and Mn2O3.49 The elemental composition of prepared Mn2O3 were compared with the theoretical values. Because XPS provides more convenient and detailed results as compared to EDX, the results from Table 3 confirmed that the prepared product is mainly Mn2O3.
3, and suggests that the prepared Mn2O3 could be primarily Mn2O3 with a small amount of other manganese oxides (Mn5O8, MnO2 and/or Mn3O4) within it.47,48 The literature says that Mn2O3 belongs to the orthorhombic system with MnO as the basic unit, where Mn3+ exhibits an octahedral coordination and O2− shows a tetrahedral coordination. Mn2O3 also suffers a phase transition from an orthorhombic structure to a layered structure of MnO2. Therefore, Mn2O3 could be considered as an individual constituent and/or as a combination of MnO and MnO2. Similarly, Mn3O4 possesses two oxidation states, Mn2+ and Mn3+, that could be individual constituents and/or a combination of MnO and Mn2O3.49 The elemental composition of prepared Mn2O3 were compared with the theoretical values. Because XPS provides more convenient and detailed results as compared to EDX, the results from Table 3 confirmed that the prepared product is mainly Mn2O3.
| Fraction of atoms | Theoretical values | Experimental values | ||||
|---|---|---|---|---|---|---|
| Mn2O3 | Mn5O8 | MnO2 | Mn3O4 | XPS | EDX | |
| Mn/O | 0.6666 | 0.6250 | 0.5000 | 0.7500 | 0.6654 | 0.7188 |
TEM was performed to rationalize the FESEM and XRD results. Fig. 7 shows the TEM graphs of the prepared Mn2O3 nanoparticles. The particles are dice shaped with different sizes. Two dice were clearly seen and drawn in [Fig. 7(a)]. These dice are composed of small discrete particles, which supports the FESEM result. Distinguishable crystal planes are observed in Fig. 7(b, e and j), indicating good crystallinity of the Mn2O3 nanoparticles. Five cross-sections of these three micrographs were analyzed using ImageJ software. The FFT images (Fig. 7c, f, h, k and m) and line intensity plots (Fig. 7 d, g, i, l, n and o) of the corresponding cross-sections revealed six planes [(020), (040), (132), (022), (343), and (222)], of respective d-spacing (0.47, 0.23, 0.25, 0.34, 0.16, and 0.27 nm). These values are well matched with COD-pdf# 96-210-5792.50
The solid-state UV-visible spectra for the prepared Mn2O3 nanoparticles has an absorption maxima at 351.84 nm, as shown in Fig. 8(a). From the optical absorption maxima (A), the absorption coefficient (α) was calculated using eqn (7):
 | (7) |
| (αhν)2 = B(hν − Eg) | (8) |
 | ||
| Fig. 8 (a) Absorption spectra, and (b) absorption coefficient (αhν)2 vs. hν for the prepared Mn2O3 nanoparticles. | ||
To determine the nature of the electrochemical reaction in the cell, CV was performed within the potential window +1.0 V to +2.2 V at scan rates of 0.6, 0.7, 0.8, 0.9, and 1.0 mV s−1 (Fig. 9(a)). A pair of well resolved redox peaks were noticed. The heights of the anodic and cathodic peaks were close to each other at every scan rate, which implied the strong reversibility of the cell reaction. At all scan rates, similar anodic peak and cathodic peaks were observed in the range of +1.68 to +1.75 V and +1.21 to +1.16 V, respectively. The reactions54 of the anodic and cathodic peaks could be assigned as follows:
Anodic reaction:
| xZn ↔ xZn2+ + 2xe− |
Cathodic reaction:
| H2O ↔ H+ + OH− |
| Mn2O3 + xZn2+ + 2xe− → ZnxMn2O3 |
| 4Zn2+ + 6OH− + SO2+4 + 5H2O ↔ Zn4(OH)6(SO4)·5H2O |
The peak heights increased with faster scan rates, and the anodic peaks shifted towards the right while cathode peaks shifted to the left, demonstrating the possible slight adsorption of Zn2+ ions onto the cathode surface responsible for Zn2+ ion storage. Dunn's method was used to test the CV using eqn (9):
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i = log i = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a + b a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν ν
| (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ν vs. log
ν vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i graph was plotted [Fig. 9(b)], and the value of the slope, b = 0.92 and 0.81 for anodic peaks and cathodic peaks, respectively, are much closer to 1.0 rather than 0.5. This indicated that the electrochemical Zn2+ storage mechanism included diffusion controlled pseudo capacitive behavior.55,56 Mn2O3 nanoparticles provided a superior non-diffusion storage mechanism limited to Zn2+ ions. The percentages of the capacitive and diffusion contribution ratios can be determined using eqn (11):
i graph was plotted [Fig. 9(b)], and the value of the slope, b = 0.92 and 0.81 for anodic peaks and cathodic peaks, respectively, are much closer to 1.0 rather than 0.5. This indicated that the electrochemical Zn2+ storage mechanism included diffusion controlled pseudo capacitive behavior.55,56 Mn2O3 nanoparticles provided a superior non-diffusion storage mechanism limited to Zn2+ ions. The percentages of the capacitive and diffusion contribution ratios can be determined using eqn (11):
 | (10) |
 | (11) |
 vs.
vs. 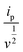 plot. The diffusion contribution or pseudo-charge storage is k1ν, and the capacitive contribution or insertion type capacity is
plot. The diffusion contribution or pseudo-charge storage is k1ν, and the capacitive contribution or insertion type capacity is  .57,58 The CV for capacitive contribution was approximately 85% that of the total contribution at a scan rate of 1.0 mV s−1 [Fig. 9(c)]. The capacitive contribution rates were increased with the scan rates. At 0.6, 0.7, 0.8 0.9, and 1.0 mV s−1, the capacitive contributions were 81, 82, 83, 84, and 85%, respectively [Fig. 9(d)], which represented the (de)intercalation dominated cell reaction.59
.57,58 The CV for capacitive contribution was approximately 85% that of the total contribution at a scan rate of 1.0 mV s−1 [Fig. 9(c)]. The capacitive contribution rates were increased with the scan rates. At 0.6, 0.7, 0.8 0.9, and 1.0 mV s−1, the capacitive contributions were 81, 82, 83, 84, and 85%, respectively [Fig. 9(d)], which represented the (de)intercalation dominated cell reaction.59
The CV experiment was performed at the electrochemical window of +1.0 to +2.2 V and a pair of redox peaks were seen within the electrochemical window of +1.0 to +1.8 V. Therefore, the BCD experiment was performed in the electrochemical window of +1.0 to +1.8 V and this window was fixed for all BCD experiments. Here, the potential window and applied current density were fixed, while time was a variable and the specific capacities were different depending on how much time was needed for every cycle. This type of BCD is very similar to the chrono-potentiometric experiment. BCD curves of the fabricated CR-2032 coin cell tested at various current density are displayed in Fig. 10(a). The specific discharge capacities decreased (293.59 ± 4.75, 269.47 ± 4.62, 252.10 ± 4.66, 225.82 ± 4.91, 195.69 ± 4.38, 173.98 ± 4.49, and 144.83 ± 4.47 mA h g−1) as the applied current density increased (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, and 0.7 A g−1), respectively. The rate capability was also performed at those current densities [Fig. 10(b)]. When the applied current density dropped back from 0.7 to 1.0 A g−1, the cell delivered a specific discharge capacity of 284.96 ± 4.91 mA h g−1, which retained 96.76% of its initial value of 293.59 ± 4.75 mA h g−1. This experiment was done on three different coin cells and the statistical values are represented in Table S1.† Cycling was done at 0.3 A g−1 current density for 1000 cycles on three different coin cells and the results are represented in Table S2.† The coulombic efficiency was maintained at an average of 98.44 ± 0.37%. After 200, 400, 600, 800, and 1000 cycles, the specific discharge capacity retention was calculated to be 96.84%, 95.73%, 94.22%, 93.18% and 90.35%, respectively.60,61 The discharge capacity is slightly lower than the charging capacity for every cycle. It could be concluded that a small amount of Zn2+ ion might have been trapped in the Mn2O3 cathode and/or formed stable complexes with it after every charging–discharging process, which blocked the available (de)intercalation sites.
 | ||
| Fig. 10 BCD of the fabricated CR-3032 coin cell. (a) Specific capacities and (b) rate capability at different current densities. (c) Cycling performance at 0.3 A g−1 for 1000 cycles. | ||
EIS was performed to find out the conductivity/resistance of the fabricated coin cell at a potential of +1.9 V at a frequency region between 300 kHz to 100 mHz. The Nyquist plot [Fig. 11(a)] was tested by using equivalent circuit R1 + Q2/R2 + Q3/R3 + W4. Here, R1 = solution resistance (Rs) in ohms, R2 = electrode resistance (Rf) due to solution electrolyte interface contribution in ohms, R3 = charge transfer resistance (Rct) in ohms, Q2 and Q3 = capacitance of the cathode in F considered as porous material, which is conventionally represented as constant phase elements (CPE), and W4 = Warburg impedance (Ws) in ohm s1/2. The values of Rs, Rf, Rct, and Ws were found to be 7.05, 50.74, 9.021 Ω, and 28.301 Ω s1/2, respectively for fresh coin cells, and those of BCD after 1000 cycles were 7.812, 67.04, 63.77 Ω, and 15.65 Ω s1/2, respectively. Fresh cells showed lower resistances compared with the used cells. The equivalent circuit almost fitted to the Nyquist plot at higher frequency but deviation was found at lower frequency. This discrepancy could be the reason for the possible development of secondary capacitors within the cell. Certain cathode materials might have separated from their current collector during the consecutive charging-discharging phase, combined with the electrolyte, passed through the separator, and moved towards the anode surface. As the resistances were comparatively higher after 1000 cycles, some detached cathode material might form a stable layer on the surface of the anode, which might be the reason for decreasing the capacity retention as the cycling continued. In addition, the mass transport system could be non-uniform within the cell. To test the validation of impedance fitting parameters, the Kramers–Kronig equation was used by checking error analysis. The plot of Zreal vs. frequency of impedance [Fig. 11(b)] completely satisfied the validation. The plot of Zim vs. frequency of impedance [Fig. 11(c)] also satisfied the validation but showed a small deviation at higher frequency. These results showed the reliability of the measurement since it satisfied the linearity, causality and stability for impedance measurements.62,63
The relationship of Zreal and the reciprocal square root of the angular frequencies (ω−1/2) is expressed in eqn (12):
 | (12) |
 vs. Zre was constructed before and after BCD cycling [Fig. 11(d)]. This portrays the resistance in the lower frequency region of the coin cell based on the movement of Zn2+ ions within the cell. The value of the slopes (σω) were 11.74 and 15.50 Ω s1/2 before and after BCD cycling, respectively.
vs. Zre was constructed before and after BCD cycling [Fig. 11(d)]. This portrays the resistance in the lower frequency region of the coin cell based on the movement of Zn2+ ions within the cell. The value of the slopes (σω) were 11.74 and 15.50 Ω s1/2 before and after BCD cycling, respectively.
The diffusion coefficient of Zn2+ ions into the bulk electrolyte was calculated using eqn (13):
| D = 0.5(RT/AFσωC)2 | (13) |
The double layer capacitance was calculated using eqn (14):
| Zre = Rs + Rct + 2σω2Cdl | (14) |
 | (15) |
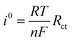 | (16) |
The Bode plot of frequency dependent impedances [Fig. 11(e)] showed that it remained at a lower resistance at higher frequency with inclined lines at lower frequency, which indicated a good capacitive of Zn2+ ion storage of the prepared Mn2O3 nanoparticles. The Bode plot of frequency dependent phase angles [Fig. 11(f)] showed that the highest phase angles were 31.02° and 37.53° before and after BCD, respectively, which represented the pseudocapacitive behavior of semiconducting Mn2O3 nanoparticles for Zn2+ ion storage within the cell.66
To understand the reaction mechanism inside the coin cell, post-mortem characterization of the cathode material was done. After BCD was done, the coin cell was broken using a sharp needle and hammer. The cathode material was taken, washed with DI water, and sent for further analysis. First, SEM images and EDX profiles of the cathodes were analyzed before (fresh cathode) and after BCD (used cathode). Fig. 12(a–d) shows SEM images of fresh and used cathodes. For the fresh cathode, particles of different sizes and shapes were present and the distribution of particles were almost homogeneous (Fig. 12(a and c)). After BCD, the cathode showed non-homogeneous distribution of particles (Fig. 12(b)), the surface of the cathode was covered by powder like substances or some foreign substances were trapped inside the cathode (Fig. 12(d)). This result implied that the cathode underwent some internal or surface changes while charging-discharging. For better understanding, EDX measurements were taken. The cathode before and after BCD showed almost similar percentages of Mn and O, with small amounts of C and F because bixbyite was mixed with PVDF and NMP, resulting in the presence of C and F with Mn and O. Zn was present in the used cathode (after BCD) while it was absent in the fresh cathode (before BCD). This might be explained in terms of the decrease of retention from 100% after BCD. There could be some intermediate product formation with the (de)intercalation of Zn2+ ions in the bixbyite framework. The reaction within the cell was not completely reversible and responsible for the presence of Zn in the form of ZnxMn2O3 within the cathode and decreased BCD cycling retention after 1000 cycles.
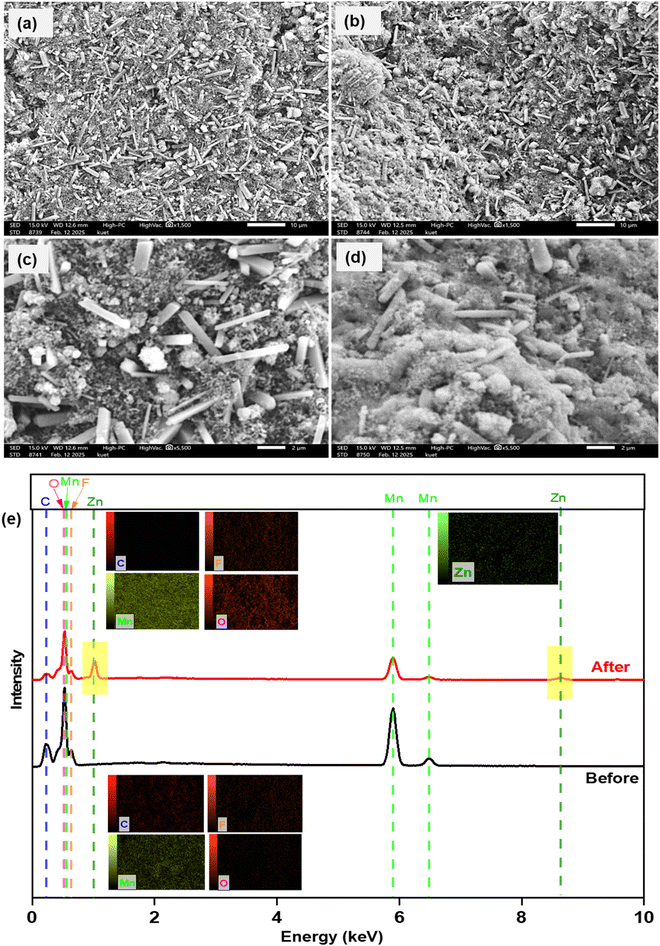 | ||
| Fig. 12 SEM images of the cathode before (a = 10 μm, c = 2 μm) and after (b = 10 μm, d = 2 μm) BCD. (e) Corresponding EDX data: inset showing elemental mapping. | ||
A part of the used cathode was sent for XPS analysis (Fig. 13). Survey scans [Fig. 13(a)] indicated the presence of Mn, O, C, Zn, F, N, and S at 3.61, 26.88, 56.28, 2.93, 8.77, 0.62, and 0.86%, respectively (by no. of atoms present). The huge amount of C was present for C-black. Fig. 13(b) indicated a narrow spectra of C 1s with Gaussian deconvolution fitting curves. The presence of sp3 C for C–C or C–H was at 284.71 eV while C–O, C–N, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O were found at 285.99, 287.01, and 288.66 eV, respectively.67 These groups arose from PVDF and NMP. A shake up satellite peak at 290.27 eV indicated the presence of π → π* and explained the aromatic character of C in NMP. Therefore, the presence of C, N, O, and F was because of the additives used for coin cell fabrication. Fig. 13(c) showed that the Mn 3 s spectra exhibited two sharp well defined peaks (88.91 and 83.45 eV) with a separation of 5.46 eV, which that Mn2O3 was in a Mn3+ oxidation state. Fig. 13(d) showed two well defined peaks at 653.55 and 641.65 eV for Mn 2p1/2 and Mn 2p3/2. The separation of 11.9 eV is slightly higher than the results obtained from the raw bixbyite micro dice [Fig. 5(d)]. Gaussian deconvolution fitting peak of Mn 2p3/2 showed the presence of Mn4+, Mn3+, and Mn2+, which is similar to the previous deconvolution peak for raw bixbyite micro dice, but the peak area of Mn4+ seems to be greater than Mn2+, which differs from raw bixbyite micro dice where the peak area of Mn2+ seems to be greater than Mn4+. Therefore, it could be said that there might be an internal chemical change during charging-discharging. Fig. 13(e) showed the presence of peaks at 533.64 and 532.01 eV for organic C
O were found at 285.99, 287.01, and 288.66 eV, respectively.67 These groups arose from PVDF and NMP. A shake up satellite peak at 290.27 eV indicated the presence of π → π* and explained the aromatic character of C in NMP. Therefore, the presence of C, N, O, and F was because of the additives used for coin cell fabrication. Fig. 13(c) showed that the Mn 3 s spectra exhibited two sharp well defined peaks (88.91 and 83.45 eV) with a separation of 5.46 eV, which that Mn2O3 was in a Mn3+ oxidation state. Fig. 13(d) showed two well defined peaks at 653.55 and 641.65 eV for Mn 2p1/2 and Mn 2p3/2. The separation of 11.9 eV is slightly higher than the results obtained from the raw bixbyite micro dice [Fig. 5(d)]. Gaussian deconvolution fitting peak of Mn 2p3/2 showed the presence of Mn4+, Mn3+, and Mn2+, which is similar to the previous deconvolution peak for raw bixbyite micro dice, but the peak area of Mn4+ seems to be greater than Mn2+, which differs from raw bixbyite micro dice where the peak area of Mn2+ seems to be greater than Mn4+. Therefore, it could be said that there might be an internal chemical change during charging-discharging. Fig. 13(e) showed the presence of peaks at 533.64 and 532.01 eV for organic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–O, responsible for NMP, and the peak at 529.81 eV indicated the presence of Mn-oxide. From Fig. 13(f), two sharp peaks at 1045.38 and 1022.32 eV indicated that Zn 2p1/2 and Zn 2p3/2 states exhibited a separation of 23.06 eV.68 Here a small percentage of Zn is present with a tiny percentage of S, is a foreign material that was not used during cathode preparation. During the coin cell fabrication, ZnSO4 was used as electrolyte but the cathode was washed with DI water after the used coin cell was broken. Therefore, the remaining Zn and S was expected to be washed off but Zn was present in an appreciable amount. This could be explained by the formation of intermediate compound ZnxMn2O3 within the cathode which complemented the EDX results [Fig. 12(e)]. A small percentage of S might be due to the stabilization of intermediate compound Zn4(OH)6(SO4)·5H2O within the cathode matrix. Fig. 14 shows the valence band spectra of used cathode. A broad peak started from 1.26 to 8.19 eV, indicating the presence of Mn–O bonds in bixbyite. Unlike raw bixbyite [Fig. 5(g)], a sharp peak at 10.42 eV confirmed the presence of a compound like ZnxMn2O3. The VBM was calculated to be 1.33 eV.69
O and C–O, responsible for NMP, and the peak at 529.81 eV indicated the presence of Mn-oxide. From Fig. 13(f), two sharp peaks at 1045.38 and 1022.32 eV indicated that Zn 2p1/2 and Zn 2p3/2 states exhibited a separation of 23.06 eV.68 Here a small percentage of Zn is present with a tiny percentage of S, is a foreign material that was not used during cathode preparation. During the coin cell fabrication, ZnSO4 was used as electrolyte but the cathode was washed with DI water after the used coin cell was broken. Therefore, the remaining Zn and S was expected to be washed off but Zn was present in an appreciable amount. This could be explained by the formation of intermediate compound ZnxMn2O3 within the cathode which complemented the EDX results [Fig. 12(e)]. A small percentage of S might be due to the stabilization of intermediate compound Zn4(OH)6(SO4)·5H2O within the cathode matrix. Fig. 14 shows the valence band spectra of used cathode. A broad peak started from 1.26 to 8.19 eV, indicating the presence of Mn–O bonds in bixbyite. Unlike raw bixbyite [Fig. 5(g)], a sharp peak at 10.42 eV confirmed the presence of a compound like ZnxMn2O3. The VBM was calculated to be 1.33 eV.69
Table 4 shows a list of specific discharge capacities of prepared Mn-based oxides with respect to the applied current density.62,63,66,70–83 Several types of Mn-oxides have been prepared for ARZIBs in the literature and some of the Mn-oxides were also doped or coated by conducting materials to increase their capacitive behavior, thereby increasing their preparation cost and complexity. Our explored material showed a comparable result with other materials in terms of the specific discharge capacity, while it showed a satisfactory value of specific discharge capacity at higher applied current density (0.3 A g−1). Besides, the preparation process was simpler and cost effective compared with other materials. As a bare compound, the prepared porous Mn2O3 micro dice showed acceptable performance as a cathode of ARZIBs compared with other results listed in Table 4.
| Cathode materials | Applied current density (A g−1) | Specific discharge capacity (mA h g−1) | References |
|---|---|---|---|
| β-MnO2 | 0.10 | 100 | 70 |
| δ-MnO2 | 0.10 | 126 | 70 |
| α-MnO2 | 0.02 | 210 | 71 |
| α-MnO2 | 0.05 | 255 | 66 |
| α-MnO2 | 0.06 | 302 | 72 |
| MnO2@MgO | 0.10 | 274 | 73 |
| α-MnO2/graphene | 0.30 | 362 | 74 |
| Mn3O4@C | 0.50 | 209 | 75 |
| Mn2O3/Mn3O4 composite | 0.10 | 122 | 76 |
| Al-doped MnO2 | 0.20 | 327 | 77 |
| Mn3O4 | 0.10 | 221 | 78 |
| MnO | 0.10 | 330 | 79 |
| Mn2O3 | 0.10 | 150 | 80 |
| α-MnO2 | 0.09 | 290 | 81 |
| δ-MnO2 | 0.10 | 269 | 82 |
| Mn3O4 | 0.10 | 239 | 83 |
| α-Mn2O3 | 0.10 | 148 | 82 |
| α-Mn2O3 | 0.20 | 137 | 82 |
| Mn3O4 | 0.10 | 219 | 62 |
| Mn3O4 | 0.10 | 240 | 63 |
| Mn2O3 | 0.30 | 255 | This work |
4. Conclusion
A simple and cost-effective ultrasonic assisted reverse micelle route was used to prepare bixbyite Mn2O3 microdice. The prepared Mn2O3 showed semiconducting properties, and was used as a cathode in fabricating CR-2032 coin cells of ARZIBs. CV data revealed that the reversible reaction within the cell involved diffusion-controlled (de)intercalation of ions between the anode and cathode by means of high capacitive behavior. It showed relatively higher capacity at lower current density. At 0.3 A g−1 current density, the battery showed an initial discharge specific capacity of 252.10 ± 4.66 mA h g−1, coulombic efficiency of 98.44 ± 0.27% and a specific capacity retention of 90.35 ± 0.30% after 1000 cycles.Data availability
Data are available upon request from the authors.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
I would like to express my sincere gratitude to the Post-Graduate Laboratory, Department of Chemistry, KUET, Bangladesh, for providing access to their state-of-the-art facilities. I am deeply thankful for the support and resources available, which were instrumental in completing this research.References
- C. Wang, Y. Zeng, X. Xiao, S. Wu, G. Zhong, K. Xu and X. Lu, J. Energy Chem., 2020, 43, 182–187, DOI:10.1016/j.jechem.2019.08.011.
- L. Li, H. Xu, Z. Li, B. Zhoong, Z. Lou and L. Wang, Adv. Mater., 2025, 37, 2414054, DOI:10.1002/adma.202414054.
- C. Li, X. Zhang, W. He, G. Xu and R. Sun, J. Power Sources, 2020, 449, 227596, DOI:10.1016/j.jpowsour.2019.227596.
- E. J. Hansen and J. Liu, Front. Energy Res., 2021, 8, 616665, DOI:10.3389/fenrg.2020.616665.
- Z. Li, Y. Zheng, L. Liu, L. Li, Z. Lou and L. Wang, Nat. Electron., 2025, 1–10, DOI:10.1038/s41928-024-01261-6.
- A. Wang, W. Zhou, A. Huang, M. Chen, Q. Tian and J. Chen, J. Colloid Interface Sci., 2021, 586, 362–370, DOI:10.1016/j.jcis.2020.10.099.
- J. Ming, J. Guo, C. Xia, W. H. Wang and N. Alshareef, Mater. Sci. Eng., R, 2019, 135, 58–84, DOI:10.1016/j.mser.2018.10.002.
- J. Shin, J. Lee, Y. Park and J. W. Choi, Chem. Sci., 2020, 11(8), 2028–2044, 10.1039/D0SC00022A.
- S. Chen, F. Tang, T. He, H. Zhang, S. Deng, Y. Li and W. Yan, Int. J. Photoenergy, 2019, 1–7, DOI:10.1155/2019/3792942.
- A. Huang, W. Zhou, A. Wang, M. Chen, Q. Tian and J. Chen, J. Energy Chem., 2021, 54, 475–481, DOI:10.1016/j.jechem.2020.06.041.
- N. Wang, H. Wan, J. Duan, X. Wang, L. Tao, J. Zhang and H. Wang, Mater. Today Adv., 2021, 11, 100149, DOI:10.1016/j.mtadv.2021.100149.
- X. Guo, J. Zhou, C. Bai, X. Li, G. Fang and S. Liang, Mater. Today Energy, 2020, 16, 100396, DOI:10.1016/j.mtener.2020.100396.
- J. Xu, X. Hu, M. A. Alam, G. Muhammad, Y. Lv, M. Wang and W. Xiong, RSC Adv., 2021, 11(56), 35280–35286, 10.1039/D1RA06808C.
- S. Dawadi, A. Gupta, M. Khatri, B. Budhathoki, G. Lamichhane and N. Parajuli, Bull. Mater. Sci., 2020, 43, 1–10, DOI:10.1007/s12034-020-02247-8.
- T. Hatakeyama, N. L. Okamoto and T. Ichitsubo, J. Solid State Chem., 2022, 205, 122683, DOI:10.1016/j.jssc.2021.122683.
- A. Zhang, X. Zhang, H. Zhao, H. Ehrenberg, G. Chen, I. Saadoune and Y. Wang, J. Colloid Interface Sci., 2024, 669, 723–730, DOI:10.1016/j.jcis.2024.05.052.
- H. Shen, B. Liu, Z. Nie, Z. Li, S. Jin, Y. Huang and H. Zhou, RSC Adv., 2021, 11(24), 14408–14414, 10.1039/D1RA00346A.
- L. Narayani, V. J. Angadi, A. Sukhdev, M. Challa, S. Matteppanavar, P. R. Deepthi and M. Pasha, J. Magn. Magn. Mater., 2019, 476, 268–273, DOI:10.1016/j.jmmm.2018.12.072.
- M. Mao, X. Wu, Y. Hu, Q. Yuan, Y. B. He and F. Kang, J. Energy Chem., 2021, 52, 277–283, DOI:10.1016/j.jechem.2020.04.061.
- D. Zhang, J. Cao, X. Zhang, N. Insin, S. Wang, J. Han and Y. Huang, Adv. Funct. Mater., 2021, 31(14), 2009412, DOI:10.1002/adfm.202009412.
- Q. Hou, D. G. Ivey and E. C. S. Inc, ECS Meeting Abstracts, 2021, 240(1), 15, DOI:10.1149/MA2021-02115mtgabs.
- K. Cai, S. H. Luo, L. Qian, X. Meng, S. X. Yan, J. Guo and X. Y. Zhou, J. Power Sources, 2023, 564, 232854, DOI:10.1016/j.jpowsour.2023.232854.
- G. Zhou, J. Yin, Z. Sun, X. Gao, F. Zhu, P. Zhao and J. Xu, RSC Adv., 2020, 10(6), 3246–3255, 10.1039/C9RA08537H.
- C. Torres-Sanchez and J. R. Corney, Ultrason. Sonochem., 2008, 15(4), 408–415, DOI:10.1016/j.ultsonch.2007.05.002.
- B. Peng, H. Wu, W. Bao, S. Guo, Y. Chen, H. Huang and J. Jow, Polym. J., 2011, 43(1), 91–96, DOI:10.1038/pj.2010.95.
- W. Cai, T. Hu, A. M. Bakry, Z. Zheng, Y. Xiao and Q. Huang, Ultrason. Sonochem., 2018, 42, 823–831, DOI:10.1016/j.ultsonch.2017.12.022.
- S. Lei, Z. Liang, L. Zhou and K. Tang, Mater. Chem. Phys., 2009, 113(1), 445–450, DOI:10.1016/j.matchemphys.2008.07.114.
- S. Lei, K. Tang, Z. Fang, Q. Liu and H. Zheng, Mater. Lett., 2006, 60(1), 53–56, DOI:10.1016/j.matlet.2005.07.070.
- Z. Zhou, F. Jiang, T. C. Lee and T. Yue, J. Alloys Compd., 2013, 581, 843–848, DOI:10.1016/j.jallcom.2013.07.207.
- H. Lu, H. Ju, Q. Yang, Z. Li, H. Ren, X. Xin and G. Xu, CrystEngComm, 2013, 15(33), 6511–6517, 10.1039/C3CE40432C.
- Y. Li, Z. Yuan, D. Li, J. Li, Y. Zhang, M. Wang and W. Han, ACS Nano, 2024, 18(6), 4733–4745, DOI:10.1021/acsnano.3c07977.
- J. Liao and Z. Ye, Batteries, 2018, 4(2), 22, DOI:10.3390/batteries4020022.
- S. A. Moon, B. K. Salunke, B. Alkotaini, E. Sathiyamoorthi and B. Kim, IET Nanobiotechnol., 2015, 9(4), 220–225, DOI:10.1049/iet-nbt.2014.0051.
- V. Sannasi and K. Subbian, J. Mater. Sci.:Mater. Electron., 2020, 31(19), 17120–17132, DOI:10.1007/s10854-020-04272-z.
- A. K. M. A. Ullah, A. S. M. F. Kibria, M. Aktor, M. N. I. Khan, A. R. M. Tarq and S. H. Firoz, Water Conserv. Sci. Eng., 2017, 1, 249–256, DOI:10.1007/s41101-017-0017-3.
- B. Wu, G. Zhang, M. Yan, T. Xiong, P. He, L. He and L. Mai, Small, 2018, 14(13), 1703850, DOI:10.1002/smll.201703850.
- C. Martinez de la Torre, J. H. Grossman, A. A. Bobko and M. F. Bennewitz, PLoS One, 2020, 15(9), e0239034, DOI:10.1371/journal.pone.0239034.
- E. A. Tokeser and O. Ozturk, J. Mater. Sci.: Mater. Electron., 2023, 34(31), 2075, DOI:10.1007/s10854-023-11402-w.
- K. H. Kim, D. K. Lee and Y. H. Choi, Mater, 2021, 14(9), 2338, DOI:10.3390/ma14092338.
- Y. K. Hsu, Y. C. Chen, Y. G. Lin, L. C. Chen and K. H. Chen, Chem. Commun., 2011, 47(4), 1252–1254, 10.1039/C0CC03902K.
- C. Julien, M. Massot, R. Baddour-Hadjean, S. Franger, S. Bach and J. P. Pereira-Ramos, Solid State Ionics, 2003, 159(3–4), 345–356, DOI:10.1016/S0167-2738(03)00035-3.
- N. Pal, A. Sharma, V. Acharya, N. K. Chourasia, S. Biring and B. N. Pal, ACS Appl. Electron. Mater., 2019, 2(1), 25–34, DOI:10.1021/acsaelm.9b00641.
- A. A. Audi and P. M. Sherwood, Surf. Interface Anal., 2002, 33(3), 274–282, DOI:10.1002/sia.1211.
- C. Yun, W. Li, X. Gao, H. Dou, T. Maity, X. Sun and J. L. MacManus-Driscoll, ACS Appl. Mater. Interfaces, 2021, 13(7), 8863–8870, DOI:10.1021/acsami.1c00607?ref=pdf.
- G. Periyasamy, I. M. Patil, B. Kakade, P. Veluswamy, J. Archana, H. Ikeda and K. Annamalai, J. Mater. Sci.:Mater. Electron., 2022, 33(11), 8644–8654, DOI:10.1007/s10854-021-06721-9.
- Q. Z. Gou, C. Li, X. Q. Zhang, B. Zhang, S. R. Zou, N. Hu and C. X. Lei, J. Mater. Sci.: Mater. Electron., 2018, 29, 16064–16073, DOI:10.1007/s10854-018-9695-7.
- M. I. Said, A. H. Rageh and F. A. Abdel-Aal, RSC Adv., 2018, 8(33), 18698–18713, 10.1039/C8RA02978D.
- G. Kumar, N. T. Tonu, P. K. Dhar and M. Mahiuddin, Pollution, 2021, 7(3), 693–707, DOI:10.22059/poll.2021.320575.1033.
- B. Zhang, P. Dong, S. Yuan, Y. Zhang, Y. Zhang and Y. Wang, Chem Bio Eng., 2024, 1(2), 113–132, DOI:10.1021/cbe.3c00120?urlappend=%3Fref%3DPDF&jav=VoR&rel=cite-as.
- Y. De Luna, A. Alsulaiti, M. I. Ahmad, H. Nimir and N. Bensalah, Front. Chem., 2023, 11, 1101459, DOI:10.3389/fchem.2023.1101459.
- E. A. Davis and N. Mott, Philos. Mag., 1970, 22(179), 0903–0922, DOI:10.1080/14786437008221061.
- H. Fritzsche, Philos. Mag. B, 1993, 68(4), 561–572, DOI:10.1080/13642819308217935.
- N. M. Hosny and A. Dahshan, Mater. Chem. Phys., 2012, 137(2), 637–643, DOI:10.1016/j.matchemphys.2012.09.068.
- D. Zhang, J. Cao, X. Zhang, N. Insin, S. Wang, J. Han and Y. Huang, Adv. Funct. Mater., 2021, 31(14), 2009412, DOI:10.1002/adfm.202009412.
- K. Lan, Q. Wei, R. Wang, Y. Xia, S. Tan, Y. Wang and D. Zhao, J. Am. Chem. Soc., 2019, 141(42), 16755–16762, DOI:10.1021/jacs.9b06962.
- G. A. Muller, J. B. Cook, H. S. Kim, S. H. Tolbert and B. Dunn, Nano Lett., 2015, 15(3), 1911–1917, DOI:10.1021/nl504764m.
- C. Chen, Y. Wen, X. Hu, X. Ji, M. Yan, L. Mai and Y. Huang, Nat. Commun., 2015, 6(1), 6929, DOI:10.1038/ncomms7929.
- D. Chao, P. Liang, Z. Chen, L. Bai, H. Shen, X. Liu and Z. X. Shen, ACS Nano, 2016, 10(11), 10211–10219, DOI:10.1021/acsnano.6b05566.
- Z. Ye, P. Li, W. Wei, C. Huang, L. Mi, J. Zhang and J. Zhang, Adv. Sci., 2022, 9(18), 2200067, DOI:10.1002/advs.202200067.
- C. Huang, Q. Wang, G. Tian and D. Zhang, Mater. Today Phys., 2021, 21, 100518, DOI:10.1016/j.mtphys.2021.100518.
- X. Liu, F. Yang, W. Xu, Y. Zeng, J. He and X. Lu, Adv. Sci., 2020, 7(21), 2002173, DOI:10.1002/advs.202002173.
- N. T. Tonu, P. Ahamed and M. A. Yousuf, Ionics, 2024, 1–15, DOI:10.1007/s11581-024-05636-9.
- N. T. Tonu, P. Ahamed and M. A. Yousuf, PLoS One, 2024, 19(6), e0305611, DOI:10.1371/journal.pone.0305611.
- M. M. Sanad and A. Y. Shenouda, J. Mater. Sci.: Mater. Electron., 2023, 34(14), 1146, DOI:10.1007/s10854-023-10555-y.
- E. Han, X. Du, P. Yang and Y. Han, Ionics, 2018, 24, 393–401, DOI:10.1007/s11581-017-2226-3.
- O. Ibukun and H. K. Jeong, New Phys.:Sae Mulli, 2018, 68, 185–188, DOI:10.3938/NPSM.68.185.
- A. Morais, J. P. C. Alves, F. A. S. Lima, M. Lira-Cantu and A. F. Nogueira, J. Photonics Energy, 2015, 5(1), 057408, DOI:10.1117/1.JPE.5.057408.
- X. Z. Zhai, J. Qu, S. M. Hao, Y. Q. Jing, W. Chang, J. Wang and Z. Z. Yu, Nano-Micro Lett., 2020, 12, 1–15, DOI:10.1007/s40820-020-0397-3.
- N. Kamarulzaman, M. F. Kasim and R. Rusdi, Nanoscale Res. Lett., 2015, 10, 346, DOI:10.1186/s11671-015-1034-9.
- D. Lakshmi and B. Nalini, J. Solid State Electrochem., 2017, 21, 1027–1034, DOI:10.1007/s10008-016-3456-4.
- E. A. Aboelazm, G. A. Ali, H. Algarni, H. Yin, Y. L. Zhong and K. F. Chong, J. Phys. Chem. C, 2018, 122(23), 12200–12206, DOI:10.1021/acs.jpcc.8b03306.
- L. Wang, X. Cao, L. Xu, J. Chen and J. Zheng, ACS Sustain. Chem. Eng., 2018, 6(12), 16055–16063, DOI:10.1021/acssuschemeng.8b02502.
- N. Palaniyandy, D. Lakshmi, G. Thenmozhi, S. Kheawhom and N. N. Musyoka, J. Mater. Sci., 2024, 59(13), 5450–5469, DOI:10.1007/s10853-024-09373-2.
- S. Y. Zhu, Y. F. Yuan, P. F. Du, C. L. Mo, G. C. Cai, B. X. Wang and S. Y. Guo, Electrochim. Acta, 2022, 419, 140396, DOI:10.1016/j.electacta.2022.140396.
- H. Chen, W. Zhou, D. Zhu, Z. Liu, Z. Feng, J. Li and Y. Chen, J. Alloys Compd., 2020, 813, 151812, DOI:10.1016/j.jallcom.2019.151812.
- J. Yao, Y. Liu, Y. Li, J. Jiang and Q. Zhu, Mater. Res. Bull., 2023, 165, 112292, DOI:10.1016/j.materresbull.2023.112292.
- Y. Zhao, S. Zhang, Y. Zhang, J. Liang, L. Ren, H. J. Fan and X. Sun, Energy Environ. Sci., 2024, 17(3), 1279–1290, 10.1039/D3EE01659E.
- L. Wang, X. Cao, L. Xu, J. Chen and J. Zheng, ACS Sustain. Chem. Eng., 2018, 6(12), 16055–16063, DOI:10.1021/acssuschemeng.8b02502.
- J. Wang, J. G. Wang, H. Liu, Z. You, C. Wei and F. Kang, J. Power Sources, 2019, 438, 226951, DOI:10.1016/j.jpowsour.2019.226951.
- T. Li, J. Tong, S. Liu, J. Liang, G. Dai, W. Sun and A. Sun, J. Colloid Interface Sci., 2024, 656, 504–512, DOI:10.1016/j.jcis.2023.11.129.
- L. Jiang, Z. Wu, Y. Wang, W. Tian, Z. Yi, C. Cai and L. Hu, ACS Nano, 2019, 13(9), 10376–10385, DOI:10.1021/acsnano.9b04165.
- B. Jiang, C. Xu, C. Wu, L. Dong, J. Li and F. Kang, Electrochim. Acta, 2017, 229, 422–428, DOI:10.1016/j.electacta.2017.01.163.
- L. Gong, Y. Zhang and Z. Li, J. Electrochem. Soc., 2022, 169(4), 040519, DOI:10.1149/1945-7111/ac638d.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra00543d |
| This journal is © The Royal Society of Chemistry 2025 |