Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rare earth-free magnetocaloric material Fe82Hf6Zr7B4Cu1 for high-temperature applications†
Anjana Vinoda,
Arvindha Babu Diraviamb,
Manivel Raja Muthuvelb and
Madhuri Wuppulluri *c
*c
aSchool of Advanced Sciences, Vellore Institute of Technology, Vellore 632014, Tamil Nadu, India
bDefence Metallurgical Research Laboratory, Hyderabad 500058, Telangana, India
cCeramic Composites Laboratory, Centre for Functional Materials, Vellore Institute of Technology, India. E-mail: madhuriw12@hotmai.com
First published on 9th May 2025
Abstract
The magnetocaloric effect (MCE) has garnered much attention in recent years, especially for rare earth (RE)-free magnetic materials. The increasing focus on these materials arises from their prospective uses in cryogenic magnetic cooling and elevated temperature environments. The study conducts a systematic experimental examination of a novel magnetocaloric material, Fe82Hf6Zr7B4Cu1 ribbons, primarily aimed at characterising their structural, magnetic, and magnetocaloric properties. X-ray diffraction (XRD) analysis confirmed the successful incorporation of hafnium in the Fe site of the Fe–Zr–B–Cu matrix. Furthermore, the magnetic properties of the ribbon were also investigated, yielding a Curie transition temperature of 678 K and a magnetic entropy change of 0.448 J kg−1 K−1 at 2.0 T. Notably, the relative cooling power and refrigeration capacity were determined to be 11.87 J kg−1 and 14.0 J kg−1, respectively, highlighting the potential of the material for high-temperature magnetocaloric applications. These findings collectively demonstrate that the novel Fe82Hf6Zr7B4Cu1 ribbon exhibits promising magnetocaloric properties, rendering it a suitable candidate for further investigation and potential applications in high-temperature magnetocaloric devices.
1. Introduction
In the realm of modern materials science, the magnetocaloric effect (MCE) is a phenomenon of utmost importance since it has the capacity to completely transform our approach to refrigeration and thermal control.1 The MCE, which is the reversible change in a material's temperature in response to an applied magnetic field, offers a viable substitute for traditional vapor-compression refrigeration.2 MCE's importance stems from its capacity to offer economical, eco-friendly, and effective cooling solutions for a variety of uses, such as air conditioning, refrigeration, and electronic cooling.3,4 Furthermore, innovative technologies like magnetic refrigeration systems, which have the potential to drastically lower energy use and greenhouse gas emissions, can be developed more quickly with the MCE.5,6 Moreover, because it offers a distinct viewpoint on the thermodynamic and magnetic characteristics of materials, the MCE is of great relevance for basic scientific research. In general, the field of MCEs is dynamic and rapidly changing, with the potential to revolutionise the way we approach refrigeration and thermal management.7An intricate thermodynamic phenomenon, the MCE is the outcome of the interaction between the magnetic and lattice degrees of freedom within a material.8 The mechanism of the MCE is presented as follows: once a magnetic field is applied to a ferromagnetic material, the magnetic moments of the atoms align, resulting in a decrease in magnetic entropy.9 An increase in lattice entropy is associated with a decrease in magnetic entropy, as the vibrational motion of the lattice is promoted by the aligned magnetic moments.10 As a result, the material's overall entropy remains constant, despite the varying distribution of entropy between the magnetic and lattice degrees of freedom. When the magnetic field is removed, the magnetic moments become arbitrary, which leads to a decrease in lattice entropy and an increase in magnetic entropy. A reversible temperature shift is the defining characteristic of the MCE, which is the result of the entropy change being reversed.6 The MCE amplitude is contingent upon the substance's intrinsic magnetic and thermodynamic properties, the temperature of the substance, and the intensity of the magnetic field.11
Magnetocaloric materials are essential for numerous applications, and a thorough comprehension of the MCE process is essential for their design and development.12 Due to their exceedingly high Curie transition temperatures (TC), magnetocaloric materials have the potential to revolutionise a diverse array of industries and applications, surpassing the temperature of room air.13 Efficiency in the operation of these materials at elevated temperatures facilitates the development of innovative refrigeration systems, heat exchangers, and thermal management solutions for extreme environments.14,15 These materials are capable of operating reliably in demanding applications due to their high TC values, which enhance their thermal stability.16 Magnetocaloric materials with TC values exceeding 500 K (ref. 17) may be employed in industrial processes that entail high temperatures, such as the cooling of chemical reactors, heat exchangers, and furnaces.16 In addition, these materials can be employed in the cooling of high-temperature electronics, propulsion systems, and thermal protection systems, as well as in other advanced aerospace applications.7 In addition, magnetocaloric materials with exceptionally high TC values can facilitate the development of innovative cryogenic refrigeration systems, superconducting applications, and quantum computing systems.18
The unique combination of high TC values, robust thermal stability, and significant magnetocaloric effects of these materials renders them an appealing choice for a wide range of applications, including energy harvesting, thermal energy storage, and advanced thermal management systems.19 For the development of refrigeration systems that are compact, efficient, and environmentally friendly, magnetocaloric materials with high TC are indispensable.1 A wide range of applications, including refrigeration, air conditioning, and electronic cooling, are suitable for these materials as a result of their high TC values, which enable them to operate efficiently near to its TC.20,21 The high TC values also result in a more efficient MCE of the magnetic moments, which are also more thermally stable.22,23 In addition, magnetocaloric materials with high TC values can be implemented in applications that require a high thermal gradient.24 Among the applications of magnetocaloric materials with high TC values are superconducting applications, electronic cooling systems, and aerospace and outer space applications.25 Generally, the development of magnetocaloric materials with high TC values is essential for the advancement of environmentally favourable, compact, and efficient refrigeration systems. This has the potential to transform a varied array of industries and applications.26
In order to advance sustainable, cost-effective, and environmentally friendly technologies, it is imperative to develop rare earth-free magnetocaloric materials.16 Traditional magnetocaloric materials are significantly dependent on rare earth elements,27–31 which are not only expensive and subject to price fluctuations, but also pose significant environmental and social concerns as a result of their extraction and processing.32,33 Alternatively, magnetocaloric materials that are devoid of rare earths provide a more environmentally favourable and sustainable alternative, which facilitates the creation of innovative applications in the fields of energy harvesting, refrigeration, and advanced magnetic devices.16 Additionally, the diminished reliance on rare earth elements facilitates the development of more efficient and compact devices, mitigates the risks associated with price volatility, and improves supply chain security.34 In the analysis, the significance of rare earth-free magnetocaloric materials is their capacity to transform a variety of industries, such as aerospace, energy, and healthcare, by offering a more sustainable, cost-effective, and efficient solution for magnetocaloric applications.
FeZrBCu alloys have emerged as promising candidates for rare earth free high-temperature magnetocaloric applications due to their distinctive combination of properties.35 These alloys are capable of efficient operation at elevated temperatures due to their high TC, which is typically greater than 600 K.36 The thermal stability of the magnetic moments is improved by the addition of Zr and B to the Fe–Cu alloy system, which leads to a more pronounced MCE.37,38 The MCE in FeZrBCu alloys is distinguished by a high refrigerant capacity (RC) and a substantial magnetic entropy change (ΔSM), rendering them appropriate for high-temperature magnetocaloric refrigeration.39 Additionally, the FeZrBCu alloys demonstrate a relatively low magnetic hysteresis, which enhances the overall efficacy of the magnetocaloric cycle and reduces energy losses.40 The high-temperature magnetocaloric properties of FeZrBCu alloys render them appealing for applications such as thermal energy harvesting, heat transfer, and high-temperature refrigeration.
Further investigation of compositional modifications has the potential to improve the performance of FeZrBCu alloys, which exhibit promising properties for high-temperature magnetocaloric applications. The substitution of hafnium (Hf) in the FeZrBCu alloy system is one such approach. Upon conducting literature review, we discovered that there is very limited research on Hf substitution in FeZrBCu alloys. The objective of our research is to address this void in knowledge by investigating the impact of Hf substitution on the Zr site at a higher concentration. This could potentially result in enhanced magnetocaloric properties and enhanced application opportunities.
In this study, the magnetocaloric properties of a novel material system, Fe82Hf6Zr7B4Cu1, with a high TC value are investigated. The material system, which is based on a rare-earth-free alloy, exhibits a high TC value and a large magnetocaloric effect. A detailed investigation of the material's magnetocaloric properties, including its temperature dependence, field dependence, and refrigerant capacity is presented.
2. Experimental procedure
Vacuum arc melting was employed to synthesise the Fe82Hf6Zr7B4Cu1 ingots. The melting process was initiated by the generation of an electric discharge between a tungsten electrode and the metal constituents in a water-cooled, dismountable copper crucible plate with trough-shaped recesses. A sample of Fe82Hf6Zr7B4Cu1 ingots was subjected to a rigorous arc melting process that involved four successive melting cycles, with each side of the sample being melted twice. In order to guarantee sample homogeneity and mitigate potential contamination, this procedure was executed in a controlled argon atmosphere. Approximately 20 g of the arc-melted alloy were fragmented and placed in a transparent quartz crucible. The wheel speed was calibrated to 3000 rpm. A pneumatically controlled crucible receptacle facilitated the precise movement of the crucible up and down, thereby enabling the sample to melt uniformly within the induction coil. The alloy was meticulously positioned in close proximity to the rotating wheel once it had reached a molten state. The molten alloy was then ejected onto the rotating copper wheel at a regulated pressure of 2 psi, enabling the quick solidification of the alloy into thin ribbons.3. Characterisation techniques
The Pan-analytical X-ray diffraction system was employed to conduct X-ray diffraction (XRD) analysis of the prepared Fe82Hf6Zr7B4Cu1 ribbons. The XRD measurements were conducted at a scanning rate of 4° min−1 using a Cu Kα source with a wavelength of 1.5406 Å. The structural properties of the samples were detailed by recording the diffraction patterns over a 2θ range of 35°–100°. The melt-spun ribbons were subjected to differential scanning calorimetry (DSC) using a TA Instruments Discovery SDT 650. A 90 μl alumina pan was used to meticulously place approximately 10–20 mg of each sample, which was subsequently heated from room temperature to 1523 K at a controlled rate of 20 °C min−1. KLA MicroSense EZ11 Vibrating sample magnetometers were employed to conduct temperature-dependent magnetisation measurements, during a temperature range of 657 K to 699 K. The measurements were performed with a constant magnetic field of 100 Oe. Isothermal magnetisation curves were measured at temperatures around the Curie transition temperature, with applied magnetic fields of up to 2.0 T.4. Results and discussion
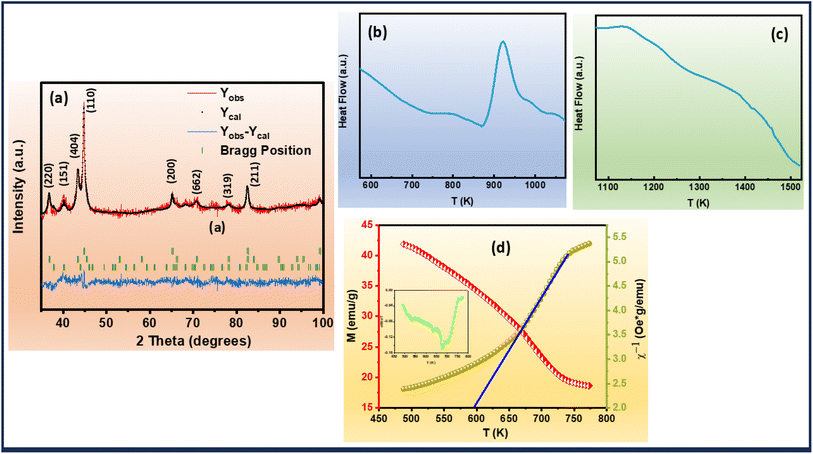
A comprehensive structural analysis of the alloys was conducted via X-ray diffraction (XRD) at room temperature, spanning the 2θ range of 35°–100°. To elucidate the phase composition and crystal structure of the ribbons, Rietveld refinement of the XRD patterns was performed, as illustrated in Fig. 1(a). The refinement revealed a complex multiphase composition, comprising three distinct phases: α-Fe, Fe2Zr, and Hf2Fe. Notably, the XRD patterns exhibited no detectable impurities, indicating high phase purity. The aforementioned observation depicted the successive hafnium (Hf) incorporation into the Fe-site of Fe–Zr–B–Cu matrix.Differential scanning calorimetry (DSC) was employed to investigate the thermal characteristics of the Fe82Hf6Zr7B4Cu ribbons. The resultant DSC curves, presented in Fig. 1(b) and (c), provide valuable insights into the thermal properties of the alloys, including the liquidus temperature (Tl) which is 1420.28 K and the initial crystallization temperature (Tx) which is 881.24 K.41 Furthermore, the glass-forming ability (GFA) of the alloys was quantitatively assessed by calculating the GFA parameter, α, using eqn (1) and which is calculated to be 0.62.42
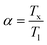 | (1) |
The composition of the alloy has a significant impact on the formation of a glassy phase in metallic systems. This can be qualitatively predicted by taking into account a number of critical factors. The enthalpy of mixing, which governs the thermodynamic stability of the alloy, the mismatch in atomic sizes among the constituent elements, which affects the topological and chemical short-range order, and the configurational entropy of the system, which influences the alloy's ability to form a disordered, glassy state, are among the factors. Researchers can acquire valuable insights into the alloying behaviour of metallic systems and identify promising compositions for glass formation by analysing these factors.
To elucidate the amorphous phase formation trend in the investigated multicomponent system, the glass-forming ability (GFA) was calculated using the PHSS parameter, a predictive tool that effectively incorporates three crucial factors influencing glass formation. Traditionally, enthalpy effects in multi-component systems have been approximated by considering solely binary interactions between species, neglecting crucial elastic and structural contributions. To accurately determine the enthalpy of mixing (ΔHC) for liquid solutions, a comprehensive approach involves summing the individual binary interaction terms, as formulated in eqn (2).
 | (2) |
| ΔHchemAB = xAxB(xBΔHinterfaceA–B + xAΔHinterfaceB–A) | (3) |
Mismatch entropy (ΔSσ) emerges as a critical factor, driven by atomic size disparities that inherently influence the alloy's thermodynamic stability and calculated by empirical relation given as in the eqn (4).44
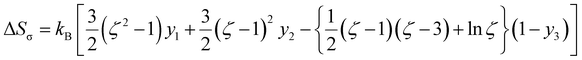 | (4) |
 , ξ is the packing fraction, kB is the Boltzmann's constant and y1, y2 and y3 are calculated by the eqn (5)–(8).
, ξ is the packing fraction, kB is the Boltzmann's constant and y1, y2 and y3 are calculated by the eqn (5)–(8).
 | (5) |
 | (6) |
 | (7) |
 | (8) |
 | (9) |
The glass forming ability of given samples are calculated using the eqn (10).
 | (10) |
 | (11) |
The magnetization–temperature (M versus T) curve of the Fe82Hf6Zr7B4Cu1 ribbons were analysed under an applied magnetic field of 100 Oe to determine the Curie transition temperature. A ferrimagnetic–paramagnetic transition is indicated by the fact that the magnetisation decreases as the temperature increases, as illustrated in Fig. 1(d). The inflection-point method was implemented to precisely ascertain the magnetic transition temperature, which was determined by identifying the temperature that corresponds to the minimum derivative of the M versus T curve.46 This was accomplished by examining the  versus T plot, which is illustrated in the inset of Fig. 1(d). The Curie transition temperature value was precisely determined using the above-mentioned method, which is 678 K.
versus T plot, which is illustrated in the inset of Fig. 1(d). The Curie transition temperature value was precisely determined using the above-mentioned method, which is 678 K.
The Curie–Weiss law, which delineates the temperature dependence of magnetic susceptibility in paramagnetic materials, facilitates a thorough comprehension of the samples' magnetic behaviour. The relationship is mathematically represented as in the eqn (12).
 | (12) |
The isothermal magnetisation curves of the ribbons Fe82Hf6Zr7B4Cu1 ribbons were measured over a wide temperature range to undertake a comprehensive investigation of their magnetic properties. The construction of comprehensive M–H curve was facilitated by the systematic increase in the magnetic field from 0 to 2.0 T. The first quadrants of the M–H curve (as shown in Fig. 2(a)) were employed to assess the variations in magnetic entropy as a function of temperature and magnetic field.48 Arrott plots were employed to conduct an extensive investigation of the alloy's magnetic transition, which serve as a valuable analytical tool for distinguishing between first-order and second-order transitions.49 The Arrott plot, depicted in Fig. 2(b), exhibits a positive slope at specific temperatures, suggesting a second-order magnetic transition. This discovery is especially noteworthy for magnetocaloric effect (MCE) applications, as second-order transitions are defined by minimal thermal and magnetic hysteresis, as per Banerjee's Criterion.9
| S = Selectronic + Slattice + Smagnetic | (13) |
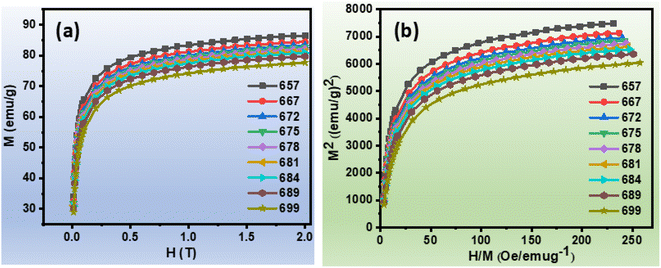 | ||
| Fig. 2 (a)Magnetisation versus magnetic field at constant temperature curve of Fe82Hf6Zr7B4Cu1 ribbons (b) Arrott curves of Fe82Hf6Zr7B4Cu1 ribbons. | ||
According to eqn (13), a system's total entropy (S) is made up of three main parts: electronic entropy (Selectronic), lattice entropy (Slattice), and magnetic entropy (Smagnetic). However, because the contributions from electronic and lattice entropy are small, the isothermal entropy change (ΔS) can be used as a trustworthy approximation of the total entropy in some situations.50 The calculation of ΔS using the magnetisation isotherms M(H,T) shown in Fig. 2(a) is made possible by this approach.
Thermodynamic theory states that the eqn (14).
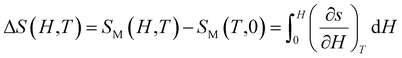 | (14) |
 | (15) |
 | (16) |
Moreover, it is possible to depict it as at discrete temperature intervals like in the eqn (17).51
 | (17) |
The magnetic entropy change (ΔSM) of the Fe82Hf6Zr7B4Cu1 ribbons as a function of temperature was examined under various magnetic fields from 0–2 T as given in Fig. S1.† This allowed for the analysis of the field dependence of ΔSM by linearly fitting the ln(ΔSM) versus ln(H) plot and extracting the slope, denoted as the n exponent, at each temperature.52 n exponent for the Fe82Hf6Zr7B4Cu1 ribbons is illustrated in Fig. S2† with a value of 1.02 observed near the Curie transition temperature (TC). The ΔSM versus T data at a magnetic field of 2.0 T is distinguished by the presence of a broad apex in the ΔSM(T) curve for Fe82Hf6Zr7B4Cu1 ribbons, which is centred near the Curie transition temperature (TC). This observation suggests a strong correlation between the temperature corresponding to the apex of the ΔSM(T) curve (Tpeak) and TC. Furthermore, the field dependence of ΔSpeakM was examined, which demonstrated a progressive increase as the magnetic field increased. The ΔSpeakM values for Fe82Hf6Zr7B4Cu1 ribbons were 0.448 J kg−1 K−1, under a field change of 2 T.
Fe82Hf6Zr7B4Cu1 stands out due to its exceptionally high Curie transition temperature of 678 K, surpassing most previously reported Fe-based alloys as shown in the Table S1.† This makes it an ideal candidate for high-temperature magnetic refrigeration applications, where materials with lower Curie transition temperatures often fail. Although its magnetic entropy change is moderate (0.46 J kg−1 K−1 at 2.0 T), this trade-off is acceptable for applications prioritizing durability and high operating temperatures, such as industrial waste heat management. The alloy's likely amorphous and nanocrystalline microstructure contributes to its thermal stability, soft magnetic properties, corrosion resistance, and scalability for fabrication. Overall, Fe82Hf6Zr7B4Cu1 unique combination of high Curie transition temperature, cost-effectiveness, and stability positions it as a superior material for high-temperature magnetocaloric applications, with potential uses in waste heat recovery and environmental cooling.
The refrigerant capacity (RC) of the Fe82Hf6Zr7B4Cu1 ribbons was assessed using the eqn (18).
 | (18) |
And relative cooling power (RCP) calculating by the eqn (19),53
| RCPFWHM = −ΔSpeakM × ΔTFWHM | (19) |
5. Conclusion
In conclusion, the Fe82Hf6Zr7B4Cu1 ribbons ribbon was successfully created using the melt spinning method, and its structural, thermal, magnetic, and magnetocaloric characteristics were thoroughly studied. The inclusion of hafnium (Hf) in the Fe site of the Fe–Zr–B–Cu matrix was validated by X-ray diffraction (XRD) research. The thermodynamic parameter PHSS, as determined by differential scanning calorimetry (DSC) study, was −0.998. It was discovered that the Curie transition temperature was 678 K and that the magnetic entropy change was 0.448 J kg−1 K−1 at 2.0 T. Relative cooling power and refrigeration capacity were determined to be 11.87 J kg−1 and 14.0 J kg−1, respectively. These findings imply that the novel Fe82Hf6Zr7B4Cu1 ribbons is a good candidate for high-temperature magnetocaloric applications due to its promising magnetocaloric applications.Conflicts of interest
There are no conflict to declare.Acknowledgements
The authors gratefully acknowledge the financial support and research facilities provided by the School of Advanced Sciences (SAS), VIT University. We also acknowledge the Defence Metallurgical Research Laboratory (DMRL), Hyderabad, for providing access to arc melting, melt spinning, XRD, DSC and VSM facilities.References
- S. Kumar, et al., Exploring Magnetocaloric Materials for Sustainable Refrigeration near Hydrogen Gas Liquefaction Temperature, Adv. Funct. Mater., 2024, 34(39), 2402513 CrossRef CAS.
- X. Miao, et al., Novel magnetocaloric composites with outstanding thermal conductivity and mechanical properties boosted by continuous Cu network, Acta Mater., 2023, 242, 118453 CrossRef CAS.
- A. Jackson, Magnetic refrigeration: an eco-friendly technology for the refrigeration at room temperature, Drugs and the Future: Brain Science, Addiction and Society, 2006, pp. 7–10, DOI:10.1016/B978-012370624-9/50005-0.
- C. Paper, C. Aprea, A. Greco, A. Maiorino and C. Masselli, Magnetic refrigeration: an eco-friendly technology for the refrigeration at room temperature, J. Phys.:Conf. Ser., 2015, 655, 012026 CrossRef.
- H. Zhang, et al., Review on the materials and devices for magnetic refrigeration in the temperature range of nitrogen and hydrogen liquefaction, Phys. B, 2019, 558, 65–73 CrossRef CAS.
- A. Vinod, D. Arvindha Babu and M. Wuppulluri, A Short Review on the Evolution of Magnetocaloric La(Fe,Si)13 and Its Fabrication through Melt Spinning, ACS Omega, 2024, 9, 11110–11128 CrossRef CAS PubMed.
- K. G. Sandeman and S. Takei, Magnetocaloric Materials and Applications, in Handbook of Magnetism and Magnetic Materials, Springer International Publishing, Cham, 2021, pp. 1–38, DOI:10.1007/978-3-030-63101-7_13-1.
- M. Zarifi, et al., Direct and indirect measurement of the magnetocaloric effect in the La0.5Ca0.5−xPbxMnO3 (0 ≤ x ≤ 0.2) manganites, J. Magn. Magn. Mater., 2020, 494, 165734 CrossRef CAS.
- P. Z. Z. Nehan, et al., The magnetocaloric effect properties for potential applications of magnetic refrigerator technology: a review, Phys. Chem. Chem. Phys., 2024, 26, 14476–14504 RSC.
- A. L. Pires and I. Introduction, Early Career Scholars In Materials Science 2019 : Reviews Magnetocaloric materials : From micro- to nanoscale, J. Mater. Res., 2019, 34, 134–157 CrossRef.
- N. Kumar, et al., Study on thermodynamic, electronic and magnetic properties of RE2 Cu2 Cd (RE=Dy-Tm) intermetallics: first-principle calculation, Bull. Mater. Sci., 2020, 43, 81 CrossRef CAS.
- M.-H. Phan and S.-C. Yu, Review of the magnetocaloric effect in manganite materials, J. Magn. Magn. Mater., 2007, 308, 325–340 CrossRef CAS.
- S. Mellari, Introduction to magnetic refrigeration: magnetocaloric materials, Int. J. Air-Cond. Refrig., 2023, 31, 5 CrossRef.
- P. Fernández-Yáñez, V. Romero, O. Armas and G. Cerretti, Thermal management of thermoelectric generators for waste energy recovery, Appl. Therm. Eng., 2021, 196, 117291 CrossRef.
- H. Yang, et al., A refrigerant-injection heat pump-based efficient integrated thermal management system for electric vehicles approaching the wide temperature range in China, Energy Convers. Manage., 2023, 288, 117102 CrossRef.
- A. Kitanovski, Energy Applications of Magnetocaloric Materials, Adv. Energy Mater., 2020, 10(10), 1903741 CrossRef CAS.
- J. Lai, et al., Machine learning assisted development of Fe2P-type magnetocaloric compounds for cryogenic applications, Acta Mater., 2022, 232, 117942 CrossRef CAS.
- A. Smith, et al., Materials challenges for high performance magnetocaloric refrigeration devices, Adv. Energy Mater., 2012, 2, 1288–1318 CrossRef CAS.
- H. Chen, et al., Evaluation of thermomagnetic generation performance of classic magnetocaloric materials for harvesting low-grade waste heat, Appl. Energy, 2022, 306, 117999 CrossRef CAS.
- A. G. A. Nnanna, Application of refrigeration system in electronics cooling, Appl. Therm. Eng., 2006, 26, 18–27 CrossRef CAS.
- R. Chein and G. Huang, Thermoelectric cooler application in electronic cooling, Appl. Therm. Eng., 2004, 24, 2207–2217 CrossRef.
- F. Jin, et al., Electron tailoring of thermal and magnetocaloric properties in Tb55TM17.5Al27.5 (TM = Fe, Co, and Ni) metallic glasses, J. Mater. Res. Technol., 2024, 33, 130–140 CrossRef CAS.
- S. Wei, H. Shen, L. Zhang, F. Cao and J. Sun, Magnetic properties and magnetocaloric effects of rare-earth based high-entropy amorphous microwires, J. Mater. Res. Technol., 2024, 33, 6216–6222 CrossRef CAS.
- G. Lei, et al., Cryogenic temperature magnetocaloric effect and critical behavior of GdDyErAlM (M=Fe, Co, Ni) high entropy amorphous alloys, J. Mater. Res. Technol., 2024, 32, 1493–1508 CrossRef CAS.
- M. Barbic, et al., Magnetocaloric materials as switchable high contrast ratio MRI labels, Magn. Reson. Med., 2019, 81, 2238–2246 CrossRef PubMed.
- K. A. GschneidnerJr, V. K. Pecharsky and A. O. Tsokol, Recent developments in magnetocaloric materials, Rep. Prog. Phys., 2005, 68, 1479–1539 CrossRef.
- Y. Zhang, A. Li, W. Hao, H.-F. Li and L. Li, Apatite-type gadolinium-based dense MGd4Si3O13 (M = Mg, Ca, and Sr) ceramics: An emerging class of sub-liquid helium temperature magnetic refrigerant, Acta Mater., 2025, 292, 121033 CrossRef CAS.
- W. Hao, R. Ji, L. Zhu, S. Huang and Y. Zhang, Structural, magnetic and cryogenic magnetocaloric properties in Gd2CrFeO6 ceramic oxide, Solid State Commun., 2025, 399, 115876 CrossRef CAS.
- F. Yang, J. Wang, R. Ji and Y. Zhang, Magnetic Properties and Low-Temperature Magnetocaloric Effect in Yb2TiO5 Oxide, J. Electron. Mater., 2025 DOI:10.1007/s11664-025-11786-x.
- J. Wang, et al., Magnetic properties and magnetocaloric effect in Tb2CoCrO6 oxide, J. Magn. Magn. Mater., 2025, 619, 172897 CrossRef CAS.
- Y. Zhang, et al., Unveiling the Structural, Electronic and Magnetic Properties of Gd 4.5 A 0.5 Si 3 O 13 (A = K, Na, and Li) Oxides With Promising Potential for Low-Temperature Magnetic Cooling, Small, 2025, 21(2), 2409981 CrossRef CAS PubMed.
- N. Haque, A. Hughes, S. Lim and C. Vernon, Rare Earth Elements: Overview of Mining, Mineralogy, Uses, Sustainability and Environmental Impact, Resources, 2014, 3, 614–635 CrossRef.
- Y. Ghorbani, I. M. S. K. Ilankoon, N. Dushyantha and G. T. Nwaila, Rare earth permanent magnets for the green energy transition: Bottlenecks, current developments and cleaner production solutions, Resour., Conserv. Recycl., 2025, 212, 107966 CrossRef CAS.
- A. Golev, M. Scott, P. D. Erskine, S. H. Ali and G. R. Ballantyne, Rare earths supply chains: Current status, constraints and opportunities, Resour. Policy, 2014, 41, 52–59 CrossRef.
- L. F. Kiss, T. Kemény, V. Franco and A. Conde, Enhancement of magnetocaloric effect in B-rich FeZrBCu amorphous alloys, J. Alloys Compd., 2015, 622, 756–760 CrossRef CAS.
- D. Arvindha Babu, Glass Forming Ability, Structure and Soft Magnetic Properties of Amorphous and Nanocrystalline Fe(Ni)-Zr(Nb)-B-Cu Melt Spun Ribbons, Indian Institute of Technology, Madras, 2018 Search PubMed.
- Y. K. Fang, et al., Magnetocaloric effect in Fe–Zr–B–M (M=Mn, Cr, and Co) amorphous systems, J. Appl. Phys., 2009, 105(7), 07A910 CrossRef.
- P. Álvarez, J. S. Marcos, P. Gorria, L. F. Barquín and J. A. Blanco, Magneto-caloric effect in FeZrB amorphous alloys near room temperature, J. Alloys Compd., 2010, 504, 150–154 CrossRef.
- W. Yang, et al., Low-Temperature Magnetic Properties and Magnetocaloric Effect of Fe–Zr–Cu Amorphous Alloys, J. Low Temp. Phys., 2020, 200, 51–61 CrossRef CAS.
- Y. Liu, X. Fu, Q. Yu, M. Zhang and J. Liu, Significant reduction of phase-transition hysteresis for magnetocaloric (La1-Ce)2Fe11Si2H alloys by microstructural manipulation, Acta Mater., 2021, 207, 116687 CrossRef CAS.
- Z. P. Lu, H. Tan, S. C. Ng and Y. Li, The correlation between reduced glass transition temperature and glass forming ability of bulk metallic glasses, Scr. Mater., 2000, 42, 667–673 CrossRef CAS.
- K. Mondal and B. S. Murty, On the parameters to assess the glass forming ability of liquids, J. Non-Cryst. Solids, 2005, 351, 1366–1371 CrossRef CAS.
- L. J. Gallego, J. A. Somoza and J. A. Alonso, Glass formation in ternary transition metal alloys, J. Phys.:Condens. Matter, 1990, 2, 6245–6250 CrossRef CAS.
- A. Takeuchi and A. Inoue, Calculations of Mixing Enthalpy and Mismatch Entropy for Ternary Amorphous Alloys, Mater. Trans. JIM, 2000, 41, 1372–1378 CrossRef CAS.
- B. Ramakrishna Rao, M. Srinivas, A. K. Shah, A. S. Gandhi and B. S. Murty, A new thermodynamic parameter to predict glass forming ability in iron based multi-component systems containing zirconium, Intermetallics, 2013, 35, 73–81 CrossRef CAS.
- P. Alvarez-Alonso, et al., High-magnetic field characterization of magnetocaloric effect in FeZrB(Cu) amorphous ribbons, J. Appl. Phys., 2015, 117, 1–5 CrossRef.
- J. Ma, et al., Critical behavior and magnetocaloric effect in quasi-two-dimensional Mn3Si2Se6, J. Alloys Compd., 2024, 999, 175004 CrossRef CAS.
- K. El Maalam, et al., Magnetocaloric Properties of Zinc-Nickel Ferrites Around Room Temperature, J. Supercond. Novel Magn., 2017, 30, 1943–1947 CrossRef.
- S. Bustingorry, F. Pomiro, G. Aurelio and J. Curiale, Second-order magnetic critical points at finite magnetic fields: Revisiting Arrott plots, Phys. Rev. B, 2016, 93, 224429 CrossRef.
- K. P. Shinde, et al., Magnetocaloric effect and Griffiths phase analysis in a nanocrystalline Ho 2 NiMnO 6 and Ho 2 CoMnO 6 double perovskite, RSC Adv., 2023, 13, 9099–9108 RSC.
- H. Zhang, et al., Correlation between Magnetocaloric Properties and Magnetic Exchange Interaction in Gd54Fe36B10−xSix Amorphous Alloys, Materials, 2023, 16, 3629 CrossRef CAS.
- Y. Li, et al., Successive magnetic transitions and magnetocaloric effect in Dy 3 Al 2 compound, J. Alloys Compd., 2015, 651, 278–282 CrossRef CAS.
- L.-W. Li, Review of magnetic properties and magnetocaloric effect in the intermetallic compounds of rare earth with low boiling point metals, Chin. Phys. B, 2016, 25, 037502 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01759a |
| This journal is © The Royal Society of Chemistry 2025 |