 Open Access Article
Open Access ArticleTernary materials discovery using human-in-the-loop generative machine learning†
Brandon Wilfong ab,
Alexander New
ab,
Alexander New c,
Gregory Bassenab,
Wyatt Bustineb,
Michael J. Pekalac,
Nam Q. Lec,
Karun K. Raoc,
Elizabeth A. Poguec,
Eddie Giengerc,
Michał J. Winiarski
c,
Gregory Bassenab,
Wyatt Bustineb,
Michael J. Pekalac,
Nam Q. Lec,
Karun K. Raoc,
Elizabeth A. Poguec,
Eddie Giengerc,
Michał J. Winiarski d,
Tyrel M. McQueen
d,
Tyrel M. McQueen *abe and
Christopher D. Stiles*c
*abe and
Christopher D. Stiles*c
aDepartment of Chemistry, Johns Hopkins University, 3400 N. Charles Street, Baltimore, 21218, Maryland, USA
bInstitute for Quantum Matter, William H. Miller III Department of Physics and Astronomy, Johns Hopkins University, 3400 N. Charles Street, Baltimore, 21218, Maryland, USA. E-mail: mcqueen@jhu.edu
cResearch and Exploratory Development Department, Johns Hopkins University Applied Physics Laboratory, 11100 Johns Hopkins Road, Laurel, 20723, Maryland, USA. E-mail: Christopher.Stiles@jhuapl.edu
dFaculty of Applied Physics and Mathematics and Advanced Materials Center, Gdansk University of Technology, Narutowicza 11/12, 80-233 Gdansk, Poland
eDepartment of Materials Science and Engineering, Johns Hopkins University, 3400 N. Charles Street, Baltimore, 21218, Maryland, USA
First published on 5th June 2025
Abstract
Machine learning (ML) approaches to materials discovery are limited by data curation, availability, and bias. These issues can be addressed through the generation of new data points representing novel material compositions and/or structures. We demonstrate the implementation of this process to produce and subsequently determine the stability of novel materials using a generative ML model. Furthermore, we successfully synthesize two predicted materials, LiZn2Pt and NiPt2Ga, and use these predictions to extrapolate to other unreported ternary compounds in the Heusler family. Our work demonstrates and expands the use of generative ML models to successfully discover and synthesize novel materials. This has broad implications for material exploration by design, as previous ML approaches to materials discovery were biased by the limits of known phase spaces and experimentalist bias, and has the potential to enable inverse-design of materials with targeted properties.
Recent advances in machine learning (ML) techniques for domain-specific learning tasks have led to an explosive adoption of data-driven scientific exploration in physics and chemistry.1–3 This is particularly true in materials development where the combinatorics of composition, stoichiometry, and structure yield too many possible materials for the community to synthesize and characterize. As such, researchers have been applying ML techniques to this problem in attempts to predict novel materials with targeted properties, such as improved batteries, solar cells, semiconductors, and superconductors.4–8 One outstanding issue with the success of ML techniques in material science applications is the lack of high-quality data that is curated, easily ingestible, complete, and high fidelity.9 To address this, the coordination of materials databases have allowed the implementation of ML workflows into material science research.10–16 Although these databases contain hundreds of thousands of known and theoretical materials with cor-responding structures and properties, the corpus of data is heavily biased toward explored phase spaces and realistically these databases contain only a small fraction of possible materials and their known properties.
To increase the success of ML-driven approaches, methods to improve materials data have been implemented to address two main issues: data completeness and data bias. One approach to address both issues simultaneously is to iteratively loop ML predictions with experimental validation thereby allowing the ML model predictions to continually evolve with the incorporation of new negative and positive data to the ML training sets.8,17,18 This “closed loop” treatment has recently been successful in the prediction and validation of new super-conductors and could be extrapolated to other property prediction problems.8 Although this approach does not require initial property labels for all materials of interest, the unlabeled, and therefore potentially interesting, material candidates must still come from the initial datasets. This restricts data de-biasing.
Therefore, a complementary strategy to expand the number of available materials, beyond what is available in current repositories, is the use of ML models or ab initio methods to generate novel materials and structures.19–27 These generative approaches can be paired with more traditional property-prediction ML models to target materials for specific design problems. To date, developing out-of-distribution material candidates with generative models and predicting properties with ML have been done independently.28–34 In this paper, we present the first successful use of a generative ML model to produce novel materials and structures, determine their thermodynamic stability, and subsequently experimentally synthesize and characterize these new materials in a single human-in-the-loop workflow. This study builds off of our prior work,35 in which we analyzed the capabilities of the generative model we used in this paper and assessed. Here, we extend those results by computationally and experimentally characterizing specific generated materials of interest.
In particular, we use a state-of-the-art generative model, the PGCGM for the generation and prediction of novel materials.23 The PGCGM is a Wasserstein GAN that can stochastically sample possible structures of ternary material systems given their constituent elements and space group.36 In this study, we use the as-released PGCGM which was trained on data taken from Materials Project (MP), Open Quantum Materials Database (OQMD), and inorganic crystal structure database (ICSD). We randomly sample constituent element sets and space groups and then use the PGCGM to generate 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116 material structures Fig. 1. As discussed in the PGCGM paper,23 following generation, these structures were post-processed to merge together spatially-adjacent atoms of the same type to one crystallographic site.
116 material structures Fig. 1. As discussed in the PGCGM paper,23 following generation, these structures were post-processed to merge together spatially-adjacent atoms of the same type to one crystallographic site.
Methods for theoretically assessing the range of possible structures a generative model can predict are limited. Such models can predict novel structures, but their predictions may lack diversity compared to their training data. Measuring the novelty and diversity of generated materials, especially in comparison to training data, remains a needed step in their use (see, e.g., ref. 23 and 26). Averting pathologies such as mode collapse remains an active area of research.33,34,37 However, because the throughput of these methods is far higher than first-principles calculations or experimental synthesis and characterization, use of generative models for predicting structures allows for a faster sampling of unknown phase spaces.
Although the PGCGM is capable of generating large numbers of potential structures, there is no guarantee that the structures will be thermodynamically stable and thus synthesizable. Therefore, we also train a stability-prediction ML model to rapidly screen identified structures for stability (Fig. 1). Specifically, we construct a set of structures from MP with computationally-predicted decomposition enthalpy, previously identified by Bartel et al.38 We use this data to train an ALIGNN model39 to predict decomposition enthalpy relative to the convex hull based on phases in the ML. The decomposition energy is the same as the energy above convex hull, except for phases that lie directly on the convex hull. In those cases, the decomposition energy is the distance from the hypothetical convex hull formed by other phases. A structure is predicted to be stable if its predicted decomposition enthalpy is negative.
We use decomposition enthalpy as a metric for stability because decomposition enthalpy takes positive values for unstable compounds and negative values for stable compounds. In contrast, the commonly used energy above hull takes a value of zero for all stable phases and does not indicate the degree of stability relative to competing phases. Thus, decomposition enthalpy provides more information about stability relative to other phases in the multicomponent system; it range of values also makes it more suitable for the loss functions used by regression-based ML methods. Outside of decomposition enthalpy and energy above hull, material stability can be characterized in other ways.40,41
In general, this process can be adapted to include any secondary prediction model for thermodynamic stability and/or a desired property prediction such as superconductivity, elastic properties, and/or magnetism; this is the reason for including the general notation of property-prediction model in the workflow shown in Fig. 1.
After screening generated structures for stability, 2652 have a predicted decomposition enthalpy less than 0.1 eV per atom, 281 are less than 0.01 eV per atom, and 195 are less than 0 eV per atom. Domain expertise is further used to down-select materials based on factors such as oxidation states of constituent elements, coordination of atoms in the generated structure, and feasibility of synthesis. This step is currently required due to the large number of prediction candidates from the PGCGM process; future work and advances in synthesizability prediction would be required to incorporate this subject matter expertise in an automated way into the prediction process. Table 1 shows select PGCGM-generated materials and their ALIGNN-predicted decomposition enthalpies (Ed). The full list of structures and predicted properties is in the ESI.† Sampled PGCGM structures may be unique and strictly theoretical, or they may reflect the theoretical structures already listed in the training data. LiZn2Pt with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m is found in the subset of MP that PGCGM was trained on (mp-867251), and in the subset of OQMD PGCGM was trained on (OQMD IDs 1042055, 1042723, and 1047136) in the P63/mmc space group. Even when the PGCGM predicts two compositions with the same stoichiometry and space group, the structures can still vary based on the precise positioning of atoms, which affects properties. The random sample z that the PGCGM takes as input enables generation of different structures with the same elements and space group.
m is found in the subset of MP that PGCGM was trained on (mp-867251), and in the subset of OQMD PGCGM was trained on (OQMD IDs 1042055, 1042723, and 1047136) in the P63/mmc space group. Even when the PGCGM predicts two compositions with the same stoichiometry and space group, the structures can still vary based on the precise positioning of atoms, which affects properties. The random sample z that the PGCGM takes as input enables generation of different structures with the same elements and space group.
| Formula | Space group | Predicted Ed (eV per atom) |
|---|---|---|
| BaH8Pt | I4/mmm | −0.1732166 |
| LiZn2Pt | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
−0.1462675 |
| HfH24W | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
−0.129171 |
| Ba3AsH6 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
−0.1043272 |
| KPdF6 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
−0.0996605 |
| RbAlS | Immm | −0.0987449 |
| NiPt2Ga | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
−0.0070151 |
In this work, LiZn2Pt was selected as the most promising candidate from the initial round of material generation, energy classification, and down-selection due to its composition and predicted structure. The selection of LiZn2Pt was due to its second-lowest Ed and Ef amongst all candidates and that the predicted structure is a Heusler, a structure type that is ubiquitous in solid-state chemistry.42–44
We considered several other material candidates as well. NaZn2Pd and NaZn2Pt appear in the list of PGCGM candidates (with predicted Ed values of −0 014375 eV per atom and −0 045241 eV per atom, respectively). Despite these negative predicted decomposition enthalpies, we were unable to successfully synthesize either. Thus, we also attempted to synthesize LiZn2Pd; this composition was targeted because there are no experimental reports of Li–Zn–Pd ternary phases, although it was not a material appearing in the PGCGM prediction list.
The X-ray powder diffraction patterns and subsequent Rietveld using the PGCGM-generated Cu2MnAl-type Heusler (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure are presented in ESI.† Importantly, the Heusler family has a range of related structures determined by the amount of order or disorder in the Heusler sublattices.43–45 Disorder in Heusler structures can be difficult to determine without synchrotron X-ray or neutron diffraction, but a qualitative approach to the X-ray diffraction offers some insight and is comprehensively shown in ESI† to justify the successful synthesis of LiZn2Pt (and LiZn2Pd) in the same structure as generated by the PGCGM. Overall, the successful synthesis of LiZn2Pt was a proof-of-concept of the ability of the human-in-the-loop workflow to help discern which regions of phase space house stable phases that have not been previously experimentally realized.
m) structure are presented in ESI.† Importantly, the Heusler family has a range of related structures determined by the amount of order or disorder in the Heusler sublattices.43–45 Disorder in Heusler structures can be difficult to determine without synchrotron X-ray or neutron diffraction, but a qualitative approach to the X-ray diffraction offers some insight and is comprehensively shown in ESI† to justify the successful synthesis of LiZn2Pt (and LiZn2Pd) in the same structure as generated by the PGCGM. Overall, the successful synthesis of LiZn2Pt was a proof-of-concept of the ability of the human-in-the-loop workflow to help discern which regions of phase space house stable phases that have not been previously experimentally realized.
Following the successful synthesis of LiZn2Pt and LiZn2Pd, several Heusler-type PGCGM predictions with negative Ef and Ed were targeted. To that end, a new ternary phase with stoichiometry NiPt2Ga was successful. Fig. 2 shows the X-ray powder diffraction pattern and Rietveld refinement for NiPt2Ga in the P4/mmm tetragonal Heusler space group. Interestingly, this is not the exact same structural prediction from the PGCGM which predicted a Cu2MnAl-type cubic Heusler similar to LiZn2Pt. These structures are obviously very closely related (ESI†), differing only by a tetragonal distortion. To confirm their proximity in energy, a comparison of DFT-computed energy for both structures was completed. The total energy for the PGCGM-predicted Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure and P4/mmm differ by ≈0.15 eV per atom with P4/mmm having lower overall energy (ESI†). Neither the Fm
m structure and P4/mmm differ by ≈0.15 eV per atom with P4/mmm having lower overall energy (ESI†). Neither the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m or P4/mmm structures for NiPt2Ga were present in the training data for the PGCGM – the P4/mmm structure of NiPt2Ga is present in OQMD (OQMD ID 1364774) but was not used to train the iteration of the PGCGM model used in this work. Thus, the successful synthesis of NiPt2Ga takes the success of the PGCGM workflow beyond informing us to regions of phase space with unreported phases and structures that are likely to be stable, but enable us to synthesize unknown materials that exist beyond the database curation of the domain expertise.
m or P4/mmm structures for NiPt2Ga were present in the training data for the PGCGM – the P4/mmm structure of NiPt2Ga is present in OQMD (OQMD ID 1364774) but was not used to train the iteration of the PGCGM model used in this work. Thus, the successful synthesis of NiPt2Ga takes the success of the PGCGM workflow beyond informing us to regions of phase space with unreported phases and structures that are likely to be stable, but enable us to synthesize unknown materials that exist beyond the database curation of the domain expertise.
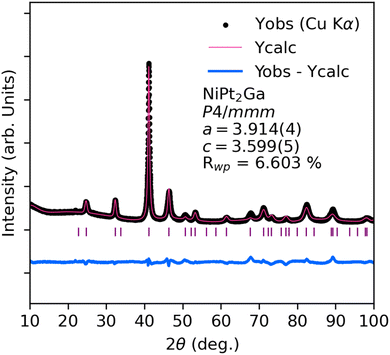 | ||
| Fig. 2 Powder X-ray diffraction of phase pure NiPt2Ga Rietveld refinement using the P4/mmm tetragonal Heusler structure. | ||
These three materials are electronically quite unusual. They all have a valence electron count (VEC) of 33 for NiPt2Ga and 35 electrons for LiZn2Pt/Pd – very high among known Heuslers (ESI†). Typically, this high VEC means that the electronic character of these Heuslers can be significantly different than the majority of Heuslers and enable access to unique regions of the band structure at the Fermi level. For example, the high VEC in LiZn2Pt and LiZn2Pd causes the Fermi level to sit directly at a band crossing between the L and Γ point which may be a source of unique transport properties. This band crossing is observed in Fig. 3 for NiPt2Ga but due to its lower VEC, it is ≈1.5 eV above the Fermi level and possible exotic properties arising from this Fermiology is not easily accessible.
Here, we have worked with materials that, although electronically unusual, belong to the well-studied Heusler class. The discovery of usable materials from truly novel classes is a challenge that still remains unsolved.26,46 Standard metrics like stable, unique, novel (SUN) assess only if a given structure is not in existing databases and do not check if the structure's materials class is novel.26 As the field progresses, we recommend the use of distance-based measurements (whether using featurizations like Magpie47 or ML model latent spaces) for determining how unlike generated materials are from known ones. This may provide additional mechanisms for going beyond current dataset limitations and mitigating dataset bias.
In general, the electronic properties of Heusler compounds are largely determined by their VEC and not their actual chemical composition, magnetism aside. For example, superconductivity in Heuslers is expected in the range of VEC of 26–29, with a peak in critical temperature (Tc) at VEC = 27.48,49 Measured magnetic susceptibility of NiPt2Ga measured down to 1.8 K shows antiferromagnetic behavior which persists up to room temperature (ESI†) with isothermal magnetization at 300 K showing antiferromagnetic-like behavior. High temperature susceptibility is required to resolve the ordering temperature as NiPt2Ga may be a candidate for study of metallic antiferromagnetism at room temperature. Magnetic susceptibility of LiZn2Pt and LiZn2Pd (ESI†) measured down to 0.4 K (for LiZn2Pt and LiZn2Pd) shows paramagnetic behavior and no anomalous magnetic transitions are revealed. Additionally, we performed a preliminary search of antiferromagnetic configurations with DFT (ESI†), none of which showed a significant decrease in energy from the ferromagnetic configuration. Overall, superconductivity is not observed in any of these compounds and in general, this is expected due to the high VEC outside the 26–29 range seemingly excluding superconductivity.
In conclusion, we have demonstrated the first successful use of a generative ML model to produce crystal structures, determine their stability through a secondary ML process, and experimentally verify these new structures. LiZn2Pt was generated using the PGCGM model in the Cu2MnAl-type Heusler structure and predicted to be stable. Subsequently, phase pure LiZn2Pt was successfully synthesized. Due to its proximity and lack of reported ternaries LiZn2Pd was also successfully synthesized. Following the successful synthesis of the aforementioned compounds, Heusler and Heusler-like PGCGM predicted structures were targeted leading to the successful synthesis of NiPt2Ga in the tetragonal Heusler structure. This work has broad implications for material exploration by design as previous ML approaches to materials discovery were biased by the limits of known phase spaces and experimentalist bias. The ability to generate and synthesize novel materials that are structurally and compositionally unique enables inverse-design of materials with targeted properties.
Data availability
We used the pretrained PGCGM available at https://github.com/MilesZhao/PGCGM/tree/main, including its scripts for validating generated structures. The code for training and evaluating our ALIGNN model is hosted at https://github.com/newalexander/generative-materials-discovery. Other relevant data, including the MP structure IDs of the training data and trained ALIGNN model, as well as the structures of the generated materials and their ALIGNN-predicted decomposition enthalpies, are hosted on FigShare.50Author contributions
C. S., A. N., and T. M. M. contributed to the conception of the work. B. W., G. B., T. M. M., E. P., and E. G. contributed to the setup and design of experiments. B. W. and G. B. synthesized samples. A. N. created the ML model with some contributions from M. P. B. W., A. N., G. B., C. S., and T. M. M. heavily contributed to the writing and revising of the manuscript. B. W., G. B, W. B., and T. M. M. collected and analyzed experimental data. W. B., K. K. R., and N. Q. L. computed electronic structure calculations for the relevant compounds. M. W. contributed to the understanding of the electronic structure and bonding in these Heusler alloys.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge internal financial support from the Johns Hopkins University Applied Physics Laboratory's Independent Research & Development (IR&D) Program for funding portions of this work. The MPMS3 system used for magnetic characterization was funded by the National Science Foundation, Division of Materials Research, Major Research Instrumentation Program, under Grant #1828490. Calculations were performed using computational resources of the Maryland Advanced Research Computing Center and the Advanced Research Computing at Hopkins (ARCH) Rockfish cluster.Notes and references
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto and L. Zdeborová, Rev. Mod. Phys., 2019, 91, 045002 CrossRef CAS.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang and L. Yang, Nat. Rev. Phys., 2021, 3, 422–440 CrossRef.
- J. Im, S. Lee, T.-W. Ko, H. W. Kim, Y. Hyon and H. Chang, npj Comput. Mater., 2019, 5, 37 Search PubMed.
- Y. Liu, B. Guo, X. Zou, Y. Li and S. Shi, Energy Storage Mater., 2020, 31, 434–450 CrossRef.
- V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione, S. Curtarolo and I. Takeuchi, npj Comput. Mater., 2018, 4, 29 CrossRef.
- C. Qin, J. Liu, S. Ma, J. Du, G. Jiang and L. Zhao, J. Mater. Chem. A, 2024, 12, 22689–22702 RSC.
- E. A. Pogue, A. New, K. McElroy, N. Q. Le, M. J. Pekala, I. McCue, E. Gienger, J. Domenico, E. Hedrick, T. M. McQueen, B. Wilfong, C. D. Piatko, C. R. Ratto, A. Lennon, C. Chung, T. Montalbano, G. Bassen and C. D. Stiles, npj Comput. Mater., 2023, 9, 181 CrossRef.
- L. Zhu, J. Zhou and Z. Sun, J. Phys. Chem. Lett., 2022, 13, 3965–3977 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B, 2002, 58, 364–369 CrossRef PubMed.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- A. O. Oliynyk and A. Mar, Acc. Chem. Res., 2018, 51, 59–68 CrossRef CAS PubMed.
- J. Graser, S. K. Kauwe and T. D. Sparks, Chem. Mater., 2018, 30, 3601–3612 CrossRef CAS.
- A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher, S. Curtarolo, A. V. Davydov, R. Agarwal, L. A. Bendersky, M. Li, A. Mehta and I. Takeuchi, Nat. Commun., 2020, 11, 5966 CrossRef CAS PubMed.
- Z. Rao, P.-Y. Tung, R. Xie, Y. Wei, H. Zhang, A. Ferrari, T. Klaver, F. Körmann, P. T. Sukumar, A. K. da Silva, Y. Chen, Z. Li, D. Ponge, J. Neugebauer, O. Gutfleisch, S. Bauer and D. Raabe, Science, 2022, 378, 78–85 CrossRef CAS PubMed.
- A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. F. Balakirev, D. E. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz and M. I. Eremets, Nature, 2019, 569, 528–531 CrossRef CAS PubMed.
- M. Somayazulu, M. Ahart, A. K. Mishra, Z. M. Geballe, M. Baldini, Y. Meng, V. V. Struzhkin and R. J. Hemley, Phys. Rev. Lett., 2019, 122, 027001 CrossRef CAS PubMed.
- D. V. Semenok, I. A. Kruglov, I. A. Savkin, A. G. Kvashnin and A. R. Oganov, Curr. Opin. Solid State Mater. Sci., 2020, 24, 100808 CrossRef CAS.
- M. Alverson, S. G. Baird, R. Murdock, E. S.-H. Ho, J. Johnson and T. D. Sparks, Digital Discovery, 2024, 3, 62–80 RSC.
- Y. Zhao, E. M. D. Siriwardane, Z. Wu, N. Fu, M. Al-Fahdi, M. Hu and J. Hu, npj Comput. Mater., 2023, 9, 38 CrossRef.
- E. Kim and S. V. Dordevic, J. Phys.: Condens. Matter, 2023, 36, 025702 CrossRef PubMed.
- Z. Ren, S. I. P. Tian, J. Noh, F. Oviedo, G. Xing, J. Li, Q. Liang, R. Zhu, A. G. Aberle, S. Sun, X. Wang, Y. Liu, Q. Li, S. Jayavelu, K. Hippalgaonkar, Y. Jung and T. Buonassisi, Matter, 2022, 5, 314–335 CrossRef CAS.
- C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, Z. Wang, A. Shysheya, J. Crabbé, S. Ueda, R. Sordillo, L. Sun, J. Smith, B. Nguyen, H. Schulz, S. Lewis, C.-W. Huang, Z. Lu, Y. Zhou, H. Yang, H. Hao, J. Li, C. Yang, W. Li, R. Tomioka and T. Xie, Nature, 2025, 639(8055), 624–632 CrossRef CAS PubMed.
- E. T. Chenebuah, M. Nganbe and A. B. Tchagang, npj Comput. Mater., 2024, 10, 198 Search PubMed.
- C. W. Park and C. Wolverton, Phys. Rev. Mater., 2020, 4, 063801 CrossRef CAS.
- A. New, M. J. Pekala, N. Q. Le, J. Domenico, C. D. Piatko and C. D. Stiles, ICML 2022 2nd AI for Science Workshop, 2022 Search PubMed.
- R. E. A. Goodall and A. A. Lee, Nat. Commun., 2020, 11, 6280 CrossRef CAS PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- T. Long, N. M. Fortunato, I. Opahle, Y. Zhang, I. Samathrakis, C. Shen, O. Gutfleisch and H. Zhang, npj Comput. Mater., 2021, 7, 66 CrossRef CAS.
- Y. Zhao, M. Al-Fahdi, M. Hu, E. M. D. Siriwardane, Y. Song, A. Nasiri and J. Hu, Adv. Sci., 2021, 8, 2100566 CrossRef CAS PubMed.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, ACS Cent. Sci., 2020, 6, 1412–1420 CrossRef CAS PubMed.
- A. New, M. Pekala, E. A. Pogue, N. Q. Le, J. Domenico, C. D. Piatko and C. D. Stiles, 1st Workshop on the Synergy of Scientific and Machine Learning Modeling @ ICML2023, 2023 Search PubMed.
- M. Arjovsky, S. Chintala and L. Bottou, Proceedings of the 34th International Conference on Machine Learning, 2017, pp. 214–223 Search PubMed.
- D. Saxena and J. Cao, ACM Comput. Surv., 2021, 54(3), 63 Search PubMed.
- C. J. Bartel, A. Trewartha, Q. Wang, A. Dunn, A. Jain and G. Ceder, npj Comput. Mater., 2020, 6, 97 CrossRef.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 185 CrossRef.
- M. Aykol, S. S. Dwaraknath, W. Sun and K. A. Persson, Sci. Adv., 2018, 4, eaaq0148 CrossRef PubMed.
- J. Jang, G. H. Gu, J. Noh, J. Kim and Y. Jung, J. Am. Chem. Soc., 2020, 142, 18836–18843 Search PubMed.
- J. K. Kawasaki, S. Chatterjee, P. C. Canfield and G. Editors, MRS Bull., 2022, 47, 555–558 CrossRef CAS.
- T. Graf, F. Casper, J. Winterlik, B. Balke, G. H. Fecher and C. Felser, Z. Anorg. Allg. Chem., 2009, 635, 976–981 Search PubMed.
- T. Graf, S. S. P. Parkin and C. Felser, IEEE Trans. Magn., 2011, 47, 367–373 CAS.
- T. Graf, C. Felser and S. S. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- T. Klimczuk, C. H. Wang, K. Gofryk, F. Ronning, J. Winterlik, G. H. Fecher, J.-C. Griveau, E. Colineau, C. Felser, J. D. Thompson, D. J. Safarik and R. J. Cava, Phys. Rev. B, 2012, 85, 174505 CrossRef.
- M. J. Winiarski, G. Kuderowicz, K. Górnicka, L. S. Litzbarski, K. Stolecka, B. Wiendlocha, R. J. Cava and T. Klimczuk, Phys. Rev. B, 2021, 103, 214501 CrossRef CAS.
- A. New, Materials-Discovery, 2024, https://figshare.com/articles/dataset/materials-discovery_zip/25783221.
Footnote |
† Electronic supplementary information (ESI) available: All experimental, computational, and machine learning methods used in this work. Additional X-ray diffraction analysis of the LiZn2Pt and LiZn2Pd phases are provided in the context of order and disorder in the Heusler structure. X-ray diffraction and Rietveld refinement of as-synthesized NiPt2Ga is presented. Microscopic analysis is performed using scanning electron microscopy (SEM) images and elemental analysis via energy dispersive spectroscopy (EDS) of as-recovered LiZn2Pt, LiZn2Pd, and NiPt2Ga phases. Magnetization measurements for all three samples are presented with LiZn2Pt and LiZn2Pd measured down to 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K in an attempt to observe superconductivity. Isothermal magnetization at various temperatures was measured for NiPt2Ga to confirm the antiferromagnetic character of the sample up to 300 K in an attempt to observe superconductivity. Isothermal magnetization at various temperatures was measured for NiPt2Ga to confirm the antiferromagnetic character of the sample up to 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. The representative crystal structures of the top 6 (excluding LiZn2Pt) candidates from the PGCGM model are shown. Band structures and DOS computations for LiZn2Pt and LiZn2Pt in the Cu2MnAl-type Heusler structure and NiPt2Ga in the P4/mmm tetragonal Heusler are presented. See DOI: https://doi.org/10.1039/d5ra00427f K. The representative crystal structures of the top 6 (excluding LiZn2Pt) candidates from the PGCGM model are shown. Band structures and DOS computations for LiZn2Pt and LiZn2Pt in the Cu2MnAl-type Heusler structure and NiPt2Ga in the P4/mmm tetragonal Heusler are presented. See DOI: https://doi.org/10.1039/d5ra00427f |
| This journal is © The Royal Society of Chemistry 2025 |


