Emulsion electrocoalescence in microfluidics: impact of local electric fields

Abstract

The mechanism of coalescence of aqueous droplet pairs under an electric field is quantitatively studied using microfluidics in quiescent conditions. We experimentally trap droplet pairs and apply electric fields with varying frequencies and formulation compositions. We find that the electrical resistance of the oil used as continuous phase controls the onset of electrocoalescence in quiescent conditions. We observe that the local field enhancement between droplets strongly depends on formulations but also on the number of droplets across the electrodes. These findings provide a better understanding of the onset of electrocoalescence and pave a route towards the rationalization of droplet-based microfluidics operations.

---

Electrocoalescence is the fusion of droplets dispersed in a continuous phase by the effect of electrostatic interactions. It is a well-established principle used in the petroleum industry for oil refining and separation from brine^1,2 and a physical mechanism proposed to explain heavy rains from atmospheric clouds.³ In the past two decades electrocoalescence also found applications in the field of droplet-based microfluidics for the precise addition of reagents and for the controlled initiation of chemical reactions in droplets.^4–8 This electrically switchable coalescence principle is important for the implementation of biological workflows that require automatized multi-step processing of material and reagents with external control.^9–12 It completes the toolbox for active control of droplet actuation by electric field, together with high-throughput droplet sorting by dielectrophoresis^13–15 and with the control of droplet production.^16–18

Obviously, electrocoalescence requires an electric field to be applied between droplets. What is the critical value of the voltage to be applied at electrodes to obtain coalescence is a very basic question that remains unanswered. Microfluidics provides means to address this question with controlled emulsions and geometries. However, already in simple geometries, the literature indicates very diverse – and sometimes inconsistent – threshold values: Zagnoni et al. obtain electrocoalescence of droplets in flow for applied fields of order 0.3 kV m⁻¹,¹⁹ Szymborski et al. at 10 kV m⁻¹,²⁰ Leary et al. at 250 kV m⁻¹,²¹ Thiam et al. at 1 MV m⁻¹,²² Priest et al. at 1.5 MV m⁻¹.²³ The results might depend on the applied frequency^7,20 or not²³ and most certainly depend on the formulations used.

The theoretical description of electrocoalescence lies in the framework of electrohydrodynamics pioneered by Melcher and Taylor.^24,25 In brief, the problem has two sides: first, the applied electric field results in a net driving force on droplets: the force originates from the dipole–dipole interaction of the polarized droplets. The ratio of conductivities and of dielectric constants control both the droplet deformation and direction of the motion.^26,27 For electrically conducting droplets immersed in a leaky dielectric the force is attractive in the direction of the field and repulsive in the orthogonal directions^28–31 bringing droplets together in line, not necessarily sufficient for full coalescence.^32–34 Second, the coalescence process, namely the destabilisation of the oil film separating the droplets is itself dependent on the electric field across the oil interface. In emulsions, droplets are stabilised against coalescence by surfactants. The (meta)-stability of the droplets is described by the interplay of interfacial forces and hydrodynamics, controlling the behaviour of colloidal systems (floculation, adhesion,…).³⁵ In electric fields, the additional attractive interaction among droplets changes the stability of the film which ruptures for a sufficiently large surface charge at the droplet interface. The instability is described similar to the stability of a thin film in spinodal dewetting,³⁶ or with analogies with electroporation mechanisms for adhesive emulsions.³⁷ The stability criterion of the film is expected to depend on formulations and as stated by Vlahovska³⁰ ‘drops with more complex interfaces, e.g. coated with surfactants are likely to display additional rich electrohydrodynamics and merit further investigation.’

Motivated by these identified unknowns and by the practical importance of the electrocoalescence principle in microfluidics, we experimentally analyze electrocoalescence. Our approach combines well established microfluidic techniques to trap droplets between microfabricated electrodes. Monodisperse droplets are produced, actuated and trapped to study their coalescence under the application of an electric field in quiescent conditions. By varying the formulations of the emulsions, we find that the electrical resistivity of the oil phase – a parameter which is neglected in microfluidics – plays a significant role. The local field between the droplet pairs is found to be orders of magnitude larger than the applied field with an amplification controlled by the electric properties of the formulations. In addition, we observed experimentally that the field enhancement is further amplified when multiple droplets are confined between the electrodes: the threshold voltage for coalescence linearly decreases with the number of droplets, thereby explaining why emulsions appear to be experimentally more unstable to electric fields than droplet pairs.

We use microfluidics to study electrocoalescence in a controlled, quiescent environment. We couple a flow focusing junction³⁸ to an array of traps^39,40 designed to obtain 36 droplet pairs (Fig. 1a and b). Once the droplet pairs are trapped in the system, the flow is stopped. An electric field parallel to the droplet pair orientation is applied across electrodes patterned using the microsolidics methods⁴¹ (Fig. 1c, ESI Fig. S1 and S2†). We first fix the formulation to a continuous phase of fluorocarbon oil HFE 7500 with 5% w/w of a non-ionic block-copolymer surfactant (Fluosurf, Emulseo) and an aqueous phase of millipore water. The voltage across the electrodes is quasistatically increased. For a fixed field frequency of 10 kHz, at low voltages, typically below 100 V, all droplet pairs remain intact (Fig. 1c). At higher voltages, the fraction r of coalesced drops, i.e. the number of coalesced droplet pairs divided by the total number of droplet traps increases with U (Fig. 1d and e, ESI Methods and Fig. S3†). r shows a sharp increase from 0 to 1 in the range 200–300 V and is a function of the applied frequency: the coalescence threshold voltage U* defined as the voltage at which half of the droplet pairs coalesced is found to increase with decreasing frequency. For a given experimental condition, the threshold U* is found to be consistent among repeats (N = 3). U* provides a means to rescale all data on a master curve (Fig. 1g), and is used as a quantitative measurement of the electrocoalescence efficiency for the different experimental conditions (surfactant concentration, oil type, droplet ionic content, amount of droplets…).

Fig. 1 Experimental workflow. (a) Micrograph of the coalescence chamber during droplet loading under a pressure control. (b) The coalescence chamber loaded with 36 droplet pairs. Droplets that were not trapped have been flushed out of the chamber. The electrodes are in black. (c–e) Zoom on the trapping array for U = 0 V (c), 340 V (d) and 380 V (e) at f = 10 kHz. (f) Fraction r of coalesced droplet pairs as a function of the applied voltage U for different frequencies f of the electric field. The continuous phase is HFE 7500 with 5% w/w surfactant while the dispersed phase is millipore water. (g) Fraction r of coalesced droplet pairs rescaled with the coalescence threshold voltage U*. Inset: coalescence threshold voltage U* as a function of the frequency f of the electric field. (N = 3). Scale bars are 200 μm.

We first test the impact of formulations on electrocoalescence, by varying the surfactant concentration in the system when using millipore water as the aqueous phase and HFE 7500 as continuous phase. We perform the experiment with surfactant concentrations of 0.1% w/w, 1% w/w and 5% w/w. r is measured for various frequencies of the electric field as a function of U, as above (ESI Fig. S3†), to obtain U* as a function of the frequency f (Fig. 2a). We confirm that for a fixed composition, U* decreases with increasing f. But at low surfactant concentrations, we observe two regimes: a strong decrease of U* at small frequencies f < f_c and a plateau at large frequency f > f_c where f_c depends on the experimental conditions. These experimental results highlight the strong influence of surfactant concentration on the electrocoalescence efficiency. We could be tempted to interpret this effect as a stabilising role of the surfactant because the droplets are more stable against coalescence at high surfactant concentrations. Yet, it must be reminded that the interfacial coverage of the surfactant is almost unchanged at these concentrations^42,43 which cannot explain such a wide variation in stabilisation efficiency (ESI Methods and Fig. S4†). We performed another set of experiments using mixtures of oils (HFE 7500 and FC 40) at fixed surfactant concentration of 5% w/w (Fig. 2b) which does not significantly change the interfacial tension and recover similar trends.

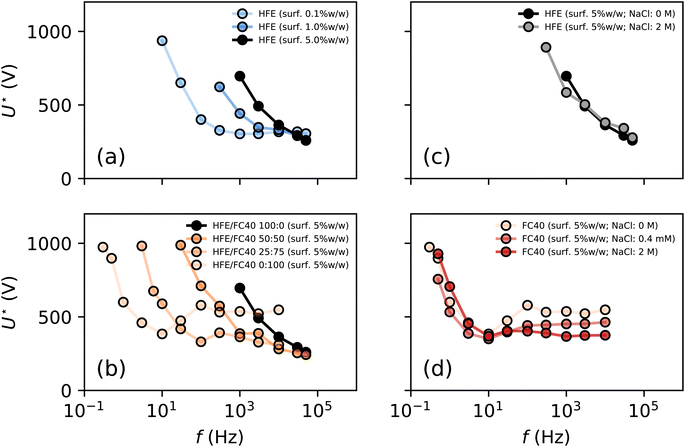Fig. 2 Formulation dependence of electrocoalescence efficiency. (a) U* is a function of the frequency of the electric field and of the surfactant concentration (for an oil phase of HFE 7500 and aqueous droplets of millipore water). (b) For a fixed surfactant concentration, U* strongly depends on the nature of the oil (here the oil properties, especially the oil resistivity (ESI Fig. S5†) are varied using mixtures of FC 40 and HFE 7500). (c and d) The aqueous phase conductivity does not significantly influence the electrocoalescence as shown in the two extreme cases of HFE 7500 (c) and FC 40 (d) with varying salt concentrations ranging 0–2 M.

The dependence of the electrical properties of the continuous phase must therefore be accounted for in the interpretation of our experimental results. The oil electrical resistivity ρ is decreased by more than one order of magnitude with surfactant (Fig. 3). For the sake of completeness, we also characterized the relative permittivity ε of the oil phase which is shown to be independent on surfactant concentration (Fig. 3). With these formulations, ρ varies over two orders of magnitude with a moderate three-fold variation of ε over the composition range (Fig. 3).

Fig. 3 Electrical properties of the continuous phase. (a and b) The electric resistivity and relative permittivity of HFE 7500 as a function of surfactant concentration. (c) Charge relaxation time scale τ for HFE 7500 solutions. The solid and dotted lines represent the average and standard deviation of the measurement without surfactant. (d and e) The electric resistivity and relative permittivity of mixtures of FC 40 and HFE 7500 at a surfactant concentration of 5% w/w. (f) Charge relaxation time scale τ for FC 40/HFE 7500 mixtures. Error bars represent the standard deviation (N = 3).

The dependence of the electrocoalescence efficiency therefore relates to the electric properties of the oil: we find that U*(f) is a function of the resistivity of the oil (ρ). Our experimental results confirm that the resistivity of the continuous phase is the main parameter controlling the electrocoalescence process. The case of FC 40 with 5% w/w surfactant appears to be non-monotonous, with a minimum at intermediate frequencies (f ∼ 10 Hz). We repeated the experiments for the two limiting cases of FC 40 and HFE 7500 with 5% w/w surfactant. We varied the electrical resistivity of the aqueous phase [small rho, Greek, circumflex] in the system by adding NaCl (0 M, 4 × 10⁻⁴ M and 2 M) and repeated the experiments for HFE 7500 and FC 40 with 5% w/w surfactant (Fig. 2c and d). We observe that: (i) the sharp dependence of U* with f at f < f_c does not depend on [small rho, Greek, circumflex], for both FC 40 and HFE 7500, (ii) the plateau value for U* at f > f_c decreases with decreasing [small rho, Greek, circumflex]. However this change in the plateau value of U* is weak: a change of four orders of magnitude of the ion concentration changes U* by less than 50%.

With the geometry of the system, obtaining an analytical description of the field distribution is not possible. In order to gain insights on the underlying mechanisms, we numerically model our experimental setup using a minimal electric model in two dimensions (COMSOL, ESI Methods and Fig. S5–S7†). We calculate the maximal value of the electric field in the domain comprising the droplets and oil phase. In the absence of droplets, the field is homogeneous and is a function of the frequency as expected from a simple voltage divider model. We define the droplets as non-deformable objects with a spacing distance of 100 nm or 1 micron between the edges of the droplets and compute the value of the field across the droplet–droplet interface for a pair of droplets. The actual spacing in the experiments is unknown as it is difficult to optically resolve here but a reasonable estimate would be below 1 micron.⁴⁴ The field across the oil film is significantly enhanced compared to the applied field, with a dependence on the thickness of the oil film and of the electric properties of the oil (ESI Fig. S6†), as expected for conducting spheres in a uniform field.⁴⁵ For a fixed gap size, the field increases at low frequency, shows a plateau and decrease at higher frequency. The cutoff frequencies are given by the PDMS/oil high-pass filter (at low frequency) as a first approximation and the water droplet charge relaxation at high frequency [small tau, Greek, circumflex] = ε₀[small epsilon, Greek, circumflex][small rho, Greek, circumflex] (only dependent on the aqueous properties here). A simple electric model qualitatively reproduces the low frequency decay (ESI Fig. S8†). The dominating capacity originates from the dielectric PDMS layer insulating the electrode from the channel (of width l_P and dielectric constant ε_P, the electrodes being spaced by a distance l). The dominating resistivity is the resistivity of the oil. Both determine the time-scale of an equivalent RC high-pass filter (ESI Fig. S8†) as:

For the range of parameters tested experimentally [small tau, Greek, circumflex] ≲ 2 μs, which confirms that the electric properties of the aqueous phase marginally influences the electrocoalescence in the range of frequency tested here (1/f > 10 μs). Hence, the droplet is approximated as a perfect conductor in all cases. We observe however that in the limit of high resistivity, the low frequency cutoff is not strictly given by the PDMS/oil RC circuit and deviations are observed, especially for the 100 nm gap (ESI Fig. S7†).

It is clear that our simple model cannot be used to predict the exact value of the field across the droplet–droplet since the gap is unknown: determining the stability condition for the film would require to compute the energy density in the film as a function of spacing distance and add it to the energy of interaction of the droplet-oil-droplet system in the absence of field which is also unknown in our case. But they provide a guide to rescale the experimental data. We rescaled the frequencies by the cutoff frequency of the PDMS/oil RC circuit (Fig. 4a).

Fig. 4 Rescaling of the experimental data. (a) Experimental data rescaled with the PDMS/oil RC constant. The data are grouped in two subsets. (b) Data rescaled adding a correction factor c. Inset: value of the correction factor c as a function of oil charge relaxation time, showing the two regimes c ∼ 1 and c ∼ 5, function of τ.

Interestingly, the data partly collapse and two regimes are observed at high conductivity and low conductivity. This effect was captured in the simulations: we improve the rescaling of the data by a correction factor c and plot c as a function of the charge relaxation time-scale of the oil τ = ρε₀ε (Fig. 4b). The correction c is shown to be small (c ∼ 1) at τ < 10⁻⁴ s and constant above (c ∼ 5), indicating that the PDMS is not the sole responsible for the capacitance in the system and that the dielectric properties of the oil eventually have to be accounted for and dominate at low conductivity.

Our results are compatible with Thiam et al.²² showing a minor effect of salt concentration on the coalescence diagram for droplet pairs in flow at small separation distances, and Priest et al.²³ showing a minor effect in static conditions. Szymborski et al. observed a weak dependence of the critical voltage for coalescence with salt concentration, with typical variations of the critical voltage in the range 100–350 V. However, it is striking to observe that the critical voltage to coalesce the emulsion is of order 100 V over 25 mm when in our case, corresponding to a field of order 100 fold smaller than in our case. The presence of multiple droplets in the coalescence chamber leads to unpredictable field distribution, thereby making the quantitative comparison irrelevant.

In order to make this link between the coalescence of droplet pairs and the coalescence in emulsion, we constructed a minimal emulsion.⁴⁴ We experimentally vary the number of droplets in a line along the direction of the field in a channel enlarged to 450 μm width with a spacing distance d of the electrodes of 510 μm (Fig. 5). We first tested the coalescence of droplet pairs, triplets and quadruplets. The threshold voltage for coalescence decreases from ∼1 kV for droplet pairs to ∼0.6 kV for quadruplets at 10 kHz (Fig. 5 and 6a).

Fig. 5 Minimal emulsions. Raw pictures showing the impact of the number of droplets on the coalescence voltage on two designs allowing for the analysis up to quadruplets (a) or septuplets (b). Coalescence of the pairs, triplets, quadruplets, up to septuplets induced by increased voltages. Experiments are performed with HFE 7500 at 1% surfactant. Voltages are applied at a frequency of 10 kHz.

Fig. 6 From single pairs to emulsion electrocoalescence: lines of droplets in a minimal emulsion are destabilized for voltages smaller than for droplets pairs as a result of local field enhancement. (a) Droplet coalescence for quadruplets analysis. (b) Droplet coalescence for septuplets device. (c) Numerical simulations show that the field is enhanced in emulsions: frequency dependence of the field enhancement. (d) The field enhancement leads to lower threshold voltages for electrocoalescence, linearly dependent on the number of droplets as a first order approximation. (e) The comparison of the field enhancement obtained in the experiments with the linear relationship obtained from the simulation shows a good agreement.

The behaviour is robust: we repeated the experiments on a device designed to generate lines of up to seven droplets. The threshold voltage further decreases down to values smaller than ∼0.4 kV for septuplets (Fig. 6b). It should also be noted that the data become more noisy in this case possibly due to lateral electrical interactions among the droplet chains.

We further used our numerical simulations to compute the field between droplets for N = 2 to 7 droplets over the whole frequency range (Fig. 6c), showing a systematic enhancement of the field with the number of droplets. For a fixed frequency, the enhancement of the field with N is close to linear with the number of interfaces: E = E_N=2(1 + α(N − 2)) where α is a frequency dependent parameter in the range 0.15–0.30 (Fig. 6d). For f = 10 kHz, α = 0.28. Knowing the coalescence threshold for a droplet pair, the threshold for N droplets follows the inverse relationship: 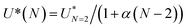. This analysis provides means to compare experiments and simulations: for all the experiments, a rescaling of the coalescence voltage by the threshold of the pairs shows that the data follow the same trend. The comparison with the experimental data shows an excellent agreement considering the crude two dimensional assumptions made in the model (Fig. 6e) and the experimental unknowns such as the exact value of the droplet spacing. Interestingly, Casas et al.⁴⁶ obtained numerical results on trains of droplets showing that the dynamics of coalescence is a function of the organisation of droplets in line. Our experiments do not directly compare to the numerical situation but the parallel between both systems is interesting to mention. Our experiments nevertheless clearly quantify the coalescence threshold in minimal emulsions, demonstrating the impact of the emulsion geometry on electrocoalescence, related to field enhancement in the oil film separating the droplets. The criterion of coalescence of a pair (N = 2) therefore controls the coalescence in more complex systems of N droplets with a significant contribution originating from the droplet environment.

To summarize our findings, we have shown that the electric parameters of the formulation used, especially the resistivity of the oil controls the coalescence efficiency by changing the cutoff frequency of the equivalent electrical circuit. The decay of the field in the film is the primary source of reduction of the electrocoalescence efficiency, mainly at low field frequency where the threshold can vary over decades. The high frequency limit where the oil can be reduced to a perfect dielectric is experimentally obtained only when the oil conductivity is large enough. For formulations used in practice, this regime might not be observed at all (e.g. with HFE 7500-based formulations). In this case, the formulation must be modelled as a leaky dielectric. We then characterized how the threshold of a pair is translated to the coalescence threshold in an emulsion at fixed formulation conditions and show that the field enhancement related to the presence of conducting droplets favors coalescence in emulsions. Our results therefore clarify the scattered reports in the literature of the coalescence threshold and highlights the key parameters affecting the performance of the electrocoalescence process in quiescent conditions.

Material and methods

Microfabrication

Microfluidic devices are fabricated in polydimethylsiloxane (PDMS) by standard soft lithography methods and replica molding.⁴⁷ Electrodes are manufactured symmetrically at both sides of the trapping array by inserting low temperature melting solder (Indium Corp.) into the electrode channels, using the microsolidics methods.⁴¹

Microfluidic droplet manipulation

A monodisperse emulsion of aqueous 50 μm droplets is produced with a flow focusing junction in a perfluorinated oil (HFE 7500 or FC 40, 3M) containing a non-ionic surfactant (Fluosurf, Emulseo). The collected emulsion is reinjected in a second microfluidic chip for droplet merging analysis (ESI Fig. S1†). The second chip consists of a reinjection nozzle with an array of 36 droplet traps. The reinjection module has a height of 27 μm while the droplet traps have a diameter of 50 μm and a height of 60 μm. The flow is controlled with pressurized air (0–200 mbar, Fluigent) and the devices are connected to flow controllers using PTFE tubing with an inner diameter of 0.3 mm (Fischer Scientific). The microfluidic chip is placed on the stage of an inverted microscope (IX71, Olympus) for imaging with a high-speed camera (v210, Phantom). Droplets are loaded in the traps by decreasing the pressure of the most right inlet. Remaining droplets which are not trapped after all the traps are loaded are removed by again increasing the pressure of the right inlet. After removal of the excess droplets the pressure of all inlets is decreased near zero to avoid oil flow in the merging chamber.

Electric actuation

One electrode in the device is grounded while an ac voltage is applied to the other electrode by a signal generator (33210A, Agilent) and a high-voltage amplifier which amplified the signal about 1000 times (623B, Trek). The output voltage of the amplifier is calibrated in function of the frequency by an oscilloscope measurement (TDS 2002C, Tektronix) with a high voltage electrode (P5100, Tektronix) (ESI Fig. S2†). The amplitude of the voltage is manually stepwise increased with 20 V every 5 s until all droplet pairs merge and an image of each setting is recorded (v210, Phantom). The applied voltage is limited to 1000 V, due to the fact that the signal generator had an internal switch in circuit when passing from 990 mV to 1 V. This internal switch causes droplet merging in some cases, therefore not allowing to perform correct interpretation of the experiment beyond this voltage. The fraction of merged droplets is measured for each applied voltage at different frequencies of the field in the range 0–50 kHz and for varying formulations (ESI Fig. S3†). All experiments are reproduced in triplicate (N = 3), to define the error bars in the reported data.

Electric characterization

The electric properties of the oil phase are characterized by impedance spectroscopy (Impedance Analyzer 7260, Materials Mates). The impedance analyzer is connected to a fluid cell which contains two opposed platinum electrodes (10 mm × 10 mm) spaced at a distance of 10 mm. The cell is filled with the formulation and a frequency scan is performed with 5 V applied. The measurements are corrected with an open and closed circuit measurement to account for the impedance of the equipment. The resistivity of the aqueous phase is determined with a conductivity meter (CDM 210, Meterlab). The data are summarized in ESI Table 2.†

Interfacial tension

The surface tension was measured with a pendant drop tensiometer (Teclis Scientific) (ESI Fig. S4†). A glass cuvette was filled with oil and surfactant while a syringe was filled with millipore water. A reversed needle with an inner diameter of 0.4 mm (100 Sterican, Braun) was used to create a rising water-in-oil droplet. The droplet size ranged from 0.2 to 6 μl. The volume was chosen such that the pendant drop reaches an equilibrium state without detaching. The densities used for calculation of the surface tension are ρ_{FC 40} = 1.85 g ml⁻¹, ρ_{HFE 7500} = 1.641 g ml⁻¹, ρ_water = 0.998 g ml⁻¹. The values of the surface tension of the pure water–oil interface were measured to be 46 mN m⁻¹ for HFE 7500 and 49 mN m⁻¹ for FC 40. The timescale of the measurement was >5000 s to reach an equilibrium state. The interfacial tension measured for oil with surfactant were at the lower limit of the method (∼5 mN m⁻¹) and we assume an accuracy of ±0.5 mN m⁻¹ on the measurement.⁴³ The data are summarized in ESI Table 2.†

Simulations

The numerical simulations are carried out by resorting to the AC/DC module of the finite-element based commercial software COMSOL Multiphysics. A 2D model, sketched on ESI Fig. S5a† of the problem is built consisting of a square domain of length L, bounded vertically by two pads of thickness t and dielectric constant ε_PDMS representing the PDMS layers. The coordinate origin is set at the center of the quare domain. Two circles representing the water droplets are positioned at y = ±(a + d)/2, where a is the radius of the circle and d is the separation distance (gap). The reduced dielectric constant and conductivity of the of the host medium containing the droplets are ε and σ = 1/ρ respectively, while those of the droplets are [small epsilon, Greek, circumflex] and [small sigma, Greek, circumflex] = 1/[small rho, Greek, circumflex]. The top edge of the domain is modeled as an electrode with an electric potential V, while the bottom edge is set to a null potential. Periodic boundary conditions are used for the left and right edges. The meshing consists in a fine mesh of free triangles (see ESI Fig. S5b† for a typical mesh realization). A square area is defined around the gap between the two droplets to achieve a finer mesh and correctly resolve the local fields. The maximum element size within the square is set to g/10 (see ESI Fig. S5c†). Additional details on the simulation are provided in the ESI Method section.†

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

JCB is cofounder and shareholder of Emulseo, producer of the surfactant used in this study.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 813786. JCB acknowledges the support of the ‘Fondation Simone et Cino Del Duca’ and of the ‘Région Nouvelle Aquitaine’ for funding. We thank Junjin Che (NTG group at CRPP) for his help with the electric characterizations of the fluids used. We thank the anonymous Referee 1 for pointing towards ref. 46.

References

1. J. S. Eow, M. Ghadiri, A. O. Sharif and T. J. Williams, Chem. Eng. J., 2001, 84, 173.
2. J. Sjöblom, S. Mhatre, S. Simon, R. Skartlien and G. Sørland, Adv. Colloid Interface Sci., 2021, 294, 102455.
3. A. Shavlov, V. Dzhumandzhi and E. Yakovenko, Plasma, 2023, 6, 127–138.
4. M. Chabert, K. D. Dorfman and J. L. Viovy, Electrophoresis, 2005, 26, 3706.
5. D. R. Link, E. Grasland-Mongrain, A. Duri, F. Sarrazin, Z. Cheng, G. Cristobal, M. Marquez and D. A. Weitz, Angew. Chem., Int. Ed., 2006, 45, 2556.
6. L. Frenz, A. El Harrak, M. Pauly, S. Bégin-Colin, A. D. Griffiths and J.-C. Baret, Angew. Chem., Int. Ed., 2008, 47, 6817–6820.
7. X. Niu, F. Gielen, A. J. DeMello and J. B. Edel, Anal. Chem., 2009, 81, 7321.
8. A. R. Abate, T. Hung, P. Marya, J. J. Agresti and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19163–19166.
9. A. Autour, E. Westhof and M. Ryckelynck, Nucleic Acids Res., 2016, 44, 2491.
10. S. L. Sjostrom, H. N. Joensson and H. A. Svahn, Lab Chip, 2013, 13, 1754.
11. C. M. Ackerman, C. Myhrvold, S. G. Thakku, C. A. Freije, H. C. Metsky, D. K. Yang, S. H. Ye, C. K. Boehm, T.-S. F. Kosoko-Thoroddsen, J. Kehe, T. G. Nguyen, A. Carter, A. Kulesa, J. R. Barnes, V. G. Dugan, D. T. Hung, P. C. Blainey and P. C. Sabeti, Nature, 2020, 582, 277.
12. K. Wu, Q. Fang, Z. Zhao and Z. Li, Anal. Chem., 2023, 95, 5069.
13. L. M. Fidalgo, G. Whyte, D. Bratton, C. F. Kaminski, C. Abell and W. T. S. Huck, Angew. Chem., Int. Ed., 2008, 47, 2042–2045.
14. J.-C. Baret, O. J. Miller, V. Taly, M. Ryckelynck, A. El-Harrak, L. Frenz, C. Rick, M. L. Samuels, J. B. Hutchison, J. J. Agresti, D. R. Link, D. A. Weitz and A. D. Griffiths, Lab Chip, 2009, 9, 1850.
15. A. Sciambi and A. R. Abate, Lab Chip, 2015, 15, 47.
16. F. Malloggi, S. A. Vanapalli, H. Gu, D. Van Den Ende and F. Mugele, J. Phys.:Condens. Matter, 2007, 19(46), 462101.
17. S. H. Tan, B. Semin and J.-C. Baret, Lab Chip, 2014, 14, 1099.
18. D. Van Assche, T. Beneyton and J.-C. Baret, Droplet, 2023, 2, e45.
19. M. Zagnoni, C. N. Baroud and J. M. Cooper, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2009, 80(4), 046303.
20. T. Szymborski, P. M. Korczyk, R. Hołyst and P. Garstecki, Appl. Phys. Lett., 2011, 99(9), 094101.
21. T. Leary, M. Yeganeh and C. Maldarelli, ACS Omega, 2020, 5, 7348.
22. A. R. Thiam, N. Bremond and J. Bibette, Phys. Rev. Lett., 2009, 102(18), 188304.
23. C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 89(13), 134101.
24. J. Melcher and G. Taylor, Annu. Rev. Fluid. Mech., 1969, 1, 111.
25. G. I. Taylor, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1966, 291, 159.
26. J. C. Baygents, N. J. Rivette and H. A. Stone, J. Fluid Mech., 1998, 368, 359–375.
27. Q. Dong and A. Sau, Physical Review Fluids, 2018, 3, 073701.
28. P. Atten, J. Electrost., 1993, 30, 259.
29. P. Atten, L. Lundgaard and G. Berg, J. Electrost., 2006, 64, 550.
30. P. M. Vlahovska, Annu. Rev. Fluid Mech., 2019, 51, 305.
31. X. Zhang, O. A. Basaran and R. M. Wham, AIChE J., 1995, 41, 1629.
32. V. Anand, V. A. Juvekar and R. M. Thaokar, Langmuir, 2020, 36, 6051 , pMID: 32306738..
33. H. Chen, W. Chen, Z. Yin and H. Fang, J. Fluid Mech., 2023, 963, A39.
34. S. Mhatre, S. Deshmukh and R. M. Thaokar, Phys. Fluids, 2015, 27, 092106.
35. J. N. Israelachvili, in The Handbook of Surface Imaging and Visualization, CRC Press, 2022, pp. 793–816.
36. S. Herminghaus, Phys. Rev. Lett., 1999, 83, 2359.
37. A. R. Thiam, N. Bremond and J. Bibette, Phys. Rev. Lett., 2011, 107, 068301.
38. S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366.
39. P. Abbyad, R. Dangla, A. Alexandrou and C. N. Baroud, Lab Chip, 2011, 11, 813.
40. E. Fradet, P. Abbyad, M. H. Vos and C. N. Baroud, Lab Chip, 2013, 13, 4326.
41. A. Siegel, D. Bruzewicz, D. Weibel and G. Whitesides, Adv. Mater., 2007, 19, 727.
42. Y. Skhiri, P. Gruner, B. Semin, Q. Brosseau, D. Pekin, L. Mazutis, V. Goust, F. Kleinschmidt, A. El Harrak, J. B. Hutchison, E. Mayot, J.-F. Bartolo, A. D. Griffiths, V. Taly and J.-C. Baret, Soft Matter, 2012, 8, 10618.
43. Q. Brosseau, J. Vrignon and J.-C. Baret, Soft Matter, 2014, 10, 3066.
44. P. Gruner, B. Riechers, B. Semin, J. Lim, A. Johnston, K. Short and J. C. Baret, Nat. Commun., 2016, 7, 1.
45. M. H. Davis, Q. J. Mech. Appl. Math., 1964, 17, 499.
46. P. S. Casas, M. Garzon, L. J. Gray and J. A. Sethian, Phys. Rev. E, 2019, 100, 063111.
47. D. C. Duffy, J. C. McDonald, O. J. A. Schueller and G. M. Whitesides, Anal. Chem., 1998, 70, 4974.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ra01597a

---