Long-range magnetic interaction of native defects in transition metal dichalcogenides

Abstract

Recent experiments have revealed weak ferromagnetism in pristine transition metal dichalcogenides (TMDs), although the underlying mechanism remains unclear. In this work, we investigate the possibility of native defects inducing ferromagnetism in TMDs, specifically WS₂ and MoS₂. Among the various native defects, we have identified that cation antisites exhibit localized magnetic moments of 2μ_B. These localized moments tend toward ferromagnetic ordering via magnetic interactions facilitated by local spin density oscillations. While the strength of the magnetic interactions is comparable to that of magnetic dopants in TMD, they are significantly weakened when the distance between the two antisites exceeds 9 Å. Therefore, our results suggest that native-defect-induced ferromagnetism in TMD is feasible only in heavily defective TMD samples.

---

1. Introduction

The discovery of two-dimensional (2D) magnetic materials such as CrI₃ and CrGeTe₃ was a great scientific and practical advance.^1,2 In the scientific aspect, the existence of the long-range magnetic order in the 2D systems has been a fundamental question, as the Mermin–Wagner theorem suggested that the 2D long-range orders are destroyed by the thermal fluctuations.³ Currently, 2D magnetism is understood based on the effect of the magnetic anisotropy by transferring the 2D system from the Heisenberg model to the Ising model.² In the practical aspect, the realization of the 2D magnetic systems could lead to new 2D-based magnetic applications.^4–9 Several 2D materials with exceptional electric and optical properties have been found over the past decades and are considered to be a new family for novel device applications.^10–13 However, magnetism has been one property missing from 2D materials. The emergence of 2D magnets is likely to open new directions in 2D materials.

Among the 2D materials, graphene and transition metal dichalcogenides (TMDs) have been intensively studied due to their exceptional properties. Although they are non-magnetic in their pristine forms, many studies have been performed to introduce magnetism in them by doping with transition metals such as Mn, V, Cr, Fe, CO, and P.^14–20 In TMDs, the long-range ferromagnetic interaction can be established by super-exchange interaction among highly localized d-states of the transition metals by antiferromagnetically coupled delocalized p-states of chalcogenides. More interestingly, ferromagnetism has been experimentally observed in graphene without any intentional doping.^21–25 Many theoretical works have studied this graphene ferromagnetism, and it is now understood to be based on the pseudo-spin-mediated long-range ferromagnetic coupling between local magnetic moments generated by native defects or hydrogen absorption.^26–28

Recent experiments have also observed a weak but room-temperature ferromagnetism in pristine (but possibly defective) TMDs such as WS₂ and MoS₂.^29–33 Because TMDs are semiconductors without the metallic pseudo-spin state that exists in graphene, the mechanism of the ferromagnetism of TMDs could be different from that in graphene. To explain the intrinsic ferromagnetism, several theoretical and experimental studies have been performed. Huo et al. proposed edge-state-induced ferromagnetism in WS₂.²⁹ Other groups have suggested that local metallic 1T phases inside the host 2H TMD can be ferromagnetically coupled and lead to ferromagnetism.^32,34

As another possible mechanism, defects could also lead to ferromagnetism in TMDs, like in graphene. Native defects such as vacancies and interstitials are inevitably generated in the growth processes and can significantly affect the properties of TMDs.^35,36 It is known that defects in TMDs could have local magnetic moments,^35,37 and a previous work suggested the possibility of magnetically-active-defect-induced ferromagnetism.³⁰ However, the detailed mechanism of defect-induced ferromagnetism, especially long-range magnetic coupling between the magnetic defects, has not been studied yet.

In this work, we have investigated the effects of native defects on the magnetic properties of TMDs such as WS₂ and MoS₂. First, we have examined isolated defects such as S vacancies (V_S), transition metal anti-sites (M_S, M = W or Mo), transition metal interstitials (M_i), and M_S and V_S complex defects (M_S–V_S), which have localized d-orbitals, and thus could have a localized magnetic moment. While V_S and M_i have no magnetic moment, M_S and M_S–V_S exhibit localized magnetic moments of 2μ_B. Second, we have studied the long-range magnetic interaction between M_S defects with respect to their relative positions. The magnetic interaction is mediated by the local spin density oscillation, and it shows that ferromagnetic couplings are favorable for most of the relative positions. However, the magnetic interaction varies with the relative position and is significantly reduced over the fourth-nearest neighboring site. Our results suggest that defect-induced ferromagnetism can be generated in heavily defective TMDs.

2. Methodology

The optimized atomic structures and relevant total energies were calculated based on spin-polarized density functional theory (DFT),^38,39 as implemented in the Vienna ab initio simulation package (VASP).^40–43 The plane augmented wave method was used to represent the ion cores,⁴⁴ and the generalized gradient approximation formulated by Perdew, Burke, and Ernzerhof was used for the exchange–correlation functional.^45,46 The wavefunctions were expanded in a plane wave basis set up to a cut-off energy of 500 eV. To model the isolated defects and the magnetic coupling between two defects, we employed a periodic 7 × 7 supercell with a 15 Å vacuum region along the z-direction, which is sufficiently large to avoid artificial interaction between periodic images. For Brillouin-zone integration, a Γ-centered 3 × 3 × 1 k-point mesh was used for ionic relaxation, and a denser 6 × 6 × 1 k-point mesh was used for precise electronic structure calculations. Atomic structures were fully relaxed until the residual forces were less than 0.02 eV Å⁻¹. The spin–orbit coupling (SOC) was incorporated using an approximation of relativistic effects by a scalar relativistic Hamiltonian with SOC in a perturbation treatment.⁴⁷ However, the inclusion of SOC was found to have a minor effect on the energy of the magnetic coupling.

The formation energy F_E(D) of a defect D was calculated as

where E(D) and E(Pure) are the total energies of the defective and pure systems, respectively, and Δn_i and μ_i are the number change and the chemical potential of the i-th element, which are added (Δn_i > 0) or removed (Δn_i < 0). The chemical potentials used were the atomic total energies of the BCC phase for W and Mo metals and the orthorhombic phase for S.

3. Results and discussion

3.1. Localized magnetic moments in native defects

We first considered native defects in WS₂ that could generate a local magnetic moment. Among the various native defects, we focused on V_S, W_S, and W_i defects as shown in Fig. 1(a)–(c), respectively, because they have unpaired d-orbitals of W atoms, so they are likely to have a localized magnetic moment. This is not the case for the other isolated native defects such as W vacancies, S interstitials, and S anti-sites. All the defects we considered are likely to be formed in W-rich (or S-poor) growth conditions. In this regard, we assume W-rich WS₂ samples in this work.

Fig. 1 Atomic structures of (a) S vacancy (V_S), (b) W antisite (W_S), (c) W interstitial (W_i), and (d) W_S–V_S complex defects in WS₂. In (a) and (d), vacancy sites are denoted by dotted blue circles. In (a) and (b), the neighboring W atoms near the defect are denoted by dotted violet lines. The W and S atoms are represented by magenta and yellow balls, respectively.

Anion vacancies, i.e., V_S in this case, have been widely observed in TMDs.^35,36,48 Our calculations also showed that V_S has the lowest formation energy, as shown in Table 1. However, V_S has no local magnetic moments, despite the existence of the non-bonding d-orbitals of the three neighboring W atoms [see Fig. 1(a)]. This is because of the inward relaxation of the three W atoms and the formation of the fully occupied bonding levels of the non-bonding d-orbitals, leaving the fully unoccupied d-levels in the gap. In pristine WS₂, the distance between two W atoms (D_W–W) is 3.18 Å. However, near the V_S defect, as shown in Fig. 1(a), D_W–W is reduced by 0.14 Å. This relaxation leads to the formation of a bonding level inside the valence band, effectively quenching the local magnetic moment.

Table 1 Defect formation energies E_F in the cation- or anion-rich conditions, and the localized magnetic moments (m) of the various defects such as S vacancies (V_S), cation interstitials (M_i), cation antisites (M_S), and cation antisite and S vacancy complex (M_S–V_S) in WS₂ and MoS₂. M stands for W in WS₂ and Mo in MoS₂

	WS2			MoS2
	EF (eV)		m (μB)	EF (eV)		m (μB)
	W-rich	S-rich		Mo-rich	S-rich
VS	1.56	2.79	0.0	1.33	2.63	0.0
Mi	5.30	7.77	0.0	3.86	6.47	0.0
MS	5.45	9.14	2.0	3.86	7.78	2.0
MS-VS	6.74	11.66	2.0	5.14	10.36	2.0

---

In the W-rich growth conditions, the sufficient W adatoms are likely to encounter the abundant V_S sites on WS₂, and the V_S sites can be filled by the W atoms, forming cation anti-site defects W_S, as shown in Fig. 1(b). The inclusion of a W atom at the V_S site restores the D_W–W (3.12 Å) near the W_S defect [see Fig. 1(b)] to a value close to that of the pristine structure. Additionally, no significant changes were observed in other bonds, such as the W–S bonds. Our calculations showed that the W_S defect exhibits a local magnetic moment of 2 μ_B, which is in good agreement with previous results.⁴⁹ Due to the different atomic environment of the W_S atom compared with that of the host W atoms, it shows different level splitting of the W_S d-orbitals. As shown in Fig. 2(a), the three d_XY, d_X²−Y², and d_Z² levels appear around the band gap, while the other two d_XZ and d_YZ levels are located below the valence band maximum (VBM). For the majority spin state, the d_XY and d_X²−Y² levels are doubly degenerate at 0.91 eV, and the single d_Z² level is located at 1.16 eV with respect to the VBM, as shown in Fig. 2(a). Note that the minority spin d_XY, d_X²−Y², and d_Z² levels are located near the conduction band minimum (CBM), showing large spin splitting. W_S has effectively six valence electrons in the d-orbitals: four originate from the valence electrons of W_S and two originate from the three neighboring W atoms. Among them, the four are filled into the d_XZ and d_YZ levels below VBM, and the doubly degenerate d_XY and d_X²−Y² levels in the gap are occupied by the remaining two electrons. Therefore, this partial electron occupation of localized d-levels induces the large spin splitting by the exchange interaction,¹⁴ and W_S can have a magnetic moment of 2μ_B.

Fig. 2 Total and projected density of states (DOS) of (a) W_S and the (b) W_S–V_S complex. Upper (lower) panel is the majority (minority) spin DOS. Black lines and gray shaded regions are total DOS, and projected DOS are shown using the corresponding colors denoted in the figures. All the projected DOSs were scaled by a factor of 10 with respect to the total DOS. The valence band maximum was set to 0.0 eV, and the Fermi level is presented by the vertical dotted lines. Isosurfaces of the spin densities for W_S and the W_S–V_S complex are shown in the insets of (a) and (b), respectively.

The inset in Fig. 2(a) shows the spatial distribution of the spin density of W_S. The majority spin is highly localized near the W_S atom, resulting in an atomic magnetic moment 1.51μ_B. For the three nearest neighboring W atoms, however, the minority spin is distributed with an atomic magnetic moment of −0.09μ_B per each W atom. For the three next nearest neighboring W atoms, the majority spin is again distributed with a smaller local magnetic moment 0.09μ_B per each W atom. The spin density oscillation is caused by the super-exchange interaction through an S atom.⁴⁹ Note that the magnetic moment on S atoms is very small because of the absence of d-orbitals. This spin density oscillation is induced by the W_S defect. Similar spin density oscillations have been found in graphene due to defects, but the spin density is distributed in much longer range, leading to long-range magnetic coupling.²⁶

Fig. 1(c) shows the atomic structure of W_i. The W adatom is stabilized on the host W site, forming a symmetrically separated two W dumbbell structure. The formation energy of W_i in the W-rich condition is similar to, but a bit smaller than that of W_S (see Table 1). However, due to the bonding between the two W atoms, similar to V_W, W_i also has no magnetic moment.

We have summarized the formation energies and magnetic moments of the isolated defects discussed above in Table 1. While W_S has a localized magnetic moment, its formation energy is relatively high. Thus, under equilibrium growth conditions, the W_S concentration [W_S] may be too low to lead to ferromagnetism in WS₂. However, under non-equilibrium growth conditions, [W_S] can be significant due to a diffusion-limited kinetic process. In the process, W_S can be formed by the migration and clustering of V_S and W_i if the following two conditions are met: (i) attractive interaction between V_S and W_i, and (ii) activation of V_S or/and W_i diffusion.^50,51 For condition (i), our calculations show that the binding energy between V_S and W_i to form W_S is quite large (about 1.41 eV), implying a strong attractive interaction. For condition (ii), previous results showed that the diffusion energy barrier is about 0.6 eV for transition metal interstitials in TMD.⁵² This is in good agreement with the fact that W_S as well as V_S are widely observed in experiments.^35,36 Hence, we will consider the effect of the anti-site defect W_S on the magnetic properties in TMD in the next section.

Until now, we have discussed isolated point defects in WS₂. In the non-equilibrium process that we considered above, large complex defects as well as W_S can be also formed by the kinetic processes of the isolated defects. The M_S–V_S complex [see Fig. 1(d)], which has been observed in experiments,³⁵ is an example. Regarding the two conditions above, (i) the binding energy between M_S and V_S is about 0.27 eV, and (ii) the V_S diffusion, for which the diffusion barrier is about 2.3 eV,⁵³ can be activated at the sample growth temperature of ∼1000 K.^15,29 While the binding energy is small, and so the W_S–V_S concentration is expected to be low even in non-equilibrium conditions, the W_S−V_S complex can exist and could lead a localized magnetic moment in WS₂. As shown in Fig. 2(b), the doubly degenerate d_XY and d_X²−Y² levels in the gap are occupied, and it has a local magnetic moment 2μ_B, similar to those of W_S. Previous works⁵⁴ have considered other large complex defects such as a W and two S vacancy complex and a six S vacancy cluster, which exhibit local magnetic moments. These results indicate that, although these complex defects could affect the magnetic properties of WS₂, the concentration of the large complex defects is so low, their effect could be insignificant even under non-equilibrium conditions. In this regard, we ignored the possible effect of large complex defects in the next section, and we focused on the long-range magnetic coupling between M_S defects, which are expected to be the most abundant magnetic defect in WS₂.

Until now, we have focused on the various defects in WS₂. We also studied the corresponding defects in MoS₂, for which the results are summarized in Table 1. Most of the results are qualitatively similar to those in WS₂. There is one thing to note: the formation energy of the Mo anti-site defect (Mo_S) is smaller than that of W_S in WS₂, so one can expect a higher Mo_S concentration. Thus, we believe that the qualitative magnetic properties induced by the native defects could be similar in both materials.

3.2. Long-range magnetic interaction of cation anti-site defects

To investigate the long-range ordering of the local magnetic moments in native defects and the defect-induced ferromagnetism in TMDs, the magnetic interaction between two M_S defects (M = W for WS₂ and Mo for MoS₂) was considered in a 7 × 7 supercell, in which the M_S concentration was 2% with respect to the total number of M atoms. This defect concentration is experimentally accessible in the TMDs.³⁵ As a measure of the magnetic interaction ΔE_m, we considered the energy differences between ferromagnetic (FM) and antiferromagnetic (AFM) ordering of the two M_S defects, i.e., ΔE_m = E^AFM − E^FM, where E^FM and E^AFM are the total energy of the FM and AFM orderings. Fig. 3(a) shows ΔE_m as a function of the distance d between two M_S defects, and the results are also summarized in Table 2. Here, the positive (negative) ΔE_m indicates that the FM (AFM) ordering is stable.

Fig. 3 Long-range magnetic interaction between two M_S defects (M = W for WS₂ and Mo for MoS₂). (a) Energy difference ΔE_m between FM and AFM ordering of the two M_S defects, i.e., ΔE_m = E^AFM − E^FM, as a function of the distance d between the two M_S defects. (b) Relative positions of the two M_S defects considered in (a). With respect to the M_S defect denoted by the black circle, the first, second, third, and fourth nearest neighboring (NN) sites are represented by the blue, green, red, and pink circles, respectively.

Table 2 Magnetic interaction ΔE_m and binding energy E_B of two anti-site defects M_S (M = W for WS₂ and Mo for MoS₂) with respect to the distance d between the two M_S defects. ΔE_m was calculated from the energy difference between the ferromagnetic E^FM and antiferromagnetic E^AFM orderings of the two defects, i.e., ΔE_m = E^AFM − E^FM. E_B was measured from the energy gain of the two defects with respect to the isolated two defects

	WS2			MoS2
	d (Å)	ΔEm (meV)	EB (eV)	d (Å)	ΔEm (meV)	EB (eV)
2 MS-1NN	3.18	239	0.27	—	—	—
2 MS-2NNAC	5.51	−17	0.12	5.52	−2.0	0.06
2 MS-2NNZZ	6.37	53	0.07	6.37	21	0.01
2 MS–3NNAC	8.42	1.4	0.04	8.43	1.4	0.03
2 MS-3NNZZ	9.55	0.6	0.02	9.55	0.6	0.01
2 MS-4NN	11.48	0.2	0.02	11.48	0.1	0.00

---

We considered various relative positions between two M_S defects up to the fourth nearest neighboring (NN) site, and the positions are represented in Fig. 3(b); with respect to the M_S defect circled in black, the first, second, third, and fourth NN sites of the other M_S defects are designated by blue, green, red, and pink circles. We denote the two n-th NN M_S defects as 2M_S-nNN_X. If more than one n-th NN site exist, the different sites are distinguished using the subscript X, which can be ZZ or AC depending on whether the two defects are aligned along the zigzag or armchair direction, respectively [see Fig. 3(b)]. For 2W_S-1NN in WS₂, the two W_S atoms were relaxed away from the S atoms but relaxed inward between them, forming a bond between the two W atoms. This lowers the total energy of the two defects by 0.27 eV. Because the distance between the two defects is close enough for their spin densities to interact [see inset of Fig. 2(a)], the magnetic interaction ΔE_m is measured to be relatively large (239 meV), as shown in Fig. 3(a) and Table 2.

For 2W_S-2NN, there are two inequivalent positions: two W_S are separated along the armchair line (2W_S-2NN_AC) or zigzag line (2W_S-2NN_ZZ) [see Fig. 3(b)]. The distance d between the two W_S defects in 2W_S-2NN_AC is shorter by 0.5 Å than that in 2W_S-2NN_ZZ. Among the relative positions that we have considered, only 2W_S-2NN_AC prefers the AFM coupling by 17 meV compared to the FM coupling. The favorable AFM coupling reflects the spin density oscillation in W_S [see inset of Fig. 2(a)]. As we mentioned above, if the majority spin is distributed on the W_S atom, the minority spin is distributed on the NN W atoms, and again the majority spin is distributed on the next NN W atoms. Thus, because of the relative position of the two W_S defects in 2W_S-2NN_AC, the spin distribution of the AFM coupling becomes compatible with the spin distribution of each W_S, as shown in Fig. 4(a). For 2W_S-2NN_ZZ, on the other hand, the spin distributions are compatible in the FM coupling [see Fig. 4(b)], and our results thus show that the energy of the FM coupling is lower by 53 meV than that of the AFM coupling.

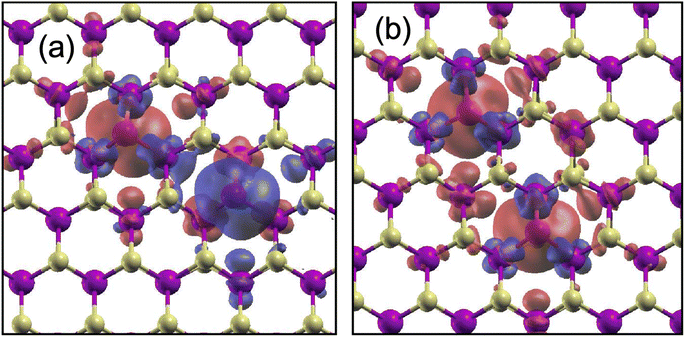Fig. 4 Spin density for (a) 2W_S-2NN_AC and (b) 2W_S-2NN_ZZ in WS₂. Red (blue) contours represent the spatial distribution of the majority (minority) spin.

The magnetic interaction is mediated by the spin density of each W_S defect. Because the spin density is localized around W_S, as shown in the inset of Fig. 2(a), ΔE_m decreases with respect to d [see Table 2 and the inset of Fig. 3(a)]. However, a finite and positive ΔE_m (FM coupling) still exists for the third and fourth NN configurations, for which d is over 8 Å. The d-dependent magnetic interaction is also reflected in the splitting of the degenerate d_XY and d_X²−Y² levels within the band gap. Fig. 5 shows the total and projected DOSs of 2W_S-2NN_ZZ, 2W_S-3NN_AC, and 2W_S-3NN_ZZ. As shown in Fig. 5(a), each W_S defect has occupied d_XY andd _X²−Y² levels and the empty d_Z2 level in the gap. For 2W_S-2NN_ZZ, the occupied d_XY and d_X²−Y² levels, which are degenerate for the isolated case, exhibit a sizable energy splitting of about 0.17 eV due to the interaction between the defect levels. The electronic structures of 2W_S-3NN_AC and 2W_S-3NN_ZZ [see Fig. 5(b) and (c)] are similar to that of 2W_S-2NN_ZZ, but the level splittings are reduced to 0.09 and 0.07 eV, respectively, as d increases.

Fig. 5 Total and projected DOS for (a) 2W_S-2NN_ZZ, (b) 2W_S-3NN_AC, and (c) 2W_S-3NN_ZZ in WS₂. Black lines and gray shaded regions are the total DOS, and projected DOS are shown using the corresponding colors denoted in the figures. All the projected DOSs were scaled by a factor of 10 with respect to the total DOS. Valence band maximum was set to 0.0 eV, and the Fermi level is presented by the vertical dotted lines.

The strength of the magnetic interaction ΔE_m is on the same order of magnitude as that of magnetic Mn dopants in TMDs, which have been considered as a source leading to ferromagnetism.¹⁴ For several TMDs, the calculated ΔE_m of the two Mn dopants are about 130–200 meV for the 1NN configuration and 5–70 meV for the 2NN_ZZ configuration, which are comparable with the ΔE_m of W_S in WS₂, as shown in Table 2 and Fig. 3(a). In this regard, we expect that the W_S defect can induce the ferromagnetism experimentally observed in undoped WS₂. However, as discussed above, ΔE_m becomes small over the defect distance d of 8 Å, so long-range ferromagnetic ordering could be possible in highly defective systems.

In addition, we considered the ΔE_m of the Mo_S defects in MoS₂. The results are very similar to those of W_S in WS₂, but there are two differences. First, the 2Mo_S-1NN configuration is unstable, and during the ionic relaxation, the two Mo_S defects are relaxed inward each other, forming bonds. This relaxation quenches the magnetic moment in Mo_S. Second, the ΔE_m is slightly smaller than that of W_S in WS₂. This difference may be caused by the small d-orbital radius of the Mo atoms. Thus, for the same defect density of M_S, MoS₂ is less likely to show ferromagnetism. However, as discussed above, the formation energy of Mo_S is smaller than that of W_S (see Table 1). As such, more abundant Mo_S defects could lead to ferromagnetism in MoS₂.

4. Conclusions

In summary, we investigated various native defects in WS₂ and MoS₂ and found that the M_S defect is the most abundant magnetic defect, exhibiting a local magnetic moment of 2μ_B, under non-equilibrium W-rich growth conditions. The spin density oscillation associated with the local magnetic moments mediates a long-range magnetic interaction between the M_S defects, which mostly leads to ferromagnetic ordering. The strength of this magnetic interaction is comparable to that of magnetic dopants in TMDs. However, the interaction decreases significantly when the defect distance exceeds 9 Å. Thus, our findings suggest that ferromagnetism in TMDs can be induced in heavily defective TMD samples with a high concentration of M_S defects.

Data availability

The data (the calculated atomic structures) supporting this article have been included as part of the ESI data.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) (NRF-2023R1A2C1006433 and RS-2023-00253716). This work was conducted during the research year of Chungbuk National University in 2023. We used the software VESTA to generate Fig. 1, 3, and 4.⁵⁵

References

1. B. Huang, et.al., Nature, 2017, 546, 270–273.
2. C. Gong, et.al., Nature, 2017, 546, 265–269.
3. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133.
4. M. Gibertini, M. Koperski, A. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419.
5. A. Soumyanarayanan, N. Reyren, A. Fert and C. Panagopoulos, Nature, 2016, 539, 509–517.
6. A. Manchon, H. Koo, J. Nitta, S. Frolov and R. Duine, Nat. Mater., 2015, 14, 871–882.
7. D. Go, J.-P. Hanke, P. Buhl, F. Freimuth, G. Bihlmayer, H.-W. Lee, Y. Mokrousov and S. Blügel, Sci. Rep., 2017, 7, 46742.
8. X. Liu and M. Hersam, Nat. Rev. Mater., 2019, 4, 669–684.
9. B. Nikolić, K. Dolui, M. Petrović, P. Plecháč, T. Markussen and K. Stokbro, First-Principles Quantum Transport Modeling of Spin-Transfer and Spin-Orbit Torques in Magnetic Multilayers, Springer International Publishing, 2018.
10. G. Eda, H. Yamaguchi, D. Voiry, T. Fujita, M. Chen and M. Chhowalla, Nano Lett., 2011, 11, 5111–5116.
11. A. Durand, T. Clua-Provost, F. Fabre, P. Kumar, J. Li, J. H. Edgar, P. Udvarhelyi, A. Gali, X. Marie, C. Robert, J. M. Gérard, B. Gil, G. Cassabois and V. Jacques, Phys. Rev. Lett., 2023, 131, 116902.
12. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
13. N. Mao, J. Tang, L. Xie, J. Wu, B. Han, J. Lin, S. Deng, W. Ji, H. Xu, K. Liu, L. Tong and J. Zhang, J. Am. Chem. Soc., 2016, 138, 300–305.
14. R. Mishra, W. Zhou, S. Pennycook, S. Pantelides and J.-C. Idrobo, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 144409.
15. F. Zhang, et.al., Adv. Sci., 2020, 7, 2001174.
16. D. Duong, S. Yun, Y. Kim, S.-G. Kim and Y. Lee, Appl. Phys. Lett., 2019, 115, 242406.
17. S. Fu, et.al., Nat. Commun., 2020, 11, 2034.
18. A. K. Jena, S. K. Mallik, M. C. Sahu, S. Sahoo, A. K. Sahoo, N. K. Sharma, J. Mohanty, S. K. Gupta, R. Ahuja and S. Sahoo, Sci. Rep., 2022, 12, 2593.
19. A. Singh, C. C. Price and V. B. Shenoy, ACS Nano, 2022, 16, 9452–9460.
20. Y. Sun, H. Zhang, Y. Zheng, P. Gao, C. Ye and F. Wang, J. Alloys Compd., 2024, 994, 174634.
21. O. V. Yazyev, Phys. Rev. Lett., 2008, 101, 037203.
22. O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408.
23. M. M. Ugeda, I. Brihuega, F. Guinea and J. M. Gómez-Rodríguez, Phys. Rev. Lett., 2010, 104, 096804.
24. J. J. Palacios, J. Fernández-Rossier and L. Brey, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195428.
25. H. Ohldag, P. Esquinazi, E. Arenholz, D. Spemann, M. Rothermel, A. Setzer and T. Butz, New J. Phys., 2010, 12, 123012.
26. H. Kim, J. Bang and J. Kang, Sci. Rep., 2018, 8, 13940.
27. H. González-Herrero, J. M. Gómez-Rodríguez, P. Mallet, M. Moaied, J. J. Palacios, C. Salgado, M. M. Ugeda, J.-Y. Veuillen, F. Yndurain and I. Brihuega, Science, 2016, 352, 437–441.
28. O. V. Yazyev and M. I. Katsnelson, Phys. Rev. Lett., 2008, 100, 047209.
29. N. Huo, Y. Li, J. Kang, R. Li, Q. Xia and J. Li, Appl. Phys. Lett., 2014, 104, 202406.
30. R. Sanikop and C. Sudakar, ACS Appl. Nano Mater., 2020, 3, 576–587.
31. X. Ding, T. Liu, S. Ahmed, N. Bao, J. Ding and J. Yi, J. Alloys Compd., 2019, 772, 740–744.
32. L. Cai, J. He, Q. Liu, T. Yao, L. Chen, W. Yan, F. Hu, Y. Jiang, Y. Zhao, T. Hu, Z. Sun and S. Wei, J. Am. Chem. Soc., 2015, 137, 2622–2627.
33. X. Mao, Y. Xu, Q. Xue, W. Wang and D. Gao, Nanoscale Res. Lett., 2013, 8, 430.
34. S. Han, Y. Park, Y. Hwang, S. Jekal, M. Kang, W. Lee, W. Yang, G. D. Lee and S. Hong, Sci. Rep., 2016, 6, 38730.
35. J. Hong, et.al., Nat. Commun., 2015, 6, 6293.
36. W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi, J. Kong, J. Lou, P. Ajayan, B. Yakobson and J.-C. Idrobo, Nano Lett., 2013, 13, 2615–2622.
37. D. Yang, X. Fan, F. Zhang, Y. Hu and Z. Luo, Nanoscale Res. Lett., 2019, 14, 192.
38. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
39. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
41. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
42. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
43. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
44. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. S. Steiner, K. Khmelevskyi, M. Marsmann and G. Kresse, Phys. Rev. B, 2016, 93, 224425.
48. L. M. V. Ildefonso, E. L. Buthers, B. S. Archanjo, C. Legnani, W. G. Quirino, D. V. P. Massote, I. O. Maciel and B. Fragneaud, J. Phys. Chem. C, 2024, 128, 7294–7305.
49. W.-F. Li, C. Fang and M. A. Van Huis, Phys. Rev. B, 2016, 94, 195425.
50. J. Bang, Y.-S. Kim, C. Park, F. Gao and S. Zhang, Appl. Phys. Lett., 2014, 104, 252101.
51. C. Si, D. Choe, W. Xie, H. Wang, Z. Sun, J. Bang and S. Zhang, Nano Lett., 2019, 19, 3612–3617.
52. H.-P. Komsa and A. V. Krasheninnikov, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 125304.
53. J. Chaste, J. Bang, I. Hnid, L. Khalil, C. Si, A. Durnez, X. Lafosse, M. Q. Zhao, A. T. Charlie Johnson, S. Zhang and A. Ouerghi, ACS Nano, 2020, 14, 13611–13618.
54. X. Zhao, X. Dai, C. Xia and T. Wang, Superlattices Microstruct., 2015, 85, 339–347.
55. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra08374a

---