Open Access Article
Open Access ArticleRheological, electrochemical, and microstructural properties of graphene oxides as flowable electrodes for energy storage applications†
André Pincot ac,
Jeffrey Chin
ac,
Jeffrey Chin ab,
Ryan Murphy
ab,
Ryan Murphy d,
F. John Burpo
d,
F. John Burpo ab,
Caspar Yi
ab,
Caspar Yi ab,
Edward Chen
ab,
Edward Chen ab,
H. Daniel Bahaghighata,
Benjamin Thompsone,
Simuck F. Yuk
ab,
H. Daniel Bahaghighata,
Benjamin Thompsone,
Simuck F. Yuk ab,
Gareth H. McKinley
ab,
Gareth H. McKinley c,
Enoch A. Nagelli
c,
Enoch A. Nagelli *ab and
Matthew Armstrong
*ab and
Matthew Armstrong *ae
*ae
aDepartment of Chemistry and Life Science, United States Military Academy, West Point, NY 10996, USA. E-mail: enoch.nagelli@westpoint.edu
bPhotonics Research Center, United States Military Academy, West Point, NY 10996, USA
cDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
dNIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA
eDepartment of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716, USA. E-mail: armstm@udel.edu
First published on 25th March 2025
Abstract
Interest in novel energy storage and conversion methods has prompted a broad interest in potential applications of conductive, complex materials such as graphene oxide slurries. Investigating the complex rheological, material, and chemical properties of chemically exfoliated graphene oxide suspensions is a potential means to address that interest. The morphological size and clustering, rheology, and electronic conductivity are determined to characterize the properties of graphene oxide (GO) suspensions from variable centrifugation speeds. The evolution of viscosity is then analyzed under oscillatory shear, steady shear, and transient shear characteristics. The resulting microstructure is then analyzed via neutron scattering analysis and imaged with scanning electron microscopy. Small-Angle Neutron Scattering (SANS) of a 500g centrifuged GO suspension determined that particle structure is locally flat sheet-like at lengths below 100 nm, crumpled aggregates of GO sheets with surface roughness at length scales from 200 nm to 2 μm, and a dense mass fractal of overlapping GO sheets extending up to length scales of 20 μm. Increased centrifugation force of the 1000g GO suspension corresponded with lower zero-shear viscosity, yield stress, and less pronounced thixotropic behavior. Rheo-dielectric measurements were conducted on 1000g and 500g GO suspensions to determine the ohmic resistance, electronic conductivity, and specific capacitance. The more fluid-like microstructure of 1000g with smaller monodispered thinning GO sheets in suspension had lower ohmic resistance and higher electronic conductivity compared to the 500g GO suspension with more polydispersed larger aggregates. The 1000g GO suspension had the highest specific capacitance of 4.63 mF cm−2 at the highest shear rate of 700 s−1 due to the higher frequency of particle–particle collisions during shear within the network of smaller and more intrinsically conductive GO sheets to store charge. Therefore, the results of this study have implications for future studies in flowable carbon nanomaterials in flow battery and flow capacitor technologies.
1 Introduction
To address the need for novel energy storage and conversion methods, the application of carbon nanoparticles (CNPs) in systems such as flow batteries has emerged as a promising approach for current and future power and energy demands.1 There exists a variety of CNP allotropes, or molecular rearrangements of carbon such as graphene nanoplatelets (GNPs) which assemble to form planar, 2D structures, carbon nanotubes (CNTs) that form extended, tube-like 1D structures, and carbon black (CB) particles which are spherical but nanoscopic and are thus considered zero-dimensional.1,2 The structure of carbon allotropes lends them unique potential in facilitating the electron flow necessary for practical electronic devices. Whether in a dry solid or liquid suspension state, aggregates of carbon particles can transfer delocalized electrons over their surface, with the conductivity of CNPs governed by the varying morphologies of their dry solid and liquid states.3–6The influence of the surface chemistry, crystal structure, and particle dimension of microstructure on the conductivity and viscosity of a nanoparticle suspension has been demonstrated in CB particles.2 When mixed into an aqueous dispersion, CNPs begin to aggregate, forming a slurry, leading to complex interactions between the individual particles. Optimizing particle agglomeration is necessary to ensure the slurry holds charge with minimal possible viscosity.2 At high viscosities, the utility of CNP slurries could be limited by the decreased ease of pumping and increased material quality requirements due to internal friction.7 Forming hierarchical structures with CB–CNT composite assemblies can act to reduce viscosity as the hybrid chains possess the advantages of both CB and CNTs, conferring decreased shear forces of CB and increased relative capacitance of CNTs at lower particle concentrations.8 Viscosity can also be tuned by coating CB with a dispersal agent, inhibiting agglomeration to promote uniform particle dispersion in the fluid. However, dispersal agents can decrease the conductive properties of the CNP slurry.9
Alternate methods of improving the conductivity of nanoparticle slurries can include the integration of other materials into the CNP dispersion. A common example of this can be seen in the mechanical mixing of poly(methyl methacrylate) (PMMA) with CB, a process that acts to increase the localization of the CNPs via the formation of small gaps for electron flow between the introduced PMMA molecules.10 While decreased shearing resistance can negatively affect the flow characteristics of liquid-phase conductive polymer composites (CPCs), covalent bonding in solid CPC structures positively affects mechanical strength while simultaneously improving electron transport for conductive polymer materials.11,12 Regardless of the particular CNP or CPC chosen for use, maximum faradaic efficiency can only be achieved by deliberately tailoring device electrodes to the unique properties of the particular slurry.13,14
Recent investigations have revealed GNPs as another viable nanomaterial for energy storage applications due to their expansive surface area affording them a high charge capacity and capacity for rapid electron exchange.1,15,16 Scalable methods for the synthesis of GO include chemical vapor deposition, direct liquid-phase exfoliation (electrochemical intercalation and shearing of graphite), and, most commonly, the Hummers' method.17–19 The most popular variant of the Hummers' method is the “modified” or “improved” Hummers' method.20–24 The aqueous GO suspension can also be reheated or evaporated to further concentrate the graphene sheets and mixed with other conductive materials such as Nafion polymer, creating more effective conductive pathways by altering the microstructure or interparticle interactions of graphene.25 However, commercially sourced GNPs come at far greater expense than CB, with the particles incurring average costs exceeding $15 USD per gram compared to $0.01 USD per gram.26–28
CNPs applied to the storage, transport, and conduction of charge must be stored within an electrolyte dispersion to allow the free flow of its constituent CNPs without the deleterious influence of the van der Waals forces and permit the agglomeration of the CNPs.29 When charged, a conductive slurry of nanoparticles can be further aggregated via water addition or, more commonly, sonication.19,30 An example of sonication can be seen in the fraying and exfoliation of nanoparticles from CNT/ZnO chains into electrolyte fluid.30 These free particles implant themselves on the exposed edges of micelles, isolating them and decrease overall fluid viscosity. Nonetheless, it is vital to balance the maximization of CNP density and the minimization of CNP chain degradation in the slurry.30 Careful sonication of the CNT dispersion is necessary as extended sonication or high frequencies can destroy the nanotubules, rendering them amorphous masses of nanofiber.31,32
As CNP agglomerates build up, the viscosity of the nanoparticle slurry generally increases, demonstrating complex thixo-elasto-visco-plastic (TEVP) flow properties.33 Thixotropy describes the time-dependent evolution of the viscosity of a fluid under shear effects on microstructure. Viscoelasticity represents the simultaneity of viscous and elastic characteristics in a material. Plasticity characterizes the threshold of non-zero yield stress above which a fluid undergoes permanent, irreversible deformation; below the threshold, the material deforms elastically.34–37 Effectively examining the rheology of CNP slurries necessitates a model of the steady-state and transient behavior of a suspension. The Generalized Newtonian Fluid (GNF) models such as the Casson, Carreau–Yasuda, and Herschel–Bulkley models can represent many aspects of steady-state flow behavior but prove unable to discern the transient viscoelastic behaviors of complex flowing materials such as GO dispersions.38,39 As such, accurately modeling the transient response phenomena produced by thixotropy and viscoelasticity requires more sophisticated constitutive models.40,41
The thinness of the monoatomic layers of GO permits exceptionally high electron mobility, facilitating the uninhibited flow of electrons through graphene sheets and resulting in outstanding conductivity, with low resistivities (corresponding to high conductivities) on the order of a mΩ cm.42 In exploring GO slurries under different flow conditions, the interplay between rheology and bulk electrochemical properties becomes a focal point, specifically the potential impact of shear-induced microstructure buildup and breakdown on ion diffusion. As GO sheets fragment in response to imposed shear stresses, the observed shear-thinning behavior may influence the ability of ions to conduct through the slurry. The dynamic stacking and restacking of numerous GO sheets in the slurry may also further contribute to the overall conductivity of the material.42,43
The flowability of GO slurries, crucial for redox flow batteries, also influences the material capacitance and electrronic conductivity. The effective particle concentration of the slurry is subject to alteration under varying flow conditions and evolving microstructure, making it a key parameter in the electrochemical performance of the material. The maintenance of a well-structured and flowable electrode comprised of nanoparticles with robust mechanical stability, characteristic of GO, is imperative for sustaining strong electrochemical performance over time.43,44 Moreover, the flowability characteristics of GO slurries can have broader implications for battery design. These include the optimal coating of substrates within flow batteries to form electrodes and the formation of conductive films.43,44 For electrochemical flow battery and flow capacitor applications, carbon nanomaterials such as GO are used as a conductive additive to electrolyte resulting in a flowable slurry electrode, therefore there is a fundamental need to study the flow rate dependent charge transfer through particle–particle interaction.45–47 For the optimization of the electrochemical performance of flowable electrodes in energy storage applications, it is critical to increase the rate of charge transfer in the slurry while lowering the viscosity. There have been recent studies that have focused on suspensions of CB to exhibit shear-thinning properties and an increase in conductivity by characterizing the shear-induced microstructure by probing the rheological and frequency-based dielectric properties with applied shear rates.48–52
The electrical percolation and mechanical percolation of suspensions can be a result of different particle–particle interactions and length scales. Results of early studies on CB showed both increasing and decreasing conductivity with increasing shear rate.49,51 The increase in conductivity was attributed to an increase in the frequency of particle–particle collisions due to shear.48,50,51 Contrary results indicating a decrease in conductivity was due to a decrease in the size of aggregates or the volume fraction of particles in the fluid.51,52 Percolation theory suggests a decrease in conductivity is a result of a decrease in agglomerate size or volume fraction of particles in a fluid.53 The conductivity with the shear of micron-sized particles such as CB has been well investigated. There are limited studies in probing the conductivity changes and microstructural properties of nano-sized CNPs such as GO in response to shear. Electron transfer can occur through a network microstructure through tunnelling or hopping during shear. Electron hopping occurs in short distances of about 1 nm at ambient temperatures, thus, nano-sized particles are the ideal material to measure it.54 Therefore, understanding the shear-dependency on viscosity, conductivity, and microstructure of a suspension can improve the performance of flowable slurries for electrochemical energy storage applications. The frequency-dependent dielectric response of GO suspensions under shear together with the changes in mechanical properties and Rheo-SANS measurements provide an insight into the role of microstructure on the conductivity of the particles in suspension. To our knowledge, there are limited multi-disciplinary studies on probing the length scales of the microstructure, transient rheological properties, and electronic conductivity and capacitance of nanometer-sized GO suspensions with shear rates.
To bridge the current gap in the robust quantitative characterization of CNP slurry electrochemistry in flow, this investigation links GO slurries' electrochemical characteristics and mechanical behavior through the collection and analysis of morphological, rheological, and electrochemical performance results. This study focuses on investigating the properties of GO in aqueous solutions at atmospheric pressure and room temperature conditions relevant operating conditions to electrochemical energy storage device applications. Fig. S9† contains Scanning Electron Microscopy (SEM) images of GO sheets after heated drying at 80 °C showing less prevalence of aggregated GO sheets settling onto substrate likely caused by the high temperature drying process. Section II details the mathematics of the ethixo-mHAWB model and the experimental parameter fitting procedure used to fit and predict the rheological data. Section 3 provides an overview of the materials and methods, with a discussion of the experimental process. Section 4 discusses the results of experiments, followed by the discussion. The remainder of the manuscript serves to conclude the study.
2 Model background and framework
2.1 Enhanced thixotropic mHAWB model
The viscoelasticity demonstrated by TEVP materials has been traditionally modeled via modifications of the Maxwell and Oldroyd-8 frameworks. While these two models can model transient behavior at relatively high shear stress,55–57 their utility does not extend to the lower range of shear stresses where complex materials can show complex time-dependent behavior. To rectify this weakness, the simple kinetic rate equation governing the evolution of the non-dimensional structure parameter can be substituted with the use of dual elastic and plastic stress terms or the incorporation of the structure parameter into a generalized viscoelastic model.58–63The elasticity and plasticity terms are resolved by splitting total strain and its time derivative, the total rate of strain, into two separate terms.59,62,64 Kinematic hardening theories of plasticity can be used to capture the plastic behavior of a material, integrating both isotropic hardening (IH) and kinematic hardening (KH) into the model description.64–69 The employment of representative equation parameters for the two hardening terms in the ethixo-mHAWB (modified Horner–Armstrong–Wagner–Beris) model used here is vital in properly modeling the dynamics of fluid systems such as slurries.69–71
Characterizing the rheology of CNP slurries plays a vital role in enhancing our understanding of the microstructural responses of slurries to stress and strain under different conditions. As a viscoelastic material, the response can be analyzed (i) at steady-state, (ii) small amplitude oscillatory shear (SAOS), representing a fairly limited region of viscoelasticity where outputs vary linearly with inputs, and (iii) large amplitude oscillatory shear (LAOS), which captures the larger spans of the viscoelastic domain.72–76 The breakdown process of the suspension provides insight into time-dependent flow characteristics. Nonlinear measurements explored by LAOS are decomposed using Fourier transforms, which typically utilize sine inputs for controlled strain and cosine inputs for controlled stress.72,77–80
The structure of CNPs can be analyzed via rheo-ultra-small-angle neutron (Rheo-USANS) scattering. This details both flow stability and the threshold at which dense agglomerates evolve into more open, smaller variants (transition state) which is informative in assessing the conductive behavior of slurries. This is expressed by the inverse Bingham number, Bi−1, which compares the bulk stress imposed on a suspension to its yield stress. At lower shear rates, Bi−1 < 1, the Bingham number indicates the accumulation of particles in relatively large, dense particles that tend to sediment under dominant yield stress, producing analytic inconsistencies. At Bi−1 > 1, corresponding to high shear rates, the aggregates are smaller, demonstrating an apparent shear-thinning as the yield stress is overcome, indicating the shear-independence of the fractal dimensions of the agglomerates.81
With the relative increase in the availability of transient experimental data for complex materials, models have been developed to represent the spectrum of TEVP behavior.56 One such model, the HAWB model, integrates a generalized White–Metzner–Cross model to better represent the viscoelasticity of deformable particles within a suspension. From the time-varying viscosity Maxwell model (TVM) model, a further improved model introducing the viscoelastic response of a material was developed in the mHAWB method.41 A subsequent modification to the kinetic equations of mHAWB to include a shear aggregation term for the structure parameter would result in the enhanced thixotropic mHAWB (ethixo-mHAWB) model shown here.41,71
A full, and more detailed ethixo-mHAWB model description can be found in the following ref. 40, 41, 71 and 73. Here, we will provide an overview of the steady state and transient constitutive equations to ground the subsequent discussion of the fitted data in the rheological underpinnings of the model. The model is a White–Metzner viscoelastic model, integrated with the Cross model to describe the viscosity as a function of shear rate.40,41,56 This baseline framework for the stress tensor evolution and the rate-dependent viscosity describes the suspension with individual GO particles, or aggregates before they begin forming larger-scale agglomerates during periods of low shear rate.
 | (1) |
 | (2) |
 | (3) |
 | (4) |
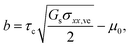 | (5) |
 | (6) |
 | (7) |
| σtot = σyx,ve + σyx,A,ve + σyx,A,e | (8) |
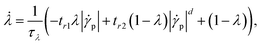 | (9) |
This thixotropic modeling incorporates the separating of strain and shear rate into elastic and plastic components from literature37,40,41,64–66 where γ = γe + γp and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =
= ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) e +
e + ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p and is further described by,
p and is further described by,
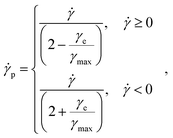 | (10) |
| γmax = γ0,Aλ, | (11) |
 | (12) |
The elastic contribution from the GO microstructure to total stress is
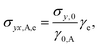 | (13) |
 | (14) |
3 Materials and methods
3.1 Graphene oxide synthesis and particle size analysis
ImageJ was used to determine the graphene particle size distribution of the GO dispersions produced via Hummer's method as described in the ESI.†86 Raman spectroscopy was conducted on the resulting GO after chemical exfoliation using Hummer's method. Refer to Fig. S5† for the Raman spectrum with the average intensity ratios of the D-Band to the G-Band corresponding to the presence of oxygenated defects on the edge and basal plane. As shown in Fig. S6 and Table S3,† Raman Spectroscopy was conducted on multiple GO film samples each with the representative spectrum and intensity ratios of D-Band to G-Band and 2D-Band to G-Band confirming the presence of multi-layer GO with oxygen functional groups resulting from the chemical exfoliation process. In order to create GO suspensions from varying centrifugation speeds, a stock 1.1 wt% GO in H2O was centrifuged at 100g for 5 min to remove any undissolved large aggregates and collecting the resulting supernatant as the basis to create 500g and 1000g GO suspensions as stated in the ESI.† As described below in Section 3.2, the 500g and 1000g GO suspensions were cast onto a SiO2/Si wafer to conduct SEM to obtain GO particle morphology images which served as the basis for particle size distribution analysis discussed later in Section 4.1. SEM images at a zoom of 950× were first adjusted for brightness/contrast and then converted to binary images. The Paintbrush tool was sparsely used to divide overlapping graphene oxide sheets when the overlaps were obvious upon visual inspection. The Fill Holes function was then used to ensure that graphene oxide sheets presented a solid surface area. The Erode function was used to remove residual pixel noise. The Analyze Particles function was used to determine Regions of Interest (ROIs); a minimum particle size of 0.5 μm2 was set as a threshold with no threshold set for maximum. A total of five images and n = 946 particles were analyzed. Moreover, the particle size GO in suspension was probed through Dynamic Light Scattering (DLS). As shown in Fig. S4,† the DLS measurement provided evidence of a clustered GO sheet network of aggregates with a particle distribution between 300 nm to 550 nm coexisting in suspension.3.2 Scanning electron microscopy
Scanning electron microscopy (SEM) was used to characterize the morphology and size of the GO sheets using a JEOL IT500HRLA SEM (JEOL USA, Peabody, MA, USA). A 30 kV beam voltage was used for imaging. All samples for SEM characterization were prepared by drop casting from a 0.2 mg mL−1 dispersion of GO and ambiently dried onto a SiO2/Si wafer. SEM image particle size analysis was conducted using ImageJ.87 Refer to Fig. S7† for SEM images and Fig. S8† for Energy Dispersive X-ray (EDX) Spectroscopy with elemental composition of the GO film from drop casting a sample of the 500g GO suspension onto a clean SiO2/Si wafer and drying at room temperature.3.3 Rheology
All rheological measurements were performed with an ARESG2 strain-controlled rheometer from TA Instruments equipped with cup and bob geometry. For rheological experiments 10 mL of the 500g, and 1000g graphene oxide suspension in water was loaded into the cup portion of the ARESG2. The dimensions of the geometry are as follows: the bob has an inner cylinder diameter measuring 27.7 mm and an outer cylinder diameter of 30.0 mm, with the bob length measuring 41.6 mm. All rheological tests were performed at 25 °C, which was maintained by a Peltier temperature controller. The shear rate never exceeded 1000 s−1 and a preshear of 300 s−1 for 30 s was used before each test to eliminate the initial thixotropic, or memory effects of the sample.40,41,71 In this work the experimental results will be shown for steady state, small amplitude oscillatory shear (SAOS, amplitude sweep at ω = 12.6 rad s−1; and frequency sweep at γ0 = 10) and large amplitude oscillatory shear (LAOS).40,41,71 The LAOS signals presented in this work are for strain and strain rate respectively,
γ(t) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt), sin(ωt),
| (15) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) = γ0ω (t) = γ0ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt), cos(ωt),
| (16) |
 | (17) |
 | (18) |
3.4 Neutron scattering
Small-angle neutron scattering (SANS) measurements were performed on the NG7-SANS beamline located at the NIST Center for Neutron Research (NCNR) in Gaithersburg, MD.87 The graphene oxide particles suspended in water (either H2O or D2O) were loaded and sealed in titanium demountable cells with a nominal path length of 1 mm. Scattering data were collected at sample-to-detector distances of 1 m, 4 m, and 13 m (lenses) to provide a combined q range from approximately 0.001 Å−1 < q < 0.5 Å−1, where q = 4πλ−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2), q is the magnitude of scattering vector, λ is the incident neutron wavelength (6 Å), and θ is the scattering angle.
sin(θ/2), q is the magnitude of scattering vector, λ is the incident neutron wavelength (6 Å), and θ is the scattering angle.
Ultra-small-angle neutron scattering (USANS) measurements were performed on the BT5-USANS instrument at the NCNR.88 The slit-smeared USANS intensity was measured over a significantly lower q-range, spanning from approximately 0.00003 Å−1 < q < 0.003 Å−1, which provided an overlapping q-region with the 13 m (lenses) SANS configuration between 0.003 Å−1 and 0.001 Å−1. The slit-smeared USANS data were de-smeared to compare the SANS and USANS on the same absolute intensities. All data were normalized to an absolute intensity I(q) with units of inverse cm−1 sr−1 (denoted here only as cm−1 as the inverse steradian is redundant in this application) after subtracting the scattering from the empty cell and blocked beam using the NCNR reduction procedures in Igor software.89 Lastly, the q-independent incoherent scattering (B) was determined at the high-q plateau and subtracted from the total intensity to give the q-dependent coherent scattering, I(q) − B. The combined SANS and USANS curves were fit using the DREAM algorithm in SasView (version 5.0.5) using a linear-weighted sum of the “lamellar” model and the “correlation length” model.90 The details of the model equation, fit parameters, and parameter uncertainties are discussed further in the ESI.†
3.5 Rheo-dielectric measurements
Dielectric spectroscopy measurements of the 500g and 1000g GO dispersions were made under steady shear with dielectric spectroscopy measurements using an ARES G2 strain-controlled rheometer outfitted with the cup and bob Couette system described above. This is coupled with an Agilent 4980A LCR meter operating between 20 Hz to 2 MHz with a redispersion of 1 MHz.91 The dielectric spectroscopy analysis resulted in impedance (Z) and phase angle (θ) measurements over the frequency range. Each run was completed after waiting 5 minutes at the steady shear (0, 0.1, 10, 100, 700 s−1) before starting any dielectric frequency sweep. Each dielectric sweep from 20 Hz to 2 MHz was performed five times at each shear rate.3.6 Model fitting and optimization
To fit the model parameters of the ethixo-mHAWB model to the rheological data, we follow the previous protocol established by Armstrong et al., and Horner et al.37,40,41,71,73,83,84 The steady-state parameters are fit to steady-state data by minimizing the normalized cost function, Fcost,ss, then held constant (during the transient parameter fit). The best-fit parameters are found using a parallel tempering algorithm, and eqn (19) shown below:71,72,83,84
 | (19) |
 | (20) |
 | (21) |
The small amplitude oscillatory shear is predicted, and Fcost,SAOS computed as follows,
 | (22) |
4 Results and discussion
4.1 Particle size distribution analysis
As seen in Fig. 1a and b, GO particle size surface areas range from 0.5–156 μm2. Nearly 33% of all GO particles are between 0.5–2 μm2 with an approximately exponential decaying particle size distribution from small-to-large surface areas. Particles between 0.5–5 μm2 comprise nearly half the total particles (48%) and particles larger than 30 μm2 are only 5% of the total distribution. These size distributions accord with previous explorations of applying 2D carbon materials to flow battery applications.92 For ImageJ processing steps from SEM images of the GO sheets see Fig. S1 and S10.†4.2 Small-angle neutron scattering
As shown in Fig. 1c, the combined USANS and SANS intensities reveal the in situ structure of a percolating network of GO sheets suspended in water. The probed q-range spans four decades, which corresponds to length scales from approximately 1 nm up to 20 μm as observed in Fig. 1c. The measured intensity (blue circles) was modeled by a summed lamellar-correlation length model (solid black line). The combined lamellar-correlation length scattering model indicates a percolated network of clustering graphene oxide sheets, which captures the high-q scattering from the flat and thin primary sheets, while also capturing the surface-fractal scaling behavior above and below a characteristic correlation length (ξ ≈ 540 nm). The reduced goodness of fit was χ2/N = 3.9, and no polydispersity was applied to any parameters. The best-fit parameters and uncertainties are given in Table S2.†The qualitative features of the apparent power-law slopes are described in Table S2 of ESI and by eqn (S2)–(S4)† are discussed in three different regions of q, demarcated by vertical dotted lines in Fig. 1c. These regions correspond to high-q (0.006 < q < 0.5 Å−1), mid-q (0.0002 < q < 0.006 Å−1), and low-q (0.00003 < q < 0.0002 Å−1). Within the high-q region, an observed power-law of I(q) ∼ q−2 indicates scattering from a uniformly flat, sheet-like region of the GO primary particles. The best-fit thickness determined from the lamellar model parameter (δ = 1.1 nm) agrees with the expected thickness of single GO sheets. In the mid-q region at length scales larger than 100 nm, a different power-law exponent (mq = −3.2 to −3.6) is observed up to an apparent correlation length of 540 nm. This region corresponds to scattering from a surface fractal with a relatively roughened topology which suggests that the graphene sheets do not remain flat in dispersion at length scales above 100 nm and instead begin to fold, crumple, or overlap. At the low-q region below the correlation length, the power-law scaling exponent (n = −3.2) continues up to the largest length scale probed by USANS (2π/qmin ≈ 20 μm). This surface-fractal scaling corresponds to scattering from the rough surface of larger GO clusters. Since a low-q plateau (Guinier region) is not observed, the maximum cluster size can be inferred to have a lower limit of its radius of gyration, Rg,max > 20 μm. Overall, the in situ structure determined from SANS and USANS agrees with the dried structure observed from SEM. Both techniques indicate the percolation of large clusters containing sheet-like graphene oxide primary particles.
Contrast variation experiments were performed to determine the neutron scattering length density (SLD) of GO particles. These experiments were accomplished by collecting SANS measurements of five different solvent ratios (20% to 100% by volume D2O in H2O) at the same GO concentration. The resulting particle SLD was estimated as ρp = 8.3 ± 0.4 × 10−6 Å−2, as shown in Fig. S2.† Using the estimated particle SLD and the known solvent SLD (ρH2O = −5.6 × 10−7 Å−2), the total scattering invariant of this two-component system could be computed and used to estimate the total volume fraction of graphene oxide sheets in the 500g sample. The scattering invariant 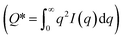 was estimated to be 2.3 × 10−4 cm−1 Å−3, and the total volume fraction of scattering centers (0.15% by volume GO) was estimated after determining the particle SLD and scattering invariant. Lastly, the specific surface area of dispersed particles in solvent (particle surface area per particle volume) is determined by Sv = CP(2π)−1(ρP – ρH2O)−2, in which CP is the Porod constant determined at the limiting high-q region from a linear fit of I(q) q4 as a function of q4 (CP = 2.9 ± 1.8 × 10−4 cm−1 Å−4). Assuming the GO particles retain a density of 0.26 g cm−3, the specific surface area of GO particles in dispersion was estimated to be Sv = 220 ± 140 m2 g−1. Details of the neutron contrast variation measurements, scattering invariant, volume fraction, Porod constant, and specific surface area estimations are described in the ESI.†
was estimated to be 2.3 × 10−4 cm−1 Å−3, and the total volume fraction of scattering centers (0.15% by volume GO) was estimated after determining the particle SLD and scattering invariant. Lastly, the specific surface area of dispersed particles in solvent (particle surface area per particle volume) is determined by Sv = CP(2π)−1(ρP – ρH2O)−2, in which CP is the Porod constant determined at the limiting high-q region from a linear fit of I(q) q4 as a function of q4 (CP = 2.9 ± 1.8 × 10−4 cm−1 Å−4). Assuming the GO particles retain a density of 0.26 g cm−3, the specific surface area of GO particles in dispersion was estimated to be Sv = 220 ± 140 m2 g−1. Details of the neutron contrast variation measurements, scattering invariant, volume fraction, Porod constant, and specific surface area estimations are described in the ESI.†
4.3 Rheology and TEVP modeling
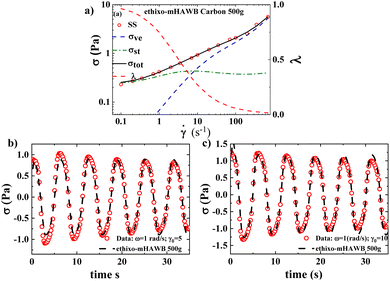
Fig. 2a–c and 3a–c show the steady state and transient data and ethixo-mHAWB model fits for both the 500g and 1000g GO suspensions respectively. The best fit parameter values of each fit, and comparison are shown in Table 1, below. Recall that the seven steady state parameters are fit to one set of steady state data; while the three transient parameters are fit to two sets of LAOS data at ω = 1 rad s−1 and γ = 5, 10 using the parallel tempering algorithm. Three of the ethixo-mHAWB model parameters are fixed as annotated in Table 1 below, based on best values for similarly structured materials from the literature.37,40,41,47,93 Visual inspection of Fig. 2a and 3a show an immediate difference in magnitude of the yield stress, and infinite shear viscosity between the 500g and 1000g GO suspension indicating that the 1000g sample demonstrates fewer effects of residual microstructure, although there is certainly some present. This may be in some part due to the higher shear forces exerted at 1000g centrifugation as well as the 500g process permitting increased particle–particle interactions due to higher sedimentation times. Inspection of Fig. 2b, c, 3b and c also show a significant difference in the magnitudes of the maximum stresses of the two sets of LAOS data, indicating that the aggregates play a significant role in the total stress even during LAOS. It is known that by changing the direction of flow twice a cycle leads to an increase in shear breakage above and beyond only increases in the magnitude of shear rate, or shear stress.37,40,41,60,94,95 By comparing the magnitude of the maximum stress of the LAOS data shown below it is clear that the 500g sample has more structure, aggregates, and agglomerates, and this increases the stress over the LAOS cycles.| Parameter | Description | 500g GO | 1000g GO |
|---|---|---|---|
| μ0,s (Pa s) | Zero shear viscosity of suspension & ind. particles | 0.071 | 0.011 |
| μ∞,s (Pa s) | Infinite shear viscosity of suspension & particles | 0.006 | 0.004 |
| τC (s) | Cross time constant | 0.047 | 0.052 |
| tr1 (s) | Ratio of shear breakdown to Brownian build-up constant | 0.384 | 0.991 |
| tr2 (s) | Ratio of shear aggregation to Brownian build-up constant | 0.133 | 0.058 |
| μA (Pa s) | Agglomerate viscosity | 0.263 | 0.079 |
| σy0 (Pa) | Yield stress | 0.229 | 0.024 |
| d | Power law for shear aggregation (fixed parameter) | 0.5 | 0.5 |
| m | Power law for effect of aggregate viscosity (fixed parameter) | 1.5 | 1.5 |
| γ∞ (Pa s) | Infinite strain (fixed parameter) | 1 | 1 |
| τλ (s) | Time constant of thixotropic evolution | 1.112 | 2.590 |
| GA (Pa) | Elastic modulus of agglomerates | 1.013 | 8.845 |
| Gs (Pa) | Elastic modulus of suspension and particles | 4.689 | 5.250 |
| Fcost (SS) | Normalized cost function of steady state fit | 0.0101 | 0.0056 |
| n (points) | Number of data points of steady state fit | 16 | 16 |
| RSS | Residual sum of squares for steady state fit | 0.0260 | 0.0081 |
| k (par.) | Number of parameters fit to steady state data | 7 | 7 |
| Fcost (trans) | Cost function of LAOS transient parameter fit | 0.0024 | 0.0011 |
| n (points) | Number of data points of transient parameter fit | 3992 | 3992 |
| RSS | Residual sum of squares for transient fit | 89.441 | 19.026 |
| k (par.) | Number of parameters (or cycles) fit to LAOS, transient data | 3 | 3 |
An analysis of Table 1 below quantifies what is shown graphically in Fig. 2 and 3. There is a significant drop in yield stress, and the infinite, zero, and aggregate viscosities. The yield stress drops by an order of magnitude due to the ostensible decrease in the amount of structure present in the 500g vs. the 1000g GO samples. In addition, analysis of the Fcost suggests that the use of the ethixo-mHAWB model for this system seems to have been more justified for the 1000g GO system.40,41,60,94,95 Which possesses lower zero-shear (or fully structured) and infinite-shear (or fully-unstructured) viscosities when compared to the 500g slurry.
Fig. 4a and c display the frequency sweeps (performed at γ0 = 10), while Fig. 4b and d show the amplitude sweeps (performed at ω = 12.6 rad s−1), for the 500g and 1000g graphene oxide systems, showing the data and ethixo-mHAWB model predictions. Qualitatively, the ethixo-mHAWB model seems to capture material viscoelasticity as the frequency increases at constant strain amplitude per Fig. 4a and c, and as the strain amplitude increases at constant frequency per Fig. 4b and d. However, Table 2 makes it clear that based on SAOS Fcost values, the model more accurately predicts the 1000g frequency and amplitude sweeps. This demonstrates again that the lower centrifugation magnitude of the 500g sample has led to a markedly different microstructure from the 1000g sample and that we are nearing the limits of the ethixo-mHAWB model's accuracy for the higher viscosity 500g system.
| Parameters | 500g GO | 1000g GO |
|---|---|---|
| Fcost,SAOS | ||
| Freq sweep; γ0 = 10 (–) | 0.0097 | 0.0121 |
| I3/I1 | 0.0100 | 0.0090 |
| Amp sweep; ω = 12.566 rad s−1 | 0.0710 | 0.0084 |
| I3/I1 | 0.0111 | 0.0117 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Fcost,LAOS | ||
| (ω = 1) | 0.0203 | 0.0033 |
| γ0 = 0 | 0.0260 | 0.0035 |
| γ0 = 1 | 0.0230 | 0.0022 |
| γ0 = 5 | 0.0087 | 0.0025 |
| γ0 = 10 | 0.0166 | 0.0031 |
| γ0 = 50 | 0.0275 | 0.0051 |
| γ0 = 100 | 0.0671 | 0.0069 |
| Fcost, averaged | 0.0337 | 0.0079 |
Fig. 5 and Table 2 below show the results of the LAOS predictions of the six sets of LAOS data at ω = 100 rad s−1 and γ0 = 5, 10, 50, and 100. Qualitatively the model predicts the 1000g LAOS data better than the 500g data. This is again corroborated by the LAOS Fcost values comparison in Table 2.
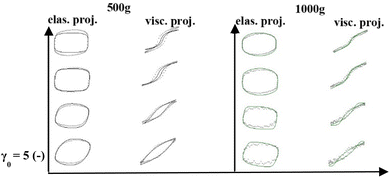
Fig. 6a and b are the Cole–Cole plots of the 500g and 1000g graphene oxide suspensions, respectively. Fig. 6c shows the color mapping of δt, a solid-like metric and Fig. 6d shows the Cole–Cole legend.93 The Cole–Cole figures are once again demonstrating significant differences in elastic and viscous properties between the 500g and 1000g samples. For example, the magnitude of the stress itself is different by one order of magnitude, and Fig. 6a shows a much more solid-like substance at all the frequency and strain amplitude combinations (from the δt color comparison), and the fact that the 500g demonstrates more persistent solid-like behavior during the oscillation at higher strains. As we follow a cycle from steps 1 through 4 over a half-period, we can see that from 1 to 2 to 3 we are in a more solid-like configuration, and moving to point 4 takes us to the more liquid-like configuration of the microstructure, as it is broken down over this portion of the LAOS cycle, with an observable structural recovery as the shear rate decreases.
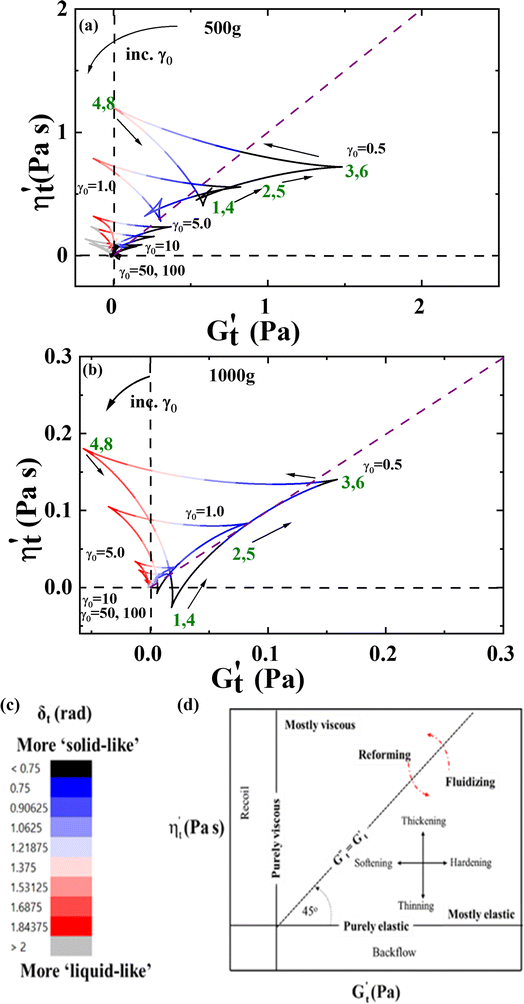 | ||
Fig. 6 (a) Cole–Cole plots of 500g; and (b) Cole–Cole plots of 1000g GO suspensions for six sets of LAOS collected at ω = 1 rad s−1 and γ0 = 0.5, 1, 5, 10, 50 and 100  ; (c) color mapping for δt; and (d) Cole–Cole interpretation legend.45,70,74,83–86 Green annotations reflect recorded properties at given step in LAOS cycle. ; (c) color mapping for δt; and (d) Cole–Cole interpretation legend.45,70,74,83–86 Green annotations reflect recorded properties at given step in LAOS cycle. | ||
Fig. 7a–d show the accumulated contour mapping of δt and λ over six sets of LAOS at ω = 1 rad s−1 and γ0 = 5, 10, 50 and 100 for both the 500g and 1000g graphene oxide samples, respectively. The y-axis on each of the subfigures is from 0–6.27 s, the amount of time for a complete LAOS period at ω = 1 rad s−1. We note that there are portions of more ‘liquid-like’ and ‘solid-like’ behavior shown for each figure. The λ values shown in the contour maps below are from the structure predictions of the ethixo-mHAWB model of each LAOS prediction, while the aforementioned δt values are computed with the Sequence of Physical Processes (SPP), using key parameters drawn from previous studies.45,70,82,93,94,96,97
4.4 Rheo-dielectric measurements
Electrochemical impedance spectroscopy (EIS) is used for determining the kinetics of electrochemical processes, resistances, and capacitances.98 From rheo-dielectric measurements, EIS analysis is conducted to determine the conductivity and capacitance of the GO dispersions under the different conditions of rheology and concentrations. This may permit us to characterize the potential performance of these slurries concerning their performance as potential flowable electrodes.All rheological measurements were performed with an ARESG2 strain-controlled rheometer from TA instruments equipped with the cup and bob geometry. In this analysis, the bob possesses an outer diameter of 27 mm, an inner diameter of 26 mm, and a length of 34 mm. For rheological experiments, 10 mL of the 500g, and 1000g GO suspension in water was loaded into the cup portion of the ARESG2. The electrical percolation threshold of the GO suspensions in H2O was determined by probing the frequency-dependent resistance to determine the conductivity. Since the GO suspensions are in a water fluid phase, the contribution of the measured resistance is electronic charge transfer without any ionic contribution.
The samples consisted of 1000g GO in H2O (∼0.9 wt% GO in H2O) and 500g sample (∼0.1 wt% GO in H2O after 500g centrifugation) within a frequency range of 20 Hz to 2 MHz. A stock solution was first made with a low centrifugation speed of 100g for 5 min to remove any undissolved large aggregates by using the resulting supernatant. There was an observed yield stress just by inverting the vial of the GO suspension and appeared to be strongly shear thinning. From the rheo-dielectric measurements, the impedance (Z) (ohms), the frequency (f) (Hz) and phase angle (φ) (radians) were determined. A brief conceptual overview of the EIS method to determine the Nyquist plot can be found in ESI Section 3.† From this data, the resulting complex plane plots of Nyquist plots of imaginary versus real impedance can be calculated using the following equations:
Re(Z) = Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(φ) cos(φ)
| (23) |
Im(Z) = Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(φ) sin(φ)
| (24) |
Since the focus of the data analysis is the determination of the real ohmic resistance for each condition, determining where the x-intercept occurs for the calculation of conductivity is the most important aspect of the Nyquist plots. Analysis of the Nyquist plots determined the ohmic resistance contribution with 0 s−1, 0.1 s−1, 1 s−1, 10 s−1, 100 s−1, and 700 s−1 shear rates. Since each rheo-dielectric measurement involves a frequency sweep from 20 Hz to 2 MHz five times at each shear rate, each Nyquist plot contains the real impedance as the x-intercepts corresponding to the ohmic resistance of the GO suspension. The x intercept of the 1000g GO sample occurred at around a frequency of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023.74 ± 0.01 Hz and the 500 g GO sample occurred at a frequency of around 12
023.74 ± 0.01 Hz and the 500 g GO sample occurred at a frequency of around 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619.15 ± 0.01 Hz. The plus or minus (±) Hz refers to the accuracy of dielectric measurement from instrumentation. Table 3 shows each average contribution. The ohmic resistance of the 500g and 1000g at zero applied shear rate is the electronic resistance of the innate microstructure of the GO suspension. The ohmic resistance decreased in the 1000g GO suspension with increasing shear rate. However, the ohmic resistance increased with increasing shear rate in the 500g GO suspension. These changes in ohmic resistance for both 1000g and 500g GO suspensions is due to the difference in the microstructure during steady shear. Determining the ohmic resistance of a flowable electrode suspension can help inform slurry electrode design to minimize ohmic power loss and maximize the electronic conductivity necessary for charge transfer in various flowable electrochemical energy storage devices. Overall, the 1000g GO suspension had a lower ohmic resistance is attributed to the higher loading of GO sheets with 0.9 wt% compared to the more dilute 0.1 wt% 500g GO since interparticle interactions tend to be strongest and most affected by the imposed flow at higher concentrations resulting in enhanced electrical percolation to facilitate the movement of electrons across finite distances despite being under shear. This is evident from the conductivity results in Table 4 comparing 1000g to 500g GO suspensions. Moreover, the rheology results in Section 4.3 show the 1000g GO suspension as being less viscous than 500g and therefore less solid-like since most of the larger particulate has been separated in the sample centrifugation process.
619.15 ± 0.01 Hz. The plus or minus (±) Hz refers to the accuracy of dielectric measurement from instrumentation. Table 3 shows each average contribution. The ohmic resistance of the 500g and 1000g at zero applied shear rate is the electronic resistance of the innate microstructure of the GO suspension. The ohmic resistance decreased in the 1000g GO suspension with increasing shear rate. However, the ohmic resistance increased with increasing shear rate in the 500g GO suspension. These changes in ohmic resistance for both 1000g and 500g GO suspensions is due to the difference in the microstructure during steady shear. Determining the ohmic resistance of a flowable electrode suspension can help inform slurry electrode design to minimize ohmic power loss and maximize the electronic conductivity necessary for charge transfer in various flowable electrochemical energy storage devices. Overall, the 1000g GO suspension had a lower ohmic resistance is attributed to the higher loading of GO sheets with 0.9 wt% compared to the more dilute 0.1 wt% 500g GO since interparticle interactions tend to be strongest and most affected by the imposed flow at higher concentrations resulting in enhanced electrical percolation to facilitate the movement of electrons across finite distances despite being under shear. This is evident from the conductivity results in Table 4 comparing 1000g to 500g GO suspensions. Moreover, the rheology results in Section 4.3 show the 1000g GO suspension as being less viscous than 500g and therefore less solid-like since most of the larger particulate has been separated in the sample centrifugation process.
| Shear rate (s−1) | 1000g GO [Ω] | 500g GO [Ω] |
|---|---|---|
| 0 | 0.84321 | 2.31628 |
| 0.1 | 0.82216 | 2.34627 |
| 1 | 0.82265 | 2.40244 |
| 10 | 0.83461 | 2.41894 |
| 100 | N/A | 2.45011 |
| 700 | 0.83231 | 2.38442 |
| Shear rate (s−1) | Conductivity [S cm−1] | |
|---|---|---|
| 1000g GO | 500g GO | |
| 0 | 0.81867 | 0.29803 |
| 0.1 | 0.83963 | 0.29422 |
| 1 | 0.83913 | 0.28734 |
| 10 | 0.82710 | 0.28538 |
| 100 | N/A | 0.28175 |
| 700 | 0.82939 | 0.28951 |
From this ohmic resistance data, the conductivity of each GO dispersion within the rheometer geometry is calculated by taking the inverse of the resistivity. Since the diameter of the bob is 27.7 mm, the cross-sectional area A of the bob is calculated at 6.02628 cm2. Eqn (S1) (seen in the accompanying ESI)† can then be used to solve for resistivity using the length of the bob l as given by instrument specifications and resistance R from Table 3 above. Taking the inverse of the resistivity value from eqn (S1)† results in the conductivity value for each test in [S cm−1] shown below in Table 4 and Fig. 10. A comparison of reported electronic conductivity values of GO from literature is included in Table S4.† Moreover, as shown in Table 4, the conductivity of the 1000g GO suspension increased with shear rate while the conductivity of the 500g GO suspension generally decreased with shear rate. As confirmed with the rheology results in Section 4.3, the 1000g GO suspension contains more of a finer microstructure comprised of less aggregates and smaller GO sheets because of the centrifugation process. The separation process resulted in a supernatant with more monodispersed GO particles with fewer graphene layer to create the 1000g suspension. These thinner GO sheets have higher intrinsic particle conductivity due to less resistance of the delocalized electrons allowing for more electron mobility through the conjugated double bond structure. Therefore, the 1000g GO suspension has smaller electrical percolation microstructure with enhanced charge transfer through shear-induced collisions of the thinner GO sheets. The thinner and smaller GO particles form a liquid-like microstructure in the 1000g suspension with shorter distances for electron transfer leading to a higher conductivity. The conductivity of the 1000g suspension increased with shear due to more intimate particle–particle points of contact through the collisions taking place between the smaller and thinner GO sheets that are in suspension. However, the conductivity of the 500g GO suspension was four times less with applied shear compared to the 1000g. This lower conductivity in 500g is from the presence of aggregates in suspension and with shear there are less points of contact between GO sheets in the microstructure. The 500g suspension is more polydispersed with larger GO particles forming larger aggregates under shear and more void space in suspension because of the fewer points of contact between the aggregates resulting in higher ohmic resistance for electron transfer and lower electronic conductivity.
Another method used to analyze the internal resistance contributions is to calculate ASR or area-specific resistance (Ω cm2). Table 5 shows the ASR values for each test under different shear rates and concentrations by multiplying the measured resistance values from Table 3 and the calculated bob area using the given instrument parameters. The ASR of the GO suspensions assess the efficacy and performance of GO as a slurry electrode for flowable electrochemical applications.
| Shear rate (s−1) | ASR [Ω cm2] | |
|---|---|---|
| 1000g GO | 500g GO | |
| 0 | 5.08142 | 13.95855 |
| 0.1 | 4.95459 | 14.13926 |
| 1 | 4.95754 | 14.47776 |
| 10 | 5.02961 | 14.57722 |
| 100 | N/A | 14.76506 |
| 700 | 5.01576 | 14.36921 |
From the results of the Nyquist plots in Fig. 8, the specific areal electrochemical capacitance (Csp) in mF cm−2 of the 500g and 1000g GO suspensions was determined. Under a constant shear rate across a cross-sectional area within a frequency range of 2 MHz to 20 Hz, the Csp was determined using the following eqn (25) where f is the frequency in Hz, Z” is the imaginary component of impedance, and A is the geometric area of the rheometer bob in cm2:101,102
 | (25) |
The specific areal capacitance as a function of frequency for the GO suspensions under shear of 0 s−1, 0.1 s−1, 1 s−1, 10 s−1, 100 s−1, and 700 s−1 is plotted in Fig. 9. Across all the applied shear rates in Fig. 9, the specific areal capacitances of the GO suspensions were the highest for 500g GO at 12.6 kHz and the highest for 1000g at 10 kHz. With increasing frequency, the time for charge transfer decreases since the distance for charges to move also decreases.103,104 In Fig. 9a, the specific areal capacitance of the 500g and 1000g GO suspensions with a zero shear rate at a low frequency of 502 Hz is 0.027 mF cm−2 and 0.028 mF cm−2, respectively. With a sweep to higher frequencies, there is a noticeable large increase in specific areal capacitance of 0.97 mF cm−2 for 500g GO at 12.6 kHz and 0.67 mF cm−2 for 1000g at 10 kHz which is due to the charge build up in the governing percolating microstructure of GO sheets as primary particles in suspension.
 | ||
| Fig. 10 Conductivity in S cm−1 comparison for 1000g GO (blue) and 500g GO (red) at different shear rates. | ||
The Csp peaks at 10 kHz and 12.6 kHz for 1000g and 500g GO suspensions, respectively, are the characteristic flip frequencies which determine the Debye relaxation time for the 1000g and 500g GO suspensions to discharge to an equilibrium within an applied electric field.105,106 The transition from long to short distance charge carrier mobility occurs at these characteristic maximum frequencies.105–107 The Csp in both the 500g and 1000g GO suspensions is mostly constant at frequencies below and above the characteristic flip frequency (∼104 kHz) at zero applied shear. The lower Csp at frequencies below the characteristic maximum flip frequency (<104 kHz) is due to the charge carriers having to move longer distances through the microstructure suspension.105,106 After applying shear to the 500g and 1000g GO suspension, the charge storage capacitance lowers when shifting to higher frequencies beyond the maximum due to charge carrier confinement within short distances.105,106 This asymmetric specific capacitance is due to a non-Debye broader relaxation or discharge time because of the charge diploes on the GO particles.105,106 Despite the lower conductivity compared to the 1000g suspension as shown in Table 3, there was a larger capacitance increase in the 500g GO suspension. This is due to the charge storage within the aggregates of GO in the 500g suspension without any leakage current at low shear rates. There is a shift to a higher flip frequency for the more viscous 500g with more aggregates in suspension since the charge transfer within the microstructure does not occur instantly since it takes time to align dipole moments within the larger GO aggregates.
The specific areal capacitance decreased drastically when sweeping to higher frequencies to 2 MHz indicating a dissipation of this charge build-up in the microstructure of the percolating large clusters of GO sheets. This governing microstructure of the GO sheets in suspension is disrupted by applying a steady shear rate to the GO suspensions thus, impacting the GO sheet–sheet interaction for charge transfer and storage. Therefore, an increase in shear rate of 0.1 s−1, 1 s−1, 10 s−1, and 100 s−1 applied to both the 500g and 1000g GO suspensions decreased the specific areal capacitance at low frequencies such as 502 Hz. Unlike the pristine 500g and 1000g suspensions, there was not a large increase in capacitance with sweeping to higher frequencies such as 10 kHz for 1000g to 12.6 kHz for 500g. The capacitances of the 500g and 1000g in the table insets in Fig. 9b–9e were lower in magnitude at 10 kHz and 12.6 kHz compared to the capacitance of the undisturbed GO suspensions in Fig. 9a. As shown in Fig. 9f, at the largest applied shear rate of 700 s−1, the specific areal capacitance of the 1000g GO suspension was the largest in magnitude across all applied shear rates with 4.63 mF cm−2. This dispersed microstructure present in the 1000g GO suspension allows for bulk charge transport and not limited to local electron transfer events among particle aggregates. The large specific capacitance at the highest shear is due to the disruption of a system spanning microstructure network of thin GO sheets resulting in an increased frequency of particle–particle collisions. At the highest shear rate of 700 s−1, there are smaller aggregates with more frequent collisions in suspension with higher inter-aggregate distance. The specific capacitance differences between the 1000g and 500g suspensions is dependent on the time scales for electron transfer as a function of the frequency-dependent dielectric response through electron transfer through either localized sites amongst particles or bulk transfer consistent with percolation and the presence of aggregates. This was evident for the 500g GO suspension which had the lowest capacitance of 0.15 mF cm−2 in higher shear rates and at a higher frequency of 12.6 kHz. Overall, there was decrease in the Csp at the characteristic maximum flip frequency with increased shear rate of 0.1 s−1, 1 s−1, 10 s−1, and 100 s−1 for all 500g GO suspensions. The same trend for Csp at the characteristic maximum flip frequency was observed for the 1000g GO suspension with shear rate until a very large increase at the highest shear rate of 700 s−1. Similarly, there was a slight increase of capacitance of the 500g GO suspension of 0.13 mF cm−2 at 100 s−1 and 0.15 mF cm−2 at the highest shear rate of 700 s−1. Therefore, there is better shear alignment with the more concentrated suspensions of GO such as 500g where interparticle interactions in the aggregates are the strongest and most affected by the imposed high shear rate at higher concentrations of sheets leading to a higher capacitance of charge storage. However, the increase in specific capacitance in the 1000g GO suspension is due to the likely formation of smaller aggregates of smaller GO sheets with more frequency of collisions during shear collectively storing charge minimizing leakage current.
The 1000g GO dispersion is found to be more conductive than the 500g GO dispersion across all shear rates. This suggests an inverse relationship between increasing centrifugal force and slurry viscosity and conductivity. The previous SANS and rheological analyses suggest that the 500g sample has more residual structure, aggregates, and agglomerates compared to the 1000g GO sample. Due to the dispersed nature of the particle network present in the 1000g GO sample, it will demonstrate less robust mechanical properties compared to the less aligned, more entangled network of the 500g sample. However, the higher centrifugation forces likely permit better intraparticle alignment of the GO flakes allowing for greater ease of electron flow resulting from enhanced conductive pathways. While it could be assumed that the decreasing size of agglomerates with an increasing shear rate would change the conductivity characteristics, it did not impact conductivity for either GO sample.
As such, we judge from the results that effective conductivity and linked properties such as resistance and impedance are not observably dependent on microstructure agglomeration states in GO dispersions. The observable timescales of structural buildup and breakdown are likely far outpaced by conduction suggesting that the flow of electrons throughout the material is contingent upon the construction of the percolated network of the GO particles themselves rather than interparticle interactions. If it is the case that electron transfer pathways are limited to the particles themselves, the resulting electronic resistance may stem from the gaps between particles in suspension.
5 Conclusions
Investigating the complex rheological, material, and chemical properties of chemically exfoliated graphene oxide suspensions after 500g and 1000g centrifugation conditions has allowed us to better understand the interwoven relationships between suspension microstructure and electrochemical characteristics. By characterizing various material properties – shape, size, morphology, structural defects, surface chemistry, and intrinsic conductivity – of the dispersed GO in flowable conditions, we have compiled and assessed an extensive dataset on electrochemically unique materials suitable for use in next-generation redox flow battery technologies. The novelty of the study is the combined rheological, material, microstructural, and electrochemical characterization of GO in suspension which has implications for applications of carbon nanomaterials as flowable electrodes for energy storage applications. Our results probe the microstructural evolution and electronic conductivity of GO sheets in suspension with shear. The more fluid-like microstructure of 1000g with smaller monodispered thinning GO sheets in suspension had lower ohmic resistance and higher electronic conductivity compared to the 500g GO suspension with polydispersed larger aggregates. Therefore, the thin GO sheets in suspension had the highest electrochemical capacitance at the highest shear rate suggesting that the higher frequency of particle–particle collisions of a network of smaller and more intrinsically conductive GO sheets can store higher electrochemical charge within the microstructural suspension.By fitting the ethixo-mHAWB model to rheometric data, we have been able to predict the complex behavior of the graphene oxide dispersion while simultaneously translating our understanding of bulk properties to a more concrete understanding of how microstructure contributes to system shear-thinning, thixotropy, and viscoelasticity. This was linked to subsequent analysis of the microstructure by SANS and SEM, revealing the aggregation behavior of the individual graphene oxide sheets from their smallest individual morphologies to the crumpled, irregular forms of larger multi-particle agglomerates. The 500g sample was found to have higher zero-shear viscosity, yield stress, and more pronounced thixotropic behavior. Analysis suggested that the more concentrated and dispersed 1000g sample demonstrated a low impedance and maximum electrochemical capacitance at the characteristic flip frequency at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023.74 ± 0.01 Hz versus 12
023.74 ± 0.01 Hz versus 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619.15 ± 0.01 Hz. Additionally, it was found that the higher concentration of GO promoted an average of 65% higher conductivity and lower resistance compared to the 500g sample. In this work, the primary particle, aggregate, and agglomerate differences between the microstructures were examined and subsequently revealed the factors most relevant to the flow and microstructural properties of the GO slurry, concurrently demonstrating an inverse correlation between increasing centrifugal force and slurry viscosity and conductivity, informing the use of such GO materials for application in future flow battery technologies. Given this understanding of the relationship between flow and electrochemical performance, the design of these prospective battery technologies can be honed to maximize their effectiveness. New lines of research can be developed in using carbon-based and other flowable nanomaterials for those applications.
619.15 ± 0.01 Hz. Additionally, it was found that the higher concentration of GO promoted an average of 65% higher conductivity and lower resistance compared to the 500g sample. In this work, the primary particle, aggregate, and agglomerate differences between the microstructures were examined and subsequently revealed the factors most relevant to the flow and microstructural properties of the GO slurry, concurrently demonstrating an inverse correlation between increasing centrifugal force and slurry viscosity and conductivity, informing the use of such GO materials for application in future flow battery technologies. Given this understanding of the relationship between flow and electrochemical performance, the design of these prospective battery technologies can be honed to maximize their effectiveness. New lines of research can be developed in using carbon-based and other flowable nanomaterials for those applications.
Data availability
Data supporting the findings of this study are available from the corresponding authors upon reasonable request. Rheological modeling, neutron scattering, and rheo-conductivity results can be accessed through the corresponding author's repository upon request.Author contributions
André Pincot: writing – original draft preparation, review and editing, investigation, visualization, software; Jeffrey Chin: writing – conceptualization, resources, investigation; Ryan Murphy: writing – conceptualization, review and editing resources, investigation, software; F. John Burpo: writing – conceptualization, review and editing, resources, supervision, project administration, investigation, visualization; Caspar Yi: writing – conceptualization, resources, investigation; Edward Chen: investigation, review and editing, visualization; H. Daniel Bahaghighat: writing – conceptualization, resources, investigation; Benjamin Thompson: writing – review and editing, investigation, visualization; Simuck F. Yuk: – review and editing, investigation; Gareth H. McKinley: writing – review and editing, supervision; Enoch A. Nagelli: writing – conceptualization, review and editing, resources, supervision, project administration, investigation, visualization; Matthew Armstrong: writing – conceptualization, review and editing, resources, supervision, project administration, investigation, visualization, software.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support and funding assistance from the U.S. Army and Army Research Lab (2020 ARL Funding through the Mathematical Science Center), and the Department of Chemistry and Life Science, United States Military Academy. Dr Jeff Horner, Dr Norman Wagner, and Dr Benjamin Thompson of the University of Delaware enabled the collection of rheological data. Dr Katie Weigandt from NIST for initial discussions and help with the NIST Center for Neutron Research (NCNR) proposal process for SANS beam time. Commercial equipment or software identified in this work does not indicate nor imply recommendation from NIST. RPM acknowledges funding from CHRNS, a national user facility jointly funded by the NCNR and NSF under Agreement No. DMR-2010792 Discussions with Dr Rogers of the University of Illinois, Urbana-Champagne led to insightful interpretations of SPP. The views expressed herein are those of the authors and do not reflect the position of the United States Military Academy, the Department of the Army, or the Department of Defense.Notes and references
- Z. Wang, et al., Region-Selective Self-Assembly of Functionalized Carbon Allotropes from Dispersion, ACS Nano, 2013, 7, 11427–11434 CAS.
- B. Akuzum, et al., Percolation Characteristics of Conductive Additives for Capacitive Flowable (Semi-Solid) Electrodes, ACS Appl. Mater. Interfaces, 2020, 12, 5866–5875 CAS.
- A. Ahmed, et al., High-performance Mn-doped ZnO loaded rGO electrode and its practical application as an electrode for self-charging supercapacitor device, J. Energy Storage, 2025, 105, 114783 Search PubMed.
- M. P. Chavhan, et al., A review of nanocomposites/hybrids made from biomass-derived carbons for electrochemical capacitors, Chem. Eng. J., 2024, 157267 CAS.
- A. Ahmed, et al., Upcycling of surgical facemasks into carbon based thin film electrode for supercapacitor technology, Sci. Rep., 2023, 13(1), 12146 CAS.
- S. Dutt, et al., Flexible and highly stable textile-based symmetric supercapacitor comprising binder-free MnO2/rGO-CF nanocomposite electrodes, J. Electron. Mater., 2023, 52(11), 7447–7458 CAS.
- K. Bashirnezhad, et al., Viscosity of Nanofluids: A Review of Recent Experimental Studies, Int. Commun. Heat Mass Transfer, 2016, 73, 114–123 CrossRef CAS.
- M. Youssry, et al., Aqueous Dispersions of Carbon Black and Its Hybrid with Carbon Nanofibers, RSC Adv., 2018, 8, 32119–32131 RSC.
- N. Hauptman, et al., Influence of Dispersing Additives on the Conductivity of Carbon Black Pigment Dispersion, J. Coat. Technol. Res., 2011, 8, 553–561 CrossRef CAS.
- R. Ou, et al., Fabrication and Electrical Conductivity of Poly (Methyl Methacrylate) (PMMA)/Carbon Black (CB) Composites: Comparison between an Ordered Carbon Black Nanowire-Like Segregated Structure and a Randomly Dispersed Carbon Black Nanostructure, J. Phys. Chem. B, 2006, 110, 22365–22373 CrossRef CAS PubMed.
- X. Liu, et al., Mapping the Electrical Conductivity of Poly (Methyl Methacrylate)/Carbon Black Composites Prior to and After Shear, ACS Appl. Mater. Interfaces, 2013, 5, 8857–8860 CrossRef CAS PubMed.
- H. Choi, et al., Electrical Percolation Threshold of Carbon Black in a Polymer Matrix and Its Application to Antistatic Fibre, Sci. Rep., 2019, 9, 6338 CrossRef PubMed.
- T. J. Petek, et al., Slurry Electrodes for Iron Plating in an All-Iron Flow Battery, J. Power Sources, 2015, 294, 620–626 CrossRef CAS.
- S. Chakraborty, et al., Surface Area Measurement of Functionalized Single-Walled Carbon Nanotubes, J. Phys. Chem., 2006, 110, 24812–24815 CrossRef CAS.
- M. Hossain, et al., Alignment of Carbon Nanotubes in Carbon Nanotube Fibers Through Nanoparticles: A Route for Controlling Mechanical and Electrical Properties, Appl. Mater. Interfaces, 2017, 9, 5530–5542 CrossRef CAS.
- S. Sasi, et al., The Effect of Graphene on the Performance of an Electrochemical Flow Capacitor, J. Mater. Chem. A, 2015, 3, 2717–2725 RSC.
- E. Bjerglund, et al., Efficient Graphene Production by Combined Bipolar Electrochemical Intercalation and High-Shear Exfoliation, ACS Omega, 2017, 2, 6492–6499 CrossRef CAS PubMed.
- X. Wang, et al., Atomic-Scale Clarification of Structural Transition of MoS2 upon Sodium Intercalation, ACS Nano, 2014, 8, 11394–11400 Search PubMed.
- Y. Zhu, et al., Mass Production and Industrial Applications of Graphene Materials, Natl. Sci. Rev., 2018, 5, 90–101 CrossRef CAS.
- M. Lavin-Lopez, et al., Influence of Different Improved Hummers Method Modifications on the Characteristics of Graphite Oxide in Order to Make a More Easily Scalable Method, Ind. Eng. Chem. Res., 2016, 55, 12836–12847 Search PubMed.
- D. Marcano, et al., Improved Synthesis of Graphene Oxide, ACS Nano, 2010, 4, 4806–4814 CrossRef CAS PubMed.
- J. Chen, et al., Graphene Materials for Electrochemical Capacitors, J. Phys. Chem., 2013, 4, 1244–1253 CAS.
- J. Lee, et. al., Hybrid Capacitive Deionization to Enhance the Desalination Performance of Capacitive Techniques, Energy Environ. Sci., 2014, 7, 3683–3689 RSC.
- O. Ruiz, et al., Graphene Oxide: A Nonspecific Enhancer of Cellular Growth, ACS Nano, 2011, 5, 8100–8107 CAS.
- C. Yi, et al., Electrosprayed Scalable 3D Graphene-CNT Electrodes for Li-Ion and Fuel Cell Applications, 2021 AIChE Annual Meeting, AIChE, 2021 Search PubMed.
- North American Carbon Black Prices Raised by $40–70 per Tonne, Focus Pigm., 2020, 2020, 4 Search PubMed.
- Multi-Walled Carbon Nanotubes, Cheap Tubes, https://www.cheaptubes.com/product-category/multi-walled-carbon-nanotubes/.
- Graphene Oxide, Cheap Tubes, https://www.cheaptubes.com/product-category/graphene-oxide/.
- G. Boulougouris, et al., Henry's Constant Analysis for Water and Nonpolar Solvents from Experimental Data, Macroscopic Models, and Molecular Simulation, J. Phys. Chem., 2001, 105, 7792–7798 CAS.
- P. Vichchulada, et al., Sonication Power for Length Control of Single-Walled Carbon Nanotubes in Aqueous Suspensions Used for 2-Dimensional Network Formation, J. Phys. Chem., 2010, 114, 12490–12495 CAS.
- K. Mukhopadhyay, et al., Conversion of Carbon Nanotubes to Carbon Nanofibers by Sonication, Carbon, 2002, 1373–1376 CAS.
- D. Yang, et al., Functionalization of Multiwalled Carbon Nanotubes by Mild Aqueous Sonication, J. Phys. Chem., 2005, 109, 7788–7794 CAS.
- A. N. Beris, Chapter 8, Hemorheology, Theory and Applications of Colloidal Suspension Rheology, ed. N. J. Wagner and J. Mewis, Cambridge U. Press, 2021, pp. 316–351 Search PubMed.
- A. S. Negi and C. O. Osuji, New Insights on Fumed Colloidal Rheology—Shear Thickening and Vorticity-Aligned Structures in Flocculating Dispersions, Rheol. Acta, 2009, 48, 871–881 CAS.
- C. O. Osuji and D. A. Weitz, Highly Anisotropic Vorticity Aligned Structures in a Shear Thickening Attractive Colloidal System, Soft Matter, 2008, 4, 1388–1392 CAS.
- C. O. Osuji, et al., Shear Thickening and Scaling of the Elastic Modulus in a Fractal Colloidal System with Attractive Interactions, Phys. Rev. E, 2008, 77, 060402 CrossRef PubMed.
- M. J. Armstrong, et al., Dynamic Shear Rheology and Structure Kinetics Modeling of a Thixotropic Carbon Black Suspension, Rheol. Acta, 2017, 56, 811–824 CrossRef CAS.
- F. Yilmaz and M. Y. Gundogdu, A Critical Review on Blood Flow in Large Arteries; Relevance to Blood Rheology, Viscosity Models, and Physiologic Conditions, Korea-Aust. Rheol. J., 2008, 20, 197–211 Search PubMed.
- A. Sequeira, and J. Janela, An Overview of Some Mathematical Models of Blood Rheology, A Portrait of State-Of-The-Art Research at the Technical University of Lisbon, 2017, pp. 65–87 Search PubMed.
- J. S. Horner, et al., Investigation of Blood Rheology under Steady and Unidirectional Large Amplitude Oscillatory Shear, J. Rheol., 2018, 62, 577–591 CrossRef CAS.
- J. S. Horner, et al., Measurements of Human Blood Viscoelasticity and Thixotropy under Steady and Transient Shear and Constitutive Modeling Thereof, J. Rheol., 2019, 63, 799–813 CrossRef CAS.
- S. Rao, J. Upadhyay, K. Polychronopoulou, R. Umer and R. Das, Reduced graphene oxide: Effect of reduction on electrical conductivity, J. Compos. Sci., 2018, 2, 25 CrossRef.
- L. Shahriary and A. A. Athawale, Graphene Oxide Synthesized by Using Modified Hummers Approach, Int. J. of Renewable Energy Environ. Eng., 2014, 2, 58–63 Search PubMed.
- Y. Shao, et al., Facile and Controllable Electrochemical Reduction of Graphene Oxide and Its Applications, J. Mater. Chem., 2010, 20, 743–748 CAS.
- M. Duduta, et al., Semi-Solid lithium rechargeable flow battery, Adv. Energy Mater., 2011, 1, 511–516 CAS.
- F. Y. Fan, et al., Polysulfide flow batteries enabled by percolating nanoscale conductor networks, Nano Lett., 2014, 14, 2210–2218 CAS.
- V. Presser, et al., The Electrochemical Flow Capacitor: A New Concept for Rapid Energy Storage and Recovery, Adv. Energy Mater., 2012, 2, 895–902 CAS.
- A. Narayanan, et al., Mechanical History Dependence in Carbon Black Suspensions for Flow Batteries: A Rheo-Impedance Study, Langmuir, 2017, 33, 1629–1638 CAS.
- U. Genz, et al., Dielectric spectroscopy of reversibly flocculated dispersions during flow, J. Colloid Interface Sci., 1994, 165, 212–220 CAS.
- M. Youssry, et al., Non-aqueous carbon black suspensions for lithium-based redox flow batteries: rheology and simultaneous rheo-electrical behavior, Phys. Chem. Chem. Phys., 2013, 15, 14476–14486 CAS.
- J. Mewis, et al., Dielectric behaviour of flowing thixotropic suspensions, Colloids Surf., 1987, 22, 249–269 Search PubMed.
- A. Helal, et al., Simultaneous Rheoelectric Measurements of Strongly Conductive Complex Fluids, Phys. Rev. Appl., 2016, 6, 06004 Search PubMed.
- S. Kirkpatrick, Percolation and Conduction, Rev. Mod. Phys., 1973, 45, 574–588 CrossRef.
- A. V. Kyrylyuk and P. Van der Schoot, Continuum percolation of carbon nanotubes in polymeric and colloidal media, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8221–8226 Search PubMed.
- J. G. Oldroyd, On the Formulation of Rheological Equations of State, Proc. R. Soc. London, Ser. A, 1950, 200, 523–541 CAS.
- R. B. Bird, et al., Dynamics of Polymeric Liquids: Fluid Mechanics, John Wiley and Sons Inc., 2nd edn, 1987, vol. 1 Search PubMed.
- A. N. Beris, and B. J. Edwards, Thermodynamics of Flowing Systems with Internal Microstructure, Oxford Univ. Press, 1994 Search PubMed.
- A. H. Barnes, Thixotropy—A Review, J. Non-Newtonian Fluid Mech., 1997, 70, 1–33 Search PubMed.
- A. Mujumdar, et al., Transient Phenomena in Thixotropic Systems, J. Non-Newtonian Fluid Mech., 2002, 102, 157–158 Search PubMed.
- K. Dullaert and J. Mewis, A Structural Kinetics Model for Thixotropy, J. Non-Newtonian Fluid Mech., 2006, 139, 21–30 CrossRef CAS.
- J. Mewis and N. J. Wagner, Thixotropy, Adv. Colloid Interface Sci., 2009, 147–148, 214–227 Search PubMed.
- P. Saramito, A New Elastoviscoplastic Model Based on the Herschel-Bulkley Viscoplastic Model, J. Non-Newtonian Fluid Mech., 2009, 158, 154–161 CrossRef CAS.
- P. R. de Souza Mendes, Modeling the Thixotropic Behavior of Structured Fluids, J. Non-Newtonian Fluid Mech., 2009, 164, 66–75 Search PubMed.
- C. J. Dimitriou, et al., Describing and Prescribing the Constitutive Response of Yield Stress Fluids Using Large Amplitude Oscillatory Shear Stress (LAOStress), J. Rheol., 2013, 57, 27–70 CAS.
- C. J. Dimitriou and G. H. McKinley, A Comprehensive Constitutive Law for Waxy Crude Oil: A Thixotropic Yield Stress Fluid, Soft Matter, 2014, 10, 6619–6644 CAS.
- C. J. Dimitriou and G. H. McKinley, A Canonical Framework for Modeling Elasto-Viscoplasticity in Complex Fluids, J. Non-Newtonian Fluid Mech., 2019, 265, 116–132 Search PubMed.
- Y. Wei, et al., A Multimode Structural Kinetics Constitutive Equation for the Transient Rheology of Thixotropic Elasto-Viscoplastic Fluids, J. Rheol., 2018, 62, 321–342 CAS.
- S. Varchanis, et al., Modeling the Rheology of Thixotropic Elasto-Viso-Plastic Materials, J. Rheol., 2019, 63, 609–639 CAS.
- A. J. Apostolidis, et al., Modeling of Human Blood Rheology in Transient Shear Flows, J. Rheol., 2015, 59, 275–298 CAS.
- G. J. Donley, et al., Yielding and Recovery of Conductive Pastes for Screen Printing, Rheol. Acta, 2019, 58, 361–382 CAS.
- M. J. Armstrong and A. Pincot, Integration of Thixotropy into Giesekus Model for Characterization of Human Blood, AIP Adv., 2021, 11, 035029 Search PubMed.
- R. H. Ewoldt, Defining Nonlinear Rheological Material Functions for Oscillatory Shear, J. Rheol., 2013, 57, 177–195 CAS.
- M. J. Armstrong and J. Tussing, A Methodology for Adding Thixotropy to Oldroyd-8 Family of Viscoelastic Models for Characterization of Human Blood, Phys. Fluids, 2020, 32(9), 094111 CAS.
- S. A. Rogers, In Search of Physical Meaning: Defining Transient Parameters for Nonlinear Viscoelasticity, Rheol. Acta, 2017, 56, 501–525 CAS.
- M. Armstrong, et al., Recent advances in biofluid mechanics and bio-and hemorheology collating recent advances in predicting complex behavior of human blood with thixo-elasto-visco-plastic models and sequence of physical process, Front. Phys., 2022, 10, 889065 Search PubMed.
- M. Armstrong, et al., Probing microstructural differences that manifest in human blood after taking aspirin using thixo-elasto-visco-plastic modeling and series of physical processes, AIP Adv., 2021, 11(11), 115226 CrossRef CAS.
- J. B. Hipp, et al., Structure-Property Relationships of Sheared Carbon Black Suspensions Determined by Simultaneous Rheological and Neutron Scattering Measurements, J. Rheol., 2019, 63, 423–436 CrossRef CAS.
- S. Naficy, et al., Graphene Oxide Dispersions: Tuning Rheology to Enable Fabrication, Mater. Horiz., 2014, 1, 326–331 RSC.
- R. H. Ewoldt, et al., New Measures for Characterizing Nonlinear Viscoelasticity in Large Amplitude Oscillatory Shear, J. Rheol., 2008, 52, 1427–1458 CrossRef CAS.
- A. Pincot, et al., Novel tensorial thixo-visco-plastic framework for rheological characterization of human blood, Sci. Rep., 2021, 11, 22004 CrossRef CAS PubMed.
- J. B. Hipp, et al., Structure-Property Relationships of Sheared Carbon Black Suspensions Determined by Simultaneous Rheological and Neutron Scattering Measurements, J. Rheol., 2019, 63, 423–436 CrossRef CAS.
- J. W. Campos, et al., Investigation of Carbon Materials for Use as a Flowable Electrode in Electrochemical Flow Capacitors, Electrochim. Acta, 2013, 98, 123–130 CrossRef CAS.
- A. Corker, et al., 3D printing with 2D colloids: designing rheology protocols to predict ‘printability’ of soft-materials, Soft Matter, 2019, 15, 1444–1456 RSC.
- M. Boota, et al., Activated Carbon Spheres as a Flowable Electrode in Electrochemical Flow Capacitors, J. Electrochem. Soc., 2014, 161, A1078 CrossRef CAS.
- D. Li, et al., Processable Aqueous Dispersions of Graphene Nanosheets, Nat. Nanotechnol., 2008, 3, 101–105 CrossRef CAS PubMed.
- W. S. Hummers and R. E. Offman, Preparation of Graphitic Oxide, J. Am. Chem. Soc., 1958, 80, 1339 CrossRef CAS.
- W. S. Rasband, ImageJ, US National Institutes of Health, Bethesda, Maryland, https://imagej.nih.gov/ij/ Search PubMed.
- C. J. Glinka, et al., The 30 m Small-Angle Neutron Scattering Instruments at the National Institute of Standards and Technology, J. Appl. Crystallogr., 1998, 31, 430–445 CrossRef CAS.
- J. G. Barker, et al., Design and Performance of a Thermal-Neutron Double-Crystal Diffractometer for USANS at NIST, J. Appl. Crystallogr., 2005, 38, 1004–1011 CrossRef CAS.
- S. R. Kline, Reduction and Analysis of SANS and USANS Data Using IGOR Pro, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- M. Doucet, et al., SasView, http://www.sasview.org/.
- J. B. Hipp, Structure, Rheology, and Electrical Conductivity of High-Structured Carbon Black Suspensions, PhD thesis, University of Delaware, 2020 Search PubMed.
- M. Mourshed, S. Mohammad Rezaei Niya, R. Ojha, G. Rosengarten, J. Andrews and B. Shabani, Carbon-based slurry electrodes for energy storage and power supply systems, Energy Storage Mater., 2021, 40, 461–489 CrossRef.
- M. J. Armstrong, et al., A Small-Scale Study of Nonlinear Blood Rheology Show Rapid Transient Transitions, J. Rheol., 2020, 59, 687–705 CAS.
- G. Donley, et al., SPP Software, University of Illinois at Urbana-Champaign, 2020, https://publish.illinois.edu/rogerssoftmatter/freeware/ Search PubMed.
- M. J. Armstrong., et al., Dynamic Shear Rheology and Structure Kinetics Modeling of a Thixotropic Carbon Black Suspension, Rheol. Acta, 2017, 56, 811–824 CrossRef CAS.
- M. J. Armstrong, et al., Structure-Rheology Elucidation of Human Blood via SPP Framework and TEVP Modeling, Korea-Aust. Rheol. J., 2021, 33, 45–63 CrossRef.
- M. J. Armstrong, Investigating and Modeling the Thixotropic Behavior, Microstructure, and Rheology of Complex Material, PhD thesis, University of Delaware, Newark, DE, 2015 Search PubMed.
- A. Lasia. Electrochemical Impedance Spectroscopy and its Application. Springer, 2020 Search PubMed.
- E. Casero, et al., Differentiation between graphene oxide and reduced graphene by electrochemical impedance spectroscopy (EIS), Electrochem. Commun., 2012, 20, 63–66 CrossRef CAS.
- H. Wang and L. Pilon, Reply to Comments on “Intrinsic Limitations of Impedance Measurements in Determining Electric Double Layer Capacitances” by H. Wang, L. Pilon [Electrochimica Acta 63 (2012) 55], Electrochim. Acta, 2012, 76, 529–531 CrossRef CAS.
- B. Pandit, S. S. Karade and B. R. Sankapal, Hexagonal VS2 Anchored MWCNTs: First Approach to Design Flexible Solid-State Symmetric Supercapacitor Device, ACS Appl. Mater. Interfaces, 2017, 9, 44880–44891 CrossRef CAS PubMed.
- L. A. Dissado and R. M. Hill, Anomalous low-frequency dispersion. Near direct current conductivity in disordered low-dimensional materials, J. Chem. Soc., 1984, 80, 291–319 CAS.
- G. Niklasson, Fractal aspects of the dielectric response of charge carriers in disordered materials, J. Appl. Phys., 1987, 62, 1–14 Search PubMed.
- H. Z. Riahi, et al., Investigations on electrical conductivity and dielectric properties of graphene oxide nanosheets synthetized from modified Hummer's method, J. Mol. Struct., 2020, 1216, 128304 CrossRef.
- T. Ahamad, et al., Influence of graphene oxide on the dielectric properties of biogenically synthesized ZnO nanoparticles, Hybrid Adv., 2023, 3, 100059 CrossRef.
- P. Kumar, et al., Dielectric Properties of Graphene Oxide Synthesized by Modified Hummers' Method from Graphite Powder, Integr. Ferroelectr., 2019, 202, 41–51 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra08308c |
| This journal is © The Royal Society of Chemistry 2025 |