Open Access Article
Open Access ArticleEnhancing the photovoltaic properties of phenylsulfonyl carbazole-based materials by incorporating a thiophene ring and end-capped acceptors for organic solar cells: a DFT approach†
Muhammad Khalid *ab,
Laiba Amirab,
Muhammad Arshadc,
Iqra Shafiqab,
Ataualpa Albert Carmo Braga
*ab,
Laiba Amirab,
Muhammad Arshadc,
Iqra Shafiqab,
Ataualpa Albert Carmo Braga d and
Khalid Abdullah Alrashidie
d and
Khalid Abdullah Alrashidie
aInstitute of Chemistry, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan. E-mail: muhammad.khalid@kfueit.edu.pk; Khalid@iq.usp.br
bCentre for Theoretical and Computational Research, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
cIndustry Solutions, Northern Alberta Institute of Technology, Edmonton, Alberta, Canada
dDepartamento de Química Fundamental, Instituto de Química, Universidade de São Paulo, Av. Prof. Lineu Prestes, 748, São Paulo, 05508-000, Brazil
eDepartment of Chemistry, College of Science, King Saud University, P. O. Box 2455, Riyadh 11451, Saudi Arabia
First published on 24th February 2025
Abstract
In the present study, phenylsulfonyl carbazole-based organic chromophores, abbreviated as PSCD1–PSCD6, were designed through tailoring the terminal group of a PSCR chromophore. Quantum chemical studies were carried out using the M06/6-311G(d,p) functional to understand the electronic, structural, chemical, and optical properties of the title chromophores. All the derivatives exhibited reduced band gaps with ΔE = 2.742–3.025 eV and significant bathochromic shifts with λmax = 496.891–545.009 nm compared with PSCR. DOS and TDM investigations revealed that the central acceptor moiety plays a crucial role in charge transfer. The minimal binding energy values for PSCD1–PSCD6 indicated a greater rate of exciton dissociation and more effective charge transfer than PSCR. The studied compounds exhibited open-circuit voltages (Voc) ranging from 1.015 to 1.720 V. PSCD4 showed a significantly reduced band gap of 2.742 eV and a red-shifted absorption maximum of 545.009 nm, among all the studied chromophores. These findings suggest that all the designed organic chromophores might be utilized as reasonable photovoltaic materials.
Introduction
Solar energy is an abundant, renewable resource that could enhance environmental health by minimizing the ecological impacts associated with fossil fuels.1,2 Through efficient harnessing, it can support the drive toward a sustainable energy future and efforts to mitigate pollution and reduce greenhouse gas emissions.3 Organic solar cells (OSCs) have emerged as a promising technology within this framework owing to their unique qualities, such as flexibility, light weight, and compatibility with roll-to-roll manufacturing.4 Typically, OSCs consist of a bulk heterojunction (BHJ) structure, where electron donor and acceptor materials are blended to enhance charge separation and energy conversion.5 By carefully designing and optimizing the morphologies of these donor and acceptor components, scientists have developed OSCs capable of achieving impressive power conversion efficiencies (PCEs) of up to 19.9%.6 This efficiency stems from the capacity of OSCs to absorb light across a broad spectrum, from the visible to the infrared region, and their molecular flexibility allows tuning of their energy gaps to maximize light absorption.7 Consequently, OSCs are considered a viable solution for eco-friendly energy generation and could contribute to the transformation of the current energy system to a sustainable, lower-impact energy grid.8,9Among the many classes of OSCs, fused-ring electron acceptors with an A1–π–A2–π–A1 configuration are widely used in OSCs.10 Various molecular configurations, such as D–π–D–π–A, A–π–D–π–A, A–π–A–π–A, D–π–A, and A–π–A, have been extensively studied to optimize the photovoltaic properties of OSCs. Introducing strong electron-withdrawing groups on terminal acceptor moieties, coupled with a donor unit core, significantly reduces band gaps and binding energies. This approach also broadens the absorption spectrum as well as enhances the exciton dissociation rate and open-circuit voltage of OSCs.11
OSCs based on (phenylsulfonyl)-7H-benzofuro[2,3-b]carbazole derivatives exhibit several advantageous properties for use in solar cells, including strong light absorption, finely tunable energy levels, and excellent charge-transport characteristics. Their potential to improve the efficiency and stability of OSCs makes them valuable candidates for further research and development in the field of photovoltaics.12 This class of materials combines the electroactive and photophysical benefits of both carbazole and benzofuran structures, resulting in high charge mobility and stability. The carbazole core possesses a rigid planar structure, which promotes effective π–π stacking interactions and efficient charge transport within the photovoltaic material. Additionally, carbazole's relatively high oxidation potential makes it suitable for use in the hole-transport layer, improving charge separation and reducing recombination losses in devices. Because of these features, carbazole is considered a highly significant and versatile building block in the development of high-performance photovoltaic materials, contributing to improving the absorption of light and efficiency of organic solar cells.
Carbazoles have been investigated for fabricating luminescent and hole-transporting materials,13 organic semiconductors, high-performance organic light emitting diodes, lasers and solar cells.14 The benzofuro[2,3-b]carbazole core enhances the conjugation length, facilitating effective charge transfer and reducing recombination losses, which is essential for improving the PCE in OSCs. Furthermore, the incorporation of phenylsulfonyl groups contributes to electron-accepting properties, thus stabilizing the molecular structure and enhancing electron affinity. Their inclusion increases exciton dissociation efficiency and allows for better alignment with donor materials in bulk heterojunctions. The resulting extended absorption spectrum and tunable HOMO–LUMO energy levels support efficient light absorption and energy conversion in the visible range. Together, these structural and electronic characteristics make phenylsulfonyl-7H-benzofuro[2,3-b]carbazole-based materials versatile and promising components in high-performance OSCs, potentially advancing the efficiency and scalability of organic photovoltaics.15
In this study, a series of phenylsulfonyl carbazole-based derivatives (PSCR and PSCD1–PSCD6) with an A1–π–A2–π–A1 framework, was designed from a 12-methyl-7-(phenylsulfonyl)-7H-benzofuro[2,3-b]carbazole (PSC) core-based compound (1).16 Structural tailoring was achieved by attaching one end of a thiophene π-spacer to the terminal of the phenylsulfonyl carbazole (PSC) acceptor (A2), while the other end π-spacer was connected to an indene malononitrile-based acceptor moiety (A1), as illustrated in Fig. 1. To understand their structure–property relationships, DFT was employed. This computational technique determines a system's geometry and ground-state characteristics on the basis of its electrical density.17 It is anticipated that these designed derivatives might possess potential electronic and photovoltaic characteristics and could be used as candidate materials for OSCs.
 | ||
| Fig. 1 Modification of the reference compound (PSCR) to design its derivatives using different end-capped acceptor moieties. | ||
Computational method
For the current investigation, a quantum chemical study was conducted with the aid of Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 software. To achieve this, the initial step was to optimize the geometries of PSCR and PSCD1–PSCD6 using the M06 functional19 with the 6-311G(d,p) basis set.20 GaussView 6.0
18 software. To achieve this, the initial step was to optimize the geometries of PSCR and PSCD1–PSCD6 using the M06 functional19 with the 6-311G(d,p) basis set.20 GaussView 6.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 was used to visualize the results and draw the structures. Several electronic and photovoltaic properties, such as the density of states (DOS), UV-visible absorption spectra, reorganization energy (RE), global reactivity descriptors, frontier molecular orbital (FMO)–based properties, non-covalent interactions (NCIs), exciton binding energy (Eb), transition density matrix (TDM), and open-circuit voltage (Voc), were calculated using the optimized geometries of entitled compounds. Various software packages, including Avogadro,22 Multiwfn,23 Origin,24 GaussSum,25 PyMOlyze,25 and Chemcraft,26 were employed to analyze and interpret the data from output files. Reorganization energies for electrons (λe) and holes (λh) were determined using the following equations:
21 was used to visualize the results and draw the structures. Several electronic and photovoltaic properties, such as the density of states (DOS), UV-visible absorption spectra, reorganization energy (RE), global reactivity descriptors, frontier molecular orbital (FMO)–based properties, non-covalent interactions (NCIs), exciton binding energy (Eb), transition density matrix (TDM), and open-circuit voltage (Voc), were calculated using the optimized geometries of entitled compounds. Various software packages, including Avogadro,22 Multiwfn,23 Origin,24 GaussSum,25 PyMOlyze,25 and Chemcraft,26 were employed to analyze and interpret the data from output files. Reorganization energies for electrons (λe) and holes (λh) were determined using the following equations:| λe = [E0− − E−] + [E0− − E0] | (1) |
| λh = [E+0 − E+] + [E0+ − E0]. | (2) |
In these calculations, E0− and E0+ represent the energies of the neutral molecule evaluated at the optimized geometries of the anion and cation, respectively; E− and E+ denote the energies of the anion and cation, correspondingly obtained from their optimized neutral molecule geomtery; E0− and E0+ are the single-point energies of the anion and cation, respectively, following optimization of their respective ions; and E0 refers to the single-point energy of the neutral molecule in its ground state.
Results and discussion
In this study, organic chromophores (PSCR and PSCD1–PSCD6) were designed via structural modeling with the aim to enhance their photovoltaic performance. For this purpose, PSCR was employed as a reference compound, which was designed using the phenylsulfonyl carbazole (PSC) central acceptor moiety.16 This core was linked to indene-based end-capped acceptor groups (2-(2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile) via a thiophene π-spacer. Six derivatives were designed by substituting different electron-withdrawing units, namely –F, –Cl, –CN, –NO2, –HSO3, and –CF3, at the ends of 2-(2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile acceptor moieties to explore their impact on the photovoltaic properties of OSCs. Fig. 1 illustrates the strategy used to design these chromophores. Fig. S1† displays the chemical structures and Table S21† lists the IUPAC names of the designed compounds. The optimized geometries are displayed in Fig. S2,† while their ChemDraw structures are illustrated in Fig. S3.† Additionally, their Cartesian coordinates are provided in Tables S1–S7.†Molecular geometric optimization and dihedral angles
The optimization of PSCR and PSCD1–PSCD6 involved calculating their structural parameters, including bond lengths and dihedral angles. A comparison between the simulated and reported experimental geometries revealed good agreement, indicating the accuracy of the used computational procedure. For the compounds PSCR and PSCD1–PSCD6, the DFT-calculated C–C bond lengths in the benzene ring ranged from 1.388 to 1.457 Å, which were in close agreement with the reported bond lengths (1.267–1.345 Å) for a benzene ring.27 The DFT-calculated bond length for the C–S bond in thiophene was 1.722 Å. Similarly, the C–N bond lengths in the terminal cyano groups of PSCR and PSCD1–PSCD6 were calculated to be 1.155 Å in all the compounds. The simulated C–C–C bond angles within the benzene ring for PSCR and PSCD1–PSCD6 were calculated as 113.3–128.3°, which were in agreement with the reported experimental values (121–141°).27 Similarly, for the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond angles in the phenylsulfonyl ring, the simulated bond angles were calculated as 122.5 Å. C–C–N bond angles were calculated to be in the range of 128.4–178.7° through DFT study. Further DFT-simulated bond lengths and bond angles are tabulated in Tables S14–S20.†
O bond angles in the phenylsulfonyl ring, the simulated bond angles were calculated as 122.5 Å. C–C–N bond angles were calculated to be in the range of 128.4–178.7° through DFT study. Further DFT-simulated bond lengths and bond angles are tabulated in Tables S14–S20.†
A dihedral angle is an angle formed between two planes that intersect along a shared bond, influencing the three-dimensional shape of a molecule. In organic chromophores, this angle significantly affects charge transfer. Furthermore, the dihedral angle is modified by the substituents linked to the molecular framework. Table S13† illustrates the dihedral angles (θ) of the studied chromophores (PSCR and PSCD1–PSCD6), while Fig. S1† shows the optimal geometries for all the compounds investigated. In this study, the values of the dihedral angle (θ1 and θ4) between the terminal acceptor (A1) and the π-spacers of the examined chromophores were found to be in the range of −174.26–2.760°, respectively. Similarly, the values of the (θ2 and θ3) dihedral angle between the π-spacers and the phenylsulfonyl carbazole central core (A2) of the studied chromophores PSCR and PSCD1–PSCD6 ranged from 24.680° to −154.41°, as shown in Table S13.† The negative values of dihedral angles indicated the planar geometry of the title chromophores, suggesting good charge transfer (Fig. 2).
Electronic properties
Analysis of frontier molecular orbitals (FMOs) provides valuable insights into the optoelectronic properties. Furthermore, this analysis helps understand intermolecular charge transfer (ICT), chemical reactivity, dynamic stability and other aspects related to molecular interactions. EHOMO and ELUMO energies are significant quantum descriptors.28 The band gap (Eg) help elucidate the increase and decrease in reactivity under the influence of various acceptor elements. Here, Eg represents the energy difference between the bonding and anti-bonding levels. The thiophene bridges play a vital role in facilitating the transfer of electron density from the core acceptor unit to terminal acceptor units.29 These terminal electron-deficient units enhance the extent of conjugation and facilitate easier delocalization of the electronic cloud across the molecules. Additionally, the studied compounds exhibited rigid and planar structures, promoting strong intermolecular interactions and improved charge mobility. HOMO/LUMO band gaps results are provided in Table 1. Fig. 3 presents the molecular orbital diagrams for the reference and designed compounds. Additionally, Fig. S3† provides visual representations of HOMO − 1, LUMO + 1, HOMO − 2, and LUMO + 2 for all the designed compounds, while Table S8† presents the corresponding energy values.| Compounds | EHOMO | ELUMO | Egap |
|---|---|---|---|
| PSCR | −6.406 | −3.381 | 3.025 |
| PSCD1 | −6.530 | −3.552 | 2.978 |
| PSCD2 | −6.545 | −3.599 | 2.946 |
| PSCD3 | −6.817 | −4.039 | 2.778 |
| PSCD4 | −6.828 | −4.086 | 2.742 |
| PSCD5 | −6.814 | −4.045 | 2.769 |
| PSCD6 | −6.682 | −3.808 | 2.874 |
 | ||
| Fig. 3 Schematic of the FMOs of PSCR and PSCD1–PSCD6 illustrating the charge density on the orbitals. | ||
The Eg for PSCR was calculated as 3.025 eV, with LUMO/HOMO energies of −3.381 and −6.406 eV, respectively. PSCD1–PSCD6 chromophores showed comparable Eg values (2.742–2.978 eV) to PSCR. Furthermore, the calculated HOMO energies of PSCD1–PSCD6 were obtained as −6.406, −6.530, −6.545, −6.682, −6.814, −6.817 and −6.828 eV, respectively whereas the LUMO energies of these molecules were −3.381, −3.552, −3.599, −3.808, −4.039, −4.045 and −4.086 eV, correspondingly. Among all the designed chromophores, PSCD4 exhibited the smallest band gap at 2.742 eV. This could likely be attributed to the powerful electron-withdrawing behavior of the nitro (–NO2) groups attached to the terminal acceptor moieties of 2-(2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. The –NO2 group displays strong resonance, facilitate efficient charge transfer due to its unpaired electrons, and has a negative inductive effect (−I). This promotes the transfer of charge density from the HOMO of the π-bridge to the LUMO of the acceptor fragment in PSCD4.30
The derivatives PSCD1 and PSCD2 displayed similar band gaps of 2.978 and 2.946 eV, respectively. The –Cl group in PSCD1 exhibited a weaker −I effect compared with the –F group in PSCD2 as fluorine is more electronegative than chlorine; therefore, a reduction in the Eg of PSCD1 was found. Consequently, the second narrowest band gap was observed in PSCD3 (2.778 eV) and PSCD5 (2.769 eV), likely owing to effective electron-withdrawing substituents –CN and –SO3H at the terminal end of the acceptor, respectively. The –CN and –SO3H groups attract electrons toward themselves, enhancing the efficiency of electronic charge delocalization within compounds. This leads to extended conjugation and increased charge-carrier mobility. A higher Eg of 2.874 eV was observed in the PSCD6 compound among all the derivatives, because of the introduction of the –CF3 group in the terminal acceptor unit of 2-(2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. The overall decreasing order of Eg in eV was as follows: PSCR (3.025) > PSCD1 (2.978) > PSCD2 (2.946) > PSCD6 (2.874) > PSCD3 (2.778) > PSCD5 (2.769) > PSCD4 (2.742). The density of charges in HOMO was spread on the bridge units, while in LUMO, it was positioned on the acceptor moieties, as indicated by the FMO surfaces of the designated compounds. In the title chromophores, the effective charge transfer suggests these chromophores could be suitable OSC candidates.
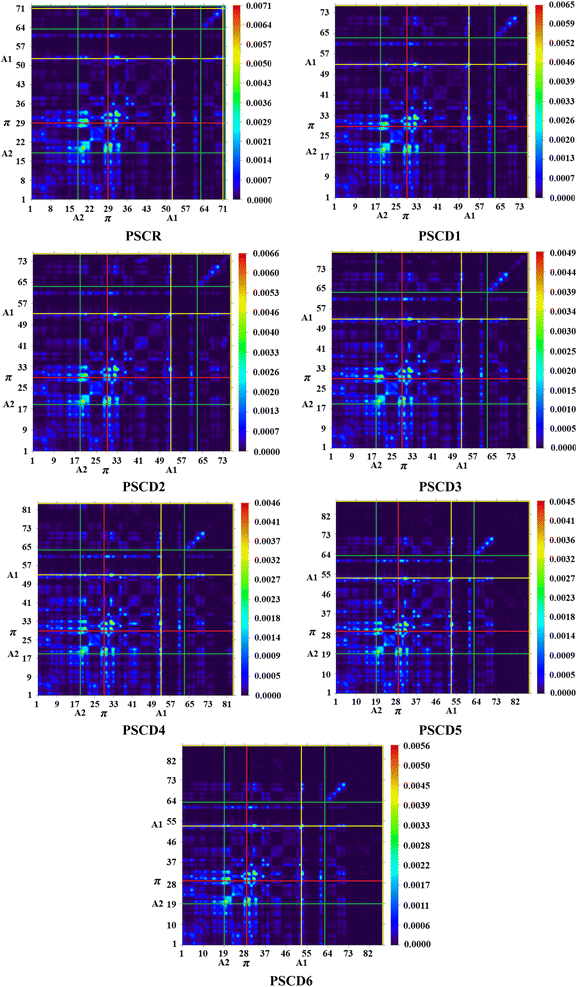
Density of states (DOS)
The DOS represents the distribution of the accessible electronic state that electrons can occupy at a specific energy level. Moreover, DOS analysis is crucial for determining the electron-transition rate in molecules.31 Thus, DOS analysis can help validate FMO results and quantify the contribution of HOMO (valence band) and LUMO (conduction band) to charge densities. A DOS plot illustrates the electron distribution across the molecules and indicates the number of positions occupied by electrons at band structures (HOMO and LUMO energy levels). Additionally, it reveals the contribution of each fragment to the formation of HOMO and LUMO.32 In this investigation, the molecules were divided into three fragments: end-capped acceptors (A1), a π-linker, and a core unit (A2). The graphical representations of the DOS analysis are provided in Fig. 4. In Fig. 4, the peaks on the left side of the graph between −6.5 and −16 are HOMOs (HOMO, HOMO − 1 and HOMO − 2, etc.), while the peaks on the left side of the map are the LUMOs (LUMO, LUMO + 1 and LUMO + 2, etc.). The black peaks in Fig. 4 show the overall density of electrons at the energy levels of both fragments. The green color represents the electron density at the π-spacer of the chromophore, whereas the red and blue peaks correspond to the acceptor region. The Fermi level shows a significant role in determining the electronic behavior of materials. It represents the energy level at which the probability of electron occupancy is 50% at absolute zero and serves as a reference point separating occupied states (below the Fermi level) from unoccupied states (above the Fermi level). In intrinsic semiconductors, the Fermi level lies midway between the valence and conduction bands, whereas in doped semiconductors, it is shifted closer to the conduction band (n-type) or the valence band (p-type).32 As the current studied compounds were n-type semiconductors, the Fermi level moved toward the conduction band, as illustrated in Fig. 4.Table S11† shows the charge distribution pattern for the terminal acceptors (A1), contributing 14.0%, 16.5%, 16.7%, 16.9%, 17.4%, 18.0%, and 19.3% to HOMO, and 15.5%, 68.5%, 69.3%, 71.6%, 75.3%, 76.1%, and 78.6% to the LUMO for PSCR and PSCD1–PSCD6, respectively. Similarly, the π-spacer contributed 1.3%, 20.4%, 20.5%, 20.8%, 22.1%, 24.1%, and 25.5% to HOMO, and 7.0%, 15.9%, 18.0%, 18.7%, 21.2%, 22.7%, and 23.1% to LUMO for all the examined compounds, respectively. Likewise, A2 contributed 55.2%, 57.9%, 60.5%, 62.3%, 62.8%, 63.1%, and 84.7% to HOMO, and 5.4%, 5.8%, 6.0%, 7.1%, 8.0%, 8.5%, and 77.5% to LUMO for the studied organic chromophores. In the valence band of all the chromophores, the electronic cloud was mostly concentrated on the linker and in conduction band this charge moved toward the terminals (acceptors).
Global reactivity parameters (GRPs)
The band gap determined on the basis of FMOs is essential for calculating GRPs of the designed compounds. Moreover, GRPs for the designed compounds (PSCR and PSCD1–PSCD6) were calculated using Koopmans' theorem.33 These parameters include the ionization potential (IP),34 electron affinity (EA),35 electronegativity (X),36 global softness (σ),37 hardness (η),38 global electrophilicity index (ω),39 chemical potential (μ),40 and charge transfer within a molecule (ΔNmax).41 Equations in Table S22† assisted in the theoretical calculations of GRPs for the studied compounds.Table 2 presents the calculated GRP values for PSCR and PSCD1–PSCD6. Efficient charge transfer depends on the molecules' IP and EA. The IP denotes the energy needed to lose an electron from the outermost shell,42 while EA represents the amount of energy emitted when a molecule gains an electron. From Table 2, it is evident that all the designed compounds exhibited high values of electron affinity and ionization potential, which supports the elevated LUMO levels in these compounds. The calculated ionization potential (IP) values in descending order were PSCD4 (6.828 eV) > PSCD3 (6.817 eV) > PSCD5 (6.814 eV) > PSCD6 (6.682 eV) > PSCD2 (6.545 eV) > PSCD1 (6.530 eV) > PSCR (6.406 eV). Conversely, a molecule with a shorter energy gap is considered softer, indicating increased reactivity and poorer stability.
| Compounds | X | μ | η | σ | ω | IP | EA | ΔNmax |
|---|---|---|---|---|---|---|---|---|
| PSCR | 4.893 | −4.983 | 1.512 | 0.330 | 7.916 | 6.406 | 3.381 | 3.295 |
| PSCD1 | 5.041 | −5.041 | 1.489 | 0.335 | 8.533 | 6.530 | 3.552 | 3.385 |
| PSCD2 | 5.072 | −5.072 | 1.473 | 0.339 | 8.732 | 6.545 | 3.599 | 3.443 |
| PSCD3 | 5.428 | −5.428 | 1.389 | 0.359 | 10.605 | 6.817 | 4.039 | 3.385 |
| PSCD4 | 5.457 | −5.457 | 1.371 | 0.364 | 10.860 | 6.828 | 4.086 | 3.980 |
| PSCD5 | 5.429 | −5.429 | 1.384 | 0.361 | 10.646 | 6.814 | 4.045 | 3.922 |
| PSCD6 | 5.245 | −5.245 | 1.437 | 0.340 | 9.572 | 6.682 | 3.808 | 3.649 |
Global softness values in descending order were PSCD4 (0.364 eV−1) > PSCD5 (0.361 eV−1) > PSCD3 (0.359 eV−1) > PSCD6 (0.340 eV−1) > PSCD2 (0.339 eV−1) > PSCD1 (0.335 eV−1) > PSCR (0.330 eV−1).
Among all the chromophores studied, PSCD4 was the most electronegative, with an electronegativity value of 5.457. Additionally, its strong acceptor nature was confirmed by a low chemical potential (μ) value of −5.457, highlighting its enhanced charge-transfer (CT) capabilities. Reactivity depends on η and σ, which are essential characteristics that are inversely proportional. Molecules with greater σ and lower η values display the shortest HOMO–LUMO energy gap, reduced stability, and enhanced reactivity.43 Remarkably, PSCD4 showed the maximum σ value of 0.364 eV−1 among the above-mentioned chromophores. Conversely, the minimum η value for PSCD4 was 1.094 eV. Furthermore, PSCD4 exhibited the highest ΔNmax at 3.980 eV. All the designed molecules showed higher softness and lower hardness values, indicating their high polarizability.
UV-visible analysis
UV-visible study is crucial for analyzing electronic transitions and identifying the configurations that contribute to them.44 The simulated UV-vis absorption properties of the titled chromophores were estimated in the gaseous phase. Additional values for the individual compounds are provided in Table S9.† Table S10† provides further detailed information, including the transition energy from the ground state (S0) to the first excited state (S1) (denoted as Eopt), the maximum absorption wavelength (λmax), the oscillator strength (fos) at λmax, and an analysis of the molecular orbital contributions and transition characteristics for the transition from S0 to S1. Fig. S4† depicts the UV-visible spectra for the designated chromophores. All the titled chromophores exhibited UV-visible spectra in the 496.891–545.009 nm range. However, the designed chromophores (PSCD1–PSCD6) demonstrated significant bathochromic shifts and lower excitation energy values compared with the reference compound PSCR. Typically, a red-shift in the absorbance spectra leads to enhanced electron mobility.In the gaseous phase, PSCR showed λmax = 496.891 nm with an E of 2.495 eV at 2.298 fos. PSCD1–PSCD6 exhibited λmax values of 504.452, 511.085, 522.083, 539.531, 541.321, and 545.009 nm, respectively. Correspondingly, they displayed lower E values of 2.458, 2.426, 2.375, 2.298, 2.290, and 2.275 eV. Moreover, their fos values were 2.289, 2.219, 2.132, 1.983, 1.921, and 1.726. Overall, all the compounds showed red shift in absorption maximum (λmax) in the following ascending order: PSCR < PSCD1 < PSCD2 < PSCD6 < PSCD3 < PSCD5 < PSCD4. These results reveal that PSCD4 exhibited the highest red-shifted values for absorption compared with the other derivatives.
Reorganization energy (RE)
The RE is a fundamental parameter in understanding the efficacy of a solar cell as it is closely linked to its charge-transfer (CT) capability. The charge-transfer phenomenon in BHJ-OSCs is governed by Marcus theory, which establishes a relationship between the RE and the charge-transfer rate (k), as presented in eqn (3):
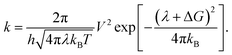 | (3) |
Transition density matrix (TDM) investigations
The TDM is important for analyzing the electronic excitations and CT phenomenon within a molecule. Additionally, it aids in understanding the interactions amid donor and acceptor components, the overlap between holes and electrons, and the extent of ICT.46 The TDM analyzes electronic excitations, from S0 to S1, and the extent of delocalization within molecules.47 Owing to the minor contribution of H atoms, they are neglected in this analysis. TDM plots for PSCD1–PSCD6 are presented in Fig. 5, with the electron cloud depicted in green, yellow and red colors against a dark background.PSCD1–PSCD6 were divided into three parts, as shown in Fig. 1: A1, A2, and the π-linker. PSCR and PSCD1–PSCD6 displayed charge transfer from A2 to the terminal moiety (A1). The π-linker unit helps with this procedure without creating any hindrance.
The electronic cloud was predominantly concentrated on the A2 entity, relatively distributed across the π-linker, and minimally localized on the terminal A1 moieties. Additionally, extensive charge dispersion occurred along the diagonal routes. Consequently, all the title compounds exhibited significantly greater charge dissociation and low coulombic interactions, which indicated their potential utilization as photovoltaic materials.
Exciton binding energy (Eb)
The least energy needed to separate a free electron and hole after their formation as an electron–hole pair, upon absorbing solar radiation, is known as the binding energy (Eb).48 A lower binding energy results in easier separation of holes and electrons from excitons, allowing charges to reach their respective electrodes more efficiently, thereby increasing the current yield.49 The binding energy value is influenced by the acceptor subunits attached to a molecule's peripheries. Highly electronegative or strong electron-withdrawing groups lower the binding energy by weakening the coulombic force between electrons and holes, as they strongly attract electrons towards themselves.50 The binding energy can be calculated using eqn (4):| Eb = EH–L − Eopt, | (4) |
| Compounds | EH–L | Eopt | Eb |
|---|---|---|---|
| PSCR | 3.025 | 2.495 | 0.530 |
| PSCD1 | 2.978 | 2.458 | 0.520 |
| PSCD2 | 2.946 | 2.426 | 0.520 |
| PSCD3 | 2.778 | 2.298 | 0.480 |
| PSCD4 | 2.742 | 2.275 | 0.467 |
| PSCD5 | 2.769 | 2.290 | 0.479 |
| PSCD6 | 2.874 | 2.375 | 0.499 |
All the designed compounds showed an improved charge-separation ability because of their low Eb values. Specifically, the Eb values of PSCR and PSCD1–PSCD6 were 0.530, 0.520, 0.520, 0.480, 0.467, 0.479, and 0.499 eV, respectively. The increasing trend of Eb for all the examined compounds was as follows: PSCD4 < PSCD5 < PSCD3 < PSCD6 < PSCD1 = PSCD2 < PSCR. Chromophores with a low Eb, allowing easier exciton dissociation and rapid charge flow, show enhanced current density, making them extremely appropriate for optoelectronic applications.51 All the title compounds in the present study had Eb values < 1.9 eV, making them suitable for optical activity and a variety of OSC applications. Among all the designed compounds, PSCD4 exhibited the lowest binding energy value (0.467 eV), indicating its excellent optoelectronic properties with significant dissociation of excitons in the S1.
Photovoltaic properties
Voc signifies the highest voltage a solar cell can generate under open-circuit conditions, when there is no current flow, with minimal external influence.52 Voc is a key factor in evaluating the PCE of OSCs.53 Fig. 6 illustrates a graphical representation of the Voc values for PSCR and PSCD1–PSCD6 in conjunction with PBDBT. The theoretical Voc values for PSCR and PSCD1–PSCD6 are calculated using the Scharber equation54 (eqn (5)):
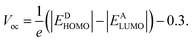 | (5) |
All the designed molecules (PSCR and PSCD1–PSCD6) demonstrated significant Voc values, as indicated in Table S12.† The EHOMO of PBDBT was −5.401 eV and ELUMO was −2.328 eV. The Voc values of PSCR and PSCD1–PSCD6 were as follows: PSCR (1.720 V), PSCD1 (1.549 V), PSCD2 (1.502 V), PSCD3 (1.062 V), PSCD4 (1.015 V), PSCD5 (1.056 V), and PSCD6 (1.293 V). These significant findings might be attributed to the terminal group alteration with efficient acceptors. The reducing order of Voc for the title chromophores was PSCR > PSCD1 > PSCD2 > PSCD6 > PSCD3 > PSCD5 > PSCD4. The predicted theoretical results of Voc reflect the efficacy of the structural modeling for enhancing the photovoltaic characteristics of the designed compounds. Literature studies reveal that the experimental-based Voc values of OSCs can be found up to 0.98 V.55 However, the calculated Voc values for the reported chromophores were found to be in the range of 1.015–1.720 V. This difference might be due to the fact that the DFT/TD-DFT investigations were performed on isolated molecules in the gaseous phase. Furthermore, experimental findings might be influenced by molecular packing, charge recombination, and other complex material interactions.
Fill factor (FF) and power conversion efficiency (PCE)
The FF is another crucial determinant of the PCE of OSCs. The FF values for PSCR and PSCD1–PSCD6 were calculated with the aid of eqn (6)55 and the results are reported in Table S12.†
 | (6) |
The equation 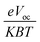 represents normalized Voc, which is an important factor calculated at standard room temperature under neutral charge conditions in molecules.56 This value is used instead of Voc in FF calculations for greater accuracy. All the newly designed molecules exhibited FF values within an optimal range, suggesting their potential effectiveness in OSC applications. Similarly, another important factor is PCE, which can be calculated using eqn (7).57
represents normalized Voc, which is an important factor calculated at standard room temperature under neutral charge conditions in molecules.56 This value is used instead of Voc in FF calculations for greater accuracy. All the newly designed molecules exhibited FF values within an optimal range, suggesting their potential effectiveness in OSC applications. Similarly, another important factor is PCE, which can be calculated using eqn (7).57
 | (7) |
The PCE is utilized to estimate the efficacy of OSCs. The open-circuit voltage (Voc), short-circuit current density (JSC), incident light power (Pin), and fill factor (FF) are proportional to PCE. The PCE of the reported chromophores falls in the range of 13.92–24.17%, as indicated in Table S12.†
Non-covalent interactions (NCIs) analysis
The study of NCIs represents a significant advancement in molecular research, providing critical insights into electron density and non-covalent interactions, including hydrogen bonding, halogen bonding, and π–π stacking.58 A quantitative measure of non-covalent interactions is derived by analyzing the reduced density gradient (s) and the Laplacian of the electron density at zero-gradient sites.59 This index can be depicted in two or three dimensions, illustrating the decreased density gradient (s) alongside the product of the electron density and the sign of λ2, which is an eigenvalue of the electron density Hessian matrix.60 The resultant plot exhibits significant spikes in areas of low electron density (ρ) and a diminished gradient, with an increased interface strength, signified by larger departures of spike amplitudes from zero. The λ2 sign is essential for analyzing NCIs: negative λ2 values indicate attractive interactions, whilst positive values signify repulsive forces, offering comprehensive insights into the characteristics of these interactions.To aid comprehension, these interactions are represented in three dimensions using the NCI isosurface (ρ). Additionally, a two-dimensional graphical depiction of the reduced density gradient (RDG), generated using Multiwfn 3.7 software, is applied to discriminate between interface types that include hydrogen bonding, van der Waals forces, and steric effects. Fig. S5† presents λ2ρ plots alongside the corresponding NCI isosurfaces, highlighting the interactions for PSCR and PSCD1–PSCD6 in chloroform, calculated at the M06/6-311G(d,p) level. The visualization incorporated scatter plots and RDG isosurfaces, with appealing interactions displayed in blue, van der Waals forces in green, and strong repellent interactions (steric effects) in red for all the designed derivatives. In the spectra, the x-axis represents the electron density as the product of λ2 and ρ, while the y-axis denotes the reduced density gradient. Spikes at the extremes of the plots are particularly notable, with the left spike with values approaching approximately −0.05 a.u., indicating strong attractive interactions, whereas the right spike, nearing 0.05 a.u., reflects strong repulsive interactions. Furthermore, in these presented plots, the higher position of the blue band compared with the red band indicates a prevalence of attractive interactions. This dominance of attractive forces plays a key role in enhancing molecular stability. In conclusion, this research stresses the critical significance of attractive interactions, especially hydrogen bonding, in regulating the stability and photovoltaic properties of the reported PSCD1–PSCD6 derivatives.
Conclusion
In summary, the organic chromophores PSCR and PSCD1–PSCD6 were designed using end-capped modifications to obtain potential photovoltaic materials. The structural modifications of the terminal acceptors incorporating various electron-withdrawing groups resulted in higher bathochromic shifts and reduced energy gaps. Quantum chemical calculations were performed to investigate the optoelectronic characteristics of the title compounds. Among all the derivatives, PSCD4 displayed the lowest Eg (2.742 eV), the widest absorption spectrum (545.009 nm), and the lowest binding energy value (0.467) owing to the introduction of the –NO2 moiety at the end of the acceptor. RE and TDM results indicated that exciton dissociation occurred with significant charge transfer in all the derivatives. Moreover, the studied compounds were blended with the donor polymer PBDBT to determine their photovoltaic potential and good Voc, FF, and PCE values were determined. These findings indicate that by employing structural modeling with efficient electron-withdrawing terminal acceptors, desired photovoltaic materials can be designed.Data availability
All data generated or analyzed during this study are included in this published article and its ESI files.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Dr Muhammad Khalid gratefully acknowledges the financial support of HEC Pakistan (project no. 20-14703/NRPU/R&D/HEC/2021). A. A. C. B. acknowledges the financial support of the São Paulo Research Foundation (FAPESP) (grants 2014/25770-6 and 2015/01491-3), the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of Brazil for academic support (grant 309715/2017-2), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Brazil, that partially supported this work (Finance Code 001). The authors thank the Researchers Supporting Project number (RSPD2025R645), King Saud University, Riyadh, Saudi Arabia.References
- M. Irfan, R. M. Elavarasan, Y. Hao, M. Feng and D. Sailan, J. Cleaner Prod., 2021, 292, 126008 CrossRef.
- M. Tawalbeh, A. Al-Othman, F. Kafiah, E. Abdelsalam, F. Almomani and M. Alkasrawi, Sci. Total Environ., 2021, 759, 143528 CrossRef CAS PubMed.
- M. Riede, D. Spoltore and K. Leo, Adv. Energy Mater., 2021, 11, 2002653 CrossRef CAS.
- J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Nat. Energy, 2016, 1, 1–7 CrossRef PubMed.
- W. Huang, P. Cheng, Y. Yang, G. Li and Y. Yang, Adv. Mater., 2018, 30, 1705706 CrossRef PubMed.
- K. Atiq, M. M. A. Iqbal, T. Hassan and R. Hussain, J. Mol. Model., 2024, 30, 13 CrossRef CAS PubMed.
- C. Coluccini, P. T. Anusha, H.-Y. T. Chen, S.-L. Liao, Y. K. Ko, A. Yabushita, C. W. Luo, Y. M. Ng and Y. L. Khung, Sci. Rep., 2019, 9, 12762 CrossRef PubMed.
- Y. Tong, Z. Xiao, X. Du, C. Zuo, Y. Li, M. Lv, Y. Yuan, C. Yi, F. Hao and Y. Hua, Sci. China: Chem., 2020, 63, 758–765 CrossRef CAS.
- Y. Liang, Z. Xu, J. Xia, S.-T. Tsai, Y. Wu, G. Li, C. Ray and L. Yu, Adv. Mater., 2010, 22, E135 CrossRef CAS PubMed.
- Y. Lin, Q. He, F. Zhao, L. Huo, J. Mai, X. Lu, C.-J. Su, T. Li, J. Wang and J. Zhu, J. Am. Chem. Soc., 2016, 138, 2973–2976 CrossRef CAS PubMed.
- Y. Zhang, Z. Liu, T. Shan, Y. Wang, L. Zhu, T. Li, F. Liu and H. Zhong, Mater. Chem. Front., 2020, 4, 2462–2471 RSC.
- M. Muppuli, K. Rajesh, D. Anitha Rexalin, K. Anandan, K. Gayathri, A. Mani, P. Devendran, V. Thayanithi, P. Kurinjinathan and M. Suresh Kumar, J. Struct. Chem., 2024, 65, 987–1001 CrossRef CAS.
- A. van Dijken, J. J. Bastiaansen, N. M. Kiggen, B. M. Langeveld, C. Rothe, A. Monkman, I. Bach, P. Stössel and K. Brunner, J. Am. Chem. Soc., 2004, 126, 7718–7727 CrossRef CAS PubMed.
- D. Avcı, S. Altürk, F. Sönmez, Ö. Tamer, A. Başoğlu, Y. Atalay, B. Zengin Kurt, D. Öztürk and N. Dege, Appl. Organomet. Chem., 2019, 33, e4725 CrossRef.
- K. Lupinska, S. Kotowicz, A. Grabarz, M. Siwy, K. Sulowska, S. Mackowski, L. Bu, Y. Bretonnière, C. Andraud, E. Schab-Balcerzak and L. Sznitko, ACS Omega, 2024, 9, 40769–40782 CrossRef CAS PubMed.
- R. Gangadharan, P. Narayanan, K. Sethusankar, V. Saravanan and A. K. Mohanakrishnan, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2016, 72, 1744–1750 CAS.
- R. D. Mills-Williams, B. D. Goddard and A. J. Archer, J. Chem. Phys., 2024, 160, 174901 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, Revision A. 02, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J. E. Del Bene, D. H. Aue and I. Shavitt, J. Am. Chem. Soc., 1992, 114, 1631–1640 CrossRef CAS.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView 5.0, Gaussian Inc., Wallingford, 2008, p. 20 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- K. J. Stevenson, J. Am. Chem. Soc., 2011, 133, 5621 CrossRef CAS.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- G. Zhurko and D. Zhurko, https://www.chemcraftprog.com, 2009.
- K. Swaminathan, P. Narayanan, K. Sethusankar, V. Saravanan and A. K. Mohanakrishnan, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2016, 72, 1739–1743 CAS.
- P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2008, 10, 3028–3042 RSC.
- S. Sadiq, R. A. Khera, A. M. Tawfeek, M. A. Ibrahim, F. Abbas, S. Ali, A. Mahal, D. Meitao and M. Waqas, J. Phys. Org. Chem., 2024, e4607 CrossRef CAS.
- A. Jezuita, K. Ejsmont and H. Szatylowicz, Struct. Chem., 2021, 32, 179–203 CrossRef CAS.
- S. A. Siddique, M. B. A. Siddique, R. Hussain, X. Liu, M. Y. Mehboob, Z. Irshad and M. Adnan, Comput. Theor. Chem., 2020, 1191, 113045 CrossRef CAS.
- A. Zahoor, N. Hadia, S. J. Akram, R. F. Mehmood, S. Sadiq, A. M. Shawky, N. S. Alatawi, A. Ahmed, J. Iqbal and R. A. Khera, RSC Adv., 2023, 13, 6530–6547 RSC.
- C. Sandoval-Yañez and J. I. Martínez-Araya, Chem. Phys. Lett., 2019, 715, 354–359 CrossRef.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- K. Fukui, Science, 1982, 218, 747–754 CrossRef CAS PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. Parthasarathi, J. Padmanabhan, M. Elango, V. Subramanian and P. Chattaraj, Chem. Phys. Lett., 2004, 394, 225–230 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- P. K. Chattaraj and D. R. Roy, Chem. Rev., 2007, 107, PR46–PR74 CrossRef CAS.
- M. Y. Mehboob, M. U. Khan, R. Hussain, K. Ayub, A. Sattar, M. K. Ahmad, Z. Irshad and M. Adnan, Spectrochim. Acta, Part A, 2021, 244, 118873 CrossRef CAS PubMed.
- J. Padmanabhan, R. Parthasarathi, V. Subramanian and P. Chattaraj, J. Phys. Chem. A, 2007, 111, 1358–1361 CrossRef CAS PubMed.
- F. A. Aloufi, R. F. Halawani, B. Jamoussi, A. K. Hajri and N. Zahi, ACS Omega, 2023, 8, 21425–21437 CrossRef CAS PubMed.
- A. U. Hassan, S. H. Sumrra, M. Zubair, G. Mustafa, S. Noreen and M. Imran, Chem. Pap., 2023, 77, 6183–6202 CrossRef CAS.
- M. M. A. Iqbal, M. Y. Mehboob, R. Hussain, M. Adnan and Z. J, Comput. Theor. Chem., 2021, 1202, 113335 CrossRef.
- M. Khalid, I. Shafiq, M. Zhu, M. U. Khan, Z. Shafiq, J. Iqbal, M. M. Alam, A. A. C. Braga and M. J, J. Saudi Chem. Soc., 2021, 25, 101305 CrossRef CAS.
- Z. Shuai, W. Li, J. Ren, Y. Jiang and H. Geng, J. Chem. Phys., 2020, 153, 080902 CrossRef CAS PubMed.
- M. Majeed, M. Waqas, R. F. Mehmood, N. S. Alatawi, M. Essid and R. A. Khera, J. Phys. Chem. Solids, 2023, 181, 111495 CrossRef CAS.
- S.-J. Lee, J. B. Park, Y. S. Kim, H.-S. Shin, A. Kotta and H.-K. Seo, Synth. Met., 2023, 294, 117302 CrossRef.
- Q. Zhao, S. Wang, Y.-H. Kim, S. Mondal, Q. Miao, S. Li, D. Liu, M. Wang, Y. Zhai and J. Gao, Green Energy Environ., 2023, 9, 949–965 CrossRef.
- H. Tang, Y. Bai, H. Zhao, X. Qin, Z. Hu, C. Zhou, F. Huang and Y. Cao, Adv. Mater., 2024, 36, 2212236 CrossRef CAS PubMed.
- M. Khalid, S. Naz, K. Mahmood, S. Hussain, A. A. C. Braga, R. Hussain, A. H. Ragab and S. R. Al-Mhyawi, RSC Adv., 2022, 12, 31192–31204 RSC.
- Z. Guo, A. K. Jena, G. M. Kim and T. Miyasaka, Energy Environ. Sci., 2022, 15, 3171–3222 RSC.
- M. U. Saeed, J. Iqbal, R. F. Mehmood, S. J. Akram, Y. A. El-Badry, S. Noor and R. A. Khera, Surf. Interfaces, 2022, 30, 101875 CrossRef CAS.
- M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794 CrossRef CAS.
- J. Fang, D. Deng, J. Zhang, Y. Zhang, K. Lu and Z. Wei, Mater. Chem. Front., 2017, 1, 1223–1228 RSC.
- R. Hussain, M. Adnan, S. Nawab, M. U. Khan, M. Khalid, Z. Irshad, K. Ayub and J. Lim, Synth. Met., 2022, 290, 117159 CrossRef CAS.
- M. Khalid, I. Shafiq, M. Imran, R. Jawaria and A. A. C. Braga, Synth. Met., 2024, 303, 117548 CrossRef CAS.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- I. Shafiq, R. Zahid, K. Mahmood, M. A. Asgha, T. Ahamad, S. Ahmed and S. C. Ojha, J. Saudi Chem. Soc., 2023, 27, 101767 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra06073c |
| This journal is © The Royal Society of Chemistry 2025 |