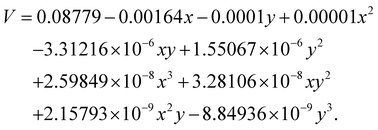DOI:
10.1039/D4NR04740K
(Paper)
Nanoscale, 2025,
17, 10239-10249
Unlocking efficiency: experimental and theoretical insights into biomass-derived carbon nanofluids with enhanced thermal conductivity†
Received
12th November 2024
, Accepted 18th March 2025
First published on 19th March 2025
Abstract
The study presents an experimental investigation, supported by theoretical analysis, into the effects of nanoparticle (NPs) concentration, particle size, and shape on the thermal conductivity (TC) of carbon nanosphere (CNS)-based nanofluids (NF). CNS was synthesized from garlic peels (Allium sativum) via pyrolysis at varying temperatures and characterized using X-ray diffraction (XRD), field emission scanning electron microscopy (FESEM), transmission electron microscopy (TEM), and other techniques. The NFs were prepared using a two-step method with different CNS concentrations in propylene glycol (PG) and deionized water (DI)/PG mixtures. Particle size distribution and colloidal stability were evaluated using dynamic light scattering (DLS) and zeta potential analysis. The TC of the NFs was measured across various temperatures, revealing a significant dependency on both particle size and concentration. All NFs exhibited enhanced thermal conductivity to the base fluid (BF), with increases of 52.60%, 101.28%, 108.51%, 114.60%, and 122.64% at 80 °C for CNS synthesized at 500 °C (AS500), 600 °C (AS600), 700 °C (AS700), 800 °C (AS800), and 900 °C (AS900), respectively. Rheological analysis showed a linear increase in dynamic viscosity (V) with rising CNS concentration within the dilute limits (0.01 to 0.1 wt%) and a strong correlation between particle size and thermal conductivity enhancement. These findings emphasize the critical role of CNS particle size in optimizing thermal performance, with potential applications in heat transfer systems. The study culminates with an exercise aimed towards presenting thermal conductivity and dynamic viscosity as surface plots. These plots provide behavioral trends for understanding the dependence of TC and V on nanoparticle size and temperature.
1. Introduction
Fluids with well-dispersed nanosized solid nanoparticles are called NFs. Due to their excellent energy absorption capacity and capacity to bypass the intermediary heat transfer stage, NFs are becoming increasingly popular.1 It has been demonstrated that the dispersion of nanoparticles in the BFs improves the fluids’ thermo-physical characteristics. Particle size is significant in determining the nanofluid's stability and thermal conductivity among all the other parameters. Numerous research studies on the impact of particle size on NF TC have been published in the literature.2–4 Many investigations have shown that as particle size increases, NFs’ thermal conductivity decreases.8,9 Earlier literature survey on this topic using nanoparticles predicted that as the particle size increases, TC also increases due to factors such as reduced interfacial resistance and enhanced phonon transport. However, several studies have also reported that a decrease in particle size can lead to an increase in thermal conductivity,5–7 primarily due to the higher surface area, improved dispersion, and increased Brownian motion, which collectively enhance heat transfer efficiency. The present study is investigating the effect of biomass-derived carbon on thermal conductivity, exploring how their size influences thermal transport properties in NFs. As the application of nanofluid is always related to a particular flow, a decisive role should be given to their viscosity it is one of the properties of the fluid and is related to molecular momentum transfer. Since less studies have explored the effect of CNS size derived from biomass, we were motivated to investigate this aspect to determine under which category this study fits. In this study, special attention is given to the aforementioned factors to enhance TC, reduce V, and examine how both are affected by particle size. In nanofluids, heat transfer happens due to Brownian motion, which refers to the unpredictable movement of nanoparticles within a bulk liquid. The TC of nanofluids increases as the particle size decreases. This is because smaller particles have a higher surface area to volume ratio and move more randomly in the base fluid. The representation of particle Brownian motion is conveyed through the Brownian diffusion coefficient, denoted as DB, which can be expressed using the Einstein–Stokes equation.8| | 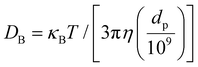 | (1) |
As eqn (1) demonstrated, the Brownian diffusion coefficient was reciprocal to particle diameter but proportional to temperature. It was inferred that the addition of particles with smaller diameters and at higher temperatures caused more violent collisions between them, improving thermal conduction in the process. The effects of temperature and particle size on the TC of the experimental sample are explained above. As a result, a rise in temperature and a decrease in particle size may increase the likelihood of collisions between bulk liquid and nanoparticle molecules and produce a quasi-convection state at specific small zones between them. It was suggested that when temperatures were high and particle sizes were small, the TC was more significant than when temperatures were low, and particle sizes were large.9,10 This is proved in our studies and further explained in sections. The choice of CNS derived from biowaste for this study is driven by the need to explore alternative carbon nanostructures with sustainable origins. While much research has been conducted on other carbon nanostructures, such as carbon nanotubes11 graphene,12 and graphene oxide,13 which are known for their exceptional thermal properties and ability to significantly enhance the TC of nanofluids, although these carbon-based materials have a significant capacity for heat transfer, they pose risks and threats to human health and the environment. CNS offers unique advantages. Compared to these nanostructures, carbon nanospheres exhibit distinct characteristics that make them an attractive option for improving TC while maintaining desirable viscosity properties. Moreover, their spherical morphology, high surface area, and ability to be synthesized from biomass waste provide a more sustainable and potentially cost-effective alternative.14 The primary focus of this study was to explore the potential of biomass-derived carbon nanospheres (CNS) from garlic peels as a sustainable and cost-effective alternative for thermal applications. While conventional nanofluids, such as metal–oxide or carbon-based nanofluids, have been extensively studied and applied in industries like automotive cooling, microelectronics, and oil extraction, research on biomass-derived carbon nanofluids is still emerging. This study aims to highlight the feasibility of waste-to-wealth approaches by demonstrating the effectiveness of CNS-based nanofluids in enhancing thermal conductivity. Future work can explore direct comparisons with widely used nanofluids to further validate the competitive performance of biomass-derived CNS. This study experimentally and theoretically investigates CNS-based nanofluids, addressing key challenges such as low thermal conductivity (TC), high dynamic viscosity (V), and nanoparticle agglomeration. By using biomass-derived CNS from garlic peel, it achieves stable dispersion, with a ∼122.64% TC enhancement at 80 °C for AS900, while maintaining viscosity within dilute limits for optimized heat transfer efficiency. This study explores how different sizes of nanoparticles influence thermophysical properties such as thermal conductivity and dynamic viscosity for improved performance. It employs mathematical modelling to predict the thermal behaviour of biomass-derived carbon nanosphere-based nanofluids, considering key factors affecting thermal conductivity enhancement. It is well known that thermal conductivity increases with an increase in CNS concentration until agglomeration or clustering occurs. The empirical Hamilton–Crosser model15 provides insights into this behavior, indicating that TC begins to decrease beyond a certain weight fraction. Most studies assume well-dispersed nanoparticles in the carrier fluid, which is achievable only at low volume fractions. The dynamic viscosity of nanofluids is typically modelled using the Brinkman model,16 which shows that V increases with an increase in weight fraction, implying a decrease in CNS size. A special case of this model is the Einstein model, which leads to similar conclusions. In this study, we do not aim to replace or refine these phenomenological models. Instead, our objective is to visualize the variation of TC and V with NP size and temperature. This was accomplished using a surface plot to fit the experimental data through a bivariate least squares approach.
2. Materials and methods
Garlic peels were collected from the local market in Bengaluru, India, for the synthesis of CNS via pyrolysis. A quartz tube furnace from NoPo Nanotechnologies Pvt. Ltd was used for CNS synthesis. Propylene glycol (PG) was used for nanofluid preparation and was purchased from Fine Chem Industries, with its properties provided in Table 1. Millipore distilled water was used for water-based tests. A magnetic stirrer from Cole-Parmer and an ultrasonicator were utilized for dispersion and mixing.
Table 1 Properties of propylene glycol
| Parameter |
Value |
| Chemical formula |
C3H8O2 |
| Thermal conductivity (@30 °C) |
(0.2166 W m−1 K−1) |
| Viscosity (@30 °C) |
0.034 mPa s at room temperature |
| Density |
1.036 g cm−3 at room temperature |
2.1. Synthesis of carbon nanosphere
The pyrolysis method was chosen over the pyrolysis method was chosen over other methods, such as hydrothermal carbonization (HTC), solvothermal synthesis, chemical vapour deposition (CVD), microwave-assisted carbonization and template-assisted carbonization. Because of its high yield of product, simplicity, and cost-effectiveness, it is ideal for large-scale production and commercialization. Adding to this, pyrolysis of biomass-based materials promotes low toxicity or no toxicity during the synthesis. One primary household and food industry waste is garlic peels (Allium sativum) from processed garlic. Garlic peels were chosen for nanoparticle synthesis due to their abundant availability, as India is the second-largest producer of garlic globally. Garlic peel is one of the major kitchen wastes and is rich in lignocellulosic content, making it a cost-effective and eco-friendly precursor for CNS synthesis. These properties make it ideal for heat transfer applications while promoting sustainability and supporting waste-to-wealth initiatives. Garlic peels were taken from local market in Bengaluru, India, after being collected, the garlic peels were sun-dried for two days to eliminate residual moisture. Subsequently, they were finely ground using an ultra-grinder (Retsch, ZM 200, Germany) operating at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and sieved at 75 μm with a laboratory sieving machine. The powder was taken in parts (∼10 g each) in a silica crucible and pyrolysed at a series of temperatures. 500, 600, 700, 800, and 900 (represented as AS500, AS600, AS700, AS800 and AS900 respectively). Under a quartz tube furnace in a continuous N2 flow to The Allium sativum peels have been pyrolysed five times in a row at temperatures ranging from 500 °C to 900 °C, highlighting the significance of pyrolysis temperature and how temperature affects the size of the nanoparticles. The resulting carbonised material was washed with ethanol and DI water to remove impurities and dried overnight at 80 °C in a hot air oven. Divyashree et al.'s17 work thoroughly analyses the production of porous nanocarbon materials and temperature impact. Fig. 1 schematically illustrates the synthesis process. Further characterisation of the obtained nanomaterials included XRD, Raman, FTIR, FESEM/EDS and TEM analysis. Then, by using these CNSs, nanofluids were prepared, and TC and V analyses were carried out.
000 rpm and sieved at 75 μm with a laboratory sieving machine. The powder was taken in parts (∼10 g each) in a silica crucible and pyrolysed at a series of temperatures. 500, 600, 700, 800, and 900 (represented as AS500, AS600, AS700, AS800 and AS900 respectively). Under a quartz tube furnace in a continuous N2 flow to The Allium sativum peels have been pyrolysed five times in a row at temperatures ranging from 500 °C to 900 °C, highlighting the significance of pyrolysis temperature and how temperature affects the size of the nanoparticles. The resulting carbonised material was washed with ethanol and DI water to remove impurities and dried overnight at 80 °C in a hot air oven. Divyashree et al.'s17 work thoroughly analyses the production of porous nanocarbon materials and temperature impact. Fig. 1 schematically illustrates the synthesis process. Further characterisation of the obtained nanomaterials included XRD, Raman, FTIR, FESEM/EDS and TEM analysis. Then, by using these CNSs, nanofluids were prepared, and TC and V analyses were carried out.
 |
| | Fig. 1 Illustration of the synthesis process. | |
2.2. Characterization
The XRD analysis was done by using Rigaku MiniFlex 600 (Japan). It was operated at 40 kV, 30 mA with graphite-filtered Cu-Kα radiation with a wavelength of 1.5406 Å. The measurements were scanned at 2θ range of 10° to 80°. An electron microscope (FESEM) and Transmission electron microscopy (TEM) were used to investigate the structural morphology of the CNS. Using energy-dispersive X-ray spectroscopy (EDS), the elemental composition of synthetic porous nanocarbon was determined. The PerkinElmer FTIR spectrum 100 was used to record the Fourier transform infrared spectrum (FTIR) between 4000 and 400 cm−1 to determine the groups present and the purity of the compounds. To determine the extent of crystallisation, HORIBA Scientific was used to obtain the Raman spectra, which were obtained using a 50× objective and a 532 nm wavelength excitation laser.
2.3. Zeta potential and dynamic light scattering
In this study, the zeta potential and cluster size of the nanoparticles were measured using the Zetasizer Nano ZS (ZEN 3600, Malvern Instruments, United Kingdom). This instrument utilises dynamic light scattering (DLS) for size measurement and electrophoretic light scattering (ELS) for zeta potential determination. For each measurement, nanoparticles were dispersed in solvent media using ultrasonication to ensure uniform suspension. The zeta potential and cluster size were measured five times for accuracy and repeatability.
2.4. Preparation of nanofluids
The preparation of the NF in this study involves two steps. First, as mentioned in section 2.1, nanoparticles are synthesized. In the second step, PG (base fluid) is mixed with AS900, AS800, AS700, AS600 and AS500. This mixture is subjected to magnetic stirring at 500 rpm for 30 minutes, followed by ultrasonication at 40 kHz, with the temperature maintained at 30 °C for 180 minutes. These NFs are called CNF1, CNF2, CNF3, CNF4 and CNF5, respectively.
2.5. Thermal conductivity measurement
In this study, a transient plane source Thermal Constants Analyzer (model TPS 500), Sweden, is used to test the validity of the current solution procedure for determining the TC of fluids with the TPS instrument. The 10-micron-thick nickel foil used to construct the hot disk sensor is structured in a double spiral pattern that conducts electricity. The sensor is double-insulated using Kapton or mica sheets. The hot disk sensor operates as a heat source, supplying constant power, and as the sample temperature sensor. The resistance across the sensor is measured as a function of time after power is delivered to the sensor element (i.e., across the concentric rings). At the same time, it is positioned horizontally between two semi-infinite materials during initialisation. A heat pulse is applied to one side of the TPS, producing a temperature gradient that enters the sample through the sensor filament. After compiling the temperature data, the Hot Disk instrument calculates the sample's TC and other thermal characteristics, including thermal diffusivity and specific heat. The resistance is converted into a temperature using nickel's resistivity, and a temperature–time variation is then utilised to solve for the TC and volumetric heat capacity using eqn (2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18
18| |  | (2) |
where Po is the total output power, D(τ) is the geometric function, α is the nickel foil's temperature coefficient of resistance and r is the sensor radius. The TC calculation using the TPS method is followed as mentioned in our previous work.19 Selection of measurement time is also very important parameter in the TC analysis longer measurement times that may cause heat to escape the sample and disperse into the surrounding air, causing errors in the TC measurement. By monitoring this temperature increase over a short period after the start of the experiment, it is possible to obtain precise information on the thermal transport properties of the surrounding material.
2.6. Dynamic viscosity measurement
Rheological investigations were conducted using the TA Instruments HR-3DISCOVERY hybrid rheometer. A 25 mm parallel plate geometry assessed V variation with temperature from 30 to 90 °C, ramping at 5 °C min−1 under a constant shear rate of 170 S−1. Additionally, a 40 mm 1.011° cone plate (Peltier plate steel) configuration was utilized to examine V changes across shear rates ranging from 20 to 140 s−1 at room temperature.
2.7. Effect of particle size and temperature on thermal conductivity
The synthesized biomass-derived CNSs, ranging in size from 28 nm to 120 nm, were dispersed separately in PG as the base fluid for the preparation of nanofluids with different particle sizes. The dispersion process involved initial magnetic stirring for preliminary mixing, followed by ultrasonication to ensure uniform distribution and stability without any surfactant. TC studies were conducted to analyze the effect of particle size, with nanofluids prepared at a fixed concentration of 0.1 wt%. The TC of the nanofluids was measured using a HOT DISK instrument over a temperature range of 30 °C to 80 °C to evaluate heat transfer performance. Additionally, the effect of concentration on TC was studied for concentrations ranging from 0.01 wt% to 0.1 wt%, and the effect of sonication time on TC was examined for durations ranging from 90 to 180 minutes at room temperature.
3. Results and discussion
3.1. Characterization studies
The synthesized NPs (AS500 to AS900) exhibited the characteristic advantages of carbon nanospheres, including favourable structural and chemical properties. However, the AS900 NPs have been chosen due to their significantly smaller particle size, higher carbon content, and enhanced zeta potential. These properties, combined with its exceptional thermophysical characteristics, such as improved TC and heat transfer efficiency, made AS900 the most suitable candidate for in-depth characterization. Consequently, AS900 was selected for further investigation, as described in the subsequent sections.
3.1.1. FESEM and EDS.
The morphologies of the NPs were characterized using FESEM (JSM-5910, JEOL) operated at 10 kV. FESEM images of all the NPs are presented in Fig. 2a–e. As the synthesis temperature increases from 500 to 900 °C, there is a noticeable formation of well-defined spherical shapes. These nanoparticles range in size from 28 nm to 128 nm. It is also confirmed by TEM as shown in the Fig. 2f and a reduction in particle size, as represented in Fig. 2g. The EDS results revealed the presence of a high carbon content in precursor, i.e, ∼86.30%, as depicted in Fig. S1(a).†
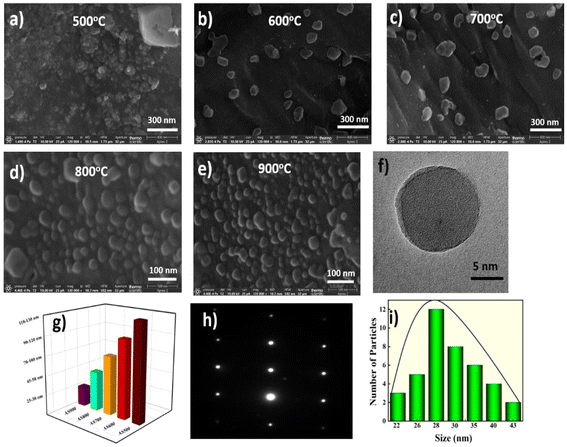 |
| | Fig. 2 (a–e) FESEM images at temperatures ranging from 500 to 900 °C, respectively. (f) TEM image of AS900, (g) the particle sizes of different nanoparticles, (h) SAED pattern of AS900, (i) histogram of AS900. | |
3.1.2. Raman spectroscopy.
Two major peaks were observed one at ∼1357 cm−1 corresponding to the D- (distortion) band as shown depicted in Fig S1(b),† indicating structural defects from sp3 hybridised carbon because of A1g mode of vibration. Another peak observed at approximately 1598 cm−1 corresponds to the G-band (graphitic band), which indicates an E2g mode of vibration. This vibration arises from the stretching of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in graphitic materials with sp2 carbon systems. The relative intensity ratio of the D-band to the G-band (ID/IG) is 0.84, signifying that the material has a high graphitic nature. This characterization is similar to findings from previous studies.20
C bonds in graphitic materials with sp2 carbon systems. The relative intensity ratio of the D-band to the G-band (ID/IG) is 0.84, signifying that the material has a high graphitic nature. This characterization is similar to findings from previous studies.20
3.1.3. X-ray diffraction (XRD).
XRD patterns of AS900 are shown in Fig S1(c).† A broadened minor hump was observed around 23°, followed by a sharp peak at 29°, corresponding to the d (002) plane in graphitic carbons (ICDD 10713739). Additionally, a peak at 43° indicates the presence of the d(100) plane found in turbostratic carbon (ICDD 10750410). Furthermore, the occurrence of multiple minor peaks at approximately 35.8°, 39.2°, 46.3°, and 47.4° are attributed to the formation of turbostratic carbon.
3.1.4. FTIR.
FTIR analysis was recorded on a spectrometer (Ni colet 6700), which was run in a range of 500 cm−1 to 4000 cm−1 in a transmittance modest resolution of 4 cm−1. Fig. S1(d)† shows the FTIR results of the sample and the purity of the sample confirmed by the functional groups. The peak present at 3377 cm−1 is attributed to –O–H stretching vibrations, the peak at 2983 cm−1 is ascribed to –C–H cm−1 stretching vibrations, and the peaks at 1601 cm−1 is attributed to –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– stretching vibrations, indicating graphitic nature, bending vibration –C–H is observed at 1416 cm−1 a peak at 1092 cm−1 are attributed to, –C–O bending. An 873 cm−1 and 710 cm−1 peak corresponds to –C
C– stretching vibrations, indicating graphitic nature, bending vibration –C–H is observed at 1416 cm−1 a peak at 1092 cm−1 are attributed to, –C–O bending. An 873 cm−1 and 710 cm−1 peak corresponds to –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– bending.21
C– bending.21
3.2. Stability characterization of nanofluid
Characterizing colloidal stability is crucial for NFs and must be assessed before conducting thermophysical property measurements. Therefore, we evaluated the colloidal stability by measuring the cluster size and zeta potential at various sonication times before beginning the thermophysical property analysis. The cluster size was measured after each sonication, and another set of test samples was used for zeta analysis. The effect of the sonication period on particle cluster size is presented in Fig. 3. The mean aggregate sizes of nanoparticles were initially 1039 nm after 90 min sonication. The average values decreased to 753.9 nm and 347.3 nm after 120 and 180 minutes of sonication of the same samples, as shown in Fig. 3, respectively. The cluster size decreases with increasing sonication period because as the duration of sonication increases, the total amount of vibrational energy supplied to the NF also increases. As a result, the rapture of the clusters increases. Fig. 4 shows the effect of sonication on zeta potential. The experiment involves varying the sonication duration, starting from 90 minutes and extending up to 180 minutes, on a NF with a concentration of 0.1 wt%. After 90 sonication, the tested value of zeta potential was −22.1 mV. Then, the zeta values increased to −30.0 mV and −31.2 mV after the sonication of 120 and 180 min, as shown in Fig. 4 respectively. The results indicate that the zeta potential value increases rapidly with the increase in the sonication period. This is because of the reduction of agglomerated nanocluster sizes and the enhancement of electrostatic charges on the nanoclusters. From the above results, it is clear that the prepared NFs are highly stable. Sonication also plays a significant role in the stability of NFs. Prolonged sonication leads to better dispersion of nanoparticles and good stability up to 180 minutes, for NFs, i.e., lesser sedimentation, however after 180 min there was slight sedimentation started for as shown in Fig. 5 Further section gives information about how sonication affects the TC.
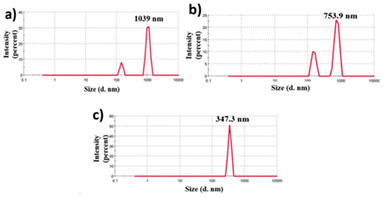 |
| | Fig. 3 Nanoparticle cluster size variation under different sonication durations: (a) 90 min, (b) 120 min, and (c) 180 min. | |
 |
| | Fig. 4 Impact of sonication duration on zeta potential (a) 90 min, (b) 120 min and (c) 180 min. | |
 |
| | Fig. 5 Digital photographs of nanofluid vials after sonication at different times. | |
3.3. Effect of sonication on thermal conductivity
Stability and TC are the two major parameters significantly enhancing the heat transfer efficiency for various applications where effect of sonication plays the dominant role. The NF is subjected to sonication at times ranging from 50 to 240 minutes. The TC of NF increases with a sonication period of up to 180 minutes. However, an increase in conductivity can be observed between 90 and 180 minutes under room temperature conditions and ceases with further sonication, as shown in Fig. 6, indicates that TC does not merely stop increasing but actually decreases beyond 180 minutes for all samples. Initially, TC rises due to sonication breaking NP clusters, leading to improved dispersion and enhanced heat transfer for instance, at 60 minutes, the TC of the 0.1 wt% sample is 0.2166 W m−1 K−1, which increases to 0.2498 W m−1 K−1 at 180 minutes. However, beyond this point, excessive sonication causes reducing the available surface area for heat transfer and lowering TC. Additionally, their interaction with the base fluid and impacting thermal transport properties. Cavitation effects from ultrasonic waves may also generate microbubbles, disrupting the homogeneity of the nanofluid and further impeding heat transfer. This decline in TC emphasizes the need to optimize sonication time to balance dispersion and stability, ensuring maximum thermal performance. However, with sonication, the energy breaks these clusters into smaller particles as shown in the Fig. 3 and allows more particles to participate in enhancing the TC. Higher TC values were obtained for nanofluid with higher concentration (0.1 wt%) due to more particles. Thus, it can be concluded that stable dispersion of AS900 in PG takes place with the ultrasonic vibration for 180 min. After 180 minutes, the TC of nanofluids declined. This is due to prolonged sonication, which can cause the particles to re-cluster as shown in the Fig. 5, reducing their overall surface area available for heat transfer, which lowers the TC.
 |
| | Fig. 6 Effect of sonication on thermal conductivity of nanofluid. | |
3.4. Effect of temperature and size on thermal conductivity
In this section, the effect of particle size and temperature on TC enhancement has been studied. To illustrate this, a concentration of 0.1 wt% was selected because experiments showed that this concentration yielded high TC, explained in the next section, 3.5. The TC studies were carried out between 20 to 80 °C. The results showed that TC increases as the particle size decreases and the temperature rises, as shown in Fig. 7a. The TC values of the NF at 20 °C are 0.2587, 0.2435, 0.2345, 0.2315, and 0.2184 W m−1 K−1 for the CNF1, CNF2. CNF3, CNF4 and CNF5, respectively. The Table 2 presents the new findings on TC values and the percentage enhancement compared to the BF for NFs with different sizes of CNS at 80 °C. It is evident from the results that as the temperature increases and the size of the nanoparticles decreases, the TC increases. This is because as the diameter of particles decreases, the space between the particles’ surfaces decreases compared to particles with a larger diameter, thereby increasing the TC of the NF. Small-sized nanoparticles efficiently scatter phonons and quantised lattice vibrations that cause thermal conduction by improving heat transfer in the material. When the size of the nanoparticles is equal to or less than the mean accessible route of phonons, this impact is very noticeable.22 Furthermore, smaller nanoparticles’ area-to-volume ratio is higher and better at resisting sedimentation. The synthesised CNS showed a highly ordered structure. This ordered structure minimises defects and boundaries within the material, which can impede thermal conduction. Additionally, the results show that as temperatures increase, the enhancement in the TC observed is attributed to increased particle mobility with accelerated Brownian motion. The enhanced Brownian motion brings augmentation in micro-convection in nanofluid.23 It should be noted that the small size of particles not only enhances the thermal conductivity due to the larger surface areas (relative to that of coarse particles) but also increases the stability and homogeneity of suspensions.24
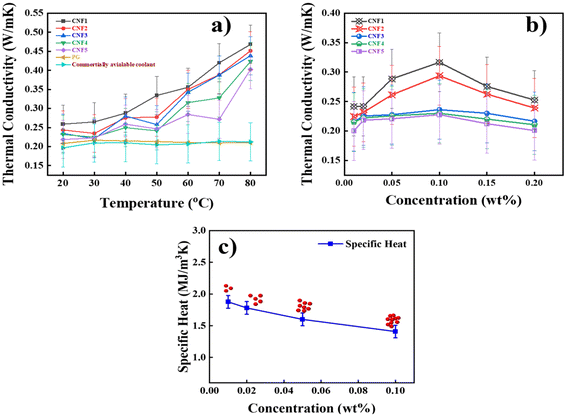 |
| | Fig. 7 TC of NFs as a function of NP (a) size and temperature (b) concentration (c) specific heat behaviour (red dot represents the concentration of nanoparticles). | |
Table 2 TC and enhancement values for NFs with different sizes at 80 °C
| Code of the NF |
Size of NPs |
Observed TC in W m−1 K−1 |
Observed TC enhancement |
| CNF5 |
120 nm |
0.4022 |
52.60% |
| CNF4 |
105 nm |
0.4231 |
101.28% |
| CNF3 |
85 nm |
0.4383 |
108.51% |
| CNF2 |
48 nm |
0.4551 |
114.60% |
|
CNF1
|
28 nm
|
0.4680
|
122.64%
|
3.5. Influence of nanoparticle concentration on thermal conductivity
In this section, we have investigated how biomass-based CNS concentration will influence the TC of NF. CNS dispersed in BF with concentrations ranging from 0.01 wt% to 0.2 wt%. The experiment was conducted at room temperature. Subsequently, the experimental results showed an increase in TC as the concentration increased from 0.01 wt% to 0.1 wt%. There is a slight increase in the TC values for CNF5, CNF4, and CNF3, whereas there is a significant increase in TC values for CNF2 and CNF1. The findings demonstrate that decreasing the size of nanoparticles improves TC of NF, as explained in the previous section 3.5. As depicted in Fig. 7b. TC increases with increasing CNS concentration up to 0.1 wt%, then it starts decreasing. This is because higher concentration allows uniformly dispersed nanoparticles with high TC to connect more easily, significantly enhancing the TC of NFs. However, the TC starts to decrease at concentrations above 0.2 wt%. This is attributed to the percolation threshold phenomena in which nanoparticles form a continuous network throughout the material. Beyond this threshold, there is a significant enhancement in the material's TC. Below this threshold, the nanoparticles are dispersed randomly within the matrix.25 Agglomeration or clustering caused by overly high NP concentrations may obstruct heat transmission pathways and lower thermal conductivity.26 Therefore, we have selected 0.1 wt% as an optimum concentration for our further studies.
3.6. Concentration-dependent specific heat behaviour in nanofluid
The specific heat capacity of NFs plays a crucial role in determining their thermal performance. In this study, we have investigated how the concentration of CNS affects the specific heat. The experiment was conducted at room temperature, and NF was prepared with various concentrations ranging from 0.01 wt% to 0.1 wt%. The results indicate that the NF exhibits a specific heat of 1.876 MJ m−3 K−1 at a lower concentration of 0.01 wt% and a low specific heat of 1.408 MJ m−3 K−1 at a higher concentration of 0.1 wt%. Findings showed that a clear trend emerges wherein an increase in concentration leads to a decrease in specific heat, as shown in Fig. 7c the red dots in Fig. 7c represent the effect of increasing nanoparticle concentration. As the concentration rises, the number of nanoparticles in the fluid also increases, resulting in a higher probability of particle interactions and agglomeration. This is because the intermolecular interaction can lead to changes in the energy required to raise the temperature of the NF. These strong solute-solvent interactions may reduce the mobility of the solvent molecule. The prepared NF exhibited excellent TC and lower specific heat, making it a promising candidate for numerous engineering applications, particularly those requiring rapid heating and cooling.
3.7. DI water and propylene glycol studies
Developing an anti-freezing NF is essential to enhance coolant performance in the automotive sector. In this study, we prepared NFs by dispersing 0.1 wt% of AS900 nanoparticles in DI water and PG mixtures at varying ratios of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 60
20, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 40
40, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, and 20
60, and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80. The combination of DI water and PG in the BF is intended to achieve optimal TC and antifreeze properties, making the NF suitable for high-efficiency coolant applications.27 The TC of these NFs was measured and compared with ASHRAE data (the ASHRAE data is given in Table 3). When DI water is mixed with PG-containing CNS nanoparticles, both DI Water and PG form hydrogen bonds with the functional groups on the surface of CNS, preventing agglomeration.
80. The combination of DI water and PG in the BF is intended to achieve optimal TC and antifreeze properties, making the NF suitable for high-efficiency coolant applications.27 The TC of these NFs was measured and compared with ASHRAE data (the ASHRAE data is given in Table 3). When DI water is mixed with PG-containing CNS nanoparticles, both DI Water and PG form hydrogen bonds with the functional groups on the surface of CNS, preventing agglomeration.
Table 3 DI water and PG TC values from ASHRAE data book28
| Temperature in °C |
TC values in W m−1 K−1 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 80 |
| 30 |
0.503 |
0.409 |
0.329 |
0.261 |
| 40 |
0.513 |
0.415 |
0.331 |
0.261 |
| 50 |
0.522 |
0.42 |
0.334 |
0.26 |
| 60 |
0.529 |
0.425 |
0.335 |
0.26 |
| 70 |
0.535 |
0.428 |
0.336 |
0.259 |
| 80 |
0.54 |
0.43 |
0.337 |
0.258 |
The results showed that the TC of the water-based NF increases compared to the BF, with the increment depending on the ratio of DI water and PG to nanoparticles, as illustrated in Fig. 8 at an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ratio, the increase is 2.3%. At a 60
20 ratio, the increase is 2.3%. At a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 ratio, it rises to 6.68%. For a 40
40 ratio, it rises to 6.68%. For a 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 ratio, the increment is 4.45%, and for a 20
60 ratio, the increment is 4.45%, and for a 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 ratio, it reaches 3.72%. The results showed the highest TC of 0.563 W m−1 K−1 for a NF with a ratio of 80
80 ratio, it reaches 3.72%. The results showed the highest TC of 0.563 W m−1 K−1 for a NF with a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 at 80 °C. As the water content increases, the TC increases because water has a higher intrinsic TC than PG. Additionally, water is denser than PG, allowing for more CNS per unit volume. Increased CNS density facilitates more efficient heat conduction pathways within the nanofluid, leading to higher TC. CNS nanoparticles can effectively transfer heat through the fluid by phonon transport mechanisms. As a result, the TC of the nanofluid is enhanced compared to the base fluid.
20 at 80 °C. As the water content increases, the TC increases because water has a higher intrinsic TC than PG. Additionally, water is denser than PG, allowing for more CNS per unit volume. Increased CNS density facilitates more efficient heat conduction pathways within the nanofluid, leading to higher TC. CNS nanoparticles can effectively transfer heat through the fluid by phonon transport mechanisms. As a result, the TC of the nanofluid is enhanced compared to the base fluid.
 |
| | Fig. 8 TC of DI water and PG mixture with different volumes and compared with ASHRAE data.28 | |
3.8. Effect of average particle size and temperature on the dynamic viscosity of nanofluid
In this study, we have explored how biomass-derived CNS size affects the V of NF. The discovery hybrid rheometer (DHR-3, USA) was used to measure V. The effect of particle size on V was investigated for all the NFs with different sizes of nanoparticles ranging from 28 nm to 128 nm at different temperatures ranging from 30 °C to 90 °C at the particle concentration 0.1 wt%. Results showed that V decreases as the size of the CNS increases from 28 nm to 128 nm, as shown in Fig. 9a. The NF CNF1 exhibited the highest V enhancement of 0.9%. In contrast, other NFs, CNF2, CNF3, CNF4, and CNF5, showed enhancements of 0.74%, 0.48%, 0.29%, and 0.17%, respectively, compared to the base fluid PG. There is a significant drop in V for the nanofluid CNF5 compared to the CNF1 nanofluid. At a constant volume fraction, smaller particles mean more particles in a specific volume of the BF, which can increase the nanofluid V. When nanoparticles are uniformly distributed in the BF due to reduced particle size, the Brownian theory emphasises that smaller particles have higher dispersion energy. As a result, the random collision between particles increases, leading to higher V. Fig. 8a also shows the variation in V with temperature: the NF with 28 nm-sized CNS dropped its V from 0.0438 mPa s to 0.00785 mPa s as the temperature increased from 30 °C to 90 °C. NF V decreases with increasing temperature. This can be attributed to the fact that with increasing temperature, the intermolecular interaction between the nanoparticles and the solvent weakens, reducing viscosity. Additionally, the thermal energy disrupts the intermolecular bonds within the NF, leading to a decrease in shear resistance. The results illustrate that both the size of the CNS and temperature play a significant role in the viscosity variations of nanofluids.29–32
 |
| | Fig. 9 Variation in dynamic viscosity with (a) temperature and size and (b) variation in shear stress with the shear rate. | |
3.9. Effect of shear rate on dynamic viscosity of nanofluid
In this study, the rheological behavior of the fluids was investigated at room temperature by varying the shear rate. In Fig. 8b, the results show the relationship between shear stress and shear rate for NFs with varying concentrations of CNS, AS900 dispersed in BF, with concentrations ranging from 0.01 wt% to 0.1 wt%. The shear stress at any given shear rate increases with increasing particle concentration, indicating that higher particle concentrations result in greater resistance to flow. The linear relationship between shear stress and shear rate for each concentration suggests that the fluids exhibit Newtonian behavior rather than shear-thickening behavior. The BF shows the lowest shear stress values, confirming that the addition of CNS increases the viscosity of the fluid, significantly impacting its rheological properties. As CNS concentration rises, more frequent particle interactions, such as collisions and frictional forces, contribute to the increase in viscosity. However, since the shear stress increases proportionally with the shear rate for all samples, the fluids maintain a Newtonian response rather than a non-Newtonian one. The increase in viscosity with concentration is attributed to the enhanced inter-particle interactions and dispersion stability of the CNS in the base fluid. At higher concentrations, the nanoparticles contribute to increased drag and energy dissipation, leading to greater viscosity. However, the absence of a nonlinear shear stress-shear rate relationship confirms that the fluids do not exhibit shear-thickening behavior. The observed rheological characteristics indicate that the nanofluids maintain Newtonian flow properties across the tested shear rate range. The next section explained about mathematical modelling for obtaining surface plots for thermal conductivity and dynamic viscosity of biomass-derived carbon nanosphere-based nanofluid as a function of the size of spherical nanoparticles and temperature in the experimental setup.
4. Theoretical modelling
The TC and V of the NF were experimentally measured, with the detailed results presented in previous sections. Building upon this experimental data, we developed an algebraic model. In order to arrive at an appropriate surface fit from the experimental data with minimal error, we considered several polynomial fits, including quadratic, cubic, quartic and quintic were considered and the two-variable least squares fit was used to get the best possible representation with the least error this entire exercise was implemented using Python programming on plotting the surfaces thus obtained along with the data points it was clear that the cubic expressions for TC and V provided the best possible fit. The coefficients of the polynomial were obtained by solving normal equations that arise in the least squares fit.
4.1. Expression for thermal conductivity and dynamic viscosity
To better understand the relationship between TC and V with temperature and nanoparticle size, mathematical models were developed. These models help predict the thermophysical properties of the NF under varying conditions, providing deeper insight into its behavior. The equations below represent the best-fit polynomial expressions derived from the experimental data, capturing the influence of temperature (x) and NP size (y) on TC and V.| |  | (3) |
and| | 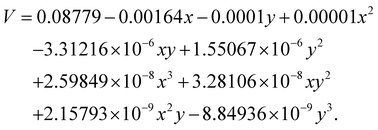 | (4) |
The data points constitute the experimental data. These data points, as well as the surface of best fit, were plotted to confirm that the surface plot is indeed the best possible fit. The surface plot thus faithfully represents the experimental data. Both models allow for a predictive framework in which TC and V can be effectively estimated based on known values of temperature and NP size, providing valuable insight into the NF's thermophysical behaviour in the experimental setup. As indicated earlier, the above expressions for TC and V are used to make three-dimensional plots for them as a function of temperature and size. The three-dimensional plots are shown in Fig. 10.
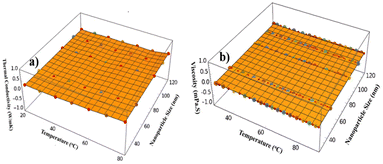 |
| | Fig. 10 Surface plot for (a) thermal conductivity and (b) dynamic viscosity. | |
4.2. Thermal conductivity and dynamic viscosity
The 3D plot of thermal conductivity illustrates how changes in NP size and temperature result in variations in TC as shown in Fig. 9a. This visualization helps identify the trend in TC due to a decrease in NP size and an increase in temperature. Quite clearly, TC increases with a decrease in size and an increase in temperature. Similarly, the 3D plot of dynamic viscosity (V) demonstrates the dependence of V on the x and y, as shown in Fig. 9b. This provides insights into how the resistance to fluid flow, as represented by V, changes with varying temperatures and particle size. These visual representations are crucial for understanding the interplay between NP characteristics and temperature on the fluid's overall behaviour. From the above plots, it is apparent that the V decreases with increasing temperature and/or increase in size. We further note that this study of NFs can also help understand thermal coolants and heat transfer systems. Given these expressions’ predictive accuracy, researchers and engineers may precisely control the operating temperature, size, and distribution of nanoparticles to obtain the necessary thermal and rheological parameters in fluids. Using experimental data and detailed analysis, these algebraic representations of thermophysical properties provide a vital instrument for forthcoming investigations for possible real-world applications. However, challenges persist, including stability, TC performance at elevated temperatures, and NP agglomeration. Future research must address these limitations to unlock the full potential of biomass-based NFs for commercial applications in advanced heat transfer systems.
5. Conclusion
In this study, garlic peel-derived carbon nanospheres were successfully synthesized via pyrolysis, with sizes ranging from 28 nm to 120 nm, and incorporated into NFs using a two-step method. The thermal properties of these NFs, including TC, V, and specific heat capacity, were systematically investigated as NP size, concentration, and temperature functions. The results revealed that TC increased with a decrease in NP size and an increase in temperature, particularly in the range of 20 °C to 80 °C. Additionally, the TC of the NFs improved with increasing NP concentration from 0.001 wt% to 0.1 wt%. Specific heat capacity, however, decreased with increasing NP concentration. Stability studies showed that sonication significantly enhanced the TC, with optimal results at 180 minutes, and the NFs remained stable for up to 270 minutes. V measurements indicated that smaller nanoparticles resulted in higher V, which decreased with increasing temperature. The shear rate experiments confirmed that the NFs exhibited Newtonian behaviour. A comparative analysis of BFs, DI water, and propylene glycol further highlighted the influence of BF composition on heat transfer performance. Mathematical modelling provided surface plots correlating TC and V with NP size and temperature, offering valuable insights for the design and optimization of NFs in thermal management applications. Overall, this work demonstrates the potential of garlic peel-derived carbon nanoparticles for enhancing the thermal properties of NFs, making them suitable for advanced heat transfer applications in engineering systems. The mathematical modelling successfully established a surface fit for thermal conductivity and viscosity using a cubic polynomial with minimal error. This approach provides an accurate representation of experimental data, aiding in the optimization of nanofluid properties for heat transfer applications.
Author contributions
Kiran Bijapur: conceptualization, methodology, writing – original draft preparation analysis; Samir Mandal: data curation, analysis, validation; PG Siddheshwar: modelling, visualization, investigation; Suryasarathi Bose: conceptualization, writing – reviewing and editing; Gurumurthy Hegde: supervision, funding acquisition, conceptualization, writing – reviewing and editing.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
References
- D. Wang, Y. Fang, W. Yu, L. Wang, H. Xie and Y. Yue, Sol. Energy Mater. Sol. Cells, 2021, 220, 110850, DOI:10.1016/j.solmat.2020.110850.
- S. Angayarkanni, V. Sunny and J. Philip, J. Nanofluids, 2015, 4, 302–330, DOI:10.1166/jon.2015.1167.
- I. Ibrahim, M. Sharifpur, J. P. Meyer and S. M. S. Murshed, Int. J. Heat Mass Transfer, 2024, 228, 125597, DOI:10.1016/j.ijheatmasstransfer.2024.125597.
- M. Hu, S. Qing, X. Zhang, H. Zhang and Z. Shi, Powder Technol., 2024, 438, 119631, DOI:10.1016/j.powtec.2024.119631.
- J. Qin, Y. Tao, Q. Liu, Z. Li, Z. Zhu and N. He, Micromachines, 2023, 14, 964, DOI:10.3390/mi14050964.
- R. Dhairiyasamy, B. Saleh, M. Govindasamy, A. A. Aly, A. Afzal and Y. Abdelrhman, Inorg. Nano-Met. Chem., 2023, 53, 78–79, DOI:10.1080/24701556.2021.1980041.
- M. Beck, Y. Yuan, P. Warrier and A. Teja, J. Nanopart. Res., 2009, 11, 1129–1136, DOI:10.1007/s11051-008-9500-2.
-
D. Ganji and A. Malvandi, Heat Transfer Enhancement Using Nanofluid Flow in Microchannels: Simulation of Heat and Mass Transfer, William Andrew, 2016 Search PubMed.
- M. Liu, M. Lin, C. Tsai and C. Wang, Int. J. Heat Mass Transfer, 2006, 49, 3028–3033, DOI:10.1016/j.ijheatmasstransfer.2006.02.012.
- W. Rashmi, A. Ismail, I. Sopyan, A. Jameel, F. Yusof, M. Khalid and N. Mubarak, J. Exp. Nanosci., 2011, 6, 567–579, DOI:10.1080/17458080.2010.487229.
- Z. Said, P. Sharma, B. Bora and A. K. Pandey, J. Taiwan Inst. Chem. Eng., 2023, 145, 104818, DOI:10.1016/j.jtice.2023.104818.
- H. Lin, Q. Jian, X. Bai, D. Li, Z. Huang, W. Huang, S. Feng and Z. Cheng, Appl. Therm. Eng., 2023, 218, 119176, DOI:10.1016/j.applthermaleng.2022.119176.
- O. Khouri, H. Goshayeshi, S. B. Mousavi, S. Hosseini Nami and S. Zeinali Heris, ACS Omega, 2024, 9, 24025–24038, DOI:10.1021/acsomega.4c02581.
- H. Hamad and S. Idrus, Polymers, 2022, 14, 783, DOI:10.3390/polym14040783.
- W. Yu and S. Choi, J. Nanopart. Res., 2004, 6, 355–361, DOI:10.1007/s11051-004-2601-7.
- A. Kuznetsov and D. Nield, Transp. Porous Media, 2010, 81, 409–422, DOI:10.1007/s11242-009-9413-2.
- D. Divyashree, S. Manaf, S. Yallappa, K. Chaitra, N. Kthyayini and G. Hegde, J. Mater. Chem. A, 2016, 25, 880–887, DOI:10.1016/j.jechem.2016.08.002.
- X. Li, D. Zhu, X. Wang, N. Wang, J. Gao and H. Li, Thermochim. Acta, 2008, 469, 98–103, DOI:10.1016/j.tca.2008.01.008.
- K. Bijapur, S. Mondal, P. G. Siddeshwar, S. Bose and G. Hegde, Nanoscale Adv., 2024, 6, 4944–4955, 10.1039/d4na00362d.
- P. Kanagavalli, G. Pandey, V. Bhat, M. Veerapandian and G. Hegde, J. Nanostruct. Chem., 2021, 11, 343–352, DOI:10.1007/s40097-020-00370-w.
-
P. Griffiths, J. Haseth and J. Winefordner, Fourier Transform Infrared Spectrometry, Wiley-Blackwell, Chichester, England, 2nd edn, 2007. DOI:10.1002/047010631x.
- W. Kim, J. Mater. Chem. C, 2015, 3, 10336–10348, 10.1039/c5tc01670c.
- H. Younes, M. Mao, S. Murshed, D. Lou, H. Hong and G. P. Peterson, Appl. Therm. Eng., 2022, 207, 118202, DOI:10.1016/j.applthermaleng.2022.118202.
- M. Chopkar, S. Sudarshan, P. K. Das and I. Manna, Metall. Mater. Trans. A, 2008, 39, 1535–1542, DOI:10.1007/s11661-007-9444-7.
- H. Xie and L. Chen, J. Chem. Eng. Data, 2011, 56, 1030–1041, DOI:10.1021/je101026j.
- J. Wang, R. Zheng, J. Gao and G. Chen, Nano Today, 2012, 7, 124–136, DOI:10.1016/j.nantod.2012.02.007.
- M. Hemmat Esfe, S. Alidoust and D. Toghraie, Mater. Today Commun., 2023, 34, 105411, DOI:10.1016/j.mtcomm.2023.105411.
-
American Society of Heating, R. &. A. Engineers and Incorporated, ASHRAE Fundamentals Handbook 2001 (SI), 2001 Search PubMed.
- V. Rudyak, Adv. Nanopart., 2013, 02, 266–279, DOI:10.4236/anp.2013.23037.
- L. Bao, C. Zhong, P. Jie and Y. Hou, Adv. Mech. Eng., 2019, 11, 1–17, DOI:10.1177/1687814019889486.
- A. Minakov, V. Rudyak and M. Pryazhnikov, Heat Transfer Eng., 2021, 42, 1024–1040, DOI:10.1080/01457632.2020.1766250.
- N. Masoumi, N. Sohrabi and A. Behzadmehr, J. Phys. D:Appl. Phys., 2009, 42, 22–37, DOI:10.1088/0022-3727/42/5/055501.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Samir
Mandal
c,
P. G.
Siddheshwar
ab,
Samir
Mandal
c,
P. G.
Siddheshwar
 d,
Suryasarathi
Bose
d,
Suryasarathi
Bose
 c and
Gurumurthy
Hegde
c and
Gurumurthy
Hegde
 *ab
*ab
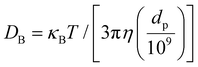
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm and sieved at 75 μm with a laboratory sieving machine. The powder was taken in parts (∼10 g each) in a silica crucible and pyrolysed at a series of temperatures. 500, 600, 700, 800, and 900 (represented as AS500, AS600, AS700, AS800 and AS900 respectively). Under a quartz tube furnace in a continuous N2 flow to The Allium sativum peels have been pyrolysed five times in a row at temperatures ranging from 500 °C to 900 °C, highlighting the significance of pyrolysis temperature and how temperature affects the size of the nanoparticles. The resulting carbonised material was washed with ethanol and DI water to remove impurities and dried overnight at 80 °C in a hot air oven. Divyashree et al.'s17 work thoroughly analyses the production of porous nanocarbon materials and temperature impact. Fig. 1 schematically illustrates the synthesis process. Further characterisation of the obtained nanomaterials included XRD, Raman, FTIR, FESEM/EDS and TEM analysis. Then, by using these CNSs, nanofluids were prepared, and TC and V analyses were carried out.
000 rpm and sieved at 75 μm with a laboratory sieving machine. The powder was taken in parts (∼10 g each) in a silica crucible and pyrolysed at a series of temperatures. 500, 600, 700, 800, and 900 (represented as AS500, AS600, AS700, AS800 and AS900 respectively). Under a quartz tube furnace in a continuous N2 flow to The Allium sativum peels have been pyrolysed five times in a row at temperatures ranging from 500 °C to 900 °C, highlighting the significance of pyrolysis temperature and how temperature affects the size of the nanoparticles. The resulting carbonised material was washed with ethanol and DI water to remove impurities and dried overnight at 80 °C in a hot air oven. Divyashree et al.'s17 work thoroughly analyses the production of porous nanocarbon materials and temperature impact. Fig. 1 schematically illustrates the synthesis process. Further characterisation of the obtained nanomaterials included XRD, Raman, FTIR, FESEM/EDS and TEM analysis. Then, by using these CNSs, nanofluids were prepared, and TC and V analyses were carried out.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18
18
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in graphitic materials with sp2 carbon systems. The relative intensity ratio of the D-band to the G-band (ID/IG) is 0.84, signifying that the material has a high graphitic nature. This characterization is similar to findings from previous studies.20
C bonds in graphitic materials with sp2 carbon systems. The relative intensity ratio of the D-band to the G-band (ID/IG) is 0.84, signifying that the material has a high graphitic nature. This characterization is similar to findings from previous studies.20
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– stretching vibrations, indicating graphitic nature, bending vibration –C–H is observed at 1416 cm−1 a peak at 1092 cm−1 are attributed to, –C–O bending. An 873 cm−1 and 710 cm−1 peak corresponds to –C
C– stretching vibrations, indicating graphitic nature, bending vibration –C–H is observed at 1416 cm−1 a peak at 1092 cm−1 are attributed to, –C–O bending. An 873 cm−1 and 710 cm−1 peak corresponds to –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– bending.21
C– bending.21


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 60
20, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 40
40, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, and 20
60, and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80. The combination of DI water and PG in the BF is intended to achieve optimal TC and antifreeze properties, making the NF suitable for high-efficiency coolant applications.27 The TC of these NFs was measured and compared with ASHRAE data (the ASHRAE data is given in Table 3). When DI water is mixed with PG-containing CNS nanoparticles, both DI Water and PG form hydrogen bonds with the functional groups on the surface of CNS, preventing agglomeration.
80. The combination of DI water and PG in the BF is intended to achieve optimal TC and antifreeze properties, making the NF suitable for high-efficiency coolant applications.27 The TC of these NFs was measured and compared with ASHRAE data (the ASHRAE data is given in Table 3). When DI water is mixed with PG-containing CNS nanoparticles, both DI Water and PG form hydrogen bonds with the functional groups on the surface of CNS, preventing agglomeration.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ratio, the increase is 2.3%. At a 60
20 ratio, the increase is 2.3%. At a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 ratio, it rises to 6.68%. For a 40
40 ratio, it rises to 6.68%. For a 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 ratio, the increment is 4.45%, and for a 20
60 ratio, the increment is 4.45%, and for a 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 ratio, it reaches 3.72%. The results showed the highest TC of 0.563 W m−1 K−1 for a NF with a ratio of 80
80 ratio, it reaches 3.72%. The results showed the highest TC of 0.563 W m−1 K−1 for a NF with a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 at 80 °C. As the water content increases, the TC increases because water has a higher intrinsic TC than PG. Additionally, water is denser than PG, allowing for more CNS per unit volume. Increased CNS density facilitates more efficient heat conduction pathways within the nanofluid, leading to higher TC. CNS nanoparticles can effectively transfer heat through the fluid by phonon transport mechanisms. As a result, the TC of the nanofluid is enhanced compared to the base fluid.
20 at 80 °C. As the water content increases, the TC increases because water has a higher intrinsic TC than PG. Additionally, water is denser than PG, allowing for more CNS per unit volume. Increased CNS density facilitates more efficient heat conduction pathways within the nanofluid, leading to higher TC. CNS nanoparticles can effectively transfer heat through the fluid by phonon transport mechanisms. As a result, the TC of the nanofluid is enhanced compared to the base fluid.