 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vanadium incorporation in ferrite nanoparticles serves as an electron buffer and anisotropy tuner in catalytic and hyperthermia applications†
T. E.
Torres
 *abcd,
D. P.
Valdés
*abcd,
D. P.
Valdés
 *ef,
S.
Hettler
*ef,
S.
Hettler
 ac,
J. M.
Nuñez
ac,
J. M.
Nuñez
 acef,
I.
Rodrigo
g,
I.
Orue
h,
J. Á.
García
g,
F.
Plazaola
acef,
I.
Rodrigo
g,
I.
Orue
h,
J. Á.
García
g,
F.
Plazaola
 i,
R. D.
Zysler
i,
R. D.
Zysler
 ef,
E.
Lima
Jr.
e,
M. H.
Aguirre
ef,
E.
Lima
Jr.
e,
M. H.
Aguirre
 abc,
G. F.
Goya
abc,
G. F.
Goya
 ab and
R.
Arenal
ab and
R.
Arenal
 abcj
abcj
aInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC – Universidad de Zaragoza, 50018, Zaragoza, Spain. E-mail: teo@unizar.es; teobaldotorresmolina@gmail.com
bDepartamento de Física de la Materia Condensada, Facultad de Ciencias Universidad de Zaragoza, 50018, Zaragoza, Spain
cLaboratorio de Microscopías Avanzadas (LMA), Universidad de Zaragoza, Calle Mariano Esquillor, 50018, Zaragoza, Spain
dDepartment of Chemistry and Chemical Biology, Rutgers, The State University of New Jersey, 123 Bevier Road, Piscataway, 08854, NJ, USA
eInstituto de Nanociencia y Nanotecnología, CNEA-CONICET, Av. E. Bustillo 9500, 8400, S.C. Bariloche, RN, Argentina
fInstituto Balseiro, UNCUYO, Av. E. Bustillo 9500, 8400, S.C. Bariloche, RN, Argentina. E-mail: daniela.valdes@ib.edu.ar
gDepartamento de Física, Universidad del País Vasco (UPV/EHU), Leioa 48940, Spain
hSGIker, Universidad del País Vasco – UPV/EHU, 48940 Leioa, Spain
iDepartamento de Electricidad y Electrónica, Universidad del País Vasco (UPV/EHU), Leioa 48940, Spain
jARAID Foundation, 50018, Zaragoza, Spain
First published on 13th March 2025
Abstract
Cancer research has gradually shifted its focus from individual therapies to a combination of them for enhanced treatment effectiveness. In particular, the increased interest in the field of catalytic medicine through nanozymes proposes promising combinations with photothermal therapy, photodynamic therapy, and magnetic fluid hyperthermia (MFH). Nanozyme activity centers around the hydroxyl radical ˙OH, the most toxic of the reactive oxygen species (ROS). With a synergistic approach in mind, we studied VxFe3−xO4 magnetic nanoparticles (MNPs) as agents for ROS production and heating. These MNPs were exhaustively characterised both morphologically and magnetically. A compositional analysis through electron microscopy and spectroscopy unveils a core–shell structure with a V-rich shell. A study of the power absorption of these MNPs fixed into a gel matrix, emulating cytosol viscosity, provides values of up to 1000 W g−1 for samples with 0.5 wt% MNPs, an AC magnetic field amplitude of 65 mT and a frequency of 350 kHz, typical in the MFH application. A concentration of the ˙OH-adduct of up to 2300 nM has been measured through electron spin resonance analysis as a result of peroxidase-like activity. Through the comparison with similarly-sized ferrite MNPs, we determined that V incorporation lowers the magnetic anisotropy and serves as an electron buffer, explaining the enhanced MFH and ROS-production results.
1 Introduction
The concept of using nanomaterials to develop artificial enzymes (“nanozymes”) was proposed approximately 16 years ago, following the discovery of intrinsic peroxidase-like (POD-like) catalytic activity in iron-oxide magnetic nanoparticles (MNPs)1 serving as heterogeneous catalysts in Fenton reactions. In the homogeneous Fenton reaction, reactive oxygen species (ROS) such as the hydroxyl (˙OH) and hydroperoxyl (˙OOH) free radicals are produced through2| Fe2+ + H2O2 → Fe3+ + ˙OH + OH− k = 63 M−1 s−1 | (1a) |
| Fe3+ + H2O2 → Fe2+ + ˙OOH + H+ k′ = 0.001 M−1 s−1 | (1b) |
One of the primary objectives of this field is to utilize ˙OH, the most toxic of the ROS, to initiate oxidative stress in biological systems at the cellular level. This process enhances membrane permeability, rendering cells more susceptible to exogenous stimuli such as heat. Given the fact that certain MNPs can also function as heating agents for magnetic fluid hyperthermia (MFH) applications, there is significant interest in studying synergistic effects between heating and enzymatic-like activity for cancer therapies.3–5
From the perspective of using MNPs as nanozymes, current research focuses on the optimization of ROS production by modifying the size, structure, morphology, and surface of the MNPs,6 as well as the material they are composed of. In particular, for experiments with a fixed MNP mass, an increased surface-to-volume ratio is desired as it provides more superficial active sites.7,8
In MFH application, an AC magnetic field with frequencies between 100 kHz and 1 MHz is applied to cells or tissues with MNPs. As these are high dynamic viscosity environments, the main relaxation contribution is given by the Néel mechanism (i.e., the orientation of the moment through an energy barrier EB).9 The relaxation process takes a characteristic time, known as the relaxation time τ, which for the Néel mechanism is10
 | (2) |
In particular, one of the usual materials chosen for MNPs in this application is magnetite (Fe3O4) because it is approved by the US Federal Drug Administration (FDA) for clinical assays.15,16 Efforts are underway to reduce Keff through divalent cationic substitution (e.g., Ni2+, Zn2+, and Mn2+).17–23 As a result of the diminished energy barrier and relaxation-to-measurement time ratio, this can lead to minor loops with an increased enclosed area,24,25 and thus, an enhanced specific loss power (SLP) with respect to the unsubstituted ferrite systems.
However, obtaining MNPs that produce considerable amounts of ROS and exhibit a satisfactory heating response in MFH is challenging. On the one hand, although ROS production is benefited from MNP size reduction, MFH imposes limitations on it, as MNPs with sizes below 30 nm result in a significant decrease in their specific loss power (SLP).25 On the other hand, although MFH may benefit from divalent cationic substitution, it is important to note that Fe2+ plays a crucial role in the POD-like activity of iron-oxide MNPs,1 and therefore, its substitution is not desirable.
Certain vanadium (V) compounds have garnered interest as potential therapeutic agents for treating major health issues such as atherosclerosis, diabetes, and cancer.26,27 Numerous studies indicate a correlation between vanadium toxicity and ROS, which can induce mitochondria-mediated cell apoptosis and affect signal transduction pathways.28–33 Its use in substituted-ferrite MNPs for MFH is just starting to be explored, procuring its genomic safety.34
In this study, we synthesised V ferrite (VxFe3−xO4) MNPs by adding a V3+ precursor in the synthesis. These MNPs were designed to exhibit a significant performance in both catalytic and MFH applications. On the one hand, the Fe2+ ion was retained in the structure, with only a small amount of V3+ introduced to lower Keff. On the other hand, the mean size 〈d〉 was targeted to be around 30 nm to achieve considerable SLP values, as ferrite systems of these sizes have been reported to exhibit such properties.25,35,36 The MNP structure was extensively characterized using various techniques, revealing a core–shell structure with a V-rich shell, which affects catalytic activity where surface ions play a key role. The performance in MFH was obtained through the determination of the SLP by AC magnetometry and ROS production was assessed by electron paramagnetic resonance (EPR) analysis, yielding considerable values in both cases. The comparison with a similarly-sized ferrite MNP makes clear the enhancing effect of V incorporation: lowering anisotropy and providing electrons for MFH and catalysis, respectively. This underscores the importance of targeted MNP design for the optimization of therapeutic applications.
2 Results and discussion
2.1 Structural and magnetic characterisation
We used the thermal decomposition method to synthesise VxFe3−xO4 MNPs. Reports on this synthesis route state that the final average MNP size and morphology depend on experimental parameters such as the boiling point of the solvent, boiling time, agitation speed, temperature ramping speed of the different steps, the chemical nature of the precursor, the precursor/surfactant/diol ratios, etc.37–42 More details on the experimental parameters used in this particular synthesis are given in section 4.1.From transmission electron microscopy (TEM) images (see Fig. S1†), we obtained the size distribution of the MNPs through statistical analysis and fitted it by a lognormal distribution, as shown in the inset of Fig. 1(a). More details on this process are given in section 4.2. We determined a mean MNP characteristic size of 〈d〉 = 33 nm and a standard deviation σ = 4 nm. The high-resolution transmission electron microscopy (HRTEM) image shown in Fig. 1(b) reveals the high crystallinity of the MNPs and enables us to confirm their FCC crystalline structure by the indexing of its fast Fourier transform (FFT) to the spinel phase, shown in the inset of Fig. 1(b). This structure is also confirmed by the analysis of a large number of MNPs through their selected-area electron diffraction ring pattern, whose indexing enables to estimate the lattice parameter of a = (8.60 ± 0.09) Å (see Fig. S1†). It is also possible to observe from the scanning transmission electron microscopy (STEM) image the presence of faceted MNPs with cubic and hexagonal projections (see Fig. 1 and Fig. S2†).
Moreover, the relative abundance of V and Fe was obtained from energy-dispersive X-ray spectroscopy (EDX) analysis in scanning electron microscopy (SEM). More details on the methodology are given in section 4.3 and one of the spectra can be found in Fig. S2.† The chemical stoichiometry formula of the material was determined to be V0.26Fe2.74O4, which reflects a good V ion incorporation if we consider that 0.3 mol were originally intended.
Regarding the magnetic behaviour of the MNPs, hysteresis loops M(H) measured at T = 5 K, shown in Fig. 2(a), provided a saturation magnetisation value of Ms(5 K) = 85 Am2 kg−1, which decreased to Ms(300 K) = 77 Am2 kg−1 at room temperature (see Fig. S2†). Despite this reduction, usually related to surface effects when considering MNPs, the Ms values obtained were only 13–16% lower than values reported for bulk magnetite, that has the highest saturation magnetisation among the ferrite compounds.43 This reflects, once again, a good crystallinity of the samples as was previously determined through HRTEM.
The magnetisation as a function of temperature M(T) curves obtained using the zero-field cooling (ZFC) and field-cooling (FC) protocols are shown in Fig. 2(b). An increment of M with T is displayed in the ZFC curve at T ≈ 90 K, associated with a Verwey transition, widely reported for other kinds of ferrite MNP systems.44–46 The absence of both a clearly-defined maximum in the ZFC curve and a Curie-like decay reflects that a fraction of the MNPs is still blocked at room temperature. Moreover, the plateau observed in the FC curve below 100 K evidenced interactions between MNPs, even if the sample was dispersed in epoxy resin at a very low concentration.
To further investigate the magnetic properties of the MNPs, ferromagnetic resonance (FMR) measurements were performed in an oriented sample.47 More details on sample preparation can be found in section 4.4. The spectra for different orientations of the sample with respect to the external magnetic field θ were recorded (see Fig. S3†) and the resonance field μ0HR was extracted from the field values where the derivative of the absorption is 0. The angular dependence of the resonance field (μ0HRvs. θ) shows a maximum at 90° and two minima at 0° and 180°, which corresponds to the definition of uniaxial symmetry. Our samples, like all ferrite compounds, exhibit cubic magnetocrystalline anisotropy. However, the effective anisotropy of the sample results from the combined contributions of magnetocrystalline, shape and surface anisotropy, among others.
Both Raikher et al. and later De Biasi et al.48,49 studied the FMR spectra of uniaxial-anisotropy MNPs based on the shape contribution to anisotropy. De Biasi et al. derived an expression for the angular variation of the resonance field from Smit and Beljers’ formalism in the linear approximation. We used their deduced expression 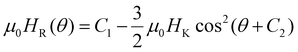 to fit our FMR data, where C1 and C2 are constants.49Fig. 2(c) shows agreement between the measured data and this fit, from which the value of the anisotropy field μ0HK = 46 mT was obtained.
to fit our FMR data, where C1 and C2 are constants.49Fig. 2(c) shows agreement between the measured data and this fit, from which the value of the anisotropy field μ0HK = 46 mT was obtained.
This uniaxial symmetry for effective anisotropy of single-domain MNPs is commonly accepted and is used to model the effective behavior of iron-oxide nanoparticle systems (with cubic magnetocrystalline anisotropy) under MFH conditions.9,24,25 It is sometimes argued that MNPs are not completely spherical and that a subtle elongation in one direction can contribute to the effective anisotropy not being cubic.14 A very recent study50 highlights that both uniaxial and cubic + uniaxial anisotropy describe the power absorption of MNPs as a function of the applied MFH field similarly. This study shows that the addition of the cubic term is relevant for low intensities of the magnetic field (less than 10 mT), which does not apply to the FMR conditions.
The anisotropy field value obtained from FMR, together with the saturation magnetisation Ms(300 K) = 77 Am2 kg−1 and a density ρ = (5–5.2) kg m−3, yields an effective magnetic anisotropy constant Keff between (0.88–0.92) × 104 J m−3 at T = 300 K. Both of the ρ limit values used correspond to the ones reported for the MnFe2O4 and Fe3O4 spinel structures in the bulk phase, respectively.43 The obtained μ0HK values are slightly below (≈16–20%) the magnetocrystalline anisotropy of bulk phase Fe3O4.
2.2 Compositional analysis
Focusing on the chemical nature of the material, Fig. 3(a) shows an X-ray photoelectron spectroscopy (XPS) survey spectrum, where we identified the intensity peaks corresponding to the Fe (Fe 2p) and V (V 2p) edges, besides those of oxygen (O 1s, both from sample and sample support) and carbon (C 1s, from the sample support). The information on the oxidation state of Fe and V in our MNPs is obtained by a detailed analysis of high-resolution XPS spectra, which are shown in Fig. 3(b)–(d). As previously reported, the oxidation states corresponding to different ions can be determined by the presence of characteristic satellite peaks. For Fe coordinated by oxygen in the cubic spinel structure (as in the ferrite compound that is being analysed), the two main peaks appear at 710.3 and 723.8 eV, which correspond to Fe 2p3/2 (L3 edge) and 2p1/2 (L2 edge) respectively. In the case of Fe3+, its fingerprint is the existence of a 2p3/2 satellite peak at a binding energy of around 719 eV, while for Fe2+ this satellite peak appears at around 715.5 eV. The absence of the satellite peak between both L3 and L2 edges51,52 is usually associated with the presence of both Fe3+ and Fe2+ species like in the case of the magnetite compound Fe3O4.Based on this evidence, it is clear that Fe3+ is present in our sample, due to the marked satellite peak at 719 eV [red peak in Fig. 3(b)]. However, the widening of the Fe 2p3/2 component reflects the presence of a multiplet splitting, commonly present in atoms with unpaired electrons, in which the coupling between the unpaired electrons in the core with the unpaired outer shell electrons creates a number of final states that will manifest in the XPS spectrum, as has been reported in detail for several transition metals, including Fe.53 In our case, ten satellite peaks have been identified in the energy range between 708 and 716 eV, five for each iron species [represented by blue peaks for Fe2+ and orange for Fe3+ in Fig. 3(b)]. From this analysis, the total content of the different Fe species corresponds to 32% for Fe2+ and 68% for Fe3+ (see Fig. S4†), which is in accordance with the relative percentages in magnetite.
Regarding V, Fig. 3(c) shows the V 2p1/2 and V 2p3/2 edges centered at 524 and 517 eV respectively, with a separation of only 7 eV. This is consistent with the presence of V5+. However, V5+ species, which lack unpaired valence electrons, typically exhibit a single sharp line. This is not the case here, as Fig. 3(c) clearly shows a broadening around 515 eV. Similar to the case of Fe 2p3/2, this broadening indicates the presence of multiplet splitting compatible with V3+, which matches previously reported spectra for this species.54 The presence of V0 species was ruled out, as its characteristic peak at around 513 eV, accompanied by a satellite peak at 519 eV, was not observed in our data.
The presence of V5+ might seem unexpected given that our vanadium precursor has only V with the +3 valence [V(acac)3]. However, it is important to note that XPS is a surface-sensitive technique with a depth range below 10 nm. Consequently, the data and compositions collected in Fig. 3 primarily reflect the surface of the MNPs, which could have oxidized, resulting in an increase in the oxidation state of both V and Fe species. Quantification indicates that V species are present as 62.5% V5+ and 37.5% V3+ (see Fig. S4†).
To further our compositional analysis, chemical composition maps were obtained using electron energy-loss spectroscopy (EELS) performed in STEM mode on individual MNPs. We show the representative analysis of an individual MNP [Fig. 4(a)], with Fe, O, and V intensity maps depicted in Fig. 4(b), accompanied by the total chemical map obtained through the sum of the individual elements. The total chemical composition map reveals that V is concentrated at the borders of the MNPs and is distributed inhomogeneously. This increased intensity at the surface is confirmed by comparing two spectra of the V–L and the O–K edges obtained from the shell and core regions, which shows a strong increase in the V–L double peak intensity in the shell region (Fig. S5†). Regarding the O–K and Fe–L edges, their intensity decreases due to the reduced thickness of the MNP at the shell. A composition line profile across the MNP indicates a V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe ratio of 1
Fe ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in the shell and 1
2 in the shell and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 in the core [see Fig. 4(c)]. This evidences that the incorporation of V was not uniform and was in fact richer in the shell of the MNPs. It is worth noting that the EDX data collected in the SEM yields a 0.26
9 in the core [see Fig. 4(c)]. This evidences that the incorporation of V was not uniform and was in fact richer in the shell of the MNPs. It is worth noting that the EDX data collected in the SEM yields a 0.26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.74 ≈ 1
2.74 ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 V
10 V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe ratio, which is similar to the ratio obtained in the core through EELS. As the shell is really thin, the core makes up the majority of the MNP and better reflects the average composition.
Fe ratio, which is similar to the ratio obtained in the core through EELS. As the shell is really thin, the core makes up the majority of the MNP and better reflects the average composition.
In addition to compositional maps, EELS data can be used to analyse the valence of the involved species. Particularly, the O–K peak is highly sensitive to the oxygen's chemical environment. The O–K spectrum corresponding to the core of the MNP (Fig. S5†) depicts a strong peak at 532 eV, typical of magnetite (Fe3O4).55 Even more, the Fe–L3 edge agrees with a magnetite structure in the core showing a highly overlapping doublet characteristic of the combination of Fe2+ and Fe3+.55 The intensities of both O–K and Fe–L are not only found to decrease in the shell region, but the spectra also change in shape. The O peak at 532 eV practically disappears and is broadened and reduced in intensity for the V-rich shell. The shape of the Fe–L edge only changes slightly as the higher-energy peak of the doublet seems to increase in intensity. The V–L edge exhibits two peaks, which appear slightly sharper and with a minor shift to higher energy in the shell region.
We could not find literature data on EELS from V ferrite specimens, but a comparison to spectra obtained from both Fe and V oxides can be used to estimate the valence and the difference between core and shell.56–58 The O–K edge of vanadium oxides indeed shows the absence of the strong peak at 532 eV observed in magnetite, but a further interpretation is difficult as it is strongly influenced by the presence of other metals.57 The same is true in the case of the Fe–L3 edge, where the peak at higher energy is attributed to Fe3+. The observed small increase of this contribution thus could suggest a higher oxidation state of Fe in the shell, but could as well be caused by the increased presence of V. A clear identification of the V valence is challenging, but the trend towards higher energy and sharper peaks observed in the shell might reflect an increase in the V oxidation state,57 which agrees with the observations of V5+ made through XPS. The identification of the valence in the shell and core regions would require reference V ferrites spectra and a more complex analysis with high spatial resolution.
2.3 Magnetic hyperthermia application
As the ultimate goal of these MNPs is their application in combined medical therapies, characterizing them in a medium that can emulate the biological environment is crucial for accurately assessing their heating performance. To mimic the intracellular viscosity,59 MNPs were fixed in polyacrylamide gels with 8% acrylamide, which has a viscosity similar to cytosol.60 AC magnetometry under typical MFH conditions was measured for these gels.Two spatial MNP configurations were used: dispersed and oriented. In the oriented configuration, MNPs were exposed to an alternating magnetic field of 40 mT during the polyacrylamide polymerization process. The oriented samples exhibit elongated arrangements aligned with the direction of the alternating field applied during preparation (see Fig. S6†). This orientation was considered to investigate whether MNPs aggregating into elongated agglomerates can enhance the SLP values with respect to the dispersed system, as supported by current consensus.24,61–63 As the SLP can be quantified from the enclosed area of the sample's hysteresis loop (see section 4.8), they were measured under MFH conditions for two MNP concentrations (0.1 and 0.5 wt%) and the aforementioned configurations (dispersed and oriented). Two MFH frequencies (f = 132, 350 kHz) and magnetic field intensity amplitudes μ0H0 up to 90 mT were used, as depicted in Fig. 5.
Across all parameter combinations, the oriented sample shows a slightly more rectangular hysteresis loop shape64,65 and higher magnetic susceptibility [Fig. 5(e)–(h)] when compared to the dispersed sample [Fig. 5(a)–(d)], yielding SLP values up to 25% higher [marked with blue arrows on Fig. 5(i) and (k)]. Additionally, the SLP as a function of the field amplitude curve reaches a saturation value around 60 mT, similar for both the oriented and dispersed samples. This indicates that, at high field amplitudes, orientation has negligible effects on the area enclosed by the hysteresis loop (i.e., on the SLP).
Interesting differences have been observed between measurements at 132 and 350 kHz. While SLP values are almost the same for the 0.1 and 0.5 wt% samples at low frequency (f = 132 kHz) [Fig. 5(i) and (k)], the SLP at high frequency (f = 350 kHz) for the 0.1 wt% samples is slightly higher than that of the 0.5 wt% one [Fig. 5(j) and (l)]. This could be related to a dipolar-interaction effect. In the sample at a concentration of 0.5 wt% in MNPs, the average distance between them is smaller than that at 0.1 wt%, which can increase the probability of agglomeration during preparation. At f = 132 kHz, the measurement time is longer than that at 350 kHz, which increases the thermal fluctuation of the magnetic moment between energy minima,25 regardless of their agglomeration. However, when the measurement time is shorter (at f = 350 kHz), the interaction effects become more pronounced. Consequently, the different behavior observed for the concentrations analysed are more apparent at higher frequencies.
Another important aspect of medical therapies is the safety conditions for the final application. When discussing MFH, the safety conditions are imposed by an upper limit to the product of the magnetic field intensity and frequency H × f, encompassing the experimental conditions in which eddy-current effects are manageable for the patient. It was initially established by Atkinson–Brezovich66 but many research groups are emphasising the necessity of redefining the threshold. A recent study establishes that H × f ≤9.59 × 109 A m−1 s−1 is safe when considering both local and systemic physiological effects of MFH.67 Taking this limit into account, the safe region is showcased through the blue rectangles for the SLP as a function of field intensity amplitude curves in Fig. 5(i)–(l). It is important to balance the parameters involved in MFH to achieve the optimal SLP performance while ensuring a safe treatment for the patient.
First of all, Fig. 5(i)–(l) illustrate something intuitive: when the frequency or MNP concentration is lower, higher field intensity amplitudes are needed to achieve a given SLP value. However, even for low frequencies or MNP concentrations, considerable SLP values within the safe limits are obtained with V ferrite MNPs (around 300 Wg−1, sometimes even higher). It is worth noting that we obtained these values for MNPs fixed in a gel matrix, with different degrees of agglomeration,68 where relaxation will be achieved through the Néel process. Even more, when we ease up on the safety conditions, SLPs up to 1000 Wg−1 were obtained.
2.4 ROS production
Based on our compositional analysis with the XPS presented in section 2.2, which indicates that there is a higher concentration of V5+ on the surface of the MNPs, a detailed catalysis study is crucial. The surface of the MNP plays a leading role in these applications. Therefore, to gather catalytic information on our MNPs, we performed EPR studies to quantify the free radicals produced by our V ferrite MNPs.To detect free radicals formed due to the POD-like activity of these MNPs through EPR, a spin-trap solution is needed to increase their half-life time. We used DMPO in a DMSO solution and detected the adduct radicals formed by the interaction of DMPO/DMSO with the original radicals. An MgO crystal with Mn2+ impurities was attached to the sample holder tubes and used as the reference signal. Six spectra were recorded at 10-minute intervals following the MNPs’ exposure to H2O2. Fig. 6(a) shows the spectra obtained at 10 and 60 minutes after the addition of H2O2, along with their corresponding fits. The full-time evolution of the spectra can be found in Fig. S7 and their fitting parameters in Table S2.†
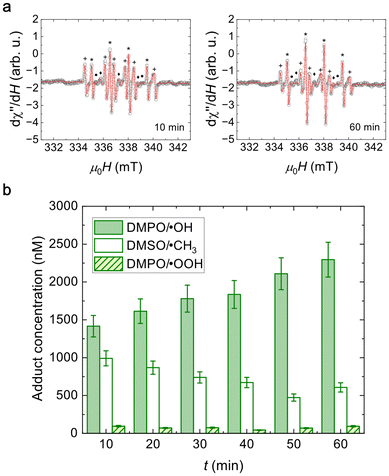 | ||
| Fig. 6 (a) EPR spectra of adducts obtained for nanoparticles in DMPO/DMSO after 10 and 60 min since H2O2 addition. (b) Adduct concentration as a function of time after addition of H2O2. | ||
As previously reported,69 each spectrum depicted in Fig. 6(a) consists of the resonance signals from five different paramagnetic species. The outer lines correspond to the central resonance lines of the Mn2+ ions in the MgO crystal used as reference. The DMPO/˙OH adduct spectrum (marked with “*”) shows four lines with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity ratio (from the convolution of 6 resonances), resulting from the hyperfine splitting due to the interaction of the electronic spin with the nuclear spin of a nitrogen and a hydrogen in DMPO. The DMPO/˙OOH adduct spectrum (marked with “•”) displays six lines surging from the convolution of 12 resonances, corresponding to the hyperfine interaction of the electron spin with the nuclear spin of a nitrogen and two hydrogens in DMPO. The DMSO/˙CH3 radical contribution (marked with “+”) arises from a secondary reaction of DMSO with the ˙OH radicals produced. Additionally, three broad lines denoted with “◆” are related to the interaction of the electron spin of oxidized DMPO with the nuclear spin of nitrogen in it (DMPO/˙N) and is intrinsic to DMPO.
1 intensity ratio (from the convolution of 6 resonances), resulting from the hyperfine splitting due to the interaction of the electronic spin with the nuclear spin of a nitrogen and a hydrogen in DMPO. The DMPO/˙OOH adduct spectrum (marked with “•”) displays six lines surging from the convolution of 12 resonances, corresponding to the hyperfine interaction of the electron spin with the nuclear spin of a nitrogen and two hydrogens in DMPO. The DMSO/˙CH3 radical contribution (marked with “+”) arises from a secondary reaction of DMSO with the ˙OH radicals produced. Additionally, three broad lines denoted with “◆” are related to the interaction of the electron spin of oxidized DMPO with the nuclear spin of nitrogen in it (DMPO/˙N) and is intrinsic to DMPO.
The net concentration of adducts formed is determined quantitatively by comparing their signals to those produced by Mn2+ impurity as described in our previous work.69 The results are presented in Fig. 6(b) and details on the calculation can be found in section 4.9.
Regarding the DMPO/˙OH adduct, we observe that a concentration of (1400 ± 200) nM is detected 10 min after the exposure to H2O2 and it increases systematically during the experiment, reaching (2300 ± 200) nM after 60 min. Contrarily, the maximum concentration of the DMSO/˙CH3 adduct is the initial one, (1000 ± 100) nM, and has a decreasing trend throughout the experiment. This is coherent with the fact that the DMSO/˙CH3 adduct is produced by a secondary reaction of DMSO with the available formed ˙OH radicals and this amount decreases with increasing DMPO/˙OH adduct formation.
Although there is DMPO/˙OOH adduct production, the concentration values are always smaller than 100 nM. This implies that V5+ in the shell of the MNPs can only produce this radical and does not play an important role in the catalytic activity of the compound. The concentration differences between DMPO/˙OH and DMPO/˙OOH adducts also lie in their respective radical formation kinetics. The formation of ˙OOH has a slower kinetic than the formation of ˙OH70 and thus limits the reaction with DMPO.
The increasing concentrations registered for the DMPO/˙OH adduct are not common for experiments with ferrite catalysts for this time span, where a saturation concentration is usually already reached at 60 min. The implications of this finding will be discussed in section 2.5, where we compare application results in our V ferrite with a similarly sized typical undoped ferrite.
2.5 The effect of V for the applications
We have evaluated the performance of the synthesised V ferrite in MFH and ROS-production applications, but in order to determine the effect of V in the structure, comparison with another MNP is needed. In fact, a similarly-sized undoped ferrite MNP is ideal for the comparison, as ROS production is greatly affected by the surface-to-volume ratio of the agents.7,8MNPs with a size of ∼30 nm were prepared through an analogous thermal decomposition synthesis, without the addition of V(acac)3. Details can be found in section 4.1. A representative TEM image of the prepared ferrite MNPs is displayed in Fig. 7(a), alongside their size distribution [Fig. 7(b)]. Their mean size is 〈d〉ferrite = 25 nm with a standard deviation of σferrite = 7 nm. Being slightly smaller than the V ferrite MNPs that we have analysed throughout this article, we expect an enhanced ROS production. The same experiments that we presented for the V ferrite were carried out with these ferrite MNPs.
 | ||
| Fig. 7 (a) TEM image of the ferrite MNPs. (b) Characteristic-size histogram. In continuous line, the lognormal fit of the distribution is shown. | ||
Regarding MFH, polyacrilamide gel phantoms at 0.1 and 0.5 wt% in ferrite MNPs were also prepared, both for dispersed and oriented configurations. Their AC hysteresis loops at 132 and 350 kHz were measured for several magnetic field intensity amplitudes. From their area and corresponding experimental frequency, the SLP was calculated and compared with the ones presented in section 2.3 for the V ferrite MNPs. The comparison is displayed in Fig. 8 for all of the 0.5 wt% gels. As the results are analogous to that for the 0.1 wt% concentration, they were included in Fig. S8† to ensure a clear and organized discussion here.
 | ||
| Fig. 8 Comparison between SLP values for ferrite and V ferrite MNPs dispersed and oriented in polyacrylamide gels, for measurements at (a) 132 and (b) 350 kHz at a MNP concentration of 0.5 wt%. | ||
We have already seen for the V ferrite that oriented samples have higher SLP values than their corresponding dispersed sample at the same concentration and under the same experimental conditions (section 2.3). The same trend was reproduced for the ferrite MNPs. However, the difference between the oriented and dispersed configuration is less pronounced for the ferrite MNPs than for V ferrite ones, which is coherent with their smaller size. As the size of the MNP decreases, their relaxation is more influenced by thermal fluctuations and this counteracts the effect of dipolar interactions on the hysteresis.25
It is also noticeable that the SLP as a function of μ0H0 saturates for the V ferrite samples in the field intensity amplitude range explored. Meanwhile, the ferrite sample needs higher amplitudes to reach its maximum (which would be the optimum) SLP value, which means that the effective energy barrier EB that an MNP needs to surpass in order to orient is bigger. This fact cannot be explained by the size difference between both samples, as EB ∝ KeffV, where V is the volume of an MNP. This implies that the V ferrite MNPs have a lower effective magnetic anisotropy than the ferrite ones,25 which corroborates the working hypothesis that, by doping the ferrite with V, the effective anisotropy can be diminished to achieve better MFH performances.
Finally, for some magnetic field amplitudes, the SLP values obtained with V ferrite are up to 1.5 times higher than the ones from the non-doped ferrite, with only a slight decrease of the effective anisotropy Keff. It is important to keep in mind that the dependence of the SLP on MNP-intrinsic parameters (such as effective anisotropy, size, saturation magnetization, dipolar interactions) and experimental conditions (AC field intensity and frequency, as well as medium viscosity) is complex. A model is needed to explain the effect of the decrease in Keff on the SLP and it is imperative to have information on MNP agglomeration to grasp interaction effects.
To measure their ROS production, ferrite MNPs were dispersed in a DMPO/DMSO solution and again six EPR spectra were taken at 10-minute intervals once H2O2 was added to the solution. The amount of adducts formed through the interaction of free radicals with DMPO and DMSO molecules was once more quantified by comparing a reference Mn2+ signal with the adduct one. The parameters obtained through the fitting of the EPR spectra corresponding to ferrite MNPs are displayed in Table S3.† The comparison between ROS produced for ferrite and V ferrite is shown in Fig. 9 for the DMPO/˙OH adduct and in Fig. S9† for the rest of the species.
 | ||
| Fig. 9 DMPO/˙OH adduct concentration as a function of time after the addition of H2O2 for ferrite and V ferrite MNPs in DMPO/DMSO. | ||
We can see that the DMPO/˙OH adduct concentration determined for the ferrite sample is initially (1100 ± 110) nM and saturates at around 1400–1500 nM at 30 min. This behaviour is typical of ferrites,69,71 that catalyse a quick ˙OH production (reflected in the DMPO/˙OH adduct formation) that suddenly becomes limited by the Fe2+ content (as the other reactant, H2O2 is in excess). This produces a saturation to a maximum value of the DMPO/˙OH adduct concentration and, when enough time is given, a diminishing of it69,71 occurs due to surpassing the half-life time of the adduct.
The difference in the DMPO/˙OH adduct concentration trends as a function of time for ferrite and V ferrite needs to be addressed as there are competing interests to take into account: the size of the MNPs and the catalyst concentration availability on their surface. Considering that the mass used in the experiments was the same for both MNPs and assuming that the catalyst density on the surface is not modified, the surface-to-volume ratio would account for an ∼1.3 increase in the production for the smaller MNPs (i.e., ferrite ones), which is not observed.
From XPS and EELS measurements, we gathered that we have a V-rich shell, which forces us to consider the different reactions taking place. Initially, we have both V3+ and V5+ but V2+ and V4+ can be obtained in small amounts as byproducts of Fenton-like reactions. We propose the reactions
| V3+ + H2O2 → V4+ + ˙OH + HO− | (3a) |
| V4+ + H2O2 → V5+ + ˙OH + HO− | (3b) |
| V4+ + H2O2 → V3+ + ˙OOH + HO+ | (3c) |
| V5+ + H2O2 → V4+ + ˙OOH + HO+ | (3d) |
Another possible route for enhanced ˙OH production is that, as Fe2+ on the surface of the MNP oxidises from its POD-like activity, an electron (e−) migration from the core of the MNP reduces it again. This happens with magnetite in the initial steps of catalysis due to its high conductivity, but as it oxidises to maghemite, conductivity decreases drastically and the electron transfer is hindered.74 We consider that this mechanism is not the greatest contribution to the enhanced ˙OH production for V ferrite because systematic studies of V incorporation in different ferrites report an impoverished electrical conductivity.75
We have already stated that the multiple oxidation states of V facilitate electron transfer to H2O2, but it can also serve to reduce Fe3+ and replenish the surface of Fe2+ as
 | (4a) |
 | (4b) |
 , yielding
, yielding| Fe3+ + V3+ → Fe2+ + V4+ ΔE = 0.433 V. | (5) |
An analogous reduction of Fe3+ is reported for Al compounds.77
To summarise, in any of the mechanisms proposed for reactions (3) and (5), V acts as an electron buffer that enhances POD-like activity by catalysing the reaction by itself or by reducing Fe3+ to recover the active Fe2+ ion.
3 Conclusions
This article presents a systematic characterisation of the structural and magnetic properties of V ferrite nanoparticles, complemented by experiments both on magnetic hyperthermia and reactive-oxygen-species production.Regarding the sample preparation, we have obtained a prominent V incorporation in the ferrite matrix of approximately 87% of the nominal value that was initially calculated for the synthesis. This allowed us to obtain a reduction in the anisotropy constant of approximately 20% compared to the value of bulk magnetite.
Regarding the composition of the prepared V ferrite nanoparticles, we have verified that there is an increased V proportion on the surface of the MNPs, providing a V-rich shell which plays an important role in catalysis applications.
Magnetic hyperthermia experiments for these V ferrite nanoparticles dispersed and oriented in polyacrylamide gels (that emulate cytosol's viscosity) show large specific loss power values of up to 1000 W g−1 for samples with 0.5 wt% in nanoparticles, a magnetic field amplitude of 65 mT and a frequency of 350 kHz. The oriented samples show larger specific loss power values in comparison with their dispersed equivalents, which highlights that for these elongated aggregates and conditions, dipolar interactions favour magnetic hyperthermia performance.
A study on the catalytic activity of the V ferrite nanoparticles through the evaluation of adduct formation provide important information on POD-like activity that is sustained through time for 1 h long experiments, reaching concentration values of up to 2300 nM for the adduct associated with the ˙OH radical.
Finally, we complemented our studies with a comparative analysis between these V ferrite and similarly-sized conventional ferrite nanoparticles. The comparison yields that the V ferrite effective anisotropy was lowered through V incorporation in the structure, enhancing the specific loss power in magnetic hyperthermia experiments. Moreover, the role of V in the catalytic activity is elucidated when the free radical production as a function of time is contrasted for both nanoparticles, serving as an electron buffer both for hydrogen peroxide in Fenton-like reactions and for the reduction of Fe3+. The performance of V ferrite nanoparticles as nanoheaters for magnetic hyperthermia and nanozymes for catalysis is promising for future combined applications.
4 Experimental
4.1 Synthesis of VxFe3−xO4 nanoparticles
The ferrite MNPs used in this work were synthesised via the thermal decomposition of Fe(III) and V(III) acetylacetonates, with trioctylamine for x = 0 (ferrite) and benzyl ether for x = 0.26 (V ferrite) as solvents. Oleic acid and oleylamine were used as surfactants.For ferrite, 6 mmol Fe(acac)3 was mixed with 18 mmol of oleic acid and 18 mmol of oleylamine in 60 ml of trioctylamine, and mechanically stirred under a nitrogen flow. The mixture was heated until reflux conditions were reached (∼350 °C) and maintained for 30 min.
For V ferrite, 2.7 mmol of Fe(acac)3 and 0.3 mmol of V(acac)3 were mixed with 9 mmol of oleic acid, 3 mmol of oleylamine, and 1.5 mmol of 1,2-octanediol in 60 ml of benzyl ether, and mechanically stirred under a nitrogen flow. The mixture was heated to 200 °C for 60 min, followed by heating until reflux conditions were reached (298 °C) and maintained for an additional 90 min.
The mixtures were then cooled to room temperature by removing the heat source. Under ambient conditions, ethanol and acetone were added, precipitating a black material, which was separated magnetically. The final product was dispersed in hexane. To modify the hydrophobic nature of the synthesised MNPs, the oleic acid coating was removed through an etching process involving several washes with methanol and hot acetone. The coating was then replaced with glucose by dispersing the uncoated MNPs with 10 times their mass in glucose in a pH = 12 ammonia solution.
4.2 TEM
The morphological and structural characterisation of the samples in this work was conducted using TEM. TEM images were acquired with a Thermo Fisher Scientific Tecnai T20 microscope equipped with a thermionic gun (LaB6 at 200 kV) and a Thermo Fisher Scientific Tecnai F30 microscope (Schottky-FEG) operating at an accelerating voltage of 200–300 kV. In the latter, selected area diffraction patterns were acquired. For all of these experiments, a drop of the MNP suspension (in either hexane or water) was deposited on a holey carbon-coated microgrid. TEM images were acquired after the solvent had fully evaporated and the sample was completely dry.Characteristic-size histograms were generated from low-magnification images, from which we gathered a significant amount of statistical data (n > 350). As faceting is not clear in these images, we approximated the area A of an MNP with that of a circle (i.e., the projection of a sphere in 2D), to obtain the MNP's characteristic size as 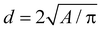 . We fitted the histogram using lognormal distribution functions.
. We fitted the histogram using lognormal distribution functions.
4.3 SEM and EDX
SEM secondary electron images were acquired with a Thermo Fisher Scientific INSPECT F microscope operating at 15 kV. The microscope is equipped with an Oxford Instruments INCA PentaFETx3 system, using which EDX spectra were recorded. The quantification software INCA Energy was used to evaluate the atomic percentages of the different elements in the sample. The software performs digital filtering and peak deconvolution to be able to identify the different peaks in the spectrum. It also carries out matrix corrections to the data to quantify. One of these corrections is the XPP correction, based on the Phi-Rho-Z method to account for the atomic number and absorption effects. Particularly, for our quantification, the software selected the V–K, O–K and Fe–L peaks.4.4 Magnetic characterisation
M(H) at room temperature and T = 5 K were conducted using a commercial vibrating sample magnetometer (Lake Shore 7400 Series VSM) and a SQUID magnetometer (MPMS5S Quantum Design), respectively. For VSM, dried powder samples were placed inside plastic capsules and for SQUID, the powder was embedded into epoxy resin at low MNP concentrations (below 0.1 wt%) to prevent dipolar interactions between MNPs.Samples for FMR measurements were prepared by embedding MNPs into epoxy resin for about 24 h under an applied field intensity of ∼800 mT to align the easy axes of the MNPs. The X-band (9.4 GHz) FMR measurements were carried out using a Bruker ELEXSYS II-E500 spectrometer at T = 300 K. The spectra were recorded by varying the sample orientation with respect to the applied field using a goniometer. This preparation and measurement protocol is analogous to the one presented in ref. 23.
4.5 STEM-EELS
HRSTEM images were acquired using a high-angle annular dark field detector (Fischione) on a CS-probe-corrected Titan microscope (Thermo Fisher Scientific) operating at 80 kV. For EELS and energy loss near edge structure (ELNES) experiments, the microscope was equipped with a Gatan Energy Filter Tridiem 866 ERS and used in conjunction with a monochromator. The experimental conditions were as follows: detector DF4, camera length 48 mm, filter entrance aperture 2.5 mm (acceptance angle 21 mrad), dispersion 0.15 eV per pixel, C3 30 mm, and spot size 16. EELS data were analyzed using custom Matlab software that applied power-law background subtraction and principal component analysis (PCA) for denoising. Quantification was performed by integrating a 30 eV-wide window and using theoretical scattering cross-sections.4.6 XPS
XPS spectra of the powdered materials were obtained using an AXIS Supra surface analysis instrument from Kratos Analytical. Due to the magnetic properties of the samples, the spectra were acquired with an electrostatic lens and without charge neutralization. For individual peak regions, a pass energy of 20 eV was used, while survey spectra were recorded at a pass energy of 160 eV. Peak analysis was performed using CasaXPS software. After subtracting the Shirley background, the peaks were fitted using a weighted sum of Lorentzian and Gaussian components.4.7 Polyacrylamide gel preparation
The gels were prepared as described in detail in ref. 60. A solution of acrylamide and bisacrylamide (30/0.8% w/v) was prepared, and a 24 μl aliquot was mixed with 25 μl of 0.375 M Tris-HCl buffer solution at pH = 8.8 for each gel. Then, 44 μl of Milli-Q water containing 0.1 or 0.5 mg of dispersed glucose-coated MNPs was added for 0.1 wt% or 0.5 wt% gels, respectively. To this mixture, 7 μl of ammonium persulfate (APS) was added as a free radical initiator, along with 6 μl of N,N,N′,N′-tetramethylethylenediamine (TEMED) to stabilize the polymerization chain reaction. This process yields ∼100 μl of polyacrylamide gel.For gels with oriented MNPs, a mixture of acrylamide, bisacrylamide, Tris-HCl buffer, and Milli-Q water with MNPs was placed into the sample holder capsules and positioned inside a coil. An AC field with an amplitude of 40 mT and a frequency of 350 kHz was applied for 2 min before adding the polymerizers (APS and TEMED), which fixed the elongated MNP arrangements.
4.8 AC magnetometry
AC magnetometry characterisation was performed at two frequencies (132 and 350 kHz) with an applied magnetic field intensity of up to 90 mT, using two different sample configurations: dispersed and oriented at 0.1 wt% and 0.5 wt% MNP concentrations. The measurements were conducted using a lab-built magnetometer capable of generating high magnetic fields to saturate the samples. This device operates over a wide frequency range (100 kHz ≤ f ≤ 1 MHz) with field intensities of 90 mT at the lower frequency end and 35 mT at the higher frequency end. Further details on the setup can be found in ref. 65.SLP was determined from the area enclosed by the hysteresis loop through
 | (6) |
4.9 Catalytic activity
The generation of DMPO and DMSO adducts was determined at room temperature using a Bruker ELEXSYS II-E500 EPR spectrometer with an X-band resonant cavity (9.4 GHz). The reaction mixtures for the EPR experiments were prepared by dispersing 120 μg of nanoparticles in 200 μl of acetate buffer solution (pH = 5) and 50 μl of DMPO/DMSO solution. The reaction was initiated by adding 10 μl of 30% H2O2 (0.49 M).To quantify the amounts of DMPO adducts, the EPR spectrum of each solution in a Quartz tube was recorded simultaneously with a MgO crystal pattern doped with a known concentration of Mn2+ attached to the tube. All spectra were fitted using EasySpin software78 following the same procedure: the baseline of each spectrum was considered cubic, the spectra computed with the “pepper” function and the resonance lines adjusted using the Nelder-Mead simplex algorithm using the reported hyperfine parameters of the identified components as seed.79 The concentrations of DMPO/DMSO adducts were obtained by comparing the EPR-fitted spectrum intensities of each species Irad with the intensity of the Mn2+ reference Iref through80
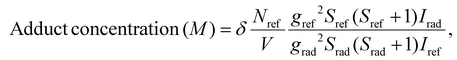 | (7) |
Author contributions
T. E. Torres: conceptualization, data curation, formal analysis, investigation, methodology, funding acquisition, writing the original draft, and writing – review & editing. D. P. Valdés: conceptualization, data curation, formal analysis, investigation, methodology, writing original draft, and writing – review & editing. S. Hettler: data curation, software, formal analysis, and writing – review & editing. J. M. Nuñez: data curation, formal analysis, and and writing – review & editing. I. Rodrigo: resources, investigation, and writing – review & editing. I. Orue: resources, investigation, and validation. J. A. García: resources, investigation, and validation. F. Plazaola: resources, investigation, validation, funding acquisition, and writing – review & editing. R. D. Zysler: resources, investigation, and validation. E. Lima Jr.: resources, investigation, formal analysis, validation, and writing original draft. M. H. Aguirre: resources, investigation, validation, and funding acquisition. G. F. Goya: resources, investigation, validation, and funding acquisition. R. Arenal: resources, investigation, validation, funding acquisition, supervision, and writing – review & editing.Data availability
Data for this article are available at Zenodo at https://doi.org/10.5281/zenodo.13913025.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Guillermo Antorrena for his valuable help and advice on the XPS analysis. T. E. T. acknowledges funding from the European Union's Horizon Europe Research and Innovation program under the Marie Sklodowska-Curie grant agreement no. 101068591. D. P. V. and J. M. N. thank CONICET-Argentina for their doctoral fellowships. The authors acknowledge funding from projects H2020-MSCA-RISE-2021 ULTIMATE-I project no. 101007825 and H2020-MSCA-RISE-2020 101007629-NESTOR and Basque Government grant no. IT-1005-16. G. F. G. acknowledges the Spanish MICIU PID2019-106947RB-C21/AEI/10.13039/501100011033. R. A. acknowledges the Spanish MICIU (PID2023-151080NB-I00/AEI/10.13039/501100011033 and CEX2023-001286-S MICIU/AEI/10.13039/501100011033), the U. Zaragoza (14446-UZ2023-CIE-02) and the DGA project E13-23R.TEM and XPS studies were conducted at the Laboratorio de Microscopias Avanzadas (LMA), U. Zaragoza, Spain.References
- L. Gao, J. Zhuang, L. Nie, J. Zhang, Y. Zhang, N. Gu, T. Wang, J. Feng, D. Yang, S. Perrett and X. Yan, Nat. Nanotechnol., 2007, 2, 577–583 CrossRef CAS PubMed.
- A. D. Bokare and W. Choi, J. Hazard. Mater., 2014, 275, 121–135 CrossRef CAS PubMed.
- C. Dai, C. Wang, R. Hu, H. Lin, Z. Liu, L. Yu, Y. Chen and B. Zhang, Biomaterials, 2019, 219, 119374 CrossRef CAS PubMed.
- S. Dong, Y. Chen, L. Yu, K. Lin and X. Wang, Adv. Funct. Mater., 2019, 30, 1907071 CrossRef.
- Q. Dai, B. Cao, S. Zhao and A. Zhang, Bioengineering, 2022, 9, 474 CrossRef CAS PubMed.
- Nanozymology: Connecting Biology and Nanotechnology, ed. X. Yan, Springer Singapore, 2020 Search PubMed.
- M. Pozzi, S. Jonak Dutta, M. Kuntze, J. Bading, J. S. Rüßbült, C. Fabig, M. Langfeldt, F. Schulz, P. Horcajada and W. J. Parak, J. Chem. Educ., 2024, 101, 3146–3155 CrossRef CAS PubMed.
- P. P. Fu, Q. Xia, H.-M. Hwang, P. C. Ray and H. Yu, J. Food Drug Anal., 2014, 22, 64–75 CAS.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921 CrossRef.
- L. Néel, Ann. Géophys., 1949, 5, 99 Search PubMed.
- W. T. Coffey, D. S. F. Crothers, J. L. Dormann, L. J. Geoghegan, Y. P. Kalmykov, J. T. Waldron and A. W. Wickstead, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15951–15965 CrossRef CAS PubMed.
- F. Bødker, S. Mørup and S. Linderoth, Phys. Rev. Lett., 1994, 72, 282 CrossRef PubMed.
- R. Yanes, O. Chubykalo-Fesenko, H. Kachkachi, D. A. Garanin, R. Evans and R. W. Chantrell, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064416 CrossRef.
- D. Gandia, L. Gandarias, L. Marcano, I. Orue, D. Gil-Cartón, J. Alonso, A. García-Arribas, A. Muela and M. L. Fdez-Gubieda, Nanoscale, 2020, 12, 16081–16090 RSC.
- D. Bobo, K. J. Robinson, J. Islam, K. J. Thurecht and S. R. Corrie, Pharm. Res., 2016, 33, 2373–2387 CrossRef CAS PubMed.
- P. Clerc, P. Jeanjean, N. Hallali, M. Gougeon, B. Pipy, J. Carrey, D. Fourmy and V. Gigoux, J. Controlled Release, 2018, 270, 120–134 CrossRef CAS.
- S. Bae, S. W. Lee and Y. Takemura, Appl. Phys. Lett., 2006, 89, 252503 CrossRef.
- M. Menelaou, K. Georgoula, K. Simeonidis and C. Dendrinou-Samara, Dalton Trans., 2014, 43, 3626 RSC.
- P. T. Yin, B. P. Shah and K. Lee, Small, 2014, 10, 4106–4112 CrossRef CAS PubMed.
- A. Apostolov, I. Apostolova and J. Wesselinowa, Eur. Phys. J. B, 2019, 92, 58 CrossRef.
- I. Castellanos-Rubio, O. Arriortua, L. Marcano, I. Rodrigo, D. Iglesias-Rojas, A. Barón, A. Olazagoitia-Garmendia, L. Olivi, F. Plazaola, M. L. Fdez-Gubieda, A. Castellanos-Rubio, J. S. Garitaonandia, I. Orue and M. Insausti, Chem. Mater., 2021, 33, 3139–3154 CAS.
- E. Mazarío, J. Sánchez-Marcos, N. Menéndez, M. Cañete, A. Mayoral, S. Rivera-Fernández, J. M. de la Fuente and P. Herrasti, J. Phys. Chem. C, 2015, 119, 6828–6834 Search PubMed.
- B. Sanz, R. Cabreira-Gomes, T. E. Torres, D. P. Valdés, E. Lima, E. De Biasi, R. D. Zysler, M. R. Ibarra and G. F. Goya, ACS Appl. Nano Mater., 2020, 3, 8719–8731 CrossRef CAS.
- D. Serantes, K. Simeonidis, M. Angelakeris, O. Chubykalo-Fesenko, M. Marciello, M. d. P. Morales, D. Baldomir and C. Martinez-Boubeta, J. Phys. Chem. C, 2014, 118, 5927–5934 CAS.
- D. P. Valdés, E. Lima, R. D. Zysler, G. F. Goya and E. De Biasi, Phys. Rev. Appl., 2021, 15, 044005 Search PubMed.
- Y. Zhao, L. Ye, H. Liu, Q. Xia, Y. Zhang, X. Yang and K. Wang, J. Inorg. Biochem., 2010, 104, 371–378 Search PubMed.
- S. Treviño, A. Díaz, E. Sánchez-Lara, B. L. Sanchez-Gaytan, J. M. Perez-Aguilar and E. González-Vergara, Biol. Trace Elem. Res., 2018, 188, 68–98 Search PubMed.
- Y. Zhang, X.-D. Yang, K. Wang and D. C. Crans, J. Inorg. Biochem., 2006, 100, 80–87 CrossRef CAS PubMed.
- X.-G. Yang, X.-D. Yang, L. Yuan, K. Wang and D. C. Crans, Pharm. Res., 2004, 21, 1026–1033 Search PubMed.
- M. A. M. Capella, L. S. Capella, R. C. Valente, M. Gefé and A. G. Lopes, Cell Biol. Toxicol., 2007, 23, 413–420 CrossRef CAS PubMed.
- G. R. Willsky, L.-H. Chi, Y. Liang, D. P. Gaile, Z. Hu and D. C. Crans, Physiol. Genomics, 2006, 26, 192–201 Search PubMed.
- C. Huang, M. Ding, J. Li, S. S. Leonard, Y. Rojanasakul, V. Castranova, V. Vallyathan, G. Ju and X. Shi, J. Biol. Chem., 2001, 276, 22397–22403 CrossRef CAS PubMed.
- D. Hu, D. Li, X. Liu, Z. Zhou, J. Tang and Y. Shen, Biomed. Mater., 2020, 16, 014101 CrossRef PubMed.
- B. Sanz-Sagué, A. Sáenz-Hernández, A. C. Moreno Maldonado, J. A. Fuentes-García, J. M. Nuñez, B. Zegura, A. Stern, K. Kolosa, I. Rozman, T. E. Torres and G. F. Goya, Chem.-Biol. Interact., 2024, 394, 110977 CrossRef PubMed.
- J.-P. Fortin, F. Gazeau and C. Wilhelm, Eur. Biophys. J., 2007, 37, 223–228 CrossRef PubMed.
- S.-h. Noh, W. Na, J.-t. Jang, J.-H. Lee, E. J. Lee, S. H. Moon, Y. Lim, J.-S. Shin and J. Cheon, Nano Lett., 2012, 12, 3716–3721 CrossRef CAS PubMed.
- M. Kosmulski, J. Colloid Interface Sci., 2004, 275, 214–224 CrossRef CAS PubMed.
- M. Kosmulski, Adv. Colloid Interface Sci., 2018, 251, 115–138 CrossRef CAS PubMed.
- M. V. Kovalenko, M. I. Bodnarchuk, R. T. Lechner, G. Hesser, F. Schäffler and W. Heiss, J. Am. Chem. Soc., 2007, 129, 6352–6353 CrossRef CAS PubMed.
- D. Kim, N. Lee, M. Park, B. H. Kim, K. An and T. Hyeon, J. Am. Chem. Soc., 2008, 131, 454–455 CrossRef PubMed.
- C. Moya, X. Batlle and A. Labarta, Phys. Chem. Chem. Phys., 2015, 17, 27373–27379 RSC.
- A. G. Roca, L. Gutiérrez, H. Gavilán, M. E. Fortes Brollo, S. Veintemillas-Verdaguer and M. d. P. Morales, Adv. Drug Delivery Rev., 2019, 138, 68–104 CrossRef CAS PubMed.
- B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, Wiley, 2008 Search PubMed.
- K. L. Lopez Maldonado, P. de la Presa, M. A. de la Rubia, P. Crespo, J. de Frutos, A. Hernando, J. A. Matutes Aquino and J. T. Elizalde Galindo, J. Nanopart. Res., 2014, 16, 2482 Search PubMed.
- G. Datt, M. Sen Bishwas, M. Manivel Raja and A. C. Abhyankar, Nanoscale, 2016, 8, 5200–5213 RSC.
- H.-M. Song, J. I. Zink and N. M. Khashab, Phys. Chem. Chem. Phys., 2015, 17, 18825–18833 RSC.
- E. De Biasi, E. Lima, C. Ramos, A. Butera and R. Zysler, J. Magn. Magn. Mater., 2013, 326, 138–146 Search PubMed.
- Y. L. Raikher and V. I. Stepanov, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6250–6259 Search PubMed.
- E. de Biasi, C. Ramos and R. Zysler, J. Magn. Magn. Mater., 2003, 262, 235–241 CrossRef CAS.
- D. Faílde, V. Ocampo-Zalvide, D. Serantes and O. Iglesias, Nanoscale, 2024, 16, 14319–14329 RSC.
- T. Fujii, F. M. F. de Groot, G. A. Sawatzky, F. C. Voogt, T. Hibma and K. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3195–3202 Search PubMed.
- T. Yamashita and P. Hayes, Appl. Surf. Sci., 2008, 254, 2441–2449 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. Lau, A. R. Gerson and R. S. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CAS.
- M. C. Biesinger, L. W. Lau, A. R. Gerson and R. S. Smart, Appl. Surf. Sci., 2010, 257, 887–898 Search PubMed.
- S.-Y. Chen, A. Gloter, A. Zobelli, L. Wang, C.-H. Chen and C. Colliex, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104103 Search PubMed.
- D. Su and R. Schlögl, Catal. Lett., 2002, 83, 115–119 CAS.
- A. Gloter, V. Serin, C. Turquat, C. Cesari, C. Leroux and G. Nihoul, Eur. Phys. J. B, 2001, 22, 179–186 CAS.
- H. Tan, J. Verbeeck, A. Abakumov and G. Van Tendeloo, Ultramicroscopy, 2012, 116, 24–33 CAS.
- M. K. Kuimova, S. W. Botchway, A. W. Parker, M. Balaz, H. A. Collins, H. L. Anderson, K. Suhling and P. R. Ogilby, Nat. Chem., 2009, 1, 69–73 Search PubMed.
- D. P. Valdés, T. E. Torres, A. C. Moreno Maldonado, G. Urretavizcaya, M. S. Nadal, M. Vasquez Mansilla, R. D. Zysler, G. F. Goya, E. De Biasi and E. Lima Jr., Phys. Rev. Appl., 2023, 19, 014042 Search PubMed.
- E. Myrovali, N. Maniotis, A. Makridis, A. Terzopoulou, V. Ntomprougkidis, K. Simeonidis, D. Sakellari, O. Kalogirou, T. Samaras, R. Salikhov, M. Spasova, M. Farle, U. Wiedwald and M. Angelakeris, Sci. Rep., 2016, 6, 37934 Search PubMed.
- L. C. Branquinho, M. S. Carrião, A. S. Costa, N. Zufelato, M. H. Sousa, R. Miotto, R. Ivkov and A. F. Bakuzis, Sci. Rep., 2013, 3, 2887 Search PubMed.
- D. P. Valdés, E. Lima, R. D. Zysler and E. De Biasi, Phys. Rev. Appl., 2020, 14, 014023 Search PubMed.
- Z. Nemati, J. Alonso, I. Rodrigo, R. Das, E. Garaio, J.-A. García, I. Orue, M.-H. Phan and H. Srikanth, J. Phys. Chem. C, 2018, 122, 2367–2381 CAS.
- I. Rodrigo, I. Castellanos-Rubio, E. Garaio, O. K. Arriortua, M. Insausti, I. n. Orue, J. A. García and F. Plazaola, Int. J. Hyperthermia, 2020, 37, 976–991 Search PubMed.
- W. J. Atkinson, I. A. Brezovich and D. P. Chakraborty, IEEE Trans. Biomed. Eng., 1984, BME-31, 70–75 Search PubMed.
- B. Herrero de la Parte, I. Rodrigo, J. Gutiérrez-Basoa, S. Iturrizaga Correcher, C. Mar Medina, J. J. Echevarría-Uraga, J. A. Garcia, F. Plazaola and I. García-Alonso, Cancers, 2022, 14, 3084 CAS.
- I. Castellanos-Rubio, I. Rodrigo, A. Olazagoitia-Garmendia, O. Arriortua, I. Gil de Muro, J. S. Garitaonandia, J. R. Bilbao, M. L. Fdez-Gubieda, F. Plazaola, I. Orue, A. Castellanos-Rubio and M. Insausti, ACS Appl. Mater. Interfaces, 2020, 12, 27917–27929 Search PubMed.
- A. C. Moreno Maldonado, E. L. Winkler, M. Raineri, A. Toro Córdova, L. M. Rodríguez, H. E. Troiani, M. L. Mojica Pisciotti, M. V. Mansilla, D. Tobia, M. S. Nadal, T. E. Torres, E. De Biasi, C. A. Ramos, G. F. Goya, R. D. Zysler and E. Lima, J. Phys. Chem. C, 2019, 123, 20617–20627 CAS.
- K. Saito, M. Takahashi, M. Kamibayashi, T. Ozawa and M. Kohno, Free Radical Res., 2009, 43, 668–676 Search PubMed.
- N. Nuñez, E. Lima, M. Vásquez Mansilla, G. F. Goya, A. Gallo-Cordova, M. d. P. Morales and E. L. Winkler, Appl. Surf. Sci., 2024, 656, 159655 Search PubMed.
- G. Fang, Y. Deng, M. Huang, D. D. Dionysiou, C. Liu and D. Zhou, Environ. Sci. Technol., 2018, 52, 2178–2185 CAS.
- L. Al-Alharbi, A. Alrooqi, M. M. Ibrahim, I. M. El-Mehasseb, T. Kumeria, A. Gobouri, T. Altalhi and H. S. El-Sheshtawy, J. Environ. Chem. Eng., 2021, 9, 105044 CAS.
- H. Dong, W. Du, J. Dong, R. Che, F. Kong, W. Cheng, M. Ma, N. Gu and Y. Zhang, Nat. Commun., 2022, 13, 5365 CAS.
- T. Zeeshan, S. Waseem, Z. Ejaz, Z. Kayani and T. E. Kuntsevich, Inorg. Chem. Commun., 2024, 162, 111687 Search PubMed.
- K. Beyer, J. grosse Austing, B. Satola, T. Di Nardo, M. Zobel and C. Agert, ChemSusChem, 2020, 13, 2066–2071 Search PubMed.
- F. Ruipérez, J. Mujika, J. Ugalde, C. Exley and X. Lopez, J. Inorg. Biochem., 2012, 117, 118–123 CrossRef PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- National Institute of Environmental Health Sciences – NIEHS, Spin Trap Database, https://tools.niehs.nih.gov/stdb/index.cfm, [online; accessed 14-August-2024].
- D. Tobia, E. Winkler, J. Milano, A. Butera, R. Kempf, L. Bianchi and F. Kaufmann, J. Nucl. Mater., 2014, 451, 207–210 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04219k |
| This journal is © The Royal Society of Chemistry 2025 |





