Open Access Article
Open Access ArticleConformation driven conductance modulation in single-stranded RNA (ssRNA)†
Arpan
De
 *a,
Arindam K.
Das
*a,
Arindam K.
Das
 b and
M. P.
Anantram
b and
M. P.
Anantram
 a
a
aDepartment of Electrical and Computer Engineering, University of Washington, Seattle, WA 98195, USA. E-mail: arpan99@uw.edu
bDepartment of Computer Science and Electrical Engineering, Eastern Washington University, Cheney, WA 99004, USA
First published on 4th July 2025
Abstract
The structural attributes of RNA, especially co-transcriptional folding, have enabled RNA origami to construct complex 3D architectures, serving as a platform to build RNA-based nanodevices. However, the potential of RNA in molecular electronics is largely unexplored, mainly due to its inherent conformational fluctuations. Although this variability poses challenges for a precise understanding of the conductance properties of RNA, it also offers opportunities for tuning RNA-based molecular devices by exploiting their dynamic nature. Accordingly, our objectives in this paper are twofold: (i) how do conformational fluctuations impact the charge transport properties of single stranded RNA (ssRNA), and (ii) how can these fluctuations be controlled? Toward that end, we first established a benchmark for ssRNA instability compared to double stranded RNA (dsRNA) based on molecular dynamics. Subsequently, we explore quantum transport across 123 distinct conformations, which show that the average conductance of ssRNA is 1.7 × 10−3 G0, but with a high standard deviation of around 5.2 × 10−3G0. We demonstrate that the conductance of ssRNA is influenced primarily by backbone bending and nucleotide positioning. Specifically, while backbone bending tends to result in higher conductance at reduced end-to-end phosphorus distances, nucleotide positioning introduces significant stochasticity. To mitigate this variability, we also demonstrate that increasing the salt concentration can stabilize ssRNA, presenting a viable strategy for minimizing conductance fluctuations. Our findings reveal that if ssRNA conductance can be switched between folded and unfolded states, it can offer two distinct conductance modes. We anticipate the programmability of ssRNA folding and durability, coupled with its conductivity, can be leveraged for advancing molecular electronics.
New conceptsAdvancement in molecular electronics relies on a precise understanding of charge transport at the nanoscale level. While DNA has been highly explored as a syn-biological electronic material, RNA remains largely unexplored despite its versatility in nanotechnology. This work provides the first comprehensive analysis of inherent conformation-driven conductance stochasticity in single-stranded RNA (ssRNA). We demonstrate that ssRNA conductance states are highly sensitive to conformational changes, particularly backbone bending and nucleotide arrangement. Importantly, we show that these conformational fluctuations can be regulated through environmental conditions such as salt concentration, offering a practical approach to control conductance variability. Our findings suggest that ssRNA programmable folding capability, combined with its variable conductance states, could enable the development of novel molecular switches and memory devices. |
Introduction
The folding and unfolding of RNA transform a simple nucleotide chain into versatile 3D molecular complexes, playing a pivotal role in numerous biological functions.1–4 For instance, RNA catalyzes peptide bond formation,5 regulates translation,6 assists in replication, and supports both protein synthesis7 and viral propagation.8 This intricate involvement of RNA complexes in modulating critical biological processes has motivated researchers to investigate its structural attributes for decades. Since 1999, a major research thrust has been prediction of secondary and tertiary structures of RNA sequences. Recently, Zhang et al. have provided a comprehensive review of state-of-the-art experimental and computational techniques for predicting RNA folding patterns.9 Other excellent discussions on different methods used to solve RNA folding problems can be found in Seetin et al.10 and Gardener et al.11 From these studies, it can be inferred that secondary structures are largely governed by Watson–Crick (WC) and wobble base pairing, but transitions to tertiary structures are more complicated. Although these computational studies shed light on the folding patterns of RNA, they do not provide any insight into the underlying charge transport properties, which is crucial for the design of next-generation nanotechnology. In this article, we aim to evaluate the impact of folding on RNA charge transport to assess the performance of RNA-based nano-devices.RNA origami has emerged as a promising method for creating nanostructures through co-transcriptional folding of RNAs.12 It enables the design of multitudes of complex RNA architectures for applications in medicine and synthetic biology. In 2018, Hoiberg et al. created an RNA octahedron via RNA origami for gene knockdown in cells.13 Additionally, Krissanaprasit et al. utilized scaffold RNAs to bind thrombin, thereby improving anticoagulant activities.14 Furthermore, Nguyen et al. demonstrated the regulation of gene expression with protein-binding RNA scaffolds.15 A pioneering study by Han et al. successfully constructed diverse multikilobase single-stranded (ss) nanostructures including a 6337-nt RNA.16 This study highlighted that self-folding of ssRNA can enable building of complex nanostructures without knots. Following up, Vallina et al. developed a multi-functional RNA origami robot, Traptamer, that can mechanically trap a fluorescent aptamer, reversibly control its fluorescence, and operate as a logic gate.17 These studies elucidate the good programmability of single-stranded RNA scaffolds. The structural advantages of ssRNAs hold great potential for applications beyond biology, for example in building electronic devices. To advance this, it is essential to understand the underlying charge transport properties of RNA. Unlike DNA, RNA charge transport has not been explored extensively. Single-molecule conductance measurements have revealed that RNAs exhibit comparable, if not higher, conductance than DNAs.18–20 Recently, Chandra et al. reported the conductance of single- and double-stranded RNAs to be around 0.001G0, where G0 is the quantum of conductance.21 However, conductance in RNA is characterized by high variability, which can be attributed to factors such as conformational changes and environmental conditions.20 This fluctuation creates challenges but also opens possibilities for optimizing RNA-based molecular devices by harnessing their natural flexibility.
In this manuscript, we have focused on unraveling the implications of structural fluctuations on short single-stranded RNA (ssRNA) conductance through rigorous charge transport analysis. First, we present a comparative statistical analysis of structural variability between single- and double-stranded RNA with molecular dynamic simulations in Fig. 1. Second, we perform charge transport calculations on 123 conformations with different backbone and nucleotide configurations, and these results are illustrated in Fig. 2–5. Finally, we show how increasing the salt concentration can effectively harness the conformational fluctuations of ssRNA in Fig. 6, offering a viable solution for realizing RNA-based electronics.
 | ||
Fig. 1 Molecular dynamics results: ssRNA vs. dsRNA. (a) 1D RMSD vs. time; dotted black lines indicate the mean RMSDs. (b) 2D RMSD vs. time. (c) End-to-end phosphorus distances vs. time. (d) Coefficient of variation (σ/μ) for the seven backbone dihedral angles. (e) Hydrogen bond heatmaps between bases of ssRNA/base-pairs of dsRNA. In (c), the dotted lines are drawn to show that ssRNA mostly fluctuates between folded and unfolded configurations, while dsRNA is comparatively stable. In (e), the color bars (in units of Å) represent average hydrogen bonds over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations. An enlarged version of the heatmaps with corresponding average H-bond numbers are provided in Fig. S5(i) and (ii) (ESI†) for ssRNA and dsRNA respectively. 000 conformations. An enlarged version of the heatmaps with corresponding average H-bond numbers are provided in Fig. S5(i) and (ii) (ESI†) for ssRNA and dsRNA respectively. | ||
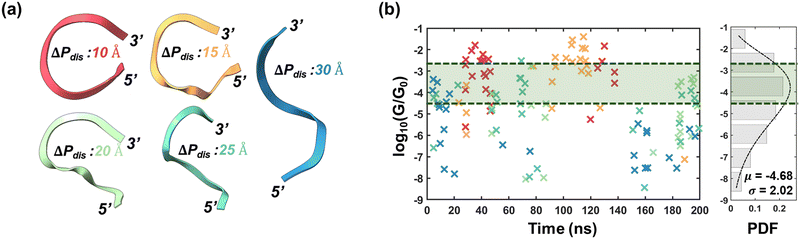 | ||
| Fig. 2 Conductance stochasticity of ssRNA. (a) Representative backbone orientations of ssRNA for nominal ΔPdis values 10, 15, 20, 25 & 30 Å. (b) Left: Conductance as a function of time. The markers (indicated by ×) are color-coordinated to panel (a). Right: Probability distribution of all the log of conductance values obtained from 123 conformations (bar plots). The dotted line is the fitted curve with gamma distribution (α = 5.3424, β = 0.8767). The green shaded regions enclosed within dotted envelopes represent the conductance dispersion limits of dsRNA of this work. The conductance values for dsRNA have been provided in Table S1 (ESI†). | ||
Molecular dynamics results: ssRNA vs. dsRNA
We have selected the 10-base ssRNA sequence 5′-GGGGGCGGGG-3′ (5′-G5CG4-3′) to investigate conductance variability induced by folding and unfolding phenomena. For reference, we have also considered a 10-base pair dsRNA structure comprising the complementary sequence of the ssRNA, 5′-G5CG4-3′/3′-C5GC4-5′. Molecular dynamics (MD) simulations were conducted for 200 ns on both structures (details in Methods), with frames captured every 2 ps, yielding a total of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations. A comparative evaluation of the structural stability of ssRNA and dsRNA is presented in Fig. 1. The root mean square deviations (1D-RMSD), calculated relative to the initial frame, are shown in Fig. 1(a), where it is evident that dsRNA exhibits greater structural stability than ssRNA, with an average RMSD of 1.95 ± 0.52 Å, compared to 5.60 ± 1.15 Å for ssRNA. This trend is further corroborated by the 2D-RMSD plots shown in Fig. 1(b). While 1D RMSD provides a reasonable estimate for structural stability, the 2D-RMSD heatmaps highlight the presence/absence of multiple low RMSD regions or stable conformation states. For ssRNA (Fig. 1(b), left), we identify six distinct patches of low RMSD (<5 Å). Among these, the biggest patch is approximately between 85–150 ns. On the contrary, the 2D-RMSD heatmap of dsRNA (Fig. 1(b), right) has a maximum value of 5.75 Å, significantly lower than the 13.32 Å observed for ssRNA. This results in the absence of low RMSD “patches” in dsRNA, underscoring its “stability throughout the MD trajectory.” To gain deeper insight into the conformational dynamics of both ssRNA and dsRNA, we employed the end-to-end phosphorus distance (ΔPdis), defined as the distance between 1st and 9th phosphorus atoms, as a key metric for analysis. The value of ΔPdis is directly proportional to the bending of the backbone. From Fig. 1(c), we observe that in the case of ssRNA, ΔPdis varies considerably (unlike dsRNA, shown in the bottom panel of Fig. 1(c)), spanning a range from 6.40 to 47.18 Å, with an average value of 21 Å. We used this average value to classify the conformations into folded (ΔPdis < 21 Å) and unfolded (ΔPdis ≥ 21 Å) states, yielding a folding probability of 47.88% (i.e., 47
000 conformations. A comparative evaluation of the structural stability of ssRNA and dsRNA is presented in Fig. 1. The root mean square deviations (1D-RMSD), calculated relative to the initial frame, are shown in Fig. 1(a), where it is evident that dsRNA exhibits greater structural stability than ssRNA, with an average RMSD of 1.95 ± 0.52 Å, compared to 5.60 ± 1.15 Å for ssRNA. This trend is further corroborated by the 2D-RMSD plots shown in Fig. 1(b). While 1D RMSD provides a reasonable estimate for structural stability, the 2D-RMSD heatmaps highlight the presence/absence of multiple low RMSD regions or stable conformation states. For ssRNA (Fig. 1(b), left), we identify six distinct patches of low RMSD (<5 Å). Among these, the biggest patch is approximately between 85–150 ns. On the contrary, the 2D-RMSD heatmap of dsRNA (Fig. 1(b), right) has a maximum value of 5.75 Å, significantly lower than the 13.32 Å observed for ssRNA. This results in the absence of low RMSD “patches” in dsRNA, underscoring its “stability throughout the MD trajectory.” To gain deeper insight into the conformational dynamics of both ssRNA and dsRNA, we employed the end-to-end phosphorus distance (ΔPdis), defined as the distance between 1st and 9th phosphorus atoms, as a key metric for analysis. The value of ΔPdis is directly proportional to the bending of the backbone. From Fig. 1(c), we observe that in the case of ssRNA, ΔPdis varies considerably (unlike dsRNA, shown in the bottom panel of Fig. 1(c)), spanning a range from 6.40 to 47.18 Å, with an average value of 21 Å. We used this average value to classify the conformations into folded (ΔPdis < 21 Å) and unfolded (ΔPdis ≥ 21 Å) states, yielding a folding probability of 47.88% (i.e., 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 out of 100
880 out of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations have ΔPdis < 21 Å). When correlating ΔPdis values with low RMSD patches in the 2D-RMSD heatmap, we observe that the ssRNA sequence exhibits stable configurations in both folded and unfolded states. For instance, for the low RMSD patches between ≈20–40 ns and ≈85–150 ns in (Fig. 1(b), left), the ssRNA sequence has a ΔPdis value of less than 21 Å. For other low RMSD patches, ΔPdis is relatively higher, suggesting shuffling between the folded and unfolded states. In contrast, dsRNA exhibits a tighter distribution of ΔPdis (see Fig. 1(c), bottom), ranging from 21.72 to 36.48 Å with a mean value of 28.4 Å which is consistent with the trends in RMSD plots in Fig. 1(a) and (b). Note that for dsRNA, we obtained two distributions of ΔPdis for 5′-3′ and 3′-5′ strands, which are very similar to each other (see Fig. S1, ESI†); in (Fig. 1(c), bottom), we show the mean ΔPdis over both strands. We also analyzed the distributions of the seven backbone dihedral angles to further characterize the structural fluctuations of ssRNA and dsRNA, as shown in Fig. 1(d). It is evident that the coefficients of variation (CV) of all dihedral angles, derived from 100
000 conformations have ΔPdis < 21 Å). When correlating ΔPdis values with low RMSD patches in the 2D-RMSD heatmap, we observe that the ssRNA sequence exhibits stable configurations in both folded and unfolded states. For instance, for the low RMSD patches between ≈20–40 ns and ≈85–150 ns in (Fig. 1(b), left), the ssRNA sequence has a ΔPdis value of less than 21 Å. For other low RMSD patches, ΔPdis is relatively higher, suggesting shuffling between the folded and unfolded states. In contrast, dsRNA exhibits a tighter distribution of ΔPdis (see Fig. 1(c), bottom), ranging from 21.72 to 36.48 Å with a mean value of 28.4 Å which is consistent with the trends in RMSD plots in Fig. 1(a) and (b). Note that for dsRNA, we obtained two distributions of ΔPdis for 5′-3′ and 3′-5′ strands, which are very similar to each other (see Fig. S1, ESI†); in (Fig. 1(c), bottom), we show the mean ΔPdis over both strands. We also analyzed the distributions of the seven backbone dihedral angles to further characterize the structural fluctuations of ssRNA and dsRNA, as shown in Fig. 1(d). It is evident that the coefficients of variation (CV) of all dihedral angles, derived from 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations, are considerably higher for ssRNA than dsRNA, which is consistent with our observations regarding RMSDs and ΔPdis values shown in Fig. 1(a)–(c). In particular, the CV of the dihedral angle between bases and backbone (χ) for ssRNA is 51.6% higher compared to dsRNA.
000 conformations, are considerably higher for ssRNA than dsRNA, which is consistent with our observations regarding RMSDs and ΔPdis values shown in Fig. 1(a)–(c). In particular, the CV of the dihedral angle between bases and backbone (χ) for ssRNA is 51.6% higher compared to dsRNA.
To further probe the backbone dihedral distributions, we have presented the residue-wise time evolutions of backbone dihedrals for ssRNA and dsRNA in Fig. S2 and S3 (ESI†) respectively. For dsRNA, the dihedrals are extremely stable with minimal fluctuations (Fig. S3, ESI†), consistent with the 2D RMSD heatmap in Fig. 1(b). In contrast, ssRNA demonstrates pronounced fluctuations in its backbone dihedrals (Fig. S2, ESI†). Specifically, the 3′-end residues’ dihedrals (primarily α, δ, ζ) show significant perturbation between ≈20–200 ns. We also observe minor variations in the interior residue dihedrals from ≈ 80 ns, coinciding with the onset of ssRNA folding (ΔPdis < 21 Å, Fig. 1(c), top). We attribute these dihedrals’ perturbations of the interior bases to the folding of the structure, which we hypothesize is triggered by fluttering of the 3′-end residues. A comparative analysis of probability densities for all dihedral angles is depicted in Fig. S4 (ESI†). In general, we observe that the pdf's of ssRNA are multimodal, in contrast to unimodal for dsRNA (with the exception of β). We also observe that while the locations of the primary peaks for ssRNA align closely with those for dsRNA, the secondary peaks for ssRNA can be attributed to folding-induced dihedral perturbations.
To further elucidate the underlying reasons for structural dynamics, we next examine hydrogen bonding between different residues. Considering each nucleotide as both a donor and an acceptor for hydrogen bonding, we have created heatmaps with the average number of hydrogen bonds, shown in Fig. 1(e), which highlights two distinct types of hydrogen bonds: (i) intra-nucleotide hydrogen bonds, formed between atoms in the backbone and base of the same nucleotide (represented by the main diagonal elements) and (ii) inter-nucleotide hydrogen bonds, formed between backbone and base of one nucleotide and those of another nucleotide. An enlarged versions of the heatmaps with corresponding average hydrogen bond numbers are provided in Fig. S5(i) and (ii) (ESI†) for ssRNA and dsRNA respectively. Inter-nucleotide hydrogen bonds can be further subdivided into two categories: bonds between adjacent nucleotides (depicted by elements on the upper and lower diagonals in Fig. 1(e)), and those between non-adjacent nucleotides (represented by all other elements except those on the main, sub, and super diagonals). The presence of hydrogen bonds between adjacent bases indicates stabilization of the ssRNA, while bonds between non-adjacent bases suggest a higher likelihood of folding. Intra-nucleotide hydrogen bonds occur only when the nucleotide comes close to the backbone during the MD trajectory. From Fig. 1(e), we can make three key observations. First, in the case of ssRNA (Fig. 1(e), top), a significant number of hydrogen bonds are observed between adjacent bases (elements on sub and super-diagonals) as well as non-adjacent bases, such as those between bases 9 & 3, 1 & 10, and 4 & 8. The former (latter) type of bonding explains the stability of the unfolded (folded) conformations, which has been explicitly demonstrated in Fig. S6 (ESI†). Second, intra-nucleotide hydrogen bonding is considerably higher for the terminal nucleotides (1 and 10), which can be attributed to the twisting of the nucleotide, bringing it in proximity to the backbone and allowing hydrogen bonds to form between the backbone and base. However, the occurrence of such twisting is less likely in the non-terminal bases, resulting in low hydrogen bonds along other diagonal elements in (Fig. 1(e), top). Finally, in dsRNA (Fig. 1(e), bottom), it is evident that hydrogen bonds within a base pair dominate those between adjacent base pairs. This explains the tight distribution of ΔPdisdsRNA in (Fig. 1(c), bottom).
Conductance variations in ssRNA
In Fig. 1, we have established the structural instability associated with ssRNA. In this section, we undertake an analysis of the impact of structural instability on the conductance of ssRNA. Toward that end, we first classified the 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ssRNA conformations into five distinct categories based on ΔPdis values, namely, 10 Å to 30 Å in steps of 5 Å with a tolerance of 10% (the nominal ΔPdis values for the five categories are 10, 15, 20, 25, and 30 Å). From each category, we have chosen frames based on the number of stacked bases, leading to a total of 123 selected conformations. The detailed frame selection methodologies for both ssRNA and dsRNA are provided in Methods.
000 ssRNA conformations into five distinct categories based on ΔPdis values, namely, 10 Å to 30 Å in steps of 5 Å with a tolerance of 10% (the nominal ΔPdis values for the five categories are 10, 15, 20, 25, and 30 Å). From each category, we have chosen frames based on the number of stacked bases, leading to a total of 123 selected conformations. The detailed frame selection methodologies for both ssRNA and dsRNA are provided in Methods.
Typical representations of the backbone orientations for the five ΔPdis categories from 10 Å to 30 Å are shown in Fig. 2(a). We performed energy-dependent decoherence probe-based charge transport calculations (details available in Methods) on the selected structures with the contacts connected to the first and last bases. We then computed the zero-bias conductance of each selected conformation with the Fermi energy corresponding to the HOMO energy. These conductance values are shown as a function of time in (Fig. 2(b), left). To better illustrate the conductance dispersion, we have also shown the probability density function (PDF) in (Fig. 2(b), right). The mean and standard deviation of the pdf of  are obtained to be −4.68 Å and 2.02 Årespectively, where G and G0 are the ssRNA conductance and quantum of conductance respectively. The high standard deviation suggests that conductance variability is closely related to conformational fluctuations. The pronounced conductance stochasticity observed in ssRNA is attributed to its ability to exhibit multiple metastable states, unlike the well-characterized dsDNA, which generally remains unfolded and exhibits a narrow conductance distribution – as supported by the dsRNA conductance data presented in this study (see Table S1, ESI†).
are obtained to be −4.68 Å and 2.02 Årespectively, where G and G0 are the ssRNA conductance and quantum of conductance respectively. The high standard deviation suggests that conductance variability is closely related to conformational fluctuations. The pronounced conductance stochasticity observed in ssRNA is attributed to its ability to exhibit multiple metastable states, unlike the well-characterized dsDNA, which generally remains unfolded and exhibits a narrow conductance distribution – as supported by the dsRNA conductance data presented in this study (see Table S1, ESI†).
Next, to explore the dependence of conductance dispersion on ΔPdis, we have presented the conductance distributions of conformations for each category of ΔPdis in Fig. S7 (ESI†). We observe that the average conductance decreases from folded (ΔPdis = 10, 15 Å) to unfolded (ΔPdis = 25, 30 Å) states. Overall, it can be inferred that folding, in general, leads to an increase in conductance along with lesser variability, a property which can be leveraged for next-generation synthetic-biology-based electronics.
Electronic properties of conformations
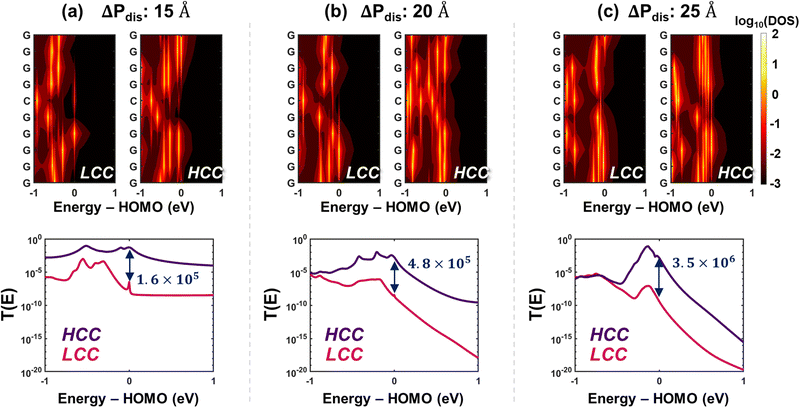
A striking observation across all categories in Fig. 2(b) is the substantial disparity between the maximum and minimum conductance values observed among the conformations. The corresponding extreme conductance values for all five ΔPdis categories are summarized in Table 1. For every ΔPdis category, the conductance spread (defined as the ratio of maximum to minimum conductance in a category) was found to range between ≈103–106G0, which is substantial and highlights the significant influence of conformation in determining conductance. To unravel the impact of conformation on conductance, we have studied the extreme conductance cases, low conductance conformation (LCC) and high conductance conformation (HCC) of ΔPdis = 15, 20, and 25 Å. For a holistic understanding of conductance fluctuations, we have compared the conformations based on four metrics.| G/G0 | ΔPdis: 10 Å | ΔPdis: 15 Å | ΔPdis: 20 Å | ΔPdis: 25 Å | ΔPdis: 30 Å |
|---|---|---|---|---|---|
| LCC: lowest conductance conformation; HCC: highest conductance conformation; G0: quantum conductance | |||||
| LCC | 2.48 × 10−6 | 7.51 × 10−8 | 8.91 × 10−9 | 3.63 × 10−9 | 1.58 × 10−8 |
| HCC | 1.62 × 10−2 | 4.00 × 10−2 | 1.70 × 10−3 | 3.00 × 10−3 | 4.12 × 10−4 |
| Ratio | 6.53 × 10 3 | 5.33 × 10 5 | 1.91 × 10 5 | 8.26 × 10 5 | 2.61 × 10 4 |
First, we analyze the structural differences between LCCs/HCCs of each category in Fig. 3. For ΔPdis = 15 Å, we notice that the distance between 3′ and 5′ ends is lower for HCC in contrast to LCC (see Fig. 3(a)). Quantitatively, the distance between the center of masses of terminal bases 1 and 10 is 10.13 Å (8.41) for LCC (HCC). This distinction becomes more pronounced for ΔPdis = 20 Å (Fig. 3(b)), where the separation between the terminal bases is 23.02 Å for LCC vs. 13.31 Å for HCC. Moreover, unlike the LCC structure, the 5′ end in HCC is close to the 7th and 8th bases (6.68 Å and 7.65 Å respectively). A similar trend can be noticed for ΔPdis = 25 Å (Fig. 3(c)). In this case, the distances between the terminal bases are 28.63 Å and 24.87 Å for LCC and HCC respectively. These results, combined with the conductance data provided in Table 1, suggest that the distance between terminal bases and conductance should be correlated. Intuitively, this is justified since a lower terminal base distance decreases the hopping length, leading to higher conductance.
However, the inter-terminal base distance alone cannot completely account for the substantial conductance ratio between LCCs and HCCs. To further address this issue, we have considered a second metric, delocalization of HOMO and HOMO−1 orbitals among the bases. A higher delocalization suggests better orbital overlapping between the bases, which in turn is indicative of better charge transport. For the three specific cases depicted in Fig. 3, we find that the proximity of bases plays a crucial role in orbital delocalization, for both folded and unfolded configurations. For ΔPdis = 15 Å, a closer observation reveals that the 1st base has moved closer to the 10th base in HCC, whereas in LCC it swings away. Consequently, the HOMO orbital is delocalized over bases 1, 7, 8, 9, 10 for HCC, while it is delocalized only over bases 3, 4, 5, 6 for LCC. The HOMO−1 orbital is also delocalized for HCC, but over bases 2, 3, 4, 5, whereas for LCC, it remains delocalized on bases 2, 3, 4. Similarly, for ΔPdis = 25 Å, we observe a delocalization over bases 1 to 8 for HCC. In contrast, the proximity of 3′ terminal bases (8, 9, 10) for LCC leads to strong orbital overlap, causing the HOMO orbital to localize near the 3′ terminal. The trends of high delocalization for HCC become more evident for the HOMO−1 orbital.
Interestingly, for ΔPdis = 20 Å, although the inter-base distances are lower in HCC than LCC (Fig. 3(b)), the HOMO orbital delocalization is more pronounced for LCC (over bases 1, 2, 3, 4, 5) than HCC (over bases 8, 9, 10). However, we find that the HOMO−1 orbital is more delocalized for HCC than LCC. To quantify orbital localization, we have computed the inverse participation ratio (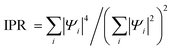 , where |Ψi|2 is the probability of finding an electron at the ith residue).22 The greater the value of IPR (maximum value is 1), the greater is the orbital localization. Table 2 summarizes the IPR values and energy levels for the first three HOMO energy levels for ΔPdis = 15, 20, 25 Å. The corresponding probabilities (|Ψi|2) are shown in Fig. S8 (ESI†). We observe from Table 2 that the IPR values of LCC and HCC at corresponding HOMO (HOMO−1) energies are 0.85 (1.00) and 1.00 (0.72) for ΔPdis = 20 Å. Additionally, the HOMO & HOMO−1 levels differ by 150 meV (≈5kBT) and 20 meV (<≈kBT) respectively for LCC and HCC. This suggests that when the Fermi energy is near the HOMO level for HCC, both HOMO and HOMO−1 orbitals can participate in electronic transport due to their relatively small energy separation. Therefore, we can conclude that for the ΔPdis = 20 Å category, small energy differences between the first few HOMOs, coupled with strong orbital delocalization, results in higher conductance of HCC. The trend of energetically close HOMOs with lower IPR values for HCCs relative to LCCs is also applicable for the other two categories (ΔPdis = 15 and 25 Å).
, where |Ψi|2 is the probability of finding an electron at the ith residue).22 The greater the value of IPR (maximum value is 1), the greater is the orbital localization. Table 2 summarizes the IPR values and energy levels for the first three HOMO energy levels for ΔPdis = 15, 20, 25 Å. The corresponding probabilities (|Ψi|2) are shown in Fig. S8 (ESI†). We observe from Table 2 that the IPR values of LCC and HCC at corresponding HOMO (HOMO−1) energies are 0.85 (1.00) and 1.00 (0.72) for ΔPdis = 20 Å. Additionally, the HOMO & HOMO−1 levels differ by 150 meV (≈5kBT) and 20 meV (<≈kBT) respectively for LCC and HCC. This suggests that when the Fermi energy is near the HOMO level for HCC, both HOMO and HOMO−1 orbitals can participate in electronic transport due to their relatively small energy separation. Therefore, we can conclude that for the ΔPdis = 20 Å category, small energy differences between the first few HOMOs, coupled with strong orbital delocalization, results in higher conductance of HCC. The trend of energetically close HOMOs with lower IPR values for HCCs relative to LCCs is also applicable for the other two categories (ΔPdis = 15 and 25 Å).
| MOs | ΔPdis: 15 Å | ΔPdis: 20 Å | ΔPdis: 25 Å | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Energy (eV) | IPR | Energy (eV) | IPR | Energy (eV) | IPR | |||||||
| LCC | HCC | LCC | HCC | LCC | HCC | LCC | HCC | LCC | HCC | LCC | HCC | |
| LCC: lowest conductance conformation HCC: highest conductance conformation IPR: inverse participation ratio. | ||||||||||||
| HOMO | −4.92 | −5.00 | 1.00 | 0.74 | −5.03 | −5.29 | 0.85 | 1.00 | −5.25 | −5.16 | 1.00 | 0.85 |
| HOMO−1 | −5.21 | −5.06 | 0.97 | 0.53 | −5.18 | −5.31 | 1.00 | 0.72 | −5.28 | −5.24 | 0.68 | 0.43 |
| HOMO−2 | −5.30 | −5.09 | 1.00 | 0.59 | −5.20 | −5.32 | 1.00 | 0.81 | −5.35 | −5.29 | 1.00 | 0.65 |
From the preceding discussions, we make two key observations: (i) while higher delocalization is typically indicative of better charge transport, conductivity is ultimately governed by the intricate interplay between inter-base distances and the extent of orbital delocalization, and (ii) although conductance is calculated with the Fermi energy at the HOMO energy level, to fully comprehend the underlying electrostatics, it is essential to analyze the energy differences among the first few HOMO energies. This additional analysis provides a more complete picture of how orbital characteristics and their variations impact charge transport in ssRNA. Our observations also extend to ΔPdis = 10 and 30 Å categories, as illustrated in Fig. S9 (ESI†).
Next, we have also analyzed the conductance trends based on density of states of the conformations. The 2D DOS heatmaps are shown in (Fig. 4, top row) and the partial DOS (PDOS) of each conformation at different energies are shown in Fig. S10–S14 (ESI†). We observe that the lower delocalization in HCC for ΔPdis = 20 Å is also reflected in the base-wise PDOS (see Fig. 4(b)), causing the total DOS at HOMO of the LCC to be higher than that of the HCC. But as we move into the HOMO band, even a small shift of 10 meV results in the total DOS as well as base-wise partial DOS of HCC to surpass those for LCC (Fig. S15, ESI†). This explains the high conductance of the HCC. For the other two categories, ΔPdis = 15 and 25 Å, the total DOS of HCCs at HOMO is substantially larger than corresponding LCCs, a trend that holds for other energies close to HOMO (see Fig. S11 and S13, ESI†). Additionally, we observe from the top row of Fig. 4 that for all ΔPdis categories, high DOS patches are concentrated near or at HOMO for the HCC. These high DOS energy levels primarily contribute to charge transport, resulting in a high transmission probability for HCCs at HOMO energy level (Fig. 4, bottom row). From the transmission profiles across different ΔPdis, we make two observations: (i) for both LCC and HCC, the transmission at HOMO energy drops with increase in ΔPdis,. This finding also holds for ΔPdis = 10 and 30 Å. (ii) The transmission in the bandgap is considerably higher for folded (ΔPdis = 10 and 15 Å) states in contrast to unfolded (ΔPdis = 25 and 30 Å) states. At lower ΔPdis, the tunneling probability between terminal bases is higher due to their proximity, while at higher ΔPdis, transport is more dependent on hopping between bases. Given that tunneling between terminal bases serves as a promising transport mechanism, conformations in folded states result in higher transmission in the bandgap, despite having negligible DOS.
The conductance of ssRNA depends primarily on the efficiency of carrier transport between the two contacts, which are bases 1 and 10 in our simulation setup. The three charge transport properties we have discussed – inter-base distance, orbital delocalization, and density of states – individually highlight the underlying reasons for significantly higher conductance (see last row in Table 1) in HCC over LCC across all ΔPdis categories. However, to comprehensively understand the rationale behind the high conductance ratio between HCC and LCC, we devised a fourth metric, probable pathways, comprising four components: (i) inter-base distance (ii) total DOS (iii) orbital overlap, and (iv) length of a path (number of nodes). To identify the most probable paths from base 1 to 10, we employed a graph network-based approach, which is explained in Methods. In this framework, individual bases are treated as nodes of a graph and the cost of a path between two nodes is based on the aforementioned charge transport properties. The cost of a node is computed based on PDOS of the bases in a path while the cost of an edge is a function of distance and orbital overlapping between successive bases in that path. We have only considered simple paths (i.e., no repeating nodes) for our analysis. A smaller path score represents more favorable pathways. The top row in Fig. 5 shows the most probable paths for HCCs and LCCs when ΔPdis = 15, 20, and 25 Å and the bottom row shows the total cost (“score”) of the top five probable paths. To validate the significance of the proposed pathways, we first compute the conductance at the HOMO level for each conformation by selectively disabling the hopping between bases involved in a specific path. We then calculate the conductance ratio by comparing the conductance of the fully connected system with that of the modified system where the hopping between bases in the chosen path is selectively turned off (see Fig. S16, ESI†). The most probable paths shown in the top row of Fig. 5 show a dramatic reduction in transmission at HOMO energy by ≈102–108 times when the paths are disrupted, underscoring the significance of these paths in facilitating charge transport. From the bottom row of Fig. 5, it is evident that the scores of the top five paths for HCCs are considerably lower than those of LCCs, particularly for the ΔPdis = 15 and 20 Å categories. Interestingly, when ΔPdis = 15 Å, while the most probable (least cost) path for HCC is a direct hop between bases 1 and 10, that for LCC is rather circuitous (1 → 2 → 3 → 4 → 9 → 10). The proximity of terminal bases in HCC allows for direct transport between the two contact bases, which is not possible in LCC due to the larger terminal base separation. We note that the most probable path agrees with the probability (|Ψ|2) of HOMO orbital (see top five pathways along with their scores in Fig. S15, ESI†). We believe that direct transport reduces the probability of scattering, which explains the higher conductivity of HCC than LCC for ΔPdis = 15 Å. For ΔPdis = 20 Å, the most probable path for HCC (1 → 7 → 8 → 9 → 10) includes a hop from base 1 to 7, which can be attributed to the proximity of these bases as shown in Fig. 5(b). This arrangement facilitates better transport in HCC compared to LCC, despite the former having lower HOMO orbital delocalization. While inter-base distances, particularly terminal-base distances, play a pivotal role in enhancing conductance, the total DOS of bases involved in a pathway can also contribute significantly toward charge transport, especially for the unfolded conformational states. For instance, when ΔPdis = 25 Å, the total DOS of all bases involved in the most probable path in HCC is considerably higher than LCC (Fig. S13, ESI†), despite the former having a longer route. A similar observation can be made for ΔPdis = 30 Å category (Fig. S15, ESI†). This demonstrates that while the length of the transport pathway (as measured by number of hops) is a factor, the higher DOS in HCC compensates for the longer route by enabling more efficient transport.
Harnessing conformational fluctuations of ssRNA
From an applications perspective, the high stochasticity in ssRNA conductance observed in Fig. 2 is undesirable. As demonstrated previously, the underlying reason for this variability is structural instability. Taking a cue from previous studies which have shown that salt concentration plays a vital role in stabilizing RNA conformations,23–26 we considered low (∼100 mM with 11 Cl− ions) and high (∼450 mM with 41 Cl− ions) salt concentrations in our calculations, as illustrated in Fig. 6. Initially, we validated our setup by computing the radial distribution functions (RDF) for Na+ ions relative to the phosphate group in ssRNA, as well as water molecules around Na+ ions (hydration shell). The computed RDFs agree with H. Knechtel et al. within a tolerance of 2–15%, as demonstrated in Fig. S17 (ESI†).23 The computed RDFs also match very closely with Stefan et al. (2.35 Å)27 The 1D-RMSD in Fig. 6(a) clearly demonstrates that the average RMSD decreases with an increase in salt concentration. Comparing the 2D RMSD heatmaps in (Fig. 6(b) with Fig. 1(b), left), we observe that increasing the salt concentration leads to a reduction in overall structural fluctuations during the MD trajectory. This is evident from the increase in low RMSD patches as the salt concentration rises. In Fig. 6(c), we plot ΔPdis as a function of time for three different salt concentrations: (i) negligible (N, Cl− = 0), (ii) low (L, Cl− = 11), and (iii) high (H, Cl− = 41). Indeed, the folding of ssRNA, as quantified by ΔPdis, has dropped from 47.88% in the “no salt” case to 36.89% and 23.44% for low and high salt concentrations respectively. The backbone structural stability is also reflected in a decreasing trend of the coefficient of variation (CV) of the six backbone dihedrals (α, β, γ, δ, ε, ζ) with increasing salt concentration (Fig. 6(d)). A lower CV of the dihedral angle χ, which signifies fluctuations of nitrogenous bases, attests to low conductance stochasticity. Finally, the hydrogen bonding analysis in Fig. 6(e) reveals the presence (absence) of more hydrogen bonds between adjacent (non-adjacent) bases at higher salt levels, explaining the increased stability of the ssRNA conformation. These observations suggest that increasing salt concentrations can be a viable approach to controlling structural fluctuations in ssRNA. This stabilization, in turn, reduces the variability in conductance, offering a more consistent performance. Such control over conductance spread could be strategically leveraged to develop ssRNA-based electronic devices, where reliable charge transport is critical for functionality.Discussion
In this study, we have systematically explored the charge transport properties of a short (10-base) single-stranded RNA (ssRNA), which is desirable for electronic applications. Although our analysis focuses on a specific ssRNA sequence, we anticipate that our findings should extend to any short ssRNA. We started by comparing the structural stability of single- and double-stranded RNAs (Fig. 1). The comparison was made using three key metrics: 1D and 2D RMSDs, end-to-end phosphorus distance (ΔPdis) and backbone dihedral angles. Our analysis revealed that while dsRNA exhibits greater stability in all three aspects, ssRNA is characterized by large conformational fluctuations. The superior stability of dsRNA can be attributed to the presence of intra-base pair hydrogen bonding which is absent in ssRNA (Fig. 1(e)). Moreover, our hydrogen bonding heatmaps depict that ssRNA is stabilized primarily by hydrogen bonds between adjacent/non-adjacent bases in an unfolded/folded state. This suggests that in short ssRNA sequences, hydrogen bonding between adjacent bases plays a critical role in determining the folding probabilities, offering a potential design rule for manipulating ssRNA structures. Next, using an MD-frame selection procedure based on stacked bases and ΔPdis, we selected 123 frames from the pool of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations to perform charge transport calculations (Fig. 2). We note that although state-of-the-art sampling methods (e.g., umbrella sampling, metadynamics, and adaptive sampling) exist which aim to achieve adequate conformational sampling while minimizing the computational cost, our frame selection procedure proved adequate to capture conformations with a wide conductance spread. S. Chandra et al. performed STM-BJ-based conductance measurements of dsRNA and DNA:RNA hybrid, each 11 bp long with a poly-GC sequence and reported a conductance of ≈1.63 × 10−3G0.20 More recently, S. Chandra et al. have also reported the conductance of 5-mer and 10-mer ssRNA to be ≈2.9– 3.6 × 10−3G0.21 Table S2 compares the single-molecule conductances of this work to the previously reported studies. Comparing the pdf in (Fig. 2(b), right) to the previously reported conductance data, we observe that the experimental conductance values are within one standard deviation of our mean computational conductance. The higher standard deviation in our work is due to our consideration of diverse configurations, which are likely non-existent in the break-junction experiments. The main goal of our study is to highlight the impact of conformational fluctuations on ssRNA conductance. This necessitates sampling a broad range of configurations. We anticipate that future experimental studies will reveal the broad range of conductance values including the high conductance states, as predicted in this work.
000 conformations to perform charge transport calculations (Fig. 2). We note that although state-of-the-art sampling methods (e.g., umbrella sampling, metadynamics, and adaptive sampling) exist which aim to achieve adequate conformational sampling while minimizing the computational cost, our frame selection procedure proved adequate to capture conformations with a wide conductance spread. S. Chandra et al. performed STM-BJ-based conductance measurements of dsRNA and DNA:RNA hybrid, each 11 bp long with a poly-GC sequence and reported a conductance of ≈1.63 × 10−3G0.20 More recently, S. Chandra et al. have also reported the conductance of 5-mer and 10-mer ssRNA to be ≈2.9– 3.6 × 10−3G0.21 Table S2 compares the single-molecule conductances of this work to the previously reported studies. Comparing the pdf in (Fig. 2(b), right) to the previously reported conductance data, we observe that the experimental conductance values are within one standard deviation of our mean computational conductance. The higher standard deviation in our work is due to our consideration of diverse configurations, which are likely non-existent in the break-junction experiments. The main goal of our study is to highlight the impact of conformational fluctuations on ssRNA conductance. This necessitates sampling a broad range of configurations. We anticipate that future experimental studies will reveal the broad range of conductance values including the high conductance states, as predicted in this work.
The significant spread of the conductance spectrum points towards the strong influence of conformational fluctuations on ssRNA charge transport. While conductance tends to increase with lower ΔPdis, the wide spread of conductances across all ΔPdis categories underscores the importance of nucleotide positioning. To probe the cause of drastic conductance disparities between two conformations with similar ΔPdis, we conducted a detailed quantum mechanical analysis on the extreme conductance conformations and observed a strong connection between the inverse participation ratio (IPR) for first few HOMOs and conductance (Fig. 3 and Table 2). Moreover, we established that the energy differences among first few HOMOs is considerably lower in high conductance conformations (HCC) over low conductance (LCC) ones (Table 2). For HCCs, with Fermi energy at HOMO level, multiple HOMO energies can partake in electronic transport. However, in certain conformations, such as when ΔPdis = 20 Å, inter-base distance dominates other electronic properties in determining ssRNA conductivity since shorter hopping distances facilitate more efficient carrier transfer between bases. This observation is corroborated by the transmission profiles shown in Fig. 4 (bottom). A higher transmission probability in the bandgap for a folded configuration suggests that the transport mechanism is dominated by direct tunneling between terminal bases. With no prospect of such tunneling in an unfolded state, transmission drops significantly. These observations suggest that while ΔPdis is a global factor which influences ssRNA conductance, inter-base distances enable local modulation of charge transport. To substantiate this hypothesis, we proposed a probable pathways metric for carrier transport based on path length, electronic properties, and inter-base distances. These pathways can offer valuable insight into the mechanisms which induce differences in conductance among conformations. Efficient charge transport favors shorter hopping distances and higher availability of states in the hopping sites. We observed that while pathways in folded structures are governed largely by inter-base distances, those in unfolded structures depend on orbital delocalization and density of states. Finally, we explored practical approaches to harness ssRNA structural fluctuations and reduce conductance stochasticity. In Fig. 6, we demonstrated that higher salt concentrations stabilize ssRNA, as reflected in multiple structural attributes.
Our study highlights that significant conductance contrast is possible on a nano-second timescale, which should spur future experimental efforts with a high time resolution. The presence of electrodes could alter the structural dynamics of a single-molecule by reducing the conformational fluctuations, resulting in a smaller ensemble of molecular configurations. Since this study is focused on unraveling the structural changes in single-molecule conductance, we considered a wide range of configurations. Incorporating electrode effects at variety of inter-electrode separation could offer additional insights into the conductance stochasticity of single molecules and should be undertaken in future studies.
Although our findings reveal the dramatic conductance fluctuations between folded and unfolded states, they also highlight the potential to achieve two distinct conductance states through controlled manipulation of ssRNA unfolding and refolding. To this end, state-of-the-art techniques such as optical and magnetic tweezers present promising methods to reversibly switch ssRNA between these two conformational states.28,29 When combined with a conductance measurement setup, this approach can pave the way for the development of ssRNA-based ultra-scaled memory devices and switches. Additionally, regulating salt concentrations offers a viable strategy to limit conformational fluctuations, ensuring more deterministic performance in applications. We anticipate that the outcomes of this study will inspire future experimental research to harness the high and low conductivity of ssRNA in its folded and unfolded states, thus contributing to the advancement of molecular electronics.
Methods
Molecular dynamics simulation setup
The structures of both ssRNA and dsRNA were created with Nucleic Acid Builder (NAB). The ssRNA sequence is: 5′-GGGGGCGGGG-3′ while the dsRNA sequence is: 5′-GGGGGCGGGG-3′/3′-CCCCCGCCC-5′. All Molecular Dynamics (MD) simulations were performed in AMBER 20 software with explicit solvent.30 We have used an RNA OL3 force field with TIP3P for water. Firstly, we perform a two-step minimization on the generated structures. In the first stage, we relax the solvent with counterions by applying a restraint of 50 kcal mol−1 force on ssRNA/dsRNA. The minimization step involves 5000 steps with 250 cycles of steepest descent followed by conjugate gradient descent with a non-bonded cutoff of 10 Å. After solvent/counterions are minimized, we perform a similar energy minimization on the whole system. Secondly, the system is heated from 0 to 300 K in a span of 1 ns. The temperature was increased linearly in 5000 steps and then kept constant for the rest of the simulations. For temperature control, we adopted the Langevin thermostat with a 1 ps−1 collision frequency. SHAKE algorithm was activated to constrain bonds involving hydrogen atoms with a convergence tolerance of 10−5. Initial velocities were also randomized. During the heating stage, we considered the NVT ensemble (constant volume) with ssRNA/dsRNA restrained with a force of 50 kcal mol−1. Following up, equilibration was performed for 1 ns on the structures and velocities obtained from the previous heating stage. During this step, the target temperature was maintained at 300 K with a Langevin thermostat with 1 ps−1 collision frequency but reduced force restraint of 0.5 kcal mol−1 on ssRNA/dsRNA to allow structural relaxation. Finally, the production stage was carried out with the final structures and velocities obtained from the equilibration step under the NPT ensemble. For both ssRNA/dsRNA, the production step lasted for 200 ns. Like the previous stages, the SHAKE algorithm and Langevin thermostat were activated. The non-bonded interaction cutoff was set at 10 Å. We have used the Particle Mesh Ewald (PME) method to account for long-range electrostatic interactions.Molecular dynamics data analysis
To explore the structural stability of ssRNA/dsRNA, we have computed the following metrics based on the MD trajectory: (i) 1D- and 2D-RMSD (ii) end-to-end phosphorus distance (ΔPdis) (iii) hydrogen bonding heatmaps and (iv) backbone dihedral angles. All the MD data analyses were performed with Cpptraj and Pytraj packages.31 Detailed descriptions of these metrics are as follows:1D- and 2D-RMSD
Pairwise RMSD of the trajectory was computed with pairwise_rmsd module in Pytraj. 1D-RMSD was derived from the first row of the 2D-RMSD matrix.End-to-end phosphorus distance (ΔPdis)
The distance between phosphorus (P) atoms of the 2nd and 10th residues was calculated using the distance module of Pytraj.Hydrogen bonding heatmaps
Hydrogen bonding was computed using the hbond function of Cpptraj by considering each residue as both a donor mask and an acceptor mask. The hydrogen bonds are detected based on the criteria: angle cutoff of 135° and distance cutoff of 3 Å. The heatmaps were generated from the average number of hydrogen bonds between any two residues and between the base and backbone over a 200 ns trajectory.Backbone dihedral angles
We extracted the six backbone dihedral angles (α, β, γ, δ, ε, ζ) along with the χ angle. The definitions of these angles are as follows:| [α: O3′(i − 1)–P–O5′–C5′] |
| [β: P–O5′–C5′–C4′] |
| [γ: O5′–C5′–C4′–C3′] |
| [δ: C5′–C4′–C3′–O3′] |
| [ε: C4′–C3′–O3′–P(i + 1)] |
| [ζ: C3′–O3′–P(i + 1)–O5′(i + 1)] |
| [χ for pyrimidines: O4′–C1′–N1–C2] |
| [χ for purines: O4′–C1′–N9–C4] |
Additionally, in salt concentration analysis, we have used the rdf module of Pytraj to compute the radial distribution function with a bin size of 0.01 Å.
Frame selection procedure
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations (frames) from the MD simulations of ssRNA. Frame selection from this vast dataset involved a two-step process. Firstly, we classify all conformations into multiple categories based on end-to-end phosphorus distance (ΔPdis), a parameter that reflects the proximity of the terminal bases and, by extension, the folding or unfolding state of the conformation. To capture the full spectrum of ssRNA conformational states, we have considered five categories of ΔPdis. However, each category contained hundreds of conformation which makes it computationally expensive to perform DFT/transport calculations on each of them. Hence, in the second step, we refined our frame selection by considering the number of stacked bases so that the impact of base positioning is accounted for in the charge transport. Following the definition in S. Chandra et al.,21 the bases are considered to be stacked when they satisfy the three following conditions: (i) |zjk| > 2 (ii) ρjk < 2.5 Å and (iii) |αkj| < 40°, where
000 conformations (frames) from the MD simulations of ssRNA. Frame selection from this vast dataset involved a two-step process. Firstly, we classify all conformations into multiple categories based on end-to-end phosphorus distance (ΔPdis), a parameter that reflects the proximity of the terminal bases and, by extension, the folding or unfolding state of the conformation. To capture the full spectrum of ssRNA conformational states, we have considered five categories of ΔPdis. However, each category contained hundreds of conformation which makes it computationally expensive to perform DFT/transport calculations on each of them. Hence, in the second step, we refined our frame selection by considering the number of stacked bases so that the impact of base positioning is accounted for in the charge transport. Following the definition in S. Chandra et al.,21 the bases are considered to be stacked when they satisfy the three following conditions: (i) |zjk| > 2 (ii) ρjk < 2.5 Å and (iii) |αkj| < 40°, where 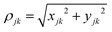 and (xjk, yjk, zjk) are distances between the center of masses of the two bases (j,k) along the x-, y-, and z-axis. αkj is the angle between normal vectors of bases (j,k). In each category, we classified the conformations into sub-categories based on number of stacked bases, which typically range from 2 to 7. From each of these sub-categories with the same number of stacked bases and almost similar ΔPdis, conformations were sorted based on the sum of all angles (Σα) between normal vectors of adjacent bases (α). A set of five frames per sub-category, representative of minimum, maximum, median, 1st, and 3rd quartile values of the sum of angles (Σα), was chosen. This yielded a total of 125 conformations.
and (xjk, yjk, zjk) are distances between the center of masses of the two bases (j,k) along the x-, y-, and z-axis. αkj is the angle between normal vectors of bases (j,k). In each category, we classified the conformations into sub-categories based on number of stacked bases, which typically range from 2 to 7. From each of these sub-categories with the same number of stacked bases and almost similar ΔPdis, conformations were sorted based on the sum of all angles (Σα) between normal vectors of adjacent bases (α). A set of five frames per sub-category, representative of minimum, maximum, median, 1st, and 3rd quartile values of the sum of angles (Σα), was chosen. This yielded a total of 125 conformations.
It is to be noted that all the selected conformations of both ssRNA and dsRNA undergo a two-step energy minimization process in AMBER 20 before charge transport calculations are performed. In the first step, the solvent and counterions are minimized over 2500 steps with restraint on ssRNA/dsRNA, while during the second step, the whole system undergoes energy minimization for 2500 steps. These energy-minimized structures are used for DFT/transport calculations.
Ab initio DFT modeling
Density functional theory (DFT) calculations have been performed in the Gaussian 16 software package with Gaussian-type orbitals.33 The hybrid functional B3LYP with a 6-31G** basis set has been used. To incorporate the solvent effect (water in this case), we have included the polarizable continuum model (PCM). For all self-consistent field (SCF) calculations, the default “tight” convergence criteria of Gaussian were used. Following this, the Fock (F) and overlap (S) matrices were extracted using readmat utility.To operate with an orthogonal atomic basis set, the Hamiltonian (H) of the system was generated from Fock (F) and overlap (S) matrices by performing Lowdin transformation as follows:
 | (1) |
The diagonal terms in H represent the onsite energies of the orbitals, while off-diagonal terms correspond to the hopping energy between orbitals. For the transport calculations, we chose to partition the whole Hamiltonian based on individual bases.
In this approach, the Hamiltonian was rearranged in the following way to obtain a modified Hamiltonian (HI):
 | (2) |
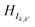 (where k ≠ k′; k, k′ ∈ [1,10]) indicate the hopping energies between orbitals in base k and k′. The dimension of HIk,k is
(where k ≠ k′; k, k′ ∈ [1,10]) indicate the hopping energies between orbitals in base k and k′. The dimension of HIk,k is  , where bj is the total number of basis sets used to represent atom j in base k and Nk is the total number of atoms in base k.
, where bj is the total number of basis sets used to represent atom j in base k and Nk is the total number of atoms in base k.
Next, a unitary transformation was applied to HI to obtain the final Hamiltonian (HDNA), which was used in the transport calculation. The transformation is expressed as follows:
| HDNA = U†HIU | (3) |
The unitary matrix U is defined as:
 | (4) |
Transport calculations
For charge transport calculations, firstly, we compute the retarded Green's function (Gr) including self-energies of contacts and decoherence probes as follows:| [E − HDNA − ΣL − ΣR − ΣB(E)]Gr = I | (5) |
 are the self-energies due to left (right) contacts while ΓL(R) represent the corresponding coupling between DNA and left (right) contacts. ΣB depicts combined self-energies of decoherence probes.
are the self-energies due to left (right) contacts while ΓL(R) represent the corresponding coupling between DNA and left (right) contacts. ΣB depicts combined self-energies of decoherence probes.
In our study, we have considered energy-dependent decoherence probes which is an improvement over the energy-independent model as shown in our previous study.34 For an energy-dependent decoherence probe, the imaginary part of ΣB is expressed as:
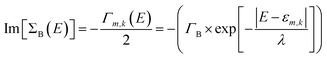 | (6) |
For all our calculations, we have chosen the following values of parameters: ΓL = ΓR = 0.1 eV; ΓB = 0.1 eV; λ = 0.1 eV. All atoms in bases 1 and 10 are connected to left and right contact respectively. The effective transmission is expressed as:
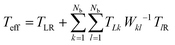 | (7) |
 , described in more detail in.35–38
, described in more detail in.35–38
Linear response conductance
The zero-bias or linear response conductance is computed from the effective transmission using the following equation: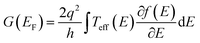 | (8) |
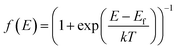 is the Fermi distribution. Conductance is calculated with the Fermi energy at the HOMO energy.
is the Fermi distribution. Conductance is calculated with the Fermi energy at the HOMO energy.
Density of states calculation
The density of states calculation involves no contact self-energies. We have considered a very small broadening (η = 0.001). Like transport calculations, we start with computing retarded Green's Function:| [(E + iη) − HDNA]Gr = I | (9) |
The local density of states (LDOS) at an energy point is calculated by solving the following equation:
 | (10) |
Wavefunction projection
To compute the probability |Ψ|2 of finding an electron on each base at any energy level, we have computed the projected wavefunction of that energy on each base.39 We first solve the following eigenvalue problem with Fock (F) and overlap (S) matrices:| FΨ = SEΨ | (11) |
To find the contribution of each base, we divide the whole system into base-wise fragments. Set of all wavefunctions pertaining to orbitals in a fragment is represented by Ψk (k ∈ [1,10]). The contribution of kth base is computed as follows:
 | (12) |
 represents the sub-matrix in the overlap matrix which corresponds to orbitals in base k and k′. The first component represents the contribution due to the orbitals in the same fragment while the last second component corresponds to overlap with other fragments.
represents the sub-matrix in the overlap matrix which corresponds to orbitals in base k and k′. The first component represents the contribution due to the orbitals in the same fragment while the last second component corresponds to overlap with other fragments.
Probable pathways calculation
(i) Inter-base distance: First, the center of mass of each base was calculated using only the atoms in the nitrogenous base, excluding those in the sugar or backbone. A 2D distance matrix, D, was then constructed, with the distances between the center of masses of all bases.
(ii) Overlap strength: Using the overlap matrix, S, obtained from DFT calculation, we extracted the submatrix  corresponding to the overlap between any two bases (k,k'). We then calculated the Frobenius norm of the matrix as:
corresponding to the overlap between any two bases (k,k'). We then calculated the Frobenius norm of the matrix as:
 | (13) |
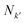 are the number of atomic orbitals in bases k and k′ respectively. A 2D overlap strength matrix SF was then generated by applying the Frobenius norm to the overlaps between every pair of bases.
are the number of atomic orbitals in bases k and k′ respectively. A 2D overlap strength matrix SF was then generated by applying the Frobenius norm to the overlaps between every pair of bases.
(iii) Available density of states: Partial density of states (PDOS) at kth base for an energy level E was calculated as:
 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 paths for each conformation.
000 paths for each conformation.
Aggregate node cost
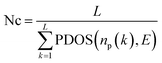
| (15) |
Aggregate edge cost

| (16) |
Path cost
| Score = Nc + Ec | (17) |
Author contributions
M. P. A. conceptualized the research problem. A. D. refined this as the work progressed. A. D. is responsible for data curation. Formal analysis of transport results was performed by A. D. and M. P. A. Formal analysis of data analysis was performed primarily by A. D. and A. K. D. with M. P. A. contributing. The methodology of transport properties was designed by M. P. A., MD was designed by A. D. and M. P. A., and the work on optimum transport path was designed by A. D. and A. K. D. All calculations were performed by A. D. The first draft was written by A. D. A. K. D. and M. P. A. extensively rewrote parts of the manuscript. The code used for transport was already available in M. P. A's group. A. D. wrote the code to determine the optimum transport path. A. D. performed the work required for visualization with input from A. K. D. and M. P. A. M. P. A. was responsible for funding acquisition. M. P. A. supervised the research work and was responsible for project administration.Conflicts of interest
The authors declare no competing interests.Data availability
All data are provided in this manuscript and ESI.†Acknowledgements
We acknowledge the support of the National Science Foundation grants GCR-2317843, FuSe-2235294 and FMRG-2328217. We also acknowledge the HYAK supercomputing facility at the University of Washington. MPA thanks Prof. Juan M Artés Vivancos (UMass) for insightful discussion on single molecule experiments. The AI tool Grammarly has been used in the process of writing this manuscript.References
- M. J. Moore, From Birth to Death: The Complex Lives of Eukaryotic mRNAs, Science, 2005, 309, 1514–1518 CrossRef CAS.
- J. L. Rinn and H. Y. Chang, Genome Regulation by Long Noncoding RNAs, Annu. Rev. Biochem., 2012, 81, 145–166 CrossRef CAS.
- P. Nissen, J. Hansen, N. Ban, P. B. Moore and T. A. Steitz, The Structural Basis of Ribosome Activity in Peptide Bond Synthesis, Science, 2000, 289, 920–930 CrossRef CAS.
- T. H. D. Nguyen, et al., The architecture of the spliceosomal U4/U6.U5 tri-snRNP, Nature, 2015, 523, 47–52 CrossRef CAS.
- H. F. Noller, V. Hoffarth and L. Zimniak, Unusual Resistance of Peptidyl Transferase to Protein Extraction Procedures, Science, 1992, 256, 1416–1419 CrossRef CAS.
- R. Giegé, M. Frugier and J. Rudinger, tRNA mimics, Curr. Opin. Struct. Biol., 1998, 8, 286–293 CrossRef.
- J. E. G. McCarthy and C. Gualerzi, Translational control of prokaryotic gene expression, Trends Genet., 1990, 6, 78–85 CrossRef CAS.
- M. Chamorro, N. Parkin and H. E. Varmus, An RNA pseudoknot and an optimal heptameric shift site are required for highly efficient ribosomal frameshifting on a retroviral messenger RNA, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 713–717 CrossRef CAS.
- J. Zhang, Y. Fei, L. Sun and Q. C. Zhang, Advances and opportunities in RNA structure experimental determination and computational modeling, Nat. Methods, 2022, 19, 1193–1207 CrossRef CAS.
- M. G. Seetin and D. H. Mathews, RNA Structure Prediction: An Overview of Methods, in Bacterial Regulatory RNA: Methods and Protocols, ed. K. C. Keiler, Humana Press, Totowa, NJ, 2012, pp. 99–122 DOI:10.1007/978-1-61779-949-5_8.
- P. P. Gardner and R. Giegerich, A comprehensive comparison of comparative RNA structure prediction approaches, BMC Bioinf., 2004, 5, 140 CrossRef.
- E. K. S. McRae, et al., Structure, folding and flexibility of co-transcriptional RNA origami, Nat. Nanotechnol., 2023, 18, 808–817 CrossRef CAS.
- H. C. Høiberg, S. M. Sparvath, V. L. Andersen, J. Kjems and E. S. Andersen, An RNA Origami Octahedron with Intrinsic siRNAs for Potent Gene Knockdown, Biotechnol. J., 2019, 14, 1700634 CrossRef.
- A. Krissanaprasit, et al., Genetically Encoded, Functional Single-Strand RNA Origami: Anticoagulant, Adv. Mater., 2019, 31, 1808262 CrossRef.
- M. T. A. Nguyen, G. Pothoulakis and E. S. Andersen, Synthetic Translational Regulation by Protein-Binding RNA Origami Scaffolds, ACS Synth. Biol., 2022, 11, 1710–1718 CrossRef CAS.
- D. Han, et al., Single-stranded DNA and RNA origami, Science, 2017, 358, eaao2648 CrossRef.
- N. S. Vallina, E. K. S. McRae, C. Geary and E. S. Andersen, An RNA origami robot that traps and releases a fluorescent aptamer, Sci. Adv., 2024, 10, eadk1250 CrossRef CAS.
- Y. Li, et al., Comparing Charge Transport in Oligonucleotides: RNA:DNA Hybrids and DNA Duplexes, J. Phys. Chem. Lett., 2016, 7, 1888–1894 CrossRef CAS.
- Y. Li, J. M. Artés and J. Hihath, Long-Range Charge Transport in Adenine-Stacked RNA:DNA Hybrids, Small, 2016, 12, 432–437 CrossRef CAS.
- S. Chandra, et al., Single-molecule conductance of double-stranded RNA oligonucleotides, Nanoscale, 2022, 14, 2572–2577 RSC.
- S. Chandra, et al., Charge transport in individual short base stacked single-stranded RNA molecules, Sci. Rep., 2023, 13, 19858 CrossRef CAS.
- M. Gonçalves, B. Amorim, F. Riche, E. V. Castro and P. Ribeiro, Incommensurability enabled quasi-fractal order in 1D narrow-band moiré systems, Nat. Phys., 2024, 20, 1933–1940 Search PubMed.
- A. Henning-Knechtel, D. Thirumalai and S. Kirmizialtin, Differences in ion-RNA binding modes due to charge density variations explain the stability of RNA in monovalent salts, Sci. Adv., 2022, 8, eabo1190 Search PubMed.
- J. F. Hopkins, S. Panja, S. A. N. McNeil and S. A. Woodson, Effect of salt and RNA structure on annealing and strand displacement by Hfq, Nucleic Acids Res., 2009, 37, 6205–6213 CrossRef CAS.
- J. J. McDermott, B. Civic and A. Barkan, Effects of RNA structure and salt concentration on the affinity and kinetics of interactions between pentatricopeptide repeat proteins and their RNA ligands, PLoS One, 2018, 13, e0209713 CrossRef CAS.
- Y.-L. Chen and L. Pollack, Salt Dependence of A-Form RNA Duplexes: Structures and Implications, J. Phys. Chem. B, 2019, 123, 9773–9785 CrossRef CAS.
- S. K. Kolev, P. St. Petkov, T. I. Milenov and G. N. Vayssilov, Sodium and Magnesium Ion Location at the Backbone and at the Nucleobase of RNA: Ab Initio Molecular Dynamics in Water Solution, ACS Omega, 2022, 7, 23234–23244 CrossRef CAS.
- C. J. Bustamante, Y. R. Chemla, S. Liu and M. D. Wang, Optical tweezers in single-molecule biophysics, Nat. Rev. Methods Primers, 2021, 1, 1–29 CrossRef.
- R. Tapia-Rojo, M. Mora and S. Garcia-Manyes, Single-molecule magnetic tweezers to probe the equilibrium dynamics of individual proteins at physiologically relevant forces and timescales, Nat. Protoc., 2024, 19, 1779–1806 CrossRef CAS.
- D. A. Case, et al., AmberTools, J. Chem. Inf. Model., 2023, 63, 6183–6191 CrossRef CAS.
- D. R. Roe and T. E. I. Cheatham, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- H. Mohammad and M. P. Anantram, Charge transport through DNA with energy-dependent decoherence, Phys. Rev. E, 2023, 108, 044403 CrossRef CAS.
- A. De, H. Mohammad and Y. Wang, et al., Performance analysis of DNA crossbar arrays for high-density memory storage applications, Sci. Rep., 2023 DOI:10.1038/s41598-023-33004-6.
- A. De et al. , Modeling and Simulation of DNA Origami based Electronic Read-only Memory. in 2022 IEEE 22nd International Conference on Nanotechnology (NANO) 385–388, 2022 DOI:10.1109/NANO54668.2022.9928676.
- H. Mohammad, et al., Role of intercalation in the electrical properties of nucleic acids for use in molecular electronics, Nanoscale Horiz., 2021, 6, 651–660 RSC.
- S. R. Patil, et al., Quantum Transport in DNA Heterostructures: Implications for Nanoelectronics, ACS Appl. Nano Mater., 2021, 4, 10029–10037 CrossRef CAS.
- J. M. Artés, Y. Li, J. Qi, M. P. Anantram and J. Hihath, Conformational gating of DNA conductance, Nat. Commun., 2015, 6, 8870 CrossRef.
- Exploring Network Structure, Dynamics, and Function using NetworkX – SciPy Proceedings. https://proceedings.scipy.org/articles/TCWV9851 (2008).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00241a |
| This journal is © The Royal Society of Chemistry 2025 |