Open Access Article
Open Access ArticlePorous carbon nitride fullerenes: a novel family of porous cage molecules†
Zacharias G.
Fthenakis
 *ab and
Nektarios N.
Lathiotakis
*ab and
Nektarios N.
Lathiotakis
 *b
*b
aIstituto Nanoscienze, Consiglio Nazionale delle Ricerche (CNR), and National Enterprise for nanoScience and nanoTechnology (NEST), Scuola Normale Superiore, 56127 Pisa, Italy. E-mail: zacharias.fthenakis@nano.cnr.it
bTheoretical and Physical Chemistry Institute, National Hellenic Research Foundation, GR-11635, Athens, Greece. E-mail: fthenak@eie.gr; lathiot@eie.gr
First published on 2nd April 2025
Abstract
A novel family of cage molecules, porous carbon nitride fullerenes (PCNFs), is designed, proposed and studied theoretically. PCNFs can be considered the zero-dimensional counterparts of two-dimensional porous graphitic carbon nitrides, in analogy with icosahedral fullerenes, being the zero-dimensional counterparts of graphene. The study is focused on two representative members of the PCNF family: icosahedral C60N60 and C120N60, which are the first members of the two main sub-families of these structures. Given the advanced potential of two-dimensional graphitic carbon nitrides for several interesting applications, it is reasonable to expect that this potential extends to their zero-dimensional counterparts. The present study demonstrates the electronic, vibrational, and thermal stability of the two representative PCNFs utilizing density functional theory and molecular dynamics simulations with ReaxFF potentials. In addition, their structural, vibrational, and electronic properties are revealed.
New conceptsMolecular design plays a vital role in the development of new molecules with novel and interesting properties, and the potential to be used in several applications, which may range from catalysis and molecular trapping to the discovery of new drugs or biomolecules. Considering the relationship between a honeycomb lattice (graphene) and Goldberg polyhedra (icosahedral fullerenes), and the structural transformations that turn a honeycomb lattice (graphene) into the geometrical structure of graphitic porous carbon nitrides, a novel family of porous cage molecules with N-terminated pores, porous carbon nitride fullerenes (PCNFs), is designed and proposed. PCNFs are the zero-dimensional (0D) counterparts of two-dimensional (2D) graphitic carbon nitrides, just as icosahedral fullerenes are the 0D counterparts of graphene. This theoretical study demonstrates their dynamic, electronic, and thermal stability, as well as their unique geometrical features. Inheriting the interesting properties of 2D graphitic carbon nitrides and having these unique geometrical features, PCNFs could be ideal structures for potentially interesting applications, such as permeation, molecular trapping, catalysis, etc., beyond those of their 2D counterparts. Therefore, PCNFs have the potential to become a promising novel class of fullerene-based cage molecules opening up new avenues in nanomaterials research and technology. |
1. Introduction
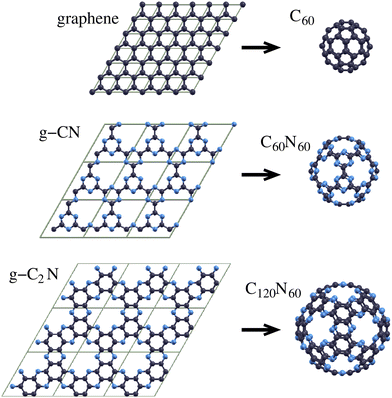
Given that fullerenes are the zero-dimensional (0D) analogues of graphene, a question that naturally arises is whether 0D fullerene analogues of two-dimensional (2D) porous graphitic carbon nitrides (g-CnNm) exist.Porous g-CnNm constitute a family of periodic graphene-based structures, incorporating substitutional N atoms in several sites of a porous graphene lattice. N atoms in these structures can be pyridinic (at the pore edges) and maybe graphitic, substituting 2- and 3-fold coordinated C atoms, respectively. Several g-CnNm have been reportedly synthesized.1–9 Two structures that have attracted considerable attention are g-CN8,9 and g-C2N,4–8 exhibiting a broad spectrum of applications, which include catalysis2,10–19 (such as photocatalytic water splitting2,16–18 and single atom catalysis19), gas separation20–26 and nanofiltration,27 water desalination,28 hydrogen storage,29 and anode materials for Li-ion batteries.30 Given that porous g-CnNm and their 0D counterparts would be structurally very similar, it is reasonable to expect that the former's intriguing properties would be inherited by the latter which may exhibit additional novel properties due to their specific cage geometry and finite size. Hence, the elevated interest in them is more than obvious.
Considering that (i) the relationship between these 0D fullerene-like structures and porous g-CnNm is analogous to the connection between icosahedral fullerenes and graphene, and (ii) the design of porous g-CnNm involves the formation of pores and substitution of appropriate C atoms with N atoms, as described above, the form of these molecules can be easily derived from Goldberg polyhedra,31 in a similar way to the design of icosahedral fullerenes. The design of such 0D structures, which we call “porous carbon nitride fullerenes” (PCNFs), involves the formation of proper pores in icosahedral fullerenes in a way that retains full icosahedral symmetry. The design process is discussed in the next section. As we show, the smallest members of icosahedral fullerenes that can be the precursors of PCNF design are C180 and C240. The PCNFs derived from them are C60N60 and C120N60, respectively, corresponding to the g-CN and g-C2N 2D structures. These PCNFs (C60N60 and C120N60) together with the corresponding 2D structures (g-CN and g-C2N, respectively) are shown in Fig. 1. In the same figure, graphene and icosahedral C60 are also shown, to emphasize the relationship between (i) graphene and C60, (ii) graphene and g-CnNm, and (iii) icosahedral fullerenes and PCNFs. In the present work, we theoretically study C60N60 and C120N60 as representatives of the PCNF family as well as C60 for comparison. Our results demonstrate the capability of this family of structures to open up new directions in nanomaterials research and technology and become the new generation of fullerene-based cage molecules.
2. Theoretical design of PCNFs
Fullerenes with rotational icosahedral symmetry are topologically equivalent to the Goldberg polyhedra,31 which contain only pentagons and hexagons. In particular, they contain exactly 12 pentagons on the vertices of an icosahedron, with its 20 equilateral triangular faces composed of hexagons in a honeycomb lattice arrangement. Each such triangular face (and in turn, the polyhedron itself) is characterized by two integer numbers (n, m), defining the lattice vector na + mb of the honeycomb lattice, which represents one of the three edges of that triangle, with a and b being the primitive lattice vectors of the honeycomb lattice.There are three classes of Goldberg polyhedra, namely (n, 0), (n, n), and (n, m) with n ≠ m. The triangular faces of the icosahedra corresponding to the first members of the (n, 0) and (n, n) classes are shown schematically in Fig. 2 with red lines. Class (n, 0) and (n, n) polyhedra (fullerenes) have full icosahedral symmetry32 (i.e. apart from the rotational icosahedral symmetry, they also have mirror symmetry), and they contain N = 20 n2 and N = 60 n2 vertices (atoms), respectively. For the Goldberg polyhedra corresponding to the triangles shown in Fig. 2, the numbers n and N are shown below each triangle. Panels (a)–(d) represent the triangles for the first (n, 0) polyhedra and panels (e)–(g) for the first (n, n) polyhedra.
Due to symmetry reasons, there is an irreducible part of each such triangle corresponding to the 1/6th of it. This irreducible part is a right triangle, shown for each case in the same figure by a green dashed line. Thus, as far as the icosahedral symmetry is retained, only the atoms in that irreducible part may behave independently, while all other atoms have an equivalent one in the irreducible part. In all cases shown in Fig. 2, the atoms in the irreducible part are numbered from 1 to 6. The atom numbered “1” (black) is the one in the pentagonal rings. The design of a fully icosahedral PCNF implies the introduction of pores into the corresponding fullerene by removing C atoms from the irreducible part of the “triangular faces” and all the equivalent C atoms in that fullerene. Then two-fold C atoms at the pore boundaries are replaced by pyridinic N atoms, and maybe some three-fold coordinated C atoms by graphitic N atoms. We should note that the above process is only for conceptualization and does not constitute a synthetic route.
The design procedure we described cannot be applied to C20 and C60, since the irreducible part of their “triangular faces” contains only one atom (see Fig. 2(a) and (e), respectively). Thus, removing that atom and its equivalents would eliminate the entire fullerene. This design procedure is also not applicable to C80. The corresponding “triangular face” of C80 has two atoms in its irreducible part (see Fig. 2(b), where these atoms are numbered “1” and “2”). If atom 1 and its equivalents are removed, atom 2 and its equivalents are left disconnected. Removing atom 2 and its equivalents results in disconnected pentagons formed by atom 1 and its equivalents. Consequently, none of the C20, C60 and C80 can be used as precursors for the formation of PCNFs. On the other hand, the next members of (n, 0) and (n, n) fullerenes, C180 and C240, respectively, can be used as precursors for the formation of the C60N60 and C120N60 PCNFs, respectively, which are studied in the present work. They are both derived by removing all pentagonal rings of C180 and C240 fullerenes, represented by atom 1 and its equivalents in Fig. 2(c) and (f), respectively. C60N60 and C120N60 are the only PCNF structures that can be derived from C180 and C240, respectively, while more than one PCNF can be derived from the next (n, 0) and (n, n) icosahedral fullerenes (e.g. the C320 and C540, respectively, and all the higher members of these fullerene subfamilies). For these fullerenes, several other options exist for removing C atoms to design PCNFs, apart from removing all pentagons, which is always an option for them.
3. Equilibrium structures – structural and vibrational properties
As already mentioned, in the present study we focus on C60N60 and C120N60 as representatives of the whole family of PCNFs. For the structural and vibrational properties, we employ density functional theory (DFT) with the state-of-the-art, range-separated, hybrid ωB97X-D33 and hybrid meta-GGA MN1534 functionals, as implemented in the Gaussian 16 code,35 with the 6-311G(d,p) basis set.The equilibrium structures for C60N60 and C120N60 are shown in Fig. 3 from two different perspectives. Their geometries obtained using the ωB97X-D and MN15 functionals are practically identical. The Cartesian coordinates of the optimal geometries are included in the ESI† (in xyz format). As we can see, they are composed of C3N3 and C4N2 hexagons, respectively, interconnected by C–C bonds. In C120N60, these interconnecting bonds and the C–C bonds within C4N2 hexagons form hexagonal carbon rings. Vibrational analysis shows that all eigenvalues of the dynamical matrix are positive (real vibrational frequencies), indicating dynamic stability. The minimum frequencies, νmin, obtained are shown in Table 1.
 | ||
| Fig. 3 Structures of (a) C60N60 and (b) C120N60 from two different viewpoints. C atoms are shown in black and N atoms in blue. | ||
| Funct. | C60N60 | C120N60 | C60 | |||
|---|---|---|---|---|---|---|
| ωB97X-D | MN15 | ωB97X-D | MN15 | ωB97X-D | MN15 | |
| d C–C, dhp | 1.520 | 1.518 | 1.478 | 1.477 | 1.448 | 1.448 |
| d C–C, dhh | 1.413 | 1.417 | 1.383 | 1.387 | ||
| d C−N | 1.327 | 1.330 | 1.325 | 1.328 | ||
| δd | 0.023 | 0.023 | 0.066 | 0.065 | ||
| D | 4.553 | 4.561 | 4.561 | 4.573 | ||
| d sphereC–C | 11.314 | 11.332 | 13.314 | 13.321 | 7.059 | 7.070 |
| d sphereN–N | 11.392 | 11.410 | 13.461 | 13.465 | ||
| IP | 9.20 | 9.23 | 8.56 | 8.08 | 8.56 | 8.01 |
| EA | 2.08 | 2.60 | 2.19 | 2.79 | 2.32 | 2.45 |
| η | 3.56 | 3.32 | 3.18 | 2.64 | 2.84 | 2.67 |
| HOMO | −9.73 | −8.68 | −8.65 | −7.61 | ||
| LUMO | −2.02 | −3.15 | −2.23 | −3.28 | ||
| Δ H–L | 7.71 | 5.53 | 6.42 | 4.32 | 6.00 | 3.92 |
| Mulliken population | ||||||
| C atoms | 0.24 | 0.20 | 0.12 | 0.095 | ||
| N atoms | −0.24 | −0.20 | −0.24 | −0.19 | ||
| ν min | 75.6 | 76.1 | 90.0 | 88.2 | 270 | 263 |
Fig. 1 shows that these structural features of C60N60 and C120N60, and their stoichiometry, are identical to those of g-CN and g-C2N, respectively. Their main morphological differences are their curvature and the pentagonal form of the pores (33333 in the Fthenakis nomenclature36,37) instead of the planarity and the hexagonal pores (333333)38 of g-CN and g-C2N. Unlike the C180 and C240 precursors, which contain pentagons and hexagons, C60N60 and C120N60 consist exclusively of hexagons.
Table 1 shows several structural properties of the two PCNFs (and C60). As we can see, the C–N bonds for both PCNFs have the same length, dC–N ≈ 1.33 Å. On the other hand, two kinds of C–C bonds were found for C120N60: those interconnecting the C4N2 hexagons with length dC–C ≈ 1.48 Å, and those interconnecting the C4N2 hexagons with length 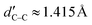 , which differ from the C–C bond lengths of C60N60 (dC–C ≈ 1.52 Å). For C60, the length of the common bonds of adjacent pentagons and hexagons (single bonds) is dhp ≈ 1.45 Å (dC–C in Table 1), and the length of the common bonds of adjacent hexagons (double bonds) is dhh ≈ 1.39 Å (
, which differ from the C–C bond lengths of C60N60 (dC–C ≈ 1.52 Å). For C60, the length of the common bonds of adjacent pentagons and hexagons (single bonds) is dhp ≈ 1.45 Å (dC–C in Table 1), and the length of the common bonds of adjacent hexagons (double bonds) is dhh ≈ 1.39 Å ( in Table 1). These values are comparable to the dC–C and
in Table 1). These values are comparable to the dC–C and  bond lengths of C60N60 and C120N60, with
bond lengths of C60N60 and C120N60, with  and
and  . This is a strong indication that the C–C bonds of C60N60 and C120N60 with lengths dC–C and
. This is a strong indication that the C–C bonds of C60N60 and C120N60 with lengths dC–C and  exhibit single and double bond characters, respectively, with the C–C bonds of C60N60 and C120N60 being weaker than those of C60, and those of C120N60 being stronger than those of C60N60. The C3N3 hexagons of C60N60 and the C4N2 hexagons of C120N60 are almost planar, with only a small outward elevation δd of the N atoms, with respect to the C atom plane (δd = 0.023 Å and 0.066 Å, respectively).
exhibit single and double bond characters, respectively, with the C–C bonds of C60N60 and C120N60 being weaker than those of C60, and those of C120N60 being stronger than those of C60N60. The C3N3 hexagons of C60N60 and the C4N2 hexagons of C120N60 are almost planar, with only a small outward elevation δd of the N atoms, with respect to the C atom plane (δd = 0.023 Å and 0.066 Å, respectively).
The diameter of the pores, defined as the diameter of the N-atom pentagon's circumscribed circle, is D ≈ 4.56 Å for both structures. Since the diameter D and the atomic environment of the pores for both C60N60 and C120N60 are practically the same, the molecular permeation properties of those pores are also expected to be similar. The local curvature is the only parameter that may differentiate these properties, varying between the two PCNFs. It is worth noting that the pore diameter falls within the range of interest for the permeation of small molecules.20–22,24,26,38 To the best of our knowledge, these pentagonal pores have not been observed in other structures and their properties make PCNFs particularly interesting.
The diameters of the two PCNFs, defined as the distance between diametrically opposite C or N atoms (dsphereC–C and dsphereN–N, respectively), are ≈11.3 and 11.4 Å for C60N60 and ≈13.3 and 13.5 Å for C120N60, i.e. the diameter of C120N60 is approximately 2 Å larger than that of C60N60, and almost twice as large as that of C60. Given the size of the PCNFs, they may hold promise as traps for small molecules or metal clusters. Molecule trapping in these systems has the potential for a wide range of applications.
4. Electronic properties
We calculate the electronic properties using the same DFT method as the one used for calculating the structural and vibrational properties of C60N60 and C120N60. Due to the icosahedral symmetry of C60N60 and C120N60, the energy levels are in most cases degenerate. In particular, the HOMOs for C60N60 and C120N60 are five- and three-fold degenerate, respectively, while the LUMOs are three- and five-fold degenerate, respectively. However, in both cases, the HOMOs are fully occupied, enhancing stability, like in the case of the aromatic ring molecules.The electron densities corresponding to all five (for C60N60) and all three (for C120N60) degenerate HOMOs are shown in Fig. 4(a) and (b), respectively, providing information on the distribution of all electrons at the HOMO energy level. As we can see, they have entirely different characters. The HOMOs of C60N60 are dominated by nitrogen sp2 lone-pair states with a minor contribution from the sp2 carbon orbitals, while for C120N60, they have the character of p⊥ orbitals. With p⊥ we mean p-orbitals directed perpendicular to the C120N60 surface locally. Moreover, one can see that the electron density of HOMOs for C120N60 is high along the C–C bonds of the C4N2 hexagons, indicating the presence of a double bond. Instead, along the C–C bonds interconnecting the C4N2 hexagons, it almost vanishes, in consistency with the presence of a single bond. These results support the discussion about the bond lengths in Section 3. It can also be seen from Fig. 4(b) that the p⊥ contribution of N atoms is relatively small compared to that of the C atoms.
The LUMOs, on the other hand, are of p⊥ orbital character for both structures, as shown in Fig. 4(c) and (d), where one of the degenerate LUMOs of C60N60 and C120N60 is shown, respectively. Although not shown, the other degenerate LUMOs have the same character differing in the location. We show the total electron density of C60N60 and C120N60 in Fig. 4(e) and (f).
Our findings on the nature of the HOMOs and LUMOs of C60N60 and C120N60 are very similar to that of the valence and conduction bands of g-CN23 and g-C2N,18 respectively. For g-CN, the valence band consists of the sp2 orbitals of the nitrogen atoms’ lone-pair electrons, lying in the structure's plane and localized on the nitrogen atoms. Instead, the conduction band is composed of pz orbitals of the C and N atoms.23 For g-C2N, the valence band is composed mainly of the pz orbitals of the C atoms, with a smaller contribution from the pz orbitals of the N atoms. Instead, the conduction band is composed mainly of pz orbitals of the N atoms.18
For both structures, there is a relatively large HOMO–LUMO gap (ΔH–L) in comparison to the differences in the other successive energy levels, indicating a clear splitting of the π occupied states from the π* unoccupied ones. The calculated HOMO, LUMO, and ΔH–L values are shown in Table 1. It is worth noting that the values of HOMO/LUMO energy levels obtained using many popular DFT approximations are, in general, not accurate predictions of the spectral properties. However, it has been demonstrated that accuracy can be substantially improved by approximations like the non-empirically tuned range-separated functionals.39–41
The drop in the HOMO–LUMO gap from C60N60 to C120N60 seems to be similar to the behavior of the gap of graphene nanoribbons, which decreases as their width increases.42 Furthermore, Mulliken population analysis reveals a weak charge transfer of ∼0.2 electrons from each N atom to C atoms in both structures, which are equally distributed to the C atoms, while the total dipole moment of PCNFs is zero, due to their icosahedral symmetry.
4.1. Ionization potentials and electron affinities
With the same DFT method, the ionization potentials (IPs) and electron affinities (EAs) of C60N60 and C120N60 were also calculated as the absolute energy differences between the neutral molecule and positive and negative ions, respectively, with full geometry relaxation. The calculated IP and EA values, as well as the values of chemical hardness η = (IP − EA)/2, are shown in Table 1. The corresponding values for C60 are also presented in the same table, showing that (a) ηPCNFs > ηC60, which indicates that C60N60 and C120N60 are electronically more stable than C60, and (b) EAPCNFs ≈ EAC60, making PCNFs promising candidates as electron acceptors in several applications, like C60. Notably, the absolute HOMO and LUMO values are relatively good measures of IPs and EAs for the state-of-the-art approximations chosen. The large ΔH–L and η values strongly suggest that the electronic state of the studied PCNF structures is particularly stable.4.2. Formation energies
The formation energies of C60N60 and C120N60 were calculated using periodic DFT calculations with the PBE functional, including D3 dispersion corrections of Grimme et al.,43 as implemented in the Quantum Espresso code.44 This methodology allows the treatment of the two molecules and their 2D counterparts at the same level of theory. We adopted the projector augmented wave method (and corresponding pseudopotentials) and kinetic energy cutoffs for the wavefunction and density of 60 and 500 Ryd, respectively. For the periodic structures, 24 × 24 × 1 k-mesh was used, while for the two molecules, Γ-point calculations were performed in a cubic supercell of a 36 Å side.The formation energy per atom, ΔE(f), of C60N60, C120N60 and C60 with respect to their 2D counterparts g-CN, g-C2N and graphene, respectively, is calculated as ΔE(f) = E0D − E2D, where E0D and E2D are the calculated total energies per atom of the 0D structures and their 2D counterparts. We found that the ΔE(f) values for C60N60, C120N60 and C60 are 0.09, 0.08 and 0.38 eV per atom, respectively. The relatively large ΔE(f) value for C60 can be explained in terms of the large bond length deviations of C60 from the bond length of graphene (d = 1.42 Å) and the corresponding relatively large bond angle deviations of the pentagonal angles (108°) from the hexagonal ones of graphene. The absence of pentagonal rings in C60N60 and C120N60 and the insignificant deviations of their bond lengths and angles from the corresponding ones of g-CN and g-C2N, respectively, significantly reduce the additional energy to form the PCNFs, which is mainly attributed to the strain energy due to the curvature. This explains the relatively small ΔE(f) values of C60N60 and C120N60.
For completeness, we also calculated the formation energies, E(f), of g-CN, g-C2N, C60N60, C120N60, and Ih-C60 fullerene with respect to graphene and N2 molecule, defined as
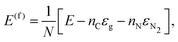 | (1) |
| 0D | 2D | |||||
|---|---|---|---|---|---|---|
| C60N60 | C120N60 | C60 | g-CN | g-C2N | Graphene | |
| E (f) (eV) | 0.38 | 0.31 | 0.38 | 0.29 | 0.23 | 0.00 |
5. Thermal stability
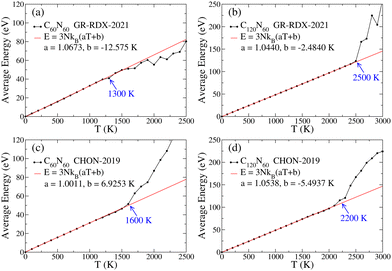
Regarding thermal stability, molecular dynamics (MD) simulations were performed utilizing the LAMMPS45 suite under NVT conditions employing the Nosé–Hoover thermostat,46,47 for 0 ≤ T ≤ 2000 K, with a 100 K increment, and the CHON-201948 and GR-RDX-202149 ReaxFF potentials. For all calculations, the time step was 0.25 ps. First, an annealing simulation was performed, under NVT conditions, using 2 × 106 time steps, from 300 K down to 0 K, followed by a conjugate gradient optimization to find the energetically optimum structure. Before each NVT simulation at a specific temperature, T, thermalization of the optimized structure at that T was performed, under NVT conditions, for 105 time steps, which was followed by an MD simulation of 2 × 106 time steps for each temperature, and the time average of the energy, E(T), for each such simulation was calculated.The obtained E(T) curves are shown in Fig. 5. A divergence in the slope of the Dulong–Petit law (E = 3NkBT) corresponding to atomic vibrations near the equilibrium positions indicates the initiation of a phase transition (usually accompanied by the coexistence of more phases), which finally leads to the fracture of the molecule. Our estimations of the transition temperature TT are shown in Fig. 5 with blue, revealing that the TT values for C60N60 and C120N60 are well above 1000 and 2000 K, respectively. Similar MD simulations for C60 with CHON-2019 predicted that TT ⪆ 3800 K, which is in agreement with older tight binding MD results,50 with 3400 < TT < 3800 K. While TT and νmin for C60N60 and C120N60 are lower than those of C60, they are still sufficiently high, to guarantee that both C60N60 and C120N60 are thermally stable at temperatures exceeding 1000 K and 2000 K, respectively.
6. On the feasibility of synthesizing C60N60 and C120N60
Although C60N60 and C120N60 were found to be extremely stable, the most important issue is their synthesis. Likely, the most promising route involves bottom-up techniques, using proper precursors, similar to the synthesis of g-CnNm. Moreover, with appropriate nanosphere precursors containing nitrogen functional groups, nitrogen-doped carbon nanospheres containing pyridinic N atoms have already been synthesized.51 Additionally, the synthesis of carbon nanospheres with g-C3N4 pores has also been reported,52,53 as well as the synthesis of spherical carbon nitride nanostructures54 with diameters ranging between 30 nm and 20 μm. In similar experimental studies, the formation of hollow mesoporous carbon nitride microspheres has also been reported.55 Therefore, the reported synthesis of both 2D g-CnNm membranes4,8,19,56,57 and carbon nanospheres58,59 as well as the minimal difference in the calculated formation energies of PCNFs compared to those of their 2D counterparts provide strong evidence for the feasibility of PCNF synthesis.7. Conclusions
In conclusion, we design and present a novel family of structures, porous carbon nitride fullerenes, representing the 0D analog of 2D porous carbon nitrides, just as fullerenes can be seen as the 0D counterparts of graphene. Our study focuses on the first members of that family of structures with icosahedral symmetry (namely C60N60 and C120N60), which are derived from the (n, 0) and (n, n) Goldberg polyhedra, respectively, following the two CN icosahedral fullerene subfamilies with N = 20n2 (C20 subfamily) and N = 60n2 (C60 subfamily), n = 1, 2, 3, …, respectively. We describe, in detail, the design process, for conceptualizing PCNFs, noting that it does not constitute a synthetic route.Performing DFT calculations with two state-of-the-art functionals (ωB97X-D and MN15), we determined the optimal geometrical properties, the HOMO and LUMO energies, the vibrational frequencies, and the IPs and EAs of C60N60 and C120N60. Our results reveal that these structures are dynamically stable, while the large values of ΔH–L and η indicate a robust electronic state. Due to their large EAs, these molecules could be used as electron acceptors. Moreover, performing molecular dynamics simulations under NVT conditions, with the CHON-2019 and GR-RDX-2021 ReaxFFs, we showed that C60N60 and C120N60 PCNFs are thermally stable well above 1000 K and 2000 K, respectively. The pore diameter (D ≈ 4.56 Å) of their 12 identical N-terminated pentagonal-like pores falls within the range of interest for the permeation of small molecules. Metallic atoms could also be captured in the pore edges for catalytic applications. The unique features of the pentagon-like pores and the particular features arising from the cage shape of these molecules make them potentially interesting for several applications well beyond their 2D counterparts. Therefore, we anticipate that the proposed novel molecules will have a pronounced impact, especially after their synthesis, opening up new directions in research and applications.
Author contributions
ZGF: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, validation, visualization, writing – original draft, and writing – review and editing. NNL: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, validation, visualization, writing – original draft, and writing – review and editing.Data availability
Data for this article are publicly available on Zenodo at https://doi.org/10.5281/zenodo.14621734.Conflicts of interest
There are no conflicts to declare.Acknowledgements
ZGF acknowledges the financial support from the project PRIN 2022 – Cod. 202278NHAM (PE11) CHERICH-C “Chemical and electrochemical energy storage materials from organic wastes: the treasure hidden in C-based materials” – CUP B53D23008590006, funded by the European Union – Next Generation EU in the context of the Italian National Recovery and Resilience Plan, Mission 4, Component 2, Investment 1.1, “Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN)”.References
- H. Montigaud, B. Tanguy, G. Demazeau, I. Alves and S. Courjault, J. Mater. Sci., 2000, 35, 2547–2552 CrossRef CAS.
- X. Wang, K. Maeda, X. Chen, K. Takanabe, K. Domen, Y. Hou, X. Fu and M. Antonietti, J. Am. Chem. Soc., 2009, 131, 1680–1681 CrossRef CAS PubMed.
- P. Kumar, E. Vahidzadeh, U. K. Thakur, P. Kar, K. M. Alam, A. Goswami, N. Mahdi, K. Cui, G. M. Bernard, V. K. Michaelis and K. Shankar, J. Am. Chem. Soc., 2019, 141, 5415–5436 CrossRef CAS PubMed.
- L. Tan, C. Nie, Z. Ao, H. Sun, T. An and S. Wang, J. Mater. Chem. A, 2021, 9, 17–33 RSC.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I.-Y. Jeon, S.-M. Jung, H.-J. Choi, J.-M. Seo, S.-Y. Bae, S.-D. Sohn, N. Park, J. H. Oh, H.-J. Shin and J.-B. Baek, Nat. Commun., 2015, 6, 6486 CrossRef CAS PubMed.
- S. S. Shinde, C. H. Lee, J.-Y. Yu, D.-H. Kim, S. U. Lee and J.-H. Lee, ACS Nano, 2018, 12, 596–608 CrossRef CAS PubMed.
- N. Fechler, N. P. Zussblatt, R. Rothe, R. Schlögl, M.-G. Willinger, B. F. Chmelka and M. Antonietti, Adv. Mater., 2016, 28, 1287–1294 CrossRef CAS PubMed.
- C. Moreira Da Silva, M. Vallet, C. Semion, T. Blin, R. Saint-Martin, J. Leroy, D. Dragoé, F. Brisset, C. Gillet, R. Guillot and V. Huc, Sci. Rep., 2023, 13, 15423 CrossRef CAS PubMed.
- J. Li, C. Cao, J. Hao, H. Qiu, Y. Xu and H. Zhu, Diamond Relat. Mater., 2006, 15, 1593–1600 CrossRef CAS.
- Y. Cao, J. Zhao, X. Zhong, G. Zhuang, S. Deng, Z. Wei, Z. Yao and J. Wang, Green Energy Environ., 2021, 6, 846–857 CrossRef CAS.
- X. Liu and L. Sheng, New J. Chem., 2022, 46, 9250–9257 RSC.
- B. L. He, J. S. Shen and Z. X. Tian, Phys. Chem. Chem. Phys., 2016, 18, 24261–24269 RSC.
- Q. Han, N. Chen, J. Zhang and L. Qu, Mater. Horiz., 2017, 4, 832–850 RSC.
- Y. Cheng, Y. Song and Y. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 6772–6782 RSC.
- S. Su, J. Ma, Z. Liu, D. Holiharimanana and H. Sun, Catalysts, 2023, 13, 578 CrossRef CAS.
- M. Ashwin Kishore, A. O. Sjåstad and P. Ravindran, Carbon, 2019, 141, 50–58 CrossRef CAS.
- H. Wang, X. Li and J. Yang, ChemPhysChem, 2016, 17, 2100–2104 CrossRef CAS PubMed.
- M. R. Ashwin Kishore and P. Ravindran, J. Phys. Chem. C, 2017, 121, 22216–22224 CrossRef CAS.
- G. F. S. R. Rocha, M. A. R. da Silva, A. Rogolino, G. A. A. Diab, L. F. G. Noleto, M. Antonietti and I. F. Teixeira, Chem. Soc. Rev., 2023, 52, 4878–4932 RSC.
- Y.-C. Rao, Z.-Q. Chu, X. Gu and X.-M. Duan, Comput. Mater. Sci., 2019, 161, 53–57 CrossRef CAS.
- Y. Qu, F. Li, H. Zhou and M. Zhao, Sci. Rep., 2016, 6, 19952 CrossRef CAS PubMed.
- Y. Qu, F. Li and M. Zhao, Sci. Rep., 2017, 7, 1483 CrossRef PubMed.
- Z. Chen, P. Li and C. Wu, RSC Adv., 2015, 5, 11791–11796 RSC.
- L. Zhu, Q. Xue, X. Li, T. Wu, Y. Jin and W. Xing, J. Mater. Chem. A, 2015, 3, 21351–21356 RSC.
- X. Chang, L. Zhu, Q. Xue, X. Li, T. Guo, X. Li and M. Ma, J. CO2 Util., 2018, 26, 294–301 CrossRef CAS.
- X. Wei, Z. Liu, Q. Hou, X. Zhang, Z. Wang, R. Zhang, Y. Yong, H. Cui and X. Li, J. Ind. Eng. Chem., 2024, 131, 329–336 CrossRef CAS.
- Y.-s Yu, R.-r Tan and H.-m Ding, Phys. Chem. Chem. Phys., 2020, 22, 16855–16861 RSC.
- M. Mehrdad and A. Moosavi, Nanotechnology, 2020, 32, 045706 CrossRef PubMed.
- P. Panigrahi, M. Desai, M. K. Talari, H. Bae, H. Lee, R. Ahuja and T. Hussain, Int. J. Hydrogen Energy, 2021, 46, 7371–7380 CrossRef CAS.
- J. Xu, J. Mahmood, Y. Dou, S. Dou, F. Li, L. Dai and J.-B. Baek, Adv. Mater., 2017, 29, 1702007 CrossRef PubMed.
- M. Goldberg, Tohoku Math. J., First Series, 1937, 43, 104–108 Search PubMed.
- R. B. King and M. V. Diudea, J. Math. Chem., 2006, 39, 597–604 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian Inc., Wallingford CT, 2016.
- Z. G. Fthenakis, Carbon, 2022, 199, 508–519 CrossRef CAS.
- Z. G. Fthenakis, Nanomaterials, 2023, 13, 2343 CrossRef CAS PubMed.
- Z. G. Fthenakis, I. D. Petsalakis and N. N. Lathiotakis, J. Membr. Sci., 2025, 713, 123329 CrossRef CAS.
- M. E. Foster and B. M. Wong, J. Chem. Theory Comput., 2012, 8, 2682–2687 CrossRef CAS PubMed.
- Z. C. Wong, W. Y. Fan, T. S. Chwee and M. B. Sullivan, Phys. Chem. Chem. Phys., 2017, 19, 21046–21057 RSC.
- L. N. Anderson, M. B. Oviedo and B. M. Wong, J. Chem. Theory Comput., 2017, 13, 1656–1666 CrossRef CAS PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- M. Kowalik, C. Ashraf, B. Damirchi, D. Akbarian, S. Rajabpour and A. C. T. van Duin, J. Phys. Chem. B, 2019, 123, 5357–5367 CrossRef CAS PubMed.
- Z. G. Fthenakis, I. D. Petsalakis, V. Tozzini and N. N. Lathiotakis, Front. Chem., 2022, 10, 951261 CrossRef CAS PubMed.
- S. G. Kim and D. Tománek, Phys. Rev. Lett., 1994, 72, 2418–2421 CrossRef CAS PubMed.
- H. Zhang, J. Hu, Y. Liu, C. Lin, X. Zhang and Y. Zhang, ACS Appl. Nano Mater., 2023, 6, 22956–22967 CrossRef CAS.
- Q. Song, J. Li, L. Wang, L. Pang and H. Liu, Inorg. Chem., 2019, 58, 10802–10811 CrossRef CAS PubMed.
- Y. Tang, X. Wang, J. Chen, X. Wang, D. Wang and Z. Mao, Carbon, 2020, 168, 458–467 CrossRef CAS.
- J. L. Zimmerman, R. Williams, V. N. Khabashesku and J. L. Margrave, Nano Lett., 2001, 1, 731–734 CrossRef CAS.
- J. Li, L. Han, X. Ye, M. Zhang, Y. Hu and T. Jiang, Particuology, 2020, 53, 186–191 CrossRef CAS.
- T. S. Miller, A. B. Jorge, T. M. Suter, A. Sella, F. Corà and P. F. McMillan, Phys. Chem. Chem. Phys., 2017, 19, 15613–15638 RSC.
- C.-Y. Wang, K. Maeda, L.-L. Chang, K.-L. Tung and C. Hu, Carbon, 2022, 188, 482–491 CrossRef CAS.
- J. Liu, S. Z. Qiao, H. Liu, J. Chen, A. Orpe, D. Zhao and G. Q. M. Lu, Angew. Chem., Int. Ed., 2011, 50, 5947–5951 CrossRef CAS PubMed.
- Z.-G. Liu, X.-X. He, J.-H. Zhao, C.-M. Xu, Y. Qiao, L. Li and S.-L. Chou, Chem. Commun., 2023, 59, 4257–4273 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nh00091b |
| This journal is © The Royal Society of Chemistry 2025 |