An ultrathin all-dielectric terahertz metamaterial with quasi-BIC induced angular dispersion
Daoye
Zheng
and
Yu-Sheng
Lin
 *
*
Sichuan University, Chengdu, 610207, China. E-mail: yusheng.lin@scupi.cn
First published on 9th April 2025
Abstract
One typical characteristic of conventional all-dielectric terahertz metamaterials is their thickness, which is designed to be dozens of, or even one hundred microns, to reduce the leakage of the resonant field to the substrate. In the frequency range of 2 THz to 3 THz, we propose a substrate-free ultra-thin all-dielectric terahertz metamaterial (UATM) composed of a silicon (Si) dual-ellipse array and silicon dioxide (SiO2) supporting layer with thicknesses of 5 μm and 2 μm, respectively. The UATM exhibits quasi-bound state in the continuum (quasi-BIC) modes related to the tilt angle and period parameters. Moreover, due to the strong electromagnetic field near the interfaces and large interaction area, the UATM exhibits a high refractive index sensitivity exceeding 1.00 THz per RIU. Furthermore, at oblique incident angles ranging from 0° to 25°, the resonant quality factor (Q-factor) of the UATM remains higher than 100, and the sensitivities to the incident angle are 22.53 and 26.17 GHz per degree with a linear range of 0.498 THz and 0.438 THz, respectively. These properties indicate the potential applications of the UATM in high sensitivity biochemical sensing and multifunctional narrowband filtering fields.
New conceptsThe majority of all-dielectric terahertz (THz) metamaterials are configured on thick substrates. To minimize the leakage of resonant energy to the substrate, their thicknesses are usually designed to be dozens of, or even one hundred microns. In this article, we propose a substrate-free ultra-thin all-dielectric terahertz metamaterial (UATM) composed of a tilted silicon (Si) dual-ellipse array and silicon dioxide (SiO2) supporting layer with thicknesses of only 5 μm and 2 μm, respectively. The UATM exhibits a quasi-bound state in the continuum (quasi-BIC) modes that relate to the tilt angle and period parameters. The ultrathin thickness and substrate-free design enable stronger electric field localization near the interfaces and larger spatial overlap area with the analyte, thereby improving the refractive index sensitivity to greater than 1 THz per RIU, higher than that of conventional THz metamaterials. Furthermore, the UATM exhibits notable angular dispersion properties. Within an incident angle range of 25°, the resonant quality factor (Q-factor) of the UATM remains higher than 100. In the linear dispersion ranges of 0.498 THz and 0.438 THz, the sensitivities to the incident angle are 22.53 and 26.17 GHz per degree. These properties indicate the UATM's application potential in highly sensitive biochemical sensing and multifunctional narrow band filtering. |
Introduction
Terahertz (THz) waves are electromagnetic waves with frequencies ranging from 0.1 THz to 10 THz. They have attracted much attention because of their potential applications in the next generation of wireless communication,1 security inspection,2 high resolution radar,3 molecule detection,4 and astronomy.5 However, their weak interactions with natural materials lead to a lack of high-performance THz devices, which is known as the “THz gap”.6 Luckily, metamaterials, artificially designed and manufactured subwavelength micro-/nanostructure arrays with novel optical properties, have the capability to flexibly and efficiently manipulate THz waves.7 Based on surface plasmon resonance and Mie scattering, well-designed metamaterials can flexibly manipulate the amplitude, phase, polarization, wavefront, and angular momentum of electromagnetic waves from the microwave to ultraviolet range.8–18 Metamaterials have been widely explored for application in electromagnetic cloaking,19,20 biochemical sensing,21–24 integrated imaging,25 customized thermal emission,26 and optical communication.27Meanwhile, benefiting from high freedom of design, metamaterials have become an ideal platform to explore the basic properties and applications of some novel physical mechanisms. Recently, bound states in the continuum (BIC), special non-radiative modes with infinite Q-factors that fall but decouple with the continuum, have been introduced in metamaterials to enhance the resonant strength and increase resonant Q-factors.28,29 In reality, a perfect BIC mode cannot be directly observed in spectra, thus quasi-BIC modes with slight coupling to the continuum, providing finite but still high Q-factors, receive more attention in real applications.30 Generally, BIC modes can be divided into symmetry-protected BIC (SP-BIC) and accidental BIC.31 The decoupling of SP-BIC to the continuum is from the orthogonality of resonant modes to the radiative channel.30 By importing asymmetry parameters, the BIC mode will gradually convert to the quasi-BIC mode. In 2018, K. Koshelev et al. proposed the classical tilted dual-ellipse structure, and demonstrated that the Q-factor of the SP-BIC mode exhibits an inverse square relationship with the asymmetric parameters of the system.32 In contrast, accidental BIC is derived from the destructive interference of radiative resonances and can be tuned by controlling the coupling strength. Fabry–Pérot BIC (FP-BIC) is a kind of typical accidental BIC that can be seen as the standing wave in a FP cavity.33 For example, G. Yang et al. configured a metamaterial on a metallic mirror and controlled the thickness of the metamaterial to realize narrowband perfect absorption.34 Friedrich–Wintgen BIC (FW-BIC) is another kind of accidental BIC, and is derived from the coupling of two or more resonances. When the two resonances are tuned to the same frequency, one mode converts into a BIC mode while the loss of another mode is doubled.35 For example, by controlling the coupling between a plasmonic mode and photonic mode, S. Azzam et al. demonstrated the FW-BIC mode in a metallic grating covered by a dielectric waveguiding layer under oblique incidence.36 In the THz band, X. Zhao et al. designed a multiple split-ring resonator (SRR) with a LC mode and dipole mode to stimulate a BIC mode featuring the disappearance of an electromagnetic induced transparency (EIT) peak.37
However, owing to the limitation of the intrinsic ohmic loss, high Q-factor resonance is not easy to be realized in metallic metamaterials, especially in the THz band.38 All-dielectric metamaterials, with much lower intrinsic loss can support higher Q-factor resonances, but most conventional metamaterials are fabricated on a thick substrate. The presence of a thick substrate leads to resonant energy leakage, thereby weakening the resonant amplitude and decreasing the Q-factor.39 Therefore, the thicknesses of all-dielectric metamaterials in the THz band are usually designed to be dozens of, or even one hundred microns, to better localize the resonant field.40–43 Even if applying lithium tantalate (LiTaO3) with a very high permittivity of 41.4, the metamaterial configured on a quartz substrate still requires a thickness of 11 μm (∼0.073 λ).44 Furthermore, the existence of a substrate will also result in the waste of the lower surface area for light–matter interaction, which directly leads to the low sensitivity of the metamaterial to the change in the background refractive index.
To overcome the above drawback, researchers have tried to fabricate three-dimensional metamaterials in which the resonant field is far from the substrate. W. Wang et al. proposed a series of vertical split ring resonators (SRRs) to enlarge the light–matter interaction areas and realized a maximum sensitivity of 788 GHz per RIU.45 H. Silalahi et al. configured a planar SRR on a patterned thick photoresist to generate floating metamaterials. The obtained sensitivity was 532 GHz per RIU.46 Nevertheless, three-dimensional metamaterials cannot fully eliminate the substrate effect, and it is still challenging in real fabrication. A more drastic method involves removing the substrate to increase the interaction area and reducing the thickness to leak the resonant field into the background environment. Recently, T. Lin et al. proposed a substrate-free metamaterial consisting of a single patterned metallic layer with a thickness of 10 μm, and realized a highest sensitivity of 0.86 THz per RIU.39 Remarkably, the Q-factors of metallic metamaterials are usually low, thus leading to a relatively low figure of merit (FOM), while dielectric metamaterials can provide a higher Q-factor but lower sensitivity. Similarly, by removing the substrate and properly optimizing the geometry design, the sensitivity of all-dielectric metamaterials can be improved. A. Leitis et al. have demonstrated the technological feasibility and fabricated a series of substrate-free metamaterials working in the mid-infrared band.47 In 2024, W. Adi et al. developed a membrane metasurface composed of a radius perturbed circle hole array to enhance the vibrational coupling to molecules in the infrared band.48 Recently, S. Rosas et al. designed a free-standing metasurface with tilted ellipse holes on a membrane and applied its scaling arrays to construct a fingerprint sensor.49 These research works usually focus on the sensing application in the infrared band, but few of them explore dielectric free-standing metamaterials in the THz band. Furthermore, the substrate-free design enables dielectric metamaterials much thinner and lighter to support further integration with micro-electro-mechanical system (MEMS) micro actuators to realize reconfigurable and multifunctional meta-devices.
In this article, we propose a substrate-free ultrathin all-dielectric THz metamaterial (UATM) consisting of Si dual-ellipse structures and a SiO2 supporting layer with thicknesses of 5 μm and 2 μm, respectively. SP-BIC and FW-BIC modes can be stimulated by properly configuring the asymmetry parameter and period parameters, respectively. Moreover, the ultrathin thickness and substrate-free design enable a strong field distribution in the background environment near the surface of the UATM and larger interaction area, thus increasing the sensitivity to more than 1.00 THz per RIU. Furthermore, the UATM exhibits a broad and linear angular dispersive range with sensitivities to the incident angle of 22.53 and 26.17 GHz per degree within a broad range exceeding 0.40 THz and within an incident angle of 25°. These results demonstrate the considerable potential of the UATM in highly sensitive sensing and multifunctional free space light filtering applications.
Design and method
As shown in the schematic diagram in Fig. 1(a), the Si dual-ellipse array with a thickness of 5 μm is configured on the buried SiO2 layer with a thickness of 2 μm, while the Si substrate layer below the buried oxide layer can be removed by using the deep reactive ion etching (DRIE) technique. The angles φ and θ are the azimuth angle and incident angle of the incident THz wave, respectively. k is the wave vector of the incident light. The geometry parameters of the UATM are shown in Fig. 1(b), where α is the rotation angle of the ellipse structures, RS and RL are the radii along the shorter axis and longer axis, and Px and Py are the periods along the x- and y-axis directions. These initial parameters are set as α = 20°, RS = 10 μm, RL = 40 μm, and Px = Py = 100 μm.To accurately measure the optical properties of the UATM, electromagnetic simulation software Lumerical finite difference time domain (FDTD) solutions is applied to calculate the resonant electromagnetic field distributions and transmission spectra. In the simulation, the incident light is x-polarized plane wave, a periodic boundary condition is applied in the x- and y-axis directions, and a perfect matched layer is applied in the z-axis direction. The complex refractive index data of Si and SiO2 in the THz band are from the built-in material database of lumerical FDTD.
Results and discussion
Fig. 1(c) shows the transmission spectra of four designs with the same unit cells. When the metamaterial (5 μm thick Si dual-ellipse array) is configured on a thick Si (500 μm in thickness) or SiO2 (500 μm in thickness) substrate, there is no obvious resonant mode in the frequency region from 2.0 THz to 3.0 THz. This is because the introduction of the substrate can promote the redshift of the resonance.50 Meanwhile, the metamaterial is not thick enough to localize a resonant electromagnetic wave with a longer wavelength, and the resonant electromagnetic field will largely leak into the substrate with a small but nonzero loss as shown in Fig. 4(a). In contrast, when the metamaterial is placed in a homogeneous air background, there are two obvious narrowband resonant modes at 2.650 THz and 2.955 THz. This indicates that the Si metamaterial with a thickness smaller than λ/20 can still support strong resonances. However, the metamaterial cannot directly float in air without any support or anchor in reality. A potentially feasible solution is employing the existing buried oxide layer in a silicon on insulator (SOI) wafer as a supporting layer. This still supports dual-resonance denoted as mode 1 and mode 2 at 2.518 THz and 2.836 THz. In contrast to the ideally floating case without any support, the two resonances show redshifts and the resonant strength is a little weaker due to the material loss in SiO2. To better under the physical mechanism of the two modes, we apply a multipole decomposition method to calculate the scattering cross sections (SCS), which can be expressed as51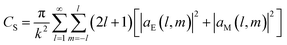 | (1) |
Mode 1 is a typical SP-BIC mode related to the asymmetry parameter α as shown in Fig. 2(a) and (b). At α = 0°, mode 1 is entirely a BIC mode with an infinite Q-factor. Upon increasing α, mode 1 gradually emerges, and blueshifts from 2.462 THz at α = 2.5° to 2.565 THz at α = 30°, while the corresponding Q-factor decreases from 540 to 51. Meanwhile, mode 2 is not sensitive to parameter α, and just slightly blueshifts 0.019 THz, as its Q-factor reduces from 160 at α = 0° to 104 at α = 30°. Moreover, the thickness of the Si metamaterial (tSi) can also affect the optical responses of the UATM, as exhibited in Fig. 2(c) and (d). At tSi = 1 μm, mode 1 is close to mode 2 in the spectra, with a Q-factor of 599, but the resonant strength is very weak. Subsequently, mode 1 gradually emerges and redshifts 0.635 THz from 2.876 THz at tSi = 1 μm to 2.241 THz at tSi = 10 μm with a Q-factor of 50. Similarly, mode 2 redshifts 0.173 THz from 2.921 THz at tSi = 1 μm to 2.748 THz at tSi = 10 μm with a decreasing Q-factor of 450 and 76, respectively. The optical properties related to tSi can be qualitatively explained by the breaking of space symmetry along the z-axis direction. At tSi = 0 μm, the structure is perfectly symmetrical along the z-axis direction, and the remaining SiO2 membrane cannot support resonances. Upon increasing tSi, the asymmetry is increased as the resonance emerges and Q-factor decreases. Notably, due to intrinsic material loss, the evolution trend of the Q-factor will not perfectly conform to an inverse square relationship.
Fig. 3 shows transmission spectra at various RL and RS values. In Fig. 3(a) and (b), mode 1 redshifts 0.357 THz from 2.837 THz at RL = 15 μm to 2.480 THz at RL = 45 μm with the Q-factor decreasing from 307 to 103. Mode 2 remains relatively stable, and slightly redshifts 0.066 THz, while the corresponding Q-factor decreases from 196 to 117 and then increases to 141. In Fig. 3(c) and (d), upon changing RS from 5.0 μm to 15 μm, mode 1 redshifts 0.315 THz from 2.718 THz to 2.403 THz with Q-factors of 216 and 89, respectively. Meanwhile, mode 2 redshifts 0.215 THz from 2.919 THz to 2.704 THz, as the Q-factor substantially decreases from 420 to 42.
The configuration of the supporting layer will also affect the optical properties of the UATM. The effect of the thickness of the SiO2 layer (tSiO2) is shown in Fig. 4(a) and (c). Upon increasing tSiO2 from 0 μm to 10 μm, mode 1 exhibits an obvious redshift of 0.455 THz from 2.649 THz at tSiO2 = 0 μm to 2.194 THz at tSiO2 = 10 μm, with a relatively stable Q-factor remaining between 113 and 128. With similar trends, mode 2 shows a redshift of 0.565 THz, from 2.954 THz at tSiO2 = 0 μm to 2.389 THz at tSiO2 = 10 μm, with a Q-factor decreasing from 322 to 93. In addition, the resonant amplitudes of both mode 1 and mode 2 decrease with increasing tSiO2, and ultimately, the metamaterial resonant modes will convert into classical thin-film interference modes. Fig. 4(b) and (d) show the optical response of the UATM at various etch depths of the Si layer (tetch). In the case of tetch < 5 μm, the Si layer is not totally etched and there is a thin Si layer between the patterned Si layer and SiO2 layer. The resonant modes are not supported at tetch = 0 μm and gradually emerge with the increase of tetch. From tetch = 1.5 μm to 5.0 μm, mode 1 blueshifts 0.407 THz from 2.111 THz to 2.518 THz with the Q-factor decreasing from 642 to 114. From tetch = 0.5 μm to 5.0 μm, mode 2 blueshifts 0.796 THz from 2.039 THz to 2.835 THz with the Q-factor decreasing from 590 to 124. Mode 3 exhibits a high Q-factor, but its resonant strength is very weak and quickly falls in the diffraction region. These decreasing trends of the Q-factors can be explained by the broken structure symmetry along the z-axis. The reduction of tSiO2 and increase of tetch can be considered as increasing asymmetry that results in the decrease of the resonant Q-factors, as the weak resonant strength is attributed to the material loss.
The interaction between adjacent unit cells related to period parameters has obvious influences on the optical properties of metamaterials. Fig. 5 shows these properties at various period configurations including changing only Px or Py, and simultaneously changing Px and Py, and the white dashed lines represent Rayleigh anomaly (RA) modes. In Fig. 5(a) and (b), upon increasing Px from 90 μm to 150 μm, mode 1 redshifts 0.775 THz from 2.675 THz to 1.900 THz with the Q-factor increasing from 63 to 522, since the coupling strength of mode 1 and RA is enhanced. In contrast, mode 2 is insensitive to the changing of Px. In Fig. 5(c) and (d), from Py = 80 μm to Py = 100 μm, mode 1 remains stable in resonant amplitude, Q-factor and resonant frequency, while mode 2 redshifts 0.731 THz from 3.357 THz to 2.626 THz. Subsequently, with the further redshift of the RA, the spectra of mode 1 and mode 2 become very close and show avoided crossing character, which indicates their strong coupling. The Q-factor of mode 2 quickly increases, and the corresponding resonant linewidth nearly disappears at Py = 113 μm, and then mode 1 and mode 2 exchange their relational locations in the spectra. The evolution trend matches the typical features of an FW-BIC. Upon further increasing Py, mode 1 decreases in the diffraction region, while mode 2 continues to exhibit a redshift with increasing Q-factor. In Fig. 5(e) and (f), upon simultaneously changing Px and Py from 90 μm to 150 μm, mode 1 redshifts 0.741 THz from 2.666 THz to 1.925 THz with the Q-factor increasing from 80 to 565, as mode 2 redshifts 1.097 THz from 3.064 THz to 1.967 THz with the Q-factor increasing from 95 to 713.
In fact, the sensitivities of mode 1 and mode 2 to the period parameters are determined by their far-field radiation patterns. Fig. 1(d) shows that mode 1 is dominated by the MD and EQ, whose radiation fields present destructive interference along the y-axis and constructive interference along the x-axis. Therefore, mode 1 is sensitive to Px but insensitive to Py. Mode 2 is dominated by the ED along the x-axis, and the radiation field is along the y-axis. Therefore, mode 2 is sensitive to Py but insensitive to Px. Upon increasing the period parameters, the coupling strength between the resonant modes and RA is enhanced to support lattice resonance, thus improving the resonant Q-factors.
Due to the ultrathin thickness, the resonant light field cannot be totally localized in the interior of the unit cells. Therefore, the field near the interface will be stronger and have the potential to improve the refractive index sensitivity of dielectric THz metamaterials. Fig. 6 shows transmission spectra of the UATM at various background refractive indices (n) and corresponding Q-factors, resonances, sensitivities and FOM. Upon changing n from 1.00 to 1.55, mode 1 redshifts 0.644 THz from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518 THz to 1.874 THz. Due to the coupling to the RA, the redshift trend is fitted as a quadratic function as expressed by f1 = 0.24879n2 − 1.80925n + 4.08003, and then R2 = 0.99999 is obtained. The corresponding Q-factor increases from 114 to 1109. Mode 2 redshifts 0.917 THz from 2.836 THz to 1.919 THz with the Q-factor increasing from 124 to 900, which can be fitted as f2 = 0.98312n2 − 4.16559n + 6.01599, and then R2 = 0.99997 is obtained. In Fig. 6(c), the sensitivity of mode 1 decreases from 1.268 THz per RIU at around n = 1.05 to 1.023 THz per RIU at around n = 1.55, with corresponding FOM of 72 and 605. Meanwhile, the sensitivity of mode 2 decreases from 2.203 THz per RIU to 1.218 THz per RIU with corresponding FOM of 119 and 572. Compared to most conventional dielectric metamaterials with substrates, even metallic metamaterials in the THz band, the UATM exhibits a higher sensitivity exceeding 1.00 THz per RIU with comparable Q-factors and FOM.
518 THz to 1.874 THz. Due to the coupling to the RA, the redshift trend is fitted as a quadratic function as expressed by f1 = 0.24879n2 − 1.80925n + 4.08003, and then R2 = 0.99999 is obtained. The corresponding Q-factor increases from 114 to 1109. Mode 2 redshifts 0.917 THz from 2.836 THz to 1.919 THz with the Q-factor increasing from 124 to 900, which can be fitted as f2 = 0.98312n2 − 4.16559n + 6.01599, and then R2 = 0.99997 is obtained. In Fig. 6(c), the sensitivity of mode 1 decreases from 1.268 THz per RIU at around n = 1.05 to 1.023 THz per RIU at around n = 1.55, with corresponding FOM of 72 and 605. Meanwhile, the sensitivity of mode 2 decreases from 2.203 THz per RIU to 1.218 THz per RIU with corresponding FOM of 119 and 572. Compared to most conventional dielectric metamaterials with substrates, even metallic metamaterials in the THz band, the UATM exhibits a higher sensitivity exceeding 1.00 THz per RIU with comparable Q-factors and FOM.
To compare the sensing performance of the UATM with those in other reports in the literature, these performances are summarized in Table 1. For convenience, we use linear functions to fit the frequency shift of the UATM. Mode 1 and mode 2 are fitted as f1 = 3.683 − 1.175n, R2 = 0.99884, and f2 = 4.447 − 1.658n, R2 = 0.99103, respectively. The work in ref. 44 used the low loss and high refractive index material LiTaO3 on a SiO2 substrate, and shows a high Q-factor of 1.2 × 105 and sensitivity of 0.489 THz per RIU in the same frequency range. In our work, the material loss is taken into consideration, and the asymmetry parameter (α = 20°) is not very small, so the Q-factor of the UATM is smaller but the sensitivity is much higher. ref. 45 and 46 propose a 3D SRR and floating SRR that enable electric fields far from the substrate and enlarge the light–matter interaction area, showing high sensitivities of 0.788 and 0.532 THz per RIU. In ref. 52 and 53, EIT and BIC are introduced into traditional SRRs, obtaining sensitivities of 0.496 and 0.674 THz per RIU. Ref. 39 proposes a free-standing metallic metamaterial with a BIC mode, realizing a high sensitivity of 0.86 THz per RIU in the frequency range of 0.2 THz to 1.4 THz. In comparison to these works, our work can realize average sensitivities of 1.175 THz per RIU and 1.658 THz per RIU (the minimum values at n = 1.55 are 1.023 THz per RIU and 1.218 THz per RIU), higher than conventional dielectric metamaterials and even some metallic metamaterials, with high Q-factors of more than 100 (higher than metallic metamaterials). These results show the considerable potential of the UATM in THz sensing applications.
| Ref. | Mechanism | Frequency range (THz) | Q-factor | Sensitivity (THz per RIU) |
|---|---|---|---|---|
| 44 | BIC + LiTaO3 on substrate | 2.0–2.5 | 1.2 × 105 | 0.489 |
| 45 | 3D SRR | 0.6–1.6 | ∼20 | 0.788 |
| 46 | Floating SRR | 0.2–1.0 | — | 0.532 |
| 52 | EIT | 1.6–2.5 | — | 0.496 |
| 53 | BIC in SRR | 1.3–2.3 | 50 | 0.674 |
| 39 | BIC + free-standing metallic metamaterial | 0.2–1.4 | 14.7 | 0.86 |
| This work | BIC + substrate free dielectric metamaterial | 1.8–2.9 | 100–1000 | 1.175, 1.658 |
Fig. 7 shows angular dispersion spectra of the UATM. Upon increasing the incident angle θ, the RA, marked as a white dashed line, gradually redshifts. At φ = 0°, mode 1 shows an obvious redshift of 0.498 THz from 2.514 THz at θ = 1° to 2.016 THz at θ = 25°. From θ = 4° to θ = 25°, mode 1 shows a high linearity for the θ value, and the linear fitting function can be expressed as f1 = −0.02253θ + 2.57066, and R2 = 0.99935 is obtained. As mode 1 and the RA get closer, the Q-factor of mode 1 increases from 112 at θ = 1° to 447 at θ = 25°, and the transmittance at the resonant frequency is lower than 20%, which means the resonance intensity is still strong. Mode 2 remains stable from θ = 0° to θ = 3° with a Q-factor of 111, and then falls in the diffraction region with a Q-factor of 67 at θ = 4°.
At φ = 90°, mode 1 remains stable between θ = 0° and θ = 6°, while mode 2 exhibits a blueshift and quickly falls into the diffraction region. Mode 3 is a quasi-BIC mode only under oblique incidence conditions. It shows a redshift of 0.172 THz from 2.774 THz at θ = 1° to 2.602 THz at θ = 6°. Remarkably, the resonant linewidth of mode 3 gradually narrows and disappears at around θ = 7°, and the coupling between mode 1 and mode 3 also generates a typical avoided crossing shape, resulting in a FW-BIC mode. Subsequently, mode 1 exhibits a high but decreasing Q-factor and quickly falls in the diffraction region. Mode 3 continues to redshift 0.438 THz from 2.397 THz at θ = 8° to 2.059 THz at θ = 25°, and the resonant frequency can be fitted as f3 = −0.02617θ + 2.70095, and R2 = 0.99794 is obtained. The Q-factor of mode 3 exhibits an obvious increase from 100 at θ = 8° to 450 at θ = 25°. The transmittance at 2.059 THz (mode 3) at θ = 25° is 0.11. This indicates that the resonant strength is still robust. The proposed UATM can potentially be integrated with MEMS microactuators to realize a tunable metamaterial with angle dependence, and then unlock the rich angular dispersion properties of quasi-BIC to construct real-time reconfigurable and multifunctional filtering devices.
Conclusion
We propose a substrate-free ultrathin all-dielectric THz metamaterial with a total thickness of 7 μm, and investigate the quasi-BIC mode with a Q-factor higher than 100. Mode 1 and mode 2 are sensitive to the period parameters Px and Py, respectively. Specifically, a FW-BIC mode can be stimulated by the strong coupling of the redshifting resonant modes driven by the RA. Meanwhile, the UATM shows high sensitivity (higher than 1 THz per RIU) to the background refractive index, providing a potential design method to enhance the sensitivity for high performance biochemical sensing based on dielectric metamaterials. Additionally, the UATM has a broad and linear angular dispersion range exceeding 0.40 THz within an incident angle range of 25°. This work provides a feasible design of ultrathin all-dielectric metamaterials with high Q-factors in the THz band and shows the application potential in highly sensitive biochemical sensing, multifunctional narrowband filtering, etc.Data availability
All data generated or analyzed during this study are included in this published article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from Guangdong Science and Technology Program (2024A0505050007) and Guangdong Basic and Applied Basic Research Foundation (2024A1515013019).References
- Y. Huang, Y. Shen and J. Wang, From Terahertz Imaging to Terahertz Wireless Communications, Engineering, 2023, 22, 106–124 CrossRef.
- J. Li, X. Li, N. T. Yardimci, J. Hu, Y. Li, J. Chen, Y. Hung, M. Jarrahi and A. Ozcan, Rapid sensing of hidden objects and defects using a single-pixel diffractive terahertz sensor, Nat. Commun., 2023, 14(1), 6791 CrossRef CAS PubMed.
- H. Matsumoto, I. Watanabe, A. Kasamatsu and Y. Monnai, Integrated terahertz radar based on leaky-wave coherence tomography, Nat. Electron., 2020, 3(2), 122–129 CrossRef.
- B. Liu, Y. Peng, Y. Hao, Y. Zhu, S. Chang and S. Zhuang, Ultra-wideband terahertz fingerprint enhancement sensing and inversion model supported by single-pixel reconfgurable graphene metasurface, PhotoniX, 2024, 5, 10 CrossRef.
- N. Wang, S. Cakmakyapan, Y. Lin, H. Javadi and M. Jarrahi, Room-temperature heterodyne terahertz detection with quantum-level sensitivity, Nat. Astron., 2019, 3(11), 977–982 CrossRef.
- H. Chen, W. J. Padilla, J. M. O. Zide, A. C. Gossard, A. J. Taylor and R. D. Averitt, Active terahertz metamaterial devices, Nature, 2006, 444(7119), 597–600 CrossRef CAS.
- S. Lee, S. Baek, T. Kim, H. Cho, S. Lee, J. Kang and B. Min, Metamaterials for Enhanced Optical Responses and their Application to Active Control of Terahertz Waves, Adv. Mater., 2020, 32(35), 2000250 CrossRef CAS PubMed.
- Q. Xu, Y. Lang, X. Jiang, X. Yuan, Y. Xu, J. Gu, Z. Tian, C. Ouyang, X. Zhang, J. Han and W. Zhang, Recent progress on structural coloration, Photon. Insights, 2024, 3(2), R03 CrossRef.
- Y. Hu, M. Tong, S. Hu, W. He, X. Cheng and T. Jiang, Spatiotemporal Lineshape Tailoring in BIC-Mediated Reconfigurable Metamaterials, Adv. Funct. Mater., 2022, 32(34), 2203680 CrossRef CAS.
- F. Ding, Y. Deng, C. Meng, P. C. V. Thrane and S. I. Bozhevolnyi, Electrically tunable topological phase transition in non-Hermitian optical MEMS metasurfaces, Sci. Adv., 2024, 10(5), eadl4661 CrossRef CAS PubMed.
- N. C. Wilson, E. Shin, R. E. Bangle, S. B. Nikodemski, J. H. Vella and M. H. Mikkelsen, Ultrathin Pyroelectric Photodetector with Integrated Polarization-Sensing Metasurface, Nano Lett., 2023, 23(18), 8547–8552 CrossRef CAS PubMed.
- S. Wang, Z. L. Deng, Y. Wang, Q. Zhou, X. Wang, Y. Cao, B. O. Guan, S. Xiao and X. Li, Arbitrary polarization conversion dichroism metasurfaces for all-in-one full Poincare sphere polarizers, Light: Sci. Appl., 2021, 10(1), 24 CrossRef CAS PubMed.
- G. V. Eleftheriades, M. Kim, V. G. Ataloglou and A. H. Dorrah, Prospects of Huygens' Metasurfaces for Antenna Applications, Engineering, 2022, 11, 21–26 CrossRef.
- S. Liu, X. Wang, J. Ni, Y. Cao, J. Li, C. Wang, Y. Hu, J. Chu and D. Wu, Optical Encryption in the Photonic Orbital Angular Momentum Dimension via Direct-Laser-Writing 3D Chiral Metahelices, Nano Lett., 2023, 23(6), 2304–2311 CrossRef CAS PubMed.
- T. J. Cui, L. Li, S. Liu, Q. Ma, L. Zhang, X. Wan, W. X. Jiang and Q. Cheng, Information Metamaterial Systems, iScience, 2020, 23(8), 101403 CrossRef PubMed.
- N. J. Ray, J. H. Yoo, H. T. Nguyen and E. Feigenbaum, All-Glass Metasurfaces for Ultra-Broadband and Large Acceptance Angle Antireflectivity: from Ultraviolet to Mid-Infrared, Adv. Opt. Mater., 2023, 11(12), 2300137 CrossRef CAS.
- Z. Chen, S. Cheng, H. Zhang, Z. Yi, B. Tang, J. Chen, J. Zhang and C. Tang, Ultra wideband absorption absorber based on Dirac semimetallic and graphene metamaterials, Phys. Lett. A, 2024, 517, 129675 CrossRef CAS.
- Z. Li, S. Cheng, H. Zhang, W. Yang, Z. Yi, Y. Yi, J. Wang, S. Ahmad and R. Raza, Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene, Phys. Lett. A, 2025, 534, 130262 CrossRef CAS.
- X. Hu, Y. Luo, J. Wang, J. Tang, Y. Gao, J. Ren, H. Yu, J. Zhang and D. Ye, Multiband Omnidirectional Invisibility Cloak, Adv. Sci., 2024, 11(28), 2401295 Search PubMed.
- W. Li, S. Cheng, H. Zhang, Z. Yi, B. Tang, C. Ma, P. Wu, Q. Zeng and R. Raza, Multi-functional metasurface: ultra-wideband/multi-band absorption switching by adjusting guided-mode resonance and local surface plasmon resonance effects, Commun. Theor. Phys., 2024, 76(6), 65701 CrossRef.
- X. Liu, W. Chen, Y. Ma, Y. Xie, J. Zhou, L. Zhu, Y. Xu and J. Zhu, Enhancing THz fingerprint detection on the planar surface of an inverted dielectric metagrating, Photonics Res., 2022, 10(12), 2836–2845 CrossRef.
- B. Liu, Y. Peng, Z. Jin, X. Wu, H. Gu, D. Wei, Y. Zhu and S. Zhuang, Terahertz ultrasensitive biosensor based on wide-area and intense light-matter interaction supported by QBIC, Chem. Eng. J., 2023, 462, 142347 CrossRef CAS.
- Z. Zeng, H. Liu, H. Zhang, S. Cheng, Y. Yi, Z. Yi, J. Wang and J. Zhang, Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals, Phot. Nano., 2025, 63, 101347 Search PubMed.
- S. Cheng, W. Li, H. Zhang, M. N. Akhtar, Z. Yi, Q. Zeng, C. Ma, T. Sun, P. Wu and S. Ahmad, High sensitivity five band tunable metamaterial absorption device based on block like Dirac semimetals, Opt. Commun., 2024, 569, 130816 CrossRef CAS.
- T. Li, C. Chen, X. Xiao, J. Chen, S. Hu and S. Zhu, Revolutionary meta-imaging: from superlens to metalens, Photonics Insights, 2023, 2(1), R01 CrossRef.
- J. Yu, R. Qin, Y. Ying, M. Qiu and Q. Li, Asymmetric Directional Control of Thermal Emission, Adv. Mater., 2023, 35(45), 2302478 CrossRef CAS PubMed.
- C. Xu, Z. Ren, J. Wei and C. Lee, Reconfigurable terahertz metamaterials: From fundamental principles to advanced 6G applications, iScience, 2022, 25(2), 27 CrossRef.
- G. Xu, H. Xing, Z. Xue, D. Lu, J. Fan, J. Fan, P. P. Shum and L. Cong, Recent Advances and Perspective of Photonic Bound States in the Continuum, Ultrafast Sci., 2023, 3, 33 CrossRef.
- D. C. Zografopoulos and O. Tsilipakos, Recent advances in strongly resonant and gradient all-dielectric metasurfaces, Mater. Adv., 2023, 4(1), 11–34 RSC.
- C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos and M. Soljačić, Bound states in the continuum, Nat. Rev. Mater., 2016, 1(9), 16048 CrossRef CAS.
- K. Koshelev, G. Favraud, A. Bogdanov, Y. Kivshar and A. Fratalocchi, Nonradiating photonics with resonant dielectric nanostructures, Nanophotonics, 2019, 8(5), 725–745 CrossRef.
- K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov and Y. Kivshar, Asymmetric Metasurfaces with High-Q Resonances Governed by Bound States in the Continuum, Phys. Rev. Lett., 2018, 121(19), 193903 CrossRef PubMed.
- M. Kang, T. Liu, C. T. Chan and M. Xiao, Applications of bound states in the continuum in photonics, Nat. Rev. Phys., 2023, 5(11), 659–678 CrossRef.
- G. Yang, S. U. Dev, M. S. Allen, J. W. Allen and H. Harutyunyan, Optical Bound States in the Continuum Enabled by Magnetic Resonances Coupled to a Mirror, Nano Lett., 2022, 22(5), 2001–2008 CrossRef CAS PubMed.
- P. Hu, J. Wang, Q. Jiang, J. Wang, L. Shi, D. Han, Z. Q. Zhang, C. T. Chan and J. Zi, Global phase diagram of bound states in the continuum, Optica, 2022, 9(12), 1353–1361 CrossRef.
- S. I. Azzam, V. M. Shalaev, A. Boltasseva and A. V. Kildishev, Formation of Bound States in the Continuum in Hybrid Plasmonic-Photonic Systems, Phys. Rev. Lett., 2018, 121(25), 253901 CrossRef CAS PubMed.
- X. Zhao, C. Chen, K. Kaj, I. Hammock, Y. Huang, R. D. Averitt and X. Zhang, Terahertz investigation of bound states in the continuum of metallic metasurfaces, Optica, 2020, 7(11), 1548 CrossRef.
- Z. Ren, Y. Hu, W. He, S. Wan, S. Hu, Z. Yu, X. Cheng, Z. Xu and T. Jiang, Overcoming High-Quality Limitations in Plasmonic Metasurfaces for Ultrasensitive Terahertz Applications, ACS Nano, 2024, 18(32), 21211–21220 CrossRef CAS PubMed.
- T. Lin, Q. Zeng, Y. Huang, S. Zhong, T. Shi, Y. Zhong, F. Sun and Q. Zhang, Substrate-Free Terahertz Metamaterial Sensors with Customizable Configuration and High Performance, Adv. Opt. Mater., 2024, 2400689 CrossRef CAS.
- S. Han, L. Cong, Y. K. Srivastava, B. Qiang, M. V. Rybin, A. Kumar, R. Jain, W. X. Lim, V. G. Achanta, S. S. Prabhu, Q. J. Wang, Y. S. Kivshar and R. Singh, All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum, Adv. Mater., 2019, 31(37), e1901921 CrossRef PubMed.
- S. Han, P. Pitchappa, W. Wang, Y. K. Srivastava, M. V. Rybin and R. Singh, Extended Bound States in the Continuum with Symmetry-Broken Terahertz Dielectric Metasurfaces, Adv. Opt. Mater., 2021, 9(7), 2002001 Search PubMed.
- T. Lin, Y. Huang, S. Zhong, T. Shi, F. Sun, Y. Zhong, Q. Zeng, Q. Zhang and D. Cui, Passive trapping of biomolecules in hotspots with all-dielectric terahertz metamaterials, Biosens. Bioelectron., 2024, 251, 116126 CrossRef CAS PubMed.
- W. Shi, J. Gu, X. Zhang, Q. Xu, J. Han, Q. Yang, L. Cong and W. Zhang, Terahertz bound states in the continuum with incident angle robustness induced by a dual period metagrating, Photonics Res., 2022, 10(3), 810 CrossRef CAS.
- Y. Wang, Z. Han, Y. Du and J. Qin, Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface, Nanophotonics, 2021, 10(2), 1295–1307 CrossRef CAS.
- W. Wang, F. Yan, S. Tan, H. Zhou and Y. Hou, Ultrasensitive terahertz metamaterial sensor based on vertical split ring resonators, Photonics Res., 2017, 5(6), 571–577 CrossRef CAS.
- H. M. Silalahi, Y. Chen, Y. Shih, Y. Chen, X. Lin, J. Liu and C. Huang, Floating terahertz metamaterials with extremely large refractive index sensitivities, Photonics Res., 2021, 9(10), 1970 CrossRef.
- A. Leitis, M. L. Tseng, A. John-Herpin, Y. S. Kivshar and H. Altug, Wafer-Scale Functional Metasurfaces for Mid-Infrared Photonics and Biosensing, Adv. Mater., 2021, 33(43), 2102232 CrossRef CAS.
- W. Adi, S. Rosas, A. Beisenova, S. K. Biswas, H. Mei, D. A. Czaplewski and F. Yesilkoy, Trapping light in air with membrane metasurfaces for vibrational strong coupling, Nat. Commun., 2024, 15, 10049 CrossRef CAS PubMed.
- S. Rosas, W. Adi, A. Beisenova, S. K. Biswas, F. Kuruoglu, H. Mei, M. Kats, D. Czaplewski, Y. Kivshar and F. Yesilkoy, Enhanced biochemical sensing with high-Q transmission resonances in free-standing membrane metasurfaces, Optica, 2025, 12(2), 178–189 CrossRef CAS.
- J. van de Groep and A. Polman, Designing dielectric resonators on substrates: Combining magnetic and electric resonances, Opt. Express, 2013, 21(22), 26285–26302 CrossRef CAS PubMed.
- P. Grahn, A. Shevchenko and M. Kaivola, Electromagnetic multipole theory for optical nanomaterials, New J. Phys., 2012, 14(9), 93033 CrossRef.
- J. Zhang, N. Mu, L. Liu, J. Xie, H. Feng, J. Yao, T. Chen and W. Zhu, Highly sensitive detection of malignant glioma cells using metamaterial-inspired THz biosensor based on electromagnetically induced transparency, Biosens. Bioelectron., 2021, 185, 113241 CrossRef CAS PubMed.
- R. Wang, L. Xu, L. Huang, X. Zhang, H. Ruan, X. Yang, J. Lou, C. Chang and X. Du, Ultrasensitive Terahertz Biodetection Enabled by Quasi-BIC-Based Metasensors, Small, 2023, 19, 2301165 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |







