Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An ultra-compact integrated phase shifter via electrically tunable meta-waveguides†
Chengkun
Dong
a,
Xiaowen
Gu
abc,
Yiyun
He
a,
Ziwei
Zhou
a,
Jiayi
Wang
a,
Zhihai
Wu
a,
Wenqi
Wang
a,
Tangsheng
Chen
bc,
Jun
Wu
 a,
Tong
Qiu
a and
Jun
Xia
a,
Tong
Qiu
a and
Jun
Xia
 *a
*a
aJoint International Research Laboratory of Information Display and Visualization, School of Electronic Science and Engineering, Southeast University, Nanjing 210096, China. E-mail: xiajun@seu.edu.cn
bNational Key Laboratory of Solid-State Microwave Devices and Circuits, Nanjing 210000, China
cNanjing Electronic Devices Institute, Nanjing 210096, China
First published on 11th March 2025
Abstract
Integrated photonics has emerged as a pivotal technology in the advancement of next-generation computing and communication devices. Thermal optical phase shifters (OPSs) have been widely used to realize a tunable Mach–Zehnder interferometer (MZI) and a micro-ring resonator (MRR), which are the building bricks for the LSI/VLSI photonic integrated circuits. Due to the thermal crosstalk and the low modulation efficiency, thermal OPSs have large-scale size and high power consumption. In this work, we embed a Mie resonant metasurface into a waveguide and use the liquid crystal to tune the phase of the propagated light, which could realize a novel integrated phase shifter based on LC meta-waveguides. We use nanofabrication to prepare the meta-waveguide integrated MZI and MRR. By applying voltage, the output of the waveguide's intensity can be changed. Compared with thermo OPSs, this new modulator has the advantages of small size (20 μm × 0.35 μm), no thermal crosstalk, low power consumption (<10 nW), and easy large-scale integration. Additionally, we apply it to the convolutional architecture and verify that it has the potential to accelerate neural network computation.
New conceptsOur study presents a major advance in the field of very large-scale integration (VLSI) of photonic integrated circuits (PICs), addressing longstanding challenges associated with the large form factors and high power consumption of on-chip components. Shrinking the area and reducing the power consumption of functional on-chip components will help photonic integrated circuits (PICs) to advance from medium-scale integration (MSI) to VLSI, driving progress in fields ranging from communication and computation to sensing. In this work, we present an ultra-compact, electrically tunable phase shifter with low power consumption, enabled by leveraging phase shifts arising from Mie-type resonances and the electrical tunability endowed by liquid crystals. Compared to current thermal optical phase shifters, the active length required for a 2π phase shift is reduced by ∼50-fold, from a few millimeters to tens of microns, and the power consumption is lowered by ∼10-fold, from hundreds of nanowatts to tens of nanowatts. Free from thermal crosstalk, we have achieved an ultra-compact Mach–Zehnder interferometer (MZI) and a micro-ring resonator (MRR), which are the two basic building bricks for photonic VLSIs. Using the proposed phase shifter, we have also demonstrated a photonic neural network for classification computing with accelerated optical convolution. |
Introduction
Integrated optical phase shifters1–3 which can control the phase of light have been widely used in various applications, including optical communication systems, quantum information processing,4 light detection and ranging (LIDAR),5,6 and sensing. Although integrated phase shifters based on the thermo-optic7,8 effects are already generally available in foundry platforms,9 their large-scale integration is limited by high power consumption and thermal crosstalk. To further enable large-scale optical phased arrays10 and optical computing architectures,11 the development of integrated optics phase shifters is progressing towards smaller size, lower power consumption, and higher efficiency.12Recently, researchers have been working on developing novel phase shifters13 based on new materials and new modulation mechanisms. One of them is based on MEMS, which tune the refractive index by moving the waveguide mechanically.14 Hermetic sealing is difficult to use in practical applications. Another promising way is using phase change materials (PCMs) as active materials.15 Normally, they consume too much energy during the phase change process. Additionally, phase shifters based on the Pockels electro-optic effect have attracted attention due to their ultrafast response and low power consumption. Materials such as lithium niobate (LN),16 barium titanate,17 and electro-optic polymers provide direct phase modulation through an external electric field without requiring mechanical movement or thermal effects. However, challenges such as material integration and fabrication complexity remain key considerations for practical implementation.
Tunable metasurfaces18–20 have shown great potential in various applications, ranging from imaging,21–23 sensing,24–26 and optical communication27–30 to LIDAR.31–33 Recently, there has been growing interest in developing dynamic metasurfaces based on phase-change materials (PCMs),34–36 which can modulate phase, amplitude, and polarization by thermal or optical stimulation. Another promising approach is to use graphene metasurfaces,37–39 which can dynamically control the polarization and phase of light by tuning the Fermi level of graphene through the electro-optic effect. Additionally, tuning free-carriers in transparent conducting oxides and semiconductors has been demonstrated to be a convincing way to dynamically tune the metasurfaces.40 Beyond these approaches, lithium niobate metasurfaces41 based on the Pockels effect have also emerged as an effective method for dynamic optical control, which enable fast, low-power modulation not only of the phase but also of the intensity and wavelength of light. These dynamic tuning methods provide real-time and broadband tuning capabilities, making them promising candidates for ultrafast optical switches, spatial light modulators, and adaptive optics.
Liquid crystal metasurfaces42 employ anisotropic liquid crystals to dynamically modulate the phase, polarization, and amplitude of light. This allows for the creation of ultra-thin, tunable optical elements that can be integrated into a wide range of applications, including displays, imaging systems, and optical communications. Furthermore, the use of liquid crystals allows for dynamic control of these optical responses, enabling real-time reconfiguration of the metasurface properties.
The newly developed liquid crystal metasurfaces43–45 are mostly aimed at dynamic phase modulation of free-space optical fields. However, applying an LC metasurface to an integrated phase shifter remains untapped. Here, we propose an on-chip integrated phase shifter based on liquid crystal meta-waveguides. Simulation results demonstrate that the phase modulation under liquid crystal deflection can reach 2π along the meta-waveguide at a 1550 nm wavelength. Based on this, we fabricated an MZI and MRR and experimentally verified the phase shift characteristics by measuring the intensity variation of the output waveguides. Compared with traditional thermal-optic phase shifters, our proposed phase shifter has advantages such as no thermal crosstalk, small size, and ease of large-scale integration. We also applied the proposed phase shifter in convolutional neural networks (CNNs), which can achieve high-speed convolution operation. All 2 × 2 convolutional kernels in modified VGG1646 have been replaced, and the classification performance of the network has not decreased. This proves that the architecture can be used to accelerate the calculation of modified VGG16. The proposed novel on-chip phase shifter is conducive to increasing the scale of integrated optics and promoting the development of optical computing and optical phased arrays.
Results and discussion
Principle
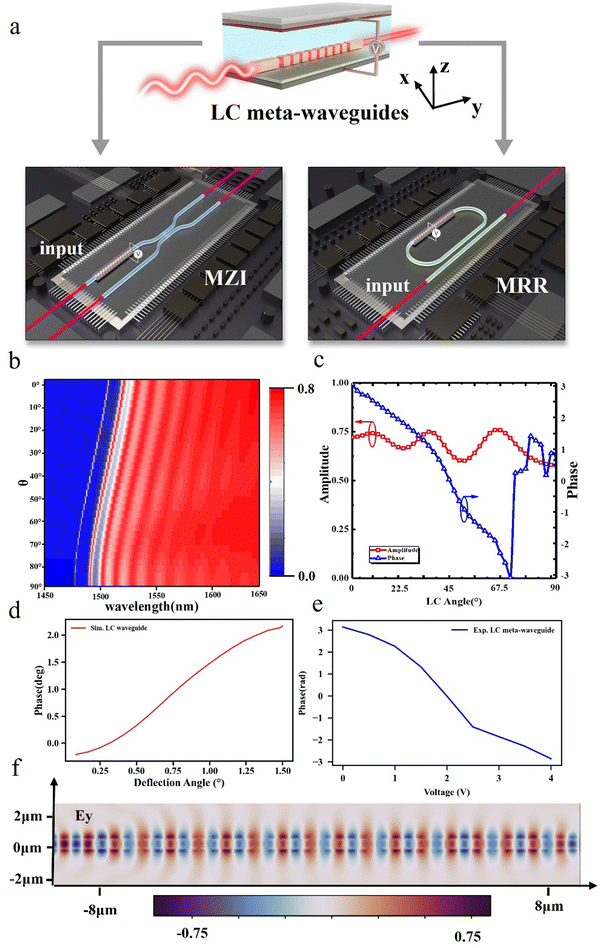
In this work, we put the metasurface integrated waveguide into the arm of the MZI and MRR to dynamically tune the phase delay inside the waveguide using a liquid crystal.Fig. 1a shows the meta-waveguides integrated with a liquid crystal. The amplitude and phase inside meta-waveguides can be modulated when applying voltage to deflect the orientation of liquid crystals. The LC molecules are influenced by the alignment layer on the surface of ITO, causing their long axes to align in the x-direction. Additionally, the metasurface exerts an orientational effect on the LC molecules, resulting in a parallel alignment of the liquid crystals.33 If the variation of the amplitude is homogeneous during the phase modulation, it can be used as a phase shifter for integrated optics. Here we design the dimensions of the meta-waveguide: the height of the meta-waveguide is 220 nm, the width of the meta-waveguide is 350 nm, the period is 400 nm, and the fill factor follows a quadratic distribution, with a maximum of 60.75% at the two ends and a minimum of 51.25% in the middle.
The phase and amplitude of the proposed LC meta-waveguide are simulated using FDTD. Fig. 1b shows the spectrum of the meta-waveguide from 1450 nm to 1650 nm under different liquid crystal deflection angles. Meta-waveguides have low transmittance at short wavelengths and high transmittance at long wavelengths. There is a blue shift in the spectrum when voltage is applied. Fig. 1c shows the changes in the amplitude and phase of the light field modulated by the designed meta-waveguide at different liquid crystal deflection angles, respectively. It can be seen that the amplitude of the meta-waveguide in the figure remains homogeneous near the wavelength of 1550 nm, while the amount of phase variation reaches 2π. Fig. 1d shows that the LC waveguide (without a metasurface structure) cannot reach 2π during LC deflection. This also proves that the metasurface structure in the waveguide has a phase enhancement effect. Fig. 1e shows the measured phase modulation of LC meta-waveguides by adding voltage at 1537.0 nm. The method of phase measurement is to use the interference optical path, which is mentioned in the following section. From the optical field diagram shown in Fig. 1f, it can be seen that the mode in the waveguide is similar to that in the meta-waveguide area, thus allowing the mode in the waveguide to evolve into the mode in the meta-waveguide.
In Fig. 2a and b, we simulated the spectral response of a meta-waveguide with a fixed period of 400 nm and varying widths in the wavelength range of 1450 nm to 1650 nm. When the width is greater than 350 nm, the LC modulation causes large amplitude fluctuations at a wavelength of 1550 nm, making it unsuitable for use in phase shifters. As shown in Fig. 1c, when the waveguide width is smaller than 350 nm, the phase modulation at a wavelength of 1550 nm is less than 2π.
In Fig. 2d and e, we also simulated the spectral response of a meta-waveguide with a fixed width of 350 nm and varying periods in the same wavelength range. Similarly, when the period is greater than 400 nm, the amplitude variation during the liquid crystal deflection process is large; as shown in Fig. 1f, when the period is smaller than 350 nm, the phase modulation is less than 2π. Therefore, to minimize amplitude variation and achieve a phase change of 2π during liquid crystal deflection at the 1550 nm wavelength, we choose a meta-waveguide period of 400 nm and a width of 350 nm. Therefore, to minimize amplitude variation and achieve a phase change of 2π during liquid crystal deflection at 1550 nm, we choose a meta-waveguide with a period of 400 nm and a width of 350 nm.
Mach–Zehnder interferometer using LC meta-waveguides
The MZI and MRR are significant integrated optical components that can be used to form optical computing arrays and optical routing networks. We applied the proposed LC meta-waveguides into them and prepared the MZI and MRR using microfabrication processes such as EBL, PECVD, etc. (see Methods). The direction of the LC alignment layer is perpendicular to the waveguide direction and is located on the upper ITO surface. The LC at the bottom, due to the anchoring effect of the meta-atomic gaps, will also be oriented perpendicular to the waveguide, so the LC molecules are considered to be parallel to both the top and bottom.Based on this, the meta-waveguide is integrated into a Mach–Zehnder interferometer to manifest the amount of phase change. The schematic is shown in Fig. 1a, where the novel MZI input part includes two waveguides, in one of which a meta-waveguide is present for realizing the phase change. There is a 3 dB directional coupler after the modulation region for interference of light on the two arms.47
 | (1) |
 | (2) |
It can be seen from eqn (1) and (2) that the intensity changes at the two output ports are in opposite phases. That is, as the phase difference increases, its transmission intensity shows an opposite trend. When the output of one port reaches the maximum value, the output of the other port is the minimum. Therefore, when the external electric field changes the liquid crystal director and thereby changes the phase modulation amount of the meta-waveguide, the intensity of the two output ports will change accordingly.
In order to eliminate the influence of liquid crystal on couplers and other waveguide structures, liquid crystal is only placed around the meta-waveguide, and the cladding material of other parts of the device is still SiO2.
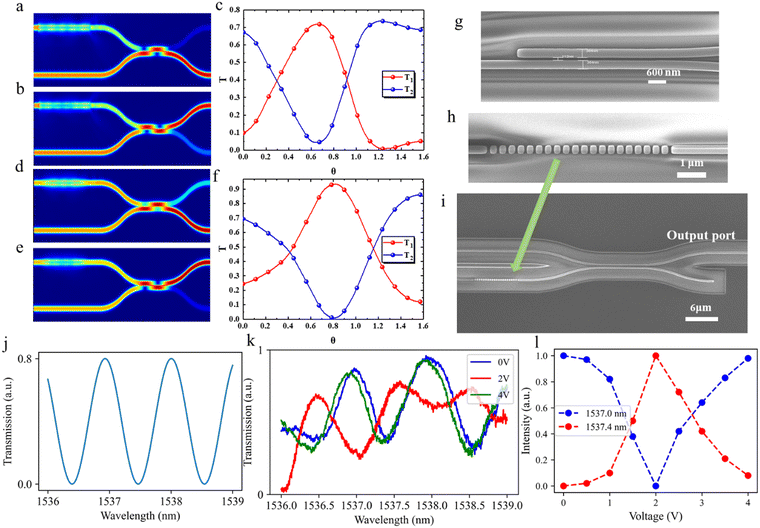
The simulation is carried out when the angle between the liquid crystal director and the z-axis changes from 0° to 90°. Fig. 3(a) and (b) show the mode field diagrams when light is output from the lower waveguide and upper waveguide, respectively. The transmittance of the output ends of both arms at 1550 nm is shown in Fig. 3(c). Maximum transmittance of the output waveguide is greater than 70% during modulation.
In addition, in order to further reduce the loss in the meta-waveguide area, we added a taper to guide the light from the waveguide to the meta-atom structure.49Fig. 3(d) and (e) show the light field distribution of the designed MZI with a taper. It can be observed that the leakage of the optical field from the waveguide region to the meta-waveguide region is reduced with the assistance of taper guidance. Fig. 3(f) shows the transmittance of the output ends of both arms at 1550 nm with a taper.50
First, the light in the optical fiber is coupled into the input waveguide using a coupling grating. Then the optical power in the input waveguide is split into two using a directional coupler and fed into the MZI dual arms. The light in one of the arms passes through the meta-waveguide where it can be phase modulated. The voltage is applied to deflect the liquid crystal molecules and thus modulate the light (more details can be seen in Fig. S3 and S4, ESI†).
The light output from the waveguide is extracted at one end of the Mach–Zehnder interferometer and a coupling grating is used at the end of the waveguide to couple the light in the waveguide into the output fiber. A spectrometer is used to detect the signal at the output waveguide.
The spectral shift of the device can indicate the phase change in the region of the meta-waveguide. Fig. 3(g–i) show the SEM image of the coupler, the SEM image of the meta-waveguide, and the SEM image of the entire MZI, respectively. Fig. 3(j) shows the calculated spectrum of one arm of the proposed MZI output. The FSR of the proposed MZI is given by:
 | (3) |
Here, λ is the operation wavelength, L1 and L1 are the lengths of two waveguides, and ng1 and ng2 are group indices of the waveguides, which are obtained from simulation in COMSOL. In the calculations, we took into account the insertion loss caused by the meta-waveguides, the initial phase difference, and the coupling loss introduced by the coupling structure. We found that the calculated FSR is approximately 1.12 nm for wavelengths ranging from 1536 nm to 1539 nm.
Fig. 3(k) shows the measured spectral response from 1536 nm to 1539 nm at voltages of 0 V, 2 V, and 4 V. The spectrum exhibits a periodic response, with the peak spacing determined by the FSR, which results from the interference in the MZI. After applying voltage, the spectrum shifted, proving a phase change in the meta-waveguide. As shown in the figure, a peak appears around 1537 nm at 0 V, a trough appears at 2 V, and another peak reappears at 4 V, from which we can infer that the half-wave voltage is 2 V. Fig. 3(l) depicts the variation of light intensity in the output waveguide of the device at different voltages for 1537.0 nm and 1537.4 nm. From the significant light intensity changes in the output waveguide, it can be seen that the phase of the LC meta-waveguide is modulated. According to the change of light intensity at 1537 nm and formula (1), we get the relationship between phase and voltage change, as shown in Fig. 1(d).
Micro-ring resonator using LC metawaveguides
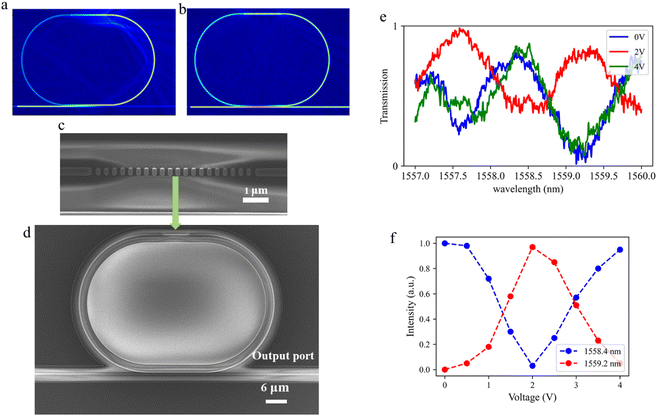
In order to further illustrate the phase modulation of the meta-waveguides, it was applied to MRR to create a tunable micro-ring resonator. We place the meta-waveguide in a symmetrical region in the ring waveguide, as shown in Fig. 4(d).Fig. 4(a) and (b) show two photonic switching states of the MRR under different LC deflection angles. The preparation and electrical testing methods of the MRR are the same as those of MZI. Fig. 4(c) and (d) show the SEM image of the meta-waveguide and MRR before liquid crystal encapsulation and the spectral changes after electrical stimulation.
As shown in Fig. 4(e), without applying any voltage, a peak appears at 1558.4 nm. When a voltage of 2 V is applied, the peak shifts to 1557.5 nm. From Fig. 4(e), the FSR of the device can also be determined to be approximately 1.8 nm, with a half-wave voltage of 2 V. Fig. 4(f) shows the output intensities at 1558.4 nm and 1559.2 nm, with the intensity variations showing opposite trends.
Phase shifters based on the thermo-optic effect51 consume a significant amount of power, resulting in thermal crosstalk that restricts the scaling of LSI/VLSI. Compared with traditional thermo-optic phase shifters, LC meta-waveguide phase shifters have no thermal crosstalk and ultra-compact size, making them suitable for large-scale integration. It can be seen from Table 1 that the energy consumption of LC meta-waveguide is 10 nW and the active area length is 10 μm, which has significant advantages over thermo-optical phase shifters.
| Thermo-optic effect12 | LC waveguide52 | BTO53 | PCM54 | LN55 | LC meta-waveguide | |
|---|---|---|---|---|---|---|
| Power consumption | 0.4 mW56 | Low | 6.24 mW | 10 nW (ESI) | ||
| Thermal crosstalk | Large | Little | Little | Little | Little | Little |
| Length of active area | ∼1000 μm | 50 μm | 150 μm | 33 μm | 400 μm | 20 μm |
| Response time | 60 ms | 20 ms | 0.1 ms (when the pulse voltage is 3 V) | 50 μs | <0.1 μs | 2–3 ms |
| Easy to integrate | N | Y | Y | N | N | Y |
LC meta-waveguides offer a compact design compared to MEMS, phase-change materials, and graphene phase shifters. MEMS phase shifters rely on mechanical movement, requiring larger components and more complex driving systems. PCM-based modulation depends on phase transitions, involving significant material structure changes over a large area. While graphene is small, it requires large planar electrodes for modulation. In contrast, LC meta-waveguides achieve phase modulation through metasurface resonances, enabling smaller device volumes. Additionally, vertical electrode structures drive the liquid crystal, further reducing the device size.
In terms of power consumption, compared to driving micro-mechanical structures, material phase transitions, or applying strong electric fields to change the conductivity or surface states of graphene, the power required to drive LC is much lower.57
The LC meta-waveguide arrays' driving method can be compatible with existing large-scale pixel LCOS chips. Additionally, the individual LC meta-waveguide phase shifters have low power consumption and a small area, making them well-suited for VLSI integration.
Convolution operation
To further validate the ability of the proposed phase shifter applied to optical computing,58 we apply the LC meta-waveguide phase shifter to the proposed convolutional architecture and use it in a network based on modified VGG16, as shown in Fig. 5(a). All 2 × 2 convolution operations in the modified network are performed using the LC meta-waveguide optical convolution accelerator (LCM-OCA).We change the addressing voltage to control the LC meta-waveguide to produce different additional phases. For each phase shifter, we can generate eight gray levels according to the experiment that can be mapped to drive voltages. The proposed convolutional architecture with the LC meta-waveguide phase shifter is based on simulations that are grounded in experimental test results. Specifically, we measured 8 discrete phase values experimentally to derive the transmission matrix R used in the convolutional architecture. The subsequent work, including system performance analysis, was performed through simulations. By modulating the additional phase of the phase shifter, we are able to change the transmission matrix R of LCM-OCA.59
 | (4) |
To validate the effectiveness of the LCM-OCA in convolutional neural networks, we used the modified VGG16 for recognizing simple colored objects and performing classification tasks (for neural network details and datasets, see ESI†).
The output obtained by processing the input vector through LCM-OCA can be considered as the result of convolution with these 2 × 2 kernels. Therefore, we replace the 2 × 2 convolution kernels in the model with these kernels, and the convolution layers that use 2 × 2 convolution kernels in the original model can be computed on LCM-OCA. We evaluate the similarity between two convolution kernels using the root mean square error (RMSE)60 between matrices. The RMSE is defined as follows:
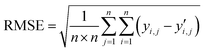 | (5) |
Here, the 2 × 2 convolution kernel n = 2, yi,j represents the parameters of the convolution kernel in the saved model, and  represents the parameters in the kernel used for replacement.
represents the parameters in the kernel used for replacement.
The confusion matrix is shown in Fig. 5(d). The variation curves of cross-entropy loss and classification accuracy of our network on the training set with training rounds are shown in Fig. 5(e). On the test set, our model achieved an accuracy of 91.82% in top-1 probability classification prediction (Table 2).
| CIFAR-10 | GoogleNet61 (%) | ResNet5062 (%) | Our model (%) | After replacement (%) | |
|---|---|---|---|---|---|
| Image category | Airplane | 51.10 | 90.80 | 92.90 | 92.90 |
| Automobile | 62.10 | 69.10 | 95.50 | 95.50 | |
| Bird | 56.70 | 72.60 | 88.90 | 89.50 | |
| Cat | 78.80 | 61.90 | 81.80 | 81.90 | |
| Deer | 49.50 | 75.40 | 94.50 | 94.20 | |
| Dog | 57.50 | 82.10 | 86.20 | 85.30 | |
| Frog | 90.20 | 76.60 | 94.60 | 94.70 | |
| Horse | 78.20 | 84.70 | 93.70 | 93.90 | |
| Ship | 95.50 | 83.20 | 95.40 | 95.40 | |
| Truck | 97.10 | 84.60 | 94.70 | 94.40 |
Our simulation demonstrated that our proposed network using 2 × 2 convolutional kernels achieved excellent performance in the classification task on the CIFAR10 dataset. This suggests that we can use the replacement method to load the convolutional neural network63 onto an LCM-OCA to accelerate convolutional calculations.
Conclusions
In conclusion, we have proposed and demonstrated an ultra-compact on-chip phase shifter based on electrically tunable meta-waveguides. Simulations demonstrate that the phase modulation of the liquid crystal meta-waveguide phase shifter can reach up to 2π and keep the amplitude homogeneity. We have prepared MZIs and MRRs based on liquid crystal meta-waveguides and verified the role of phase modulation by measuring changes in the light intensity of the output waveguide. We also apply the liquid crystal meta-waveguide phase shifter to the convolutional architecture and apply this architecture to accelerate the operation of the modified VGG16 network. Based on our measured results, we simulated the overall neural network, which proves that it is possible to realize complex operations.Methods
First, EBL is used to prepare waveguide and meta-waveguide structures on silicon-on-insulator (SOI) substrates. The top layer of single crystal silicon is then etched using dry etching. The plasma enhanced chemical vapor deposition (PECVD) is then used to deposit silicon oxide, and finally, EBL is used to window the meta-waveguide area. How to remove the silicon oxide above the meta-waveguide area is a challenge. If only dry etching is used, the bottom silicon oxide may be over-etched. Therefore, here we use a combination of dry etching and wet etching to better remove the top silicon oxide. Then the liquid crystal was packaged, using a process similar to the LCOS packaging process.64The device is powered as follows: the ground of the electrode is connected to the silicon substrate, and the high level is applied to ITO.65 During the test, a square wave signal with a frequency of 1 kHz and a voltage from 0–4 V was applied. Subsequently, the packaging of LC is compatible with the packaging process of LCOS. Due to the removal of the silicon dioxide above the meta-waveguide area, the LC can make direct contact with the meta-waveguides.66
Author contributions
C. D. fabricated the initial meta-waveguide device, performed simulation and optical characterization, and wrote the first draft of the manuscript. X. G. conducted the nanofabrication of the device. Y. H. proposed a modified neural network architecture and performed simulation. Z. Z. performed liquid crystal cell fabrication. J. W. Z. W. and W. W. performed electro-optical characterization. T. C., J. W. and T. Q. provided comments on the revision of the manuscript. J. X. conceived the idea and supervised the work. All authors contributed to the manuscript preparation.Data availability
The data that support the findings of this study are available from the corresponding authors upon request. Source data are provided in this paper.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Key R&D Program of China (grant no. 2021YFF0701100), the National Natural Science Foundation of China (grant no. 62075040), and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (grant no. SJCX22_0047). We acknowledge Keyang Yang for his help with the discussion and verification of initial ideas. Chengkun Dong also acknowledges the support from the China Scholarship Council.References
- W. Bogaerts, D. Perez, J. Capmany, D. A. B. Miller, J. Poon, D. Englund, F. Morichetti and A. Melloni, Programmable photonic circuits, Nature, 2020, 586, 207–216 CrossRef CAS PubMed.
- C. V. Poulton, M. J. Byrd, P. Russo, E. Timurdogan, M. Khandaker, D. Vermeulen and M. R. Watts, Long-Range LiDAR and Free-Space Data Communication With High-Performance Optical Phased Arrays, IEEE J. Sel. Top. Quantum Electron., 2019, 25, 7700108 CAS.
- W. R. Clements, P. C. Humphreys, B. J. Metcalf, W. S. Kolthammer and I. A. Walmsley, Optimal design for universal multiport interferometers, Optica, 2016, 3, 1460–1465 CrossRef.
- J. W. Wang, F. Sciarrino, A. Laing and M. G. Thompson, Integrated photonic quantum technologies, Nat. Photonics, 2020, 14, 273–284 CrossRef CAS.
- P. Y. Hsieh, S. L. Fang, Y. S. Lin, W. H. Huang, J. M. Shieh, P. C. Yu and Y. C. Chang, Metasurfaces on silicon photonic waveguides for simultaneous emission phase and amplitude control, Opt. Express, 2023, 31, 12487–12496 CrossRef CAS PubMed.
- X. S. Zhang, K. Kwon, J. Henriksson, J. H. Luo and M. C. Wu, A large-scale microelectromechanical-systems-based silicon photonics LiDAR, Nature, 2022, 603, 253–258 CrossRef CAS PubMed.
- S. A. Miller, Y. C. Chang, C. T. Phare, M. C. Shin, M. Zadka, S. P. Roberts, B. Stern, X. C. Ji, A. Mohanty and O. A. J. Gordillo, et al., Large-scale optical phased array using a low-power multi-pass silicon photonic platform, Optica, 2020, 7, 3–6 CrossRef CAS.
- J. Carolan, C. Harrold, C. Sparrow, E. Martín-López, N. J. Russell, J. W. Silverstone, P. J. Shadbolt, N. Matsuda, M. Oguma and M. Itoh, et al., Universal linear optics, Science, 2015, 349, 711–716 CrossRef CAS PubMed.
- C. Wang, M. Zhang, B. Stern, M. Lipson and M. Loncar, Nanophotonic lithium niobate electro-optic modulators, Opt. Express, 2018, 26, 1547–1555 CrossRef CAS PubMed.
- L. B. Shao, M. J. Yu, S. Maity, N. Sinclair, L. Zheng, C. Chia, A. Shams-Ansari, C. Wang, M. Zhang and K. J. Lai, et al., Microwave-to-optical conversion using lithium niobate thin-film acoustic resonators, Optica, 2019, 6, 1498–1505 CrossRef CAS.
- J. Wen, J. Y. Jiang, J. Y. Ma, S. Q. Feng, Q. K. Gong, W. A. Xiao, X. J. Lian and L. Wang, The State-of-the-Art Phase-Change Integrated Photonic Devices With Electrically Driven Microheaters, IEEE Trans. Electron Devices, 2024, 71, 955–964 CAS.
- S. Shekhar, W. Bogaerts, L. Chrostowski, J. E. Bowers, M. Hochberg, R. Soref and B. J. Shastri, Roadmapping the next generation of silicon photonics, Nat. Commun., 2024, 15, 751 CrossRef CAS PubMed.
- J. Capmany, J. Mora, I. Gasulla, J. Sancho, J. Lloret and S. Sales, Microwave Photonic Signal Processing, J. Lightwave Technol., 2013, 31, 571–586 Search PubMed.
- G. Joa, P. Edinger, S. J. Bleiker, X. J. Wang, A. Y. Takabayashi, H. Sattari, N. Quack, M. Jezzini, P. Verheyen, G. Stemme, et al., Wafer-Level Vacuum Sealing for Packaging of Silicon Photonic MEMS, in Conference on Silicon Photonics XVI, Electr Network, Mar 06-11, 2021; 2021; vol. 11691.
- C. Ríos, Q. Y. Du, Y. F. Zhang, C. C. Popescu, M. Y. Shalaginov, P. Miller, C. Roberts, M. Kang, K. A. Richardson and T. Gu, et al., Ultra-compact nonvolatile phase shifter based on electrically reprogrammable transparent phase change materials, Photonix, 2022, 3, 26 CrossRef.
- C. Wang, M. Zhang, X. Chen, M. Bertrand, A. Shams-Ansari, S. Chandrasekhar, P. Winzer and M. Loncar, Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages, Nature, 2018, 562, 101–104 CrossRef CAS PubMed.
- S. Abel, F. Eltes, J. E. Ortmann, A. Messner, P. Castera, T. Wagner, D. Urbonas, A. Rosa, A. M. Gutierrez and D. Tulli, et al., Large Pockels effect in micro-and nanostructured barium titanate integrated on silicon, Nat. Mater., 2019, 18, 42–47 CrossRef CAS PubMed.
- S. Abdollahramezani, O. Hemmatyar, M. Taghinejad, H. Taghinejad, A. Krasnok, A. A. Eftekhar, C. Teichrib, S. Deshmukh, M. A. El-Sayed and E. Pop, et al., Electrically driven reprogrammable phase-change metasurface reaching 80% efficiency, Nat. Commun., 2022, 13, 1696 CrossRef CAS PubMed.
- H. S. Ee and R. Agarwal, Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate, Nano Lett., 2016, 16, 2818–2823 CrossRef CAS PubMed.
- S. X. Yu, L. Li, G. M. Shi, C. Zhu and Y. Shi, Generating multiple orbital angular momentum vortex beams using a metasurface in radio frequency domain, Appl. Phys. Lett., 2016, 108, 241901 CrossRef.
- P. X. Zheng, Q. Dai, Z. L. Li, Z. Y. Ye, J. Xiong, H. C. Liu, G. X. Zheng and S. Zhang, Metasurface-based key for computational imaging encryption, Sci. Adv., 2021, 7, eabg0363 CrossRef PubMed.
- S. Y. Zhang, C. L. Wong, S. W. Zeng, R. Z. Bi, K. Tai, K. Dholakia and M. Olivo, Metasurfaces for biomedical applications: imaging and sensing from a nanophotonics perspective, Nanophotonics, 2021, 10, 259–293 CAS.
- D. D. Wen, F. Y. Yue, G. X. Li, G. X. Zheng, K. L. Chan, S. M. Chen, M. Chen, K. F. Li, P. W. H. Wong and K. W. Cheah, et al., Helicity multiplexed broadband metasurface holograms, Nat. Commun., 2015, 6, 8241 CrossRef PubMed.
- Q. Ma, G. D. Bai, H. B. Jing, C. Yang, L. L. Li and T. J. Cui, Smart metasurface with self-adaptively reprogrammable functions, Light: Sci. Appl., 2019, 8, 98 CrossRef PubMed.
- D. Conteduca, I. Barth, G. Pitruzzello, C. P. Reardon, E. R. Martins and T. F. Krauss, Dielectric nanohole array metasurface for high-resolution near-field sensing and imaging, Nat. Commun., 2021, 12, 3293 CrossRef CAS PubMed.
- M. L. Tseng, A. Jahani, A. Leitis and H. Altug, Dielectric Metasurfaces Enabling Advanced Optical Biosensors, ACS Photonics, 2021, 8(1), 47–60 CrossRef CAS.
- J. B. Wu, Z. Shen, S. J. Ge, B. W. Chen, Z. X. Shen, T. F. Wang, C. H. Zhang, W. Hu, K. B. Fan and W. Padilla, et al., Liquid crystal programmable metasurface for terahertz beam steering, Appl. Phys. Lett., 2020, 116, 131104 CrossRef CAS.
- M. Z. Liu, P. C. Huo, W. Q. Zhu, C. Zhang, S. Zhang, M. W. Song, S. Zhang, Q. W. Zhou, L. Chen and H. J. Lezec, et al., Broadband generation of perfect Poincare beams via dielectric spin-multiplexed metasurface, Nat. Commun., 2021, 12, 2230 CrossRef CAS PubMed.
- I. Kim, J. Jang, G. Kim, J. Lee, T. Badloe, J. Mun and J. Rho, Pixelated bifunctional metasurface-driven dynamic vectorial holographic color prints for photonic security platform, Nat. Commun., 2021, 12, 3614 CrossRef CAS PubMed.
- Y. H. Yang, J. Seong, M. Choi, J. Park, G. Kim, H. Kim, J. Jeong, C. H. Jung, J. Kim and G. Jeon, et al., Integrated metasurfaces for re-envisioning a near-future disruptive optical platform, Light: Sci. Appl., 2023, 12, 152 CrossRef CAS PubMed.
- S. Q. Li, X. W. Xu, R. M. Veetil, V. Valuckas, R. Paniagua-Domínguez and A. I. Kuznetsov, Phase-only transmissive spatial light modulator based on tunable dielectric metasurface, Science, 2019, 364, 1087–1090 CrossRef CAS PubMed.
- J. Park, B. G. Jeong, S. I. Kim, D. Lee, J. Kim, C. Shin, C. B. Lee, T. Otsuka, J. Kyoung and S. Kim, et al., All-solid-state spatial light modulator with independent phase and amplitude control for three-dimensional LiDAR applications, Nat. Nanotechnol., 2021, 16, 69–76 CrossRef CAS PubMed.
- N. X. Li, C. P. Ho, J. Xue, L. W. Lim, G. Y. Chen, Y. H. Fu and L. Y. T. Lee, A Progress Review on Solid-State LiDAR and Nanophotonics-Based LiDAR Sensors, Laser Photonics Rev., 2022, 16, 2100500 Search PubMed.
- Y. F. Zhang, C. Fowler, J. H. Liang, B. Azhar, M. Y. Shalaginov, S. Deckoff-Jones, S. S. An, J. F. B. Chou, C. M. Roberts and V. Liberman, et al., Electrically reconfigurable non-volatile metasurface using low-loss optical phase-change material, Nat. Nanotechnol., 2021, 16, 661–666 CrossRef CAS PubMed.
- C. H. Chu, M. L. Tseng, J. Chen, P. C. Wu, Y. H. Chen, H. C. Wang, T. Y. Chen, W. T. Hsieh, H. J. Wu and G. Sun, et al., Active dielectric metasurface based on phase-change medium, Laser Photonics Rev., 2016, 10, 986–994 CrossRef CAS.
- A. Karvounis, B. Gholipour, K. F. MacDonald and N. I. Zheludev, All-dielectric phase-change reconfigurable metasurface, Appl. Phys. Lett., 2016, 109, 051103 CrossRef.
- M. S. Islam, J. Sultana, M. Biabanifard, Z. Vafapour, M. J. Nine, A. Dinovitser, C. M. B. Cordeiro, B. W. H. Ng and D. Abbott, Tunable localized surface plasmon graphene metasurface for multiband superabsorption and terahertz sensing, Carbon, 2020, 158, 559–567 CrossRef CAS.
- Y. Yao, R. Shankar, M. A. Kats, Y. Song, J. Kong, M. Loncar and F. Capasso, Electrically Tunable Metasurface Perfect Absorbers for Ultrathin Mid-Infrared Optical Modulators, Nano Lett., 2014, 14, 6526–6532 CrossRef CAS PubMed.
- N. Dabidian, I. Kholmanov, A. B. Khanikaev, K. Tatar, S. Trendafilov, S. H. Mousavi, C. Magnuson, R. S. Ruoff and G. Shvets, Electrical Switching of Infrared Light Using Graphene Integration with Plasmonic Fano Resonant Metasurfaces, ACS Photonics, 2015, 2, 216–227 CrossRef CAS.
- G. K. Shirmanesh, R. Sokhoyan, R. A. Pala and H. A. Atwater, Dual-Gated Active Metasurface at 1550 nm with Wide (>300°) Phase Tunability, Nano Lett., 2018, 18, 2957–2963 CrossRef PubMed.
- J. H. Zhang, J. Y. Ma, M. Parry, M. Cai, R. Camacho-Morales, L. Xu, D. N. Neshev and A. A. Sukhorukov, Spatially entangled photon pairs from lithium niobate nonlocal metasurfaces, Sci. Adv., 2022, 8, eabq4240 CrossRef CAS PubMed.
- T. Badloe, J. Kim, I. Kim, W. S. Kim, W. S. Kim, Y. K. Kim and J. Rho, Liquid crystal-powered Mie resonators for electrically tunable photorealistic color gradients and dark blacks, Light: Sci. Appl., 2022, 11, 118 CrossRef CAS PubMed.
- Y. V. Izdebskaya, Z. W. Yang, M. K. Liu, D. Y. Choi, A. Komar, D. N. Neshev and I. V. Shadrivov, Magnetic tuning of liquid crystal dielectric metasurfaces, Nanophotonics, 2022, 11, 3895–3900 CrossRef CAS PubMed.
- M. Sharma, L. Michaeli, D. Ben Haim and T. Ellenbogen, Liquid Crystal Switchable Surface Lattice Resonances in Plasmonic Metasurfaces, ACS Photonics, 2022, 9, 2702–2712 CrossRef CAS.
- A. Komar, R. Paniagua-Domínguez, A. Miroshnichenko, Y. F. Yu, Y. S. Kivshar, A. I. Kuznetsov and D. Neshev, Dynamic Beam Switching by Liquid Crystal Tunable Dielectric Metasurfaces, ACS Photonics, 2018, 5, 1742–1748 CrossRef CAS.
- S. K. Khare and V. Bajaj, Time-Frequency Representation and Convolutional Neural Network-Based Emotion Recognition, IEEE Trans. Neural Networks Learn. Syst., 2021, 32, 2901–2909 Search PubMed.
- H. L. Zhou, J. J. Dong, J. W. Cheng, W. C. Dong, C. R. Huang, Y. C. Shen, Q. M. Zhang, M. Gu, C. Qian and H. S. Chen, et al., Photonic matrix multiplication lights up photonic accelerator and beyond, Light: Sci. Appl., 2022, 11, 30 CrossRef CAS PubMed.
- Y. Z. Wang, F. Zhang, X. Tang, X. Chen, Y. X. Chen, W. C. Huang, Z. M. Liang, L. M. Wu, Y. Q. Ge and Y. F. Song, et al., All-Optical Phosphorene Phase Modulator with Enhanced Stability Under Ambient Conditions, Laser Photonics Rev., 2018, 12, 1800016 CrossRef.
- T. Ma, A. B. Khanikaev, S. H. Mousavi and G. Shvets, Guiding Electromagnetic Waves around Sharp Corners: Topologically Protected Photonic Transport in Metawaveguides, Phys. Rev. Lett., 2015, 114, 127401 CrossRef PubMed.
- D. A. Sulway, Y. Yonezu, L. M. Rosenfeld, P. Jiang, T. Aoki and J. W. Silverstone, High-performance, adiabatically nanotapered fiber-chip couplers in silicon at 2 microns wavelength, Opt. Express, 2023, 31, 25350–25358 CrossRef CAS PubMed.
- S. Chung, H. Abediasl and H. Hashemi, A Monolithically Integrated Large-Scale Optical Phased Array in Silicon-on-Insulator CMOS, IEEE J. Solid State Circ., 2018, 53, 275–296 Search PubMed.
- L. Van Iseghem, E. Picavet, A. Y. Takabayashi, P. Edinger, U. Khan, P. Verheyen, N. Quack, K. B. Gylfason, K. De Buysser and J. Beeckman, et al., Low power optical phase shifter using liquid crystal actuation on a silicon photonics platform, Opt. Mater. Express, 2022, 12, 2181–2198 CrossRef CAS.
- J. Geler-Kremer, F. Eltes, P. Stark, D. Stark, D. Caimi, H. Siegwart, B. J. Offrein, J. Fompeyrine and S. Abel, A ferroelectric multilevel non-volatile photonic phase shifter, Nat. Photonics, 2022, 16(7), 491–497 CrossRef CAS.
- Z. R. Fang, R. Chen, J. J. Zheng, A. I. Khan, K. M. Neilson, S. J. Geiger, D. M. Callahan, M. G. Moebius, A. Saxena and M. E. Chen, et al., Ultra-low-energy programmable non-volatile silicon photonics based on phase-change materials with graphene heaters, Nat. Nanotechnol., 2022, 17(8), 842–848 CrossRef CAS PubMed.
- P. Ying, H. Y. Tan, J. W. Zhang, M. B. He, M. Y. Xu, X. Y. Liu, R. Y. Ge, Y. T. Zhu, C. Liu and X. L. Cai, Low-loss edge-coupling thin-film lithium niobate modulator with an efficient phase shifter, Opt. Lett., 2021, 46, 1478–1481 CrossRef PubMed.
- H. Larocque, L. Ranzani, J. Leatham, J. Tate, A. Niechayev, T. Yengst, T. Komljenovic, C. Fodran, D. Smith and M. Soltani, Beam steering with ultracompact and low-power silicon resonator phase shifters, Opt. Express, 2019, 27, 34639–34654 CrossRef CAS PubMed.
- S. Y. Xiao, T. Wang, T. T. Liu, C. B. Zhou, X. Y. Jiang and J. F. Zhang, Active metamaterials and metadevices: a review, J. Phys. D:Appl. Phys., 2020, 53, 503002 CrossRef CAS.
- W. T. Gu, X. Y. Gao, W. C. Dong, Y. L. Wang, H. L. Zhou, J. Xu and X. L. Zhang, All-optical complex-valued convolution based on four-wave mixing, Optica, 2024, 11, 64–72 CrossRef CAS.
- X. Y. Meng, G. J. Zhang, N. N. Shi, G. Y. Li, J. Azana, J. Capmany, J. P. Yao, Y. C. Shen, W. Li and N. H. Zhu, et al., Compact optical convolution processing unit based on multimode interference, Nat. Commun., 2023, 14, 3000 CrossRef CAS PubMed.
- D. S. K. Karunasingha, Root mean square error or mean absolute error? Use their ratio as well, Inf. Sci., 2022, 585, 609–629 CrossRef.
- A. Sekhar, S. Biswas, R. Hazra, A. K. Sunaniya, A. Mukherjee and L. X. Yang, Brain Tumor Classification Using Fine-Tuned GoogLeNet Features and Machine Learning Algorithms: IoMT Enabled CAD System, IEEE J. Biomed. Health, 2022, 26, 983–991 Search PubMed.
- A. K. Sharma, A. Nandal, A. Dhaka, L. Zhou, A. Alhudhaif, F. Alenezi and K. Polat, Brain tumor classification using the modified ResNet50 model based on transfer learning, Biomed. Signal Process. Control, 2023, 86, 105299 CrossRef.
- J. X. Gu, Z. H. Wang, J. Kuen, L. Y. Ma, A. Shahroudy, B. Shuai, T. Liu, X. X. Wang, G. Wang and J. F. Cai, et al., Recent advances in convolutional neural networks, Pattern Recogn., 2018, 77, 354–377 CrossRef.
- Z. C. Zhang, Z. You and D. P. Chu, Fundamentals of phase-only liquid crystal on silicon (LCOS) devices, Light: Sci. Appl., 2014, 3, e213 CrossRef.
- K. Yin, E. L. Hsiang, J. Y. Zou, Y. N. Q. Li, Z. Y. Yang, Q. Yang, P. C. Lai, C. L. Lin and S. T. Wu, Advanced liquid crystal devices for augmented reality and virtual reality displays: principles and applications, Light: Sci. Appl., 2022, 11, 161 CrossRef CAS PubMed.
- Y. Y. Ji, F. Fan, M. Chen, L. Yang and S. J. Chang, Terahertz artificial birefringence and tunable phase shifter based on dielectric metasurface with compound lattice, Opt. Express, 2017, 25(10), 11405–11413 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00592a |
| This journal is © The Royal Society of Chemistry 2025 |