Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comprehensive analysis of nanomagnetism models for the evaluation of particle energy in magnetic hyperthermia
N.
Maniotis
 *a,
M.
Maragakis
b and
N.
Vordos
b
*a,
M.
Maragakis
b and
N.
Vordos
b
aDepartment of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece. E-mail: nimaniot@physics.auth.gr
bDepartment of Physics, Democritus University of Thrace, Kavala, Greece
First published on 27th May 2025
Abstract
Magnetic nanoparticles (MNPs) have attracted significant research interest due to their unique magnetic properties, which differ from their bulk counterparts and enable applications in information technology, environmental protection, and biomedicine. Among these applications, magnetic particle hyperthermia (MPH) has emerged as a promising therapeutic approach for cancer treatment. This review provides a comprehensive analysis of nanomagnetism models used to evaluate the heating potential of MNPs in MPH. Specifically, we examine (i) theoretical approaches for estimating the magnetic properties of nanoparticle systems and (ii) numerical simulation strategies that predict their response to externally applied magnetic fields. Common modeling frameworks typically focus on key magnetic parameters such as total energy, magnetization, anisotropy, and hysteresis loop morphology. However, precise characterization of these properties remains challenging due to their dependence on multiple interrelated factors, including particle size, shape, composition, and interparticle interactions. To address these challenges, this review discusses various analytical and numerical models that aid in the qualitative and quantitative assessment of MNP behavior under alternating magnetic fields. By critically evaluating these methodologies, we aim to enhance the understanding of magnetic field-driven heating mechanisms and contribute to the optimization of MNPs for hyperthermia-based therapeutic applications. Looking forward, the integration of advanced multiphysics simulations, combining magnetization dynamics with biological, thermal, and fluidic environments, is anticipated to revolutionize the predictive accuracy and translational potential of MPH technologies.
Introduction
Magnetic particle hyperthermia (MPH) is an innovative and minimally invasive cancer treatment that utilizes a magnetic fluid, also known as ferrofluid, as a localized heat source.1–4 This ferrofluid consists of a stable colloidal suspension of magnetic nanoparticles (MNPs), which can be directly injected into the tumor or delivered through intravenous administration via passive or active (functionalized) targeting.5,6 Those systems are usually of iron oxide nanoparticles that are suspended – very finely distributed – in water. After administration, magnetic nanoparticles can be directed toward the tumor site either through passive targeting mechanisms—such as the enhanced permeability and retention (EPR) effect—or via active targeting strategies involving surface functionalization with ligands that bind to tumor-specific receptors.7 Once accumulated to the tumor area, nanoparticles are exposed to an external alternating magnetic field (AMF) that causes reversal of their magnetic moments, activating mechanisms of energy transfer in the form of heat.8,9Due to their unique properties, MNPs have gained significant research attention which emerges from their nanoscale dimensions and differentiates them from their bulk counterparts. Beyond the advantages of miniaturization in high-tech applications and enhanced surface-area-to-volume ratios in conventional technologies,10–13 MNPs exhibit a novel magnetic behavior driven by their reduced dimensionality.14–16 As the size of a material approaches the nanometer scale, surface effects become increasingly substantial, often rivaling or surpassing bulk contributions.17–19 In order to ensure both stability and biocompatibility, MNPs are commonly coated or functionalized with biocompatible materials such as polyethylene glycol (PEG), dextran, or starch.16,20,21 These coatings not only stabilize the particles by reducing surface energy and preventing agglomeration but also improve their dispersion and circulation time in biological environments.22 Furthermore, structural defects resulting from broken crystalline symmetry play a crucial role in determining magnetic properties, while additional physical effects emerge when the particle size reaches the material's intrinsic characteristic length scales. These size-dependent effects make MNPs highly sensitive to variations in size, shape, and chemical composition, necessitating specialized theoretical and computational approaches to accurately describe their behavior.23–26
The collective magnetic properties of MNPs arise from a complex interplay between intrinsic parameters such as the magnetic moment and anisotropy and external experimental conditions like the applied magnetic field and the measurement timescale.27 While significant progress has been made in understanding these properties, accurately modeling the dynamic response of MNPs under alternating magnetic fields—particularly in the context of MPH—remains a challenge. The difficulty primarily stems from the wide range of relevant length and time scales involved, making conventional atomistic simulations computationally demanding and often impractical.28 Moreover, large-scale simulations of dense nanoparticle systems encounter limitations due to the complex interactions between particles and externally applied magnetic fields, as well as the lack of universally reliable models, valid for these type of interactions.29–32
A key challenge in simulating realistic MNP systems is that neither atomic-scale models nor continuum-based approaches alone can fully capture the intricate magnetic behaviors at intermediate scales. The mesoscopic regime—spanning approximately from 10−9 to 10−6 meters—bridges the gap between atomistic simulations and macroscopic continuum models.33,34 Within this scale, individual nanoparticle dynamics are still relevant, yet the system is too large to be efficiently simulated using purely atomistic methods. Mesoscopic modeling provides an effective way to address this challenge by considering local equilibrium at the microscopic level while capturing emergent behaviors on longer timescales.35 One of the most widely used techniques at this scale is micromagnetic modeling,36 which provides a phenomenological framework for determining equilibrium magnetization configurations in MNPs based on applied field conditions,37 particle geometry,38 and material properties.39 The field of numerical micromagnetics continues to evolve, with ongoing advancements improving its predictive capabilities.40,41
Given the complexity of MNP interactions and their strong dependence on microstructural and morphological factors, a combination of analytical and numerical approaches is necessary to effectively model their heating potential in hyperthermia applications. This review provides a comprehensive analysis of mesoscopic models designed to estimate and optimize key magnetic properties relevant to MPH, including anisotropy, total energy, magnetization, and hysteresis loop area. Special emphasis is placed on numerical simulations, which enable the study of non-local magnetic interactions and dynamic processes that cannot be resolved analytically. By critically assessing these modeling strategies, we aim to enhance the understanding of field-driven heating mechanisms in MNPs, ultimately contributing to the development of more efficient hyperthermia-based therapies.
Single particle approximations: analytical models in MPH
When magnetic nanoparticles are exposed to an external AMF, as used in MPH, the total energy they acquire primarily originates from two key contributions. Firstly, there is the Zeeman energy, which corresponds to the energy transferred to the nanoparticles by the external field. Secondly, there is the anisotropy energy, which arises due to the deviation of the nanoparticle's magnetic moment from its preferred easy-axis direction, under the influence of the alternating field. This misalignment imposes an additional energy cost on the system. Since MNPs in MPH applications experience continuously changing magnetic fields, their magnetization dynamics is translated to hysteresis losses, which contribute to the dissipation of energy as heat, an essential feature for hyperthermia treatment. Analyzing the total energy involved in this process requires first considering a single nanoparticle, before extending the analysis to an ensemble.Let us consider a ferromagnetic nanoparticle of volume V, with a saturation magnetization Ms and an effective anisotropy constant Keff. Unlike bulk ferromagnetic materials that exhibit multi-domain structures, nanoparticles below a critical radius rc (which depends on the material and its shape) exist in a single-domain state to minimize their total energy (Fig. 1). Since the critical dimension for most materials falls within the nanometer range, MNPs used in MPH are typically assumed to be single-domain entities. Their energy dissipation, governed by hysteresis losses and relaxation mechanisms, plays a crucial role in determining their heating efficiency under an AMF.
 | ||
Fig. 1 Schematic representation of magnetic domain structures in nanoparticles based on their size. Particles with a radius r larger than a critical value rc exhibit a multi-domain structure (left), where multiple magnetic domains are separated by domain walls. When the particle radius is smaller than rc, it becomes a single-domain particle (right), where all atomic spins align coherently, resulting in a net magnetic moment ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) p in a single direction.43 p in a single direction.43 | ||
In the single-domain model, all spins are parallel to one another and the magnetic moment μ can be described as a single giant magnetic moment:
| |μ|=MsV | (1) |
Another approximation is that the magnetic nanoparticle is assumed to have a uniaxial magnetocrystalline anisotropy according to which the crystal system has a single-axis of high symmetry. Assuming these approximations, the energy of a magnetic nanoparticle placed in an AMF H is given by the following equation which was first introduced by Stoner and Wohlfarth:44
E(θ,φ) = KeffV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(θ) − μ0MsVH sin2(θ) − μ0MsVH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ − φ) cos(θ − φ) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft), where H0 and f are the field amplitude and frequency respectively. According to the Stoner–Wohlfarth model, E(θ) behavior can be estimated by assuming zero thermal effects (i.e. at T = 0 K) and a constant “easy” axis angle with the magnetic field orientation (specific value of φ) which is a reasonable hypothesis for a single particle. Normally, eqn (2) is solved through energy minimization processes without applying time-dependent temperature variations. In order to take into account the thermal energy contribution kBT at temperatures higher than 0 K in the energy solution, the dimensionless parameters
sin(2πft), where H0 and f are the field amplitude and frequency respectively. According to the Stoner–Wohlfarth model, E(θ) behavior can be estimated by assuming zero thermal effects (i.e. at T = 0 K) and a constant “easy” axis angle with the magnetic field orientation (specific value of φ) which is a reasonable hypothesis for a single particle. Normally, eqn (2) is solved through energy minimization processes without applying time-dependent temperature variations. In order to take into account the thermal energy contribution kBT at temperatures higher than 0 K in the energy solution, the dimensionless parameters  and
and  are introduced. The parameter σ is usually referred as anisotropy barrier. Then, the reduced magnetic energy normalized to kBT is:
are introduced. The parameter σ is usually referred as anisotropy barrier. Then, the reduced magnetic energy normalized to kBT is: | (3) |
If the external magnetic field is applied along the “hard” axis (φ = π/2), then the energy is expressed as E = K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + μ0HMs
θ + μ0HMs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and the angle θ that minimizes the energy in this case is found by:
θ, and the angle θ that minimizes the energy in this case is found by:
The unique way that these conditions are satisfied is when  where μ0HK corresponds to the anisotropy field representing the field at which μ reaches its maximum value i.e. reaches saturation. When the applied magnetic field μ0H is higher than the anisotropy field, the energy landscape displays only one minimum, which defines the equilibrium position, i.e., along the anisotropy axis direction. Conversely, when μ0H is lower than μ0HK, the energy profile as a function of θ displays two minima at positions (θ1, E1), (θ2, E2) and two maxima as depicted in Fig. 2 for φ = 30°. The upper maximum point at position (θ3, E3) is known as the saddle point.
where μ0HK corresponds to the anisotropy field representing the field at which μ reaches its maximum value i.e. reaches saturation. When the applied magnetic field μ0H is higher than the anisotropy field, the energy landscape displays only one minimum, which defines the equilibrium position, i.e., along the anisotropy axis direction. Conversely, when μ0H is lower than μ0HK, the energy profile as a function of θ displays two minima at positions (θ1, E1), (θ2, E2) and two maxima as depicted in Fig. 2 for φ = 30°. The upper maximum point at position (θ3, E3) is known as the saddle point.
 | ||
| Fig. 2 Schematic representation of the energy landscape variation with the “easy” axis-magnetic moment angle (double-well approximation) for ξ = 0.5 and φ = 30°. The red arrows show the magnetic moment orientation. When ξ ≠ 0, θ1, θ2, and θ3 values deviate slightly from 0, 180 and 90 degrees which correspond to parallel antiparallel and perpendicular orientation, with respect to the “easy” axis, respectively. Although this deviation exists, we can approximately employ 0 and 180 degrees as the minimum energy positions without a significant deviation from the realistic experimental behavior.45 | ||
As described, the total energy minimization and the estimation of E(θ) behavior can be done analytically in the case of a single nanoparticle. However, in the case of an assembly of magnetic nanoparticles, where the system is characterized by a random distribution in φ values, this analytical solution is not valid and computational techniques should be utilized.43,46 On this, the most frequently used technique is the Monte Carlo (MC) minimization method. This simulation approach is based on the generation of random numbers (random sampling) to obtain numerically the minimization of a given energy functional. In magnetic nanoparticles, the random numbers coincide with “easy” axis orientations because they are used to generate trial orientations of the magnetization vector relative to the easy axis and the minimization proceeds for the energy function E(θ,φ) given by eqn (2). The described methodology was employed in a characteristic system of iron oxide (Fe3O4) magnetic nanoparticles47 at room temperature T = 300 K, for magnetic fields amplitudes typically used in MPH and a frequency equal to 300 kHz. Since the applied magnetic field is alternating, the considered case is essentially quasi-static, and therefore, the conditions ruling the system are expressed by an energy minimization processes.
The results of the above procedure are more clearly comprehended by Fig. 3 where the E/kBT ratio is plotted versus θ for various values of H in the range typically used in biomedical applications and more specifically for magnetic hyperthermia protocols.48–50 For ξ = 0, a value that corresponds to the absence of magnetic fields or for infinite temperatures, μ can take two equivalent equilibrium values at θ1 = 0° and θ2 = 180°, i.e., along its “easy” axis. For a finite positive value of ξ, the magnetic field favors one of the two minima. Increasing ξ, moves the abscissa of this minimum progressively so that the parallel orientation of μ to the magnetic field is favored. In the example shown in Fig. 3, when the applied magnetic field is higher than the anisotropy field, the energy landscape (as a function of the angle θ between easy axis and μ) displays only one minimum, which defines the equilibrium position, i.e., along the anisotropy axis direction (curves corresponding to an applied magnetic field amplitude of 40 and 50 mT in Fig. 3). Conversely, when the applied magnetic field is smaller than the anisotropy field, the energy profile as a function of θ displays two minima and two maxima (curves corresponding to an applied magnetic field amplitude of 10 and 20 mT).
 | ||
| Fig. 3 Magnetic energy as a function of angle θ for various values of μ0H at T = 300 K and f = 300 kHz. The results were obtained after energy minimization with the Monte Carlo method for a single Fe3O4 magnetic nanoparticle.45 The transformation of the energy profile under increasing external magnetic field strength is visually demonstrated by clearly showing the disappearance of the metastable state and the emergence of a single energy minimum aligned with the easy axis. | ||
In order to calculate the total energy, we examined the case where nanoparticles have reached saturation and, thus, magnetization was assumed to be independent to the applied magnetic field H and equal to a constant value Ms. In order to expand the validity of this approach and thoroughly study the magnetic properties of nanoparticles, the dependence of magnetization on H should be introduced through analytical relationships of the M(H) curve. First, let us consider a case of zero or very low anisotropy barrier, i.e. KeffV/kBT ≪ 1 and Keff ≤ 1 kJ m−3 where the virgin magnetization curve is given by:
| M(H) = MsL(ξ) | (4) |
 being the Langevin function which intrinsically neglects the anisotropy of magnetic nanoparticles and introduces the Zeeman term as the main contribution of the total energy in eqn (2). Eqn (4) is valid in the case of very small nanoparticles with dimensions lying in the superparamagnetic regime which are characterized by a low KeffV product. On the other hand, the Langevin function fails to describe the magnetization of magnetic nanoparticles with effective anisotropy above 1 kJ m−3 and/or large nanoparticles with dimensions lying in the superparamagnetic to ferromagnetic transition range. Using theories for domain stability in fine particles and bulk properties available in the literature, one can determine the characteristic size up to which single-domains are stable. This series of magnetic “phases” as a function of size is shown in Fig. 4 for different ferromagnets, which includes a “single-domain” size Dsd, below which the material will not support a multi-domain particle, and a size Dsp defined by the superparamagnetic effect, below which a spontaneous flip in magnetization occurs due to thermal effects at room temperature.
being the Langevin function which intrinsically neglects the anisotropy of magnetic nanoparticles and introduces the Zeeman term as the main contribution of the total energy in eqn (2). Eqn (4) is valid in the case of very small nanoparticles with dimensions lying in the superparamagnetic regime which are characterized by a low KeffV product. On the other hand, the Langevin function fails to describe the magnetization of magnetic nanoparticles with effective anisotropy above 1 kJ m−3 and/or large nanoparticles with dimensions lying in the superparamagnetic to ferromagnetic transition range. Using theories for domain stability in fine particles and bulk properties available in the literature, one can determine the characteristic size up to which single-domains are stable. This series of magnetic “phases” as a function of size is shown in Fig. 4 for different ferromagnets, which includes a “single-domain” size Dsd, below which the material will not support a multi-domain particle, and a size Dsp defined by the superparamagnetic effect, below which a spontaneous flip in magnetization occurs due to thermal effects at room temperature.
 | ||
| Fig. 4 Nanomagnetic size effects: top graphs outline the collective magnetic features exhibited by the hysteresis loops and spin configurations in each one of the three regions with surface spins also sketched at the outer layer of the particle. Main graph shows the magnetic transitions occurring as MNPs grow in diameter. transition area between red and blue bars corresponds to transition from (SPM) superparamagnetism to (SD) ferromagnetism-single-domain particles while the rightmost edge of blue bars corresponds to the critical diameter above which the formation of (MD) multiple domains is energetically favored. Next to the bar charts effective anisotropy and room temperature saturation magnetization values are given as collected from ref. 47. | ||
For MPH applications, it is a prerequisite to know the magnetic status of the MNPs since the energy release and thus the heating mechanism differs for particles possessing or not hysteresis.
The second case emerges for  and μ0HK > μ0H and assumes the neglection of excited energy states inside each energy well, therefore, magnetization calculations only depend on the position of the two energy minima E1 and E2 and the energy maximum E3 as depicted in Fig. 2. This approach is known as the double-well (DW) approximation and has been applied not only in the study of magnetic nanosystems,51,52 but also in many fields of physics such as quantum mechanics,53–55 neural networks56,57 and protein structure prediction.58–60 The values of E1, E2 and E3 are obtained after solving eqn (2) either for random or parallel (φ = 0) orientation of the magnetic field with respect to the “easy” axis. When applied magnetic field is below μ0HK, the magnetization can switch from the one minimum to the other at a rate ν1 expressed by:
and μ0HK > μ0H and assumes the neglection of excited energy states inside each energy well, therefore, magnetization calculations only depend on the position of the two energy minima E1 and E2 and the energy maximum E3 as depicted in Fig. 2. This approach is known as the double-well (DW) approximation and has been applied not only in the study of magnetic nanosystems,51,52 but also in many fields of physics such as quantum mechanics,53–55 neural networks56,57 and protein structure prediction.58–60 The values of E1, E2 and E3 are obtained after solving eqn (2) either for random or parallel (φ = 0) orientation of the magnetic field with respect to the “easy” axis. When applied magnetic field is below μ0HK, the magnetization can switch from the one minimum to the other at a rate ν1 expressed by:
 | (5) |
Similarly, the switching rate ν2 from the opposite direction is given by:
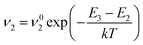 | (6) |
 where γ is the gyromagnetic ratio and Heff is the effective magnetic field, which encompasses contributions from the anisotropy field, external field, and internal demagnetizing fields. For the sake of simplicity, these frequencies are kept constant and equal to 1/τ0, where τ0 is a typical time value for ferromagnetic resonance61 set equal to 10−10 s. In the case of small magnetic field amplitudes H i.e. low values of ξ (as in MPH application) the two energy minima can be approached as θ1 = 0° and θ2 = 180°. Thus, the energy differences ΔE1 and ΔE2 between each minimum and the saddle point can estimated by eqn (5) and (6), for the case of φ = 0, as ΔE2,1 = KeffV(1 ± H0/HK)2. Calling P1 the occupation probability of position E1 and P2 the corresponding one of position E2, the time evolution of P1 is estimated by:62
where γ is the gyromagnetic ratio and Heff is the effective magnetic field, which encompasses contributions from the anisotropy field, external field, and internal demagnetizing fields. For the sake of simplicity, these frequencies are kept constant and equal to 1/τ0, where τ0 is a typical time value for ferromagnetic resonance61 set equal to 10−10 s. In the case of small magnetic field amplitudes H i.e. low values of ξ (as in MPH application) the two energy minima can be approached as θ1 = 0° and θ2 = 180°. Thus, the energy differences ΔE1 and ΔE2 between each minimum and the saddle point can estimated by eqn (5) and (6), for the case of φ = 0, as ΔE2,1 = KeffV(1 ± H0/HK)2. Calling P1 the occupation probability of position E1 and P2 the corresponding one of position E2, the time evolution of P1 is estimated by:62 | (7) |
Considering ∂/∂t = (∂/∂H)(∂H/∂t) and M = Ms(P1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 + (1 − P1)cos
θ1 + (1 − P1)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2) eqn (7) becomes:
θ2) eqn (7) becomes:
 | (8) |

A time dependent applied magnetic field H(t) of frequency f with a sweeping rate 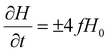 is assumed. For negative sweeping rates, the magnetic field reversal occurs (demagnetization process). For very large values of effective anisotropy and for “easy” axis alignment along the direction of the applied magnetic field (φ = 0), the analytical solution of eqn (8) converges to:
is assumed. For negative sweeping rates, the magnetic field reversal occurs (demagnetization process). For very large values of effective anisotropy and for “easy” axis alignment along the direction of the applied magnetic field (φ = 0), the analytical solution of eqn (8) converges to:
| M = Ms × tanh(ξ) | (9) |
The above analysis was applied in Fe3O4 nanoparticles, used previously as a model system, to generate the virgin magnetization curve M(H). Fig. 5 depicts the calculated M(H) curves for different values of effective anisotropy. Initially, a Monte Carlo simulation is applied for various values of effective anisotropy in order to estimate E1(Keff), E2(Keff) and E3(Keff) from energy minimization. Then, for each Keff value the corresponding (θ1, E1), (θ2, E2) and (θ3, E3) are substituted in eqn (5) and (6) to estimate ν1 and ν2, respectively. Lastly, the differential eqn (8) is solved numerically.
 | ||
| Fig. 5 Monte Carlo simulation resulted curves of magnetization of Fe3O4 magnetic nanoparticle with diameter 40 nm versus external field varied from 0 to 0.1 T and for different values of the effective anisotropy. The magnetic field is applied along the easy axis (φ = 0).45 | ||
The solutions of this equation for different Keff values reveal a progressive evolution of the magnetization curves from the Langevin function (0 kJ m−3) to the tanh function of eqn (9), (250 kJ m−3). When the particle's anisotropy is relatively small, the curve of magnetization follows the Langevin function where the magnetic moments can take all the possible orientations (θ ∈ R). Following effective anisotropy increment, the obtained magnetization also increases.
For large values of Keff, the magnetic moments of nanoparticles have only two stable orientations, parallel and antiparallel to nanoparticle's “easy” axis (the two minima of the energy landscape at θ1 and θ2). In the presence of magnetic field this behavior saturates faster, compared to the small anisotropy case, the magnetization and thus the Langevin function is replaced by the faster growing function tanh. Each one of the Keff values used in simulations satisfied the prerequisite for the application of DW approximation as soon as they resulted to anisotropy fields higher than the applied magnetic field (0.1 T).
Numerical solutions of eqn (8) based on multiple demagnetization and magnetization cycles  provide the full hysteresis loop for specific values of the involved parameters (Keff, V, Ms, H0, f, T) but only for the case of oriented particle (φ = 0). When the field is applied at an arbitrary angle φ relative to the easy axis different expressions should be given. Those expressions are crucial when modeling ensembles of non-interacting nanoparticles with random orientations. Unlike the aligned case the critical field at which the barrier vanishes depends on φ. The analytic expression for ΔE2,1 is more complex, but in the following we will present some useful approximations.
provide the full hysteresis loop for specific values of the involved parameters (Keff, V, Ms, H0, f, T) but only for the case of oriented particle (φ = 0). When the field is applied at an arbitrary angle φ relative to the easy axis different expressions should be given. Those expressions are crucial when modeling ensembles of non-interacting nanoparticles with random orientations. Unlike the aligned case the critical field at which the barrier vanishes depends on φ. The analytic expression for ΔE2,1 is more complex, but in the following we will present some useful approximations.
Starting from the original Stoner–Wohlfarth model, described by eqn (2) and holds at zero temperature, the critical (switching) field Hsw where an irreversible jump of the magnetization direction occurs, is given by the condition  This equations system has no algebraic closed-form for arbitrary φ. The explicit solution involves solving a transcendental equation, by eradicating the angle θ, which leads to
This equations system has no algebraic closed-form for arbitrary φ. The explicit solution involves solving a transcendental equation, by eradicating the angle θ, which leads to
Hsw = HK[cos2/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ + sin2/3 φ + sin2/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ]−3/2 φ]−3/2 | (10) |
Although there are no analytic equations, analyzing the energy difference numerically with the help of eqn (2) and (10) it turns out that the expression:
 | (11) |
In the updated model at finite temperature:
• The system is assumed to be in one of two wells (θ = 0 or π).
• The transition rates between wells are governed by Arrhenius-type equations.
• The magnetization at time t M(t,φ) is a statistical average of the projection of magnetic moments in those wells onto the field direction.
The magnetization will be then given by:
M(t,φ) = Ms(P1(φ,t)cos(θ1 − φ) + (1 − P1(φ,t))cos(θ2 − φ)) ⇒ M(t,φ) = Ms(2P1(φ,t) − 1)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ φ | (12) |
To get the total magnetization Mtotal for a randomly oriented ensemble of non-interacting particles presenting known volume and anisotropy distributions P(V) and P(K) respectively, one has to simply integrate according to:
 | (13) |
Both approximations (aligned and random orientation) are derived assuming thermally assisted transitions within Néel–Arrhenius-like dynamics and also that the particle does not switch deterministically, but rather probabilistically due to thermal fluctuations. This means it is especially valid when the barrier height is a few kBT or more: ΔE ≥ 10kBT. If the barrier is too small, thermal fluctuations cause rapid switching and the rate equation approach may no longer be meaningful. An example is presented in Fig. 6 for a spherical iron oxide nanoparticle with diameter equal to 40 nm. Suggestively, the used magnetic field amplitude and frequency are typical values of magnetic hyperthermia schemes. A simpler approach for solving the DW system is, owing to the nonlinearities of the treatment, to work for a given value of the angle φ and to make a numerical average over all possible φ values (at least, in the presence of complete randomness of the directions of the easy axes). In each case, the proposed methodology can be treated by any software, keeping in mind that the core of the script should be the numerical solution of a first-order differential equation.
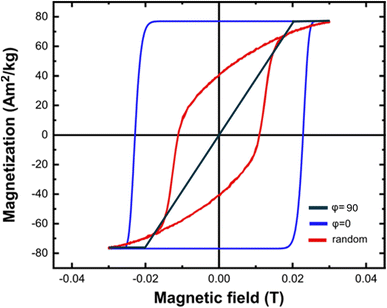 | ||
| Fig. 6 Magnetization versus magnetic field loops calculated when the “easy” axes are aligned with the magnetic field (blue colored loop, φ = 0), when easy axes are randomly oriented in space (red colored loop) and when magnetic field is applied vertically to the “easy” axis (black colored line). Hysteresis loops are obtained after solving eqn (8) for Keff = 9 kJ m−3, V = 3 × 10−23 m3, Ms = 80 emu g−1, μ0H0 = 0.03 T, f = 300 kHz and T = 300 K.45 | ||
The dependency of the coercive field and the hysteresis loop area to magnetic nanoparticles properties (size, anisotropy, magnetization) and applied magnetic field parameters (amplitude, frequency) is determined by fitting the numerical results to analytical equations. In the case of φ = 0, the following analytical expression for the coercive field is obtained:63
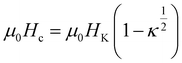 | (14) |
 | (15) |
It is clear from eqn (15) that κ is a crucial parameter, strongly affected by the temperature, which considers the sweeping rate of the magnetic field. For the case of random magnetic field orientation, the coercive field is given by:
| μ0Hc = 0.48μ0HK(b − κn) | (16) |
Similar to the coercive field, the estimation of the hysteresis loop area A is obtained by:
| A = 4a × μ0HK(1−κ1/2)Ms | (17) |
| A = 4a × 0.48μ0HK(b−κn)Ms | (18) |
The key feature of hysteresis loop area formulas is the dimensionless parameter α which is called “squareness” and characterizes the relative area of the hysteresis loop with respect to the ideal square one. The parameter α is proportional to the degree of alignment. For α = 1 the system is perfectly optimized and the “easy” axes of all magnetic nanoparticles is aligned to the magnetic field direction. In a sense, α represents the degree of optimization of a given system. The maximum hysteresis area Amax that can be obtained is:
| Amax = 4μ0HmaxMs | (19) |
| System | M s (300 K)a (A m2 kg−1) | μ 0 H max (mT) | A max (mJ g−1) | A exp (mJ g−1) | α | Reference |
|---|---|---|---|---|---|---|
| a Bulk magnetization per unit mass at 300 K. b μ 0 H max magnetic field of experiments. c A max theoretical maximum hysteresis area that could have been measured, which was calculated using eqn (19). d A exp hysteresis area experimentally measured under these conditions. e Calculated as α = Aexp/Amax. f Randomly-oriented iron oxide nanoparticles synthesized by bacteria. g Iron oxide nanoparticles synthesized by bacteria and aligned with the magnetic field. | ||||||
| FexOy MNPs | ≤92 | 13.8 | 5 | 1.5 | 0.3 | 64 |
| Magnetosomes-Af | ≤92 | 12.5 | 5 | 1.3 | 0.26 | 65 |
| Magnetosomes-Bg | ≤92 | 12.5 | 5 | 2.3 | 0.46 | 65 |
| Co MNPs | 162 | 31.2 | 20.6 | 3.25 | 0.16 | 18 |
| FeCo MNPs | 240 | 29 | 27.8 | 1.5 | 0.054 | 66 |
| Fe MNPs | 218 | 66 | 57.5 | 5.6 | 0.097 | 67 |
| CoFe2O4 | 75 | 31.1 | 9.35 | 0.63 | 0.067 | 68 |
Many-particles approximations: numerical models in MPH
Understanding MNPs magnetization dynamics is crucial for optimizing their heating efficiency. Due to the complex nature of inhomogeneous magnetization in nano-systems, the use of dynamical micromagnetic approaches is necessary. In this regard, full-scale numerical micromagnetic simulations have become essential for accurately modeling the response of a large number of MNPs under AMF. Over the past decade, advancements in computational power and the development of specialized micromagnetic software packages—such as OOMMF, LLG, MicroMagus, MuMax, and NMAG—have enabled detailed investigations into the magnetization dynamics of nanoparticles in MPH (Dmytriiev et al. 2012; Leliaert et al. 2018; Leliaert and Mulkers 2019; Stavrou et al. 2019; Sundara Mahalingam et al. 2019). Micromagnetic modeling in MPH is based on Brown's equation, which defines the total energy of a ferromagnet, and the Landau–Lifshitz–Gilbert (LLG) equation, which governs the magnetization dynamics under an external field. By solving these equations numerically, researchers can predict hysteresis losses which are critical for designing MNPs with optimized heating performance for hyperthermia applications.Under the assumption of micromagnetic theory, Brown69 derived a set of equations after employing the magnetic Gibbs free energy, such as:
| E = ∫(Eex + Ea + Ez + Ed + Edip) | (20) |
This integral in eqn (20) runs over the total volume of the ferromagnetic body. The details of constituent energies are mathematically described by eqn (21)–(25) and are theoretically defined as follows: exchange energy Eex (eqn (21)) indicates the interaction of spins with nearest neighbors. Volume anisotropy energy Ea (eqn (22)) indicates the crystal structure and depends on the crystal type of specimen material i.e. uniaxial or cubic symmetry. The Zeeman energy Ez (eqn (23)) indicates an externally applied magnetic field H. The term Ed indicates the dipolar nature of the individual magnetic nanoparticles that produce a demagnetizing field, also called the stray field, and triggers a demagnetizing energy contribution (eqn (24)), while Edip refers to the magneto-dipolar interaction between moments (eqn (25)). In the case of an assembly of N magnetic nanoparticles, the energies involved are given by the following expressions:
 | (21) |
 | (22) |
 | (23) |
 | (24) |
 | (25) |
Eqn (20) generates an effective magnetic field Heff which accounts for all relevant contributions to the magnetic Gibbs free energy E such as the externally applied magnetic field H, the demagnetizing field Hdi, the dipolar magnetic field and the exchange field. When a ferromagnetic material is placed in a magnetic field it's magnetization vector Mi “moves” due to the influence of Heff. This motion is well described by the Landau–Lifshitz theorem70 which is expressed by the following equation:
 | (26) |
This equation describes the precession of magnetization vector Mi in an effective field Heff. On the other hand, hysteresis curves tell us that beyond a certain value of an applied magnetic field, any magnetic sample can become saturated, i.e., all moments in the material are aligned along the field direction and thus, precession alone cannot describe this process. Energy dissipation (or damping) must be included to allow for magnetization to relax toward the saturated state. This is the reason why Gilbert71 included a phenomenological damping parameter in eqn (26) to express the experimentally noticeable damping in ferromagnetic materials. Consequently, the LLG equation is given by:
 | (27) |
Moreover, thermal field is added so the effects of finite temperature on magnetisation are considered. This is done by including a random noise field.72 The magnitude of the noise field is assumed to be the same in all three directions (isotropic), with a zero mean. The subsequent thermal fluctuations are also assumed to be uncorrelated. In other words, this assumption amounts to presuming the thermal noise to be white, with a flat power distribution in all frequencies. Mathematically, these assumptions can be written as follows: 〈Hth〉 = 0,  and 〈Hth(t)Hth(t + τ)〉 = |Hth|2δ(τ). An important point to stress is the time-dependence of the noise field: the exact magnitude of the noise field depends on the frequency of observation, and therefore the selection of the time-step in the discrete simulation is critical.
and 〈Hth(t)Hth(t + τ)〉 = |Hth|2δ(τ). An important point to stress is the time-dependence of the noise field: the exact magnitude of the noise field depends on the frequency of observation, and therefore the selection of the time-step in the discrete simulation is critical.
When thermal agitation is active, the system has a chance to overcome the barrier before its height is reduced to zero and the jump has some probability of taking place at an earlier time.73 In addition, the chances for this to occur should be higher the lower the field rate of change, because the system spends more time in front of the barrier to overcome, a process that is also imposed by the magnitude of magnetic anisotropy.3 As shown in Fig. 7, additional energy states are raised due to the thermal interactions between particles defining an inhomogeneously magnetized material. Nevertheless, in literature, the hysteresis loop is considered independent of the field rate. Thus, the estimation of specific absorption rate values (SAR), a key measure used for characterizing the heating efficiency of nanoparticles in MPH, from hysteresis loop area A, leads to a direct proportionality between SAR and frequency f, revealed through the linear relationship: SAR = A × f. However, this relationship is far from true since, as we explained rate-independent hysteresis is just a zero-temperature approximation, and so A should be described as a function of frequency A(f) at higher temperatures and for low frequencies.
 | ||
| Fig. 7 Schematic diagram of additional energy states emerged for a DW magnetic nanoparticle when thermal field is activated in the micromagnetic approach.45 | ||
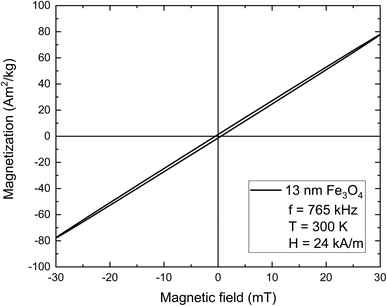
In74 the dynamic hysteresis loops are derived from micromagnetic simulations for the various frequency values and are depicted in Fig. 8 together with the loop obtained at 0 K which is independent on frequency. From the results is shown that there are two frequency regimes. One low frequency regime until ≈400 kHz where the hysteresis area increases with frequency due to the increase of the phase delay in the magnetization response. After this critical value of frequency, MNPs magnetization reaches the maximum phase delay i.e. the maximum relaxation time of spins. The whole process is dictated by thermal phenomena. At low frequency values thermal fluctuations dominate and, thus, the magnetic moments of MNPs need more time to surpass the anisotropy barrier. On the other hand, at room temperature and in the presence of an AMF, magnetic moments will overcome the barrier before its height is decreased and the jump has some finite probability of happening before AMF amplitude reach to zero. The increase in frequency diminishes the temperature influence and induces a kind of small hardening to the MNPs loop.
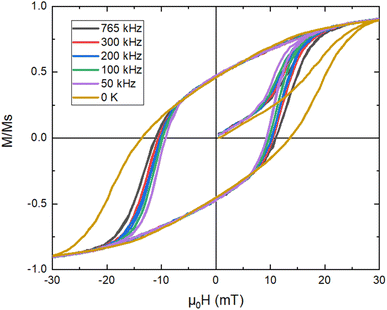 | ||
| Fig. 8 AC hysteresis loops for 30 mT magnetic field amplitude and for various frequencies (50–765 kHz). The largest loop corresponds to 0 K and is independent of the frequency.35 | ||
This behaviour is also illustrated in Fig. 9 through the dependence of the coercive field μ0Hc with frequency, where Hc is the magnitude of the reverse magnetic field strength. The results were also fitted with eqn (16).
 | ||
| Fig. 9 Dependence of the hysteresis loop with frequency and fitting of obtained data. The fitting curve and the corresponding equation are shown with red color.35 | ||
The SAR dependence on frequency is obtained by employing the equation SAR = μ0∮M(H)dH × f where the integral gives the hysteresis loop area. The results for 0 and 300 K are presented in Fig. 10.
 | ||
| Fig. 10 SAR dependence on frequency for 0 and 300 K. At the low frequencies (LF) regime and room temperature, the hysteresis loop area is not constant with frequency and thus SAR(f) diverges from linearity. An exponential trend is observed until the critical frequency value of 400 kHz. Above this value, the linear trend is restored at the high frequency (HF) regime. At 0 K a rate-independent loop results to a linear behavior of the SAR(f) function in both regimes. Note here that SAR is estimated in watts per iron mass which is the percentage of iron in the magnetic nanoparticles mass. The system under study were an assembly of 40 nm magnetite nanoparticles exposed to an AMF with an amplitude equal to 30 mT.74 | ||
In the LF regime the exponential fitting is given by: SAR = S0 × eηf where S0 was found equal to 70 W gFe−1 and corresponds to the hysteresis losses of the static (zero frequency) loop and η is a fitting constant. Thus, in the LF regime the SAR (f) relationship is more suitably described by an exponential trend rather than a linear relationship usually employed in literature, and is valid only in the HF regime.
To illustrate the temperature effect on the hysteresis loop we show in Fig. 11 some M(H) curves for various temperatures from 0 K to 400 K with a step of 100 K and magnetic field variations from −30 mT to 30 mT as above. The value of frequency is now fixed at the value of 765 kHz which is a typical value used in MPH. The M(H) curves, obtained by micromagnetic simulations, in Fig. 11 illustrate the influence of the thermal fluctuations on the hysteresis curves. For low-temperatures case, the system is in the blocked state and exhibits ferromagnetic-like hysteresis losses that originate from the overcoming of the anisotropy energy barrier while for the high temperatures thermal excitations are large enough to promote the reversible jumping over the anisotropy barrier without energy losses. The magnetic moments fluctuate because of the thermal energy and consequently fluctuations are reduced the smaller the temperature. Thus, the physical tendency of both saturation magnetization and coercive field decrease with temperature increase is observed from the simulations and coincides with theory. Magnetization saturation and coercive field values are depicted in Table 2.
 | ||
| Fig. 11 Dynamic hysteresis loops of single domain magnetite MNPs estimated by micromagnetic simulations at various temperatures and compared to the one observed at 0 K. The applied field amplitude and frequency were equal to 30 mT and 765 kHz respectively. The value of anisotropy constant was equal to 9 kJ m−3, a value also used in analytical models as depicted in Fig. 4 for magnetite. The decrease of hysteresis loop area and thus the decrease of hysteresis losses is obvious with temperature increase. | ||
| T (K) | M s (A m2 kg−1) | μ 0 H c (mT) |
|---|---|---|
| 0 | 50 | 25 |
| 100 | 48 | 22 |
| 200 | 45 | 21 |
| 300 | 40 | 18 |
| 400 | 34 | 12 |
Another interesting plot that may be followed from the temperature dependent hysteresis loop curves is the one for the variation of saturation magnetization with temperature. The temperature dependence of the magnetization, investigated by using a combination of different experimental methods, is an important source of information regarding the anomalies and/or singularities linked to the dimensional confinement in magnetic nanoparticles. The deviation shown by magnetic material if compared with its highest magnetization state is given by the spin-wave excitation, also called magnon. The latter is basically originated by the sinusoidal-type distribution of the spin orientation states within the material, which are forming a certain angle with respect to each other; thus, a more energetically unfavorable situation of anti-parallel coupling is avoided. Departing from the spin-wave theory, Bloch proposed an expression75 aiming to describe the thermal dependence of the saturation magnetization Ms(T) in a bulk material,
 | (28) |
 and measured in K−n where Q is 1, 2, and 4 for single cubic, bcc, and fcc systems, respectively, and S is the total electron spin. The exponent n = 3/2 fits well to experimental results in ferromagnetic materials and some spinel ferrites such as MnxFe3−xO4 (0.2 ≤ x ≤ 2).76
and measured in K−n where Q is 1, 2, and 4 for single cubic, bcc, and fcc systems, respectively, and S is the total electron spin. The exponent n = 3/2 fits well to experimental results in ferromagnetic materials and some spinel ferrites such as MnxFe3−xO4 (0.2 ≤ x ≤ 2).76
By taking the saturation magnetization data that occurred from Fig. 11 and analyze them using Bloch's law and determine the Bloch's constant and exponent, B and n respectively, directly from the fitting (B and n are left as free-fitting parameters) of the saturation magnetization to temperature plot with eqn (28) as illustrated in Fig. 12.
The Bloch's law, given by eqn (28), indicates that the decrease in the saturation magnetization with increasing temperature due to spin-wave excitations is described by a power law in T. Our data seem to follow the predicted behavior as displayed in the plot of Fig. 12. There, the solid red line represent the fit of the eqn (28) and the agreement between the latter and numerical data is optimized (R2 = 0.995) for n = 2 a value that deviates from Bloch's law n = 3/2. In the case of nanoparticles and clusters, some theoretical calculations have shown that the exponent n is higher than 3/2, and reaches 2 as a consequence of the reduction in the size of the particles.75 Going back to eqn (28), such deviations are numerically reflected in the temperature exponent and the B constant value, which are increased with respect to the bulk values, indicating a decrease in the Curie temperature of the studied system. The main idea behind the explanation of this effect is that the lack of full coordination at the surface of the MNPs may lead to larger spin deviations in this region than in the central part of the MNP. The effect of the limited number of degrees of freedom at the surface leads to an energy gap in the spin-wave spectrum resulting in a flat magnetization curve at low temperatures. In other words, the magnetization decreases faster at higher temperatures in the nanoparticles than in the bulk material, due to lacking coordination at the surface. Both micromagnetic calculations45,77 and experimental results78 have repeatedly shown this behavior. Bloch's constant B is also left as a free-fitting parameter, determined from the fitting procedure and found equal to 3.03 × 10−6 K−2 a value that has been already reported in the literature for single domain ferromagnetic nanoparticles.79
The explained methodology can be extended to optimize the structural and magnetic properties of magnetic nanoparticles used in MPH (crystal symmetry, grain size, anisotropy, saturation magnetization, coercive field).36,72,77,80–82 Since nanoparticles synthesis, characterization and evaluation procedures can be quite costly and time-consuming, the use of numerical simulations instead of experimental measurements to rapidly and accurately examine a large number of parameters and properties and finally, obtain the optimum ones, comes as an advantageous opportunity. Offered possibilities of employing modern numerical methods and suitable computer software are in position to easily deliver a reliable prediction on the hysteresis behavior of any system designed to operate as an MPH agent.
Discussion on rate equations and numerical models
In the study of magnetic hyperthermia, understanding and predicting the behavior of magnetic nanoparticles under alternating magnetic fields is crucial for optimizing heating efficiency. Researchers employ various modeling approaches to describe the dynamic magnetization processes, ranging from full-scale numerical simulations based on the Landau–Lifshitz–Gilbert (LLG) equation to analytical approximations like the rate equation model under the double-well potential framework. While both approaches provide valuable insights, analytical models offer several distinct advantages when dealing with the physical realities of hyperthermia experiments, especially considering the immense number of particles involved.In a typical magnetic hyperthermia experiment, the sample contains a massive number of nanoparticles. For instance, in one milligram of MNPs, the number of individual particles can exceed 1013, assuming a typical particle mass on the order of 10−22 kg. The total number of particles per unit volume can be estimated by dividing the sample's saturation magnetization (e.g., measured in A m−1) by the magnetic moment of a single particle (A m2). This huge number of particles underscores a fundamental limitation of direct numerical simulations: it is computationally infeasible to model each particle individually. Numerical simulations using the LLG equation (implemented in software like OOMMF or MuMax3) solve the time evolution of the magnetization vector for individual or assemblies of magnetic moments under the influence of external and internal magnetic fields. These methods are highly accurate and account for detailed micromagnetic interactions, including exchange coupling, dipole–dipole interactions, thermal noise, and anisotropy effects. However, this accuracy comes with significant computational cost:
(1) Particle scale modeling LLG simulations are generally restricted to simulating a few particles or a small grid of magnetic cells. Simulating 1013 particles, as in a real hyperthermia sample, is completely infeasible due to limitations in memory and processing power.
(2) Statistical limitations: since LLG simulations model only a tiny fraction of the actual system, they may not accurately capture the collective response of an ensemble with distributed particle sizes, anisotropies, or orientations.
(3) Neglect of thermal fluctuations or approximations: including thermal effects requires stochastic LLG formulations, which significantly increase computational complexity and often require simplifications that reduce realism.
(4) No explicit particle count: these simulations often model a continuous magnetization distribution rather than discrete particles. As such, they cannot explicitly incorporate the actual number of particles, limiting their usefulness in estimating macroscopic quantities like specific absorption rate (SAR) per unit volume.
In the double-well approximation, the time-dependent magnetization M(t) is obtained by solving the rate equation. This approach offers several key advantages:
(1) Scalability: since each particle is treated independently (under the assumption of negligible interparticle interactions), the model can be scaled to an arbitrary number of particles. One can directly calculate the macroscopic magnetization by summing or integrating over the contributions of all particles, weighted by distributions in size, anisotropy, and orientation.
(2) Direct incorporation of particle number: unlike LLG models, analytical models can explicitly include the number of particles per unit volume. This allows direct estimation of heating power or SAR by calculating:
| SAR = Nsμ0∮M(H)dH × f |
(3) Inclusion of distributions: analytical models can easily accommodate realistic distributions of particle properties (e.g., log-normal size distribution, random orientation of easy axes, or Gaussian anisotropy distribution). These distributions are integrated into the final magnetization response using statistical mechanics tools, something that becomes highly complex in LLG simulations.
(4) Faster computation: analytical solutions or numerical integration of rate equations is many orders of magnitude faster than LLG-based simulations, making it feasible to explore wide parameter spaces (e.g., different field amplitudes, frequencies, temperatures) efficiently.
(5) Thermal effects naturally included: since the flipping rates are based on thermal activation over energy barriers, the role of temperature is naturally incorporated without the need for stochastic differential equations.
Analytical models are rooted in equilibrium and nonequilibrium statistical mechanics. The double-well system is a prototypical example of a bistable system in statistical physics, where the populations of each state evolve with time according to thermally activated transition rates. This connection allows for a principled approach to modeling macroscopic observables like net magnetization, entropy production, or hysteresis losses, using well-established tools. Averaging over distributions is done through integrals of the form presented in eqn (13). Such ensemble averaging is essential for comparison with experiments where particle heterogeneity is the norm.
On the other hand, LLG simulations provide microscopic detail and are valuable for understanding local magnetization dynamics and complex particles interactions such as the magnetostatic and dipolar interaction leading to strong demagnetizing fields. Moreover, the main advantages are:
• It captures full vector dynamics including precession, damping, and transient behavior.
• Works well at very high frequencies or short timescales.
• Necessary when anisotropy is complex or field varies non-sinusoidally.
If researchers working in this field aim in understanding and optimizing magnetic hyperthermia heating efficiency, rate equations methods are typically preferable, unless they study effects that require full LLG dynamics such as high-speed switching, precession-dominated regimes and most importantly strong interactions between nanoparticles.
Linear response theory
In MPH, the linear response theory (LRT) is a model that aims to describe the dynamic response of an assembly of small (<20 nm) superparamagnetic nanoparticles using the Néel–Brown relaxation time, a concept that will be further analyzed below. The starting assumption of LRT is that the magnetic system responds linearly with the magnetic field and its magnetization can be put in the form M(t) = χH(t) where χ is the complex susceptibility.83 When an alternating magnetic field of sufficiently high frequency is applied, the magnetisation of a superparamagnetic particle lags behind the applied field. As a result of this phase lag, the susceptibility, χ = χ′ − iχ′′ is an imaginary quantity with the real part χ′ representing the in-phase component, and the imaginary part, χ′′ the quadrature or loss-component are given by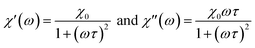 where χ0 is the equilibrium magnetic susceptibility. The equilibrium susceptibility depends on the applied magnetic field.75,84,85 A conservative approach consists in treating χ0 as the chord susceptibility represented by a Langevin function L(ξ) = cothξ − 1/ξ implemented in the following expression:
where χ0 is the equilibrium magnetic susceptibility. The equilibrium susceptibility depends on the applied magnetic field.75,84,85 A conservative approach consists in treating χ0 as the chord susceptibility represented by a Langevin function L(ξ) = cothξ − 1/ξ implemented in the following expression:  where
where  is the initial susceptibility and ϕ the fraction of saturation magnetisation Ms of the magnetic nanoparticles to the bulk magnetisation Md: φ = Ms/Md. Although χ′ decreases with increasing frequency, the imaginary part, χ′′, peaks at an angular frequency
is the initial susceptibility and ϕ the fraction of saturation magnetisation Ms of the magnetic nanoparticles to the bulk magnetisation Md: φ = Ms/Md. Although χ′ decreases with increasing frequency, the imaginary part, χ′′, peaks at an angular frequency  where τ is the relaxation time of the particles. These relationships are identical to the Debye spectra of polar molecules in the absence of a constant field. Note here that, ferromagnets exhibit magnetic resonance at frequencies ≈ 108 to 1010 Hz yielding a change of sign to negative value of χ′(ω) and a sharp peak of χ′′(ω).86,87
where τ is the relaxation time of the particles. These relationships are identical to the Debye spectra of polar molecules in the absence of a constant field. Note here that, ferromagnets exhibit magnetic resonance at frequencies ≈ 108 to 1010 Hz yielding a change of sign to negative value of χ′(ω) and a sharp peak of χ′′(ω).86,87
When an external magnetic field that provides sufficient energy is applied to a system of superparamagnetic nanoparticles suspended in a liquid carrier, the magnetic moment of the latter may be displaced from its preferred orientation. The whole system of the liquid and the magnetic nanoparticles is called magnetic fluid or “ferrofluid’’.88 Consequently, as the magnetic moment returns to the equilibrium state, thermal energy is released. There are two possible relaxation mechanisms of the magnetic moment, Néel and Brownian.89 In Néel relaxation which is associated with the anisotropy energy, the magnetic moment alternates between parallel and anti-parallel directions within the MNPs, while the physical orientation of the particle remains fixed. In the Brownian relaxation mechanism, which relates to the hydrodynamic properties of the magnetic fluid, the physical orientation of the particle changes, while the magnetic moment remains unaltered with respect to the particle rotation axis. In the Néel mechanism, the relaxation time, τN, is given by:63
 | (29) |
 | (30) |
 where R is the nanoparticle radius and δ is the thickness of the surfactant. Néel relaxation dominates over a short range of particle sizes as the fastest process. Above a certain critical size, Brown relaxation mechanism, depicted by eqn (30) takes over. In the region of that critical size, where both processes are equally probable, the net relaxation time τ is given by their geometric mean:37
where R is the nanoparticle radius and δ is the thickness of the surfactant. Néel relaxation dominates over a short range of particle sizes as the fastest process. Above a certain critical size, Brown relaxation mechanism, depicted by eqn (30) takes over. In the region of that critical size, where both processes are equally probable, the net relaxation time τ is given by their geometric mean:37 | (31) |
The energy deposition premises an AMF with reversal times comparable to the effective relaxation time. Then, thermal energy is deposited due to delay in the relaxation of magnetic moment. Although both mechanisms are present in the heating process, a transition between both mechanisms occurs when τB = τN and depends on several parameters including the crystal and hydrodynamic volume of the MNPs, the frequency of the AC field, the energy barrier and the viscosity of the medium. Specifically, Néel relaxation mechanism is dominant for smaller particles of low anisotropy, suspended in viscous medium, at high frequencies of the AMF, while Brownian relaxation mechanism is favored for larger particle sizes with high anisotropy, in a medium of low viscosity and at low AMF frequencies. When the MNPs are immobilized in a medium, for instance in tumor tissue, or form agglomerations, Brownian relaxation mechanism is suppressed and Néel relaxation is the only occurring mechanism.90 Exploitation of magnetic particles that deposit energy through Néel relaxation mechanism is encouraged in medical applications, since Brownian relaxation mechanism is influenced by the local environment, which introduces further implications in treatment planning.10,85,91–94
The computation of power dissipation in a magnetic fluid due to susceptibility losses is accomplished by usage of thermodynamics theory. Rosensweig developed a model that calculates the volumetric power dissipation rate through analytical relationships.13,89 The model applies at low fields, hence within the linear response regime of magnetization. According to the first law of thermodynamics, the internal energy U for a system of fixed density can be expressed as the sum of the heat Q added to the system and the magnetic work W applied on the system. For a unit volume:
| dU = δQ + δW. |
Assuming an adiabatic process δQ = 0 and the differential internal energy of the system equals to the differential magnetic work
| dU = δW = H × dB | (32) |
| ΔU = −μ0∮MdH. | (33) |
The magnetization M of the magnetic fluid can be expressed in terms of the complex magnetic susceptibility χ = χ′ − iχ′′. The external magnetic field H(t) and resulting magnetization M(t) are given by:
H(t) = H0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt = Re[H0eiωt] and M(t) = Re[χH0eiωt] = H0(χ′ ωt = Re[H0eiωt] and M(t) = Re[χH0eiωt] = H0(χ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt + χ′′ ωt + χ′′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt) ωt) | (34) |
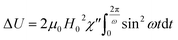 | (35) |
Only the χ′′ component of magnetic susceptibility also referred as the loss component is present in eqn (35). Thus, the time dependent magnetization will be given by the equation:95
 | (36) |
It has been demonstrated by Rosensweig that the volumetric power dissipation is then given by the product of the internal energy ΔU and cyclic frequency f = ω/2π:
| P = fΔU = μ0πχ′′fH02. | (37) |
 in eqn (37) yields the following expression for the volumetric power dissipation corresponding to an aqueous monodispersion assembly of magnetic nanoparticles:
in eqn (37) yields the following expression for the volumetric power dissipation corresponding to an aqueous monodispersion assembly of magnetic nanoparticles: | (38) |
Then the SAR in watt per magnetic material mass would be given by  where ϕ is the magnetic nanoparticles volume fraction inside the magnetic fluid and ρMNPs is the MNPs density. It is important to point out that, although according to eqn (38) the heating efficiency depends on the magnetic field amplitude squared, a dependence on the amplitude cube has been found in literature74,96,97 for higher frequencies as it is depicted in Fig. 13. In addition, the power dissipation and thus the SAR of the MNPs is maximized for ωτ = 1. This condition is satisfied when the relaxation time of the nanoparticles is equal to the AC field time constant and determines the critical frequency of the system.98,99
where ϕ is the magnetic nanoparticles volume fraction inside the magnetic fluid and ρMNPs is the MNPs density. It is important to point out that, although according to eqn (38) the heating efficiency depends on the magnetic field amplitude squared, a dependence on the amplitude cube has been found in literature74,96,97 for higher frequencies as it is depicted in Fig. 13. In addition, the power dissipation and thus the SAR of the MNPs is maximized for ωτ = 1. This condition is satisfied when the relaxation time of the nanoparticles is equal to the AC field time constant and determines the critical frequency of the system.98,99
 | ||
| Fig. 13 SAR index dependence on magnetic field amplitude and frequency of single domain MNPs. SAR data points are presented with red and blue color and are fitted with best fitting curve (green dotted line) for two typical frequency values used in MPH, namely 375 and 765 kHz, respectively.40 | ||
In several articles, eqn (38) is defined as applying to “relaxation losses” of superparamagnetic MNPs. In these articles, “relaxation losses” are opposed – as if it was a different process – to the “hysteresis losses” of ferromagnetic NPs. This distinction can lead to confusion as all the losses, whether the MNPs are in the superparamagnetic regime or in the ferromagnetic regime (>20 nm), are always “hysteresis losses” insofar as they are simply given by the hysteresis loop area. By drawing the parametric plot (H(t), M(t)) we can find the hysteresis loop. Basic mathematics indicates that eqn (34) and (36) correspond to the parametric equation of an ellipse in the (H, M) plane that forms an angle between its long axis and the abscise axis. A typical hysteresis loop resulted after employing LRT to a specific MNPs system is showing in Fig. 14. Thus, LRT is simply one model among several that aims to calculate the hysteresis loop area and shape when the magnetic response is linear with the applied magnetic field. In63 the authors suggested putting an end to the distinction between hysteresis losses and relaxation losses and, rather, making a distinction between different kinds of models aiming at calculating the hysteresis area.
In real systems a magnetic fluid contains nanoparticles of different sizes that can be reasonably described by a log-normal distribution:72,93–96 with normalization condition
with normalization condition 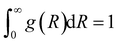 where σ is the standard deviation, R0 the median of ln
where σ is the standard deviation, R0 the median of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R and the mean nanoparticle radius Rm is given by:
R and the mean nanoparticle radius Rm is given by:  The volumetric power dissipation
The volumetric power dissipation ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) of a polydispersion is obtained by integrating over the distribution function:
of a polydispersion is obtained by integrating over the distribution function:  The size distribution of nanoparticles should be considered in the calculation of power dissipation, in order to avoid overestimated results. The degradation of power dissipation for increasing standard deviation, implies that narrow size distributions are desired for optimum heating efficiency.97–100 It is important to point out that the effective relaxation time depends exponentially on the particle volume and anisotropy in systems where Néel relaxation is the primary heating mechanism. Thus, the influence of both parameters on heating efficiency is very significant. Tailoring highly anisotropic nanoparticles allows for the tuning of effective relaxation time on higher levels, enabling highly efficient systems at lower frequencies and smaller sizes.101–103 Though LRT becomes inaccurate under strong interparticle interactions and spatial magnetization complexities, it offers simplicity and speed for estimations and evaluations in SPM systems where dipolar interactions do not dominate.
The size distribution of nanoparticles should be considered in the calculation of power dissipation, in order to avoid overestimated results. The degradation of power dissipation for increasing standard deviation, implies that narrow size distributions are desired for optimum heating efficiency.97–100 It is important to point out that the effective relaxation time depends exponentially on the particle volume and anisotropy in systems where Néel relaxation is the primary heating mechanism. Thus, the influence of both parameters on heating efficiency is very significant. Tailoring highly anisotropic nanoparticles allows for the tuning of effective relaxation time on higher levels, enabling highly efficient systems at lower frequencies and smaller sizes.101–103 Though LRT becomes inaccurate under strong interparticle interactions and spatial magnetization complexities, it offers simplicity and speed for estimations and evaluations in SPM systems where dipolar interactions do not dominate.
Conclusions
A thorough understanding and accurate assessment of the intrinsic magnetic properties of nanoscale systems are crucial for both fundamental research and application-driven design. In this context, the magnetic behavior of individual nanoparticles can be effectively described using simplified analytical models, such as the macrospin approximation and double well (DW) models. These approaches assume that the entire nanoparticle behaves as a single giant magnetic moment, capable of switching between two energy minima (metastable states) separated by an energy barrier. The thermally activated magnetization reversals between these states, characterized by saddle points in the energy landscape, provide a theoretical basis for estimating the magnetization of a single nanoparticle. Additionally, numerical techniques, such as Monte Carlo simulations, are employed to refine these models and extend their predictive capabilities.However, when dealing with many-body systems, where interactions between multiple nanoparticles become significant, analytical energy minimization techniques are no longer sufficient. Instead, micromagnetic simulations and dynamical models are required to capture the complex magnetization dynamics. A widely used approach is the LLG equation, which governs the precessional motion of magnetization in interacting nanoparticle systems. By utilizing micromagnetic simulation software—such as OOMMF, MuMax, NMAG, and MicroMagus—hysteresis loops of nanoparticle assemblies can be computed, enabling the evaluation of their collective magnetic properties.
In the case of MPH applications, the presence of an externally applied AMF introduces additional complexity to the magnetization dynamics. To optimize heating efficiency for therapeutic use, the arrangement and interactions of nanoparticles under a dynamic magnetic field must be carefully examined. Molecular dynamics simulations complement micromagnetic models by providing insights into nanoparticle alignment and aggregation under field influence, which directly affects their heating performance. Moreover, in LRT, the dominant relaxation mechanism depends on factors such as nanoparticle size, magnetic anisotropy, and surrounding medium viscosity. Optimizing these relaxation processes is essential to maximize heat dissipation while ensuring efficient energy absorption under clinical operating conditions during a magnetic hyperthermia scheme.
Due to the inherent complexity of magnetization dynamics in these systems, only relatively simple cases—such as single-domain nanoparticles described by the macrospin approximation—can be solved analytically. In contrast, micromagnetic simulations offer a more realistic and comprehensive representation by incorporating all relevant energy contributions, including exchange energy, anisotropy energy, Zeeman energy, magnetostatic interactions, and dipolar interactions. This enables precise predictions of the spatial and temporal evolution of magnetization under external stimuli.
Micromagnetic modeling continues to be an invaluable tool for advancing nanoscale magnetic research, bridging the gap between theoretical predictions and experimental observations. The future of numerical simulations in this field lies in the development of multiphysics approaches, integrating magnetization dynamics with additional physical processes such as heat transfer, fluid dynamics, and mechanical stress effects. While current software solutions are making strides toward such integration, a fully optimized, general-purpose multiphysics package remains an ongoing challenge. Enhancing user-friendly interfaces will also be essential for facilitating the use of micromagnetic simulations in both fundamental research and applied technologies.
Looking ahead, numerical simulations are expected to further expand their role as the primary tool for designing and optimizing magnetic nanoparticles, particularly for biomedical applications such as MPH. The increasing interest in nanoscale and many-body magnetic systems underscores the necessity of simulation-driven design, enabling the tailoring of magnetic properties for next-generation nanoparticle-based therapies. Beyond the current state-of-the-art, future efforts are anticipated to focus on the development of comprehensive multiphysics frameworks capable of simultaneously modeling magnetization dynamics, heat transfer, fluid flow, and even biological interactions at cellular and tissue levels. This holistic approach will allow for the accurate prediction of nanoparticle behavior under realistic physiological conditions, bridging the gap between theoretical models and clinical applications. Furthermore, coupling micromagnetic simulations with experimental feedback loops and machine learning techniques is expected to significantly accelerate the discovery and optimization of MNPs, delivering customized solutions tailored to specific patient needs and tumor microenvironments. Ultimately, such advances will not only enhance the therapeutic efficiency and safety of MPH treatments but will also open new pathways in the broader field of nanomedicine, establishing numerical simulations as a cornerstone in the rational design of multifunctional nanomaterials for biomedical innovation.
Data availability
Data for this article, including origin data are available at the site of the MagnaCharta Lab of the Physics Department of Aristotle University of Thessaloniki at https://magnacharta.auth.gr/.Conflicts of interest
There are no conflicts to declare.References
- Q. A. Pankhurst, N. K. T. Thanh, S. K. Jones and J. Dobson, J. Phys. D Appl. Phys., 2009 DOI:10.1088/0022-3727/42/22/224001.
- L. S. Arias, J. P. Pessan, A. P. M. Vieira, T. M. T. De Lima, A. C. B. Delbem and D. R. Monteiro, Antibiotics, 2018 DOI:10.3390/antibiotics7020046.
- E. A. Périgo, G. Hemery, O. Sandre, D. Ortega, E. Garaio, F. Plazaola and F. J. Teran, Appl. Phys. Rev., 2015 DOI:10.1063/1.4935688.
- O. Hosu, M. Tertis and C. Cristea, Magnetochemistry, 2019, 5, 55 CrossRef CAS.
- V. Socoliuc, D. Peddis, V. I. Petrenko, M. V. Avdeev, D. Susan-Resiga, T. Szabó, R. Turcu, E. Tombácz and L. Vékás, Magnetochemistry, 2020, 6, 2 CrossRef CAS.
- M. F. El-Amin, A. M. Saad, A. Salama and S. Sun, Geofluids, 2024 DOI:10.1155/2017/3602593.
- I. Hilger, Int. J. Hyperthermia, 2013, 29(8), 828–834 CrossRef PubMed.
- A. Das, S. Mohanty, R. Kumar and B. K. Kuanr, ACS Appl. Mater. Interfaces, 2020, 12, 42016–42029 CrossRef CAS PubMed.
- E. Myrovali, N. Maniotis, T. Samaras and M. Angelakeris, Nanoscale Adv., 2020, 2, 408–416 RSC.
- Z. W. Tay, P. Chandrasekharan, A. Chiu-Lam, D. W. Hensley, R. Dhavalikar, X. Y. Zhou, E. Y. Yu, P. W. Goodwill, B. Zheng, C. Rinaldi and S. M. Conolly, ACS Nano, 2018, 12, 3699–3713 CrossRef CAS PubMed.
- H. Calipinar and D. Ulas, Procedia Comput. Sci., 2019, 158, 1011–1018 CrossRef.
- M. A. Ahsan, V. Jabbari, M. A. Imam, E. Castro, H. Kim, M. L. Curry, D. J. Valles-Rosales and J. C. Noveron, Sci. Total Environ., 2020, 698, 134214 CrossRef CAS PubMed.
- R. R. Shah, T. P. Davis, A. L. Glover, D. E. Nikles and C. S. Brazel, J. Magn. Magn. Mater., 2015, 387, 96–106 CrossRef CAS PubMed.
- A. P. Guimarães, Principles of Nanomagnetism, 2009 Search PubMed.
- M. Ashraf, I. Khan, M. Usman, A. Khan, S. S. Shah, A. Z. Khan, K. Saeed, M. Yaseen, M. F. Ehsan, M. N. Tahir and N. Ullah, Chem. Res. Toxicol., 2020, 33, 1292–1311 Search PubMed.
- A. A. Petryk, A. J. Giustini, R. E. Gottesman, P. A. Kaufman and P. J. Hoopes, Int. J. Hyperthermia, 2013, 29, 845–851 CrossRef CAS PubMed.
- H. Gavilán, K. Simeonidis, E. Myrovali, E. Mazarío, O. Chubykalo-Fesenko, R. Chantrell, L. Balcells, M. Angelakeris, M. P. Morales and D. Serantes, Nanoscale, 2021, 13, 15631–15646 RSC.
- M. Zeisberger, S. Dutz, R. Müller, R. Hergt, N. Matoussevitch and H. Bönnemann, J. Magn. Magn. Mater., 2007 DOI:10.1016/j.jmmm.2006.11.178.
- X. Gao, A. Avellan, S. Laughton, R. Vaidya, S. M. Rodrigues, E. A. Casman and G. V. Lowry, Environ. Sci. Technol., 2018, 52, 2888–2897 CrossRef CAS PubMed.
- J. Pearce, A. Giustini, R. Stigliano and P. J. Hoopes, J. Nanotechnol. Eng. Med., 2013 DOI:10.1115/1.4024904.
- A. Skumiel, K. Kaczmarek, D. Flak, M. Rajnak, I. Antal and H. Brząkała, J. Mol. Liq., 2020, 304, 112734 CrossRef CAS.
- K. Vamvakidis, N. Maniotis and C. Dendrinou-Samara, Nanoscale, 2021, 13, 6426–6438 RSC.
- P. Appa Rao, K. Srinivasa Rao, T. R. K. Pydi Raju, G. Kapusetti, M. Choppadandi, M. Chaitanya Varma and K. H. Rao, J. Alloys Compd., 2019, 794, 60–67 CrossRef CAS.
- M. Vicentini, R. Ferrero and A. Manzin, Int. J. Therm. Sci., 2024, 203, 109151 CrossRef CAS.
- Suriyanto, E. Y. K. Ng and S. D. Kumar, Biomed. Eng. Online, 2017, 16, 36 CrossRef CAS PubMed.
- S. Ruta, R. Chantrell and O. Hovorka, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- P. Allia, G. Barrera and P. Tiberto, Phys. Rev. B, 2018, 98, 1–14 CrossRef.
- S. Erokhin, D. Berkov, N. Gorn and A. Michels, Phys. Rev. B: Condens. Matter Mater. Phys., 2012 DOI:10.1103/PhysRevB.85.024410.
- Y. Fernández-Afonso, L. Asín, L. Beola, M. Moros, J. Jesús, M. De La Fuente, R. M. Fratila, V. G. Grazú and L. Gutiérrez, ACS Appl. Bio Mater., 2022, 2022, 1879–1889 CrossRef PubMed.
- G. T. Landi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014 DOI:10.1103/PhysRevB.89.014403.
- J. G. Ovejero, D. Cabrera, J. Carrey, T. Valdivielso, G. Salas and F. J. Teran, Phys. Chem. Chem. Phys., 2016, 18, 10954–10963 RSC.
- B. Mehdaoui, R. P. Tan, A. Meffre, J. Carrey, S. Lachaize, B. Chaudret and M. Respaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 174419 CrossRef.
- L. V. Zhigilei, A. N. Volkov and A. M. Dongare, in Encyclopedia of Nanotechnology, 2016 Search PubMed.
- U. Jeong, X. Teng, Y. Wang, H. Yang and Y. Xia, Adv. Mater., 2007, 19(1), 33–66 CrossRef CAS.
- K. Wu and J. P. Wang, AIP Adv., 2017 DOI:10.1063/1.4978458.
- K. Brzuszek, C. A. Ross and A. Janutka, J. Magn. Magn. Mater., 2024, 599, 172070 CrossRef CAS.
- P. Allia, G. Barrera and P. Tiberto, Phys. Rev. Appl., 2019, 12, 034041 CrossRef CAS.
- P. M. Zélis, G. A. Pasquevich, S. J. Stewart, M. B. F. Van Raap, J. Aphesteguy, I. J. Bruvera, C. Laborde, B. Pianciola, S. Jacobo and F. H. Sánchez, J. Phys. D Appl. Phys., 2013, 46, 125006 CrossRef.
- D. Faílde, V. Ocampo-Zalvide, D. Serantes and Ò. Iglesias, Nanoscale, 2024, 16, 14319–14329 RSC.
- J. Leliaert and J. Mulkers, J. Appl. Phys., 2019 DOI:10.1063/1.5093730.
- G. Barrera, P. Allia and P. Tiberto, Nanoscale, 2021, 13, 4103–4121 RSC.
- K. Simeonidis, C. Martinez-Boubeta, D. Serantes, S. Ruta, O. Chubykalo-Fesenko, R. Chantrell, J. Oró-Solé, L. Balcells, A. S. Kamzin, R. A. Nazipov, A. Makridis and M. Angelakeris, ACS Appl. Nano Mater., 2020, 3, 4465–4476 CrossRef CAS PubMed.
- N. Maniotis, A. Nazlidis, E. Myrovali, A. Makridis, M. Angelakeris and T. Samaras, J. Appl. Phys., 2019, 125(10), 103903 CrossRef.
- E. C. Stoner and E. P. Wohlfarth, Philos. Trans. R. Soc. London, Ser. A, 1948, 240, 599–642 CrossRef.
- N. Maniotis and K. Simeonidis, Analytical Approaches of Magnetic Hybrid Nanoparticles Using Numerical Modelling and Simulation Tools, in Handbook of Magnetic Hybrid Nanoalloys and their Nanocomposites, Springer, Cham, 2022, DOI:10.1007/978-3-030-34007-0_54-1.
- D. Serantes, Open Surf. Sci. J., 2012 DOI:10.2174/1876531901204010071.
- N. Maniotis, Numerical simulation and characterization of systems for Magneto-thermal and Magneto-mechanical interaction with the living matter, Aristotle University of Thessaloniki, 2020 Search PubMed.
- M. Angelakeris, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 1642–1651 CrossRef CAS PubMed.
- B. Kozissnik, A. C. Bohorquez, J. Dobson and C. Rinaldi, Int. J. Hyperthermia, 2013, 29(8), 706–714 CrossRef PubMed.
- A. Makridis, S. Curto, G. C. Van Rhoon, T. Samaras and M. Angelakeris, J. Phys. D Appl. Phys., 2019, 52, 255001 CrossRef CAS.
- G. Barrera, P. Allia and P. Tiberto, Nanoscale Adv., 2023, 5, 4080–4094 RSC.
- D. Soukup, S. Moise, E. Céspedes, J. Dobson and N. D. Telling, ACS Nano, 2015, 9, 231–240 CrossRef CAS PubMed.
- E. Kasapoglu, M. B. Yücel and C. A. Duque, Nanomaterials, 2023, 13, 892 CrossRef CAS PubMed.
- M. Roda-Llordes, A. Riera-Campeny, D. Candoli, P. T. Grochowski and O. Romero-Isart, Phys. Rev. Lett., 2024, 132, 023601 CrossRef CAS PubMed.
- R. N. Valani and Á. G. López, Chaos, Solitons Fractals, 2024, 186, 115253 CrossRef.
- S. Gu, M. Cieslak, B. Baird, S. F. Muldoon, S. T. Grafton, F. Pasqualetti and D. S. Bassett, Sci. Rep., 2018, 8, 1–15 Search PubMed.
- C. Liu, L. Zhu and M. Belkin, Appl. Comput. Harmon. Anal., 2022, 59, 85–116 CrossRef.
- E. Callaway, Nature, 2022, 608, 15–16 CrossRef CAS PubMed.
- D. Chakravarty, J. W. Schafer, E. A. Chen, J. F. Thole, L. A. Ronish, M. Lee and L. L. Porter, Nat. Commun., 2024, 15, 1–13 Search PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596(7873), 583–589 CrossRef CAS PubMed.
- S. Chikazumi, Physics of Ferromagnetism, International Series of Monographs on Physics, Oxford University Press, 2nd edn, 2009, ISBN-13978-0199564811 Search PubMed.
- N. A. Usov and Y. B. Grebenshchikov, J. Appl. Phys., 2009 DOI:10.1063/1.3173280.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921 CrossRef.
- R. Hergt, R. Hiergeist, I. Hilger, W. A. Kaiser, Y. Lapatnikov, S. Margel and U. Richter, J. Magn. Magn. Mater., 2004 DOI:10.1016/j.jmmm.2003.09.001.
- R. Hergt, R. Hiergeist, M. Zeisberger, D. Schüler, U. Heyen, I. Hilger and W. A. Kaiser, J. Magn. Magn. Mater., 2005, 80–86 CrossRef CAS.
- L. M. Lacroix, R. B. Malaki, J. Carrey, S. Lachaize, M. Respaud, G. F. Goya and B. Chaudret, J. Appl. Phys., 2009 DOI:10.1063/1.3068195.
- B. Mehdaoui, A. Meffre, L. M. Lacroix, J. Carrey, S. Lachaize, M. Gougeon, M. Respaud and B. Chaudret, J. Magn. Magn. Mater., 2010 DOI:10.1016/j.jmmm.2010.05.012.
- J. P. Fortin, F. Gazeau and C. Wilhelm, Eur. Biophys. J., 2008 DOI:10.1007/s00249-007-0197-4.
- W. Brown, Micromagnetics, Wiley, New York, London, 1963 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Phys. Z. Sowjetunion, 1935, 8, 153 Search PubMed.
- T. L. Gilbert, Phys. Rev., 1955, 100, 1243 Search PubMed.
- T. Schrefl, J. Fidler, D. Suess, W. Scholz and V. Tsiantos, Handb. Adv. Magn. Mater., pp. 128–146 Search PubMed.
- G. Bertotti, Hysteresis in magnetism: for physicists, materials scientists, and engineers, Academic press, 1998 Search PubMed.
- N. Maniotis, AIP Adv., 2023, 13(6), 065122 CrossRef CAS.
- N. Modaresi, R. Afzalzadeh, B. Aslibeiki, P. Kameli, A. Ghotbi Varzaneh, I. Orue and V. A. Chernenko, J. Magn. Magn. Mater., 2019, 482, 206–218 CrossRef CAS.
- M. M. Leiva, S. Larumbe, A. V. Martinez, M. Monteserín, A. V. Martínez, S. Burgui and L. F. Martín, J. Nanosci. Nanotechnol., 2021, 21, 1–37 CrossRef PubMed.
- R. Ferrero, M. Vicentini and A. Manzin, Nanoscale Adv., 2024, 6, 1739–1749 RSC.
- K. Vamvakidis, S. Mourdikoudis, A. Makridis, E. Paulidou, M. Angelakeris and C. Dendrinou-Samara, J. Colloid Interface Sci., 2018 DOI:10.1016/j.jcis.2017.10.001.
- F. R. Arantes and D. R. Cornejo, J. Nanopart. Res., 2013 DOI:10.1007/S11051-013-1859-Z.
- A. Manzin, R. Ferrero and M. Vicentini, Adv. Theory Simul., 2021 DOI:10.1002/adts.202100013.
- S. Sundara Mahalingam, B. V. Manikandan and S. Arockiaraj, J. Phys.: Conf. Ser., 2019, 1172, 012070 CrossRef.
- R. Bjørk, E. B. Poulsen, K. K. Nielsen and A. R. Insinga, J. Magn. Magn. Mater., 2021, 535, 168057 CrossRef.
- A. Balousis, N. Maniotis and T. Samaras, Nanomaterials, 2021, 11, 1–11 CrossRef PubMed.
- A. Rajan, M. Sharma and N. K. Sahu, Sci. Rep., 2020 DOI:10.1038/s41598-020-71703-6.
- H. Chen, D. Billington, E. Riordan, J. Blomgren, S. R. Giblin, C. Johansson and S. A. Majetich, Appl. Phys. Lett., 2020, 117, 073702 CrossRef CAS.
- X. R. Wang, Z. Z. Sun and J. Lu, Nanoscale Magnetic Materials and Applications, 2009, pp. 1–34 Search PubMed.
- F. Gazeau, J. C. Bacri, F. Gendron, R. Perzynski, Y. L. Raikher, V. I. Stepanov and E. Dubois, J. Magn. Magn. Mater., 1998, 186, 175–187 CrossRef CAS.
- I. Raouf, S. Khalid, A. Khan, J. Lee, H. S. Kim and M. H. Kim, J. Therm. Biol., 2020, 91, 102644 CrossRef CAS PubMed.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- I. M. Obaidat, V. Narayanaswamy, S. Alaabed, S. Sambasivam and C. V. V. Muralee Gopi, Magnetochemistry, 2019, 5, 67 CrossRef.
- C. G. Hadjipanayis, M. J. Bonder, S. Balakrishnan, X. Wang, H. Mao and G. C. Hadjipanayis, Small, 2008, 4, 1925–1929 CrossRef CAS PubMed.
- In Magnetic Nanostructured Materials, ed. A. A. El-GendyJosé, M. Barandiarán and R. L. Hadimani, 2018 Search PubMed.
- N. Chekina, D. Horák, P. Jendelová, M. Trchová, M. J. Bene, M. Hrubý, V. Herynek, K. Turnovcová and E. Syková, J. Mater. Chem., 2011 10.1039/c1jm10621j.
- H. F. Rodrigues, G. Capistrano, F. M. Mello, N. Zufelato, E. Silveira-Lacerda and A. F. Bakuzis, Phys. Med. Biol., 2017, 62, 4062–4082 CrossRef CAS PubMed.
- Y. Hadadian, A. P. Ramos and T. Z. Pavan, Sci. Rep., 2019 DOI:10.1038/s41598-019-54250-7.
- A. Makridis, S. Curto, G. C. Van Rhoon, T. Samaras and M. Angelakeris, J. Phys. D Appl. Phys., 2019, 52, 255001 CrossRef CAS.
- A. Makridis, N. Maniotis and K. Simeonidis, Magn. Nanopart., 2024, 261–297 Search PubMed.
- I. Conde-Leboran, D. Baldomir, C. Martinez-Boubeta, O. Chubykalo-Fesenko, M. Del Puerto Morales, G. Salas, D. Cabrera, J. Camarero, F. J. Teran and D. Serantes, J. Phys. Chem. C, 2015 DOI:10.1021/acs.jpcc.5b02555.
- L. Asín, M. R. Ibarra, A. Tres and G. F. Goya, Pharm. Res., 2012, 29, 1319–1327 CrossRef PubMed.
- M. Nabil, P. Decuzzi and P. Zunino, R. Soc. Open Sci., 2015 DOI:10.1098/rsos.150447.
- K. M. Krishnan, IEEE Trans. Magn., 2010, 46, 2523–2558 CAS.
- S. L. Saville, B. Qi, J. Baker, R. Stone, R. E. Camley, K. L. Livesey, L. Ye, T. M. Crawford and O. Thompson Mefford, J. Colloid Interface Sci., 2014, 424, 141–151 CrossRef CAS PubMed.
- G. Vallejo-Fernandez and K. Ogrady, Appl. Phys. Lett., 2013, 103, 142417 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |