Open Access Article
Open Access ArticleCritical role of precursor flux in modulating nucleation density in 2D material synthesis revealed by a digital twin†
Abhinav
Sinha‡
 a,
Manvi
Verma‡
a,
Manvi
Verma‡
 a,
Nandeesh Kumar
K. M.
a,
Nandeesh Kumar
K. M.
 a,
Keerthana S.
Kumar
a,
Keerthana S.
Kumar
 a,
Ananth
Govind Rajan
a,
Ananth
Govind Rajan
 *b and
Akshay
Singh
*b and
Akshay
Singh
 *a
*a
aDepartment of Physics, Indian Institute of Science, Bengaluru, Karnataka 560012, India. E-mail: aksy@iisc.ac.in
bDepartment of Chemical Engineering, Indian Institute of Science, Bengaluru, Karnataka 560012, India. E-mail: ananthgr@iisc.ac.in
First published on 23rd April 2025
Abstract
Chemical vapor deposition (CVD) is the most widespread approach for two-dimensional (2D) material synthesis, yet control of nucleation density remains a major hurdle towards large-area growth. We find that precursor flux, a function of gas velocity and precursor concentration, is the critical parameter controlling nucleation. We observe that for a vertically aligned substrate, the presence of a cavity/slot in the substrate-supporting plate creates an enhanced growth zone for 2D-MoS2. The effect of this confined space on nucleation density is experimentally verified by electron microscopy. To understand this intriguing observation, we developed a hyper-realistic multiphysics computational fluid dynamics model, i.e., a digital twin of our CVD reactor, which reveals that space confinement achieves nearly-zero gas velocities. Digital twin-informed calculations indicate a significantly lower metal precursor flux at the confined space during the initial stages of growth, while precursor concentration is uniform across the substrate. The digital twin also makes an important prediction regarding a large time-lag between the set temperature, reactor environmental temperature, and substrate temperature, with implications for nucleation and growth. We offer a framework for designing confined spaces to control nucleation via regulating precursor flux, and for simulating reactor parameters for rapid optimization via the digital-twin model.
Introduction
Transition metal dichalcogenides (TMDs) are exemplary two-dimensional (2D) materials, promising for electronic and optoelectronic applications,1–3 as well as for catalysis, including carbon dioxide reduction4 and hydrogen evolution reactions.5 Mechanical exfoliation6 and chemical vapor deposition (CVD)7–9 are the most common methods used for the synthesis of TMD monolayers (MLs). CVD can potentially provide high uniformity, repeatability, control of layer number, and scalability to large areas. However, CVD is a complex multiscale process involving heating precursors (gaseous or solid), vapor-phase transport by an inert carrier gas to the substrate, and subsequent reaction and deposition. Obtaining high-quality MLs using CVD is challenging due to reactor-to-reactor variability and local changes in temperature, concentration, and flow fields.10,11 Even a seemingly minor variation in these experimental parameters can significantly impact the quality of the growth.12–14 However, multiphysics simulation studies that model the complex transport phenomena occurring in a CVD reactor and use them to develop new growth strategies are lacking.There is a critical need to connect experimental parameters, such as the set temperature and gas flow rate, to mesoscopic variables such as the local temperature, concentration, and fluid flow profiles, and finally to thermodynamic variables and experimental observations of growth. For example, temperature impacts evaporation rates of the precursors,15,16 growth rate, and shape of the synthesized 2D material.17,18 However, the temperature profile inside a CVD reactor is expected to be non-uniform, with implications for non-stoichiometric growth. Similarly, obtaining a quantitative model of the vapor pressure (concentration) profile is critical for modifying nucleation and growth kinetics. Furthermore, the velocity profile of the carrier gas influences the concentration profile at the substrate,19,20 as well as sticking coefficients.21 Therefore, developing a digital twin (in silico CVD reactor) for a real CVD system will lead to an informed modification of experimental parameters and improve reproducibility, thus going beyond the currently practiced experimental trial-and-error paradigm. Previous simulation studies have mostly aimed at understanding the reaction pathways controlling growth via density functional theory22,23 (DFT), though some recent studies focus on computational fluid dynamics (CFD) aspects.24–26 However, the effect of the complete reactor geometry in modulating gas flow dynamics, along with precursor concentration and temperature models in a multiple temperature zone setup, is still critically missing.
Importantly, the combined role of local velocity and concentration, i.e. a treatment of precursor flux, is critically missing. For example, confined space geometries have been utilized in CVD processes to modulate precursor concentration and velocity profiles.27–30 Gas flow velocity and temperature field simulations have been performed for the case of single heating zone reactors,31 and limited to horizontally positioned substrates.32,33 However, velocity, concentration, and temperature profiles have been treated separately, leading to an incomplete understanding of the CVD process, including nucleation and growth.
Large-scale device fabrication requires large-area growth of superior quality 2D materials. Reducing nucleation density proportionally increases the edge lengths, and results in fewer and sparsely occurring grain boundaries, hence improving optoelectronic and electronic properties. Furthermore, a comprehensive understanding of the dynamics of nucleation, controlled by the dynamics of temperature, is critically important. Random, uninhibited nucleation results in a high nucleation density, limiting the size of the obtained flakes.34,35 A higher precursor concentration at the substrate initiates a “self-seeding” nucleation mechanism, which may also result in multi-layer growth.36 Thus, a controlled nucleation density is the key to achieving desired ML growth and flake size.34
Here, we experimentally perform oxygen-assisted three-zone atmospheric pressure CVD (AP-CVD) of ML MoS2 and create the corresponding digital twin: a comprehensive computational fluid dynamics (CFD) model including heat, mass, and momentum transport equations. For a vertically aligned substrate (normal to the incoming gas flow), we find that the presence of a slot (cavity) in the supporting plate creates an excellent growth zone for MoS2, compared to no growth observed on the rest of the substrate, and on the substrate which does not have a slot. We create a COMSOL Multiphysics© finite element model by accounting for fluid flow dynamics, evaporation of chalcogen and metal oxide precursors, realistic substrate geometries, and temperature profiles. Using this hyper-realistic model, we observed no significant concentration gradients for the vertically aligned substrate. However, a velocity dead-zone is created in the slot area, wherein we find direct evidence of reduced nucleation density via electron microscopy. Thus, precursor flux, which is a function of gas velocity, precursor concentration and concentration gradient, emerges as the critical parameter controlling nucleation density. Furthermore, informed by our digital twin, we observed a large time lag between the set temperature, reactor temperature, and substrate temperature, with consequences on growth uniformity and nucleation. Thus, using this model, we make several critical observations on nucleation density, spatial temperature profiles, and gas flow. The deep study of precursor flux, enabled by the digital twin, will lead to the synthesis of higher quality 2D materials and faster optimization of the nucleation/growth process.
Results and discussion
The setup used for ML MoS2 growth (on SiO2/Si substrates) is shown in Fig. 1a. The reactor is a quartz tube (60 mm diameter). Three heated zones provide independent control over the evaporation temperature of the precursors and growth temperature at the substrate, with the zones separated by 75 mm wide insulation barriers. Inert carrier gas (Ar or N2) transports the vaporized precursors to the substrate placed downstream. We also introduce a small amount of oxygen (O2) into the system (see Methods for details of the growth process), as it is shown to improve the growth.37 Before heating, the reactor is flushed with high-purity inert gas to obtain reduced levels of residual moisture and O2 (see ESI Section I and Video V1† for corresponding simulations of the tube environment). Fig. 1b shows a model of the reactor, as used for the simulations with appropriate boundary conditions and sources. Chalcogen (sulfur) powder and transition metal oxide (MoO3) powders are placed in alumina boats in the first and second heating zones, respectively.To ensure maximum precursor impingement on the growing surface, the substrate is placed vertically in the third heating zone. As we will see later, vertical placement also enables minimum spatial variation in the precursor concentration, providing a more uniform growth environment. In contrast, for a horizontally placed substrate, even with small dimensions (1 × 1 cm2), a concentration gradient is expected32,33 (also see ESI Section II†). This gradient is most pronounced during the nucleation stage and critically affects the type of growth obtained. To support the substrate in a vertical configuration, we created a slot (a groove, 1 mm deep, 1–2 mm wide) in the bottom supporting alumina plate, and supported it at the back using an alumina boat (see Fig. 1b, lower left).
Remarkably, the presence of the slot is decisive toward obtaining ML MoS2 growth under similar growth conditions across different growth runs and substrates. Fig. 1c and d show optical microscopy images of 300 nm SiO2/Si substrates after CVD growth, when the substrate is placed inside the slot, and without the slot, respectively. A Raman peak shift of ∼20 cm−1, along with typical optical contrast, confirms the presence of ML MoS2 (ref. 38) (see ESI Section III† for optical spectroscopy and SEM characterization). The presence of ML MoS2 flakes only in the case of the slotted configuration is striking and points toward the significant effect of the slot on modifying the local growth environment.
Development of the multiphysics digital twin
We used COMSOL Multiphysics© to develop a coupled 3D model of gas-flow, precursor concentration, and temperature distribution for a realistic simulation of the CVD process. To understand the gas flow dynamics and the precursor concentration inside the slot, we carefully modeled the source geometry, substrate supports, and specific materials of various assemblies. The synthesis process can be divided into four broad parts: nitrogen flushing, reactor heating, precursor vaporization, and reaction and deposition. We developed an integrated model for the first three of the mentioned processes, simulating the actual experimental conditions as closely as possible (see Methods for mesh sizes for simulations and specific COMSOL modules used). The deposition process is modeled by considering evaporation and downstream transport of the powder precursors to the substrate.In the context of CVD, transfer of physical quantities inside a physical system is a combination of convection (due to inert carrier gas flow) and diffusion25,26 (due to concentration gradients). The governing equation for describing such a physical phenomenon is the diffusion-convection equation (DCE):
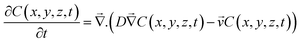 | (1) |
 is the carrier gas velocity (m s−1), D is the precursor diffusivity in the carrier gas (m2 s−1),39 and x (m) is the coordinate along the reactor. Using the DCE, we can also model precursor evaporation with the addition of a source term:
is the carrier gas velocity (m s−1), D is the precursor diffusivity in the carrier gas (m2 s−1),39 and x (m) is the coordinate along the reactor. Using the DCE, we can also model precursor evaporation with the addition of a source term: | (2) |
Understanding concentration profiles and fluid flow inside the reactor
We first examine precursor and O2 spatiotemporal profiles at the substrate. We note that our synthesis process minimizes precursor evaporation prior to the set temperature being realized (see ESI Section IV† for corresponding axial simulations of MoO3 and O2). Hence, for the purpose of modeling precursor evaporation, we allow the precursors to evaporate only after heating is completed (30 min).Fig. 2 shows the MoO3/S8 ratio and O2 profiles at the substrate after 5 minutes of the beginning of growth, with and without the slot. Elemental sulfur (S) in its vaporized form exists as S8 (octa-sulfur) molecules.43 Hence, the concentrations of sulfur and oxygen depicted are those of S8 and O2 species, respectively, and are discussed as such in the rest of the manuscript. Elemental concentrations may be obtained by multiplying S8 and O2 concentrations by a factor of 8 and 2, respectively. Importantly, the presence of the slot does not result in a spatially varying precursor profile at the substrate for any of the simulated species, and thus, we have indicated the average values of precursor concentration. Furthermore, the slot does not affect the average surface concentration of the reacting species compared with the non-slotted configuration (MoO3/S8 ratio (Fig. 2a and c) and O2 (Fig. 2b and d)). A similar trend was observed throughout the growth time (see ESI Section IV and Videos V2, V3, and V4† for simulated profiles along the length of the reactor and at other time steps during growth).
Precursor concentration gradients are not the underlying reason for the observed drastic changes in growth between slotted and non-slotted configurations. Concentration, velocity fields, and temperature are the primary parameters affecting nucleation and growth, amongst which concentration and temperature are similar for both slotted and non-slotted configurations. Hence, we must take a careful look at the velocity profiles near the substrate.
First, we calculate the Reynolds and Mach numbers to understand the type of carrier gas flow (laminar vs. turbulent and incompressible vs. compressible, respectively) in our reactor. The Reynolds number (Re) is a nondimensional number that quantifies the ratio of inertial to viscous forces in a flow field, calculated as
 | (3) |
 | (4) |
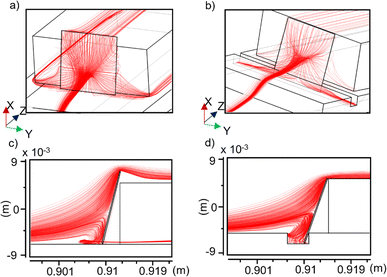
Now, we simulate the carrier gas velocity streamlines (while accounting for simulated temperature profiles), representative of the fluid flow direction at any given point. In any given volume element, the evaporated precursor atoms will be imparted momentum in the direction tangential to the nearby streamlines. Hence, streamlines serve as useful tools for visualizing and understanding the local growth environment near the substrate. Note that the ratio of substrate area and reactor cross section is very small (∼0.04), and hence only streamlines within a small radial cross section interact with the substrate. For discussion, we have indicated (Fig. 3) only those sets of streamlines that impinge on the surface of the substrate, and ignored the ones that fall outside or go around.
A comparison between Fig. 3a (slotted) and 3b (non-slotted) reveals that the carrier gas, upon encountering the substrate, is pushed down toward the slot, whereby its velocity decreases due to the slot geometry. Thus, a region of very low velocity, hereafter referred to as a “velocity dead-zone” (stationary zone), is created near the slot. Due to the lower flow velocity and laminar nature of fluid flow, streamlines bend inside the slot (Fig. 3d). For the non-slotted configuration (Fig. 3c), streamlines show a reversal of the flow at the bottom of the substrate, leading the flow away from the surface before turning sideways to continue the forward flow. This reverse current is suppressed in Fig. 3d due to the slot geometry confining the flow inside it. This can directly affect the nucleation density at the substrate, as we will see later.
Next, we examined the velocity profiles directly at the substrate surface. Note that during heating and growth, the velocity inside the reactor is in a steady state, and hence we plot the steady-state magnitudes of the velocity components. Fig. 4a and d show the transverse velocity profiles over the substrate, distinctly showing an overall reduction in magnitude in the case when a slot is present. This effect is more pronounced in the region of the substrate physically inside the slot, where the velocity is almost two orders of magnitude lower than in the nearby region (physically outside the slot). Fig. 4b and e show surface plots of the normal component of the velocity at the substrate. It can be seen in Fig. 4b that a lower velocity region exists toward the bottom of the substrate where it is in contact with the alumina plate. With the slotted configuration in Fig. 4e, this area extends out. The significant changes in the local growth environment due to modified gas flow dynamics should directly affect the delivery of the precursor on the substrate.
To corroborate our understanding of the non-trivial influence of the carrier gas velocity profile and precursor concentration, we calculated the incoming precursor flux (J, at the substrate) analytically. The steady-state nucleation rate46 goes as Q0 ∝ J2 (see ESI Section V† for a detailed derivation). Hence, a decreased precursor flux to the substrate would result in an overall reduction in the nucleation density.
Using data obtained from the multiphysics simulations, particularly precursor concentration, surface temperature during the estimated nucleation window (roughly between 1 and 5 minutes of growth, see ESI Section IV†), and the velocity components at the substrate, we obtained the precursor flux at each substrate surface element (governed by the mesh size employed for simulations). Earlier studies have indicated that TMD nucleation is governed primarily by the concentration and adsorption–desorption equilibrium of the transition metal precursor.15,47,48 With this in mind, Fig. 4c and f show the calculated MoO3 flux, incoming at the substrate at 5 minutes of growth, for the non-slotted and slotted configurations, respectively (see ESI Section V† for MoO3 flux profiles throughout the growth, S flux profiles, and details of the flux calculations). In the presence of a slot, the MoO3 flux reduces to 1/3rd of the value compared to the case without a slot. Interestingly, the spatial variation in the precursor flux and the surface velocity follows a similar trend.
To directly measure the nucleation density, we performed scanning electron microscopy (SEM) of the substrates. Fig. 4g–j correspond to slotted and non-slotted configurations, respectively, under similar optimized growth conditions (see ESI Section VI† for comparison at other vertical distances from the slot). A comparison of Fig. 4g and i, which are taken at similar vertical positions on the substrate, well away from the slot, shows similar density, size and shape of nucleation sites. A more careful observation reveals the presence of small MoS2 flakes with a triangular shape. Due to an increased rate of nucleation in this region, the growth of MoS2 flakes is limited to a maximum edge length of ∼1–2 μm. On the contrary, Fig. 4h (in the slot) and 4j (without slot), which are at the same vertical positions on the substrate, show remarkably different depositions. In Fig. 4h, the nucleation density is reduced, and MoS2 triangular flakes with edge length ≥30 μm are observed. Interestingly, for the substrate placed without a slot (Fig. 4j), a deposition similar to Fig. 4g and i is observed. This is direct evidence that a slot-induced, confined space reaction environment leads to a decrease in the nucleation density. Statistical analysis indicates an order of magnitude reduction in nucleation density in the slot region (ESI† Section VI). Hence, reduced precursor flux leads to reduced nucleation density in the slot. Thus, precursor flux, and not just the precursor concentration, is the decisive parameter controlling nucleation.
Predicting temperature variations in the CVD reactor
Temperature has a significant impact on nucleation and ML growth. Even in analytical calculations for the impingement rates discussed above, the rate of nucleation depends exponentially on the temperature of the substrate. Thus, a complete understanding of the dynamic heating process and local temperatures in a CVD reactor is necessary. In our COMSOL model, we accounted for the heating rate and heat diffusion between neighboring heating zones, as well as the realistic thermal conductivity of the materials in the reactor (alumina, quartz, and inert gas). Such a model is valuable even for simulating the post-deposition cooling process, with an effect on uncontrolled deposition.Fig. 5 and Video V5† depict the time-dependent simulated axial temperature profile along the reactor. The set temperatures of all three zones are achieved in 30 minutes (onset of the growth time in our CVD process). We observe that there is finite heat leakage via the insulation zones, and the temperatures of the areas near the insulation zones are less than at the centers of the heating zones. Furthermore, due to the presence of heating sources at the radial boundaries, a radial temperature gradient forms in the reactor (see ESI Section VII†).
Remarkably, the temperature (Fig. 5c) of the substrate assembly (combination of the substrate, alumina boat, and plate) is much lower than the center of the heating zone. The set temperature and the substrate temperature show a lag of nearly ∼250 °C. Furthermore, the zone-center temperature and the substrate temperature show a lag of nearly ∼150 °C. This temperature difference is significant considering the above-mentioned exponential relation between nucleation and temperature, and can lead to markedly different types of growth. As a critical experimental insight, we observe that by the onset of growth, the substrate is still not at the desired temperature, and doesn't reach the set temperature even till the growth is finished (Fig. 5e and ESI Section VII†). We note that such an observation is very challenging to make experimentally and leads to a more comprehensive understanding of the observed growth. Through careful selection of holder materials and adjustment of the growth process, such effects may be minimized, or even tuned.
We attribute this significant time-lag to the large heat capacity of the substrate assembly, compared to the inert environment. The specific heat capacities of inert gas (N2) and alumina are similar. However, the large difference in density leads to a larger heat capacity for alumina boats and supports, compared to that of the surrounding inert atmosphere (see ESI Section VII†). Fig. 5e shows time-dependent plots for the heat source and the average surface temperature at the substrate, with and without alumina supports. The average temperature at the substrate significantly lags behind the source due to the alumina supports, while it follows the source temperature closely in the absence of alumina (with air being replaced for alumina in the simulations) as the supporting material. We note that “without alumina supports” is a hypothetical setting used in the simulation, where the substrate is unsupported. In reality, such a system can be created by using a holder with one or a few contact points on the substrate.
We believe that such temperature differentials and dynamics will also arise in other CVD reactors depending upon the specific material used as the substrate holder, and especially since most reactors use alumina or quartz. Additionally, since nucleation occurs in the initial stages of growth in a very narrow time frame, nucleation is sensitive to the instantaneous temperature rather than the average temperature over the growth time scale. Similarly, such temperature variation could also be found in the precursor alumina boats, which implies that the actual temperature of precursor evaporation may be much lower than expected. Also, large temperature gradients might lead to deposition of the unreacted material and bulk/secondary deposition, resulting in poor quality of growth. In short, low temperature differentials are expected to lead to controllable film growth, and conversely, high temperature differentials can lead to particle formation and higher growth rates. The significant temperature differentials between the substrate and local inert gas environment may also give rise to thermo-diffusion or the Ludwig–Soret effect,49,50 which can lead to the aggregation of heavier (MoO3) and lighter (S) precursors in the colder and warmer regions of the as-formed thermal boundary layer close to the substrate.51,52
Conclusions
In summary, we report the non-trivial effect of transition metal precursor flux in modulating the 2D TMD nucleation density in a confined-space microreactor (vertically placed substrate in a slot). This unique insight is enabled by the development of a hyper-realistic digital-twin CFD model, accounting for specific reactor and substrate holder geometries, evaporation and transport of precursor species, and reactor heating. Significant modifications in the carrier gas flow near the slot (velocity-dead zone), revealed by the digital twin, impact precursor delivery during the nucleation and growth stages. Thus, the precursor flux is the critical parameter controlling nucleation, wherein the reduction of nucleation density is experimentally verified by electron microscopy. Furthermore, we predict a significant time lag between the actual substrate temperature and the set temperature, explained by the high heat capacity of the substrate holder. Thus, such a multiscale model offers a better understanding of the actual growth temperature and local temperature variations at different places in the reactor, allowing local tunability and control.Laminar flow (present in our system) is universally preferred for vapor deposition techniques including CVD,25,53 Metal Organic CVD (MOCVD)54,55 and even physical vapor deposition systems.56 In contrast, turbulent flow can lead to non-uniform thickness and degrade film quality.57,58 For such widely used laminar flow systems, our conclusions, which are based on modified gas flow dynamics due to geometrical confinement, will be valid. The exact modification of streamlines in a smooth, laminar flow of carrier gas would, of course, depend on the specific holder assembly in question but can be predicted in a similar manner to our CVD system. It should be noted that the digital-twin model is centered on transport phenomena (heat/mass transfer and fluid flow) and is independent of specific reaction kinetics. This allows for a generally applicable understanding of how macroscopic experimental parameters may affect microscopic variables such as the residence time and nucleation density. This digital-twin model may also be integrated with density functional theory (DFT) calculations and reactive molecular dynamics (MD) simulations to relate a set of macroscopic growth parameters to microscopic physical quantities. These simulations can be used to relate optical and structural properties (such as defects) to growth conditions and reactor configurations. This study motivates exploration of complex substrate holder geometries and introduction of additional physical features to the reactor to controllably modify the local growth environment for high-quality material synthesis. Since such studies are challenging to conduct in practice, the as-simulated profiles will lead to informed decision making. Scalable and reproducible synthesis of 2D-TMDs is crucial for reliable technological applications. However, a proportional scaling of the reactor is expected to alter the type of growth obtained. In this case, the precursor flux emerges as a tuning knob to directly control nucleation density, leading to well-controlled growth. Additionally, for wafer-scale growths, due to the large wafer diameter, temperature inhomogeneities can occur across a wafer. Such temperature variations can be significant and can alter vapor pressure and precursor delivery across the wafer. Detailed modelling of wafer-scale reactors can be performed via the digital twin and lead to practically useful insights. Overall, our combined experimental–theoretical work paves the way for informed, predictive, and reproducible growth of high-quality and large-area 2D materials via regulating precursor flux, direct control of nucleation density, and the development of a hyper-realistic digital-twin model.
Methods
Experimental details
Monolayer MoS2 was grown in a split tube type, horizontal, three-zone furnace. Sulfur (Sigma-Aldrich, CAS no. 7704-34-9, 99.98%) and MoO3 (Sigma-Aldrich, CAS no. 1313-27-5, 99.97%) powder precursors were used and placed in the first and second zone, respectively. The substrates are sonicated in acetone, IPA, and DI water at 50 °C for 10 minutes each and nitrogen-dried. The substrate was placed vertically inside a slot (groove/cavity) in an alumina plate, supported by another alumina block. Ultra-high purity inert gas (N2) was used to flush the reactor of ambient air, moisture, and other contaminants. The exhaust is open to the atmosphere, and the process takes place at atmospheric pressure with a constant N2 flow.The three zones were individually heated to 200 °C, 530 °C, and 750 °C in 30 minutes with a 100/2 sccm N2/O2 flow. Ultra-high purity N2 (impurity <10 ppm) and O2 (impurity <5 ppm) were used throughout the complete process. During growth, the flow rate is 100/2 sccm (N2/O2) for the first 5 minutes and 100 sccm (N2) for 15 minutes. After 20 minutes of growth, the flow rate is increased to 100 sccm to flush out unreacted precursors and prevent secondary growth during the cooling phase. The furnace lid is opened for rapid cooling, assisted by a wall-mounted fan. After cooling down using UHP N2 flow, we evacuate the reactor for ∼2 hours before taking out the sample. Surface coverage and morphology of the as-grown ML MoS2 were observed using a scanning electron microscope (Ultra55 FE-SEM Karl Zeiss) at 5 kV accelerating voltage. Raman and photoluminescence (PL) measurements were carried out on a HORIBA LabRamHR Raman/PL setup using a 532 nm laser.
Multiphysics simulations
Simulations were performed using COMSOL Multiphysics, which utilized the CFD, heat transfer, and chemical reaction engineering modules. The submodules, laminar flow, heat transfer for fluids, transport of diluted species, and transport of concentrated species were used to model the physics inside the CVD tube. Tables S–I in the ESI† provide information about the materials used for modelling individual components of the digital twin. The simulation was performed on a mesh termed “Coarser” in COMSOL with a total of 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905 elements within the volume of the tube and with an average element quality of 0.6268 in skewness (0 being the worst and 1 being the best). The mesh was fine enough to realize the slot in the model. Running each simulation on a workstation with a 12th Gen Intel i9 with 16 cores took three and a half hours.
905 elements within the volume of the tube and with an average element quality of 0.6268 in skewness (0 being the worst and 1 being the best). The mesh was fine enough to realize the slot in the model. Running each simulation on a workstation with a 12th Gen Intel i9 with 16 cores took three and a half hours.
Abbreviations
| 2D | Two-dimensional |
| TMD | Transition metal dichalcogenide |
| ML | Monolayer |
| CVD | Chemical vapor deposition |
| CFD | Computational fluid dynamics |
| MoS2 | Molybdenum disulfide |
| DFT | Density functional theory |
| MOCVD | Metal–organic chemical vapor deposition |
| AP-CVD | Atmospheric pressure chemical vapor deposition |
| SEM | Scanning electron microscopy |
| DCE | Diffusion-convection equation |
| RMD | Reactive molecular dynamics |
Data availability
Data and codes for the manuscript are uploaded to the link https://osf.io/xjqy6/?view_only=d0d31958b0db434995875c44d7c4a3b6.Author contributions
Abhinav Sinha (ABS), MV, AS, and AGR developed the overall modeling framework. The inert gas flushing and precursor evaporation model was developed by MV, ABS, AS, and AGR. The temperature model was developed by ABS, KSK, and AS. All simulations were performed by ABS and NK. MV, KSK, and AS developed the experimental framework. MV and KSK performed chemical vapor deposition. MV and KSK carried out optical microscopy, scanning electron microscopy and optical spectroscopy characterization. MV, ABS, AS, and AGR discussed and prepared the manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AS acknowledges funding from DST Nanomission CONCEPT (Consortium for Collective and Engineered Phenomena in Topology) grant and Anusandhan National Research Foundation (ANRF) grant (CRG-2022-003334). The authors acknowledge the financial support received from the I-STEM program funded by the Office of the Principal Scientific Adviser to the Government of India for providing the COMSOL license. ABS and NK acknowledge the Kotak IISc AI-ML Centre (KIAC-UG Computation Lab) for computational resources. AGR acknowledges financial support from the Department of Science and Technology (DST) and the Ministry of Electronics and Information Technology (MeitY) via the National Supercomputing Mission (NSM) under grant DST/NSM/R&D_HPC_Applications/Extension Grant/2023/16. AGR also thanks the Infosys Foundation, Bengaluru, for an Infosys Young Investigator grant. KSK acknowledges the DST-INSPIRE Fellowship. The authors also acknowledge the Micro Nano Characterization Facility (MNCF), Centre for Nano Science and Engineering (CeNSE) for use of characterization facilities. The authors thank Madhavan Nampoothiri for useful discussions regarding the precursor flux calculations.References
- I. Datta, S. H. Chae, G. R. Bhatt, M. A. Tadayon, B. Li, Y. Yu, C. Park, J. Park, L. Cao, D. N. Basov, J. Hone and M. Lipson, Low-Loss Composite Photonic Platform Based on 2D Semiconductor Monolayers, Nat. Photonics, 2020, 14(4), 256–262, DOI:10.1038/s41566-020-0590-4.
- A. Singh, S. S. Jo, Y. Li, C. Wu, M. Li and R. Jaramillo, Refractive Uses of Layered and Two-Dimensional Materials for Integrated Photonics, ACS Photonics, 2020, 7(12), 3270–3285, DOI:10.1021/acsphotonics.0c00915.
- S. Pak, A.-R. Jang, J. Lee, J. Hong, P. Giraud, S. Lee, Y. Cho, G.-H. An, Y.-W. Lee, H. Suk Shin, S. M. Morris, S. Cha, J. Inn Sohn and J. Min Kim, Surface Functionalization-Induced Photoresponse Characteristics of Monolayer MoS 2 for Fast Flexible Photodetectors, Nanoscale, 2019, 11(11), 4726–4734, 10.1039/C8NR07655C.
- Y. Zhao, Y. Chen, P. Ou and J. Song, Basal Plane Activation via Grain Boundaries in Monolayer MoS2 for Carbon Dioxide Reduction, ACS Catal., 2023, 13(19), 12941–12951, DOI:10.1021/acscatal.3c03113.
- J. Zhu, Z.-C. Wang, H. Dai, Q. Wang, R. Yang, H. Yu, M. Liao, J. Zhang, W. Chen, Z. Wei, N. Li, L. Du, D. Shi, W. Wang, L. Zhang, Y. Jiang and G. Zhang, Boundary Activated Hydrogen Evolution Reaction on Monolayer MoS2, Nat. Commun., 2019, 10(1), 1348, DOI:10.1038/s41467-019-09269-9.
- L. Ottaviano, S. Palleschi, F. Perrozzi, G. D'Olimpio, F. Priante, M. Donarelli, P. Benassi, M. Nardone, M. Gonchigsuren, M. Gombosuren, A. Lucia, G. Moccia and O. A. Cacioppo, Mechanical Exfoliation and Layer Number Identification of MoS 2 Revisited, 2D Mater., 2017, 4(4), 045013, DOI:10.1088/2053-1583/aa8764.
- J.-K. Huang, J. Pu, C.-L. Hsu, M.-H. Chiu, Z.-Y. Juang, Y.-H. Chang, W.-H. Chang, Y. Iwasa, T. Takenobu and L.-J. Li, Large-Area Synthesis of Highly Crystalline WSe2 Monolayers and Device Applications, ACS Nano, 2014, 8(1), 923–930, DOI:10.1021/nn405719x.
- T. Li, W. Guo, L. Ma, W. Li, Z. Yu, Z. Han, S. Gao, L. Liu, D. Fan, Z. Wang, Y. Yang, W. Lin, Z. Luo, X. Chen, N. Dai, X. Tu, D. Pan, Y. Yao, P. Wang, Y. Nie, J. Wang, Y. Shi and X. Wang, Epitaxial Growth of Wafer-Scale Molybdenum Disulfide Semiconductor Single Crystals on Sapphire, Nat. Nanotechnol., 2021, 16(11), 1201–1207, DOI:10.1038/s41565-021-00963-8.
- P. Yan, J. Wang, G. Yang, N. Lu, G. Chu, X. Zhang and X. Shen, Chemical Vapor Deposition of Monolayer MoS2 on Sapphire, Si and GaN Substrates, Superlattices Microstruct., 2018, 120, 235–240, DOI:10.1016/j.Spmi.2018.05.049.
- L. Tang, J. Tan, H. Nong, B. Liu and H.-M. Cheng, Chemical Vapor Deposition Growth of Two-Dimensional Compound Materials: Controllability, Material Quality, and Growth Mechanism, Acc. Mater. Res., 2021, 2(1), 36–47, DOI:10.1021/accountsmr.0c00063.
- A. Senkić, J. Bajo, A. Supina, B. Radatović and N. Vujičić, Effects of CVD Growth Parameters on Global and Local Optical Properties of MoS2 Monolayers, Mater. Chem. Phys., 2023, 296, 127185, DOI:10.1016/j.matchemphys.2022.127185.
- Y. J. Cho, Y. Sim, J.-H. Lee, N. T. Hoang and M.-J. Seong, Size and Shape Control of CVD-Grown Monolayer MoS2, Curr. Appl. Phys., 2023, 45, 99–104, DOI:10.1016/j.cap.2022.11.008.
- H. Liu, Y. Zhu, Q. Meng, X. Lu, S. Kong, Z. Huang, P. Jiang and X. Bao, Role of the Carrier Gas Flow Rate in Monolayer MoS2 Growth by Modified Chemical Vapor Deposition, Nano Res., 2017, 10(2), 643–651, DOI:10.1007/s12274-016-1323-3.
- B. Zheng and Y. Chen, Controllable Growth of Monolayer MoS 2 and MoSe 2 Crystals Using Three-Temperature-Zone Furnace, IOP Conf. Ser.:Mater. Sci. Eng., 2017, 274, 012085, DOI:10.1088/1757-899X/274/1/012085.
- W. Wang, X. Zeng, S. Wu, Y. Zeng, Y. Hu, J. Ding and S. Xu, Effect of Mo Concentration on Shape and Size of Monolayer MoS2 Crystals by Chemical Vapor Deposition, J. Phys. D: Appl. Phys., 2017, 50(39), 395501, DOI:10.1088/1361-6463/aa81ae.
- A. Arafat, M. S. Islam, N. Ferdous, A. S. M. J. Islam, M. M. H. Sarkar, C. Stampfl and J. Park, Atomistic Reaction Mechanism of CVD Grown MoS2 through MoO3 and H2S Precursors, Sci. Rep., 2022, 12(1), 16085, DOI:10.1038/s41598-022-20531-x.
- D. Zhu, H. Shu, F. Jiang, D. Lv, V. Asokan, O. Omar, J. Yuan, Z. Zhang and C. Jin, Capture the Growth Kinetics of CVD Growth of Two-Dimensional MoS2, npj 2D Mater. Appl., 2017, 1(1), 1–8, DOI:10.1038/s41699-017-0010-x.
- A. Zafar, Z. Zafar, W. Zhao, J. Jiang, Y. Zhang, Y. Chen, J. Lu and Z. Ni, Sulfur-Mastery: Precise Synthesis of 2D Transition Metal Dichalcogenides, Adv. Funct. Mater., 2019, 29(27), 1809261, DOI:10.1002/adfm.201809261.
- K. Momeni, Y. Ji and L.-Q. Chen, Computational Synthesis of 2D Materials Grown by Chemical Vapor Deposition, J. Mater. Res., 2022, 37(1), 114–123, DOI:10.1557/s43578-021-00384-2.
- P. Mishra and N. Verma, A CFD Study on a Vertical Chemical Vapor Deposition Reactor for Growing Carbon Nanofibers, Chem. Eng. Res. Des., 2012, 90(12), 2293–2301, DOI:10.1016/j.cherd.2012.05.006.
- P. Chakraborty and M. R. Zachariah, Sticking Coefficient and Processing of Water Vapor on Organic-Coated Nanoaerosols, J. Phys. Chem. A, 2008, 112(5), 966–972, DOI:10.1021/jp076442f.
- A. Govind Rajan, J. H. Warner, D. Blankschtein and M. S. Strano, Generalized Mechanistic Model for the Chemical Vapor Deposition of 2D Transition Metal Dichalcogenide Monolayers, ACS Nano, 2016, 10(4), 4330–4344, DOI:10.1021/acsnano.5b07916.
- S. Ghorai and A. Govind Rajan, From Molecular Precursors to MoS2 Monolayers: Nanoscale Mechanism of Organometallic Chemical Vapor Deposition, Chem. Mater., 2024, 36(6), 2698–2710, DOI:10.1021/acs.chemmater.3c02675.
- S. Bhowmik and A. Govind Rajan, Chemical Vapor Deposition of 2D Materials: A Review of Modeling, Simulation, and Machine Learning Studies, iScience, 2022, 25(3), 103832, DOI:10.1016/j.isci.2022.103832.
- M. H. Johari, M. S. Sirat, M. A. Mohamed, A. F. Mustaffa and A. R. Mohmad, Computational Fluid Dynamics Insights into Chemical Vapor Deposition of Homogeneous MoS2 Film with Solid Precursors, Cryst. Res. Technol., 2023, 58(10), 2300139, DOI:10.1002/crat.202300139.
- K. Momeni, Y. Ji, N. Nayir, N. Sakib, H. Zhu, S. Paul, T. H. Choudhury, S. Neshani, A. C. T. van Duin, J. M. Redwing and L.-Q. Chen, A Computational Framework for Guiding the MOCVD-Growth of Wafer-Scale 2D Materials, npj Comput. Mater., 2022, 8(1), 1–8, DOI:10.1038/s41524-022-00936-y.
- M. Suleman, S. Lee, M. Kim, V. H. Nguyen, M. Riaz, N. Nasir, S. Kumar, H. M. Park, J. Jung and Y. Seo, NaCl-Assisted Temperature-Dependent Controllable Growth of Large-Area MoS2 Crystals Using Confined-Space CVD, ACS Omega, 2022, 7(34), 30074–30086, DOI:10.1021/acsomega.2c03108.
- D. Tian, L. Kang, Z. Zhang, L. Meng, X. Li and W. Yan, Controlled Synthesis of Continuous MoS2 Films via Space-Confined Vapor Deposition, Chem. Phys., 2023, 571, 111923, DOI:10.1016/j.chemphys.2023.111923.
- B. Ryu, Y. Liu, H. Pu, Y. Wang, X. Shi, S. Soo Lee and J. A. Chen, Facile Approach for Site-Selective and Large-Area Growth of MoS2 through Heterogeneous Nucleation, Appl. Surf. Sci., 2023, 607, 155066, DOI:10.1016/j.apsusc.2022.155066.
- Z. Duan, T. Chen, J. Shi, J. Li, K. Song, C. Zhang, S. Ding, B. Li, G. Wang, S. Hu, X. He, C. He, H. Xu, X. Liu, C. Jin, J. Zhong and G. Hao, Space-Confined and Substrate-Directed Synthesis of Transition-Metal Dichalcogenide Nanostructures with Tunable Dimensionality, Sci. Bull., 2020, 65(12), 1013–1021, DOI:10.1016/j.scib.2020.03.002.
- L. Tang, T. Li, Y. Luo, S. Feng, Z. Cai, H. Zhang, B. Liu and H.-M. Cheng, Vertical Chemical Vapor Deposition Growth of Highly Uniform 2D Transition Metal Dichalcogenides, ACS Nano, 2020, 14(4), 4646–4653, DOI:10.1021/acsnano.0c00296.
- Y. Sharifi and L. E. K. Achenie, Effect of Substrate Geometry on the Deposition Rate in Chemical Vapor Deposition, J. Cryst. Growth, 2007, 304(2), 520–525, DOI:10.1016/j.jcrysgro.2007.03.046.
- B. Huet, X. Zhang, J. M. Redwing, D. W. Snyder and J.-P. Raskin, Multi-Wafer Batch Synthesis of Graphene on Cu Films by Quasi-Static Flow Chemical Vapor Deposition, 2D Mater., 2019, 6(4), 045032, DOI:10.1088/2053-1583/ab33ae.
- H. Kim, D. Ovchinnikov, D. Deiana, D. Unuchek and A. Kis, Suppressing Nucleation in Metal–Organic Chemical Vapor Deposition of MoS2 Monolayers by Alkali Metal Halides, Nano Lett., 2017, 17(8), 5056–5063, DOI:10.1021/acs.nanolett.7b02311.
- W. Chen, J. Zhao, J. Zhang, L. Gu, Z. Yang, X. Li, H. Yu, X. Zhu, R. Yang, D. Shi, X. Lin, J. Guo, X. Bai and G. Zhang, Oxygen-Assisted Chemical Vapor Deposition Growth of Large Single-Crystal and High-Quality Monolayer MoS2, J. Am. Chem. Soc., 2015, 137(50), 15632–15635, DOI:10.1021/jacs.5b10519.
- D. Zhou, H. Shu, C. Hu, L. Jiang, P. Liang and X. Chen, Unveiling the Growth Mechanism of MoS2 with Chemical Vapor Deposition: From Two-Dimensional Planar Nucleation to Self-Seeding Nucleation, Cryst. Growth Des., 2018, 18(2), 1012–1019, DOI:10.1021/acs.cgd.7b01486.
- K. S. Kumar, A. K. Dash, H. Sabreen H, M. Verma, V. Kumar, K. Watanabe, T. Taniguchi, G. S. Gautam and A. Singh, Understanding Interplay of Defects, Oxygen and Strain in 2D Materials for next-Generation Optoelectronics, 2D Mater., 2024, 11(4), 045003, DOI:10.1088/2053-1583/ad4e44.
- M. Mondal, A. K. Dash and A. Singh, Optical Microscope Based Universal Parameter for Identifying Layer Number in Two-Dimensional Materials, ACS Nano, 2022, 16(9), 14456–14462, DOI:10.1021/acsnano.2c04833.
- J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, The Molecular Theory of Gases and Liquids, Wiley, 1954 Search PubMed.
- E. A. Gulbransen, K. F. Andrew and F. A. Brassart, Vapor Pressure of Molybdenum Trioxide, J. Electrochem. Soc., 1963, 110(3), 242, DOI:10.1149/1.2425719.
- D.-Y. Peng and J. Zhao, Representation of the Vapour Pressures of Sulfur, J. Chem. Thermodyn., 2001, 33(9), 1121–1131, DOI:10.1006/jcht.2001.0835.
- M. Ohring, Chapter 3 – Thin-Film Evaporation Processes, in Materials Science of Thin Films, ed. Ohring, M., Academic Press, San Diego, 2nd edn, 2002, pp. 95–144, DOI:10.1016/B978-012524975-1/50006-9.
- J. R. Lyons, An Estimate of the Equilibrium Speciation of Sulfur Vapor over Solid Sulfur and Implications for Planetary Atmospheres, J. Sulfur Chem., 2008, 29(3–4), 269–279, DOI:10.1080/17415990802195615.
- J. P. Holman, Heat Transfer, McGraw-Hill, Scientific Research Publishing, New York, 10th edn, 2009, https://scirp.org/reference/referencespapers?referenceid=2298536, accessed 2024-06-26 Search PubMed.
- H. Schlichting and K. Gersten, Boundary-Layer Theory, Springer Science & Business Media, 2003 Search PubMed.
- I. V. Markov, Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy, World Scientific, 2003 Search PubMed.
- T. Wang, J. Guo, Y. Zhang, W. Yang, X. Feng, J. Li and P. Yang, Synthesis of High-Quality Monolayer MoS2 via a CVD Upstream Deposition Strategy for Charge Capture and Collection, Cryst. Growth Des., 2024, 24(7), 2755–2763, DOI:10.1021/acs.cgd.3c01369.
- B. Ding, C. Zhu, T. Wang, L. Li, Z. Li, L. Cheng, S. Feng, G. Zhang, Y. Zang, J. Hu, L. Li and C. Xia, Large-Area Growth of Monolayer MoS2 by Using Atmospheric-Pressure Chemical Vapor Deposition with Nucleation Controlling Process, Surf. Interface Anal., 2024, 56(1), 22–31, DOI:10.1002/sia.7264.
- M. A. Rahman and M. Z. Saghir, Thermodiffusion or Soret Effect: Historical Review, Int. J. Heat Mass Transfer, 2014, 73, 693–705, DOI:10.1016/j.ijheatmasstransfer.2014.02.057.
- N. G. Kafoussias and E. W. Williams, Thermal-Diffusion and Diffusion-Thermo Effects on Mixed Free-Forced Convective and Mass Transfer Boundary Layer Flow with Temperature Dependent Viscosity, Int. J. Eng. Sci., 1995, 33(9), 1369–1384, DOI:10.1016/0020-7225(94)00132-4.
- H.-M. YEH, Enrichment of Heavy Water by Thermal Diffusion, Chem. Eng. Commun., 1998, 167(1), 167–179, DOI:10.1080/00986449808912699.
- N.-Y. R. Ma and A. L. Beyerlein, The 2H Thermal Diffusion Isotope Effect in Benzene and Methanol, J. Chem. Phys., 1983, 78(11), 7010–7011, DOI:10.1063/1.444651.
- Z.-H. Han, Q.-B. Wang, Q.-Q. Xu, X.-H. Qiu, T. Cheng, D.-S. Jiao and J.-Z. Yin, The Effect of Sulfuration Reaction Rates with Sulphur Concentration Gradient Dependence on the Growth Pattern and Morphological Evolution of MoS2 in Laminar Flow, Nanoscale, 2024, 16(30), 14402–14417, 10.1039/D4NR01772B.
- F. Esposito, M. Bosi, G. Attolini, F. Rossi, R. Fornari, F. Fabbri and L. Seravalli, Influence of the Carrier Gas Flow in the CVD Synthesis of 2-Dimensional MoS2 Based on the Spin-Coating of Liquid Molybdenum Precursors, Nanomaterials, 2024, 14(21), 1749, DOI:10.3390/nano14211749.
- C. Park, G. W. Shim, W. Hong and S.-Y. Choi, MOCVD Growth of Hierarchical Nanostructured MoS2: Implications for Reactive States as the Large-Area Film, ACS Appl. Nano Mater., 2023, 6(10), 8981–8989, DOI:10.1021/acsanm.3c01622.
- G. M. Hanket, B. E. McCandless, W. A. Buchanan, S. Fields and R. W. Birkmire, Design of a vapor transport deposition process for thin film materials, J. Vac. Sci. Technol., A, 2006, 24(5), 1695–1701 CrossRef CAS.
- H. Van Santen, C. R. Kleijn and H. E. A. Van Den Akker, On Turbulent Flows in Cold-Wall CVD Reactors, J. Cryst. Growth, 2000, 212(1), 299–310, DOI:10.1016/S0022-0248(00)00033-6.
- M. Kavousanakis, N. Cheimarios, G. Kokkoris and A. G. Boudouvis, On the Effect of Self-Sustained Periodic Flows on Film Thickness Non-Uniformity during CVD, Comput. Chem. Eng., 2022, 161, 107775, DOI:10.1016/j.compchemeng.2022.107775.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5na00202h |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |