DOI:
10.1039/D4MO00117F
(Research Article)
Mol. Omics, 2025,
21, 38-50
GRL–PUL: predicting microbe–drug association based on graph representation learning and positive unlabeled learning
Received
24th June 2024
, Accepted 31st October 2024
First published on 4th November 2024
Abstract
Extensive research has confirmed the widespread presence of microorganisms in the human body and their crucial impact on human health, with drugs being an effective method of regulation. Hence it is essential to identify potential microbe–drug associations (MDAs). Owing to the limitations of wet experiments, such as high costs and long durations, computational methods for binary classification tasks have become valuable alternatives for traditional experimental approaches. Since validated negative MDAs are absent in existing datasets, most methods randomly sample negatives from unlabeled data, which evidently leads to false negative issues. In this manuscript, we propose a novel model based on graph representation learning and positive-unlabeled learning (GRL–PUL), to infer potential MDAs. Firstly, we screen reliable negative samples by applying weighted matrix factorization and the PU-bagging strategy on the known microbe–drug bipartite network. Then, we combine muti-model attributes and constructed a microbe–drug heterogeneous network. After that, graph attention auto-encoder module, an encoder combining graph convolutional networks and graph attention networks, is introduced to extract informative embeddings based on the microbe–drug heterogeneous network. Lastly, we adopt a modified random forest as the final classifier. Comparison experiments with five baseline models on three benchmark datasets show that our model surpasses other methods in terms of the AUC, AUPR, ACC, F1-score and MCC. Moreover, several case studies show that GRL–PUL could capably predict latent MDAs. Notably, we further verify the effectiveness of a reliable negative sample selection module by migrating it to other state-of-the-art models, and the experimental results demonstrate its ability to substantially improve their prediction performance.
1 Introduction
Human microorganisms, including bacteria, archaea, fungi, protozoa, and viruses, are widely present throughout the human body, and most of them can exert either beneficial or harmful effects.1 Numerous studies have shown that maintaining a balanced microbial environment is crucial for human health.2,3 For example, the gut microbiota can modulate the host's immune system,4,5 and the mycobacteria are associated with diabetes.6 Conversely, despite our knowledge of the importance of microorganisms, there remains a significant gap in our ability to regulate them using methods such as pharmaceuticals,7 due to a lack of understanding of their complex relationships.8 Traditional biomedical experiments are protracted, demanding, and costly,9–11 exacerbating the dilemma of microbe–drug association (MDA) identification.
With the improvement of datasets and the enhancement of computational power in recent years, computational models have emerged as an effective method for predicting MDAs. For instance, Zhu et al.12 proposed a model named HMDAKATZ combining heterogeneous networks with the KATZ method. Long et al.13 introduced graph convolutional networks (GCNs) into MDA prediction. Liu et al.14 performed multiple level attention to learn embedding from the bipartite graph. Tan et al.15 adopted a double auto-encoder to learn different kinds of features. Ma et al.16 constructed two heterogeneous microbe–drug networks to enrich the input features. Liang et al.17 predicted MDAs by combining nuclear norm minimization and graph attention networks. Recently, some researchers18–20 set out to focus on extracting the features of subgraphs, which brings a novel research direction for link prediction tasks in bioinformatics.
Although those methods can achieve great performance in association prediction tasks, there are still some deficiencies in their models, especially in their negative sampling strategies. As shown in Table 1, labeled positive samples are a mere fraction compared to the number of unlabeled samples† in existing MDA datasets. Currently, mainstream prediction models naturally assume a low proportion of true positive samples in unlabeled data and randomly select a subset of samples from a large pool of unlabeled data as negative samples. Although simple, such an approach cannot avoid the potential false negative issues associated with collecting negative samples, thus leading to biased classifiers. Utilizing validated positive samples to select highly reliable negative samples and thoroughly learning their features have become crucial steps in MDA prediction. In recent years, some researchers have set out to alleviate false negative issues in biological association prediction tasks. Zeng et al.21 used deep forests combined with a two-step positive unlabeled learning method to predict disease-associated circular RNAs. They trained two deep forest models respectively for negative sampling and MDA identification. Peng et al.22 designed a PU learning algorithm based on XGBoost and spy positives technique to predict microbe-disease associations. Those spy samples consist of the positive samples that have the smallest distance to the cluster center formed by the K-means clustering algorithm. Tian et al.23 combined the process of negative sampling based on self-defined hardness function with model training based on an MLP classifier to predict microbe–drug associations. They dynamically adjust the probability of being sampled as reliable negative samples based on the deviation between the MLP predictions and the true labels of the samples. Although significant advancements have been achieved by the aforementioned works, the research of PU learning in the realm of bioinformatics association prediction, particularly with regard to MDA identification, remains underexplored.
Table 1 Statistics of microbe–drug association
| Dataset |
Microbe |
Drug |
Association |
πpos (%) |
| πpos indicates the percentage of positive associations in each dataset. |
| MDAD |
173 |
1373 |
2470 |
1.04 |
| aBiofilm |
140 |
1720 |
2884 |
1.12 |
| DrugVirus |
95 |
175 |
933 |
5.61 |
Hence, we proposed a model named graph representation learning and positive unlabeled learning (GRL–PUL), as illustrated in Fig. 1, to predict potential MDAs. Firstly, a negative sampling module is presented to select reliable negative samples via the utilization of weighted matrix factorization and the PU-bagging technique. Then, a microbe–drug heterogeneous network is constructed after fusing and concatenating functional similarity and genome sequence attributes for microbes and molecular structure similarity, Gaussian kernel similarity, and network topological attributes for drugs. Subsequently, we constructed a modified graph auto-encoder module via decoupling GCN and incorporating a graph attention network to attain informative embeddings of the heterogeneous network. Finally, we combined the random forest classifier and LPU (learning classifiers from only positive and unlabeled data) strategy24 to obtain the probability of MDAs. To verify our model's effectiveness, we conducted a series of experiments on three benchmark datasets in comparison with several representative methods. The evaluation results prove our model's excellent ability in MDA prediction. It is worth emphasizing that to validate the effectiveness of the negative sample selection module, we integrated it into several advanced models. The results demonstrated that our proposed negative sampling module significantly improves the models’ performance. In brief, our contributions are as follows:
 |
| | Fig. 1 The overall framework of GRL–PUL includes four steps: (A) GRL–PUL introduces weighted matrix factorization (WMF) to obtain latent factors for each microbe and drug based on the known microbe–drug bipartite network, which is applied using the Hadamard product to form the features of microbe–drug pairs for the PU-bagging strategy to select reliable negative samples; (B) a heterogeneous network of microbe–drug is built by fusing and concatenating muti-model attributes; (C) GRL–PUL adopts the GAAE module, whose encoder performs a decoupling operation on the traditional GCN layer and combines GCN and GAT to learn informative embeddings; (D) the final unbiassed results of potential MDAs are obtained from GRL–PUL's PURF module, where the random forest and LPU strategy are combined to correct prediction biases. | |
• We designed a novel negative sampling module based on weighted matrix factorization and the PU-bagging technique to identify reliable negative samples, which not only performs excellently in our proposed model but also shows strong performance when applied to other models.
• We proposed a graph representation learning method, whose encoder combining graph convolutional networks and graph attention networks, has an excellent ability to learn informative features from the constructed microbe–drug heterogeneous network.
• We built an improved classifier based on the random forest and LPU strategy to obtain the final positive likelihood score of potential MDAs.
• We further conducted comprehensive experiments to verify the effectiveness of our model, and the results demonstrate that our model outperforms five representative models.
2 Materials and methods
2.1 Data collection and preprocessing
In the present study, we utilize three different microbe–drug association datasets named MDAD,25 aBiofilm,26 and DrugVirus,27 which have been experimentally validated and collected from previous research, to evaluate the predictive performance of GRL–PUL. The statistics of these datasets are shown in Table 1.
Then, we construct a microbe–drug bipartite network and bipartite graph adjacency matrix Ä ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nm for each dataset, where Nd and Nm represent the number of drugs and microbes. For any given drug di and microbe mj, Äij will be 1 if there is a known association between drug di and microbe mj, and 0 otherwise. Furthermore, the symmetric adjacency matrix A ∈
Nd×Nm for each dataset, where Nd and Nm represent the number of drugs and microbes. For any given drug di and microbe mj, Äij will be 1 if there is a known association between drug di and microbe mj, and 0 otherwise. Furthermore, the symmetric adjacency matrix A ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×(Nd+Nm) is obtained using the formula:
(Nd+Nm)×(Nd+Nm) is obtained using the formula:
| |  | (1) |
and ·
T denotes the operation of matrix transposition.
2.2 Construction of microbe–drug heterogeneous networks
In this section, we extract the integrated similarity and network features of drugs, as well as the functional similarity and genome sequence features of microbes. By combining these various features, we construct a microbe–drug heterogeneous network, which is then used as the primary feature.
2.2.1 Extraction of the microbial functional similarity attribute.
We adopt the Kamneva tool28 to obtain the functional similarity of microbes. Initially, we constructed a microbial protein–protein functional association network and retrieved the genetic neighbor scores from the STRING database.29 The functional similarity between microbe mi and microbe mj, represented by Sm(mi,mj), is determined by computing the percentage of the link score connecting the two microbes relative to the total link scores of the two microbial gene families. Finally, we constructed a functional similarity feature matrix of microbe Sm ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×Nm.
Nm×Nm.
2.2.2 Extraction of the microbial genome sequence attribute.
Genome sequences provide the blueprint for essential microbial and viral components. We encoded the original genome sequences which are obtained from the NCBI database30 by one-hot coding. To ensure uniform length, all sequences are padded with zeros. Eventually, we employed principal component analysis (PCA)31 to reduce the dimensionality to match the number of microbes Nm and obtain the microbe sequence feature matrix Fm ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×Nm.
Nm×Nm.
2.2.3 Extraction of the drug integrated similarity attribute.
The integrated similarity attribute of a drug is comprised of the molecular structure similarity and drug Gaussian kernel similarity.
2.2.3.1 Molecular structure similarity.
To calculate the pairwise drug structural similarity, we used the SIMCOMP232 tool based on the maximum common substructure to compute the molecular structural similarity DSstruct(di,dj) between drug di and drug dj. After that, the similarity matrix DSstruct ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd is constructed.
2.2.3.2 Drug Gaussian kernel similarity.
With the objective of enriching the drug similarity feature, we introduced Gaussian interaction profile kernel similarity, which can map data to a multidimensional space and compute the similarity between data nodes. The Gaussian kernel similarity between drug di and drug dj is calculated as follows:
Nd×Nd is constructed.
2.2.3.2 Drug Gaussian kernel similarity.
With the objective of enriching the drug similarity feature, we introduced Gaussian interaction profile kernel similarity, which can map data to a multidimensional space and compute the similarity between data nodes. The Gaussian kernel similarity between drug di and drug dj is calculated as follows:| | | DSgauss(di,dj) = exp(−μ‖DIP(di) − DIP(dj)‖2), | (2) |
in which DIP denotes the drug–drug association matrix and DIP(di) represents (i.e. the i-th row of the drug–drug association matrix) the drug–drug interaction profile of drug di. μ is the kernel bandwidth control parameter and is defined using the following formula:| |  | (3) |
where μ′ is the original bandwidth and is generally set to 1. Ultimately, we obtained the drug Gaussian kernel similarity DSgauss ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd.
2.2.3.3 Drug integrated similarity.
We fused the molecular structure similarity DSstruct and the drug Gaussian kernel similarity DSgauss, and calculated the integrated similarity of the drug (denoted as Sd) as below:
Nd×Nd.
2.2.3.3 Drug integrated similarity.
We fused the molecular structure similarity DSstruct and the drug Gaussian kernel similarity DSgauss, and calculated the integrated similarity of the drug (denoted as Sd) as below:| |  | (4) |
2.2.4 Extraction of the drug network topological attribute.
For the purpose of better capturing the inter-node features for drugs, we further employed the random walk with restart33 (RWR) algorithm on the drug–drug association network. The RWR algorithm is defined as:| | | p(t+1)i = (1 − θ)p(t)iTprob + θp(0)i, | (5) |
where θ is the restart probability and Tprob is the transition matrix. p(0)i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×1 refers to the initial probability vector of node i, in which the j-th element is defined as follows:
Nd×1 refers to the initial probability vector of node i, in which the j-th element is defined as follows:| | 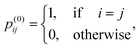 | (6) |
and p(t)ij is the likelihood of node i transferring to node j at time t. After the algorithm converges through iteration, a matrix Fd ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd representing the drug network topological attribute is procured.
Nd×Nd representing the drug network topological attribute is procured.
2.2.5 Multi-modal attribute construction.
All the aforementioned features, i.e. the microbe functional similarity feature Sm, the microbe genome sequence feature Fm, the drug integrated similarity feature Sd and the drug network topological feature Fd, are normalized separately in order to endow them with comparability. We then fused them into two kinds of models. The first model Xsimilarity ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×(Nd+Nm) is composed of a similarity feature and is defined as follows:
(Nd+Nm)×(Nd+Nm) is composed of a similarity feature and is defined as follows:| |  | (7) |
The second model Xsecond ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×(Nd+Nm) is composed of the microbe functional similarity and drug network topological feature, and is defined as follows:
(Nd+Nm)×(Nd+Nm) is composed of the microbe functional similarity and drug network topological feature, and is defined as follows:| |  | (8) |
Eventually, we concatenated both models to form the final feature X ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×2(Nd+Nm):
(Nd+Nm)×2(Nd+Nm):| | | X = [Xsimilarity,Xsecond]. | (9) |
2.3 Selection of reliable negative MDAs
In supervised learning, the quantity and quality of positive and negative samples are crucial to the model's performance. As shown in Table 1, the known microbe–drug associations constitute only a small portion of all samples in the existing MDA databases, leaving numerous microbe–drug pairs unobserved. Due to technical or cost-related reasons, there are no absolutely verified negative samples nowadays. Hence, it is essential to select high-quality and reliable negative samples for model training. To address and alleviate the issue at hand, we proposed a module based on weighted matrix factorization and a PU-bagging strategy, which is named MFPUB for short. Weighted matrix factorization is adopted to learn latent factor matrices for microbes and drugs, and then the PU-bagging strategy is combined with a random forest to identify reliable negative samples based on the latent factor matrices. The detailed process of MFPUB is shown in Algorithm 1.
2.3.1 Matrix factorization based on a bipartite network.
Matrix factorization used to be commonly employed in recommendation systems.34 Inspired by previous studies,35 we introduced weighted matrix factorization to extract latent features from the microbe–drug bipartite network. The objective function is set as follows:| |  | (10) |
where Ui represents the i-th row of the microbe latent factor matrix U and Vj represents the j-th row of the drug latent factor matrix V. Wij represents the confidence in the predicted relationship between microbe i and drug j. When Äij = 1, Wij is set to 1; otherwise, it is equal to ω.‡α and λ are weight parameters balancing the reconstruction loss and regularization. ‖·‖F denotes the Frobenius norm. In order to accelerate convergence speed and enhance the credibility of those samples already validated through wet experiments, we adopted weighted alternating least squares. Thus, these two update rules are run alternately until convergence:| | | Ui = (λI + αVTWiV)−1(αVTWiÄ·i), | (11) |
Here, Wi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd is a diagonal matrix with diagonal elements that satisfy the equation Wixx = Wix (i.e. the element in row x and column x of Wi is equal to row i and column x of W), and Ä·i ∈
Nd×Nd is a diagonal matrix with diagonal elements that satisfy the equation Wixx = Wix (i.e. the element in row x and column x of Wi is equal to row i and column x of W), and Ä·i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×1 represents the i-th column of Ä,
Nd×1 represents the i-th column of Ä,| | | Vj = (λI + αUTWjU)−1(αUTWjÄTj·), | (12) |
Here, Wj ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×Nm is a diagonal matrix with diagonal elements that satisfy the equation Wjxx = Wxj (i.e. the element in row x and column x of Wj is equal to row x and column j of W), and Äj· ∈
Nm×Nm is a diagonal matrix with diagonal elements that satisfy the equation Wjxx = Wxj (i.e. the element in row x and column x of Wj is equal to row x and column j of W), and Äj· ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 1×Nm represents the j-th row of Ä.
1×Nm represents the j-th row of Ä.
Finally, we obtained the microbe latent factor matrices U ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×K and the drug latent factor matrices V ∈
Nm×K and the drug latent factor matrices V ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×K, while K is the size of the latent factor of each microbe and drug.
Nd×K, while K is the size of the latent factor of each microbe and drug.
2.3.2 PU-bagging strategy.
The bagging strategy has demonstrated strong robustness in classification tasks. However, using the same subset randomly selected from unlabeled samples throughout the process as negative samples may lead to errors. To alleviate the false negative problem, positive unlabeled learning combined with random forests has emerged as an effective approach.36,37 In the PU-bagging strategy, each base learning process utilized a training dataset comprising two subsets:| | | Straini = SP ∪ SUi, i = 1, 2, 3,…,n. | (13) |
Here, SUi is the potential negative training subset, which is constructed by randomly selecting from the unknown microbe–drug pair set, and SP is the positive sample set. The sizes of SP and SUi are equal. In each iteration, predictions are made on the remaining unlabeled samples to obtain their probability values after fitting the model with the training set Straini. At the end of n iterations, we calculated their average, and used the minimum value of positive samples as the threshold to filter out unlabeled samples with probability values lower than this threshold, considering them as reliable negative samples S−.
|
Algorithm 1 Algorithm of the MFPUB model |
Input: The bipartite graph adjacency matrices Ä ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nm, hidden factor dimension K, maximum iteration max_iter, the params of the loss function α and λ, weight matrix W, and epoch of the random forest epochRF; Nd×Nm, hidden factor dimension K, maximum iteration max_iter, the params of the loss function α and λ, weight matrix W, and epoch of the random forest epochRF; |
|
Output: Reliable negative samples S−; |
1: Initialize microbe latent factor matrices U ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×K and drug latent factor matrices V ∈ Nm×K and drug latent factor matrices V ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×K; Nd×K; |
| 2: fori = 1 tomax_iterdo |
| 3: update Ui according to eqn (11); |
| 4: update Vi according to eqn (12); |
| 5: end for |
6: fuse Ui and Vi according to each microbe–drug association using the Hadamard product, forming the microbe–drug pair feature Fmd ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd×Nm)×K; (Nd×Nm)×K; |
| 7: forj = 0 toepochRFdo |
| 8: Build a set of potential negative samples SUj by randomly selecting an equal number of samples from the unlabeled data SU as the known samples SP; |
| 9: Train a new random forest classifier with SUj ∪ SP; |
| 10: Using the trained classifier, predict the probability values of the remaining unlabeled samples and record their probability values; |
| 11: end for |
| 12: using the last trained classifier, predict the probability values of all positive samples, and choose the minimum probability value of the positive samples as threshold t; |
| 13: select those with not-null probability values lower than the threshold t as candidate negative samples Scandi_neg; |
| 14: randomly select a portion of Scandi_neg as reliable negative samples S− with the same size as positive samples; and |
| 15: return reliable negative samples S−. |
2.4 GAAE module
Graph auto-encoders (GAEs),38 widely applied in bioinformatic tasks,39–41 have demonstrated their powerful ability to learn latent representations. In this section, we propose a graph attention auto-encoder (GAAE) module to comprehensively characterize the integrated features of microbe–drug heterogeneous networks.
2.4.1 Encoder.
Noteworthily, previous research42,43 usually adopted graph convolutional networks as encoders to learn embeddings from the input features. However, the static weights they employ may result in the loss of some important features during the training process. Recently, some variational graph convolutional networks have been proposed to solve the problems in the field of bioinformatics.44,45 Motivated by Gasteiger et al.46 separating the neural network from the propagation scheme, we decoupled the GCN model into linear transformation and message propagation. Subsequently, a graph attention layer47 is added between the linear transformation layer and the information propagation layer.
As mentioned above, the input feature matrix is defined as X = [![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 1,
1,![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 2,…,
2,…,![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) Nd+Nm]T, where the feature of node vi is denoted as
Nd+Nm]T, where the feature of node vi is denoted as ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i ∈
i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2(Nd×Nm). It will be fed into a neural network with a parameter set θ consisting of a single linear transformation layer. The linear transformation proceeds as follows:
2(Nd×Nm). It will be fed into a neural network with a parameter set θ consisting of a single linear transformation layer. The linear transformation proceeds as follows:
| | | H = fθ(X), fθ(X) = XW1st + b. | (14) |
Here, the input feature matrix is transformed into the latent factor matrix
H ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×Fvia
(Nd+Nm)×Fvia linear transformation operation
fθ(·), while
F is the dimension of the embedded representation of the node.
W1st ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2(Nd+Nm)×F
2(Nd+Nm)×F is the first learnable weight matrix and
b is the bias.
As for the graph attention layer, we utilized a linear mapping layer to transform the latent factor matrix H = [![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) 1,
1,![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) 2,…,
2,…,![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) Nd+Nm]T,
Nd+Nm]T, ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) i ∈
i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F, into the higher-level feature
F, into the higher-level feature  . To begin with, a shared linear transformation, parametrized by a weight matrix Wattn ∈
. To begin with, a shared linear transformation, parametrized by a weight matrix Wattn ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F×F, is applied to each node. Thereafter, we performed self-attention on the nodes to calculate attention scores:
F×F, is applied to each node. Thereafter, we performed self-attention on the nodes to calculate attention scores:
| | eij = LeakyReLU(![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) T[Wattn T[Wattn![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) i‖Wattn i‖Wattn![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) j]), j]), | (15) |
where
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 1×2F
1×2F is a learnable shared parameter and ‖ denotes the concatenation operation. The attention coefficient between node
i and node
j (one of the first-order neighbors of node
i) is computed by normalizing the attention scores across all first-order neighbors of node
i (including node
i) using the softmax function:
| |  | (16) |
where
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) i
i is the first-order neighborhood of node
i. Then, we computed a linear combination of the features corresponding to attention coefficients:
| | 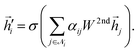 | (17) |
Here,
σ(·) represents the activation function, while in this study we employ LeakyReLU activation. Additionally,
W2nd ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F×F
F×F represents the second learnable weight matrix.
Finally, the node embeddings Zi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F will be obtained after applying Laplacian propagation, and the encoder function is defined as follows:
F will be obtained after applying Laplacian propagation, and the encoder function is defined as follows:
| |  | (18) |
where
Ā =
A +
I,
D is the degree matrix of
Ā, and
Tattn ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd+Nm
Nd+Nm denotes the attention coefficient matrix.
2.4.2 Decoder.
Similar to previous work,43,48 we used the inner product as the decoder. The computational formula of the reconstructed adjacency matrix  is defined below:where φ(·) is the sigmoid function and ·T represents transpose.
2.4.3 Loss function.
We calculated the binary cross entropy between the input graph and reconstructed graph as the loss function, which is defined as follows:| |  | (20) |
In the adjacency matrix A, y serves as a binary indicator taking values of either 0 or 1, while ŷ denotes the output values within the reconstructed adjacency matrix Â, which ranges from 0 to 1.
2.5 Random forest classifier enhanced by PU learning
Using the GAAE module, we obtained the node embeddings of microbe–drug heterogeneous networks. Then each microbe–drug pair is represented by applying the Hadamard product, which is an operation that takes two matrices of the same dimensions and produces another matrix where each element is the product of the corresponding elements in the original two matrices, between node embedding of the microbe and node embedding of the drug. After calculating the representations of microbe–drug pairs, positive unlabeled learning based on a random forest classifier (PURF),49 adopting the LPU strategy,24 is implemented to predict potential microbe–drug association. We first trained the PURF classifier using a training set and obtained the function g(x) = p(s = 1|x) learned from positive and unlabeled samples, while s = 1 shows that the sample is labeled. However, our purpose is to learn an objective function f(x) = p(y = 1|x) as closely as possible, while y = 1 shows that there is indeed an association between the drug and the microbe in the real world. Aiming at reaching the goal, LPU adopts a novel computing method whose corn derivation process is shown as follows:| | | p(s = 1|x) = p(y = 1 ∧ s = 1|x) | (21) |
| | | = p(y = 1|x)p(s = 1|y = 1,x) | (22) |
| | | = p(y = 1|x)p(s = 1|y = 1). | (23) |
It is clear that the final result follows by dividing each side by p(s = 1|y = 1) which represents the probability of a positive example being labeled. In order to compute c = p(s = 1|y = 1), a constant factor based on the “selected completely at random” assumption,50 we randomly hold out a 10% ratio of the positive sample from the training set before training the random forest classifier. After the classifier is fitted, using the remaining training set, the constant probability c is calculated by averaging the probability predicted by the fitted classifier:| |  | (24) |
where H denotes the hold out set and n represents its cardinality.
3 Results
In this section, we first introduce the details of the experimental setup and evaluation metrics. Secondly, we compare the model we proposed with other representative models. Then, hyperparameter sensitivity analysis and model ablation study are conducted to evaluate the impact of individual hyperparameters and components on the overall performance of GRL–PUL. Additionally, it is worth noting that we transferred the reliable negative sample selection strategy to other models for the purpose of verifying its effectiveness. Ultimately, we conduct case studies for two important drugs and two pathogenic microbes and visualization of embeddings learned from sample sets formed by different negative sampling strategies.
3.1 Experimental setup and evaluation metrics
In this study, we perform 5-fold cross-validation (5-CV) on three independent datasets, MDAD, aBiofilm, and DrugVirus, to evaluate the performance of prediction models. In 5-CV, for each dataset, all known microbe–drug pairs are categorized as positive samples and are grouped into positive set SP. Then SP is randomly divided into five equal parts, four of which form the positive samples in the training set and the remaining one is sorted into the test set. Similar to the positive samples, reliable negative samples, which are selected by our designed MFPUB module and have the same size as the positive samples, are partitioned into the training set and the test set with a ratio of 80% to 20%. This process is repeated five times, each time with a different fold as the test set. The final performance metric is the average of the results from all five iterations.
In 5-CV, we separately obtained true positives (TPs), false positives (FPs), true negatives (TNs) and false negatives (FNs). Moreover, we employed five evaluation metrics, namely the area under the receiver operating characteristic curve (AUC), area under the precision–recall curve (AUPR), accuracy (ACC), F1 score (F1-score) and Matthews correlation coefficient (MCC), which have been generally used as evaluation metrics in previous work.23,51,52 Their calculation formulas are below:
| |  | (25) |
| |  | (26) |
| |  | (27) |
| | 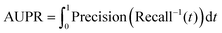 | (28) |
| |  | (29) |
| |  | (30) |
| |  | (31) |
3.2 Performance comparison with other models
To demonstrate the performance of GRL–PUL, we compared it with five representative approaches, which are briefly introduced below:
• GCNMDA:13 a computational method employing a GCN and conditional random field to predict microbe–drug associations.
• Graph2MDA:53 a multi-modal variational graph auto-encoder model for predicting microbe–drug associations.
• MKGCN:54 a computational model utilizing multiple kernel matrices to predict microbe–drug associations.
• OGNNMDA:55 a novel model utilizing an unusual multi-layer encoder for enhanced prediction of microbe–drug associations.
• SCSMDA:23 a computational approach consisting of a fusion of contrastive learning strategy and self-defined negative sampling method to improve its capability of predicting microbe–drug associations.
As mentioned above, we performed 5-CV on each model in the experiments, which is trained with the setting adjusted and optimized by the original authors. The performance comparisons are illustrated in Fig. 2. GRL–PUL demonstrated the best performance across all metrics, including the AUC, AUPR, ACC, F1-score, and MCC on both MDAD and aBiofilm datasets. On the DrugVirus dataset, Graph2MDA and MKGCN achieved superior values for the AUC and ACC due to their biased predictions. However, overall, the GAAE still exhibited superior performance.
 |
| | Fig. 2 Performance comparison of GRL–PUL with five competitive models on three datasets, including the AUC, AUPR, ACC, F1-score and MCC. | |
3.3 Hyper-parameter sensitivity analysis
As described previously, there are several critical hyper-parameters in GRL–PUL, including the size of latent factor matrices learned by MFPUB (K), the reliability of unlabeled samples (ω), the parameter (α) and (λ) balancing the reconstruct loss and L2-norm, the size of embeddings learned by the GAAE module (F) and the learning rate of the GAAE module (lrGAAE). To evaluate the influence of these parameters on the effectiveness of our model, we performed 5-CV five times on the MDAD dataset, while the results were measured using the above five metrics (i.e. AUC, AUPR, ACC, F1-score and MCC).
K is the length of the latent factor vector for each microbe and drug, obtained using the MFPUB module. We set the value of K to vary from {10, 30, 50, 70, to 90}. ω, ranging from {0.05, 0.075, 0.1, 0.125, to 0.15}, is set to measure the contribution of the labels of unlabeled samples to the graph reconstruction process in the MFPUB module. α and λ are the weight coefficients in eqn (10), which plays a role in balancing the weight of regularization and reconstruction loss. The value of α is chosen from {1 × 10−4, 2 × 10−4, 3 × 10−4, 4 × 10−4, to 5 × 10−4}, while λ is chosen from {2 × 10−3, 4 × 10−3, 6 × 10−3, 8 × 10−3, to 1 × 10−2}. Similar to K, the size of embedding learned by the GAAE module (F) is searched from {32, 64, 128, 256, to 512}. Regarding the learning rate of GAAE (lrGAAE), we experimented with the values {1 × 10−4, 5 × 10−4, 1 × 10−3, 5 × 10−3 and 1 × 10−2}. As shown in Fig. 3, we achieved the best prediction performance of our model with the settings: K = 50, ω = 0.1, α = 2 × 10−4, λ = 6 × 10−3, F = 256, and lrGAAE = 5 × 10−4. In subsequent experiments, we will maintain this setup to achieve optimal model performance.
 |
| | Fig. 3 Impact of hyper-parameters on GRL–PUL performance. | |
3.4 Model ablation study
Model ablation study is performed by altering or eliminating parts of a model to assess the significance of each part on the model's overall effectiveness. From the above descriptions, our proposed model comprises some important parts. Ablation studies are consequently applied to test their effectiveness. Based on the original model, we developed the following four variants:
• GRL–PUL w/o MFPUB: it selects negative samples randomly instead of employing the MFPUB module.
• GRL–PUL w/o the GAT-layer: it encodes input features by a single-layer GCN without adding a GAT layer.
• GRL–PUL w/o LT: it aggregates information using only a single-layer GAT before propagation, without initially performing linear transformation (LT) on the input features.
• GRL–PUL w/o PURF: it uses an inner product decoder to reconstruct a relational graph without utilizing the random forest combining PU learning strategy as the final classifier.
The intuitive representation of GRL–PUL and its four variants’ performances are shown in Table 2. Obviously, the comparison reveals that GRL–PUL exceeds all variants in five evaluation indicators, demonstrating that the negative samples selected by MFPUB are more likely to be true negative samples and that the encoder of GAAE can better characterize the original features. Simultaneously, the PURF module plays an important role in effectively enhancing performance prediction.
Table 2 Performance of GRL–PUL and its variants on three datasets
| Model |
MDAD |
DrugVirus |
aBiofilm |
| AUC |
AUPR |
ACC |
F1-score |
MCC |
AUC |
AUPR |
ACC |
F1-score |
MCC |
AUC |
AUPR |
ACC |
F1-score |
MCC |
| Bold data represent the maximum value for that metric in the current dataset, while underlined data indicate the second-best value. |
| GRL–PUL w/o MFPUB |
0.989089 |
0.988319 |
0.942551 |
0.943672 |
0.885890 |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) |
0.892347 |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) |
0.992691 |
0.992615 |
0.950555 |
0.951284 |
0.901581 |
| GRL–PUL w/o GAT-layer |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) |
0.902558 |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) |
0.806644 |
0.821309 |
0.622400 |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) |
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) . .![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif) ![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) ![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) |
| GRL–PUL w/o LT |
0.988884 |
0.989430 |
0.942146 |
0.942688 |
0.884574 |
0.908008 |
0.895960 |
0.811465 |
0.826934 |
0.633795 |
0.992596 |
0.992742 |
0.951908 |
0.952186 |
0.904027 |
| GRL–PUL w/o PURF |
0.974439 |
0.982294 |
0.948016 |
0.946006 |
0.898589 |
0.843739 |
0.842563 |
0.778771 |
0.773024 |
0.560761 |
0.973426 |
0.980269 |
0.935922 |
0.934025 |
0.873514 |
| GRL–PUL |
0.998961
|
0.998855
|
0.983239
|
0.983232
|
0.966527
|
0.917283
|
0.908112
|
0.829681
|
0.840402
|
0.666336
|
0.998956
|
0.998780
|
0.983391
|
0.983421
|
0.966839
|
3.5 Performance comparison between different negative sampling strategies
To validate the effectiveness and generalizability of the negative sampling module we proposed, we applied it to several state-of-the-art models and selected reliable negative samples for them. We conducted a series of experiments to compare the performance of several models utilizing different negative sampling strategies (i.e. random negative sampling and our proposed MFPUB module). In each experiment, we ensured the use of an equal number of positive and negative samples. The comparison prediction results of each model are clearly visible in Table 3, from which we can see, for example, MDASAE56 using reliable negative samples selected by MFPUB surpass the original model by 1.79%, 2.95%, 1.71%, 1.46% and 3.16% in terms of the AUC, AUPR, ACC, F1-score and MCC. In the MKGCN model, which originally treats all unlabeled samples as negative samples, the introduction of the MFPUB module addresses inherent biases by selecting high-quality negative samples. This adjustment leads to a 0.05% increase in AUC, a 3.10% increase in AUPR, a 31.40% increase in the F1 score, and a 26.47% increase in MCC, although ACC decreases by 0.73%. These improved models reveal outstanding performance, demonstrating that selecting reliable negative samples for model training can enhance predictive performance and that MFPUB can effectively select reliable negative samples.
Table 3 The performance of models trained using different negative sampling strategies to select negative samples on the MDAD dataset
| Metrics |
MDASAE |
MKGCN |
OGNNMDA |
| Random |
MFPUB |
Random |
MFPUB |
Random |
MFPUB |
| AUC |
0.973161 |
0.990536 ↑ |
0.993763 |
0.994317 ↑ |
0.958868 |
0.972979 ↑ |
| AUPR |
0.961752 |
0.990170 ↑ |
0.966081 |
0.995993 ↑ |
0.961380 |
0.977517 ↑ |
| ACC |
0.932882 |
0.948823 ↑ |
0.993108 |
0.985830 ↓ |
0.904049 |
0.919838 ↑ |
| F1-score |
0.936848 |
0.950536 ↑ |
0.750120 |
0.985637 ↑ |
0.904747 |
0.919143 ↑ |
| MCC |
0.872655 |
0.900206 ↑ |
0.768562 |
0.971976 ↑ |
0.808712 |
0.839977 ↑ |
3.6 Case study
To further validate the predictive effectiveness of GRL–PUL, we performed, based on the MDAD dataset, case studies on two clinically important drugs (i.e. curcumin and epigallocatechin gallate) and two problematic pathogenic microbes due to multidrug resistance (i.e. Staphylococcus aureus and Pseudomonas aeruginosa) as that described in previous research.57 After obtaining association prediction scores by GRL–PUL, the top-ranked 20 candidate associations will be verified by the MeSH§ and DrugBank datasets¶ as well as existing publications. The verification results are shown in Tables 4, 5, 6 and 7, respectively, demonstrating that GRL–PUL exhibits a satisfactory prediction ability in case studies including both drugs and microbes.
Table 4 The top-ranked 20 curcumin-associated microbes and their evidence
| Microbe |
PMID |
Microbe |
PMID |
|
Burkholderia cenocepacia
|
19146953 |
Klebsiella variicola
|
26139614 |
|
Serratia marcescens
|
24262582 |
Pseudomonas japonica
|
26139614 |
|
Burkholderia multivorans
|
19146953 |
Escherichia coli
|
24262582 |
|
Candida albicans
|
28473808 |
Streptomyces gordonii
|
Unconfirmed |
|
Proteus mirabilis
|
24262582 |
Achromobacter xylosoxidans
|
Unconfirmed |
|
Aeromonas hydrophila
|
26139614 |
Citrobacter freundii
|
26139614 |
|
Streptococcus mutans
|
23778072 |
Vibrio harveyi
|
23354447 |
|
Pseudomonas aeruginosa
|
27108548 |
Escherichia coli
|
24262582 |
|
Enterobacter ludwigi
|
26139614 |
Baker's yeast |
Unconfirmed |
|
Raoultella ornithinolytica
|
26139614 |
Thermus thermophilus
|
Unconfirmed |
Table 5 The top-ranked 20 epigallocatechin gallate-associated microbes and their evidence
| Microbe |
PMID |
Microbe |
PMID |
|
Raoultella ornithinolytica
|
26139614 |
Burkholderia multivorans
|
19146953 |
|
Klebsiella variicola
|
26139614 |
Enterobacter cancerogenus
|
26139614 |
|
Aeromonas hydrophila
|
26139614 |
Enterobacter ludwigi
|
26139614 |
|
Burkholderia cenocepacia
|
19146953 |
Human immunodeficiency virus 1 |
Unconfirmed |
|
Streptococcus pneumoniae
|
28402019 |
Candida albicans
|
19898545 |
|
Eikenella corrodens
|
21150103 |
Staphylococcus epidermidis
|
16189116 |
|
Streptococcus mutans
|
22169220 |
Vibrio harveyi
|
Unconfirmed |
|
Pseudomonas japonica
|
26139614 |
Acinetobacter baumannii
|
Unconfirmed |
|
Clostridium perfringens
|
Unconfirmed |
Mycobacterium tuberculosis
|
Unconfirmed |
|
Serratia marcescens
|
26139614 |
Vibrio cholerae
|
Unconfirmed |
Table 6 The top-ranked 20 Staphylococcus aureus-associated drugs and their evidence
| Drug |
PMID |
Drug |
PMID |
| HE4 |
26221537 |
Cefalonium |
26828772 |
| 2,3-Dehydrosilybin |
26273725 |
Fenclonine |
25658642 |
|
D-Glutamine |
25658642 |
Pefloxacin |
2830840 |
|
L-Tryptophan |
28819217 |
L-Phenylalanine-D-lysine |
27161246 |
| Prolificin A |
22170780 |
Copper sulfate |
28756196 |
| Ethyl acetate |
26004723 |
BisEDT-RIP |
15572191 |
|
L-Pipecolic acid |
25658642 |
D-Aspartic acid |
25658642 |
| 2,3-Dihydroxybenzoic acid |
25319566 |
D-tert-Leucine |
25658642 |
| Azithromycin |
23070152 |
Ferrous |
Unconfirmed |
| Citropin 1.1 |
16289474 |
Biphenyl |
25007234 |
Table 7 The top-ranked 20 Pseudomonas aeruginosa-associated drugs and their evidence
| Drug |
PMID |
Drug |
PMID |
| Asperdiol |
22905751 |
Dimethyl sulfoxide |
27645245 |
| GL13K |
23917321 |
Garlic extract |
15716452 |
| Cynarin |
26370951 |
7-Fluoroindoline-2,3-dione |
22251040 |
|
N-(2-Oxothiolan-3-yl)butanamide |
20453898 |
Phenyl-arginine-b-naphthylamide |
24176982 |
| Oleic acid |
23844805 |
5-Fluoroindole |
22251040 |
| IDR-1018 |
24852171 |
5,7,8,4-Tetramethoxyflavone |
Unconfirmed |
|
N-(4-Hydroxyphenyl)butanamide |
20453898 |
1-(Pyrazin-2-yl)ethan-1-one |
19855933 |
| Anthraflavic acid |
Unconfirmed |
Cathelicidin |
18591225 |
| 13-Methyltetradecanoic acid |
18318842 |
Carnitine hydrochloride |
Unconfirmed |
| LF11-215 |
26149536 |
Octadecyl gallate |
24016798 |
3.7 Visualization of embeddings
To further demonstrate that the GAAE module and MFPUB module contribute to learning more valuable features, we employed the t-SNE method58 to map the embeddings learned using GCNMDA,13 Graph2MDA,53 and GRL–PUL using the random negative sampling strategy and the MFPUB module respectively into a two-dimensional space. From Fig. 4, it is evident that GRL–PUL utilizing the MFPUB module for selecting reliable samples outperforms other models in acquiring discriminative embeddings. As observed in Fig. 4(a) and (d), regardless of the adopted negative sampling strategy, there are no distinct boundaries between the positive and negative samples in the feature space of GCNMDA, which is significantly inferior to that of Graph2MDA and GRL–PUL. However in Fig. 4(b) and (e), it is obvious that positive samples are mixed with relatively more negative samples while random negative sampling is employed, and the MFPUB module shows significant alleviation of this issue. Furthermore, we can also observe the same phenomenon from Fig. 4(c) and (f). The result demonstrates that selecting more reliable positive samples and enhancing the capability of graph representation learning are two crucial factors for improving MDA prediction performance and that GRL–PUL containing the MFPUB module and the GAAE module makes effective improvements in both aspects.
 |
| | Fig. 4 The t-SNE visualizations of the embeddings learnt by GCNMDA, Graph2MDA and GRL-PUL, which adopt random negative sampling strategy, are presented in (a), (b) and (c) respectively. The results after incorporating the MFPUB module into these models are shown in (d), (e), and (f). | |
4 Conclusion
A substantial amount of research has revealed that microbes and drugs play an essential role in human health. Leveraging microbe–drug associations which still require further excavation can effectively promote disease prevention and treatment. In this paper, we propose the GRL–PUL model to predict potential MDAs. Apart from obtaining muti-model attributes to construct microbe–drug heterogeneous networks, GRL–PUL utilizes the MFPUB module to select reliable negative samples, the GAAE module to learn information-rich embeddings from the heterogeneous network and the PURF module to calculate the probability of MDAs. Although the model we proposed has shown superiority over mainstream models in various aspects, there is still potential to enhance its overall performance on small-scale and sparse datasets by optimizing the structure of the graph representation learning module.
Author contributions
Jinqing Liang and Yuping Sun contributed to the conception and methodology of the study, analysis and manuscript preparation; Jinqing Liang contributed to the original draft and performed the experiment; Jinqing Liang, Yuping Sun, and Jie Ling contributed to reviewing and editing; Yuping Sun helped performed the analysis with constructive discussions and contributed to the supervision and funding acquisition of the study.
Data availability
The data that support the findings of this study are openly available in MDAD: a special resource for microbe–drug associations at https://doi.org/10.3389/fcimb.2018.00424,22 aBiofilm: a resource of anti-biofilm agents and their potential implications in targeting antibiotic drug resistance at https://doi.org/10.1093/nar/gkx1157,23 and Discovery and development of safe-in-man broad-spectrum antiviral agents at https://doi.org/10.1016/j.ijid.2020.02.018.24
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (62002070).
References
- H. M. P. Consortium, Structure, function and diversity of the healthy human microbiome, Nature, 2012, 486(7402), 207–214 CrossRef
 .
.
- M. Ventura, S. O’flaherty, M. J. Claesson, F. Turroni, T. R. Klaenhammer and D. Van Sinderen,
et al., Genome-scale analyses of health-promoting bacteria: probiogenomics, Nat. Rev. Microbiol., 2009, 7(1), 61–71 CrossRef CAS
 .
.
- G. A. Ogunrinola, J. O. Oyewale, O. O. Oshamika and G. I. Olasehinde, The human microbiome and its impacts on health, Int. J. Microbiol., 2020, 2020(1), 8045646 Search PubMed
 .
.
- A. L. Kau, P. P. Ahern, N. W. Griffin, A. L. Goodman and J. I. Gordon, Human nutrition, the gut microbiome and the immune system, Nature, 2011, 474(7351), 327–336 CrossRef CAS PubMed
 .
.
- F. Sommer and F. Bäckhed, The gut microbiota—masters of host development and physiology, Nat. Rev. Microbiol., 2013, 11(4), 227–238 CrossRef CAS PubMed
 .
.
- L. Wen, R. E. Ley, P. Y. Volchkov, P. B. Stranges, L. Avanesyan and A. C. Stonebraker,
et al., Innate immunity and intestinal microbiota in the development of Type 1 diabetes, Nature, 2008, 455(7216), 1109–1113 CrossRef CAS
 .
.
- J. A. Gimenez-Bastida, L. M. Carreras, A. Moya-Pérez and J. M. L. Llopis, Pharmacological efficacy/toxicity of drugs: a comprehensive update about the dynamic interplay of microbes, J. Pharm. Sci., 2018, 107(3), 778–784 CrossRef CAS PubMed
 .
.
- M. Ramirez, S. Rajaram, R. J. Steininger, D. Osipchuk, M. A. Roth and L. S. Morinishi,
et al., Diverse drug-resistance mechanisms can emerge from drug-tolerant cancer persister cells, Nat. Commun., 2016, 7(1), 10690 CrossRef CAS
 .
.
- J. Cummings, G. Lee, A. Ritter, M. Sabbagh and K. Zhong, Alzheimer's disease drug development pipeline: 2020, Alzheimer's Dementia, 2020, 6(1), e12050 CrossRef
 .
.
- C. P. Adams and V. V. Brantner, Estimating the cost of new drug development: is it really $802 million?, Health Aff., 2006, 25(2), 420–428 CrossRef PubMed
 .
.
- S. M. Paul, D. S. Mytelka, C. T. Dunwiddie, C. C. Persinger, B. H. Munos and S. R. Lindborg,
et al., How to improve R&D productivity: the pharmaceutical industry's grand challenge, Nat. Rev. Drug Discovery, 2010, 9(3), 203–214 CrossRef CAS PubMed
 .
.
-
L. Zhu, G. Duan, C. Yan and J. Wang, Prediction of microbe—drug associations based on KATZ measure, In: 2019 IEEE international conference on bioinformatics and biomedicine (BIBM), IEEE, 2019, pp. 183–187.
- Y. Long, M. Wu, C. K. Kwoh, J. Luo and X. Li, Predicting human microbe–drug associations via graph convolutional network with conditional random field, Bioinformatics, 2020, 36(19), 4918–4927 CrossRef CAS PubMed
 .
.
- D. Liu, J. Liu, Y. Luo, Q. He and L. Deng, MGATMDA: Predicting microbe-disease associations via multi-component graph attention network, IEEE/ACM Trans. Comput. Biol. Bioinf., 2021, 19(6), 3578–3585 Search PubMed
 .
.
- Y. Tan, J. Zou, L. Kuang, X. Wang, B. Zeng and Z. Zhang,
et al., GSAMDA: a computational model for predicting potential microbe–drug associations based on graph attention network and sparse autoencoder, BMC Bioinf., 2022, 23(1), 492 CrossRef
 .
.
- Q. Ma, Y. Tan and L. Wang, GACNNMDA: a computational model for predicting potential human microbe–drug associations based on graph attention network and CNN-based classifier, BMC Bioinf., 2023, 24(1), 35 CrossRef PubMed
 .
.
- M. Liang, X. Liu, Q. Chen, B. Zeng and L. Wang, NMGMDA: a computational model for predicting potential microbe–drug associations based on minimize matrix nuclear norm and graph attention network, Sci. Rep., 2024, 14(1), 650 CrossRef CAS
 .
.
- Z. Zhou, L. Zhuo, X. Fu and Q. Zou, Joint deep autoencoder and subgraph augmentation for inferring microbial responses to drugs, Briefings Bioinf., 2024, 25(1), bbad483 CrossRef
 .
.
- M. Li, Z. Wang, L. Liu, X. Liu and W. Zhang, Subgraph-Aware Graph Kernel Neural Network for Link Prediction in Biological Networks, IEEE J. Biomed. Health Inf., 2024, 28, 4373–4381 Search PubMed
 .
.
-
K. Zhang, F. Huang, L. Liu, Z. Xiong, H. Zhang, Y. Quan and W. Zhang, Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, International Joint Conferences on Artificial Intelligence Organization, 2024, pp. 6161–6169.
- X. Zeng, Y. Zhong, W. Lin and Q. Zou, Predicting disease-associated circular RNAs using deep forests combined with positive-unlabeled learning methods, Briefings Bioinf., 2020, 21(4), 1425–1436 CrossRef CAS PubMed
 .
.
- L. Peng, L. Huang, G. Tian, Y. Wu, G. Li and J. Cao,
et al., Predicting potential microbe-disease associations with graph attention autoencoder, positive-unlabeled learning, and deep neural network, Front. Microbiol., 2023, 14, 1244527 CrossRef PubMed
 .
.
- Z. Tian, Y. Yu, H. Fang, W. Xie and M. Guo, Predicting microbe–drug associations with structure-enhanced contrastive learning and self-paced negative sampling strategy, Briefings Bioinf., 2023, 24(2), bbac634 CrossRef
 .
.
-
C. Elkan and K. Noto, Learning classifiers from only positive and unlabeled data, In: Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, 2008, pp. 213–220.
- Y. Z. Sun, D. H. Zhang, S. B. Cai, Z. Ming, J. Q. Li and X. Chen, MDAD: a special resource for microbe–drug associations, Front. Cell. Infect. Microbiol., 2018, 8, 424 CrossRef CAS
 .
.
- A. Rajput, A. Thakur, S. Sharma and M. Kumar, aBiofilm: a resource of anti-biofilm agents and their potential implications in targeting antibiotic drug resistance, Nucleic Acids Res., 2018, 46(D1), D894–D900 CrossRef CAS PubMed
 .
.
- P. I. Andersen, A. Ianevski, H. Lysvand, A. Vitkauskiene, V. Oksenych and M. Bjørås,
et al., Discovery and development of safe-in-man broad-spectrum antiviral agents, Int. J. Infect. Dis., 2020, 93, 268–276 CrossRef CAS PubMed
 .
.
- O. K. Kamneva, Genome composition and phylogeny of microbes predict their co-occurrence in the environment, PLoS Comput. Biol., 2017, 13(2), e1005366 CrossRef PubMed
 .
.
- D. Szklarczyk, A. L. Gable, K. C. Nastou, D. Lyon, R. Kirsch and S. Pyysalo,
et al., The STRING database in 2021: customizable protein-protein networks, and functional characterization of user-uploaded gene/measurement sets, Nucleic Acids Res., 2021, 49(D1), D605–D612 CrossRef CAS PubMed
 .
.
- S. T. Sherry, M. H. Ward, M. Kholodov, J. Baker, L. Phan and E. M. Smigielski,
et al., dbSNP: the NCBI database of genetic variation, Nucleic Acids Res., 2001, 29(1), 308–311 CrossRef CAS PubMed
 .
.
- J. Yang, D. Zhang, A. F. Frangi and J.-Y. Yang, Two-dimensional PCA: a new approach to appearance-based face representation and recognition, IEEE Trans. Pattern Anal. Mach. Intell., 2004, 26(1), 131–137 CrossRef PubMed
 .
.
- M. Hattori, N. Tanaka, M. Kanehisa and S. Goto, SIMCOMP/SUBCOMP: chemical structure search servers for network analyses, Nucleic Acids Res., 2010, 38(suppl_2), W652–W656 CrossRef CAS
 .
.
- D. K. Jain, Z. Zhang and K. Huang, Random walk-based feature learning for micro-expression recognition, Pattern Recognit. Lett., 2018, 115, 92–100 CrossRef
 .
.
- Y. Koren, R. Bell and C. Volinsky, Matrix factorization techniques for recommender systems, Computer, 2009, 42(8), 30–37 Search PubMed
 .
.
-
Z. Shen, Z. Jiang and W. Bao, CMFHMDA: Collaborative matrix factorization for human microbe-disease association
prediction, in: Intelligent Computing Theories and Application: 13th International Conference, ICIC 2017, Liverpool, UK, August 7–10, 2017, Proceedings, Part II 13. Springer, 2017, pp. 261–269.
- H. Wei, Y. Xu and B. Liu, iPiDi-PUL: identifying Piwi-interacting RNA-disease associations based on positive unlabeled learning, Briefings Bioinf., 2021, 22(3), bbaa058 CrossRef PubMed
 .
.
- X. Chen, C. C. Zhu and J. Yin, Ensemble of decision tree reveals potential miRNA-disease associations, PLoS Comput. Biol., 2019, 15(7), e1007209 CrossRef PubMed
 .
.
-
T. N. Kipf and M. Welling, Variational graph auto-encoders, arXiv, 2016, preprint, arXiv:161107308 DOI:10.48550/arXiv.1611.07308.
-
S. Purkayastha, I. Mondal, S. Sarkar, P. Goyal and J. K. Pillai, Drug-drug interactions prediction based on drug embedding and graph auto-encoder, In: 2019 IEEE 19th International Conference on Bioinformatics and Bioengineering (BIBE), IEEE, 2019, pp. 547–552.
- Z. Liu, Q. Chen, W. Lan, H. Pan, X. Hao and S. Pan, GADTI: graph autoencoder approach for DTI prediction from heterogeneous network, Front. Genet., 2021, 12, 650821 CrossRef
 .
.
- Q. Liang, W. Zhang, H. Wu and B. Liu, LncRNA-disease association identification using graph auto-encoder and learning to rank, Briefings Bioinf., 2023, 24(1), bbac539 CrossRef
 .
.
- S. Zhou, W. Sun, P. Zhang and L. Li, Predicting pseudogene-miRNA associations based on feature fusion and graph auto-encoder, Front. Genet., 2021, 12, 781277 CrossRef CAS
 .
.
- A. B. Silva and E. J. Spinosa, Graph convolutional auto-encoders for predicting novel lncRNA-disease associations, IEEE/ACM Trans. Comput. Biol. Bioinf., 2021, 19(4), 2264–2271 Search PubMed
 .
.
- H. Fu, F. Huang, X. Liu, Y. Qiu and W. Zhang, MVGCN: data integration through multi-view graph convolutional network for predicting links in biomedical bipartite networks, Bioinformatics, 2022, 38(2), 426–434 CrossRef CAS PubMed
 .
.
-
S. Chu, G. Duan and C. Yan, Predicting miRNA-disease associations based on graph convolutional network with path learning, in: 2023 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), IEEE, 2023, pp. 474–479.
-
J. Gasteiger, A. Bojchevski and S. Günnemann, Predict then propagate: Graph neural networks meet personalized pagerank, arXiv, 2018, preprint, arXiv:181005997 DOI:10.48550/arXiv.1810.05997.
- P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio,
et al., Graph attention networks, stat, 2017, 1050(20), 10–48550 Search PubMed
 .
.
- B. Yang and H. Chen, Predicting circRNA-drug sensitivity associations by learning multimodal networks using graph auto-encoders and attention mechanism, Briefings Bioinf., 2023, 24(1), bbac596 CrossRef
 .
.
- Y. Zhang, Y. Qiu, Y. Cui, S. Liu and W. Zhang, Predicting drug–drug interactions using multi-modal deep auto-encoders based network embedding and positive-unlabeled learning, Methods, 2020, 179, 37–46 CrossRef CAS PubMed
 .
.
- J. Bekker and J. Davis, Learning from positive and unlabeled data: A survey, Mach. Learn., 2020, 109(4), 719–760 CrossRef
 .
.
- Y. Zhang, F. Ye, D. Xiong and X. Gao, LDNFSGB: prediction of long non-coding rna and disease association using network feature similarity and gradient boosting, BMC Bioinf., 2020, 21, 1–27 CrossRef
 .
.
- Z. Lou, Z. Cheng, H. Li, Z. Teng, Y. Liu and Z. Tian, Predicting miRNA-disease associations via learning multimodal networks and fusing mixed neighborhood information, Briefings Bioinf., 2022, 23(5), bbac159 CrossRef
 .
.
- L. Deng, Y. Huang, X. Liu and H. Liu, Graph2MDA: a multi-modal variational graph embedding model for predicting microbe–drug associations, Bioinformatics, 2022, 38(4), 1118–1125 CrossRef CAS
 .
.
- H. Yang, Y. Ding, J. Tang and F. Guo, Inferring human microbe–drug associations via multiple kernel fusion
on graph neural network, Knowl.-Based Syst., 2022, 238, 107888 CrossRef
 .
.
- J. Zhao, L. Kuang, A. Hu, Q. Zhang, D. Yang and C. Wang, OGNNMDA: a computational model for microbe–drug association prediction based on ordered message-passing graph neural networks, Front. Genet., 2024, 15, 1370013 CrossRef CAS PubMed
 .
.
- L. Fan, L. Wang and X. Zhu, A novel microbe–drug association prediction model based on stacked autoencoder with multi-head attention mechanism, Sci. Rep., 2023, 13(1), 7396 CrossRef CAS
 .
.
- H. Huang, Y. Sun, M. Lan, H. Zhang and G. Xie, GNAEMDA: microbe–drug associations prediction on graph normalized convolutional network, IEEE J. Biomed. Health Inf., 2023, 27(3), 1635–1643 Search PubMed
 .
.
- L. Van der Maaten and G. Hinton, Visualizing data using t-SNE, J. Mach. Learn. Res., 2008, 9(11), 2579–2605 Search PubMed
 .
.
Footnotes |
| † It is extremely difficult to exhaustively determine through wet experiments that a specific microbe–drug pair has no association, which is common in existing biological association identification tasks. Therefore, labeled negative samples are virtually absent in current MDA datasets. |
| ‡ The reliability of unlabeled samples ω, whose optimal value is 0.1, is the confidence coefficient of unlabeled samples. See the details in Section 3.3. |
| § See more on https://www.ncbi.nlm.nih.gov/mesh. |
| ¶ See more on https://go.drugbank.com/. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  * and
Jie
Ling
* and
Jie
Ling
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nm for each dataset, where Nd and Nm represent the number of drugs and microbes. For any given drug di and microbe mj, Äij will be 1 if there is a known association between drug di and microbe mj, and 0 otherwise. Furthermore, the symmetric adjacency matrix A ∈
Nd×Nm for each dataset, where Nd and Nm represent the number of drugs and microbes. For any given drug di and microbe mj, Äij will be 1 if there is a known association between drug di and microbe mj, and 0 otherwise. Furthermore, the symmetric adjacency matrix A ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×(Nd+Nm) is obtained using the formula:
(Nd+Nm)×(Nd+Nm) is obtained using the formula:
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×Nm.
Nm×Nm.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×Nm.
Nm×Nm.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd is constructed.
Nd×Nd is constructed.

![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd.
Nd×Nd.

![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×1 refers to the initial probability vector of node i, in which the j-th element is defined as follows:
Nd×1 refers to the initial probability vector of node i, in which the j-th element is defined as follows: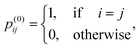
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd representing the drug network topological attribute is procured.
Nd×Nd representing the drug network topological attribute is procured.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×(Nd+Nm) is composed of a similarity feature and is defined as follows:
(Nd+Nm)×(Nd+Nm) is composed of a similarity feature and is defined as follows:
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×(Nd+Nm) is composed of the microbe functional similarity and drug network topological feature, and is defined as follows:
(Nd+Nm)×(Nd+Nm) is composed of the microbe functional similarity and drug network topological feature, and is defined as follows:
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×2(Nd+Nm):
(Nd+Nm)×2(Nd+Nm):
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nd is a diagonal matrix with diagonal elements that satisfy the equation Wixx = Wix (i.e. the element in row x and column x of Wi is equal to row i and column x of W), and Ä·i ∈
Nd×Nd is a diagonal matrix with diagonal elements that satisfy the equation Wixx = Wix (i.e. the element in row x and column x of Wi is equal to row i and column x of W), and Ä·i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×1 represents the i-th column of Ä,
Nd×1 represents the i-th column of Ä,![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×Nm is a diagonal matrix with diagonal elements that satisfy the equation Wjxx = Wxj (i.e. the element in row x and column x of Wj is equal to row x and column j of W), and Äj· ∈
Nm×Nm is a diagonal matrix with diagonal elements that satisfy the equation Wjxx = Wxj (i.e. the element in row x and column x of Wj is equal to row x and column j of W), and Äj· ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 1×Nm represents the j-th row of Ä.
1×Nm represents the j-th row of Ä.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×K and the drug latent factor matrices V ∈
Nm×K and the drug latent factor matrices V ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×K, while K is the size of the latent factor of each microbe and drug.
Nd×K, while K is the size of the latent factor of each microbe and drug.![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×Nm, hidden factor dimension K, maximum iteration max_iter, the params of the loss function α and λ, weight matrix W, and epoch of the random forest epochRF;
Nd×Nm, hidden factor dimension K, maximum iteration max_iter, the params of the loss function α and λ, weight matrix W, and epoch of the random forest epochRF;![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nm×K and drug latent factor matrices V ∈
Nm×K and drug latent factor matrices V ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd×K;
Nd×K;![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd×Nm)×K;
(Nd×Nm)×K;![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 1,
1,![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 2,…,
2,…,![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) Nd+Nm]T, where the feature of node vi is denoted as
Nd+Nm]T, where the feature of node vi is denoted as ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i ∈
i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2(Nd×Nm). It will be fed into a neural network with a parameter set θ consisting of a single linear transformation layer. The linear transformation proceeds as follows:
2(Nd×Nm). It will be fed into a neural network with a parameter set θ consisting of a single linear transformation layer. The linear transformation proceeds as follows:![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) (Nd+Nm)×Fvia linear transformation operation fθ(·), while F is the dimension of the embedded representation of the node. W1st ∈
(Nd+Nm)×Fvia linear transformation operation fθ(·), while F is the dimension of the embedded representation of the node. W1st ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2(Nd+Nm)×F is the first learnable weight matrix and b is the bias.
2(Nd+Nm)×F is the first learnable weight matrix and b is the bias.
![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) 1,
1,![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) 2,…,
2,…,![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) Nd+Nm]T,
Nd+Nm]T, ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) i ∈
i ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F, into the higher-level feature
F, into the higher-level feature  . To begin with, a shared linear transformation, parametrized by a weight matrix Wattn ∈
. To begin with, a shared linear transformation, parametrized by a weight matrix Wattn ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F×F, is applied to each node. Thereafter, we performed self-attention on the nodes to calculate attention scores:
F×F, is applied to each node. Thereafter, we performed self-attention on the nodes to calculate attention scores:![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) T[Wattn
T[Wattn![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) i‖Wattn
i‖Wattn![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) j]),
j]),![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) ∈
∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 1×2F is a learnable shared parameter and ‖ denotes the concatenation operation. The attention coefficient between node i and node j (one of the first-order neighbors of node i) is computed by normalizing the attention scores across all first-order neighbors of node i (including node i) using the softmax function:
1×2F is a learnable shared parameter and ‖ denotes the concatenation operation. The attention coefficient between node i and node j (one of the first-order neighbors of node i) is computed by normalizing the attention scores across all first-order neighbors of node i (including node i) using the softmax function:
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) i is the first-order neighborhood of node i. Then, we computed a linear combination of the features corresponding to attention coefficients:
i is the first-order neighborhood of node i. Then, we computed a linear combination of the features corresponding to attention coefficients: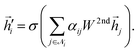
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F×F represents the second learnable weight matrix.
F×F represents the second learnable weight matrix.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) F will be obtained after applying Laplacian propagation, and the encoder function is defined as follows:
F will be obtained after applying Laplacian propagation, and the encoder function is defined as follows:
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nd+Nm denotes the attention coefficient matrix.
Nd+Nm denotes the attention coefficient matrix.





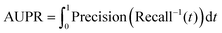




![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[6 with combining low line]](https://www.rsc.org/images/entities/char_0036_0332.gif)
![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif)
![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) .
.![[9 with combining low line]](https://www.rsc.org/images/entities/char_0039_0332.gif)
![[5 with combining low line]](https://www.rsc.org/images/entities/char_0035_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[8 with combining low line]](https://www.rsc.org/images/entities/char_0038_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.



