Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling the oxygen exchange mechanism on La2Ce2O7†
Yizhou
Shen
 ,
Vincent
Thoréton
,
Vincent
Thoréton
 and
Reidar
Haugsrud
*
and
Reidar
Haugsrud
*
Department of Chemistry, Centre for Materials Science and Nanotechnology, University of Oslo, Gaustadalléen 21, NO-0349 Oslo, Norway
First published on 4th December 2024
Abstract
Understanding the mechanism of the oxygen exchange rate between the gas-phase and the oxide surface is essential to utilize electrochemical transport of oxygen in ceria-based materials for sustainable technologies. This contribution applies pulse isotope exchange (PIE) to investigate the oxygen exchange mechanism on La2Ce2O7 and 5% Pr-substituted La2Ce2O7. The oxygen exchange kinetics is rate-limited by the dissociation of adsorbed molecular oxygen. Pr substitution increases the surface kinetics, presumably due to an increased concentration of electronic defects that enhances charge transfer of electronic defects at the surface. Humidity decreases the exchange rate due to the selective dissociative adsorption of water molecules into surface oxygen vacancies, forming hydroxide defects. This effect diminishes with increasing temperature due to the exothermic nature of hydration.
1. Introduction
The exchange of oxygen between the gas-phase and the oxide surface, as well as the transport of oxide ions and electrons in the bulk of the oxide, are mutually important for the performance of solid oxide fuel and electrolyzer cells (SOFC and SOEC), interconverting chemical and electrical energy.1–4 Nevertheless, which functional properties of oxides promote the oxygen reduction reaction (ORR) and why, remain subjects of debate.Rare-earth (RE) substituted ceria, Ce1−xRExO2−δ, is among the best oxide ion conductors, and the partial reducibility of Ce(IV) yields electronic defects, jointly giving rise to various functional properties.5 Moreover, these materials are ideal for fundamental studies and have been central in developing the understanding of oxygen exchange mechanisms.6–25 Substitution with multivalent RE cations (>5 atomic%) introduces impurity electron bands, further facilitating ionization of adsorbed oxygen species at the surface, increasing the oxygen exchange rate, ℜ0, by orders of magnitude.21,26–30 In several ceria-based materials, the apparent activation energy of ℜ0 has been reported to be significantly higher at high temperatures (above 700 to 800 °C) compared to lower temperatures (Ea > 2 eV vs. Ea < 1.5 eV, respectively).23,31–33 In this respect, it has been speculated whether the omnipresent water vapor influences the oxygen exchange mechanism in the low-temperature range.33
Although debated, the crystal structure of La2Ce2O7 has been reported as a disordered fluorite structure, closely related to pristine ceria,34–37 and can consequently be regarded as 50% La-substituted CeO2, i.e., Ce0.5La0.5O∼1.75. Unlike ceria, the material exhibits predominantly ionic conductivity even at low oxygen partial pressures (e.g., <10−20 atm at 700 °C38,39). Its ionic conductivity at 600 °C is approximately one order of magnitude lower than GDC, but only a factor of three lower than YSZ.38–40 La2Ce2O7 dissolves hydroxide defects up to high temperatures (∼800 °C) and demonstrates appreciable proton conductivity under humidified conditions.39,41–44 Thus, La2Ce2O7 exhibits conductivity characteristics interesting for diverse applications.45–47
There are a few studies on the oxygen exchange kinetics of ceria with La (≪50%) and co-doped with Pr.48–50 La substitution increases the oxygen exchange coefficient, ks (relation to ℜ0 shown in the ESI†), of Pr-doped ceria and its apparent activation energy.50 It has been speculated that this behavior indicates a change in the point defects controlling the rate-determining process, e.g., shifting from oxygen vacancies to electronic defects.50,51
Oxygen vacancies and electronic defects play crucial roles in the fundamental processes involved in oxygen exchange, and material properties that affect the concentration of these defects are essential.21,52 Recently, the interaction between the electronic band structure at the surface and adsorbed oxygen species has been emphasized. Electron transfer from the surface to adsorbed oxygen species is facilitated by the reduction of the material's band gap, which, in the case of Pr-substituted ceria, is attributed to the generation of a Pr impurity band within the band gap.27–30,50
The materials being studied here, La2Ce2O7 (LaC) and 5% Pr-substituted La2Ce2O7, La2Ce1.95Pr0.05O7−δ (5PrLaC) represent extremes of oxygen-deficient, ceria-like disordered fluorite structures, substituting 50% of Ce(IV) with the more basic La(III). Additionally, Pr substitution may promote the formation of electronic defects through Pr(III)–Pr(IV) redox transitions. Accordingly, these materials serve as suitable model systems to investigate the individual effects of these parameters on oxygen exchange kinetics. Moreover, the significant bulk concentration and conductivity of protons in lanthanum cerates in the presence of water vapor, even at temperatures above 700 °C (approximately 1 mol% at 700 °C in 0.025 atm H2O), make these materials particularly interesting for studying the effects of water vapor on oxygen exchange kinetics.39,44
On these bases, we investigated the oxygen exchange mechanism and potential effects of water vapor on the exchange rate of La2Ce2O7-based materials utilizing pulse isotope exchange (PIE) measurements. Building on our experimental findings and a further discussion of the literature data for ceria-based materials, we address the understanding of the oxygen exchange properties of this technologically important class of materials.
2. Gas-phase isotope studies
Oxygen exchange between the gas-phase and the oxide surface involves a series of elementary steps. Initially, gas-phase transport occurs towards the surface, followed by oxygen adsorption and potential dissociation into various adsorbed species. Additional steps required for oxygen exchange include the transfer of electrons to the adsorbed oxygen species, surface diffusion, and incorporation of oxide ions. These steps may all limit the overall rate of oxygen exchange.The exchange reaction at the oxide surface can be described by Kröger–Vink notation as:53
 | (1) |
 represents oxygen vacancies,
represents oxygen vacancies,  lattice oxide ions and h˙ electron holes. At equilibrium, the reaction rates of oxygen entering and leaving the surface are equal and characterized by ℜ0 (in mol O m−2 s−1), i.e., the equilibrium oxygen exchange rate.
lattice oxide ions and h˙ electron holes. At equilibrium, the reaction rates of oxygen entering and leaving the surface are equal and characterized by ℜ0 (in mol O m−2 s−1), i.e., the equilibrium oxygen exchange rate.
Several techniques have been developed to investigate the oxygen exchange kinetics, including electrical conductivity relaxation (ECR),54,55 isotope exchange followed by depth profiling (IEDP) with secondary ion mass spectrometry (SIMS)56,57 and gas phase analysis methodologies (GPA).58,59 ECR measurements provide information on chemical diffusion and surface exchange coefficients, while IEDP with SIMS gives insight into the oxygen tracer surface exchange and diffusion coefficients. GPA, on the other hand, involves continuous monitoring of isotopologue transients in a labeled atmosphere surrounding the oxides in chemical equilibrium with the reaction conditions. Under the steady-state approximation, ℜ0 can principally be broken down into the rates of dissociative adsorption, ℜdis, and incorporation, ℜinc, providing further insight into the underlying exchange mechanism.60,61
During PIE measurements, powder samples are pre-equilibrated at the chosen oxygen partial pressure, pO2, and temperature in a packed-bed quartz reactor under a constant laminar gas flow. An 18O enriched pulse with the same pO2 as during pre-annealing is introduced upstream through the powder bed for oxygen exchange. The fractions of 16O and 18O (f16g and f18g) are determined from the concentrations of the diatomic isotopologues 16O2, 16O18O and 18O2 (f32g, f34g and f36g) at the reactor outlet by means of a quadrupole mass spectrometer (Pfeiffer QME Prisma 220). Provided there is chemical equilibrium between the gas-phase and the oxide and that the requirements of the PIE model are fulfilled,60 the simultaneous decrease in f36g along with the increase in f34g and f32g reflects the scrambling of 16O and 18O as a consequence of dissociation and incorporation (in addition to recombination and desorption) of chemisorbed surface oxygen species into the oxide lattice. The requirement for chemical equilibrium should be recognized in relation to the kinetic parameters derived from gas-phase isotope analysis methods, as these parameters represent balanced exchange rate coefficients.
To investigate the effects of water vapor on the exchange rate, the powder was equilibrated in carrier gas mixtures containing 3% H2O. However, the labeled oxygen pulse used for the exchange experiments was bottle-dry. In this way, the humidity present during the oxygen exchange is determined by the amount of adsorbed hydroxide defects on the surface of the powder. The amount of adsorbed hydroxide defects on the powder surface varies with temperature, following the thermodynamics of the interactions between water and the oxide surface. These interactions involve the chemisorption of water molecules, potential dissociation, and incorporation of these species to form hydroxide defects. We emphasize that the influence of water encountered herein is solely qualitative in nature. It serves as a basis for further discussion and analysis. To gain comprehensive understanding of these interactions and their effects on the oxygen exchange rate, additional quantitative studies are necessary.
3. Experimental
LaC was synthesized via solid-state synthesis. Stoichiometric amounts of cerium(IV) oxide nanopowders (particle size <50 nm, 99.95% purity; Sigma-Aldrich) and lanthanum(III) oxide (≥99.9% purity; Sigma-Aldrich), pre-dried at 900 °C, were dispersed in isopropanol and mixed in a roller mill (Model 12VS, Capco) for 24 hours.The resulting suspension was dried and then calcined at 1000 °C for 3 hours. The powders were shaped into pellets through uniaxial pressing, followed by sintering at 1580 °C in air for 4 hours, with heating and cooling rates of 3 °C min−1, giving a relative density of >94% (determined by Archimedes’ method). Finally, the dense pellets were crushed and sieved into three fractions with particle sizes: 90–125 μm, 40–60 μm, and <20 μm. We assume that the agglomerates maintain the relative density of the sintered pellets before crushing.
5PrLaC was synthesized according to a Pechini-based route. Stoichiometric amounts of lanthanum(III) nitrate hexahydrate (≥99.9%; Sigma-Aldrich) and praseodymium nitrate hexahydrate (99.9%; Sigma-Aldrich) were dissolved in deionized water, followed by mixing with citric acid (99%; Sigma-Aldrich) under continuous stirring at 80 °C. The molar ratio between the cations and citric acid was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.
2.
After evaporating the water, the precursor was further annealed at 250 °C, resulting in a xerogel, which was calcined at 1000 °C for 3 hours in air. Sintering at 1580 °C in air yielded a relative density of 93%, and the fractioning procedures were the same as for LaC.
X-ray diffraction (XRD) and scanning electron microscopy (SEM) images of the powder products are presented in the ESI.†
The PIE procedure was conducted following the method described by Bouwmeester et al.,60,62 with the detailed procedure outlined in the ESI.† The temperature range used to extract kinetic parameters was from 650 to 950 °C, which is significantly lower than the sintering temperature. The temperature range measured varied slightly depending on the materials and gas composition. The temperature at which the interaction between oxygen in the gas-phase and the surface becomes detectable with the quadrupole mass spectrometer (QMS) is referred to as the onset temperature, Tonset (°C).
The pO2 range was between 0.005 and 0.21 atm for both dry and wet carrier gases. The water vapor pressure pH2O (0.03 atm) in the wet carrier gas was determined by the temperature of the water reservoir through which the carrier gas flowed before entering the reactor. One should note that to enable accurate measurements at the lowest pO2, 99% 18O gas was used as the source for the isotope mixtures, different from the more conventional isotope enrichment of >97% 18O for the higher pO2.
The PIE measurements were conducted in the surface-controlled regime. This was verified through separate gas-phase isothermal isotope exchange (IIE) experiments, which showed that the average particle sizes were considerably smaller than the characteristic length, l, where l = D/ks (D is the bulk self-diffusion coefficient). Accordingly, it was assumed that there is no concentration gradient of oxygen isotopes in the oxide bulk, i.e., bulk diffusion has virtually no effect on the measurements of oxygen surface exchange.
4. Results
Fig. 1 and 2 depict representative examples of the evolution of the pulse response in PIE as a function of temperature for LaC and 5PrLaC in bottle-dry and wet (0.03 atm H2O) carrier gases at 0.02 atm O2. The fraction of 36O2, f36g, gradually decreases above 500–600 °C (Tonset) because of the scrambling of adsorbed 16O and 18O at the surface and the incorporation of 18O into the bulk of the oxide. Tonset is lower for the doped compared to the undoped material.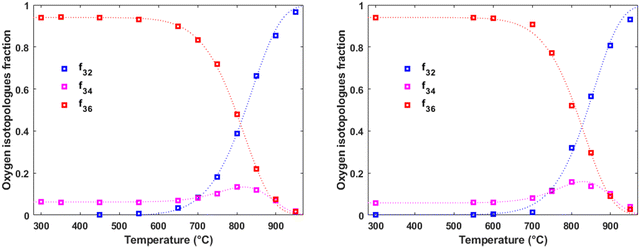 | ||
| Fig. 1 Oxygen isotopologue fractions as a function of temperature for La2Ce2O7 at pO2 = 0.02 atm in dry carrier gas (on the left) and wet carrier gas (on the right), respectively. In both cases, dry pulses were employed. The dotted lines represent the fits to the models (see ESI,† Section S1 and eqn (S17), (S22)–(S24)). The constant level of 16O18O up to Tonset is due to the purity of the isotope-labeled gas (97% 18O), reflecting the distribution of the isotopologues. | ||
 | ||
| Fig. 2 Oxygen isotopologue fractions as a function of temperature for La2Ce1.95Pr0.05O7-δ at pO2 = 0.02 atm in dry carrier gas (on the left) and wet carrier gas (on the right), respectively. In both cases, dry pulses were employed. The dotted lines represent the fits to the models (see ESI,† Section S1 and eqn (S17), (S22)–(S24)). | ||
The presence of water vapor slightly increases Tonset and alters the profile shape accordingly. It is worth noting that the increased formation of 16O18O qualitatively indicates slower incorporation relative to dissociative adsorption and associative desorption.
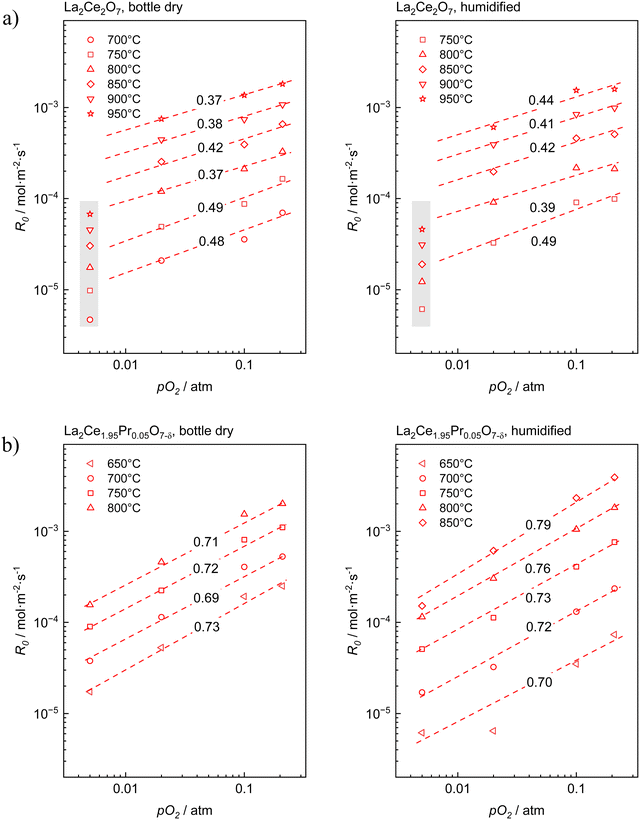
Fig. 3 presents the oxygen partial pressure dependence of ℜ0 for both bottle-dry and humidified conditions for (a) LaC and (b) 5PrLaC, including the pO2dependences obtained from linear fitting of the data according to double logarithmic representations. Fig. 4 displays the isobaric temperature dependence of ℜ0 corresponding to the exchange rates in Fig. 3 for the lowest and highest measured pO2. Generally, there is some scatter in the data with respect to functional dependences, especially for LaC. Nevertheless, one may conclude from Fig. 3 and 4 that the overall exchange rate is slightly higher for the Pr-substituted material and, moreover, that the rate generally decreases and becomes more activated under humidified conditions.
The oxygen partial pressure dependence for 5PrLaC is relatively consistent, varying in the range  . For LaC, the data points for the three highest oxygen partial pressures follow an essentially
. For LaC, the data points for the three highest oxygen partial pressures follow an essentially  dependence, whereas the data at 0.005 atm O2 deviate and are lower than expected according to the functional dependence from higher pO2. With the present scatter, there is no distinct difference between the pO2 dependences in both bottle-dry and humidified conditions for the two materials.
dependence, whereas the data at 0.005 atm O2 deviate and are lower than expected according to the functional dependence from higher pO2. With the present scatter, there is no distinct difference between the pO2 dependences in both bottle-dry and humidified conditions for the two materials.
For the temperature dependence of ℜ0 in Fig. 4: firstly, the apparent activation energy decreases when going from undoped to 5% Pr-doped La2Ce2O7. Secondly, the data at 0.005 atm O2 for LaC, which deviate from the “linear” dependence at higher pO2, exhibit lower apparent activation energies than those at higher oxygen partial pressures. Finally, the apparent activation energy measured across the temperature range increases going from bottle-dry to humidified conditions, and particularly so for the Pr-doped material. This is emphasized in Fig. 5, which presents the temperature dependence of ℜ0 at 0.02 atm O2. Notably, the wet data deviate from linear Arrhenius behavior, as the difference in ℜ0 between wet and dry carrier gases gradually diminishes with increasing temperature. For 5PrLaC, the apparent activation energy decreases from approximately 190 to 130 kJ mol−1, whereas it remains essentially constant for LaC (∼150 kJ mol−1).
 | ||
| Fig. 5 Temperature dependence of the overall oxygen surface exchange rates of La2Ce2O7 and La2Ce1.95Pr0.05O7−δ at pO2 = 0.02 atm in dry and wet carrier gases. In both cases, dry pulses were employed. | ||
5. Discussion
Preliminary understanding of the oxygen exchange mechanism may be obtained by visually analyzing the development of the oxygen isotopologues in the PIE profiles (cf.Fig. 1 and 2). Low f34 levels indicate that the scrambling of dissociated oxygen species adsorbed on the surface is sluggish relative to the incorporation of these surface species. In other words, one of the elementary reactions involved in oxygen dissociation limits the overall oxygen exchange.More quantitative approaches involve addressing the pO2 dependence of ℜ0 using chemical kinetics, as different sequences of elementary reactions lead to different dependences on the oxygen partial pressure.63,64 For the Pr-doped material, Fig. 3 shows that 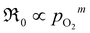 , m ∈ [0.5–1], supporting that the rate-determining step (rds) involves the dissociation of molecular oxygen.21 The behavior of the undoped material is less conclusive due to more scattered data, and even more so, whether or not the data points at 0.005 atm of oxygen are included. Leaving the 0.005 atm dataset out, the oxygen partial pressure dependences are consistently lower (
, m ∈ [0.5–1], supporting that the rate-determining step (rds) involves the dissociation of molecular oxygen.21 The behavior of the undoped material is less conclusive due to more scattered data, and even more so, whether or not the data points at 0.005 atm of oxygen are included. Leaving the 0.005 atm dataset out, the oxygen partial pressure dependences are consistently lower (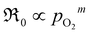 , m ∈ [0.37–0.49]) for LaC compared to the Pr-substituted material, indicating differences in the overall oxygen exchange mechanism.
, m ∈ [0.37–0.49]) for LaC compared to the Pr-substituted material, indicating differences in the overall oxygen exchange mechanism.
Although the 36O2 pulse is dry, there are distinct differences between the detailed effects of reaction conditions on the exchange rates for bottle-dry and wet carrier gases (cf.Fig. 1–5).
Considering commonly applied reaction mechanisms for oxygen exchange on similar ceria-based materials, the adsorption of gaseous oxygen molecules with the transfer of one electronic defect can be denoted as:63,65–67
| O2,g + *↔ O2,ad | (2) |
| O2,ad ↔ O2,ad− + h˙ | (3) |
Whether electrons or electron holes are involved in the elementary reactions other than the rate-determining step does not alter the oxygen partial pressure dependence of the overall exchange rate since these reactions are at quasi equilibrium.63,68–71 For dissociative adsorption, one may differentiate between mechanisms mediated by oxygen vacancies (4-a) and (5-a) and those that are not (4-b) and (5-b):
 | (4-a) |
 | (4-b) |
 | (5-a) |
 | (5-b) |
The reactions are outlined both with electrons from the valence band (formation of holes) and the conduction band in the reactions in eqn (4) and (5), respectively. The adsorbed peroxide species formed during dissociation are incorporated along with the transfer of another electronic defect:
 | (6) |
For the reactions in eqn (2)–(6), * denotes adsorption sites different from  . O2,g and O2,ad represent neutral diatomic oxygen species in the gas-phase and adsorbed on the surface, respectively. O−2,ad and O−ad refer to charged, adsorbed oxygen species, i.e., a superoxide and a peroxide species, respectively.
. O2,g and O2,ad represent neutral diatomic oxygen species in the gas-phase and adsorbed on the surface, respectively. O−2,ad and O−ad refer to charged, adsorbed oxygen species, i.e., a superoxide and a peroxide species, respectively.
For the scheme facilitated by oxygen vacancies, one oxygen species incorporates directly as part of the dissociation. The leftover adsorbed peroxide species formed in the reactions can either be incorporated through the consecutive reaction in eqn (6) or recombine with another adsorbed species and desorb as an oxygen molecule. Despite potential recombination and desorption, oxygen exchange is completed by the direct incorporation of the oxygen species into the oxygen vacancy. Since the incorporation of oxygen takes place simultaneously with dissociation in both eqn (4-a) and (5-a)via oxygen vacancies, parallel to the incorporation in eqn (6), this has been denoted as a parallel-like mechanism in the literature.61,72 The reactions in (4-b) and (5-b) exclusively represent dissociation and must be followed by the incorporation reaction (eqn (6)) to complete the exchange between gas-phase oxygen and oxide ions in the surface sublattice. Accordingly, these reactions imply a serial scheme.72,73
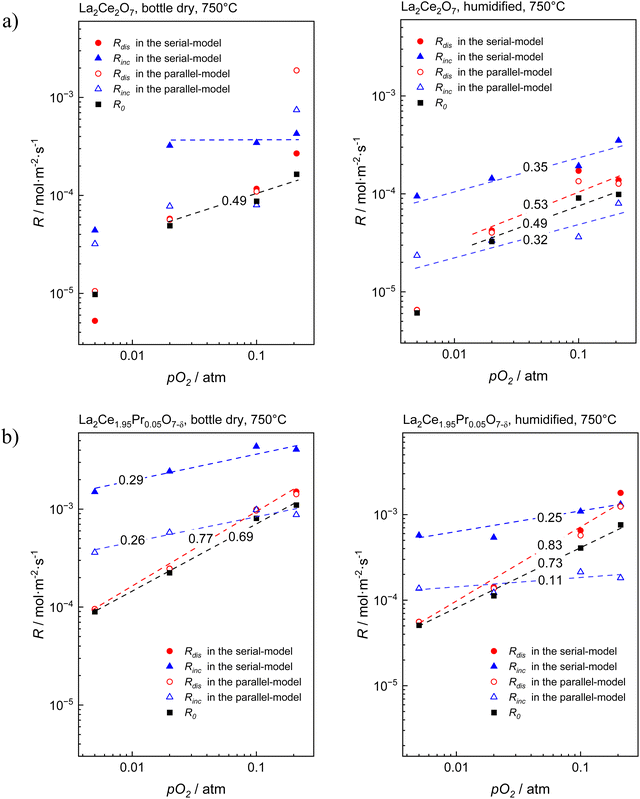
Bouwmeester et al.60,61 have demonstrated that ℜ0 can be deconvoluted into individual pairs of ℜdis and ℜinc from the time dependence of the fractions of oxygen isotopes and isotopologues in the pulse response. The relationship between these rate constants differs for the parallel (eqn (7), with p in superscript for parallel) and serial mechanism (eqn (8), with s in superscript for serial):
 | (7) |
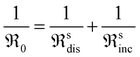 | (8) |
The relative influence of dissociation and incorporation can be illustrated using contour plots, as introduced by den Otter et al.72Fig. 6 displays a contour plot of the ratios between ℜ0 and ℜdis, corresponding to the fraction of the oxygen incorporated (exchanged between the gas-phase and surface) relative to that dissociatively adsorbed according to the serial and parallel models, respectively. 5PrLaC shows a higher fraction of incorporation relative to dissociation than for LaC. Additionally, the presence of water vapor decreases the relative rate of incorporation for both materials.
 | ||
Fig. 6 Contour plot of the ratio of the overall oxygen exchange rate (hetero exchange rate) to the dissociative adsorption rate at 750 °C and 0.02 atm of O2. p1 and p2 are the independent probabilities of each oxygen atom in a dissociated oxygen molecule being incorporated into the oxide. Further derivation and interpretation of the contour plot can be found in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72,74,75 72,74,75 | ||
As shown in Fig. 7 and 8, the temperature and oxygen partial pressure dependences of the rate constants are deconvoluted according to eqn (7) and (8), corresponding to the parallel and serial mechanisms, respectively. The pairs of rate constants exhibit rather similar functional behavior, but their relative contributions to the overall exchange rate vary. For the serial mechanism, the incorporation is generally faster than dissociative adsorption, whereas for the parallel mechanism, the rates are more similar.
 | ||
| Fig. 7 Temperature dependence of the deconvoluted oxygen surface exchange rates in dry and wet carrier gases at pO2 = 0.02 atm, for (a) La2Ce2O7 and (b) La2Ce1.95Pr0.05O7. The entire dataset is presented in the Section S5 (ESI†). | ||
 | ||
| Fig. 8 Oxygen partial pressure dependence of the deconvoluted oxygen surface exchange rates in dry and wet carrier gases for (a) La2Ce2O7 and (b) La2Ce1.95Pr00.05O7. The entire dataset is presented in the Section S5 (ESI†). | ||
The temperature dependences for the dissociation and incorporation display some notable trends. Firstly, the exchange rates are higher for the doped material. Secondly, the apparent activation energy is higher under humidified compared to bottle-dry conditions (cf.Fig. 5). This is most significant for the Pr-substituted material and is also more pronounced for incorporation than for dissociative adsorption. Under bottle-dry conditions, the activation energy for the dissociative adsorption is, generally, higher for LaC compared to for 5PrLaC, a trend that reverses under humidified conditions.
Examples of pO2 dependence on the rate constants are shown in Fig. 8. Overall, the oxygen partial pressure dependence is relatively consistent and corresponds to the behavior expected for dissociative adsorption and incorporation (see also ESI,†Fig. 6 and 7). The dissociation rates largely reflect ℜ0, but with slightly stronger oxygen partial pressure dependences. The individual behavior manifests the differences in the exchange mechanism between the pristine and doped material,  and
and  , respectively. The pO2 dependence of ℜinc is scattered but generally decreases with increasing temperature in the range m ∈ [0, 0.05], becoming essentially invariant at the higher temperatures
, respectively. The pO2 dependence of ℜinc is scattered but generally decreases with increasing temperature in the range m ∈ [0, 0.05], becoming essentially invariant at the higher temperatures  .
.
Generally, dissociative adsorption governs the oxygen exchange for the serial mechanism, as ℜsdis is significantly lower than ℜsinc. Since these values are more similar when deconvoluting of ℜ0 according to the parallel-like mechanism, and the incorporation rate is independent of pO2, ℜpdis eventually surpasses ℜsinc. In other words, reaction (4-a) or (5-a) contributes relatively more than reaction (6) to the overall oxygen incorporation at the highest oxygen partial pressures. Since incorporation is realized as part of the dissociation, oxygen exchange is maintained.
The defect structure of the surface influences the temperature and pO2 dependences of the exchange rate. However, since these surface properties are rarely known, one has to rely on the properties of bulk and evaluate potential deviations from it based on developed theories for space charge layers. Merkle, Maier and coworkers21,76 have discussed potential differences in the defect chemistry between the bulk and the surface, including ceria-based materials, relevant to the present investigation. Based on their findings and other literature reporting negligible surface charges for ceria-based materials, as well as the fact that the La acceptor totally dominates the defect structure of La2Ce2O7, we have assumed, as a first approximation, that the pO2 dependence of the concentration of point defects at the surface corresponds to that of the bulk material. It should, however, be recognized that the surfaces of ceria-based materials tend to be more reduced than the bulk.30
Previous research has demonstrated that the total electrical conductivity of La2Ce2O7 is independent of pO2 under oxidizing conditions, reflecting predominant oxide ion conductivity.38,39,77–79 This behavior was, as adopted herein, rationalized by considering lanthanum cerate as 50% La-substituted CeO2. The doping reaction, wherein La3+ substitutes for Ce4+ and is charge-compensated by formation of oxygen vacancies, can be described as follows:
 | (9) |
The simplified, limiting electroneutrality (bulk) within the present experimental window is thereby given by:
 | (10) |
The pO2 dependence of the minority electronic defect concentration can be determined from the equilibrium constant of the redox reactions:
 | (11) |
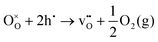 | (12) |
Combined with the limiting electroneutrality conditions in eqn (10), the concentrations of electrons and electron holes are accordingly proportional to  and
and 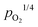 , respectively.
, respectively.
Returning to the elementary reactions, rate expressions for the reactions in eqn (2)–(6) can now be derived. Provided that dissociative adsorption is limiting, the elementary reactions in eqn (2), (3) and (6) reach quasi-equilibrium. As PIE represents tracer measurements, the exchange coefficients derived from the isotope profiles reflect the equilibrium exchange rates, ℜ0, and can be expressed as:80
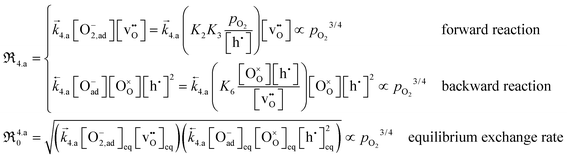 | (13) |
 | (14) |
 | (15) |
 | (16) |
It is apparent from eqn (13) and (14) that if valence band electrons are involved (leading to the formation of holes) in the rate-determining step, it is not possible to distinguish whether oxygen vacancies participate in the dissociation reaction, as both mechanisms result in  . This dependence matches relatively well with the observed pressure dependence of ℜ0 for the Pr-doped material (cf.Fig. 8b), but the deconvoluted experimental data are mostly on the higher side of a 3/4 dependency. There are several possible explanations for the stronger pressure dependence: (i) the defect structure deviates somewhat from that of the bulk, (ii) the first ionization step may be partly constrained, and (iii) if the adsorption and dissociation occur directly at the oxygen vacancy, with the transfer of three electronic species, bypassing the initial adsorption step. Nonetheless, it will be evident later that the influence of humidity points toward the contribution of oxygen vacancies in the rate-determining step.
. This dependence matches relatively well with the observed pressure dependence of ℜ0 for the Pr-doped material (cf.Fig. 8b), but the deconvoluted experimental data are mostly on the higher side of a 3/4 dependency. There are several possible explanations for the stronger pressure dependence: (i) the defect structure deviates somewhat from that of the bulk, (ii) the first ionization step may be partly constrained, and (iii) if the adsorption and dissociation occur directly at the oxygen vacancy, with the transfer of three electronic species, bypassing the initial adsorption step. Nonetheless, it will be evident later that the influence of humidity points toward the contribution of oxygen vacancies in the rate-determining step.
If instead conduction band electrons are involved in the rate-determining step, eqn (15) and (16) show that different pressure dependences emerge for the parallel-like and serial dissociation mechanisms. For the LaC data, ℜdis is proportional to  (cf.Fig. 8a), which corresponds to the dependence expected for the serial mechanism where conduction band electrons are the ionization source of the oxygen species (eqn (16)). Overall, evaluation of the oxygen partial pressure dependences indicates that pristine LaC follows the serial mechanism with conduction band electrons ionizing the oxygen species, whereas for the Pr-doped material, valence band electrons predominate.
(cf.Fig. 8a), which corresponds to the dependence expected for the serial mechanism where conduction band electrons are the ionization source of the oxygen species (eqn (16)). Overall, evaluation of the oxygen partial pressure dependences indicates that pristine LaC follows the serial mechanism with conduction band electrons ionizing the oxygen species, whereas for the Pr-doped material, valence band electrons predominate.
Deviating effects of water vapor on oxygen exchange kinetics have been reported in the literature.81–86 In this respect, it is important to recognize the conceptual differences in the exchange of oxygen between surface oxide ions and (i) the oxide ion in water, and (ii) the oxygen molecules. The former represents an acid–base reaction involving no net transfer of electronic species, while the latter, overall, is a redox reaction. We will now attempt to gain further insight to the exchange mechanism through the effects of humidity on the data.
Since water vapor decreases the oxygen exchange rate and increases the apparent activation energy without significantly changing the dependence on oxygen partial pressure, we infer that hydroxide groups adsorb onto oxygen vacancies, partly blocking the adsorption of oxygen (eqn (4-a) and (5-a)). La2Ce2O7 favorably dissolves hydroxide defects via dissociative adsorption of water into oxygen vacancies,39,44 and the surface of the lanthanum cerate is relatively basic, generally promoting hydration.87 On these bases, we presume that hydroxide groups are relatively strongly bonded to oxygen vacancies during annealing in wet carrier gas and, at least partly, remain adsorbed during the 36O2 pulse, although it is dry. Since hydration of surface oxygen vacancies is exothermic, the concentration of hydroxide defects at the surface decreases with increasing temperature, gradually reducing the effect of humidity on the exchange rate. This is consistent with the diminishing difference between the dry and wet datasets as the temperature rises (cf.Fig. 5), supporting the rationale behind the water effect.
A close evaluation of the effects of humidified conditions reveals that the activation energy of ℜdis for LaC is independent of the level of humidification. In contrast, the activation energy increases for ℜinc for LaC, similarly also for both ℜdis and ℜinc for 5PrLaC (see Fig. 4). Since dissociative adsorption according to the serial mechanism (eqn (4-b) and (5-b)) is the only elementary reaction not involving oxygen vacancies, these findings again support the hypothesis that hydroxide groups block oxygen vacancies. Further, it indirectly supports that the pristine and Pr-substituted La2Ce2O7 follow different exchange mechanisms. Finally, the fact that both ℜdis and ℜinc for 5PrLaC exhibit higher apparent activation energies under humidified compared to bottle-dry conditions, shows that the oxygen exchange for the doped material is facilitated by oxygen vacancies and follows the parallel-like mechanism.
In interpreting the oxygen partial pressure dependence of the faster elementary steps, the reactions are at equilibrium and depend on the concentration of the defects taking part. If we assume that electron holes enter the incorporation step (eqn (6)), then the corresponding reaction rate follows a  dependence; otherwise, if electrons do, the reaction rate will be independent of pO2. Despite scattering, the behaviour of the incorporation data generally reflects this trend (cf.Fig. 8).
dependence; otherwise, if electrons do, the reaction rate will be independent of pO2. Despite scattering, the behaviour of the incorporation data generally reflects this trend (cf.Fig. 8).
So far, we have not directly addressed the effects of Pr substitution, i.e., the overall slightly increased exchange rates and the apparent activation energy decreasing from ∼150 kJ mol−1 to ∼120 kJ mol−1 under dry conditions. Presumably, the bond strength between Pr(III) and oxygen is weaker than for the Ce(IV)-oxygen bond, which would promote the oxygen exchange compared to LaC. Moreover, the addition of Pr(III) will increase the level of acceptor dopants and, consequently, the concentration of oxygen vacancies. However, given the low concentration of Pr, relative to the inherently high oxygen vacancy concentration in lanthanum cerates, we believe that this minute change in composition does not affect the vacancy concentration sufficiently, nor the potential effect of weaker metal–oxygen bonds, enough to account for the changes in ℜ0. Therefore, it is plausible to suggest that the effects of Pr doping are related to its multiple valence states. Similar effects of Pr on the oxygen exchange rate have been observed for other rare-earth substituted ceria materials, scaling with the concentration of Pr.21 The nominal Pr concentration in the present study is below the reported threshold where the formation of continuous Pr impurity bands are suggested to form within the CeO2 bandgap.27,28,88 Nevertheless, the electronic conductivity has been shown to increase significantly for ceria-based materials, even with Pr levels below 5%, indicating that even low Pr concentrations affect the level of electronic defects in ceria-based materials.21 Moreover, Schaube et al.,21 reported an enrichment of Pr at the surface relative to nominal bulk values for Pr-substituted CeO2. Provided that 5PrLaC behaves similarly, we speculate that the Pr concentration at the surface reaches levels where its multiple oxidation states will affect the surface electronic states, to some extent enhancing the overlap with the electronic states of the adsorbate. Overall, this would increase the oxygen exchange rate and decrease its activation energy.26–28
According to the differences in the behaviour of the two materials, the electronic defect responsible for the ionization of the adsorbed oxygen species, indeed, changes from conduction band electrons for pristine lanthanum cerate to valence band electrons for the Pr-doped version. Whether valence band or conduction band electrons ionize the adsorbed oxygen species depends on the overlap between electron band structure of the surface and that of adsorbed oxygen species – more specifically, the position of the adsorbate energy level relative to the conduction and valence band for the surface cations, and, not least, the Fermi level. Thereby, the encountered change in the oxygen exchange mechanism between the two materials may support that the Pr concentration on the surface is enriched compared to the nominal values and sufficient to alter the electronic properties at the surface.
As pointed out earlier, the effect of water on the apparent activation energy is stronger for the Pr-doped material compared to the pristine LaC (cf.Fig. 5). Presumably, this is also related to the Pr3+/Pr4+ couple, and one may speculate whether this effect relates to the balance between hydration and hydrogenation at the surface.
Finally, one should compare the results from the present study with relevant literature. There is significant scatter in the literature data when comparing rates and activation energies of oxygen exchange kinetics; even for identical compositions, exchange rates may vary by orders of magnitude.21 Despite this, it is still useful to compare lanthanum cerates to relevant literature on rare-earth-substituted ceria. Nicollet et al.50 reported that the activation energy increases with increasing concentration of La, with values in the range of 1 eV for La0.1(Ce0.9Pr0.1)0.9O2−δ. This is generally lower than the activation energy determined here for the lanthanum cerates, and the present data consequently supports the claim of Nicollet et al.50 Comparing the data from Schaube et al.21 to the current study for similar compositions and conditions, the oxygen exchange rates and activation energies are in the same ballpark.
6. Conclusion
The oxygen surface exchange mechanism for La2Ce2O7 and La2Ce1.95Pr0.05O7−δ has been investigated using the pulse isotope exchange technique. The exchange is rate-limited by oxygen vacancy-mediated dissociation of adsorbed oxygen species.Water vapor decreases the oxygen exchange rate and increases its apparent activation energy. This behavior reflects preferential, exothermic dissociative adsorption of water, blocking surface oxygen vacancies.
The activation energy is lower, and the exchange rate is higher for 5 mol% Pr-doped La2Ce2O7 compared to that of nominal La2Ce2O7, implying that electronic species introduced by the redox-active Pr ions facilitate the transfer of electronic species during the exchange process.
The effect of water on oxygen exchange is more prominent for 5 mol% Pr-doped La2Ce2O7, indicating that the hydrogenation mediated by the Pr3+/Pr4+ couple at the surface affects the charge transfer process.
Author contributions
Yizhou Shen: writing – original draft, conceptualization, investigation, formal analysis, visualization. Vincent Thoréton: review & editing, supervision. Reidar Haugsrud: writing – review & editing, conceptualization, supervision.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.Acknowledgements
The authors acknowledge the support of the FRINATEK project 262393 “Fundamentals of Surface Kinetics in High Temperature Electrochemistry” (FUSKE) of the Research Council of Norway.References
- Z. Shao and S. M. Haile, Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group, 2010, vol. 3, pp. 255–258 Search PubMed.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS.
- Q. Xu, Z. Guo, L. Xia, Q. He, Z. Li, I. Temitope Bello, K. Zheng and M. Ni, Energy Convers. Manag., 2022, 253, 115175 CrossRef CAS.
- E. P. Murray, T. Tsai and S. A. Barnett, Nature, 1999, 400, 649–651 CrossRef CAS.
- W. C. Chueh, A. H. McDaniel, M. E. Grass, Y. Hao, N. Jabeen, Z. Liu, S. M. Haile, K. F. McCarty, H. Bluhm and F. El Gabaly, Chem. Mater., 2012, 24, 1876–1882 CrossRef CAS.
- R. Schmitt, A. Nenning, O. Kraynis, R. Korobko, A. I. Frenkel, I. Lubomirsky, S. M. Haile and J. L. M. Rupp, Chem. Soc. Rev., 2020, 49, 554–592 Search PubMed.
- H. Inaba and H. Tagawa, Solid State Ionics, 1996, 83, 1–16 Search PubMed.
- C. Sánchez-Bautista, A. J. Dos Santos-García, J. Peña-Martínez and J. Canales-Vázquez, Solid State Ionics, 2010, 181, 1665–1673 CrossRef.
- B. Matović, M. Stojmenović, J. Pantić, A. Varela, M. Žunić, N. Jiraborvornpongsa and T. Yano, J. Asian Ceram. Soc., 2014, 2, 117–122 CrossRef.
- P. Shuk and M. Greenblatt, Solid State Ionics, 1999, 116, 217–223 CrossRef CAS.
- L. Li, G. Li, Y. Che and W. Su, Chem. Mater., 2000, 12, 2567–2574 CrossRef CAS.
- M. A. Małecka, L. Kepiński and M. Maczka, J. Solid State Chem., 2008, 181, 2306–2312 CrossRef.
- W. Miśta, M. A. Małecka and L. Kepiński, Appl. Catal., A, 2009, 368, 71–78 CrossRef.
- V. Grover, A. Banerji, P. Sengupta and A. K. Tyagi, J. Solid State Chem., 2008, 181, 1930–1935 CrossRef CAS.
- B. Zachau-Christiansen, ECS Proc. Vol., 1993, 1993–4, 104–111 CrossRef.
- M. Melchionna and P. Fornasiero, Mater. Today, 2014, 17, 349–357 CrossRef CAS.
- T. Montini, M. Melchionna, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116, 5987–6041 CrossRef CAS PubMed.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63–94 CrossRef CAS.
- V. V. Kharton, F. M. Figueiredo, L. Navarro, E. N. Naumovich, A. V. Kovalevsky, A. A. Yaremchenko, A. P. Viskup, A. Carneiro, F. M. B. Marques and J. R. Frade, J. Mater. Sci., 2001, 36, 1105–1117 CrossRef CAS.
- A. Bueno-López, K. Krishna, M. Makkee and J. A. Moulijn, J. Catal., 2005, 230, 237–248 CrossRef.
- M. Schaube, R. Merkle and J. Maier, J. Mater. Chem. A, 2019, 7, 21854–21866 CAS.
- L. Li, X. Lin, G. Li and H. Inomata, J. Mater. Res., 2001, 16, 3207–3213 CrossRef CAS.
- E. Ruiz-Trejo, J. D. Sirman, Y. M. Baikov and J. A. Kilner, Solid State Ionics, 1998, 113–115, 565–569 CAS.
- Z. Zhan, T.-L. Wen, H. Tu and Z.-Y. Lu, J. Electrochem. Soc., 2001, 148, A427 Search PubMed.
- S. A. Acharya, J. Power Sources, 2012, 198, 105–111 CrossRef CAS.
- J. J. Kim, S. R. Bishop, D. Chen and H. L. Tuller, Chem. Mater., 2017, 29, 1999–2007 CrossRef CAS.
- S. R. Bishop, T. S. Stefanik and H. L. Tuller, Phys. Chem. Chem. Phys., 2011, 13, 10165–10173 RSC.
- S. R. Bishop, T. S. Stefanik and H. L. Tuller, J. Mater. Res., 2012, 27, 2009–2016 CrossRef CAS.
- D. Chen, S. R. Bishop and H. L. Tuller, J. Electroceram., 2012, 28, 62–69 CrossRef CAS.
- Q. Lu, G. Vardar, M. Jansen, S. R. Bishop, I. Waluyo, H. L. Tuller and B. Yildiz, Chem. Mater., 2018, 30, 2600–2606 CAS.
- P. S. Manning, J. D. Sirman and J. A. Kilner, Solid State Ionics, 1996, 93, 125–132 CAS.
- K. Kowalski, Defect Diffus. Forum, 2009, 289–292, 769–774 CAS.
- S. P. Waldow, B. J. Statham, H. F. Wardenga, T. E. Weirich, A. Klein and R. A. De Souza, ACS Appl. Mater. Interfaces, 2020, 12, 36768–36777 CAS.
- E. Reynolds, P. E. R. Blanchard, Q. Zhou, B. J. Kennedy, Z. Zhang and L. Y. Jang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(13), 132101 CrossRef.
- L. E. Kalland, S. T. Norberg, J. Kyrklund, S. Hull, S. G. Eriksson, T. Norby, C. E. Mohn and C. S. Knee, Phys. Chem. Chem. Phys., 2016, 18, 24070–24080 RSC.
- H. Yamamura, H. Nishino, K. Kakinuma and K. Nomura, J. Ceram. Soc. Jpn., 2003, 111(1300), 902–906 CrossRef CAS.
- F. J. Trindade, S. Damasceno, L. Otubo, M. R. Felez, D. Z. De Florio, F. C. Fonseca and A. S. Ferlauto, ACS Appl. Nano Mater., 2022, 5, 8859–8867 CrossRef CAS.
- S. A. Ismail, L. Jiang, P. Zhong, T. Norby and D. Han, J. Alloys Compd., 2022, 899, 163306 CrossRef CAS.
- V. Besikiotis, C. S. Knee, I. Ahmed, R. Haugsrud and T. Norby, Solid State Ionics, 2012, 228, 1–7 CrossRef CAS.
- B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CAS.
- L. Yan, W. Sun, L. Bi, S. Fang, Z. Tao and W. Liu, Int. J. Hydrogen Energy, 2010, 35, 4508–4511 CrossRef CAS.
- W. Sun, S. Fang, L. Yan and W. Liu, Fuel Cells, 2012, 12, 457–463 CrossRef CAS.
- Z. Zhu, B. Liu, J. Shen, Y. Lou and Y. Ji, J. Alloys Compd., 2016, 659, 232–239 CrossRef CAS.
- L. E. Kalland, A. Løken, T. S. Bjørheim, R. Haugsrud and T. Norby, Solid State Ionics, 2020, 354, 115401 CrossRef CAS.
- Y. Ling, J. Chen, Z. Wang, C. Xia, R. Peng and Y. Lu, Int. J. Hydrogen Energy, 2013, 38, 7430–7437 CrossRef CAS.
- J. De Wang, Y. H. Xie, Z. F. Zhang, R. Q. Liu and Z. J. Li, Mater. Res. Bull., 2005, 40, 1294–1302 CrossRef.
- Y. Zhang, J. Xu, X. Xu, R. Xi, Y. Liu, X. Fang and X. Wang, Catal. Today, 2020, 355, 518–528 CrossRef CAS.
- C. Madhuri, K. Venkataramana, A. Nurhayati and C. V. Reddy, Curr. Appl. Phys., 2018, 18, 1134–1142 Search PubMed.
- A. Kalpana Devi, G. Ram Kumar, C. Prerna, K. Amarsingh Bhabu, V. Sabarinathan and T. R. Rajasekaran, J. Mater. Sci.: Mater. Electron., 2020, 31, 10628–10638 CrossRef CAS.
- C. Nicollet, D. Kalaev and H. L. Tuller, Solid State Ionics, 2019, 331, 96–101 CrossRef CAS.
- W. C. Jung and H. L. Tuller, Adv. Energy Mater., 2011, 1, 1184–1191 CrossRef CAS.
- J. A. Kilner, Solid State Ionics, 2000, 129, 13–23 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Phys. – Adv. Res. Appl., 1956, 3, 307–435 Search PubMed.
- C. B. Gopal and S. M. Haile, J. Mater. Chem. A, 2014, 2, 2405–2417 RSC.
- Z. Li, T. Norby and R. Haugsrud, J. Am. Ceram. Soc., 2012, 95, 2065–2073 CrossRef CAS.
- J. A. Kilner, B. C. H. Steele and L. Ilkov, Solid State Ionics, 1984, 12, 89–97 CrossRef CAS.
- R. J. Chater, S. Carter, J. A. Kilner and B. C. H. Steele, Solid State Ionics, 1992, 53–56, 859–867 CrossRef CAS.
- M. V. Ananyev, E. S. Tropin, V. A. Eremin, A. S. Farlenkov, A. S. Smirnov, A. A. Kolchugin, N. M. Porotnikova, A. V. Khodimchuk, A. V. Berenov and E. K. Kurumchin, Phys. Chem. Chem. Phys., 2016, 18, 9102–9111 RSC.
- Z. Li, R. Haugsrud and T. Norby, Solid State Ionics, 2011, 184, 42–46 CrossRef CAS.
- H. J. M. Bouwmeester, C. Song, J. Zhu, J. Yi, M. Van Sint Annaland and B. A. Boukamp, Phys. Chem. Chem. Phys., 2009, 11, 9640–9643 RSC.
- C. Y. Yoo and H. J. M. Bouwmeester, Phys. Chem. Chem. Phys., 2012, 14, 11759–11765 RSC.
- C. L. Song, J. X. Yi and Y. Yan, Chinese J. Chem. Phys., 2019, 32, 474–484 CrossRef CAS.
- R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2002, 4, 4140–4148 RSC.
- R. A. De Souza, Phys. Chem. Chem. Phys., 2006, 8, 890–897 RSC.
- Y. M. Choi, H. Abernathy, H. T. Chen, M. C. Lin and M. Liu, Chem. Phys. Chem., 2006, 7, 1957–1963 CrossRef CAS.
- C. Yang, X. Yu, S. Heißler, P. G. Weidler, A. Nefedov, Y. Wang, C. Wöll, T. Kropp, J. Paier and J. Sauer, Angew. Chem., Int. Ed., 2017, 56, 16399–16404 CrossRef CAS.
- Z. Wu, M. Li, J. Howe, H. M. Meyer and S. H. Overbury, Langmuir, 2010, 26, 16595–16606 CrossRef CAS.
- R. Merkle, M. F. Hoedl, G. Raimondi, R. Zohourian and J. Maier, Annu. Rev. Mater. Res., 2021, 51, 461–493 CrossRef CAS.
- L. Wang, R. Merkle, Y. A. Mastrikov, E. A. Kotomin and J. Maier, J. Mater. Res., 2012, 27, 2000–2008 CrossRef CAS.
- M. M. Kuklja, E. A. Kotomin, R. Merkle, Y. A. Mastrikov and J. Maier, Phys. Chem. Chem. Phys., 2013, 15, 5443–5471 RSC.
- Z. Guan, D. Chen and W. C. Chueh, Phys. Chem. Chem. Phys., 2017, 19, 23414–23424 RSC.
- M. W. Den Otter, B. A. Boukamp and H. J. M. Bouwmeester, Solid State Ionics, 2001, 139, 89–94 CrossRef CAS.
- H. J. M. B. and A. J. B. B. A. Boukamp, in Proceedings of the Second International Symposium on Ionic and Mixed Conducting Ceramics, ed. W. L. W. and H. L. T. T. A. Ramanarayanan, The Electrochemical Society, 1994, p. 141.
- K. Klier, J. Novakova and P. Jiru, J. Catal., 1963, 484, 479–484 CrossRef.
- G. K. Boreskov and V. S. Muzykantov, Ann. N. Y. Acad. Sci., 1973, 213, 137–170 CrossRef CAS PubMed.
- D. Poetzsch, R. Merkle and J. Maier, Adv. Funct. Mater., 2015, 25, 1542–1557 CrossRef CAS.
- E. Suda, B. Pacaud and M. Mori, J. Alloys Compd., 2006, 408–412, 1161–1164 CrossRef CAS.
- H. Tinwala, P. Shah, K. Siddhapara, D. Shah and J. Menghani, J. Cryst. Growth, 2016, 452, 54–56 CrossRef CAS.
- K. Sandhya, N. S. Chitrapriya, P. K. Aswathy and D. N. Rajendran, Mater. Today: Proc., 2019, 10, 112–120 CAS.
- J. Maier, Solid State Ionics, 1998, 112, 197–228 CrossRef CAS.
- R. A. De Souza, J. Mater. Chem. A, 2017, 5, 20334–20350 RSC.
- S. J. Cooper, M. Niania, F. Hoffmann and J. A. Kilner, Phys. Chem. Chem. Phys., 2017, 19, 12199–12205 RSC.
- M. J. Pietrowski, R. A. De Souza, M. Fartmann, R. Ter Veen and M. Martin, Fuel Cells, 2013, 13, 673–681 CrossRef CAS.
- M. Molinari, S. C. Parker, D. C. Sayle and M. S. Islam, J. Phys. Chem. C, 2012, 116, 7073–7082 CrossRef CAS.
- N. Sakai, K. Yamaji, T. Horita, H. Kishimoto, Y. P. Xiong and H. Yokokawa, Phys. Chem. Chem. Phys., 2003, 5, 2253–2256 RSC.
- N. Sakai, K. Yamaji, T. Horita, Y. P. Xiong, H. Kishimoto and H. Yokokawa, J. Electrochem. Soc., 2003, 150, A689 CrossRef CAS.
- T. Norby, M. Widerøe, R. Glöckner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC.
- H. L. Tuller and A. S. Nowick, J. Phys. Chem. Solids, 1977, 38, 859–867 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00840e |
| This journal is © The Royal Society of Chemistry 2025 |