Open Access Article
Open Access ArticleSubstitution-induced changes in the structure, vibrational, and magnetic properties of BiFeO3
I.
Kallel
a,
Z.
Abdelkafi
 *a,
N.
Abdelmoula
a,
H.
Khemakhem
a,
N.
Randrianantoandro
b and
E. K.
Hlil
c
*a,
N.
Abdelmoula
a,
H.
Khemakhem
a,
N.
Randrianantoandro
b and
E. K.
Hlil
c
aLaboratory of Multifunctional Materials and Applications (LaMMA), LR16ES18, Faculty of Sciences of Sfax, University of Sfax, B.P. 1171, 3000 Sfax, Tunisia. E-mail: zied_abdelkafi@yahoo.fr
bInstitut des Molécules et Matériaux du Mans – UMR 6283, CNRS – Le Mans Université, Avenue Olivier Messaien, Le Mans 72085, France
cInstitut Néel, Université Grenoble Alpes, CNRS, BP 166, F-38042 Grenoble cedex 9, France
First published on 19th June 2025
Abstract
To address practical progress and prospective applications of BiFeO3, particularly in the development of data storage devices, we substituted it with the perovskite BaTi0.9Zr0.1O3 to form the system (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3, limiting x to the range of 0–0.4. We prepared these compositions using the solid-state reaction method, highlighting the correlation between their structure, vibrational properties, and magnetic response. X-ray diffraction and Raman scattering spectra reveal the structural transition from the R3c rhombohedral to Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic with increasing the content of BaTi0.9Zr0.1O3. Mössbauer spectroscopy investigation indicates that the substitution of Fe3+ ions with Ti4+ and Zr4+ weakens the Dzyaloshinskii–Moriya (DM) interaction. Thus, the DM interaction becomes subordinate to the exchange interaction in the G-type antiferromagnetic order of Fe3+ ions within the BFO structure, potentially suppressing the cycloidal spin configuration in the samples x = 0.1, 0.2, and 0.3. The mean hyperfine magnetic fields decreased with the increasing (x) of BaTi0.9Zr0.1O3, and a paramagnetic phase was observed for x = 0.4. The decrease of quadrupole splitting/shift (ΔEQ/2ε) for x = 0.1, 0.2, and 0.3 indicates a transition toward a higher-symmetry environment around Fe3+ due to the substitution. This result proves the structural transition from the R3c rhombohedral to Pm
m cubic with increasing the content of BaTi0.9Zr0.1O3. Mössbauer spectroscopy investigation indicates that the substitution of Fe3+ ions with Ti4+ and Zr4+ weakens the Dzyaloshinskii–Moriya (DM) interaction. Thus, the DM interaction becomes subordinate to the exchange interaction in the G-type antiferromagnetic order of Fe3+ ions within the BFO structure, potentially suppressing the cycloidal spin configuration in the samples x = 0.1, 0.2, and 0.3. The mean hyperfine magnetic fields decreased with the increasing (x) of BaTi0.9Zr0.1O3, and a paramagnetic phase was observed for x = 0.4. The decrease of quadrupole splitting/shift (ΔEQ/2ε) for x = 0.1, 0.2, and 0.3 indicates a transition toward a higher-symmetry environment around Fe3+ due to the substitution. This result proves the structural transition from the R3c rhombohedral to Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic observed by X-ray diffraction and Raman spectroscopy as the content of BaTi0.9Zr0.1O3 increases. Using Rietveld refinement data of X-ray diffraction, the calculation of the tilt angle (ω) reveals a decrease in the level of the rhombohedral structure. For compositions exceeding x = 0.1, the decrease in ω with the substitution rate leads to a reduction in remanent magnetization. However, the enhancement of remanent magnetization (Mr ∼ 0.34 emu g−1) was observed for x = 0.1. Moreover, hysteresis loops for the compositions x = 0.1 and 0.2 exhibit smaller field coercivity at 2 K compared to 300 K, which could identify the presence of magnetoelectric coupling in this system.
m cubic observed by X-ray diffraction and Raman spectroscopy as the content of BaTi0.9Zr0.1O3 increases. Using Rietveld refinement data of X-ray diffraction, the calculation of the tilt angle (ω) reveals a decrease in the level of the rhombohedral structure. For compositions exceeding x = 0.1, the decrease in ω with the substitution rate leads to a reduction in remanent magnetization. However, the enhancement of remanent magnetization (Mr ∼ 0.34 emu g−1) was observed for x = 0.1. Moreover, hysteresis loops for the compositions x = 0.1 and 0.2 exhibit smaller field coercivity at 2 K compared to 300 K, which could identify the presence of magnetoelectric coupling in this system.
1. Introduction
The domain of magnetoelectric multiferroics continues to attract significant interest due to the coupling of ferroelectric and magnetic order characteristics, considering the potential applications in a range of multifunctional areas such as high energy-storage performance,1 data storage2 and neuromorphic computing.3 One of the most extensively researched multiferroics, bismuth ferrite BiFeO3 (BFO), bears both magnetic and ferroelectric properties at room temperature (RT), with high Néel (TN ∼ 630 K) and Curie (TC ∼ 1100 K) temperatures.4 It presents a significant polarization of about 100 μC cm−2 (ref. 5) resulting from the displacement of Fe and Bi atoms.6 Neutron diffraction studies prove a negative magnetostriction that reduces the spontaneous polarization caused by the suppressed displacement of Fe below TN.7The structure of BFO was classified as rhombohedral distorted perovskite, which is affiliated with the R3c space group. This structure is typified by ionic displacements from centrosymmetric position and antiphase tilt of octahedral FeO6 (a−a−a− in Glazer notation), which occurs across the same direction [001].8 Besides, the magnetic structure of BFO is G-type antiferromagnetic, with all six nearest magnetic neighbors oriented antiferromagnetically, which exhibits a superimposed spin cycloid with an incommensurate period of 62 nm.9 As a result, weak ferromagnetism arises from the Dzyaloshinskii–Moriya interaction, which averages to zero in the bulk of BFO.10,11 This state has a negative impact on the observation of the linear magnetoelectric effect,10–12 hindering its potential use in devices. Several attempts have been made to suppress the cycloid by using different techniques in order to recover a nonzero macroscopic magnetization as well as the linear magnetoelectric effect.13–18 A high magnetic field has been used to destroy the cycloidal spin structure, causing a transition from the cycloidal modulated spin structure to a homogeneous G-type antiferromagnetic structure.17 Similarly, the thin film BFO induces the destruction of the spin cycloid due to the epitaxial strain.18 Several efforts have been made to improve the magnetization in BFO, mostly focusing on the potential of chemical substitution to release a weak remanent magnetization of BFO, typically within the range of Mr ∼ 0.1 to 0.3 emu g−1.13–16 The origin of weak magnetization in the compound (Bi0.8La0.2)(Fe,Ga)O3-43%PbTiO313 was explained by the Landau–Ginzburg theory,17 in which an energy perturbation is sufficient to make a transition from a cycloidal spin structure to a homogenous one. Based on this theory, Park et al.19 have shown that the (1 − x)BaTiO3-xBiFeO3 solid solution nanostructures exhibit magnetoelectric characteristics, leading to a decrease in coercive field (Hc) at low temperatures relative to RT. In the same work, a high value of remanent magnetization (Mr ∼ 0.75 emu g−1) was observed for the composition x = 0.2. In addition, in the work of A. Singh16 on the (1 − x)BiFeO3-xBaTiO3 ceramics, an evolution of remanent magnetization was observed. Notably, a significant remanent magnetization of 0.16 emu g−1 was detected for the composition x = 0.2. To the best of our knowledge, there have been no previous reports on the solid solution (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3, specifically examining structural, vibrational and magnetic proprieties.
In our recent work, BaZr0.1Ti0.9O3 substituted BFO was studied, particularly for x = 0.1.20 In this study, we have shown that the coupling between hyperfine field (Hhf) and polarization (P) (calculated from Rietveld refined atomic) occurs via magnetoelastic coupling within the lattice. Moreover, we have demonstrated that the evolution of Hhf as a function of P below TN exhibits a linear trend, and the magnetoelectric coupling coefficient value (αME) is around 1.84 × 10−9 s m−1. In this present work, we aim to extend this study by increasing the substitution rate in the (1 − x)BiFeO3-xBaZr0.1Ti0.9O3 system. Thus, the substitution rates of interest in this work are x = 0, x = 0.1, x = 0.2, x = 0.3 and x = 0.4. In light of earlier research, we propose a coherent mechanism to reach a comprehensive correlation between crystalline structural distortion, vibrational band, and magnetic properties within this system.
2. Experimental procedure
The system (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3 within the range of 0 ≤ x ≤ 0.4 was synthesized via solid-state reaction. The chemical equation for the synthesis of these samples is the following:BaCO3, TiO2, ZrO2, Bi2O3, and Fe2O3 were used as starting reagents. These powders were accurately weighed in stoichiometric ratios and mixed thoroughly in an agate mortar for 1 hour. The resulting mixture was rapidly calcined at temperatures of 873 K, 973 K, and 1103 K for 1 hour in air, with intermediate grindings for 1 hour. After calcination, the powders were mixed for another hour and pressed under 100 MPa into pellets with dimensions of 8 mm in diameter and approximately 1.5 mm in thickness. These pellets were then sintered in air for 2 hours at 1223 K. A ceramic BFO sample was synthesized following the solid-state technique reported by Achenbach et al.21 The X-ray diffraction (XRD) measurements were carried out with an EMPYREAN X-ray diffractometer using Cu-Kα1,2 radiations (λ1 = 1.5406 Å, λ2 = 1.544 Å). Structural analyses were performed via powder XRD, using an 18 KW Cu-rotating anode. The microstructural analysis was conducted using a JEOL JSM 6510 LV scanning electron microscope (SEM) with an X-Max N20 detector. The SEM-energy dispersive spectroscopy (SEM-EDS) mapping was performed using Zeiss GeminiSEM 560 equipped with a field emission gun (FEG) and an Oxford Instruments energy-dispersive X-ray spectroscopy (EDS) detector. Raman spectra were recorded at RT in the spectral range of 50 to 700 cm−1 in a micro-Raman spectrometer (LABRAM HR-800), working in a backscattering configuration, equipped with an Argon Ion Laser line, at 514.5 nm. 57Fe Mössbauer spectra were displayed in transmission geometry with a constant acceleration spectrometer, via a 57Co source diffused in a rhodium matrix. Isomer shift values were referenced to α-Fe. Mössbauer experiments were carried out in transmission geometry at RT. The samples were placed in a furnace under vacuum. Mössbauer data were analyzed using the MOSFIT program,22 which permits the use of a distribution of hyperfine structures as components of the spectrum. M–H hysteresis loops were recorded at RT using a SQUID Quantum Design magnetometer.
3. Results and discussion
3.1. X-Ray diffraction studies
To examine the structural transition in the solid solution, we performed an X-ray diffraction (XRD) study of the (1 − x)BiFeO3-xBaTi0.9Zr0.1O3 system in the range 0 ≤ x ≤ 0.4. Fig. 1 illustrates the evolution of X-ray diffraction for all compositions. From this figure, the observed high-intensity peaks confirm the phase purity and good crystalline nature of all the synthesized ceramics, without any detected phase parasites except for a slight impurity (Bi25FeO39) in BFO marked with an asterisk (*) in the corresponding figure. We notice from Fig. 2 that both peaks (104) and (110) emerge into a single peak (110), accompanied by the fusion of peaks (006) and (202) into a single peak (111) as the substitution rate increases from x = 0 to x = 0.4. Similarly, within the range of 65° < 2θ < 68°, we observe the disappearance of the peak (208) as x evolves. All these observations indicate a significant transformation in the profile structure from rhombohedral to the cubic with the substitution content. Additionally, Fig. 3 reveals the progressive disappearance of the peak superlattice reflection (113) as x increases. This peak results from antiphase rotation of oxygen octahedra about the [001] axis. All these features confirm that the rhombohedral structure with R3c space group is the stable phase of (1 − x)BiFeO3-xBaTi0.9Zr0.1O3 only for x values ranging from 0 to 0.2.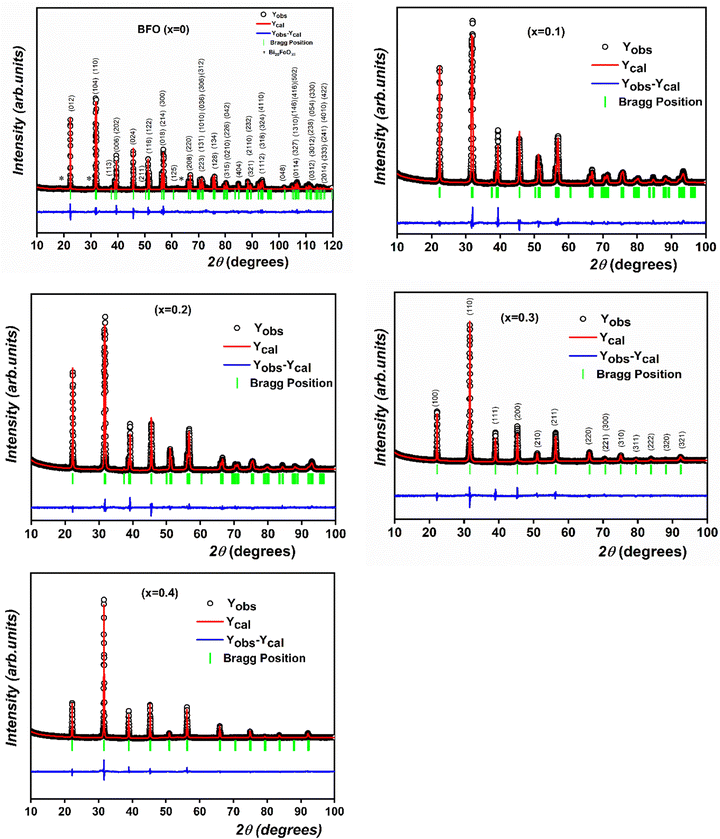 | ||
| Fig. 1 The observed, calculated and difference Rietveld's refinement for XRD patterns of (1 − x)BiFeO3-xBaTi0.9Zr0.1O3 system in the range 0 ≤ x ≤ 0.4. | ||
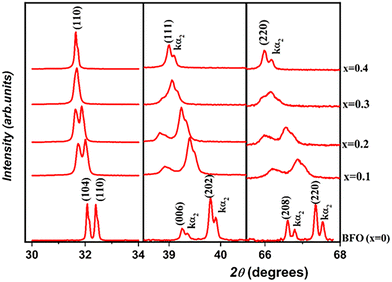 | ||
| Fig. 2 Evolution of (104), (110), (006), (202), (208) and (220) peaks as a function of substitution rate (0 ≤ x ≤ 0.4). | ||
To further analyze the XRD data, Rietveld refinement of the patterns of all prepared compositions was performed using the FullProf program.23 The observed, calculated and the difference refined XRD patterns of compositions with x = 0, 0.1, 0.2, 0.3 and 0.4 are illustrated in Fig. 1. The results of the Rietveld refinement are summarized in Table 1. All peaks were indexed to the noncentrosymmetric distorted rhombohedral structure with R3c space for compositions 0 ≤ x ≤ 0.2, whereas the compositions 0.2 < x ≤ 0.4 are indexed with the centrosymmetric cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space. As illustrative examples, Fig. 1 displays the XRD pattern of BFO indexed to the R3c space group, whereas the pattern for the composition x = 0.3 is indexed to the Pm
m space. As illustrative examples, Fig. 1 displays the XRD pattern of BFO indexed to the R3c space group, whereas the pattern for the composition x = 0.3 is indexed to the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.
m space group.
| x | 0 | 0.10 | 0.20 | 0.30 | 0.40 |
|---|---|---|---|---|---|
| Space group | R3c |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|||
| a = b ≠ c, α = β = 90°, γ = 120° | a = b = c, α = β = γ =90° | ||||
| a (Å) | 5.58397(5) | 5.59783(12) | 5.61909(12) | 3.99914(14) | 4.00505(9) |
| c (Å) | 13.88305(15) | 13.8859(4) | 13.9156(3) | — | — |
| Bi/Ba (z) | 0.2951(8) | 0.2938(5) | 0.2883(4) | 0 | 0 |
| Fe/Ti/Zr (x = y) | 0 | 0 | 0 | 0.5 | 0.5 |
| Fe/Ti/Zr (z) | 0.0162(9) | 0.0175(5) | 0.0145(5) | 0.5 | 0.5 |
| O (x) | 0.233(2) | 0.2267(15) | 0.2173(15) | 0.5 | 0.5 |
| O (y) | 0.343(2) | 0.3437(13) | 0.3445(12) | 0.5 | 0.5 |
| O (z) | 1/12 | 1/12 | 1/12 | 0 | 0 |
| Fe–O–Fe (deg) | 157.0(7) | 158.2(4) | 161.7(4) | 180 | 180 |
| ω (deg) | 12.03(57) | 10.758(39) | 8.870(41) | — | — |
| Polarization P (μC cm−2) | 61.72(26) | 55.89(15) | 50.30(14) | — | — |
| R wp (%) | 19.8 | 11.4 | 11.0 | 17.1 | 16.1 |
| χ 2 | 4.78 | 3.85 | 2.81 | 3.78 | 3.13 |
In order to compare the variation of unit cell parameters with compositions (x) of the two phases, we have calculated equivalent elementary perovskite cell parameters from the refined hexagonal c and a parameters using the following relationships24 and
and  for the rhombohedral phase. The evolution of the elementary perovskite cell parameters as a function of compositions (x) is shown in Fig. 4a and the ratio c/a is depicted in Fig. 4b. From Fig. 4a, a remarkable variation of the parameters with substitution rate (x) is observed. This variation is attributed to the disparate ionic radii, either at site A (Bi3+ (1.17 Å)/Ba2+ (1.42 Å)) or at site B (Fe3+ (0.645 Å)/Ti4+ (0.605 Å)/Zr4+ (0.72 Å)) resulting in lattice distortion. Furthermore, the parameter c shows a clear change up to x = 0.2, revealing the occurrence of a phase transition. On the other hand, from Fig. 4b, the c/a ratio demonstrates a systematic decrease with increasing x until it reaches the value of 1 for compositions with x = 0.3 and 0.4, indicating the reduction in lattice distortion from rhombohedral to cubic structure. This distortion necessarily impacts the Wyckoff positions of atoms in the (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3 system. In our structural study, Bi3+/Ba2+ and Fe3+/Ti4+/Zr4+ ions are positioned at the 6(a) Wyckoff site while O2− ions reside at the 18(b) sites for compositions with the space group R3c. Following the approach outlined by Megaw et al.,24 the coordinates of all atoms within the asymmetric unit cell of the R3c space group can be expressed as functions of displacement parameters s, t, d, and e. These parameters are represented in the Wyckoff positions as: Bi3+/Ba2+ (0, 0, 1/4 + s), Fe3+/Ti4+/Zr4+ (0, 0, t), and O2− (1/6 − 2e − 2d, 1/3 − 4d, 1/12). In the cubic phase associated with the Pm
for the rhombohedral phase. The evolution of the elementary perovskite cell parameters as a function of compositions (x) is shown in Fig. 4a and the ratio c/a is depicted in Fig. 4b. From Fig. 4a, a remarkable variation of the parameters with substitution rate (x) is observed. This variation is attributed to the disparate ionic radii, either at site A (Bi3+ (1.17 Å)/Ba2+ (1.42 Å)) or at site B (Fe3+ (0.645 Å)/Ti4+ (0.605 Å)/Zr4+ (0.72 Å)) resulting in lattice distortion. Furthermore, the parameter c shows a clear change up to x = 0.2, revealing the occurrence of a phase transition. On the other hand, from Fig. 4b, the c/a ratio demonstrates a systematic decrease with increasing x until it reaches the value of 1 for compositions with x = 0.3 and 0.4, indicating the reduction in lattice distortion from rhombohedral to cubic structure. This distortion necessarily impacts the Wyckoff positions of atoms in the (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3 system. In our structural study, Bi3+/Ba2+ and Fe3+/Ti4+/Zr4+ ions are positioned at the 6(a) Wyckoff site while O2− ions reside at the 18(b) sites for compositions with the space group R3c. Following the approach outlined by Megaw et al.,24 the coordinates of all atoms within the asymmetric unit cell of the R3c space group can be expressed as functions of displacement parameters s, t, d, and e. These parameters are represented in the Wyckoff positions as: Bi3+/Ba2+ (0, 0, 1/4 + s), Fe3+/Ti4+/Zr4+ (0, 0, t), and O2− (1/6 − 2e − 2d, 1/3 − 4d, 1/12). In the cubic phase associated with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, the Bi3+/Ba2+ ions are situated at the 1(a) site (0, 0, 0), Fe3+/Ti4+/Zr4+ ions occupy the 1(b) site (1/2, 1/2, 1/2), and O2− ions are located at the 3(c) sites (1/2, 1/2, 0). In the event of local disorder within the structure, the cations and anions may also be present at alternative Wyckoff sites. Therefore, the determination of Wyckoff positions allows us to deduce the antiphase rotation (tilt, (ω)) as well as the lattice-scale polarization (P).
m space group, the Bi3+/Ba2+ ions are situated at the 1(a) site (0, 0, 0), Fe3+/Ti4+/Zr4+ ions occupy the 1(b) site (1/2, 1/2, 1/2), and O2− ions are located at the 3(c) sites (1/2, 1/2, 0). In the event of local disorder within the structure, the cations and anions may also be present at alternative Wyckoff sites. Therefore, the determination of Wyckoff positions allows us to deduce the antiphase rotation (tilt, (ω)) as well as the lattice-scale polarization (P).
 | ||
| Fig. 4 (a) Variation in unit cell parameters for compositions 0 ≤ x ≤ 0.4. (b) The evolution of ratio (c/a) as a function of x. | ||
The configuration of the antiphase rotation (tilt, (ω)) of the adjacent FeO6 oxygen octahedra around the [001] direction is achieved in the R3c space group (a−a−a− in Glazer's notations) as observed in the rhombohedrally distorted perovskite of BFO.8 However, this configuration is not present in the cubic case with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (a0a0a0 in Glazer's notations). In this case, the calculation of ω is based on the following relation:24
m space group (a0a0a0 in Glazer's notations). In this case, the calculation of ω is based on the following relation:24
| ω = tan−1(4e31/2) | (1) |
On the other hand, the lattice-scale polarization (P) can be calculated from the displacement of both Fe3+/Ti4+/Zr4+ (tc) and Bi3+/Ba2+ (sc) cations from their centrosymmetric position along the direction [001] for the noncentrosymmetric rhombohedral structure. The polarization is then determined by evaluating the displacement c(s − t).6 The calculated polarizations are summarized in Table 1. We notice that the calculated polarization is reduced with BaZr0.1Ti0.9O3 substitution until x = 0.2. Thus, we can point out the role of the stereochemical activity of the Bi lone electron pair that leads to the ferroelectric order.
3.2. Microstructural studies
The surface morphology and microstructure of samples x = 0.1, x = 0.2, x = 0.3, and x = 0.4 were analyzed using scanning electron microscopy (SEM). The SEM surface micrographs of these samples, as depicted in Fig. 5, show a dense morphology with few voids. Each sample presents distinctive morphologies and boundaries. The histogram representing the grain size distribution is in the inset of each SEM image. The histograms indicate the average grain sizes of around 1.5 μm, 2 μm, 3.5 μm and 1.5 μm for x = 0.1, x = 0.2, x = 0.3 and x = 0.4, respectively. | ||
| Fig. 5 SEM micrograph of the surface of (1 − x)BiFeO3-xBaZr0.1Ti0.9O3 ceramic for compositions 0.1 ≤ x ≤ 0.4. | ||
As an example, we illustrate the SEM-energy dispersive spectroscopy (SEM-EDS) elements of samples with x = 0.1 and x = 0.3 in Fig. 6a and b, respectively. This analysis confirms the presence of all elements across the grains. Here, the presence of carbon in the EDS mapping is due to the carbon paint used to fix the sample onto the microscope holder. The distribution of Zr exhibits the lowest intensity, which is attributed to its low concentration, following the chemical equation. The distributions of Bi, Ba, and Ti appear less intense compared to that of Fe in the EDS maps, indicating the formation of Fe-rich regions. This nonuniform distribution suggests a microscopic segregation, which can be explained by the immiscibility between the BaTi0.9Zr0.1O3 and BiFeO3 phases. In fact, the introduction of multiple elements with considerable differences in electronegativity and chemical valence was also observed in the substituted system BiFeO3–BaTiO3, leading to the development of microscopic segregation.25–27
3.3. Raman scattering spectra
Raman scattering spectroscopy is a highly effective technique for investigating structural distortions. This technique allows for the examination of distortions within a space group through band shifts, as well as the characterization of distortions related to a phase transition, involving phenomena such as band splitting and soft modes. At RT, BFO adopts a rhombohedral R3c space group with two formulas in one primitive cell. By comparison to the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure, the rhombohedral structure can be described by an antiphase tilt of the adjacent FeO6 octahedron and a displacement of both Fe3+ and Bi3+ cations from their centrosymmetric position along the direction [001]. According to group theory, the 10 atoms in the unit cell of the rhombohedral R3c (C3v) structure lead to 13 Raman phonon modes:28ΓRaman,R3c = 4A1 + 9E.
m structure, the rhombohedral structure can be described by an antiphase tilt of the adjacent FeO6 octahedron and a displacement of both Fe3+ and Bi3+ cations from their centrosymmetric position along the direction [001]. According to group theory, the 10 atoms in the unit cell of the rhombohedral R3c (C3v) structure lead to 13 Raman phonon modes:28ΓRaman,R3c = 4A1 + 9E.
Fig. 7 depicts the Raman scattering spectra of the composition 0 ≤ x ≤ 0.4 at RT. From this figure, we can see that all Raman modes broaden as x increases. This observation can be attributed to lattice anharmonicity and disorder caused by variations in the occupancy of the Bi and Fe sites. On the other hand, the A1-1 mode (∼140 cm−1) is likely dominated by the Bi–O covalent bond. This bond is responsible for controlling the ferroelectric phase of BFO.29 In our case, the Raman spectra provide evidence that the A1-1 mode decreases in intensity with the substitution rate up to composition x = 0.2, which later disappears completely starting from x = 0.3. This observation suggests a reduction in the stereochemical activity of the 6s2 lone pair electrons associated with Bi3+ ions, which occurs due to the substitution of Bi3+ by Ba2+. This decrease in stereochemical activity impacts the long-range ferroelectric ordering and consequently reduces the ferroelectric characteristics of the system. This trend supports the XRD study, where the polarization deduced from lattice parameters diminishes with the substitution rate x. Furthermore, the vibration mode (A1-3) detected around 230 cm−1 is possibly associated with the tilts of the FeO6 octahedron or ω.29 The decrease in its intensity with x is consistent with the reduction of the tilt ω obtained previously through the refinements of XRD pattern refinements. The vanishing of the mode (A1-3) observed in the compositions x = 0.3 and 0.4 suggests their cubic symmetry.
 | ||
| Fig. 7 Raman spectra of all composition of (1 − x)BiFeO3-xBaZr0.1Ti0.9O3 system (0 ≤ x ≤ 0.4) recorded at RT. | ||
As previously mentioned in the XRD section, the system (1 − x)BiFeO3-xBaTi0.9Zr0.1O3 transforms into a cubic phase when x exceeds 20%. In the cubic phase, the irreducible representation for the optical phonons is denoted as Γopt = 3F1u + F2u. Here, the F1u mode is infrared active, while F2u is considered a “silent mode” as it remains inactive in both Raman and infrared spectroscopy. Therefore, we anticipate the absence of Raman active modes in the cubic phase. However, in the cubic phase for x = 0.3 and 0.4, the mode of the rhombohedral structure remains active in the cubic phase, which is caused by the breakdown of the Raman selection rule and substitutional disorder at the cation site. These modes essentially reflect the phonon density of states.30
3.4. Magnetic properties using Mössbauer spectroscopy and hysteresis loops
To highlight the effect of Ba(Ti0.9Zr0.1)O3 substitution on the spin cycloidal structure of BFO and to find the oxidation state of the Fe ions and their structural environment, we carried out 57Fe Mössbauer spectrometry at RT.5 The obtained Mössbauer spectra for (1 − x)BiFeO3-xBaZr0.1Ti0.9O3, where 0 ≤ x ≤ 0.4 are shown in Fig. 8a. Here, the BFO spectrum is shown as a reference in order to emphasize the effects of Ba(Ti0.9Zr0.1)O3 substitution. For our prepared pure BFO ceramic (x = 0), the spectrum is fitted by the model proposed by D. Lebeugle et al.,5 which links the observed spectral asymmetry to the spiral magnetic structure of Fe3+ ions. With this model we obtained the hyperfine parameter values, Hhf = 498 kOe, ΔEQ = 0.51 mm s−1 and δ = 0.40 mm s−1 at RT. These values confirm that Fe is found only as Fe3+ in the octahedral environment. They agree with those obtained in ref. 5 from BFO single crystals at the same temperature. | ||
| Fig. 8 (a) Mössbauer spectra of (1 − x)BiFeO3-xBaZr0.1Ti0.9O3 system (0 ≤ x ≤ 0.4) recorded at RT (b) hyperfine field distribution. | ||
The Fig. 8a shows also symmetrical lines Mössbauer spectra with line-width broadening for samples with x = 0.1, 0.2 and 0.3. This may indicate the presence of Fe3+ sites distribution in the sample. Indeed, the substitution of BFO with Ba(Ti0.9Zr0.1)O3 introduces chemical disorder due to the random replacement of Fe3+ ions with Ti4+ and Zr4+ ions within the BFO structure. This disorder reduces spectral asymmetry and broadens the line widths, making the cycloidal model less effective for fitting the spectra. In response to these changes, we adopted a fitting model based on a discrete distribution of magnetic sextets. In this model, the step size of the hyperfine field distribution and the line width of the sextuplet are fixed, while the isomer shift and quadrupole shift values are fitted but remain common across all sextets.
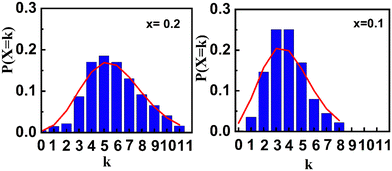
Fig. 8b shows the obtained hyperfine distribution obtained as a result of the fitting. In order to study the effect of the substitution on the environment of the Fe3+ ions, we carried out an analysis with a Poisson distribution. We considered that the value of the area of each sextuplet of the hyperfine field distribution (Fig. 8b) represents the probability P(X = k) that a Fe3+ site is surrounded by k nearest Ti4+ or Zr4+ neighbors, such that:
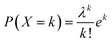 | (2) |
Mössbauer spectrometry results indicate that the substitution of Fe3+ ions with Ti4+ and Zr4+ induces cationic disorder, which weakens or even suppresses the cycloidal magnetic structure. As shown in Fig. 9, analysis of this disorder using a Poisson distribution reveals an increase in variance from λ = 3.9 to 5.7 as the substitution level rises from x = 0.1 to 0.2. This increase suggests a higher degree of disruption in the cycloidal magnetic structure of Fe3+ ions, driven by the Dzyaloshinskii–Moriya (DM) interaction, which becomes subordinate to the exchange interaction. For x > 0.3, the cationic distribution broadens further, indicating an escalation in structural disorder, while magnetic interactions between Fe3+ ions progressively weaken.
Fig. 10 illustrates the evolution of mean hyperfine parameters as a function of the substitution rate x. The mean hyperfine field decreases with increasing x, confirming the substitution of Fe3+ by non-magnetic Ti4+ and Zr4+ ions. The nearly constant isomer shift indicates that the valence state of Fe remains unchanged upon substitution.
 | ||
| Fig. 10 Substitution rate dependence of mean hyperfine parameters values. Hhf: hyperfine field, δ: isomer shift, ΔEQ/2ε: quadrupole splitting/shift. | ||
The quadrupole splitting/shift (ΔEQ/2ε) arises from the interaction between the nuclear quadrupole moment (eQ) and the electric field gradient (∇![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ) at the nucleus, providing insight into the local symmetry of the Mössbauer absorber, in this case, 57Fe nuclei. A low ΔEQ value, close to zero, typically corresponds to a highly symmetric environment. The observed decrease in ΔEQ/2ε for x ≠ 0 suggests a significant modification in the local symmetry, indicating a transition toward higher-symmetry environment around Fe3+ due to substitution. This result confirms the structural transition from the R3c rhombohedral to Pm
) at the nucleus, providing insight into the local symmetry of the Mössbauer absorber, in this case, 57Fe nuclei. A low ΔEQ value, close to zero, typically corresponds to a highly symmetric environment. The observed decrease in ΔEQ/2ε for x ≠ 0 suggests a significant modification in the local symmetry, indicating a transition toward higher-symmetry environment around Fe3+ due to substitution. This result confirms the structural transition from the R3c rhombohedral to Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic observed by XRD and Raman spectroscopy with increasing substitution rate.
m cubic observed by XRD and Raman spectroscopy with increasing substitution rate.
At x = 0.4, the Mössbauer spectrum exhibits paramagnetic behavior, with a Néel temperature below 300 K.19 The obtained hyperfine parameter values are, δ = 0.38 mm s−1 and ΔEQ = 0.47 mm s−1 at RT.
Fig. 11 depicts the M–H cycles for (1 − x)BiFeO3-xBaTi0.9Zr0.1O3 ceramics with x ranging from 0 to 0.4 at 300 K and 2 K. Various parameters such as Ms at 60 kOe, Mr, and Hc are extracted from these cycles and tabulated in Table 2 at 300 K and 2 K. In the pure BFO, the observation of a low value of remanent magnetization is due to the presence of a small quantity of Bi25FeO39 detected in XRD analysis.5 This finding is consistent with the results reported in the work of Saha et al.31 From Fig. 11, the value of Mr for x = 0.1 and x = 0.2 shows an improvement in the magnetic order compared to BFO due to the suppression of spin cycloid structure, as investigated by Mössbauer spectroscopy. Furthermore, Mössbauer data show no evidence of Fe2+, ruling out the possibility that the increase in Mr for x = 0.1 and x = 0.2 is due to the presence of Fe2+.32
 | ||
| Fig. 11 Field (H) dependence of magnetization (M) of (1 − x)BiFeO3-xBaZr0.1Ti0.9O3 system (0 ≤ x ≤ 0.4) measured at 2 and 300 K. | ||
| x | M s (emu g−1) at 60 kOe | M r (emu g−1) | H c (Oe) | |||
|---|---|---|---|---|---|---|
| 300 K | 2 K | 300 K | 2 K | 300 K | 2 K | |
| 0 | 1.01 | 1.12 | 0.026 | 0.029 | 335 | 390 |
| 0.1 | 1.28 | 1.52 | 0.34 | 0.38 | 2120 | 1850 |
| 0.2 | 0.9 | 1.1 | 0.11 | 0.22 | 2000 | 1500 |
| 0.3 | 0.61 | 0.81 | 0.016 | 0.017 | 450 | 415 |
| 0.4 | 0.68 | 1.44 | 0 | 0.004 | 0 | 60 |
As mentioned in section XRD, the same trend for Mr and the tilt angle ω is expected. According to the XRD studies, the tilt angle exhibits a systematic decrease with increasing substitution x. However, Mr reaches a maximum at the composition x = 0.1 both at 2 K and 300 K (Fig. 12a). The nonmonotonic dependence of Mr with the tilt angle ω was detected. The substitution of Fe3+ by nonmagnetic Zr4+/Ti4+ reduces the amount of the interaction DM in the composition x = 0.1, as obtained in the Mössbauer spectroscopy studies. This feature allows the activation of the weak ferromagnetism set in BFO. In fact, we can explain the appearance of the weak ferromagnetism similarly to the system (1 − x)BiFeO3-xPbTiO3, which is due to the broken cycloid spin structure (as schematized in Fig. 7 of the work of V. F. Freitas et al.33). Thus, we can suggest the complete destruction of the spin cycloid at x = 0.1 which explains the highest value of Mr for x = 0.1. After the complete suppression of the cycloid, the reduction in Mr for x > 0.10, is attributed to the decrease of the tilt angle. According to Mössbauer spectroscopy investigation, the interaction DM is significantly weakening and yields to the exchange interaction in the G-type antiferromagnetic order of Fe3+ ions within the BFO structure. For the composition x = 0.3, the magnetic interactions between Fe3+ ions progressively weaken, and the remanent magnetization Mr approaches zero (as shown in Fig. 12a). For higher doping, i.e., for x = 0.4, Mr completely vanishes, suggesting a paramagnetic phase, consistent with the results observed in the Mössbauer studies.
 | ||
| Fig. 12 (a) Variation of remnant magnetization (Mr) (b) the evolution of the coercive field (Hc) as a function of x at 2 and 300 K. | ||
In Fig. 12b, the value of the coercive field Hc at 300 K is higher than 2 K, respectively, for the compositions x = 0.1 and 0.2. This result suggests the existence of magnetoelectric coupling in the compositions x = 0.1 and x = 0.2. Indeed, according to the work of Park et al.,19 the presence of magnetoelectric coupling in the (1 − x)BiFeO3-xBaTiO3 solid solution nanostructures could potentially explain the decrease in coercivity at low temperatures compared to the value at RT. Referring to the expression of Hc given by the following equation:34
 | (3) |
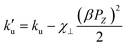 | (4) |
 denotes effective uniaxial magnetic anisotropy, β represents the magnetoelectric coefficient associated with the Dzyaloshinsky–Moriya magnetic field, PZ is the spontaneous polarization, and χ⊥ indicates the magnetic susceptibility in the direction perpendicular to the antiferromagnetic vector.13,17 In the same figure, according to the work of K. Chakrabarti et al.,35 we can attribute the origin of the highest value of the coercive field Hc for the composition x = 0.1 at 2 K and 300 K to significant magnetoelastic and magnetocrystalline anisotropy. The highest values of Ms and Mr are also observed at x = 0.1 in the (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3 system. The comparison of these changes with the system (1 − x)BiFeO3-xBaTiO319 is interesting, where the highest values of Ms and Mr match the lowest values of Hc at x = 0.2. This difference can be attributed to the effect of Zr since the ionic radius of Zr4+ (0.72 Å) is larger than that of Ti4+ (0.605 Å). This introduces local structural distortions and strain within the lattice, enhancing the magnetocrystalline anisotropy. In Fig. 12b, the substantial decrease in coercive field Hc at x = 0.3 and x = 0.4 is due to the change of magnetocrystalline anisotropy, as the rhombohedral structure emerges toward a highly symmetric cubic phase. This result agrees with the Mössbauer spectroscopy analysis.
denotes effective uniaxial magnetic anisotropy, β represents the magnetoelectric coefficient associated with the Dzyaloshinsky–Moriya magnetic field, PZ is the spontaneous polarization, and χ⊥ indicates the magnetic susceptibility in the direction perpendicular to the antiferromagnetic vector.13,17 In the same figure, according to the work of K. Chakrabarti et al.,35 we can attribute the origin of the highest value of the coercive field Hc for the composition x = 0.1 at 2 K and 300 K to significant magnetoelastic and magnetocrystalline anisotropy. The highest values of Ms and Mr are also observed at x = 0.1 in the (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3 system. The comparison of these changes with the system (1 − x)BiFeO3-xBaTiO319 is interesting, where the highest values of Ms and Mr match the lowest values of Hc at x = 0.2. This difference can be attributed to the effect of Zr since the ionic radius of Zr4+ (0.72 Å) is larger than that of Ti4+ (0.605 Å). This introduces local structural distortions and strain within the lattice, enhancing the magnetocrystalline anisotropy. In Fig. 12b, the substantial decrease in coercive field Hc at x = 0.3 and x = 0.4 is due to the change of magnetocrystalline anisotropy, as the rhombohedral structure emerges toward a highly symmetric cubic phase. This result agrees with the Mössbauer spectroscopy analysis.
4. Conclusion
Ceramics from the system (1 − x)BiFeO3-(x)BaTi0.9Zr0.1O3 with x = 0–0.4 were prepared using a conventional solid-state sintering procedure. We thoroughly investigated the crystalline structure and the magnetic properties using XRD, Raman scattering spectroscopy, Mössbauer spectroscopy analysis reveals that the substitution of Fe3+ ions with Ti4+ and Zr4+ induces cationic disorder, which weakens the Dzyaloshinskii–Moriya (DM) interaction. Consequently, the DM interaction becomes subordinate to the exchange interaction in the G-type antiferromagnetic order of Fe3+ ions within the BFO structure. This modification may lead to the suppression of the cycloidal spin structure of Fe3+ ions in samples with x = 0.1, 0.2 and 0.3. The same analysis indicates a paramagnetic state of composition x = 0.4. On the other hand, the magnetic coercivity (Hc) of the compositions x = 0.1 and 0.2 decreases at low temperatures compared to RT. The reason for this effect is related to the magnetoelectric coupling. From Rietveld refinement data, it was demonstrated that the tilt angle (ω) decreases with the substitution rate in the rhombohedral phase and becomes zero in the cubic phase. This decrease results in a reduction of magnetic properties deduced from the M–H response, except for the composition with x = 0.1, which shows an enhancement compared to BFO. Hence, this composition provides a significant remnant magnetization (Mr) equal to 0.34 emu g−1. As a result, substituted BFO could potentially be suitable for the development of several devices, particularly in the field of data storage.Author contributions
All authors contributed to the present manuscript. Material synthesis, data collection, and analysis were carried out by Imen Kallel, Zied Abdelkafi, Najmeddine Abdelmoula, Hamadi Khemakhem and Nirina Randrianantoandro. Futhermore, El-Kebir Hlil contributed to the interpretation of the Magnetic properties section. The initial draft of the manuscript was prepared by Imen Kallel in collaboration with Zied Abdelkafi, and all other authors provided comments on previous versions of the manuscript. All authors read and approved the final draft of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data available in the article are true and valid, as recognized by the authors. The data that support the findings of this study are available from all authors upon reasonable request.Acknowledgements
The authors acknowledge the financial support provided by the Laboratory of Multifunctional Materials and Applications (LaMMA), (LR16ES18), Faculty of Sciences of Sfax, University of Sfax, (Tunisia). They also thank Anthony Rousseau (IMMM, Le Mans Université, France) for his assistance with SEM and EDS mapping using the Zeiss GeminiSEM 560 at the microscopy platform of the Institut des Molécules et Matériaux du Mans (IMMM), Le Mans Université, France.References
- R. Montecillo, C.-S. Chen, Y.-T. Lee, P.-Y. Chen and C.-S. Tu, J. Eur. Ceram. Soc., 2023, 43, 1941–1951 CrossRef CAS.
- A. Raza Khan, G. M. Mustafa, S. Kumail Abbas, S. Atiq, M. Saleem, S. M. Ramay and S. Naseem, Results Phys., 2020, 16, 102956 CrossRef.
- H. Sun, Z. Luo, C. Liu, C. Ma, Z. Wang, Y. Yin and X. Li, J. Materiomics, 2022, 8, 144–149 CrossRef.
- G. Catalan and J. F. Scott, Adv. Mater., 2009, 21, 2463–2485 CrossRef CAS.
- D. Lebeugle, D. Colson, A. Forget, M. Viret, P. Bonville, J. F. Marucco and S. Fusil, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 024116 CrossRef.
- S. M. Selbach, T. Tybell, M.-A. Einarsrud and T. Grande, Adv. Mater., 2008, 20, 3692–3696 CrossRef CAS.
- S. Lee, M. T. Fernandez-Diaz, H. Kimura, Y. Noda, D. T. Adroja, S. Lee, J. Park, V. Kiryukhin, S. W. Cheong, M. Mostovoy and J.-G. Park, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 060103 CrossRef.
- A. Glazer, Acta Crystallogr., Sect. B, 1972, 28, 3384–3392 CrossRef CAS.
- I. Sosnowska, T. P. Neumaier and E. Steichele, J. Phys. C-Solid State Phys., 1982, 15, 4835 CrossRef CAS.
- A. M. Kadomtseva, A. K. Zvezdin, Y. F. Popov, A. P. Pyatakov and G. P. Vorob’ev, J. Exp. Theor. Phys. Lett., 2004, 79, 571–581 CrossRef CAS.
- I. Sosnowska and A. K. Zvezdin, J. Magn. Magn. Mater., 1995, 140–144, 167–168 CrossRef CAS.
- C. Ederer and N. A. Spaldin, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 71, 060401 CrossRef.
- N. Wang, J. Cheng, A. Pyatakov, A. K. Zvezdin, J. F. Li, L. E. Cross and D. Viehland, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 72, 104434 CrossRef.
- J.-H. Lee, H. J. Choi, D. Lee, M. G. Kim, C. W. Bark, S. Ryu, M.-A. Oak and H. M. Jang, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 045113 CrossRef.
- A. Singh, A. Gupta and R. Chatterjee, Appl. Phys. Lett., 2008, 93, 022902 CrossRef.
- A. Singh, A. Senyshyn, H. Fuess, S. J. Kennedy and D. Pandey, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 024108 CrossRef.
- B. Ruette, S. Zvyagin, A. P. Pyatakov, A. Bush, J. F. Li, V. I. Belotelov, A. K. Zvezdin and D. Viehland, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 064114 CrossRef.
- F. Bai, J. Wang, M. Wuttig, J. Li, N. Wang, A. P. Pyatakov, A. K. Zvezdin, L. E. Cross and D. Viehland, Appl. Phys. Lett., 2005, 86, 032511 CrossRef.
- T.-J. Park, G. C. Papaefthymiou, A. J. Viescas, Y. Lee, H. Zhou and S. S. Wong, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 024431 CrossRef.
- I. Kallel, H. Khemakhem, Z. Sassi, N. Abdelmoula, E.-K. Hlil and N. Randrianantoandro, J. Phys. D: Appl. Phys., 2022, 55, 065303 CrossRef CAS.
- G. D. Achenbach, W. J. James and R. Gerson, J. Am. Ceram. Soc., 1967, 50, 437 CrossRef CAS.
- J. Teillet and T. Varret, unpublished Mosfit program (Université du Maine, France, 1984).
- J. Rodríguez-Carvajal, FULLPROF,version 2015, Laboratoire Leon Brillouin, CEA-CNRS, France, https://www.ill.eu/sites/fullprof.
- H. D. Megaw and C. N. W. Darlington, Acta Crystallogr., Sect. A, 1975, 31, 161–173 CrossRef.
- D. Wang, Z. Fan, W. Li, D. Zhou, A. Feteira, G. Wang, S. Murakami, S. Sun, Q. Zhao, X. Tan and I. M. Reaney, ACS Appl. Energy Mater., 2018, 1, 4403–4412 CrossRef CAS.
- H. Li, J. Zhao, Y. Li, L. Chen, X. Chen, H. Qin, H. Zhou, P. Li, J. Guo and D. Wang, ACS Appl. Mater. Interfaces, 2024, 16, 9078–9087 CrossRef CAS PubMed.
- Z. Yang, Y. Li, B. Wang, J. Pan, A. K. Kleppe and D. A. Hall, J. Materiomics, 2024, 10, 57–69 CrossRef.
- R. Haumont, J. Kreisel and P. Bouvier, Phase Transitions, 2006, 79, 1043–1064 CrossRef CAS.
- P. Hermet, M. Goffinet, J. Kreisel and P. Ghosez, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 75, 220102 CrossRef.
- K. K. Mishra, V. Sivasubramanian, R. M. Sarguna, T. R. Ravindran and A. K. Arora, J. Solid State Chem., 2011, 184, 2381–2386 CrossRef CAS.
- S. Saha, K. L. Routray, T. K. Nayak and B. Dash, Braz. J. Phys., 2024, 54, 147 CrossRef CAS.
- M. Shu, D. Wang, S. Li, B. Yang, L. Yin, W. Song, J. Yang, X. Zhu and Y. Sun, J. Appl. Phys., 2020, 128, 164101 CrossRef CAS.
- V. F. Freitas, T. G. M. Bonadio, G. S. Dias, O. A. Protzek, A. N. Medina, L. F. Cótica, I. A. Santos, D. Garcia and J. A. Eiras, J. Appl. Phys., 2013, 113, 114105 CrossRef.
- A. H. Morrish, IEEE Press, Piscataway, 2001.
- K. Chakrabarti, K. Das, B. Sarkar and S. K. De, J. Appl. Phys., 2011, 110, 103905 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |