Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Near-bandgap emission in [HOC2H4NH3]2PbI4 perovskite under hydrostatic pressure: emission of a free exciton and a polaronic exciton†
Filip
Dybała
a,
Robert
Kudrawiec
 *a,
Maciej P.
Polak
*a,
Maciej P.
Polak
 b,
Artur P.
Herman
b,
Artur P.
Herman
 a,
Adam
Sieradzki
a,
Adam
Sieradzki
 c and
Mirosław
Mączka
c and
Mirosław
Mączka
 d
d
aDepartment of Semiconductor Materials Engineering, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, Wrocław 50-370, Poland. E-mail: robert.kudrawiec@pwr.edu.pl
bDepartment of Materials Science and Engineering, University of Wisconsin-Madison, Madison, Wisconsin 53706-1595, USA
cDepartment of Experimental Physics, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, Wrocław 50-370, Poland
dInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, ul. Okólna 2, Wrocław 50-422, Poland
First published on 6th December 2024
Abstract
Two-dimensional metal-halide perovskites, including EA2PbI4 (EA = HOC2H4NH3+, ethanolammonium), are very soft materials and therefore they exhibit unique excitonic properties, significantly different from those known for conventional semiconductor quantum wells or two-dimensional van der Waals crystals. These differences should be even more pronounced for excitonic properties under hydrostatic pressure. In this work, we show that photoluminescence studies of EA2PbI4 under hydrostatic pressure at low temperatures very clearly reveal the nature of excitonic transitions in this crystal. The near-bandgap emission (NBE) consists of two peaks, one of which is related to the recombination of free excitons (FE), and the other observed at lower energy is assigned to a polaronic exciton, i.e., FE containing a large polaron (FEP). As hydrostatic pressure increases, the polaron formation energy increases and therefore the FEP emission is enhanced and redshifts by a factor of 1.5 relative to the FE emission. In the configuration diagram that was adapted to explain the NBE, the observed changes in emissions under hydrostatic pressure can be explained by a shift of the FEP potential minimum on both the energy axis and the configuration coordinate axis. This allows us to explain the spectral shifts of FE and FEP, as well as the appearance of additional peaks for FE and FEP emission.
1. Introduction
Two-dimensional (2D) hybrid organic–inorganic metal halide perovskites are materials with very specific characteristics in the context of exciton formation and their properties. This makes them attractive candidates for a wide range of applications, as recently discussed.1 Due to the atomic structure of perovskites, i.e. corner-sharing AB6 octahedra (A = Sn, Pb; B = Cl, Br, I) arranged in layers separated by an organic dielectric part,2–4 they were often compared to epitaxial quantum wells. This qualitatively explains the much higher exciton binding energy in 2D perovskites compared to 3D analogues. High exciton binding energies are also observed in 2D layers of inorganic van der Waals crystals.5 However, even in this case it is difficult to assert strong similarities between excitons in these systems. This is primarily due to the soft ionic lattice of hybrid organic–inorganic perovskites, which is a very important feature that distinguishes them from both conventional semiconductor quantum wells and 2D layered van der Waals crystals.The consequence of the high softness of hybrid perovskites is that the electron (hole) generated in the conduction (valence) band causes significant lattice distortion around itself. As a result, such a quasiparticle can no longer be considered a free electron (hole), but rather an electron (hole) “dressed with phonons”. Therefore, in many perovskites we deal with negative and positive polarons instead of free electrons and holes.6–15 A distinction is made between small polarons when the lattice distortion covers one octahedron and large polarons when the distortion is much larger.12,16 The formation energy of negative and positive polarons is different and depends on the composition of perovskites and their crystallographic structure. Therefore, depending on the perovskite, we deal with different polarons. In a given perovskite there might be one type of polarons or two types of polarons (e.g. only small polarons or both small and large polarons). Currently, although many researchers study polarons in perovskites, the effect of hydrostatic pressure on their formation energy and the energies of excitons containing such polarons has yet to be investigated.
The photo-induced formation of polarons instead of free carriers has important consequences for excitons and optical properties of 2D perovskites. In general, free excitons (FE) and self-trapped excitons (STE) are distinguished in the emission spectra of perovskites,3,4,15–26 but often without going deeper into the nature of STEs, assuming only excitonic self-localization on the lattice distortion caused by the ‘transfer’ of an electron from the valence band to the conduction band. In the context of a better understanding of polarons in perovskites and their distinction into small and large type,12,16 a significant difference should be observed between STEs consisting of different polarons, i.e., small and large polarons. Additionally, a distinction between intrinsic STEs and STEs additionally localized on point defects or impurities (i.e., extrinsic STEs) can be made.3 There is rather a consensus among researchers that the broad emission with a large Stokes shift (∼300–800 meV), which is observed for many 2D perovskites,3,4,18–25 is related to STEs consisting of small polarons. These can be both intrinsic and extrinsic STEs.3 This also does not rule out the possibility that defect-related emission in this spectral range may occur in some perovskites.27 In the case of near-bandgap emission (NBE), FEs can be expected, but there is no consensus among researchers on the nature of this emission, especially since in many perovskites more than one emission peak in this spectral range is observed. Therefore, additional experiments are needed to better understand the nature of NBE. Due to the soft ionic lattice of perovskites, photoluminescence (PL) measurements under hydrostatic pressure are an appropriate approach to investigate the nature of excitons, including their self-localization.
So far, PL measurements at high hydrostatic pressure have been performed for many 2D perovskites,28–37 including [HOC2CH4NH3]2PbI4 (EA2PbI4) up to 10 GPa,38 but measurements at low temperatures are rare, while low temperatures are needed to observe multi-peak NBE. In this work we performed careful PL studies of NBE for EA2PbI4 under hydrostatic pressure at various temperatures in order to identify the nature of this emission. In general, this perovskite has not been intensively studied,39–43 but recently have attracted significant attention since the presence of a high-dielectric organic component leads to a pronounced decrease of the dielectric confinement and subsequent narrowing of the band gap and decrease of the exciton binding energy to ∼13 meV.41 Therefore, optical studies of this compound under hydrostatic pressure seems to be very important. In this work to explain the observed changes in PL spectra, an exciton configuration diagram is adopted and its evolution under hydrostatic pressure is proposed.
2. Methods
2.1 Crystal growth
In order to grow single crystals of EA2PbI4 (EA = HOC2H4NH3+), 2 mmol of PbI2 (0.46 g) and 5 mmol of ethanolamine (0.305 g) were dissolved on a hot plate at 40 °C in a mixture of propylene carbonate and hydroiodic acid with the volume ratio 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.7. The clear yellow solution containing EA2PbI4 precursor was transferred to a glass vial. The closed vial was then kept at 50 °C and the red plate-like crystals, which grew at the bottom of the vial, were separated from the liquid after 5 days and dried at room temperature. Fig. S2 (ESI†) shows good agreement of the experimental powder diffraction pattern of the ground crystals with the theoretical pattern calculated based on the single-crystal data published by Mercier et al.,44 confirming purity of the bulk sample.
2.7. The clear yellow solution containing EA2PbI4 precursor was transferred to a glass vial. The closed vial was then kept at 50 °C and the red plate-like crystals, which grew at the bottom of the vial, were separated from the liquid after 5 days and dried at room temperature. Fig. S2 (ESI†) shows good agreement of the experimental powder diffraction pattern of the ground crystals with the theoretical pattern calculated based on the single-crystal data published by Mercier et al.,44 confirming purity of the bulk sample.
2.2 Photoluminescence and reflectance measurements
For PL and reflectance (R) measurements, the sample was placed inside a closed-cycle cryostat, which allows optical measurements from 10 to 350 K. For PL measurements, the sample was excited with a 325 nm line from a HeCd laser (Kimmon IK3501R-G) with a power of 0.25 mW, which, when focused on the sample, gives an excitation density of ∼0.3 W cm−2. PL spectra were recorded using a 0.5 m Andor monochromator with a 600 g mm−1 diffraction grating blazed at 500 nm and a Si CCD camera cooled down to −70 °C by Peltier elements. For R measurements the sample was illuminated with a white light from a halogen lamp. A 0.5 m monochromator (Zolix Omni-λ series) was used to disperse the reflected light from the sample. The light was detected by a silicon photodiode using the lock-in technique with an SR830 DSP lock-in amplifier.2.3 Measurements under hydrostatic pressure
For PL measurements under hydrostatic pressure, the sample was mounted in diamond anvil cells (DAC) (Diacell® CryoDAC-Nitro). This DAC system is placed in a cryostat enabling measurements at different temperatures. The pressure inside the DAC can be controlled by the pressure on the appropriate membrane. A schematic representation of this system with a photo is shown in Fig. S3 in the ESI.† To determine the pressure inside the DAC a ruby sphere was used. The sample and ruby sphere were excited with a 325 nm HeCd laser (Kimmon IK3501R-G) and the PL signal was analysed using a 0.5 m Andor monochromator with a 600 g mm−1 diffraction grating blazed at 500 nm and a Si CCD camera cooled down to −70 °C by Peltier elements. The excitation density was estimated to be ∼1 W cm−2 before DAC. Daphne oil was used as the pressure transmitting medium ensuring good hydrostatic conditions up to ∼4 GPa. Therefore, in PL measurements we tried not to exceed this pressure significantly.2.4 DFT calculations
The first principles density functional theory (DFT) calculations were performed with the Vienna ab initio simulation package (VASP)45–47 with the use of the recommended PAW potentials,48i.e. including d electrons for Pb. The structure of perovskites and layered systems tend to be best described with functionals focused on proper treatment of van der Waals (vdW) interactions49 and the use of vdW functionals has been a standard practice in halide perovskites.50,51 When studying pressure dependencies, proper description of the system's geometry is crucial. Since the EA2PbI4 has not been extensively studied within DFT, we assessed the performance of the semilocal PBEsol52 and two state-of-the-art vdW functionals − rev-vdW-DF253 and SCAN + rVV10.54 various functionals, using the experimentally obtained crystallographic structure data from ref. 55 as a reference. PBEsol underestimated the out-of-plane lattice constant by 1.7% and incorrectly predicted the longer in-plane lattice to be the shorter one, underestimating it by 2%, while predicting the shorter one almost exactly as in the experimental data. The vdW functionals, rev-vdW-DF2 and SCAN + rVV10 performed much better than PBEsol and almost identical to each other, both correctly optimizing the short and long in-plane lattice constant, underestimating their lengths by just 0.7% and 1.1%, and 1.5% for the out-of-plane lattice constant. As the more recent and more rigorously derived of the two, SCAN + rVV10 was chosen as the functional of choice for all geometry optimization under pressure. The electronic band structure was calculated using the HSE06 functional. The α parameter was adjusted to 0.43 in order to reproduce the experimentally obtained value at low temperature and zero pressure and was kept constant for all calculations. Since spin–orbit coupling is extremely important in a proper description of the band structure, it has been included in all calculations. The energy cut off of 550 eV and a Γ-centered 4 × 4 × 4 k-point mesh was used. For geometry optimization the forces were converged down to 1 meV Å−1, and for the band structure the energy was converged to 10−6 eV. The k-point path in reciprocal space for the monoclinic crystal structure as shown in ref. 56 was used. In order to obtain the energy of valence band maximum relative to vacuum as a function of pressure, the bulk geometry optimized for each pressure was translated into slab supercells consisting of two layers (116 atoms), with surface perpendicular to the [100] direction and followed by 20 Å of vacuum. The macroscopic average potential57 in the direction perpendicular to the slab was used to align the potentials so that the reference vacuum potential was zero.3. Results and discussion
Fig. 1(a) shows a comparison of the R spectrum and the PL spectrum for the EA2PbI4 crystal over a wide spectral range at selected temperatures. The temperature evolutions of the R and PL spectra are shown in Fig. 1(b) and (c), respectively. The optical transition associated with the FE dominates the R spectrum. As the temperature increases, this transition shifts towards higher energies and, as in other perovskites, due to increase of the electron–phonon interaction and Pb–I bond length.58–60 It is worth emphasizing here that for this crystal we did not observe a phase transition in differential scanning calorimetry measurements in the investigated temperature range, see Fig. S1 in ESI.† Therefore, this is a suitable material for studying the nature of NBE because there are no additional complications related to the phase transition, which could be associated with discontinuities in peak position and intensity.61,62 The spectral position and broadening of the FE transition were extracted from the R spectra, fitting them with formula given by eqn (1) | (1) |
 | (2) |
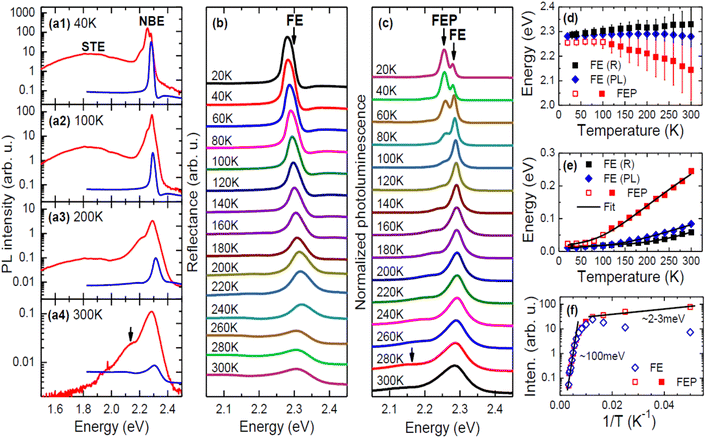 | ||
| Fig. 1 (a1)–(a4) Comparison of R (blue lines) and PL (red lines) spectra of EA2PbI4 at selected temperatures (PL spectra are presented on a logarithmic scale to better highlight weak emission). (b) Temperature dependence of R spectrum in the region of free exciton transition. (c) Temperature dependence of NBE plotted on a linear scale. (d) Temperature dependence of the FE energy determined from reflectance measurements and their analysis using eqn (1) (black squares) and PL measurements (blue solid diamonds) and the energy of the STE containing a large polaron determined from photoluminescence measurements (red squares). (e) Temperature dependence of the FE broadening determined from reflectance measurements (black squares) and PL measurements (blue solid diamonds) and the broadening of the STE containing a large polaron determined from PL measurements (red squares). (f) Analysis of PL intensity for the FE (blue diamonds) and the STE containing a large polaron (red squares). The red squares in panels (d)–(f) refer to the same peak but to emphasize its different behaviour up to 100 K they are drawn as open and above this temperature as solid. | ||
A broad emission with a large Stokes shift was identified in the PL spectra and attributed to the recombination of STEs consisting of small polarons, see Fig. 1(a). This emission is much weaker than the NBE and is not discussed in this article. Based on the comparison of the R spectrum with the PL spectrum (Fig. 1(a)), the high-energy peak in PL can be assigned to the FE. However, as the temperature increases, the spectral position of this peak deviates progressively from the energy of the FE transition visible in the R spectrum. A direct comparison of the energy of the FE transition observed in R and PL is shown in Fig. 1(d) along with the broadening of these transitions in the form of vertical bars. Taking into account the broadenings of these transitions, it can be assumed that they are consistent and the differences in energy position result from the nature of these two experiments. In R, which is an absorption-like experiment, phonon broadening affects the peak position differently than in PL, which is an emission-like experiment. It should be emphasized that this type of behavior is unusual in regular semiconductors where the FE energies in R and PL are the same, but considering the soft ionic character of perovskites, this may be a typical feature and can be observed in other 2D perovskites. Previous literature reports directly comparing R spectra with PL spectra in 2D perovskites are not numerous,63,64 especially as a function of temperature, but those that exist do not contradict our observations. Additionally, PL reabsorption often reported in perovskites65–67 may contribute to the difference in the FE transition energy observed in R and PL spectra. Due to the large electron–phonon coupling in perovskites, phonon replicas can be expected on the high-energy side of the reflectance spectrum, but such transitions are not clearly visible in our reflectance spectra. So far, such transitions have been rarely reported for absorption68 and/or reflectance spectra but it is very possible that lower temperatures are needed for their clear observation and with increasing temperature, phonon replicas contribute to the broadening of the main transition (FX in this case). As a result, this may be an additional cause of the shift between the PL peak and the transition energy determined from fitting the reflectance spectrum with eqn (1). It is worth noting here that this difference at low temperature is negligible and increases with temperature.
Below the FE emission, the second peak, which was assigned to a polaronic exciton (i.e., FE containing a large polaron (FEP)) is clearly visible. At low temperatures this peak is stronger than the FE emission but is quenched very quickly with temperature, suggesting a very low activation energy for this emission. On the other hand, this emission does not disappear completely and is clearly visible even at room temperature, see the proper arrow in Fig. 1(a) and (c). The intensity analysis presented in Fig. 1(f) clearly indicates two regimes of the activation energy (Ea), which can be determined with the formula:
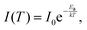 | (3) |
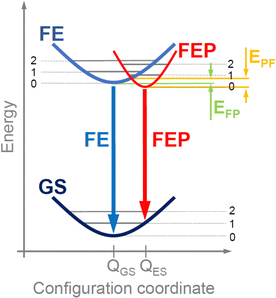
As a result of the transfer of an electron from the valence band to the conduction band (i.e., generation of an electron–hole pair), we are dealing with a local deformation of the crystal lattice. In the configuration diagram in the exciton image, this deformation can be described by the excited state with a minimum at QES (see red parabola in Fig. 2), which is attributed to the FEP, while for a FE the minimum is at QGS (see blue parabola in Fig. 2). If the polaron formation energy is negative, the energy minimum for FEP is at a lower energy than for FE (situation in Fig. 2). Thus, there is an effective energy transfer from FE to FEP and vice versa, with a potential EFP barrier for energy transfer from FE to FEP and a potential EPF barrier for energy transfer from FEP to FE. The height of these barriers depends on the polaron formation energy and will be higher for small polarons than for large polarons. For NBE, the FEP is formed with a large polaron and only an electron or hole polaron is needed. Therefore, the low-energy PL peak in NBE is attributed to the FEP. Two activation energies can be expected for such a transition: one related to the EPF barrier energy and the other related to the exciton binding energy. In general, these energies depend on the material.
In the case of EA2PbI4, at low temperature, FEP dominates due to the lower energy for FEP, but as the temperature increases, excitons localize less and less to the lattice deformation and the relative intensity of FE emission in relation to FEP emission increases, see in Fig. 1(f) that the intensity of FEP (red open squares) decreases up to 100 K while the intensity of FE (blue open diamonds) increases in this temperature range. This is evidence of energy transfer between FEP and FE with an activation energy of ∼2–3 meV corresponding to the EPF barrier. Due to the fact that the energy minimum for FEP is at a lower energy than for FE (see Fig. 2), the transfer of FE to FEP does not stop above 100 K and therefore FEP emission is still visible above this temperature, but its broadening increases with temperature much more than that of FE (see the red squares in Fig. 1(e)). Differences in broadening of FE and FEP emission can be easily explained in the configuration diagram by the greater contribution of optical phonons to the FEP emission with increasing temperature. It is also worth noting that temperature rise can be represented within this configuration diagram. This allows us to explain the broadening of the PL spectra and the differences in spectral positions for FE observed in PL and R. Summarizing the above considerations, it can be assumed that the adopted configuration diagram explains the emission spectra very well and can be a starting point for explaining PL measurements under hydrostatic pressure.
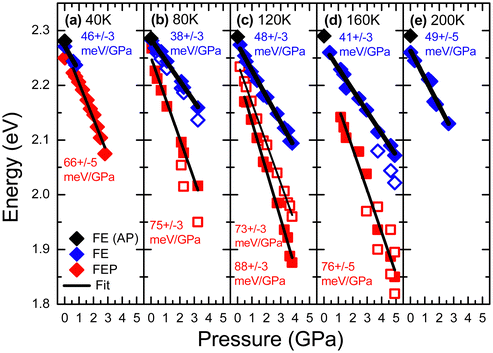
PL measurements for EA2PbI4 were performed at various hydrostatic pressures for five selected temperatures (40, 80, 120, 160 and 200 K) and a summary of these measurements is presented in Fig. 3. At 40 K and low pressures (0.02 GPa), the PL spectrum is dominated by FEP emission and additionally weak FE emission is visible, which is consistent with measurements without hydrostatic pressure, see Fig. 1. As the hydrostatic pressure increases, the emission shifts towards the red, FE disappears very quickly, and the FEP emission broadens significantly and at higher pressures two peaks can be distinguished for this emission. At temperatures of 40, 80 and 120 K, the PL spectra behave very similarly. At low pressure, FE emission dominates. As the pressure increases, the FE emission weakens in favor of FEP emission. Both emissions redshift with increasing pressure and broaden significantly. At higher pressures additional peaks can be distinguished for FEP, see grey arrows in Fig. 3. At 200 K the PL spectra with increasing pressure behave similarly, i.e. the FE emission redshifts, but the FEP emission is no longer clearly visible at this temperature as well as at higher temperatures not shown in this figure. PL measurements for EA2PbI4 under hydrostatic pressure at room temperature were reported in ref. 38 and there, as in our case, it was found that the FE emission dominates in the PL spectra. These observations are consistent with PL measurements as a function of temperature for this crystal (see Fig. 1), which show that at high temperatures the FE emission dominates in the PL spectra, and the FEP emission broadens greatly and is no longer as intense but is present, and this is in accordance with the proposed configuration diagram. In addition, the continuous changes in the spectral position of the peaks indicate continuous changes in the electronic band structure and exclude phase transitions, which generally result in discontinuous changes in the electronic band structure.
 | ||
| Fig. 3 PL spectra of EA2PbI4 measured under different hydrostatic pressures at (a) 40 K, (b) 80 K, (c) 120 K, (d) 160 K, and (e) 200 K. | ||
The spectral positions of FE and FEP emissions along with the locations of additional peaks are shown in Fig. 4. These results were fitted with linear relationships, on the basis of which the pressure coefficients for FE and FEP emissions were determined. The values of these coefficients are given in the figure. It is clearly visible that the pressure coefficient for FEP is approximately 1.5 times higher than for FE. This behavior of the pressure coefficients for FE and FEP and the appearance of these additional peaks can be explained very well in a configuration diagram taking into account hydrostatic pressure, see Fig. 5.
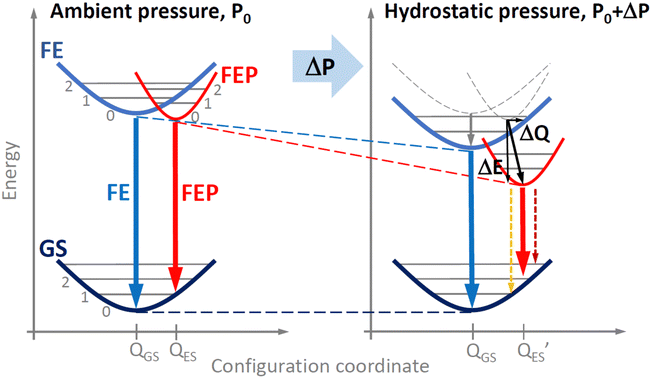 | ||
| Fig. 5 Pressure induced changes in configuration diagram for free exciton and free exciton–polaron transition in EA2PbI4. | ||
As the pressure increases, the energy gap narrows, which shifts the excitonic emission towards the red. Additionally, as the pressure increases, the polaron formation energy changes, which translates into the location of the FEP potential on the configuration diagram, see Fig. 5. Based on our experimental results, we conclude that both ΔE and ΔQ change and hence the pressure coefficient for FEP is approximately ∼1.5 times greater than that for FE. The satellite peaks for FEP emission (see grey arrows in Fig. 3 and open points in Fig. 4) indicate a change in the FEP potential in the configuration diagram on the configuration coordinate axis by ΔQ. Additionally, it cannot be ruled out that the FEP state with n = 1 participates in this emission. This scenario becomes more likely at higher pressures when the n = 1 state for FEP is lower than the n = 0 state for FE. As the temperature increases, these satellite peaks are not resolved very well, but they contribute to the broadening of the FEP emission.
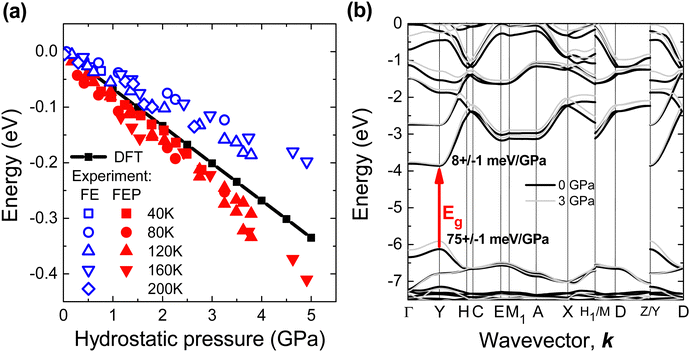
The relative changes in the spectral position of FE and FEP with increasing pressure are shown in Fig. 6(a) together with the changes in the energy gap obtained from DFT calculations. In such a comparison, the problem of underestimating the energy gap in DFT calculations and not taking into account the exciton binding energy is eliminated. According to DFT calculations, the fundamental energy gap (Eg) is a direct gap and other direct optical transitions are separated by high energy (∼1 eV), see Fig. 6(b). Therefore, the R spectrum is dominated by the FE absorption at the Y point of the Brillouin zone and the same excitonic transition is observed in PL spectra. The pressure coefficient for FE should be very similar to pressure coefficient for Eg. In our case the calculated pressure coefficient is ∼40% higher than the pressure coefficient for FE observed in PL and this discrepancy can be attributed to an imperfect pseudopotential in the DFT calculations under hydrostatic pressure. However, the pressure coefficient for FEP is still higher than the calculated pressure coefficient for Eg, which can be explained by the increase in polaron formation energy with increasing hydrostatic pressure. Therefore, the pressure coefficient for FEP is higher than that for FE.
According to DFT calculations for EA2PbI4, hydrostatic pressure mainly changes the valence band, see Fig. 6(b), but in general the band position changes are different for different perovskites.71 Also, the formation energy of positive and negative polarons depend on the perovskite72,73 and this energy can change differently with the hydrostatic pressure. Hence, the relationships between FE and FEP may be different for different perovskites and therefore similar studies for other perovskites are needed as different relationships between FE, FEP and STE emission can be expected. This study clearly demonstrates that PL measurements under hydrostatic pressure at low temperature can distinguish individual peaks in the NBE and their different pressure dependences, which helps identify the nature of these peaks.
It is worth noting here that a self-trap exciton additionally trapped on a shallow donor (or acceptor) can be visible in the NBE region for the studied perovskite and other perovskites as it was already reported.14 In our case, such emission cannot be completely excluded by analyzing the photoluminescence spectra with temperature and therefore FEP can overlap with such emission. However, the behavior of FEP emission with increasing pressure clearly indicates that we are not dealing here with an exciton bound to a shallow donor (or acceptor) only because such an exciton should spectrally follow the FE peak. Our measurements clearly show that the spectral shift of FEP is much larger than FE, and most importantly, this spectral shift is followed by strong quenching of FE emission. This behavior is very well explained by the configuration diagram in which the EFP and EPF potential barriers are comparable at atmospheric pressure (see Fig. 2), but with the increase of hydrostatic pressure, the EPF potential barrier increases significantly compared to the EFP potential barrier, which is responsible for the transfer of FE to FEP and causes the quenching of FE emission. It is worth adding here that even if we are dealing with excitons bound on shallow donors (or acceptors), the formation of a large polaron described by the configuration diagram explains the evolution of FEP emission with temperature and pressure.
A more advanced description can be obtained using DFT methods. In this case, calculations of polaron formation energy and exciton binding energy with pressure seem to be very important. This will certainly help to obtain a more complete picture of the optical response from perovskites and we hope that our experimental studies will motivate such calculations, which are still very challenging and beyond the scope of this work.
4. Conclusions
In conclusions, the NBE was carefully studied under hydrostatic pressure at different temperatures. FE and FEP emissions were identified in the NBE region. This emission is very well explained in the configuration diagram, where the pressure-induced changes in the PL spectrum can be attributed to the shift of the FEP potential on the scale of energy and configuration coordinates. This shows that the configuration diagram has great potential in explaining emission processes in perovskites under hydrostatic pressure.Author contributions
Filip Dybała: measurements under hydrostatic pressure, data analysis, writing – review & editing. Robert Kudrawiec: conceptualization, data analysis, project administration, validation, writing – original draft, writing – review & editing, formal analysis. Maciej P. Polak: DFT calculations, writing – review & editing. Artur P. Herman: PL and R measurements, review & editing. Adam Sieradzki: DSC measurements, review & editing; Mirosław Mączka: crystal growth, writing – review & editing.Data availability
The data that support the findings of this study are available on request from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. K. and A. P. H. acknowledge for financial support from the National Science Centre in Poland through OPUS Grant No. 2020/39/B/ST3/02704.References
- A. Kostopoulou, I. Konidakis and E. Stratakis, Nanophotonics, 2023, 12, 1643 CrossRef PubMed and references therein.
- N. Mercier, Angew. Chem., Int. Ed., 2019, 58, 17912 CrossRef.
- M. D. Smith, B. A. Connor and H. I. Karunadasa, Chem. Rev., 2019, 119(5), 3104–3139 CrossRef.
- G. Zhou, B. Su, J. Huang, Q. Zhang, Z. Xi and Z. Xia, Mater. Sci. Eng., R, 2020, 141, 10054 CrossRef.
- G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001 CrossRef.
- M. Bonn, K. Miyata, E. Hendry and X.-Y. Zhu, ACS Energy Lett., 2017, 2(11), 2555–2562 CrossRef.
- J. Yin, H. Li, D. Cortecchia, C. Soci and J.-L. Brédas, ACS Energy Lett., 2017, 2(2), 417–423 CrossRef.
- F. Zheng and L. Wang, Energy Environ. Sci., 2019, 12, 1219–1230 RSC.
- D. Ghosh, E. Welch, A. J. Neukirch, A. Zakhidov and S. Tretiak, J. Phys. Chem. Lett., 2020, 11(9), 3271–3286 CrossRef PubMed.
- W. P. D. Wong, J. Yin, B. Chaudhary, X. Y. Chin, D. Cortecchia, S.-Z. A. Lo, A. C. Grimsdale, O. F. Mohammed, G. Lanzani and C. Soci, ACS Mater. Lett., 2020, 2(1), 20–27 CrossRef.
- D. Meggiolaro, F. Ambrosio, E. Mosconi, A. Mahata and F. DeAngelis, Adv. Energy Mater., 2020, 10, 1902748 CrossRef.
- L. R. V. Buizza and L. H. Herz, Adv. Mater., 2021, 33, 2007057 CrossRef.
- W. Tao, Y. Zhang and H. Zhu, Acc. Chem. Res., 2022, 55(3), 345–353 CrossRef PubMed.
- S. H. Parra, D. B. Straus, B. T. Fichera, N. Iotov, Ch. R. Kagan and J. M. Kikkawa, ACS Nano, 2022, 16(12), 21259–21265 CrossRef PubMed.
- M. Baskurt and J. Wiktor, J. Phys. Chem. C, 2023, 127(49), 23966–23972 CrossRef CAS.
- D. Emin, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13691 CrossRef PubMed.
- M. D. Smith, A. Jaffe, E. R. Dohner, A. M. Lindenberg and H. I. Karunadasa, Chem. Sci., 2017, 8, 4497 RSC.
- M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51(3), 619–627 CrossRef PubMed.
- R. Gautier, M. Paris and F. Massuyeau, J. Am. Chem. Soc., 2019, 141(32), 12619–12623 CrossRef PubMed.
- S. Li, J. Luo, J. Liu and J. Tang, J. Phys. Chem. Lett., 2019, 10(8), 1999–2007 CrossRef PubMed.
- Z. Xu, X. Jiang, H.-p Cai, K. Chen, X. Yao and Y. Feng, J. Phys. Chem. Lett., 2021, 12(43), 10472–10478 CrossRef PubMed.
- Y. Lekina, D. G. Bradley, Y. Xiao, A. Thanetchaiyakup, X. Zhao, J. Kaur, S. Chakraborty, H. S. Soo, J. V. Hanna and Z. X. Shen, J. Phys. Chem. C, 2023, 127(33), 16496–16507 CrossRef.
- Ch Yang, Q. Wei, Y. Gong, M. Long, G. Zhou, G. Xing and B. Wu, J. Phys. Chem. Lett., 2023, 14(44), 10046–10053 CrossRef PubMed.
- F. Jiang, Z. Wu, M. Lu, Y. Gao, X. Li, X. Bai, Y. Ji and Y. Zhang, Adv. Mater., 2023, 35, 2211088 CrossRef PubMed.
- Y. Han, X. Cheng and B.-B. Cui, Mater. Adv., 2023, 4, 355–373 RSC.
- K. Fedoruk, D. Drozdowski, M. Maczka, J. K. Zareba, D. Stefańska, A. Gagor and A. Sieradzki, Inorg. Chem., 2022, 61(39), 15520–15531 CrossRef CAS PubMed.
- S. Kahmann, E. K. Tekelenburg, H. Duim, M. E. Kamminga and M. A. Loi, Nat. Commun., 2020, 11, 2344 CrossRef CAS PubMed.
- Y. Wang, X. Lü, W. Yang, T. Wen, L. Yang, X. Ren, L. Wang, Z. Lin and Y. Zhao, J. Am. Chem. Soc., 2015, 137(34), 11144–11149 CrossRef CAS.
- G. Liu, L. Kong, W. Yang and H.-K. Mao, Mater. Today, 2019, 27, 91–106 CrossRef CAS.
- Y. Fang, L. Zhang, L. Wu, J. Yan, Y. Lin, K. Wang, W. L. Mao and B. Zou, Angew. Chem., Int. Ed., 2019, 58, 15249 CrossRef CAS.
- Y. Qin, Z. Lv, S. Chen, W. Li, X. Wu, L. Ye, N. Li and P. Lu, J. Phys. Chem. C, 2019, 123(36), 22491–22498 CrossRef CAS.
- Y. Liang, Y. Zang, X. Huang, C. Tian, X. Wang and T. Cui, J. Phys. Chem. C, 2020, 124(16), 8984–8991 CrossRef.
- Z. Ma, F. Li, L. Sui, Y. Shi, R. Fu, K. Yuan, G. Xiao and B. Zou, Adv. Opt. Mater., 2020, 8, 2000713 CrossRef.
- Y. Wang, S. Guo, H. Luo, C. Zhou, H. Lin, X. Ma, Q. Hu, M.-H. Du, B. Ma, W. Yang and X. Lü, J. Am. Chem. Soc., 2020, 142(37), 16001–16006 CrossRef.
- A. Celeste and F. Capitani, J. Appl. Phys., 2022, 132(22), 220903 CrossRef.
- M. Maczka, S. Sobczak, P. Ratajczyk, F. F. Leite, W. Paraguassu, F. Dybała, A. P. Herman, R. Kudrawiec and A. Katrusiak, Chem. Mater., 2022, 34, 7867–7877 CrossRef.
- X. Zhao, F. Gao, W. Li, Z. Li, Y. Zhang, K. Li, H. Hu, W. Cai, J. Zhang and X. Bu, J. Mater. Chem. C, 2024, 12, 4599–4605 RSC.
- Y. Fang, L. Zhang, Y. Yu, X. Yang, K. Wang and B. Zou, CCS Chem., 2020, 3(8), 2203–2210 CrossRef.
- N. Mercier, S. Poiroux, A. Riou and P. Batail, Inorg. Chem., 2004, 43(26), 8361–8366 CrossRef PubMed.
- A. Lemmerer and D. G. Andreas, CrystEngComm, 2010, 12(4), 1290–1301 RSC.
- B. Cheng, T.-T. Li, P. Maity, P.-Ch Wei, D. Nordlund, K.-T. Ho, D.-H. Lien, Ch-H. Lin, R.-Z. Liang, X. Miao, I. A. Ajia, J. Yin, D. Sokaras, A. Javey, I. S. Roqan, O. F. Mohammed and J.-H. He, Commun. Phys., 2018, 1, 80 CrossRef.
- J. Yin, P. Maity, R. Naphade, B. Cheng, J.-H. He, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, ACS Nano, 2019, 13(11), 12621–12629 CrossRef PubMed.
- X. Chen, H. Lu, K. Wang, Y. Zhai, V. Lunin, P. C. Sercel and M. C. Beard, J. Am. Chem. Soc., 2021, 143(46), 19438–19445 CrossRef.
- N. Mercier, S. Poiroux, A. Riou and P. Batail, Inorg. Chem., 2004, 43(26), 8361–8366 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558(R) CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef.
- D. A. Egger and L. Kronik, J. Phys. Chem. Lett., 2014, 5(15), 2728–2733 CrossRef PubMed.
- S. X. Tao, X. Cao and P. A. Bobbert, Sci. Rep., 2017, 7, 14386 CrossRef PubMed.
- C.-G. Zhao, G. M. Dalpian, Z. Wang and Z. Zunger, Phys. Rev. B, 2020, 101, 155137 Search PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- I. Hamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103(R) CrossRef.
- H. Peng, Z.-H. Yang, J. P. Perdew and J. Sun, Phys. Rev. X, 2016, 6, 041005 Search PubMed.
- B. Cheng, T.-Y. Li, P. Maity, P.-Ch Wei, D. Nordlund, K.-T. Ho, D.-H. Lien, Ch-H. Lin, R.-Z. Liang, X. Miao, I. A. Ajia, J. Yin, D. Sokaras, A. Javey, I. S. Roqan, O. F. Mohammed and J.-H. He, Commun. Phys., 2018, 1, 80 CrossRef.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49(2), 299–312 CrossRef.
- A. Baldereschi, S. Baroni and R. Resta, Phys. Rev. Lett., 1988, 61, 734 CrossRef PubMed.
- R. Saran, A. Heuer-Jungemann, A. G. Kanaras and R. J. Curry, Adv. Opt. Mater., 2017, 5, 1700231 CrossRef.
- A. Francisco-López, B. Charles, O. J. Weber, M. I. Alonso, M. Garriga, M. Campoy-Quiles, M. T. Weller and A. R. Goñi, J. Phys. Chem. Lett., 2019, 10(11), 2971–2977 CrossRef.
- J. Xu, S. Yu, X. Shang and X. Chen, Adv. Photon. Res., 2023, 4, 2200193 CrossRef.
- A. Pieni
![[a with combining cedilla]](https://www.rsc.org/images/entities/char_0061_0327.gif) żek, F. Dybała, M. P. Polak, Ł. Przypis, A. P. Herman, J. Kopaczek and R. Kudrawiec, J. Phys. Chem. Lett., 2023, 14(28), 6470–6476 CrossRef.
żek, F. Dybała, M. P. Polak, Ł. Przypis, A. P. Herman, J. Kopaczek and R. Kudrawiec, J. Phys. Chem. Lett., 2023, 14(28), 6470–6476 CrossRef. - C. Stavrakas, S. J. Zelewski, K. Frohna, E. P. Booker, K. Galkowski, K. Ji, E. Ruggeri, S. Mackowski, R. Kudrawiec, P. Plochocka and S. D. Stranks, Adv. Energy Mater., 2019, 9, 1901883 CrossRef.
- S.-C. Wu, C.-S. Wu, C.-H. Chien, T.-W. Zhang, C.-X. Yang, C. Liu, M.-H. Li, C.-F. Lin, Y.-H. Wu, B.-H. Lin, Y.-H. Chou, Y.-C. Chang, P. Chen and H.-C. Hsu, Adv. Funct. Mater., 2023, 33, 2213427 CrossRef.
- Y. Lekina, B. Febriansyah, X. Fan, L. You, S. Morris, J. Wang, J. England, X. Huang, J. Yan and Z. X. Shen, J. Phys. Chem. C, 2021, 125(41), 22630–22642 CrossRef.
- H. Diab, Ch Arnold, F. Lédée, G. Trippé-Allard, G. Delport, Ch Vilar, F. Bretenaker, J. Barjon, J.-S. Lauret, E. Deleporte and D. Garrot, J. Phys. Chem. Lett., 2017, 8(13), 2977–2983 CrossRef.
- D. Hong, J. Li, S. Wan, I. G. Scheblykin and Y. Tian, J. Phys. Chem. C, 2019, 123(19), 12521–12526 CrossRef.
- Y. Fang, H. Wei, Q. Dong and J. Huang, Nat. Commun., 2017, 8, 14417 CrossRef.
- S. Neutzner, F. Thouin, D. Cortecchia, A. Petrozza, C. Silva and A. R. S. Kandada, Phys. Rev. Mater., 2018, 2, 064605 CrossRef.
- J. Tan, D. Li, J. Zhu, N. Han, Y. Gong and Y. Zhang, Nanoscale, 2022, 14, 16394–16414 RSC.
- S. Dai, X. Xing, V. G. Hadjiev, Z. Qin, T. Tong, G. Yang, Ch Wang, L. Hou, L. Deng, Z. Wang, G. Feng and J. Bao, Today Phys., 2023, 30, 100926 Search PubMed.
- S. Wang, M. Huang, Y.-N. Wu and S. Chen, Adv. Theory Simul., 2021, 4, 2100060 CrossRef.
- B. Chen, R. Chen and B. Huang, Adv. Energy Sustainability Res., 2023, 4, 2300018 CrossRef.
- Y. Yamada and Y. Kanemitsu, NPG Asia Mater., 2022, 14, 48 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00743c |
| This journal is © The Royal Society of Chemistry 2025 |