Single-cell impedance spectroscopy of nucleated cells

Abstract

Single-cell microfluidic impedance spectroscopy is widely used to characterise single cells, but the intrinsic electrical properties are rarely determined owing to the limited number of data points across a wide frequency bandwidth. To address this shortcoming, we have developed a system with an extended frequency range (to 550 MHz) that measures the impedance spectrum of single nucleated cells at high throughput. The system was evaluated using HL60 cells treated with glutaraldehyde or cytochalasin D, and THP-1 cells differentiated into macrophages. The impedance data was fitted to the double-shell model to obtain cell membrane capacitance and cytoplasm conductivity. It is shown that reducing the conductivity of the suspension media significantly enhances the dielectric relaxations of the cell membrane, allowing small differences between control and chemically modified cells to be discriminated.

---

1. Introduction

The electrical properties of single cells have been widely used as potential label-free markers of cell phenotype, and microfluidic impedance cytometry (MIC) can rapidly characterise the electrical properties of individual cells, for a recent review see.¹ MIC has been used to explore a range of cell properties including viability,^2,3 identification of leukocyte types in whole blood,^4,5 activation state of macrophages,^6,7 parasite invasion of red blood cells,^8,9 identification of cancer cells,^10,11 and antimicrobial susceptibility.^12,13

In microfluidic impedance cytometry, cells are usually measured at two or at most three discrete frequencies, and categorisation is typically made according to the value of the impedance signals, for example, amplitude, phase, and/or electrical opacity (the ratio of high to low frequency impedance). However, this limited range of measurements is insufficient to determine the intrinsic electrical properties of each single cell (e.g. membrane capacitance), which requires fitting the frequency-dependent impedance data to a set of Debye relaxations,¹⁴ using, for example, a multi-shell model. Too few frequency points and/or a limited frequency range leads to poor fits that return cell electrical properties with a high degree of uncertainty, limiting the applicability of the method to distinguish small changes between different cells. To address this, the properties of single cells need to be measured across a wide range of frequencies. Early work by Sun et al.¹⁵ used maximum length sequence (MLS) analysis to measure the properties of polystyrene beads with 512 evenly distributed frequencies between approximately 1 kHz and 500 kHz, but this method had a limited frequency bandwidth. Some groups have attempted to extrapolate particle dielectric parameters from a limited range of frequencies. For example, Chai et al.¹⁶ used giant liposomes of known radius, membrane permittivity and cytoplasm conductivity and fitted a single dispersion to four discrete frequencies up to 1.2 MHz. The dielectric properties of the liposomes were extracted using the single-shell model.¹⁷ Zhao et al.^18,19 used a constriction channel to measure the capacitance of single cells at two low frequencies, up to 250 kHz. Using equivalent electrical circuits and without considering the nucleus in the model, they claimed to extract the cell membrane capacitance. Haandbæk et al.²⁰ characterised different yeast cell phenotypes at frequencies up to 20 MHz, fitting data to a shell model including the cell wall.

We recently described a single-cell dielectric spectroscopic method capable of characterising the properties of thousands of single cells in the frequency range from 200 kHz to 50 MHz with 8 simultaneous frequencies.²¹ The system was evaluated using model particles that have no nucleus (red blood cells (RBCs) and ghosts), where the 50 MHz upper frequency limit was sufficient to fit the data to the single-shell model. However, this frequency range is insufficient to fully characterise the electrical properties of nucleated mammalian cells suspended in physiological saline, where the frequency needs to extend to >500 MHz. In this paper, we describe an improved system capable of high-speed multi-frequency characterisation of nucleated cells. In order to extract the dielectric properties of each individual cell, single-cell spectra were fitted to the double-shell model by post-processing the data, although real-time machine learning methods could also be used.²² Throughput is around 250 cells per second and the system performance was demonstrated by measuring the intrinsic dielectric properties of different cells.

Classically, the dielectric properties of nucleated (mammalian) cells are usually measured in low-conductivity media. This is done for several reasons: to minimise issues with electrode polarisation which is much worse for a high conductivity media (thin double layer), and also to minimise Joule heating in the medium, particularly for single-cell electrorotation studies where the electric field can be very high. Furthermore, because the cell membrane characteristic relaxation frequencies decrease in a low-conductivity suspending medium, it is easier to generate the maximum frequency of the measurement system e.g. 10 MHz. To avoid osmotic stress, cells are resuspended in a non-metabolising sugar solution. However, single-cell impedance cytometry is generally performed using physiological saline to maximise the current through the micro-channel and the signal to noise (SNR). To avoid issues with electrode polarisation reference beads can be used to calibrate the transfer function of the system.^20,21 However, as shown here, there is a trade-off between optimising the suspending medium conductivity for SNR (high conductivity) and the ability to resolve discrete Debye relaxations (lower conductivity).

2. Theory

2.1. Shell model and mixture theory

The multi-shell model developed by Irimajiri et al.²³ has been widely used to determine the intrinsic dielectric properties of cells from experimental impedance data, both for the case of cell suspensions²⁴ and for single-cell electrorotation measurements.²⁵ In this model the complex permittivity of a cell in suspension is related to the cell and suspending media by Maxwell mixture's theory (MMT):where a general complex permittivity is defined as , 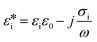φ_cell is the volume fraction of the cell in the measurement volume, and the Clausius–Mossotti factor of a cell is defined as:

The complex permittivity of the cell is modelled as a series of concentric shells, as illustrated in Fig. 1(a), which shows the double-shell model as applied to a nucleated cell. This model relates the dielectric parameters of each individual shell to the complex dielectric properties of the cell according to:^14,26

where the subscript “1” indicates cell membrane. The factor y_a is given by y_a = (R_a/r_cell)³, with r_cell the cell radius, d₁ the thickness of the cell membrane and R_a = r_cell − d₁. The parameter E_a is a factor that depends on layer dimensions and dielectric parameters, see ESI† for full derivation of the double-shell model. Note that the cell membrane capacitance C_mem, cytoplasm conductivity σ_cyt, and cell diameter d are determined from C₁ = ε₁/d₁, σ₂, and 2r_cell in the model shown in Fig. 1(a). Substituting eqn (3) into eqn (2) gives the Clausius–Mossotti factor for the cell as a function of the suspending media, cell dielectric properties and dimensions.

Fig. 1 Double-shell model and calculated Clausius–Mossotti factor 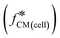(a). Diagram showing the multi-shell model used to characterise a nucleated cell, subscript 1: cell membrane, 2: cytoplasm, 3: nuclear envelope, 4: nucleoplasm, med: media – see ESI† for further details. Note that the cell membrane capacitance C_mem, cytoplasm conductivity σ_cyt, and cell diameter d correspond to C₁ (ε₁/d₁), σ₂, and 2r_cell. (b) and (c). Plots of the real and imaginary parts of the Clausius–Mossotti factor for a “typical” cell as a function of frequency for different suspending media conductivities, modelled using the double-shell model. Cell parameters were: diameter = 12 μm; membrane capacitance = 12.4 mF m⁻²; cytoplasm conductivity = 0.3 S m⁻¹; for other parameters, see ESI† Table S1. (d)–(g) Illustration showing how changes in cell dielectric parameters influence the real and imaginary parts of . Diameter range (orange region), 8–24 μm, membrane capacitance (red region), 5.3–19.5 mF m⁻², and cytoplasm conductivity (blue region), 0.1–0.5 S m⁻¹. Plots are calculated for 0.32 S m⁻¹ and 1.6 S m⁻¹ conductivity electrolyte. The black curves are for “typical” values of cell dielectric parameters, as in (b) and (c).

Fig. 1(b) and (c) shows example plots of calculated using the double-shell model for a “typical” nucleated cell (for details, see figure legend) suspended in electrolytes of different conductivities (corresponding to four-fold dilutions of physiological saline). The figure demonstrates how the spectrum changes with suspending medium conductivity. The real part of the polarizability is always negative except for the lowest conductivity, and the magnitude of the frequency dispersion (peak in the imaginary part) is the greatest at the lowest conductivity.

Fig. 1(d)–(g) demonstrate how variations in cell dielectric properties manifest themselves in different frequency windows for the highest and lowest suspending medium conductivities. The low-frequency limit of the Clausius–Mossotti factor (∼100 kHz) is dominated by the cell volume (assuming the particle to be a perfect insulator) and to a lesser degree by the membrane capacitance. For a fixed specific membrane capacitance, the low frequency relaxation is particle size dependent, moving to higher frequencies for smaller cells. Higher membrane capacitance shifts this relaxation peak to a lower frequency whilst the cytoplasm conductivity impacts the spectra at high frequencies >10 MHz.

Comparing the spectra for these two conductivities shows that the relative changes due to variations in cell dielectric parameters are more pronounced in the lower conductivity. In terms of impedance measurements, the absolute value of the current between the two electrodes is lower (by approximately a factor of 5), but the relative change in impedance is greater at 0.32 S m⁻¹ than in physiological saline (1.6 S m⁻¹). The single-shell model (Fig. S1†), shows similar trends in terms of conductivity but also illustrates that this is inadequate for modelling a nucleated mammalian cell and would lead to incorrect values of cell membrane and cytoplasm dielectric properties. Fig. 1 also demonstrates that in order to measure and characterise nucleated cells, it is imperative that the measurement frequency extends to hundreds of MHz to allow accurate data fitting with the double-shell model.

2.2. Experimental principle

The microfluidic impedance cytometer along with the workflow is shown in Fig. 2. The measurement chip is made from glass and consists of a microchannel 30 μm in height and 40 μm in width, with several micrometer-sized electrodes. An AC voltage is applied to one set of electrodes while the opposite sensing electrodes measure the differential current (ESI† Fig. S2). As a cell transits through the channel, a bipolar Gaussian differential signal is generated, with an amplitude related to the cell impedance at that applied frequency.

Fig. 2 System overview and measurement principle. Cells suspended in saline flow along the microchannel where microelectrodes measure the differential current at different frequencies ranging from 250 kHz to 550 MHz. After gating and calibration, the frequency spectrum was fitted to the double-shell model to give cell diameter and cell dielectric parameters (membrane capacitance: C_mem, cytoplasm conductivity: σ_cyt).

The current in the empty channel should ideally be invariant with frequency, but the actual system consists of many circuit elements, which means that the impedance of the empty cell is non-linear. To overcome these non-linearities, polystyrene beads of known size and dielectric properties are used as internal calibration particles.^20,21 Because the complex permittivity of the bead is known and fixed, the complex permittivity of the cell can be determined from the ratio of particle volumes.²¹ For spherical cells dispersed in a suspending media at a low volume fraction, (φ_cell < 0.01), the differential complex current of the mixture is given by:²¹

and the ratio of the complex current between a cell (unknown) and a bead (known) is:Because φ_bead/φ_cell = r³_bead/r³_cell, the Clausius–Mossotti factor can be expressed asEqn (2) and (6) are two different expressions of the same parameter, . The equations show that the dielectric spectrum of the cell can be determined from the experimentally measured differential currents ( and ) provided the frequency-dependent dielectric properties of the beads (r_bead and ) are known according to:

The impedance signal is the differential current for the cell/bead multiplied by the Clausius–Mossotti factor for the bead (right-hand side of eqn (7)). Given that the radius and dielectric properties of the bead are known then from eqn (7), the radius and unknown dielectric parameters of the cell can be determined by fitting the data to the shell model. In this case, the experimental data was fitted using the least-squares minimisation algorithm “pattern-search” (MATLAB). The fit determines cell size and the volume ratio of nucleus to cell, along with dielectric parameters (ε₁ to ε₄, and σ₂ to σ₄). For the fitting, these parameters were allocated starting values and boundaries as in ESI† Table S2. The cell membrane conductivity, σ₁ was fixed to 10⁻¹⁰ S m⁻¹ (assuming a viable cell).

3. Methods

3.1. Experiment setup

The impedance chips (Fig. 2) were fabricated using standard photolithography and thermo-compression bonding as outlined elsewhere.²⁷ Electrodes (Pt) were patterned onto 700 μm glass wafers followed by deposition and patterning of a thick resist to create channels 40 μm wide and 30 μm high. A pair of wafers were bonded together and the final microfluidic chips were clamped into a custom PEEK holder to provide electrical and fluidic connections. An overview of the chip fabrication protocol is shown in Fig. S3.†

Cells were suspended at a concentration of 5 × 10⁵ ml⁻¹ in saline of different conductivities and mixed with polystyrene reference beads (latex carboxylate-modified polystyrene beads, Sigma Aldrich) at a concentration of around 2.5 × 10⁵ ml⁻¹. The suspension was pumped through the microfluidic chip at a flow rate of 30 μl min⁻¹. A lock-in amplifier (UHFLI, Zurich Instruments) generated an applied voltage V_AC in the frequency range from 250 kHz to 550 MHz. The current signals from the chips were amplified with custom electronics and demodulated with the lock-in. For single-cell spectroscopy, eight frequencies were applied simultaneously to the impedance electrodes. Data was processed using custom MATLAB scripts to extract the signal amplitude at different frequencies for each particle.

Two different conductivity saline solutions were used (a) normal physiological saline at 1.6 S m⁻¹ (0.9% w/v) with an osmolarity of 280 to 300 mOsm and (b) 5× diluted saline (0.32 S m⁻¹) with D-mannitol (in water) to adjust the osmolarity to the range of 280 to 300 mOsm. Prior to use, the solutions were filtered through a 0.22 μm filter.

3.2. Cells

Two different cells were used in the experiments, HL60 and THP-1. The cells were grown in the same culture media, consisting of RPMI 1640 + Glutamax (Gibco) media, 10% fetal bovine serum (FBS, Gibco), and 1% penicillin-streptomycin (Sigma Aldrich) in a humidified incubator at 37 °C and 5% CO₂. Cells were harvested for treatment and measurement at a concentration of 5 × 10⁵ cells per ml.

HL60 cells were treated with glutaraldehyde (GA, 11428743, Thermo Scientific Chemicals) as follows. GA-DPBS solution at a concentration of 1% v/v was added to a 1 ml suspension of cells in DPBS (11590476, Gibco). The sample was kept at room temperature for 30 minutes and then resuspended in saline (conductivity 0.32 S m⁻¹ or 1.6 S m⁻¹). Cytochalasin D (CytoD, C2618, Sigma Aldrich) was used to disrupt HL60 cell cytoskeletons. Stock solutions of CytoD were dissolved in DMSO (A13280.36, Thermo Scientific Chemicals) and added to 1 ml cell samples in 0.32 S m⁻¹ or 1.6 S m⁻¹ media to adjust the concentration to 10 μM. After incubating the cells at 37 °C incubator for 10 minutes, the sample was kept at room temperature for around 1 minute so that the conductivity would return to the correct value. The untreated group was added to the same amount of DMSO and also kept at 37 °C for 10 minutes, following the same protocol as the treated group.

THP-1 differentiation was achieved by adding phorbol 12-myristate 13-acetate (PMA, P1585, Sigma Aldrich) into the cell suspension (in culture media) followed by incubation at 37 °C, 5% CO₂ for 48 h. THP-1 cells were harvested at a concentration of 5 × 10⁵ ml⁻¹ and resuspended in fresh culture media. Stock PMA dissolved in DMSO was added to adjust the concentration to 200 ng ml⁻¹. The untreated THP-1 group was added to the same amount of DMSO as a control. The two different cell suspensions were both moved to 6-well flasks and placed in an incubator. After 48 h, the differentiated macrophages (M0) were bathed in a thin layer of TrypLE Express (12605010, Gibco) and placed in an incubator for 10 minutes, then resuspended in culture media without PMA at 5 × 10⁵ ml⁻¹ for further measurement. A control group was also resuspended in culture media at the same concentration. Samples were resuspended in 0.32 S m⁻¹ conductivity saline.

4. Results

4.1. Mean dielectric properties and influence of suspending media conductivity

Fig. 3(a) and (b) show example impedance-frequency spectra for a population of untreated HL60 cells (solid dots) and cells fixed with glutaraldehyde (unfilled circles). Glutaraldehyde treatment of cells cross-links both membrane lipids and proteins,²⁸ making the cells non-viable. The data was collected using two frequencies, a fixed reference frequency of 18 MHz and a second frequency that was swept between 250 kHz and 550 MHz at 18 discrete frequencies. Beads and cells were gated using the 18 MHz phase scatter data to maximise the signal to noise ratio (SNR), defined as the mean square ratio of noise to particle sub-populations (Fig. S4†). The spectrum is, therefore, the mean value of impedance at each frequency for the population of cells. The data is the normalised Clausius–Mossotti factor determined using eqn (7) scaled by the ratio of the volume of cells to beads. The numbers of cells at each frequency point are summarised in Table S3.† Data was collected using independent batches of cells on different days. The solid curves (untreated cells) and dashed curves (fixed cells) are best fits to the double-shell model for the real (blue) and imaginary (red) parts of the spectrum. The cell diameter (d), membrane capacitance (C_mem) and cytoplasm conductivity (σ_cyt) were extracted from the fit as described in section 2.2. Table 1 summarises the data set for untreated and fixed cells suspended in saline at 0.32 S m⁻¹ (R² > 0.98), and 1.6 S m⁻¹ (R² > 0.90). For physiological saline, the fixed and unfixed cell diameters were similar. The two key dielectric parameters (C_mem and σ_cyt) were also close (C_mem: 11.07 mF m⁻²vs. 11.52 mF m⁻², σ_cyt: 0.31 S m⁻¹vs. 0.33 S m⁻¹). In the lower-conductivity media, there were slight differences between untreated and fixed cell diameter; C_mem and σ_cyt decreased after glutaraldehyde exposure (C_mem: 9.14 mF m⁻² reducing to 6.32 mF m⁻²; σ_cyt: 0.33 S m⁻¹ reducing to 0.07 S m⁻¹). The mean ± SD of σ_cyt calculated from three repeat experiments decreased from 0.29 ± 0.04 S m⁻¹ to 0.08 ± 0.02 S m⁻¹ after glutaraldehyde exposure (Table S4†). This is consistent with previous studies showing that C_mem and σ_cyt of RBCs (no nucleus) decreased after fixing.^29–31 A plot demonstrating that the single-shell model does not fit the data is presented in ESI† Fig. S5 and Table S5. It shows that the double-shell model is required to fit the data for nucleated cells.

Fig. 3 Plots of the normalised Clausius–Mossotti factor (real and imaginary) for HL60 cells suspended in low and high-conductivity saline. The spectra (blue: real part, red: imaginary part) for untreated (solid lines with dots) and fixed cells (dashed lines with circles) were measured in two different saline conductivities (a) 0.32 S m⁻¹ with 7 μm diameter beads and (b) 1.6 S m⁻¹ with 5 μm diameter beads. (c) Normalised impedance spectra (blue: real part, red: imaginary part) of untreated HL60 cells (solid lines with dots) and CytoD-treated (dashed lines with circles) cells in 0.32 S m⁻¹ media with 7 μm beads. This is a representative plot for three repeats (n = 3). In (a), (b) and (c), dots and circles are individual data points. Solid and dashed lines fit to the double-shell model. (d) Mean and S.D of C_mem for untreated and CytoD treated cells for three independent repeats (n = 3), demonstrating a significant change (***, p ≤ 0.001, Students' t-test) in membrane capacitance. The suspending media relative permittivity was set to 80, cell membrane conductivity was fixed to 10⁻¹⁰ S m⁻¹, membrane thickness to 5 nm and nuclear envelope thickness to 20 nm. Bead permittivity = 2.5ε₀, conductivity = 0.57 mS m⁻¹.

Table 1 Parameter set from fits for untreated and fixed HL60 cells as in Fig. 3(a) and (b). For confidence intervals (CI) see Table S6 in ESI†

		Diameter (d, μm)	Membrane capacitance (Cmem, mF m^−2)	Cytoplasm conductivity (σcyt, S m^−1)
1.6 S m^−1	Untreated	11.6	11.07	0.31
	Fixed	11.7	11.52	0.33
0.32 S m^−1	Untreated	12.0	9.14	0.33
	Fixed	12.6	6.32	0.07
	CytoD	11.7	7.11	0.33

---

HL60 cells were also treated with cytochalasin D (CytoD), a compound that disrupts the cytoskeleton. Cells were measured in 0.32 S m⁻¹ saline and an example data set (n = 3) is shown in Fig. 3(c). The electrical opacity (|Z_3MHz|/|Z_150kHz|) of treated cells was also measured separately (n = 3), see data in Fig. S6.† The treated groups (unfilled circles) have a small but significant difference in the spectra compared with the control cells (solid dots). The optimal frequency for discrimination between the treated and untreated groups was found to occur at a frequency of around 6 MHz (for methodology, see ESI†). The best fits using the double-shell model (solid and dotted lines) are summarised in Table 1. C_mem is reduced after treatment, but σ_cyt remains unchanged. The results summarised in Fig. 3(d) demonstrate a statistically significant difference (data from three independent biological repeats). The membrane capacitance C_mem = 9.27 ± 0.30 mF m⁻² for the untreated group and 7.01 ± 0.19 mF m⁻² for the CytoD group. These findings contrast with previously reported impedance measurements of CytoD-exposed cells suspended in physiological saline where no significant change was observed.³² However, Jaffe and Voldman³³ used a dielectrophoresis spring system to measure a few hundred cells treated with CytoD and demonstrated a small but significant difference in cell polarizability. Liu et al.³⁴ used a constriction channel to measure cell electrical properties and concluded that treated cells had a higher membrane capacitance. However, this method applies significant stress on a cell, changing its shape and potentially influencing the membrane capacitance.³⁵ Importantly, the data in Fig. 3(c) demonstrates that measuring the impedance of cells suspended in a lower conductivity electrolyte increases the sensitivity of the system allowing small changes in cell electrical properties to be determined.

4.2. Single-cell spectroscopy

Single-cell spectra were measured by applying eight simultaneous frequencies spaced logarithmically apart (251 kHz, 761 kHz, 2.31 MHz, 6.99 MHz, 21.2 MHz, 64.1 MHz, 194.3 MHz, 575 MHz). A suspension of HL60 cells consisting of a 50/50 mixture of normal and GA fixed, along with reference beads was measured in 0.32 S m⁻¹ or 1.6 S m⁻¹ saline. Cells were obtained from the same batch for each conductivity. Each single-cell spectrum was normalised against the mean bead impedance and then fitted to the double-shell model as described in section 2.2. Fig. 4(a) and (b) show examples of single-cell spectra for cells in the two different conductivities. Similar to the population mean data (Fig. 3(a) and (b)), the change in the normalised for the untreated and fixed cells in 0.32 S m⁻¹ saline is very clear. However, this difference is barely visible for cells suspended in physiological saline. The fitting results from Fig. 4(a) and (b) are summarised in Table 2. The spectrum for 1000 individual cells from one sample of each type was fitted to the double-shell model and the results are shown on the scatter plots in Fig. 4(c) and (d). For the lower of the two suspending conductivities (Fig. 4(c)), the cell distribution has a low coefficient of variance, with clear separation in size and membrane capacitance. The fixed cells had lower C_mem and σ_cyt (mean ± SD) compared with the untreated cells; see Table 3. However, the values of C_mem and σ_cyt determined from single-cell data were slightly different from those obtained by the population mean method (section 4.1). For example, the mean ± SD of C_mem determined from three repeats using the population mean method is 9.28 ± 0.30 mF m⁻² (Table S4†), while the mean value calculated from 1000 individual cells using the single cell method is 10.47 ± 1.26 mF m⁻² (Table 3). This difference may be because the limited set of frequencies (8) in the single cell data set reduces the accuracy of the fits, particularly at the low frequency end of the spectrum where the size of the cell is determined. These results contrast with the higher conductivity saline results where the subpopulations overlap, making discrimination impossible.

Fig. 4 Single-cell impedance spectra for HL60 cells in low and high-conductivity saline. (a) and (b) are examples of normalised (blue: real part, red: imaginary part) for untreated (solid line with dots) and fixed cells (dashed line with circles) measured in saline of conductivity 0.32 S m⁻¹ and 1.6 S m⁻¹, respectively. (c)-i and (d)-i are scatter plots (d vs. C_mem) for 1000 individual untreated (blue) and fixed (red) HL60 cells. (c)-ii and (d)-ii Histogram of σ_cyt in two different conductivity media. Mean ± SD are summarised in Table 3.

Table 2 Fitting results for untreated and fixed single-cells in 0.32 S m⁻¹ and 1.6 S m⁻¹ saline (Fig. 4(a) and (b)). For confidence intervals (CI), see Table S7 in ESI†

		Diameter (d, μm)	Membrane capacitance (Cmem, mF m^−2)	Cytoplasm conductivity (σcyt, S m^−1)
0.32 S m^−1	Untreated	12.5	10.31	0.24
	Fixed	11.3	6.26	0.07
1.6 S m^−1	Untreated	11.4	10.23	0.36
	Fixed	11.6	9.26	0.43

---

Table 3 Single-cell fitting results (mean ± SD) for untreated and fixed cells in two different conductivity saline (Fig. 4(c) and (d)). CV: coefficient of variation

		Diameter (d, μm)	Membrane capacitance (Cmem, mF m^−2)	Cytoplasm conductivity (σcyt, S m^−1)
0.32 S m^−1	Untreated	11.8 ± 0.7, CV = 0.06	10.47 ± 1.26, CV = 0.12	0.22 ± 0.10, CV = 0.45
	Fixed	12.6 ± 0.8, CV = 0.06	6.02 ± 0.84, CV = 0.14	0.07 ± 0.03, CV = 0.43
1.6 S m^−1	Untreated	11.9 ± 0.6, CV = 0.05	10.64 ± 3.68, CV = 0.35	0.37 ± 0.08, CV = 0.22
	Fixed	12.0 ± 0.5, CV = 0.04	9.15 ± 3.20, CV = 0.35	0.38 ± 0.09, CV = 0.24

---

4.3. Differentiated macrophages

Macrophages play an essential role in the immune system as they recognise, engulf and digest pathogens. Monocytes migrate to the site of inflammation, where they differentiate into macrophages,³⁶ and identifying differentiated macrophages from monocytes is important for the study of immune processes and diseases. In this work, a monocytic leukaemia cell line (THP-1) was differentiated into a macrophage (M0) by exposure to phorbol 12-myristate 13- acetate (PMA).^37,38

Protocols for differentiating THP-1 cells vary widely.^38–41 In this work, cells were exposed to PMA (200 ng ml⁻¹) for 48 h followed by washing and resuspension, as in Fig. 5(a). Fig. S7(a) and (b)† show images of THP-1 and M0 cells in culture media. THP-1 cells float and have regular round shapes, while M0 cells attach to the flask bottom and have a spreading morphology. To measure cell size, THP-1 and M0 cells were dyed with Trypan blue and imaged with a microscope (Fig. 5(b) and (c)). The average diameter of THP-1 cells (30 cells) was 14.3 ± 1.4 μm and M0 cells was 18.0 ± 2.9 μm (30 cells); M0 cells become enlarged after differentiation.

Fig. 5 Single-cell analysis of THP-1 cells differentiated into macrophages (M0) following 48 h exposure to PMA in saline (0.32 S m⁻¹). (a) Experimental workflow for THP-1 cells differentiation. (b) and (c) are images of cells dyed with Trypan blue after harvesting from the plates and ready to be measured. The average diameter (mean ± SD) of 30 THP-1 cells is 14.3 ± 1.4 μm, and 18.0 ± 2.9 μm for 30 M0 cells. (d) Shows a scatter plots (d vs. C_mem) for 1000 individual THP-1 cells (blue) and M0 cells (red). (e) Show a histogram of σ_cyt for two different cell subpopulations. (f) Plots of the mean ± SD of diameter, membrane capacitance and cytoplasm conductivity for each set of 1000 cells (three-repeat experiments). Blue dots are THP-1 cells and red are M0 cells. Statistical analysis of d, C_mem and σ_cyt from Student's t-test (*, p ≤ 0.05; **, p ≤ 0.01; ns, not significant).

Fig. 5(d) shows a scatter plot of diameter (d) vs. C_mem for the THP-1 and M0 population (see Fig. S8† for other data sets). The differentiated M0 cells have a broader distribution in size and membrane capacitance. Fig. 5(e) shows a histogram of σ_cyt, showing that the two groups have a similar range but differ in their mean value (mean ± SD: THP-1: 0.15 ± 0.04 S m⁻¹; M0: 0.14 ± 0.04 S m⁻¹). Fig. 5(f) shows mean ± SD for three repeats with 1000 cells in each group.

There is a significant difference in cell diameter (**, p ≤ 0.01), accompanied by a change in cytoplasm conductivity (*, p ≤ 0.05), but the mean change in membrane capacitance is not significant. The variability in this parameter may reflect differences in cell states since the differentiation ability of THP-1 cells is influenced by passage number. These results differ from the work of Soe et al.⁴² who used dielectrophoresis (DEP) to characterise macrophage phenotypes and reported that the membrane capacitance of THP-1 monocytes and M0 cells were different (11.1 and 12.8 mF m⁻²), but these values were determined from a single DEP cross-over frequency measurement in very low conductivity media.

5. Conclusion

This work shows that the complete dielectric properties of nucleated cells suspended in a high conductivity electrolyte can be measured in a system with an extended frequency range of up to 550 MHz. Data for nucleated cells cannot be accurately fitted to a single-shell model; only to the double-shell model. HL60 cells modified with GA or CytoD were measured both in low (0.32 S m⁻¹) and high-conductivity (1.6 S m⁻¹) saline, demonstrating that the lower conductivity media significantly improves the resolution of the system, making it possible to discriminate untreated from treated cells. Experimentally this is consistent with the work of Ostermann et al.⁴³ who showed that a low conductivity measurement buffer (1 : 4 PBS: 0.28 M sucrose) enhanced discrimination of viable and necrotic U937 cells. Fitting to the double-shell model at 0.32 S m⁻¹ showed that the membrane capacitance of the cross-linked cells was 30% less than untreated cells in saline. The reduction in cytoplasm conductivity was greater, demonstrating a decrease in cytoplasmic ion concentration in the non-viable cells. Cells treated with CytoD had a significantly reduced membrane capacitance but unchanged cytoplasm conductivity. These differences could not be observed in cells suspended in physiological saline.

Single-cell measurements of nucleated cells were also made by applying 8 simultaneous frequencies. In 0.32 S m⁻¹ saline, untreated and fixed cells could be easily discriminated through changes in membrane capacitance and cytoplasm conductivity, consistent with the data for the mean population. Analysis of the electrical properties of THP-1 cells and their differentiation into macrophages demonstrated moderate changes in size and cytoplasm conductivity, with a higher variance in the membrane capacitance.

In conclusion, we have developed a new high-frequency single-cell impedance cytometer capable of analysing many hundreds of single nucleated cells in a short time frame. Resuspension of cells in an electrolyte with conductivity 5× lower than physiological saline improves discrimination between different cell types and significantly increases the accuracy of the double shell fits. Analysis of many individual nucleated cells by impedance spectroscopy can be used to extract dielectric data using the double-shell model. The work highlights the shortcoming of the single-shell model for a nucleated cell and demonstrates the requirement for enhanced frequency bandwidth in order to provide accurate fits.

Data availability

Data for this article can be accessed at [https://doi.org/10.5258/SOTON/D3368].

Conflicts of interest

There are no conflicts of interest.

Acknowledgements

The authors acknowledge Katie Chamberlain for fabrication of the impedance chips, Dr Emily Swindle for the gift of HL60 cells, and Dr. Liku Tezera and Anika Assaraf for the gift of THP-1 cells.

References

1. C. Honrado, et al., Single-cell microfluidic impedance cytometry: from raw signals to cell phenotypes using data analytics, Lab Chip, 2021, 21(1), 22–54.
2. J. Zhong, et al., Multi-frequency single cell electrical impedance measurement for label-free cell viability analysis, Analyst, 2021, 146(6), 1848–1858.
3. Y. Feng, et al., Neural network-enhanced real-time impedance flow cytometry for single-cell intrinsic characterisation, Lab Chip, 2022, 22(2), 240–249.
4. D. Holmes, et al., Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry, Lab Chip, 2009, 9(20), 2881–2889.
5. J. L. Prieto, et al., Monitoring sepsis using electrical cell profiling, Lab Chip, 2016, 16(22), 4333–4340.
6. K. Torres-Castro, et al., Multichannel Impedance Cytometry Downstream of Cell Separation by Deterministic Lateral Displacement to Quantify Macrophage Enrichment in Heterogeneous Samples, Adv. Mater. Technol., 2023, 8(8), 2201463.
7. A. Salahi, et al., Single-cell assessment of the modulation of macrophage activation by ex vivo intervertebral discs using impedance cytometry, Biosens. Bioelectron., 2022, 210, 114346.
8. C. Honrado, et al., Dielectric characterisation of Plasmodium falciparum-infected red blood cells using microfluidic impedance cytometry, J. R. Soc., Interface, 2018, 15(147), 20180416.
9. E. Du, et al., Electric impedance microflow cytometry for characterisation of cell disease states, Lab Chip, 2013, 13(19), 3903–3909.
10. J. S. McGrath, et al., Electrophysiology-based stratification of pancreatic tumorigenicity by label-free single-cell impedance cytometry, Anal. Chim. Acta, 2020, 1101, 90–98.
11. T.-K. Chiu, et al., A low-sample-loss microfluidic system for the quantification of size-independent cellular electrical property—Its demonstration for the identification and characterisation of circulating tumour cells (CTCs), Sens. Actuators, B, 2017, 246, 29–37.
12. D. C. Spencer, et al., A fast impedance-based antimicrobial susceptibility test, Nat. Commun., 2020, 11(1), 5328.
13. T. Tang, et al., Machine learning-based impedance system for real-time recognition of antibiotic-susceptible bacteria with parallel cytometry, Sens. Actuators, B, 2023, 374, 132698.
14. H. Morgan and N. G. Green, AC electrokinetics: colloids and nanoparticles, Research Studies Press, 2003.
15. T. Sun, et al., High speed multi-frequency impedance analysis of single particles in a microfluidic cytometer using maximum length sequences, Lab Chip, 2007, 7(8), 1034–1040.
16. H. Chai, et al., Evaluating the Accuracy of Impedance Flow Cytometry with Cell-Sized Liposomes, ACS Sens., 2023, 8(7), 2681–2690.
17. H. Morgan, et al., Single cell dielectric spectroscopy, J. Phys. D: Appl. Phys., 2007, 40(1), 61–70.
18. Y. Zhao, et al., A microfluidic system enabling continuous characterisation of specific membrane capacitance and cytoplasm conductivity of single cells in suspension, Biosens. Bioelectron., 2013, 43, 304–307.
19. Y. Zhao, et al., Development of microfluidic impedance cytometry enabling the quantification of specific membrane capacitance and cytoplasm conductivity from 100,000 single cells, Biosens. Bioelectron., 2018, 111, 138–143.
20. N. Haandbæk, et al., Characterisation of Single Yeast Cell Phenotypes Using Microfluidic Impedance Cytometry and Optical Imaging, ACS Sens., 2016, 1(8), 1020–1027.
21. D. Spencer and H. Morgan, High-Speed Single-Cell Dielectric Spectroscopy, ACS Sens., 2020, 5(2), 423–430.
22. C. Honrado, et al., Automated biophysical classification of apoptotic pancreatic cancer cell subpopulations by using machine learning approaches with impedance cytometry, Lab Chip, 2022, 22(19), 3708–3720.
23. A. Irimajiri, T. Hanai and A. Inouye, A dielectric theory of “multi-stratified shell” model with its application to a lymphoma cell, J. Theor. Biol., 1979, 78(2), 251–269.
24. K. Asami, et al., Dielectric spectroscopy of biological cells, Bioelectrochem. Bioenerg., 1996, 40(2), 141–145.
25. M. Sancho, et al., Interaction between cells in dielectrophoresis and electrorotation experiments, Biomicrofluidics, 2010, 4(2), 022802.
26. A. Mansoorifar, et al., Accuracy of the Maxwell–Wagner and the Bruggeman–Hanai mixture models for single cell dielectric spectroscopy, IET Nanobiotechnol., 2017, 11(7), 874–882.
27. D. Spencer and H. Morgan, Positional dependence of particles in microfludic impedance cytometry, Lab Chip, 2011, 11(7), 1234–1239.
28. D. Heard and G. Seaman, The action of lower aldehydes on the human erythrocyte, Biochim. Biophys. Acta, 1961, 53(2), 366–374.
29. K. Cheung, S. Gawad and P. Renaud, Impedance spectroscopy flow cytometry: on-chip label-free cell differentiation, Cytometry, Part A, 2005, 65(2), 124–132.
30. A. Salahi, et al., Modified Red Blood Cells as Multimodal Standards for Benchmarking Single-Cell Cytometry and Separation Based on Electrical Physiology, Anal. Chem., 2022, 94(6), 2865–2872.
31. Z. Gagnon, et al., Bovine red blood cell starvation age discrimination through a glutaraldehyde-amplified dielectrophoretic approach with buffer selection and membrane cross-linking, Electrophoresis, 2008, 29(11), 2272–2279.
32. J. Chen, et al., Single-cell electro-mechanical shear flow deformability cytometry, Microsyst. Nanoeng., 2024, 10(1), 173.
33. A. Jaffe and J. Voldman, Multi-frequency dielectrophoretic characterisation of single cells, Microsyst. Nanoeng., 2018, 4, 23.
34. Y. Liu, et al., Development of microfluidic platform capable of characterising cytoplasmic viscosity, cytoplasmic conductivity and specific membrane capacitance of single cells, Microfluid. Nanofluid., 2020, 24(6), 1–11.
35. J. M. Meacham, et al., Enhanced intracellular delivery via coordinated acoustically driven shear mechanoporation and electrophoretic insertion, Sci. Rep., 2018, 8(1), 3727.
36. F. Gatto, et al., PMA-Induced THP-1 Macrophage Differentiation is Not Impaired by Citrate-Coated Platinum Nanoparticles, J. Nanomater., 2017, 7(10), 332.
37. Z. N. Mohd Yasin, et al., Macrophage polarisation in THP-1 cell line and primary monocytes: A systematic review, Differentiation, 2022, 128, 67–82.
38. T. Starr, et al., The phorbol 12-myristate-13-acetate differentiation protocol is critical to the interaction of THP-1 macrophages with Salmonella Typhimurium, PLoS One, 2018, 13(3), e0193601.
39. M. Daigneault, et al., The identification of markers of macrophage differentiation in PMA-stimulated THP-1 cells and monocyte-derived macrophages, PLoS One, 2010, 5(1), e8668.
40. P. B. Aldo, et al., Effect of culture conditions on the phenotype of THP-1 monocyte cell line, Am. J. Reprod. Immunol., 2013, 70(1), 80–86.
41. E. W. Baxter, et al., Standardised protocols for differentiation of THP-1 cells to macrophages with distinct M(IFNgamma+LPS), M(IL-4) and M(IL-10) phenotypes, J. Immunol. Methods, 2020, 478, 112721.
42. M. T. M. Soe, K. L. Spiller and M. Noh, Dielectrophoretic characterisation of macrophage phenotypes, Electrophoresis, 2022, 43(23–24), 2440–2452.
43. M. Ostermann, et al., Label-free impedance flow cytometry for nanotoxicity screening, Sci. Rep., 2020, 10(1), 142.

---

Footnote

† Electronic supplementary information (ESI) available: Please see the file ‘Supplementary.pdf’ for ESI. The ESI includes the derivation of the double-shell model, plots of simulations for single-shell model, opacity plots of HL60 treated with/without CytoD, images of THP-1 and M0 cells, tables of parameter settings for shell model simulations and model fitting, and explanations for SNR, CI, differential amplifier circuit and chip fabrication and so on. See DOI: https://doi.org/10.1039/d5lc00111k

---