Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Eco-friendly NaCl glycerol-based deep eutectic electrolyte for high-voltage electrochemical double layer capacitor†
Daniele
Motta
 a,
Alessandro
Damin
a,
Alessandro
Damin
 a,
Hamideh
Darjazi
a,
Hamideh
Darjazi
 bc,
Stefano
Nejrotti
bc,
Stefano
Nejrotti
 ag,
Federica
Piccirilli
ag,
Federica
Piccirilli
 de,
Giovanni
Birarda
de,
Giovanni
Birarda
 d,
Claudia
Barolo
d,
Claudia
Barolo
 acg,
Claudio
Gerbaldi
acg,
Claudio
Gerbaldi
 bc,
Giuseppe Antonio
Elia
bc,
Giuseppe Antonio
Elia
 bc and
Matteo
Bonomo
bc and
Matteo
Bonomo
 *acf
*acf
aDepartment of Chemistry, NIS Interdepartmental Centre and INSTM Reference Centre, Università di Torino, Torino 10135, Italy. E-mail: matteo.bonomo@uniroma1.it
bGAME Lab, Department of Applied Science and Technology – DISAT, Politecnico di Torino, Torino 10129, Italy
cNational Reference Center for Electrochemical Energy Storage (GISEL) – INSTM, Firenze 50121, Italy
dElettra Synchrotron Light Source, Basovizza 34149, Trieste, Italy
eArea Science Park, Padriciano 34149, Trieste, Italy
fDepartment of Basic and Applied Sciences for Engineering (SBAI), Sapienza Università di Roma, Roma 00161, Italy
gInstitute of Science, Technology and Sustainability for Ceramics (ISSMC-CNR), Via Granarolo 64, 48018 Faenza, Italy
First published on 31st March 2025
Abstract
Herein, we propose eco-friendly electrolytes based on sodium chloride as a hydrogen bond acceptor and glycerol as a hydrogen bond donor, as alternatives to toxic, flammable and unsustainable electrolytes commonly used in electrochemical energy storage systems. By means of an in-depth multi-technique investigation, including Raman and FT-FIR spectroscopy, of the formulated electrolytes, we point out the effect of the structuring of the system on the transport and electrochemical properties. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 molar ratio mixture proves to be a deep eutectic solvent (DES), showing good room temperature ionic conductivity (0.186 mS cm−1) and electrochemical stability (≈3 V). When implemented as electrolyte in an activated-carbon electrochemical double layer capacitor, this DES exhibits superior performance compared to mixtures with different molar ratio and those containing ethylene glycol as the hydrogen bond donor, with a high operational voltage (2.6 V), a specific capacitance of 14.1 F g−1, and a remarkable cycling stability. These findings highlight the potential of glycerol-based DESs as alternative electrolytes for sustainable electrochemical energy storage applications.
10 molar ratio mixture proves to be a deep eutectic solvent (DES), showing good room temperature ionic conductivity (0.186 mS cm−1) and electrochemical stability (≈3 V). When implemented as electrolyte in an activated-carbon electrochemical double layer capacitor, this DES exhibits superior performance compared to mixtures with different molar ratio and those containing ethylene glycol as the hydrogen bond donor, with a high operational voltage (2.6 V), a specific capacitance of 14.1 F g−1, and a remarkable cycling stability. These findings highlight the potential of glycerol-based DESs as alternative electrolytes for sustainable electrochemical energy storage applications.
Green foundation1. This work advances the field of green chemistry by developing an eco-friendly deep eutectic solvent (DES) as a sustainable alternative to toxic, flammable, and unsustainable electrolytes commonly used in electrochemical energy storage systems. It promotes the use of renewable and non-toxic materials while preserving key electrochemical properties.2. The proposed DES is composed of sodium chloride, an inherently sustainable salt, and (bio) glycerol, a byproduct of various industrial processes, particularly biodiesel production. This DES not only offers a sustainable alternative to conventional organic electrolytes but also enhances the eco-friendliness of its own electrolyte category. 3. Since obtaining a greener DES than ours is actually challenging, tailored studies could investigate the recyclability of the DES after use in energy storage devices to close the loop and reduce waste. Additionally, expanding the range of electrochemical application of this DES would pave the way for further sustainable and large-scale use. |
Introduction
The urgent need to address the energy crisis and environmental pollution has driven the scientific community and companies to prioritize alternative energy sources over fossil fuels. Besides, the fluctuating prices of non-renewables, influenced by recent global events, have further highlighted the importance of sustainable energy solutions.1 In this scenario, solar and wind power play and will play a key role with an expected share of 24.7% of global electricity generation in 2028, twice as much as now.2 However, the intermittency and unpredictability of these energy sources3 force the integration of the related technologies with electrochemical energy storage systems (EESSs), such as metal-ion batteries (MIBs) and electrochemical double-layer capacitors (EDLCs).4 Moreover, these technologies are becoming increasingly significant in the automotive market,5 primarily due to the electric vehicle sales growth in the last few years, especially from 2022 to 2023 with a growth of 35%.6MIBs generally rely on an electrolyte composed of a mixture of linear and cyclic organic carbonates, such as dimethyl carbonate and ethylene carbonate, with a metal salt.7 Although this type of electrolytes can achieve high electrochemical performances, there are some drawbacks associated with their thermal stability.8 Indeed, in addition to the low thermal stability of the common fluorinated salts used, such as LiPF6 in lithium-ion batteries,9 organic carbonate solvents are highly flammable and can cause thermal runaways.10 On top of that, conventional organic electrolytes are not environmentally friendly, since they are usually fossil-derived, and they pose a risk to health and the environment due to their inherent toxicity.11 Similarly to MIBs, commercial EDLCs are based on organic electrolytes, mainly consisting of a conductive salt, such as tetraethylammonium tetrafluoroborate (TEABF4), dissolved in acetonitrile or propylene carbonate solvents. These electrolytes present an operation potential window between 2.5 and 2.8 V, which can ensure high energy density.12 Here again, using organic solvents in EDLCs has toxicity, volatility, safety, and sustainability drawbacks, as they are derived from fossil fuels.13 However, since organic electrolytes show a sub-optimal ionic conductivity (in the order of mS cm−1), thus leading to EDLCs with limited power density, an alternative for this application is represented by aqueous electrolytes. However, the latter are not fully compatible with commercial EDLCs due to the low electrochemical stability of water (operation voltage commonly restricted to about 1.0 V), which limits the energy density of the systems.14 Recently, significant effort has been devoted to developing highly concentrated aqueous electrolytes, called “water-in-salt” electrolytes, to promote interionic attractions over water-ion interactions, aiming to extend the electrochemical stability.15 In this scenario, the design of innovative and eco-friendly electrolytes with good ionic conductivity and high operational voltage is crucial for the advancement of sustainable EESS.
In recent years, deep eutectic solvents (DESs)16 have joined ionic liquids (ILs) as alternative electrolytes in several applications,17 among which their use as next-generation electrolytes is of particular interest owing to their low volatility, low flammability and good thermal and electrochemical stability.18,19 A DES is a mixture of two or more compounds for which the eutectic point temperature is deeper than the eutectic point expected for an ideal liquid mixture,20 a concept common with numerous definitions currently found in the literature.21 This unique thermodynamic behavior is due to the establishment of specific intermolecular interactions, mainly hydrogen bonds, between at least one hydrogen bond donor (HBD) and one hydrogen bond acceptor (HBA). Differently from other electrolytes, such as ILs and those based on volatile organic compounds (VOCs), these mixtures can be easily prepared without stringent conditions since they have been proven to be stable in air and humidity, thus contributing to a drastic cost reduction in the production phase.22 Another advantage of this class is the claimed biodegradable nature, although some evidence shows that not all DESs are “readily biodegradable” or non-toxic.23 Indeed, it must be considered that the resulting mixture may not necessarily be harmless in the case of green precursors and that mixtures with metal salts may inherently pose toxicity concerns.17
Recent advancements in novel eutectic electrolytes have shown highly promising results, particularly in post-lithium MIBs batteries.24 Notably, the ZnCl2-ethylene glycol DES has achieved remarkable outcomes enabling a dendrite-free Zn anode and significantly extending the lifespan of zinc-ion batteries.25 Alternatively, electrochemical properties of simpler binary systems like this can be enhanced by incorporating additives, such as water within hybrid eutectic co-solvents,26 or by creating more complex systems involving three or more components.27
Notwithstanding their remarkable features, the main issue that hinders the exploitation of DESs as electrolytes in EESS is their high viscosity, which jeopardizes the ionic conductivity and, thus, the overall system performance.28 Moreover, despite the electrochemical stability window of DESs being wider than expected from protic solvents, it is still smaller than ILs and organic electrolytes.29 Consequently, it is crucial to investigate the correlation between structure and properties further to harness the potential of these electrolytes as eco-friendly alternatives to traditional organic ones and ILs. This approach could pave the way for designing new DESs capable of overcoming the limitations mentioned above, always considering the potential environmental implications of their use.
Differently from the hazardous, toxic and not sustainable HBAs that have been widely used until now,21 in combination with a variety of HBDs, the aim of the work is to propose a truly green electrolyte. In the present work, we formulated novel formulations based on the combination of NaCl (as HBA) with two different HBDs, namely ethylene glycol (EG) and glycerol (Gly). Indeed, while sodium chloride is an inherently sustainable salt, glycerol can be obtained as a byproduct from different industrial processes, especially biodiesel production through transesterification.30,31 Unfortunately, this is not (yet) the same for ethylene glycol since it is currently produced starting from ethylene, which is a petrochemical derivative.32 However, above the fact that the production of ethylene33 and ethylene oxide34 (the forefather of EG) from bioethanol have been proposed, there is much research devoted to the production of this solvent from cellulose and biomass, and especially to the techno-economic evaluation of these synthesis pathways.35 The only noteworthy example of glycerol-based DES electrolyte relies on the most used HBA, choline chloride (ChCl), and it has been tested in supercapacitor showing a specific capacitance of 30 F g−1 at room temperature, but with a quite limited operational voltage (1.9 V operating at a current density of 1 A g−1).36
Before implementation in a complete EDLC, we conducted a multi-technique investigation of the formulations to determine the eventual formation of DESs and correlate the structural properties with the physical, chemical, and electrochemical ones. More in detail, we exploit differential scanning calorimetry (DSC) to assess the mixture's melting temperature and to disclose whether they resemble a DES or salt-in-solvent system. On top of that, Raman spectroscopy was employed to delve into the molecular interactions, figuring out the impact of the HBA on the HBDs conformations, with our findings indicating that this technique can be a reliable method for verifying DES formation.37,38 As a further piece of evidence, the mixtures were analyzed to evaluate their physicochemical and electrochemical properties. Even though EG-based mixtures demonstrated higher ionic conductivity (and lower viscosity) than Gly-based mixtures, in the last ones, the formation of more stable structures strongly impacts electrochemical stability. The interactions established between NaCl and Gly make less room for secondary decomposition reactions that can be noticed in EG-based mixtures. Indeed, based on the multi-technique characterization, only NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 can be considered an actual DES among all the formulated mixtures. Furthermore, it turned out to be the best electrolyte among those studied since the EDLC made with this electrolyte and activated carbon (AC) electrodes can operate stably at high voltage, showing remarkable results for such an eco-friendly electrolyte.
10 can be considered an actual DES among all the formulated mixtures. Furthermore, it turned out to be the best electrolyte among those studied since the EDLC made with this electrolyte and activated carbon (AC) electrodes can operate stably at high voltage, showing remarkable results for such an eco-friendly electrolyte.
Experimental
Materials
Glycerol (CAS no. 56-81-5, BioRenewable, ≥99.5%) and sodium chloride (CAS no. 7647-14-5, ≥99%) were purchased from Sigma Aldrich, while ethylene glycol (CAS no. 107-21-1, ≥99.5%) from TCI. Glycerol and ethylene glycol were pre-treated with a 15-minute vacuum drying process to minimize excess water content before use.Preparation
The mixtures were prepared by stirring the components under heating at 40 °C in closed vials until a homogeneous and transparent phase is formed. This temperature was chosen to avoid any unwanted degradation. The NaCl–EG molar ratio varied between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 and 1
18 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, while the NaCl–Gly molar ratio between 1
12, while the NaCl–Gly molar ratio between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and 1
14 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8. More concentrated mixtures showed the presence of undissolved NaCl, therefore they were not considered. The water content, determined by Karl-Fischer coulometric titration, was found <0.2% w/w for all the mixtures (Table S1†).
8. More concentrated mixtures showed the presence of undissolved NaCl, therefore they were not considered. The water content, determined by Karl-Fischer coulometric titration, was found <0.2% w/w for all the mixtures (Table S1†).
Spectroscopic characterization
Raman spectra were acquired using a laser with λ = 785 nm, associated with the Renishaw Raman Microscope 1000 instrument, after calibrating it with monocrystalline silicon, by applying 1% laser power with a 5× NIR objective lens for 10 acquisitions, each lasting 20 seconds. For both polyols, the region 100–1800 cm−1 was examined. The regions of interest were manipulated by truncation, baseline subtraction and normalization to the most intense peak, to highlight the spectral changes. Since the band intensities, as well as the background, depend on non-constant scattering phenomena (considering the liquid nature of the samples), subtracting the baseline from the spectra is quite challenging, especially throughout the whole spectrum. However, it is possible to subtract the baseline more easily and analyze the intensities of the bands by limiting the analyzed region. For the interpretation of the spectra resulting from Gly-based mixtures, we relied on the simulation of the spectra of each conformation.Far-infrared measurements were performed exploiting the SISSI-Bio source at Elettra Synchrotron,39 delivering light from the THz to the visible range. The ATR (Attenuated Total Reflectance) technique was employed, using a single reflection monolithic diamond crystal. Samples were dropped onto the crystal and enclosed in a sealed chamber, allowing the entire interferometer (Bruker Vertex 70V) to operate under vacuum while keeping the sample in air. The signal was acquired with a helium-cooled bolometer operating at −267.15 °C to ensure optimal sensitivity. The signal in the spectral range from 10 to 600 cm−1 was collected by acquiring 256 scans at a speed of 10 kHz. For each solvent, three measurements were taken and averaged. Absorbance was calculated using as reference the ATR signal of the clean crystal. After subtracting the residual atmospheric absorption (Opus 8.5 Bruker Optics), data were further corrected for the optical path using the refractive indices of the mixtures and following the methodology used by Zunzunegui-Bru et al.40 Lastly, the spectral curves were cut between 40 and 360 cm−1, and a baseline correction was applied using a rubberband method with 128 points (performed with Opus 8.5 by Bruker Optics).
Physicochemical investigation
Melting temperatures were determined with a TAQ200 DSC, acquiring the thermogram between −80 °C and 30 °C with a ramp rate of 10 °C min−1. Before the measurement, each sample underwent two cycles between −80 °C and −50 °C to promote complete crystallization and the presence of a well-defined melting peak. The calorimetry analysis was successful with EG-based mixtures, whereas for Gly-based ones the glassy-like behavior (i.e., mixtures could undergo extended undercooling) was more pronounced thus leading to thermograms without any detectable solid–liquid transitions. Consequently, for those mixtures the melting points were measured using a cold thermometer glass, immersed in the mixtures through the bulb, following an established procedure in our laboratories.37 Each mixture was firstly frozen by immersing the vial in a Dewar flask containing liquid nitrogen (−196 °C) and taking advantage of headspace cooling, without ever allowing its contact with the nitrogen to avoid the fast cooling and so the formation of the glassy state. Once the mixture was frozen, it was allowed to warm up slowly to room temperature. The temperature at which it was possible to extract the bulb from the solid was recorded as the melting point. The reported values are the average of 3 measurements each.Viscosities were measured with a Discovery HR10 rheometer between 20 °C and 90 °C (75 °C for ethylene glycol to avoid any decomposition) with a ramp rate of 5 °C min−1 (Peltier Plate); a 0.9939° cone plate with a diameter of 40 mm were used for the measurements. The shear rate was set at 20 s−1. Before each measurement, a conditioning procedure, at RT with a shear rate of 10 s−1 for 300 s, was performed to evenly distribute the mixture and likely remove any trapped air.
The ionic conductivities were measured with an Hach® Sension + 5071 between 25 °C and 85 °C (75 °C for ethylene glycol, due to possible thermal instability) by means of electrochemical impedance spectroscopy (EIS) in the frequency range between 10 Hz and 1 MHz and with a sinus amplitude of 10 mV. A KCl 0.1 M aqueous solution was used to calibrate the instrument.
Electrochemical analyses
Cyclic voltammetry (CV) curves were acquired to estimate the electrochemical stability window (ESW) of the mixtures. CVs were performed through a BioLogic SP-150 potentiostat with a scan rate of 1 mV s−1. A three-electrode set-up was employed with a carbon disc as the working electrode, a Pt wire as the counter-electrode and AgCl/Ag as the reference electrode. To evaluate the electrochemical performance in EDLC (CV and galvanostatic charge/discharge) symmetrical T-configuration cells (Swagelok Cell) were used. The measurements were made employing two identical activated carbon electrodes. The activated carbon electrodes were prepared by mixing with water a commercial YP50F (Kuraray) activated carbon with C65 (Imerys) conductive carbon additive and PTFE (Sigma Aldrich) as binder in an 85/10/5 ratio. Once a homogenous down-like dispersion was obtained, the material was calendared in a thin self-standing film of 0.5 mm and cut into 12 mm diameter disks with a metal die and left to dry under vacuum using the BUCHI Glass Oven B-585 for 24 hours before use. The cells were assembled inside a UNIlabplus glove box (MBRAUN). Once the cells were prepared, the analyses were carried out with the VMP3 BioLogic instrument. CV curves of complete cells were acquired with the same scan rate of the ESW measurements (1 mV s−1), while the galvanostatic charge/discharge (GCD) technique was performed on the more promising electrolytes at 0.5, 1 and 2 mA cm−2, with an upper cut-off voltage ranging from 2 to 3 V.1H NMR
1H NMR spectra were acquired on a Jeol ECZR600 and spectrometer working at 14.1 T (1H operating frequency: 600 MHz), in DMSO-d6, using the residual solvent peak as an internal reference (DMSO-d5 1H: 2.54 ppm).Results and discussion
Thermal properties
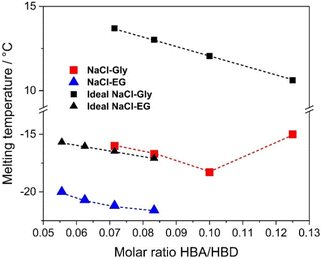
An appropriate thermal analysis is mandatory to obtain the melting point of the formulated mixtures and consequently assign the eutectic point, i.e. the HBA/HBD molar ratio which presents the lowest melting point among those investigated. However, an accurate analysis by means of DSC is not feasible for the Gly-based mixtures41,42 since they exhibit a glass-like behavior (zero-enthalpy phenomenon) and can be easily supercooled without showing any solid–liquid phase transition in the thermograms.43 It should be pointed out that many authors in literature reported melting temperatures of similar mixtures, but without showing any DSC traces, undermining the reliability of the available data. To overcome this hurdle, an ad hoc method, detailed in the Experimental section, was employed to detect the melting temperatures of Gly-based mixtures which are summarized in Table S2.† As can be graphically noticed from the trend of the melting temperatures as a function of the molar ratio sketched in Fig. 1, the lowest melting temperature does not belong to the more concentrated mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8), but to NaCl–Gly 1
8), but to NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (−18.3 °C), which is significantly lower than the melting point of an ideal system (following the cryoscopic depression rule), indicating the likely formation of an eutectic system. Even though similar issues with thermograms have been reported for EG-systems,44 we were successful in disclosing the melting point of NaCl–EG mixtures by DSC (Fig. S1†). Such mixtures show a decrease in the melting temperature as the concentration of NaCl increases (Table S2†), following a cryoscopic depression from −20.0 °C (molar ratio 1
10 (−18.3 °C), which is significantly lower than the melting point of an ideal system (following the cryoscopic depression rule), indicating the likely formation of an eutectic system. Even though similar issues with thermograms have been reported for EG-systems,44 we were successful in disclosing the melting point of NaCl–EG mixtures by DSC (Fig. S1†). Such mixtures show a decrease in the melting temperature as the concentration of NaCl increases (Table S2†), following a cryoscopic depression from −20.0 °C (molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18) to −21.6 °C (molar ratio 1
18) to −21.6 °C (molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12), with a typical deviation from the ideality,21 as shown in Fig. 1.
12), with a typical deviation from the ideality,21 as shown in Fig. 1.
Spectroscopic characterization of NaCl–Gly mixtures
According to the literature, DESs are generally described based on the intermolecular (mainly hydrogen bond) interactions between the HBD and the HBA. Essentially, this means that the possibility of a structural change of the HBD inside the eutectic mixture, and how this can affect the formation or not of a eutectic system, the transport properties and electrochemical stability, is never considered. To fill this gap, we performed Raman analysis on the pure solvent and on all formulations in the region 100–1800 cm−1 to assess possible changes in the molecule conformations. Once spectral variations in the different formulations have been established, we analyzed the components underneath specific bands to verify and validate the formation of the DES (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10). Besides, by doing that, we aimed at establishing a correlation between the structural features of the molecules (and thus the resulting intermolecular interactions) and the transport and electrochemical properties which will be discussed in the following paragraphs. Different glycerol conformers exist due to the dihedral angles involving the two C–C–C–O torsions. Each terminal CH2OH group can rotate around the other backbone carbon–carbon bond. These two torsion angles can be divided into three staggered regions known as α, β and γ. The combination of different rotation angles in the molecule allows glycerol to show up in 6 possible conformations called αα, αβ, αγ, ββ, βγ and γγ.45 According to the molecular dynamics simulations conducted by Chelli et al. in 1999,46 the most plentiful conformations in the liquid phase are αα, αγ and γγ, with percentages of 48%, 46% and 4.4%, respectively. Moreover, they noticed that in the glassy state, the population of conformers is naturally identical to that of the supercooled liquid near the glass transition, differently from the crystalline state in which αα conformer is the only one present.47,48 However, in 2000 the same group49 found a different population in the liquid phase by deconvoluting the experimental IR spectrum according to the DFT computed normal modes for several conformations. Specifically, they obtained the best fit by using 70% of αα, 27% of αγ and 3% of γγ, demonstrating the complexity of univocally defining glycerol conformations in the liquid phase. This behavior is corroborated by the analysis conducted by Towey et al.,50 who combined neutron diffraction experiments and computational modelling to determine glycerol conformations in the liquid phase. The simulation that turned out to be the more accurate had 83.5% of αβ, 10.4% of αγ, 4.3% of βγ and 1.8% of γγ, a distribution completely different from the previous results. Another aspect to underline is the challenges in rationalizing the relationship between conformations and the Raman spectrum, which was attempted by Chelli et al.49 but not with the same valuable results obtained with the IR spectrum. The key finding that can be confidently stated based on these studies is that there is a high probability that α-type conformations are more prevalent than β- and γ-type ones, even without knowing which ones. However, despite this issue, Mendelovici et al.51 carried out the band component analysis, and by using a fitting function, they could assign the principal bands in the region 100–1800 cm−1 (Table S4†).
10). Besides, by doing that, we aimed at establishing a correlation between the structural features of the molecules (and thus the resulting intermolecular interactions) and the transport and electrochemical properties which will be discussed in the following paragraphs. Different glycerol conformers exist due to the dihedral angles involving the two C–C–C–O torsions. Each terminal CH2OH group can rotate around the other backbone carbon–carbon bond. These two torsion angles can be divided into three staggered regions known as α, β and γ. The combination of different rotation angles in the molecule allows glycerol to show up in 6 possible conformations called αα, αβ, αγ, ββ, βγ and γγ.45 According to the molecular dynamics simulations conducted by Chelli et al. in 1999,46 the most plentiful conformations in the liquid phase are αα, αγ and γγ, with percentages of 48%, 46% and 4.4%, respectively. Moreover, they noticed that in the glassy state, the population of conformers is naturally identical to that of the supercooled liquid near the glass transition, differently from the crystalline state in which αα conformer is the only one present.47,48 However, in 2000 the same group49 found a different population in the liquid phase by deconvoluting the experimental IR spectrum according to the DFT computed normal modes for several conformations. Specifically, they obtained the best fit by using 70% of αα, 27% of αγ and 3% of γγ, demonstrating the complexity of univocally defining glycerol conformations in the liquid phase. This behavior is corroborated by the analysis conducted by Towey et al.,50 who combined neutron diffraction experiments and computational modelling to determine glycerol conformations in the liquid phase. The simulation that turned out to be the more accurate had 83.5% of αβ, 10.4% of αγ, 4.3% of βγ and 1.8% of γγ, a distribution completely different from the previous results. Another aspect to underline is the challenges in rationalizing the relationship between conformations and the Raman spectrum, which was attempted by Chelli et al.49 but not with the same valuable results obtained with the IR spectrum. The key finding that can be confidently stated based on these studies is that there is a high probability that α-type conformations are more prevalent than β- and γ-type ones, even without knowing which ones. However, despite this issue, Mendelovici et al.51 carried out the band component analysis, and by using a fitting function, they could assign the principal bands in the region 100–1800 cm−1 (Table S4†).
To interpret the experimental data (Fig. 2a), the spectra of the individual conformers (Fig. S2†) were simulated, also including the presence of an implicit solvent (i.e., ethylene glycol) to get as close as possible to the experimental conditions. Since determining the conformational population of liquid glycerol falls outside the scope of this investigation, these spectra were used to extrapolate information about the variability of specific spectral regions among the formulated mixtures. However, among these, only the region 750–900 cm−1, in which the C–C stretching of the molecule is present, is informative, undergoing significant changes in the peak intensities as the HBA concentration varies (Fig. 2b). Indeed, the region of the C–O stretching (1000–1160 cm−1) and C–C–O rocking (356–600 cm−1), which would have been ideal for analysis as they are directly connected to intermolecular hydrogen bonds, do not present any notable changes (Fig. S3†). Presumably, since these spectral regions are sensitive to both molecular conformations and the surrounding chemical environment (which could cause shifts in Raman spectra), a compensatory effect occurs, leading to minimal, if not negligible, variations in those. Going into more detail, the band at 821 cm−1 decreases as the NaCl concentration increases, while there is a slight growth of the band at 793 cm−1. Nevertheless, from the normalized spectra, the variations in the intensity ratios could be highlighted, but it was not possible to actually see the changes in each band. Consequently, we carried out the deconvolution of the bands of the pure HBD, and then we used its parameters to fit the formulated mixture bands. As shown in Fig. 2c, the deconvolution of the selected region involves the use of four curves, centered at 793 cm−1, 869 cm−1, 821 cm−1 and 850 cm−1 respectively. Once the fitting had been conducted for all the mixtures, the integrated areas relating to each component were extracted and compared (Fig. 2d). Each value was then related to the area of the total curve and plotted as a function of concentration. The most significant structural alteration of the HBD occurs with the initial addition of HBA; actually, beyond NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14, such pronounced variations in peak intensities are no longer noted, except for NaCl–Gly 1
14, such pronounced variations in peak intensities are no longer noted, except for NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, which represents a marked discontinuity in the plot. Specifically, the band at 821 cm−1, probably the most traceable to the αβ conformation (Table S3†), is largely unaffected by the concentration of the HBA, while the bands at 869 cm−1 and 793 cm−1 seem interrelated and inversely related to the band at 850 cm−1, as if there were an exchange between the conformations that dominate the central region (presumably αα and αγ) with those that are prevalent in the external region (presumably ββ, βγ and γγ). Given the uncertainty in defining the conformer population, we cannot assume the percentage conversion of a particular conformation, but we can infer that there is at least a reorganization within the system, with a peculiar arrangement for the eutectic composition. Of course, even in the case of EG-based mixtures the addition of NaCl induces significant spectral variations (Fig. S4†), particularly in the region 450–580 cm−1, which is sensitive to the population of the two different conformers (gauche and trans). This structural change is attributable to the coordination of sodium to the hydroxyl groups of ethylene glycol, highlighted by the spectral changes in the region 810–920 cm−1 (Fig. S4†). However, as the amount of salt increases, the variations clearly become more pronounced, without any discontinuity in the trend. This is due to the formation of salt-in-solvent systems, without a peculiar situation forming as for NaCl–Gly mixtures, among which the 1
10, which represents a marked discontinuity in the plot. Specifically, the band at 821 cm−1, probably the most traceable to the αβ conformation (Table S3†), is largely unaffected by the concentration of the HBA, while the bands at 869 cm−1 and 793 cm−1 seem interrelated and inversely related to the band at 850 cm−1, as if there were an exchange between the conformations that dominate the central region (presumably αα and αγ) with those that are prevalent in the external region (presumably ββ, βγ and γγ). Given the uncertainty in defining the conformer population, we cannot assume the percentage conversion of a particular conformation, but we can infer that there is at least a reorganization within the system, with a peculiar arrangement for the eutectic composition. Of course, even in the case of EG-based mixtures the addition of NaCl induces significant spectral variations (Fig. S4†), particularly in the region 450–580 cm−1, which is sensitive to the population of the two different conformers (gauche and trans). This structural change is attributable to the coordination of sodium to the hydroxyl groups of ethylene glycol, highlighted by the spectral changes in the region 810–920 cm−1 (Fig. S4†). However, as the amount of salt increases, the variations clearly become more pronounced, without any discontinuity in the trend. This is due to the formation of salt-in-solvent systems, without a peculiar situation forming as for NaCl–Gly mixtures, among which the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio is a eutectic point.
10 ratio is a eutectic point.
Raman spectroscopy proved to be highly effective in highlighting the conformational changes in glycerol induced by NaCl. However, due to the set-up of the adopted instrument, exploring intermolecular hydrogen bonds at low Raman shift (Fig. 2a) would be challenging and unreliable. To overcome this issue, FIR spectroscopy was employed. Indeed, this technique is well-established, particularly for ILs,52,53 as a valuable tool for investigating this spectral region. Between 40–360 cm−1, glycerol spectral bands undergo significant changes following on from the increase with each addition of NaCl (Fig. 3a), confirming alterations in the HBD–HBD interactions, as expected in the case of a different conformational population, and a reorganization of the system. As shown in Fig. 3b, the deconvolution of the spectra reveals seven curves, one of which, at 214 cm−1, is likely attributed to trace amounts of water in the mixtures (Fig. S5†). The most responsive bands to NaCl concentration are those at 300 cm−1, 220 cm−1, and 136 cm−1. By plotting the area ratios A(300 cm−1)/A(220 cm−1) and A(136 cm−1)/A(220 cm−1) as a function of the concentration, in Fig. 3c, a minimum appears in both trends at molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, resembling the eutectic behavior (Fig. 1). Once more, as already evidenced by Raman spectroscopy, this concentration represents a unique condition, i.e. the eutectic composition, specifically characterized by a greater increase of the band at 220 cm−1 at the expense of the bands at 300 cm−1 and 136 cm−1. Therefore, the investigation through spectroscopic techniques strongly suggested that NaCl induces not only variations of the surrounding hydrogen bond environment of glycerol, as evidenced by FIR spectroscopy, but also of the population of conformers within the HBD, highlighted by Raman spectroscopy. Moreover, both techniques demonstrate how the spectral discontinuities can be correlated with the thermal ones, i.e. the eutectic point, setting aside the spectroscopic nature of the bands discussed, which is being investigated in independent computational work.
10, resembling the eutectic behavior (Fig. 1). Once more, as already evidenced by Raman spectroscopy, this concentration represents a unique condition, i.e. the eutectic composition, specifically characterized by a greater increase of the band at 220 cm−1 at the expense of the bands at 300 cm−1 and 136 cm−1. Therefore, the investigation through spectroscopic techniques strongly suggested that NaCl induces not only variations of the surrounding hydrogen bond environment of glycerol, as evidenced by FIR spectroscopy, but also of the population of conformers within the HBD, highlighted by Raman spectroscopy. Moreover, both techniques demonstrate how the spectral discontinuities can be correlated with the thermal ones, i.e. the eutectic point, setting aside the spectroscopic nature of the bands discussed, which is being investigated in independent computational work.
 | ||
| Fig. 3 (a) Experimental FIR spectra of pure Gly and Gly-based mixtures. (b) Deconvolution bands (c) A(300 cm−1)/A(220 cm−1) and A(136 cm−1)/A(220 cm−1) as a function of the molar ratio. | ||
Transport properties
The extensive interactions through hydrogen bonding (but also van der Waals and electrostatic interactions to a lesser extent) between HBA and HBD do not affect the thermal properties of the mixtures only, but also their transport properties.29 Generally, because of these extensive networks, DESs have higher viscosity and lower ionic conductivity than conventional electrolytes.28 To gain deeper insight into the correlation between the structure and properties of the mixtures, and since transport properties of an electrolyte play a crucial role in the final performances of EESS, viscosity measurements were performed between 20 °C and 90 °C (80 °C for EG-based mixtures) to understand as this varies with the temperature (Table 1). As expected, viscosity decreases as the temperature increases, following the Vogel–Fulcher–Tammann (VFT) equation (Fig. S6 and 7†):where η0 describes the viscosity of the fluid at a relatively very low temperature, B is a parameter linked to the activation energy (Ea), and T0 is the ideal glass-transition temperature (zero configurational entropy).54 Albeit the rationalization of transport properties (viscosity and ionic conductivity) could have also been carried out using the Arrhenius equation, the latter would not have accounted for the glassy nature of the HBDs used, which leads to a temperature dependence of these properties deviating from expected behaviour near their glass transition. The parameters extrapolated from the experimental data are listed in Table S6† for each mixture. The coefficient of regression (R2) is >0.999 for Gly-based mixtures, while it is >0.96 for EG-based mixtures due to the noise caused by their lower viscosities at high temperature, which are close to the limit of the sensitivity of the instrument geometry. Through this model, more accurate viscosity values were extracted in the same temperature range. For EG-based mixtures the viscosity values at room temperature increase with the concentration as expected from “salt-in-solvent” mixtures, as the free volume available for the movement of the molecules is reduced.28 On the contrary, Gly-based mixtures do not behave in the same way since the viscosity increases in order 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 < 1
10 < 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 < 1
14 < 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 < 1
12 < 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, not following the concentration trend. The explanation could lie in the formation of a DES (1
8, not following the concentration trend. The explanation could lie in the formation of a DES (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10), which led to a different conformational population of the mixtures, as suggested by Raman spectroscopy, causing a quite lower viscosity than expected. Specifically, an increase in the β- and γ-type conformations at the expense of the α-type conformation might weaken the hydrogen bond network, ultimately resulting in a less viscous system. Moreover, Gly-based mixtures are more viscous (by two orders of magnitude) than EG-based mixtures, as expected from the viscosity of pure HBDs: this is clearly detectable from parameter B (linked to the activation energy), which is about two times higher (Table S6†). The other aspect related to transport properties is ionic conductivity (Table 2), which severely impacts the final electrochemical capacity of the EESS. As for the viscosity, the ionic conductivities trend of the mixtures follows the VFT equation (Fig. S8 and 9†):
10), which led to a different conformational population of the mixtures, as suggested by Raman spectroscopy, causing a quite lower viscosity than expected. Specifically, an increase in the β- and γ-type conformations at the expense of the α-type conformation might weaken the hydrogen bond network, ultimately resulting in a less viscous system. Moreover, Gly-based mixtures are more viscous (by two orders of magnitude) than EG-based mixtures, as expected from the viscosity of pure HBDs: this is clearly detectable from parameter B (linked to the activation energy), which is about two times higher (Table S6†). The other aspect related to transport properties is ionic conductivity (Table 2), which severely impacts the final electrochemical capacity of the EESS. As for the viscosity, the ionic conductivities trend of the mixtures follows the VFT equation (Fig. S8 and 9†):where σ0 is the ionic conductivity at infinite temperature, B is a parameter linked to the activation energy, Ea, and T0 is the ideal glass-transition temperature (zero configurational entropy). The parameters extrapolated from the experimental data of each mixture are listed in Table S7,† with regression coefficients (R2) > 0.999. We extracted the ionic conductivities in the same temperature range for all the formulations. For EG-based mixtures the ionic conductivity values at room temperature increase with concentration, as expected from “salt-in-solvent” mixtures, in analogy with the decrease observed for viscosity values. Instead, for Gly-based mixtures the ionic conductivity increases with the concentration until NaCl–Gly 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and then remains constant for NaCl–Gly 1
10 and then remains constant for NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8, again demonstrating a discontinuity in the property at the eutectic composition. Hence, our DES has the highest ionic conductivity among the mixtures, and the reason is understandable, as envisaged by the previously discussed drop in viscosity. The ionic conductivities of Gly-based mixtures are, as expected, lower than EG-based mixtures, owing to their higher viscosities. This is also evident from parameter B, which is more negative for Gly-based mixtures (Table S7†).
8, again demonstrating a discontinuity in the property at the eutectic composition. Hence, our DES has the highest ionic conductivity among the mixtures, and the reason is understandable, as envisaged by the previously discussed drop in viscosity. The ionic conductivities of Gly-based mixtures are, as expected, lower than EG-based mixtures, owing to their higher viscosities. This is also evident from parameter B, which is more negative for Gly-based mixtures (Table S7†).
| Mixture | Molar ratio | Viscosity, η (mPa s) | ||||||
|---|---|---|---|---|---|---|---|---|
| 25 °C | 35 °C | 45 °C | 55 °C | 65 °C | 75 °C | 85 °C | ||
| NaCl–EG | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
22.5 | 14.6 | 10.2 | 7.46 | 5.71 | 4.52 | — |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
23.1 | 15.1 | 10.5 | 7.71 | 5.90 | 4.67 | — | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
23.9 | 15.5 | 10.7 | 7.74 | 5.83 | 4.54 | — | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
31.7 | 20.1 | 13.8 | 10.1 | 7.69 | 6.09 | — | |
| NaCl–Gly | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
1114 | 480.8 | 234.8 | 126.6 | 73.8 | 46.0 | 30.2 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
1137 | 487.1 | 237.5 | 128.2 | 75.1 | 47.0 | 31.1 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
1019 | 440.4 | 216.4 | 117.7 | 69.4 | 43.7 | 29.1 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8 |
1143 | 495.6 | 242.9 | 131.2 | 76.7 | 47.8 | 31.4 | |
| Mixture | Molar ratio | Ionic conductivity, σ (mS cm−1) | ||||||
|---|---|---|---|---|---|---|---|---|
| 25 °C | 35 °C | 45 °C | 55 °C | 65 °C | 75 °C | 85 °C | ||
| NaCl–EG | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 18 |
3.75 | 4.71 | 5.61 | 6.44 | 7.21 | 7.92 | — |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 16 |
4.03 | 5.40 | 6.77 | 8.11 | 9.40 | 10.6 | — | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
4.21 | 5.92 | 7.84 | 9.92 | 12.1 | 14.4 | — | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
4.55 | 6.12 | 7.77 | 9.46 | 11.1 | 12.8 | — | |
| NaCl–Gly | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 14 |
0.158 | 0.332 | 0.618 | 1.05 | 1.65 | 2.45 | 3.46 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12 |
0.166 | 0.359 | 0.678 | 1.16 | 1.82 | 2.70 | 3.80 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
0.186 | 0.376 | 0.684 | 1.14 | 1.77 | 2.60 | 3.66 | |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8 |
0.186 | 0.389 | 0.729 | 1.24 | 1.97 | 2.95 | 4.21 | |
As a further step towards the comprehension of how the structure impacts on the transport properties, we evaluated the relation between ionic conductivity and viscosity through the Walden law. This claims that the product of the molar conductivity Λm and the viscosity ηα (where α corresponds to the Walden plot's slope) is constant for infinitely diluted electrolyte solutions, although the approach fits well even with more concentrated systems. Based on this rule, it is possible to draw the Walden plot, log Λmversus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η−1, which is a qualitative method to establish the ionicity of a liquid, which refers to the number of “free” ions in solution.55 The diagonal in the Walden plot represents the so-called ideal KCl line, which is arbitrarily assigned to 1 M aqueous KCl, even though the definition of the ionicity based on this line is questionable since only a point for this solution actually lies on the diagonal.56 In accordance with the position of the Walden plot of the mixtures it is possible to define three cases: (i) superionic liquid, (ii) good ionic liquid and (iii) poor ionic liquid when far above, close or far below the diagonal, respectively.57,58 As shown in the Walden plot reported in Fig. 4, all our mixtures show good ionicity at the respective concentration range, with a slightly higher ionicity in the case of the Gly-based mixtures, meaning that no ionic association limits the mass transfer in these systems.
η−1, which is a qualitative method to establish the ionicity of a liquid, which refers to the number of “free” ions in solution.55 The diagonal in the Walden plot represents the so-called ideal KCl line, which is arbitrarily assigned to 1 M aqueous KCl, even though the definition of the ionicity based on this line is questionable since only a point for this solution actually lies on the diagonal.56 In accordance with the position of the Walden plot of the mixtures it is possible to define three cases: (i) superionic liquid, (ii) good ionic liquid and (iii) poor ionic liquid when far above, close or far below the diagonal, respectively.57,58 As shown in the Walden plot reported in Fig. 4, all our mixtures show good ionicity at the respective concentration range, with a slightly higher ionicity in the case of the Gly-based mixtures, meaning that no ionic association limits the mass transfer in these systems.
Electrochemical investigation
Once the structural and transport properties of the mixtures and the differences induced by the variation of HBA and HBD molar ratio were elucidated, we conducted a thorough electrochemical characterization aiming at understanding how these structural differences could affect electrochemical stability. Three-electrode cyclic voltammograms of all the mixtures are depicted in Fig. 5.It should be noted that no supporting electrolyte was added to the mixture to avoid the further modulation of the hydrogen bond networking of the system and to be as adherent as possible to the experimental condition of an electrolyte tested in EESS. Furthermore, the good conductivity of the electrolyte allowed us to adopt this strategy. ESWs of EG-based electrolytes range between 2.6 and 2.8 V, while the ones of Gly-based electrolytes are slightly wider, up to 2.8–3.0 V. Furthermore, in the case of the diol, the CV profiles are not completely flat, with some bumps evident (Fig. S10†), probably due to unwanted reactions that irreversibly occur both in oxidation and in reduction scans. On the other hand, for Gly-based mixtures there are no side reactions inside the windows, and the cathodic limits are at slightly lower potentials, thus leading to wider ESWs. The disparity in stability between the two HBDs underscores the presence of a unique structuring in the case of glycerol, which is lacking with ethylene glycol. In other words, ethylene glycol molecules are freer within the systems and, consequently, more subjected to parasitic reactions than glycerol counterparts. Comparing with literature is challenging due to the lack of reliability in assessing the electrochemical stability of this type of electrolyte. Indeed, the ESWs of certain DESs are reported using CV at 100 mV s−1, which is a much less demanding condition compared to the one we employed (1 mV s−1). Moreover, electrochemical stability is often evaluated directly within the final electrochemical system, where interactions with engineered cathodes and anodes may either positively or negatively impact it. Despite these hurdles, our mixtures exhibit, overall, wider ESWs than traditional DESs based on ChCl59 or zinc salts (e.g., ZnCl2 or ZnTFSI)60 as HBAs and carboxylic acids, amides, or alcohols as HBDs. On the contrary, the ESWs remain narrower when lithium salts (e.g., LiTFSI or LiPF6)61 are exploited as HBAs, which, although providing superior performances (4–5 V), are less sustainable and more toxic62 than NaCl.
To comprehensively evaluate the potential of these novel mixtures, we subjected them to an in-depth electrochemical characterization (CV and GCD) as electrolytes in supercapacitors with AC carbon electrodes, thereby providing a thorough understanding of their overall performance and paving the way for the optimization of their future applications. The CVs were acquired for all the formulated mixtures, increasing stepwise the upper cut-off voltage from 2.2 up to 3.0 V, with the aim of finding the best conditions for cycling the EDLC. Limited electrochemical stability of EG-based mixtures, used as the electrolyte in the AC symmetric cells (Fig. S11†), is evidenced by the presence of secondary (faradaic) reactions most likely associated with the degradation of the electrolyte. This behavior would lead to low coulombic efficiency and poor capacitance retention despite the good capacitance (around 20 F g−1 at 3 V). Differently, Gly-mixtures show excellent stability even in the complete device, as shown in Fig. 6, and a capacitance of about 7 F g−1 at 3 V, even though at relatively high voltage (>2.6 V) the polyol seems to be starting to lose reversibility, showing a reduced electrochemical stability, as we expected by using AC electrodes instead of the glassy carbon electrodes63 employed for the determination of the ESW. However, this striking diversity in electrochemical stability between Gly-based mixtures and EG-based ones (within the AC symmetric cell) provides further compelling evidence of the differing nature of the mixtures, as discussed above. In particular, the development of more structured DES or DES-like systems gives rise to electrolytes that demonstrate significantly improved stability compared to their less structured salt-in-solvent counterparts, highlighting the critical role of molecular organization on electrochemical performances.
 | ||
| Fig. 6 CV curves of NaCl–Gly electrolytes in AC supercapacitors acquired at 1 mV s−1 with different operational voltages (2.2, 2.4, 2.6, 2.8, 3 V). | ||
Moreover, to find the optimal condition for a long-cycling test, a short GCD (10 cycles) were performed consecutively at 0.5, 1 and 2 mA cm−2 (chosen according to the currents reached in the CVs) for the cut-off voltages of 2, 2.2, 2.4, 2.6, 2.8, and 3 V. As shown in Fig. 7a it is evident that at 0.5 mA cm−2 the faradaic contribution is not negligible, and the decomposition of the electrolytes occurs even at low voltages (2.2 V). On the other hand, at both 1 and 2 mA cm−2, the cut-off voltage could be extended up to 2.6 V (at least), without any strong faradaic behavior (i.e., coulombic efficiency around 99%), except for NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 which shows significant faradaic phenomena already at 2.6 V. Among all the electrolytes, NaCl–Gly 1
8 which shows significant faradaic phenomena already at 2.6 V. Among all the electrolytes, NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 better maintains the capacitance and the coulombic efficiency at higher voltages, showing the most promising performances at 1 mA cm−2 (Fig. 7b). Before further investigating this electrolyte, 1H NMR analysis was performed on NaCl–Gly 1
10 better maintains the capacitance and the coulombic efficiency at higher voltages, showing the most promising performances at 1 mA cm−2 (Fig. 7b). Before further investigating this electrolyte, 1H NMR analysis was performed on NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 post-cycling. A solution was prepared by immersing the separator of the post-mortem EDLC in DMSO for 24 h to guarantee a complete extraction of adsorbed species. From the resulting 1H NMR spectrum (Fig. S12†), no peaks related to glycerol oxidation products (e.g., carbonyl or carboxyl groups) are detectable, indicating that chlorine gas evolution could be responsible for the anodic limit of the ESW. This result appears to be in contrast with the formation of aldehydes assumed by Sinclair et al.64 However, unlike the anodic limit, the cathodic one could be consistent and linked to the reduction of the polyol, specifically to its dehydration (which leads to hydrogen evolution), as demonstrated for ethylene glycol. Indeed, the formation of 2-chloro-1,3-propanediol65 witnessed by 1H NMR spectrum is likely related to such dehydration reaction, which is hindered by the presence of chloride and hence by the formation of a secondary adduct.
10 post-cycling. A solution was prepared by immersing the separator of the post-mortem EDLC in DMSO for 24 h to guarantee a complete extraction of adsorbed species. From the resulting 1H NMR spectrum (Fig. S12†), no peaks related to glycerol oxidation products (e.g., carbonyl or carboxyl groups) are detectable, indicating that chlorine gas evolution could be responsible for the anodic limit of the ESW. This result appears to be in contrast with the formation of aldehydes assumed by Sinclair et al.64 However, unlike the anodic limit, the cathodic one could be consistent and linked to the reduction of the polyol, specifically to its dehydration (which leads to hydrogen evolution), as demonstrated for ethylene glycol. Indeed, the formation of 2-chloro-1,3-propanediol65 witnessed by 1H NMR spectrum is likely related to such dehydration reaction, which is hindered by the presence of chloride and hence by the formation of a secondary adduct.
Lastly, a deeper investigation of the NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 electrolyte was carried out to evaluate the performance of the DES in EDLC. Specifically, a long GCD (1000 cycles) was performed at 1 mA cm−2 at 2.4, 2.6, and 2.8 V (Fig. 7c). In all three cases, during the initial 100 cycles, a notable drop in specific capacitance is observed, likely due to decomposition reactions taking place into the porous of the electrodes, partially degrading the AC surface and reducing the area available for ion storage. Indeed, after this stage, the electrolyte reaches a stable state, exhibiting exceptional capacitance retention.
10 electrolyte was carried out to evaluate the performance of the DES in EDLC. Specifically, a long GCD (1000 cycles) was performed at 1 mA cm−2 at 2.4, 2.6, and 2.8 V (Fig. 7c). In all three cases, during the initial 100 cycles, a notable drop in specific capacitance is observed, likely due to decomposition reactions taking place into the porous of the electrodes, partially degrading the AC surface and reducing the area available for ion storage. Indeed, after this stage, the electrolyte reaches a stable state, exhibiting exceptional capacitance retention.
Particularly, NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 achieve the best performances at the intermediate voltage 2.6 V with a specific capacitance of 14.1 F g−1 at the 100th cycle, a remarkable capacitance retention of 96% at the 1000th cycle and an average coulombic efficiency >98.0% (Fig. 7d). Thus, at this voltage, there is the optimal trade-off between stabilization of the electrode–electrolyte interface phenomena, which are more pronounced at 2.8 V, and the increased capacitance induced by the higher voltage compared to 2.4 V.
10 achieve the best performances at the intermediate voltage 2.6 V with a specific capacitance of 14.1 F g−1 at the 100th cycle, a remarkable capacitance retention of 96% at the 1000th cycle and an average coulombic efficiency >98.0% (Fig. 7d). Thus, at this voltage, there is the optimal trade-off between stabilization of the electrode–electrolyte interface phenomena, which are more pronounced at 2.8 V, and the increased capacitance induced by the higher voltage compared to 2.4 V.
Table 3 provides a comparison of the performance parameters, including operating voltage, specific capacitance, and cycling stability, for the DES used in this study alongside key results from previous literature on alternative liquid electrolytes. Notably, the operating voltage and cycling stability of the NaCl–Gly system are comparable to, or even exceed, those of other DES electrolytes, as well as water-in-salt systems. Even if delivering slightly higher specific capacitances, the latter suffer from poor thermal stability, high cost and corrosivity issue due to the high concentrations required. While the higher viscosity of our DES limits its capacitance, this should not overshadow its significant advantages in terms of sustainability and environmental friendliness, along with its ease of production, compared to ILs (which, in turns, can operate within a wider voltage and deliver better performance). By avoiding unsustainable or fluorinated salts, as well as toxic or fossil fuel-derived compounds, it provides a greener and more eco-conscious alternative for EDLC applications. Furthermore, ILs usually required an atmosphere-controlled (e.g. a glovebox) and energy-demanding formulation processes which jeopardize their industrial scalability and negatively impact on the overall costs.
| Operating voltage | Specific capacitance | Capacitance retention | Electrodes | Comments | Ref. | |
|---|---|---|---|---|---|---|
| DES electrolytes | ||||||
| NaCl–glycerol | 2.6 V | 14.1 F g−1 at 1 mA cm−2 (63 mA g−1) | 96% after 1000 cycles | AC | Highest sustainability | This work |
| Lowest costs environmental friendliness | ||||||
| ChCl–urea–water | 2.2 V | 157 F g−1 at 1 A g−1 | 88% after 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles 000 cycles |
AC | Fossil fuel-based | 66 |
| LiTFSI-N-methylacetamide | 2.5 V | 157 F g−1 at 347 mA g−1 | — | AC | High toxicity | 67 |
| Fluorinated and unsustainable solvent fossil fuel-based | ||||||
| LiClO4–acetamide–water | 2.3 V | 42.5 F g−1 at 4 A g−1 | 91% after 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles 000 cycles |
Graphene/MoS2 | Safety issue | 68 |
| Fossil fuel-based | ||||||
| Ionic liquid electrolytes | ||||||
| EMIMTFSI | 3.5 V | 190 F g−1 at 2 A g−1 | 89% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles 000 cycles |
Graphene | High toxicity unsustainable and fluorinated solvent costly and energy-demanding preparation process | 69 |
| EMIMBF4 | 172 F g−1 at 2 A g−1 | 90% after 1M cycles | ||||
| BMIMPF6 | 4 V | 387 F g−1 at 1 A g−1 (60 °C) | 5000 cycle | Carbon nanosponge | Fossil fuel-based | 70 |
| Water-in-salt electrolytes | ||||||
| LiTFSI | 2.2 V | 44 F g−1 at 5 A g−1 | 80% after 6000 cycle | Polyaniline-derived carbon nanorod | Unsustainable and fluorinated salt | 71 |
| Thermal instability | ||||||
| NaClO4 | 2.4 V | 26.3 F g−1 at 1 A g−1 | 93.2% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles 000 cycles |
NaMnO/AC | High cost | 72 |
| Safety issue | ||||||
| NaNO3 | 2.1 V | 32.7 F g−1 at 1 A g−1 | 83.1% after 9000 cycles | AC | Thermal instability | 73 |
Conclusions
Throughout this paper, we successfully highlight the potential of glycerol-based deep eutectic solvents as eco-friendly electrolytes for electrochemical energy storage systems, with a particular focus on their use in activated carbon-based electrochemical double-layer capacitors. By exploring novel formulations based on sodium chloride with glycerol or ethylene glycol, we demonstrated the feasibility of designing electrolytes that balance environmental benefits with desirable and tunable electrochemical properties. To make this electrolyte a starting point for the design of new eco-friendly electrolytes, a thorough spectroscopic characterization has been conducted. The interplay between Raman and FTIR spectroscopy in the FIR range revealed that the structural conformations of glycerol, as well as its chemical surrounding (i.e., intermolecular hydrogen bonds), play a pivotal role in defining the eutectic behavior and subsequent performance of the electrolytes. The reorganization induced by sodium chloride affects not only the spectroscopic properties (for which a more thorough investigation is currently undergoing in our team) but, more importantly, the transport and electrochemical properties of the mixtures. This is further evidenced by the superior ionicity and electrochemical stability of DES and DES-like mixtures compared to ethylene glycol-based salt-in-solvent counterparts. Among the tested glycerol mixtures, NaCl–Gly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 stands out as a promising DES, exhibiting a lower viscosity (1019 mPa s), higher ionic conductivity (0.186 mS cm−1) and a working voltage comparable to commercial EDCLs' one (up to 2.6 V). These findings underscore the potential of glycerol-based deep eutectic solvents as eco-friendly alternatives to commercial electrolytes, paving the way for further advancements in sustainable electrochemical energy storage.
10 stands out as a promising DES, exhibiting a lower viscosity (1019 mPa s), higher ionic conductivity (0.186 mS cm−1) and a working voltage comparable to commercial EDCLs' one (up to 2.6 V). These findings underscore the potential of glycerol-based deep eutectic solvents as eco-friendly alternatives to commercial electrolytes, paving the way for further advancements in sustainable electrochemical energy storage.
Author contributions
Daniele Motta: writing – original draft; visualization; investigation; data curation. Alessandro Damin: visualization; project administration; methodology; formal analysis. Hamideh Darjazi: writing – review & editing; methodology. Stefano Nejrotti: writing – review & editing; methodology. Federica Piccirilli: writing – review & editing; resources; investigation. Giovanni Birarda: software; investigation. Claudia Barolo: validation; supervision. Claudio Gerbaldi: validation; supervision. Giuseppe Antonio Elia: writing – review & editing; supervision; funding acquisition; formal analysis. Matteo Bonomo: writing – review & editing; supervision; project administration; methodology; funding acquisition; conceptualization.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study has received support from GENESIS project funded by the Ministero dell'Università e della Ricerca within the PRIN 2022 program and from Project CH4.0 under the MUR program “Dipartimento di Eccellenza 2023–2027” (CUP D13C22003520001).References
- B. Zakeri, K. Paulavets, L. Barreto-Gomez, L. G. Echeverri, S. Pachauri, B. Boza-Kiss, C. Zimm, J. Rogelj, F. Creutzig, D. Ürge-Vorsatz, D. G. Victor, M. D. Bazilian, S. Fritz, D. Gielen, D. L. McCollum, L. Srivastava, J. D. Hunt and S. Pouya, Energies, 2022, 15, 1–23 Search PubMed.
- IEA, 2023, https://www.iea.org/reports/tracking-clean-energy-progress-2023.
- G. Notton, M. L. Nivet, C. Voyant, C. Paoli, C. Darras, F. Motte and A. Fouilloy, Renewable Sustainable Energy Rev., 2018, 87, 96–105 Search PubMed.
- A. Dutta, S. Mitra, M. Basak and T. Banerjee, Energy Storage, 2023, 5, 1–36 CrossRef.
- W. Liu, T. Placke and K. T. Chau, Energy Rep., 2022, 8, 4058–4084 Search PubMed.
- International Energy Agengy, Geo, 2015, 9–10 Search PubMed.
- S. Zhang, T. Long, H. Z. Zhang, Q. Y. Zhao, F. Zhang, X. W. Wu and X. X. Zeng, ChemSusChem, 2022, 15, e202200999 CrossRef CAS PubMed.
- J. Zhang, X. Yao, R. K. Misra, Q. Cai and Y. Zhao, J. Mater. Sci. Technol., 2020, 44, 237–257 Search PubMed.
- H. Yang, G. V. Zhuang and P. N. Ross, J. Power Sources, 2006, 161, 573–579 CrossRef CAS.
- Q. Wang, P. Ping, X. Zhao, G. Chu, J. Sun and C. Chen, J. Power Sources, 2012, 208, 210–224 CrossRef CAS.
- M. Cvjetko Bubalo, S. Vidović, I. Radojčić Redovniković and S. Jokić, J. Chem. Technol. Biotechnol., 2015, 90, 1631–1639 Search PubMed.
- A. González, E. Goikolea, J. A. Barrena and R. Mysyk, Renewable Sustainable Energy Rev., 2016, 58, 1189–1206 CrossRef.
- T. S. Bhat, P. S. Patil and R. B. Rakhi, J. Energy Storage, 2022, 50, 104222 CrossRef.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- J. Han, A. Mariani, S. Passerini and A. Varzi, Energy Environ. Sci., 2023, 16, 1480–1501 RSC.
- A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Chem. Commun., 2003, 70–71 RSC.
- M. E. Di Pietro and A. Mele, J. Mol. Liq., 2021, 338, 116597 CrossRef CAS.
- C. Zhang, L. Zhang and G. Yu, Acc. Chem. Res., 2020, 53, 1648–1659 CAS.
- J. Wu, Q. Liang, X. Yu, L. Qiu-Feng, L. Ma, X. Qin, G. Chen and B. Li, Adv. Funct. Mater., 2021, 31, 1–25 Search PubMed.
- M. A. R. Martins, S. P. Pinho and J. A. P. Coutinho, J. Solution Chem., 2019, 48, 962–982 CrossRef CAS.
- D. O. Abranches and J. A. P. Coutinho, Annu. Rev. Chem. Biomol. Eng., 2023, 14, 141–163 CAS.
- R. Puttaswamy, C. Mondal, D. Mondal and D. Ghosh, Sustainable Mater. Technol., 2022, 33, e00477 CAS.
- S. Nejrotti, A. Antenucci, C. Pontremoli, L. Gontrani, N. Barbero, M. Carbone and M. Bonomo, ACS Omega, 2022, 7, 47449–47461 CAS.
- K. Qu, X. Lu, N. Jiang, J. Wang, Z. Tao, G. He, Q. Yang and J. Qiu, ACS Energy Lett., 2024, 9, 1192–1209 CrossRef CAS.
- L. Geng, J. Meng, X. Wang, C. Han, K. Han, Z. Xiao, M. Huang, P. Xu, L. Zhang, L. Zhou and L. Mai, Angew. Chem., Int. Ed., 2022, 61, 1–9 Search PubMed.
- C. Li, R. Kingsbury, A. S. Thind, A. Shyamsunder, T. T. Fister, R. F. Klie, K. A. Persson and L. F. Nazar, Nat. Commun., 2023, 14, 3067 CAS.
- X. Song, Y. Ge, H. Xu, S. Bao, L. Wang, X. Xue, Q. Yu, Y. Xing, Z. Wu, K. Xie, T. Zhu, P. Zhang, Y. Liu, Z. Wang, Z. Tie, J. Ma and Z. Jin, J. Am. Chem. Soc., 2024, 146, 7018–7028 CAS.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082 CAS.
- A. Sharma, R. Sharma, R. C. Thakur and L. Singh, J. Energy Chem., 2023, 82, 592–626 CAS.
- H. W. Tan, A. R. Abdul Aziz and M. K. Aroua, Renewable Sustainable Energy Rev., 2013, 27, 118–127 CAS.
- Z. Pirzadi and F. Meshkani, Fuel, 2022, 329, 125044 CrossRef CAS.
- S. Rebsdat and D. Mayer, Ullmann's Encyclopedia of Industrial Chemistry, John Wiley & Sons, Ltd, 2001 Search PubMed.
- I. Rossetti, M. Compagnoni, G. De Guido, L. A. Pellegrini, G. Ramis and S. Dzwigaj, Can. J. Chem. Eng., 2017, 95, 1752–1759 CrossRef CAS.
- D. Ripamonti, A. Tripodi, F. Conte, A. Robbiano, G. Ramis and I. Rossetti, J. Environ. Chem. Eng., 2021, 9, 105969 CrossRef CAS.
- M. K. Wong, S. S. M. Lock, Y. H. Chan, S. J. Yeoh and I. S. Tan, Chem. Eng. J., 2023, 468, 143699 CrossRef CAS.
- W. Wang, M. M. Sabugaa, S. Chandra, Y. P. Asmara, B. A. Alreda, N. Ulloa, Y. Elmasry and M. M. Kadhim, J. Energy Storage, 2023, 71, 108141 CrossRef.
- F. Cappelluti, A. Mariani, M. Bonomo, A. Damin, L. Bencivenni, S. Passerini, M. Carbone and L. Gontrani, J. Mol. Liq., 2022, 367, 120443 CrossRef CAS.
- M. Bonomo, L. Gontrani, A. Capocefalo, A. Sarra, A. Nucara, M. Carbone, P. Postorino and D. Dini, J. Mol. Liq., 2020, 319, 114292 CrossRef CAS.
- G. Birarda, F. Piccirilli, H. Vondracek, D. E. Bedolla, S. Chiaramaria, L. Vaccari and E.-S. Triesteo, Biomedical Vibrational Spectroscopy 2022: Advances in Research and Industry, 2022, vol. 1195707 Search PubMed.
- E. Zunzunegui-Bru, S. R. Alfarano, P. Zueblin, H. Vondracek, F. Piccirilli, L. Vaccari, S. Assenza and R. Mezzenga, ACS Nano, 2024, 18, 21376–21387 CrossRef CAS PubMed.
- A. S. D. Ferreira, R. Craveiro, A. R. Duarte, S. Barreiros, E. J. Cabrita and A. Paiva, J. Mol. Liq., 2021, 342, 117463 Search PubMed.
- B. L. Kuhn, G. C. Paveglio, S. Silvestri, E. I. Muller, M. S. P. Enders, M. A. P. Martins, N. Zanatta, H. G. Bonacorso, C. Radke and C. P. Frizzo, New J. Chem., 2019, 43, 1415–1423 RSC.
- Y. E. Ryabov, Y. Hayashi, A. Gutina and Y. Feldman, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 1–4 CrossRef.
- F. Gabriele, M. Chiarini, R. Germani and N. Spreti, J. Mol. Liq., 2023, 385, 122332 Search PubMed.
- O. Bastiansen, H. Borgiel and E. Saluste, Acta Chem. Scand., 1949, 3, 415–421 CrossRef CAS.
- R. Chelli, P. Procacci, G. Cardini and S. Califano, Phys. Chem. Chem. Phys., 1999, 1, 879–885 RSC.
- H. Koningsveld, Recl. Trav. Chim. Pays-Bas, 1968, 87, 243–254 CrossRef.
- T. Kusukawa, G. Niwa, T. Sasaki, R. Oosawa, W. Himeno and M. Kato, Bull. Chem. Soc. Jpn., 2013, 86, 351–353 CrossRef CAS.
- R. Chelli, F. L. Gervasio, C. Gellini, P. Procacci, G. Cardini and V. Schettino, J. Phys. Chem. A, 2000, 104, 5351–5357 CrossRef CAS.
- J. J. Towey, A. K. Soper and L. Dougan, Phys. Chem. Chem. Phys., 2011, 13, 9397–9406 RSC.
- E. Mendelovici, R. L. Frost and T. Kloprogge, J. Raman Spectrosc., 2000, 31, 1121–1126 CrossRef CAS.
- K. Fumino, T. Peppel, M. Geppert-Rybczyńska, D. H. Zaitsau, J. K. Lehmann, S. P. Verevkin, M. Köckerling and R. Ludwig, Phys. Chem. Chem. Phys., 2011, 13, 14064–14075 RSC.
- K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929 RSC.
- P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259 CAS.
- A. Mariani, M. Bonomo, X. Gao, B. Centrella, A. Nucara, R. Buscaino, A. Barge, N. Barbero, L. Gontrani and S. Passerini, J. Mol. Liq., 2021, 324, 115069 CAS.
- C. Schreiner, S. Zugmann, R. Hartl and H. J. Gores, J. Chem. Eng. Data, 2010, 55, 1784–1788 CAS.
- Y. Wang, W. Chen, Q. Zhao, G. Jin, Z. Xue, Y. Wang and T. Mu, Phys. Chem. Chem. Phys., 2020, 22, 25760–25768 CAS.
- K. R. Harris, J. Phys. Chem. B, 2019, 123, 7014–7023 CAS.
- D. Julião, M. Xavier and X. Mascarenhas, Mater. Today Energy, 2024, 42, 101432 Search PubMed.
- R. Al-Farsi and M. Hayyan, Renewable Sustainable Energy Rev., 2023, 184, 113505 CAS.
- K. Zhou, X. Dai, P. Li, L. Zhang, X. Zhang, C. Wang, J. Wen, G. Huang and S. Xu, Prog. Mater. Sci., 2024, 146, 101338 CAS.
- A. Mauger, C. M. Julien, A. Paolella, M. Armand and K. Zaghib, Mater. Sci. Eng., R, 2018, 134, 1–21 Search PubMed.
- K. Xu, S. P. Ding and T. R. Jow, J. Electrochem. Soc., 1999, 146, 4172–4178 CAS.
- N. S. Sinclair, X. Shen, E. Guarr, R. F. Savinell and J. S. Wainright, J. Electrochem. Soc., 2021, 168, 106506 CAS.
- Z. Wu, B. Gong and J. Cao, Preparation method of 2-MCPD, D5-2-MCPD and 13C3-2-MCPD, CN Pat., CN114853564B, 2024 Search PubMed.
- S. Azmi, M. F. Koudahi and E. Frackowiak, Energy Environ. Sci., 2022, 15, 1156–1171 CAS.
- A. Boisset, J. Jacquemin and M. Anouti, Electrochim. Acta, 2013, 102, 120–126 CAS.
- C. W. Lien, B. Vedhanarayanan, J. H. Chen, J. Y. Lin, H. H. Tsai, L. D. Shao and T. W. Lin, Chem. Eng. J., 2021, 405, 126706 CAS.
- C. Li, X. Zhang, K. Wang, X. Sun, G. Liu, J. Li, H. Tian, J. Li and Y. Ma, Adv. Mater., 2017, 29, 1604690 Search PubMed.
- X. Wang, H. Zhou, E. Sheridan, J. C. Walmsley, D. Ren and D. Chen, Energy Environ. Sci., 2016, 9, 232–239 RSC.
- D. Xiao, Q. Wu, X. Liu, Q. Dou, L. Liu, B. Yang and H. Yu, ChemElectroChem, 2019, 6, 439–443 CAS.
- X. Bu, Y. Zhang, L. Su, Q. Dou, Y. Xue and X. Lu, Ionics, 2019, 25, 6007–6015 CrossRef CAS.
- J. Guo, Y. Ma, K. Zhao, Y. Wang, B. Yang, J. Cui and X. Yan, ChemElectroChem, 2019, 6, 5433–5438 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4gc06369d |
| This journal is © The Royal Society of Chemistry 2025 |