Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying the prospect of a visible-light-absorbing oxysulfide photocatalyst by probing transient absorption and photoluminescence†
Ryota
Shoji‡
a,
Vikas
Nandal‡
 *b,
Kazuhiko
Seki
*b,
Kazuhiko
Seki
 *b,
Xiaoping
Tao
c,
Akihiro
Furube
*b,
Xiaoping
Tao
c,
Akihiro
Furube
 d,
Takashi
Hisatomi
d,
Takashi
Hisatomi
 c,
Hiroaki
Yoshida
ef,
Tsuyoshi
Takata
c,
Masanori
Kaneko
g,
Koichi
Yamashita
g,
Kazunari
Domen
c,
Hiroaki
Yoshida
ef,
Tsuyoshi
Takata
c,
Masanori
Kaneko
g,
Koichi
Yamashita
g,
Kazunari
Domen
 ch and
Hiroyuki
Matsuzaki
ch and
Hiroyuki
Matsuzaki
 *a
*a
aResearch Institute for Material and Chemical Measurement, National Metrology Institute of Japan (NMIJ), National Institute of Advanced Industrial Science and Technology (AIST), 1-1-1 Higashi, Tsukuba, Ibaraki 305-8565, Japan. E-mail: hiroyuki-matsuzaki@aist.go.jp
bGlobal Zero Emission Research Center, National Institute of Advanced Industrial Science and Technology (AIST), 16-1 Onogawa, Tsukuba, Ibaraki 305-8569, Japan. E-mail: nk.nandal@aist.go.jp; k-seki@aist.go.jp
cResearch Initiative for Supra-Materials, Interdisciplinary Cluster for Cutting Edge Research, Shinshu University, 4-17-1 Wakasato, Nagano-shi, Nagano 380-8553, Japan
dInstitute of Post-LED Photonics, Tokushima University, 2-1 Minamijosanjima-cho, Tokushima 770-8506, Japan
eMitsubishi Chemical Corporation, Science & Innovation Center, 1000 Kamoshida-cho, Aoba-ku, Yokohama, Kanagawa 227-8502, Japan
fJapan Technological Research Association of Artificial Photosynthetic Chemical Process (ARPChem), 2-11-16 Yayoi, Bunkyo-ku, Tokyo 113-8656, Japan
gGraduate School of Nanobioscience, Yokohama City University, 22-2 Seto, Kanazawa-ku, Yokohama, Kanagawa 236-0027, Japan
hOffice of University Professors, The University of Tokyo, 2-11-16 Yayoi, Bunkyo-ku, Tokyo 113-8656, Japan
First published on 27th December 2024
Abstract
Photocatalytic water splitting is an emerging renewable technology for producing green hydrogen fuel from sunlight and water on a large scale. Identifying charge-carrier transport properties is critical for establishing a design pathway for exciting visible-light-absorbing oxysulfide-based photocatalysts. Herein, the dynamics of distinct charge carriers in the Gd2Ti2O5S2 (GTOS) photocatalyst is revealed by transient optical spectroscopies (transient diffuse reflectance (TDR) and transient photoluminescence (TPL) spectroscopies) and theoretical modeling. We demonstrate that TDR and TPL signals can probe the evolution of photoexcited mobile electrons and holes separately for GTOS. The decay of optical signals primarily originates from bimolecular recombination of mobile electrons with detrapped holes from shallow trap states close to the valence band. Using different estimated parameters, the effects of the size reduction and charge carrier extraction rate ke (surface to electrolyte) on the internal quantum efficiency (IQE) are determined. Our results indicate that the IQE can be tremendously improved by simultaneously reducing particle size and increasing ke. After particle size reduction, we show that the high apparent quantum yield (∼30%) GTOS was achieved by improving ke (from surface treatment and optimizing the cocatalyst loading method) as compared to Y2Ti2O5S2 (0.7%). Our work presents a comprehensive methodology that identifies the critical photophysical properties of visible-light-absorbing photocatalysts for efficient and scalable particulate photocatalyst-based solar water splitting systems.
Broader contextAmbient-solar-energy-driven water splitting via particulate photocatalysts is an emerging candidate technology to attain stable and stoichiometric generation of H2 and O2. Currently, the commercial prospects of such a system are hindered by the inability of the existing photocatalysts (e.g., Al-doped SrTiO3) to absorb sunlight in the visible spectral range, despite showing a high external quantum efficiency. Consequently, the solar-to-hydrogen (STH) energy conversion efficiency is less than 1%, far less than the 10% target set by a technoeconomic analysis (TEA) report (J. H. Kim et al., Chem. Soc. Rev., 2019, 48, 1908–1971). To improve the STH energy conversion efficiency, major research is now focused on tuning/characterizing the photophysical properties of visible-light-absorbing photocatalysts, including (oxy)sulfides such as Gd2Ti2O5S2 and Y2Ti2O5S2. Herein, transient diffuse reflectance and photoluminescence spectroscopies are used in conjunction with theoretical modeling to identify the decay of distinct (mobile and trapped) photoexcited charge carriers in Gd2Ti2O5S2. Discussions based on a detailed characterization and performance prediction indicate that simultaneous improvements in the bulk and surface charge carrier transport properties are imperative for realizing high water splitting activity. The insights gained from this work can be applied and contribute to the development of efficient photocatalytic/photoelectrode water splitting systems. |
1. Introduction
The development of renewable energy technologies is of utmost importance for addressing increasing energy demands and carbon emissions and realizing socioeconomic prosperity across the globe. Photocatalytic water splitting is a promising method for harvesting abundant solar energy into carbon-free H2 fuel, which can easily be stored and transferred for later use.1–4 Among various configurations, particulate water splitting systems safely generate H2 and O2 gases on a large scale (∼100 m2) for extended periods of operation under ambient solar illumination.5 Photocatalyst sheets comprise an ultraviolet-light-absorbing Al-doped SrTiO3 photocatalyst and cocatalysts for the oxygen and hydrogen evolution reactions. If the photocatalyst has an appropriate bandgap energy, it can absorb solar energy to produce electrons and holes in the conduction band (CB) and valence band (VB), respectively.6–10 A fraction of these charge carriers might be lost via the recombination and/or trapping processes, whereas the rest of the charges are transported to the water via the cocatalyst at the surface of the photocatalyst. Charge carrier loss mechanisms have been eliminated by facet-selective cocatalyst loading of Al-doped SrTiO3 to achieve an external quantum efficiency approaching the theoretical limit.11 However, because a large region of the visible-light spectrum was not used, the solar-to-hydrogen (STH) energy conversion efficiency of this system was less than 1%. Therefore, the development of narrow-bandgap-energy semiconductors is critical for realizing efficient and cost-effective STH production.Extensive research in past decades was focused on the development of photocatalysts such as oxides, chalcopyrites, (oxy)halides, (oxy)nitrides, and (oxy)sulfides by tailoring the VB energy and/or CB energy for visible-light-induced water splitting.4 Among these materials, (oxy)sulfide-based photocatalysts such as Ln2Ti2S2O5 (Ln = Pr, Nd, Sm, Gd, Tb, Dy, Ho, Er) produced H2 or O2 gas from aqueous solution in the presence of a sacrificial agent under visible light without any degradation.12,13 Most of these materials were challenged by their inability to perform overall water splitting (OWS) under single-step excitation. Recently, Wang et al. demonstrated that the Y2Ti2O5S2 (YTOS) particulate photocatalyst [with a particle size as large as tens of micrometers; prepared by a solid-state reaction (SSR) method] produced H2 and O2 in a stoichiometric ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for 20 h after Rh/Cr2O3 and IrO2 cocatalysts were loaded.14 The external quantum efficiency (EQE) of the OWS reaction was less than 1%, suggesting a substantial charge carrier loss mechanism. Using carrier dynamics analysis, our group revealed that the EQE of YTOS can be improved by reducing the particle size and increasing the carrier lifetime (by optimizing the fabrication procedure and doping with foreign elements).15 Lin et al. synthesized plate-like YTOS particles with size as large as a few micrometers using flux methods; the YTOS particles were then loaded with Rh and Co3O4 cocatalysts by an impregnation technique.16 Because of the reduced particle size, the EQE of the H2 and O2 evolution half-reactions was 5.9% and 7.3%, respectively, at an excitation wavelength of 420 nm. Gd2Ti2O5S2 (GTOS) with a light-absorption edge of ∼650 nm has shown immense potential to split water under visible light.13 Plate-like GTOS particles prepared using flux and chemical etching processes stably produced H2 with a high EQE of 30% at 420 nm in an aqueous methanol solution (hole scavenger).17 Such enhanced activity was attributed to the intimate contact between the GTOS surface and Pt cocatalyst (deposited by microwave heating) for efficient electron extraction. Given such advancements in oxysulfides, identifying the major components of charge carrier decay using multiple spectroscopic techniques and predicting the design requirements are critical for the future development of efficient visible-light-driven OWS systems.
1 for 20 h after Rh/Cr2O3 and IrO2 cocatalysts were loaded.14 The external quantum efficiency (EQE) of the OWS reaction was less than 1%, suggesting a substantial charge carrier loss mechanism. Using carrier dynamics analysis, our group revealed that the EQE of YTOS can be improved by reducing the particle size and increasing the carrier lifetime (by optimizing the fabrication procedure and doping with foreign elements).15 Lin et al. synthesized plate-like YTOS particles with size as large as a few micrometers using flux methods; the YTOS particles were then loaded with Rh and Co3O4 cocatalysts by an impregnation technique.16 Because of the reduced particle size, the EQE of the H2 and O2 evolution half-reactions was 5.9% and 7.3%, respectively, at an excitation wavelength of 420 nm. Gd2Ti2O5S2 (GTOS) with a light-absorption edge of ∼650 nm has shown immense potential to split water under visible light.13 Plate-like GTOS particles prepared using flux and chemical etching processes stably produced H2 with a high EQE of 30% at 420 nm in an aqueous methanol solution (hole scavenger).17 Such enhanced activity was attributed to the intimate contact between the GTOS surface and Pt cocatalyst (deposited by microwave heating) for efficient electron extraction. Given such advancements in oxysulfides, identifying the major components of charge carrier decay using multiple spectroscopic techniques and predicting the design requirements are critical for the future development of efficient visible-light-driven OWS systems.
Herein, transient diffuse reflectance (TDR) and transient photoluminescence (TPL) spectroscopies are used in conjunction with theoretical analyses to elucidate the decay dynamics of photogenerated charge carriers of the GTOS particulate photocatalyst. Crystalline GTOS particles synthesized using Gd2S3, TiO2, Gd2O3, and I2 were excited with a pump photon energy of 3.1 eV and probed with a photon energy of 0.24 eV at different fluence intensities PFL. The decay rates of the TDR signal S(t) and the TPL signal as functions of time t were found to increase with increasing PFL. In addition, S(t) follows a power-law decay behavior such that S(t) ∝ t−α in the late sub-microsecond time range, where α is the exponent. These decay characteristics are attributed to the bimolecular recombination of mobile electrons and detrapped holes from shallow trap states with an exponential density of states close to the VB. Additional hole trap states obeying a shallow Gaussian distribution with respect to the VB are revealed using a combination of TDR and TPL analyses in the nanosecond time range. Various performance-affecting parameters, such as the recombination/trapping rate constant, doping density, trap-state parameters, and charge carrier lifetime, were determined. The influence of these parameters on water-splitting activity and a potential design route to improve it are predicted for GTOS, which is compared with the YTOS photocatalyst.
2. Results and discussion
2.1. Sample preparation
GTOS particles were synthesized using an SSR method with precursors Gd2S3, TiO2, Gd2O3, and I2. I2 was included as a precursor for its efficient mass transfer ability (i.e., its ability to promote crystal growth and reduce grain boundaries). The fabrication details are included in the Experimental section. A scanning electron microscopy (SEM) image shows plate-like particles with a nonuniform distribution and sizes ranging from hundreds of nanometers to a few micrometers [Fig. 1(a)]. The corresponding X-ray diffraction (XRD) pattern indicates that the synthesized particles are composed mainly of GTOS crystalline phases with dominant peaks arising from the 002, 004, and 103 planes [Fig. 1(b)]. GTOS exhibits a tetragonal structure with space group I4/mmm. Refinement of XRD data and estimation of the crystallographic structure for GTOS are provided in Fig. S1 and Table S1 of the ESI.† The XRD data are consistent with previously reported data for YTOS. The GTOS crystals are expected to be arranged in a Ruddlesden–Popper phase, where the perovskite (having Ti2O5 octahedra) and rocksalt (composed of Gd2S2) layers are stacked alternatingly along the c axis. From XRD refinement, the estimated lattice parameters are a = 3.802 Å, b = 3.802 Å, and c = 22.908 Å. On the basis of the XRD, transmission electron microscopy (TEM), and selected-area electron diffraction results, it was concluded that the flux method led to preferential growth of YTOS crystals along the a and b axes.16 Similar conclusions have been reported for GTOS prepared by a flux method.17 Therefore, we assign the basal plane as the ab plane and the side facets as the ac and bc planes [Fig. 1(a)]. Fig. 1(c) shows the atomic structure of GTOS, where Y was replaced with Gd in a tetragonal structure of YTOS. Density functional theory (DFT) calculations using the Perdew–Burke–Ernzerhof (PBE)18 exchange–correlation functional and the Heyd–Scuseria–Ernzerhof (HSE06)19 functional were carried out to obtain the electronic and optical properties of GTOS (Fig. S2–S5, ESI†). Details of the DFT calculations are included in the Experimental section. The GTOS conventional unit cell with optimized lattice parameters a = 3.812 Å, b = 3.812 Å, and c = 23.072 Å [Fig. 1(c)] is shown in the ESI.† Calculations of the electronic band structure using the PBE functional provided an underestimated bandgap energy of 0.755 eV at Γ and Z k-mesh points (Fig. S2, ESI†). However, the bandgap energy was estimated to be 1.875 eV using computationally expensive HSE06 calculations [Fig. 1(d)], which is consistent with the estimates based on the light-absorption edge and PL peak energy. Irrespective of the functional type, partial density of states (PDOS) calculations suggested that the major contributors to the CB and VB are Ti-3d and S-3p orbitals, respectively; similar results were obtained for YTOS.15 The PDOS of the valence orbitals of different GTOS elements are shown in Fig. S3 of the ESI.† On the basis of the parabolic fit in Fig. 1(d), the calculated effective masses for electrons (holes) are 0.55me (0.81me), 0.57me (0.55me), and 48.2me (73.1me) along Γ–X, Γ–N, and Γ–Z, respectively. The imaginary part of the dielectric function (Fig. S4, ESI†) was calculated using the PBE functional and was further used to implement a bandgap correction method.20 In Fig. S5 of the ESI,† various optical parameters obtained after bandgap correction (i.e., the dielectric function, refractive index, extinction coefficient, reflectivity, and absorption coefficient spectra) are presented. These spectral features govern the light absorption and reflection properties of GTOS and are also critical for the analysis of transient optical spectroscopy measurements. For instance, the determination of absorption coefficient αabs at a pump photon energy of 3.1 eV is critical for accurately estimating the parameters of the GTOS. The absorption coefficient αabs is on the order of 104 cm−1 in the energy range from 2.75 to 4 eV [Fig. 1(e)], which is one order of magnitude lower than the αabs values of other direct-bandgap organic and hybrid photoactive materials but greater than the αabs of the indirect-bandgap semiconductor Si.21 Recently, the optical properties of GTOS were confirmed by a more expensive calculation.22 The diffuse reflectance (DR) spectrum shows that the GTOS particles absorb visible light with an energy greater than 1.88 eV [Fig. 1(f)], which is consistent with the bandgap calculated from DFT calculations using the HSE06 functional.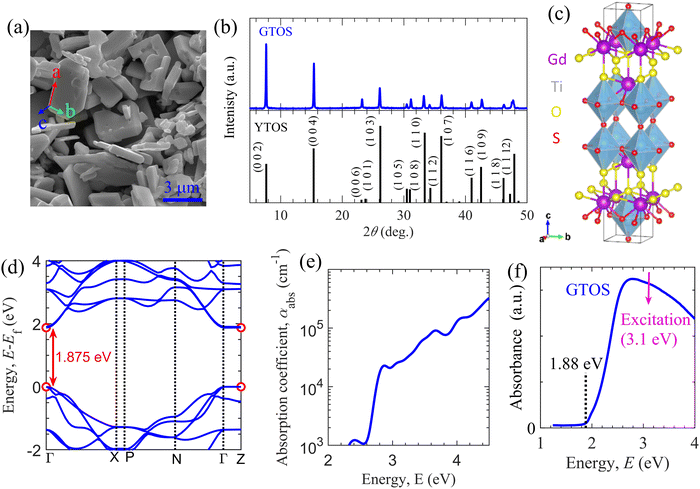 | ||
| Fig. 1 Properties of the GTOS photocatalyst. (a) SEM image of GTOS particles. (b) Measured (top) and simulated (bottom) XRD patterns of GTOS and YTOS photocatalysts. (c) Conventional cell after relaxation of the unit cell of GTOS with space group I4/mmm. (d) Electronic band structure obtained from DFT and HSE06 calculations. (e) Absorption coefficient obtained by the PHS method (see Fig. S5, ESI† for details). (f) Diffuse reflectance spectra of GTOS, indicating an optical bandgap energy of 1.88 eV and a pump photon energy of 3.1 eV. | ||
2.2. Transient optical measurements
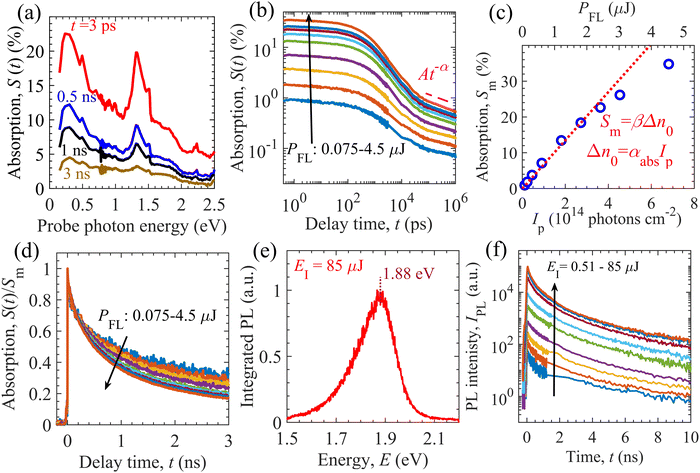
We carried out TDR and TPL measurements to identify the dominant relaxation processes of photogenerated charge carriers in the GTOS photocatalyst. Measurement details are provided in the Experimental section. For the TDR measurement, the GTOS sample was excited by pump photons with an energy of 3.1 eV at different fluence intensities PFL. The probe photon energy was varied from 0.15 to 2.8 eV to obtain the TDR spectra, S(t), at PFL = 3 μJ per pulse, where t is the delay time of the probe light with respect to the pump light [Fig. 2(a)]. The TDR spectra show a major absorption signal S(t) peak at 0.24 eV. In addition, another S(t) peak with a lower intensity is detected at 1.31 eV. The intensity of both S(t) peaks decreases as t increases from 3 ps to 3 ns. The determination of the exact nature of the charged species from TDR spectra is often complicated and nontrivial. Previously, our group reported that mobile electrons can be identified using a probe photon energy in the range of 0.15–0.36 eV for a wide range of photocatalytic materials such as BiVO4,23 SrTiO3,24 Ta3N5,25–27 and Y2Ti2O5S2.15,28 We therefore measured the decay kinetics of S(t) at 0.24 eV for various PFLs [Fig. 2(b)]. The S(t) kinetics exhibits a PFL dependence for delay times as long as 1.5 ns [Fig. S6(a), ESI†]. The PFL dependence might have originated from bimolecular recombination of mobile electrons in the CB with mobile holes in the VB. The S(t) features power-law decay in the sub-microsecond time range such that S(t) = At−α. The amplitude A increases with increasing PFL; however, the exponent α remains independent of PFL [Fig. S7(c), ESI†]. Such power-law S(t) decay has previously been identified and used to obtain the characteristic energy (E0 = kBT/α) of exponential-tail trap states near the VB for the Ta3N5-based photoanode25,26,29 and oxysulfide-based photocatalysts.15–17,28 In these n-type doped photocatalysts, the power-law S(t) decay of mobile electrons was the result of (1) hole detrapping from exponential tail-trap states to the VB and (2) their band-to-band (bimolecular) recombination with electrons. If E0 is sufficiently smaller than 10kBT, the trap-assisted recombination of charge carriers can be ignored against the detrapping of holes. In the opposite case, for E0 > 10kBT, trap-assisted recombination of charge carriers is dominant over detrapping and the asymptotic power-law decay is not realized. Therefore, we assume shallow trap states and ignore trap-assisted recombination. Moreover, the maximum absorption signal Sm at t ∼ 0.4 ps increases linearly with increasing PFL and increasing pump photon intensity Ip [Fig. 2(c)], as per the relations Sm = βΔn0 and Δn0 = αabsIp (using the Lambert–Beer law), respectively, where αabs is the absorption coefficient at a pump photon energy of 3.1 eV and Δn0 is the photogenerated charge carrier density. These results suggest that charge carrier recombination within the instrumental response time (IRT) of the TDR measurement (0.25 ps) is negligible for a PFL as high as 2.4 μJ per pulse. Hereafter, the instrumental response time (IRT) is defined as a full width at half maximum of the instrumental response function (IRF) of the TDR and TPL measurements (Gauss function). We estimated Ip = 4.54 × 1014 cm−2 at PFL = 3 μJ per pulse by measuring the beam profile of the pump and probe lights. In the early nanosecond time range, the S(t) decays faster with increasing PFL [Fig. 2(d)]. Early nanosecond decay analysis shows that the S(t) is proportional to t−1, as per the relation 1/S(t) = 1/Sm + [kr/β + kr(neq + Nt)]t (Fig. S6, ESI†). This result confirms that the PFL-dependent S(t) decay is governed by bimolecular recombination between mobile charge carriers. Early nanosecond decay analysis enabled an initial guess of parameters such as the bimolecular recombination rate constant kr, proportionality constant β, and the sum of the equilibrium electron density (equivalent to n-type doping density) neq and trap density Nt.TPL measurements were also performed to probe the photophysical properties of the GTOS photocatalyst. The IRT of TPL measurement (67 ps) is larger than that of TDR measurement (0.25 ps). The sample was excited by a pump light with a photon energy of 3.1 eV, which was identical to that used in the TDR measurements. Such excitation led to the generation of mobile charge carriers in the CB and VB. The excitation intensity EI ranged from 0.51 to 85 μJ per pulse. After pulsed excitation, some of the photoexcited charge carriers relaxed via a radiative recombination process and emitted a TPL signal IPL. The integrated photoluminescence (PL) spectrum was obtained by the numerical integration of the IPL up to 10 ns. For EI = 85 μJ per pulse, the integrated PL spectrum shows a maximum at 1.88 eV, which agrees well with the light-absorption-edge energy [Fig. 1(c)]. The integrated PL spectrum displays an asymmetric spectral shape from 1.5 to 2.1 eV [Fig. 2(e)]. The TPL signal decays faster with increasing time t before ∼2 ns, in comparison to TPL decaying after ∼2 ns [see Fig. 2(f)]. In addition, the initial TPL decay in the sub-nanosecond time range could be affected by an IRT of 67 ps. The peak energy of the integrated PL spectrum and the EI-dependent IPL decay confirm that a portion of the photogenerated charge carriers relaxed via a band-to-band bimolecular recombination process, consistent with the TDR observations. In addition, the maximum IPL at t ∼ 40 ps increases linearly and quadratically with increasing EI (or Δn0) (Fig. S8, ESI†). Ideally, the linear dependence of the maximum IPL on Δn0 might originate from the recombination of equilibrium electrons with excess photogenerated holes, whereas the quadratic behavior might be attributable to the recombination of excess photogenerated holes and electrons.
2.3. Theoretical modeling
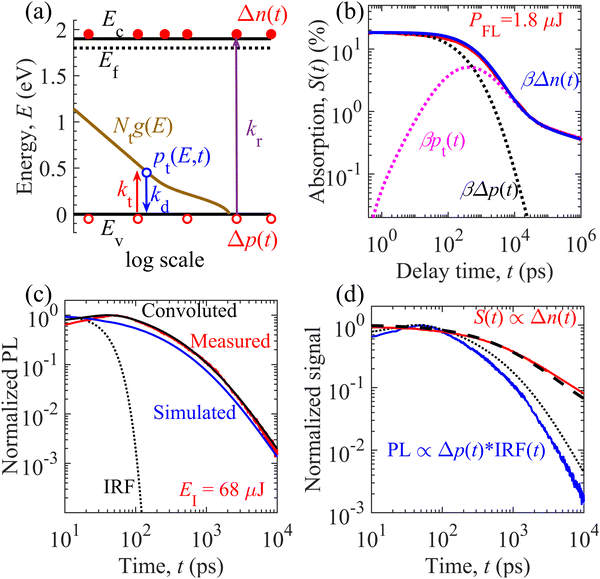
We carried out numerical calculations to simulate and analyze both the TDR and TPL decays of the GTOS photocatalyst using an identical model. Such theoretical analysis can quantify the decay kinetics of distinct charge carrier species (mobile and trapped) as well as estimate performance-influencing material parameters of the GTOS. On the basis of spectroscopic observations, we considered an identical charge carrier relaxation model [Fig. 3(a)] for simultaneously evaluating the TDR and TPL decays. The model highlights mainly three relaxation processes: (1) band-to-band bimolecular recombination of mobile charge carriers, (2) trapping of mobile holes to shallow trap states, and (3) detrapping of holes from trap states to the VB. The shallow trap states are modeled as the sum of Gaussian-tail and exponential-tail trap states, which are defined by respective trap density Nt and characteristic energy E0. Additional details of the model are provided in the Experimental section. By fine-tuning parameters from initial guesses (Fig. S6 and S7, ESI†), the time profiles for densities of mobile electrons Δn(t), mobile holes Δp(t), and total trapped holes pt(t) are simulated and calibrated to the S(t) decay kinetics in the sub-picosecond to microsecond time range for various PFLs [Fig. 3(b) and Fig. S9, ESI†]. The results show that the S(t) data acquired at a probe photon energy of 0.24 eV originated from the decay of mobile electrons such that S(t) = βΔn(t). In addition to bimolecular recombination with electrons, mobile holes become trapped in shallow states with increasing time t before 400 ps [pink dotted curve in Fig. 3(b)]. Δp(t) decays rapidly compared with Δn(t). In addition, pt(t) increases with increasing time t. At t ∼ 400 ps, the hole detrapping rate eventually becomes balanced with the hole trapping rate. After 400 ps, the detrapping rate dominates the trapping rate and results in a decrease of pt(t) via recombination with electrons. The detrapped holes undergo bimolecular recombination with the mobile electrons, leading to similar decay features for Δn(t) and pt(t). The onset of the balanced state is shortened from 900 to 200 ps when the PFL increases from 0.075 to 4.5 μJ per pulse (Fig. S9, ESI†). Because of the distinct trap location with respect to the VB, the holes are detrapped from the Gaussian-tail and exponential-tail trap states to the VB in the nanosecond and sub-microsecond time ranges, respectively. Energy mapping of the charge carrier species is carried out at different time scales (Fig. S10, ESI†).The time profile of the TPL signal was simulated at various EIs. The parameters estimated from the TDR analysis were used as initial guesses and were fine-tuned for calibration of convoluted results with the measured TPL signal [Fig. 3(c) and Fig. S11, ESI†]. The convoluted data represent the convolution of numerical simulations corresponding to kr[neq + Δn(t)]Δp(t) and the IRF. Fine-tuning of the parameters was achieved by simultaneously comparing the convoluted and measured TPL decays in the high and low EI ranges. For instance, in the high EI range, neq is smaller than Δn(t) and the above TPL expression can be approximated as krΔn(t)Δp(t). This finding suggests that kr and Δn0 determine the decay characteristics in the sub-nanosecond time range in the high EI range. If Δn0 is known in advance, kr can be estimated through analysis of the TPL decay in the high EI range in the early time range. However, neq is higher than Δn(t) and the TPL can be simplified as krneqΔp(t) in the low EI range. As a result, krneq is expected to govern the decay rate in the sub-nanosecond time range in the low EI range. If kr is determined in the high EI range, neq can be estimated through analysis of the TPL decay in the low EI range in the early time range. In addition, shallow trap states are quantified by analysis of TPL decay primarily in the nanosecond time range. Such insights enable us to obtain parameters from TPL decay analysis. Irrespective of pump excitation, the mobile holes deplete faster than the mobile electrons (Fig. S9 and S12, ESI†). Therefore, the measured TPL signal follows the fast decay kinetics of minority mobile holes Δp(t) (Fig. S12, ESI†) rather than the slow decay kinetics of majority mobile electrons Δn(t). With similar parameter values (Table S2, ESI†), the simultaneous evaluation of TDR and TPL signals provides a unique capability to probe mobile electrons Δn(t) and holes Δp(t), respectively, in the nanosecond time range [Fig. 3(d)]. Because of hole detrapping from Gaussian-tail trap states, the simulated decay of the TPL signal is relatively slower than the simulated decay of the TPL signal in the absence of Gaussian-tail trap states (Fig. S13, ESI†). This result suggests that the holes are repopulated among the VB and Gaussian-tail trap states. Because of repopulation, the TPL decay by radiative recombination with mobile electrons becomes slower.
2.4. Performance predictions
TDR and TPL signal decay analyses provide various unknown parameters for visible-light-absorbing GTOS photocatalysts. These parameters can play a critical role in enhancing the performance of a GTOS-based solar water splitting reactor. In principle, the internal quantum efficiency (IQE) determines the ratio of charge carriers extracted by the electrolyte and photogenerated charge carriers under steady-state illumination conditions. The extracted charge carrier density is typically influenced by the charge transfer efficiency in the bulk and across the photocatalyst/electrolyte interface. The diffusion length of minority charge carriers [LD = (μkBTτ/q)0.5]30 should be greater than the average particle size of the photocatalyst, where μ, τ, kB, T and q are the charge carrier mobility, charge carrier lifetime, Boltzmann constant, temperature and elementary electronic charge, respectively. In such a scenario, the majority of charge carriers can reach the photocatalyst surface before the recombination process and realize high charge transfer efficiency in the bulk. Trap-assisted recombination can be ignored when shallow trap states are present; consequently, the τ of n-type doped photocatalysts such as GTOS is given by the inverse of the product of kr and neq [τ = 1/(krneq)] under the low-level photocarrier generation condition (Δn0 < neq). Although shallow trap states slow the transient decay kinetics of the mobile carrier density after pulsed excitation, they do not influence the lifetime of mobile carriers in steady states (see the ESI† for details) as long as neq is determined under the presence of trap states; the value of neq can be influenced by the presence of shallow trap states, but the relation τ = 1/(krneq) rigorously holds. On the basis of TDR analysis, kr, neq, and τ are estimated to be 1.7 × 10−10 cm3 s−1, 5 × 1018 cm−3, and 1.11 ns, respectively; these values are well supported by the TPL signal decay analysis. The exact determination of μ for a particulate-based GTOS photocatalyst is experimentally challenging and unknown at the present stage. With the estimated τ, the LD is 53 nm for a μ of 1 cm2 V−1 s−1, which is less than the maximum particle size of ∼3 μm and less than the thickness of ∼0.5 μm [Fig. 1(a)]. In comparison with the minority charge carrier lifetime of YTOS, that of GTOS is shorter because of the high neq [Fig. 4(a)]. In addition, GTOS exhibits a larger amplitude A of power-law S(t) decay, which indicates that the shallow trap state density is larger than that of YTOS; the decay component associated with trapped carriers increases with increasing trap-state density. The exact spatial locations of trap states are ambiguous and cannot be directly determined by TDR analysis. However, in a previous study, the doping of Sc onto the surface of YTOS was found to modulate the exponential-tail-trap-state-induced power-law S(t) decay and to lead to an enhancement of the H2 evolution activity.28 We speculate that, like YTOS, GTOS could have a considerable fraction of exponential-tail trap states present at its surface.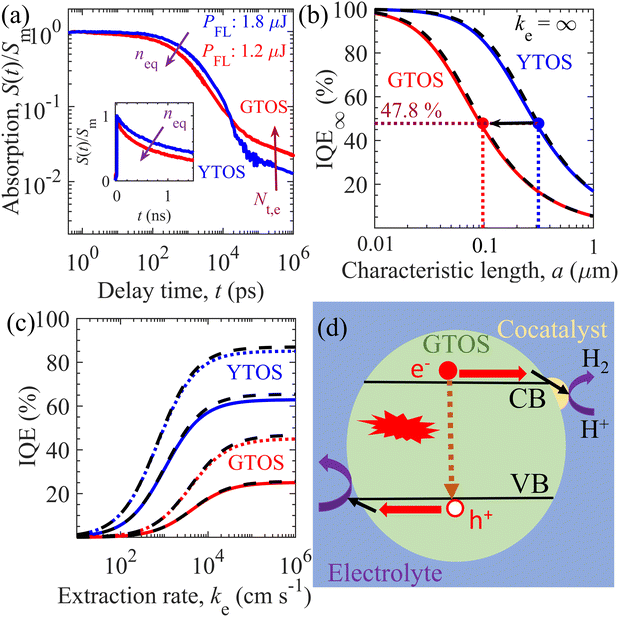 | ||
| Fig. 4 Performance predictions of the GTOS and YTOS photocatalysts. (a) Normalized TDR signal decay of the GTOS and YTOS samples at a pump fluence intensity PFL of 1.2 μJ and 1.8 μJ per pulse, respectively. Initial density of photogenerated charge carriers, Δn0, inside GTOS (4.45 × 1018 cm−3) and YTOS (4.74 × 1018 cm−3) is almost the same under the above-mentioned PFL. The arrow direction indicates an increase of the equilibrium electron density neq and the exponential-tail trap state density Nt,e. The particle size of the GTOS and YTOS is less than 3 μm and 10 μm, respectively. (b) Variation of IQE at an ideal carrier extraction velocity ke = ∞(IQE∞) versus the characteristic length a of GTOS and YTOS. Here, a = R/3 and R/2 for spherical and cylindrical particles, respectively, with radius R of the photocatalysts. (c) Influence of ke on the IQE [from eqn (1)] of GTOS and YTOS with a of 0.2 μm (solid lines) and 0.1 μm (dotted lines). In (b) and (c), the solid and dotted lines correspond to IQEs originating from the 3D transport of charge carriers in a spherical particle. The dashed black lines correspond to the IQEs originating from the 2D transport of charge carriers in a cylindrical particle. (d) Proposed charge carrier relaxation/transport mechanism for the best performing GTOS photocatalysts. Here, electrons (e−) and holes (h+) are extracted efficiently (shown by black arrows near the CB and VB; corresponding to high ke), resulting in the minimization of bulk recombination (represented by a dashed arrow) to improve the IQE for a high hydrogen evolution reaction. | ||
Under steady-state AM1.5 solar illumination, the theoretical limit of STH energy conversion efficiency ηmax is 20.9% for GTOS and YTOS photocatalysts because both oxysulfides exhibit a bandgap energy of ∼1.9 eV.15 For simplicity, we consider that 100% light absorption occurs on the light-absorption edge at 650 nm for the generation of mobile charge carriers in GTOS and YTOS during water splitting. Under this condition, the STH energy conversion efficiency η is obtained as η (%) = ηmax (%) × IQE. Moreover, particulate photocatalysts such as Al-doped SrTiO3 exhibited light reflection of less than 5% during OWS activity.11 To achieve η of 10% using a photocatalyst with a bandgap energy of ∼1.9 eV, designing a photocatalyst and its surface to minimize charge transport losses and realize an IQE of 47.8% is critical.15 According to the SEM image, the GTOS [Fig. 1(a)] and YTOS (ref. 16) prepared by a flux method exhibited a plate-like structure rather than the conventional bulky structure. The IQE is derived by considering three-dimensional (3D) and two-dimensional (2D) transport of charge carriers inside spherical (3D) and cylindrical (2D) particles (see the ESI† for details), respectively. IQE is correlated with the diffusion length of charge carriers LD, characteristic length a, and the extraction rate of minority holes from the photocatalyst surface to water ke with the following relation (see the ESI† for details):
| IQE (%) = (IQE∞−1 + a/(keτ))−1 × 100 | (1) |
Here, IQE∞ = LD2/3a2[3a/LD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coth(LD/3a) − 1] and LD/a[I1(2a/LD)/I0(2a/LD)] are the bulk 3D and 2D charge-transport-limited IQE (ratio) for a high ke, respectively, and I1(z) and I0(z) are the modified Bessel functions of the first kind of order one and zero for variable z, respectively. The characteristic length a is the ratio of the volume to the external surface area; as a result, a = R/3 and R/2 for spherical and cylindrical particles with radius R, respectively. On the basis of eqn (1), Fig. 4(b) and (c) predict the influence of the characteristic length and charge carrier extraction rate ke on the IQE of GTOS and YTOS. In addition, Fig. S14 of the ESI† shows the effect of LD and particle size (2R) on IQE∞. IQE∞ can be improved significantly either by increasing LD or reducing particle size (2R). For GTOS and YTOS, the charge carrier lifetime τ is controlled by bimolecular recombination of photogenerated holes and equilibrium (dark) electrons under AM 1.5G solar illumination. Therefore, LD (or IQE∞) improvement can be achieved by reducing equilibrium electron density neq. Considering a μ of 1 cm2 V−1 s−1, the LD is 53 and 178 nm for GTOS and YTOS, respectively. Because of the different LDs, the optimum characteristic length to achieve an IQE of 47.8% is ∼314 nm and ∼97 nm for YTOS and GTOS, respectively [Fig. 4(b)]. In addition, the IQE increases with decreasing characteristic length (or particle size) as more charge carriers are transported to the surface rather than recombination. Similarly, the IQE increases with increasing carrier extraction rate ke, which depends on the characteristic length [Fig. 4(c)]. Despite efficient charge carrier separation in the bulk, the IQE can be strongly suppressed by decreasing ke. Interestingly, the results indicate that IQE trends against ke are similar for 3D and 2D charge carrier transport for the given characteristic length a. Our results show that optimization of the bulk and surface properties is imperative to improve the water-splitting activity of emerging visible-light-absorbing photocatalysts and could be used as a design strategy for the efficient production of H2 fuel from sunlight and water.
coth(LD/3a) − 1] and LD/a[I1(2a/LD)/I0(2a/LD)] are the bulk 3D and 2D charge-transport-limited IQE (ratio) for a high ke, respectively, and I1(z) and I0(z) are the modified Bessel functions of the first kind of order one and zero for variable z, respectively. The characteristic length a is the ratio of the volume to the external surface area; as a result, a = R/3 and R/2 for spherical and cylindrical particles with radius R, respectively. On the basis of eqn (1), Fig. 4(b) and (c) predict the influence of the characteristic length and charge carrier extraction rate ke on the IQE of GTOS and YTOS. In addition, Fig. S14 of the ESI† shows the effect of LD and particle size (2R) on IQE∞. IQE∞ can be improved significantly either by increasing LD or reducing particle size (2R). For GTOS and YTOS, the charge carrier lifetime τ is controlled by bimolecular recombination of photogenerated holes and equilibrium (dark) electrons under AM 1.5G solar illumination. Therefore, LD (or IQE∞) improvement can be achieved by reducing equilibrium electron density neq. Considering a μ of 1 cm2 V−1 s−1, the LD is 53 and 178 nm for GTOS and YTOS, respectively. Because of the different LDs, the optimum characteristic length to achieve an IQE of 47.8% is ∼314 nm and ∼97 nm for YTOS and GTOS, respectively [Fig. 4(b)]. In addition, the IQE increases with decreasing characteristic length (or particle size) as more charge carriers are transported to the surface rather than recombination. Similarly, the IQE increases with increasing carrier extraction rate ke, which depends on the characteristic length [Fig. 4(c)]. Despite efficient charge carrier separation in the bulk, the IQE can be strongly suppressed by decreasing ke. Interestingly, the results indicate that IQE trends against ke are similar for 3D and 2D charge carrier transport for the given characteristic length a. Our results show that optimization of the bulk and surface properties is imperative to improve the water-splitting activity of emerging visible-light-absorbing photocatalysts and could be used as a design strategy for the efficient production of H2 fuel from sunlight and water.
To validate the IQE model of eqn (1), Fig. S15 of the ESI† displays the comparison of simulated IQE (using parameters in Table S3, ESI†) and previously reported experimental EQE data for different GTOS- and YTOS-based photocatalyst systems. For GTOS, theoretical IQE predictions using ke = ∞ are close to the measured EQE [Fig. S15(a), ESI†] for the optimized sample (prepared by the flux method), indicating good contacts between cocatalysts and the GTOS surface for charge carrier transfer for water splitting activity. To achieve the ideal limit of ke (= ∞), the GTOS surface was subjected to acid treatment before Pt and IrO2 cocatalyst deposition by the microwave method in ethylene glycol for hydrogen and oxygen evolution reactions.17Fig. 4(d) displays the schematic illustration of charge carrier relaxation/transport behind the optimized GTOS sample (corresponding to ke = ∞). Here, the water splitting activity is controlled by bulk charge carrier recombination rather than ke. This indicates that a further EQE improvement can be achieved by improving the bulk properties like charge carrier lifetime and diffusion length by reducing the equilibrium electron density with p-type dopants. In contrast, for YTOS, the measured EQE is significantly less than the calculated IQE using ke = ∞. This suggests that EQE could be limited by poor charge transfer from the YTOS surface to electrolyte, which led to significant recombination of photogenerated charge carriers. Overall, our results identify performance bottlenecks from the bulk and surface properties of GTOS and YTOS photocatalyst systems to achieve high water splitting activity, respectively.
2.5. Influence of the I2 precursor and preparation methods
SSR- and flux-based methods have been the predominant methods used to prepare oxysulfide photocatalysts such as GTOS and YTOS.16,17 In the present study, a GTOS photocatalyst with a plate-like morphology was realized by an SSR method with the additional I2 precursor [Fig. 1(a)]. We observe that the preparation conditions (i.e., temperature and additional precursors) can strongly affect the properties of oxysulfide photocatalysts (discussion included in the ESI† as well as Table S4, Fig. S16, and S17 of the ESI†). For instance, in the samples prepared using the SSR method, the n-type doping density (charge carrier lifetime) of GTOS is almost two orders higher (lower) than that of YTOS, which might be explained by GTOS having a greater density of vacancies as a result of being processed at higher temperatures than YTOS. We observed that the flux materials resulted in a decrease and increase of the doping density neq for the respective SSR-based GTOS and YTOS samples. This observation suggests that, depending on the thermal processing conditions, the flux materials can be used to reduce the neq of GTOS and YTOS. The charge carrier lifetime [1/(krneq)] of the SSR-based YTOS is substantially longer (12.25 ns) than that of the flux-based YTOS (1.11 ns), whereas the influence of flux material on the lifetime (0.33 ns) of GTOS is inconsequential.To deconvolute the effects of the processing temperature and I2 precursor, GTOS samples prepared by an SSR method in the presence and absence of I2 precursors at a fixed temperature of 973 K were investigated; these samples are designated as GTOS (973 K, I2) and GTOS (973 K), respectively. The major effects of the I2 precursor are a decrease of the recombination rate constant kr and an improvement of the charge carrier lifetime, in addition to a decrease of the exponential-tail trap state density. On the basis of the above discussion, GTOS samples prepared by the SSR method at a processing temperature of 973 K and in the presence of the I2 precursor exhibited a longer charge carrier lifetime and a nonsegregated plate-like structure.
3. Conclusions
In summary, TDR and TPL spectroscopies were performed, and their kinetics were theoretically analyzed to reveal the charge carrier dynamics of an emerging visible-light-absorber GTOS photocatalyst. Distinct charge carrier species (mobile and trapped) were identified by simultaneous evaluation of the TDR and TPL signal decay characteristics. The TDR signal at a probe photon energy of 0.24 eV and the TPL signal decay were found to be dominated by the decay of photogenerated mobile electrons and mobile holes, respectively. The pump-fluence-intensity-dependent TDR signal decay in the early nanosecond time range was attributed to the bimolecular recombination of mobile electrons with holes detrapped from Gaussian-tail trap states. However, the power-law TDR decay in the sub-microsecond time range was governed by the recombination of mobile electrons with holes detrapped from exponential-tail trap states. These trap states are located close to the valence band and participate in the trapping and detrapping processes of photogenerated holes. Various parameters, such as the rate constants for recombination and trapping, equilibrium electron density, charge carrier lifetime, and the trap-state parameters of GTOS, were determined by TDR decay analysis. The parameters estimated from the TDR decay analysis are consistent with the values obtained from the TPL decay analysis. In addition, we discussed the critical role of bulk and surface properties in efficient water splitting. Our detailed analysis of spectral data offers a unique methodology for characterizing emerging visible-light-absorbing photocatalysts, which is critical for the design of highly efficient solar-water-splitting systems.4. Experimental section
4.1. Fabrication of GTOS
The GTOS powder was prepared by a traditional solid-state reaction (SSR) in a sealed evacuated quartz tube. Gd2O3 (Wako Pure Chemical Industries, 99.99%), Gd2S3 (High Purity Chemicals, 99.9%), and TiO2 (High Purity Chemicals, 99.99%) were combined at a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. I2 (Wako Pure Chemical Industries, 99.9%) and sulfur powder (High Purity Chemicals, 99.99%) were added to the other starting reagents at a concentration of 5 wt% for the sample with I2 and without I2, respectively. These materials were mixed in an Ar-filled recirculating glove box with an O2 concentration of less than 3 ppm. The resultant mixture was sealed in an evacuated quartz tube, heated to 973 K at a heating rate of 5 K min−1, and then maintained at this temperature for 96 h. After the annealing process, the sample was allowed to cool naturally. To remove the iodine species or excess sulfur adsorbed onto the surface, the GTOS powder was annealed in air at 473 K for 1 h, thoroughly rinsed with distilled water, and dried under vacuum at 313 K.
6. I2 (Wako Pure Chemical Industries, 99.9%) and sulfur powder (High Purity Chemicals, 99.99%) were added to the other starting reagents at a concentration of 5 wt% for the sample with I2 and without I2, respectively. These materials were mixed in an Ar-filled recirculating glove box with an O2 concentration of less than 3 ppm. The resultant mixture was sealed in an evacuated quartz tube, heated to 973 K at a heating rate of 5 K min−1, and then maintained at this temperature for 96 h. After the annealing process, the sample was allowed to cool naturally. To remove the iodine species or excess sulfur adsorbed onto the surface, the GTOS powder was annealed in air at 473 K for 1 h, thoroughly rinsed with distilled water, and dried under vacuum at 313 K.
4.2. Sample characterization
Powder XRD patterns were collected using a Rigaku MiniFlex 300. UV-Visible DRS data were acquired using a JASCO V-670 UV-visible system. The morphology of the samples was investigated using a FE-SEM (Phenom Pharos, ThermoFisher Scientific).4.3. Density functional theory calculations
Structural optimizations, along with electronic structure and dielectric function analyses, were performed on the GTOS primitive cell (11 atoms per cell) using the Vienna Ab initio Simulation Package (VASP).31 Calculations of the electronic structure were based on the projected augmented wave (PAW)32 method and the Perdew–Burke–Ernzerhof (PBE)18 exchange–correlation functional. The electronic wave functions were expanded using a plane-wave basis set with a kinetic energy cutoff of 520 eV. A Γ-centered k-point mesh of 7 × 7 × 9 was used for the structural optimization, and an 11 × 11 × 15 k-point mesh was used for the dielectric function calculations in the independent-particle approximation using the PBE functional. For calculations of the PDOS, band structure, and effective mass, a 4 × 4 × 6 k-point mesh was used with the HSE0619 functional, incorporating a Hartree–Fock screening parameter of 0.2. After structural optimization, the transformation of the optimized primitive cell back into the conventional cell revealed lattice constants of a = b = 3.813 Å and c = 23.072 Å. The convergence criteria were set at 10−8 eV for electronic configurations and 10−2 eV Å−1 for ionic forces. The post-processing of VASP calculated data was carried out using the VASPKIT code.334.4. Transient diffuse reflectance spectroscopy
Transient diffuse reflectance (TDR) spectroscopy, which is similar to transient absorption (TA) spectroscopy, was used to investigate the photocarrier dynamics of the various photocatalysts. During the TDR measurement, a TA signal was acquired in the diffuse-reflectance mode because of the opaque nature of the photocatalyst powder samples. The TA intensity is presented herein in units of percentage absorption [absorption (%)], calculated as 100 × (1 − R/R0), where R and R0 are the intensities of the diffusely reflected light with and without pump excitation, respectively.Femtosecond TDR measurements (t < 3 ns) were carried out using a Ti:Al2O3 laser with a regenerative amplifier (Spectra-Physics, Solstice, a central wavelength of ∼800 nm, a pulse width of ∼100 fs, a pulse energy of ∼3.5 mJ per pulse, and a repetition rate of 1 kHz) as a light source. The output from the laser was split into four paths. These four paths were used for excitation of two optical parametric amplifiers (OPAs: Spectra-Physics, TOPAS Prime), the white-light-continuum generation based on focusing the fundamental light (800 nm) onto a sapphire plate, and second- and third-harmonic generation of the fundamental light (800 nm) using β-BaB2O4 crystals. The second-harmonic light (400 nm) was used as a pump light, and the intensity of this light was varied between 0.075 and 4.5 μJ per pulse using neutral-density filters. For the probe light ranging from 440 to 8214 nm, a white-light continuum spanning the range from 440 to 1600 nm and infrared (IR) light longer than 1600 nm generated from the OPA equipped with a difference-frequency-generation crystal were used. The delay time between the probe and pump pulses could be adjusted to be as long as 3 ns by changing the optical path length of the pump pulse. The GTOS powder sample was held in a CaF2 cuvette with dimensions of 45 mm × 10 mm × 1 mm. An amplified Si photodetector (Thorlabs, PDA36A-EC) and an InGaAs photodetector (Thorlabs, PDA20CS-EC) were used to probe the wavelength ranges of 440–1100 nm and 1100–1600 nm, respectively. For the probe from 440 to 1600 nm, diffusely reflected light from the sample was passed through a grating monochromator (Princeton Instruments, Acton SP2150) prior to data acquisition, whereas a liquid-N2-cooled HgCdTe photodetector (Kolmar Technologies, KMPV11-1-J1) was used to probe the range from 1600 to 8214 nm. The diameter of the pump beam where it met the sample was approximately 1 mm, and the area irradiated by this beam was evaluated using a beam profiler (Newport, LBP2-HR-VIS2). With estimated pump beam area, the normalized pump intensity was 225.40 μJ cm−2 per pulse at a pump fluence intensity PFL of 3 μJ per pulse. The photogenerated charge carrier density was estimated by considering the light penetration depth (408 nm) obtained from the absorption coefficient (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) at 400 nm and the irradiated area of the excitation light as per the Lambert–Beer law.
500 cm−1) at 400 nm and the irradiated area of the excitation light as per the Lambert–Beer law.
During the TDR measurements for t > 3 ns, a continuous-wave IR light emitted at 5250 nm (0.24 eV) from a quantum cascade laser (Thorlabs, QD5250CM1 AB152) was used as the probe light source. The pump light of 400 nm was identical to that used in the measurements for t < 3 ns described above. The diffusely reflected light from the sample was detected using a liquid-N2-cooled fast HgCdTe photodetector (Kolmar Technologies, KV104-0.25-A-2/11, a bandwidth of 80 MHz). The signal from this detector was preamplified using a voltage amplifier (Femto, DHPVA-200), amplified using a voltage amplifier (Femto, DUPVA-1-60), and then subsequently processed and recorded with a digital oscilloscope (Lecroy, WaveRunner 6200 A). The pump-induced signal (AC signal) was selectively extracted using the AC-coupled mode of the amplifier (Femto, DUPVA-1-60). The DC offset of the signal from the detector was independently recorded with a digital multimeter (National Instruments, USB-4065) to calculate the absorption value [absorption (%)]. Using this process, very weak TA signals (<0.01%) could be detected with a time resolution of a few nanoseconds.
4.5. Transient photoluminescence measurements
Transient photoluminescence (TPL) measurements were carried out using a streak camera (Hamamatsu Photonics, StreakScope C4334) equipped with a monochromator to detect the PL spectra and kinetics of GTOS. The GTOS powder sample was placed in a quartz cell with dimensions of 58 mm × 12.5 mm × 1.0 mm (GL Sciences, quartz cell with screw cap, F15-SQF-1). A Ti:Al2O3 laser with a regenerative amplifier (Spectra-Physics, Solstice, a central wavelength of ∼800 nm, a pulse width of ∼100 fs, a pulse energy of ∼3.5 mJ per pulse, and a repetition rate of 1 kHz) was used as a light source. The second-harmonic light (400 nm) generated from the fundamental light (800 nm) using a β-BaB2O4 (BBO) crystal was used as the excitation light. The excitation light intensity was varied using neutral-density filters from 0.51 μJ per pulse to 85 μJ per pulse. The time resolution of the system was 67 ps. The irradiated area of the excitation light at the sample position was estimated using a beam profiler (Newport LBP2-HR-VIS2). With the estimated pump beam area, the normalized pump intensity was 204.55 μJ cm−2 per pulse at an excitation intensity EI of 85 μJ per pulse. The photogenerated charge carrier density was estimated by considering the light penetration depth (408 nm) obtained from the absorption coefficient (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) at 400 nm and the irradiated area of the excitation light as per the Lambert–Beer law.
500 cm−1) at 400 nm and the irradiated area of the excitation light as per the Lambert–Beer law.
4.6. Modeling and simulations
Fig. 3a displays the charge carrier relaxation model of the n-type GTOS photocatalyst. In this model, the relaxation of photogenerated charge carriers is dominated by band-to-band bimolecular recombination of holes and electrons and by trapping and detrapping of holes. Mobile electrons and holes are generated in their respective CB and VB by the pump fluence intensity PFL (in TDR) and the excitation intensity EI (in TPL). The initial density of mobile electrons/holes Δn0 is modulated by varying the PFL or EI. Shallow trap states close to the VB energy of Ev for trapping and detrapping of holes are composed of the sum of Gaussian-tail and exponential-tail trap states such that the trap density is given by Ntg(E) = Ntg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−E2/(2E0,g2)][2/(πE0,g2)]0.5 + Nt,e
exp[−E2/(2E0,g2)][2/(πE0,g2)]0.5 + Nt,e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/E0,e)/E0,e. The total trap density is obtained from
exp(−E/E0,e)/E0,e. The total trap density is obtained from 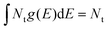 , which is the sum of the trap density from Gaussian-tail Nt,g and exponential-tail Nt,e components. E, E0,g, and E0,e are the energy inside the bandgap (with respect to Ev), Gaussian characteristic energy, and the exponential characteristic energy, respectively. Trapping and detrapping of holes proceed with respective rate constants kt and kd. In addition, mobile holes and mobile electrons undergo the bimolecular recombination process with rate constant kr. The dynamics of mobile electron density Δn(t), mobile hole density Δp(t), and trapped hole density pt(E,t) with time t are determined from the numerical simulations (using the Runge–Kutta fourth-order method implemented in MATLAB) of eqn (2)–(4):
, which is the sum of the trap density from Gaussian-tail Nt,g and exponential-tail Nt,e components. E, E0,g, and E0,e are the energy inside the bandgap (with respect to Ev), Gaussian characteristic energy, and the exponential characteristic energy, respectively. Trapping and detrapping of holes proceed with respective rate constants kt and kd. In addition, mobile holes and mobile electrons undergo the bimolecular recombination process with rate constant kr. The dynamics of mobile electron density Δn(t), mobile hole density Δp(t), and trapped hole density pt(E,t) with time t are determined from the numerical simulations (using the Runge–Kutta fourth-order method implemented in MATLAB) of eqn (2)–(4):| dpt(E,t)/dt = ktΔp(t)[Ntg(E) − pt(E,t)] − kdpt(E,t)[Nv − Δp(t)]. | (2) |
Here, the first and second terms on the right-hand-side represent the trapping and detrapping of holes, respectively. Under the steady-state condition (i.e., dpt(E,t)/dt = 0), the detrapping rate constant is evaluated as kd = kt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−E/kBT), where kB and T are the Boltzmann constant and temperature, respectively. Nv is the effective density of states for the VB. The time evolution of mobile holes is given by
exp(−E/kBT), where kB and T are the Boltzmann constant and temperature, respectively. Nv is the effective density of states for the VB. The time evolution of mobile holes is given by
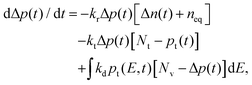 | (3) |
 , respectively. The time evolution of electrons is governed by bimolecular recombination in accordance with
, respectively. The time evolution of electrons is governed by bimolecular recombination in accordance with| dΔn/dt = −krΔp(t)[Δn(t) + neq]. | (4) |
At t = 0.4 ps, Δn(t) and Δp(t) are equal to Δn0, which is determined by the Lambert–Beer law. The trapped hole density pt(E,t) = 0 at t = 0.4 ps as the charge carriers are expected to be produced in the continuum CB and VB after pump laser irradiation. The initial guess of parameters is obtained from early nanosecond absorption signal decay analysis (Fig. S6, ESI†). With the fine-tuning of the parameters, the numerically simulated Δn(t) is in reasonable agreement with the experimental TDR data for various PFL. Table S2 of the ESI† provides the estimated parameters of GTOS from the TDR signal decay analysis.
The TPL signal decay analysis was independently carried out using the aforementioned charge carrier relaxation model. The TPL signal was generated from the band-to-band recombination of mobile charge carriers. Therefore, the TPL signal intensity was given and simulated using the relation IPL = krΔp(t)[Δn(t) + neq]. The simulated TPL signal was convoluted with the instrumental response function (IRF) = A0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−t2/(2σ2)]/(2πσ2)0.5, where constants A0 and σ are fixed at 1.1 × 10−24 and 28.28 ps, respectively. After convolution, the simulated TPL signal was matched with experimental data for various EI values and various parameters of the GTOS photocatalyst were determined. The estimated parameters from TDR signal decay analysis were similar to those obtained from the TPL signal decay analysis.
exp[−t2/(2σ2)]/(2πσ2)0.5, where constants A0 and σ are fixed at 1.1 × 10−24 and 28.28 ps, respectively. After convolution, the simulated TPL signal was matched with experimental data for various EI values and various parameters of the GTOS photocatalyst were determined. The estimated parameters from TDR signal decay analysis were similar to those obtained from the TPL signal decay analysis.
Author contributions
H. M., K. S., and K. D. conceived the idea and initiated the research. X. T. (with the help of T. H., H. Y., T. T., and K. D.) prepared the sample and characterized materials by SEM, XRD, and DRS measurements. M. K. and K. Y. conducted DFT calculations. R. S. and H. M. performed TDR and TPL experiments. V. N. and K. S. performed the theoretical modeling and analyzed the data with R. S., H. M. and A. F.. V. N. and R. S. wrote the manuscript with contributions from the other authors. All authors contributed to the scientific discussion and editing of the manuscript.Data availability
The data that support the findings of this study are available upon reasonable request to the authors.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was funded by the Artificial Photo-Synthesis Project of the New Energy and Industrial Technology Development Organization (NEDO).References
- Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511–518 CrossRef CAS.
- Y. Goto, T. Hisatomi, Q. Wang, T. Higashi, K. Ishikiriyama, T. Maeda, Y. Sakata, S. Okunaka, H. Tokudome, M. Katayama, S. Akiyama, H. Nishiyama, Y. Inoue, T. Takewaki, T. Setoyama, T. Minegishi, T. Takata, T. Yamada and K. Domen, Joule, 2018, 2, 509–520 CrossRef CAS.
- J. H. Kim, D. Hansora, P. Sharma, J.-W. Jang and J. S. Lee, Chem. Soc. Rev., 2019, 48, 1908–1971 RSC.
- Q. Wang and K. Domen, Chem. Rev., 2020, 120, 919–985 CrossRef CAS PubMed.
- H. Nishiyama, T. Yamada, M. Nakabayashi, Y. Maehara, M. Yamaguchi, Y. Kuromiya, Y. Nagatsuma, H. Tokudome, S. Akiyama, T. Watanabe, R. Narushima, S. Okunaka, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Nature, 2021, 598, 304–307 CrossRef CAS.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 RSC.
- S. Chen, T. Takata and K. Domen, Nat. Rev. Mater., 2017, 2, 17050 CrossRef CAS.
- T. Hisatomi, J. Kubota and K. Domen, Chem. Soc. Rev., 2014, 43, 7520–7535 RSC.
- M. Schröder, K. Kailasam, J. Borgmeyer, M. Neumann, A. Thomas, R. Schomäcker and M. Schwarze, Energy Technol., 2015, 3, 1014–1017 CrossRef.
- T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414 CrossRef CAS.
- M. Goga, R. Seshadri, V. Ksenofontov, P. Gütlich and W. Tremel, Chem. Commun., 1999, 979–980 RSC.
- A. Ishikawa, T. Takata, T. Matsumura, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. B, 2004, 108, 2637–2642 CrossRef CAS.
- Q. Wang, M. Nakabayashi, T. Hisatomi, S. Sun, S. Akiyama, Z. Wang, Z. Pan, X. Xiao, T. Watanabe, T. Yamada, N. Shibata, T. Takata and K. Domen, Nat. Mater., 2019, 18, 827–832 CrossRef CAS PubMed.
- V. Nandal, R. Shoji, H. Matsuzaki, A. Furube, L. Lin, T. Hisatomi, M. Kaneko, K. Yamashita, K. Domen and K. Seki, Nat. Commun., 2021, 12, 7055 CrossRef CAS.
- L. Lin, P. Kaewdee, V. Nandal, R. Shoji, H. Matsuzaki, K. Seki, M. Nakabayashi, N. Shibata, X. Tao, X. Liang, Y. Ma, T. Hisatomi, T. Takata and K. Domen, Angew. Chem., Int. Ed., 2023, 62, e202310607 CrossRef CAS PubMed.
- H. Yoshida, Z. Pan, R. Shoji, V. Nandal, H. Matsuzaki, K. Seki, L. Lin, M. Kaneko, T. Fukui, K. Yamashita, T. Takata, T. Hisatomi and K. Domen, Angew. Chem., Int. Ed., 2023, 62, e202312938 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- M. Nishiwaki and H. Fujiwara, Comput. Mater. Sci., 2020, 172, 109315 CrossRef CAS.
- S. De Wolf, J. Holovsky, S.-J. Moon, P. Löper, B. Niesen, M. Ledinsky, F.-J. Haug, J.-H. Yum and C. Ballif, J. Phys. Chem. Lett., 2014, 5, 1035–1039 CrossRef CAS PubMed.
- M. Kaneko, V. Nandal, K. Yamashita and K. Seki, AIP Adv., 2024, 14, 95115 CrossRef CAS.
- Y. Suzuki, D. H. K. Murthy, H. Matsuzaki, A. Furube, Q. Wang, T. Hisatomi, K. Domen and K. Seki, J. Phys. Chem. C, 2017, 121, 19044–19052 CrossRef CAS.
- D. H. K. Murthy, H. Matsuzaki, Q. Wang, Y. Suzuki, K. Seki, T. Hisatomi, T. Yamada, A. Kudo, K. Domen and A. Furube, Sustainable Energy Fuels, 2019, 3, 208–218 RSC.
- T. Higashi, H. Nishiyama, V. Nandal, Y. Pihosh, Y. Kawase, R. Shoji, M. Nakabayashi, Y. Sasaki, N. Shibata, H. Matsuzaki, K. Seki, K. Takanabe and K. Domen, Energy Environ. Sci., 2022, 15, 4761–4775 RSC.
- Y. Pihosh, V. Nandal, R. Shoji, R. Bekarevich, T. Higashi, V. Nicolosi, H. Matsuzaki, K. Seki and K. Domen, ACS Energy Lett., 2023, 8, 2106–2112 CrossRef CAS.
- D. H. K. Murthy, H. Matsuzaki, Z. Wang, Y. Suzuki, T. Hisatomi, K. Seki, Y. Inoue, K. Domen and A. Furube, Chem. Sci., 2019, 10, 5353–5362 RSC.
- H. Yoshida, Z. Pan, R. Shoji, V. Nandal, H. Matsuzaki, K. Seki, T. Hisatomi and K. Domen, J. Mater. Chem. A, 2022, 10, 24552–24560 RSC.
- Y. Pihosh, V. Nandal, T. Higashi, R. Shoji, R. Bekarevich, H. Nishiyama, T. Yamada, V. Nicolosi, T. Hisatomi, H. Matsuzaki, K. Seki and K. Domen, Adv. Energy Mater., 2023, 13, 2301327 CrossRef CAS.
- R. F. Pierret, Semiconductor Device Fundamentals, Addison-Wesley, 1996 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B, 2006, 73, 45112 CrossRef.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ey00187g |
| ‡ R. S. and V. N. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |