 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards utility-scale electronic structure with sample-based quantum bootstrap embedding
Joel
Bierman
a and
Yuan
Liu
 *abc
*abc
aDepartment of Electrical and Computer Engineering, North Carolina State University, Raleigh, NC 27606, USA. E-mail: q_yuanliu@ncsu.edu
bDepartment of Computer Science, North Carolina State University, Raleigh, NC 27606, USA
cDepartment of Physics, North Carolina State University, Raleigh, NC 27607, USA
First published on 22nd January 2026
Abstract
One of the main applications for which quantum computers are hoped to find utility is in simulating ground state energies and other observables of molecular chemical systems. The recently proposed sample-based diagonalization method is a readily implementable method for this task on current-day hardware using short circuit depths and has been demonstrated on as many as 85 qubits in recent studies. In this work, we combine the recently proposed quantum bootstrap embedding (QBE) method with sampled-based diagonalization (QBE-SQD) and present the first benchmarking study of the QBE method on real quantum hardware, ibm_pittsburgh, a Heron r3 processor with 156 qubits. Our test system is a hydrogen ring with 8 hydrogen atoms in the cc-pVDZ basis. We show that for this system, QBE-SQD using an active space of (8e, 19o) per fragment with a 43 qubit footprint produces a ground state energy accuracy which exceeds that of an SQD calculation with an (8e, 30o) active space with a 67 qubit footprint when using a comparable number of Slater determinants. This demonstrates that the use of quantum bootstrap embedding techniques is a promising path towards extending the capabilities of state-of-the-art quantum eigensolvers on near-term devices.
1 Introduction
One of the key areas where quantum computers are expected to demonstrate an advantage over classical computers is the simulation of physical quantum systems such as the electronic structure problem in molecular chemistry and materials science.1–3 That is, we want to compute observables for the ground state of the Hamiltonian | (1) |
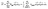 | (2) |
 are the particle creation and annihilation operators, respectively, for orbital p. hpq and vpqsr are the one- and two-body integral tensor elements defined as
are the particle creation and annihilation operators, respectively, for orbital p. hpq and vpqsr are the one- and two-body integral tensor elements defined as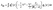 | (3) |
 | (4) |
As the quality and quantity of qubits on quantum computers have improved in recent years, experiments relevant to such physical systems on quantum computers are shifting from small-scale proof-of-concept simulations4–6 to near utility-scale experiments at the limits of what can be accomplished on a classical computer.7,8 Simultaneously, quantum error correction experiments demonstrating logical qubits achieving error rates modestly lower than those of their physical unencoded counterparts are beginning to emerge.9–11 While this progress is encouraging, these simulations are run on quantum devices which lack fault-tolerance for the number of logical qubits needed to demonstrate quantum utility. Current-day devices can at most utilize error mitigation schemes such as zero-noise extrapolation, probabilistic error cancellation, and dynamical decoupling.12–14 This precludes the demonstration of algorithms such as quantum phase estimation15–19 (QPE), which is expected to require hundreds of logical qubits with logical error rates several orders of magnitude below what is achievable on current-day devices in order to demonstrate an advantage over classical computers.2
Embedding methods such as density matrix embedding theory20–23 (DMET) and quantum bootstrap embedding24–31 (QBE) provide a feasible approach to simulate large-scale electronic structure problems on small quantum computers. These methods take the approach of fragmenting a large system into several subsystems and variationally optimize the energy subject to a set of constraints related to the self-consistency of each of these fragment wavefunctions. Consequentially, one only has to run an eigensolver subroutine for each of the smaller fragments rather than the system as a whole. In the classical setting, the superlinear scaling of both approximate and exact eigensolvers implies that the memory footprint and runtime associated with running eigensolvers for the collection of fragments can often be made less severe than for the large unfragmented system. It could even be reasonably argued that the potential benefits of using embedding are even more pronounced in the quantum setting due to additional constraints of current-day machines. These include (1) a limited number of qubits, (2) non-negligible error rates which limit the size of individual circuits that can be run, and (3) limited qubit-connectivity that can limit the expressivity of ansatz circuits. The use of DMET in combination with SQD has recently been demonstrated on real quantum hardware.32 However it remains to be seen which embedding method works better on quantum computers.
To unleash the power of quantum embedding methods on near-term quantum hardware, the choice of quantum eigensolvers is important. Even for small fragments, phase estimation has a high-overhead cost that often requires a deep depth circuit. Variational quantum eigensolver33–35 (VQE) was proposed as an alternative phase estimation to be run on near-term quantum devices. Even though VQE does not explicitly require deep circuits, it is known to suffer from other issues which present a formidable barrier to its use for large-scale (dozens to hundreds of qubits) simulations on any quantum computer, both near-term and long-term. It has been estimated that for utility-scale systems (∼102 qubits), measuring the energy of a molecular Hamiltonian a single time on a quantum computer could have a wall clock runtime on the order of days to months.36 Even if these resource estimates could be improved drastically, the barren plateaus problem37–39 where the variance of the gradient of the cost function landscape vanishes exponentially with the size of the system, could still make convergence to the global minimum exponentially slow.
The long runtime expected from variational methods for simulating physical systems has led to the emergence of quantum selective configuration interaction (QSCI) methods,8,40–42 which avoid this long runtime problem by not measuring expectation values of observables on the quantum computer at all. Instead, this class of methods reduces the role of the quantum computer to finding an optimal subspace onto which the Hamiltonian can be projected and subsequently diagonalized on a quantum computer. This has allowed QSCI to be demonstrated with simulations as large as 85 qubits under the name sample-based diagonalization (SQD).41 Similarly, adapting quantum Monte Carlo methods to quantum computers has been proposed as a means to avoid the optimization challenges of VQE.43 Meanwhile, much attention has been paid towards developing ways of enhancing existing eigensolvers by reducing their qubit footprint on the quantum computer. Orbital optimization methods,44–47 for example, introduce the matrix elements of a single-particle wavefunction rotation operator as additional parameters to be optimized in a larger minimization problem. These methods tend to generate more compact basis sets than those generated by canonical molecular orbitals.
By combining bootstrap embedding with a quantum eigensolver such as SQD, we can potentially reduce the impact of the constraints of current quantum hardware. This presents the opportunity to either simulate systems larger than what can be achieved with SQD alone or simulate similar system sizes with higher accuracy. Another benefit of using SQD as the eigensolver in QBE lies in evaluating the matching conditions. When VQE or QPE is the eigensolver, one either uses (i) coherent matching (SWAP test), or incoherent matching by (ii) measuring the full qubit RDM on the overlapping region, or (iii) the corresponding fermionic 1-RDM.24 The first of these needs more than doubling the qubit count and implementing a sequence of controlled SWAP gates that are not easily mapped to the heavy-hex topology of IBM machines without too much overhead. The second involves exponentially costly state tomography. The third of these is likely to incur a significant (but polynomial) measurement overhead as well. Instead, in SQD, after the eigensolver subroutine is finished, one obtains the 1-RDM needed for the matching conditions at negligible cost.
The potential challenge in combining bootstrap embedding with SQD is that noise on the quantum device, the limited ansatz expressiveness, and limited sampling have the potential to disrupt the convergence of the BE optimization that is necessary for the advantages of bootstrap embedding to be realized.
In this work, we combine sample-based diagonalization with bootstrap embedding and investigate the extent to which QBE-SQD can be used to enhance the capabilities of SQD. We present the first benchmarking study of QBE-SQD on real quantum hardware in chemically realistic basis sets for a moderate size molecular system H8 across different bond lengths. This system provides a good test of the performance of the methods from weakly to strongly correlated regimes. By comparing QBE-SQD on the 156-qubit Heron r3 processor ibm_pittsburgh with vanilla SQD, we show that QBE-SQD using an active space of (8e, 19o) per fragment with a 43 qubit footprint produces a ground state energy accuracy at near-equilibrium geometries which exceeds that of an SQD calculation in a larger active space (8e, 30o) with a 67 qubit footprint by several mHa when using a comparable number of Slater determinants while maintaining a stronger usable signal for the configuration recovery process. This demonstrates that the use of QBE techniques is a promising path towards extending the capabilities of state-of-the-art quantum eigensolvers on near-term devices. For stretched bond geometries, we show that the convergence of bootstrap embedding becomes increasingly challenging, increasing the density matching error as the bonds are progressively stretched. We show that this effect can be mitigated by only optimizing the chemical potential.
The rest of the paper is organized as follows. Sec. 2 reviews background information relevant to bootstrap embedding and sample-based diagonalization individually and details how these methods may be combined. Sec. 3 details our experimental set-up and results on ibm_pittsburgh. Sec. 4 ends with concluding discussions of the implication of the results and potential future directions of research.
2 Methods
In Sections 2.1 and 2.2, we review background information for sample-based diagonalization (SQD) and quantum bootstrap embedding (QBE), respectively. In Sec. 2.3 we describe how sample-based diagonalization and bootstrap embedding may be combined.2.1 Sample-based diagonalization
Quantum Selective Configuration Interaction (QSCI) methods,40 of which sampled-based diagonalization8,42,48 (SQD) is a particular example, use quantum computers to find an estimate for the support of the ground state |ψ0〉 of a Hamiltonian Ĥ, modeling some physical system, and then offload the diagonalization of Ĥ in this approximate support to a classical computer.This is done by sampling from an ansatz circuit UA|Ψi〉 (where |Ψi〉 is a reference state that is usually taken to be the Hartree–Fock state) in the computational basis {|x〉} to obtain a measurement outcome probability distribution P(x) = |〈x|UA|Ψi〉|2 and measurement outcomes χ. In the presence of noise, one would instead obtain a noisy probability distribution ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (x) and a set of noisy measurement outcomes χ.
(x) and a set of noisy measurement outcomes χ.
Many of the elements of χ will not have the correct spin-z and particle numbers due to noise on the device and will thus not be usable in their current form. Instead of naively post-selecting based on measurement outcomes with the correct quantum numbers, the original SQD work48 proposed passing elements in χ to a self-consistent configuration recovery subroutine wherein individual bits in basis states with incorrect spin and particle numbers are flipped according to a probability distribution that depends on a current best estimate of the average occupation number of the orbital for which that bit encodes. This probability distribution is chosen to more heavily weight bits whose values xp are more distant from the current best guess of np, the average occupation number of spin-orbital p.
This set of recovered bitstrings is denoted as χR. From here, one classically subsamples K batches of bitstrings from χR of size Nb to obtain d(k) unique basis states, where k = 1, 2, …, K. Each of these sets of basis states defines a subspace S(k) onto which the Hamiltonian Ĥ can be projected
 | (5) |
 | (6) |
 | (7) |
Importantly, these “quantum-assisted” selective CI methods do not require measuring any observables on the quantum computer and in this way they sidestep the long runtimes associated with VQE and its variants. It is important to note two main drawbacks of QSCI methods. Because the diagonalization step is done classically in a subspace spanned by a subset of the basis states sampled on the quantum computer, the true ground state which we are trying to approximate must be well-approximated by a state with polynomial support. If this was not the case, then not only would an exponential number of measurements need to be conducted on the quantum computer, but the diagonalization step itself would be classically intractable as well. Thus, it is likely that there are many quantum systems which cannot be well-approximated using QSCI methods.
The second is that the ansatz UA|Ψi〉 from which we are drawing samples must have a support that has sufficient overlap with the support of a state which well-approximates the true ground state. The samples we draw from it must also produce a compact diagonalization subspace. That is, we do not want to draw a large number of unimportant basis states. At a minimum, we want QSCI to be more efficient in terms of subspace size than, for instance, classical SCI methods. Choosing an ansatz with these properties is not necessarily trivial and how best to achieve both of them is an open question.
2.2 Bootstrap embedding
Bootstrap embedding24–28 is a method wherein it is assumed that the entanglement of a large molecular system has a structure that is sufficiently local under some easy-to-find basis such that the system can be broken down into non-disjoint subsystems. The correlation energy between fragments is approximately recovered by enforcing matching conditions on overlapping regions of neighboring fragments. For instance, one can match the qubit or 1-electron RDMs.In this work, we focus on matching conditions that use the fermionic 1-RDM as this method is the most straightforward to apply when using SQD as the eigensolver. In particular we match the “center” of a fragment with the “edge” of its neighbor. The intuition behind this is that the center region of a fragment should be insulated from the error associated with the fragmentation, whereas the edge of the fragment is spatially closer to where the molecule was fragmented and thus should suffer from a larger approximation error. By enforcing the constraint that the RDMs of all edges of all fragments match the RDMs of the centers of all fragments for which their overlap is non-zero, we reduce the error associated with the edge regions.
These matching conditions are not, however, sufficient for minimizing the error in correlation energy incurred from the fragmentation process. To this end, for each fragment “A”, a set of bath orbitals |b(A)i〉 is defined through the Schmidt decomposition of the Hartree–Fock state:
 | (8) |
The number of fragments is denoted by Nfrag. The set of edge orbitals in two fragments are denoted as fragment “A” and fragment “B” using  and
and  , respectively. The sets of center orbitals in these fragments are likewise denoted by
, respectively. The sets of center orbitals in these fragments are likewise denoted by  . A Hamiltonian in the embedded basis for fragment A is denoted as ĤA. A trial wavefunction for the fragment-bath subsystem associated with fragment A is denoted by |ΨA〉. For all Nfrag fragments, we want to perform the minimization problem
. A Hamiltonian in the embedded basis for fragment A is denoted as ĤA. A trial wavefunction for the fragment-bath subsystem associated with fragment A is denoted by |ΨA〉. For all Nfrag fragments, we want to perform the minimization problem
 | (9) |
 | (10) |
 for all B ≠ A. We also require that the total number of electrons occupying the union of the center regions for all the fragments sums to the number of electrons in the unfragmented system, Ne:
for all B ≠ A. We also require that the total number of electrons occupying the union of the center regions for all the fragments sums to the number of electrons in the unfragmented system, Ne: | (11) |
 | (12) |
 | (13) |
 | (14) |
![[small klambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e11a.gif) (A) enter as the arguments of an optimization that can be carried out using a wide range of optimizers such as gradient descent or quasi-Newton methods.
(A) enter as the arguments of an optimization that can be carried out using a wide range of optimizers such as gradient descent or quasi-Newton methods.
2.3 QBE-SQD
In contrast to the cases using either VQE or QPE with quantum bootstrap embedding, where it is necessary to evaluate the matching conditions using either the SWAP test or the qubit or fermionic RDMs,24 the fragment wavefunctions output by QBE-SQD are already in a classical form which can be used to readily produce 1-RDMs at negligible cost. This is because the role of the quantum computer in SQD is to inform the subspace in which a classical diagonalization subroutine is performed. This allows one to utilize the 1-RDM matching condition as given in eqn (10) and the particle number constraint in eqn (11) in much the same way as that for BE-FCI or other classical solvers.For clarity, we outline the entire QBE-SQD procedure in Fig. 1. In step 1, the system is fragmented and the bath orbitals are generated via the Schmidt decomposition of the mean-field state. The effective potential λ(A) is initialized to 0. SQD is then run for the effective Hamiltonians Ĥ(A)emb + λ(A) for each of the fragments in step 2. SQD returns the embedded subsystem wavefunctions |ψ(A)〉 which we use to evaluate the matching conditions. The evaluated mismatch is used to evaluate whether or not the BE optimization has converged. If the method has converged, we stop the method. Otherwise, the mismatch is used to calculate an updated effective potential λ(A) for each of the fragments. This is then used to generate the effective Hamiltonian for which SQD performs the diagonalization. This loop is repeated until convergence, at which point we return the ground state energy.
3 Results
3.1 Simulation and experimental details on ibm_pittsburgh
All experiments were run using code produced by adding the PySCF49 2.9.0 implementation of the SQD solver provided by the qiskit-addon-sqd 0.11.0 package as a solver to the bootstrap embedding package QuEmb.50 Qiskit51 2.1.0 is used for all quantum experiments. Classical SHCI (semistochastic heat bath configuration interaction) calculations are carried out using the solve_hci function of qiskit-addon-dice-solver 0.3.0, which performs the variational stage of SHCI for a fixed ε1 using DICE.52,53 We use block2 (ref. 54) to carry out DMRG (density matrix renormalization group)55 calculations with a bond dimension of 500. CASCI (complete active space configuration interaction) calculations are carried out using PySCF.Our test system is a hydrogen ring, i.e. 8 equally spaced hydrogen atoms arranged in a ring with radius r = 1.3, 1.8, 2.2 Å in the cc-pVDZ basis, as illustrated in Fig. 2. The r = 1.3 Å geometry tests the accuracy for near-equilibrium geometries whereas r = 1.8, 2.2 Å represent progressively stretched geometries. Nominally, treating this system would require 80 spin-orbitals without any fragmentation or active space truncation. For both SQD and QBE-SQD we use the 2-LUCJ ansatz with parameters taken to be double-factorized t1 and t2 amplitudes from a classical CCSD calculation using PySCF and ffsim56 0.0.45 as described in ref. 48. In the case of QBE-SQD, these CCSD parameters are re-computed for every fragment at every BE iteration using the given effective fragment Hamiltonians at the given iteration. Representative (the exact numbers can fluctuate mildly from fragment to fragment and from iteration to iteration) gate counts and circuit depths are provided in Table 1. The LUCJ ansatz uses nearest-neighbor coupling terms mapped to the qubits illustrated in Fig. 3b. Fig. 3a indicates the qubits used for QBE-SQD. Fig. 3b indicates the qubits used for SQD (8e, 30o). No error mitigation techniques are used aside from the configuration recovery process.48 Both BE-FCI and QBE-SQD use the default orbital localization technique of QuEmb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Löwdin localized orbitals. Furthermore, the “BE2” fragmentation scheme is used for all experiments. This method loops over all atoms and considers fragments to consist of an atom and its nearest neighbors.
Löwdin localized orbitals. Furthermore, the “BE2” fragmentation scheme is used for all experiments. This method loops over all atoms and considers fragments to consist of an atom and its nearest neighbors.
| Method | Qubits | Circuit depth | 2-Qubit gates | 1-Qubit gates |
|---|---|---|---|---|
| QBE-SQD r = 1.3 Å | 43 | 505 | 1638 | 8244 |
| QBE-SQD r = 1.8 Å | 43 | 497 | 1638 | 8526 |
| QBE-SQD r = 2.2 Å | 43 | 496 | 1642 | 8512 |
| SQD (8e, 30o) r = 1.3 Å | 67 | 752 | 3876 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| SQD (8e, 30o) r = 1.8 Å | 67 | 744 | 3868 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117 117 |
| SQD (8e, 30o) r = 2.2 Å | 67 | 749 | 3906 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 738 738 |
3.2 QBE-SQD
QBE fragments this hydrogen ring into 8 subsystems by looping over all atoms and taking a fragment to be a particular atom and its nearest neighbors. Thus, we get 8 fragments, each of which consists of 30 fragment spin-orbitals. The singular value decomposition adds 8 bath orbitals to each fragment for a total of 38 spin-orbitals per embedded subsystem. Five batches and five configuration recovery iterations are used for each fragment. A batch size of 2500 samples is used for each fragment batch sample eigensolver call. The actual number of Slater determinants used in the diagonalization fluctuates from fragment to fragment and iteration to iteration; however we note that the number of Slater determinants typically falls within the range of 15% to 24% of the embedded subsystem FCI dimension size every time the classical diagonalization subroutine is run.We use 105 shots per circuit run for each fragment. With this configuration, each call to SQD in QBE uses approximately 30 seconds of QPU runtime. Fig. 4a illustrates the convergence of the energy and density matching errors for H8 with a radius of 1.3 Å as a function of the bootstrap embedding optimization iteration. We compare bootstrap embedding using SQD as the eigensolver on ibm_pittsburgh to bootstrap embedding using classical full configuration interaction (BE-FCI). The top figure plots the convergence of the BE ground state energy error (as compared to unfragmented DMRG in the cc-pVDZ basis with an active space of (8e, 40o)) as a function of the BE iteration, whereas the bottom figure plots the norm of the error vector associated with the RDM constraint terms in eqn (12). We note that in both measures of the convergence, QBE-SQD closely agrees with BE-FCI.
 | ||
| Fig. 4 Convergence of QBE-SQD and BE-FCI for the 8-atom hydrogen ring using the full RDM matching conditions. The geometries tested consist of ring radii of (a) 1.3 Å, (b) 1.8 Å, and (c) 2.2 Å. | ||
Fig. 4b and c illustrate the analogous comparisons for r = 1.8 Å and r = 2.2 Å, respectively. It is at these stretched geometries where differences in the convergence behavior of QBE-SQD and BE-FCI emerge. For instance, at r = 1.8 Å, the convergence of QBE-SQD closely matches that of BE-FCI up until iteration 3, after which they begin to diverge slightly, but still agree to within approximately 1 mHa. This is to be expected given the noise on the quantum device and the fixed batch size. For moderately stretched geometries, the number of nearly degenerate Slater determinants increases, which leads to a larger number of Slater determinants that contribute non-negligibly to the exact ground state. Because the batch size for QBE-SQD is kept at 2.5 × 103 for all geometries, we do not systematically expand the number of Slater determinants used for each fragment wavefunction and the accuracy decreases as a result. We also note that compared to the r = 1.3 Å density matching error convergence, the r = 1.8 Å convergence is both less consistently monotonic and less accurate. Whereas both QBE-SQD and BE-FCI can converge the density matching error to 2 × 10−4 and an energy error to 16 mHa at the near-equilibrium geometry, at this stretched geometry, BE-FCI can only converge the density matching error to 2 × 10−3 and the energy error to 20 mHa at iteration 5. This indicates that the decreased energy accuracy is a property of bootstrap embedding more generally rather than being completely attributable to either the noise on the quantum device or the quality of the subspace spanned by the Slater determinants that SQD selects. The picture for the further stretched r = 2.2 Å geometry is qualitatively similar except notably that QBE-SQD can converge the energy to approximately 10 mHa.
We note that aside from utilizing other orbital localization schemes, another way to improve the convergence of the BE optimization procedure is to forgo optimization of the parameters associated with the 1-RDM matching entirely and only optimize the chemical potential (the diagonal 1-RDM elements in the third summation term in eqn (12)). One might be (reasonably) worried that neglecting the RDM matching constraints would compromise the accuracy of the energy at the end of the optimization. We demonstrate that this is not the case for the system studied in this work. For all three geometric configurations studied in this work, optimizing only the chemical potential converges more quickly to a more accurate energy. We can see from comparing Fig. 4a and 5a that the improvement in the energy accuracy for the r = 1.3 Å geometry is modest, improving upon the RDM matching scheme by less than 1 mHa. The difference is more pronounced for the two stretched geometries that were not observed to converge to the same density matching error as the equilibrium case. For example, we can see from comparing Fig. 4b and 5b that using the chemical potential optimization improves the energy accuracy by approximately 6 mHa for the r = 1.8 Å geometry. The corresponding improvement for the r = 2.2 Å geometry is approximately 3.6 mHa.
 | ||
| Fig. 5 Convergence of QBE-SQD and BE-FCI for the 8-atom hydrogen ring using only chemical potential optimization. The geometries tested consist of ring radii of (a) 1.3 Å, (b) 1.8 Å, and (c) 2.2 Å. | ||
We note that it was found in ref. 57 that the use of Löwdin localized orbitals in combination with extended basis sets such as cc-pVDZ can lead to poor spatial localization of the orbitals, which leads to poor convergence of the BE optimization. The use of intrinsic atomic orbitals (IAOs) (as the authors suggest) could improve upon the results we were able to achieve in our current work. We further note that ref. 29 reported a ∼ 6 mHa error per hydrogen atom for a hydrogen chain of length 30 for 3-atom BE fragments using the cc-pVDZ basis. This is qualitatively consistent with our results, which achieved energy errors of approximately 1 to 2.5 mHa per atom. Notably, this work was published several years before the work revealing that IAOs offer more consistent convergence than localized orbitals with large basis sets.
3.3 Comparison with SQD
One might also be interested in how the energy accuracy of QBE-SQD compares to SQD. To this end, we have run SQD in an active space of (8e, 30o) for the hydrogen ring (r = 1.3, 1.8, 2.2 Å). These radii correspond to H–H distances of 0.995, 1.3777, and 1.6838 Å, respectively. Classical SHCI for an active space of (8e, 30o) is also run. These active spaces are truncated according to their mean-field orbital energies.We note that in this section, a CASCI calculation in an (8e, 30o) active space is used as the reference energy, whereas in the previous section a DMRG (8e, 40o) calculation was used to assess the accuracy of QBE-SQD. This is primarily to keep the comparison with SQD (8e, 30o) fair. However, in the interest of keeping track of how far these energies differ from our best available reference energy, we explicitly state the values of these two reference energies to five decimal places. CASCI (8e, 30o) calculations yield total energies of −4.37710, −4.29319, and −4.16879 Ha for the r = 1.3, 1.8, and 2.2 Å geometries, respectively. The corresponding DMRG (8e, 40o) energies are −4.38533, −4.30252, and −4.17430 Ha.
Ten circuit runs are performed for each geometry for SQD. 105 shots are used per circuit run with five batches and five configuration recovery iterations. For each circuit run, the classical diagonalization and configuration recovery steps are performed for a variety of batch sizes of 5 × 102 and n × 103 for n = 1, 2, 3, 4, 5 in order to study the convergence of the energy accuracy as a function of the number of Slater determinants used. We note that nominally this system consists of 80 spin-orbitals and 8 electrons when no active space truncation is used. However, when using an active space of (8e, 40o) was attempted, none of the 105 measurement outcomes yielded a basis state with the correct particle and spin numbers, resulting in no usable signal for SQD. These circuits used a total of 89 qubits, circuit depths of 1042, 6856 2-qubit gates, and 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 1-qubit gates. Moreover, the average occupation particle number was approximately 40, indicating that the output was almost entirely noise. When the active space is truncated to (8e, 30o), 8 out of the 10 circuit runs had a non-zero usable signal for r = 1.3 Å, 3 for r = 1.8 Å, and 4 for r = 2.2 Å.
650 1-qubit gates. Moreover, the average occupation particle number was approximately 40, indicating that the output was almost entirely noise. When the active space is truncated to (8e, 30o), 8 out of the 10 circuit runs had a non-zero usable signal for r = 1.3 Å, 3 for r = 1.8 Å, and 4 for r = 2.2 Å.
The results for the r = 1.3 Å geometry are shown in Fig. 6. In this figure, the reported number of Slater determinants for SQD is that used by the solution state, which may deviate slightly from the maximum number of Slater determinants used by all batch states for all configuration recovery iterations. We observe that the number of Slater determinants used by QBE-SQD for each fragment may fluctuate considerably throughout the optimization process. For this reason, the number of Slater determinants used by QBE-SQD is taken to be the maximum number among all fragments for all batch samples for all optimization iterations for an individual fragment. We observe that QBE-SQD agrees with the CASCI (8e, 30o) calculation to approximately 8 mHa. Thus, QBE-SQD is observed to outperform SQD by approximately 7 mHa (when the number of Slater determinants is comparable) despite using a fraction of the number of qubits.
We include classical SHCI using fixed selective cut-off values of ε1 = 10−4 and 10−5 to assess the compactness of the subspace found by SQD. The implementation used is the one provided in qiskit-addon-dice-solver 0.3.0, which acts as a wrapper for DICE hard-coded to only carry out the variational stage and skip the perturbative stage of SHCI. In this implementation, one has the option of providing a list of α and β substrings to use in the initialization. We have observed that when the Hartree–Fock state is used as the initialization, SHCI frequently converges to the first excited state for stretched bond geometries. This effect was noted previously.48 Providing substrings (for both α and β corresponding to the Hartree–Fock state and excitations into the lowest unoccupied orbital in the Hartree–Fock state (i.e. HOMO to LUMO excitations)) is effective at mitigating this effect. We find that SHCI outperforms both QBE-SQD and SQD for all geometries studied. We note that qiskit-addon-sqd uses the PySCF implementation of SCI, which is known to be inefficient in terms of the number of Slater determinants used. This is likely a significant factor in the compactness of the SQD subspace size.
Looking at the results for the r = 1.8 Å geometry in Fig. 6, the first feature that we note is that when using a comparable number of Slater determinants, QBE-SQD is less accurate than SQD by approximately 1 to 3 mHa when using the full 1RDM matching constraint; however when optimizing only the chemical potential, QBE-SQD outperforms SQD by approximately 3 mHa. SQD achieves an accuracy of approximately 8 to 10 mHa at this comparison point and 1 mHa at a batch size of 5 × 103.
We now move on to the comparison for the r = 2.2 Å geometry in the lower panel of Fig. 6. Here we observe that when using the full 1RDM matching constraints, QBE-SQD outperforms SQD (when using a comparable number of Slater determinants) by approximately 2 to 5 mHa. When only the chemical potential constraint is enforced, this gap is extended to approximately 5 to 8 mHa. QBE-SQD is seen to differ from CASCI by approximately 5 mHa when using the full 1RDM matching constraints and approximately 2 mHa when only the chemical potential is optimized.
3.4 Role of configuration recovery
The energy accuracy as a function of the number of Slater determinants does not, however, paint the entire picture of the resource requirements for each of these two methods. The degree to which each of these methods relies on the configuration recovery process is also a relevant quantity.To this end, we have plotted the average number of Slater determinants used at each configuration recovery iteration for SQD (8e, 30o) with a batch size of 103 and QBE-SQD. This choice of SQD batch size corresponds roughly to solution states whose numbers of Slater determinants are comparable to the number of Slater determinants used by QBE-SQD per fragment. Two particular fragment instances in the QBE-SQD optimization process are chosen to be representative of the range of possible outcomes in terms of the number of Slater determinants used in the 0th iteration. These results are plotted in Fig. 7. We observe that in the absence of error mitigation outside of configuration recovery, the number of Slater determinants in the 0th configuration recovery iteration is typically on the order of 101. Starting at the 1st iteration, this number jumps drastically to being on the order of 106. For QBE-SQD, the number of Slater determinants at the 0th iteration can range anywhere from 105 to 106. This confirms our intuition regarding the benefits of using bootstrap embedding on a quantum computer: fragmenting the system reduces the qubit footprint linearly without sacrificing the accuracy too much, but reduces the average number of errors per circuit run which in turn significantly strengthens the signal used by the classical diagonalization. Consider a simplified error model where the probabilities of error for n gates are modeled as independent, biased coin flips with probability of error p. The probability that no gate errors occur is (1 − p)n, where for small n, p is approximately 1 − np. However, when n is not small (as is the case here where the gate counts are on the order of 103 to 104), the probability that no gate error occurs drops exponentially with n. Embedding methods afford us the opportunity to linearly decrease the maximum qubit footprint thus reducing the overall gate count n linearly (for circuits such as LUCJ whose gate count scales linearly with the number of qubits), which in turn exponentially improves the average number of errors per circuit.
 | ||
| Fig. 7 The number of Slater determinants (averaged over 5 batches) used by SQD (8e, 30o) and 2 fragment instances (f7 and f4) of QBE-SQD throughout the configuration recovery process. | ||
4 Conclusions
In this work, we have performed what are, to our knowledge, the first experimental demonstrations of the quantum bootstrap embedding method for the ground state electronic structure on real quantum hardware. To achieve this, we employed sampled-based diagonalization as an eigensolver subroutine. We have benchmarked the resulting QBE-SQD method on a hydrogen ring consisting of 8 atoms in the cc-pVDZ basis. These results have been compared to those of the classical methods DMRG, SHCI (DICE), CASCI, and BE-FCI.We have shown evidence that QBE-SQD can outperform SQD with a much smaller circuit volume. By examining the number of Slater determinants during the configuration recovery process, we have discovered that this favored performance is because the fragmentation process in QBE naturally reduces the impact of noise on near-term quantum hardware at a faster rate than the energy accuracy reduction from the fragmentation itself. These results together suggest that quantum bootstrap embedding provides a feasible pathway toward a utility-scale electronic structure on quantum computers.
Looking forward, several challenges remain towards realizing this goal of large utility-scale quantum computational chemistry. One challenge is the performance of QBE-SQD for strongly correlated systems, for example, the H8 ring at stretched bond distances, where the optimization in bootstrap embedding is more difficult than it is for equilibrium ones. It is known that the use of Löwdin localized orbitals in combination with large basis sets such as cc-pVDZ can lead to suboptimal BE convergence,57 which we have also noted in the current work. An optimal choice of basis set or orbital localization method that can minimize the BE error and maximize the convergence rate would be desired.
It has been claimed that there are circuits one can sample from, which will generate more compact subspaces than some classical SCI methods using LUCJ circuits with optimized parameters.48 However, such circuits were not found to be able to outperform DMRG and it is unclear whether or not the classical SCI methods used represent the current state of the art. This raises several important questions for the practicality of SQD for utility-scale simulations. Can one systematically and efficiently find such circuits that outperform not just SHCI, but the best available classical methods? How shallow are these circuits? Are the probability distributions resulting from such circuits such that the measurement overhead is tractable? Additionally, there is the issue that SQD in its current form can only sample a number of basis states which scales polynomially with the system size. How restrictive is this in practice? Can one find relevant chemical systems whose ground states require only a polynomial number of basis states, but for which all classical methods fail to describe accurately? Can one develop a “more coherent” version of SQD for which this limitation is less restrictive? We note that there have been recent attempts to address this question. These include Krylov diagonalization methods,8,58 Hamiltonian simulation-based methods,59,60 and LUCJ circuits with numerically optimized parameters.61
From a quantum software development viewpoint, there is also a lack of cohesive integration of classical HPC and quantum hardware for quantum chemistry applications. QBE-SQD must make (at a minimum) dozens of calls to the quantum eigensolver with large classical diagonalization subroutines done on a classical HPC cluster in between such calls. Under the current paradigm where only a small number of quantum computers are available through cloud computing, the wait time in the queue for these machines can be on the order of hours or even days for a single job, which becomes a significant bottleneck when a large number of such job submissions is necessary. Furthermore, when the number of Slater determinants used by SQD in the classical diagonalization subroutine becomes large, the use of many nodes on a large HPC cluster will likely become necessary. Thus, for large-scale demonstrations of QBE-SQD, the options available to an experimentalist would be to (1) have a reserved on-site quantum computer and HPC cluster, (2) use quantum cloud computing and absorb the cost of reserving large amounts of idle classical HPC time, or (3) design the software and job scheduling interactively between quantum and classical computers in such a way that the classical HPC job is canceled after each quantum job submission and then restarted at a checkpoint once the quantum job finishes. We look forward to future development to push forward the frontier of quantum computational chemistry.
Author contributions
JB: conceptualization, investigation, methodology, software, visualization, formal analysis, writing-original draft, writing-review and editing. YL: conceptualization, investigation, methodology, funding acquisition, project administration, resources, supervision, writing - review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
Raw data, the QBE-SQD source code, and scripts to generate the plots are available at the GitHub repository at https://github.com/JoelHBierman/qbe_sqd_data and on Zenodo (DOI: https://doi.org/10.5281/zenodo.18225640). The QuEmb source code can be found at the repository: https://github.com/oimeitei/quemb. The Qiskit source code can be found at the repository: https://github.com/Qiskit/qiskit. The qiskit-ibm-runtime source code can be found at the repository: https://github.com/Qiskit/qiskit-ibm-runtime. The ffsim source code can be found at the repository: https://github.com/qiskit-community/ffsim. The source code for qiskit-addon-sqd and qiskit-addon-dice-solver can be found at https://github.com/Qiskit/qiskit-addon-sqd and https://github.com/Qiskit/qiskit-addon-dice-solver, respectively. The PySCF source code can be found at the repository: https://github.com/pyscf. The block2 source code can be found at the repository: https://github.com/block-hczhai/block2-preview.Acknowledgements
The authors thank Antonio Mezzacapo, Minh Tran, Javier Robledo Moreno, Yingzhou Li, Jianfeng Lu, James Brown, Shaun Weatherly, Minsik Cho, Leah Weisburn, and Oskar Weser for helpful discussions. The authors acknowledge the high-performance computing services and quantum hardware access through the IBM Innovation Center at NC State University. The authors acknowledge the Arc V3 high-performing computing resources access granted by the Computer Science Department at NC State University. This work was supported by the U.S. Department of Energy, Office of Science, Advanced Scientific Computing Research, under contract number DE-SC0025384. This work was partially supported by the Wellcome Leap as part of the Quantum for Bio (Q4Bio) Program. Use of AI disclosure: troubleshooting and implementation of pieces of the code for this work were assisted by the use of Microsoft Copilot.Notes and references
- V. E. Elfving, B. W. Broer, M. Webber, J. Gavartin, M. D. Halls, K. P. Lorton and A. Bochevarov, arXiv preprint arXiv:2009.12472, 2020 Search PubMed.
- M. Reiher, N. Wiebe, K. M. Svore, D. Wecker and M. Troyer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7555–7560 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 015003 Search PubMed.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242–246 Search PubMed.
- A. J. McCaskey, Z. P. Parks, J. Jakowski, S. V. Moore, T. D. Morris, T. S. Humble and R. C. Pooser, Npj Quantum Inf., 2019, 5, 1–8 Search PubMed.
- Y. Nam, J.-S. Chen, N. C. Pisenti, K. Wright, C. Delaney, D. Maslov, K. R. Brown, S. Allen, J. M. Amini, J. Apisdorf, K. M. Beck, A. Blinov, V. Chaplin, M. Chmielewski, C. Collins, S. Debnath, K. M. Hudek, A. M. Ducore, M. Keesan, S. M. Kreikemeier, J. Mizrahi, P. Solomon, M. Williams, J. D. Wong-Campos, D. Moehring, C. Monroe and J. Kim, Npj Quantum Inf., 2020, 6, 1–6 Search PubMed.
- Y. Kim, A. Eddins, S. Anand, K. X. Wei, E. van den Berg, S. Rosenblatt, H. Nayfeh, Y. Wu, M. Zaletel, K. Temme and A. Kandala, Nature, 2023, 618, 500–505 CrossRef CAS PubMed.
- J. Yu, J. R. Moreno, J. T. Iosue, L. Bertels, D. Claudino, B. Fuller, P. Groszkowski, T. S. Humble, P. Jurcevic and W. Kirbyet al., arXiv preprint arXiv:2501.09702, 2025 Search PubMed.
- R. Acharya, D. A. Abanin, L. Aghababaie-Beni, I. Aleiner, T. I. Andersen, M. Ansmann, F. Arute, K. Arya, A. Asfaw, N. Astrakhantsev, J. Atalaya, R. Babbush, D. Bacon, B. Ballard, J. C. Bardin, J. Bausch, A. Bengtsson, A. Bilmes, S. Blackwell, S. Boixo, G. Bortoli, A. Bourassa, J. Bovaird, L. Brill, M. Broughton, D. A. Browne, B. Buchea, B. B. Buckley, D. A. Buell, T. Burger, B. Burkett, N. Bushnell, A. Cabrera, J. Campero, H.-S. Chang, Y. Chen, Z. Chen, B. Chiaro, D. Chik, C. Chou, J. Claes, A. Y. Cleland, J. Cogan, R. Collins, P. Conner, W. Courtney, A. L. Crook, B. Curtin, S. Das, A. Davies, L. De Lorenzo, D. M. Debroy, S. Demura, M. Devoret, A. Di Paolo, P. Donohoe, I. Drozdov, A. Dunsworth, C. Earle, T. Edlich, A. Eickbusch, A. M. Elbag, M. Elzouka, C. Erickson, L. Faoro, E. Farhi, V. S. Ferreira, L. F. Burgos, E. Forati, A. G. Fowler, B. Foxen, S. Ganjam, G. Garcia, R. Gasca, E. Genois, W. Giang, C. Gidney, D. Gilboa, R. Gosula, A. G. Dau, D. Graumann, A. Greene, J. A. Gross, S. Habegger, J. Hall, M. C. Hamilton, M. Hansen, M. P. Harrigan, S. D. Harrington, F. J. H. Heras, S. Heslin, P. Heu, O. Higgott, G. Hill, J. Hilton, G. Holland, S. Hong, H.-Y. Huang, A. Huff, W. J. Huggins, L. B. Ioffe, S. V. Isakov, J. Iveland, E. Jeffrey, Z. Jiang, C. Jones, S. Jordan, C. Joshi, P. Juhas, D. Kafri, H. Kang, A. H. Karamlou, K. Kechedzhi, J. Kelly, T. Khaire, T. Khattar, M. Khezri, S. Kim, P. V. Klimov, A. R. Klots, B. Kobrin, P. Kohli, A. N. Korotkov, F. Kostritsa, R. Kothari, B. Kozlovskii, J. M. Kreikebaum, V. D. Kurilovich, N. Lacroix, D. Landhuis, T. Lange-Dei, B. W. Langley, P. Laptev, K.-M. Lau, L. Le Guevel, J. Ledford, J. Lee, K. Lee, Y. D. Lensky, S. Leon, B. J. Lester, W. Y. Li, Y. Li, A. T. Lill, W. Liu, W. P. Livingston, A. Locharla, E. Lucero, D. Lundahl, A. Lunt, S. Madhuk, F. D. Malone, A. Maloney, S. Mandrà, J. Manyika, L. S. Martin, O. Martin, S. Martin, C. Maxfield, J. R. McClean, M. McEwen, S. Meeks, A. Megrant, X. Mi, K. C. Miao, A. Mieszala, R. Molavi, S. Molina, S. Montazeri, A. Morvan, R. Movassagh, W. Mruczkiewicz, O. Naaman, M. Neeley, C. Neill, A. Nersisyan, H. Neven, M. Newman, J. H. Ng, A. Nguyen, M. Nguyen, C.-H. Ni, M. Y. Niu, T. E. O’Brien, W. D. Oliver, A. Opremcak, K. Ottosson, A. Petukhov, A. Pizzuto, J. Platt, R. Potter, O. Pritchard, L. P. Pryadko, C. Quintana, G. Ramachandran, M. J. Reagor, J. Redding, D. M. Rhodes, G. Roberts, E. Rosenberg, E. Rosenfeld, P. Roushan, N. C. Rubin, N. Saei, D. Sank, K. Sankaragomathi, K. J. Satzinger, H. F. Schurkus, C. Schuster, A. W. Senior, M. J. Shearn, A. Shorter, N. Shutty, V. Shvarts, S. Singh, V. Sivak, J. Skruzny, S. Small, V. Smelyanskiy, W. C. Smith, R. D. Somma, S. Springer, G. Sterling, D. Strain, J. Suchard, A. Szasz, A. Sztein, D. Thor, A. Torres, M. M. Torunbalci, A. Vaishnav, J. Vargas, S. Vdovichev, G. Vidal, B. Villalonga, C. V. Heidweiller, S. Waltman, S. X. Wang, B. Ware, K. Weber, T. Weidel, T. White, K. Wong, B. W. K. Woo, C. Xing, Z. J. Yao, P. Yeh, B. Ying, J. Yoo, N. Yosri, G. Young, A. Zalcman, Y. Zhang, N. Zhu, N. Zobrist and Google Quantum AI and Collaborators, Nature, 2025, 638, 920–926 Search PubMed.
- Z. Ni, S. Li, X. Deng, Y. Cai, L. Zhang, W. Wang, Z.-B. Yang, H. Yu, F. Yan, S. Liu, C.-L. Zou, L. Sun, S.-B. Zheng, Y. Xu and D. Yu, Nature, 2023, 616, 56–60 CrossRef CAS PubMed.
- V. V. Sivak, A. Eickbusch, B. Royer, S. Singh, I. Tsioutsios, S. Ganjam, A. Miano, B. L. Brock, A. Z. Ding, L. Frunzio, S. M. Girvin, R. J. Schoelkopf and M. H. Devoret, Nature, 2023, 616, 50–55 Search PubMed.
- K. Temme, S. Bravyi and J. M. Gambetta, Phys. Rev. Lett., 2017, 119, 180509 CrossRef PubMed.
- L. Viola and S. Lloyd, Phys. Rev. A, 1998, 58, 2733–2744 Search PubMed.
- N. Ezzell, B. Pokharel, L. Tewala, G. Quiroz and D. A. Lidar, Phys. Rev. Appl., 2023, 20, 064027 Search PubMed.
- S. Paesani, A. Gentile, R. Santagati, J. Wang, N. Wiebe, D. Tew, J. O’Brien and M. Thompson, Phys. Rev. Lett., 2017, 118, 100503 Search PubMed.
- N. Wiebe and C. Granade, Phys. Rev. Lett., 2016, 117, 010503 Search PubMed.
- D. S. Abrams and S. Lloyd, Phys. Rev. Lett., 1999, 83, 5162–5165 CrossRef CAS.
- J. D. Whitfield, J. Biamonte and A. Aspuru-Guzik, Mol. Phys., 2011, 109, 735–750 CrossRef CAS.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- G. Knizia and G. K.-L. Chan, Phys. Rev. Lett., 2012, 109, 186404 CrossRef PubMed.
- G. Knizia and G. K.-L. Chan, J. Chem. Theory Comput., 2013, 9, 1428–1432 Search PubMed.
- Z.-H. Cui, T. Zhu and G. K.-L. Chan, J. Chem. Theory Comput., 2019, 16, 119–129 CrossRef PubMed.
- T. E. Reinhard, U. Mordovina, C. Hubig, J. S. Kretchmer, U. Schollwöck, H. Appel, M. A. Sentef and A. Rubio, J. Chem. Theory Comput., 2019, 15, 2221–2232 Search PubMed.
- Y. Liu, O. R. Meitei, Z. E. Chin, A. Dutt, M. Tao, I. L. Chuang and T. Van Voorhis, J. Chem. Theory Comput., 2023, 19, 2230–2247 Search PubMed.
- H.-Z. Ye, N. D. Ricke, H. K. Tran and T. Van Voorhis, J. Chem. Theory Comput., 2019, 15, 4497–4506 Search PubMed.
- H.-Z. Ye, H. K. Tran and T. Van Voorhis, J. Chem. Theory Comput., 2020, 16, 5035–5046 Search PubMed.
- M. Welborn, T. Tsuchimochi and T. Van Voorhis, J. Chem. Phys., 2016, 145, 074102 Search PubMed.
- O. R. Meitei and T. Van Voorhis, J. Chem. Theory Comput., 2023, 19, 3123–3130 Search PubMed.
- H.-Z. Ye and T. Van Voorhis, J. Phys. Chem. Lett., 2019, 10, 6368–6374 Search PubMed.
- H.-Z. Ye, H. K. Tran and T. Van Voorhis, J. Chem. Theory Comput., 2021, 17, 3335–3347 Search PubMed.
- L. P. Weisburn, M. Cho, M. Bensberg, O. R. Meitei, M. Reiher and T. Van Voorhis, J. Chem. Theory Comput., 2025, 21, 4591–4603 Search PubMed.
- A. Shajan, D. Kaliakin, A. Mitra, J. Robledo Moreno, Z. Li, M. Motta, C. Johnson, A. A. Saki, S. Das, I. Sitdikov, A. Mezzacapo and K. M. Merz, J. Chem. Theory Comput., 2025, 21, 6801–6810 Search PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, Nat. Commun., 2014, 5, 4213 Search PubMed.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth and J. Tennyson, Phys. Rep., 2022, 986, 1–128 Search PubMed.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- J. F. Gonthier, M. D. Radin, C. Buda, E. J. Doskocil, C. M. Abuan and J. Romero, Phys. Rev. Res., 2022, 4, 033154 CrossRef CAS.
- M. Cerezo, A. Sone, T. Volkoff, L. Cincio and P. J. Coles, Nat. Commun., 2021, 12, 1791 CrossRef CAS PubMed.
- S. Wang, E. Fontana, M. Cerezo, K. Sharma, A. Sone, L. Cincio and P. J. Coles, Nat. Commun., 2021, 12, 6961 CrossRef CAS PubMed.
- M. Ragone, B. N. Bakalov, F. Sauvage, A. F. Kemper, C. Ortiz Marrero, M. Larocca and M. Cerezo, Nat. Commun., 2024, 15, 7172 CrossRef CAS PubMed.
- K. Kanno, M. Kohda, R. Imai, S. Koh, K. Mitarai, W. Mizukami and Y. O. Nakagawa, arXiv preprint arXiv:2302.11320, 2023 Search PubMed.
- S. Barison, J. R. Moreno and M. Motta, Quantum Sci. Technol., 2025, 10, 025034 Search PubMed.
- D. Danilov, J. Robledo-Moreno, K. J. Sung, M. Motta and J. Shee, arXiv preprint arXiv:2503.05967, 2025 Search PubMed.
- W. J. Huggins, B. A. O'Gorman, N. C. Rubin, D. R. Reichman, R. Babbush and J. Lee, Nature, 2022, 603, 416–420 CrossRef CAS PubMed.
- J. Bierman, Y. Li and J. Lu, J. Chem. Theory Comput., 2023, 19, 790–798 CrossRef CAS PubMed.
- J. Bierman, Y. Li and J. Lu, J. Chem. Theory Comput., 2024, 20, 3131–3143 CrossRef CAS PubMed.
- J. R. Moreno, J. Cohn, D. Sels and M. Motta, arXiv preprint arXiv:2302.11588, 2023 Search PubMed.
- L. Zhao, J. Goings, K. Shin, W. Kyoung, J. I. Fuks, J.-K. Kevin Rhee, Y. M. Rhee, K. Wright, J. Nguyen, J. Kim and S. Johri, Npj Quantum Inf., 2023, 9, 1–9 Search PubMed.
- J. Robledo-Moreno, M. Motta, H. Haas, A. Javadi-Abhari, P. Jurcevic, W. Kirby, S. Martiel, K. Sharma, S. Sharma, T. Shirakawa, I. Sitdikov, R.-Y. Sun, K. J. Sung, M. Takita, M. C. Tran, S. Yunoki and A. Mezzacapo, Sci. Adv., 2025, 11, eadu9991 CrossRef CAS PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Wiley Interdiscip. Rev. Comput. Mol. Sci, 2017, 8, e1340 CrossRef.
- M. Cho, O. R. Meitei, L. P. Weisburn, O. Weser, S. Weatherly, A. Alexiu, R. Hanscam, H. K. Tran, H.-Z. Ye, M. Welborn, N. Ricke, T. Tsuchimochi, A. Trofimov, T. Orkhon, N. Whelpley, C. Luo and T. Van Voorhis, J. Phys. Chem. A, 2025, 129, 6538–6551 CrossRef PubMed.
- A. Javadi-Abhari, M. Treinish, K. Krsulich, C. J. Wood, J. Lishman, J. Gacon, S. Martiel, P. D. Nation, L. S. Bishop, A. W. Cross, B. R. Johnson and J. M. Gambetta, Quantum computing with Qiskit, 2024 Search PubMed.
- S. Sharma, A. A. Holmes, G. Jeanmairet, A. Alavi and C. J. Umrigar, J. Chem. Theory Comput., 2017, 13, 1595–1604 Search PubMed.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, J. Chem. Theory Comput., 2016, 12, 3674–3680 CrossRef CAS PubMed.
- H. Zhai, H. R. Larsson, S. Lee, Z.-H. Cui, T. Zhu, C. Sun, L. Peng, R. Peng, K. Liao, J. Tölle, J. Yang, S. Li and G. K.-L. Chan, J. Chem. Phys., 2023, 159, 234801 CrossRef CAS PubMed.
- H. Zhai and G. K.-L. Chan, J. Chem. Phys., 2021, 154, 224116 CrossRef CAS PubMed.
- The ffsim developers, ffsim: Faster simulations of fermionic quantum circuits ., https://github.com/qiskit-community/ffsim.
- H. K. Tran, L. P. Weisburn, M. Cho, S. Weatherly, H.-Z. Ye and T. Van Voorhis, J. Chem. Theory Comput., 2024, 20, 10912–10921 CrossRef CAS PubMed.
- S. Piccinelli, A. Baiardi, M. Rossmannek, A. C. Vazquez, F. Tacchino, S. Mensa, E. Altamura, A. Alavi, M. Motta and J. Robledo-Morenoet al., arXiv preprint arXiv:2508.02578, 2025 Search PubMed.
- K. Sugisaki, S. Kanno, T. Itoko, R. Sakuma and N. Yamamoto, Phys. Chem. Chem. Phys., 2025, 27, 20869–20884 Search PubMed.
- M. Mikkelsen and Y. O. Nakagawa, Phys. Rev. Res., 2025, 7, 043043 CrossRef CAS.
- T. Shirakawa, J. Robledo-Moreno, T. Itoko, V. Tripathi, K. Ueda, Y. Kawashima, L. Broers, W. Kirby, H. Pathak and H. Paiket al., arXiv preprint arXiv:2511.00224, 2025 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |




