An improved machine learning strategy using structural features to predict the glass transition temperature of oxide glasses

Abstract

We present a physics-informed machine learning approach to predict the glass transition temperature (T_g) of sodium borosilicate glasses. Four models—random forest, extreme gradient boosting, support vector machines, and K-nearest neighbors—were trained using both compositional and structural features derived from statistical mechanics. Incorporating these structural descriptors significantly improved model performance. This is evident from reduction in mean absolute error (14.85 K → 13.76 K), root mean square error (21.78 → 19.12) and increase in R² (0.88 → 0.91) measured on testing the dataset for the random forest model. Similar performance improvement was seen for other models as well. Building on this, we propose a three-step predictive strategy that enhances generalization across compositions and accurately predict the T_g of unseen compositions, achieving a mean absolute error of approximately 8 K and an R² value of around 0.98. Our method demonstrates improved accuracy when benchmarked against GlassNet, which represents the current state-of-the-art in property prediction for glasses. These results highlight the importance of considering structural information in improving prediction capabilities of machine learning models for composition-specific small datasets. This approach can assist in the rapid screening and design of glass materials, reducing the reliance on time-consuming experiments and guiding future research toward targeted property optimization.

---

1 Introduction

Glasses have a lot of applications in modern life, such as medicine, engineering, science, etc.^1,2 Synthesizing glasses usually involves significant time, labor, chemicals, and energy consumption, contributing to a considerable carbon footprint. Furthermore, the glasses must be characterized and tested to determine their suitability for real-life applications. Glass transition temperature (T_g) is one of the important characteristic temperatures of glasses. It is the temperature interval in which a glass loses its brittleness while heating. Glasses behave as rigid and brittle solids below T_g. At the same time, they exhibit viscous liquid-like behavior above T_g. At a fundamental level, knowing T_g provides insights into the relationship between glasses' composition, structure, and physical properties. T_g is closely related to glass forming ability, which is crucial to developing novel glass compositions for various applications.³T_g is also of great importance from the industry perspective. It dictates the temperature range in which glasses can be safely processed and used in various applications such as fiber drawing, molding, and shaping. It helps to decide the annealing temperature to relieve internal stresses and prevent glass cracking.⁴ The change in thermal expansion at T_g is an important consideration when designing glass sealants in solid oxide fuel cells, microelectronicz devices, and other systems where thermal stresses can be problematic during operation.^5,6

Experimentally, T_g of glasses is measured via thermal characterization techniques such as differential thermal analysis (DTA), differential scanning calorimetry (DSC), and dilatometry. On the other hand, classical computational methods can help in predicting glass properties using molecular dynamics studies and density functional theory (DFT).⁷ These computational methods help in understanding the atomic-scale mechanisms of glasses; however, they have limitations. Limited system size, unrealistic cooling rates, dependency on the choice of interatomic potentials, and high computational cost are major disadvantages of these theoretical methods.⁸ Machine learning (ML) has shown promising results in the property prediction of various materials.^9–12 Reducing costs, saving time, and exploring unconventional compositions would reduce the carbon footprints and accelerate the material design.^13–16 ML methods can handle large datasets while capturing complex, nonlinear relationships between the composition and material properties. Tools like SHapley Additive exPlanations (SHAP) and partial dependence plots (PDP) can further be used to visualize and interpret the outputs of these models.¹⁷

Previous studies have attempted T_g prediction of glasses using a range of approaches. O'Donnell et al. employed a linear fitting approach to predict T_g of oxide glasses, though their study was limited to fewer than 100 bioactive glasses.¹⁸ Cassar et al. used artificial neural networks for T_g prediction of multicomponent oxide glasses.¹⁹ The model was trained on more than 55 000 glasses containing up to 45 chemical elements. For high T_g glasses, the uncertainty in predictions was found to be high compared to low T_g glasses. This model was purely trained on compositional data. Alcobaca et al. developed ML models using a dataset of 43 240 oxide glasses,²⁰ but they considered only compositional features as input without additional feature engineering. Similarly, Ravinder et al. used deep learning to model glass properties on a dataset of 100 000 glasses,²¹ again relying solely on compositional features. In a closely related study, Bishnoi et al. applied Gaussian processes to predict a range of glass properties using a large dataset, also emphasizing compositional inputs.²² Zhang et al. developed a T_g prediction model with more than 15 features, although their focus was primarily on Fe-based metallic glasses.²³ In 2023, Cassar developed GlassNet, which is a multitask deep neural network model trained on more than 218 000 different glass compositions using 98 features.²⁴ This model is capable of predicting 85 properties of glasses ranging from oxides, chalcogenides, halides and others. Many researchers reported T_g prediction of polymers using various ML methods.^25–27

ML models applied on large datasets with too many compositional features may give overall good performance metrics; however, their performance may be poor in specific composition domains.^19,28 On the other hand, when focusing on specific glass systems, preprocessing often reduces the dataset to a very small size,²⁹ which makes the model training a challenging task.¹¹ Furthermore, the properties of the glasses cannot be fully explained based on their composition alone; many glass properties depend on the glass's local structure, the interaction of ingredients, thermal history, testing conditions, etc.^30–32 Thus, a research gap remains in exploring features beyond composition for ML studies, particularly in composition-specific domains where datasets are small. This gap is addressed in the present work using physics-informed models that can integrate domain knowledge, aligning predictions with established theories and published literature.^33,34

In the present work, widely employed ML models have been used to predict the T_g of sodium borosilicate glasses. The structural features were obtained using principles of statistical mechanics. The effect of distribution of the structural units on predicted T_g was determined. The current work aims to improve ML models' performances for T_g predictions of glasses in specific composition domains with the help of statistical mechanical calculations. The work is hoped to provide fruitful insights into the inter-ingredient interactions that affect the T_g of sodium borosilicate glasses. The results would help accelerate the glass design with minimal experimental efforts. This cost-effective approach would help reduce carbon footprints and mitigate environment-related problems.

2 Methodology

2.1 Data source

The dataset used in the present work was extracted from the SciGlass database (v2.0.1), which contains composition and property data of around 420 000 glass compositions, including 268 000 oxide glasses and melts, 18 500 halide glasses, and 38 500 chalcogenide glasses.³⁵ For the present work, data were fetched using the GlassPy (v0.5.3) python module.²⁴ The data were accessed on 22^nd May 2025.

2.2 Data preprocessing

2.2.1 Feature extraction. The data, including SiO₂, B₂O₃, and Na₂O as key ingredients, were extracted, with the target property being T_g. Microsoft Excel was used to filter and keep only required columns and rows. Any data involving glasses with any other elements were excluded to ensure accuracy and relevance. It was ensured that the selected data contained no missing values. Additionally, it was confirmed that the mole fractions of all ingredients for each sample sum up to unity. Mole fractions were later converted to mole percentages (by multiplying with 100) as per requirements for the statistical mechanical calculations (discussed later). Inconsistency was observed in the reported T_g values for the same compositions by different research groups. Only unique compositions were retained by replacing multiple T_g values with their median. These data cleaning steps along with the requirements by the statistical calculations discussed in next subsection have greatly reduced the size of the dataset. Such reduction in dataset size is common while dealing with specific composition–property data.²⁹ The final dataset contained 500 data points.

2.2.2 Feature engineering. Feature engineering is an important step to make ML models more effective using domain knowledge. For the present work, the distribution of different structural units corresponding to SiO₂ and B₂O₃ was calculated using the StatMechGlass python package.⁸ This distribution of structural units arises due to modifier oxides, such as Na₂O, interacting with network formers, such as SiO₂ and B₂O₃. The StatMechGlass package uses a statistical mechanical framework to calculate the distribution of structural units. It considers both the entropic (Si/B ratio) and the enthalpy contribution (energy barrier) to model the interaction of Na₂O with SiO₂ and B₂O₃. The smg.smg_structure(glass_comp, T_g) function from the StatMechGlass framework was employed in the present work to calculate the percentage of various structural units in borosilicate glasses. The instructions for installing StatMechGlass and other packages can be found in the readme.md file available in the link provided in the “Data availability” section. The details of using this package, its mathematical foundation and effectiveness in predicting glass structure are given elsewhere.^8,33 Basic processes governing structural units are discussed in subsection 3.2. It was found that the StatMechGlass module requires the values of all three glass components to be non-zero to calculate the structural distribution of the glasses with given compositions. So, all those rows where any of SiO₂, B₂O₃ and Na₂O was equal to zero were removed, which further reduced the dataset size. This clean dataset was used as the input for the StatMechGlass module. The function smg.smg_structure(glass_comp, T_g) returns the percentage of various silicate units as S0, S1, S2, S3 and S4 while borate units as B0, B1, B2, B3, B4. These features were then appended to the dataset and used as input descriptors for model training. The column headers for silicate units were renamed as more familiar and standard notations used in glass science, i.e., Q⁴, Q³, Q², Q¹ and Q⁰. In glass science, Q⁴, Q³, Q², Q¹ and, Q⁰, represent SiO₄ tetrahedra with 4, 3, 2, 1, and 0 bridging oxygen (BO) atoms, respectively. Similarly, structural units in the borate network were denoted as B⁴, B³, B², B¹, and B⁰.

2.3 ML models

Four standard ML models, support vector machines (SVM), K-nearest neighbors (KNN), extreme gradient boosting (XGB), and random forest (RF), were used as starting codes and further amended to optimize their performance. SVM uses kernels to map input data into a high-dimensional space and tries to fit a hyperplane that minimizes prediction errors while ensuring generalization.³⁶ KNN, a simple and interpretable instance-based algorithm, predicts values by averaging the target values of the K number of nearest neighbors. KNN may struggle with high-dimensional or noisy data, however its predictions are interpretable.³⁷ The choice of K and the distance metric (e.g., Euclidean distance) are important parameters that affect the model's prediction performance. XGB, a tree-based, gradient-boosting algorithm, sequentially improves weak decision trees to minimize residual errors, while employing regularization for robustness and scalability.³⁸ It employs regularization techniques and efficiently handles missing values, making it robust and scalable. RF is another tree-based ML technique that builds multiple decision trees using random subsets of data and features.³⁹ It reduces overfitting, improves accuracy and is effective for regression tasks with continuous data.¹¹ Data processing and analysis were performed using Python. Its Integrated Development and Learning Environment (IDLE) was used to edit and compile codes. ML modeling was done using the Scikit-learn package. Other major libraries used in the present work include pandas, numpy, xgboost, seaborn, matplotlib and SHAP.

All the mentioned ML models were tested on three feature sets, (a) set 1 – compositional features only, (b) set 2 – structural features only (silicate and borate units), and (c) set 3 –both compositional and structural features together. The dataset with each set of features was divided into a ratio of 80 : 20 for training and testing purposes. To make the study more robust, 5-fold cross-validation was employed. In this method, training data are further divided into five parts. Four parts are used for training; the remaining is reserved for validation. Cross-validated performance metrics are the average of performance metrics after each iteration.⁴⁰ The optimized model selected this way is finally run on the hold-out testing set to assess its generalization. The root mean squared error (RMSE), mean absolute error (MAE), and R² values were used to evaluate the models' performance. The models' hyperparameters were tuned by grid search. In the preliminary trials, a broad range of hyperparameters were tried. However, to settle a balance between computational time and performance of the models, the most influencing hyperparameters were selected for final grid search (Table 1). SHAP algorithm was used to interpret and visualize the outputs of ML models. For the validation purposes, a subset of 20 samples was selected from the full dataset using quantile-based binning to ensure a diverse representation of glass compositions across the full range of T_g. One composition from each T_g bin was randomly chosen to span the entire distribution. The remaining data formed the training and testing sets as discussed above. Such stratified sampling helps evaluate model generalization across different T_g regimes. We compared our results against GlassNet, which represents the current state-of-the-art in property prediction for glasses. The codes and datasets used for this study are available in the link given in the Data availability section.

Table 1 Performance metrics computed on the test set for various models across different feature sets

Feature set	Model	MAE	R ^2	RMSE	Best parameters
Set 1 (composition only)	RF	14.85	0.88	21.78	{‘Bootstrap’: true, ‘max_depth’: 10, ‘n_estimators’: 100, ‘random_state’: 42}
	XGB	15.75	0.87	22.24	{‘learning_rate’: 0.1, ‘n_estimators’: 50}
	SVM	22.37	0.78	28.94	{‘C’: 10, ‘kernel’: ‘rbf’}
	KNN	17.82	0.84	24.98	{‘n_neighbors’: 7, ‘weights’: ‘distance’}
Set 2 (structural units only)	RF	13.76	0.91	19.12	{‘Bootstrap’: true, ‘max_depth’: 10, ‘n_estimators’: 200, ‘random_state’: 42}
	XGB	14.60	0.89	20.67	{‘learning_rate’: 0.2, ‘n_estimators’: 200}
	SVM	20.61	0.82	26.48	{‘C’: 0.1, ‘kernel’: ‘linear'}
	KNN	16.31	0.87	22.67	{‘n_neighbors’: 7, ‘weights’: ‘distance'}
Set 3 (all features)	RF	13.38	0.91	18.76	{‘Bootstrap’: true, ‘max_depth’: 10, ‘n_estimators’: 200, ‘random_state’: 42}
	XGB	15.01	0.88	21.56	{‘learning_rate’: 0.2, ‘n_estimators’: 200}
	SVM	19.80	0.84	25.35	{‘C’: 1, ‘kernel’: ‘linear'}
	KNN	16.42	0.87	22.53	{‘n_neighbors’: 7, ‘weights’: ‘distance’}

---

3 Results and discussion

3.1 Data distribution

The distribution of compositional variables is represented by plotting histograms, as shown in Fig. 1(a–c). The distribution of SiO₂ is slightly skewed, with values more concentrated toward the higher range (60–75 mol%), indicating the predominance of silica-rich compositions in the current dataset. In contrast, B₂O₃ values are primarily concentrated in the lower mol% range (10–40 mol%) but exhibit a wide spread range extending up to 95 mol%. Na₂O is also concentrated towards lower concentrations, with a few compositions exceeding 50 mol%. This is intuitive as Na₂O is a network modifier and too high modifier amounts at the cost of the glass former will lead to low glass forming ability. T_g values range nearly from 500 to 900 K, as shown in Fig. 1(d).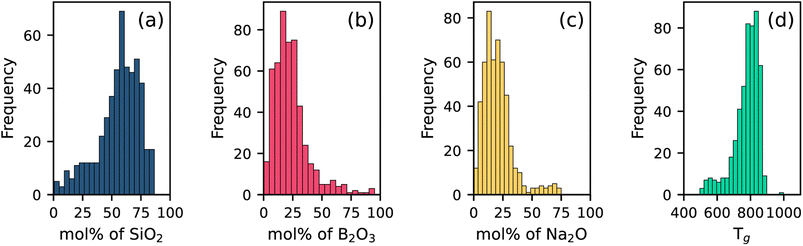

Fig. 1 Histograms showing the distribution of (a) SiO₂ (b) B₂O₃ (c) Na₂O and (d) T_g (K) values in the used dataset.

The group of taller bars towards relatively high T_g represents silica-rich compositions, while a group of shorter bars toward lower T_g represents borate-rich compositions. To elucidate this, Fig. 2(a) shows the ternary graphs representing the distribution of T_g of glasses according to their compositions.

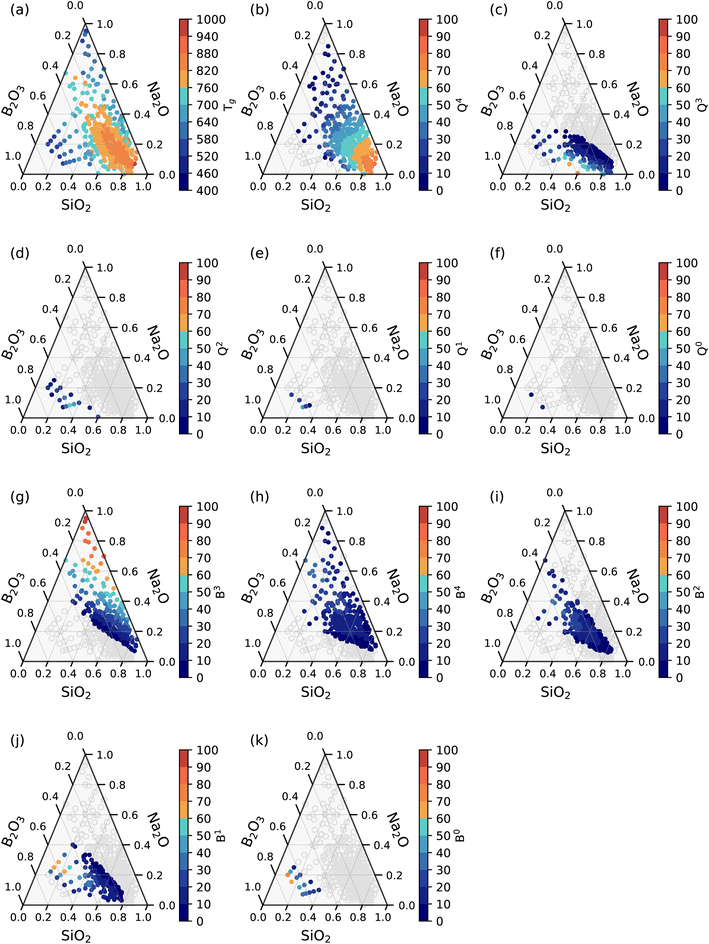Fig. 2 Ternary graphs showing the distribution of (a) T_g and (b–k) various structural units in SiO₂–B₂O₃–Na₂O glasses.

Each dot in this graph represents a sample from the dataset. Red and orange dots represent compositions with T_g > 760 K, which arise from glasses containing higher concentrations of SiO₂. On the other hand, light and dark blue dots represent glasses with relatively lower T_g, which can be seen for the borate-rich glasses and the soda (Na₂O)-rich compositions due to the modifier nature of Na₂O.

3.2 Structural evolution

Bodker et al., in their research, have shown the potential of statistical mechanical calculations to predict the structural evolution of ternary alkali borosilicate glasses with good accuracy.⁴¹ Leveraging the potential of these calculations, the distribution of structural units within glass compositions in our dataset was calculated. The StatMechGlass package considers the following reaction mechanisms for the structural evolution in silica network of the alkali-borosilicate glasses:⁸

2Qⁿ + M₂O → 2Qⁿ⁻¹ (1)

Here, M₂O represents the alkali oxide (Na₂O in the present case), and Qⁿ is the silica tetrahedra with n = 0, 1, 2, 3, 4. Similarly, borate structural units can be denoted as Bⁿ units. Boron can exist in both 3-fold and 4-fold coordination in glasses.⁴² Reaction mechanisms governing the conversion of one type of borate structural units into another are given as:

2B³ + M₂O → 2B⁴ (2)

2B³ + M₂O → 2B² (3)

The relative dominance of these reaction mechanisms is influenced by the modifier concentration.⁴³Fig. 2(b–k) represents calculated structural units of glasses as a function of their compositions. Values <5% are represented by the ovals in a light gray color to improve clarity and focus on the more relevant data points only. Q⁴ is found to be the most abundant structural unit in the glasses, with moderate to higher SiO₂ content (50% and more). Q³ units are the second most widely occurring structural units in silica networks. At the same time, Q² and Q¹ are present in fewer samples at higher Na₂O content, while Q⁰ units are quite rare in glasses of the present dataset. These structural units could have been present in greater quantity at higher Na₂O concentrations in binary alkali silicate glasses. However, in borosilicate glasses, partial Na₂O is consumed to modify the borate network as well. Hence, the tendency to form SiO₂ tetrahedra with three and four NBOs reduces. Similarly, B⁰ units in the present glass dataset are rare, existing only at higher B₂O₃ and low Na₂O content. It may also be due to fewer samples in this composition domain. B² units are high in low borate-containing glasses with moderate to high Na₂O content. Glasses with low B₂O₃ content (<30%) exhibit the coexistence of B⁴, B³ and B² units with a minor number of B² and B¹ units. Glasses containing more than 30% B₂O₃ exhibit both B² and B¹ units. The variation in the number of structural units of each kind with respect to Na₂O content is due to the competition of Na₂O interaction with both the borate and the silicate network.

3.3 ML for T_g prediction

3.3.1 Using only compositional features as input (set 1). Performance metrics computed on the test set and the best hyperparameters for the ML models are given in Table 1. A good-performing model is characterized by lower MAE and higher R² values. Tree-based models (RF and XGB) performed better than KNN and SVM. Results indicate that RF predicts T_g closer to the actual values (low MAE) and tries to fit more data points (high R² value) for this set of features compared to any other model. SVM performed poorer both in terms of MAE as well as R² across all the feature sets.

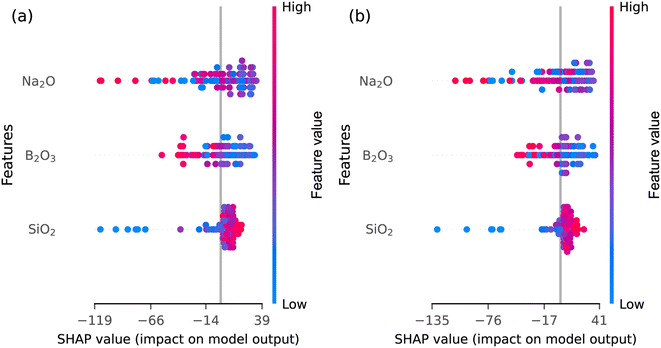
Fig. 3 shows the SHAP summary (beeswarm) plots of the SHAP values for RF and XGB models for compositional features. The data points are stacked (top to bottom) in order of decreasing contribution of the features towards the prediction of T_g. Na₂O is observed to have the highest contribution towards T_g in both models. In a SHAP summary plot, blue dots represent lower feature values, and red dots represent higher ones. If a feature contributes to lowering the predicted value, its blue dots will be more concentrated towards the negative SHAP value side, while its red dots will be towards the positive SHAP value side.

Fig. 3 SHAP summary plots for compositional features from the (a) RF and (b) XGB model.

The SHAP summary plot for Na₂O shows a mix of red and blue dots spread across the x-axis, indicating its nonlinear contribution to the predicted T_g. This aligns with the relatively low performance of ML models when using only compositional features. Both models agree on the contribution of the constituent oxides and consistently indicate that the predicted T_g increases with SiO₂ content, with a few exceptions. A deeper understanding of how features influence the predicted T_g can be gained from partial dependence plots (PDPs), as shown in Fig. 4.

Fig. 4 Partial dependence plots for compositional features (a) SiO₂ (b) Na₂O and (c) B₂O₃ in RF and XGB models.

Both RF and XGB models exhibit similar overall trends for compositional features, though variations exist in local regions of the curves. T_g remained largely unaffected up to ∼30 mol% of SiO₂, after which it showed a sharp increase, continuing up to ∼50 mol%, before nearly saturating at higher concentrations (Fig. 4(a)). This aligns with the SHAP analysis, which indicated that SiO₂ generally contributes positively to T_g prediction. Below ∼30 mol% SiO₂, the glass compositions are correspondingly enriched in either B₂O₃ or Na₂O. In the former case, T_g is low as borate glasses exhibit lower T_g compared to silicate glasses.¹ On the other hand, if compositions have high Na₂O content, the silicate network is fragmented into clusters, again leading to low T_g. But once sufficient SiO₂ is present, a continuous network of Si–O–Si bonds forms, leading to a sharp increase in network rigidity and hence T_g. Beyond ∼50 mol%, the network is already well-connected, so the effect of further SiO₂ additions gradually saturates.

T _g reaches a maximum at around 20 mol% of Na₂O, beyond which it decreases (Fig. 4(b)). This supports the SHAP summary plot, where Na₂O exhibited a nonlinear influence on T_g, with positive and negative contributions spread across the range of SHAP values. It also aligns with the nonlinear variation in the experimentally determined T_g of borosilicate glasses containing alkali metal oxides.⁴⁴ From a structural viewpoint, Na₂O initially increases T_g by stabilizing tetrahedral BO₄ units and enhancing cross-linking between borate and silicate species. However, at higher concentrations, excess Na₂O starts breaking Si–O–Si linkages and generating more NBOs, which reduces network connectivity and lowers T_g.

The dependence of T_g on B₂O₃ is also nonlinear: it initially increases up to ∼15 mol%, then decreases up to ∼40 mol%, and has minimal effect on T_g at higher concentrations (Fig. 4(c)). As observed in the SHAP analysis, this nonlinear role of B₂O₃ in T_g prediction is further supported by its complex behavior in PDP plots. At any given B₂O₃ content, T_g depends on the relative fractions of SiO₂ and Na₂O in the remaining composition. If the remaining composition is SiO₂-rich, higher T_g is expected and vice versa. However, various probable structural arrangements (BO₃, BO₄) at different concentrations of Na₂O add more complexity. The high non-linearity in T_g with respect to B₂O₃ suggests that compositional features alone are insufficient to fully interpret the T_g variations. Thus, it is worthwhile to consider the distribution of various silicate and borate structural units in order to interpret these variations as discussed in the next subsection.

Overall, PDPs confirm the nonlinear influences captured by SHAP analysis and also pinpoint composition ranges where sharp transitions in T_g occur, while necessitating further analysis by expanding the input feature space.

3.3.2 Including structural features as input (set 2 and set 3). Interestingly, using structural features as input variables gives rise to better T_g prediction by the models. All models showed improvement in MAE (>7%) and R² with the inclusion of structural features as input. Beeswarm plots for the RF and XGB models for Set 2 (Structural features) are given in Fig. 5. Q⁴ has the highest and most clear impact on T_g prediction according to the RF model. The smooth transition from blue to red as SHAP values shift from negative to positive suggests that a higher fraction of Q⁴ units increases the T_g. Although Q⁰ appears at the top of the list for the XGB model, from domain knowledge, it is known that these are the least abundant structural units for most of the glasses in the present dataset. Q⁰ units exist only at very high alkali oxide content in glasses.¹ Considering this fact, Q⁴ is effectively the most important feature with a clear impact on T_g, similar to that in the RF model.

Fig. 5 SHAP summary plots for structural features from (a) RF and (b) XGB model.

B ¹ is another feature that clearly impacts predicted T_g values in both models. It contributes to lowering T_g, as evidenced by red dots on the negative SHAP value side and blue dots on the positive side. B² and Q³ units in both models show a nonlinear trend indicated by mixed red and blue dots on the summary plots. B⁰, B⁴, Q¹ and Q² are the bottom four features with the least importance in both models. The RF model incorporates contributions from both silicate and borate structural units, as evidenced by a balanced distribution of both types of structural units among its top five features. In contrast, the XGB model assigns higher importance to silicate units (the top three are silicate units) than to the borate structural units.

Fig. 6 presents PDP plots for structural features, offering clearer insights into their influence on T_g. The Q⁴ units consistently increased T_g across the entire range for both models, reinforcing the SHAP analysis, where Q⁴ had the strongest positive contribution to T_g. This trend is expected, as a higher fraction of Q⁴ units indicates greater connectivity and stronger bonding in the glass network, leading to a higher T_g. The contribution of Q³ towards T_g is largely neutral according to the RF model. The XGB model exhibits a sharp decrease in T_g with Q³ up to ∼10% after which further changes in Q³ have minimal impact. Q² and Q¹ units show only a minor effect on T_g, influencing predictions only at their low values, beyond which T_g remains primarily unchanged. From the borate network, B¹ units exhibit a negative influence on T_g, consistent across both models in PDP analysis, supporting their trend in the SHAP plots. B² and B³ units initially increase T_g, but their effect either saturates or reverses at higher values. B⁰ units, on the other hand, have a negligible impact on T_g except at low values, where they tend to increase T_g. Better performance metrics of the ML models with structural features than with compositional features indicate that these models may be applied to glasses with any composition, provided their structural unit distribution is calculable. It must be stressed here that the same amount of different alkali oxides does not result in the same distribution of structural units in different glass systems.⁴⁵ Depending on the characteristics of alkali oxides, their interaction with different glass formers would differ. The distribution of structural units in the present work is calculated considering the enthalpy barriers by Na₂O towards its interaction with silicate and borate network.⁸ This approach allowed us to capture the non-linear and system-specific evolution of structural units, thereby improving the reliability of model predictions across diverse glass compositions. Thus, the improved performance of structure-based models emphasizes the importance of including structural features in property prediction for composition-specific small datasets.

Fig. 6 Partial dependence plots for compositional features (a–e) Qⁿ units (f–j) Bⁿ units.

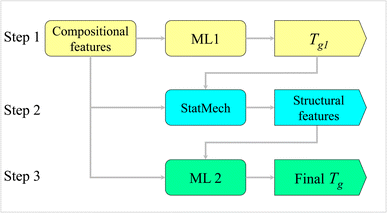
3.4 Three-step prediction strategy

Based on the improved prediction results using structural features, a three-step prediction framework was designed as shown in Fig. 7. The steps involved are given below:

Fig. 7 Three-step workflow for improved T_g predictions.

(i) Apply ML model trained on compositional data (ML1) for prediction of initial T_g from the compositions. Name it T_g1.

(ii) Use StatMechGlass package to calculate distribution of structural units using composition and T_g1.

(iii) Use ML model trained on compositional and structural data (ML2) to predict final T_g.

As RF has given the best T_g predictions using compositions alone as well as including structural features, it has been used for predictions at both step (i) and step (iii) as given above. This strategy was applied to the validation set of 20 compositions that were not part of training and testing of the models. The performance metrics of the model using this strategy on unseen data are given in Table 2.

Table 2 Performance comparison of GlassNet, regular RF model and three-step ML strategy on validation set

Model	Trained on	Validation MAE (K)	Validation R^2	Validation RMSE
GlassNet	Compositional and physicochemical data	15.40	0.93	20.06
Regular ML (RF)	Compositional data	10.59	0.96	15.59
Three-step ML	Structural data	9.15	0.97	12.84
	Both compositional and structural data	8.32	0.98	11.69

---

We compared our model with the state-of-the-art GlassNet model and a traditional ML method (RF on compositional features only). The inclusion of structural features improved the predictive performance of the RF model. Our three-step strategy reduced errors, achieving better MAE, RMSE and R² compared to GlassNet for the studied composition system. This clear improvement in the performance of our model demonstrates that our framework provides superior T_g prediction accuracy for sodium borosilicate glasses. However, it must be noted here that GlassNet is not exclusively trained on this dataset and performance metrics are subject to variation in other composition domains. The importance of our results lies in the fact that the validation set contains diverse ranges of compositions (SiO₂ (min 10 mol%, max 82 mol%); B₂O₃ (min 5.2 mol%, max 45 mol%); Na₂O (min 4.5 mol%, max 70 mol%)) as well as T_g (min 526 K, max 884 K).

Although T_g1 is a predicted value and will introduce uncertainty in the calculated structural unit values, the gain achieved in the final T_g prediction by using structural features together with compositional features overcomes the noise introduced due to T_g1 and leads to more accurate T_g prediction. It is worth mentioning here that decision-tree-based algorithms such as RF and XGB partition the input space based on the training data. Consequently, while these models perform well within the domain of the training data, their ability to extrapolate beyond this range is limited. Therefore, predictions outside the training domain should be interpreted with caution. As statistical mechanics calculations can be extended to derive the structural features of more complex glass systems, it would be worthwhile to check the influence of structural features on other properties of other glass systems by implementing the proposed three-step ML prediction strategy.

4 Conclusion

Statistical mechanical calculations beneficially transformed the composition–property database into a structure–property database for predicting the T_g of ternary sodium borosilicate glasses. Structural features dictate T_g of glasses more profoundly than compositional features, improving ML models' prediction capabilities. Q⁴ and B¹ structural units in borosilicate glasses clearly influence T_g more than other structural units. RF exhibited better performance than KNN, SVM and XGB for T_g prediction across all the feature sets. The three-step prediction strategy worked well even on unseen data. Our results showed improved performance compared to the state-of-the-art GlassNet model for predicting T_g specifically for sodium borosilicate glasses. Thus, it is worthwhile to consider structural features to improve the predictive performance of the ML model for composition-specific small datasets. The proposed workflow may be generalized to predict other properties of sodium borosilicate glasses and may also be extended to other glass systems.

Author contributions

SSD – conceptualization, data curation, methodology, validation, visualization, and writing – original draft. KS – conceptualization, methodology, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The codes and datasets supporting this study are available at Zenodo: https://doi.org/10.5281/zenodo.17077656.

Acknowledgements

The authors are thankful to Thapar Institute of Engineering and Technology, Patiala (India) and “TIET-UQ Centre of Excellence in Data Science and AI” for the financial support under the project ID DSAI2025-EE-1018. The authors are also thankful to Dr Xin Yu (The University of Queensland, Australia) for valuable discussions.

References

1. J. Shelby, Introduction to Glass Science and Technology, Royal Society of Chemistry, Cambridge, 2005.
2. A. Varshneya and J. Mauro, Fundamentals of inorganic glasses. Fundamentals of Inorganic Glasses, Wiley, United States, 2019.
3. J. Russo, F. Romano and H. Tanaka, Phys. Rev. X, 2018, 8, 021040.
4. O. Narayanaswamy, Viscosity and Relaxation, Elsevier, 1986, vol. 3, pp. 275–318.
5. X.-V. Nguyen, C.-T. Chang, G.-B. Jung, S.-H. Chan, W.-T. Lee, S.-W. Chang and I.-C. Kao, Int. J. Hydrogen Energy, 2016, 41, 21812–21819.
6. C. Thieme, M. Schlesier, E. Oji Dike and C. Rüssel, Sci. Rep., 2017, 7, 3344.
7. F. Lodesani, M. C. Menziani, H. Hijiya, Y. Takato, S. Urata and A. Pedone, Sci. Rep., 2020, 10, 2906.
8. M. S. Bødker, C. J. Wilkinson, J. C. Mauro and M. M. Smedskjaer, SoftwareX, 2022, 17, 100913.
9. A. Jain, Curr. Opin. Solid State Mater. Sci., 2024, 33, 101189.
10. X. Zhong, B. Gallagher, S. Liu, B. Kailkhura, A. Hiszpanski and T. Y.-J. Han, npj Comput. Mater., 2022, 8, 204.
11. P. Xu, X. Ji, M. Li and W. Lu, npj Comput. Mater., 2023, 9, 42.
12. G. Huang, Y. Guo, Y. Chen and Z. Nie, Materials, 2023, 16, 5977.
13. Y. Wang, Y. Tian, T. Kirk, O. Laris, J. H. Ross, R. D. Noebe, V. Keylin and R. Arróyave, Acta Mater., 2020, 194, 144–155.
14. X. Li, G. Shan, J. Zhang and C.-H. Shek, J. Mater. Chem. C, 2022, 10, 17291–17302.
15. X. Li, C.-H. Shek, P. K. Liaw and G. Shan, Prog. Mater. Sci., 2024, 146, 101332.
16. D. Chang, W. Lu and G. Wang, Chemom. Intell. Lab. Syst., 2022, 228, 104621.
17. A. V. Ponce-Bobadilla, V. Schmitt, C. S. Maier, S. Mensing and S. Stodtmann, Clin. Transl. Sci., 2024, 17, e70056.
18. M. D. O'Donnell, Acta Biomater., 2011, 7, 2264–2269.
19. D. R. Cassar, A. C. de Carvalho and E. D. Zanotto, Acta Mater., 2018, 159, 249–256.
20. E. Alcobaca, S. M. Mastelini, T. Botari, B. A. Pimentel, D. R. Cassar, A. C. P. de Leon Ferreira and E. D. Zanotto, et al. , Acta Mater., 2020, 188, 92–100.
21. R. Ravinder, K. H. Sridhara, S. Bishnoi, H. S. Grover, M. Bauchy, Jayadeva, H. Kodamana and N. M. A. Krishnan, Mater. Horiz., 2020, 7, 1819–1827.
22. S. Bishnoi, R. Ravinder, H. S. Grover, H. Kodamana and N. M. A. Krishnan, Mater. Adv., 2021, 2, 477–487.
23. J. Zhang, M. Zhao, C. Zhong, J. Liu, K. Hu and X. Lin, Nanoscale, 2023, 15, 18511–18522.
24. D. R. Cassar, Ceram. Int., 2023, 49, 36013–36024.
25. A. Afantitis, G. Melagraki, K. Makridima, A. Alexandridis, H. Sarimveis and O. Iglessi-Markopoulou, J. Mol. Struct., 2005, 716, 193–198.
26. W. Liu and C. Cao, Colloid Polym. Sci., 2009, 287, 811–818.
27. X. Chen, L. Sztandera and H. M. Cartwright, Int. J. Intell. Syst., 2007, 23, 22–32.
28. C. Liu and H. Su, Mater. Today Commun., 2024, 40, 109691.
29. L. dos Santos Vitoria, D. R. Cassar, S. de Souza Lalic and M. L. F. Nascimento, J. Non-Cryst. Solids, 2024, 629, 122870.
30. G. Sharma, S. Danewalia, N. Bansal, S. Khan, N. Pandher and K. Singh, Mater. Sci. Eng. B, 2024, 306, 117461.
31. P. Jha, S. Danewalia and K. Singh, J. Therm. Anal. Calorim., 2017, 128, 745–754.
32. M. Zaki, Jayadeva and N. M. A. Krishnan, Front. Mater., 2024, 11, year.
33. M. L. Bødker, M. Bauchy, T. Du, J. C. Mauro and M. M. Smedskjaer, npj Comput. Mater., 2022, 8, 192.
34. Y.-T. Shih, Y. Shi and L. Huang, J. Non-Cryst. Solids, 2022, 584, 121511.
35. EPAM Systems, Epam/SciGlass, 2019, https://github.com/epam/SciGlass, Accessed: May, 22, 2025.
36. W.-C. Lu, X.-B. Ji, M.-J. Li, L. Liu, B.-H. Yue and L.-M. Zhang, Adv. Manuf., 2013, 1, 151–159.
37. I. Triguero, D. García-Gil, J. Maillo, J. Luengo, S. García and F. Herrera, Data Min. Knowl. Discov., 2019, 9, e1289.
38. M. Bowles, Machine Learning with Spark and Python: Essential Techniques for Predictive Analytics, John Wiley & Sons, 2019.
39. S. J. Rigatti, J. Insur. Med., 2017, 47, 31–39.
40. Z. Xiong, Y. Cui, Z. Liu, Y. Zhao, M. Hu and J. Hu, Comput. Mater. Sci., 2020, 171, 109203.
41. M. S. Bødker, S. S. Sørensen, J. C. Mauro and M. M. Smedskjaer, Front. Mater., 2019, 6, 175.
42. G. Kaur, P. Sharma, V. Kumar and K. Singh, Mater. Sci. Eng. C, 2012, 32, 1941–1947.
43. Y. Yiannopoulos, G. D. Chryssikos and E. Kamitsos, Phys. Chem. Glasses, 2001, 42, 164–172.
44. S. Singh, G. Kalia and K. Singh, Mol. Struct., 2015, 1086, 239–245.
45. G. S. Henderson, Can. Mineral., 2005, 43, 1921–1958.

---