Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Navigating materials design spaces with efficient Bayesian optimization: a case study in functionalized nanoporous materials
Panagiotis
Krokidas
 *a,
Vassilis
Gkatsis†
*a,
Vassilis
Gkatsis†
 ab,
John
Theocharis†
ab,
John
Theocharis†
 c and
George
Giannakopoulos
c and
George
Giannakopoulos
 ad
ad
aInstitute of Informatics and Telecommunications, National Centre for Scientific Research “Demokritos”, Agia Paraskevi, 15310, Greece. E-mail: p.krokidas@iit.demokritos.gr
bDepartment of Informatics and Telecommunications, National and Kapodistrian University, Athens, Greece
cPhysics Department, National and Kapodistrian University, Athens, Greece
dSciFY PNPC, Athens, Greece
First published on 3rd November 2025
Abstract
Machine learning (ML) has the potential to accelerate the discovery of high-performance materials by learning complex structure–property relationships and prioritizing candidates for costly experiments or simulations. However, ML efficiency is often offset by the need for large, high-quality training datasets, motivating strategies that intelligently select the most informative samples. Here, we formulate the search for top-performing functionalized nanoporous materials (metal–organic and covalent–organic frameworks) as a global optimization problem and apply Bayesian Optimization (BO) to identify regions of interest and rank candidates with minimal evaluations. We highlight the importance of a proper and efficient initialization scheme of the BO process, and we demonstrate how BO-acquired samples can also be used to train an XGBoost regression predictive model that can further enrich the efficient mapping of the region of high performing instances of the design space. Across multiple literature-derived adsorption and diffusion datasets containing thousands of structures, our BO framework identifies 2×- to 3×-more materials within a top-100 or top-10 ranking list, than random-sampling-based ML pipelines, and it achieves significantly higher ranking quality. Moreover, the surrogate enrichment strategy further boosts top-N recovery while maintaining high ranking fidelity. By shifting the evaluation focus from average predictive metrics (e.g., R2, MSE) to task-specific criteria (e.g., recall@N and nDCG), our approach offers a practical, data-efficient, and computationally accessible route to guide experimental and computational campaigns toward the most promising materials.
1 Introduction
The advent of Machine Learning (ML) has introduced powerful capabilities in the discovery and development of novel materials,1 particularly through its ability to uncover complex structure–property relationships. In this context, ML models can learn to map structural and chemical information to macroscopic material properties, enabling fast and efficient predictions. As a result, experimental or computationally expensive methods can be reserved for only the most promising candidates. In the field of functionalized nanoporous materials, recent studies have showcased the potential of artificial intelligence—from conventional ML models capable of high-accuracy property prediction,2,3 to emerging approaches based on Large Language Models (LLMs),4,5 and generative models capable of proposing entirely new material structures.6Despite these advances, ML-driven discovery remains constrained by several challenges. Chief among them is the paradox between the promise of ML to reduce experimental costs and the substantial data requirements it imposes. Generating sufficiently large, high-quality datasets—whether through experiments or simulations—can be prohibitively expensive, undermining the very efficiency ML aims to deliver.7–9 To address this, significant effort has been invested in smart sampling strategies, broadly referred to as Active Learning (AL),10,11 which aim to minimize the number of required samples while maximizing predictive accuracy.
However, despite their conceptual appeal, many AL strategies often struggle to consistently outperform passive learning approaches,12 in which ML models are trained on randomly selected samples. In fact, random sampling remains a surprisingly strong benchmark.11 Moreover, maximizing predictive performance (e.g., via R2, mean squared error) may not always align with the practical goals of materials scientists. In many cases, the primary objective is not to model the entire design space, but rather to identify regions containing top-performing materials. As we demonstrate in this work, standard ML metrics often fail to reflect performance in this specific task.
Identifying high-performing sub-regions can be formulated as an optimization problem in which a sampling algorithm iteratively selects new points, not to reduce uncertainty as in active learning, but to maximize an acquisition function. An acquisition function is a heuristic that quantifies the utility of evaluating a candidate point, balancing exploration of uncertain regions with exploitation of high-predicted-value regions. Bayesian Optimization (BO) provides a principled solution in this context, serving as a global optimizer over complex design spaces.13–16 In this work, we adapt BO not only to identify the single best-performing instance, but also to recover an ensemble of the top-N performers (e.g., top-10 or top-100), reflecting the practical needs of materials scientists who often require multiple candidates rather than a solitary optimum. We address the following core research questions:
(1) How many samples are needed to identify regions within large design spaces (containing thousands to hundreds of thousands of materials) that contain top-performing candidates? We note that this number depends strongly on the task at hand, the complexity of the underlying structure–property relationships, and the choice of feature representation.
(2) How many samples are required to identify the single best-performing material in such spaces?
(3) How does our approach compare to an ML model trained on an equal number of randomly selected samples, particularly in terms of ranking the top-performing materials and identifying the global optimum?
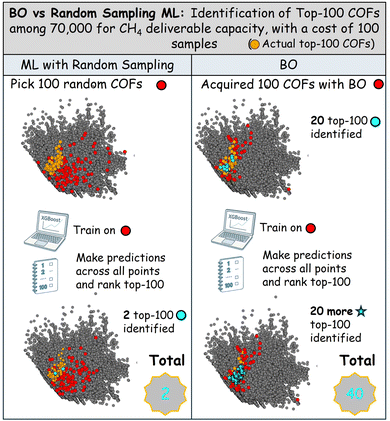
While BO is a powerful framework, it can incur substantial computational expense.17 To mitigate this, we introduce frugality-oriented elements. Here, frugality refers primarily to minimizing the number of costly experimental or simulation evaluations required to identify high-performing materials, which is the main bottleneck, but we also consider simple strategies to reduce computational overhead. First, we quantify how the choice of initial samples influences BO's convergence and overall performance. Unlike our baseline method (Random Sampling ML), BO is always initialized with a simple yet effective, informed strategy that combines one central point and two diverse points, ensuring both representativeness and diversity in the initial sampling. This primarily supports experimental efficiency by ensuring informative early evaluations. Next, we evaluate batch sampling strategies—selecting multiple candidates per iteration—to strike an optimal balance between predictive accuracy and runtime efficiency. Batching reduces computational cost by limiting the number of surrogate retrainings, while also enabling parallel experiments in principle. Finally, we show that, by training a machine-learning surrogate (e.g., XGBoost) on the BO-acquired samples after the campaign, we can predict and rank the remainder of the design space. This enrichment step mainly reduces experimental effort by identifying additional top-N candidates without further evaluations, while also providing a lightweight ranking at low computational cost. Fig. 1 summarizes our approach.
We evaluate our method across a diverse collection of literature-based datasets involving gas adsorption and diffusion in functionalized nanoporous materials, including metal–organic frameworks (MOFs) and covalent–organic frameworks (COFs). In all cases, our BO framework outperforms random-sampling-based ML pipelines in both identifying and ranking top-performing candidates. Notably, we not only measure success in terms of top-performer recovery but also assess the quality of the ranking (nDCG; see Section 2.4).
2 Methodology
2.1 The premise
As outlined in the introduction, the premise of this work is that researchers in a laboratory often operate within a specific experimental budget while seeking the best or top-performing materials from a vast design space of nanoporous materials. Typically, this budget, represented by N (the number of new materials evaluated), is significantly smaller than the total number of materials available in the design space (N ≪ N′, where N′ denotes the total number of available materials). Consequently, identifying the best or top-performing materials by randomly selecting and testing N samples relies purely on chance. ML offers an alternative: it can use these N randomly selected samples to train a model, predict performance across the entire design space, and rank all available materials based on predicted performance.Inspired by recent advancements in Bayesian Optimization (BO) applied to MOFs and related materials, we investigate the potential of BO to guide researchers in allocating their N experiments. The goal is to iteratively direct experiments toward regions of the design space with higher performance, progressively converging on areas of interest and improving efficiency in identifying exceptional materials.
2.2 Problem formulation
Suppose a set M containing all nanoporous materials m ∈ M. Each material m can be uniquely identified by a set of n feature properties f (hereby called features). Each point in this multi-dimensional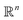 space corresponds to the design of one material and each material may differ slightly or greatly from the others in terms of a target property value. So:
space corresponds to the design of one material and each material may differ slightly or greatly from the others in terms of a target property value. So: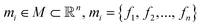 | (1) |
We define a machine learning model as the process p that learns the mapping from the general material space 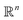 to this target property y, so:
to this target property y, so:
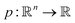 | (2) |
Let the dataset used to train this machine learning model be denoted as Dtrain which consists of N data points, same as the budget for experiments. This can be defined as:
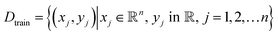 | (3) |
Similarly we can define the test dataset Dtest and the evaluation dataset Deval. Now lets consider a method for evaluating this model. Let us denote this method as 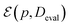 which takes the ML model p and evaluation dataset and provides a measure of the performance of the model. The logic and metrics used for the evaluation are described in detail in the Evaluation metrics section.
which takes the ML model p and evaluation dataset and provides a measure of the performance of the model. The logic and metrics used for the evaluation are described in detail in the Evaluation metrics section.
Our goal is to use the least amount of data, less than or equal to the available budget, in order to achieve the best performance score. In practical terms, this problem is inherently multi-objective: we aim to minimize the number of samples required for training while simultaneously maximizing the predictive performance of the model. The trade-off between these two goals is the central question addressed in this work.
2.3 AI methodologies
BO is an iterative process where at each iteration we train an ML model (called a surrogate model) with the currently acquired data, we use this model to make predictions about a specific data property on the whole dataset. Finally an acquisition function is being utilized to select the most informative data point and add it to the dataset. The surrogate's uncertainty quantification is central to this process, since the acquisition function balances exploration (sampling uncertain regions) with exploitation (sampling high-predicted-value regions). Practically, the surrogate model represents our current beliefs about the target property that we are trying to maximize (or minimize) and the acquisition function seeks to select data points from areas of the data space that we lack knowledge of. By transferring this scheme to our problem, we state that BO determines which experiments should be performed by designating the most promising candidate materials in terms of target property value maximization.
We adopt the open-source implementation of Gantzler et al.,19 which is built on the BoTorch library20 for Gaussian process–based Bayesian optimization, as the foundation for our framework; in Section 2.5, we detail the extensions we introduce on top of this BO implementation.
In the following paragraph we make clarifications concerning the details of our method.
As our surrogate model we have selected a Gaussian Process (GP) model due to its efficiency in representing the uncertainty of knowledge. The model consists of two parts, a mean function and a kernel (covariance function)
| Y(x) ∼ GP(μ(x), K(x, x′)) | (4) |
| μ(x) = C | (5) |
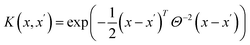 | (6) |
The acquisition function that we have selected is Expected Improvement (EI):
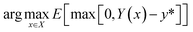 | (7) |
At the conclusion of the BO process, users gain access to a curated set of high-performing materials from the design space. As we will demonstrate later, these selected points form an information-rich dataset containing instances of optimal performance. This dataset can then be used to train the same predictive model employed in the random sampling approach (XGBoost), enabling it to make predictions across the entire design space and further expand the list of high-performing materials with additional suggested candidates. Consequently, the final selection of top-performing materials is derived from a combined dataset consisting of BO-acquired samples and XGBoost predictions trained exclusively on these samples. As we will show in later sections, this strategy proves highly effective, as the trained model excels at distinguishing and identifying high-performing instances, further enhancing the optimization process. A graphical representation of our pipeline is depicted on Fig. 1.
Recent works have applied BO directly to nanoporous materials design. Deshwal et al.22 demonstrated that BO can efficiently navigate a database of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 COFs to identify those with highest methane deliverable capacity, outperforming random search, evolutionary algorithms, and one-shot ML baselines, while also acquiring a significant fraction of the top-performing structures after relatively few evaluations. Gantzler et al.19 extended this idea by employing multi-fidelity BO for COFs in Xe/Kr separations, showing that combining low-cost approximate evaluations with high-fidelity simulations accelerates the search. Together, these studies established BO as a powerful framework for adsorption and diffusion problems in porous materials. In this work, we demonstrate how three complementary elements—diversity-preserving initialization, batch-mode acquisitions, and surrogate enrichment with XGBoost—can be combined into a coherent framework, whose integration provides a practical and effective workflow for materials discovery.
000 COFs to identify those with highest methane deliverable capacity, outperforming random search, evolutionary algorithms, and one-shot ML baselines, while also acquiring a significant fraction of the top-performing structures after relatively few evaluations. Gantzler et al.19 extended this idea by employing multi-fidelity BO for COFs in Xe/Kr separations, showing that combining low-cost approximate evaluations with high-fidelity simulations accelerates the search. Together, these studies established BO as a powerful framework for adsorption and diffusion problems in porous materials. In this work, we demonstrate how three complementary elements—diversity-preserving initialization, batch-mode acquisitions, and surrogate enrichment with XGBoost—can be combined into a coherent framework, whose integration provides a practical and effective workflow for materials discovery.
2.4 Evaluation metrics
We trained and evaluated our regressor across the various training dataset sizes that will be presented in a following section, aiming to determine the minimum number of training samples required to effectively capture the most promising region of the design space in terms of target property maximization. In this section, we define what constitutes a promising area and outline the evaluation metrics used to assess our machine learning model's ability to identify it.In our experiments, where the design space is finite and the target property values for all candidate materials are known, we can easily rank the materials in descending order and extract the top-N (where N is either 100 or 10, in this work). Ideally, our model's predictions should rank the same materials within the top-N while closely approximating their actual target property values. To evaluate our model's performance in these tasks, we employed the following metrics.
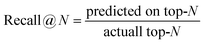 | (8) |
 | (9) |
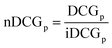 | (10) |
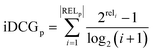 | (11) |
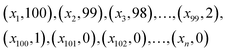 | (12) |
2.5 Beyond baseline BO: practical additions
In this section, we summarize a set of additions to standard Bayesian optimization. Some of these strategies (e.g., diverse initialization, batch acquisitions) have appeared in the literature, while others (e.g., enrichment of BO findings with predictions) are introduced here. Taken together, they provide a clear improvement in efficiency and make our BO framework more practical for materials discovery. We present them as recommended extensions that practitioners may find useful when applying BO to large design spaces.However, purely random initialization can introduce statistical variability, potentially leading to inconsistencies in performance when applying BO to real-case scenarios. To mitigate this, in our work we employ an informed initialization strategy rather than random selection, following the approach of Gantzler et al.19 Specifically, we first determine a central sample by computing the mean of all feature values and selecting the candidate whose features are closest to this mean, which serves as a representative point of the design space. Next, to ensure diversity in the initial training set, we apply a diverse-set selection procedure that, starting with the central sample, iteratively identifies additional samples that maximize the minimum Euclidean distance from the already selected points.
This procedure guarantees that the initial three samples are simultaneously representative and diverse, providing the Gaussian process surrogate model with a robust starting dataset for BO. In our case, three such samples were selected. As shown in the SI (Table S1), this approach yields performance comparable to the average of 20 BO runs with different random initializations (three points each, 100 steps), in identifying the top-100 instances for all datasets considered in this work. We emphasize that this comparison was performed deliberately to confirm that our initialization scheme does not bias performance upward relative to random initialization, but rather offers a practical and robust one-shot alternative in settings where repeated BO restarts are not feasible.
We note that the notion of ‘diversity’ depends on the chosen feature representation; different fingerprints (e.g., chemical vs. geometric) can yield different diverse sets.24 The present work adopts the feature sets provided in the literature datasets considered here, but in general, the effectiveness of a diversity-based initialization strategy depends on the availability of a feature representation that meaningfully captures structural and chemical differences.
Fig. S1 in the SI compares single-sample BO with batch sizes of 5 and 10 samples per iteration, evaluating their performance in terms of recall@100 and best-sample identification as functions of sample size and computational time. The test case involves the dataset by Mercado et al.,25 comprising 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 COFs evaluated for methane deliverable capacity. Based on this analysis, we adopt a batch size of 5 samples per BO iteration throughout this work, as it provides an effective balance between computational efficiency and performance. Notably, this configuration achieves the same recall@100 and identifies the best-performing COF using 700 samples at just one-tenth of the computational time compared to single sampling. We note that batch BO itself is well established in the literature, particularly through methods such as q-EI.26,27 Here, we adopt a simpler strategy: selecting the top-k EI points per iteration. This makes batching straightforward to implement in similar workflows while retaining the benefits of parallelism and reduced runtime.
000 COFs evaluated for methane deliverable capacity. Based on this analysis, we adopt a batch size of 5 samples per BO iteration throughout this work, as it provides an effective balance between computational efficiency and performance. Notably, this configuration achieves the same recall@100 and identifies the best-performing COF using 700 samples at just one-tenth of the computational time compared to single sampling. We note that batch BO itself is well established in the literature, particularly through methods such as q-EI.26,27 Here, we adopt a simpler strategy: selecting the top-k EI points per iteration. This makes batching straightforward to implement in similar workflows while retaining the benefits of parallelism and reduced runtime.
Fig. 1 summarizes our approach, as was described in Section 2.5.1–2.5.3.
2.6 Datasets
In this section we summarize all the datasets used in this work. Mercado et al.25 reported a database of approx. 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 COF, where they report the uptake and deliverable capacity of CH4 in them, through Monte Carlo simulations. The same COFs database was used by Deshwal et al.,22 for methane uptake values, for the development of a BO routine that identifies the best candidate material. The same structure database was employed in the 2023 work by Aksu and Keskin2 for where they report a high-throughput and ML scheme for the identification of COFs with CH4/H2 separation performance. Here, we use CH4 uptake and deliverable capacity as target values. Orhan et al.28 reported a 5600 MOFs databases in their high throughput screening work for O2/N2 materials. The target properties we considered were the diffusivity and uptake of O2, and the diffusion selectivity of O2/N2. Another database we considered was the one developed by Majumdar et al.29 which includes more than 20
000 COF, where they report the uptake and deliverable capacity of CH4 in them, through Monte Carlo simulations. The same COFs database was used by Deshwal et al.,22 for methane uptake values, for the development of a BO routine that identifies the best candidate material. The same structure database was employed in the 2023 work by Aksu and Keskin2 for where they report a high-throughput and ML scheme for the identification of COFs with CH4/H2 separation performance. Here, we use CH4 uptake and deliverable capacity as target values. Orhan et al.28 reported a 5600 MOFs databases in their high throughput screening work for O2/N2 materials. The target properties we considered were the diffusivity and uptake of O2, and the diffusion selectivity of O2/N2. Another database we considered was the one developed by Majumdar et al.29 which includes more than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hypothetical MOFs, along with various gas properties, of which we kept H2 uptake capacity, CO2 uptake, N2 uptake, CO2 working capacity, and CO2/N2 selectivity. This database was employed, also, by Daoo et al.30 in their work on Active Learning methods for high-performing MOFs for the separation of C2H2/C2H4 and C3H6/C3H8. We kept as target properties the C2H2 and C2H4 uptakes. Villajos et al. in their 2023 work31 reported an extended dataset for H2 adsorption at cryogenic temperatures, where they provide 3600 MOFs with crystallographic and porous properties, along with volumetric and gravimetric capacities. In our work we consider as target property the gravimetric capacity. Aksu and Keskin2 reported a high-throughput computational screening combined with ML for the identification of high-performing COFs as adsorbents for CH4/H2 separations in pressure-swing and vacuum-swing adsorption (PSA and VSA, respectively). In our work we considered as target properties the CH4 and H2 uptakes at 1 bar pressure.
000 hypothetical MOFs, along with various gas properties, of which we kept H2 uptake capacity, CO2 uptake, N2 uptake, CO2 working capacity, and CO2/N2 selectivity. This database was employed, also, by Daoo et al.30 in their work on Active Learning methods for high-performing MOFs for the separation of C2H2/C2H4 and C3H6/C3H8. We kept as target properties the C2H2 and C2H4 uptakes. Villajos et al. in their 2023 work31 reported an extended dataset for H2 adsorption at cryogenic temperatures, where they provide 3600 MOFs with crystallographic and porous properties, along with volumetric and gravimetric capacities. In our work we consider as target property the gravimetric capacity. Aksu and Keskin2 reported a high-throughput computational screening combined with ML for the identification of high-performing COFs as adsorbents for CH4/H2 separations in pressure-swing and vacuum-swing adsorption (PSA and VSA, respectively). In our work we considered as target properties the CH4 and H2 uptakes at 1 bar pressure.
3 Results and discussion
3.1 A first demonstration case for a fixed number of 100 samples: “COFs with high deliverable capacity as target property” as a testbed of comparison”
In this section, we evaluate our BO approach using the methane deliverable capacity dataset from Mercado et al.25 as a testbed. We compare our method against a conventional ML approach in the context of a lab operating on a limited budget of 100 samples.A ranking of the top-100 predicted values compared with the actual top-100 reveals that the conventional ML (Random Sampling ML) approach identifies only 2 of the true top-100 performing COFs. In contrast, the BO approach successfully selects 20 COFs within the top-100 tier. Moreover, when the XGBoost model is trained on the BO-acquired samples, it identifies an additional 20 top-performing COFs, boosting the overall count to 40.
This result highlights the value of using Bayesian Optimization (BO) to acquire high-interest samples, as it complements and enhances subsequent ML-based ranking. Although the XGBoost model trained on BO-acquired samples exhibits lower overall predictive performance—achieving an R2 of 0.70 compared to 0.85 for the model trained on randomly selected samples, along with a higher MSE (see Fig. S2 in the SI)—its focused training on a promising subregion of the design space makes it particularly effective at accurately identifying and ranking the top-performing COFs.
This becomes evident when evaluating the models specifically on the top-100 region: the XGBoost model trained on BO-selected samples achieves better R2 and lower MSE than the one trained on random samples Fig. S2, despite its lower global metrics. This illustrates that common evaluation metrics such as R2 and MSE, when applied over the entire dataset or random subsets, can be misleading in assessing a model's true utility. In scenarios where the goal is to discover rare but high-value regions in the design space, average performance across the whole dataset does not reflect the model's effectiveness in those critical areas.
Thus, our approach uses BO for targeted sample acquisition in a large design space and then employs ML to enrich the top-100 findings, through predictions (Fig. 2).
3.2 All dataset results
In this section, we apply our BO approach and benchmark it against the Random Sampling ML baseline across all literature datasets introduced in the Methodology section. The comparison is carried out as a function of the evaluation budget, ranging from 1000 to 2000 sample evaluations. Performance is assessed in terms of the top-100 or top-10 candidates identified (depending on the design space size), as well as the single best material discovered, each reported as a function of the available evaluation budget.First, we evaluate the methane uptake dataset for COFs from Mercado et al.25 As shown in Fig. 3(a), although the XGBoost model trained on randomly selected samples (Random Sampling ML) gradually improves its recall@100 with increasing sample size, even 1000 samples yield only marginal gains (recall@100 ≈ 50). In stark contrast, our BO framework achieves a recall@100 of 93 from the very first iterations. Remarkably, BO pinpoints the single best-performing COF with just 50 samples, whereas the random sampling strategy fails to identify the top candidate even after 1000 evaluations.
Moreover, it is worth mentioning that the nDCG values are considerably higher for BO, highlighting the ability of our approach to not only find more of the top-100 instances, but ensure a more accurate positioning of them, closer to the actual ranks of the materials, in terms of their performance (see Fig. S3).
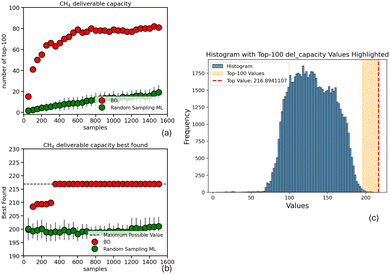
Fig. 4(a) demonstrates that for the more challenging methane deliverable capacity target, BO still vastly outperforms the conventional ML approach based on Random Sampling ML in terms of recall@100. The BO approach identifies up to 80 of the top-100 COFs—slightly lower than the performance for methane uptake—that creates a clear performance gap with the Random Sampling ML, which at 1500 samples identifies 19 top-100. This highlights BO's superior ability to target high-interest regions in complex design spaces.
Fig. 4(b) further emphasizes this advantage when it comes to identifying the single best-performing COF. For methane deliverable capacity, BO requires approximately 300 samples to reliably pinpoint the best COF, compared to just 50 samples for methane uptake. In contrast, the Random Sampling ML approach shows a steady but limited improvement in the best COF value as more samples are added, indicating its difficulty in effectively exploiting additional data to locate the optimum. Moreover, nDCG is consistenly higher for BO, reaching almost 1, while Random Sampling ML maxes below 0.9 (Fig. S3). These results confirm that BO is a highly effective sampling strategy, particularly in challenging scenarios where the design space is vast and the optimal regions are hard to exploit using conventional methods.
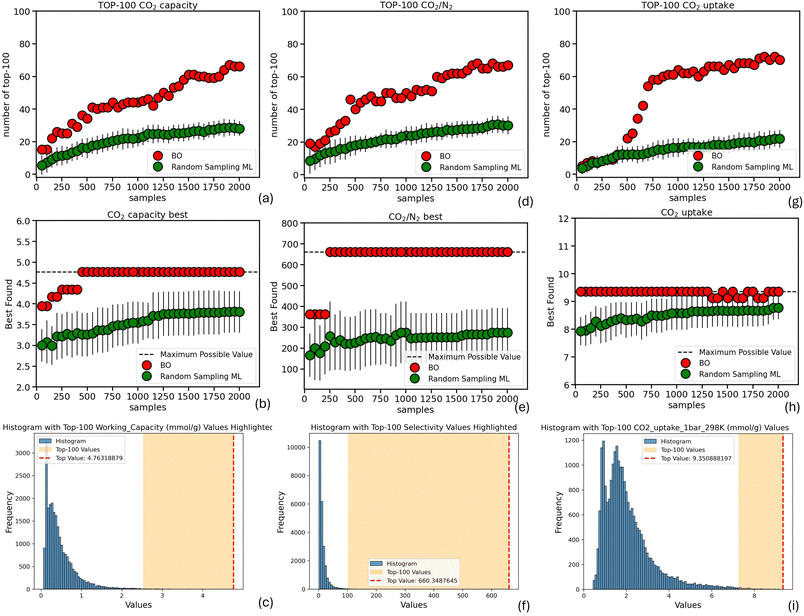
Fig. 5–7 summarize the results for the remaining datasets considered in this work. The first two columns of Fig. 5 illustrate the number of samples required by both Bayesian Optimization (BO) and Random Sampling ML to identify the top-100 and top-1 performing MOFs for ethylene and ethane uptake, respectively, based on the dataset from Daoo and Singh.30 It is evident that, in both cases, BO successfully identifies significantly more of the top-100 performing materials with the same number of samples. Furthermore, BO is able to identify the single best-performing MOF within the very first steps, whereas Random Sampling ML exhibits only marginal improvements throughout the search (up to 1600 samples). Even in the case of H2 uptake (Fig. 5(g) and (h)), based on the dataset reported by Majumdar et al.,29 where random sampling shows a comparable ability to BO in identifying top-100 materials after approximately 1000 samples, it fails to identify the best-performing MOF—even after 2000 samples—highlighting the greater efficiency of the BO strategy. Again, the nDCG values of BO remain consistently higher than those of random sampling across all three cases (Fig. S3), highlighting BO's superior ability not only to identify the region containing the top-performing materials, but also to rank them in a manner that more closely reflects their true performance.
The same strong performance in identifying top-performing MOFs is observed when our BO method is applied to the three datasets reported by Majumdar et al.,29 targeting CO2 working capacity, CO2/N2 selectivity, and CO2 uptake (Fig. 6). We draw the reader's attention particularly to the case of CO2/N2 selectivity, where the underlying distribution illustrates the difficulty of the task. Despite this challenge, BO achieves significantly higher identification performance and successfully discovers the best-performing MOF early in the search process. Once again, the nDCG values for BO are considerably higher than those for random sampling (Fig. S3), further demonstrating its superior ranking capabilities.
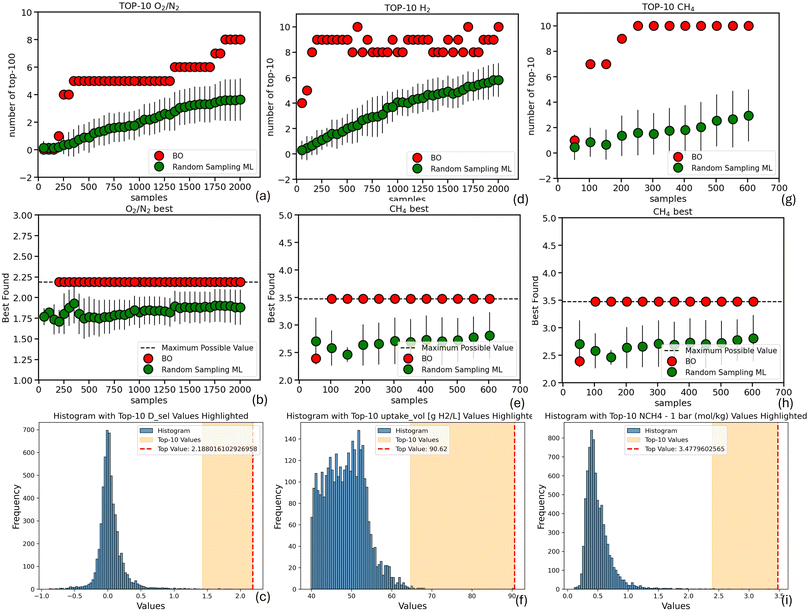
Finally, Fig. 7 presents the results for three additional datasets: O2/N2 diffusion selectivity in MOFs (from Orhan et al.28), H2 uptake in MOFs (from Villajos et al.31), and CH4 uptake in COFs (from Aksu and Keskin2). Due to the relatively smaller size of these datasets, we focused on the identification of the top-10 performing materials, reducing the evaluation threshold by an order of magnitude compared to previous cases. Even under this more stringent setting, our BO approach consistently outperforms random sampling, both in terms of identifying top performers and in ranking them effectively. BO successfully identifies a greater portion of the top-10 candidates with fewer samples, and—as confirmed by the nDCG scores—produces rankings that more closely reflect the true order of performance.
4 Conclusions
We have presented a frugality-oriented Bayesian Optimization (BO) framework tailored to the practical needs of materials scientists seeking not just a single optimum, but an ensemble of top-N performers from vast design spaces of functionalized nanoporous materials. By integrating three practical elements—(i) a diversity-preserving initialization scheme, (ii) batch-mode acquisitions to reduce retraining overhead, and (iii) a surrogate enrichment step in which an XGBoost model is trained on BO-acquired samples to predict and rerank the remainder of the space—we achieve a data-efficient workflow that dramatically reduces the number of expensive evaluations required. Across eight literature-derived datasets (MOFs and COFs spanning adsorption, diffusion, and selectivity targets), our BO framework recovers up to 2×–5× more true top-N candidates than a conventional ML pipeline trained on random samples (as measured by recall@N), and produces more accurate rankings (nDCG). Moreover, our BO method locates the single best performer with just 100–200 evaluations, whereas the random-sampling approach often still fails to find it after 2000 samples. By prioritizing task-specific metrics (recall@N, nDCG) over global measures (e.g., R2, MSE), we directly address the experimental goal of discovering rare, high-value materials under strict budget constraints. It is worth mentioning, in general, when comparing BO and Random Sampling ML, that BO is by construction a sequential process, whereas random sampling allows fully independent evaluations. In principle, if very large-scale parallel evaluation were available, random sampling could exploit this more directly and achieve faster turnaround despite lower sample efficiency. In practice, however, such scenarios remain largely hypothetical in materials discovery, where evaluations are typically costly and parallel resources are limited. Under these realistic conditions, BO provides a clear advantage by reducing the total number of evaluations required. The result is a robust and practical workflow—effective across diverse chemistries and objectives, and built entirely on standard Gaussian process and XGBoost tools. While our benchmarking focused on Random-Sampling ML as a baseline—reflecting its widespread use in prior literature and practice—we note that other strategies, such as uncertainty-based or diversity-driven active learning,11 have also been explored for chemical design spaces. Incorporating such baselines in future work would provide additional perspective, but our present goal was to highlight the benefits of useful extensions to BO relative to the most common ML pipeline.We envisage several concrete extensions to further enhance our framework's practical utility. First, integrating multi-objective BO methods—such as those by Kim et al.32 and Hoang et al.33—would enable simultaneous optimization of multiple performance criteria (e.g., selectivity vs. capacity). Second, replacing the Gaussian process surrogate with alternative probabilistic models (e.g., Bayesian Neural Networks34 or Gradient Boosting models with uncertainty estimation35) could alleviate the computational and scaling limitations of GPs. Third, human-in-the-loop strategies, as in HypBO,36 would allow domain experts to steer the sampling process in real time, potentially accelerating convergence in difficult regions. Finally, minimizing the effective design space—following the ZoMBI algorithm of Siemenn et al.17 —offers a promising route to reduce memory overhead, runtime, and the number of required samples, thereby addressing both the computational and the sampling costs. We are actively exploring these directions, though detailed implementation lies beyond the scope of this work.
Author contributions
Panagiotis Krokidas: conceptualization, formal analysis, methodology, software, supervision, writing; Vassisis Gkatsis: data curation, methodology, software, writing; John Theocharis: conceptualization, methodology, software; George Giannakopoulos: supervision, writing, methodology.Conflicts of interest
There are no conflicts to declare.Data availability
The codes for our (a) Bayesian optimization implementation as described in this manuscript and (b) the evaluation metrics estimation underlying this work are freely available for general use under the Apache License 2.0. They are deposited at https://github.com/insane-group/BO_for_Design_Space_Exploration and archived on Zenodo with DOI: https://doi.org/10.5281/zenodo.17491026. The datasets used in this work were obtained from literature, as cited in this manuscript.Supplementary information: details of the XGBoost and Gaussian process models, comparison of efficient vs. random initialization, batch sampling performance, additional R², MSE and nDCG analyses, and computational setup used in this work. See DOI: https://doi.org/10.1039/d5dd00237k.
Acknowledgements
This work was supported by the European Union's Horizon Europe research and innovation programme under grant agreement No. 101135927 (NOUS).Notes and references
- R. Batra, C. Chen, T. G. Evans, K. S. Walton and R. Ramprasad, Nat. Mach. Intell., 2020, 2, 704–710 CrossRef.
- G. O. Aksu and S. Keskin, J. Mater. Chem. A, 2023, 11, 14788–14799 RSC.
- Y. He, E. D. Cubuk, M. D. Allendorf and E. J. Reed, J. Phys. Chem. Lett., 2018, 9, 4562–4569 CrossRef CAS.
- Z. Zheng, O. Zhang, C. Borgs, J. T. Chayes and O. M. Yaghi, J. Am. Chem. Soc., 2023, 145, 18048–18062 CrossRef CAS PubMed.
- Y. Kang and J. Kim, Nat. Commun., 2024, 15, 1–13 Search PubMed.
- A. S. Fuhr and B. G. Sumpter, Front. Mater., 2022, 9, 1–13 Search PubMed.
- A. Nandy, C. Duan and H. J. Kulik, Curr. Opin. Chem. Eng., 2022, 36, 100778 CrossRef.
- R. Chang, Y. X. Wang and E. Ertekin, npj Comput. Mater., 2022, 8, 242 CrossRef.
- B. Zong, J. Li, T. Yuan, J. Wang and R. Yuan, J. Materiomics, 2025, 11, 100916 CrossRef.
- F. Di Fiore, M. Nardelli and L. Mainini, Arch. Comput. Methods Eng., 2024, 31, 2985–3013 CrossRef.
- A. Jose, E. Devijver, N. Jakse and R. Poloni, J. Am. Chem. Soc., 2024, 146, 6134–6144 CrossRef CAS PubMed.
- H. Liu, B. Yucel, B. Ganapathysubramanian, S. R. Kalidindi, D. Wheeler and O. Wodo, Digital Discovery, 2024, 3(10), 1997–2009 RSC.
- J. Schrier, A. J. Norquist, T. Buonassisi and J. Brgoch, J. Am. Chem. Soc., 2023, 145, 21699–21716 CrossRef CAS.
- S. R. Chitturi, A. Ramdas, Y. Wu, B. Rohr, S. Ermon, J. Dionne, F. H. Jornada, M. Dunne, C. Tassone, W. Neiswanger and D. Ratner, npj Comput. Mater., 2024, 10, 1–12 CrossRef.
- Y. Wu, A. Walsh and A. M. Ganose, Digital Discovery, 2024, 3, 1086–1100 RSC.
- T. Loutas, A. Oikonomou and C. Rekatsinas, Compos. Struct., 2025, 351, 118597 CrossRef.
- A. E. Siemenn, Z. Ren, Q. Li and T. Buonassisi, npj Comput. Mater., 2023, 9, 92 CrossRef.
- T. Chen and C. Guestrin, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 2016, pp. 785–794 Search PubMed.
- N. Gantzler, A. Deshwal, J. R. Doppa and C. M. Simon, Digital Discovery, 2023, 2, 1937–1956 RSC.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, Adv. Neural Inf. Process. Syst., 2020, 33, 21524–21538 Search PubMed.
- M. Haddadnia, L. Grashoff and F. Strieth-Kalthoff, Digital Discovery, 2025, 1417–1422 RSC.
- A. Deshwal, C. M. Simon and J. R. Doppa, Mol. Syst. Des. Eng., 2021, 6, 1066–1086 RSC.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 1–10 CrossRef.
- R. Mercado, R. S. Fu, A. V. Yakutovich, L. Talirz, M. Haranczyk and B. Smit, Chem. Mater., 2018, 30, 5069–5086 CrossRef CAS.
- D. Ginsbourger, R. L. Riche and L. Carraro, A Multi-points Criterion for Deterministic Parallel Global Optimization based on Gaussian Processes, Institut National Polytechnique de Grenoble Technical Report hal-00260579, 2008 Search PubMed.
- D. Ginsbourger, R. L. Riche and L. Carraro, Computational Intelligence in Expensive Optimization Problems, Springer, Berlin, Heidelberg, 2010, vol. 2, pp. 131–162 Search PubMed.
- I. B. Orhan, H. Daglar, S. Keskin, T. C. Le and R. Babarao, ACS Appl. Mater. Interfaces, 2022, 14, 736–749 CrossRef CAS.
- S. Majumdar, S. M. Moosavi, K. M. Jablonka, D. Ongari and B. Smit, ACS Appl. Mater. Interfaces, 2021, 13, 61004–61014 CrossRef CAS.
- V. Daoo and J. K. Singh, ACS Appl. Mater. Interfaces, 2024, 16, 6971–6987 CrossRef CAS.
- J. A. Villajos, M. Bienert, N. Gugin, F. Emmerling and M. Maiwald, Mater. Adv., 2023, 4, 4226–4237 RSC.
- J. Kim, M. Li, Y. Li, A. Gómez, O. Hinder and P. W. Leu, Digital Discovery, 2023, 3, 381–391 RSC.
- K. T. Hoang, S. Boersma, A. Mesbah and L. S. Imsland, Renewable Energy, 2025, 247, 122988 CrossRef.
- Y. L. Li, T. G. Rudner and A. G. Wilson, 12th International Conference on Learning Representations, ICLR, 2024 Search PubMed.
- T. Duan, A. Avati, D. Y. Ding, K. K. Thai, S. Basu, A. Ng and A. Schuler, 37th International Conference on Machine Learning, ICML 2020, 2020, PartF168147-4, pp. 2670–2680 Search PubMed.
- A. Cissé, X. Evangelopoulos, S. Carruthers, V. V. Gusev and A. I. Cooper, Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence (IJCAI-24), 2024, pp. 3881–3889 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |