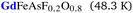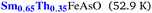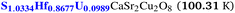A straightforward gradient-based approach for designing superconductors with high critical temperature: exploiting domain knowledge via adaptive constraints

Abstract

Materials design aims to discover novel compounds with desired properties. However, prevailing strategies face critical trade-offs. Conventional element-substitution approaches readily and adaptively incorporate various domain knowledge but remain confined to a narrow search space. In contrast, deep generative models efficiently explore vast compositional landscapes, yet they struggle to flexibly integrate domain knowledge. To address these trade-offs, we propose a gradient-based material design framework that combines these strengths, offering both efficiency and adaptability. In our method, chemical compositions are optimised to achieve target properties by using property prediction models and their gradients. In order to seamlessly enforce diverse constraints—including those reflecting domain insights such as oxidation states, discretised compositional ratios, types of elements, and their abundance, we apply masks and employ a special loss function, namely the integer loss. Furthermore, we initialise the optimisation using promising candidates from existing datasets, effectively guiding the search away from unfavourable regions and thus helping to avoid poor solutions. Our approach demonstrates a more efficient exploration of superconductor candidates, uncovering candidate materials with higher critical temperature than conventional element-substitution and generative models. Importantly, it could propose new compositions beyond those found in existing databases, including new hydride superconductors absent from the training dataset but which share compositional similarities with materials found in the literature. This synergy of domain knowledge and machine-learning-based scalability provides a robust foundation for rapid, adaptive, and comprehensive materials design for superconductors and beyond.

---

1 Introduction

Materials design is crucial for technological innovation such as the discovery of new superconductor materials. High-temperature superconductors (HTS) are especially promising because they reduce cooling costs and enable higher magnetic fields. They are also expected to be applied in fusion power generation, electric power cables, and superconducting maglev trains.^1,2

Exploiting physical insights—such as selection of elements based on their oxidation states and the fact that materials with too many elements are impractical—can narrow this search, making materials design more efficient. A traditional technique in materials design is elemental substitution (i.e., doping).^3–6 In this approach, one starts with a promising host material and partially substitutes certain elements to tune the properties. Substituted elements are typically chosen based on physical insights—such as oxidation states—to ensure charge neutrality and other key constraints.

Machine learning (ML) has become a widely used approach for materials discovery, offering faster property predictions than conventional Density Functional Theory (DFT) calculations and thus enabling high-throughput screening. In the context of HTS development, some studies^7–15 have focused on training superconducting transition temperature (T_c) prediction models using the SuperCon dataset,¹⁶ which comprises a large set of known superconductors. Some studies^17–19 combine ML-based T_c prediction with experimental tests and report the discovery of novel superconducting materials.

Recently, deep generative models have gained prominence in materials design,^20–23 including the quest to discover novel superconductors.^24,25 These models propose new compounds by learning the statistical distribution of existing data, thus enabling the exploration of a vast chemical space. Several studies^26,27 employ diffusion models²⁸—a deep generative model widely used in the computer vision field²⁹—to generate superconductor candidates. SuperDiff,²⁷ a diffusion model for superconductors, generates candidate superconductors by gradually removing noise from a noisy composition. Moreover, SuperDiff can generate conditioned outputs based on reference compounds using Iterative Latent Variable Refinement (ILVR).³⁰ While conventional generative methods only explore materials within existing databases, SuperDiff can generate new materials based on promising reference compounds.

Moreover, there are strategies that guide deep generative models toward desired properties, such as label-based conditional generation,³¹ Universal Guidance³² (UG), Classifier Guidance (CG)³³ and Classifier-Free Guidance (CFG).³⁴ While CG and UG use a separate property predictor to steer the generation process, CFG does not require such a predictor. Although the label-based conditional generation and CFG have both been extensively validated in image generation, their reliance on labels within the dataset limits their flexibility in materials design. By contrast, CG can be conditioned on labels not present in the target dataset using models trained on other datasets. Xie et al.²⁰ employ a strategy similar to CG, combining a diffusion model with a formation energy prediction model. Applying CG to T_c prediction models and superconducting material generation models such as SuperDiff has the potential to enable HTS design.

A gradient-based method^35–38 that uses prediction models and their gradients to optimise inputs has recently attracted attention. This method is similar to CG and UG but simpler, as it does not require training a generative model. Moreover, this method allows for more flexible and adaptive conditional optimisation.³⁸ While there is no study of applying this technique to composition optimisation, it could be a promising approach for materials design.

Despite these advances, significant trade-offs remain. Elemental substitution can incorporate physical knowledge but may limit exploration to a relatively narrow search space. Deep generative models can explore a broader chemical space efficiently, yet they struggle to flexibly integrate physical knowledge—such as atomic valence constraints or converting compositional ratios to integers—in an adaptive manner. On the other hand, the gradient-based method has a risk of falling into poor solutions, though this method has the potential to introduce various physical knowledge in an adaptive manner.

In this paper, to address these issues, we adopt a gradient-based method and propose a straightforward materials-design method called Knowledge-Integrated Adaptive Gradient-based Optimisation (KIAGO). This framework combines the adaptive application of domain knowledge with computational efficiency to directly optimise chemical compositions (Fig. 1). KIAGO does not require training a deep generative model, making it more straightforward to implement. Specifically, we adopt two property prediction models—one for T_c and another for formation energy—to maximise T_c while enhancing stability, thereby proposing realistic materials. Unlike CFG and label-based conditional generation, KIAGO can optimise formation energy (which is not included in the SuperCon dataset) by using a separately trained formation energy prediction model. Additionally, by conducting an intensive search around promising materials, KIAGO mitigates the risk of being trapped at poor results. Moreover, by applying masks and a specialised loss function to enforce integer values, we can effectively embed physical insights (e.g., ensuring the retention of specific elements, oxidation states, the number of elements, or integer compositional ratios), thus providing a versatile framework that accommodates diverse constraints in adaptive manners.

Fig. 1 Overview of Knowledge-Integrated Adaptive Gradient-based Optimisation (KIAGO). KIAGO simultaneously maximises T_c and minimises the formation energy by optimising the input composition using two pretrained models and their gradients. Through the use of fixed composition vectors, masks, and specialised loss functions, KIAGO enables flexible control of the composition in three ways: (1) element control. Specific elements can be fixed and excluded from the optimisation target to perform conditional optimisation. KIAGO is also able to control which elements appear during the optimisation via masks. Here, we fix the composition of barium and exclude helium from the optimisation using the mask; (2) restricting the maximum number of elements. We first rank elements by their abundance in the composition and create a mask to keep only the most abundant ones up to a specified cutoff. All other elements are set to zero, ensuring that the total number of elements never exceeds the chosen limit. In this figure, we select the three most abundant elements to build a mask, which then restricts the final composition to those three elements. (3) Normalising the compositional ratios to small integers. Here, we use the loss function L_int⁴ to guide the normalised composition to a composition consisting of four atoms.

To validate the effectiveness of KIAGO, we performed experiments to propose promising HTS. Our approach significantly outperformed both generative models (SuperDiff and SuperDiff with CG) and conventional elemental substitution techniques in proposing high-T_c candidates efficiently. In particular, we found that SuperDiff with CG tended to generate materials with lower T_c values because the T_c distribution in the original data constrained them. In contrast, our method proposed high-T_c candidates without being limited by the original distribution. Additionally, KIAGO could keep some part of the composition fixed while optimising others, relevantly replace elements according to their oxidation states, and maintain charge neutrality perfectly. Additionally, KIAGO proposed candidate compositions that shared the same elements as hydride superconductors reported in other literature despite their absence from the SuperCon dataset. These results highlight its potential for discovering novel materials.

2 KIAGO

2.1 Overview

Knowledge-Integrated Adaptive Gradient-Based Optimisation (KIAGO) is a gradient-based method that uses pre-trained models and their gradients to directly optimise the input representation—in this case, the normalised compositional vector of candidate materials. Rather than merely searching for compositions that yield favourable properties, KIAGO introduces three key strategies to enhance material quality and provide fine-grained control: (1) initialisation from promising materials to mitigate the risk of being trapped at poor results; (2) masking to control elemental types; (3) special loss functions for conversion to integers and atomic-count constraints.

2.2 Gradient-based method

A gradient-based method can adopt any predictive model, provided the chain rule of differentiation is valid from input to output. To propose superconducting materials with high-T_c, we employ a T_c predictor f_Tc. We also use a formation-energy predictor f_Ef to propose compounds that are both high-T_c and thermodynamically feasible. We introduce a hyperparameter α and define the loss L as

L = −f_Tc(x̂) + αf_Ef(x̂) (1)

Here, x̂ ∈ [0, 1]^N_elem is a compositional vector spanning N_elem elements. Minimising L aims to increase T_c while lowering the formation energy. However, simple minimisation poses several issues: (1) it may converge to poor solutions, (2) it lacks control over the number and type of elements, and (3) it does not ensure integer ratios in the final composition.

2.3 Initialisation based on promising materials

To avoid converging to poor solutions, we adopt a strategy of starting the optimisation from various initial states including those corresponding to known promising materials. We can reduce this risk by focusing on the areas of existing high-performance compounds. Such a strategy goes beyond doping-like approaches that only alter part of an existing material, enabling a broader range of materials to be explored. Specifically, we perturb known superconductors by substituting elements randomly and adding new elements to the composition. This technique effectively explores the local neighbourhood of promising materials.

2.4 Controlling the types of elements present

We next control which elements appear in the composition by combining a fixed composition vector and a mask (Fig. 1(1)). First, we split x̂ into a fixed portion x_const and an optimisable portion x̂_opt:Here, σ is a normalisation function that ensures each element is non-negative and the total sum is 1. A possible approach was to use the softmax function. However, to emphasize elements that remain unused, we instead chose to use normalisation after applying Rectified Linear Unit (ReLU).

Because x_const remains unchanged, its specified composition remains fixed during optimisation. We further introduce a mask M_elem(M_elem ∈ {0, 1}^N_elem) to select the allowable elements. Concretely, we set

x̂_opt = x̂_base*M_elem, (6)

where is a trainable parameter, and the asterisk (*) denotes element-wise multiplication. This mask enforces strict control over which elements can be used, thus guiding the optimisation toward compositions that meet specified domain constraints.

2.5 Controlling the number of element types in the composition

To achieve realistic composition, we use a mask to limit how many elements can appear in the composition (Fig. 1(2)). To do this, we sort the compositional values in ascending order and create a mask M^max_elem(M^max_elem ∈ {0, 1}^N_elem), which sets to zero any element index beyond the allowed maximum elements n^max_elem.

∑M^max_elem = n^max_elem (7)

2.6 Integer loss

We construct a loss function that guides the composition into integer-compatible values during optimisation (Fig. 1(3)). Such values {c_n^N_unit} are those for which the product of the normalised composition and the unit cell size N_unit becomes an integer ratio. For instance, if N_unit = 4, then the feasible set {c_n⁴} is {0.00, 0.25, 0.50, 0.75, 1.00}.

The integer loss measures how far each compositional ratio of element i(x̂ⁱ) is from its nearest value in {c_n^N_unit}.

{c_n^N_unit} = {n/N_unit}_{n=0,1,…,Nunit}x̂ⁱ ∈ {x̂^H, x̂^He, x̂^Li, …, x̂^N_elem} (9)

As an example, Fig. 2 shows the result of applying L_int⁴ to Ca_0.23Sr_0.27O_0.50. We assume N_unit = 4 and guide the compositions toward the nearest values in {0.00, 0.25, 0.5, 0.75, 1.00}. Because it is difficult to fix N_unit in advance, we evaluate multiple candidates for N_unit and choose the one that yields the smallest loss. Concretely, we define L_integer as follows:

Fig. 2 An overview of the integer loss L_int⁴ under the assumption that each unit cell contains four atoms. The numbers shown inside the dashed box represent all possible different combinations between the integer-compatible set {c_n⁴} and the composition values. The total loss is obtained by selecting the minimum among these combinations for each element (indicated by the black underline) and summing them.

This flexible approach selects a suitable integer grid even when the optimal cell size is unknown.

2.7 Optimisation procedure

KIAGO divides its optimisation into two stages. First, as in Sections 2.3 and 2.4, we construct an initial x̂_base and control which elements appear while iteratively minimising the following loss L_1st. This process yields x̂^1st_*.

L_1st = −f_Tc(x̂) + αf_Ef(x̂) (13)

Next, we introduce the conversion to integers and a maximum-atom constraint. We use x̂^1st_* to build the mask M^max_elem, then iteratively minimise the loss L_2nd.

L_2nd = −f_Tc(x̂′) + αf_Ef(x̂′) + βL_{integer,{Nunit}}(x̂′) (16)

Here, β is a hyperparameter. We take x̂′(x̂^2nd_*) as the final solution.

3 Results

3.1 Implementation details

We used PyTorch³⁹ to implement KIAGO. KIAGO optimises a total of 4096 candidate compositions across 1000 steps using Adam optimiser.⁴⁰ We first perform 500 steps of optimisation using eqn (12)–(14), followed by another 500 steps using eqn (15)–(17) with α = 4 (selected based on tuning) and β = 1.

To predict the superconducting transition temperature (T_c), we employ a ResNet18 model⁴¹ trained on normalised compositions of SuperCon and Crystallography Open Database (COD).^42–51 Each composition is represented by a periodic table-based feature map, which has four channels corresponding to the s, p, d, and f orbitals.¹² SuperCon comprises more than 26 000 composition–T_c pairs and is widely used for T_c prediction. Although SuperCon lacks explicit structural information, it is used to propose novel superconductor candidates, some of which are later verified experimentally.^17–19 We also use COD as a source of non-superconductors to regularize training and reduce false positives.

For each element, we set flags at the positions of its row and column on the periodic table, as well as at its relevant orbital channels. We then multiply these element-level feature maps by the respective compositional ratios to create the final input representation. Further details are available in Section S.1. For formation energy, we used ElemNet,⁵² which is originally implemented in TensorFlow 1.x⁵³ and we re-implemented it in PyTorch. Since ElemNet only covers elements up to atomic number 86, we apply a mask to exclude elements beyond that range. Additional technical specifics are given in Section S.2.

We compared KIAGO against two baselines: a conventional elemental-substitution (C-ES) approach and SuperDiff, a diffusion-based generative model. The C-ES method randomly replaces some elements with others of identical oxidation states. For SuperDiff, we used the official implementation and trained on the same data for our T_c prediction model, but without normalising compositions. Following the official code, we conducted 1000 diffusion steps. According to the original SuperDiff, we conditioned generations of compositions on existing superconductors using Iterative Latent Variable Refinement (ILVR). We applied scale factors of 1, 2, 4, and 6 to yield a total of 4096 samples. We also incorporated Classifier Guidance (CG) using T_c prediction model and ElemNet into SuperDiff to compare it directly with KIAGO. Normally, the classifier used for CG must be trained on data with noise, which would make Universal Guidance (UG) the better choice for off-the-shelf models. However, we found that UG did not work well and CG still improved T_c using models without noise-augmented training. Therefore, we decided to use CG. Although neither model is strictly a classifier, we refer to this approach as CG for convenience. Note that this is not proposed in the original paper.²⁷ At each inference step, we used eqn (13) with α = 4 for gradient guidance, and we tuned the guidance weight from 1 × 10⁻⁷ to 1.0, ultimately selecting 1 × 10⁻³. Additional details of SuperDiff are provided in Section S.3.

After generating candidate compositions, we applied a multi-step screening procedure to ensure realistic materials. First, we used SMACT⁵⁴ to filter compositions with charge neutrality and electronegativity balance, following Yuan et al.²⁷ Next, we selected only those with formation energies (predicted by ElemNet) less than zero. We also removed compositions containing ten or more elements since the preprocessed SuperCon data have at most nine. Finally, we evaluated T_c values using the same ResNet18 predictor used in KIAGO and SuperDiff with CG.

To assess thermodynamic stability of the proposed materials, we use the energy above the convex hull per atom (ΔE_hull). Our method proposes compositions rather than crystal structures, so validating ΔE_hull with DFT total energies is not feasible. Instead, we estimate ΔE_hull from formation energies predicted by ElemNet. Concretely, we predict formation energies for compositions from the Materials Project⁵⁵ and the Alexandria Materials Database,^56–59 and compute ΔE_hull by building phase diagrams with pymatgen.⁶⁰

3.2 Mitigating the risk of convergence to non-promising solutions

In this section, we investigated whether our initialisation scheme could mitigate the risk of converging to non-promising local minima in the first stage (eqn (12)–(14)). Specifically, we aimed to determine whether our method can produce more promising local optima than a purely random initialisation. In our method, we began with the superconductor LaNiAsO from the SuperCon dataset. With a probability of 0.22, we replaced elements of its composition with different elements chosen according to their occurrence frequencies in SuperCon. We then selected random elements with random compositional ratios (from 0.0 to 0.3) for those elements, normalised the resulting composition, and used it as the initialisation. By contrast, the random initialisation selects four elements, to match the number of atoms in LaNiAsO, uniformly at random and assigns them random compositional values.

Fig. 3 shows the optimisation results. Our initialisation scheme yields higher T_c values than random initialisation. Although our method can still become trapped in local optima, it proposes more promising solutions than the random approach. Hence, our approach partially mitigates the inherent challenge of local minima in gradient-based methods. See Section S.4 for details on the variability across different random seeds.

Fig. 3 Comparison of optimisation results under different initialisation methods. Both approaches employ Adam optimiser⁴⁰ with a learning rate of 0.001. (Left) Initialisation by adding noise to an existing superconductor (LaNiAsO). (Right) Random initialisation, in which seven elements are chosen arbitrarily and assigned random compositional values.

3.3 Converting compositional ratios to integers via loss-based approach

In this section, we compared the integer conversion method based on a loss function L_{integer,{Nunit}} with a rule-based integer conversion method. We aimed to determine which approach reduced the drop in T_c in the second stage (eqn (15)–(17)). In the loss-based method, we follow eqn (16) to maximise T_c while minimising E_f. Specifically, we guided the composition toward an integer representation by selecting an optimal total number of atoms from a set of integers smaller than the specified maximum atom count. We optimised them for 500 steps for integer conversion. By contrast, the rule-based approach multiplies the normalised composition by the specified number of atoms and then rounds each value to the nearest integer.

Table 1 shows the results comparing the rule-based approach and L_{integer,{Nunit}}. Because it remains closer to the pre-conversion to integers composition, rounding with a larger total number of atoms is generally advantageous. Although the rule-based method fully exploits this by always rounding at the maximum atom count, L_{integer,{Nunit}} does not always do so, yet it still performs better.

Table 1 Comparison between the rule-based approach and L_{integer,{Nunit}} for converting compositional ratios to integers. The table shows the average change in T_c before and after conversion to integers under certain maximum numbers of atoms, based on a total of 61 440 samples derived from 15 different superconducting materials

Max. num. atoms	L integer,{Nunit} (K)	Rule-based (K)
15	−3.59	−7.65
20	−0.81	−4.30
25	−0.93	−2.23
50	−0.43	−1.38
100	−0.13	−0.31

---

3.4 Generating superconductors with higher T_c based on existing ones

In this section, we investigated whether our method could propose superconductors with higher T_c values based on known superconductors as initial candidates. For KIAGO, we start with existing superconductors and introduce noise to the compositions described in Section 3.2. We used Adam optimiser with learning rate of 0.03 for KIAGO. We set {N_unit} = {1, 2, …, 25} and n^max_elem = 10. SuperDiff conditions on existing superconductors via Iterative Latent Variable Refinement (ILVR). The conventional elemental-substitution (C-ES) approach randomly replaces a subset of elements with others sharing the same oxidation state. For each base material of superconductor, we select copper-based, iron-based, and other superconductors that pass charge-neutrality and electronegativity screening by SMACT, then randomly choose from these sets as base materials.

Table 2 presents the differences in predicted T_c between the generated superconductors and their base materials. KIAGO achieves the most efficient exploration of higher T_c values compared to other methods. By contrast, there are experiments where SuperDiff does not yield any valid materials passing all screenings. This limitation may stem from the fact that many entries in SuperCon do not pass charge-neutrality and electronegativity checks; hence, the model struggles to generate valid compositions. The C-ES method also fails to propose sufficiently high T_c compounds, likely because its rule-based approach cannot fully explore the vast compositional space. In contrast, KIAGO proposes many materials showing substantial T_c increases. For completeness, Section S.6 includes all screening-pass rates.

Table 2 Differences in T_c (K) between the average T_c of the highest top-30 proposed superconductors and the base superconductors in the experiments of proposing superconductors based on existing ones. SD, SD w/ CG, and C-ES denote SuperDiff, SuperDiff with classifier guidance, and conventional elemental substitution, respectively. After screening 4096 samples, the T_c prediction model was used to calculate T_c. ‘N/A’ indicates that none of the samples passed the screening

Base materials from SuperCon	KIAGO	SD	SD w/ CG	C-ES
	Top-30	Top-30	Top-30	Top-30
	ΔTc (K)	ΔTc (K)	ΔTc (K)	ΔTc (K)
LaNiAsO	104.39	−1.42	−0.47	13.54
SrFe1.88Ni0.12As2	97.91	26.76	4.53	21.88
Sr4V2Fe2As2O6	97.49	−13.77	−13.66	−5.45
LaPt2B2C	86.73	−5.01	−4.66	6.90
HgBa2Ca2Cu3O8	17.07	−29.43	−1.18	−12.11
CeBiS2O	92.12	N/A	−0.31	2.04
Bi2Sr2CuO6	129.63	18.34	26.76	43.78
TlSr2CaCu2O7	76.32	5.21	12.42	18.60

---

Table 3 describes example compositions. Both KIAGO and C-ES yield integer-total compositions, allowing straightforward induction of possible crystal structures. However, SuperDiff and SuperDiff with CG frequently produce non-integer totals, making immediate structural analysis more challenging. For several candidates proposed by KIAGO, we computed the convex-hull distance ΔE_hull using ElemNet. Ca₅Cu₄Sr₅O₁₁ (127.16 K) and MgCa₄Cu₄Ba₃TlO₁₀ (142.90 K) showed ΔE_hull < 0.06 (eV per atom), suggesting possible thermodynamic stability.

Table 3 Samples of proposed superconductors

Method	Samples
KIAGO	Ca4Co3Sr3W3F2As8 (115.65 K)
	Ca5Cu4Sr5O11 (127.16 K)
	MgCa4Cu4Ba3TlO10 (142.90 K)
	Cu6Sr3Pt3B5O7 (87.52 K)
SD	Ni0.99LaO1.01As0.99 (3.65 K)
	Ni0.82Ge0.25La0.97C1.59As0.44Se0.14 (1.23 K)
	Ca0.28Cu1.39Sr2.04Pb0.91Bi1.15O7.03 (76.03 K)
	Ca1.84Sc0.17Cu2.91Ba2.05HgO8.05 (127.46 K)
SD w/ CG	CaCu2.02Sr1.69Y0.41Tl1.04O6.95 (87.78 K)
	Co0.3Ni0.69La0.83Ce0.16O0.94As0.97 (4.85 K)
	La0.6Ce0.43Nd0.15Bi1.03O0.98S2.01 (2.54 K)
	Ni0.9Ge0.11La0.96C0.29O0.87As0.8 (5.96 K)
C-ES	La4Bi4O4S8 (4.61 K)
	CaCu2BaTlCO7 (86.78 K)
	V2Sr4YHfO6As2 (36.65 K)
	La2Hf2Ir2B4C2 (18.46 K)

---

Interestingly, SuperDiff with CG does not necessarily generate higher-T_c compounds than SuperDiff alone. Table 4 shows how T_c changes in guidance and denoising under different weights for guidance. During generation, high guidance weights raise T_c in the guidance step but then revert it in the ILVR and denoising step. We attribute this to the T_c distribution in SuperCon, where low- or moderate-T_c compounds dominate (median: 12.5 K). As a result, extremely high T_c values are treated as noise, prompting the model to restore them to more typical levels. Furthermore, larger weight for guidance cause a stronger mismatch with the training distribution, reducing the fraction of generated compositions that contain fewer than ten elements. This interplay of denoising and guidance likely hampers SuperDiff with CG's ability to reach stable, high-T_c solutions. For the results without ILVR, please refer to Section S.3.

Table 4 Total changes in T_c resulting from guidance, ILVR, and denoising during the 1000 steps in SuperDiff w/ CG. “Guide weight” denotes the weight for guidance. “Denoise ΔT_c”, “ILVR ΔT_c” and “Guide ΔT_c” represent the cumulative change in T_c per step due to denoising, ILVR, or the guidance. “Sum” is the total of these values. “Screening ratio” denotes the ratio of the number of screened samples to the total number of samples

Guide weight w	Denoise ΔTc (K)	ILVR ΔTc (K)	Guide ΔTc (K)	Sum (K)	Screening ratio
—	84.8	37.4	—	122.2	0.13
1.0 × 10^−5	80.2	43.0	0.0	123.2	0.09
1.0 × 10^−4	75.9	46.9	0.4	123.1	0.10
1.0 × 10^−3	79.2	39.8	3.2	122.3	0.08
1.0 × 10^−2	77.1	13.2	33.8	124.1	0.11
1.0 × 10^−1	42.5	−197.1	279.3	124.7	0.12
1.0	−63.5	−1409.6	1611.0	137.9	0.00
1.0 × 10^1	−101.7	−3945.1	4190.5	143.7	0.00
1.0 × 10^2	−42.2	−3746.6	3925.2	136.4	0.00

---

3.5 Elemental substitution

In this section, we implemented elemental substitution to improve T_c. Here we replaced one metal element based on its oxidation state while retaining the rest of the composition. Specifically, we chose a single metal element from an existing superconductor and kept the remaining composition fixed.

We implemented this approach in KIAGO by treating the preserved composition as a fixed vector x_const. We then randomly initialise the substituting element and apply a mask based on its oxidation state. For example, when substituting Y³⁺, we only allow elements having a +3 oxidation state, such as gallium or aluminum. To achieve this, we used a mask that has one value on elements having a +3 oxidation state and set all others to zero. To simplify evaluation, we excluded the preserved elements from the mask. We use Adam optimiser with learning rate of 0.03 for KIAGO. Note that we did not perform conversion to integers on the substituting element, so we set β = 0. By contrast, SuperDiff does not explicitly support elemental substitution, so we approximated it by conditioning the generation process with ILVR.

In addition to the screening described in Section 3.1, we assessed whether the intended elemental substitution was correctly carried out. First, we checked whether the preserved composition remains within 1% of its original ratio. Second, we checked that the total composition of the newly substituted element (or elements) stays within 1% of the original substituted metal's ratio. To simplify evaluation, we excluded the preserved elements from the substituted element candidates. We then evaluated the T_c of compositions that pass both this substitution check and the previous screening.

Tables 5–7 summarize the probability of correct element evaluation, the charge-neutrality evaluation, and the resulting T_c values, respectively. Notably, KIAGO and C-ES achieve 100% correct substitutions (Table 5), indicating that these methods incorporate domain knowledge effectively. Consequently, as shown in Table 6, their proposed materials always satisfy charge neutrality. Moreover, KIAGO demonstrates high search efficiency, yielding the best results in most experiments (Table 7). SuperDiff, however, cannot reliably perform elemental substitution, indicating that generative models like SuperDiff are not well suited when strict domain knowledge must be enforced.

Table 5 Success rate of elemental substitution in proposed materials. We defined a successful elemental substitution as satisfying both of the following criteria: (1) the preserved composition remains within 1% of its original ratio, and (2) the total composition of the newly substituted element (or elements) stays within 1% of the original substituted metal's ratio

Base materials from SuperCon	Substitute target	KIAGO	SD	SD w/ CG	C-ES
CeFeAsF0.2O0.8	Ce^3+	1.00	0.00	0.00	1.00
LaFeAsO	La^3+	1.00	0.01	0.00	1.00
SrFe2As2	Sr^2+	1.00	0.01	0.00	1.00
Bi2CaSr2Cu2O8	Bi^3+	1.00	0.23	0.20	1.00
CeNiC2	Ce^4+	1.00	0.00	0.00	1.00
LaNiC2	La^3+	1.00	0.01	0.01	1.00
MgCoNi3	Co^2+	1.00	0.00	0.00	1.00
RuSr2GdCu2O8	Sr^2+	1.00	0.03	0.03	1.00
RuSr2YCu2O8	Y^3+	1.00	0.03	0.03	1.00
Y2Fe3Si5	Y^3+	1.00	0.00	0.00	1.00
YIrSi	Y^3+	1.00	0.00	0.00	1.00

---

Table 6 Success rate with respect to charge neutrality in proposed materials resulting from elemental substitution

Base materials from SuperCon	Substitute target	KIAGO	SD	SD w/ CG	C-ES
CeFeAsF0.2O0.8	Ce^3+	1.00	0.03	0.02	1.00
LaFeAsO	La^3+	1.00	0.02	0.02	1.00
SrFe2As2	Sr^2+	1.00	0.03	0.05	1.00
Bi2CaSr2Cu2O8	Bi^3+	1.00	0.01	0.01	1.00
CeNiC2	Ce^4+	1.00	0.07	0.06	1.00
LaNiC2	La^3+	1.00	0.03	0.04	1.00
MgCoNi3	Co^2+	1.00	0.71	0.63	1.00
RuSr2GdCu2O8	Sr^2+	1.00	0.05	0.06	1.00
RuSr2YCu2O8	Y^3+	1.00	0.08	0.07	1.00
Y2Fe3Si5	Y^3+	1.00	0.18	0.26	1.00
YIrSi	Y^3+	1.00	0.28	0.48	1.00

---

Table 7 Differences in T_c (K) between the average T_c of the highest top-30 proposed superconductors and the base superconductors in experiments of elemental substitution. After screening 4096 samples, the T_c prediction model was used to calculate T_c. ‘N/A’ indicates that none of samples passed the screening

Base materials from SuperCon	Substitute target	KIAGO	SD	SD w/ CG	C-ES
		Top-30	Top-30	Top-30	Top-30
		ΔTc (K)	ΔTc (K)	ΔTc (K)	ΔTc (K)
CeFeAsF0.2O0.8	Ce^3+	14.17	N/A	N/A	9.96
LaFeAsO	La^3+	33.88	1.24	N/A	31.10
SrFe2As2	Sr^2+	31.54	N/A	N/A	19.25
Bi2CaSr2Cu2O8	Bi^3+	18.72	0.15	−1.11	6.10
CeNiC2	Ce^4+	13.10	N/A	−0.02	4.33
LaNiC2	La^3+	10.53	N/A	N/A	4.90
MgCoNi3	Co^2+	31.66	N/A	0.13	7.23
RuSr2GdCu2O8	Sr^2+	−3.38	−0.23	−0.16	5.64
RuSr2YCu2O8	Y^3+	45.96	−0.89	1.53	37.74
Y2Fe3Si5	Y^3+	5.57	N/A	N/A	1.50
YIrSi	Y^3+	6.09	3.42	N/A	3.86

---

Next, we compare the highest-T_c compounds in the SuperCon dataset that have undergone the same elemental substitution with the compounds proposed by KIAGO. Table 8 shows that, in most element-substitution experiments, KIAGO proposes materials with higher T_c than any element-substituted materials in the SuperCon dataset. This result highlights the potential of our approach to surpass known substitution strategies and discover more promising superconductors.

Table 8 Comparison between materials proposed by KIAGO and the highest-T_c compounds from the SuperCon dataset under the same element-substitution conditions. All T_c values are prediction values by our T_c prediction model. Blue elements indicate the substituted elements

Base materials from SuperCon	Substitute target	Proposed samples	Best in SuperCon
CeFeAsF0.2O0.8 (39.8 K)	Ce^3+
LaFeAsO (13.4 K)	La^3+
SrFe2As2 (17.3 K)	Sr^2+
Bi2CaSr2Cu2O8 (81.0 K)	Bi^3+
CeNiC2 (3.0 K)	Ce^4+
LaNiC2 (2.4 K)	La^3+
MgCoNi3 (7.4 K)	Co^2+
RuSr2GdCu2O8 (33.7 K)	Sr^2+
RuSr2YCu2O8 (34.4 K)	Y^3+
Y2Fe3Si5 (2.3 K)	Y^3+
YIrSi (2.8 K)	Y^3+

---

For several candidates proposed by KIAGO, we computed the convex-hull distance ΔE_hull using ElemNet. Element-substituted derivatives of Y₂Fe₃Si₅ and CeFeAsF_0.2O_0.8—namely Pr_0.3995Gd_0.3859Dy_0.3634Ho_0.361Hf_0.2428Sm_0.2474Fe₃Si₅ (T_c = 5.3 K) and Ag_0.1752Sm_0.6868Tb_0.138FeAsF_0.2O_0.8 (T_c = 51.66 K)—exhibit convex-hull distances of ΔE_hull = 0.02 and 0.00 eV per atom, respectively, indicating potential thermodynamic stability.

In this section, we limit our discussion to single-element substitution. However, our method can also support multi-element substitution. For example, in Ti₂O₄, two Ti⁴⁺ atoms and one O²⁻ atom contribute a total charge of +6. This can be replaced by two X³⁺ atoms, resulting in a composition like X₂O₃. Here, X denotes any element with a +3 oxidation state. Such substitutions are feasible as long as the total charge is preserved, and our oxidation-state-based masking mechanism can accommodate them.

3.6 Proposing novel hydride superconductors

In this section, we focused on proposing novel hydride superconductors (HSC). Many known HSC are binary or ternary systems containing hydrogen and just one or two other elements, with hydrogen comprising a large fraction of the composition. Thus, we constrained KIAGO to compositions that have at least 40% hydrogen to expand the space around existing materials, form binary or ternary compounds, and possess a total atom count of 15 or fewer. HSC are often tested under high pressure, where Pauling's electronegativity rules may not hold. For instance, LaH₁₀ has been experimentally confirmed but fails SMACT-based screening for electronegativity and charge neutrality, because SMACT assumes each element has a single fixed valence. Then, we assumed each atom of the same element could adopt different valences. For example, hydrogen can be both +1 and −1, making LaH₁₀ = {La²⁺, H¹⁻ × 6, H¹⁺ × 4}, which is thus electrically neutral. However, allowing multiple valences can lead to a combinatorial explosion, so we imposed a maximum total of 15 atoms per composition. We used these criteria (charge neutrality under variable valences, ternary or binary composition, and a total of 15 or fewer atoms) as a replacement for SMACT-based screening.

For initialisation for KIAGO, we began with HSC from the SuperCon dataset. With a probability of 0.29, we replaced elements of its composition with different elements chosen according to their occurrence frequencies in SuperCon. We then selected random elements with random compositional ratios (from 0.0 to 0.03) for those elements, normalised the resulting composition, and used it as the initialisation. We also set {N_unit} = {1, 2, …, 15}.

In Table 9, we present the average T_c of the top five proposed hydride superconductors. Compared with other methods, KIAGO efficiently generates hydride superconductors. Table 10 shows the probability of proposing materials that meet specific criteria—namely, having at least 40% hydrogen content, three or fewer elements, and a total atom count of 15 or below. These results indicate that KIAGO not only explores the search space efficiently but also strictly adheres to the specified constraints.

Table 9 Average T_c for the top-5 proposed superconductors

Base materials from SuperCon	KIAGO	SD	SD w/ CG	C-ES
	Top-5	Top-5	Top-5	Top-5
	T c (K)	T c (K)	T c (K)	T c (K)
PdH	4.06	0.00	0.46	2.82
PtH	2.73	0.00	0.44	2.82
LaH10	3.84	0.00	0.00	0.00
H2S	2.97	0.14	0.58	0.00
H4Si	3.11	0.00	0.00	0.00

---

Table 10 Ratio of proposed materials satisfying the following three conditions: (1) hydrogen (H) content is 40% or more, (2) composed of three or fewer elements, and (3) 15 atoms or less

Base materials from SuperCon	KIAGO	SD	SD w/ CG	C-ES
PdH	1.00	0.03	0.04	1.00
PtH	1.00	0.03	0.05	1.00
LaH10	1.00	0.02	0.02	1.00
H2S	1.00	0.04	0.05	1.00
H4Si	1.00	0.03	0.02	1.00

---

Table 11 lists HSC proposed by KIAGO. Notably, KIAGO also proposed materials made of the same elements as those in known compounds from the SuperCon dataset. In addition, it suggested materials that are not in the SuperCon dataset but have been reported in other literature.

Table 11 Candidates of hydride superconductor proposed by KIAGO. The ‘Similar formula in Refs’ and ‘T_c in Refs’ columns show the composition and T_c of superconductors experimentally confirmed or calculated by DFT in other studies, respectively, which are composed of the same elements as the proposed materials

Proposed formula	Predicted Tc (K)	Similar formula in dataset	T c (K) in SuperCon	Similar formula in refs	T c (K) in refs
SiH	0.7	SiH4	17.0	—	—
ZrH	0.5	—	—	ZrH3	6.7^EXP^61
V3H2	1.8	—	—	VH	6.5 ∼ 10.7^DFT^62
ScH	2.8	—	—	ScH2	38^DFT^63

---

4 Limitation

Our method relies heavily on the accuracy of the prediction models. Although our current T_c predictor achieves competitive performance compared with other methods (see Section S.1.3), the predicted T_c values for the proposed materials inevitably contain some error. We provide composition-level estimates (e.g., ElemNet-based ΔE_hull); however, DFT-validated, structure-dependent metrics remain unavailable. ElemNet was trained on compositions with up to seven constituent elements, and its ability to generalise to systems with more elements is inherently limited, making such predictions partially extrapolative. Nevertheless, as demonstrated in high-entropy alloy systems, moderate extrapolation can still yield reasonably accurate results.⁶⁴ Moreover, since the SuperCon dataset lacks pressure information—crucial for hydride superconductors—our model cannot address pressure effects, which could pose another limitation.

Improving the prediction model's accuracy must involve ensemble methods,¹⁴ better model architectures, or enhanced datasets. Importantly, our method does not depend on any specific model architecture. Given the rapid pace of machine-learning advances, more accurate models will likely become available soon, and substituting them into our framework should alleviate current limitations. Additionally, datasets are also improving at a fast rate, offering further opportunities for refinement. Incorporating crystal structure prediction (CSP)^65,66 from composition may mitigate the limitation of missing structural information, while multi-modal learning^7,67 at the fine-tuning stage may enable models to consider essential factors such as pressure.

5 Conclusion

In this paper, we introduced KIAGO, a gradient-based method for proposing high-T_c superconductors that unify domain knowledge with efficient computational strategies. Unlike classifier guidance-based generative models, KIAGO does not require to train additional generative models, making it a more straightforward solution. By initialising the optimisation from promising superconductors, we mitigate the risk of converging to poor local minima—an issue often encountered in gradient-based methods—and achieve higher optimisation efficiency. A key strength of KIAGO lies in its ability to incorporate diverse domain knowledge via masking. We demonstrated this by precisely controlling elemental substitutions and restricting our search to hydride superconductors. These results underscore the adaptability of KIAGO: it not only capitalises on existing knowledge, like traditional doping strategies but also explores a broader chemical space more effectively than previous approaches. Overall, KIAGO paves the way for discovering new materials by exploiting domain knowledge and machine learning's scalability. This synergy has the potential to accelerate advancements in high-T_c superconductivity and beyond, offering a robust framework for rapid and adaptive materials design.

Author contributions

A. F. performed the experiments and drafted the manuscript; A. L. and K. S. contributed to discussions; S. W. supervised the research and provided project administration.

Conflicts of interest

There are no conflicts to declare.

Data availability

The code used to implement the optimisation framework in this study is available at Zenodo: https://doi.org/10.5281/zenodo.17319338, which archives the GitHub repository at https://github.com/AkiraTOSEI/KIAGO. This version corresponds to the release v0.3.0, accessed on 10 October 2025. Trained models for the T_c predictor and formation energy predictor are also provided in this repository. The SuperCon dataset is available at https://mdr.nims.go.jp/collections/5712mb227 and we used version 220808. The ElemNet training data can be obtained from http://cucis.ece.northwestern.edu/projects/DataSets/ElemNet/data.tar.gz, and the COD database can be accessed at https://www.crystallography.net/cod/ and we accessed the COD dataset on March 22, 2023. The Alexandria Materials Database and the Materials Project were accessed on 8 October 2025. Supplementary information: details on predictive-model training and performance, information on SuperDiff with Classifier Guidance (SD w/ CG), and additional experimental results for KIAGO. See DOI: https://doi.org/10.1039/d5dd00250h.

Acknowledgements

The authors gratefully acknowledge support from the Doctoral Student Special Incentives Program, Graduate School of Engineering, The University of Tokyo (SEUT-RA).

Notes and references

1. J. R. Hull, Rep. Prog. Phys., 2003, 66, 1865.
2. D. Uglietti, Supercond. Sci. Technol., 2019, 32, 053001.
3. J. Skakle, Mater. Sci. Eng., R, 1998, 23, 1–40.
4. Y. Yao, C. Song, P. Bao, D. Su, X. Lu, J. Zhu and Y. Wang, J. Appl. Phys., 2004, 95, 3126–3130.
5. S. C. Erwin, L. Zu, M. I. Haftel, A. L. Efros, T. A. Kennedy and D. J. Norris, Nature, 2005, 436, 91–94.
6. R. Terzioglu, G. Aydin, N. Soylu Koc and C. Terzioglu, J. Mater. Sci.: Mater. Electron., 2019, 30, 2265–2277.
7. V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione, S. Curtarolo and I. Takeuchi, npj Comput. Mater., 2018, 4, 29.
8. K. Matsumoto and T. Horide, Appl. Phys. Express, 2019, 12, 073003.
9. S. Zeng, Y. Zhao, G. Li, R. Wang, X. Wang and J. Ni, npj Comput. Mater., 2019, 5, 84.
10. Y. Dan, R. Dong, Z. Cao, X. Li, C. Niu, S. Li and J. Hu, IEEE Access, 2020, 8, 57868–57878.
11. T. D. Le, R. Noumeir, H. L. Quach, J. H. Kim, J. H. Kim and H. M. Kim, IEEE Trans. Appl. Supercond., 2020, 30, 1–5.
12. T. Konno, H. Kurokawa, F. Nabeshima, Y. Sakishita, R. Ogawa, I. Hosako and A. Maeda, Phys. Rev. B, 2021, 103, 014509.
13. J. Zhang, Z. Zhu, X.-D. Xiang, K. Zhang, S. Huang, C. Zhong, H.-J. Qiu, K. Hu and X. Lin, J. Phys. Chem. C, 2022, 126, 8922–8927.
14. A. Taheri, H. Ebrahimnezhad and M. H. Sedaaghi, Mater. Today Commun., 2022, 33, 104743.
15. J. Zhang, K. Zhang, S. Xu, Y. Li, C. Zhong, M. Zhao, H.-J. Qiu, M. Qin, X.-D. Xiang and K. Hu, et al. , J. Energy Chem., 2023, 78, 232–239.
16. N. I. for Materials Science, SuperCon, version 220808, https://mdr.nims.go.jp/collections/5712mb227.
17. C. Pereti, K. Bernot, T. Guizouarn, F. Laufek, A. Vymazalová, L. Bindi, R. Sessoli and D. Fanelli, npj Comput. Mater., 2023, 9, 71.
18. E. A. Pogue, A. New, K. McElroy, N. Q. Le, M. J. Pekala, I. McCue, E. Gienger, J. Domenico, E. Hedrick and T. M. McQueen, et al. , npj Comput. Mater., 2023, 9, 181.
19. D. Kaplan, A. Zheng, J. Blawat, R. Jin, R. J. Cava, V. Oudovenko, G. Kotliar, A. M. Sengupta and W. Xie, Eur. Phys. J. Plus, 2025, 140, 58.
20. T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, arXiv, 2021, preprint, arXiv:2110.06197,  DOI:10.48550/arXiv.2110.06197.
21. Z. Ren, S. I. P. Tian, J. Noh, F. Oviedo, G. Xing, J. Li, Q. Liang, R. Zhu, A. G. Aberle and S. Sun, et al. , Matter, 2022, 5, 314–335.
22. C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, S. Shysheya, J. Crabbé, L. Sun and J. Smith, et al., arXiv, 2023, preprint, arXiv:2312.03687,  DOI:10.48550/arXiv.2312.03687.
23. Z. Yang, W. Ye, X. Lei, D. Schweigert, H.-K. Kwon and A. Khajeh, npj Comput. Mater., 2024, 10, 296.
24. C. Zhong, J. Zhang, X. Lu, K. Zhang, J. Liu, K. Hu, J. Chen and X. Lin, ACS Appl. Mater. Interfaces, 2023, 15, 30029–30038.
25. E. Kim and S. Dordevic, J. Phys.: Condens. Matter, 2023, 36, 025702.
26. D. Wines, T. Xie and K. Choudhary, J. Phys. Chem. Lett., 2023, 14, 6630–6638.
27. S. Yuan and S. Dordevic, Sci. Rep., 2024, 14, 10275.
28. J. Ho, A. Jain and P. Abbeel, Adv. Neural Inf. Process. Syst., 2020, 33, 6840–6851.
29. F.-A. Croitoru, V. Hondru, R. T. Ionescu and M. Shah, IEEE Trans. Pattern Anal. Mach. Intell., 2023, 45, 10850–10869.
30. J. Choi, S. Kim, Y. Jeong, Y. Gwon and S. Yoon, arXiv, 2021, preprint, arXiv:2108.02938,  DOI:10.48550/arXiv.2108.02938.
31. A. Brock, J. Donahue and K. Simonyan, arXiv, 2018, preprint, arXiv:1809.11096,  DOI:10.48550/arXiv.1809.11096.
32. A. Bansal, H.-M. Chu, A. Schwarzschild, S. Sengupta, M. Goldblum, J. Geiping and T. Goldstein, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, 2023, pp. 843–852.
33. P. Dhariwal and A. Nichol, Adv. Neural Inf. Process. Syst., 2021, 34, 8780–8794.
34. J. Ho and T. Salimans, arXiv, 2022, preprint, arXiv:2207.12598,  DOI:10.48550/arXiv.2207.12598.
35. S. Ren, W. Padilla and J. Malof, Adv. Neural Inf. Process. Syst., 2020, 33, 38–48.
36. K. R. Allen, T. Lopez-Guevara, K. Stachenfeld, A. Sanchez-Gonzalez, P. Battaglia, J. Hamrick and T. Pfaff, arXiv, 2022, preprint, arXiv:2202.00728,  DOI:10.48550/arXiv.2202.00728.
37. R. Hwang, J. Y. Lee, J. Y. Shin and H. J. Hwang, Proceedings of the AAAI Conference on Artificial Intelligence, 2022, pp. 4504–4512.
38. A. Fujii, H. Tsunashima, Y. Fukuhara, K. Shimizu and S. Watanabe, arXiv, 2023, preprint, arXiv:2304.13860,  DOI:10.48550/arXiv.2304.13860.
39. A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga and A. Lerer, NIPS 2017 Workshop Autodiff, 2017.
40. D. P. Kingma and J. Ba, arXiv, 2014, preprint, arXiv:1412.6980,  DOI:10.48550/arXiv.1412.6980.
41. K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
42. Crystallography Open Database (COD), https://www.crystallography.net/cod/, accessed: March 22, 2023.
43. A. Vaitkus, A. Merkys, T. Sander, M. Quirós, P. A. Thiessen, E. E. Bolton and S. Gražulis, J. Cheminf., 2023, 15, 123.
44. A. Merkys, A. Vaitkus, A. Grybauskas, A. Konovalovas, M. Quirós and S. Gražulis, J. Cheminf., 2023, 15, 25.
45. A. Vaitkus, A. Merkys and S. Gražulis, Appl. Crystallogr., 2021, 54, 661–672.
46. M. Quirós, S. Gražulis, S. Girdzijauskaitė, A. Merkys and A. Vaitkus, J. Cheminf., 2018, 10, 23.
47. A. Merkys, A. Vaitkus, J. Butkus, M. Okulič-Kazarinas, V. Kairys and S. Gražulis, Appl. Crystallogr., 2016, 49, 292–301.
48. S. Gražulis, A. Merkys, A. Vaitkus and M. Okulič-Kazarinas, Appl. Crystallogr., 2015, 48, 85–91.
49. S. Gražulis, A. Daškevič, A. Merkys, D. Chateigner, L. Lutterotti, M. Quiros, N. R. Serebryanaya, P. Moeck, R. T. Downs and A. Le Bail, Nucleic Acids Res., 2012, 40, D420–D427.
50. S. Gražulis, D. Chateigner, R. T. Downs, A. Yokochi, M. Quirós, L. Lutterotti, E. Manakova, J. Butkus, P. Moeck and A. Le Bail, Appl. Crystallogr., 2009, 42, 726–729.
51. R. T. Downs and M. Hall-Wallace, Am. Mineral., 2003, 88, 247–250.
52. D. Jha, L. Ward, A. Paul, W.-k. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593.
53. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/, Software available from tensorflow.org.
54. D. W. Davies, K. T. Butler, A. J. Jackson, J. M. Skelton, K. Morita and A. Walsh, J. Open Source Softw., 2019, 4, 1361.
55. M. K. Horton, P. Huck, R. X. Yang, J. M. Munro, S. Dwaraknath, A. M. Ganose, R. S. Kingsbury, M. Wen, J. X. Shen and T. S. Mathis, et al. , Nat. Mater., 2025, 1–11.
56. Alexandria Materials Database, https://alexandria.icams.rub.de/, accessed: September 28, 2025.
57. J. Schmidt, L. Pettersson, C. Verdozzi, S. Botti and M. A. Marques, Sci. Adv., 2021, 7, eabi7948.
58. J. Schmidt, N. Hoffmann, H.-C. Wang, P. Borlido, P. J. Carriço, T. F. Cerqueira, S. Botti and M. A. Marques, Adv. Mater., 2023, 35, 2210788.
59. H.-C. Wang, J. Schmidt, M. A. Marques, L. Wirtz and A. H. Romero, 2D Materials, 2023, 10, 035007.
60. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
61. H. Xie, W. Zhang, D. Duan, X. Huang, Y. Huang, H. Song, X. Feng, Y. Yao, C. J. Pickard and T. Cui, J. Phys. Chem. Lett., 2020, 11, 646–651.
62. Q. Zhuang, X. Jin, Q. Lv, Y. Li, Z. Shao, Z. Liu, X. Li, H. Zhang, X. Meng, K. Bao and T. Cui, Phys. Chem. Chem. Phys., 2017, 19, 26280–26284.
63. Y.-K. Wei, J.-N. Yuan, F. I. Khan, G.-F. Ji, Z.-W. Gu and D.-Q. Wei, RSC Adv., 2016, 6, 81534–81541.
64. K. Miyamoto, K. Shimizu, A. K. A. Lu and S. Watanabe, e-J. Surf. Sci. Nanotechnol., 2025, 23, 188–192.
65. S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, ACS Cent. Sci., 2020, 6, 1412–1420.
66. R. Jiao, W. Huang, P. Lin, J. Han, P. Chen, Y. Lu and Y. Liu, Adv. Neural Inf. Process. Syst., 2023, 36, 17464–17497.
67. C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572.

---