Active learning path-dependent properties using a cloud-based materials acceleration platform

Abstract

Solid state materials are central to many modern technologies in which a given material may be exposed to a variety of environments. The material properties often vary with the sequence of environments in an irreversible manner, resulting in a quintessential path-dependency in experimental observables. While sequential learning techniques have been effectively deployed for accelerating learning of state properties of materials, they often use a consistent environment path in all experiments. To elevate such techniques for making optimal decisions in experimental investigations of path-dependent properties, we introduce an iterated expected information gain acquisition function that optimizes over entire experimental trajectories. This approach is implemented within a cloud-based Materials Acceleration Platform architecture utilizing an event-driven stateful broker coupled with remote HELAO (Hierarchical Experimental Laboratory Automation and Orchestration) instances and an AI science manager. The platform's efficacy was demonstrated through a case study optimizing multi-step spectro-electrochemical experiments to identify optically stable potential windows in (Co–Ni–Sb)O_z metal oxides. The system successfully integrated AI-driven experiment design, remote laboratory automation, and cloud-based data infrastructure, validating the platform's capability for managing complex, adaptive, path-dependent workflows in materials discovery.

---

1 Introduction

The acceleration of experiments involving state-changing materials, such as electrochemical stability assessments or corrosion studies, is fundamentally linked to experimental provenance—the concept that a material's current properties are significantly influenced by its history of processing and measurement. Prominent examples include the optimization of multi-step charging protocols to preserve battery capacity¹ and the development of break-in procedures to enhance the efficiency and durability of proton exchange membrane fuel cells (PEMFCs).^2,3 In such scenarios, the specific sequence and duration of applied conditions (e.g., charging rates, potentials) define unique paths for conditioning materials into desired states. For PEMFCs, the machine learning-based diagnosis of break-in processes remains underdeveloped,⁴ given protocols potentially varying across wide ranges of temperature, humidity, current density, and potential, in addition to the number and duration of steps involved.

The substantial cost associated with measurement time, coupled with the general scarcity of experimental data⁵ for such path-dependent phenomena, positions sequential learning techniques as highly suitable for the efficient exploration of these complex parameter spaces. While active experimental design has been pursued for many settings without path dependency,^6–8 effective experiment selection in our setting must explicitly account for the path-dependence of predicted properties; the outcome of a future measurement is contingent not only on the current state but also on the sequence of preceding observations. To address this challenge, acquisition strategies must consider the influence of experimental history on both the observations themselves and the accessibility of subsequent data points.

We introduce an acquisition function termed iterated expected information gain (iEIG), extending the classical EIG concept.^9–11 This function evaluates the anticipated reduction in uncertainty over a trajectory of potential observations. It explicitly incorporates the compounding effect of early experimental decisions on the informativeness and feasibility of subsequent measurements, which is particularly relevant when initial observations constrain or enable access to parts of an experimental path. Consequently, the total information gain accrued over a path becomes a more pertinent objective than its pointwise equivalent.

This active learning strategy is deployed within a cloud-based Materials Acceleration Platform (MAP), i.e., a self-driving laboratory.^12–14 While early distributed MAPs demonstrated remote control,¹⁵ and cloud-server management for shared hardware,¹⁶ recent architectures utilize “stateless” brokers¹⁷ to integrate diverse resources across institutions. Although stateless designs offer resilience, event-driven “stateful” brokers¹⁸ provide a verifiable event log essential for data provenance, aligning with modern cloud data pipelines (e.g., AWS, Azure, GCP) that inherently support scalability and reliability. Our implementation couples a stateful, event-driven cloud broker with remote instances of the Hierarchical Experimental Laboratory Automation and Orchestration (HELAO) system¹⁹ and an AI science manager operating in a closed loop. The platform's utility is demonstrated via a case study involving the optimization of multi-step spectro-electrochemical experiments to identify optically stable potential windows in (Co–Ni–Sb)O_z metal oxides.

2 Methodology

2.1 Materials synthesis and characterization

A pseudo-ternary materials system comprising Co–Ni–Sb oxides was selected based on its diverse Pourbaix stability domains calculated via the Materials Project²⁰ (Fig. S2). Material libraries were synthesized on FTO-coated glass substrates using reactive RF magnetron co-sputtering from elemental metal targets (Co, Ni, Sb) in a partial pressure environment of 4.8 mTorr Ar and 1.2 mTorr O₂. Following deposition, the libraries underwent annealing at 610 °C for 1 hour in air. Compositions and film thicknesses across each library were characterized using X-ray fluorescence (XRF) on a uniformly spaced grid of 296 points with an EDAX Orbis MicroXRF system. To access a broad range of composition with moderate variation in thickness, only data points with thicknesses within two standard deviations of the mean pseudo-ternary oxide thickness (490 nm ± 40 nm) were included in the study. Pseudo-binary (Co–Sb, Ni–Sb, Ni–Co) oxide libraries contained an average of 60 points within this thickness window, while pseudo-ternary (Co–Ni–Sb) oxide libraries contained an average of 260 points.

2.2 Spectro-electrochemical measurements

Operando spectro-electrochemical measurements were performed utilizing a modified scanning electrochemical cell²¹ shown in Fig. 1, featuring a 1.8 mm diameter measurement area. The system incorporated automated components for high-throughput operation, including an automated z-stage (Thorlabs MLJ250), counter and working electrode chamber vent valves (Bio-Chem 100T2NC12), and peristaltic pumps (Masterflex C/L) for rapid filling and controlled electrolyte flow. A leak-free Ag/AgCl reference electrode (Innovative Instruments LF1-45) ensured stable potential measurements. Experiments were conducted in two electrolytes: 0.1 M H₂SO₄ (pH 1) and 0.2 M K₂HPO₄/KH₂PO₄ buffer (pH 7), both containing 0.25 M Na₂SO₄ as a supporting electrolyte.

Fig. 1 A planar optical flow cell derived from the scanning droplet cell design to accommodate gasket-sealed operation. Electrolyte is pulled into the cell through the primary flow path (“Electrolyte In” to “Electrolyte Out”). Red arrows show the secondary low-flow path which establishes contact with a membrane separating working and counter electrode chambers. An optical fiber is terminated at a gasket-sealed quartz window above the working electrode chamber.

Operationally, the working electrode chamber was located beneath a quartz window positioned below the fiber optic terminal. The entire cell assembly was mounted to a fixed arm and kept at constant elevation. Motorized X-, Y-, and Z-stages control the translation and height of the sample composition library beneath the cell assembly. During operation, the composition library was translated to a given sample location then raised to engage the cell assembly. The assembly was gasket-sealed around the working electrode chamber aperture, then filled with electrolyte. Electrolyte was pulled into the working chamber and out through two flow paths: one high-flow path directly across the working electrode chamber, and a low-flow path that established liquid contact with the counter electrode membrane or separator frit. An independent flow path and peristaltic pump was used for the counter electrode chamber. For every sample composition, electrolyte flow was constant throughout the series of spectro-electrochemical measurements, then stopped and both working and counter chambers drained at a higher pump rate prior to disengaging the cell assembly. When switching between electrolytes, the cell assembly was purged with the working electrolyte at ∼2 mL per minute for three minutes, enough for 30 changeovers of the ∼200 μL working electrode chamber volume. Human interaction was required in replacing the electrolyte reservoir and mounting the binary and ternary composition libraries to the motorized stage. A connectorized white light LED (Doric Lenses LEDC2_385/W35) was used as the illumination source. An integrating sphere (Spectral Products AT-IS-1) was positioned about 2 m below the bottom side of the composition library and connected to a spectrometer (Spectral Products SM303) for transmission measurements.

An optical “instability” metric, β(V), was defined to quantify spectral changes during chronoamperometry (CA) relative to an initial open-circuit potential (OCV) measurement. Specifically, β(V) represents the mean relative change in absorbance, ΔA(V, λ) averaged over the wavelength range 430–700 nm during the final 5 seconds of each 85-second CA step,

where the relative change in absorbance is defined as:
here, I(V,λ) is the transmitted intensity at potential V and wavelength λ, I₀(λ) is the initial intensity measured at OCV, and n is the number of spectrometer channels (Spectral Products SM303) within the 430–700 nm range determined by the white LED source (Doric LEDC2_450/white). This metric quantifies relative spectral changes without distinguishing between reversible and irreversible processes.

For each catalyst composition and pH, a sequence of eleven 85-second CA steps was executed at potentials evenly spaced between 0.0 V and 2.0 V vs. RHE. Each CA step was preceded by a 5-second OCV measurement. The starting potential V₀ and the initial potential sweep direction for the sequence were determined by the active learning algorithm. The potential was stepped systematically in the chosen direction until a limit (0.0 V or 2.0 V vs. RHE) was reached, after which the direction reversed to scan back towards the opposite limit, without revisiting intermediate potentials. The initial potential step was measured only once during the sequence. Fig. 2 depicts an example measurement sequence.

Fig. 2 An example measurement sequence request made by the AI science manager (active learning algorithm) to the automated instrumentation (HELAO) using the cloud-deployed data requests API. We illustrate the eleven 85-second CA steps at evenly spaced potentials (column 1), the transmitted intensity at a given potential (column 2), and the relative changes in absorbance (column 3), which are used in eqn (1).

2.3 Active learning framework

The AI science manager aimed to identify optically stable potential windows within the pseudo-ternary (Co–Ni–Sb)O_z composition space. Eight material libraries were investigated in distinct closed-loop active learning runs. The AI manager was provided the parameter space encompassing acquirable compositions, selectable starting potentials V₀, and initial potential step directions. The initial surrogate model was seeded using prior data from Ni–Co (pH 1: 52 points; pH 7: 50 points) and Co–Sb (pH 1: 61 points) pseudo-binary oxide systems.

The probabilistic surrogate model characterizes the optical instability metric as an unknown function where X is the 5-dimensional design space and the co-domain consists of optical instability metric measurements, real values in . The design space X consists of five-dimensional elements, , including: fraction of Co, fraction of Ni, pH value, potential V, and initial step direction. The composition dimension molar fraction of Sb is constrained by fraction of Sb = 1 – (fraction of Co + fraction of Ni). Each query of the black-box function f at input design point x yields a noisy observation β of the optical instability metric f(x), written as β ∼ f(x) + ε, where 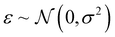represents Gaussian noise (i.e., a perturbation of the deterministic metric).

A Gaussian process (GP) Bayesian model models this black-box function. Given a dataset of T optical instability metric observations from T design points, denoted as D = {(x₁, β₁), …, (x_T, β_T)}, the GP posterior predictive distribution for an input x is written as p(β|x, D), with variance denoted as Var[p(β∣x,D)]. To make predictions, we can use the mean of our optical instability forecast, (where denotes an expectation).

The acquisition function maximizes the expected information gain (EIG) about f for any design point x ∈ X. For homoscedastic noise and a Gaussian posterior, maximizing EIG is equivalent to maximizing the posterior predictive variance:

Intuitively, we want to modify the EIG to produce an acquisition function that selects design points which are both highly informative and unlikely to terminate prematurely due to instabilities. In practice, this means the acquisition function should favor compositions, starting potentials, and sweep directions that maximize expected reduction in model uncertainty while extending the number of stable steps in each scan. To incorporate a sequence of potential steps V until an instability, we employ an “expected-EIG acquisition function” using the iterated expected information gain. For a tuple x̄ representing a potential scan (defined by composition, pH value, starting potential V₀, and potential scan direction V_d), the iterated-EIG (iEIG) is:

where we assume that a scan consists of m steps, i = 1, …, m, and we define to be a binary variable indicating the stability of potential V_i within a given scan x̄ ( for stable, for unstable). This acquisition function is approximated as follows: first, for i = 1, …, m, each term in the sum (in eqn (3)) is computed similar to the vanilla EIG expression, where

EIG_f(x̄,V_i) = EIG_f(x) ∝ log(Var[p(β|x,D)]), (4)

i.e., the log variance of the posterior predictive distribution at the input x corresponding to potential V_i. Second, for a given scan x̄, over each i = 1, …, m, the expression is approximated via posterior sampling (similar to Thompson sampling^22,23), where we draw a posterior sample from our model and record the sequence of stable potential probabilities (starting from potental V₁ and proceeding to potential V_i−1). Note that, once a stability of zero (s_i = 0) has been observed, then the stability indicator variable remains at zero for the remainer of the scan (i.e., , for all i′ > i). Inuitively, the iEIG_f(x̄) acquisition function value is calculated from a sum of the EIG_f(x) values multiplied by its probability of stability, taken over the potential scan.

We use the iEIG acquisition function to guide sequential experiments, as it balances expected information gain against the risk of path-dependent instabilities that can prematurely terminate measurement sequences—e.g., environment-induced sample destruction. The iEIG acquisition function explicitly balances these two considerations: it prioritizes queries that are expected to yield the largest reduction in model uncertainty (as in the classical EIG formulation), while simultaneously incorporating the probability of encountering instabilities along a potential scan. This “iterated” extension is essential in our experimental setup, where each query corresponds to a trajectory of sequential measurements rather than an isolated point.

In Fig. 3, we illustrate the iEIG acquisition function for a single composition and pH value, and compare it against a standard EIG acquisition function over the same scanning range. Note that both scanning up and scanning down lead to path-dependent measurements—i.e., can run into an instability—but our acquisition function aims to choose a design point (e.g., composition, initial voltage, scanning direction) that is expected to be both informative and take a larger number of measurements before hitting such an instability. In Fig. 4, we illustrate the acquisition optimization process, showing the queried value over the course of three time steps.

Fig. 3 Illustration of the iEIG acquisition function, on a single composition and pH value, at a single time step. We show the standard EIG acquisition function (top), the iEIG acquisition function over a downwards scan (middle), and the iEIG acquisition function over an upwards scan (bottom), each over a range of potential, or starting potential, values. Vertical dotted colored lines denote the locations of the acquisition function maximizers for the three acquisition functions, with maximum values shown as horizontal dashed lines. The iEIG acquisition function selects the maximizer over the bottom two axes (i.e., over both the “scanning down” and “scanning up” directions).

Fig. 4 Illustration of the iEIG acquisition function, over three time steps (t = 5, 6, 7) on one plate. We show the previously measured observations (red squares), the acquisition function optimizer over the composition space (gold star), and the acquisition function values over the ternary composition space (blue shaded circles). For each composition in this figure, the maximizer of the iEIG acquisition function (over the full set of starting potentials) is shown. Note that in this figure, this maximizer is only shown over the ternary composition space.

3 Data infrastructure

The platform's data infrastructure utilized two primary AWS DynamoDB tables: a ‘lab table’ for tracking completed experiments, parameters, and associated data, and a ‘data requests table’ for managing the status of active learning campaigns.

Upon completion of an experiment and subsequent data upload to AWS S3 by HELAO, an AWS EventBridge trigger invoked an AWS Lambda function. This function inserted metadata—including the S3 location of raw data and experiment details—into the lab DynamoDB table, adhering to the ESAMP (Event-Sourced Architecture for Materials Provenance) paradigm.²⁴ A second Lambda function initiated data processing routines, generating performance metrics. These metrics were then associated with corresponding experiment requests within the data requests database.

The machine learning model iteratively updated its predictions based on newly available data. A Python client interfaced with the data requests API to retrieve processed data, then a Python script retrained the model, and computed acquisition scores (iterated-EIG values) for unevaluated design points. These scores were subsequently stored back into the data requests database. The HELAO orchestrator queried this database, identified the highest-priority acquisition score, and executed the corresponding spectro-electrochemical experiment sequence. Each entry in the data requests database contained a unique ID, experiment input parameters (composition, pH, V₀, V_d), the calculated acquisition score, and ultimately, the resulting performance metrics upon experiment completion. This closed-loop system enabled dynamic prioritization and execution of experiments driven by the AI model. Fig. 5 provides a schematic overview of the interactions between instrument orchestration (HELAO), data orchestration (cloud services), and AI modeling entities.

Fig. 5 Overview diagram showing the cloud-deployed Data Orchestration module (middle), connecting the Instrument Orchestration module (left) and AI Science Manager (right). The Data Orchestration module interacts with the AI Science Manager to handle acquisition requests and data access, sends measurement requests to the Instrument Orchestration module, stores corresponding instrument measurements, and carries out analysis and logging steps.

4 Discussion

As the experimental campaign required hundreds of hours of automated measurements, we had the resources to conduct only a single run of experimentation, for which we applied our proposed method. In lieu of direct comparisons against alternative baselines—such as random search (RS) or Bayesian experimental design with expected information gain (EIG)—we evaluated our approach using online metrics that assessed the quality of the probabilistic model and acquisition strategy, providing evidence that the method was functioning as intended. We also note that common baselines such as Bayesian optimization (BO), as well as RS and EIG, are not well suited to this setting. Our aim was to learn the full function landscape rather than identify a single optimum, which makes BO less suitable as it tends to concentrate sampling around candidate extrema. RS and EIG, though exploratory, do not account for path dependence and therefore often produce unstable trajectories that degrade model quality. Consequently, to evaluate the proposed iEIG method, we defined performance metrics to validate its ability to efficiently learn the path-dependent landscape.

Evaluating the performance of the online experimental procedure involves assessing both the probabilistic surrogate model p(β∣x, D) and the experimental design efficacy. This evaluation is complex due to the unavailability of the true underlying function f(x) and the corruption of measurements following instability events during potential scans of V, limiting ground truth access to a subset of observed measurements.

To assess the quality of our surrogate model, we utilize two distinct approaches. The first approach involves evaluating the error of the probabilistic surrogate model throughout the course of the experiments. Specifically, we compare the predicted value of a given measurement before a query is performed with the true measurement observed during experimentation. Recall that our Gaussian process model predicts the mean of our optical instability forecast, , which is then compared against a noisy draw of the ground truth optical instability measurement β ∼ f(x) + ε. Therefore, we anticipate that there will always be a lower bound on the possible error, owing to aleatoric uncertainty.

This type of error metric has been used in prior online experimentation studies,^8,14,25 and it can be computed online during the course of the experiment without the need to wait until the conclusion of the experiment or rely on synthetic experimental setups.

In Fig. 6, we show the results of this error metric over the course of our eight composition libraries. The first six experimental scenarios involve binary combinations of (Co–Ni, Co–Sb, and Ni–Sb) oxides, while the final two experimental scenarios involve ternary (Co–Ni–Sb) oxide combinations. Specifically, we plot the absolute error,

where β_t is the observed optical instability metric for a given queried input point in our experiment, x_t. It is worth noting that our model is trained across all eight scenarios, with the input points x_t ∈ X (fraction of Co, fraction of Ni, fraction of Sb, pH value, and potential V) being consistent across these eight different experimental settings.

Fig. 6 Absolute error of model predictions on each subsequent query, over all experiments. Top: for each plate, the subset of experimental compositions within the full set of ternary combinations are illustrated. Bottom: the absolute error, as defined in eqn (5), is shown for each query (excluding instabilities) on each plate.

Several interesting behaviors emerge as we examine the results over the course of the training. In general, we observe a decrease in error as additional measurements are acquired for a given composition space. This trend is relatively consistent across all experiments, and suggests that the model improves as it gains more observational data. For example, the elevated error observed in the first Ni–Co plate reflects its position as the very first experiment in the sequence, when the model had little prior data. More generally, early experiments begin with higher error that decreases as observations accumulate, with brief increases only when the design space expands substantially (e.g., from binary to ternary systems).

In our second approach, we record an error metric that cannot be computed online during the experiments, but can be computed after the experiments are finished. This approach still adheres to our constraints, as it avoids using corrupted measurements that occur after encountering an instability. In this approach, we take a held-out set of data, denoted D_k, from the full ternary (Co–Ni–Sb) oxide composition space, where we have ground truth measurements from the end of the experimental regime. This held-out dataset serves as a consistent reference set with which we can estimate the error of our model over the course of the full experiment.

In this approach, we compute the mean absolute error over predictions on our held-out set, defined as

where the held-out data D_k = {(x_i,β_i)}_i=1k consists of k input points x_i with corresponding true measurements β_i.

We show the results of this metric over the course of all eight experimental scenarios in Fig. 7. In addition to evaluating this metric on a common held-out dataset from the full ternary (Ni–Co–Sb) oxide composition space (solid lines), we also compute it on plate-specific held-out datasets for each experimental plate (dashed lines). The plate-specific held-out datasets reveal how model accuracy improves during each set of plate experiments, while the common dataset provides a consistent benchmark across plates and more directly reflects the objective of learning unseen compositions—e.g., in ternary space. Together, these two evaluations distinguish between within-plate learning dynamics and cross-plate generalization.

Fig. 7 Mean absolute error of model predictions on fixed held-out datasets given measurements on the ternary space, shown over all experiments. Top: for each plate, the subset of experimental compositions within the full set of ternary combinations are illustrated. Bottom: the solid lines depict the mean absolute error, as defined in eqn (6), on a common held-out dataset derived from the final ternary plate, and the dashed lines depict the mean absolute error on a plate-specific held-out dataset, for a sequence of queries (excluding instabilities) from each plate. Note that, for the final ternary plate, the solid and dashed lines are equivalent (as the plate-specific dataset is equal to the held-out dataset) and thus only one line is shown.

In general, we observe that the held-out error decreases smoothly as the experiment progresses, reflecting the continual improvement of the model as more data points are observed. The only exception to this smooth decrease occurs in the first Ni–Sb binary experiment and the first ternary-combination experiment, where a temporary increase in error was observed. Notably, in the final ternary experiment, we see a large decrease in error. This is expected, as the common held-out set (solid lines in Fig. 7) was sourced from a ternary composition space with a similar pH value.

Overall, these findings demonstrate the robustness of our probabilistic surrogate model and experimental design procedure, as well as the ability of the model to adapt to the challenges posed by the experimental environment. The consistent reduction in error, especially following space expansion and brief anomalies, supports the validity of the active learning approach in guiding the experimental process effectively.

The cloud-based active learning platform successfully orchestrated the spectro-electrochemical stability campaign, acquiring 9755 CA measurements across 887 unique composition-pH combinations over 11 days. The platform demonstrated robust integration of the AI science manager, HELAO orchestrator, cloud data infrastructure, and remote hardware. Experiment selection was efficiently guided by the iterated-EIG acquisition function, prioritizing informative measurements based on model uncertainty and stability predictions. The optical instability metric employed does not account for irreversible spectral changes. To date, the Materials Project Pourbaix application^20,26 provides the largest repository of aqueous electrochemistry data, where Pourbaix energetics are derived from the thermodynamics of dissolved molecular species and bulk solid state materials, without consideration of the electrode–electrolyte interface. Given the lack of kinetic passivation in the calculations, it is interesting to consider the nature of the relationship between the optical instability metric and the Pourbaix energetics. As we show in the SI, these data are poorly correlated, with no apparent predictability of the optical instability results based on the computational data, highlighting the critical role of experimentation in mapping the electrochemical behavior of solid state materials.

5 Conclusion

This work presents a cloud-based, state-tracking broker architecture successfully managing distributed MAPs. It integrates remote laboratory automation via HELAO, AI-driven active learning using a novel iterated-EIG acquisition function suitable for path-dependent properties, and event-driven data management leveraging commercial cloud services. The platform enables automated, closed-loop optimization of experiments, demonstrated by accelerating the exploration of optical stability in (Co–Ni–Sb)O_z metal oxides. While the specific optical metric used in the case study showed limitations in correlating with thermodynamic Pourbaix stability for the (Co–Ni–Sb)O_z system, the campaign successfully validated the platform's core capability to manage complex, adaptive workflows across distributed components, including handling path-dependent experimental sequences. This architecture advances the development of interconnected, self-driving laboratories poised to address complex materials discovery challenges.

Glossary

AWS – Amazon Web Services, Inc. is a subsidiary of Amazon that provides on-demand cloud computing platforms and APIs to individuals, companies, and governments, on a metered, pay-as-you-go basis. Clients will often use this in combination with autoscaling.

EventBridge – Amazon EventBridge is a serverless event bus that makes it easy to connect applications together using data from your own applications.

DynamoDB – Amazon DynamoDB is a managed NoSQL database service provided by Amazon Web Services (AWS). It supports key-value and document data structures and is designed to handle a wide range of applications requiring scalability and performance.

S3 – Amazon Simple Storage Service (S3) is a service offered by Amazon Web Services (AWS) that provides object storage through a web service interface. Amazon S3 uses the same scalable storage infrastructure that Amazon (https://amazon.com) uses to run its e-commerce network.

HELAO – Hierarchical Experimental Laboratory Automation and Orchestration, an open-source automation and orchestration software which facilitates parallel and distributed operation of devices and instruments through an interconnected network of web services deployed via FastAPI.

ESAMP – An event-sourced architecture for materials provenance management and application to accelerated materials discovery.

Conflicts of interest

Modelyst LLC implements custom data management systems in a professional context. John M. Gregoire is presently employed by Lila Sciences, a company engaged in AI for materials science.

Data availability

The laboratory instrument orchestration code can be found at the https://github.com/High-Throughput-Experimentation/helao-async/tree/683a3b39e5884ec6729f299227805fbc75ad92f6 repository. The model and acquisition function code can be found at the https://github.com/al-path-dependent/al-path-dependent repository. The data orchestration code can be found at the https://github.com/modelyst/CLOMAP-data-orchestration repository. Optical and electrochemical measurement data generated from the closed-loop campaign is available at https://doi.org/10.22002/qrkev-fyr45.

Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00325c.

Acknowledgements

This work was primarily supported by the Toyota Research Institute, and also based on infrastructure provided by the Liquid Sunlight Alliance, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Fuels from Sunlight Hub under Award DE-SC0021266. The authors acknowledge Benjamin Moss for providing guidance on the spectroelectrochemical measurement protocol and interpretation of data. Generative AI was used in the form of Google's Gemini 2.5 large language model which was applied to the final draft of this manuscript to clarify and unify the writing styles across separate author contributions.

References

1. P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins, Z. Yang, P. K. Herring, M. Aykol, S. J. Harris, R. D. Braatz, S. Ermon and W. C. Chueh, Nature, 2020, 578, 397–402.
2. F. A. de Bruijn, V. Dam and G. Janssen, Fuel cells, 2008, 8, 3–22.
3. J. Zhao and X. Li, Energy Convers. Manage., 2019, 199, 112022.
4. F. Van Der Linden, E. Pahon, S. Morando and D. Bouquain, J. Power Sources, 2023, 575, 233168.
5. M. Aykol, P. Herring and A. Anapolsky, Nat. Rev. Mater., 2020, 5, 725–727.
6. A. Wang, H. Liang, A. McDannald, I. Takeuchi and A. G. Kusne, Oxford Open Mater. Sci., 2022, 2, itac006.
7. A. G. Kusne, A. McDannald and B. DeCost, Digital Discovery, 2024, 3, 2211–2225.
8. K. Tran, W. Neiswanger, K. Broderick, E. Xing, J. Schneider and Z. W. Ulissi, J. Chem. Phys., 2021, 154 DOI:10.1063/5.0044989.
9. D. V. Lindley, Ann. Math. Stat., 1956, 27, 986–1005.
10. K. Chaloner and I. Verdinelli, Stat. Sci., 1995, 273–304.
11. P. Müller, Handbook of Statistics, 2005, vol. 25, pp. 509–518.
12. G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish, H. Hao, S. Lo, S. Pablo-García, E. M. Rajaonson and M. Skreta, et al., Chem. Rev., 2024, 124, 9633–9732.
13. N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, T. He, D. Milsted, M. J. McDermott, M. Gallant, E. D. Cubuk and A. Merchant, et al., Nature, 2023, 624, 86–91.
14. A. A. Volk and M. Abolhasani, Nat. Commun., 2024, 15, 1378.
15. R. A. Skilton, R. A. Bourne, Z. Amara, R. Horvath, J. Jin, M. J. Scully, E. Streng, S. L. Y. Tang, P. A. Summers, J. Wang, E. Pérez, N. Asfaw, G. L. P. Aydos, J. Dupont, G. Comak, M. W. George and M. Poliakoff, Nat. Chem., 2015, 7, 1–5.
16. D. E. Fitzpatrick, C. Battilocchio and S. V. Ley, Org. Process Res. Dev., 2016, 20, 386–394.
17. M. Vogler, J. Busk, H. Hajiyani, P. B. Jørgensen, N. Safaei, I. E. Castelli, F. F. Ramirez, J. Carlsson, G. Pizzi, S. Clark, F. Hanke, A. Bhowmik and H. S. Stein, Matter, 2023, 6, 2647–2665.
18. M. J. Statt, B. A. Rohr, D. Guevarra, S. K. Suram and J. M. Gregoire, Digital Discovery, 2024, 3, 238–242.
19. D. Guevarra, K. Kan, Y. Lai, R. J. R. Jones, L. Zhou, P. Donnelly, M. Richter, H. S. Stein and J. M. Gregoire, Digital Discovery, 2023, 2, 1806–1812.
20. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. a. Persson, APL Mater., 2013, 1, 011002.
21. A. Shinde, D. Guevarra, J. A. Haber, J. Jin and J. M. Gregoire, J. Mater. Res., 2015, 30, 442–450.
22. D. J. Russo, B. Van Roy, A. Kazerouni, I. Osband, Z. Wen et al., Foundations and Trends® in Machine Learning, 2018, vol. 11, pp. 1–96.
23. K. Kandasamy, W. Neiswanger, R. Zhang, A. Krishnamurthy, J. Schneider and B. Poczos, International Conference on Machine Learning, 2019, pp. 3222–3232.
24. M. J. Statt, B. A. Rohr, K. Brown, D. Guevarra, J. Hummelshøj, L. Hung, A. Anapolsky, J. M. Gregoire and S. K. Suram, Digital Discovery, 2023, 2, 1078–1088.
25. S. A. Miskovich, W. Neiswanger, W. Colocho, C. Emma, J. Garrahan, T. Maxwell, C. Mayes, S. Ermon, A. Edelen and D. Ratner, Mach. Learn.: Sci. Technol., 2024, 5, 015004.
26. K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 235438.

---