Leveraging feature gradient for efficient acquisition function maximization in material composition design

Abstract

Bayesian optimization (BO) has been widely employed for alloy composition design, but faces unique challenges in this domain when maximizing the acquisition function (AF), which is a critical step for selecting the best candidate. While various optimization methods exist for maximizing AF, material composition design presents difficulties that include the need to translate compositions into material features, rapid polynomially expanding design spaces as component numbers increase, and compositional constraints (e.g., sum to 100%). To address this issue, we propose a strategy that leverages numerical feature gradient for efficient AF maximization in material composition design. By establishing a differentiable pipeline from alloy compositions, through material features and model predictions, to AF values, our strategy enables efficient navigation from initial compositional guesses to optimal solutions. This approach reduces the complexity of the inner optimization problem from rapid polynomial (i.e., in the case of full enumeration) to empirically observed linear scale with respect to the number of components, making it efficient for medium-scaled design spaces (up to 10 components) while showing potential for scaling to larger compositional spaces. Additionally, initiating the process with randomly generated compositions promotes more diverse solutions, as evidenced by a slower decay of compositional state entropy compared to traditional enumeration-based approaches. Furthermore, the flexibility of our method allows for tailoring the optimization process by adjusting key settings, such as the number of initial compositions, the choice of AFs, surrogate models, and the formulas used to calculate material features. We envision this strategy as a scalable and modular methodology for advancing materials design, particularly in the composition design of high-entropy alloys, ceramics, and perovskites, where elemental compositions can be adjusted as continuous variables.

---

1. Introduction

Artificial intelligence and machine learning have emerged as powerful techniques for the accelerated composition design of new materials.^1–6 These techniques include sampling-based experimental design,^7–9 evolutionary algorithms,^10–12 Bayesian optimization (BO), and generative design methods.^5,13 Among these methods, BO has garnered significant attention due to its efficiency, minimal reliance on large training datasets, and ease of implementation.^{1,2,4,14–16} BO has facilitated the development of various advanced materials, including high-entropy alloys,¹⁷ invar alloys,⁵ metallic glasses, electro-ceramics^18,19 and perovskites.^20,21 Notably, many state-of-the-art self-driving laboratories also utilize BO as a recommendation system to guide the subsequent experiments or simulations.^10,22–27 BO's efficiency stems from its ability to balance exploration and exploitation by defining acquisition functions (AFs) that incorporate predicted mean values and associated uncertainties.^28,29 Within this framework, candidates in the search space are ranked based on their AF values, with the highest-ranking option recommended.

However, maximizing AF values (often referred as inner loop optimization,^28,30 Section 2 in the ESI†) is often challenging. While BO traditionally assumes continuous input variables, material composition design often involves discrete variables (e.g., discretized component percentages) and transforming raw compositions into material features. These characteristics complicate the maximization process, rendering standard gradient-based approaches difficult to apply directly. Consequently, many existing compositional design works rely on evaluating the AF values across the entire design space to identify the optimal candidate.^2,18,31–33 This approach, known as exhaustive enumeration (brute force), becomes increasingly intractable as the size of the compositional space shows a rapid polynomial growth with the number of components for material composition design³⁴ (Section 1 in the ESI†). Consequently, this limitation has constrained the search space in many studies to fewer than 10⁷ possible compositions,^18,35–37 which is far smaller than the full potential compositional space of high-entropy materials.^{5,34,35,38,39} Moreover, this exhaustive enumeration frequently leads to the repeated selection of similar compositions across consecutive experimental iterations, concentrating the search around narrow compositional regions and resulting in compositions with marginally improved material properties.^1,2

Various approaches have been proposed to address the challenge of AF maximization, including local search,⁴⁰ probabilistic reparameterization,⁴¹ and applying continuous relaxation and then discretize (round) for discrete domains.⁴² Among these approaches, gradient-based methods have demonstrated promising performance in maximizing AF values.^30,43,44 In composition design, obtaining gradient from surrogate models like Gaussian Process Regression (GPR) with respect to raw compositions might seem straightforward. However, a common practice in materials informatics involves transforming raw compositions into material features,^37,45,46 where the composition values often have constraints (e.g., ensuring components sum to 100%). These features are defined using various mathematical formulas related to elemental properties and mole fractions, such as (weighted) minimum/maximum operations, along with mole averages of atomic radius, valence electron number, and electronegativity.^46–48 While these transformations enhance the performance of machine learning surrogate models,^{17,35,37,49,50} improving the efficiency of composition design,^35,37,50 they also complicate both the definition and propagation of gradients. This complexity arises because feature transformations may involve non-differentiable operations (such as min/max), making closed-form gradient calculation through features challenging. As a result, computing and leveraging gradients for AF maximization becomes a challenging task within this workflow. This difficulty has led many works to adopt alternative strategies, such as exhaustive enumeration^32,33 or heuristic methods.⁵¹

To address this inner loop optimization challenge in material composition design, we proposed a strategy that leverages numerically computed feature gradient for efficient AF maximization (Section 3 in the ESI†). By establishing an end-to-end piecewise differentiable pipeline from alloy compositions, through material features and model predictions, to the AF values, our strategy enables efficient navigation from initial compositional guesses to optimal solutions. This approach reduces the complexity of the inner optimization problem from a rapid polynomial to a linear scale with respect to the number of components, making it feasible for medium-scaled design spaces (up to 10 components) with the potential for scaling to larger compositional spaces. Additionally, initiating the process with randomly generated compositions promotes more diverse solutions, as indicated by a slower decay of compositional state entropy compared to traditional enumeration-based approach. This broader exploration mitigates the issue of compositional concentration. Even though our results indicate possible incomplete maximization of AF values (i.e., the algorithm may not always find the global maximum of the AF, but rather identify the largest local maximum from a subset of all possible local maxima), the search spans a wider range of promising compositional regions, allowing for stable performance with smaller deviations across parallel BO runs. This proposed method, leveraging gradients propagated through feature transformations, is applicable to the composition design of a wide array of materials, including ceramics, metallic glasses, and high-entropy perovskites, where elemental compositions can be adjusted as continuous variables.

The remainder of this article is structured as follows: We first present our feature gradient methodology in Section 2. Next, we describe the benchmark environments used to evaluate our approach in Section 3. We then demonstrate the efficacy of our approach in Section 4. This is followed by a discussion part regarding various key settings in Section 5. Finally, we summarize our contributions and outline promising directions for future research.

2. Feature gradient strategy for efficient acquisition function maximization

Fig. 1a presents a flowchart illustrating our proposed method for composition design that leverages feature gradient ∇_cε(c) and its propagation through the prediction pipeline to efficiently maximize AFs. This method uses a well-established GPR model with a Matérn 5/2 kernel as the surrogate model, denoted g(·), which provides alloy property predictions and their associated uncertainties within the inner loop of the BO framework. Rather than using raw compositions c as inputs, we compute material features by applying mathematical transformations ε(·) that combine elemental properties and mole fractions, such as weighted averages. These computed material features then serve as the inputs for the GPR model, (g(ε(c))). Using the GPR model's predictions of target properties and associated uncertainties, an AF value, α(g(ε(c))), is estimated.

Fig. 1 Schematic pipeline of the proposed BO strategy for composition design, utilizing feature gradient, ∇_cε(c), to efficiently maximize AFs. (a) The complete differentiable pipeline, ∇_cα(g(ε(c))), linking alloy compositions (values represent atomic percentages in (a1)), material features, GPR predictions, and AF values (AFVs). AF maximization in (a3) is achieved efficiently using the gradient information, with a rejection sampling step in (a2) to generate feasible initial compositions, ensuring they fall within the desired design space. (b) Illustration showing that this gradient-based approach yields a broader set of candidate compositions by identifying multiple distinct local maxima, as opposed to traditional enumeration-based methods which tend to focus on a narrower set of options. This results in more balanced exploration of the compositional space, rather than strict exploitation of a single optimum.

The complete feature set is formed by the combination of elemental properties and feature transformation functions, totaling 240 distinct features. The elemental property set includes 30 metrics, spanning from fundamental atomic characteristics to complex physicochemical properties (Table S5†). The feature transformation functions comprise 8 formulations (Table S1†), including weighted averages, max/min operations, etc. These transformations enable the integration of compositions with elemental properties to create material features that effectively capture composition–property relationships through enhanced information sharing among constituent elements.

The mapping from compositions, through material features and GPR predictions, to AF values that we considered in this work, including Expected Improvement (EI), Probability of Improvement (POI) and Upper Confidence Bound (UCB), can be implemented as a differentiable computational graph. This allows for end-to-end gradient computation through a chain, linking the alloy compositions, material features, GPR predictions, and AF values, as expressed by ∇_cα(g(ε(c))) (Fig. 1a(1)). Although deriving an analytical form for this chain is challenging, we utilize numerical differentiation to obtain gradient values, leveraging PyTorch's differentiation tools.^52,53 The details, including the mean and uncertainty predictions of GPR, the definitions of considered AFs (EI, POI and UCB), the computation of feature transformations (ε(c)), and the numerical evaluation of gradients through features and GPR predictions to AF values, are provided in Section 3 of the ESI.†

Using this numerical gradient ∇_cα(g(ε(c))), AF maximization is achieved efficiently, as demonstrated in Fig. 1a(2). Optimization methods, such as Sequential Least Squares Programming (SLSQP), guide the search toward local optima. Starting from random initial composition guesses, this gradient-based approach rapidly identifies compositions that locally maximize the AFs. The SLSQP method incorporates linear compositional constraints (e.g., positive concentrations) into the optimization objective through the Lagrange Multiplier method, essentially constructing an equivalent Lagrangian formulation of the constrained optimization of scalar AFs. This incorporation of constraints ensures that compositions proposed by the gradient-guided search remain realizable throughout the optimization process. In composition design, constraints such as element solubility and the requirement that total mole fractions sum to 100% often lead to a rugged compositional space. To address this, we include a rejection sampling⁵⁴ step to generate feasible initial compositions. This sampling ensures that the initial compositions are well-distributed within the feasible design space, improving the effectiveness of the optimization process.

Random initial sampling of compositions also helps to prevent the optimization from converging prematurely to specific regions, promoting broader exploration of the design space. Consequently, this strategy yields a diverse set of optima compared to traditional enumeration-based approaches (detailed in Table S3†), as schematically illustrated in Fig. 1b.

Finally, Table 1 presents pseudo-code for our BO method, which incorporates feature gradient for efficient AF maximization. The code is available at https://github.com/wsxyh107165243/FeatureGradientBO. By optimizing the AF with feature gradient, our method significantly accelerates the BO process, allowing for efficient exploration of large compositional spaces with greatly reduced computational effort.

Table 1 Pseudo code of BO with feature gradient for composition design of alloys

---

3. Benchmark testing models

To evaluate our proposed method, we developed three distinct test environments, each utilizing neural networks trained on high-quality alloy composition-property datasets. Each test environment is tailored to a specific class of alloys: shape memory alloys (SMAs), titanium alloys (Ti), and high-entropy alloys (HEAs). These well-trained neural networks serve as the ground truth within the outer loop of the BO process. Within each BO outer loop iteration, the composition proposed by our method is input into these neural networks to obtain property predictions, which are considered as the material properties and subsequently added to the set of evaluated compositions in the BO framework. The initial dataset for launching the BO process (40 compositions, which also serves as the training dataset for the GPR surrogate) is significantly smaller than the dataset used to train the neural networks. This setup allows the neural network predictions to effectively serve as substitution for actual material synthesis and characterizations.

The SMAs environment focuses on phase change alloys used in thermal management devices, targeting key properties such as high enthalpy change (ΔH) for greater energy density, low thermal hysteresis (ΔT) for rapid response, and the working temperature T_w (defined as the average of martensite and austenite transformation peak temperatures, M_p and A_p) near the operating temperature. A figure of merit (FOM_sma) is defined as: 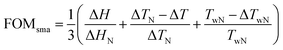, where ΔH_N, ΔT_N and T_wN are normalization factors for enthalpy change, hysteresis, and the deviation from the target working temperature, respectively. ΔT_wN is the difference between the objective working temperature and the predicted working temperature.

The Ti environment evaluates mechanical properties, specifically yield strength (σ_Y), ultimate strength (σ_U), and Vickers hardness (ν). These properties are optimized through a figure of merit (FOM_ti) defined as: 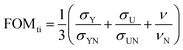, where σ_YN, σ_UN and ν_N are normalization factors for yield strength, ultimate strength, and Vickers hardness, respectively.

The HEAs environment focuses on yield strength (σ_Y), ultimate strength (σ_U), and elongation (ε), with the goal of balancing strength and ductility. The figure of merit (FOM_hea) for this environment is defined as: , where ε_N is the normalization factor for elongation. These figures of merit (FOMs) combine multiple properties into single objectives for the BO algorithms to optimize, reflecting practical material development priorities and providing a complex, multi-objective optimization landscape suitable for testing our composition optimization algorithms. It should be noted that our current implementation uses an equally weighted sum of multiple properties as the figure of merit, which serves as optimization objective for method validation but does not directly address multi-objective optimization, which is a limitation of the current approach.

The neural networks used in these environments were implemented with an architecture inspired by the approach outlined in ref. 55. Each neural network begins with a convolutional section followed by a residual connection, after which process conditions are concatenated with the outputs before entering the fully connected section. The convolutional section consists of two layers with a kernel size of 1 × N_feature × N_feature, and batch normalization is applied after each layer to enhance model robustness. The resulting output is flattened and passed through two fully connected layers, configured as (N_elem × N_feature) × 128 and 128 × 1, incorporating Exponential Linear Units (ELUs) for nonlinear activation and a dropout layer to improve stability. The networks were trained using the Adam optimizer with a batch size of 16.

For training, we used 501 composition-property pairs for HEAs, 603 pairs for Ti alloys, and 295 pairs for SMAs, ensuring reliable model performance. These data were collected from both our laboratory and published literature, with details provided in the Section 6 of the ESI.† The nine neural networks (three per alloy type) were trained as detailed in the Methods section and in Section 6 of the ESI.† Before training, each dataset was randomly split into training (70%), validation (15%), and test (15%) subsets. As shown in left panels of Fig. 2, training was performed for up to 1000 epochs with a learning rate of 5 × 10⁻⁴. The training loss and validation R² scores demonstrated significant improvements during the initial 500 epochs, with diminishing returns in later epochs. The R² score on the test set at the 500th epoch closely matched that of the validation set, confirming stable training. Consequently, 500 epochs were selected as the optimal training duration for building the neural networks. The performance of these networks, as shown in right panels of Fig. 2, was further evaluated using 10-fold cross-validation, yielding R² values between 0.443 and 0.917 and MAE values between 0.187 and 0.492. It is worth noting that the neural network performance shows lower accuracy for Ti alloy tensile strength prediction (R² = 0.443). This reduced performance likely stems from the variability in tensile strength measurements, which are highly sensitive to specimen preparation, testing conditions, and structural variations. These neural networks are then integrated to form FOMs specific to each alloy class, which will be optimized using BO algorithms.

Fig. 2 (Left panels) Training processes of neural networks for nine properties across three material systems, illustrating the convergence of training and validation metrics. (Right panels) Results of 10-fold cross-validation for the nine neural networks, demonstrating R² and mean absolute error (MAE) values, indicative of generally good predictive performance across different properties, with the exception of tensile strength in Ti alloys which shows moderate performance. All data are normalized and presented in arbitrary units (a.u.) to facilitate comparison across different property scales.

4. Results

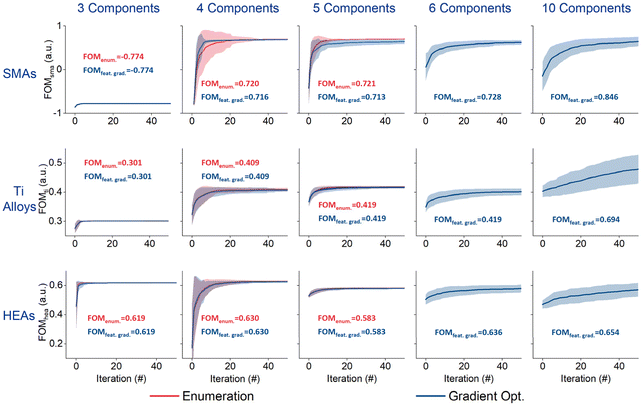
Our aim here is to identify compositions with high FOM values through iterative interactions with the test environments, a process often referred to as outer compositional optimization. The ability for BO to handle the vast space of multicomponent alloys largely depends on the efficiency of AF maximization (i.e., inner loop maximization). We compared the traditional enumeration approach with our feature gradient strategy for the inner loop across all test environments. For this comparison, we conducted 96 parallel trajectories of outer compositional optimization, each starting from different initial compositions. The optimization performance, represented by the best-so-far FOM value as a function of iteration (interactions with the test environment), is shown in Fig. 3. Compositional constraints and step sizes are detailed in Tables S6–S8 in the ESI.† To demonstrate the advantages of our strategy, we increased the size of the design space and the complexity of the search landscape by varying the number of components from 3 to 10.

Fig. 3 Comparison of outer compositional optimization trajectories between enumeration and gradient-based methods for the inner loop across all test environments, with the number of components varying from 3 to 10. The y-axis in each plot represents the best-so-far FOM value achieved up to each iteration, reflecting the progressive improvement in material performance throughout the BO process. The best FOM values and corresponding compositions after 50 iterations (i.e., interactions with the test environment) are shown in each panel.

For alloys with 3–5 components, the total number of possible compositions remains within 10¹⁰, allowing for a direct comparison of the performance of both optimization methods. In these scenarios, our feature gradient strategy for inner optimization achieved results comparable to the enumeration approach, as shown in Fig. 3.

As the number of components increased, however, enumeration became increasingly computationally impractical. Therefore, for compositions with higher numbers of components, only the gradient-based inner optimization trajectories are presented. Our results demonstrate that the proposed feature gradient strategy is scalable and efficient for composition design involving up to 10 components. This scalability is achieved by empirically scaling the number of initial compositional guesses linearly with the number of components, suggesting potential applicability for even larger systems. Expanding the search space often increases the likelihood of discovering compositions with enhanced properties, especially in the case of Ti alloys shown in Fig. 3. The scalability underscores the advantages of using gradient-based optimization in complex compositional spaces, where direct enumeration becomes computationally prohibitive.

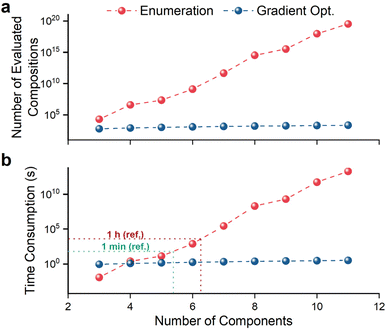
For multi-component alloys, the number of possible compositions shows rapid polynomial growth with the number of components (see Section 1 in the ESI†), making inner loop optimization increasingly challenging. Comparing the computation time for inner loop optimization between the traditional enumeration approach and our feature gradient method provides valuable insights. Based on our hardware, the estimated time to calculate the AF value for a single composition (t₀) is approximately 6 × 10⁻⁷ seconds. In the enumeration approach, the number of evaluated compositions (N) corresponds to the entire design search space, resulting in a time consumptions (t) of approximately t₀ × N. As shown in Fig. 4, both N and t increase with the number of components (N_elem).

Fig. 4 Comparison of the number of evaluated compositions (a) and corresponding time consumption (b) as a function of the number of components for the traditional enumeration approach and the proposed feature gradient method. Results are based on the test environment of SMAs.

For our feature gradient strategy, as the gradient calculation must be included, the time to evaluate a single gradient t_grad is ∼1.5 × 10⁻³ seconds using the same hardware. However, by employing gradient-based optimization methods like SLSQP, the number of evaluated compositions (N) is significantly reduced. In our approach, N depends on the number of initial compositions, and to our experience, scales linearly with the number of components (N_elem), at approximately 20 × N_elem. For example, with a training set of 40 compositions, we observed that the SLSQP algorithm typically requires ∼10 gradient calculations to find the near zero-gradient composition from a random initial composition point. Therefore, with a 4-component system (N_elem = 4), the total computation time would be approximately 10 × 20 × N_elem × t_grad ≈ 10 × 20 × 4 × (1.5 × 10⁻³) = 1.2 seconds per inner loop in BO framework. Overall, the time consumption for our feature gradient method remains far lower than that of the enumeration method.

Fig. 4 illustrates the number of evaluated compositions and corresponding time consumption as a function of component count for both strategies. Our results demonstrate that the proposed method achieves substantially higher efficiency and lower time consumption in the inner loop, particularly as the number of components increases. The computational complexity of our method is primarily determined by the number of initial random guesses in the inner loop, exhibiting only a weak, linear correlation with the number of components. For up to six components, the enumeration method remains feasible, with a computational time of around one hour. However, based on the intersection of the two curves in Fig. 4b, when the target component number exceeds four, our feature gradient strategy becomes the preferred approach.

By leveraging the high efficiency of our feature gradient strategy for AF maximization, we can initiate the search from multiple randomly generated compositions, enabling several parallel search routes. Each route progresses along the gradient ascent direction until the gradient value, ∇_cα(g(ε(c))) approaches zero. With a sufficiently large number of starting compositions (e.g., 20 × N_elem), the optimized solutions are more likely to approximate the global optimum. This multi-starting point approach efficiently explores diverse regions of the AF landscape in each inner loop, which subsequently leads to solutions that are both well-distributed across the design space and possess desirable material properties through the outer loop process. This approach addresses a key limitation of traditional enumeration-based BO, which often selects similar compositions repeatedly across consecutive iterations, thereby concentrating the search on narrow compositional regions.^1,2 In contrast, our gradient-based strategy promotes broader exploration, yielding a more comprehensive coverage of the entire composition design space.

To quantitatively evaluate the broader exploration behavior of our strategy, we introduced state entropy as a metric, following the definition from:^56,57

where x⊂[Doublestruck R]^q, x^k-NN_i is the k-th nearest neighbor (k-NN) of x_i within a set {x_i}^N_i=1, C_k = log k − Ψ(k) is a bias correction term, Ψ is the digamma function, Γ is the gamma function, q is the dimensionality of x, and [small pi, Greek, circumflex] ≈ 3.14159. In our analysis, this set {x_i}^N_i=1 specifically refers to the materials actually selected by each optimization strategy during the experimental iterations of the BO process. For q > 0, we simplify to the following approximation:
which we use as the measurement of state entropy. State entropy quantifies the diversity and distribution of explored compositions. Higher entropy indicates more comprehensive exploration of the compositional space, while lower entropy reflects concentrated sampling in limited regions.

The state entropy analysis from multiple parallel optimization trajectories strongly supports our findings, as shown in Fig. 5a–c. Notably, in all three test environments (SMAs, Ti alloys, and HEAs), our strategy consistently maintains higher state entropy values, demonstrating a broader exploration of the compositional space. The higher state entropy values observed in our feature gradient strategy arise from its fundamental operational characteristics. While enumeration-based methods deterministically identify the single global maximum of the AF, our approach identifies multiple local maxima dependent on randomly selected initial compositions. For each inner loop, we perform multiple gradient-based ascent runs (20 × N_elem), potentially discovering diverse local maxima across the compositional space. These identified local maxima constitute a subset from the power set of all local maxima within the whole compositional design space, and may vary across parallel inner loops. This introduces an inherent stochasticity as initial compositions are randomly selected and the GPR landscape is often multimodal. Consequently, the feature gradient method explores diverse promising regions, manifesting as higher state entropy values even though it may not guarantee finding the exact global maximum in every iteration.

Fig. 5 State entropy as a function of iteration number for all three test environments: (a) SMAs, (b) Ti alloys, and (c) HEAs, with four components in each case. (d) A representative optimization trajectory comparing the enumeration and feature gradient methods. The corresponding t-SNE analysis of all explored compositions is shown in (e). The x and y axes in (e) represent the first and second dimensions of the t-SNE projection with no specific physical meaning (axis labels omitted for clarity). Each point represents a composition, with color indicating FOM value (higher values in red). The upper panel shows compositions explored by the enumeration method, while the lower panel shows those explored by the gradient method. The t-SNE analysis highlights the broader exploration achieved by the feature gradient method.

To further visualize this broader exploration, we performed t-SNE (t-Distributed Stochastic Neighbor Embedding) analysis on two representative optimization trajectories from both methods in the 4-component SMAs environment (Fig. 5d). t-SNE preserves short Euclidean distances and represents higher compositional similarity in a 2-dimensional space, allowing high-dimensional compositional data to be effectively visualized. The broader exploration achieved by our strategy is evident in the more scattered compositions within the light pink region of Fig. 5e. Additional pairwise distribution analysis of elemental compositions (Fig. S2, ESI†) further corroborates these findings, showing that the enumeration method produces more peaked compositional distributions concentrated in limited regions, while the gradient optimization approach maintains broader, more uniform exploration across the compositional space.

A key observation is that our strategy promotes broader exploration while also achieving more stable performance across parallel optimization tests, even though complete global maximization is not guaranteed. This trade-off suggests that sacrificing the guarantee of finding the exact argmax significantly reduces computational time in the inner loop, with only negligible losses in material performance. Such a balance is particularly valuable in scenarios where computational efficiency takes precedence over marginal improvements in solutions. Furthermore, we demonstrate that the increased exploration enabled by our strategy enhances the robustness of BO, making it less sensitive to the selection of initial data. This robustness is further supported by the consistently higher state entropy values achieved by our method.

Our results show that the proposed strategy offers a computational advantage in finding near-optimal AF values, outperforming the enumeration-based method by significantly reducing computational time through the use of feature gradient and gradient ascent, which require evaluating only a small subset of compositions. Additionally, systematic state entropy analysis confirms that our approach achieves broader exploration of the design space, reducing the risk of premature convergence and enhancing the robustness of BO. This improved efficiency and reduced dependency on initial data highlight the potential of our method to advance computational materials design.

5. Discussion

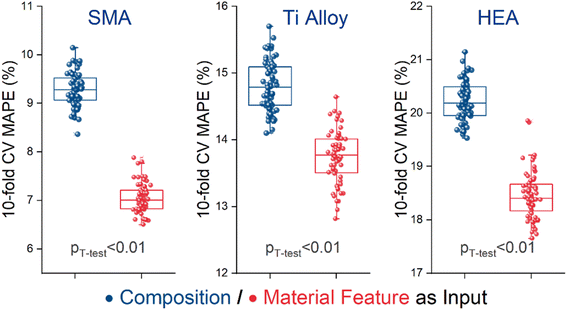
A key innovation of our strategy lies in the use of feature gradient to guide the optimization process. While raw compositions can serve as inputs to the surrogate model, material features offer a compelling alternative, as they potentially capture richer physical information.^17,58 Although incorporating material features in the inner loop introduces additional computational costs, it often enhances model performance and accelerates optimization. Thus, it is essential to quantitatively assess their impact on model accuracy. To systematically compare the effectiveness of these two input types, we conducted extensive cross-validation experiments across three datasets: SMAs, Ti alloys, and HEAs, following the procedure outlined in Table S4 (Section 5 in the ESI).† For each dataset and input type, 64 parallel tests were performed, with each test randomly sampling 100 experimental composition-property data points. These data points were used for 10-fold cross-validation to calculate the mean absolute percentage error (MAPE), which served as the primary metric for model performance. This normalized metric enables direct comparison of predictive accuracy across different material systems with varying property magnitudes. The results, shown in Fig. 6, consistently demonstrate superior performance when using material features compared to raw compositions across all three datasets. Additional analysis using mean absolute error (MAE) shows similar trends across all material systems, confirming the robustness of this finding (Fig. S3, ESI†). Statistical analysis via paired t-tests (p < 0.01) further confirms the significance of this improvement. This enhanced predictive capability for unseen compositions supports the inclusion of feature gradient in our strategy, despite the additional computational challenges they introduce in the inner loop optimization process.

Fig. 6 Comparative analysis of predictive performance between models using raw compositions (blue) and material features (red) as inputs for predicting martensitic transformation temperature (SMAs), Vickers hardness (Ti alloys), and yield strength (HEAs). Box plots show the distribution of mean absolute percentage error (MAPE) values from 10-fold cross-validation across 64 comparative experiments for each dataset. The MAPE metric was chosen to enable comparison across properties with different value scales. Statistical significance of the performance differences was confirmed through paired t-tests (p_t-test < 0.01, meaning that there is less than 1% probability that the differences were due to chance).

Our strategy involves hyperparameters that need to be determined for effective deployment. One key hyperparameter is the number of randomly initialized starting compositions for inner loop optimization. In the inner loop, gradient ascent is performed on these starting compositions, with a larger number of starting points enabling a more thorough exploration of the composition design space. While increasing the number of starting compositions can lead to better acquisition function values, it also results in higher computational costs. Experimental results across different numbers of starting compositions (10, 20, 40, and 80) demonstrate consistent improvements in the FOM with more starting points, as shown in Fig. 7. As this budget increases, the gradient-based results increasingly approximate towards the enumeration-based results. This convergence occurs because with more initial composition points distributed throughout the compositional space, gradient ascent can identify more of the local optima that would otherwise only be found through exhaustive enumeration. When the budget increases to a sufficient level where gradient ascent identifies all local maxima across the compositional space, the optimization result becomes effectively consistent with the enumeration-based method. The inset in Fig. 7 illustrates this convergence trend, showing how the performance increases as the number of initial compositions increases from 10 to 80, with diminishing marginal returns at higher values, indicating a saturation effect. To balance the trade-off between achieving higher FOM values and managing computational costs, we empirically propose that the number of starting compositions should scale linearly with the number of components, following the formula 20 × N_elem. This scaling provides a practical balance between BO performance and computational efficiency.

Fig. 7 Comparative analysis of final BO performance on the SMAs test environment (with 4 components) under varying numbers of starting compositions for the inner loop. The y-axis (final FOM_sma) represents the maximum figure of merit value achieved up to the final experimental iteration. Different colors (red, yellow, blue, and purple) represent box plots for varying numbers of initial compositions to start gradient ascent (10, 20, 40, and 80 respectively). Box plots represent the distribution of final FOM values across parallel tests, while the inset illustrates the trend of mean FOM values as a function of the number of starting compositions.

The differentiable pipeline proposed in this work connects alloy compositions, material features, surrogate models, and AFs. While we demonstrated the effectiveness of our strategy using EI as the AF, it is important to note that this methodology is not limited to EI. Other AFs that are analytically differentiable, such as Upper Confidence Bound (UCB, with trade-off parameter κ = 1.96) and Probability of Improvement (POI), can also be integrated into our feature gradient strategy. This mathematical property broadens the applicability of our feature gradient strategy to a range of AFs, each offering unique exploration–exploitation trade-offs. To explore this broader applicability, we extended our experiments to include UCB and POI as AFs. Using the same experimental procedures as for EI, we conducted comparative tests on the SMA dataset with four components. The results, shown in Fig. 8a, indicate consistent optimization performance across all tested AFs when using the feature gradient strategy. All three AFs exhibit similar trends: an initial phase of steep improvement during the first 10 experimental iterations, followed by stable convergence. Among the tested AFs, UCB demonstrated marginally faster initial convergence, while POI showed slightly higher variance in the early stages. However, all three AFs converged to similar final FOM values (approximately 0.7), with overlapping confidence intervals during the stable phase. These results highlight the robustness of our feature gradient strategy and its consistent effectiveness regardless of the choice of AF.

Fig. 8 (a) Optimization trajectories using UCB (trade-off parameter κ = 1.96) and POI acquisition functions in the SMA test environment with four components. (b) Optimization trajectories considering a broader range of functional forms for calculating material features, compared to the trajectory using only the molar average function. In all plots, the y-axis (FOM_sma) represents the best figure of merit achieved up to each iteration (best-so-far FOM). Inset figure plots the FOM difference between considering feature functionals and using only the molar average function: FOM_diff = FOM_{with functionals} − FOM_{only weighted avg.}.

For material features, various mathematical formulas beyond the traditional weighted averaging approach can be employed. This broader class of functions (Table S1†) expands the feature space beyond linear combinations of elemental properties, potentially capturing non-linear relationships and richer physical information. However, this generalization complicates the calculation from initial compositions to final AF values. To evaluate the impact of this generalization on the optimization outcomes, we examined its influence on the FOM values obtained through BO. We utilized eight mathematical formulas commonly used in HEAs research⁵⁹ and combined them with 30 elemental properties, generating a pool of 240 elemental property–formula combinations. Genetic algorithms were applied for feature subset selection, optimizing the 10-fold cross-validation (R²) to identify the most promising combinations. Comparative experiments between traditional weighted averaging and expanded mathematical functionals revealed notable differences in optimization performance (Fig. 8b). The approach employing a broader range of formulas exhibited superior performance during the initial stages of optimization, with a significant positive performance difference observed within the first three BO iterations (inset of Fig. 8b). This result underscores the potential benefits of incorporating more sophisticated mathematical formulas into feature calculations. However, the increased complexity of these functionals significantly amplifies the computational burden in traditional enumeration-based inner loop optimization, potentially limiting its practical implementation. This observation highlights the strong advantage of the feature gradient strategy, which efficiently handles these complex formulas while maintaining computational tractability. By enabling the practical use of advanced mathematical formulas, the gradient-based approach not only enhances BO performance but also ensures computational efficiency, providing a robust framework for advancing materials design.

Apart from the AF, another key factor for successful BO is the choice of surrogate model, which directly impacts the effectiveness of the property prediction and optimization process. While Gaussian Process Regression (GPR) remains the most widely used surrogate model, alternative approaches, such as Random Forest (RF), have gained attention for their robust predictive performance and reduced sensitivity to hyperparameter tuning. However, the non-differentiability of RF models poses a significant challenge for inner loop optimization, particularly when employing efficient gradient-based strategies. This limitation highlights the need for differentiable alternatives, such as Deep Gaussian Processes (DGPs),^60,61 which not only preserve differentiability but also excel in capturing complex composition–property relationships. Additionally, DGPs offer enhanced computational efficiency when handling larger datasets, making them a promising option for high-dimensional materials design problems. Choosing an appropriate surrogate model therefore requires striking a careful balance between predictive accuracy, computational efficiency, and differentiability to enable effective inner loop optimization. This balance is especially critical in materials design, where the intricate complexity of composition–property relationships necessitates both precise modeling and computationally tractable optimization methods.

In the supplementary, we further briefly discuss various design choices, including the use of 20 × N_elem and random sampling, as well as potential issues with gradient failure. We note that for EI, a common challenge is that AF values gradually approach 0 as experimental iterations proceed. This occurs because the probability of finding improvements diminishes with better solutions found, leading to numerical difficulties with vanishing EI values and gradients.⁶² Additionally, determining which elemental properties are most relevant for specific performance metrics presents a significant challenge. The potential elemental feature space is large,^63,64 encompassing hundreds of candidates, many of which may have minimal correlation with the target performance. Feature selection, which involves identifying the optimal subset of elemental properties that meaningfully influence performance, remains an active research area in materials informatics. Our selection of 30 candidate elemental properties represents a balance between domain knowledge, empirical experience, and computational tractability, though more sophisticated features could potentially enhance performance further. Notably, some acquisition functions, such as entropy-based functions, may not be differentiable, limiting our method's applicability in such cases. Currently, our research focuses on pure numerical experiments, with the validity of recommendations ensured by BO itself. We do not conduct further material synthesis or characterization experiments, and it is important to note that a better AF score does not necessarily lead to improved experimental results. This limitation is partly related to our current approach of encoding multiple material properties into a single FOM with equal weights. While this formulation serves our purpose of testing optimization strategies on complex landscapes, it may not reflect specific application preferences.

6. Conclusion

In summary, to address the challenges in acquisition function (AF) maximization within Bayesian optimization (BO) for materials composition design challenges that include rapid polynomially expanding compositional spaces, complex material feature transformations, and compositional constraints, we have developed a method leveraging numerically computed feature gradients for efficient AF maximization. By establishing a differentiable pipeline from alloy compositions, through material features and model predictions, to AF values, our strategy enables efficient navigation from initial compositional guesses to optimal solutions. Additionally, initiating the process with randomly generated compositions promotes broader exploration of the design space, yielding more diverse solutions. Our approach significantly improves inner loop efficiency while enabling extensive exploration of the compositional space during BO. Moreover, the flexibility of our method allows for tailoring the optimization process by adjusting key hyperparameters, such as the number of initial compositions, the choice of AFs, surrogate models, and the formulas used to calculate material features. We envision the utility of this method extending beyond alloys to the composition design of ceramics, metallic glasses, and high-entropy perovskites, where continuous compositional tuning plays a critical role. This strategy represents a scalable and versatile approach for advancing materials design.

A limitation of our method is its reliance on a single aggregated FOM, which may not effectively capture trade-offs between competing material properties for specific applications. Addressing this limitation would expand the applicability of our approach to more complex materials design scenarios where such trade-offs are essential. Further improvements to this approach could include several promising directions. First, extending the framework to handle multi-objective optimization problems, allowing for the exploration of Pareto-optimal solutions and preference-based optimization rather than using naive weighted property combinations. Second, enhancing the sampling strategies in the inner loop. Advanced methods for generating diverse initial compositions as starting points for gradient ascent could further improve the optimization result. Such strategies might include diversity-promoting sampling techniques that better cover the compositional space. Additionally, developing adaptive sampling approaches that dynamically adjust the number of initial points based on the complexity of the acquisition function landscape, for example by increasing sampling density with more evaluated compositions during sequential BO iterations, would enhance the method's efficacy. These enhancements would collectively address both the balance between competing objectives and the effectiveness of inner optimization, potentially leading to even more effective materials discovery.

Data availability

The datasets used in this study were derived from multiple sources: SMAs data was collected through experimental work conducted in our laboratory over several years; HEAs data was obtained from a published dataset in ref. 55; and Ti alloys data was collected from various research literature (see ref. 63 for details). Prior to neural network training, all input compositions, processing conditions, features, and output properties were standardized to follow the standard normal distribution. All three alloy datasets (SMAs, HEAs, and Ti alloys), along with the complete implementation code for feature transformation, neural network training, and Bayesian optimization with feature gradient, are publicly available in our GitHub repository (see Section 2) and archived at Zenodo (https://doi.org/10.5281/zenodo.15630210).

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge the support of National Key Research and Development Program of China (2021YFB3802100), National Natural Science Foundation of China (No. 51931004, 52173228, and 52271190) and Innovation Capability Support Program of Shaanxi (2024ZG-GCZX-01(1)-06). The authors thank Turab Lookman (AiMaterials Research LLC) and Yan Zhang (Northwest Institute for Non-ferrous Metal Research) for discussion. The authors also express sincere gratitude to the anonymous reviewers for their suggestions that improved the quality of this manuscript.

References

1. T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design, npj Comput. Mater., 2019, 5(1), 21.
2. C. Wen, Y. Zhang, C. Wang, D. Xue, Y. Bai, S. Antonov, L. Dai, T. Lookman and Y. Su, Machine learning assisted design of high entropy alloys with desired property, Acta Mater., 2019, 170, 109–117.
3. P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins and Z. Yang, Closed-loop optimization of fast-charging protocols for batteries with machine learning, Nature, 2020, 578(7795), 397–402.
4. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021, 590(7844), 89–96.
5. Z. Rao, P.-Y. Tung, R. Xie, Y. Wei, H. Zhang, A. Ferrari, T. Klaver, F. Körmann, P. T. Sukumar and A. Kwiatkowski da Silva, Machine learning–enabled high-entropy alloy discovery, Science, 2022, 378(6615), 78–85.
6. T. Yang, D. Zhou, S. Ye, X. Li, H. Li, Y. Feng, Z. Jiang, L. Yang, K. Ye and Y. Shen, Catalytic Structure Design by AI Generating with Spectroscopic Descriptors, J. Am. Chem. Soc., 2023, 145(49), 26817–26823.
7. A. Gelman, J. B. Carlin, H. S. Stern, and D. B. Rubin, Bayesian Data Analysis, Chapman and Hall/CRC, 1995.
8. M. D. Morris and T. J. Mitchell, Exploratory designs for computational experiments, J. Stat. Plann. Inference, 1995, 43(3), 381–402.
9. C. Schenk and M. Haranczyk, A novel constrained sampling method for efficient exploration in materials and chemical mixture design, Comput. Mater. Sci., 2025, 252, 113780.
10. M. Hernández-del-Valle, C. Schenk, L. Echevarría-Pastrana, B. Ozdemir, E. Dios-Lázaro, J. Ilarraza-Zuazo, D.-Y. Wang and M. Haranczyk, Robotically automated 3D printing and testing of thermoplastic material specimens, Digital Discovery, 2023, 2(6), 1969–1979.
11. Z. Li and N. Birbilis, NSGAN: a non-dominant sorting optimisation-based generative adversarial design framework for alloy discovery, npj Comput. Mater., 2024, 10(1), 112.
12. B. J. Bucior, A. S. Rosen, M. Haranczyk, Z. Yao, M. E. Ziebel, O. K. Farha, J. T. Hupp, J. I. Siepmann, A. Aspuru-Guzik and R. Q. Snurr, Identification schemes for metal–organic frameworks to enable rapid search and cheminformatics analysis, Cryst. Growth Des., 2019, 19(11), 6682–6697.
13. P. Dang, J. Hu, Y. Xian, C. Li, Y. Zhou, X. Ding, J. Sun and D. Xue, Elastocaloric Thermal Battery: Ultrahigh Heat-Storage Capacity Based on Generative Learning-Designed Phase-Change Alloys, Adv. Mater., 2025, 2412198.
14. A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher and S. Curtarolo, On-the-fly closed-loop materials discovery via Bayesian active learning, Nat. Commun., 2020, 11(1), 5966.
15. D. Shin, A. Cupertino, M. H. de Jong, P. G. Steeneken, M. A. Bessa and R. A. Norte, Spiderweb nanomechanical resonators via Bayesian optimization: inspired by nature and guided by machine learning, Adv. Mater., 2022, 34(3), 2106248.
16. S. Kaappa, C. Larsen and K. W. Jacobsen, Atomic structure optimization with machine-learning enabled interpolation between chemical elements, Phys. Rev. Lett., 2021, 127(16), 166001.
17. Y. Zhang, C. Wen, C. Wang, S. Antonov, D. Xue, Y. Bai and Y. Su, Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models, Acta Mater., 2020, 185, 528–539.
18. D. Xue, P. V. Balachandran, J. Hogden, J. Theiler, D. Xue and T. Lookman, Accelerated search for materials with targeted properties by adaptive design, Nat. Commun., 2016, 7(1), 1–9.
19. J. He, C. Yu, Y. Hou, X. Su, J. Li, C. Liu, D. Xue, J. Cao, Y. Su and L. Qiao, Accelerated discovery of high-performance piezocatalyst in BaTiO3-based ceramics via machine learning, Nano Energy, 2022, 97, 107218.
20. H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, Efficient search of compositional space for hybrid organic–inorganic perovskites via Bayesian optimization, npj Comput. Mater., 2018, 4(1), 51.
21. J. Moon, W. Beker, M. Siek, J. Kim, H. S. Lee, T. Hyeon and B. A. Grzybowski, Active learning guides discovery of a champion four-metal perovskite oxide for oxygen evolution electrocatalysis, Nat. Mater., 2024, 23(1), 108–115.
22. Z. Vangelatos, H. M. Sheikh, P. S. Marcus, C. P. Grigoropoulos, V. Z. Lopez, G. Flamourakis and M. Farsari, Strength through defects: A novel Bayesian approach for the optimization of architected materials, Sci. Adv., 2021, 7(41), eabk2218.
23. A. Dave, J. Mitchell, S. Burke, H. Lin, J. Whitacre and V. Viswanathan, Autonomous optimization of non-aqueous Li-ion battery electrolytes via robotic experimentation and machine learning coupling, Nat. Commun., 2022, 13(1), 5454.
24. O. Schilter, D. P. Gutierrez, L. M. Folkmann, A. Castrogiovanni, A. García-Durán, F. Zipoli, L. M. Roch and T. Laino, Combining Bayesian optimization and automation to simultaneously optimize reaction conditions and routes, Chem. Sci., 2024, 15(20), 7732–7741.
25. B. Ozdemir, M. Hernández-del-Valle, M. Gaunt, C. Schenk, L. Echevarría-Pastrana, J. P. Fernández-Blázquez, D.-Y. Wang and M. Haranczyk, Toward 3D printability prediction for thermoplastic polymer nanocomposites: Insights from extrusion printing of PLA-based systems, Addit. Manuf., 2024, 95, 104533.
26. F. Häse, L. M. Roch and A. Aspuru-Guzik, Next-generation experimentation with self-driving laboratories, Trends Chem., 2019, 1(3), 282–291.
27. M. M. Flores-Leonar, L. M. Mejía-Mendoza, A. Aguilar-Granda, B. Sanchez-Lengeling, H. Tribukait, C. Amador-Bedolla and A. Aspuru-Guzik, Materials Acceleration Platforms: On the way to autonomous experimentation, Curr. Opin. Green Sustainable Chem., 2020, 25, 100370.
28. P. I. Frazier, A tutorial on Bayesian optimization, arXiv, 2018, preprint, arXiv:1807.02811,  DOI:10.48550/arXiv.1807.02811.
29. T. Lookman, P. V. Balachandran, D. Xue, J. Hogden and J. Theiler, Statistical inference and adaptive design for materials discovery, Curr. Opin. Solid State Mater. Sci., 2017, 21(3), 121–128.
30. J. Wilson, F. Hutter and M. Deisenroth, Maximizing acquisition functions for Bayesian optimization, Adv. Neural Inf. Process. Syst., 2018, 31, 9906–9917.
31. Y. Tian, R. Yuan, D. Xue, Y. Zhou, Y. Wang, X. Ding, J. Sun and T. Lookman, Determining multi-component phase diagrams with desired characteristics using active learning, Advanced Science, 2021, 8(1), 2003165.
32. J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. Batchelor, T. Löffler, V. A. Mints, L. Banko, M. Arenz and A. Savan, Bayesian optimization of high-entropy alloy compositions for electrocatalytic oxygen reduction, Angew. Chem., 2021, 133(45), 24346–24354.
33. X. Mi, L. Dai, X. Jing, J. She, B. Holmedal, A. Tang and F. Pan, Accelerated design of high-performance Mg-Mn-based magnesium alloys based on novel Bayesian optimization, J. Magnesium Alloys, 2024, 12(2), 750–766.
34. B. Cantor, Multicomponent and high entropy alloys, Entropy, 2014, 16(9), 4749–4768.
35. C. Wen, Y. Zhang, C. Wang, H. Huang, Y. Wu, T. Lookman and Y. Su, Machine-Learning-Assisted Compositional Design of Refractory High-Entropy Alloys with Optimal Strength and Ductility, Engineering, 2024, 46, 214–223.
36. K. Yuan, J. Shi, W. Aftab, M. Qin, A. Usman, F. Zhou, Y. Lv, S. Gao and R. Zou, Engineering the thermal conductivity of functional phase-change materials for heat energy conversion, storage, and utilization, Adv. Funct. Mater., 2020, 30(8), 1904228.
37. G. L. Hart, T. Mueller, C. Toher and S. Curtarolo, Machine learning for alloys, Nat. Rev. Mater., 2021, 6(8), 730–755.
38. M. Suvarna, T. Zou, S. H. Chong, Y. Ge, A. J. Martín and J. Pérez-Ramírez, Active learning streamlines development of high performance catalysts for higher alcohol synthesis, Nat. Commun., 2024, 15(1), 5844.
39. Y. Xian, P. Dang, Y. Tian, X. Jiang, Y. Zhou, X. Ding, J. Sun, T. Lookman and D. Xue, Compositional design of multicomponent alloys using reinforcement learning, Acta Mater., 2024, 274, 120017.
40. C. Oh, J. Tomczak, E. Gavves and M. Welling, Combinatorial Bayesian optimization using the graph cartesian product, Adv. Neural Inf. Process. Syst., 2019, 32, 2914–2924.
41. S. Daulton, X. Wan, D. Eriksson, M. Balandat, M. A. Osborne and E. Bakshy, Bayesian optimization over discrete and mixed spaces via probabilistic reparameterization, Adv. Neural Inf. Process. Syst., 2022, 35, 12760–12774.
42. E. C. Garrido-Merchán and D. Hernández-Lobato, Dealing with categorical and integer-valued variables in Bayesian optimization with gaussian processes, Neurocomputing, 2020, 380, 20–35.
43. B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. De Freitas, Taking the human out of the loop: A review of Bayesian optimization, Proc. IEEE, 2015, 104(1), 148–175.
44. J. Wu, M. Poloczek, A. G. Wilson and P. Frazier, Bayesian optimization with gradients, Adv. Neural Inf. Process. Syst., 2017, 30, 5273–5284.
45. H. Zhang, H. Fu, W. Li, L. Jiang, W. Yong, J. Sun, L. Q. Chen and J. Xie, Empowering the Sustainable Development of High-End Alloys via Interpretive Machine Learning, Adv. Mater., 2024, 2404478.
46. Q. Wei, B. Cao, L. Deng, A. Sun, Z. Dong and T.-Y. Zhang, Discovering a formula for the high temperature oxidation behavior of FeCrAlCoNi based high entropy alloys by domain knowledge-guided machine learning, J. Mater. Sci. Technol., 2023, 149, 237–246.
47. Q. Wei, B. Cao, H. Yuan, Y. Chen, K. You, S. Yu, T. Yang, Z. Dong and T.-Y. Zhang, Divide and conquer: Machine learning accelerated design of lead-free solder alloys with high strength and high ductility, npj Comput. Mater., 2023, 9(1), 201.
48. D. H. Mok, H. Li, G. Zhang, C. Lee, K. Jiang and S. Back, Data-driven discovery of electrocatalysts for CO2 reduction using active motifs-based machine learning, Nat. Commun., 2023, 14(1), 7303.
49. X. Wan, Z. Li, W. Yu, A. Wang, X. Ke, H. Guo, J. Su, L. Li, Q. Gui and S. Zhao, Machine learning paves the way for high entropy compounds exploration: challenges, progress, and outlook, Adv. Mater., 2023, 2305192.
50. K. N. Sasidhar, N. H. Siboni, J. R. Mianroodi, M. Rohwerder, J. Neugebauer and D. Raabe, Enhancing corrosion-resistant alloy design through natural language processing and deep learning, Sci. Adv., 2023, 9(32), eadg7992.
51. F. Archetti, and A. Candelieri, Bayesian Optimization and Data Science, Springer, 2019.
52. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, Pytorch: An imperative style, high-performance deep learning library, Adv. Neural Inf. Process. Syst., 2019, 32, 8026–8037.
53. M. Balandat, B. Karrer, D. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, BoTorch: A framework for efficient Monte-Carlo Bayesian optimization, Adv. Neural Inf. Process. Syst., 2020, 33, 21524–21538.
54. B. D. Flury, Acceptance–rejection sampling made easy, SIAM Rev., 1990, 32(3), 474–476.
55. J. Wang, H. Kwon, H. S. Kim and B.-J. Lee, A neural network model for high entropy alloy design, npj Comput. Mater., 2023, 9(1), 60.
56. H. Singh, N. Misra, V. Hnizdo, A. Fedorowicz and E. Demchuk, Nearest neighbor estimates of entropy, Am. J. Math. Manag. Sci., 2003, 23(3–4), 301–321.
57. Y. Seo, L. Chen, J. Shin, H. Lee, P. Abbeel, and K. Lee, State entropy maximization with random encoders for efficient exploration, International Conference on Machine Learning, PMLR, 2021, pp. 9443–9454.
58. S. Zhai, H. Xie, P. Cui, D. Guan, J. Wang, S. Zhao, B. Chen, Y. Song, Z. Shao and M. Ni, A combined ionic Lewis acid descriptor and machine-learning approach to prediction of efficient oxygen reduction electrodes for ceramic fuel cells, Nat. Energy, 2022, 7(9), 866–875.
59. Y. Zhang, C. Wen, P. Dang, T. Lookman, D. Xue and Y. Su, Toward ultra-high strength high entropy alloys via feature engineering, J. Mater. Sci. Technol., 2024, 200, 243–252.
60. A. Damianou, and N. D. Lawrence, Deep gaussian processes, Artificial intelligence and statistics, PMLR, 2013, pp. 207–215.
61. S. W. Ober, C. E. Rasmussen, and M. van der Wilk, The promises and pitfalls of deep kernel learning, Uncertainty in Artificial Intelligence, PMLR, 2021, pp. 1206–1216.
62. S. Ament, S. Daulton, D. Eriksson, M. Balandat and E. Bakshy, Unexpected improvements to expected improvement for Bayesian optimization, Adv. Neural Inf. Process. Syst., 2023, 36, 20577–20612.
63. Y. Jia, Y. Xian, Y. Xu, P. Dang, X. Ding, J. Sun, Y. Zhou, and D. Xue, Universal Semantic Embeddings of Chemical Elements for Enhanced Materials Inference and Discovery, arXiv, 2025, preprint, arXiv:2502.14912,  DOI:10.48550/arXiv.2502.14912.
64. Y. Zhang, C. Wen, P. Dang, X. Jiang, D. Xue and Y. Su, Elemental numerical descriptions to enhance classification and regression model performance for high-entropy alloys, npj Comput. Mater., 2025, 11(1), 75.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00080g

---