Open Access Article
Open Access ArticleAutomated structural analysis of small angle scattering data from common nanoparticles via machine learning
Graham
Roberts
 a,
Mu-Ping
Nieh
a,
Mu-Ping
Nieh
 bc,
Anson W. K.
Ma
bc,
Anson W. K.
Ma
 bc and
Qian
Yang
bc and
Qian
Yang
 *a
*a
aSchool of Computing, University of Connecticut, Storrs, CT, USA. E-mail: qyang@uconn.edu
bChemical & Biomolecular Engineering Department, University of Connecticut, Storrs, CT, USA
cPolymer Program, Institute of Materials Science, University of Connecticut, Storrs, CT, USA
First published on 30th April 2025
Abstract
Billions of dollars have been invested in recent years to build up national scattering facilities around the world with more advanced configurations and faster data collection for small angle scattering (SAS), a technique that enables in situ structural analysis of nanoparticles (NP) under stringent sample environments. However, the interpretation of experimental SAS data is typically a slow process that requires significant domain expertise, leading to high-throughput scattering facilities such as synchrotron scattering centers collecting large quantities of data that may potentially be left unanalyzed. Here, we present a fast and data-efficient machine learning (ML) framework for identifying basic NP morphologies (spherical, cylindrical and discoidal geometries) and their corresponding structural parameters. The trained models take as input scattering curves with minimal pre-processing, and are able to identify morphology and structural dimensions from experimental curves with comparable accuracy to human experts. Critically, design choices that facilitate the practical application of ML models in scattering facilities are discussed, including ease of training, extrapolability outside of the parameter range of training data, and verifiability of predictions. The enhanced data analysis efficiency enabled by applying ML models to real-time in situ analysis of SAS data has the potential to revolutionize the utilization of synchrotron and neutron scattering facilities for probing nanostructures.
The properties of nanomaterials are closely related to not only their chemical compositions but also their structures. Small angle scattering (SAS), including small angle X-ray scattering (SAXS) and small angle neutron scattering (SANS), is a powerful NP characterization method that can provide global and internal morphology and structure.1,2 Many governments have invested billions of US dollars3,4 to design and construct scattering infrastructures of high-flux synchrotron or neutron sources, where statistically meaningful SAS data are attainable in seconds to a few minutes. Timely analysis of SAS data, however, is a time consuming and challenging endeavor for nanoscience researchers. Analyzing a single curve can range from several minutes to weeks or more of work; for this reason, a large portion of collected SAS curves (especially SAXS curves) is never analyzed. It also prevents experimentalists from being able to incorporate real-time feedback to adjust subsequent experiments. Thus, there is an increasing need and demand for automated analysis tools that can quickly recover the morphology and structure of the NP from a given scattering curve.
One typical SAS analytical method involves selecting a NP morphology based on user expertise and fitting the data to a known scattering model for that morphology. SAS data are represented by the scattering intensity, I, as a function of the scattering vector,  , where λ and θ are the wavelength and scattering angle, respectively. The forward model is derived from the square of the Fourier transform of a density function of the assumed morphology, and is parameterized by the structural parameters of the morphology, such as sphere radius. Fitting a scattering curve to a model identifies these parameters by solving a non-convex optimization problem to maximally match the I(q) obtained by the forward model with the observed data. This process relies on the researcher first selecting the correct morphology, and if not, repeating the process until they find a morphology for which a good fit can be found. Selecting the correct morphology is difficult for a multitude of reasons. One reason is that many morphologies exist along a single continuous manifold, with no clear boundary between them. For example, the scattering curve for a solid particle is equivalent to one for a particle with a shell in the limit that the shell becomes infinitely thin, or with any shell thickness if the shell's scattering length density is to similar to that of the solvent the particles are suspended in. Another reason is that even particles with distinct morphologies may exhibit scattering curves that are virtually indistinguishable in some parameter ranges, such as large flat disks versus large core–shell spheres, or small spheres versus small cylinders/disks with small aspect ratios.
, where λ and θ are the wavelength and scattering angle, respectively. The forward model is derived from the square of the Fourier transform of a density function of the assumed morphology, and is parameterized by the structural parameters of the morphology, such as sphere radius. Fitting a scattering curve to a model identifies these parameters by solving a non-convex optimization problem to maximally match the I(q) obtained by the forward model with the observed data. This process relies on the researcher first selecting the correct morphology, and if not, repeating the process until they find a morphology for which a good fit can be found. Selecting the correct morphology is difficult for a multitude of reasons. One reason is that many morphologies exist along a single continuous manifold, with no clear boundary between them. For example, the scattering curve for a solid particle is equivalent to one for a particle with a shell in the limit that the shell becomes infinitely thin, or with any shell thickness if the shell's scattering length density is to similar to that of the solvent the particles are suspended in. Another reason is that even particles with distinct morphologies may exhibit scattering curves that are virtually indistinguishable in some parameter ranges, such as large flat disks versus large core–shell spheres, or small spheres versus small cylinders/disks with small aspect ratios.
Machine learning (ML) has proven to be a powerful tool for analyzing data, particularly when the analysis is very time consuming for human researchers. Applying ML to SAS analysis has garnered significant interest from the community in recent years,5,6 and the potential integration of ML into SAS workflows to enable accelerated analysis for applications such as automated design of experiments and active learning of phase diagrams has been demonstrated.7 ML approaches for deriving the morphology of unconventional structures that do not correspond to simple forward models have recently been successful in tackling challenging inverse analysis problems.8 However, these specialized methods can be more computationally expensive than necessary for in situ and large-scale analysis of conventional materials. For conventional structures, existing works focusing on morphology classification and structural parameter prediction typically attempt to explore the efficacy of using various ML algorithms to build a single multi-class classifier over a large set of candidate morphologies.9–15 While reasonable overall accuracies are achieved given large training datasets, this approach tends to result in lower accuracy in distinguishing between common but similar morphologies such as spheres and core–shell spheres. Neural network-based approaches also require about an order of magnitude larger datasets than classical models and more expensive training procedures.13–15
In this work we demonstrate a machine learning (ML) pipeline for SAS analysis that is designed to capture hierarchical relationships between similar morphologies, thus increasing multi-class classification accuracy, while utilizing less training data and enabling fast inference, making it a practical approach for integration with experiments at scattering facilities. This pipeline is illustrated in Fig. 1. The first stage is a hierarchical multi-class classification model which identifies the morphology of the particle. We focus this work on six common but potentially difficult-to-distinguish morphologies: cylinder, disk, sphere, and their core–shell counterparts, and demonstrate how our hierarchical approach is well-suited to physics-informed multi-class classification. The second stage is a set of regression models, one for each morphology and applicable structural parameter such as radius, length, and shell thickness. Finally and importantly, the predicted morphology and structural parameters can be passed into the corresponding forward model to verify the correctness of the ML predictions and ensuring their trustworthiness. Optionally, the predicted parameters can be used to initialize fitting in the traditional manner to enable rapid fine-tuning. We demonstrate our pipeline first on thousands of simulated curves, including structures with parameter ranges dramatically different from our training set, to demonstrate the robustness of our ML models to extrapolated data. Then, we demonstrate the accuracy of our ML pipeline in making predictions on experimental curves drawn from the literature, while having been trained entirely on simulated data. Our light-weight ML models use only classical algorithms without deep learning, making them easy to train. Most importantly, they are capable of making predictions on thousands of scattering curves within seconds, significantly enhancing the efficiency with which SAS data can be analyzed and potentially unlocking new experimental designs for scattering science.
1 Methods
1.1 Dataset generation
We train our machine learning models using simulated data generated by the SASView open source library for small angle scattering data.16 The prediction capability of machine learning models depends on the quality of the data used to train them. We simulate our data with class balance between morphologies to ensure our model and performance metrics are not affected by imbalance in the dataset. To improve our model performance, we intentionally leverage physical understanding of the morphologies being considered to over-sample data theoretically near decision boundaries in the classification task. We also create a dataset for testing the extrapolation capabilities of the classifier (i.e., outside the range of the training data) that contains scattering curves corresponding to larger aspect ratios and shell-to-total ratios than those in our training data, as explained below.There are several steps in our data generation process. First, we determine parameter ranges to vary our simulations over. We then simulate the curves using SASView,16 sampling at random over the selected parameter range, and using a q-vector ranging from 3.7 × 10−3 to 2.6 × 10−1 (Å−1). It should be noted that polydispersity is one of the varied parameters, and it has a similar effect as instrument resolution on the scattering patterns. Therefore, the simulated data with adjusted polydispersity would reflect truthfully the experimental data. We also vary the scattering length density, which varies the contrast between the studied objects and matrix, leading to similar effects on the scattering curve to variations in scale. Next, we screen the simulated data and remove any with non-physical simulation artifacts, such as sharp pulses in the scattering curve caused by numerical approximations (such as integration or near-zero values). Then, we shift the data to mitigate the effects of confounding variables such as concentration and background intensity. This is a simple vertical shift in log space to maintain the structure of the curve and the relative values between features. Finally, these scattering curves are the “feature vectors” that we use as input to our machine learning models, which we train to predict the corresponding “labels” for each curve (the morphology in the classification step, and the structural parameters in the regression step).
While traditional k-fold cross-validation was used for model selection, with k = 5, we make a critical departure from convention by using only 20% of the data for training and the majority 80% for validation. Due to the hierarchical nature of our multi-class classification algorithm (discussed in the next section), there are an exponentially large number of possible final hyperparameter sets corresponding to the hyperparameters for each of the intermediate classifiers. Using significantly more validation data than training data helps to avoid overfitting the model selection process.17 We find empirically that this 20–80 split significantly outperforms the more traditional 80–20 split in our problem.
1.2 Classification
Our classification method leverages physical knowledge to solve the multi-class classification problem hierarchically along physically-motivated decision boundaries. The first binary classification problem decides between spherical curves and cylindrical curves. Next, each branch decides between solid and core shell curves. It is worth noting that there is a continuous change between solid and core–shell scattering curves in several different cases. The first is in the limit that the shell thickness approaches zero. The second is in the case that the core diameter or length approaches zero, so that the shell takes up the entire volume. The last is in the case that the scattering length density of the shell is equal to either the scattering length density of the solvent or of the core. In all of these cases a technically core–shell morphology is indistinguishable from a solid. Finally, in the last level of the classification problem, we separate cylinders from disks. There is again a continuous distribution bridging the cylinder and disk classes, which meet in the case where the diameter and length are equal. We find empirically that better performance can be achieved by first resolving the challenging decision boundary between solid and core–shell morphologies before moving on to the final decision separating cylinders and disks. We also tested other potential orderings of the hierarchical classification, such as first separating all solids from all core–shell morphologies, but the hierarchical structure depicted in Fig. 3 achieved the best validation performance and was thus chosen as our final model. A binary kernel support vector classifier (SVC) is trained for each decision within the tree, and hyperparameters are independently optimized for each SVC.18,19 We note that support vector classifiers are significantly easier to train than neural network models since they involve solving a convex optimization problem.1.3 Regression
We use kernel ridge regression18 (KRR), a classical machine learning algorithm for nonlinear regression, to build models for predicting structural parameters from the scattering curves. The choice of kernel (radial basis function, polynomial, and cosine) and kernel hyperparameters are optimized using 10-fold cross-validation. A separate KRR model was trained for each parameter for each morphology. Each regression model was trained on scattering curves of the correct morphology in the respective training set. We also generate a separate calibration dataset to enable statistically rigorous uncertainty quantification of regression predictions using conformal prediction.20,21For many structural parameters, such as the radius of spheres, the scattering curves vary smoothly with respect to the structural parameter and predictive regression models are easy to train; a few exceptions to this occur for core–shell morphologies. The training, validation and test datasets are drawn from the same 3 × 3 grid as the classification task, but we do not explore extrapolation of the regression models since the ranges of each parameter are defined by the effective probing range for our q-range. The regression data are the same data used for classification with no additional pre-processing steps, enabling data to be directly passed from the classifier to the regressor in the pipeline.
2 Results
2.1 Classification
Simulated data from the software package SASView16 are used to build a training set containing 2000 scattering curves of each morphology (six morphologies in total), and a test set containing 1000 curves of each morphology. The performance of our hierarchical classification model is compared against those of several off-the-shelf multi-class classification algorithms that have been tuned for optimal hyperparameters: support vector classifiers (SVC), k-nearest neighbors (KNN), and random forest (RF).18,19,22 Standard soft-margin SVC finds the classification boundary which maximizes the width of a margin around it, with as few points inside the margin and incorrect predictions as possible. When used for multiclass classification, either a one-vs-all or one-vs-rest ensemble of binary models is used to make a final class prediction. This is different from our hierarchical multi-class classification approach, which trains a binary SVC classifier over different subsets of data for each decision in our hierarchical classification tree. KNN is a simple classifier in which the predicted class of a new test point is voted on by its k nearest neighbors in the training set. For KNN, the similarity metric we use for defining nearest neighbors is the Euclidean distance in n-dimensional feature space, where n is the number of features, e.g. the number of distinct q values sampled. RF classifiers are ensembles of decision trees, each of which hierarchically splits data based on features that maximally distinguish between classes. We note that our hierarchical approach is again conceptually different from decision-tree based methods: our algorithm splits on predicted labels, not given features. All off-the-shelf classifiers are provided by the scikit-learn library.23We first measure the expected predictive performance of our model when interpolating within the parameter space spanned by the training data. We divide the data set into a 3 × 3 grid of bins according to the aspect ratio and the shell-to-total ratio, as described in Methods. Four of the bins are used for both training and test, and the bin with the smallest aspect ratio and shell-to-total ratio data is sampled twice as much as the other three for training, since these data are closest to the true decision boundary between cylinders and disks, and between solid and core–shell. The other five bins containing curves from parameter space outside the range of training data are reserved for testing only.
The performance of our hierarchical classification model compared against those of off-the-shelf multi-class classification algorithms is shown in Table 1. All test sets have balanced class distributions and thus prediction accuracy (number of correct classifications divided by total number of datapoints) is an appropriate performance metric. We also report the F1-score averaged over all classes (macro F1-score),24 which captures more information on the per-class performance than accuracy. The F1-score is defined as the harmonic mean of precision and recall, or equivalently,
| Hierarchical (ours) | SVC | KNN | RF | |
|---|---|---|---|---|
| Accuracy|F1 | Accuracy|F1 | Accuracy|F1 | Accuracy|F1 | |
| Full test set | 0.88|0.88 | 0.86|0.86 | 0.81|0.80 | 0.74|0.73 |
| Extrapolation only | 0.86|0.85 | 0.83|0.82 | 0.77|0.76 | 0.71|0.69 |
| Scale extrapolation | 0.86|0.86 | 0.85|0.84 | 0.79|0.77 | 0.74|0.72 |
We first test the model performance on data selected from all nine data bins equally. We also measure the performance of each model when tested only on data in the extrapolation test set consisting of the five highest aspect and/or shell-to-total ratio bins, from which no training data were drawn. Our hierarchical model yields higher accuracy in both extrapolation (>0.86) and the full test dataset (>0.88) than other off-the-shelf-classifiers. As expected, extrapolation was more challenging for all models. However, our model was able to achieve the same performance in extrapolation as the next best performing model (SVC with one-vs-rest multi-class classification) over the full test set. Finally, we report the extrapolation performance of our model on a third test set, called scale extrapolation, in which the scale parameter is varied between 0.5 and 1.5. Since scale can be an arbitrary constant that depends on experimental conditions and choices of units, we would like to demonstrate that our classification model is robust to differences in scale, even though this invariance is not explicitly enforced by the algorithm. In our training data, the scale parameter is held constant but scattering length density is varied. Our results in Table 1 show that this variation is sufficient to allow our classification model to be robust to changes in scale.
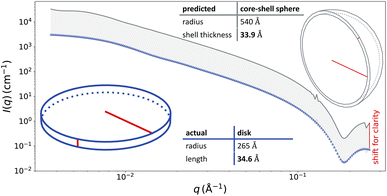
Due to the degeneracy of SAS data, such that scattering curves can be possibly described by scattering models corresponding to multiple different morphologies, the ability of ML models to achieve “acceptable” classifications is higher than that automatically measured by comparing with test set labels. One example of such an acceptable misclassification is when a NP with an ultra thin shell, or a null contrast between the core and the shell, is mistaken as a solid NP. A more rare situation is shown in Fig. 4. Here, a curve simulated using a disk morphology was predicted to be a core–shell sphere and can be fit well by a core–shell sphere model. The ground truth scattering curve corresponding to the disk morphology and the predicted best fit scattering curve using a core–shell sphere morphology share similar key features: two slope transitions of the scattering intensity from plateau to q Å−2 decay and then from q Å−2 decay to q Å−4 decay, followed by a minimum intensity and a high-q peak from low-q to high-q. As a result, both the discoidal and core–shell spherical models can fit the data indistinguishably well, taking into account measurement uncertainty and polydispersity. The intuition for why this occurs is revealed by the structural parameters. The true disk morphology has a large radius and is relatively thin. The best fit core–shell sphere morphology has an even larger radius, with a predicted shell thickness almost equivalent to the ground truth disk thickness. One could imagine that local regions of the shell on the predicted core–shell sphere have a similar morphology to the ground truth disk – similar to predicting that the morphology is in the shape of the earth's crust when the ground truth is a single tectonic plate.
To further validate the prevalence of these types of degeneracy, we randomly sampled ten misclassified curves and found that five of them were able to be fit by the “incorrect” predicted models well. This suggests that the accuracy of our ML prediction should be higher than the values listed in Table 1, presumably larger than 0.9, presenting a significant breakthrough in determining morphology from SAS data.
Finally, in Table 2, we compare our classification results to the performance of two state-of-the-art classifiers11,13 from the literature. Both of these publications report recall, which measures how many datapoints of a given class are classified correctly. As with most works in the literature, these methods simultaneously consider a large number of possible morphologies. While this increases the complexity of the multi-class classification problem so that a direct one-to-one performance comparison should not be made, we can see that our model achieves better performance on every mutually considered morphology while requiring an order of magnitude less training data per class. Our algorithm is also easy and fast to train – a new training dataset of a similar size can be automatically generated in minutes, and similarly a full new hierarchical classification model can be trained (including hyperparameter tuning) in minutes. Thus, what we have developed is an algorithmic approach that can be easily customized to new experiments, rather than a single pre-trained model that may have trouble extrapolating to new experimental requirements. We note that the smaller subset of morphologies being considered by the hierarchical tree is an advantage that correlates well with how small angle scattering is used in practice. Typically, an experimentalist will have a general idea of the subset of morphologies they expect and knowledge of the q-range their experiment will include. With this information, our approach enables a customized hierarchical classification model and set of regression models to be quickly and automatically built for each new experiment.
| Algorithmic approach | # Training curves per class | Recall | Notes | |
|---|---|---|---|---|
| Transformer neural network (SASformer)13 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Cylinder | 0.91 | Cylinders and disks are considered the same morphology. Covers a broad set of 55 classes |
| Sphere | 0.88 | |||
| CS-Cylinder | 0.82 | |||
| CS-Sphere | 0.78 | |||
| Weighted k-nearest neighbors + Gaussian processes + stochastic gradient descent11 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Sphere | 0.51 | Covers 39 classes, of which only sphere and core–shell sphere are shared with our paper |
| CS-Sphere | 0.80 | |||
| Hierarchical model + support vector classifier | 1660 | Cylinder | 0.94 | This work |
| Disk | 0.87 | |||
| Sphere | 0.98 | |||
| CS-Cylinder | 0.83 | |||
| CS-Disk | 0.84 | |||
| CS-Sphere | 0.85 | |||
2.2 Regression
For each morphology, we trained separate regression models for each structural parameter of interest (such as radius, length and shell thickness). The test performance of these models are displayed in Table 3. The performance metrics used are R2 score and the mean absolute percentage error (MAPE):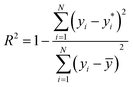 | (1) |
 | (2) |
 is its corresponding predicted value, and ȳ is the mean label value over the data. An R2 score of 1 indicates a perfectly predictive model, while R2 ≤ 0 indicates a model worse than a constant trivial model that simply predicts ȳ for all datapoints. Most morphologies have structural parameters that the regression models can capture with an R2 > 0.9, although the presence of shells does hinder the ability of some structural parameters to be identifiable from the scattering curves. For context, in Table 3 we also provide baseline values for R2 and MAPE that correspond to a trivial constant model; these baseline values capture information about the spread of the labels in the training data and provide a measure of the difficulty of the learning problem. In all cases the R2 should be higher than that of the baseline and the MAPE lower.
is its corresponding predicted value, and ȳ is the mean label value over the data. An R2 score of 1 indicates a perfectly predictive model, while R2 ≤ 0 indicates a model worse than a constant trivial model that simply predicts ȳ for all datapoints. Most morphologies have structural parameters that the regression models can capture with an R2 > 0.9, although the presence of shells does hinder the ability of some structural parameters to be identifiable from the scattering curves. For context, in Table 3 we also provide baseline values for R2 and MAPE that correspond to a trivial constant model; these baseline values capture information about the spread of the labels in the training data and provide a measure of the difficulty of the learning problem. In all cases the R2 should be higher than that of the baseline and the MAPE lower.
| Morphology | Param | R 2 | Base. R2 | MAPE | Base. MAPE |
|---|---|---|---|---|---|
| Cylinder | Radius | 0.97 | −0.08 | 0.16 | 1.09 |
| Length | 0.917 | −0.08 | 0.104 | 0.664 | |
| Disk | Radius | 0.960 | −0.011 | 0.078 | 0.491 |
| Length | 0.938 | −0.232 | 0.262 | 1.27 | |
| Sphere | Radius | 1.0 | −0.002 | 0.005 | 0.883 |
| CS-Cylinder | Radius | 0.895 | −0.027 | 0.107 | 0.384 |
| Length | −0.17 | −1.45 | 0.330 | 0.377 | |
| Shell | 0.448 | −1.09 | 0.251 | 0.387 | |
| CS-Disk | Radius | 0.354 | −0.745 | 0.193 | 0.246 |
| Length | 0.693 | −0.209 | 0.262 | 0.641 | |
| Shell | 0.274 | −0.05 | 0.312 | 0.463 | |
| CS-Sphere | Radius | 0.908 | −0.009 | 0.189 | 0.964 |
| Shell | 0.502 | −0.177 | 0.334 | 0.621 |
2.3 Experimental data
The classification and regression models have also been evaluated with a collection of eight experimental SAS curves obtained from literature. The experimental curves drawn from the literature had a variety of different q-ranges. To match the experimental data to the expected input to our ML models, we first remove all data outside of our q-range. We then use linear interpolation to match the grid sampling of q in our feature vector. Finally, if there are missing values at low-q or high-q, we use a constant fit to extrapolate at those values. The intensity at all missing low-q values are set to equal the intensity at the lowest available q, since it is desirable for scattering curves to have a plateau at low q. Similarly, the intensity at all missing high-q values are set to equal the intensity at the highest available q. Finally, we apply the same vertical shift to the scattering curve as we did to the simulated training data.Fig. 5 and Table 4 show the outcomes from the classification and regression models and their performance evaluated on these experimental curves. Our ML models classify most morphologies accurately and predict reasonable values for corresponding structural parameters. The misclassifications are justified as follows. In (A) and (D), our model predicts a core–shell morphology with a vanishingly small shell, which effectively agrees with the reported corresponding solid morphologies. In (C), the reported morphology (flexible cylinder) is not one of the six morphologies considered by our classification model; however, the predicted morphology (core–shell cylinder) gives a close representation. In (E), the correct spherical shape is predicted by our model, but no shell is detected in contrast to the reported morphology. We note in this case a separate manual optimization by a human expert found a smaller shell than the reported value. Using the SAS models of the morphology identified by ML, reasonable fits to the experimental data could still be found. We also find that the corresponding estimated structural parameters are generally in good agreement with reported values, yielding reasonable predicted curves in comparison with the corresponding experimental ones. We include with each parameter prediction the 95% confidence intervals calculated with a calibration dataset using conformal prediction, which provides statistically rigorous uncertainty estimates.20,21 Note that several curves (A, C, and D) have no clear plateau at low q due to the probing range, resulting in high uncertainty in the largest parameter, which is to be expected. Finally, we use the predicted morphology and structural parameters to initialize further fitting of the data using traditional optimization methods. Since the ML models provided reasonable initial estimates, this enabled fast convergence during the optimization and reduced the risk of being trapped in an undesirable local minima. We show in Fig. 5 that this fine-tuning procedure achieved good agreement with experimental data in all cases.
 | ||
| Fig. 5 We test our trained ML models on several experimental scattering curves from the literature. The red triangles correspond to the input experimental curves. The teal lines are the scattering curves simulated by SASView using the structural parameters predicted by the ML model. The black lines are simulated scattering curves using the best fit from SASView, optimized starting from our predictions. All morphologies and parameter values are listed in Table 4. | ||
| Curve | Parameter | Prediction (95% CI) | Prediction + opt. | Manual + opt. | Literature |
|---|---|---|---|---|---|
| A | Morph. | CS-Cylinder | CS-Cylinder | Cylinder | Cylinder |
| Radius (Å) | 64 (19, 111) | 98.52 | 77.59 | 100 | |
| Length (Å) | 878 (166, 1646)* | 450.82 | 308.57 | 410 | |
| Shell (Å) | 14 (0**, 77) | 5.03 | N/A | N/A | |
| B | Morph. | Disk | Disk | Disk | Disk |
| Radius (Å) | 123 (90, 157) | 142.82 | 145 | 145 | |
| Length (Å) | 55 (40, 69) | 52.71 | 51 | 51 | |
| C | Morph. | CS-Cylinder | CS-Cylinder | Cylinder | Flex. cylinder |
| Radius (Å) | 53 (35, 71) | 19 | 22 | 13 | |
| Length (Å) | 801 (275, 1354)* | ≥1600 | ≥1600 | ≥1000 | |
| Shell (Å) | 0** | ≈0 | N/A | N/A | |
| D | Morph. | CS-Disk | CS-Disk | Disk | Disk |
| Radius (Å) | 575 (362, 783)* | 656.7 | ≥1000 | ≥3000 | |
| Length (Å) | 168 (80, 266) | 117.9 | 120 | 110 | |
| Shell (Å) | 52 (3100) | 286.5 | N/A | N/A | |
| E | Morph. | Sphere | Sphere | CS-Sphere | CS-Sphere |
| Radius (Å) | 146 (145, 147) | 146.3 | 115 | 130 | |
| Shell (Å) | N/A | N/A | 32 | 70 | |
| F | Morph. | Disk | Disk | Disk | Disk |
| Radius (Å) | 124 (90, 158) | 154.2 | 154.2 | 141 | |
| Length (Å) | 54 (40, 68) | 52.5 | 50.0 | 42 | |
| G | Morph. | CS-Sphere | CS-Sphere | CS-Sphere | CS-Sphere |
| Radius (Å) | 135 (111, 158) | 104.7 | 104.7 | 98 | |
| Shell (Å) | 84 (11, 160) | 36.4 | 36.4 | 36 | |
| H | Morph. | CS-Sphere | CS-Sphere | CS-Sphere | CS-Sphere |
| Radius (Å) | 96 (77, 114) | 45.1 | 45.0 | 73 | |
| Shell (Å) | 42 (0**, 139) | 45.7 | 45.0 | 25 |
3 Discussion
Our ML pipeline is able to accurately and automatically identify the morphology and structural parameters of NP in a matter of seconds, enabling in situ analysis. We highlight several key design decisions in our ML framework that make it particularly suited for practical application at scattering facilities. First, our method is designed to increase accuracy by focusing on a small number of morphologies of interest in a particular experiment, the typical use case for scattering scientists, rather than a general classifier over all possible morphologies. This allows our model to focus on capturing hierarchical and other relationships between the selected morphologies to derive better multi-class classification boundaries with fewer data. For example, the set of solid spheres should be considered a subset of the set of particles with core–shell spheres, since the former are a special case of the latter in which the shell has either no contrast or no thickness, or the core becomes vanishingly small. Cylinders and disks also fall on the same continuous manifold, with an intuitive boundary where diameter becomes greater than length. We use a physics-informed hierarchical scheme for multi-class classification that is able to capture and leverage these relationships among morphologies, as shown in Fig. 3. We demonstrate that using a series of binary classifiers separating scattering curves into increasingly smaller subsets outperforms classical multi-class classification methods, which typically involve extensions of binary classifiers using one-vs-one or one-vs-all schemes, non-parametric nearest neighbor approaches, or decision tree-based methods that split data on input features.9 We note in particular that our hierarchical method differs from decision trees in that our tree nodes split based on a fully trained binary classifier, and not just on input features. Each split can itself utilize any classification method, including SVC, KNN, and RF. Crucially, these models are tuned for hyperparameters separately. This enables two things. First, the final overall multi-class classification boundary can be much more complex, since it does not assume the same complexity (controlled by tuned hyperparameters) at each segment of the boundary. It is possible, for example, to learn a much simpler boundary between spheres and cylinders/disks, than between spheres and core–shell spheres. Second, while the final overall classification boundary can be complex, each individual decision boundary that is being learned can be simple since each stage of the hierarchical classifier can focus on a limited number of differences between logical subsets of morphologies, rather than all differences at once. This allows us to utilize less training data for greater accuracy, since simpler boundaries require fewer datapoints to learn. This is in contrast to neural network-based approaches, which also enable flexibility in the decision boundary but typically requires an order of magnitude more training data.13,15Our second key design decision is to construct the model specifically to extrapolate well to structural parameter ranges outside of those sampled by the training data. It is especially important to develop ML methods that are robust to extrapolation in scientific contexts, where it is likely that new data of interest is different from existing known data. We achieve this by designing the splitting of data into training, validation, and test sets to capture extrapolation, as described in detail in the Methods section. When there are no good physics-based estimates for the structural parameters in a particular experiment, models that are trained to extrapolate well rather than simply interpolate correctly are of greater practical utility. Additionally, even when structural parameter ranges can be reasonably constrained a priori, models that can extrapolate better are more likely to have captured underlying patterns in the data, thus exhibiting increased performance overall.31
Finally, our ML pipeline highlights the verification capabilities of a framework that simultaneously classifies morphologies and predicts corresponding structural parameters. The structural parameters suggested by regression are typically sufficiently accurate that even if further optimization is needed, the optimizer will quickly converge due to initialization at good initial values. Researchers are encouraged to verify the output of the ML models using the predicted morphology's forward model to ensure confidence in the results. We find that even in cases where the model used to generate a simulated scattering curve disagrees with the results of the classifier, a correct match is often found due to the inherent degeneracy of SAS curves.
4 Conclusion
As scattering instrumentation becomes more advanced, the rate of data collection is outstripping that of data analysis by human experts, creating a research bottleneck. This work demonstrates ML models which rapidly and automatically identify both the morphology and structural parameters of NP from SAS measurements, enabling in situ analysis of scattering data. Our hierarchical classification algorithm for morphology prediction leads to better predictive performance than standard off-the-shelf ML algorithms, especially when extrapolating outside of the parameter space of the training data. Furthermore, our method utilizes only classical ML approaches, which require less training data, are easier to train, and have faster inference time than more complex neural network-based approaches. Empirical results on both simulated and experimental data from the literature demonstrate that our ML models, which were trained solely on simulated data, are sufficiently accurate for analysis of experimental data. We discuss how our and similar ML frameworks that simultaneously predict morphology and structural parameters are compatible with verification and refinement of ML predictions to ensure trust in scientific conclusions. Our approach highlights how carefully designed ML pipelines for inverse analysis of scattering data can enable practical implementation in laboratories, significantly increasing the efficiency with which data is analyzed and potentially transforming experimental paradigms in scattering science.Data availability
Data and source code for this article, including all training and test curves as well as scripts to reproduce experiments, are available in the AutomatedSAS Github repository, DOI: https://doi.org/10.5281/zenodo.15283677.Author contributions
Conceptualization: Mu-Ping Nieh, Anson W. K. Ma, Qian Yang; Data curation: Graham Roberts, Mu-Ping Nieh; formal analysis: Graham Roberts, Mu-Ping Nieh; funding acquisition: Mu-Ping Nieh, Qian Yang; investigation: Graham Roberts; methodology: Graham Roberts, Mu-Ping Nieh, Qian Yang; project administration: Qian Yang; resources: Mu-Ping Nieh, Qian Yang; software: Graham Roberts; supervision: Qian Yang; validation: Graham Roberts; visualization: Graham Roberts; writing – original draft: Graham Roberts; writing – review & editing: Mu-Ping Nieh, Anson W. K. Ma, Qian Yang.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Q. Y. and G. R. acknowledge support from the Air Force Research Laboratory, Materials and Manufacturing Directorate (AFRL/RXMS) via contract no. FA8650-20-C-5206. (Distribution A. Approved for public release: distribution unlimited. (SAF-2023-0827) Date Approved 09-07-2023.) This work is also supported by Oak Ridge National Laboratory via subcontract no. CW52476. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement no. 654000.Notes and references
- D. S. Sivia, Elementary scattering theory: for X-ray and neutron users, Oxford University Press, 2011 Search PubMed.
- G. Squires, Introduction to the Theory of Thermal Neutron Scattering, Cambridge Univ, 1978 Search PubMed.
- T. Mason, D. Abernathy, I. Anderson, J. Ankner, T. Egami, G. Ehlers, A. Ekkebus, G. Granroth, M. Hagen, K. Herwig, J. Hodges, C. Hoffmann, C. Horak, L. Horton, F. Klose, J. Larese, A. Mesecar, D. Myles, J. Neuefeind, M. Ohl, C. Tulk, X.-L. Wang and J. Zhao, Phys. B, 2006, 385–386, 955–960 CrossRef CAS.
- P. Adams, J. F. Ankner, L. Anovitz, A. Banerjee, E. Begoli, H. Bilheux, J. J. Billings, R. Boehler, S. Calder, B. C. Chakoumakos, T. R. Charlton, W.-R. Chen, Y. Cheng, L. Coates, M. J. Cuneo, L. L. Daemen, C. R. Dela Cruz, C. Do, A. Moreira dos Santos, N. Dudney, G. Ehlers, M. R. Fitzsimmons, F. X. Gallmeier, A. Geist II, V. Graves, B. Haberl, L. He, W. T. Heller, K. Herwig, J. P. Hodges, C. Hoffmann, K. Hong, A. Huq, A. Johs, U. C. Kalluri, J. Katsaras, A. I. Kolesnikov, A. Y. Kovalevskyi, J. O. J. L. Labbe, J. Liu, E. Mamontov, M. E. Manley, M. McDonnell, M. A. McGuire, D. A. A. Myles, S. Nagler, J. C. Neuefeind, D. P. Olds, K. Page, A. Payzant, L. Petridis, S. V. Pingali, S. Qian, A. Ramirez Cuesta, J. B. Roberto, L. Robertson, P. Rosenblad, T. Saito, G. Sala, G. S. Smith, C. Stanley, A. D. Stoica, A. Tennant, C. Tulk, T.-M. Usher-Ditzian, S. Vazhkudai, J. Warren, H.-W. Wang, Z. Wang, D. J. Wesolowski and T. J. Williams, First Experiments: New Science Opportunities at the Spallation Neutron Source Second Target Station, 2019 Search PubMed.
- D. Ratner, B. Sumpter, F. Alexander, J. J. Billings, R. Coffee, S. Cousineau, P. Denes, M. Doucet, I. Foster, A. Hexemer, D. Hidas, X. Huang, S. Kalinin, M. Kiran, A. G. Kusne, A. Mehta, A. Ramirez-Cuesta, S. Sankaranarayanan, M. Scott, M. Stevens, Y. Sun, J. Thayer, B. Toby, D. Ushizima, R. Vasudevan, S. Wilkins and K. Yager, Roundtable on Producing and Managing Large Scientific Data with Artificial Intelligence and Machine Learning, Office of Basic Energy Sciences (BES), 2019 Search PubMed.
- M. Doucet, A. M. Samarakoon, C. Do, W. T. Heller, R. Archibald, D. A. Tennant, T. Proffen and G. E. Granroth, Mach. Learn.: Sci. Technol., 2020, 2, 023001 Search PubMed.
- P. A. Beaucage and T. B. Martin, Chem. Mater., 2023, 35, 846–852 CrossRef CAS.
- Z. Ye, Z. Wu and A. Jayaraman, JACS Au, 2021, 1, 1925–1936 CrossRef CAS PubMed.
- C. Do, W.-R. Chen and S. Lee, MRS Adv., 2020, 5, year Search PubMed.
- D. Franke, C. M. Jeffries and D. I. Svergun, Biophys. J., 2018, 114, 2485–2492 CrossRef CAS PubMed.
- R. K. Archibald, M. Doucet, T. Johnston, S. R. Young, E. Yang and W. T. Heller, J. Appl. Crystallogr., 2020, 53, 326–334 CrossRef CAS.
- P. Tomaszewski, S. Yu, M. Borg and J. Rönnols, 2021 Swedish Workshop on Data Science (SweDS), 2021, pp. 1–6 Search PubMed.
- B. Yildirim, J. Doutch and J. M. Cole, Digital Discovery, 2024, 3, 694–704 RSC.
- H. A. Aty, R. Strutt, N. Mcintyre, M. Allen, N. E. Barlow, M. Páez-Pérez, J. M. Seddon, N. Brooks, O. Ces and I. R. Gould, Digital Discovery, 2022, 1, 98–107 RSC.
- Y. Li, L. Liu, X. Zhao, S. Zhou, X. Wu, Y. Lai, Z. Chen, J. Chen and X. Xing, Radiation Detection Technology and Methods, 2024, 1–17 Search PubMed.
- The SASView Project, SASView, https://www.sasview.org Search PubMed.
- A. Y. Ng, ICML, 1997, pp. 245–253 Search PubMed.
- J. F. Trevor Hastie and R. Tibshirani, Elements of Statistical Learning, Springer, New York, 2009 Search PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006 Search PubMed.
- G. Shafer and V. Vovk, J. Mach. Learn. Res., 2008, 9, 371–421 Search PubMed.
- A. N. Angelopoulos and S. Bates, A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification, arXiv, 2022, preprint, arXiv:2107.07511, DOI:10.48550/arXiv.2107.07511 [cs].
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- X.-Z. Wu and Z.-H. Zhou, Proceedings of the 34th International Conference on Machine Learning – Volume 70, 2017, pp. 3780–3788 Search PubMed.
- T. Zech, E. Metwalli, K. Götz, I. Schuldes, L. Porcar and T. Unruh, Part. Part. Syst. Char., 2022, 39, 2100172 CrossRef CAS.
- A. Hu, T.-H. Fan, J. Katsaras, Y. Xia, M. Li and M.-P. Nieh, Soft Matter, 2014, 10, 5055–5060 RSC.
- H. D. Burrows, M. Knaapila, A. P. Monkman, M. J. Tapia, S. M. Fonseca, M. L. Ramos, W. Pyckhout-Hintzen, S. Pradhan and U. Scherf, J. Phys.: Condens. Matter, 2008, 20, 104210 CrossRef.
- Z. Chen, P. A. FitzGerald, Y. Kobayashi, K. Ueno, M. Watanabe, G. G. Warr and R. Atkin, Macromolecules, 2015, 48, 1843–1851 CrossRef CAS.
- M.-P. Nieh, V. A. Raghunathan, S. R. Kline, T. A. Harroun, C.-Y. Huang, J. Pencer and J. Katsaras, Langmuir, 2005, 21, 6656–6661 CrossRef CAS PubMed.
- E. J. Cornel, G. N. Smith, S. E. Rogers, J. E. Hallett, D. J. Growney, T. Smith, P. S. O'Hora, S. van Meurs, O. O. Mykhaylyk and S. P. Armes, Soft Matter, 2020, 16, 3657–3668 RSC.
- O. Bousquet and A. Elisseeff, J. Mach. Learn. Res., 2002, 2, 499–526 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |