Exploring the transferability of machine-learning models for analyzing XRD data of shocked microstructures: from single crystal to polycrystals

Abstract

This study explores the transferability of machine-learning models to analyze X-ray diffraction (XRD) profiles of shock-loaded single-crystal and polycrystalline data. Transferability in this context refers to the ability of these models to accurately predict microstructural descriptors for crystal orientations and structures not included in its training data. Supervised machine-learning models were trained on XRD profiles and microstructural descriptors from atomistic simulations to extract properties like pressure, temperature, phase fractions, and dislocation density. We assessed two aspects of transferability: (1) the ability of models trained on specific single crystal orientations to predict microstructural descriptors for other orientations, and (2) the capacity of models trained on single crystal data to analyze polycrystalline structures. Results show promising accuracy in predicting certain descriptors within the same orientation and improved transferability to new orientations and polycrystalline systems when trained on multiple orientations. However, the accuracy of these predictions depends on the microstructural descriptor being targeted and the specific crystal orientations included in the training dataset. This work highlights the potential and limitations of machine learning for analyzing XRD data of shock-loaded materials and emphasizes the need for diverse training data to enhance model transferability and robustness.

---

1 Introduction

Diffraction techniques have been widely used for materials characterization¹ across numerous scientific domains, including fields such as biology^2,3 and materials science.^2,4–6 X-ray diffraction (XRD) methods have been used for phase identification in crystalline materials^4,5,7 as well as characterization of the length scale and strain state of crystalline materials.^8–11 XRD methods have also been utilized in dynamic experiments like shock tests to extract material strength¹² or characterize defect formation.^13,14 However, analyzing XRD profiles of materials subjected to high strain rates is challenging. Peak broadening, phase transformations, and residual stresses caused by extreme deformation complicate interpretation of lattice parameters and phase identification.^15,16 Additionally, heterogeneous deformation, texture development, and experimental difficulties in preserving shock-induced microstructures add complexity, often necessitating advanced analysis techniques.

Machine-learning methods offer robust alternative approaches for interpreting diffraction datasets, overcoming the biases of manual methods^17,18 (such as peak width analysis or Rietveld refinement) while also providing access to microstructural descriptors that are hard or impossible to extract otherwise.¹⁹ Hence, researchers have successfully applied machine-learning techniques to XRD data for tasks related to the identification of phases and structures,²⁰ the classification of diffraction patterns,^21,22 the determination of crystal symmetry,^23,24 or the extraction of defect statistics.^19,25 Though most existing works provide robust structural characterizations comparable to traditional methods, several limitations hinder their widespread application and reliability for diffraction analysis. Notably, a key limitation of interest here is the substantial requirement for large, high-quality, and representative datasets with accurate labels that directly impacts the ability of these models to generalize to new and unseen data.²⁶ Acquiring datasets that encompass a wide range of material conditions, including variations in crystallographic orientation, texture, and microstructural representation, can be challenging. The lack of sufficient representation of diverse material states in the training data directly limits the transferability of models to novel or out-of-distribution samples. For instance, a model trained to identify phases in one specific material system may not be directly applicable to a different material with distinct crystallographic structures or defect characteristics.¹⁶ The process of data generation is often resource-intensive, particularly when it involves experimental data collection.

In this paper, we are particularly interested in the transferability of machine-learning models trained on limited data for analyzing XRD data. Transferability, in this context, refers to the ability of a machine-learning model, once trained on a specific dataset with a particular crystallographic orientation, to accurately predict microstructural descriptors for other crystal orientations and structures that were not part of its training data. Given that XRD data can be complex and varied, it is crucial to understand how well a model can be trained on a limited amount of crystallographic data and still provide reliable predictions and insights when applied to different sets of XRD data. To that end, we performed atomistic simulations of shock loading in four single-crystal orientations and one polycrystalline copper (Cu) microstructure, generating paired XRD profiles and microstructural descriptors including pressure, temperature, phase fractions, and dislocation density. Using supervised, machine-learning workflows, we extracted these descriptors from the XRD profiles and assessed the ability of machine-learning models trained on single-crystal simulations to predict results for other orientations and for polycrystalline structures not part of the training data.

2 Methods

2.1 Shock simulations

To generate complex microstructural states in shock-loaded single crystal and polycrystalline Cu, we carried out molecular dynamics (MD) simulations using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).²⁷ We used an Embedded Atom Method (EAM) interatomic potential²⁸ to describe the shock response of Cu. This potential has been shown to accurately reproduce the shock Hugoniot for Cu²⁹ as well as the defect-evolution behavior during various stages of shock loading and spall failure.^15,30–32 The four single-crystal simulations had dimensions of 40 nm × 40 nm × 100 nm (approximately 13 million atoms) with the longest dimension oriented along the 〈111〉, 〈110〉, 〈100〉, and 〈112〉 crystallographic directions respectively. These longest dimensions correspond to the loading directions for the shock simulations. For the polycrystalline simulations, we created the microstructure using Voronoi tessellation³³ with dimensions of 50 nm × 50 nm × 100 nm (approximately 21 million atoms), an average grain diameter of 20 nm and randomly selected grain orientations. The dimensions for the single crystal and polycrystalline systems were selected to be large enough to eliminate any size effects on the deformation behavior of the systems.³⁴ All shock simulations were performed with periodic boundary conditions in the X and Y directions and free boundaries in the Z (loading) direction. Examples of shocked structures are shown in Fig. 1(a).

Fig. 1 (a) Shocked single crystal and polycrystalline microstructures colored by structure type, where red corresponds to stacking faults, blue to BCC, and gray to disorder. Atoms identified as FCC have been removed. Dashed lines illustrate how the system is divided into bins. (b) Simulated XRD profiles for the same microstructures. (c) Example of the temporal evolution of pressure generated through shock loading where time I corresponds to the “shock-compressed state” and time II is the “zero-stress state”.

Prior to shock loading for both the single-crystal and polycrystalline Cu structures, the simulation cells were equilibrated for a minimum of 50 ps at 300 K and zero stress using an isobaric–isothermal ensemble (NPT). Shock simulations were performed by driving a 3 nm-thick section at one end (bottom) of the simulation cell inwards into the sample along the Z direction with a constant velocity of 1 km s⁻¹ for a duration of 10 ps. This shock setup recreates the shock wave propagation behavior in plate impact shock experiments,³⁵ which are used to study the shock compression and spall failure behavior of materials. All MD simulations were performed with a timestep of 2 fs. Microstructural states were saved every 1 ps for a total duration of 50 ps for the 〈111〉 loading direction single-crystal system (51 saved states) and every 4 ps for a total duration of 40 ps for all of the other structures (11 saved states). Data from the 〈111〉 loading direction simulation was used in two formats: the complete dataset derived from the 51 saved states, and a truncated dataset composed of only the same timesteps that were saved during shock-loading simulations for other crystallographic orientations. An example of the temporal evolution of pressures generated for this loading condition is provided in Fig. 1(c). In this evolution, the compressive wave moves toward the back surface, creating a “shock-compressed state” at the end of the pulse. This compression wave reflects off the back surface as a release wave. Additionally, a second release wave (tail) follows the compressive wave at the end of the shock pulse. With the propagation of the two release waves, the system briefly reaches a “zero-stress state” (II in Fig. 1(c)). The interaction of release waves can cause triaxial tension, leading to void nucleation if stresses are high enough.^15,16,34,35

2.2 Simulated X-ray diffraction

XRD profiles, I(2θ) (i.e. mean diffraction intensity vs. diffraction angle), were generated using the LAMMPS diffraction package³⁶ for two different system configurations. In one configuration, XRD profiles were generated for each stored timestep using the entire simulation cell at once. In the other configuration, 20 XRD profiles were generated for 20 binned regions per stored timestep, where a given simulation cell was divided into 20 bins (2 along the X direction, 2 along the Y direction, and 5 along the Z direction) prior to the initiation of the shock wave. An illustration of the bin distribution is provided in Fig. 1(a). We used a wavelength of 1.54 Å corresponding to Cu Kα with a reciprocal mesh spacing of 0.003 Å⁻¹ and diffraction angles from ranging from 30° to 60°. This range of angles captures the {111} and {200} peaks with good resolution. Each XRD profile was normalized such that the maximum intensity was set to 1. Example profiles are shown in Fig. 1(b), where two sharp peaks correspond to two distinct atomic planes, those being the {111} (2θ = 43.15°) and {200} (2θ = 50.35°) planes. The positions of these features agree well with experimentally measured powder diffraction data for Cu.³⁷

The microstructures were characterized using algorithms implemented in OVITO.³⁸ We used common neighbor analysis³⁹ to extract the phase fractions of face-centered cubic (FCC), body-centered cubic (BCC), hexagonal close-packed (HCP), and disordered phases. Additionally, we employed the dislocation extraction algorithm (DXA)^40,41 to determine the type and density of dislocations. We also used the Crystal Analysis Tool⁴² to identify surface atoms, stacking faults, and twin stacking faults.

Microstructural characteristics were extracted for the entire simulation cells as well as for the binned regions within the simulation cells. We defined a total of six descriptors, s_i, describing the state of a microstructure during shock loading: pressure, total dislocation density, disordered phase fraction, FCC phase fraction, HCP phase fraction, and temperature. These descriptors were chosen because they generally correlate directly with macroscopic mechanical properties, influencing yield strength, ductility, and toughness of shocked materials and with microstructure response during shock compression and spall failure. These descriptors also serve as means to quantify the contributions from the strained crystalline phase (FCC atoms), defects such as dislocations, stacking faults (HCP atoms), and disordered atoms to the diffraction patterns. Additionally, as discussed later in this paper, within this set of microstructural descriptors, the difficulty of the regression task is expected to vary, with varying degrees of overlapping modifications to the XRD profiles due to changes in each individual descriptor. We normalized the descriptor's values based on the minimum and maximum values from the training set. This normalization was applied across all timesteps and bins for the simulations used to train the machine-learning model. For data from simulations that were not included in the machine-learning model training, the normalization of the descriptors was performed according the maximum and minimum values used for normalizing the training data.

2.3 Supervised learning for microstructure analysis

In order to link the state of the microstructure, s_i, to the XRD profiles, I(2θ), we used the supervised machine-learning workflow^25,26 shown in Fig. 2. This workflow consists of (i) a convolutional autoencoder that reduces the dimensionality of the XRD profiles, , to a latent vector, , where L_D < M and (ii) a multilayer perceptron (MLP) that maps Z to a set of material state descriptors s_i. A latent dimension size of 20 (L_D = 20) was selected after performing a sensitivity study that examined the impact of different sizes of the learned latent representation on the performance of both the autoencoder and the MLPs (see ESI S8† for the selection of the optimal size of the latent representation). Details of the architectures of the convolutional autoencoder and MLP along with notes on model training are provided in ESI S1.† ESI S7† includes a comparison of the performance of the proposed machine-learning architecture with a simpler workflow that uses a decision tree regression model to directly regress microstructural descriptors from XRD profiles. For the purposes of this work, only the XRD profiles and microstructural descriptors from the binned regions of the simulations were used.

Fig. 2 Schematic of the supervised machine-learning workflow employed for this work. (a) Single-crystal and polycrystalline atomic structures with complex distributions of defects and material states are produced during shock. (b) Simulated XRD profiles are generated from the atomistic structures. (c) An encoder is used to reduce the dimensionality of the XRD profiles I into a set of latent variables Z of dimension L_D. This learned latent representation is being used to regress material state descriptors s using a multilayer perceptron.

3 Results & discussion

3.1 Effect of crystal orientation on shock behavior

We first look at the distributions of microstructure state descriptors in the shock-compressed state for the 〈111〉 loading orientation in Fig. 3(a). In that state, the microstructure can be divided into three regions: (i) a region with zero stress (bin V) which has near-zero dislocation density and is at ambient temperature, (ii) the shock front (bins III and IV) which has a sharp gradient in temperature and dislocation density, and (iii) the plastic wave region (bins I and II) which has high dislocation density and high temperature. Bin I has broad {111} and {200} peaks due to high dislocation density (∼7 × 10¹⁷ m⁻²) and stacking faults (around 10% of the bin volume), high stress (51 GPa), and increased temperature (∼959 K); bin II displays both wide and sharp peaks from dislocation density variations; bin III shows sharp peaks with low dislocation density (∼0.38 × 10¹⁷ m⁻²), a lower temperature, and peak splitting due to stacking faults; bin IV exhibits peak splitting due to the coexistence of shocked and un-shocked material; and finally bin V shows the standard XRD spectrum for pristine, un-shocked material.

Fig. 3 Single crystal Cu shock loaded along 〈111〉 in the (a) shock-compressed state and (b) zero-stress state, with the microstructure, Z stress, dislocation density, temperature, and fitted diffraction patterns of each bin shown. The five bins (I–V) taken along the Z direction are shown by dashed lines. The microstructure is colored by structure, where gray atoms correspond to FCC atoms, red to disordered atoms, and green for stacking faults.

Fig. 3(b) shows the same analysis for the {111} loading orientation in the zero-stress state. Bins I, II, and III have returned to near-zero stress with high, uniform dislocation densities and temperatures, resulting in broadening of XRD peaks shifted to lower 2θ. Bin IV, despite having a similar dislocation density, shows much broader peaks due to a higher fraction of disordered atoms (around 47%). Bin V's peak positions resemble the ambient system, balancing the effects of compressive stress and elevated temperature effects.

Each loading orientation produces distinct shock waves with varying pressures, wave propagation, and microstructure evolution during shock loading and spall failure.^43,44 Fig. S8 in ESI S9† illustrates these differences by plotting the differences in the distributions in the stresses, dislocation densities, and temperature for the four orientations during different stages of the shock simulation (shock compression and spall failure). Table 1 summarizes the system-averaged peak pressures, shock velocities, and dislocation densities for each orientation. An equivalent table that provides the maximum and minimum values for the binned regions of several state descriptors and histograms of the different microstructure state descriptors from the binned regions of all of the simulations are provided in ESI S2.† All of these tabulated results highlight significant differences in the microstructure state descriptors due to the shock-loading orientation.

Table 1 Peak pressure, average shock velocity, and peak dislocation density for different shock-loading orientations of single-crystal Cu

Loading orientation	Pressure (GPa)	Shock velocity (km s^−1)	Dislocation density (10^17 m^−2)
〈111〉	42.93	6.817	4.296
〈110〉	53.36	6.754	3.689
〈100〉	49.93	5.449	1.407
〈112〉	53.55	6.107	3.941

---

3.2 Extracting microstructural information from XRD during shock

As illustrated in Fig. 4(a), shock-loading conditions create highly modified XRD profiles with variable peak shapes and distributions, making traditional, peak-width characterization challenging and inconsistent,^17,18 especially in cases with significant peak overlap (see profile at 15 ps in Fig. 4(a)) or similar profiles (see profiles between 35 and 50 ps). However, as shown in Fig. 4(b), the low-dimensional representation Z of the XRD profiles, processed by our convolutional autoencoder and ordered via principal component analysis (PCA) prior to visualization (the first two components account for nearly 75% of the explained variance in the entire dataset), consistently and clearly differentiates the XRD profiles as they evolve in time, indicating unique fingerprints contained in each individual profile. This raises the question: can machine-learned models extract microstructure state descriptors from XRD profiles during shock in the same way humans use features like peak positions, shapes, and widths?

Fig. 4 (a) Simulated XRD profiles created from the same bin at different time steps during the 〈111〉 single-crystal shock simulation, (b) projection of the XRD profiles for the same bin and simulation as (a) into PC scores Z₁ and Z₂ created by an autoencoder trained on the complete 〈111〉 single-crystal shock simulation which was then ordered via principal component analysis (PCA) prior to visualization. The first two components account for nearly 75% of the explained variance in the entire dataset (46.6% and 27.7% for the first and second components respectively).

We begin by evaluating the ability of our machine-learning model to predict the full set of microstructural descriptors from XRD profiles for specific shock orientations on single-crystal data. Fig. 5(a) presents parity plots and latent projections from models trained on the complete 〈111〉 shock-loading orientation simulation (see Table S1 in ESI S1.3† for a list of the different training dataset descriptions). We observe that the MLP model accurately predicts pressure, dislocation density, FCC phase fraction, and temperature from previously unseen XRD profiles in the validation set. Notably, pressure predictions exhibit the highest regression accuracy among these descriptors. This trend could be attributed to the large number of training data available to the machine-learning model with values ranging from tensile pressures of −11 GPa to compressive pressures of 53 GPa during the various stages of shock compression and spall failure. The model's performance for dislocation density and FCC phase fraction predictions is somewhat lower due the presence of outliers, as evidenced in their respective parity plots. Models trained on other orientations show comparable regression accuracy (see details in ESI S3†). This success highlights the ability of our supervised approach to extract meaningful fingerprints from XRD data and use them to create robust regression models for predicting microstructure state descriptors.¹⁹

Fig. 5 (a) Parity plots of models trained with latent projections of XRD profiles from the 〈111〉 oriented shock simulations for pressure, total dislocation density, FCC phase fraction, and temperature. Data points shown are from the validation set created during model training. R² scores and MSE for the parity plots are superimposed on their respective plot. (b) Projections of the 〈111〉 shock-loading direction data into a latent space learned by an autoencoder which was ordered via PCA prior to visualization, with the color of each point corresponding to that point's normalized value of the pressure, total dislocation density, FCC phase fraction, or temperature respectively.

Fig. 5(b) provides further insight into the model's performance by visualizing the distribution of these descriptors along two latent dimensions (Z₁, Z₂), which are the first two PC scores from the PCA transformation of the latent encoding learned by the autoencoder. While the full latent space comprises 20 dimensions (L_D = 20), this two-dimensional representation offers a glimpse into the model's internal organization of the data. Interestingly, this visualization reveals an absence of clear clustering or distinct organizational patterns across all of the descriptors, suggesting that the latent space captures descriptor variation in a continuous manner across all of the latent dimensions (see the clear relationship between Z₂ and pressure while no clear trend is observed between Z₁ or Z₂ and temperature). This smooth variation of microstructural descriptors across the latent dimensions implies complex dependencies during shock loading, which could impact the model's predictability for certain descriptor combinations or extreme cases. The lack of distinct clusters also indicates that the model's performance may be more consistent across the parameter space, rather than exhibiting sharp transitions in accuracy between different regimes.

3.3 Transferability of predictions from one shock-loading orientation to another

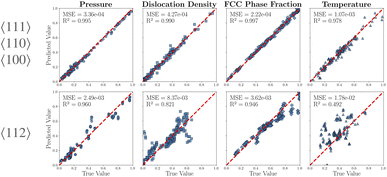
We now examine the transferability of models trained on data from one shock-loading orientation to predict results for different shock-loading orientations. Fig. 6 illustrates this comparison. The top row shows validation set parity plots for a model trained with the truncated dataset for orientation 〈111〉 (i.e. the dataset was truncated to have the same number of time steps as the other datasets. See further definitions and explanation of those datasets in ESI S1.3†). The lower rows display parity plots when applying this same model (i.e. trained using the truncated data for the 〈111〉 orientation) to datasets from the other orientations: 〈110〉, 〈100〉, and 〈112〉. These results reveal that the model's ability to make accurate predictions across different shock-loading orientations varies depending on the specific property being predicted and the combination of training and target orientations. For instance, the model trained on 〈111〉 data predicts pressures for the 〈110〉 and 〈112〉 orientations with relatively high accuracy but performs poorly when predicting pressures for the 〈100〉 orientation (based on the R² and MSE values). Similar variations in performance are observed for total dislocation density and FCC phase fraction predictions across different orientations. Transferability performance was comparable for models trained with different shock-loading orientation data (see ESI S4†). This can potentially be explained by the fact that the ability of the machine-learning model to predict pressures relies on the ability to predict the nucleation and evolution of defects (dislocation densities, stacking faults, etc.) during the various stages of the simulation. The shock compression data for the 〈111〉 system shows a one-wave structure i.e. there is no separation between the elastic and plastic waves. In contrast, the shock wave structures for the other 〈110〉, 〈100〉, and 〈112〉 orientations show a distinct two-wave (clear separation between the elastic and plastic waves). These variations could be responsible for the deviations in the predicted values for pressure (as well as the other descriptors) for the other three loading orientations when trained with the 〈111〉 data. In contrast to predictions of pressure, temperature predictions consistently show poor accuracy across all orientations. The evolution of temperatures in the simulations is largely related to the plastic work done in (i) the nucleation and evolution of dislocations in the system during the various stages of loading and (ii) nucleation and evolution of voids during spall failure. As illustrated in Fig. S8b in ESI S9,† a large fraction of the system undergoing spall failure (where the temperatures are very high) also have low dislocation densities (very similar to an un-shocked region). This can be attributed to the distributions of voids in the system (as illustrated in the polycrystal example in Fig. 2(a)) and the fraction of the material that is disordered. These complex relationships between void fraction, disorder, dislocation density, and temperature may be the source of the machine-learning frameworks difficulty in capturing the temperature profiles for different loading orientations outside of the training set. Enhancing the predictions of temperature (and dislocation densities) may require the inclusion of additional information beyond the XRD profiles (such as void fraction), which may be used in a future work.

Fig. 6 Parity plots comparing the performance of a model trained with the truncated timestep series from the 〈111〉 shock-loading orientation (top row) for predicting the microstructural descriptors (from left to right: pressure, total dislocation density, FCC fraction, and temperature) from different shock-loading orientation simulations (from top to bottom: 〈111〉 (validation set), 〈110〉, 〈100〉, and 〈112〉). Values shown in parity plots are normalized based on the maximum and minimum values from the model training dataset.

A key issue arises when the range of expected values for a particular microstructural descriptor varies substantially between the training dataset and the target dataset. This discrepancy can lead to significant prediction errors. For instance, the parity plot for total dislocation density in the 〈100〉 shock-loading orientation reveals a stark contrast between the normalized true values (ranging from 0.0 to 0.35) and the model's predictions (spanning 0.0 to 1.0). This overestimation occurs because the model, trained on XRD profiles associated with higher dislocation densities, applies these learned relationships to data from the 〈100〉 orientation, which actually exhibits significantly lower total dislocations. Conversely, underprediction can occur when the target dataset contains descriptor values exceeding those in the training set, as seen in the pressure predictions for the 〈110〉 shock-loading orientation. This type of limitation can be exacerbated when there are significant differences in the coupled evolution of descriptors between the training and target datasets. For example, a model that is trained with data from a shock simulation of a material that was initially at room temperature may struggle to predict the temperature of a pristine material at an elevated temperature, as the training data for the model only includes elevated temperatures alongside the other microstructural changes that occur during shock loading. These observations underscore the importance of carefully considering the range and distribution of descriptor values in both training and target datasets to improve the model's transferability and accuracy across different shock-loading orientations.

Training models with data from multiple shock-loading orientations can improve the generalization and predictions for new data, especially when different simulations cover various ranges of microstructural descriptors. Fig. 7 presents a comparison of model performance when trained on multiple single-crystal (SC) shock-loading orientations. Additional results using different combined datasets are presented in ESI S5.† The top row of Fig. 7 shows validation set parity plots for a model trained using multiple orientations: 〈111〉, 〈110〉, and 〈100〉, while the bottom row displays predictions using a single orientation: 〈112〉. Comparing these results to those of Fig. 6, we observe nearly identical performance across the four microstructural descriptors, with slight improvements in accuracy for pressure, total dislocation density, and FCC phase fraction while temperature predictions remain poor. As expected, these results, along with the additional results presented in ESI S4 and S5,† reveal that, in most cases, training models with multiple single-crystal shock-loading orientations can improve prediction accuracy for unseen orientations compared to models trained on a single orientation. This improvement in transferability is particularly evident when the training set encompasses a wide range of microstructural descriptor values, allowing the model to better generalize to new orientations. These findings underscore the importance of diverse training data in enhancing model transferability and robustness in predicting microstructural descriptors across various shock-loading orientations.

Fig. 7 Top row: validation set parity plots for a model trained with 〈111〉, 〈110〉, and 〈100〉 orientations. Bottom row: parity plots for dataset 5 (〈112〉 orientation) created using a model trained with the orientations from the top row.

As illustrated in our results, expanding the training set will not improve transferability if the target dataset contains descriptors or features that are absent in the expanded training set. A visible example of this assertion can be observed in the performance of the proposed machine-learning workflow on predictions of the temperature. Fig. 5–7 all illustrate that machine-learning models are capable of predicting the temperature of structures from simulations that were included in the training set, indicating that the temperature is somehow encoded within the XRD profiles and that this encoding can be precisely decoded. However, as discussed previously and illustrated in Fig. 6 and 7, increasing the range of training data will not address deficiencies in the information present within the training set. Accurate predictions of some descriptors (such as temperature and dislocation density for arbitrary shock conditions) may require additional information beyond the XRD profile, such as information on void fraction.

3.4 Transferability of predictions from single crystal to polycrystalline structures

The previous sections have demonstrated the efficacy of our machine-learning workflow in extracting microstructural descriptors from XRD profiles generated during shock loading of single-crystal structures. Building upon these findings, we now address a crucial question: Can models trained with data from single-crystal shock-loading simulations accurately predict microstructural descriptors from polycrystalline shock-loading simulations? To investigate this question, Fig. 8 presents multiple sets of parity plots, each row representing predictions for the microstructural properties of the polycrystalline structure during shock, made by models trained with different sets of single crystal shock simulation data. The top row showcases reference parity plots created using a model trained with polycrystalline data, with points corresponding to the validation portion of the dataset. Analysis of this model's performance reveals that regression accuracy for pressure and FCC phase fraction is comparable to the validation set accuracies observed in models trained with individual single-crystal shock simulations. However, prediction accuracy for total dislocation density and temperature is slightly lower, indicating that these descriptors are more challenging to extract from XRD profiles of polycrystalline microstructures. Examining the subsequent rows of Fig. 8, which represent models trained with single-crystal data (either from single or multiple orientations), confirms this expectation. While prediction accuracies for pressure and FCC phase fraction remain comparable to those shown in Fig. 6 and 7, performance for total dislocation density and temperature deteriorates. See ESI S6† for regression model accuracy metrics for models trained with all of the different training datasets utilized in this work when predicting the descriptors from the polycrystalline shock simulation.

Fig. 8 Parity plots comparing the microstructural state descriptor regression accuracy for the state descriptors from the nanocrystalline shock-loading simulation for (top row) a model trained with dataset 11, (top middle) a model trained with dataset 4, (bottom middle) a model trained with dataset 8, and (bottom) a model trained with dataset 6. Values shown in parity plots are normalized based on the maximum and minimum values from their respective model training datasets.

This comparative analysis provides valuable insights into how different microstructural descriptors are encoded within XRD profiles and how the presence of grain boundaries in polycrystalline structures, the main microstructural feature differing between the single-crystal and polycrystalline systems, affects these encodings.⁴⁵ For instance, temperature parity plots for all single-crystal-trained models show a consistent over-prediction in the low-temperature regime for polycrystalline structures. Increased temperatures typically increases d-spacing, which shifts peaks to the left, whereas grain boundaries have some atoms with closer d-spacing than equilibrium, and some farther leading to peak broadening. Our results here suggests that, under shock conditions and for (nanostructured) polycrystalline microstructures, the alterations in XRD profiles caused by grain boundaries in polycrystalline microstructures mimic the effects of increased temperature in single crystal shock simulations. While the overall prediction for the FCC phase fraction is relatively good, FCC phase fraction parity plots for single-crystal-trained models tend to over-predict in bins with the highest FCC phase presence in polycrystalline simulations. This over-prediction indicates that grain boundaries and the resulting disordered atoms affect XRD profiles differently than disordered atoms created during shock wave propagation through single-crystal microstructures.

Overall, the transferability of models trained on single-crystal data to predict descriptors in polycrystalline systems shows promise for certain microstructural properties, particularly pressure and FCC phase fraction. One effective approach to enhance the transferability of models for predicting unseen orientations or polycrystalline systems is to incorporate a broader variety of microstructure and defect configurations to create a balanced training dataset where different descriptors and microstructural features are present in roughly equal amounts. Polycrystalline materials, in contrast to single crystals, exhibit a rich tapestry of defect structures, including grain boundaries, dislocation networks, and voids, which can significantly influence the evolution of the dynamic response. By integrating these additional microstructural features and defect configurations into the training dataset, the machine-learning model can be better equipped to generalize its predictions across a wider range of conditions, including those found in polycrystalline systems. Furthermore, to facilitate improved transferability from single crystal orientations to polycrystalline systems, one could develop additional configurations that encompass a diverse array of defect structures, such as dislocation walls for instance. This comprehensive approach would not only enhance the model's predictive accuracy but also provides deeper insights into the complex behavior of materials under various loading conditions. These findings underscore both the potential and limitations of applying single-crystal trained models to polycrystalline systems, necessitating careful consideration of microstructural differences when developing machine-learning approaches for materials science applications.

In addition, improving the transferability of the trained models to unseen initial microstructures or loading orientations may be possible with the use of transfer-learning methods.⁴⁶ However, the use of transfer learning requires the existence of some labeled data within the target dataset that can be used for the transfer learning process, as well as the supposition that the labeled data that exists in the target dataset is representative of the differences between the training data and the target data. For the purpose of this work, transferability tests were performed primarily to determine the performance of trained models on data from unseen shock-loading orientations under the assumption that no labeled data would exist for these unseen datasets, and as such no attempt at transfer learning was performed and such attempts are left for future works.

4 Conclusions

This study examines the effectiveness and transferability of machine-learning models for predicting microstructural descriptors from XRD profiles using shock-loaded Cu data as an exemplar. Models were trained on simulated XRD profiles and corresponding descriptors for both single-crystal and polycrystalline Cu samples. For single-crystal samples, models demonstrated high accuracy in predicting descriptors such as pressure, dislocation density, FCC phase fraction, and temperature within the same shock orientation. The machine-learned fingerprints and their relationships with some microstructure state descriptors (such as pressure or phase fractions) are partially transferable. Transferability to different orientations varied, with accuracy depending on both the descriptor and specific orientations involved. Training on multiple orientations generally enhanced prediction accuracy for unseen orientations, while applying single-crystal-trained models to polycrystalline samples showed promise, particularly for predicting pressure and FCC phase fraction. Yet, the presence of grain boundaries in polycrystalline samples complicated predictions, especially for total dislocation density and temperature. These findings underscore the potential and limitations of using machine learning for XRD data analysis: while the models provide a powerful tool for extracting microstructural information, it is crucial to consider microstructural differences and data ranges when training and applying these models. It is also important to note that the machine-learning model architectures and model hyperparameters play a large role in the performance of these workflows, and that changes to the workflow proposed in this work could significantly alter regression performance (see ESI S7† for a comparison to a simpler direct-regression workflow). Moving forward, several strategies can be employed to improve the robustness, adaptability, and transferability of machine-learning models for XRD data analysis such as incorporating diverse training data from multiple crystal orientations and microstructures, applying data augmentation, or employing transfer-learning strategies.

Data availability

Data for this article, including atomistic simulation results, machine-learning workflows, and trained models are available from the Materials Data Facility repository at https://doi.org/10.18126/jezj-6852. For additional details or to request specific datasets or codes used in the study, please contact the corresponding author at E-mail: rdingre@sandia.gov.

Author contributions

Daniel Vizoso: data curation (supporting), methodology (equal), formal analysis (equal), software (lead), writing – original draft preparation (equal), writing – review and editing (equal). Phillip Tsurkan: data curation (lead), formal analysis (equal), writing – review and editing (equal). Ke Ma: data curation (supporting), formal analysis (equal). Avinash M. Dongare: conceptualization (equal), funding acquisition (equal), writing – review and editing (equal). Rémi Dingreville: conceptualization (equal), methodology (equal), funding acquisition (equal), writing – original draft preparation (equal), writing – review and editing (equal).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Mark Rodriguez from Sandia National Laboratories and the anonymous reviewers during the evalution of this paper for providing insightful comments and suggestions during the preparation of this manuscript. R. D. and D. V. acknowledge funding under the Beyond Fingerprinting Sandia Grand Challenge Laboratory Directed Research and Development (GC LDRD) program. P. T. and A. M. D would like to acknowledge financial support from the Department of Energy, National Nuclear Security Administration under Award No. DE-NA0003857. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author(s) and do not necessarily reflect the views of the National Nuclear Security Administration. In addition, P. T. acknowledges support provided by the U.S. Department of Education Graduate Assistance in Areas of National Need (GAANN) fellowship, with Project Director Bryan Huey under Grant No. P200A210093. The authors also acknowledge the support from the high performance computing center at the University of Connecticut, Storrs campus. The development of the machine-learning framework is supported by the Center for Integrated Nanotechnologies (CINT), an Office of Science user facility operated for the U.S. Department of Energy (DOE). This article has been authored by an employee of National Technology & Engineering Solutions of Sandia, LLC under Contract No. DE-NA0003525 with the U.S. Department of Energy. The employee owns all right, title, and interest in and to the article and is solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan.

Notes and references

1. J. Epp, Materials Characterization Using Nondestructive Evaluation (NDE) Methods, Woodhead Publishing, 2016, pp. 81–124.
2. G. M. Vanacore, A. W. P. Fitzpatrick and A. H. Zewail, Nano Today, 2016, 11(2), 228–249.
3. M. T. B. Clabbers and J. P. Abrahams, Crystallogr. Rev., 2018, 24(3), 176–204.
4. R. Balasubramaniam and A. V. R. Kumar, Corros. Sci., 2000, 42(12), 2085–2101.
5. P. Sciau, A. Kania, B. Dkhil, E. Suard and A. Ratuszna, J. Phys.: Condens. Matter, 2004, 16(16), 2795.
6. Y. Zhu, T.-R. Kuo, Y.-H. Li, M.-Y. Qi, G. Chen, J. Wang, Y.-J. Xu and H. M. Chen, Energy Environ. Sci., 2021, 14(4), 1928–1958.
7. S. S. Shankar, A. Rai, B. Ankamwar, A. Singh, A. Ahmad and M. Sastry, Nat. Mater., 2004, 3(7), 482–488.
8. T. Ungár, J. Mater. Sci., 2007, 42, 1584–1593.
9. A. Monshi, M. R. Foroughi and M. R. Monshi, World J. Nano Sci. Eng., 2012, 2(3), 154–160.
10. A. R. Bushroa, R. G. Rahbari, H. H. Masjuki and M. R. Muhamad, Vacuum, 2012, 86(8), 1107–1112.
11. K. Mongkolsuttirat and J. Buajarern, J. Phys.: Conf. Ser., 2021, 1719(1), 012054.
12. S. J. Turneaure and Y. M. Gupta, J. Appl. Phys., 2011, 109(12), 123510.
13. C. L. Williams, C. Kale, S. A. Turnage, L. S. Shannahan, B. Li, K. N. Solanki, R. Becker, T. C. Hufnagel and K. T. Ramesh, Phys. Rev. Mater., 2020, 4(8), 083603.
14. Z. Fan, Z. Song, B. Jóni, G. Ribárik and T. Ungár, Crystals, 2023, 13(8), 1252.
15. M. J. Echeverria, S. Galitskiy, A. Mishra, R. Dingreville and A. M. Dongare, Comput. Mater. Sci., 2021, 198, 110668.
16. A. Mishra, C. Kunka, M. J. Echeverria, R. Dingreville and A. M. Dongare, Sci. Rep., 2021, 11(1), 9872.
17. C. Weidenthaler, Nanoscale, 2011, 3(3), 792–810.
18. C. Kunka, B. L. Boyce, S. M. Foiles and R. Dingreville, Nanoscale, 2019, 11(46), 22456–22466.
19. C. Kunka, A. Shanker, E. Y. Chen, S. R. Kalidindi and R. Dingreville, npj Comput. Mater., 2021, 7(1), 67.
20. J.-W. Lee, W. B. Park, J. H. Lee, S. P. Singh and K.-S. Sohn, Nat. Commun., 2020, 11(1), 86.
21. J. A. Aguiar, M. L. Gong and T. Tasdizen, Comput. Mater. Sci., 2020, 173, 109409.
22. H. Wang, Y. Xie, D. Li, H. Deng, Y. Zhao, M. Xin and J. Lin, J. Chem. Inf. Model., 2020, 60(4), 2004–2011.
23. K. Kaufmann, C. Zhu, A. S. Rosengarten, D. Maryanovsky, T. J. Harrington, E. Marin and K. S. Vecchio, Science, 2020, 367(6477), 564–568.
24. L. C. O. Tiong, J. Kim, S. S. Han and D. Kim, npj Comput. Mater., 2020, 6(1), 196.
25. D. Vizoso, G. Subhash, K. Rajan and R. Dingreville, Chem. Mater., 2023, 35(3), 1186–1200.
26. D. Vizoso and R. Dingreville, J. Appl. Phys., 2025, 137(13), 131101.
27. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
28. Y. Mishin, M. J. Mehl, D. A. Papaconstantopoulos, A. F. Voter and J. D. Kress, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(22), 224106.
29. E. M. Bringa, J. U. Cazamias, P. Erhart, J. Stölken, N. Tanushev, B. D. Wirth, R. E. Rudd and M. J. Caturla, J. Appl. Phys., 2004, 96(7), 3793–3799.
30. E. M. Bringa, K. Rosolankova, R. E. Rudd, B. A. Remington, J. S. Wark, M. Duchaineau, D. H. Kalantar, J. Hawreliak and J. Belak, Nat. Mater., 2006, 5(10), 805–809.
31. S. J. Fensin, E. K. Cerreta, G. T. Gray III and S. M. Valone, Sci. Rep., 2014, 4(1), 5461.
32. K. Ma, J. Chen and A. M. Dongare, J. Appl. Phys., 2021, 129(17), 175901.
33. P. M. Derlet and H. Van Swygenhoven, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(1), 014202.
34. K. Mackenchery, R. R. Valisetty, R. R. Namburu, A. Stukowski, A. M. Rajendran and A. M. Dongare, J. Appl. Phys., 2016, 119(4), 044301.
35. M. A. Meyers and C. T. Aimone, Prog. Mater. Res., 1983, 28(1), 1–96.
36. S. P. Coleman, D. E. Spearot and L. Capolungo, Modell. Simul. Mater. Sci. Eng., 2013, 21(5), 055020.
37. H. E. Swanson, N. T. Gilfrich and M. I. Cook, Joint Committee on Chemical Analysis by Powder Diffraction Methods, ASTM Special Technical Publication, 48-G, 1957, p. 60.
38. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18(1), 015012.
39. J. D. Honeycutt and H. C. Anderson, J. Phys. Chem., 1987, 91(19), 4950–4963.
40. A. Stukowski and K. Albe, Modell. Simul. Mater. Sci. Eng., 2010, 18(2), 025016.
41. A. Stukowski, V. V. Bulatov and A. Arsenlis, Modell. Simul. Mater. Sci. Eng., 2012, 20(8), 085007.
42. A. Stukowski, JOM, 2013, 66, 399–407.
43. C. M. Liu, C. Xu, Y. Cheng, X. R. Chen and L. C. Cai, Comput. Mater. Sci., 2015, 110, 359–367.
44. W. Zhu, Z. Song, X. Deng, H. He and X. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(2), 024104.
45. T. Ungár, S. Ott, P. Sanders, A. Borbély and J. Weertman, Acta Mater., 1998, 46(10), 3693–3699.
46. S. Niu, Y. Liu, J. Wang and H. Song, IEEE Trans. Artif. Intell., 2020, 1(2), 151–166.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00400k

---