Open Access Article
Open Access ArticleBitBIRCH: efficient clustering of large molecular libraries†
Kenneth López
Pérez‡
,
Vicky
Jung‡
,
Lexin
Chen
 ,
Kate
Huddleston
and
Ramón Alain
Miranda-Quintana
,
Kate
Huddleston
and
Ramón Alain
Miranda-Quintana
 *
*
Department of Chemistry & Quantum Theory Project, University of Florida, Gainesville, Florida 32611, USA. E-mail: quintana@chem.ufl.edu
First published on 13th March 2025
Abstract
The widespread use of Machine Learning (ML) techniques in chemical applications has come with the pressing need to analyze extremely large molecular libraries. In particular, clustering remains one of the most common tools to dissect the chemical space. Unfortunately, most current approaches present unfavorable time and memory scaling, which makes them unsuitable to handle million- and billion-sized sets. Here, we propose to bypass these problems with a time- and memory-efficient clustering algorithm, BitBIRCH. This method uses a tree structure similar to the one found in the Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH) algorithm to ensure O(N) time scaling. BitBIRCH leverages the instant similarity (iSIM) formalism to process binary fingerprints, allowing the use of Tanimoto similarity, and reducing memory requirements. Our tests show that BitBIRCH is already >1000 times faster than standard implementations of the Taylor–Butina clustering for libraries with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. BitBIRCH increases efficiency without compromising the quality of the resulting clusters. We explore strategies to handle large sets, which we applied in the clustering of one billion molecules under 5 hours using a parallel/iterative BitBIRCH approximation.
000 molecules. BitBIRCH increases efficiency without compromising the quality of the resulting clusters. We explore strategies to handle large sets, which we applied in the clustering of one billion molecules under 5 hours using a parallel/iterative BitBIRCH approximation.
Introduction
Clustering is an unsupervised machine learning (ML) technique that organizes unlabeled data into groups, or clusters, of related points.1–3 This can be critical to obtain insights into the structure and organization of the data,3 which could also be used to aid the development of supervised ML models.4,5 This is essential in developing more accurate predictive models.4 In chemical applications, during the data generation and curation process, clustering can assist in identifying regions of chemical space that are lacking within the dataset.6,7 By ensuring that a representative range of chemical space is covered in the training and validation datasets, one can reduce biases and ensure that the model performs well on diverse data, broadening generalizability and enhancing the robustness of the model.8In drug design, the importance of clustering is highlighted when considering the “molecular similarity principle”, which states that structurally similar molecules will often share similar chemical properties or biological activities.9–11 By identifying similar compounds, clustering can help predict the behavior and properties of existing and new structures, expediting virtual screening.12 The preponderant molecular representations for small molecules in drug design are binary fingerprints.13 Fingerprints encode molecular information using bitstrings (arrays of on and off bits),13 this simplicity is particularly attractive in the exploration of large chemical spaces, but also leads to robust results in Structure–Activity Relationship (SAR) studies.14–16 There are multiple ways to generate fingerprints from a molecular graph or structure (MACCS,17 ECFP,18 RDKit,19 MAP,20etc.), so it is important to emphasize that the results discussed below apply to any type of binary encoding. Tanimoto similarity21,22 is widely used in cheminformatics tasks,23–26 including clustering.27,28 From this binary fingerprint representations, it is easy to calculate the Tanimoto similarity10,21 between any two molecules A and B, T(A, B), as:
 | (1) |
Pharmaceutical applications typically use one of a handful of clustering algorithms, with spectral,29,30 hierarchical,31,32 and Jarvis-Patrick33,34 clustering as common choices. However, arguably the most popular option is the Taylor–Butina clustering. All of these methods rely on the construction of the similarity matrix between the molecules, and then use some notion of neighborhood/locality to group the points.27 Taylor–Butina does this in perhaps the simplest and most intuitive way, requiring a single parameter: a similarity threshold used to count the number of neighbors of each potential cluster centroid.27,35 At every iteration, the molecule with most neighbors is identified as the best potential centroid and, together with all its available neighbors, they form a cluster. This procedure is repeated until exhausting all molecules, or until no molecules remain that are closer than the pre-specified threshold. This results in clusters that are easily interpretable, as they contain molecules that are closely related to the corresponding centroid.27 However, the fact that we need to compute the similarity matrix means that all these methods scale as O(N2) in both time and memory,36 with this scaling potentially preventing their application to ever-increasing sectors of chemical space.
These time and memory bottlenecks are not unique to chemical applications of clustering, so it is not strange that methods with more favorable scaling have proliferated. One particularly attractive alternative is the Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH) algorithm.37 BIRCH solves the memory problems by using a Clustering Feature (CF) to encapsulate the cluster information in a compact way that still allows computing critical indicators, like the cluster centroids, radius, and diameter.37 The time scaling is then improved using a CF-tree data structure, that allows to efficiently distribute the molecules into their corresponding clusters: the “leaves” of the tree37 (there has been a renewed interest in the cheminformatics/drug-design communities in using tree structures to accelerate similarity searches, especially in conjunction with low-dimensional molecular representations38). These are very attractive features, however, they cannot be immediately transferred to drug-design applications for two main reasons. First, BIRCH was originally conceived for continuous inputs, which is in stark contrast with the discreet on/off character of the molecular fingerprint components. Moreover, the stored information in the CF limits BIRCH to the Euclidean distance, thus preventing the use of the Tanimoto similarity, or any other cheminformatic similarity index.
In this contribution we propose a novel clustering algorithm with the ease of interpretation of Taylor–Butina, but leveraging the advantages of the CF and CF-tree structures, resulting in more attractive memory and time scaling algorithm. Given the close relation with BIRCH, we termed our method: BitBIRCH. As discussed below, we can adapt the tree structure from the CF-tree without many changes (although BitBIRCH uses a more efficient criterion to split the tree nodes). The biggest challenge comes from the cluster representation, since we need an alternative to the CF that allows computing all the cluster's properties from the collection of bitstrings. The solution to this comes from our work on quantifying the chemical diversity of large datasets by comparing an arbitrary number of molecules at the same time. We started applying this idea with extended similarity39,40 indices, which were successfully applied to dissecting epigenetic libraries,41 chemical space sampling,42 activity cliffs,43 and even in the study of Molecular Dynamics simulations.44,45 Recently, we expanded on this framework with the introduction of the instant similarity (iSIM) formalism.46 iSIM shows how the average of the pairwise comparisons over a library can be calculated from two simple ingredients: the number of points in the set and a cumulative vector obtained after adding the fingerprints column wise. This is precisely what is needed to replace the CF by a Bit Feature (BF) that encapsulates the cluster's information, and to be able to use the Tanimoto similarity in a BIRCH-like context. In the next sections, we discuss how iSIM can lead to a cluster's centroid, radius, and diameter, and how to include information in the BF that allows to cluster a large set in a truly online way. Our estimates show that already for only 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules BitBIRCH is >1000 times faster than the RDKit implementation of Taylor–Butina. We also compare these methods using several clustering quality metrics, which show that BitBIRCH's improved time and memory efficiency do not diminish the final clustering results, with our algorithm outperforming Taylor–Butina in multiple instances. Finally, we discuss alternative formulations of BitBIRCH capable of handling billion-sized sets in just a few hours.
000 molecules BitBIRCH is >1000 times faster than the RDKit implementation of Taylor–Butina. We also compare these methods using several clustering quality metrics, which show that BitBIRCH's improved time and memory efficiency do not diminish the final clustering results, with our algorithm outperforming Taylor–Butina in multiple instances. Finally, we discuss alternative formulations of BitBIRCH capable of handling billion-sized sets in just a few hours.
Results and discussion
BitBIRCH, instant similarity, and Taylor–Butina
BitBIRCH and BIRCH are based on two key features: (a) the use of a reduced, vector-like, representation to encode the information about each cluster, (b) a (CF-)tree structure to traverse and store the data. The latter is similar between both algorithms, with the most salient difference being the way to assign sub-clusters after splitting a node (details about this and the full pseudo-code are discussed in the ESI, Section S1†). As far as the simplified cluster representation, BIRCH uses the CF, while for BitBIRCH we propose the Bit Feature (BF). Let be the jth cluster, containing Nj elements. Each of these elements, x(j,k), is a q-dimensional vector, that is: x(j,k) = [x(j,k)1,…,x(j,k)q]. From now onwards, bold lowercase symbols will always represent vectors with q components/features (In all the numerical results discussed below, unless otherwise explicitly mentioned, we worked with fingerprints with q = 2048.) Then, the CF27 of the jth cluster, CFj, has three elements:
be the jth cluster, containing Nj elements. Each of these elements, x(j,k), is a q-dimensional vector, that is: x(j,k) = [x(j,k)1,…,x(j,k)q]. From now onwards, bold lowercase symbols will always represent vectors with q components/features (In all the numerical results discussed below, unless otherwise explicitly mentioned, we worked with fingerprints with q = 2048.) Then, the CF27 of the jth cluster, CFj, has three elements:| CFj = [Nj,lsj,ssj] | (2) |
 | (3) |
 | (4) |
This is all that is needed to calculate either the radius or diameter of each cluster if the separation between the points is measured using the Euclidean distance. However, it is clear that for binary inputs (like molecular fingerprints) a new strategy is needed. First, we want to quantify similarity in different ways. Second, for binary data lsj = ssj, meaning that they carry exactly the same information, and storing both vectors is unnecessary, independently of the chosen metric.
The BFj, on the other hand, is represented with a four-component structure:
| BFj = [Nj,lsj,cj,molsj] | (5) |
The other new inclusion in the BFj is the cluster centroid, cj. Since cluster membership is determined by comparing the new molecules being inserted in the tree with the cluster centroids, having the latter pre-calculated is more efficient than having to calculate them on-demand. Moreover, since we do not need the ssj, we can store the cj at no extra memory cost, compared to the CFj. The centroid can be easily calculated from Nj and lsj if we remember that, by definition, the center of a cluster is the point that, on average, is the closest to all the elements in the set. For instance, from the Tanimoto formula (eqn (1)), we see that for every bit position, we should maximize the number of on–on coincidences, while minimizing the number of on–off mismatches. Thus, from the lsj we can determine cj as:
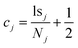 | (6) |
All that is left now is showing that Nj and lsj are enough to calculate the diameter and radius of the cluster. The diameter of a cluster, Dj, is defined as the average of all the pairwise inter-point separations:
 | (7) |
The key insight is that we can use the recently introduced instant similarity (iSIM)46 to calculate the instant Tanimoto value of the set, iT(X(j)), which is the average of the Tanimoto values over the cluster. In short, each element of lsj contains information about the number of on bits in a column, so  corresponds to all the possible on–on matches, while
corresponds to all the possible on–on matches, while  is the number of on–off mismatches in the rth column, respectively. We can then write:
is the number of on–off mismatches in the rth column, respectively. We can then write:
 | (8) |
| Dj = 1 − iT(X(j)) | (9) |
A similar argument can be made for the radius of the cluster, Rj, defined as the average separation between all the points in the cluster and its centroid:
 | (10) |
However, we can use iSIM to rewrite this as (see Section S1 of the ESI† for a detailed derivation):
 | (11) |
In other words, Dj and Rj can be calculated with just the number of elements and linear sum of a cluster thanks to iSIM. In the remaining of this contribution, we will discuss BitBIRCH based on Rj, since this is the closest to the sphere-exclusion algorithm. Also, for simplicity, instead of referring to a radial threshold, we will be referring to a similarity threshold, calculated as 1 − Rj. It is worth noting that while we will mainly focus on the Tanimoto index, the ESI† shows that BitBIRCH can also be used with other popular similarity indices like Sokal–Michener and Russel–Rao (see Section S7†). While the overall behaviour of these indices is quite consistent, Tanimoto is both the most well-behaved and robust for the range of similarity thresholds considered. Likewise, even though the results in this paper correspond to 2048 bits RDKit fingerprints, in the ESI† we discuss the performance of BitBIRCH with other fingerprint types.
As shown in Fig. 1, BitBIRCH retains the attractive O(N) scaling of BIRCH, due to the combination of the BF and tree structure, in stark contrast with the already-mentioned O(N2) time (also shown in Fig. 1) and memory requirements of the Taylor–Butina algorithm. The Taylor–Butina implementation in RDKit19 took more than 8 hours to cluster 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules (each with 2048 features) in the University of Florida's HiPerGator cluster, and we were unable to allocate enough memory to cluster more than 500
000 molecules (each with 2048 features) in the University of Florida's HiPerGator cluster, and we were unable to allocate enough memory to cluster more than 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, since it required more than 4 TB of RAM. On the other hand, BitBIRCH was able to cluster 450
000 molecules, since it required more than 4 TB of RAM. On the other hand, BitBIRCH was able to cluster 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules in 2.2 minutes, and easily handled one million molecules in ∼5 minutes.
000 molecules in 2.2 minutes, and easily handled one million molecules in ∼5 minutes.
 | ||
| Fig. 1 Computing time needed to cluster subsets of the Pubchem library up to one million molecules with the Taylor–Butina (RDKit implementation) and BitBIRCH algorithms. | ||
Despite the great difference in computing time, BitBIRCH and Taylor–Butina are in close agreement over the global structure of the data. Thus, the valuable insights and intuition built upon the sphere-exclusion method are also available through the BitBIRCH approach, but at a much lower computational cost. In Fig. 2 we show how the number of clusters found by each method follows the same trends over diverse conditions. We considered clusters that had more than a minimum number of elements (min_size = 1, 2, 3, 5, and 10), in order focus on denser subsets. While the general agreement in the number of clusters is very good for all the considered libraries (see also ESI, Section S3†), Taylor–Butina and BitBIRCH are particularly close when more singleton-like clusters are removed (min_size = 10).
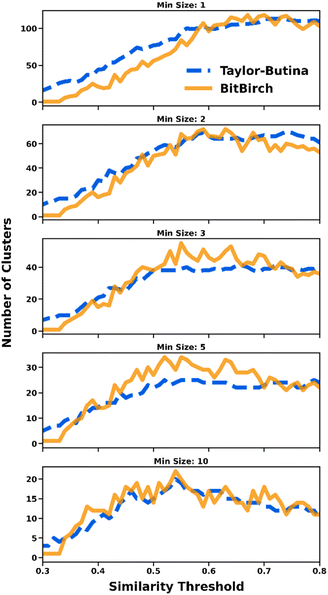 | ||
| Fig. 2 Comparison of numbers of clusters for the ChEMBL 262_Ki19 library with more than min_size (=1, 2, 3, 5, 10) elements found by the Taylor–Butina (dashed blue line) and BitBIRCH (continuous orange line) algorithms for different similarity thresholds. | ||
This global similarity is also present at the local level, if we compare set representatives from the top 10 most populated clusters found by both algorithms. Fig. 3 presents a heat-map with the Tanimoto comparisons between the medoids found by Taylor–Butina and BitBIRCH (for details on how to find the medoids, check the ESI, Section S1†). Overall, there is a close relation between the “core” molecules identified by these methods, especially for the denser clusters. As discussed in the ESI,† this trend persists for the other ChEMBL subsets considered in this work. Moreover, in the ESI† we also discuss other tests showing the agreement between these two methods, including the Jaccard–Tanimoto set comparison between the most populated clusters, and the analysis of these trends over multiple coincidence thresholds.
 | ||
| Fig. 3 Comparison of the medoids' similarity of the top 10 most populated clusters in the ChEMBL 262_Ki19 library found by the Taylor–Butina and BitBIRCH algorithms (similarity threshold = 0.65, min_size = 10). | ||
Clustering performance
Having established that the BitBIRCH and Taylor–Butina algorithms offer similar views on the nature of the data, we now compare the quality of the resulting clusterings. We used three main internal cluster validation measures:49 the Calinski–Harabasz (CHI),50 Davies–Bouldin (DBI),51 and Dunn (DI)52 indices. The CHI depends on the ratio of between- and within-cluster dispersions, with bigger values indicating a better clustering.50 This index can be re-formulated with Tanimoto as a similarity measure: | (12) |
DBI values are usually easier to interpret, since they are bounded in the [0, 1] interval, with lower values corresponding to tighter and more separated clusters.51 However, calculating this index demands computing all the pairwise similarities between the cluster representatives. This is problematic, since for most practical values of the similarity threshold the number of clusters is proportional to the number of molecules (NC ∼ O(N)), or in other words, the DBI calculation will roughly scale as O(N2). Even if we include the DBI analysis as a way to benchmark the performance of BitBIRCH, this index is not a viable option for ultra-large libraries; calculating it is more demanding than actually performing the clustering. The DI also suffers from this problem, since it demands calculating the separation between all pairs of clusters. Still, we report DI values for all the 30 ChEMBL subsets here and in the ESI,† keeping in mind that higher DI values indicate more well-separated clusters (more details about the expressions used to calculate the DBI and DI are included in the ESI, Section S4†).
Fig. 4 shows the mentioned quality clustering metrics for the ChEMBL 233 library. The CHI values in Fig. 4A indicate that BitBIRCH outperforms Taylor–Butina for lower similarity thresholds (<0.6), with both methods giving clusters of the same quality until slightly over the 0.7 threshold, a range that covers most practical applications. This observation is supported when a Wilcoxon signed-rank test is done, the CHIs for the thirty ChEMBL libraries are significantly higher for BitBIRCH at low thresholds (p < 0.05) and there is no statistically significant difference at thresholds in the [0.5, 0.7] range, depending on the minimum size of the considered clusters (see Figs. S4.31 and S4.32 in the ESI†). The shaded areas in Fig. 4A–C indicate the standard deviation of the corresponding index values calculated after removing clusters with more than 1, 2, 3, 5, and 10 molecules. Interestingly, the BitBIRCH results are consistently more robust to the removal of outliers and singleton-like clusters than those of Taylor–Butina, which is once again more prevalent for looser thresholds. The DBI analysis (Fig. 4B) is similar to the CHI, now with a region of BitBIRCH that gives markedly better results until a 0.65 threshold, and then essentially equivalent results to Taylor–Butina around the 0.75 region. This observation for ChEMBL_233 also applies to all the 30 studied libraries, with Wilcoxon tests showing that there is no statistical difference at threshold values in [0.5, 0.7], while at low thresholds, the DBI score is significantly lower for BitBIRCH (see Section S4 in the ESI†). The DI results are even more promising (Fig. 4C), with BitBIRCH consistently outperforming Taylor–Butina almost up to a 0.8 threshold. Overall, the DI is statistically higher for BitBIRCH in the [0.3, 0.8] range (ESI, Section S4†). It is reassuring to see that these different metrics agree on the relative performance of both algorithms, with the CHI and DI plots, in particular, presenting very similar features. Essentially, for the range of similarity thresholds that are usually explored in drug design53 and ML applications, BitBIRCH performs better or, at worst, equal to Taylor–Butina.
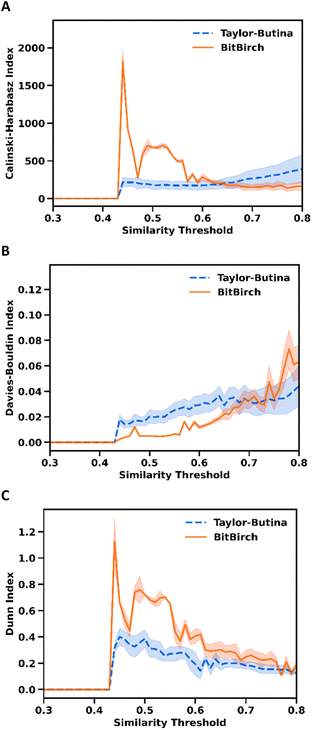 | ||
| Fig. 4 Comparison of Taylor–Butina (blue dashed line) and BitBIRCH (orange continuous line) clustering results for the ChEMBL 233_Ki9 library. Dark lines and shaded regions indicate the average and standard deviation over min_size = 1, 2, 3, 5, 10 values, respectively. (A) Calinski–Harabasz, (B) Davies–Bouldin, and (C) Dunn indices. | ||
As a final test on the potential variability of BitBIRCH, we studied how the distribution of the clusters in chemical space changes under different conditions (for this, we used a PCA projection into the first two principal components to conveniently visualize the cluster results). For the natural products of the ChEMBL33 (ref. 47) library (Fig. 5) we observe that from a relatively loose threshold (0.35) to a much stricter one (0.8), the relative positions of the most populated clusters remain sensibly constant. This is especially clear for the 0.5–0.8 range, where not only the position of the clusters, but also the average similarities of the cluster members (calculated with iSIM, see color scale in Fig. 5) is largely preserved. This indicates that BitBIRCH results are quite robust to changes in the similarity threshold. At least at a general level, we do not have to carefully fine-tune this parameter, especially within the [0.5, 0.8] interval.
Tackling ultra-large libraries
As shown above, the standard BitBIRCH implementation can easily handle millions of molecules, but now we explore iterative/parallel scheme to tackle much larger sets.This parallel method is inspired by the (optional) refinement step at the end of traditional BIRCH implementations37 and clustering ensembles.54 The basic idea is that the cluster centroids could be used as representatives of their corresponding sets. Centroids are used as input in a second clustering step. So, the BitBIRCH-parallel recipe is quite simple: (1) separate the data into non-overlapping splits (we usually consider 10 splits, as discussed below); (2) use BitBIRCH to cluster each of these splits; (3) collect the cluster centroids and cluster them with BitBIRCH. This parallel/iterative approach is an approximation to just clustering all the data in one go, but the question remains: how much does the quality of the clustering suffer after this iterative procedure?
First, Fig. 6A shows that for the 30 ChEMBL subsets considered here, the final number of clusters found by the standard and the parallel BitBIRCH methods (with 10 initial splits) is quite consistent, which reflects the ability of the simpler method to capture the same global structure as the exact BitBIRCH. In the ESI† we also present a detailed comparison between the local structure of the clusters found by these algorithms (ESI, Section S5†). The CHI (Fig. 6B) and DBI (Fig. 6C) analysis reveal a promising pattern: in general, both methods have very similar performance, with the parallel approach being even slightly favoured in some cases, as reported in other ensemble-like approaches.55,56 Even more reassuring, according to the DI (Fig. 6D), in most cases BitBIRCH-parallel finds better-separated and more compact clusters. The statistical analysis supports these observations, with the corresponding CHI and DBI values being statistically equivalent (p = 0.16 and p = 0.45, respectively), while the parallel DIs are significantly higher than BitBIRCH (p < 0.05) in the respective Wilcoxon's tests (details on ESI, S5†).
Since by all the considered metrics the iterative/parallel approximation does not diminish the quality of the final results, we chose it to analyse a library with one billion molecules. As noted above, 4 TB were insufficient to cluster 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules with Taylor–Butina. But even ignoring the memory issues, the trend in Fig. 1 (O(Taylor–Butina) = 2 × 10−7N2) suggests that it will take ∼6342 years to cluster one billion molecules. Using the BitBIRCH algorithm without any modifications (O(BitBIRCH) = 2.94 × 10−4N) this estimate improves to only 3.4 days, which is already a practical time, but we wanted to test how much one could improve upon this result with the parallel BitBIRCH implementation. The one billion molecules were selected from the ZINC22 (ref. 48) library and clustered using the parallel strategy using 1000 splits (1
000 molecules with Taylor–Butina. But even ignoring the memory issues, the trend in Fig. 1 (O(Taylor–Butina) = 2 × 10−7N2) suggests that it will take ∼6342 years to cluster one billion molecules. Using the BitBIRCH algorithm without any modifications (O(BitBIRCH) = 2.94 × 10−4N) this estimate improves to only 3.4 days, which is already a practical time, but we wanted to test how much one could improve upon this result with the parallel BitBIRCH implementation. The one billion molecules were selected from the ZINC22 (ref. 48) library and clustered using the parallel strategy using 1000 splits (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules each). While the average time to cluster a split was 4.34 min, to compute the total time we will consider the slowest one, 18.76 min, since it is the limiting step before clustering the centroids. On average, each split clustering yielded 26
000 molecules each). While the average time to cluster a split was 4.34 min, to compute the total time we will consider the slowest one, 18.76 min, since it is the limiting step before clustering the centroids. On average, each split clustering yielded 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 centroids (lowest: 5430; highest: 84
653 centroids (lowest: 5430; highest: 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649). Then, the final clustering took 242 min between the centroid aggregation and clustering, resulting in a total of 2
649). Then, the final clustering took 242 min between the centroid aggregation and clustering, resulting in a total of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 081
081![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662 clusters with more than 10 molecules. The total time to obtain the final clustering assignations of the billion molecules was 4.35 hours; a much more attractive time than the unmanageable Taylor–Butina estimate, and even the days required for this task using the unmodified BitBIRCH.
662 clusters with more than 10 molecules. The total time to obtain the final clustering assignations of the billion molecules was 4.35 hours; a much more attractive time than the unmanageable Taylor–Butina estimate, and even the days required for this task using the unmodified BitBIRCH.
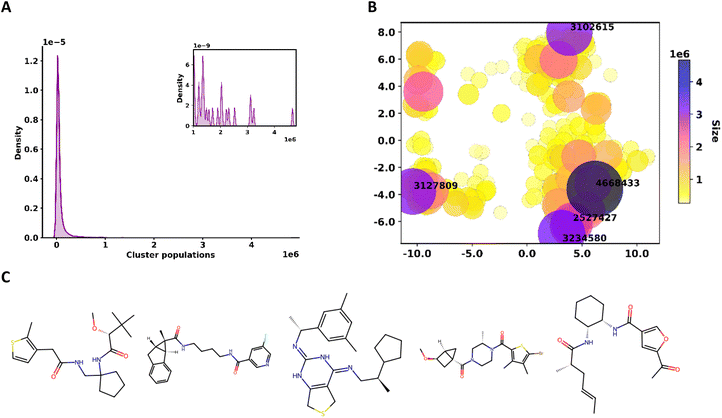
In Fig. 7A we present a summary of the cluster population distribution for the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 largest clusters, indicating a strong preference for smaller “pockets” of molecules. The distribution of the larger clusters (Fig. 7B) shows a relatively uneven location of the more populated centers (darker and bigger circles in Fig. 7B), which dominate the boundaries of the two-dimensional PCA projection. The asymmetric distribution of the denser clusters is also showcased by the “voids” observed in the central region of this chemical sub-space. In Fig. 7C, we show the structures of the medoids (most similar molecules to the rest of the molecules in the set) of each of the top five most populated clusters.
000 largest clusters, indicating a strong preference for smaller “pockets” of molecules. The distribution of the larger clusters (Fig. 7B) shows a relatively uneven location of the more populated centers (darker and bigger circles in Fig. 7B), which dominate the boundaries of the two-dimensional PCA projection. The asymmetric distribution of the denser clusters is also showcased by the “voids” observed in the central region of this chemical sub-space. In Fig. 7C, we show the structures of the medoids (most similar molecules to the rest of the molecules in the set) of each of the top five most populated clusters.
Materials and methods
The timing comparisons between Taylor–Butina and BitBirch were done on the first 1 million molecules from the PubChem 2005 library. For clustering performance calculations, 30 ChEMBL target-oriented subsets curated by van Tilborg et al. were used (details on ESI, Section S2†).57 For the PCA clustering visualization changes with similarity threshold, the natural products from ChEMBL33 (ref. 47) (n = 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087) were used. For the billion molecules clustering, random tranches from the ZINC22 2D48 database (https://cartblanche.docking.org/tranches/2d) were taken until 1 billion was reached (see ESI, Section S7†). In all cases, 2048-bit RDKit19 fingerprints were generated from SMILES, corrupted SMILES were discarded from the databases. The statistical comparison between the clustering performance metrics for the methods was done using SciPy's58 Wilcoxon test,59 alternative hypothesis evaluated depended on the case. All the calculations (except the statistical analysis and plotting) were run in University of Florida's HiperGator supercomputer. The BitBIRCH code is available at: https://github.com/mqcomplab/bitbirch.
087) were used. For the billion molecules clustering, random tranches from the ZINC22 2D48 database (https://cartblanche.docking.org/tranches/2d) were taken until 1 billion was reached (see ESI, Section S7†). In all cases, 2048-bit RDKit19 fingerprints were generated from SMILES, corrupted SMILES were discarded from the databases. The statistical comparison between the clustering performance metrics for the methods was done using SciPy's58 Wilcoxon test,59 alternative hypothesis evaluated depended on the case. All the calculations (except the statistical analysis and plotting) were run in University of Florida's HiperGator supercomputer. The BitBIRCH code is available at: https://github.com/mqcomplab/bitbirch.
Conclusions
We have developed an alternative to the BIRCH and Taylor–Butina algorithms, BitBIRCH, capable of handling binary data with the similarity metrics that are used in drug design and ML applications targeting small molecules. Key components of BitBIRCH include the tree structure derived from the BIRCH method, as well as the ability to use the BF to encode the cluster's information. The tree is critical to ensure the O(N) time scaling, by reducing the total number of comparisons required to allocate each new molecule to their corresponding cluster. The BF, on the other hand, is what allows to reduce the memory usage, by providing a convenient proxy to the cluster's properties required to assign new molecules or create new sub-divisions. This is possible thanks to the iSIM formalism since having the chance to calculate the average of the pairwise Tanimoto comparisons is what opens the door to the cluster's radius and diameter. As noted before, while we focused on Tanimoto similarity, iSIM can be used to calculate the average pairwise with other similarity indices; BitBIRCH can trivially incorporate other criteria, like Russel–Rao and Sokal–Michener. Likewise, this methodology is applicable to any type of fingerprints.The comparison of BitBIRCH with the RDKit implementation of Taylor–Butina showcases the differences in efficiency between these methods. We saw that 4 TB of memory were insufficient for Taylor–Butina to cluster more than 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, while BitBIRCH was able to easily handle millions.
000 molecules, while BitBIRCH was able to easily handle millions.
Moreover, RDKit took more than 8 hours to cluster those 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, with BitBIRCH requiring ∼2.2 minutes to complete the same task. If we follow the trends in Fig. 1, we see that for 1
000 molecules, with BitBIRCH requiring ∼2.2 minutes to complete the same task. If we follow the trends in Fig. 1, we see that for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules, BitBIRCH is >1000 times faster than Taylor–Butina. Compare this to other linear clustering algorithms, like linclust, that only got to a 1000× speedup over their previous alternatives for billions of points, thus showcasing how much faster BitBIRCH is compared to Taylor–Butina. One of the key characteristics of BitBIRCH is that the increase in time and memory efficiency do not diminish the clustering quality compared to the O(N2) alternatives. First, we saw that BitBIRCH and Taylor–Butina partition the chemical space in similar ways (total number of clusters, etc.). Moreover, a more detailed analysis over 30 subsets of the ChEMBL library showed that BitBIRCH outperforms Taylor–Butina for lower similarity thresholds according to the CHI and DBI metrics, with both methods being statistically indistinguishable in the [0.5, 0.7] range. The DI, on the other hand, favors BitBIRCH up to a 0.8 threshold. So, for all the clustering metrics considered, BitBIRCH performs better or, at worst, with the same quality as Taylor–Butina. BitBIRCH also proved to be more robust to changes in the computational conditions (similarity threshold, minimum number of molecules in a cluster).
000 molecules, BitBIRCH is >1000 times faster than Taylor–Butina. Compare this to other linear clustering algorithms, like linclust, that only got to a 1000× speedup over their previous alternatives for billions of points, thus showcasing how much faster BitBIRCH is compared to Taylor–Butina. One of the key characteristics of BitBIRCH is that the increase in time and memory efficiency do not diminish the clustering quality compared to the O(N2) alternatives. First, we saw that BitBIRCH and Taylor–Butina partition the chemical space in similar ways (total number of clusters, etc.). Moreover, a more detailed analysis over 30 subsets of the ChEMBL library showed that BitBIRCH outperforms Taylor–Butina for lower similarity thresholds according to the CHI and DBI metrics, with both methods being statistically indistinguishable in the [0.5, 0.7] range. The DI, on the other hand, favors BitBIRCH up to a 0.8 threshold. So, for all the clustering metrics considered, BitBIRCH performs better or, at worst, with the same quality as Taylor–Butina. BitBIRCH also proved to be more robust to changes in the computational conditions (similarity threshold, minimum number of molecules in a cluster).
Finally, we explored alternatives to tackle billion-sized libraries in even more efficient ways. The fingerprint folding approach compromised the clustering results, with even one-fold, leading to worse DI values than the original BitBIRCH method. We found a more promising route with the parallel/iterative clustering strategy, it separates the data into different splits, which are then clustered and whose resulting centroids are then clustered again. This led to performances remarkably close to the unmodified BitBIRCH algorithm, while considerably boosting the efficiency of the method. We tested this with 1 billion molecules from the ZINC22 library, which we were able to cluster in 4.35 hours (in stark contrast with the estimated 6342 years it would take the RDKit Taylor–Butina implementation to complete this task).
Data availability
The software used in the paper can be found in: https://github.com/mqcomplab/bitbirch (DOI: 10.5281/zenodo.14977624). Benchmark data can be found in: https://github.com/molML/MoleculeACE/tree/main/MoleculeACE/Data/benchmark_data.Author contributions
Kenneth López Pérez: code optimization, manuscript, and data analysis. Vicky Jung: code optimization, conceptualization, and data analysis. Lexin Chen: manuscript, data analysis. Kate Huddleston: manuscript, and code optimization. Ramón Alain Miranda-Quintana: conceptualization, main code contributor, code optimization, manuscript, data analysis, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
KLP, LC, KH, and RAMQ thank the National Institute of General Medical Sciences of the National Institutes of Health for support under award number R35GM150620. VJ thanks the UF AI Scholars Program for a fellowship.References
- A. E. Ezugwu, A. M. Ikotun, O. O. Oyelade, L. Abualigah, J. O. Agushaka, C. I. Eke and A. A. Akinyelu, Eng. Appl. Artif. Intell., 2022, 110, 104743 CrossRef.
- G. J. Oyewole and G. A. Thopil, Artif. Intell. Rev., 2023, 56, 6439–6475 CrossRef PubMed.
- A. K. Jain, M. N. Murty and P. J. Flynn, ACM Comput. Surv., 1999, 31, 264–323 CrossRef.
- L. Cheng, N. B. Kovachki, M. Welborn and T. F. Miller, J. Chem. Theory Comput., 2019, 15, 6668–6677 CrossRef CAS PubMed.
- B. Zhang, in Third IEEE International Conference on Data Mining, IEEE Comput. Soc, 2003, pp. 451–458 Search PubMed.
- D. Domingo-Fernández, Y. Gadiya, S. Mubeen, D. Healey, B. H. Norman and V. Colluru, J. Cheminf., 2023, 15, 107 Search PubMed.
- H. Hadipour, C. Liu, R. Davis, S. T. Cardona and P. Hu, BMC Bioinf., 2022, 23, 132 CrossRef CAS PubMed.
- J. T. Leonard and K. Roy, QSAR Comb. Sci., 2006, 25, 235–251 CrossRef CAS.
- H. Eckert and J. Bajorath, Drug Discovery Today, 2007, 12, 225–233 CrossRef CAS PubMed.
- M. A. Johnson and G. M. Maggiora, Concepts and applications of molecular similarity, Wiley-Interscience, 1st edn, 1990 Search PubMed.
- Y. C. Martin, J. L. Kofron and L. M. Traphagen, J. Med. Chem., 2002, 45, 4350–4358 CrossRef CAS PubMed.
- P. Beroza, J. J. Crawford, O. Ganichkin, L. Gendelev, S. F. Harris, R. Klein, A. Miu, S. Steinbacher, F.-M. Klingler and C. Lemmen, Nat. Commun., 2022, 13, 6447 CrossRef CAS PubMed.
- D. Bajusz, A. Rácz and K. Héberger, in Comprehensive Medicinal Chemistry II, Elsevier, 2017, vol. 3 Search PubMed.
- K.-Z. Myint, L. Wang, Q. Tong and X.-Q. Xie, Mol. Pharm., 2012, 9, 2912–2923 CrossRef CAS PubMed.
- G. B. McGaughey, R. P. Sheridan, C. I. Bayly, J. C. Culberson, C. Kreatsoulas, S. Lindsley, V. Maiorov, J.-F. Truchon and W. D. Cornell, J. Chem. Inf. Model., 2007, 47, 1504–1519 CrossRef CAS PubMed.
- R. D. Brown and Y. C. Martin, J. Chem. Inf. Comput. Sci., 1997, 37, 1–9 CrossRef CAS.
- J. L. Durant, B. A. Leland, D. R. Henry and J. G. Nourse, J. Chem. Inf. Comput. Sci., 2002, 42, 1273–1280 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- G. Landrum and J. Penzotti, 2018, preprint, http://www.rdkit.org/.
- A. Capecchi, D. Probst and J.-L. Reymond, J. Cheminf., 2020, 12, 43 CAS.
- D. J. Rogers and T. T. Tanimoto, Science, 1960, 132, 1115–1118 CrossRef CAS PubMed.
- P. Jaccard, New Phytol., 1912, 11, 37–50 CrossRef.
- B. Zhang, M. Vogt, G. M. Maggiora and J. Bajorath, J. Comput.-Aided Mol. Des., 2015, 29, 937–950 CrossRef CAS PubMed.
- D. C. Anastasiu and G. Karypis, Int. J. Data Sci. Anal., 2017, 4, 153–172 CrossRef.
- D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2015, 7, 20 Search PubMed.
- R. Todeschini, V. Consonni, H. Xiang, J. Holliday, M. Buscema and P. Willett, J. Chem. Inf. Model., 2012, 52, 2884–2901 CrossRef CAS PubMed.
- D. Butina, J. Chem. Inf. Comput. Sci., 1999, 39, 747–750 CrossRef CAS.
- P. Thiel, L. Sach-Peltason, C. Ottmann and O. Kohlbacher, J. Chem. Inf. Model., 2014, 54, 2395–2401 CrossRef CAS PubMed.
- E. Liu, Z. Z. Zhang, X. Cheng, X. Liu and L. Cheng, BMC Med. Genomics, 2020, 13, 50 CrossRef CAS PubMed.
- S. Gan, D. A. Cosgrove, E. J. Gardiner and V. J. Gillet, J. Chem. Inf. Model., 2014, 54, 3302–3319 CrossRef CAS PubMed.
- A. Böcker, S. Derksen, E. Schmidt, A. Teckentrup and G. Schneider, J. Chem. Inf. Model., 2005, 45, 807–815 CrossRef PubMed.
- B. S. S. Sowjanya Lakshmi and R. K. V. P, in Soft Computing and Signal Processing, 2023, pp. 127–137 Search PubMed.
- A. Vathy-Fogarassy, A. Kiss and J. Abonyi, in Applications of Fuzzy Sets Theory, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 195–202 Search PubMed.
- M. G. Malhat, H. M. Mousa and A. B. El-Sisi, in 2014 9th International Conference on Informatics and Systems, IEEE, 2014, pp. DEKM-61–DEKM-66 Search PubMed.
- R. Taylor, J. Chem. Inf. Comput. Sci, 1995, 35, 59–67 CrossRef CAS.
- S. Hernández-Hernández and P. J. Ballester, Biomolecules, 2023, 13, 498 CrossRef PubMed.
- T. Zhang, R. Ramakrishnan and M. Livny, ACM SIGMOD Record, 1996, vol. 25, pp. 103–114 Search PubMed.
- K. E. Kirchoff, J. Wellnitz, J. E. Hochuli, T. Maxfield, K. I. Popov, S. Gomez and A. Tropsha, in Advances in Information Retrieval, 2024, pp. 34–49 Search PubMed.
- R. A. Miranda-Quintana, D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2021, 13, 32 Search PubMed.
- R. A. Miranda-Quintana, A. Rácz, D. Bajusz and K. Héberger, J. Cheminf., 2021, 13, 33 Search PubMed.
- E. A. Flores-Padilla, K. E. Juárez-Mercado, J. J. Naveja, T. D. Kim, R. Alain Miranda-Quintana and J. L. Medina-Franco, Mol. Inf., 2022, 41, 2100285 CrossRef CAS PubMed.
- K. López-Pérez, E. López-López, J. L. Medina-Franco and R. A. Miranda-Quintana, Molecules, 2023, 28, 6333 CrossRef PubMed.
- T. B. Dunn, E. López-López, T. D. Kim, J. L. Medina-Franco and R. A. Miranda-Quintana, Mol. Inf., 2023, 42(7), e2300056 CrossRef PubMed.
- L. Chang, A. Perez and R. A. Miranda-Quintana, Phys. Chem. Chem. Phys., 2022, 24, 444–451 RSC.
- A. Rácz, L. M. Mihalovits, D. Bajusz, K. Héberger and R. A. Miranda-Quintana, J. Chem. Inf. Model., 2022, 62, 3415–3425 CrossRef PubMed.
- K. López-Pérez, T. D. Kim and R. A. Miranda-Quintana, Digital Discovery, 2024, 3, 1160–1171 RSC.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2012, 40, D1100–D1107 CrossRef CAS PubMed.
- B. I. Tingle, K. G. Tang, M. Castanon, J. J. Gutierrez, M. Khurelbaatar, C. Dandarchuluun, Y. S. Moroz and J. J. Irwin, J. Chem. Inf. Model., 2023, 63, 1166–1176 CrossRef CAS PubMed.
- O. Arbelaitz, I. Gurrutxaga, J. Muguerza, J. M. Pérez and I. Perona, Pattern Recognit., 2013, 46, 243–256 CrossRef.
- C. T. Harabasz and M. Karoński, in Communications in Statistics, 1974, vol. 3, pp. 1–27 Search PubMed.
- D. L. Davies and D. W. Bouldin, IEEE Trans. Pattern Anal. Mach. Intell., 1979, PAMI-1, 224–227 Search PubMed.
- J. C. Dunn, J. Cybern., 1973, 3, 32–57 CrossRef.
- G. Zahoránszky-Kőhalmi, C. G. Bologa and T. I. Oprea, J. Cheminf., 2016, 8, 16 Search PubMed.
- A. Strehl and J. Ghosh, J. Mach. Learn. Res., 2002, 3, 583–617 Search PubMed.
- J. Wu, H. Liu, H. Xiong, J. Cao and J. Chen, IEEE Trans. Knowl. Data Eng., 2015, 27, 155–169 Search PubMed.
- N. Nguyen and R. Caruana, in Seventh IEEE International Conference on Data Mining (ICDM 2007), IEEE, 2007, pp. 607–612 Search PubMed.
- D. van Tilborg, A. Alenicheva and F. Grisoni, J. Chem. Inf. Model., 2022, 62, 5938–5951 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. Pietro Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G. L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- D. Rey and M. Neuhäuser, in International Encyclopedia of Statistical Science, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 1658–1659 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00030k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |