Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
GraphXForm: graph transformer for computer-aided molecular design†
Jonathan
Pirnay‡
ab,
Jan G.
Rittig‡
c,
Alexander B.
Wolf‡
d,
Martin
Grohe
e,
Jakob
Burger
 d,
Alexander
Mitsos
cfg and
Dominik G.
Grimm
d,
Alexander
Mitsos
cfg and
Dominik G.
Grimm
 *ab
*ab
aTechnical University of Munich, TUM Campus Straubing for Biotechnology and Sustainability, Bioinformatics, Petersgasse 18, 94315 Straubing, Germany
bUniversity of Applied Sciences Weihenstephan-Triesdorf, Bioinformatics, Petersgasse 18, 94315 Straubing, Germany. E-mail: dominik.grimm@hswt.de
cProcess Systems Engineering (AVT.SVT), RWTH Aachen University, Forckenbeckstraße 51, 52074 Aachen, Germany
dTechnical University of Munich, TUM Campus Straubing for Biotechnology and Sustainability, Laboratory of Chemical Process Engineering, Uferstraße 53, 94315 Straubing, Germany
eChair of Computer Science 7, RWTH Aachen University, Ahornstraße 55, 52074 Aachen, Germany
fJARA Center for Simulation and Data Science (CSD), Aachen, Germany
gForschungszentrum Jülich GmbH, Institute of Climate and Energy Systems ICE-1: Energy Systems Engineering, Jülich 52425, Germany
First published on 14th March 2025
Abstract
Generative deep learning has become pivotal in molecular design for drug discovery, materials science, and chemical engineering. A widely used paradigm is to pretrain neural networks on string representations of molecules and fine-tune them using reinforcement learning on specific objectives. However, string-based models face challenges in ensuring chemical validity and enforcing structural constraints like the presence of specific substructures. We propose to instead combine graph-based molecular representations, which can naturally ensure chemical validity, with transformer architectures, which are highly expressive and capable of modeling long-range dependencies between atoms. Our approach iteratively modifies a molecular graph by adding atoms and bonds, which ensures chemical validity and facilitates the incorporation of structural constraints. We present GraphXForm, a decoder-only graph transformer architecture, which is pretrained on existing compounds and then fine-tuned using a new training algorithm that combines elements of the deep cross-entropy method and self-improvement learning. We evaluate GraphXForm on various drug design tasks, demonstrating superior objective scores compared to state-of-the-art molecular design approaches. Furthermore, we apply GraphXForm to two solvent design tasks for liquid–liquid extraction, again outperforming alternative methods while flexibly enforcing structural constraints or initiating design from existing molecular structures.
1 Introduction
Molecular design plays an important role across many fields, such as drug discovery, materials science, and chemical engineering. The immense chemical search space, estimated to contain between 1060 and 10100 potential molecules,1 renders manual approaches to molecular design both arduous and resource-intensive.Advancements in deep learning have significantly impacted molecular design, enabling efficient navigation of the chemical space with the help of neural networks.2–6 A prevalent paradigm is to represent molecules as strings of text, such as SMILES7 or SELFIES,8 and use neural network architectures from language modeling, such as recurrent neural networks (RNNs) or transformers,9 to generate novel molecular structures. These architectures are typically pretrained on large datasets of existing molecules to learn general underlying patterns in the strings and then fine-tuned on specific objective functions via reinforcement learning (RL) for downstream tasks.10–14
To address the challenge of capturing long-range dependencies in sequential data that RNNs face, transformers9 have been successfully applied due to their ability to model long-range dependencies more efficiently and as they are widely used in language modeling today.12 However, transformers are resource-intensive, and fine-tuning them with RL further constrains the model sizes that are practical in real-world applications.12,15,16 In general, chemical language models may propose string representations of molecules with invalid chemical structures – for example, when SMILES syntax or valence constraints are violated – which has led to numerous works aimed at circumventing this problem.8,17–19 Despite recent evidence that invalid SMILES can actually be beneficial from a language modeling perspective,20 they can harm the RL component of the pipeline as they can increase sample complexity and necessitate reward shaping to account for them. Moreover, the sequential nature of string synthesis makes it challenging to enforce structural constraints – such as ensuring a minimum number of specific atom types, restricting bonding patterns, or initiating design from predefined molecular substructures – often requiring scaffold-constrained techniques.21,22
An alternative approach is to represent molecules directly as graphs, where atoms are nodes and bonds are edges, and to develop models that modify a molecular graph or design it directly.23–33 Working at the graph level allows explicit encoding of atomic interactions and bonding rules, ensuring chemical validity, and makes it straightforward to start from existing structures and modify them. For example, graph-based methods like Graph GA27 employ genetic algorithms to modify molecular graphs directly, even outperforming several neural-based string-synthesis methods without relying on neural networks. As a deep learning example, Zhou et al.26 use deep Q-learning34 with a simple feedforward network to optimize graphs from scratch by adding or removing atoms and bonds.
We propose to combine and extend the strengths of both paradigms: employing transformers for their ability to capture long-range dependencies in sequence data, and leveraging pretraining on existing molecules, all while working directly on the molecular graph. More specifically, we use graph transformers32,35 and formulate molecule design as a sequential task, where a molecular graph – starting from an arbitrary structure – is iteratively extended by placing atoms and adding bonds.
To this end, we introduce GraphXForm, a decoder-only graph transformer architecture that guides these incremental decisions, predicting the next modification based on the current molecular graph. Pretrained on existing compounds, we propose a fine-tuning approach for downstream tasks that combines elements of the deep cross-entropy method36 and self-improvement learning.37 Unlike commonly used deep RL methods like REINFORCE,38 this approach allows for stable training of deep transformers with many layers.
We test GraphXForm for two molecular applications: (1) drug development and (2) solvent design. While algorithmic advances in molecular design have been primarily focused on de novo drug development and corresponding benchmarks,11,39–41 other areas such as materials science and chemical engineering have recently gained attention. Recent applications include catalyst,42 fuel,33,43 polymer,44,45 surfactant,46 chemical reaction substrate,47 and solvent48 design. Thus, we test GraphXForm in both established and newer application areas.
First, we consider drug design by evaluating GraphXForm on the goal-directed tasks of the well-established GuacaMol benchmark.39 The benchmark includes multiple design tasks such as drug rediscovery, isomer identification, and multi-property optimization. Based on these different design objectives, we demonstrate the soundness of GraphXForm and its competitive performance with state-of-the-art molecular design approaches.
Secondly, we apply GraphXForm for the design of solvents, which play a vital role in industrial chemical processes such as reactions, separations, and extractions. While König-Mattern48 recently applied a graph-based genetic algorithm for solvent design, the use of generative ML-based approaches remains underexplored. Therefore, our goal is to compare newer design methods and expand their capabilities by considering molecular structure constraints. Specifically, we evaluate GraphXForm on two liquid–liquid extraction tasks. The objective function in these tasks is defined by a separation factor based on activity coefficients at infinite dilution. For both downstream tasks, we compare GraphXForm to state-of-the-art molecular design approaches (Graph GA,27 REINVENT-Transformer,12 Junction Tree VAE,25 and STONED49). Additionally, we demonstrate GraphXForm's flexibility and stability by incorporating structural constraints conceptually suited for solvent design, such as preventing certain bonding patterns or preserving molecular substructures, allowing GraphXForm to propose design candidates with highly tailored properties. This capability highlights the strength of our approach in tackling design tasks that are difficult for existing methods.
Our contributions are summarized as follows:
• We formulate molecular design as a sequential task, where an initial structure (e.g., a single atom) is iteratively modified by adding atoms and bonds.
• We introduce a graph transformer architecture that takes a molecular graph as input and outputs probability distributions for atom and bond placement. This approach maintains the notion of using transformers for molecular design while moving away from string-based methods.
• We propose a training algorithm that enables the stable and efficient fine-tuning of deep graph transformers on downstream tasks.
• We demonstrate that our method outperforms state-of-the-art molecular design techniques on well-established drug design benchmarks and two solvent design tasks.
• We show that our method can be easily adapted to meet structural constraints by preserving or excluding specific molecular moieties and starting the design from initial structures.
Our code for pretraining and fine-tuning is available at: https://github.com/grimmlab/graphxform.
2 Methods and modeling
In this section, we introduce GraphXForm. In Section 2.1, we formally set up the molecular design task as the sequential construction of a graph. As in a deep reinforcement learning setup, the goal is to find a policy network that guides these sequential decisions. In Section 2.2, we introduce our algorithm for training the policy network, before describing the used transformer architecture in Section 2.3.2.1 Molecular design
 represents the bonds and their orders between atoms, i.e., we have that
represents the bonds and their orders between atoms, i.e., we have that  is the bond order between the i-th and the j-th atom. In particular, B is symmetric with zero diagonal and nonzero columns and rows (i.e., each atom is connected to at least one other atom and not to itself). For example, given the alphabet Σ = (C, N, O) the molecule with SMILES representation C
is the bond order between the i-th and the j-th atom. In particular, B is symmetric with zero diagonal and nonzero columns and rows (i.e., each atom is connected to at least one other atom and not to itself). For example, given the alphabet Σ = (C, N, O) the molecule with SMILES representation C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O can be given as (a, B) with a = (1, 3) and
O can be given as (a, B) with a = (1, 3) and 
We denote by  the space of all molecular graphs m = (a, B) as described above. Accordingly, let
the space of all molecular graphs m = (a, B) as described above. Accordingly, let  be the subspace of molecular graphs that are chemically valid, that is, all non-hydrogen atoms follow the octet rule. We refer to following the octet rule as satisfying the ‘valence constraints' throughout the paper. In this framework, ionization can be incorporated straightforwardly by extending the alphabet with additional atom types that allow for an adjusted number of non-hydrogen bonds. For instance, to model ionized carbon atoms, we can include the types C+ and C− in Σ, which are designated with a positive or negative charge and are permitted to form up to five and three non-hydrogen bonds, respectively. Chirality can be handled in an analogous manner. We refer to the ESI† for the complete alphabet used.
be the subspace of molecular graphs that are chemically valid, that is, all non-hydrogen atoms follow the octet rule. We refer to following the octet rule as satisfying the ‘valence constraints' throughout the paper. In this framework, ionization can be incorporated straightforwardly by extending the alphabet with additional atom types that allow for an adjusted number of non-hydrogen bonds. For instance, to model ionized carbon atoms, we can include the types C+ and C− in Σ, which are designated with a positive or negative charge and are permitted to form up to five and three non-hydrogen bonds, respectively. Chirality can be handled in an analogous manner. We refer to the ESI† for the complete alphabet used.
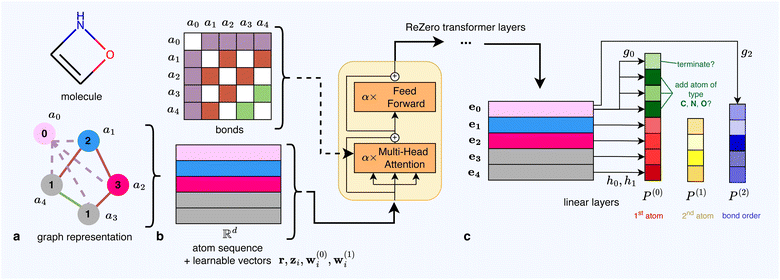
On a high level, a single molecule is constructed by the agent as follows: the agent observes an initial molecule m(0) and then performs some action x(0) on it, resulting in a new molecule m(1). Then, the agent observes m(1), decides on an action x(1) leading to molecule m(2), and so on. This iterative design process ends on some molecule m(T) once the agent decides to perform a special action DONTCHANGE, which does not alter the molecular graph but rather marks the design as completed.
We formalize this as follows. Let m(t) = (a(t), B(t)) be some molecule with atoms a(t) ∈ {1, …, k}n(t) and bond matrix  as above. We transition to a new molecule m(t+1) = (a(t+1), B(t+1)) by performing some action
as above. We transition to a new molecule m(t+1) = (a(t+1), B(t+1)) by performing some action  on m(t). An action x(t) in the action space
on m(t). An action x(t) in the action space  is of one of the following three types:
is of one of the following three types:
(1) x(t) = DONTCHANGE, which terminates the design of the molecule. In particular, m(t+1) = m(t) and n(t+1) = n(t).
(2) x(t) = ADDATOM(j, l, o), with j ∈ {1, …, k}, l ∈ {1, …, n(t)}, and  This action adds an atom of type Σj to the graph and connects it to the l-th atom with a bond of order o. In particular, we set n(t+1) = n(t) + 1. For the new molecule m(t+1) = (a(t+1), B(t+1)), the atom vector
This action adds an atom of type Σj to the graph and connects it to the l-th atom with a bond of order o. In particular, we set n(t+1) = n(t) + 1. For the new molecule m(t+1) = (a(t+1), B(t+1)), the atom vector  is obtained by appending j to a(t). The second entry l ∈ {1, …, n(t)} indicates that we bond this new (n + 1)-th atom to the l-th atom with order o, i.e.,
is obtained by appending j to a(t). The second entry l ∈ {1, …, n(t)} indicates that we bond this new (n + 1)-th atom to the l-th atom with order o, i.e.,  is obtained by appending a zero row and column to B(t) and setting Bn+1,l(t+1) = Bl,n+1(t+1) = o.
is obtained by appending a zero row and column to B(t) and setting Bn+1,l(t+1) = Bl,n+1(t+1) = o.
(3) x(t) = ADDBOND(j, l, o), meaning that we are adding a bond of order  between existing, unbonded atoms j and l. In particular, we have n(t+1) = n(t) and a(t+1) = a(t). The bond matrix B(t+1) is obtained from B(t) by setting
between existing, unbonded atoms j and l. In particular, we have n(t+1) = n(t) and a(t+1) = a(t). The bond matrix B(t+1) is obtained from B(t) by setting 
Given a molecule m(0) and a sequence of actions x(0), …, x(t−1), we will also write (m(0), x(0), …, x(t−1)) for the molecule  that results from m(0) by sequentially applying the actions x(0), …, x(t−1) to m(0). In general, the action sequence x(0), …, x(t−1) is not unique to get from m(0) to m(t).
that results from m(0) by sequentially applying the actions x(0), …, x(t−1) to m(0). In general, the action sequence x(0), …, x(t−1) is not unique to get from m(0) to m(t).
Starting from a molecule in  by removing chemically invalid actions from the action space (which would lead to violation of valence constraints) at each step, we can guarantee staying in the space of chemically valid molecules. Once the agent chooses the action DONTCHANGE, the design process is considered complete. We note that starting from an appropriate initial atom, it is in fact possible to reach every target molecule in the chemically valid space
by removing chemically invalid actions from the action space (which would lead to violation of valence constraints) at each step, we can guarantee staying in the space of chemically valid molecules. Once the agent chooses the action DONTCHANGE, the design process is considered complete. We note that starting from an appropriate initial atom, it is in fact possible to reach every target molecule in the chemically valid space  (i.e., all molecular graphs that can be constructed from the alphabet Σ and that satisfy the valence constraints) when starting from any atom that exists in the target molecule. For an illustrative molecule construction, see Fig. 1.
(i.e., all molecular graphs that can be constructed from the alphabet Σ and that satisfy the valence constraints) when starting from any atom that exists in the target molecule. For an illustrative molecule construction, see Fig. 1.
 | (1) |
 , where chemically invalid molecules are mapped to −∞. As in previous work,12,13,26 we pose the corresponding learning problem to eqn (1) in the terms of deep RL: the agent's decision at each step is guided by a policy that maps a chemically valid molecule to a probability distribution over possible actions. The policy is modeled by a neural network: we write
, where chemically invalid molecules are mapped to −∞. As in previous work,12,13,26 we pose the corresponding learning problem to eqn (1) in the terms of deep RL: the agent's decision at each step is guided by a policy that maps a chemically valid molecule to a probability distribution over possible actions. The policy is modeled by a neural network: we write  for a policy depending on network parameters θ, that maps a valid molecule
for a policy depending on network parameters θ, that maps a valid molecule  to a probability distribution πθ(m) over
to a probability distribution πθ(m) over  The goal is to find πθ that, given any initial molecule m(0), maximizes the expectation
The goal is to find πθ that, given any initial molecule m(0), maximizes the expectation | (2) |
Our graph-based approach allows us to extend this concept of action masking to enforce additional constraints, such as particular bonding patterns, minimum/maximum number of atoms and their types, or restricting structural motifs like rings. We explore these constraints in detail in Section 3. We note that it is possible to simply assign an objective value of −∞ to molecules that violate these constraints after the design process. However, the ability to preemptively avoid constraint-violating regions by masking actions during the design process reduces the search space.
2.2 Learning algorithm
We now introduce our method for training the policy neural network πθ. Our proposed learning algorithm is a hybrid of the deep cross-entropy method (CEM)36 and self-improvement learning (SIL),37,50–52 a sampling-based approach to expert iteration.53 Both the deep CEM and SIL train the neural network over multiple epochs in a self-improving loop. In each epoch, the current policy is used to generate a set of action sequences, from which the best sequences are selected as ‘pseudo-labels’ to serve as the dataset for supervised training. The network is then trained for one epoch to assign higher probabilities to these sequences, and the updated network is subsequently used to generate new action sequences. Unlike many deep RL algorithms, this approach does not require reward shaping or value approximation. Moreover, training in a supervised way provides stability and facilitates the use of larger, decoder-only transformer architectures.9There are key differences between SIL and the deep CEM. The deep CEM is formulated for problems with a single instance (as in our molecular design task) and retains a fixed percentage of the best action sequences in each epoch, which are obtained through simple sampling from the policy's predicted distributions at each step. In contrast, SIL is typically applied to problems with infinitely many instances and employs more advanced sequence decoding techniques – such as sequence sampling without replacement54 – to improve solution quality and diversity while maintaining efficient decoding speed.
In our proposed approach, we seek to develop a method that works for single-instance problems, as in the deep CEM, while retaining the diverse sampling mechanism used in SIL methods.37,52 In particular, we adopt the Take a Step and Reconsider (TASAR) method37 to sample action sequences, as detailed below. The pseudocode for our approach is presented in Algorithm 1, and we describe the key steps as follows:
(1) We begin with a policy network πθ. The parameters θ can be initialized randomly or, e.g., pretrained in an unsupervised manner on existing molecules (see Section 3.1). Additionally, we assume an initial molecule  in the space of chemically valid molecules
in the space of chemically valid molecules  from which the construction starts. In practice, we typically choose m0 to consist of a single carbon atom.
from which the construction starts. In practice, we typically choose m0 to consist of a single carbon atom.
(2) Throughout training, we maintain a set BESTFOUND containing the best molecules discovered so far. This set is initially initialized with the starting molecule m0.
(3) In each epoch, we sample action sequences from the policy using the TASAR method.37 Specifically, β action sequences are sampled without replacement using stochastic beam search54 with a beam width  These sequences are then evaluated using the objective function. The best action sequence among the β samples is followed for a predefined number σ of actions. Subsequently, alternative, previously unseen actions are sampled from the resulting partial sequence to further explore and potentially improve the solution, and the process continues. Sampling without replacement ensures that unique action sequences are generated, effectively exploring the search space (particularly for shorter sequences55). Although different action sequences may result in the same molecule, this does not pose an issue for TASAR since the policy is concerned with generating action sequences rather than the molecular structure itself. By sampling sequences without replacement, the policy is encouraged to produce diverse outputs, even if the resulting molecules are identical.
These sequences are then evaluated using the objective function. The best action sequence among the β samples is followed for a predefined number σ of actions. Subsequently, alternative, previously unseen actions are sampled from the resulting partial sequence to further explore and potentially improve the solution, and the process continues. Sampling without replacement ensures that unique action sequences are generated, effectively exploring the search space (particularly for shorter sequences55). Although different action sequences may result in the same molecule, this does not pose an issue for TASAR since the policy is concerned with generating action sequences rather than the molecular structure itself. By sampling sequences without replacement, the policy is encouraged to produce diverse outputs, even if the resulting molecules are identical.
(4) After sampling, the set BESTFOUND serves as the training dataset for supervised learning (lines 6–8). Similarly to how decoder-only models in language modeling are trained to predict the next token from partial text, we sample batches of intermediate molecules and train the network with a cross-entropy loss to predict the next action for the corresponding molecule.
(5) In the next epoch, the process is repeated with the updated network weights.
2.3 Policy network architecture
The policy network receives a molecule as input and predicts a probability distribution over possible next actions using a simplified version of the Graphormer.35 This model treats the molecule's atoms as an unordered set of nodes and processes them through a stack of transformer layers with the attention mechanism augmented by bonding information. The resulting latent representations of the nodes are then used to predict action distributions.• Action level 0: the agent decides whether to end the design process (choosing DONTCHANGE) or to modify the molecule. In the latter case, it selects the first atom j, which can be an already present one for ADDBOND(j, l, o) or a new one from the alphabet for ADDATOM(j, l, o).
• Action level 1: given a modification is intended, the agent selects a second atom l from the current molecule, indicating a new bond between j and l.
• Action level 2: finally, the agent determines the order o of the bond between j and l.
Fig. 2 provides an illustration, and we elaborate on the architecture below:
 are the atoms, and
are the atoms, and  is the bond matrix. Each atom ai ∈ {1, …, k} corresponds to an atom type selected from an alphabet Σ = (Σ1, …, Σk).
is the bond matrix. Each atom ai ∈ {1, …, k} corresponds to an atom type selected from an alphabet Σ = (Σ1, …, Σk).
Following the Graphormer35 model, we introduce a ‘virtual atom’ a0 = 0 into the molecular graph, which is connected to every atom via a special ‘virtual bond’ (see Fig. 2). This virtual bond is represented in the bond matrix by an integer outside the range of standard bond orders. The virtual atom functions similarly to the special [CLS]-token in BERT56 and accumulates sequence-level information for downstream tasks. Conceptually, the virtual atom acts as an additional message proxy between nodes in the molecular graph.
The atom sequence (a0, a1, …, an) is first embedded into latent representations (â0, â1, …, ân) in  where each âi is a learnable vector corresponding to the atom type. We then augment these representations with additional learnable embeddings that encode the current action level and other relevant information.
where each âi is a learnable vector corresponding to the atom type. We then augment these representations with additional learnable embeddings that encode the current action level and other relevant information.
Specifically, we introduce a learnable vector  to represent the current action level. For each atom i ∈ 1, …, n, we further include the embeddings wi(0) and wi(1), which indicate whether the i-th atom has been selected at action levels 0 and 1, respectively. Moreover, let
to represent the current action level. For each atom i ∈ 1, …, n, we further include the embeddings wi(0) and wi(1), which indicate whether the i-th atom has been selected at action levels 0 and 1, respectively. Moreover, let  be an embedding that reflects the total number of bonds (i.e., the degree) formed by the i-th atom. The final augmented sequence
be an embedding that reflects the total number of bonds (i.e., the degree) formed by the i-th atom. The final augmented sequence
| (â0 + r,â1 + z1 + w1(0) + w1(1), …, ân + zn + wn(0) +wn(1)) | (3) |
To incorporate bonding information within the transformer layers, let  be the computed self-attention matrix in a layer (for any attention head) corresponding to the input sequence (a0, a1, …, an). As in Graphormer,35 and similar to the Molecule Attention Transformer,32 we augment the attention matrix A by introducing bond-specific information. This is done by adding a learnable bias to the attention scores before applying the softmax operation. Specifically, for 0 ≤ i, j ≤ n, the attention score Aij between the i-th and j-th sequence elements is modified as follows:
be the computed self-attention matrix in a layer (for any attention head) corresponding to the input sequence (a0, a1, …, an). As in Graphormer,35 and similar to the Molecule Attention Transformer,32 we augment the attention matrix A by introducing bond-specific information. This is done by adding a learnable bias to the attention scores before applying the softmax operation. Specifically, for 0 ≤ i, j ≤ n, the attention score Aij between the i-th and j-th sequence elements is modified as follows:
| Aij ← Aij + bij, | (4) |
 is a learnable scalar that only depends on the bond order Bij for i, j > 0 (and not on the indices i, j). In particular, for the special bonds involving the virtual atom (i.e., if i = 0 or j = 0), bij = b is a learnable scalar shared across all atoms. We note that bij for each bond order is learned independently across layers and attention heads.
is a learnable scalar that only depends on the bond order Bij for i, j > 0 (and not on the indices i, j). In particular, for the special bonds involving the virtual atom (i.e., if i = 0 or j = 0), bij = b is a learnable scalar shared across all atoms. We note that bij for each bond order is learned independently across layers and attention heads.
 corresponds to the original atom ai. These embeddings are then used to simultaneously predict three probability distributions, P(0), P(1), and P(2), each corresponding to one of the action levels. The agent selects an action based on the distribution associated with the current action level.
corresponds to the original atom ai. These embeddings are then used to simultaneously predict three probability distributions, P(0), P(1), and P(2), each corresponding to one of the action levels. The agent selects an action based on the distribution associated with the current action level.
The unnormalized log-probabilities (logits) for these distributions are computed as follows:
• Action level 0 (P(0)): we denote the logits for P(0) as
 | (5) |
The first k + 1 logits, (p0(0), p1(0), …, pk(0)), are obtained by projecting the vector e0 through a linear layer  Here, p0(0) corresponds to the DONTCHANGE action, and for 1 ≤ j ≤ k, the logit pj(0) corresponds to adding a new atom of type Σj (i.e., serving as the first parameter j in ADDATOM(j, ·, ·)). The remaining logits, q1(0), …, qn(0), are computed by applying a linear layer
Here, p0(0) corresponds to the DONTCHANGE action, and for 1 ≤ j ≤ k, the logit pj(0) corresponds to adding a new atom of type Σj (i.e., serving as the first parameter j in ADDATOM(j, ·, ·)). The remaining logits, q1(0), …, qn(0), are computed by applying a linear layer  independently to each of the embeddings e1, …, en. For 1 ≤ j ≤ n, the logit qj(0) corresponds to selecting the first parameter j for the ADDBOND(j, ·, ·) action.
independently to each of the embeddings e1, …, en. For 1 ≤ j ≤ n, the logit qj(0) corresponds to selecting the first parameter j for the ADDBOND(j, ·, ·) action.
• Action level 1 (P(1)): the logits (q1(1), …, qn(1)) for this level are obtained by applying a linear layer  independently to each of e1, …, en. Here, ql(1) represents the choice of the second parameter l for either ADDATOM(j, l, ·) or ADDBOND(j, l, ·).
independently to each of e1, …, en. Here, ql(1) represents the choice of the second parameter l for either ADDATOM(j, l, ·) or ADDBOND(j, l, ·).
• Action level 2 (P(2)): the logits (p1(2), …, py(2)), which correspond to the bond order o in either ADDATOM(j, l, o) or ADDBOND(j, l, o), are computed by projecting e0 using a linear layer  where y is a predefined maximum bond order.
where y is a predefined maximum bond order.
After the agent selects an action at the current action level, the chosen information is fed back into the network by updating the learnable vectors r,wi(0) and wi(1). This updated state is then used for the subsequent forward pass when predicting the next action level.
The multi-step action prediction allows us to easily mask actions (i.e., setting their probability to zero in the policy) that would lead to invalid molecules. While checking for actions that would violate constraints adds a small amount of computational overhead, it has a significant benefit: invalid molecules can be immediately disregarded, preventing the network from wasting resources on infeasible designs. Masking invalid actions not only reduces the search space but also speeds up training by avoiding the need for the model to learn through trial and error how to avoid invalid molecules.
3 Results and discussion
We begin by outlining the experimental setup and hyperparameters for our method. Our first case study tackles the goal-directed design tasks from the well-established GuacaMol benchmark.39 In our second case study, we explore two solvent design tasks by detailing the goals, their underlying objective functions, and the property prediction methods used. To contextualize our results, we also present preliminary baselines obtained by screening available molecules and compare our findings with those of other approaches.3.1 GraphXForm: pretraining and fine-tuning
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. Each SMILES string is converted into an action sequence in our graph formulation; since the conversion is not unique, we select one possible sequence arbitrarily. These sequences are used to train the model in a self-supervised manner – predicting the next action given previous actions – as outlined in lines 6–8 of Algorithm 1. Training is performed with a dropout rate of 0.1, a batch size of 512, and over a total of 1.5 million batches.
000 molecules. Each SMILES string is converted into an action sequence in our graph formulation; since the conversion is not unique, we select one possible sequence arbitrarily. These sequences are used to train the model in a self-supervised manner – predicting the next action given previous actions – as outlined in lines 6–8 of Algorithm 1. Training is performed with a dropout rate of 0.1, a batch size of 512, and over a total of 1.5 million batches.
Petraining the network on existing molecules establishes a prior that captures the characteristics of real molecules, which is crucial for most generative methods such as REINVENT10,12 or JT-VAE.25
 , we fine-tune the pretrained policy network using the learning algorithm described in Section 2.2. We train only the weights of the final linear layers g0, g2, h0, h1. Unless stated otherwise, we initialize the molecule m0 as a single carbon atom. We set s = 100 as the number of top molecules to retain throughout training. For the TASAR sampling procedure, we use a beam width of β = 512 and a step size of σ = 12; that is, after every four added atoms or bonds, TASAR seeks better alternative solutions. At the end of each epoch, we train the network on 20 batches of size 64, sampled uniformly from the top 100 molecules. We intentionally keep the number of training batches per epoch relatively low to prevent premature overfitting, though in most runs increasing the number of batches does not harm performance and may even speed up convergence.
, we fine-tune the pretrained policy network using the learning algorithm described in Section 2.2. We train only the weights of the final linear layers g0, g2, h0, h1. Unless stated otherwise, we initialize the molecule m0 as a single carbon atom. We set s = 100 as the number of top molecules to retain throughout training. For the TASAR sampling procedure, we use a beam width of β = 512 and a step size of σ = 12; that is, after every four added atoms or bonds, TASAR seeks better alternative solutions. At the end of each epoch, we train the network on 20 batches of size 64, sampled uniformly from the top 100 molecules. We intentionally keep the number of training batches per epoch relatively low to prevent premature overfitting, though in most runs increasing the number of batches does not harm performance and may even speed up convergence.
3.2 Case study 1: drug design
Graph GA27 employs a genetic algorithm that directly operates on the molecular graph, mutating atoms and fragments using crossover rules derived from graph matching. This non-learning method is highly effective at making fine-grained local modifications, and it has been shown to outperform several SMILES-based learning approaches.11,27,39
In contrast, REINVENT-Transformer12 designs molecules by synthesizing SMILES strings in an autoregressive manner. This method uses a transformer network that is pretrained in a self-supervised fashion on known molecules and then fine-tuned with reinforcement learning via a variant of the REINFORCE algorithm.38 We include REINVENT-Transformer in our comparisons because, like GraphXForm, it relies on pretrained transformers and generates molecules autoregressively. However, while REINVENT-Transformer constructs molecules token by token from a predefined vocabulary, GraphXForm operates directly on the molecular graph by adding atoms and bonds.
GraphXForm outperforms both Graph GA and REINVENT-Transformer in different drug design tasks. As shown in Table 1, GraphXForm finds molecules with significantly higher scores for the three MPO cases compared to Graph GA and REINVENT-Transformer. For the scaffold hop task, GraphXForm achieves the best possible score of 1 similar to Graph GA. Considering the performance across all 20 tasks of the GuacaMol benchmark (see ESI Table 1†), GraphXForm attains a total summed score of 18.227, compared to 17.983 for Graph GA. Furthermore, ESI Table 1† demonstrates that our method overall outperforms other classic baselines from the original GuacaMol paper, as well as a recent optimization method that utilizes multiple GPT agents for drug design.63 These results underscore the robust molecular optimization capabilities of GraphXForm.
3.3 Case study 2: solvent design
The first solvent design task focuses on the separation of isobutanol (IBA) from water, a common liquid–liquid extraction process. The chosen solvent should be largely immiscible with water (i.e., low solubility exhibited for both the solvent in water and water in the solvent) and possess high affinity for IBA. As is common practice in chemical engineering, we use the partition coefficient P∞IBA at small mole fractions of IBA in both phases xIBA:
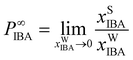 | (6) |
 | (7) |
To ensure the formation of two phases, i.e., a miscibility gap between the solvent and water, we use the following constraint:
| γ∞S,W × γ∞W,S > exp(4). | (8) |
This constraint guarantees a phase split between the water and solvent, assuming that the activity coefficient profiles follow the two-parameter Margules gE model.64 Although the activity coefficients of all conceivable solvent/water mixtures will not necessarily follow this model, the constraint still serves as a useful indicator for miscibility gaps.
The partition coefficient and the miscibility gap constraint are then combined to form the following scalar objective function:
 | (9) |
Our second solvent design task centers on an extraction process presented by Peters et al.,65 who carried out a solvent screening using COSMO-RS as a property predictor. Here, an enzymatic reaction in aqueous medium converts 3,5-dimethoxy-benzaldehyde (DMBA) molecules to (R)-3,3′,5,5′-tetra-methoxy-benzoin (TMB). The task is to find an organic solvent that forms a two-phase system with water. Similar to the IBA task, an optimal solvent should have a high affinity for the product TMB, enabling it to pull TMB out of the aqueous phase. At the same time, however, the solvent should have a low affinity for the educt DMBA. Designing a suitable solvent for this task is extremely challenging because DMBA and TMB possess similar chemical structures and polarities.
Again assuming small concentrations of DMBA and TMB as well as low mutual solubility between the solvent and water, we define the following partition coefficients similarly to our IBA task:
 | (10) |
Following Peters et al.,65 we maximize the ratio P∞TMB/P∞DMBA, while additionally enforcing the miscibility gap constraint from eqn (8) leading to the following scalar objective:
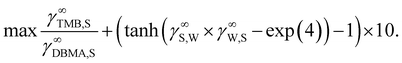 | (11) |
We note that further thermodynamic properties, e.g., boiling and melting points, and sustainability indicators, such as biodegradability and toxicity, are highly relevant for the practical effectiveness of solvents. Such properties could be considered as part of the objective function or as additional constraints in future work.
We note that many GNN models and other ML models such as transformers have been developed for activity coefficient prediction,71–73 also considering the composition-dependency and thermodynamic consistency.74–77 We here chose the GH-GNN as it is specialized for activity coefficients at infinite dilution and was trained on a much larger experimental database than the other models, thus covering a larger chemical space,69 which is desirable for molecular design. This model has shown high prediction accuracy, outperforming well-established methods for predicting activity coefficients at infinite dilution such as UNIFAC78 or COSMO-RS,79cf. Medina et al.69. Future work could investigate further additional activity coefficient models or directly predicting partition coefficients with ML.80,81
JT-VAE adopts a VAE, a widely used generative model in ML-guided molecular design.82–84 VAEs use an encoder–decoder structure, where the encoder maps molecules into a continuous latent space, and the decoder reconstructs them from this representation. Particularly when the objective function is derived from a trained network, the molecular latent space can facilitate exploration of the molecular space. That is, different optimization strategies can be employed to discover points in the latent space that correspond to promising novel molecules. These strategies include random sampling, Bayesian optimization, and GAs.33,82,84 In our work, we use JT-VAE in combination with GAs. JT-VAE operates on molecular graphs and their non-cyclic abstractions (junction trees), and it has demonstrated a high rate of decoding latent vectors into chemically valid molecules. Since we consider only molecules that conform to the alphabet Σ, we train JT-VAE on a subset of the QM9 dataset85,86 consisting of approximately 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules with at most nine heavy atoms.
000 molecules with at most nine heavy atoms.
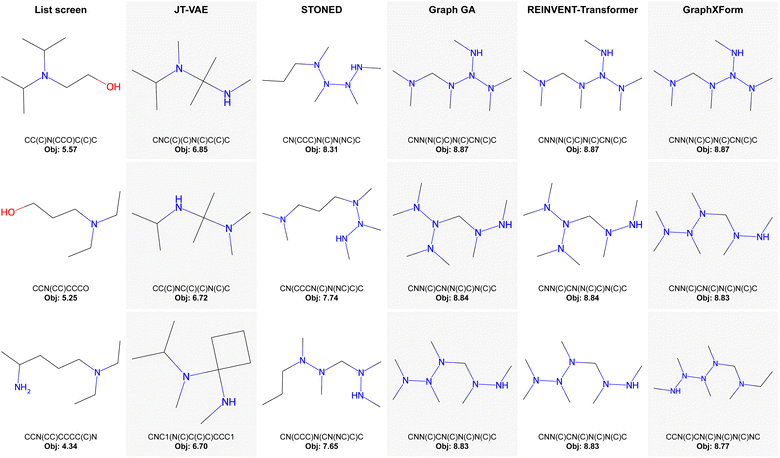 | ||
| Fig. 3 IBA task, unconstrained: top three molecules (with their corresponding SMILES string and objective value) identified by each method across all runs. | ||
| Method | IBA (cf.eqn (9)) | TMB/DMBA (cf.eqn (11)) | ||||||
|---|---|---|---|---|---|---|---|---|
| Max best | Mean best | Max top 20 | Mean top 20 | Max best | Mean best | Max top 20 | Mean top 20 | |
| JT-VAE25 | 6.85 | 6.41 ± 0.66 | 6.04 | 5.68 ± 0.57 | 2.16 | 1.56 ± 0.54 | 1.44 | 1.20 ± 0.23 |
| STONED49 | 8.31 | 7.42 ± 0.94 | 6.72 | 6.28 ± 0.41 | 2.39 | 1.68 ± 0.65 | 1.91 | 1.45 ± 0.49 |
| Graph GA27 | 8.87 | 7.13 ± 3.01 | 8.67 | 6.80 ± 3.22 | 8.40 | 8.14 ± 0.27 | 8.07 | 7.95 ± 0.32 |
| REINVENT-Transformer12 | 8.87 | 8.32 ± 0.52 | 8.66 | 8.09 ± 0.45 | 7.41 | 6.52 ± 1.17 | 7.22 | 6.42 ± 0.96 |
| GraphXForm (ours) | 8.87 | 8.87 ± 0.00 | 8.60 | 8.58 ± 0.04 | 8.65 | 8.65 ± 0.00 | 8.41 | 8.39 ± 0.01 |
In the IBA task, GraphXForm, REINVENT-Transformer, and Graph GA all identified the same best molecule, which has an objective value of 8.87. However, GraphXForm consistently found this molecule in every run, highlighting its stability. For example, in contrast, while Graph GA has a slightly higher average value for the best 20 molecules found, its mean best objective over all runs is only 7.13.
For the more challenging TMB/DMBA task, GraphXForm outperforms all other methods across every metric. Notably, Graph GA outperforms REINVENT-Transformer overall, likely due to the latter's sensitivity to initialization during RL fine-tuning. This factor is also reflected in its relatively high standard deviation. We also observe that the designs produced by Graph GA and GraphXForm exhibit substantial structural similarity, although GraphXForm makes additional refinements that lead to improved scores.
Interestingly, the JT-VAE and STONED methods identified molecules with significantly lower objective values for the TMB/DMBA task when compared to other methods, with maximum values of approximately 2.16 and 2.39, respectively. However, their results for the IBA task (6.85 and 7.53) were closer to those of the other methods. We attribute this discrepancy to the nature of the tasks: the TMB/DMBA task is inherently more challenging and requires larger molecules with more complex branching, while the best-performing molecules in the IBA task were smaller. As JT-VAE was trained only on molecules with up to nine heavy atoms, its ability to explore larger molecules seems limited. Similarly, STONED struggled to effectively explore larger molecular structures.
In summary, GraphXForm demonstrates highly promising results in both solvent design tasks, outperforming its comparison partners in terms of identifying the best candidates and ensuring robustness in the design process. In the following sections, we further explore the flexibility of GraphXForm by imposing structural constraints on the designed molecules and starting the design process from initial molecular structures.
A straightforward approach to enforcing such constraints is to assign an objective value of −∞ to any designed molecules that violate them, effectively discarding those candidates. In contrast, because GraphXForm operates directly on the molecular graph – transitioning from one molecule to the next without waiting for the completion of a string – we can flexibly restrict the search space by simply masking actions that would lead to constraint violations.
To examine how structural constraints affect the performance of GraphXForm in finding molecules with high objective values, we impose the following constraints: rings are limited to five or six atoms, and the following bonding patterns are disallowed: single bonds between two nitrogen atoms; single bonds between two oxygen atoms; a carbon atom single-bonded to two nitrogen atoms, unless the carbon is also double-bonded to an oxygen atom, forming a urea functional group; and a carbon atom single-bonded to a nitrogen atom, an oxygen atom, a hydrogen atom, and one other non-hydrogen functional group. We acknowledge that these constraints do not cover all aspects of synthetic accessibility, chemical stability, safety, or environmental impact. Rather, they serve as illustrative examples to demonstrate the capabilities of GraphXForm in incrementally limiting the designs to promising candidate structures that can be further evaluated by experts.
For the IBA task, the top three molecules designed by GraphXForm under these constraints are shown in the top row of Fig. 5. With constraints in place, we achieve a ‘mean best’ value of 7.28 ± 0.00 and a ‘mean top 20’ value 6.85 ± 0.02, which are only slightly lower than the values obtained without structural constraints. We also conducted constrained design runs with REINVENT-Transformer as a string-based counterpart; however, it reached only a ‘mean best’ value of 6.36 ± 0.39, with its overall best molecule scoring 6.92.
 | ||
| Fig. 5 Top three molecules designed by GraphXForm under structural constraints on specific bonding patterns and ring sizes. | ||
The bottom row of Fig. 5 displays the top three molecules identified by GraphXForm under the structural constraints for the TMB/DMBA task. Under these constraints, GraphXForm achieves a ‘mean best’ value of 8.54 ± 0.00 and a ‘mean top 20’ value of 8.31 ± 0.06. Notably, these results remain superior to those of the other methods without structural constraints, as reported in Table 2.
These findings further demonstrate GraphXForm's flexibility and its ability to consistently design promising molecules.
We repeat a similar experiment for the TMB/DMBA task. During list screening, we observed that the top three structures were all long-chain alcohols. However, long-chain alcohols tend to have melting points above room temperature, making them unsuitable as solvents for the intended processes. The melting point can be lowered by, e.g., adding branches. To address this, we again initiated three runs starting from the best molecule identified in the screening. These runs allowed the addition of up to 3, 5, and 7 atoms, thereby simulating branching of the long-chain alcohol. Additionally, we constrained the design process so that the resulting molecule remains an alcohol by preventing any modifications to the hydroxy group (an oxygen atom bonded to one hydrogen atom). The results, shown in the second row of Fig. 6, indicate that while no improvement in the objective function is observed when adding only 3 atoms, a notable enhancement occurs when 5 or 7 atoms are added.
This approach provides a powerful tool for cases where it is preferable to build upon an existing molecule rather than starting from scratch. We note that enabling the agent to remove atoms or bonds would not be beneficial when designing from a single atom, as it would introduce unnecessary redundancies into the search space. However, in scenarios where the design process begins with an existing molecule, allowing removal could offer additional flexibility and enable greater deviations from the initial structure. Extending the action space to include atom and bond removal is straightforward within our framework; however, we leave the exploration of this possibility for future work.
4 Conclusion
We presented GraphXForm, a method for molecular design that follows the successful paradigm of self-supervised pretraining followed by (RL-based) fine-tuning, but operates directly on molecular graphs. By doing so, we addressed challenges faced by string-based methods, such as chemical validity or accommodating structural constraints. We introduced a technique derived from self-improvement learning to fine-tune a deep graph-transformer model. Based on the established drug design GuacaMol benchmark39 and two solvent design tasks, we showed that GraphXForm can outperform state-of-the-art molecule design techniques. Additionally, our approach can flexibly adhere to specified structural constraints, such as bond types and functional groups, and can adaptively start the design process from existing molecular structures.Looking ahead, several promising avenues for future development exist. First, we plan to expand the atom alphabet of GraphXForm and pretrain the network on significantly larger databases. Although these enhancements can be integrated into our current framework, we intentionally limited the atom set in this study to ensure comparability with other methods. Second, we aim to extend the action space by allowing the agent to remove bonds and atoms. While not necessary for our present investigation – and admittedly introducing further action symmetries – this addition would offer the model more possibilities when modifying starting molecules.
Additionally, future work could involve evaluating GraphXForm on a broader range of molecular design tasks and incorporating more design considerations. For instance, recent trends in ML-based drug development emphasize increased sample efficiency11,60,61,88 and the integration of synthesizability models.62,89 Although sample efficiency was not the primary focus of our current study, our method inherently maintains a kind of experience replay buffer, suggesting that techniques targeting replay buffers60,61 could be readily applied to further enhance GraphXForm. Furthermore, tweaking TASAR parameters (e.g., using a shallower beam width β or a higher step size σ) and allowing more training batches in each fine-tuning epoch can help to make the method more sample-efficient.
We also aim to incorporate more constraints to ensure the suitability of the designed molecules for specific applications. In the case of solvents for liquid–liquid separation processes, this includes recognizing that numerous factors – such as boiling and melting points – are critical to a solvent's effectiveness. This, however, will depend on the availability of reliable property predictors.
Finally, since many structural constraints (e.g., presence of certain atoms, bonds, or formal groups) on the molecular graph can be flexibly formulated and implemented in a general manner within the current framework, we envision integrating GraphXForm with large language models to create a user-friendly design interface. This would allow researchers to formulate constraints in natural language, which would then be translated into the appropriate configuration for the model.
Data availability
All our code and data for pretraining and fine-tuning GraphXForm is available at https://github.com/grimmlab/graphxform. DOI of code and data release: https://doi.org/10.5281/zenodo.15016002.Author contributions
J. P.: conceptualization; methodology – concept and implementation of environment, network architecture, learning algorithm, adaptation of benchmark methods; analysis; validation; visualization; writing – original draft. J. G. R.: conceptualization; methodology – concept and implementation of objective functions and surrogate models, adaptation of benchmark methods; analysis; validation; writing – original draft. A. B. W.: conceptualization; methodology – concept and implementation of environment and objective functions, adaptation of benchmark methods; analysis; validation; visualization; writing – original draft. M. G.: resources; funding acquisition; writing – review & editing. J. B.: conceptualization; resources; supervision; project administration; funding acquisition; writing – review & editing. A. M.: conceptualization; resources; supervision; project administration; funding acquisition; writing – review & editing. D. G. G.: conceptualization; resources; supervision; project administration; funding acquisition; writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 466417970 and 466387255 – within the Priority Programme “SPP 2331: Machine Learning in Chemical Engineering”. This work was performed as part of the Helmholtz School for Data Science in Life, Earth and Energy (HDS-LEE). Simulations were performed with computing resources granted by RWTH Aachen University under project “thes1232”. The authors gratefully acknowledge the Competence Center for Digital Agriculture (KoDA) at the University of Applied Sciences Weihenstephan-Triesdorf for providing additional computational resources. Furthermore, the authors thank Herbert Riepl for suggesting structural constraints.References
- G. Schneider and U. Fechner, Nat. Rev. Drug Discovery, 2005, 4, 649–663 CAS.
- T. Fu, W. Gao, C. Coley and J. Sun, Advances in Neural Information Processing Systems, 2022, vol. 35, pp. 12325–12338 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 Search PubMed.
- M. H. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef CAS PubMed.
- E. J. Bjerrum and R. Threlfall, arXiv, 2017, preprint, arXiv:1705.04612, DOI:10.48550/arXiv.1705.04612.
- X. Zhang, L. Wang, J. Helwig, Y. Luo, C. Fu, Y. Xie, M. Liu, Y. Lin, Z. Xu and K. Yan, et al., arXiv, 2023, preprint, arXiv:2307.08423, DOI:10.48550/arXiv.2307.08423.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2020, 1, 045024 Search PubMed.
- A. Vaswani, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 1–14 Search PubMed.
- W. Gao, T. Fu, J. Sun and C. Coley, Advances in Neural Information Processing Systems, 2022, vol. 35, pp. 21342–21357 Search PubMed.
- P. Xu, T. Fu, W. Gao and J. Sun, Artificial Intelligence and Data Science for Healthcare: Bridging Data-Centric AI and People-Centric Healthcare, 2024 Search PubMed.
- E. Mazuz, G. Shtar, B. Shapira and L. Rokach, Sci. Rep., 2023, 13, 8799 CrossRef CAS PubMed.
- A. Gupta, A. T. Müller, B. J. Huisman, J. A. Fuchs, P. Schneider and G. Schneider, Mol. Inf., 2018, 37, 1700111 CrossRef PubMed.
- P. Henderson, R. Islam, P. Bachman, J. Pineau, D. Precup and D. Meger, Proceedings of the AAAI Conference on Artificial Intelligence, 2018 Search PubMed.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, arXiv, 2017, preprint, arXiv:1707.06347, DOI:10.48550/arXiv.1707.06347.
- N. O'Boyle and A. Dalke, ChemRxiv, 2018, preprint, DOI:10.26434/chemrxiv.7097960.v1.
- A. H. Cheng, A. Cai, S. Miret, G. Malkomes, M. Phielipp and A. Aspuru-Guzik, Digital Discovery, 2023, 2, 748–758 RSC.
- H. Dai, Y. Tian, B. Dai, S. Skiena and L. Song, International Conference on Learning Representations, 2018, https://openreview.net/forum?id=SyqShMZRb Search PubMed.
- M. A. Skinnider, Nat. Mach. Intell., 2024, 6, 437–448 CrossRef.
- M. Langevin, H. Minoux, M. Levesque and M. Bianciotto, J. Chem. Inf. Model., 2020, 60, 5637–5646 CrossRef CAS PubMed.
- J. Arús-Pous, A. Patronov, E. J. Bjerrum, C. Tyrchan, J.-L. Reymond, H. Chen and O. Engkvist, J. Cheminf., 2020, 12, 1–18 Search PubMed.
- Y. Wang, Z. Li and A. Barati Farimani, in Machine Learning in Molecular Sciences, Springer, 2023, pp. 21–66 Search PubMed.
- Y. Li, L. Zhang and Z. Liu, J. Cheminf., 2018, 10, 1–24 Search PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, 35th International Conference on Machine Learning, ICML 2018, 2018, vol. 5, pp. 3632–3648 Search PubMed.
- Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Sci. Rep., 2019, 9, 10752 CrossRef PubMed.
- J. H. Jensen, Chem. Sci., 2019, 10, 3567–3572 RSC.
- N. De Cao and T. Kipf, arXiv, 2018, preprint, arXiv:1805.11973, DOI:10.48550/arXiv.1805.11973.
- C. Zang and F. Wang, Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2020, pp. 617–626 Search PubMed.
- Z. Zhang, Q. Liu, C.-K. Lee, C.-Y. Hsieh and E. Chen, Chem. Sci., 2023, 14, 8380–8392 RSC.
- O. Mahmood, E. Mansimov, R. Bonneau and K. Cho, Nat. Commun., 2021, 12, 3156 CrossRef CAS PubMed.
- Ł. Maziarka, T. Danel, S. Mucha, K. Rataj, J. Tabor and S. Jastrzebski, Workshop on Graph Representation Learning, Neural Information Processing Systems, 2019 Search PubMed.
- J. G. Rittig, M. Ritzert, A. M. Schweidtmann, S. Winkler, J. M. Weber, P. Morsch, K. A. Heufer, M. Grohe, A. Mitsos and M. Dahmen, AIChE J., 2023, 69, e17971 CrossRef CAS.
- V. Mnih, arXiv, 2013, preprint, arXiv:1312.5602, DOI:10.48550/arXiv.1312.5602.
- C. Ying, T. Cai, S. Luo, S. Zheng, G. Ke, D. He, Y. Shen and T.-Y. Liu, Advances in Neural Information Processing Systems, 2021, vol. 34, pp. 28877–28888 Search PubMed.
- A. Z. Wagner, arXiv, 2021, preprint, arXiv:2104.14516, DOI:10.48550/arXiv.2104.14516.
- J. Pirnay and D. G. Grimm, European Conference on Artificial Intelligence 2024, 2024, pp. 1927–1934 Search PubMed.
- R. J. Williams, Mach. Learn., 1992, 8, 229–256 Search PubMed.
- N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, J. Chem. Inf. Model., 2019, 59, 1096–1108 CrossRef CAS PubMed.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy and M. Veselov, et al. , Front. Pharmacol, 2020, 11, 565644 CAS.
- M. Thomas, N. M. O'Boyle, A. Bender and C. De Graaf, J. Cheminf., 2024, 16, 64 CAS.
- O. Schilter, A. Vaucher, P. Schwaller and T. Laino, Digital Discovery, 2023, 2, 728–735 RSC.
- S. M. Sarathy and B. A. Eraqi, Proc. Combust. Inst., 2024, 40, 105630 CrossRef CAS.
- S. Jiang, A. B. Dieng and M. A. Webb, npj Comput. Mater., 2024, 10, 139 CrossRef CAS.
- T. Yue, L. Tao, V. Varshney and Y. Li, Digital Discovery, 2025 10.1039/D4DD00395K.
- M. Nnadili, A. N. Okafor, T. Olayiwola, D. Akinpelu, R. Kumar and J. A. Romagnoli, Ind. Eng. Chem. Res., 2024, 63, 6313–6324 CrossRef CAS.
- A. Nigam, R. Pollice, G. Tom, K. Jorner, J. Willes, L. Thiede, A. Kundaje and A. Aspuru-Guzik, Advances in Neural Information Processing Systems, 2023, vol. 36, pp. 3263–3306 Search PubMed.
- L. König-Mattern, E. I. S. Medina, A. O. Komarova, S. Linke, L. Rihko-Struckmann, J. S. Luterbacher and K. Sundmacher, Chem. Eng. J., 2024, 495, 153524 CrossRef.
- A. Nigam, R. Pollice, M. Krenn, G. dos Passos Gomes and A. Aspuru-Guzik, Chem. Sci., 2021, 12, 7079–7090 RSC.
- J. Huang, S. S. Gu, L. Hou, Y. Wu, X. Wang, H. Yu and J. Han, The 2023 Conference on Empirical Methods in Natural Language Processing, 2023 Search PubMed.
- A. Corsini, A. Porrello, S. Calderara and M. Dell'Amico, The Thirty-eighth Annual Conference on Neural Information Processing Systems, 2024, https://openreview.net/forum?id=buqvMT3B4k Search PubMed.
- J. Pirnay and D. G. Grimm, Transactions on Machine Learning Research, 2024, https://openreview.net/forum?id=agT8ojoH0X Search PubMed.
- T. Anthony, Z. Tian and D. Barber, Advances in Neural Information Processing Systems, 2017, vol. 30 Search PubMed.
- W. Kool, H. Van Hoof and M. Welling, International Conference on Machine Learning, 2019, pp. 3499–3508 Search PubMed.
- K. Shi, D. Bieber and C. Sutton, International Conference on Machine Learning, 2020, pp. 8785–8795 Search PubMed.
- J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, Proceedings of the 2019 conference of the North American chapter of the association for computational linguistics: human language technologies, 2019, vol. 1, pp. 4171–4186 Search PubMed.
- T. Bachlechner, B. P. Majumder, H. Mao, G. Cottrell and J. McAuley, Uncertainty in Artificial Intelligence, 2021, pp. 1352–1361 Search PubMed.
- M. Davies, M. Nowotka, G. Papadatos, N. Dedman, A. Gaulton, F. Atkinson, L. Bellis and J. P. Overington, Nucleic Acids Res., 2015, 43, W612–W620 CrossRef CAS PubMed.
- M. Thomas, N. M. O'Boyle, A. Bender and C. De Graaf, arXiv, 2022, preprint, arXiv:2212.01385, DOI:10.48550/arXiv.2212.01385.
- J. Guo and P. Schwaller, JACS Au, 2024, 4, 2160–2172 CrossRef CAS PubMed.
- J. Guo, P. Schwaller, NeurIPS, Workshop on AI for New Drug Modalities, 2024, https://openreview.net/forum?id=bm3aARS2Nw Search PubMed.
- W. Gao, S. Luo and C. W. Coley, arXiv, 2024, preprint, arXiv:2410.03494, DOI:10.48550/arXiv.2410.03494.
- X. Hu, G. Liu, Y. Zhao and H. Zhang, Advances in Neural Information Processing Systems, 2024, vol. 36 Search PubMed.
- J. Wisniak, Chem. Eng. Sci., 1983, 38, 969–978 CrossRef CAS.
- M. Peters, M. Zavrel, J. Kahlen, T. Schmidt, M. Ansorge-Schumacher, W. Leitner, J. Büchs, L. Greiner and A. C. Spiess, Eng. Life Sci., 2008, 8, 546–552 CrossRef CAS.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, 34th International Conference on Machine Learning, ICML 2017, 2017, vol. 3, pp. 2053–2070 Search PubMed.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans, T. Sommer and P. Friederich, Commun. Mater., 2022, 3, 93 CrossRef CAS PubMed.
- J. G. Rittig, Q. Gao, M. Dahmen, A. Mitsos and A. M. Schweidtmann, in Machine Learning and Hybrid Modelling for Reaction Engineering, ed. D. Zhang and E. A. Del Río Chanona, Royal Society of Chemistry, 2023, pp. 159–181 Search PubMed.
- E. I. S. Medina, S. Linke, M. Stoll and K. Sundmacher, Digital Discovery, 2023, 2, 781–798 RSC.
- J. Gmehling, D. Tiegs, A. Medina, M. Soares, J. Bastos, P. Alessi, I. Kikic, M. Schiller and J. Menke, DECHEMA Chemistry Data Series, 2008, vol. 9 Search PubMed.
- J. G. Rittig, K. Ben Hicham, A. M. Schweidtmann, M. Dahmen and A. Mitsos, Comput. Chem. Eng., 2023, 171, 108153 CrossRef CAS.
- B. Winter, C. Winter, J. Schilling and A. Bardow, Digital Discovery, 2022, 1, 859–869 RSC.
- J. Damay, F. Jirasek, M. Kloft, M. Bortz and H. Hasse, Ind. Eng. Chem. Res., 2021, 60, 14564–14578 CrossRef CAS.
- J. G. Rittig, K. C. Felton, A. A. Lapkin and A. Mitsos, Digital Discovery, 2023, 2, 1752–1767 RSC.
- B. Winter, C. Winter, T. Esper, J. Schilling and A. Bardow, Fluid Phase Equilib., 2023, 568, 113731 CrossRef CAS.
- J. G. Rittig and A. Mitsos, Chem. Sci., 2024, 15, 18504–18512 RSC.
- T. Specht, M. Nagda, S. Fellenz, S. Mandt, H. Hasse and F. Jirasek, Chem. Sci., 2024, 15, 19777–19786 RSC.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- A. Klamt, F. Eckert and W. Arlt, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 101–122 CrossRef CAS PubMed.
- W. J. Zamora, A. Viayna, S. Pinheiro, C. Curutchet, L. Bisbal, R. Ruiz, C. Ràfols and F. J. Luque, Phys. Chem. Chem. Phys., 2023, 25, 17952–17965 RSC.
- T. Nevolianis, J. G. Rittig, A. Mitsos and K. Leonhard, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-3t818.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- C. Bilodeau, W. Jin, T. Jaakkola, R. Barzilay and K. F. Jensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1608 Search PubMed.
- D. M. Anstine and O. Isayev, J. Am. Chem. Soc., 2023, 145, 8736–8750 CrossRef CAS PubMed.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- National Center for Biotechnology Information, PubChem Compound Database, 2024, https://pubchem.ncbi.nlm.nih.gov/ Search PubMed.
- J. G. Rittig, M. Franke and A. Mitsos, AI for Accelerated Materials Design-NeurIPS, 2024 Search PubMed.
- J. Guo and P. Schwaller, AI for Accelerated Materials Design - NeurIPS 2024, 2024, https://openreview.net/forum?id=J63EUbjhSw Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00339j |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |